Бином ⭐ Ньютона: формула, доказательство, ее применение
Формула бинома Ньютона
Определение 1Бином Ньютона имеет вид формулы, с помощью которой целую неотрицательную степень n суммы двух переменных раскладывают на отдельных слагаемые:
(a+b)n=∑k=0nnkan-kbk=n0an+n1an-1b+…+nkan-kbk+…+nnbn
Здесь nk≡Cnk=n!k!(n-k)! обозначает биномиальные коэффициенты, n из множества неотрицательных целых чисел.
Данная формула, записанная таким образом, существует давно. Эти знания были доступны еще математикам Индии и Персии. Формула бинома была сформулирована и введена в использование Ньютоном с целью демонстрации обобщенного случая при показателе степени в виде некоего числа из множества действительных. Спустя время формула была распространена и на комплексные числа. Общий случай бинома является рядом, не имеющим окончания.
Пример 1Пример записи формулы бинома Ньютона:
Упростить и ускорить процесс, при котором раскладывают степень на слагаемые, можно, если прибегнуть к треугольнику Паскаля.
Заметим, что формула бинома Ньютона представляет собой частный случай разложения функции (1+x)r в ряд Тейлора:
(1+x)r=∑k=0∞rkxk,
Здесь для r допустимы какие-либо значения из множества комплексных чисел, то есть это может быть число со знаком минус или вещественное число. Для того чтобы определить коэффициенты записанного разложения, следует воспользоваться следующей формулой:
rk=1k!∏n=0k-1(r-n)=r(r-1)(r-2)⋯(r-(k-1))k!
Рассмотрим полученную последовательность элементов:
(1+z)α=1+αz+α(α-1)2z2+…+α(α-1)⋯(α-n+1)n!zn+….
Сделаем вывод, что схождение данного ряда возможно при соблюдении условия:
|z|≤1.
Рассмотрим частный случай, когда:
z=1m
α=x·m
В такой ситуации справедливо следующее тождество:
1+1mxm=1+x+xm(xm-1)2 m2+…+xm(xm-1)⋯(xm-n+1)n! mn+….
В том случае, когда m→∞, допустим переход к пределу. Целесообразно воспользоваться вторым замечательным пределом:
limm→∞1+1mm=e
Основываясь на записанных выше свойствах, представим следующее тождество:
ex=1+x+x22+…+xnn!+…
Данное соотношение и его объяснение первым удалось вывести Эйлеру.
Допустимо обобщение бинома Ньютона таким образом, что результатом является полином Ньютона.
Определение 2Полином Ньютона представляет собой возведение в степень суммы какого-либо количества слагаемых:
(x1+x2+⋯+xm)n=∑kj⩾0k1+k2+⋯+km=nnk1,k2,…,kmx1k1…xmkm,
Здесь nk1,k2,…,km=n!k1!k2!⋯km!. В таком виде записаны мультиномиальные коэффициенты.
Суммируются индексы kj, имеющие целое значение и являющиеся неотрицательными. При сложении они дают n. Таким образом, сумма берется по всем композициям числа n длины m. Применение полинома Ньютона возможно при условии, что:
xj0=1
Это выполняется даже в том случае, когда xj=0.
Имеется два способа доказательства мультиномиальной теоремы:
- индукция по n;
- комбинаторные соображения и комбинаторный смысл, которыми обладает мультиномиальный коэффициент.
В том случае, когда m=2 , можно выразить k2=n-k1 . В итоге получается бином Ньютона.
Предположим, что:
Bn(as)=Bn(a1,…,an)
B0=1
При этом для полных полиномов Белла характерно биномиальное разложение:
Bn(as+bs)=∑i+j=nni, jBi(as)Bj(bs).
Биномиальные коэффициенты
Определение 3С математической точки зрения биномиальные коэффициенты являются коэффициентами в разложении бинома Ньютона (1+x)n по степеням x.
Возможно несколько вариантов для обозначения коэффициента при xk:
- nk;
- Cnk.
Записанные выражения следует читать, как «биномиальный коэффициент из n по k», либо «число сочетаний из n по k». Запись Cnk переводится, как «C из n по k»:
(1+x)n=n0+n1x+n2x2+…+nnxn=∑k=0nnkxk,
Соотношение справедливо в случае натуральных степеней n.
Допустимо определять биномиальные коэффициенты для каких-либо показателей n из множества действительных. Если взять некое действительное число n, то можно определить биномиальные коэффициенты в виде коэффициентов разложения выражения (1+x)n для получения степенного ряда, не имеющего окончания:
(1+x)n=∑k=0∞nkxk,
При неотрицательных целых n каждый из коэффициентов nk, если k > n, принимает нулевое значение. По этой причине записанное разложение является конечной суммой.
По этой причине записанное разложение является конечной суммой.
Существует определение биномиального коэффициента с точки зрения комбинаторики.
Определение 4Биномиальным коэффициентом nk в случае неотрицательных целых чисел n и k является число сочетаний из n по k, то есть число всех (нестрогих) подмножеств (выборок) с размерностью k в n-элементном множестве.
С биномиальными коэффициентами можно встретиться при решении задач в классе по краткому курсу комбинаторики и теории вероятностей. В качестве обобщения биноминальных коэффициентов используют мультиномиальные коэффициенты.
Путем определения коэффициентов в разложении (1+x)n в степенную последовательность, выводят явные формулы для биномиальных коэффициентов nk.
В случае, когда n является действительным числом, а k взято из множества целых чисел, получим, что:
Здесь k! представляет собой обозначение факториала числа k.
Запишем верные равенства, когда n и k являются неотрицательными числами:
В том случае, когда речь идет о целых показателях со знаком минуса, коэффициенты разложения бинома (1+x)-n определяют таким образом:
Треугольник Паскаля изображен на рисунке:
Источник: ru.wikipedia.org
Рассмотрим тождество:
nk=n-1k-1+n-1k
С его помощью можно расставить биномиальные коэффициенты для неотрицательных целых чисел n, k таким образом, что получится треугольник Паскаля. В нем каждое число является результатом сложения пары вышестоящих чисел:
n=0: 1 n=1: 1 1 n=2: 1 2 1 n=3: 1 3 3 1 n=4:1 4 6 4 1⋮ ⋮ ⋮ ⋮ ⋮
При делении чисел, расположенных в каждой из строк треугольника Паскаля, на 2n, каждая из строк в процессе стремления n к бесконечности обратится в функцию нормального распределения.
В том случае, когда значение n зафиксировано, производящая функция последовательности биномиальных коэффициентов n0, n1, n2,… имеет следующий вид:
∑k=0∞nkxk=(1+x)n.
В том случае, когда значение k зафиксировано, производящая функция последовательности коэффициентов 0k, 1k, 2k,… определяется, как:
∑n nkyn= yk(1-y)k+1.
Двумерная производящая функция биномиальных коэффициентов nk для целых n,k имеет следующий вид:
∑n,knkxkyn=11-y-xy,или∑n=0∞∑k=0nnkxkyn=11-y-xy.
Запишем несколько следствий, вытекающих из теоремы Люка:
- коэффициент nk является нечетным ⇔ когда k записано в двоичном виде, единицы не находятся в таких разрядах, в которых в числе n имеются нули;
- коэффициент nk не является кратным простому числу p⇔ когда число k записано в p-ичной форме, любой из разрядов не превышает соответствующий разряд числа n;
- в ряду последовательных биномиальных коэффициентов n0, n1, …, nn:
- каждое из чисел не является кратным данному простому p⇔ число n можно записать, как mpk-1 при натуральном числе m, которое меньше по сравнению с p;
- каждое из чисел, за исключением первого и последнего, является кратным данному простому p⇔n=pk;
- количество чисел, которые являются нечетными, определяется, как степень 2 с показателем, равным числу 1 в двоичной записи числа n;
- допустимо равное количество четных и нечетных чисел;
- количество чисел, которые не являются кратными простому p, определяется, как (a1+1)⋯(am+1), где числа a1, …,am представляют собой разряды p-ичной записи числа n, m=⌊logpn⌋+1,при⌊·⌋ в виде функции «пол», обозначающей длину рассматриваемой записи.

Перечислим важные тождества, которые пригодятся в решении задач:
1) nk=n-1k-1+n-1k.
2) nk=(-1)k-n+k-1k.
3) Правило симметрии: nk=nn-k.
4) Исключение из скобок: nk=nkn-1k-1.
5) Замена индексов: nmmn-k=nkkn-m.
6) (n-k)nk=nn-1k.
Рассмотрим бином Ньютона, а также следствия, которые вытекают из формулы:
n0+n1+…+nn=2n,
Здесь выполняется следующее условие:
n∈ℕ.
Запишем основные тождества:
- ∑j=knnj(-1)j=(-1)k n-1k-1.
- n0-n1+…+(-1)nnn=0,приn∈ℕ.
- n0+n2+…+n2⌊n/2⌋=2n-1,приn∈ℕ.
- ∑k=-aa(-1)k2ak+a3=(3a)!(a!)3,
Обобщенный вид:
∑krm+ksn-k=r+sm+n
Разберем свертку Вандермонда и следствия, которые из нее вытекают. Формула имеет вид:
∑krm+ksn-k=r+sm+n
Здесь m,n∈ℤ,аr,s∈ℝ.
Получить записанное тождество можно путем определения коэффициента при xm+n в процессе разложения:
(1+x)r(1+x)s
При этом важно учитывать следующее тождество:
(1+x)r+s=(1+x)r(1+x)s.
Здесь суммируют все целые k такие, для которых выполняется условие:
rm+ksn-k≠0.
В случае каких-либо действительных r, s количество слагаемых, отличных от нуля, в сумме является конечным.
n0aa-n1a+1a+…+(-1)nnna+na=(-1)nan
Тождество можно записать в общем виде:
∑i=0p(-1)ipi∏m=1ni+smsm=0
Условием является:
∑m=1nsm<p.
Следующее тождество имеет вид:
n02+n12+…+nn2=2nn.
Перечислим другие важные тождества:
- ∑k=1n(-1)k-1knk=∑k=1n1k=Hn (n-е гармоническое число).
- С помощью мультисекции ряда в виде (1+x)n можно записать тождество для суммы биномиальных коэффициентов с произвольным шагом s и смещением t(0⩽t<s). Это будет конечная сумма, состоящая из s слагаемых: nt+ nt+s+ nt+2s+…= 1s∑j=0s-12cos πjsncos π(n-2t)js.
Перечислим следствия:
- n3=∑i=2n-1(n-i)(2n-i+1)2=∑i=2n-1(n-i)2An1-i-112;
- n4=∑i=3n-1(n-i)2n(n-1)-∑i0=1i-2i023=∑i=3n-1(n-i)2An2-i-1223;
- nk=∑i=k-1n-1(n-i)2Ank-2-i-1k-2k!-1,приAnk, равным числу размещений из n по k.

Рассмотрим стандартный алгоритм действий для определения биномиальных коэффициентов. Принцип решения заключается в применении рекуррентной формулы:
nk=n-1k+n-1k-1
При этом на каждом этапе n нужно хранить значения nk при k=0,1, …,n¯.
Когда значение k зафиксировано, биномиальные коэффициенты можно определить таким образом:
nk=nn-k·n-1k
Здесь начальное значение kk=1.
В том случае, когда значение n зафиксировано, определить коэффициенты nk можно следующим способом:
nk=n-k+1k·nk-1
При этом исходное условие:
n0=1.
Доказательство
Докажем формулу бинома Ньютона. Умножить скобки можно путем взятия из каждой по одному слагаемому и сложения всех произведений, которые получились в итоге. Разберем значение коэффициента при akbn-k.
Существует определенное количество способов выбора a (из скобок) на первом шаге, равное n. На втором шаге число способов равно n-1 и так далее до n-k+1 на k-м шаге. С другой стороны, для каждой из вариаций вычислены и все ее порядковые перестановки, количество которых составляет k!. Путем нормирования получим в точности:
С другой стороны, для каждой из вариаций вычислены и все ее порядковые перестановки, количество которых составляет k!. Путем нормирования получим в точности:
Cnk.
Далее разберем доказательство по методу индукции по n. Запишем базу индукции:
n=0
Получим:
(a+b)0=1=00a0b0
Запишем шаг индукции. Предположим, что соотношение для n является справедливым:
(a+b)n=∑k=0nnkan-kbk
В таком случае, требуется представить доказательства справедливости утверждения для n+1:
(a+b)n+1=∑k=0n+1n+1kan+1-kbk
Построим доказательство таким образом:
(a+b)n+1=(a+b)(a+b)n=(a+b)∑k=0nnkan-kbk=∑k=0nnkan-k+1bk + ∑k=0nnkan-kbk+1
Выберем слагаемое, которое входит в состав первой суммы, если k имеет нулевое значение:
∑k=0nnkan-k+1bk=an+1+∑k=1nnkan-k+1bk
Выберем слагаемое, которое включено во вторую сумму, если соблюдается равенство k=n:
∑k=0nnkan-kbk+1=bn+1+∑k=0n-1nkan-kbk+1=bn+1+∑k=1nnk-1an-k+1bk
На следующем шаге следует выполнить сложение сумм, которые получились в результате преобразований. Получим:
Получим:
an+1+∑k=1nnkan-k+1bk + bn+1+∑k=1nnk-1an-k+1 bk=an+1+bn+1+∑k=1nnk+nk-1an-k+1bk=
∑k=00n+1kan+1-kbk + ∑k=n+1n+1n+1kan+1-kbk + ∑k=1nn+1kan+1-kbk=∑k=0n+1n+1kan+1-kbk
Формула бинома Ньютона доказана.
Применение формулы Бинома Ньютона при решении примеров и задач
Задача 1На тарелке имеется 12 конфет. Из общего количества 4 штуки являются шоколадными. Остальные конфеты представлены в виде карамелек. Гостю предлагается выбрать из всего ассортимента 2 шоколадные конфеты и 3 карамельки. Требуется вычислить количество способов, с помощью которых гость может сделать выбор.
Решение
Заметим , что по условию задачи, имеется несколько событий. В первом случае — это выбор шоколадных конфет, а во втором — карамелек. Не имеет значение, в каком порядке гость выбирает конфеты. Исходя из этого, можно воспользоваться формулой сочетания, применительно к первому и второму событиям.
Из 4 шоколадных конфет нужно выбрать 2 штуки. Выполнить действие допустимо следующим количеством способов C42:
C42=4!2!2!=3·41·2=6
Далее посчитаем число выборок для карамелек. Всего таких конфет на тарелке:
Всего таких конфет на тарелке:
12 – 4 = 8
Требуется выбрать 3 карамельки, согласно условию задания. В этом случае воспользуемся формулой сочетания из 8 по 3:
C83=8!3!5!=6·7·81·2·3=56
Исходя из того, что действия по выбору шоколадных конфет и карамелек не зависят друг от друга, с помощью правила умножения вычислим общее количество способов и запишем ответ:
C42·C83=6·56=336
Ответ: 336.
Задача 2Имеется некий двучлен в степени n. Его требуется разложить в виде многочлена при условии, что:
n=0, 1, 2, …,5.
Решение
Первые 4 разложения по порядку целесообразно выполнить, используя формулы квадрата и куба разности:
(a+b)0=1
(a+b)1=1·a+1·b
(a+b)2=1·a2+2·a·b+1·b2
(a+b)3=1·a3+3·a2·b+3·a·b2+1·b3
Записать бином 4 и 5 степени можно с помощью треугольника Паскаля:
(a+b)4=1·a4+4·a3·b+6·a2·b2+4·a·b3+1·b4
(a+b)5=1·a5+5·a4·b+10·a3·b2+10·a2·b3+5·a·b4+1·b5
Задача 3В саду гуляют 5 уток. Кормление птиц осуществляют попарно. Требуется определить число способов выбора двух уток из общего количества.
Кормление птиц осуществляют попарно. Требуется определить число способов выбора двух уток из общего количества.
Решение
Заметим, что в данном случае не имеет значение, в каком порядке осуществляют кормление уток. Исходя из этого, вычислим C52:
C52=5!2!·3!=5·4·3·2·12·1·3·2·1=10
Ответ: 10.
Задача 4В хозяйстве имеется всего 150 гусей. Для кормления необходимо выбрать две птицы из общего количества. Нужно вычислить количество способов такого выбора.
Решение
Заметим, что в данном случае не имеет значение, в каком порядке выбирать гусей, чтобы покормить. Тогда вычислим C1502:
C1502=150!2!·148!=150·149·148·…·12·1·148·…·1=150·1492·1=11175
Ответ: 11175.
Дифференциальное и интегральное исчисления для втузов, т.2
Дифференциальное и интегральное исчисления для втузов, т.2
ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА XIII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 1. Постановка задачи. Уравнение движения тела при сопротивлении среды, пропорциональном скорости. Уравнение цепной линии § 2. Определения § 3. Дифференциальные уравнения первого порядка (общие понятия) § 4.  (n) = f(x) (n) = f(x)§ 18. Некоторые типы дифференциальных уравнений второго порядка, приводимых к уравнениям первого порядка. Задача о второй космической скорости § 19. Графический метод интегрирования дифференциального уравнения второго порядка § 20. Линейные однородные уравнения. Определения и общие свойства § 21. Линейные однородные уравнения второго порядка с постоянными коэффициентами § 22. Линейные однородные уравнения n-го порядка с постоянными коэффициентами § 23. Неоднородные линейные уравнения второго порядка § 24. Неоднородные линейные уравнения второго порядка с постоянными коэффициентами § 25. Неоднородные линейные уравнения высших порядков § 26. Дифференциальное уравнение механических колебаний § 27. Свободные колебания. Векторное и комплексное изображение гармонических колебаний § 28. Вынужденные колебания § 29. Системы обыкновенных дифференциальных уравнений § 30. Системы линейных дифференциальных уравнений с постоянными коэффициентами § 31.  Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки§ 32. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 33. Разностный метод приближенного решения дифференциальных уравнений, основанный на применении формулы Тейлора.. Метод Адамса § 34. Приближенный метод интегрирования систем дифференциальных уравнений первого порядка ГЛАВА XIV. КРАТНЫЕ ИНТЕГРАЛЫ § 2. Вычисление двойного интеграла § 3. Вычисление двойного интеграла (продолжение) § 4. Вычисление площадей и объемов с помощью двойных интегралов § 5. Двойной интеграл в полярных координатах § 6. Замена переменных в двойном интеграле (общий случай) § 7. Вычисление площади поверхности § 9. Момент инерции площади плоской фигуры § 10. Координаты центра масс площади плоской фигуры § 11. Тройной интеграл § 12. Вычисление тройного интеграла § 13. Замена переменных в тройном интеграле § 14.  Момент инерции и координаты центра масс тела Момент инерции и координаты центра масс тела§ 15. Вычисление интегралов, зависящих от параметра Упражнения к главе XIV ГЛАВА XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ § 2. Вычисление криволинейного интеграла § 3. Формула Грина § 4. Условия независимости криволинейного интеграла от пути интегрирования § 5. Поверхностный интеграл § 6. Вычисление поверхностного интеграла § 7. Формула Стокса § 9. Оператор Гамильтона. Некоторые его применения Упражнения к главе XV ГЛАВА XVI. РЯДЫ § 1. Ряд. Сумма ряда § 2. Необходимый признак сходимости ряда § 3. Сравнение рядов с положительными членами § 4. Признак Даламбера § 5. Признак Коши § 6. Интегральный признак сходимости ряда § 7. Знакочередующиеся ряды. Теорема Лейбница § 8. Знакопеременные ряды. Абсолютная и условная сходимость § 9. Функциональные ряды § 10. Мажорируемые ряды § 11. Непрерывность суммы ряда § 12. Интегрирование и дифференцирование рядов § 13.  Степенные ряды. Интервал сходимости Степенные ряды. Интервал сходимости§ 15. Ряды по степеням x-a § 16. Ряды Тейлора и Маклорена § 17. Примеры разложения функций в ряды § 18. Формула Эйлера § 19. Биномиальный ряд § 20. Разложение функции ln(1+x) в степенной ряд. Вычисление логарифмов § 21. Вычисление определенных интегралов с помощью рядов § 22. Интегрирование дифференциальных уравнений с помощью рядов § 23. Уравнение Бесселя § 24. Ряды с комплексными членами § 25. Степенные ряды с комплексной переменной § 26. Решение дифференциального уравнения первого порядка методом последовательных приближений (метод итераций) § 27. Доказательство существования решения дифференциального уравнения. Оценка погрешности при приближенном решении § 28. Теорема единственности решения дифференциального уравнения Упражнения к главе XVI ГЛАВА XVII. РЯДЫ ФУРЬЕ § 2. Примеры разложения функций в ряды Фурье § 3. Одно, замечание о разложении периодической функции в ряд Фурье § 4.  Ряды Фурье для четных и нечетных функций Ряды Фурье для четных и нечетных функций§ 5. Ряд Фурье для функции с периодом 2l § 6. О разложении непериодической функции в ряд Фурье § 7. Приближение в среднем заданной функции с помощью тригонометрического многочлена § 8. Интеграл Дирихле § 9. Сходимость ряда Фурье в данной точке § 10. Некоторые достаточные условия сходимости ряда Фурье § 11. Практический гармонический анализ § 12. Ряд Фурье в комплексной форме § 13. Интеграл Фурье § 14. Интеграл Фурье в комплексной форме § 15. Ряд Фурье по ортогональной системе функций § 16. Понятие о линейном функциональном пространстве. Аналогия между разложением функций в ряд Фурье и разложением векторов Упражнения к главе XVII ГЛАВА XVIII. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ § 1. Основные типы уравнений математической физики § 2. Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод уравнений электрических колебаний в проводах § 4.  Уравнение распространения тепла в стержне. Формулировка краевой задачи Уравнение распространения тепла в стержне. Формулировка краевой задачи§ 5. Распространение тепла в пространстве § 6. Решение первой краевой задачи для уравнения теплопроводности методом конечных разностей § 7. Распространение тепла в неограниченном стержне § 8. Задачи, приводящие к исследованию решений уравнения Лапласа. Формулировка краевых задач § 9. Уравнение Лапласа в цилиндрических координатах. Решение задачи Дирихле для кольца с постоянными значениями искомой функции на внутренней и внешней окружностях § 10. Решение задачи Дирихле для круга § 11. Решение задачи Дирихле методом конечных разностей Упражнения к главе XVIII ГЛАВА XIX. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ И НЕКОТОРЫЕ ЕГО ПРИЛОЖЕНИЯ § 1. Начальная функция и ее изображение § 2. Изображение функций … § 3. Изображение функции с измененным масштабом независимой переменной. Изображение функций sin at, cos at § 4. Свойство линейности изображения § 5. Теорема смещения § 6. Изображение функций … § 7.  Дифференцирование изображения Дифференцирование изображения§ 8. Изображение производных § 9. Таблица некоторых изображений § 10. Вспомогательное уравнение для данного дифференциального уравнения § 11. Теорема разложения § 12. Примеры решения дифференциальных уравнений и систем дифференциальных уравнений операционным методом § 13. Теорема свертывания § 14. Дифференциальные уравнения механических колебаний. Дифференциальные уравнения теории электрических цепей § 15. Решение дифференциального уравнения колебаний § 16. Исследование свободных колебаний § 17. Исследование механических и электрических колебаний в случае периодической внешней силы § 19. Теорема запаздывания § 20. Дельта-функция и ее изображение Упражнения к главе XIX ГЛАВА XX. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ § 1. Случайное событие. Относительная частота случайного события. Вероятность события. Предмет теории вероятностей § 2. 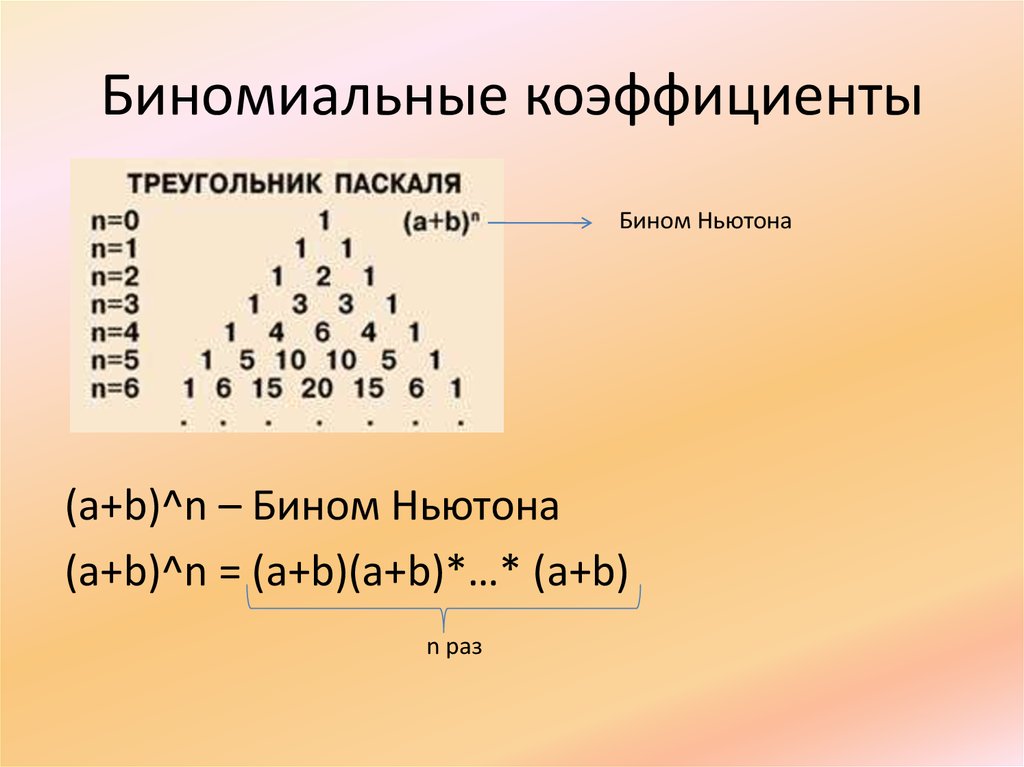 Классическое определение вероятности и непосредственный подсчет вероятностей Классическое определение вероятности и непосредственный подсчет вероятностей§ 3. Сложение вероятностей. Противоположные случайные события § 4. Умножение вероятностей независимых событий § 5. Зависимые события. Условная вероятность. Полная вероятность § 6. Вероятность гипотез. Формула Байеса § 7. Дискретная случайная величина. Закон распределения дискретной случайной величины § 8. Относительная частота и вероятность относительной частоты при повторных испытаниях § 9. Математическое ожидание дискретной случайной величины § 10. Дисперсия. Среднеквадратичное отклонение. Понятие о моментах § 11. Функции от случайных величин § 12. Непрерывная случайная величина. Плотность распределения непрерывной случайной величины. Вероятность попадания случайной величины в заданный интервал § 13. Функция распределения, или интегральный закон распределения. Закон равномерного распределения вероятностей § 14. Числовые характеристики непрерывной случайной величины § 15.  Нормальный закон распределения. Математическое ожидание нормального распределения Нормальный закон распределения. Математическое ожидание нормального распределения§ 16. Дисперсия и среднеквадратичное отклонение случайной величины, подчиненной нормальному закону распределения § 17. Вероятность попадания значения случайной величины в заданный интервал. Функция Лапласа. Интегральная функция распределения для нормального закона § 19. Выражение нормального закона распределения через срединное отклонение. Приведенная функция Лапласа § 20. Правило трех сигм. Шкала вероятностей распределения ошибок § 21. Среднеарифметическая ошибка § 22. Мера точности. Соотношение между характеристиками распределения ошибок § 23. Двумерная случайная величина § 24. Нормальный закон распределения на плоскости § 25. Вероятность попадания двумерной случайной величины в прямоугольник со сторонами, параллельными главным осям рассеивания, при нормальном законе распределения § 26. Вероятность попадания двумерной случайной величины в эллипс рассеивания § 27.  Задачи математической статистики. Статистический материал Задачи математической статистики. Статистический материал§ 28. Статистический ряд. Гистограмма § 29. Определение подходящего значения измеряемой величины § 30. Определение параметров закона распределения. Теорема Ляпунова. Теорема Лапласа Упражнения к главе XX ГЛАВА XXI. МАТРИЦЫ. МАТРИЧНАЯ ЗАПИСЬ СИСТЕМ И РЕШЕНИЙ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ § 1. Линейные преобразования. Матрица § 2. Общие определения, связанные с понятием матрицы § 3. Обратное преобразование § 4. Действия над матрицами. Сложение матриц § 5. Преобразование вектора в другой вектор с помощью матрицы § 6. Обратная матрица § 7. Нахождение матрицы, обратной данной § 8. Матричная запись системы линейных уравнений § 9. Решение системы линейных уравнений матричным методом § 10. Ортогональные отображения. Ортогональные матрицы § 11. Собственный вектор линейного преобразования § 12. Матрица линейного преобразования, при котором базисные векторы являются собственными векторами § 13.  Преобразование матрицы линейного преобразования при переходе от одного базиса к другому Преобразование матрицы линейного преобразования при переходе от одного базиса к другому§ 14. Квадратичные формы и их преобразования § 15. Ранг матрицы. Существование решений системы линейных уравнений § 16. Дифференцирование и интегрирование матриц § 17. Матричная запись системы дифференциальных уравнений и решений системы дифференциальных уравнений с постоянными коэффициентами § 18. Матричная запись линейного уравнения n-го порядка § 19. Решение систем линейных дифференциальных уравнений с переменными коэффициентами методом последовательных приближений с использованием матричной записи Упражнения к главе XXI ПРИЛОЖЕНИЯ |
Биномиальная теорема
9.4 Биномиальная теорема
Цели обучения
- Оценивать выражения, включающие факториалы.
- Вычислить биномиальные коэффициенты.
- Расширьте степени биномов, используя теорему о биномах.

Факториалы и биномиальный коэффициент
Начнем с определения факториала Произведение всех натуральных чисел, меньших или равных данному натуральному числу, обозначаемому н !. натурального числа n , обозначаемого n !, как произведение всех натуральных чисел, меньших или равных n .
n!=n(n−1)(n−2)⋯3⋅2⋅1
Например,
7!=7⋅6⋅5⋅4⋅3⋅2⋅1=5,040 Семь факториал5! =5⋅4⋅3⋅2⋅1=120 Пять факториал3!=3⋅2⋅1=6 Три факториал1!=1=1 Один факториал
Мы определяем нулевой факториалФакториал нуля определяется как равный 1; 0!=1. быть равным 1,
0!=1 Ноль факториал
Факториал отрицательного числа не определен.
Примечание : В большинстве современных калькуляторов вы найдете функцию факториала. Некоторые калькуляторы не имеют специальной кнопки. Однако обычно его можно найти в системе меню, если оно предусмотрено.
Факториал также можно выразить с помощью следующего рекуррентного соотношения:
n!=n(n−1)!
Например, факториал числа 8 можно представить как произведение 8 и 7!:
8!=8⋅7!=8⋅7⋅6⋅5⋅4⋅3⋅2⋅1=40 320
При работе с соотношениями, включающими факториалы, часто бывает так, что многие из факторов сокращаются.
Пример 1
Оценка: 12!6!.
Решение:
12!6!=12⋅11⋅10⋅9⋅8⋅7⋅6⋅5⋅4⋅3⋅2⋅16⋅5⋅4⋅3⋅2⋅1=12⋅11⋅10 ⋅9⋅8⋅7⋅6!6!=12⋅11⋅10⋅9⋅8⋅7=665,280
Ответ: 665,280
Биномиальный коэффициентЦелое число, вычисляемое по формуле: (nk)=n!k !(n−k)!., обозначаемый nCk=(nk), читается как « n выберите k ” и задается следующей формулой:
nCk=(nk)=n!k!(n−k)!
Эта формула очень важна в области математики, называемой комбинаторикой. Он дает количество способов, которыми k элементов могут быть выбраны из набора n элементов, где порядок не имеет значения. В этом разделе нас интересует возможность расчета этой величины.
Пример 2
Вычислите: (73).
Решение:
Используйте формулу для биномиального коэффициента,
(nk)=n!k!(n−k)!
, где n=7 и k=3. После замены ищите факторы для отмены.
(73)=7!3!(7−3)!=7!3! 4!=7⋅6⋅5⋅4!3! 4!=2106=35
Ответ: 35
Примечание : Проверьте в системе меню вашего калькулятора функцию, которая вычисляет это количество. Найдите обозначение nCk в подразделе вероятности.
Найдите обозначение nCk в подразделе вероятности.
Попробуйте! Рассчитать: (85).
Ответ: 56
(нажмите, чтобы посмотреть видео)
Рассмотрим следующий бином, возведенный в степень 3 rd мощность в развернутом виде:
(x+y)3=x3+3x2y+3xy2+y3
Сравните это со следующими вычислениями,
(30)=3!0!(3−0)! =3!1⋅3!=1(31)=3!1!(3−1)!=3⋅2!1⋅2!=3(32)=3!2!(3−2)!=3 ⋅2!2! 1!=3(33)=3!3!(3−3)!=3!3! 0!=1
Обратите внимание на связь между этими вычислениями и коэффициентами расширенного бинома. Это наблюдение обобщается в следующем разделе.
Биномиальная теорема
Рассмотрим разложение (x+2)5:
(x+2)5=(x+2)(x+2)(x+2)(x+2)(x+2)
Быстро понимаешь, что это очень утомительное вычисление, включающее множество применений распределительное свойство. Биномиальная теорема Описывает алгебраическое разложение двучленов, возведенных в степень: (x+y)n= Σk=0n (nk) xn−kyk. предоставляет метод разложения биномов в степени без прямого умножения каждого множителя:
(x+y)n=(n0)xny0+(n1)xn−1y1+(n2)xn−2y2+…+(nn−1)x1yn−1 +(nn)x0yn
Более компактно можно записать
(x+y)n= Σk=0n (nk) xn−kyk Биномиальная теорема
Пример 3
Разложить по биномиальной теореме: (x+2)5.
Решение:
Используйте биномиальную теорему, где n=5 и y=2.
(x+2)5=(50)x520+(51)x421+(52)x322+(53)x223+(54)x124+(55)x025
Иногда бывает полезно определить закономерность, возникающую в результате применения биномиальной теоремы . Обратите внимание, что степени переменной x начинаются с 5 и уменьшаются до нуля. Степени постоянного члена начинаются с 0 и увеличиваются до 5. Биномиальные коэффициенты можно вычислить в стороне и оставить читателю в качестве упражнения.
(х+2)5=(50)х520+(51)х421+(52)х322+(53)х223+(54)х124+(55)х025=1х5х1+5х4х2+10х3х4+10х2х8+ 5×1×16+1×1×32=x5+10×4+40×3+80×2+80x+32
Ответ: x5+10×4+40×3+80×2+80x+32
Бином может иметь отрицательные члены, и в этом случае мы получить чередующийся ряд.
Пример 4
Расширьте, используя биномиальную теорему: (u−2v)4.
Решение:
Используйте биномиальную теорему, где n=4, x=u и y=−2v, а затем упростите каждый член.
(u−2v)4=(40)u4(−2v)0+(41)u3(−2v)1+(42)u2(−2v)2+(43)u1(−2v)3+( 44)u0(−2v)4=1×u4×1+4u3(−2v)+6u2(4v2)+4u(−8v3)+1×1(16v4)=u4−8u3v+24u2v2−32uv3+16v4
Ответ: u4−8u3v+24u2v2−32uv3+16v4
Попробуйте! Расширьте, используя биномиальную теорему: (a2−3)4.
Ответ: a8−12a6+54a4−108a2+81
(нажмите, чтобы посмотреть видео)
Далее изучаем коэффициенты разложений (x+y)n, начиная с n=0:
(x+y )0=1(x+y)1=x+y(x+y)2=x2+2xy+y2(x+y)3=x3+3x2y+3xy2+y3(x+y)4=x4+4x3y +6x2y2+4xy3+y4
Запишите коэффициенты в виде треугольного массива и обратите внимание, что каждое число ниже является суммой двух чисел над ним, всегда оставляя 1 на каждом конце.
Это треугольник Паскаля. Треугольный массив чисел, соответствующих биномиальным коэффициентам.; он обеспечивает быстрый метод вычисления биномиальных коэффициентов. Используйте это в сочетании с биномиальной теоремой, чтобы упростить процесс расширения биномов, возведенных в степени. Например, чтобы расширить (x−1)6, нам потребуются еще две строки треугольника Паскаля,
. Биномиальные коэффициенты, которые нам нужны, выделены синим цветом. Используйте эти числа и биномиальную теорему, чтобы быстро разложить (x−1)6 следующим образом:
(x-1)6=1×6(-1)0+6×5(-1)1+15×4(-1)2+20×3(-1)3+15×2(-1)4+6x(-1)5 +1×0(−1)6=x6−6×5+15×4−20×3+15×2−6x+1
Пример 5
Расширить, используя биномиальную теорему и треугольник Паскаля: (2x−5)4.
Решение:
Из треугольника Паскаля видно, что при n=4 биномиальные коэффициенты равны 1, 4, 6, 4 и 1. Используйте эти числа и биномиальную теорему следующим образом:
(2x−5)4 =1(2x)4(-5)0+4(2x)3(-5)1+6(2x)2(-5)2+4(2x)1(-5)3+1(2x)0 (−5)4=16×4⋅1+4⋅8×3(−5)+6⋅4×2⋅25+4⋅2x(−125)+1⋅625=16×4−160×3+600×2−1000x+625
Ответ: 16×4−160×3+600×2−1000x+625
Ключевые выводы
- Чтобы вычислить факториал натурального числа, умножьте это число на все натуральные числа, меньшие его: 5!=5⋅4⋅3⋅ 2⋅1=120. Помните, что мы определили 0!=1.
- Биномиальные коэффициенты — это целые числа, вычисляемые по формуле: (nk)=n!k!(n−k)!.
- Биномиальная теорема предлагает метод разложения биномов, возведенных в степени, без непосредственного умножения каждого множителя: (x+y)n= Σk=0n (nk) xn−kyk.
- Используйте треугольник Паскаля для быстрого определения биномиальных коэффициентов.
Тематические упражнения
6!
4!
10!
9!
6!3!
8!4!
13!9!
15!10!
12!3! 7!
10!2! 5!
п!(п-2)!
(n+1)!(n−1)!
- 4! +3!
- (4+3)!
- 4!−3!
- (4−3)!
1×2×3×4×5×6×7
1×2×3×4×5
15×14×13
10×9×8×7
13
8×7
н(п-1)(п-2)
1×2×3×⋯×n×(n+1)
(64)
(84)
(72)
(95)
(90)
(1312)
(n0)
(нн)
(n1)
(nn−1)
10C8
5С1
12C12
10C5
нСn-2
нСn-3
Часть A: Факториалы и биномиальный коэффициент
Оценить.
Перепишите, используя факториал.
Рассчитайте указанный биномиальный коэффициент.
(4x−3)3
(2x−5)3
(х2+у)3
(х+1у)3
(х+3)4
(х+5)4
(x−4)4
(х-2)4
(х+2у)4
(x3−y)4
(х+1)5
(х-3)5
(х-2)6
(х+1)6
(x−1)7
(х+1)7
(5x−1)4
(3x−2)4
(4у+в)4
(3у-в)4
(у-5в)5
(2u+3v)5
(а-б2)5
(а2+b2)4
(а2+b4)6
(а5+b2)5
(х+2)3
(х-2)4
(x−y)4, x,y≥0
(х+2у)5, х,у≥0
(х+у)7
(х+у)8
(х+у)9
(х-у)7
(х-у)8
(х-у)9
Часть B: Биномиальная теорема
Расширить с помощью биномиальной теоремы.
Определите факториалы целых чисел 5, 10, 15, 20 и 25.
 Что растет быстрее: обычная показательная функция an=10n или факториальная функция an=n!? Объяснять.
Что растет быстрее: обычная показательная функция an=10n или факториальная функция an=n!? Объяснять.Исследуйте и обсудите историю биномиальной теоремы.
Часть C: Дискуссионная доска
Ответы
720
3 628 800
120
17 160
15 840
н2-н
- 30
- 5 040
7!
15!12!
13!12!
п!(п-3)!
15
21
1
1
п
45
1
n2−n2
64×3−144×2+108x−27
x38+3x2y4+3xy22+y3
х4+12х3+54х2+108х+81
x4-16×3+96×2-256x+256
x4+8x3y+24x2y2+32xy3+16y4
х5+5х4+10х3+10х2+5х+1
x6-12×5+60×4-160×3+240×2-192x+64
x7-7×6+21×5-35×4+35×3-21×2+7x-1
625×4-500×3+150×2-20x+1
256u4+256u3v+96u2v2+16uv3+v4
u5−25u4v+250u3v2−1,250u2v3+3,125uv4−3,125v5
a5−5a4b2+10a3b4−10a2b6+5ab8−b10
a12+6a10b4+15a8b8+20a6b12+15a4b16+6a2b20+b24
х3+32х2+6х+22
x2-4xxy+6xy-4yxy+y2
x7+7x6y+21x5y2+35x4y3+35x3y4+21x2y5+7xy6+y7
x9+9x8y+36x7y2+84x6y3+126x5y4+126x4y5+84x3y6+36x2y7+9xy8+y9
x8-8x7y+28x6y2-56x5y3+70x4y4-56x3y5+28x2y6-8xy7+y8
Ответ может отличаться
Биномиальная теорема · Предварительное исчисление
Биномиальная теорема · Предварительное исчислениеВ этом разделе вы:
- Примените биномиальную теорему.

Многочлен с двумя членами называется биномом. Мы уже научились умножать двучлены и возводить двучлены в степени, но возведение двучленов в большую степень может быть утомительным и занимать много времени. В этом разделе мы обсудим короткий путь, который позволит нам найти (x+y)n
без умножения бинома на самого себя n
раз.
Идентификация биномиальных коэффициентов
В разделе «Принципы подсчета» мы изучили комбинаций . В ярлыке для нахождения (x+y)n,
нам нужно будет использовать комбинации, чтобы найти коэффициенты, которые появятся в разложении бинома. В этом случае мы используем обозначение (nr)
вместо C(n,r),
, но его можно рассчитать таким же образом. Итак,
(nr)=C(n,r)=n!r!(n−r)!
Комбинация (номер)
называется биномиальным коэффициентом . Пример биномиального коэффициента: (52)=C(5,2)=10.
Биномиальные коэффициенты
Если n
и r
являются целыми числами, большими или равными 0, где n≥r,
, то биномиальный коэффициент равен
(nr)=n(n,r)=n! г!(п-г)!
Всегда ли биномиальный коэффициент является целым числом?
Да. Точно так же, как количество комбинаций всегда должно быть целым числом, биномиальный коэффициент всегда будет целым числом.
Точно так же, как количество комбинаций всегда должно быть целым числом, биномиальный коэффициент всегда будет целым числом.
Нахождение биномиальных коэффициентов
Найдите каждый биномиальный коэффициент.
- (53)
- (92)
- (97)
Используйте формулу для расчета каждого биномиального коэффициента. Вы также можете использовать функцию nCr
на вашем калькуляторе.
(nr)=C(n,r)=n!r!(n−r)!
- (53)=5!3!(5−3)!=5⋅4⋅3!3!2!=10
- (92)=9!2!(9−2)!=9⋅8⋅7!2!7!=36
- (97)=9!7!(9−7)!=9⋅8⋅7!7!2!=36
Анализ
Обратите внимание, что мы получили одинаковый результат для частей (b) и (c). Если вы внимательно посмотрите на решение для этих двух частей, вы увидите, что в итоге вы получите те же два факториала в знаменателе, но в обратном порядке, как и в случае с комбинациями.
(номер)=(nn−r)
Найдите каждый биномиальный коэффициент.
- (73)
- (114)
- 35
- 330
Использование биномиальной теоремы
Когда мы расширяем (x+y)n
путем умножения, результат называется биномиальным расширением и включает биномиальные коэффициенты. Если бы мы хотели расширить (x+y)52,
мы могли бы умножить (x + y)
сам по себе пятьдесят два раза. Это может занять несколько часов! Если мы исследуем некоторые простые биномиальные расширения, мы можем найти шаблоны, которые приведут нас к сокращению пути для нахождения более сложных биномиальных расширений.
(x+y)2=x2+2xy+y2(x+y)3=x3+3x2y+3xy2+y3(x+y)4=x4+4x3y+6x2y2+4xy3+y4
Сначала рассмотрим показатели степени. С каждым последующим членом показатель степени x
уменьшается, а показатель степени для y
увеличивается. Сумма двух показателей равна n
Сумма двух показателей равна n
за каждый термин.
Далее рассмотрим коэффициенты. Обратите внимание, что коэффициенты увеличиваются, а затем уменьшаются симметрично. Коэффициенты следуют шаблону:
(n0),(n1),(n2),…,(nn).
Эти закономерности приводят нас к теореме о биноме , которую можно использовать для расширения любого бинома.
(x+y)n=∑k=0n(nk)xn−kyk=xn+(n1)xn−1y+(n2)xn−2y2+…+(nn−1)xyn−1+yn
Еще один способ увидеть коэффициенты — изучить разложение бинома в общем виде, x+y,
в последовательные степени 1, 2, 3 и 4.
(x+y)1=x+y(x+y)2=x2+2xy+y2(x+y)3=x3+3x2y+3xy2+y3(x+y)4=x4+4x3y+6x2y2+ 4xy3+y4
Можете ли вы угадать следующее разложение бинома (x+y)5?
См. [ссылка], которая иллюстрирует следующее:
Чтобы определить разложение на (x+y)5,
мы видим n=5,
таким образом, будет 5+1 = 6 слагаемых. Суммарная степень каждого члена равна 5. В порядке убывания степеней x
.
шаблон выглядит следующим образом:
- Ввести
x5,
, а затем для каждого последующего члена уменьшайте показатель степени на
хна 1 до
x0=1.
- Представить
y0=1,
, а затем увеличьте показатель степени на
уна 1 до
y5достигнуто.
x5, x4y, x3y2, x2y3, xy4, y5
Следующим расширением будет
(х+у)5=х5+5х4у+10х3у2+10х2у3+5ху4+у5.
Но откуда берутся эти коэффициенты? Биномиальные коэффициенты симметричны. Мы можем видеть эти коэффициенты в массиве, известном как Треугольник Паскаля , показанном в [ссылка].
Чтобы сгенерировать треугольник Паскаля, мы начинаем с записи 1. В строке ниже, строке 2, мы записываем две единицы. В 3-м -м -м ряду обвяжите концы рядов единицами и прибавьте 1+1
., чтобы найти среднее число, 2. В энном
ряд, обвязать концы ряда 1 изн. Каждый элемент треугольника представляет собой сумму двух элементов непосредственно над ним.
Каждый элемент треугольника представляет собой сумму двух элементов непосредственно над ним.
Чтобы увидеть связь между треугольником Паскаля и биномиальными коэффициентами, давайте вернемся к разложению биномов в общем виде.
Биномиальная теорема
Биномиальная теорема — это формула, которую можно использовать для расширения любого бинома.
(x+y)n=∑k=0n(nk)xn−kyk=xn+(n1)xn−1y+(n2)xn−2y2+…+(nn−1)xyn−1+yn
Дан двучлен, запишите его в развернутой форме.
- Определить значение
n
по показателю степени.
- Оценить
k=0 от
до
k=n, используя формулу биномиальной теоремы.
- Упростить.
Расширение бинома
Пишите в расширенной форме.
- (х+у)5
- (3x−y)4
- Заменитель
n=5
в формулу.
k=0 от Оцените
Оценитедо
k=5слагаемых. Упрощать.
(x+y)5=(50)x5y0+(51)x4y1+(52)x3y2+(53)x2y3+(54)x1y4+(55)x0y5(x+y)5=x5+5x4y+10x3y2+10x2y3+5xy4+y5
- Замена
n=4
в формулу. Оцените
k=0 отдо
k=4слагаемых. Обратите внимание, что
3xна месте, которое было занято
хи тот
–yнаходится на том месте, которое было занято
у.Итак, подставляем их. Упрощать.
(3x−y)4=(40)(3x)4(−y)0+(41)(3x)3(−y)1+(42)(3x)2(−y)2+(43) (3x)1(−y)3+(44)(3x)0(−y)4(3x−y)4=81×4−108x3y+54x2y2−12xy3+y4
Анализ
Обратите внимание на чередующиеся знаки в части b. Это происходит потому, что (−y)
в нечетных степенях отрицательно, а (−y)
в четных степенях положительно. Это будет происходить всякий раз, когда бином содержит знак вычитания.
Пишите в развернутом виде.
- (х-у)5
- (2x+5 лет)3
- x5-5x4y+10x3y2-10x2y3+5xy4-y5
- 8×3+60x2y+150xy2+125y3
Использование биномиальной теоремы для нахождения одного термина
Расширение бинома с высоким показателем степени, например (x+2y)16
может быть длительным процессом.
Иногда нас интересует только определенный член биномиального разложения. Нам не нужно полностью расширять бином, чтобы найти один конкретный термин.
Обратите внимание на структуру коэффициентов в разложении (x+y)5.
(х+у)5=х5+(51)х4у+(52)х3у2+(53)х2у3+(54)ху4+у5
Второй член равен (51)x4y.
Третий член равен (52)x3y2.
Мы можем обобщить этот результат.
(номер)xn−ryr
(r+1)-й член биномиального разложения
(r+1)-й
член биномиального разложения of (x+y)n
равно:
(nr)xn−ryr
Учитывая бином, напишите конкретный термин без полного раскрытия.
- Определить значение
n
по показателю степени.
- Определить (г+1).
- Определить р.
- Заменить
r
в формуле для
(r+1)-й-й член биномиального разложения.
Запись заданного члена биномиального разложения
Найдите десятый член (x+2y)16
без полного разложения бинома.
Поскольку мы ищем десятый член, r+1=10,
мы будем использовать r=9
в наших расчетах.
(nr)xn−ryr
(169)x16−9(2y)9=5 857 280x7y9
Найдите шестой член (3x−y)9
без полного раскрытия бинома.
−10,206x4y5
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с биномиальным расширением.
- Биномиальная теорема
- Пример биномиальной теоремы
Ключевые уравнения
| Биномиальная теорема | (x+y)n=∑k−0n(nk)xn−kyk |
| (г+1)й |
| член биномиального разложения | (номер)xn−ryr |
Ключевые понятия
Раздел Упражнения
Устный
Что такое биномиальный коэффициент и как он рассчитывается?
Биномиальный коэффициент — это альтернативный способ обозначения комбинации C(n,r).
Он определяется как (nr)= C(n,r) =n!r!(n−r)!.
Какую роль играют биномиальные коэффициенты в биномиальном разложении? Они ограничены любым типом номера?
Что такое биномиальная теорема и для чего она используется?
Биномиальная теорема определяется как (x+y)n=∑k=0n(nk)xn−kyk
и может использоваться для расширения любого бинома.
Когда полезно использовать биномиальную теорему? Объяснять.
Алгебраический
Для следующих упражнений оцените биномиальный коэффициент.
(62)
15
(74)
35
(109)
10
(2511)
(176)
12 376
(200199)
В следующих упражнениях используйте биномиальную теорему для раскрытия каждого бинома.
(4a−b)3
64a3−48a2b+12ab2−b3
(5а+2)3
(3а+2б)3
27а3+54а2б+36аб2+8б3
(2x+3г)4
(4x+2y)5
1024×5+2560x4y+2560x3y2+1280x2y3+320xy4+32y5
(3x−2y)4
(4x−3y)5
1024×5−3840x4y+5760x3y2−4320x2y3+1620xy4−243y5
(1x+3г)5
(x−1+2y−1)4
1×4+8x3y+24x2y2+32xy3+16y4
(х-у)5
В следующих упражнениях используйте биномиальную теорему, чтобы записать первые три члена каждого бинома.
(а+б)17
а17+17а16б+136а15б2
(x−1)18
(a−2b)15
a15−30a14b+420a13b2
(x−2y)8
(3а+б)20
3 486 784 401a20+23 245 229 340a19b+73 609 892 910a18b2
(2а+4б)7
(x3-y)8
x24-8x21y+28x18y
В следующих упражнениях найдите указанный член каждого двучлена, не раскрывая его полностью.
Четвертый член (2x−3y)4
Четвертый член (3x−2y)5
−720x2y3
Третий член (6x−3y)7
Восьмой член (7+5y)14
220 812 466 875 000y7
Седьмой член (a+b)11
Пятый член (x−y)7
35x3y4
Десятый член (x−1)12
Девятый член (a−3b2)11
1 082 565a3b16
Четвертый член (x3−12)10
Восьмой член (y2+2x)9
1152y2x7
Графический
В следующих упражнениях используйте биномиальную теорему, чтобы разложить бином f(x)=(x+3)4.
Затем найдите и изобразите каждую указанную сумму на одном наборе осей.
Найти и построить график f1(x),
такое, что f1(x)
является первым членом разложения.
Найдите и начертите f2(x),
такое, что f2(x)
представляет собой сумму первых двух членов разложения.
f2(x)=x4+12×3
Найдите и начертите f3(x),
такое, что f3(x)
представляет собой сумму первых трех членов разложения.
Найдите и начертите f4(x),
такое, что f4(x)
представляет собой сумму первых четырех членов разложения.
f4(x)=x4+12×3+54×2+108x
Найдите и начертите f5(x),
такое, что f5(x)
представляет собой сумму первых пяти членов разложения.
Расширения
В разложении (5x+3y)n,
каждый член имеет вид (nk)an–kbk, где k
последовательно принимает значение 0,1,2, …, n.
Если (nk)=(72),
, каков соответствующий терм?
590,625x5y2
В разложении (a+b)n,
коэффициент при an−kbk
совпадает с коэффициентом какого другого члена?
Рассмотрим разложение (x+b)40.
Чему равен показатель степени b
в k-м
члене?
к-1
Найдите (nk−1)+(nk)
и запишите ответ в виде биномиального коэффициента в виде (nk).
Докажи это. Подсказка: Используйте тот факт, что для любого целого числа p
такое, что p≥1, p!=p(p−1)!.
(nk−1)+(nk)=(n+1k);
Доказательство:
(nk−1)+(nk)=n!k!(n−k)!+n!(k−1)!(n−(k−1))!=n!k! (n−k)!+n!(k−1)!(n−k+1)!=(n−k+1)n!(n−k+1)k!(n−k)!+kn !k(k−1)!(n−k+1)!=(n−k+1)n!+kn!k!(n−k+1)!=(n+1)n!k!( (n+1)−k)!=(n+1)!k!((n+1)−k)!=(n+1k)
Какое выражение нельзя разложить с помощью биномиальной теоремы? Объяснять.
- (х2-2х+1)
- (а+4а−5)8
- (x3+2y2−z)5
- (3×2−2y3)12
Выражение (x3+2y2−z)5
нельзя расширить с помощью биномиальной теоремы, потому что его нельзя переписать как бином.
Глоссарий
- Биномиальный коэффициент
- количество способов выбрать r объектов из n объектов, где порядок не имеет значения; эквивалентно
C(n,r),
обозначается как
(номер)
- биномиальное разложение
- результат расширения
(x+y)n
путем умножения
- Биномиальная теорема
- формула, с помощью которой можно расширить любой бином
Эта работа находится под лицензией Creative Commons Attribution 4.0 International License.
Вы также можете бесплатно скачать на http://cnx.org/contents/[email protected]
Атрибуция:
- По вопросам, касающимся этой лицензии, обращайтесь по адресу [email protected].
- Если вы используете данный учебник в качестве библиографической ссылки, то цитировать его следует следующим образом:
Колледж OpenStax, Precalculus.




 С. Дифференциальное и интегральное исчисления для втузов, т. 2: Учебное пособие для втузов.—13-е изд.— М.: Наука, Главная редакция физико-математической литературы, 1985. — 560 с.
С. Дифференциальное и интегральное исчисления для втузов, т. 2: Учебное пособие для втузов.—13-е изд.— М.: Наука, Главная редакция физико-математической литературы, 1985. — 560 с.

 Что растет быстрее: обычная показательная функция an=10n или факториальная функция an=n!? Объяснять.
Что растет быстрее: обычная показательная функция an=10n или факториальная функция an=n!? Объяснять.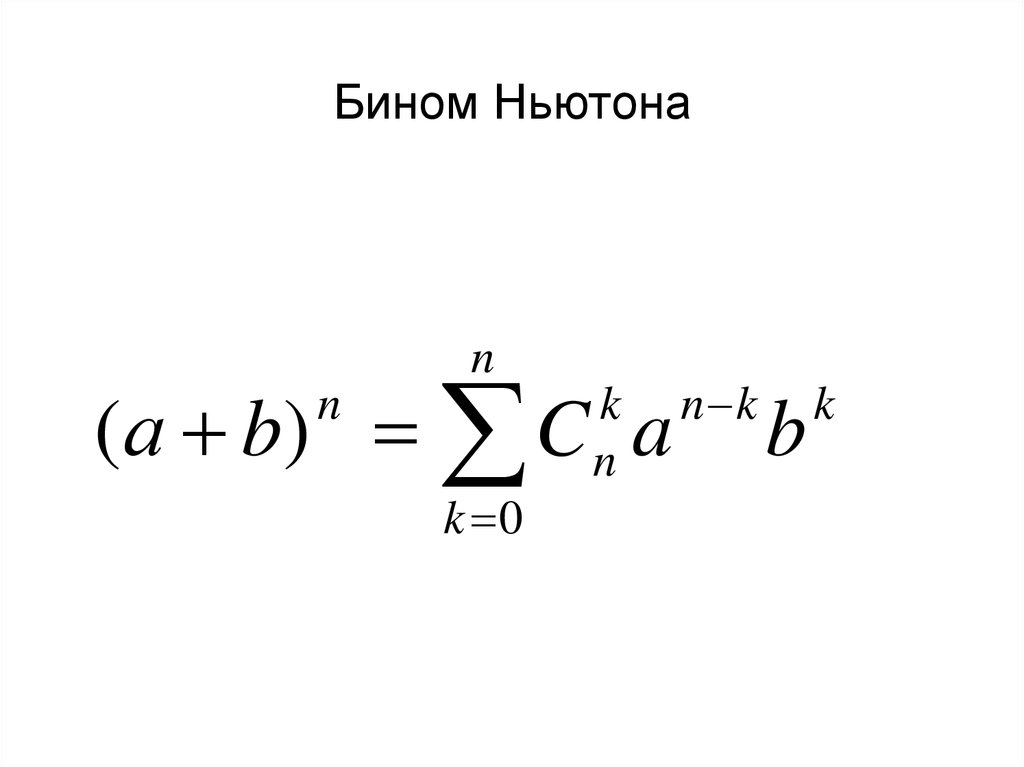
 Оцените
Оцените