Действия с иррациональными числами: Иррациональные числа — урок. Алгебра, 8 класс.

Действия над иррациональными числами.

Это означает, что

можно записать все под одним корнем, например:

√2・√3=√(2・3)=√6

Так же помним, что если перед корнем стоит множитель, а от перестановки множителей произведение не меняется, то

 5

√2・4√3=

5

・√2・4・√3=

5

・4・√2・√3=20√6

Если видите знак корня в знаменателе дроби – избавляйтесь от нее!

Для начала напомню вам два правила:

 Иррациональность бывает двух типов:

11. 

В знаменателе стоит иррациональное число, над которым выполняют действие умножения (или вообще не выполняют никакого действия).

22. В знаменателе стоит число, участвующее в сложении или вычитании.

Для избавления от иррациональности в знаменателе в первом случае вам необходимо умножить и числитель и знаменатель дроби (основное свойство дроби) на точно такой же корень:

 Во втором случае вам необходимо и числитель и знаменатель дроби умножить на сопряженное выражение (точно такое же выражение, но с другим действием, производимым с числами):

Советую так же изучить статью, которая подскажет вам, как быть, если под знаком корня вы увидите сумму или разность, содержащую иррациональное число.

Задания, предложенные в тестах:
В5, РТ-19 (2 этап)
А11, РТ-20 (2 этап)

«действия над иррациональными числами»

Действия над иррациональными числами

Цели: формировать умение различать рациональные и иррациональные числа и осуществлять действия над ними.

Ход урока

I. Организационный момент.

II. Устная работа.

– Вычислите:

а) 0,15 + 1,37; д) –3,8 – 5,7;

б) 1,27 + 3,3; е) 2,9 – 6,3;

в) 6,42 – 3,2; ж) 1,7 – 0,95;

г) –8 + 4,7; з) –1,25 – 5,8.

III. Тест с последующей проверкой.

«+» – согласен с утверждением;

«–» – не согласен с утверждением.

1) Всякое целое число является натуральным.

2) Всякое натуральное число является рациональным.

3) Число –7 является рациональным.

4) Сумма двух натуральных чисел всегда является натуральным числом.

5) Разность двух натуральных чисел всегда является натуральным числом.

6) Произведение двух целых чисел всегда является целым числом.

7) Частное двух целых чисел всегда является целым числом.

8) Сумма двух рациональных чисел всегда является рациональным числом.

9) Частное двух рациональных чисел всегда является рациональным числом.

10) Всякое иррациональное число является действительным.

11) Действительное число не может быть натуральным.

12) Число 2,7(5) является иррациональным.

13) Число π является действительным.

14) Число 3,1(4) меньше числа π.

15) Число –10 принадлежит одновременно множеству целых, рациональных и действительных чисел.

К л ю ч: – + + + – + – + + + – – + – +

IV. Объяснение нового материала.

Привести примеры из учебника, показывающие, как осуществлять арифметические действия над иррациональными числами.

V. Формирование умений и навыков.

1. № 283, № 284 (а), № 287.

2. № 288, № 290.

В классе с высоким уровнем подготовки можно дополнительно разобрать вопрос о том, каким числом представляется сумма или разность рациональных и иррациональных чисел. Для этого нужно решить ряд задач.

1) № 292.

Р е ш е н и е

– Сложим данные иррациональные числа в столбик:

Получили число, дробная часть которого представлена группой цифр, состоящих из одной, двух, трёх и т. д. троек, разделённых шестёрками. Очевидно, что данное число является иррациональным.

2) Может ли сумма двух иррациональных чисел быть числом рациональным?

Р е ш е н и е

– В предыдущей задаче мы выполнили сложение двух иррациональных чисел и получили в сумме иррациональное число. Но это не означает, что сумма любых двух иррациональных чисел является иррациональным числом.

Нужно подобрать такие два иррациональных числа, которые в сумме дали бы бесконечную десятичную периодическую дробь. В качестве первого слагаемого можно взять число из предыдущей задачи: 1,323223222… Тогда вторым слагаемым может быть число 1,676776777… (группы цифр состоят из одной, двух, трёх и т. д. семёрок, разделённых шестёрками).

То есть в сумме получим число 2,(9) или 3.

Значит, можно подобрать два таких иррациональных числа, которые в сумме дают рациональное число.

3) Может ли разность двух иррациональных чисел быть числом рациональным?

4) Если число а – рациональное, а число b – иррациональное, то каким числом будет сумма а + b и разность а – b?

VI. Итоги урока.

В о п р о с ы у ч а щ и м с я:

– Какие множества чисел вы изучили? Как они связаны между собой?

– В виде какой десятичной дроби может быть представлено любое рациональное число?

– Существуют ли иррациональные числа, которые могут быть представлены в виде периодической десятичной дроби?

– В виде каких десятичных дробей представляются иррациональные числа?

Домашнее задание: № 284 (б), № 289, № 291.

Д о п о л н и т е л ь н о: № 293.

Операции с действительными числами: рациональные и иррациональные числа

Операции с действительными числами являются частью основных арифметических действий, которым обучают в школе. Вещественное число — это количество, которое можно начать с бесконечного десятичного расширения. В отличие от натуральных чисел 1, 2, 3, …, которые образуются в результате счета, действительные числа используются для измерения постоянно меняющихся величин, таких как размер и время. Таким образом, действительные числа — это рациональные числа и иррациональные числа. Они отличаются словом «действительный» от комплексных чисел, включая символ i или \(\sqrt{-1}\), которые используются для упрощения математической интерпретации эффектов, подобных тем, которые наблюдаются в электрических явлениях. Иррациональные числа, а также положительные и отрицательные целые числа и дроби (или рациональные числа) входят в категорию действительных чисел.

Существует 4 основных операции над рациональными числами:

1. Сложение рациональных чисел

Сложение объединяет две величины в одну величину или сумму в самой простой форме. Давайте представим, что у вас есть группа из двух ящиков и группа из трех ящиков. Когда вы объедините две группы, вы получите группу из пяти блоков.

Пример: 2/9 + 4/9 = 6/9 — математическое представление этого понятия.

2. Вычитание рационального числа

Противоположностью сложения является вычитание. Чтобы найти разницу между двумя величинами, мы вычитаем одну из другой, а не складываем их вместе. Предположим, вы начинаете с группы из пяти ящиков, как в предыдущем примере. После удаления трех ящиков из этой группы у вас останется два. Выражаясь математически:

Пример: 2/9 – 1/9 = 1/9 – это математическое представление этой концепции.

Узнать о типах чисел

3. Умножение рационального числа

Умножение также объединяет несколько величин в одну величину, которая называется произведением. Умножение, по сути, можно представить как сумму многочисленных сложений. Произведение x и y является результатом сложения x и y вместе y раз. Произведение двух дробей равно произведению числителей, деленному на произведение знаменателей.

\({a\over{b}}\times{c\over{d}} = {ac\over{bd}}\)

Пример: \({2\более{3}}\times{4\over{5}} = {2\times4\over{3\times5}} = {8\over{15}}\)

4. Деление рационального числа

Деление является противоположностью умножения. Вы разделяете количество на меньшее значение, называемое частным, вместо того, чтобы умножать два или более числа вместе, чтобы получить большее значение. Умножение на обратную дробь идентично делению на нее. 1 деленное на число равно обратной величине. Мультипликативное обратное число есть величина, обратная этому числу. Обратное число и его произведение равно единице. Существует обратное значение для всех чисел, кроме 0,9.0003

\({a\over{b}}\div{c\over{d}}= {a\over{b}}\times{d\over{c}} = {ad\over{bc}} \)

Пример: \({2\over{3}}div{4\over{5}} = {2\times5\over{3\times4}} = {10\over{12}}\)

Узнать о среднем арифметическом

Существует 4 основных операции над иррациональными числами:

1. Сложение иррациональных чисел

r + s может быть или не быть иррациональным числом. Это означает, что операция сложения двух иррациональных чисел не всегда приводит к иррациональному числу.

Иррациональное число + Иррациональное число = Иррациональное / Рациональное число.

Пример. Рассмотрим два иррациональных числа \(2 + \sqrt{3} и 5 + \sqrt{3}\). Сложение числа приведет к \(2 + \sqrt{3} + 5 + \sqrt{3} = 7 + 2\sqrt{3}\). Это снова иррациональное число. Теперь рассмотрим еще два иррациональных числа \(2 + \sqrt{3} \text{ и } 2 – \sqrt{3}\). Сложение числа приведет к \(2 + \sqrt{3} + 2 – \sqrt{3} = 4\). Это рациональное число.

2. Вычитание иррациональных чисел

Если r — одно иррациональное число, а s — другое иррациональное число, то r – s могут быть иррациональными числами, а могут и не быть. Это означает, что операции вычитания между двумя иррациональными числами не всегда приводят к иррациональному числу.

Иррациональное число – Иррациональное число = Иррациональное / Рациональное число.

Пример. Рассмотрим два иррациональных числа \(5 + \sqrt{3} и 2 + \sqrt{3}\). Вычитание числа приведет к \(5 + \sqrt{3} – (2 + \sqrt{3}) = 3\). Это рациональное число. Теперь рассмотрим еще два иррациональных числа \(2 + \sqrt{3} \text{ и } 2 – \sqrt{3}\). Вычитание числа приведет к \(2 + \sqrt{3} – (2 – \sqrt{3}) = 2\sqrt{3}\). Это рациональное число.

3. Умножение иррациональных чисел

Если r — одно иррациональное число, а s — другое иррациональное число, то rs может быть, а может и не быть иррациональным числом. Это означает, что любое произведение двух иррациональных чисел не всегда дает иррациональное число.

Иррациональное число × Иррациональное число = Иррациональное / Рациональное число.

Рассмотрим два иррациональных числа \(2\sqrt{3} \text{ и } \sqrt{3}\). Умножение числа даст \(2\sqrt{3} × \sqrt{3} = 2 × 3 = 6\).

Это рациональное число. Теперь рассмотрим еще два иррациональных числа \(2\sqrt{3} \text{ и } \sqrt{2}\). Умножение чисел даст \(2\sqrt{3} × \sqrt{2} = 2\sqrt{6}\). Это иррациональное число.

4. Деление иррациональных чисел

Если r — одно иррациональное число, а s — другое иррациональное число, то r/s могут быть иррациональными числами, а могут и не быть. Это означает, что деление двух иррациональных чисел не всегда приводит к иррациональному числу.

Иррациональное число ÷ Иррациональное число = Иррациональное / Рациональное число.

Рассмотрим два иррациональных числа \(2\sqrt{3} \text{ и } \sqrt{3}\). Умножение числа приведет к \(2\sqrt{3} ÷ \sqrt{3} = {2\sqrt{3}}\times{1\over{\sqrt{3}}} = 2\).

Это рациональное число. Теперь рассмотрим еще два иррациональных числа \(2\sqrt{3} \text{ и } \sqrt{2}\). Умножение чисел даст \(2\sqrt{3} × \sqrt{2} = 2\sqrt{6}\). Это иррациональное число.

Читать о двоичных числах

Существует 4 основных операции над рациональными и иррациональными числами:

1. Сложение рациональных и иррациональных чисел

Неповторяющиеся числа 900 на завершающий признак иррационального не влияет добавление рационального числа к иррациональному числу. В результате сложение рациональных и иррациональных чисел дает иррациональное число.

Рациональное число + Иррациональное число = Иррациональное число.

Пример. Рассмотрим одно рациональное и одно иррациональное число, 5 и e соответственно. Сложение обоих дает нам 5 + e. Это иррациональное число.

2. Вычитание рациональных и иррациональных чисел

Неповторяющийся и непрерывный признак иррационального числа не изменяется при вычитании рационального числа из иррационального числа. В результате вычитание рациональных и иррациональных чисел дает иррациональное число.

Рациональное число – Иррациональное число = Иррациональное число.

Пример. Рассмотрим одно рациональное и одно иррациональное число, 5 и e соответственно. Вычитание обоих дает нам 5 – e. Это иррациональное число.

3. Умножение рациональных и иррациональных чисел

На неповторяющийся и непрерывный характер иррационального числа не влияет умножение ненулевого рационального числа на иррациональное число. В результате произведение является иррациональным числом.

Рациональное число * Иррациональное число = Иррациональное число.

Пример. Рассмотрим одно рациональное и одно иррациональное число, 5 и \(\sqrt{3}\) соответственно. Вычитание обоих дает нам \(5\sqrt{3}\) . Это иррациональное число.

4. Деление рационального и иррационального числа

Неповторяющийся и непрерывный характер иррационального числа не затрагивается делением ненулевого рационального числа на иррациональное число. В результате произведение является иррациональным числом.

Рациональное число ÷ Иррациональное число = Иррациональное число

Пример. Рассмотрим одно рациональное и одно иррациональное число, 5 и \(\pi\) соответственно. Вычитание обоих дает нам \({5\over{\pi}}\). Это иррациональное число.

Прочтите о взаимно простых числах

Давайте посмотрим на некоторые примеры операций над действительными числами, которые встречаются на экзаменах.

Пример 1: Как найти иррациональное число между двумя иррациональными числами.

Решение:  Предположим, что у нас есть два иррациональных числа a и b, тогда иррациональные числа между ними будут квадратом обоих иррациональных чисел и извлекут квадратный корень из их среднего. Если квадратный корень иррационален, то мы получаем желаемое число. Если у нас нет нужного вам номера, мы можем повторить процедуру, используя один из исходных номеров и вновь сгенерированный номер.

Найти рациональные числа между \(\sqrt{2} \text{ и } \sqrt{3}\)

Разница между \(\sqrt{2} \text{ и } \sqrt{3\). 6 находится между \(4\sqrt{2}\text{ и } 4\sqrt{3} \text{ и } \frac{3}{2} \text{ находится между } \sqrt{2} \text{ и } \sqrt{3}\).

Пример 2: Укажите, являются ли следующие утверждения верными или ложными.

Сумма рационального числа и рационального числа рациональна.

Сумма рационального числа и иррационального числа иррациональна.

Сумма иррационального числа и иррационального числа иррациональна.

Произведение рационального числа на рациональное число рационально.

Произведение рационального числа на иррациональное число иррационально.

Произведение иррационального числа на иррациональное число иррационально.

Решение:  Сумма рационального числа и рационального числа рациональна — всегда верно.

Сумма рационального числа и иррационального числа иррациональна — всегда верно.

Сумма иррационального числа и иррационального числа иррациональна- Только иногда верно.

Произведение рационального числа на рациональное число рационально — всегда верно.

Произведение рационального числа на иррациональное число иррационально – Неверно.

Произведение иррационального числа на иррациональное число иррационально- Только иногда верно.

Надеюсь, эта статья об операциях над действительными числами была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!

Q.1 Что такое операции над рациональными числами?

Ответ 1 Арифметические операции — это дисциплина математики, которая занимается изучением чисел и их операций, которые полезны во всех других разделах математики. Сложение, вычитание, умножение и деление являются наиболее распространенными операциями. Рациональные числа являются частью системы счисления. Понимание рациональных чисел является базовой математикой и важной темой алгебры. Все целые числа, а также все дроби, конечные десятичные дроби и повторяющиеся десятичные дроби входят в число рациональных чисел. Каждое рациональное число можно представить в виде дроби a/b, где a и b — целые числа.

Q.2 Что такое пример рационального числа?

Ответ 2 Число получается делением двух целых чисел (целое число — это число без дробной части). «Отношение» — это корень слова. В арифметике рациональное число — это число, которое может быть выражено как частное p/q двух чисел с q ​​= 0. Множество рациональных чисел также включает все целые числа, которые могут быть выражены как частное с целым числом в качестве числителя и 1 в качестве знаменателя. Рациональные числа — это либо завершающие, либо повторяющиеся десятичные дроби в десятичной форме. 1/7 = 0,142857, например, где 142857 не повторяется бесконечно. Каждое рациональное число можно представить в виде дроби a/b, где a и b — целые числа. 3 можно выразить, например, как 3/1, -0. 175 представлено -7/40, а 1 1/6 представлено 7/6. Хотя все рациональные числа являются натуральными числами, целыми числами и целыми числами, не все рациональные числа являются натуральными числами, целыми числами или целыми числами.

Q.3 Что означает иррациональное в математике?

Ответ 3 Иррациональные числа являются частным случаем чисел во всей системе счисления. Иррациональные числа в некотором роде противоположны рациональным. Это действительные числа, которые мы не можем записать в виде отношения \({p\over{q}}\), где p и q — целые числа, где q не может быть равно нулю. Например, \(\sqrt{2} = 1,414213….\) иррационально, потому что мы не можем записать это как часть целых чисел. Следовательно, иррациональные числа являются повторяющимися числами. Давайте теперь посмотрим, как мы можем определить иррациональные числа.

Q.4 Что такое сумма и произведение двух рациональных чисел?

Ответ 4 Рациональное число можно представить в виде дроби, в которой числитель и знаменатель являются целыми числами (знаменатель не равен нулю). Поскольку целые числа закрыты при сложении и умножении, сложение двух рациональных чисел равносильно сложению двух таких дробей, в результате чего получается еще одна дробь того же типа.

В.5 Как разделить два рациональных числа?

Ответ 5 Деление противоположно умножению. Вы разделяете количество на меньшее значение, называемое частным, вместо того, чтобы умножать два или более числа вместе, чтобы получить большее значение. Умножение на обратную дробь идентично делению на нее. 1 деленное на число равно обратной величине. Мультипликативное обратное число есть величина, обратная этому числу. Обратное число и его произведение равно единице. Существует обратное значение для всех чисел, кроме 0,9.0269 \({a\over{b}}\div{c\over{d}}= {a\over{b}}\times{d\over{c}} = {ad\over{bc}}\ )

Операции над действительными числами — GeeksforGeeks

Действительные числа — это те числа, которые представляют собой комбинацию рациональных чисел и иррациональных чисел в системе счисления математики. С этими числами можно выполнять все арифметические операции, такие как сложение, вычитание, умножение и т. д. Кроме того, мнимые числа не являются действительными числами. Мнимые числа используются для определения комплексных чисел. Чтобы получить действительные числа, во-первых, мы должны понимать рациональные числа и иррациональные числа. Рациональные числа — это те числа, которые можно записать как p/q, где p — числитель, q — доминатор, а p и q — целые числа. Например, 5 можно записать как 5/1, так что это рациональное число, а иррациональные числа — это те числа, которые нельзя записать в виде p/q.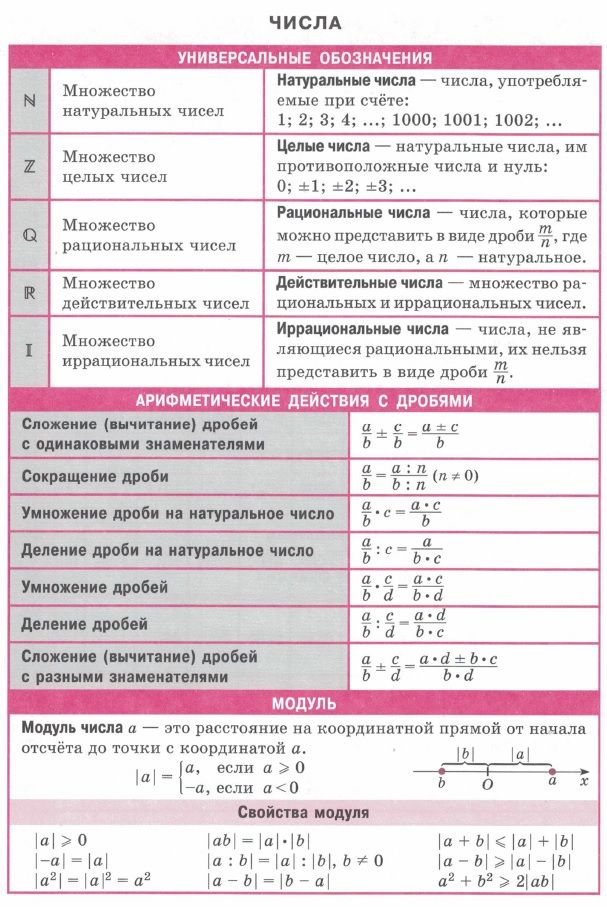

Например, √3 является иррациональным числом, его можно записать как 1,73205081 и продолжать до бесконечности, и его нельзя записать в виде дроби, это неконечная форма и неповторяющиеся десятичные дроби. А если объединить рациональные числа и иррациональные числа, то они стали действительными числами.

Пример: 12, -8, 5,60, 5/1, π(3,14) и т. д.

Действительные числа могут быть положительными и отрицательными, и это обозначается буквой R. эта категория.

Операции с действительными числами

Четыре основных математических действия: сложение, деление, умножение и вычитание. Теперь мы разберемся в этих операциях как с рациональными, так и с иррациональными числами.

Операция над двумя рациональными числами

Когда мы выполняем арифметические операции над двумя рациональными числами, такие как сложение, вычитание, деление и умножение, результатом будут рациональные числа.

Пример:

0,25 + 0,25 = 0,50 можно записать как 50/100, что является формой p/q.

0,20 – 0,10 = 0,10 можно записать как 10/100, что является формой p/q.

0,4, умноженное на 184, равно 73,6 и может быть записано как 736/10.

0,252 разделить на 0,4 равно 0,63 и может быть записано как 63/100.

Операции над двумя иррациональными числами

Когда мы выполняем арифметические операции, такие как сложение, вычитание, умножение или деление над двумя иррациональными числами, результатом могут быть рациональные или иррациональные числа.

Пример:

√2 + √3 = 3,14 можно записать как 314/100, что является рациональным числом.

√3 – √3 = 0 или 5√4 – 4√3 = 3,07, что можно записать как 307/100, что является рациональным числом.

Когда √5 умножается на √5, мы получаем 5, что является рациональным числом, или когда √3 умножается на √5, мы получаем √15, что является иррациональным числом. Когда √8 делится на √8, мы получаем 8, что является рациональным числом, или если √5 делится на √3, то мы получаем (√5)/(√3), что является иррациональным числом.

Операция над рациональным числом и иррациональным числом

Сложение

Когда мы складываем иррациональное число и рациональное число, результатом будет иррациональное число. Если к 2√5 прибавить 3, получится иррациональное число.

Вычитание

Когда мы выполняем вычитание иррационального числа и рационального числа, результатом будет иррациональное число. Если 5√6 вычесть из 3, то получится иррациональное число.

Когда мы выполняем эту операцию, результат может быть иррациональным или рациональным. Если 3 умножить на √5, то получится 3√5, что является иррациональным числом, а если √12 умножить на √3, то результатом будет √36, и его можно записать как 6, что является рациональным числом.

Деление

При делении рационального числа на иррациональное или наоборот, результатом всегда будет иррациональное число. Если 4 разделить на √2, получится 4√2, что является иррациональным числом.

Свойства действительных чисел

У нас есть четыре свойства: коммутативность, ассоциативность, дистрибутивность и тождественность. Предположим, что a, b и c — три действительных числа. Тогда эти свойства можно описать как

Коммутативное свойство

Если a и b — числа, то a + b = b + a для сложения и a × b = b × a для умножения.

Дополнение:

а + b = b + а;

5 + 6 = 6 + 5

Умножение:

a × b = b × a;

4 × 2 = 2 × 4

Ассоциативное свойство

Если a, b и c — действительные числа, то форма будет иметь вид

a + (b + c) = (a + b) = c для сложения и (a.b)c = a(b.c) для умножения

Дополнение:

а + (b + c) = (a + b) = c ;

5 + (3 + 2) = (5 + 3) + 2

Умножение:

(a.b)c = a(b.c) ;

(4×2)×6 = 4×(2×6)

Если a, b и c — действительные числа, то окончательная форма будет

a (b + c) = ab + ac и (a + b) c = ac + ab

5 (2+3)=5×2+5×3 ответ будет 25 как для левого, так и для правого члена.

Сложение: a + 0 = 0 (0 — аддитивная идентичность)

Умножение: a×1=1×a=1 (1 — мультипликативная идентичность)

Вещественные числа

Целые числа: {… – 3, -2, -1,0,1,2,3…}

Целые числа: {0,1,2, 3…}

Натуральные числа: {1,2,3…}

Иррациональные числа: √2, π, 0,102012…

Примеры задач

Вопрос 1. Докажите, что 3√7 — иррациональное число.

Решение:

Предположим противное, что 7√7 рационально.

То есть, мы можем найти взаимно простые a и b (b ≠ 0) такие, что 7√7 = ab

Переставляя, мы получаем √7 = ab/7

Поскольку 7, a и b целые числа, ab/7 рационально, поэтому √7 рационально.

Но это противоречит тому, что √7 иррационально.

Итак, мы заключаем, что 7√7 иррационально.

Вопрос 2. Объясните, почему (17 × 5 × 13 × 3 × 7 + 7 × 13) является составным числом?

Решение:

17 × 5 × 13 × 3 × 7 + 7 × 13 …(i)

= 7 × 13 × (17 × 5 × 3 + 1)

= 7 × 7 (255 + 1)

= 7 × 13 × 256

Число (i) делится на 2, 11 и 256, имеет более 2 простых делителей.

Следовательно, (17 × 5 × 13 × 3 × 7 + 7 × 13) — составное число.

Вопрос 3. Докажите, что 3 + 2√3 иррациональное число.

Решение:

Предположим противное, что 3 + 2√3 рационально.

Итак, мы можем найти целые числа a и b (b ≠ 0).

Такие, что 3 + 2√3 = ab, где a и b взаимно просты.

Преобразовывая уравнения, мы получаем, что поскольку a и b целые числа, мы получаем a ² b−32 является рациональным и, следовательно, √3 является рациональным.

No related posts.