Электростатика | Формулы по физике
Электрический заряд
Найти
Известно, что:
qne =
Вычислить ‘q’Закон Кулона
Найти
Известно, что:
Fkq1q2r =
Вычислить ‘F’Постоянная Кулона
Найти
Известно, что:
kπε_0 =
Вычислить ‘k’Относительная диэлектрическая проницаемость
Найти
εF_вакF_окр =
Вычислить ‘ε’Электрическое поле
Найти
Известно, что:
EFq =
Вычислить ‘E’Электрическое поле точечного заряда в вакууме
Найти
Известно, что:
Ekq_0r =
Вычислить ‘E’Электрическое поле точечного заряда в окружающей среде
Найти
Известно, что:
E_окрkq_0εr =
Вычислить ‘E_окр’Электрическое поле вне заряженной сферы
Найти
Известно, что:
Ekσ4πRr =
Вычислить ‘E’Электрическое поле вне заряженной сферы
Найти
Известно, что:
Ekqr =
Вычислить ‘E’Электрическое поле бесконечной заряженной плоскости
Найти
Известно, что:
Ek2πσ =
Вычислить ‘E’Электрическое поле бесконечной заряженной плоскости
Найти
Известно, что:
Eσε_0 =
Вычислить ‘E’Электрическое поле конденсатора
Найти
Известно, что:
Ekπσ =
Вычислить ‘E’Работа в электрическом поле
Найти
Известно, что:
AFΔ_d =
Вычислить ‘A’Потенциальная энергия системы двух точечных зарядов
Найти
Известно, что:Wkq0qεr =
Вычислить ‘W’Работа в электрическом поле — разность потенциальных энергий
Найти
Известно, что:
AW1W2 =
Вычислить ‘A’Потенциал электростатического поля
Найти
Известно, что:
φWq =
Вычислить ‘φ’Напряжение — разность потенциалов
Найти
Известно, что:
Uφ1φ2 =
Работа переноса заряда
Найти
Известно, что:
AqU =
Вычислить ‘A’Потенциал электростатического поля вокруг точечного заряда
Найти
Известно, что:
φkq0εr =
Вычислить ‘φ’Напряжённость электростатического поля
Найти
Известно, что:
EUΔ_d =
Вычислить ‘E’Результирующее электрическое поле
НайтиИзвестно, что:
EE0E1 =
Вычислить ‘E’Электрический момент
Найти
Известно, что:
pql =
Вычислить ‘p’Электрическая ёмкость
Найти
Известно, что:
Cqφ =
Вычислить ‘C’Электрическая ёмкость шара
Найти
Известно, что:
CεRk =
Электрическая ёмкость двух проводников
Найти
Известно, что:
CqU =
Вычислить ‘C’Электрическая ёмкость плоского конденсатора
Найти
Известно, что:
Cεε0Sd =
Вычислить ‘C’Электрическая ёмкость сферического конденсатора
Найти
Известно, что:
Cπεε0R1R2 =
Вычислить ‘C’Потенциальная энергия заряженного плоского конденсатора
Найти
Известно, что:
WqE1d =
Вычислить ‘W’Потенциальная энергия заряженного плоского конденсатора
Найти
Известно, что:
WqEd =
Вычислить ‘W’Потенциальная энергия заряженного плоского конденсатора
Найти
Известно, что:
WqU =
Вычислить ‘W’Потенциальная энергия заряженного плоского конденсатора
Найти
Известно, что:
WCU =
Вычислить ‘W’Потенциальная энергия заряженного плоского конденсатора
Найти
Известно, что:
WqC =
Вычислить ‘W’Потенциальная энергия заряженного плоского конденсатора
Найти
Известно, что:
Wεε0EV =
Вычислить ‘W’Потенциальная энергия заряженного плоского конденсатора
Найти
Известно, что:
Wεε0ESd =
Вычислить ‘W’Плотность энергии электрического поля
Найти
Известно, что:
ω_pWV =
Вычислить ‘ω_p’Плотность энергии электрического поля
Найти
Известно, что:
ω_pε0εE =
Вычислить ‘ω_p’Основные формулы по физике — КВАНТОВАЯ ФИЗИКА
Начало развития квантовой физики связано с решением немецким ученым Максом Планком проблемы излучения абсолютно черного тела. Необходимо знать гипотезу Планка о квантовании энергии осцилляторов и уяснить, что на основании формулы Планка могут быть получены законы Стефана- Больцмана и Вина.
Необходимо знать гипотезу Планка о квантовании энергии осцилляторов и уяснить, что на основании формулы Планка могут быть получены законы Стефана- Больцмана и Вина.
Развитие гипотезы Планка привело к созданию представлений о квантовых свойствах света. Кванты света называются фотонами. С позиций квантовой теории света объясняется такое явление как фотоэффект. Здесь следует знать формулу Эйнштейна для фотоэффекта.
Дальнейшее развитие квантовой физики связано с построением теории строения атома. О сложном строении атома говорят исследования спектров излучения разряженных газов.
Смотрите также основные формулы механике
Таблица сновных формул квантовой физики
|
Физические законы, формулы, переменные |
Формулы квантовой физики |
|||
|
Закон Стефана-Больцмана: σ — постоянная Стефана-Больцмана: |
|
|||
|
Энергетическая светимость (излучательность) серого тела: |
||||
|
Закон смещения Вина: |
||||
|
Импульс фотона: |
||||
|
Энергия фотона: |
||||
|
Формула Эйнштейна для фотоэффекта: |
||||
|
Красная граница фотоэффекта: |
|
|||
|
Сериальные формулы спектра водородоподобного атома |
||||
|
Длина волны де Бройля: где р — импульс частицы. В классическом приближении (при v<<c): p = mv; m — масса частицы; v — скорость частицы; с — скорость света в вакууме. В релятивистском случае (при ): |
|
|||
|
Связь импульса с кинетической энергией Wк в релятивистском приближении: |
||||
|
Плотность вероятности нахождения частицы в соответствующем месте пространства |
||||
|
Волновая функция, описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме |
||||
|
Энергия частицы в бесконечно глубокой одномерной потенциальной яме |
||||
|
Электропроводность собственных полупроводников |
||||
|
Постоянная Холла для полупроводников типа алмаза, германия, кремния |
Формула количества теплоты в физике
Содержание:
- Определение и формула количества теплоты
- Формула расчета теплоты при изменении температуры
- Формула количества теплоты при фазовых переходах
- Единицы измерения количества теплоты
- Примеры решения задач
Определение и формула количества теплоты
Внутреннюю энергию термодинамической системы можно изменить двумя способами:
- совершая над системой работу,
- при помощи теплового взаимодействия.

Передача тепла телу не связана с совершением над телом макроскопической работы. В данном случае изменение внутренней энергии вызвано тем, что отдельные молекулы тела с большей температурой совершают работу над некоторыми молекулами тела, которое имеет меньшую температуру. В этом случае тепловое взаимодействие реализуется за счет теплопроводности. Передача энергии также возможна при помощи излучения. Система микроскопических процессов (относящихся не ко всему телу, а к отдельным молекулам) называется теплопередачей. Количество энергии, которое передается от одного тела к другому в результате теплопередачи, определяется количеством теплоты, которое предано от одного тела другому.
Определение
Теплотой называют энергию, которая получается (или отдается) телом в процессе теплообмена с окружающими телами (средой). Обозначается теплота, обычно буквой Q.
Это одна из основных величин в термодинамике. Теплота включена в математические выражения первого и второго начал термодинамики. Говорят, что теплота – это энергия в форме молекулярного движения.
Говорят, что теплота – это энергия в форме молекулярного движения.
Теплота может сообщаться системе (телу), а может забираться от нее. Считают, что если тепло сообщается системе, то оно положительно.
Формула расчета теплоты при изменении температуры
Элементарное количество теплоты обозначим как $\delta Q$. Обратим внимание, что элемент тепла, которое получает (отдает) система при малом изменении ее состояния не является полным дифференциалом. Причина этого состоит в том, что теплота является функцией процесса изменения состояния системы.
Элементарное количество тепла, которое сообщается системе, и температура при этом меняется от Tдо T+dT, равно:
$$\delta Q=C d T(1)$$
где C – теплоемкость тела. Если рассматриваемое тело однородно, то формулу (1) для количества теплоты можно представить как:
$$\delta Q=c m d T=\nu c_{\mu} d T(2)$$
где $c=\frac{C}{m}$ – удельная теплоемкость тела, m – масса тела,
$c_{\mu}=c \cdot \mu$ — молярная теплоемкость,
$\mu$ – молярная масса вещества,
$\nu=\frac{m}{\mu}$ – число молей вещества.
Если тело однородно, а теплоемкость считают независимой от температуры, то количество теплоты ($\Delta Q$), которое получает тело при увеличении его температуры на величину $\Delta t = t_2 — t_1$ можно вычислить как:
$$\Delta Q=c m \Delta t(3)$$
где t2, t1 температуры тела до нагрева и после. Обратите внимание, что температуры при нахождении разности ($\Delta t$) в расчетах можно подставлять как в градусах Цельсия, так и в кельвинах.
Формула количества теплоты при фазовых переходах
Переход от одной фазы вещества в другую сопровождается поглощением или выделением некоторого количества теплоты, которая носит название теплоты фазового перехода.
Так, для перевода элемента вещества из состояния твердого тела в жидкость ему следует сообщить количество теплоты ($\delta Q$) равное:
$$\delta Q=\lambda d m$$
где $\lambda$ – удельная теплота плавления, dm – элемент массы тела. При этом следует учесть, что тело должно иметь температуру, равную температуре плавления рассматриваемого вещества.
При кристаллизации происходит выделение тепла равного (4).
При этом следует учесть, что тело должно иметь температуру, равную температуре плавления рассматриваемого вещества.
При кристаллизации происходит выделение тепла равного (4).
Количество теплоты (теплота испарения), которое необходимо для перевода жидкости в пар можно найти как:
$$\delta Q=r d m$$
где r – удельная теплота испарения. При конденсации пара теплота выделяется. Теплота испарения равна теплоте конденсации одинаковых масс вещества.
Единицы измерения количества теплоты
Основной единицей измерения количества теплоты в системе СИ является: [Q]=Дж
Внесистемная единица теплоты, которая часто встречается в технических расчетах. [Q]=кал (калория). 1 кал=4,1868 Дж.
Примеры решения задач
Пример
Задание. Какие объемы воды следует смешать, чтобы получить 200 л воды при температуре t=40С, если температура одной массы воды t1=10С, второй массы воды t2=60С?
Решение. Запишем уравнение теплового баланса в виде:
Запишем уравнение теплового баланса в виде:
$$Q=Q_{1}+Q_{2}(1.1)$$
где Q=cmt – количество теплоты приготовленной после смешивания воды; Q1=cm1t1 — количество теплоты части воды температурой t1 и массой m1; Q2=cm2t2— количество теплоты части воды температурой t2 и массой m2.
Из уравнения (1.1) следует:
$$ \begin{array}{l} \mathrm{cmt}=\mathrm{cm}_{1} t_{1}+\mathrm{~cm}_{2} t_{2} \rightarrow \mathrm{mt}=\mathrm{m}_{1} t_{1}+\mathrm{~m}_{2} t_{2} \rightarrow \\ \rightarrow \rho \mathrm{Vt}=\rho V_{1} t_{1}+\rho \mathrm{V}_{2} t_{2} \rightarrow \mathrm{Vt}=V_{1} t_{1}+V_{2} t_{2}(1.2) \end{array} $$
При объединении холодной (V1) и горячей (V2) частей воды в единый объем (V) можно принять то, что:
$$$
V=V_{1}+V_{2}(1. 3)
$$$
3)
$$$
Так, мы получаем систему уравнений:
$$ \left\{\begin{array}{c} V t=V_{1} t_{1}+V_{2} t_{2} \\ V=V_{1}+V_{2} \end{array}\right. $$
Решив ее получим:
$$ \begin{array}{l} V_{1}=\frac{\left(t_{2}-t\right)}{t_{2}-t_{1}} V \\ V_{2}=\frac{\left(t-t_{1}\right)}{t_{2}-t_{1}} V \end{array} $$
Проведем вычисления (это можно сделать, не переходя в систему СИ):
$$ \begin{array}{l} V_{1}=\frac{(60-40)}{60-10} 200=80 \text { (л) } \\ V_{2}=\frac{(40-10)}{60-10} 200=120 \text { (л) } \end{array} $$
Ответ. V1=80 л, V2=120 л.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. {*}\right)
\end{array}
$$
{*}\right)
\end{array}
$$
Ответ. $\Delta Q$=1700 Дж
Читать дальше: Формула напряженности магнитного поля.
Формулы ⚠️ по физике 8 класс: список, пояснения по разделам
Содержание:
- Формулы по физике за 8 класс: основные разделы
-
Тепловые явления
- Закон сохранения энергии
- Формула вычисления количества теплоты
- Формула вычисления количества теплоты при сгорании топлива
- Количество теплоты плавления (кристаллизации)
- Формула вычисления абсолютной влажности
- Вычисление относительной влажности воздуха
- КПД тепловой машины
-
Электрические явления
- Закон Ома для участка цепи
- Вычисление удельного сопротивления проводника
- Законы последовательного соединения проводников
- Законы параллельного соединения проводников
- Вычисление величины заряда
- Нахождение работы электрического тока
- Формула электрической мощности
- Закон Джоуля-Ленца
-
Электромагнитные явления
- Правило правой руки
- Правило буравчика
-
Световые явления
- Закон отражения света
- Закон преломления
- Вычисление абсолютного и относительного показателя преломления вещества
- Оптическая сила линзы
-
Примеры задач с решением
- Задачи из раздела «Тепловые явления»
- Задачи из раздела «Электрические явления»
- Задачи из раздела «Электромагнитные явления»
- Задачи из раздела «Световые явления»
- Расчет оптической силы линзы
Содержание
- Формулы по физике за 8 класс: основные разделы
-
Тепловые явления
- Закон сохранения энергии
- Формула вычисления количества теплоты
- Формула вычисления количества теплоты при сгорании топлива
- Количество теплоты плавления (кристаллизации)
- Формула вычисления абсолютной влажности
- Вычисление относительной влажности воздуха
- КПД тепловой машины
-
Электрические явления
- Закон Ома для участка цепи
- Вычисление удельного сопротивления проводника
- Законы последовательного соединения проводников
- Законы параллельного соединения проводников
- Вычисление величины заряда
- Нахождение работы электрического тока
- Формула электрической мощности
- Закон Джоуля-Ленца
-
Электромагнитные явления
- Правило правой руки
- Правило буравчика
-
Световые явления
- Закон отражения света
- Закон преломления
- Вычисление абсолютного и относительного показателя преломления вещества
- Оптическая сила линзы
-
Примеры задач с решением
- Задачи из раздела «Тепловые явления»
- Задачи из раздела «Электрические явления»
- Задачи из раздела «Электромагнитные явления»
- Задачи из раздела «Световые явления»
- Расчет оптической силы линзы
Формулы по физике за 8 класс: основные разделы
В 8 классе школьники на уроках физики изучают следующие разделы:
- Тепловые явления.

- Электрические явления.
- Электромагнитные явления.
- Световые явления.
Рассмотрим подробно основные законы и формулы каждого из разделов. Дадим все необходимые пояснения к ним.
Тепловые явления
Определение
Явления, которые связаны с изменением температуры тела, приводящей к его нагреванию или охлаждению, называют тепловыми.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В качестве примера можно привести нагревание и охлаждение воздуха, таяние льда, плавление металлов и др.
Закон сохранения энергии
Закон сохранения энергии постулирует, что в природе не происходит возникновения или исчезновения энергии. Энергия существует всегда, просто она превращается из одного вида в другой, передается от одного тела другому, и при этом ее значение сохраняется.
Уравнение, иллюстрирующее закон сохранения механической энергии, выглядит так:
\(E_{k_1}+E_{p_1}=E_{k_2}+E_{p_2}\)
и означает следующее:
Сумма кинетической и потенциальной энергии тел, которые находятся в замкнутой системе и взаимодействуют между собой силами тяготения и упругости, остается постоянной.
В данном уравнении \(E_{k_1}\) и \(E_{k_2}\) — кинетическая энергия тела, \(E_{p_1}\) и \(E_{p_2}\) — потенциальная энергия тела.
Полная механическая энергия (E) будет определяться по формуле:
\(E=E_k+E_p\)
где \(E_k\) — кинетическая энергия, \(E_p\) — потенциальная.
Формула вычисления количества теплоты
Внутренняя энергия тела может изменяться двумя путями:
- за счет совершения работы;
- без совершения работы, за счет теплопередачи.
Определение
Энергия, которую получает или теряет тело при теплопередаче, называется количеством теплоты.
Определяется по формуле:
\(Q=c\times m\times\left(t_2-t_1\right)\)
где Q — количество теплоты, измеряемое в джоулях, c — удельная теплоемкость, m — масса тела, \(t_1\) — начальная, \(t_2\) — конечная температуры.
Формула вычисления количества теплоты при сгорании топлива
Определение
Количеством теплоты при сгорании топлива называется величина, которая равняется количеству энергии, выделяемой при полном сгорании топлива.
Для определения количества теплоты при сгорании топлива необходимо знать удельную теплоту сгорания q — количество теплоты, которое выделяет 1 килограмм топлива при полном сгорании.
Формула выглядит так:
\(Q=q\times m\)
где Q — количество теплоты при сгорании топлива, измеряется в джоулях, m — масса топлива.
Количество теплоты плавления (кристаллизации)
Определение
Количество теплоты плавления или кристаллизации — это физическая величина, которая показывает, какое количество теплоты необходимо для плавления тела при условии, что оно находится в условиях температуры плавления и нормальном атмосферном давлении.
Для определения количества теплоты плавления нужно знать удельную теплоту плавления (\lambda) — величину, показывающую, какое количество теплоты необходимо дать кристаллическому телу массой 1 кг, чтобы при температуре плавления полностью перевести его в жидкое состояние.
Количество теплоты плавления определяется по формуле:
\(Q=\lambda\times m,\)
Количество теплоты кристаллизации находят таким образом:
\(Q=-\lambda\times m\)
где Q — количество теплоты плавления или кристаллизации, измеряется в джоулях, m — масса тела.
Формула вычисления абсолютной влажности
Определение
Влажностью воздуха называется содержание водяного пара в атмосфере, которое возможно за счет непрерывного испарения воды с поверхности водоемов.
Абсолютная влажность (ρ) показывает плотность водяного пара, т.е. сколько граммов водяного пара содержится в воздухе объемом 1 кубический метр при заданных условиях. 3}\).
3}\).
Вычисление относительной влажности воздуха
Определение 6
Относительная влажность воздуха \((\varphi)\) — это отношение абсолютной влажности воздуха (ρ) к плотности насыщенного водяного пара при той же температуре (\(ρ_0\)), выражается в процентах.
Насыщение водяного пара зависит от:
- температуры;
- количества водяных паров;
- давления.
Соответственно, относительную влажность воздуха можно вычислить при помощи формулы:
\(\varphi=\frac p{p_0}\times100\%\)
КПД тепловой машины
С помощью коэффициента полезного действия (КПД) двигателя определяют экономичность различных тепловых двигателей.
Определение
КПД называется отношение совершенной двигателем полезной работы к энергии, полученной от нагревателя.
КПД двигателя находят по формуле:
\(\eta=\frac{Q_1-Q_2}{Q_1}\times100\%\)
где \eta — КПД, выражается в процентах; \(Q_1\) — количество теплоты, полученное от нагревателя, \(Q_2\) — количество теплоты, отданное телом холодильнику.
Электрические явления
Раздел «Электрические явления» учебника 8-го класса рассматривает основные закономерности и параметры, характерные для работы электроцепей.
Закон Ома для участка цепи
В 1827 году немецкий физик Георг Ом вывел и доказал опытным путем зависимость силы тока от напряжения и сопротивления. Эта зависимость называется законом Ома и звучит так: сила тока на участке электрической цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна его сопротивлению.
Формула, отражающая эту зависимость, выглядит так:
\(I=\frac UR\)
где I — сила тока на участке цепи, измеряется в амперах, U — напряжение на участке электроцепи, R — сопротивление участка цепи.
Вычисление удельного сопротивления проводника
Зависимость сопротивления проводника от его размера и материала, из которого он изготовлен, впервые изучил Ом. Он доказал, что сопротивление прямо пропорционально длине проводника, обратно пропорционально площади его поперечного сечения и зависит от материала изготовления. 2 называют удельным сопротивлением вещества (p).
2 называют удельным сопротивлением вещества (p).
Сопротивление проводника определяем по формуле:
\(R=\frac{pl}S\)
где R — сопротивление проводника, измеряется в омах, l — длина проводника, S — площадь сечения.
Законы последовательного соединения проводников
Следующие закономерности справедливы для последовательно соединенных проводников в любом количестве:
\(I=I_1=I_2\)
\(U=U_1+U_2\)
\(R=R_1+R_2\)
где \(I_1, U_1, R_1\) — сила тока, напряжение и сопротивление на одном участке цепи, \(I_2, U_2, R_2\) — сила тока, напряжение и сопротивление на другом участке цепи.
Сила тока измеряется в амперах, напряжение — в вольтах, сопротивление — в омах.
Законы параллельного соединения проводников
Для параллельного соединения действуют следующие закономерности:
\(I=I_1+I_2\)
\(U=U_1=U_2\)
\(R=\frac{R_1\times R_2}{R_1+R_2}\)
где \(I_1, U_1, R_1\)1 — сила тока, напряжение и сопротивление первого участка цепи, \(I_2, U_2, R_2\) — сила тока, напряжение и сопротивление второго участка цепи.
Единицы измерения основных характеристик электроцепи одинаковые при последовательном и параллельном соединениях.
Вычисление величины заряда
Определение
Электрический заряд (q) — это физическая величина, которая описывает особенность частиц или тел выступать источником электромагнитных полей и участвовать в электромагнитном взаимодействии.
Измеряется в кулонах, вычисляется по формуле:
\(q=I\times t, \)
где I — сила, t — время прохождения тока.
Нахождение работы электрического тока
Определение
Работа электрического тока — это физическая величина, которая показывает, какая работа была совершена электрическим полем при перемещении зарядов по проводнику.
Работа электрического тока обозначается символом A, измеряется в джоулях, рассчитывается по формуле:
\(A=U\times I\times t\)
где I — сила тока в проводнике, U — напряжение на концах проводника, t — время протекания тока через проводник. 2\times R\times\Delta t\)
2\times R\times\Delta t\)
где Q — количество теплоты, выделяемое за время \((\Delta t)\), в течение которого ток течет в проводнике, измеряется в джоулях, I — сила тока в проводнике, R — сопротивление проводника.
Электромагнитные явления
Раздел «Электромагнитные явления» разбирает физические процессы, которые связаны с электрическим током и образующимся вокруг него магнитным полем.
Правило правой руки
Определение
Если обхватить проводник с током ладонью правой руки и направить большой палец, отставленный на 90 градусов по направлению силы тока в проводнике, оставшиеся четыре пальца покажут направление линий магнитного поля проводника.
Правило буравчика
Световые явления
В разделе «Световые явления» рассматривается свет, его источники и распространение в пространстве, а также основные физические законы, согласно которым свет распространяется в среде. Рассмотрим подробнее каждый из них.
Рассмотрим подробнее каждый из них.
Закон отражения света
Закон отражения света от зеркальной поверхности звучит так: падающий и отраженный лучи лежат в одной плоскости с перпендикуляром, который проведен к границе раздела двух сред в точке падения луча.
Угол падения alpha равен углу отражения \(\beta\):
\(<\alpha=<\beta\)
Закон преломления
Определение
Преломлением света называется изменение направления светового луча на границе сред при переходе его из одной среды в другую.
Законы преломления света:
- Лучи, падающий и отраженный, лежат в одной плоскости с перпендикуляром, который проведен к границе раздела двух сред в точке падения луча.
- Угол преломления может быть меньше или больше угла падения — в зависимости от того, из какой среды и в какую луч переходит.
Закон открыл в 1621 году голландский математик В. Снеллиус.
Снеллиус.
Вычисление абсолютного и относительного показателя преломления вещества
Определение
Абсолютный показатель преломления вещества (n) — это показатель преломления вещества относительно вакуума.
Он показывает, во сколько раз скорость света в вакууме больше, чем в среде.
Определяется по формуле:
\(n=\frac cv\)
где c — скорость света в вакууме, v — скорость света в данной среде.
Относительный показатель преломления вещества показывает, во сколько раз скорость света в первой среде отличается от скорости во второй среде.
Оптическая сила линзы
Определение
Линзы — это прозрачные тела, созданные для управления световыми лучами с помощью изменения их направления, которые представляют собой ограниченные с двух сторон сферические поверхности.
Линзы характеризует величину, которую называют оптической силой линзы, измеряется в диоптриях (D). 6 \)Дж.
6 \)Дж.
Задача на вычисление абсолютной влажности
Задача
Какой будет абсолютная влажность воздуха, если относительная влажность равна 50% при температуре 20 градусов?
Решение:
Смотрим в таблице, сколько пара может содержаться при температуре 20 градусов. Обнаруживаем значение 17 г. Так как у нас относительная влажность равна 50%, необходимо 17 / 2, получаем 8,5 г/м3. Абсолютная влажность равна 8,5 г/м3.
Задача на вычисление относительной влажности воздуха
Задача
Какой будет относительная влажность при том условии, что при температуре 30 градусов в воздухе содержалось 17 г воды?
Решение:
\(\varphi=17*100/30=56%\)
Задача на вычисление КПД тепловой машины
Задача
Какой КПД у теплового двигателя, который совершил полезную работу 70 кДж, если при полном сгорании топлива выделилась энергия 200 кДж?
Решение:
\(\eta=70/200*100%=35%\)
Задачи из раздела «Электрические явления»
Задача на вычисление удельного сопротивления проводника
Задача
Чему будет равно сопротивление проводника, в котором течет ток силой 600 мА при напряжении на концах 1,2 кВ?
Решение:
\(R=1200/0,6=200 Ом. 2/80*600=363000 \)Дж.
2/80*600=363000 \)Дж.
Для решения задач по правилам правой руки и буравчика, важно знать условные обозначения:
Задачи из раздела «Световые явления»
Задача на вычисление абсолютного показателя преломления вещества
Расчет оптической силы линзы
Задача
Какой будет оптическая сила линз объектива фотоаппарата, если его фокусное расстояние составляет 58 мм?
Решение:
58 мм=0,058 м.
\(D=1/0,058=17,24 дптр.\)
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 4)
ФОРМУЛЫ по физике
p=Fвнешt=mV
A=Fscos
A={S под граф. Fs(s)}
P=A/t=FVcpcos
=Aпол/Aзатр= Pпол/Pзатр
Ek=mV2/2
Ek=A
Eп=mgh
[Пружина] Eп=kx2/2
E=Ek+Eп=const
E=E2-E1=Aвнеш+Aтр
АБС. УПР.УДАР
УПР.УДАР
m1V1-m2V2=-m1U1+m2U2
Ek1+Ek2[до]=Ek1+Ek2[после]
Если m1=m2, то V1=U2 V2=U1
АБС.НЕУПР.УДАР
m1V1-m2V2=(m1+m2)U[m1>m2]
[до] Ek1+Ek2=Ek1
[после] Ek2=0.5(m1V1-m2V2)2/(m1+m2)
Q= Ek1-Ek2
РАВН.ВРАЩЕНИЕ
an=V2/R=2R=(2/T)2R=(2)2R
ТЯГОТЕНИЕ
G=6.67e-11м3/кгс
G=9.81м/с2
F=Gm1m2/r2
[внутри З] g=g0r/R3
[сверху] g=g0R32/(R3+h)2
g0=GMпл/Rпл2
V1косм={g0R}
V2косм=2’V1
СТОЯЧИЕ МОМЕНТЫ
M=Fd
[в 1 точке] M=0
[к 1 телу] F=0
ВОДИЧКА
pатм=1e5Па
p=Fn/s
p=pатм+gh
pстенки=0. 5pдна.ср
5pдна.ср
[пресс] F2=F1S2/S1
[сообщ. cос.] p1=p2
FA=жgVпогр.части
КОЛЕБАНИЯ
0=2
x=Acos(0t+0)
V=x|; a=V|
V0=A0; a0=A02
Ep=kx2/2
E=kA2/2=m02A2/2
МАЯТНИК
T=2/0=2{L/g}
[при движении] T=2{L/|g-a0|}
[если есть F] T=2{L/|g+F/m|}
ПРУЖИНКА
T=2/0=2{m/k}
ГАЗЫ
NA=6.02e23моль-1
[мол. Объем; н.у.] V0=22.4e-3 м3/моль
[больцмана] k=1.38e-23Дж/К
[универ.
газ. const] R=kNA=8. 31Дж/мольК
31Дж/мольК
m1мол=/NA
N=NA/m=NA
=m/
[конц.] n=N/V=NA/
[ср. скорость] Vкв={3kT/m1}={3RT/}
tноль=2730C=1K
p=nkT
p=nm1Vкв2/3=2n/3
[E поступ. движ. мол.] =3kT/2=m1Vкв2/2
(p1+p2…)V=(m1/1+m2/2…)RT
ТЕПЛОЁМК.ГАЗОВ
[t‘ёмкость] C=Q/T
[уд.t’ёмк.] c=C/m
[мол.t’ёмк] C=C/=c
ЗАРЯДЫ
qe=-qp=1.6e-19Кл
me=9.11e-31кг
mp=1.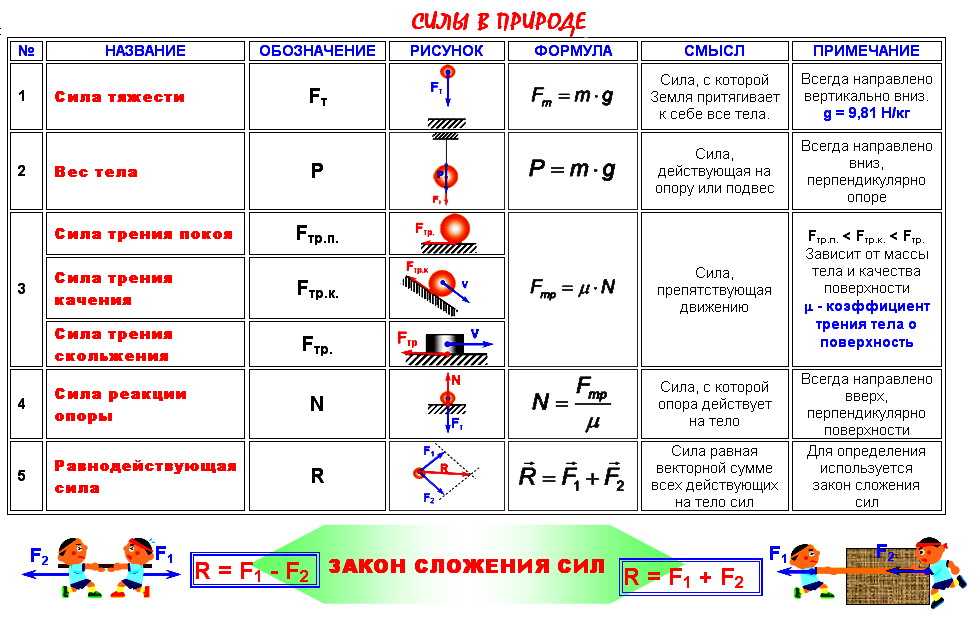 67e-27кг
67e-27кг
0=8.85e-12ф/м
k=(40)-1=9e9м/ф
F=kq1q2/r2
[пов. плотн. q] =q/t;Кл/м2
[напр.] E=F/q
[1заряд] E=kq/r2
[плоскость] E=0.5/0
[внутри сферы] E=0
[вне сферы] E=kq/r2
ПОТЕНЦИЯ
[1заряд] =kq/r
[внутри сферы] =kq/R
[вне сферы] =kq/r
U=1-2=A12/q
[А поля] A=qU
E=U/d
Fk=qE
КОНДЕНСАТОР
C=q/;ф
C=40R
E=/(0)
=U=Ed=qd/(0S)=d/(0)
[плоский] C=0S/d
[послед] C-1=;q=const;U=
[парал] C=;q=;U=const
[провод] W=0. 5q=0.5C2=0.5q2/C
5q=0.5C2=0.5q2/C
[-||-] W=0.5qU=0.5CU2=0.5q2/C
ЗАКОН ОМА
I=q/t
I=[S под I(t)]
[плотность] j=I/sпров=|qe|nV
I=U/R
R=элl/s
[послед] R=;I=const;U=
[парал] R-1=-1;I=;U=const
I=IAmax+Iш
IAmaxRA=IшRш
[расширь шкалу A в n] Rш=RA/(n-1)
UVmaxRдоб=UдобRV
[расширь шкалу V в n] Rдоб=RV(n-1)
=Aст/q0
I=/(R+r)
[ток течет +—]
ТОК И ТЕПЛО
A=qU=iUt
Q=A=I2Rt=U2t/r
P=A/t=IU=2R/(R+r)
[полная] P0=I2(R+r)
[полезная] Pп=I2R=IU=e2R/(R+r)2
=Pп/P0=R/(R+r)
[при
R=r;=50%]
Pп.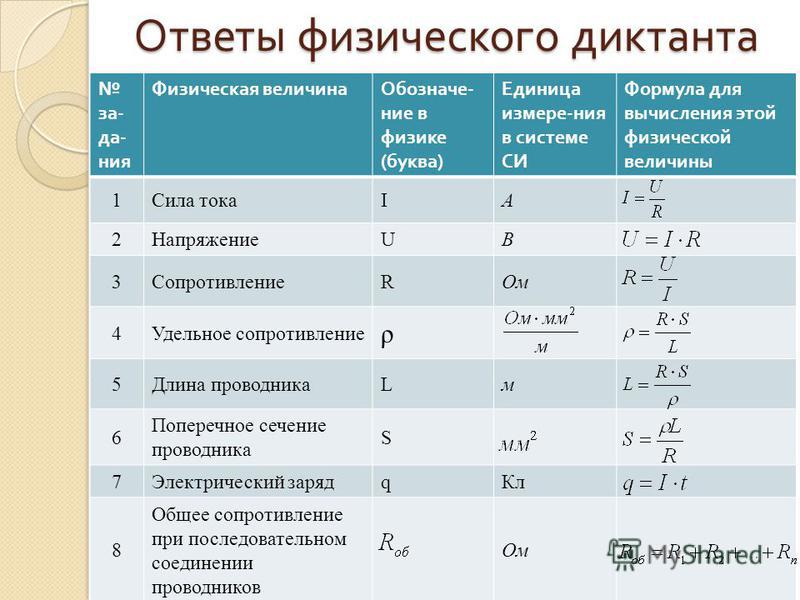 V)
V)
сам=LI
[если L=const] сам=-/t=-LI/t
W=0.5I=0.5LI2=0.52/L
КОНТУР
Umax=qmax/C
[t=0] W=CUmax2/2=0.5qmax2/C
[t=T/4] W=LImax2/2
[t=T/2] q=qmax;U=Umax;I=0
T=2{LC}
=T-1
q=qmaxsin(t+0)
U=q/C=Umaxsin(t+0)
I=q|
[с-скор.света] =cT=c/
ПЕРЕМЕННЫЙ ТОК
=maxsin(t+0)
T=2/
[реактивные] XL=L;XC=(C)-1
[общее] Z={R2+(XL-XC)2}
Iэфф=I0/2
Uэфф=U0/2
ОПТИКА
c=3e8м/с
[Vсвета в вещ-ве] V=c/n
nпадsin(пад)=nпрелsin(прел)
[предел,луч скользит] sinпр=nпрел/nпад
[опт. сила,дптр]
D=F-1
сила,дптр]
D=F-1
[d-предмлинза]
[-изобрлинза]
[F-фок.расст]
±d-1±-1=±F-1
[лин.увел]|/d|=A1B1/AB
Dобщ=
Электромагнетизм в физике: основные формулы
Основные формулы электромагнетизма
Кратность электрического заряда
Здесь q — заряд (Кл), N — число не скомпенсированных элементарных зарядов в заряде q (безразмерное), — элементарный заряд (Кл).
Поверхностная плотность заряда
Здесь — поверхностная плотность заряда , q — заряд на поверхности (Кл), S — площадь этой поверхности .
Закон Кулона
Здесь F — сила взаимодействия точечных зарядов (Н), — коэффициент пропорциональности, и — модули взаимодействующих зарядов (Кл), — относительная диэлектрическая проницаемость среды (безразмерная), —электрическая постоянная, r — расстояние между зарядами (м).
Напряженность электрического поля
Здесь Е — напряженность электрического поля (Н/Кл или В/м), F — сила, действующая на заряд (Н), q — заряд (Кл).
Напряженность поля точечного заряда
Здесь Е — напряженность поля (Н/Кл или В/м), k — коэффициент пропорциональности , q — модуль заряда (Кл), — относительная диэлектрическая проницаемость среды (безразмерная), — электрическая постоянная (Ф/м), r — расстояние от точки с напряженностью Е до заряда q (м).
Напряженность поля бесконечной равномерно заряженной плоскости
Здесь Е — напряженность электрического поля (В/м), — поверхностная плотность зарядов на плоскости , £0— электрическая постоянная (Ф/м), — диэлектрическая проницаемость среды (безразмерная).
Напряженность поля двух разноименно и равномерно заряженных плоскостей с одинаковой поверхностной плотностью зарядов (напряженность поля плоского конденсатора)
Все величины те же, что и в предыдущей формуле.
Работа перемещения заряда в однородном электрическом поле
Здесь А — работа перемещения заряда (Дж), Е — напряженность однородного поля (Н/Кл или В/м), q — перемещаемый заряд (Кл), d — проекция перемещения на силовую линию однородного поля (м).
Потенциал электрического поля
Здесь — потенциал электрического поля (В), — потенциальная энергия заряда (Дж), q — заряд, обладающий этой энергией в электрическом поле (Кл).
Потенциал поля точечного заряда
Все величины те же, что и в аналогичной формуле напряженности.
Разность потенциалов
Здесь — разность потенциалов между двумя точками поля (В), U — напряжение (В), А — работа перемещения заряда (Дж), q — перемещаемый заряд (Кл).
Связь напряженности с разностью потенциалов в однородном электрическом поле
Здесь Е — напряженность электрического поля (Н/Кл или В/м), — разность потенциалов между двумя точками поля (В), U — напряжение между этими точками (В), d — проекция расстояния между этими точками на силовую линию поля (м).
Электроемкость проводника
Здесь С — емкость проводника (Ф), q — заряд проводника (Кл), — его потенциал (В).
Емкость сферического проводника
Здесь С — емкость сферического проводника (Ф), — электрическая постоянная (Ф/м), — относительная диэлектрическая проницаемость среды (безразмерная), R — радиус сферы (м).
Емкость конденсатора
Здесь С — емкость конденсатора (Ф), q — его заряд (Кл), — разность потенциалов между его обкладками (В), U — напряжение между обкладками (В).
Емкость плоского конденсатора
Здесь С — емкость плоского конденсатора (Ф), — электрическая постоянная (Ф/м), — относительная диэлектрическая проницаемость среды (безразмерная), S — площадь обкладок конденсатора , d — расстояние между обкладками (м).
Последовательное соединение конденсаторов
q — одинаков на всех конденсаторах
Если все конденсаторы имеют одинаковую емкость С, то
Здесь q — заряд конденсаторов (Кл), — общее напряжение на батарее конденсаторов (В), — напряжения на отдельных конденсаторах (В), N — число конденсаторов (безразмерное), — общая емкость батареи конденсаторов (Ф), — емкости отдельных конденсаторов (Ф).
Параллельное соединение конденсаторов
U — одинаково на всех конденсаторах
Если все конденсаторы имеют одинаковую емкость С, то
Здесь U — напряжение на конденсаторах (В), — общий заряд батареи конденсаторов (Кл), — заряды отдельных конденсаторов (Кл), N — число конденсаторов (безразмерное), — емкость батареи конденсаторов (Ф), , — емкости отдельных конденсаторов (Ф).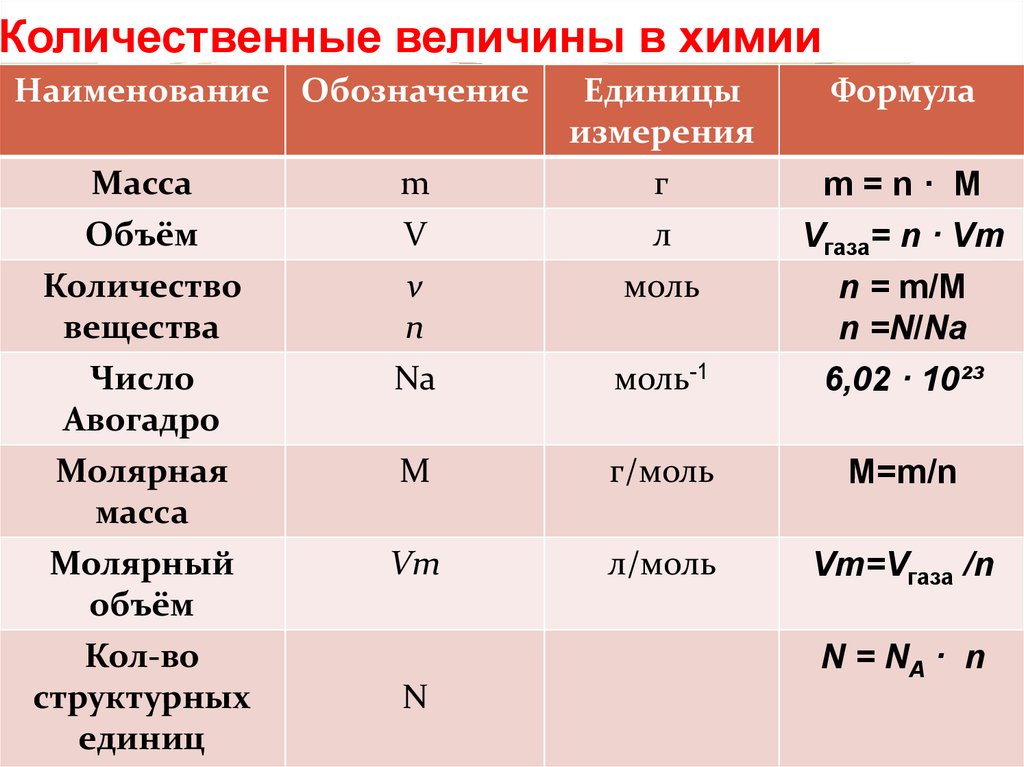
Формулы энергии электрического поля проводника
Здесь — энергия электрического поля (Дж), С — емкость проводника (Ф), — потенциал проводника (В), q — заряд проводника (Кл).
Формулы энергии электрического поля конденсатора
Здесь — энергия электрического поля конденсатора (Дж), С — емкость конденсатора (Ф), q — заряд на его обкладках (Кл), U — напряжение на обкладках конденсатора (В).
Формула энергии системы точечных зарядов
Здесь — энергия системы N точечных зарядов (Дж), — заряды, входящие в систему (Кл), — потенциалы полей, созданных в точке, где находится один из зарядов, остальными зарядами системы (В).
Формулы силы тока
Здесь I — сила постоянного тока (A), q — заряд, прошедший через поперечное сечение проводника (Кл), t — время прохождения заряда (с), n — концентрация свободных электронов , е — модуль заряда электрона (Кл), v — скорость упорядоченного движения электронов по проводнику (м/с), S — площадь поперечного сечения проводника .
Формулы плотности тока
Здесь j — плотность тока , I — сила тока (A), S — площадь поперечного сечения проводника , п — концентрация свободных электронов в проводнике , е — модуль заряда электрона (Кл), v — скорость упорядоченного движения свободных электронов (м/с).
Формулы сопротивления проводника
Здесь R — сопротивление проводника (Ом), U — напряжение на нем (В), I — сила тока в проводнике (А), — удельное сопротивление (Ом • м), l — длина проводника (м), S — площадь поперечного сечения проводника .
Зависимость сопротивления металлического проводника от температуры
Здесь R — сопротивление проводника при температуре t °C (Ом), — сопротивление проводника при О °C (Ом), а — температурный коэффициент сопротивления , t — температура по шкале Цельсия, — изменение абсолютной температуры проводника при нагревании от О °C = 273 К до абсолютной температуры Т (К).
Закон Ома для однородного участка цепи
Здесь I — сила тока (A), U — напряжение (В), R — сопротивление участка (Ом).
Последовательное соединение проводников
I — одинакова во всех проводниках
Если все проводники имеют одинаковое сопротивление, то
для двух последовательных проводников
Здесь I — сила тока (А), — общее напряжение на всех последовательно соединенных проводниках (В), ,…, — напряжения на отдельных проводниках (В), — общее сопротивление всех последовательно соединенных проводников (Ом), — сопротивления отдельных проводников (Ом), N — количество проводников (безразмерное).
Параллельное соединение проводников
U — одинаково на всех проводниках
Если все проводники имеют одинаковое сопротивление, то
общее сопротивление двух параллельных проводников
общее сопротивление трех параллельных проводников
— для двух параллельных проводников
Здесь U — напряжение на проводниках (В), — сила тока в неразветвленном участке цепи (А), — сила тока в отдельных проводниках (А), — общее сопротивление параллельных проводников (Ом), — сопротивления отдельных проводников (Ом), N — количество проводников (безразмерное).
Закон Ома для неоднородного участка цепи
Здесь I — сила тока (А), — разность потенциалов на концах участка (В), — ЭДС, действующая в участке (В), R — сопротивление участка (Ом).
Формула ЭДС
Здесь — ЭДС (В), — работа сторонних сил (Дж), q — перемещаемый заряд (Кл).
Закон Ома для всей цепи
в случае соединенных последовательно одинаковых источников тока
в случае соединенных параллельно одинаковых источников тока
Здесь I — сила тока в цепи (А), — ЭДС источника тока (В), R — сопротивление внешней части цепи (Ом), r — внутреннее сопротивление или сопротивление источника тока (Ом), N — количество одинаковых источников тока (безразмерное).
Сила тока короткого замыкания
при R = О
Все величины названы в предыдущей формуле.
Расчет сопротивления шунта к амперметру
Здесь — сопротивление шунта (Ом), — сопротивление амперметра (Ом), — число, показывающее, во сколько раз измеряемая амперметром сила тока I больше силы тока , на которую он рассчитан (безразмерное число).
Расчет добавочного сопротивления к вольтметру
Здесь — добавочное сопротивление (Ом), — сопротивление вольтметра (Ом), — число, показывающее, во сколько раз измеряемое напряжение U больше напряжения , на которое рассчитан вольтметр (безразмерное число).
Работа тока
Здесь А — работа тока (Дж), U — напряжение на участке цепи (В), I — сила тока в цепи (A), t — время прохождения тока (с), q — прошедший по цепи заряд (Кл), — разность потенциалов на концах участка цепи (В), R — сопротивление участка цепи (Ом), — ЭДС источника тока (В), Р — мощность тока (Вт).
Мощность тока
Здесь Р — мощность тока (Вт), U — напряжение (В), I — сила тока (A), R — сопротивление (Ом), — ЭДС источника тока (В), А — работа тока (Дж), t — время (с).
Закон Джоуля — Ленца
Здесь Q — количество теплоты (Дж). Остальные величины названы в предыдущей формуле.
Коэффициент полезного действия (КПД) электрической цепи
Здесь — КПД электрической цепи (% или безразмерный), U — напряжение на внешнем участке цепи (В), R — сопротивление внешнего участка цепи (Ом), r — внутреннее сопротивление или сопротивление источника тока (Ом), — ЭДС источника тока (В).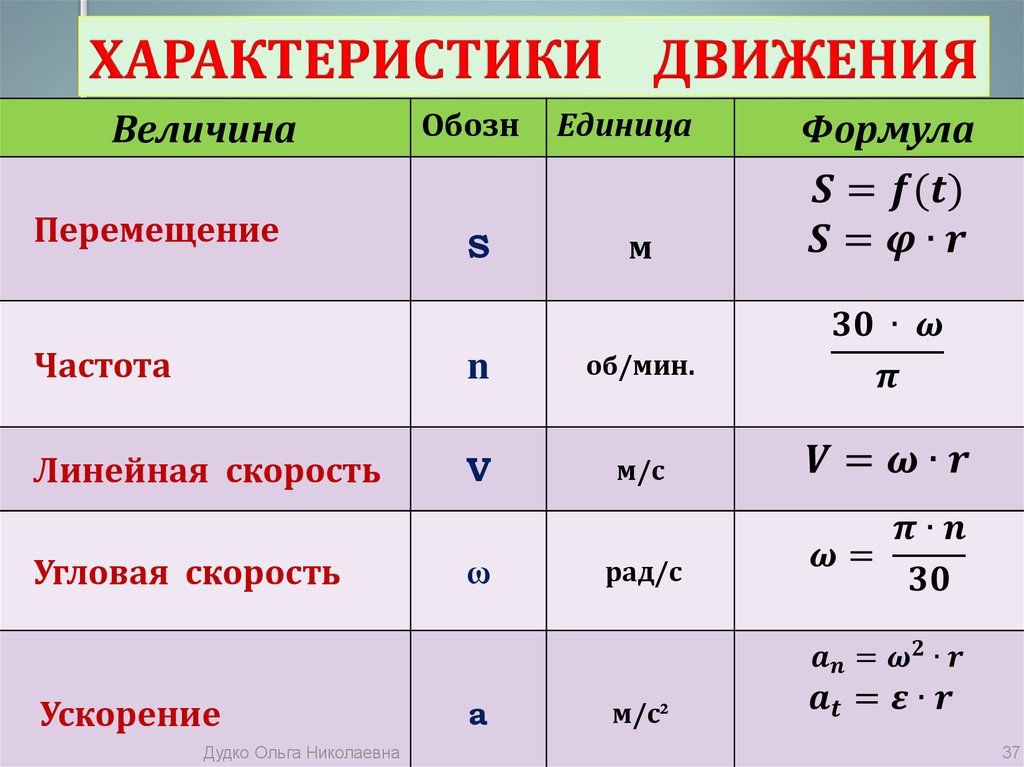
Закон Фарадея для электролиза
Здесь m — масса вещества, выделившегося на электроде (кг), k — электрохимический эквивалент этого вещества (кг/Кл), q — заряд, прошедший через электролит, I — сила тока в электрохимической ванне (A), t — время электролиза (с), F — число Фарадея (Кл/моль), М — молярная масса выделившегося вещества (кг/моль, n — валентность этого вещества (безразмерная).
Формулы индукции магнитного поля
Здесь В — индукция магнитного поля (Тл), — максимальный момент сил, вращающих контур с током в магнитном поле (Н • м), I — сила тока в контуре (A), S — площадь контура — максимальная сила Ампера, действующая на проводник с током в магнитном поле (Н), l — длина проводника в магнитном поле (м).
Формула силы Ампера
Здесь — сила Ампера, действующая на проводник с током в магнитном поле (Н), В — индукция магнитного поля (Тл), I — сила тока в проводнике (А), l — длина проводника в магнитном поле (м), — угол между направлением тока в проводнике и вектором магнитной индукции (рад).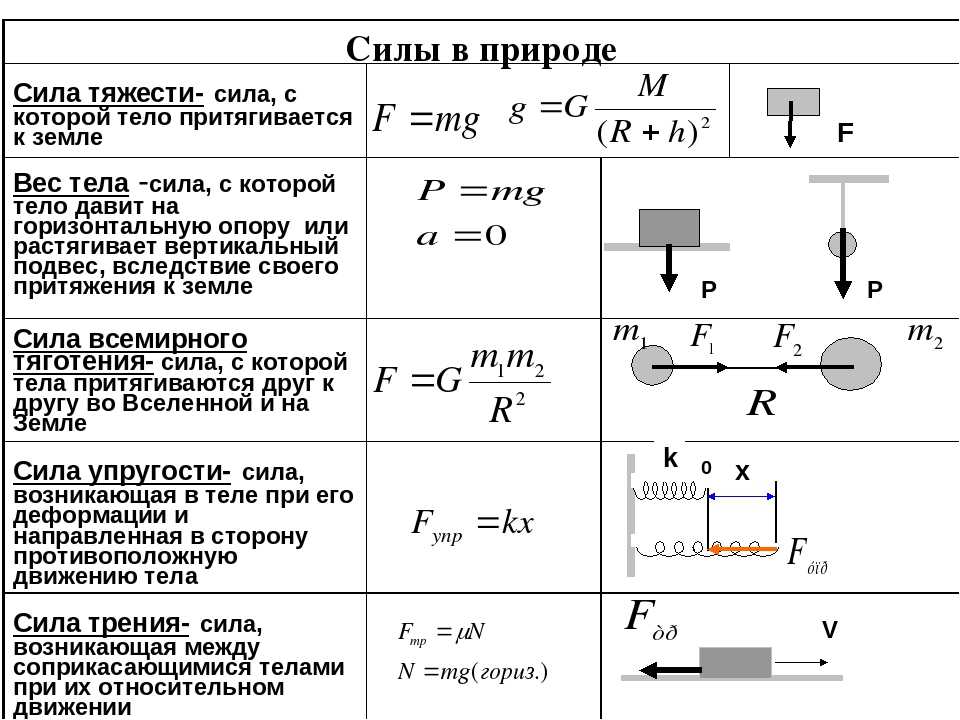
Формула момента сил, вращающих контур с током в магнитном поле
Здесь М — момент сил, вращающих контур с током в магнитном поле (Н • м), В — индукция магнитного поля (Тл), I — сила тока в контуре (A), S — площадь контура — угол между нормалью к плоскости контура и вектором магнитной индукции (рад).
Формула силы Лоренца, действующей на заряд, движущийся в магнитном попе
Здесь — сила Лоренца, действующая на заряд, движущийся в магнитном поле (Н), В — индукция магнитного поля (Тл), q — заряд (Кл), v — скорость заряда (м/с), — угол между векторами магнитной индукции и скорости (рад).
Формула магнитного потока
Здесь Ф — магнитный поток сквозь поверхность (Вб), S — площадь поверхности — угол между нормалью к поверхности и вектором магнитной индукции (рад), L — индуктивность контура (Гн), I — сила тока в контуре (А).
Формула ЭДС электромагнитной индукции
Здесь — ЭДС индукции в контуре (В), — скорость изменения магнитного потока, пересекающего контур (Вб/с), N — число витков в контуре (безразмерное), — первая производная магнитного потока по времени (Вб/с).
Формула ЭДС индукции в проводнике, движущемся поступательно в магнитном поле
Здесь — ЭДС индукции в проводнике (В), В — индукция магнитного поля (Тл), v — скорость проводника в магнитном поле (м/с), l — длина проводника в магнитном поле (м), — угол между векторами скорости и магнитной индукции (рад), — максимальная ЭДС индукции, когда проводник движется перпендикулярно линиям магнитной индукции.
Формула ЭДС индукции в контуре, вращающемся в магнитном поле
Здесь — ЭДС индукции во вращающемся контуре (В), В — индукция магнитного поля (Тл), — угловая скорость вращения (рад/с), S — площадь контура, N — число витков в контуре (безразмерное), — угол между вектором индукции и нормалью к плоскости контура, —максимальная ЭДС индукции, когда угол между нормалью к плоскости контура и вектором магнитной индукции равен 90°, т.е. когда плоскость контура параллельная линиям магнитной индукции.
Формула ЭДС самоиндукции
Здесь — ЭДС самоиндукции в контуре (В), L — индуктивность контура (Гн), — скорость изменения силы тока в контуре (А/с), — первая производная силы тока по времени.
Формула магнитной проницаемости магнетика
Здесь — магнитная проницаемость магнетика (безразмерная), В — индукция магнитного поля в магнетике (Тл), — индукция магнитного поля в вакууме (Тл).
Формула энергии магнитного поля
Здесь — энергия магнитного поля (Дж), L — индуктивность контура (Гн), I — сила тока в контуре (А).
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:
Что на нем и как его использовать
Оба экзамена AP Physics C предоставляют отличный информационный лист с экзаменационным буклетом в день экзамена. Этот информационный лист содержит множество формул и уравнений, которые используются в физике, а это означает, что он может быть чрезвычайно полезен при подготовке и сдаче экзаменов AP Physics C.
На трехстраничном листе с уравнениями, представленном на экзаменах AP Physics C, содержится много информации, поэтому важно ознакомиться с информацией, содержащейся на листе, и узнать, как использовать ее в своих интересах во время экзаменов AP.
Вот почему мы разработали таблицу уравнений PrepScholar AP Physics C. Наш лист содержит все формулы и информацию, которые вы увидите в официальном листе уравнений College Board Physics C, а также пояснения к уравнениям, чтобы вы знали, когда их использовать. Этот лист предназначен для использования в качестве учебного пособия при подготовке к экзамену AP Physics C.
Чтобы еще больше помочь вам в изучении тонкостей справочных таблиц AP Physics C, в этой статье мы также сделаем следующее:
- Объясните, как использовать таблицу уравнений AP Physics C, раздел за разделом
- Дайте три совета по использованию листа уравнений для подготовки к экзаменам AP Physics C
- Дайте три совета по использованию листа уравнений во время реальных экзаменов AP.
Начнем!
Да, верно: на самом деле есть два экзамена AP Physics C. Но изучение нашей таблицы уравнений поможет свести к минимуму это чувство «потери воли к жизни».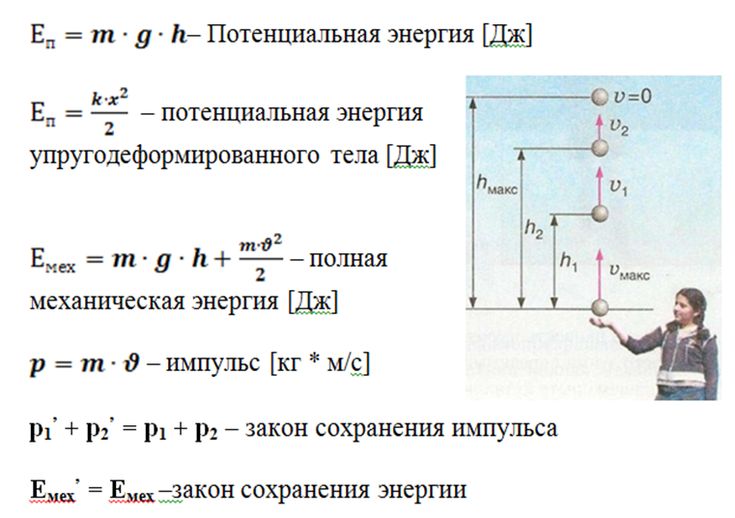 Вероятно.
Вероятно.
Экзамен AP по физике C
На самом деле существует два экзамена AP Physics C: один посвящен механике, а другой — электричеству и магнетизму. Оба экзамена AP Physics C оценивают применение учащимися научных практик, относящихся к основным идеям курса об изменениях, силовых взаимодействиях, полях и сохранении.
В частности, курсы AP Physics C проверяют студентов по следующим темам курса:
AP Физика С: Механика | AP Физика C: Электричество и магнетизм |
Кинематика | Электростатистика |
Законы движения Ньютона | Проводники, конденсаторы, диэлектрики |
Работа, энергия и мощность | Электрические цепи |
Системы частиц и импульса | Магнитные поля |
Вращение | Электромагнетизм |
Колебания | |
Гравитация |
Оба экзамена AP Physics C длятся 1 час 30 минут и состоят из одного раздела с несколькими вариантами ответов и одного раздела со свободным ответом.
Раздел множественного выбора состоит из 35 вопросов и длится 45 минут на обоих экзаменах. Раздел бесплатных ответов на обоих экзаменах AP Physics C состоит из трех вопросов и длится в общей сложности 45 минут. Разделы экзамена с множественным выбором и свободным ответом оцениваются в 50% от общего балла экзамена каждый.
Хорошей новостью является то, что лист уравнений механики AP Physics C и лист уравнений электричества и магнетизма AP Physics C одинаковы , так что вам не нужно будет использовать два разных документа для подготовки к тесту.
Вот как будет выглядеть формуляр, который вы получите в день экзамена!
Лист формул AP Physics C
Лист формул AP Physics C предоставляется сдающим оба экзамена AP Physics C как часть экзаменационного буклета, а лист формул для каждого экзамена то же самое. Лист уравнений, предоставленный во время экзамена, ни в коем случае не является исчерпывающей таблицей физических уравнений, а вместо этого содержит уравнения, обычно используемые в физике, а также константы, коэффициенты преобразования, символы единиц измерения, значения часто используемых функций и префиксы единиц измерения.
Мы предоставили собственную версию формуляра AP Physics C, которая включает всю информацию, указанную в официальном бланке формул AP Physics C, который вы получите при сдаче экзамена. В качестве бонуса наш лист формул содержит дополнительные описания каждого уравнения, которые появляются в официальном листе формул, чтобы помочь вам работать с листом формул во время подготовки к экзамену.
Несмотря на то, что и наш лист формул AP Physics C, и официальный лист формул, предоставленный на экзамене, содержат много информации, которая будет полезна на экзамене, важно помнить, что таблица формул предназначена для дополнения — она не предназначена для глубокого и тщательного понимания физики, связанной с каждой задачей теста. Имея это в виду, продолжайте читать, чтобы узнать, как правильно использовать информацию, представленную в каждом разделе листа формул AP Physics C, когда вы действительно сдаете экзамен.
Как использовать формулы на листе уравнений AP Physics C
Лист формул AP Physics C состоит из нескольких страниц и занимает разделен на пять разделов: константы и коэффициенты преобразования, префиксы, символы единиц измерения, значения тригонометрических функций для обычных углов и уравнения.
Раздел уравнений листа формул является самым длинным и разделен на подразделы в зависимости от типа формулы. Подразделы в части уравнений информационного листа — это механика, электричество и магнетизм, геометрия и тригонометрия, а также исчисление. Каждый раздел листа с формулами также можно использовать для разных целей на экзамене.
Давайте подробнее рассмотрим каждый из основных разделов ниже.
Константы и коэффициенты преобразования
Константы и коэффициенты преобразования, включенные в лист формул AP Physics C, будут полезны при выполнении различных расчетов на экзамене AP. Эти величины, иногда называемые «физическими константами» или «универсальными константами», известны тем, что имеют неизменное значение независимо от контекста в природе.
В таблицу формул включены следующие константы:
- Масса протона
- Масса нейтрона
- Масса электрона
- Номер Авогадро
- Универсальное содержание газа
- постоянная Больцмана
- Величина заряда электрона
- 1 электрон-вольт
- Скорость света
- Универсальная гравитационная постоянная
- Ускорение силы тяжести на поверхности Земли
- 1 единая атомная единица массы
- постоянная Планка
- Вакуумная диэлектрическая проницаемость
- Постоянная закона Кулона
- Вакуумная проницаемость
- Магнитная постоянная
- давление 1 атмосфера
Некоторые константы не имеют единиц измерения, но те константы, которые имеют единицы измерения, возможно, потребуется преобразовать и выразить в других единицах измерения на экзамене.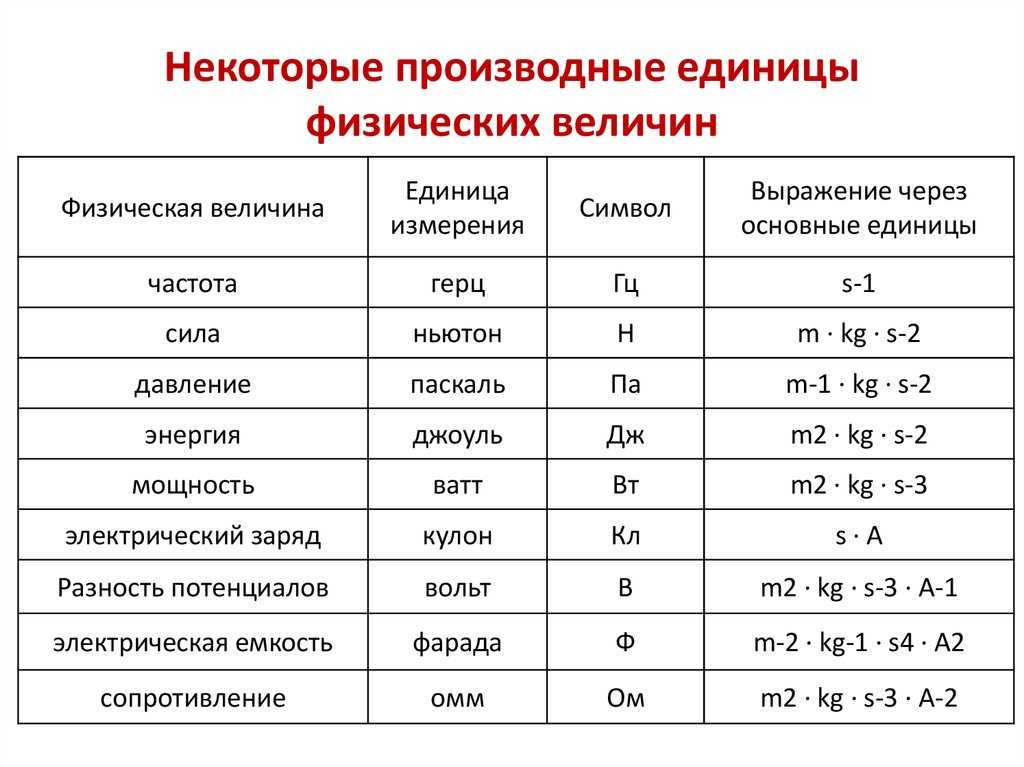 Вот где коэффициенты преобразования пригодятся на экзамене. Коэффициенты преобразования, включенные в таблицу уравнений, можно использовать для преобразования констант из одних единиц в другие посредством умножения или деления.
Вот где коэффициенты преобразования пригодятся на экзамене. Коэффициенты преобразования, включенные в таблицу уравнений, можно использовать для преобразования констант из одних единиц в другие посредством умножения или деления.
Префиксы, обозначения единиц измерения и тригонометрические функции для общих углов
С экзамен. Префикс сочетается со словом, обозначающим конкретную единицу измерения, чтобы выразить значение или измерение, когда вы отвечаете на экзаменационные вопросы, , например, килограмм (префикс) и грамм (единица измерения), или гига (префикс) и ватт (значение Ед. изм). Если вы не можете вспомнить значение (в десятках тысяч!) определенного префикса, таблица префиксов на листе формул может помочь освежить вашу память.
В таблице префиксов также указан символ для каждого префикса, который можно комбинировать с правильным символом единицы при ответе на экзаменационные вопросы . Например, правильно указывать значение в миллисекундах 90 257 или 90 258 мс и в гигагерцах 90 257 или 90 258 ГГц.
Например, правильно указывать значение в миллисекундах 90 257 или 90 258 мс и в гигагерцах 90 257 или 90 258 ГГц.
И, наконец, таблица префиксов также предоставляет коэффициент или научное обозначение для каждого префикса. Они отображаются как число 10 с показателем степени, например 10 9 или 10 12 . Вы можете рассчитывать на то, что на экзамене AP Physics C вы сможете выразить самые большие и самые маленькие измерения, используя экспоненциальную запись.
Последний раздел на первой странице таблицы уравнений содержит тригонометрические функции для обычных углов. Они пригодятся при решении задач по геометрии, тригонометрии и исчислению на экзамене AP. В таблице представлены значения sin, cos и tan в различных степенях, которые вы можете использовать для быстрой справки при решении задач на тесте AP Physics C.
Уравнения
Большая часть таблицы формул, которую вы получите во время экзаменов AP Physics C, содержит распространенные уравнения, используемые в физике. Эти уравнения разбиты на следующие области: механика, электричество и магнетизм, геометрия и тригонометрия.
Эти уравнения разбиты на следующие области: механика, электричество и магнетизм, геометрия и тригонометрия.
Каждый раздел уравнений также содержит ключ с символами, который поможет вам вспомнить, что означает каждый символ в данном уравнении. Кроме того, хотя это не включено в официальный лист формул, который вы получите во время экзамена AP Physics C, наша версия листа формул содержит краткое объяснение каждого уравнения и того, как его можно использовать во время экзамена.
Уравнения механики
Раздел таблицы уравнений AP Physics C содержит 31 часто используемое уравнение механики. Эти уравнения можно использовать для определения, описания, расчета и определения на экзамене следующего:
- Кинематические соотношения, угловые кинематические соотношения
- Импульс, полный импульс, угловой момент для вращающегося объекта и импульс для одиночного объекта, движущегося с некоторой скоростью
- Импульс
- Сила, сила трения, работа, совершаемая над объектом силой, и сила тяжести
- Кинетическая энергия, кинетическая энергия вращающегося объекта,
- Потенциальная энергия, потенциальная энергия пружинящего объекта и гравитационная потенциальная энергия
- Мощность
- Крутящий момент
- Момент инерции
- Простое гармоническое движение
Уравнения электричества и магнетизма
Следующая таблица на листе формул включает 29 общих уравнений электричества и магнетизма. Эти уравнения можно использовать для определения, определения, описания и расчета следующих параметров во время экзамена:
Эти уравнения можно использовать для определения, определения, описания и расчета следующих параметров во время экзамена:
- Величина электростатической силы
- Электрические поля и свойства электрических полей
- Разность потенциалов, потенциал за счет множественных точечных зарядов и электростатическая потенциальная энергия
- Конденсаторы и емкости
- Сопротивление, эквивалентное сопротивление и определение мощности или скорости тепловых потерь через резистор
- Токи и плотность тока
- Магнитная сила, магнитные поля и магнитный поток
Ищете помощь в подготовке к экзамену AP?
Наши индивидуальные услуги онлайн-репетиторов AP помогут вам подготовиться к экзаменам AP. Найди лучшего репетитора, получившего высокий балл на экзамене, к которому ты готовишься!
Формулы, связанные с законами
В разделе электричества и магнетизма также представлены формулы, связанные со следующими законами:
- Закон Кулона
- Закон Гаусса
- Закон Ома
- Закон Ампера
- Закон Био-Савара
- Закон Фарадея
Геометрические и тригонометрические функции
Наконец, таблица из 14 геометрических и тригонометрических функций на листе уравнений может быть использована для расчета следующего на экзамене AP по физике C: 9018 а области С 90 прямоугольник
Лист уравнений AP Physics C охватывает много идей и практик, относящихся к физике, поэтому важно хорошо разобраться с тем, что содержится на листе уравнений, и подумать, как лучше всего использовать его в качестве ресурса при подготовке и сдаче экзамена. экзамен.
экзамен.
Продолжайте читать наши советы о том, как использовать таблицу уравнений для подготовки к экзамену AP Physics C!
3 совета по использованию листа формул AP Physics C в качестве учебного пособия стоит просмотреть перед сдачей экзамена. Вот три совета по использованию таблицы уравнений в качестве учебного пособия!
Совет 1. Практикуйтесь в преобразованиях
Чем быстрее вы сможете правильно выполнять задания на экзамене AP, тем больше времени у вас будет на проверку своей работы и правильность ответов. Использование листа уравнений для практики обычных преобразований во время подготовки к экзамену может помочь вам выполнять преобразования, даже не обращаясь к листу формул во время экзамена.
А поскольку время теста AP Physics C ограничено, каждая сэкономленная секунда на счету!
Решая несколько практических задач, специально требующих преобразования, и используя таблицу уравнений, вы легче вспомните распространенные переводные коэффициенты в день экзамена.
Совет 2. Выберите специальные практические вопросы
Если вы знаете, что вам трудно запомнить или правильно использовать определенные уравнения, которые появляются в справочных таблицах AP Physics C, возможно, стоит немного попрактиковаться с ними. перед сдачей экзамена. Вам придется использовать уравнения, которые включены в формуляр во время фактического экзамена, , так что освежение тех, с которыми у вас проблемы, поможет вам более эффективно использовать свое время.
Чтобы освоиться с некоторыми из этих сложных для запоминания уравнений, попробуйте выбрать конкретные вопросы прошлых AP, которые требуют от вас использования этих уравнений. Потренируйтесь отвечать на вопросы, используя уравнения, а затем проверьте свою работу, чтобы убедиться, что вы используете их правильно. Это позволит вам хорошо разбираться в большинстве уравнений, с которыми вы можете столкнуться на реальном экзамене.
Совет 3.
 Запомните символы
Запомните символы Возможно, вам будет трудно запомнить все уравнения, представленные в справочных таблицах AP Physics C (их более 90!), но вы, вероятно, сможете запомнить, что означает каждый символ. за. Различные таблицы уравнений, представленные на листе уравнений, содержат ключ символов, который указывает, что означает каждый символ, используемый в уравнении.
Запоминание значений различных символов может помочь вам быстро интерпретировать формулы, переменные и константы, которые упоминаются в экзаменационных вопросах, что позволит вам тратить меньше времени на просмотр таблицы уравнений во время теста.
Если вы будете следовать нашим советам, вы не почувствуете себя так в день экзамена. Но на всякий случай вот несколько дополнительных советов, которые помогут вам успешно сдать экзамен AP Physics C.
3 Советы по использованию листа уравнений AP Physics C в день экзамена
Правильное использование листа уравнений и во время, отведенное на экзаменах AP Physics C, имеет решающее значение для получения хорошей оценки. Прочтите наши три совета по использованию листа формул AP Physics в день экзамена!
Прочтите наши три совета по использованию листа формул AP Physics в день экзамена!
Совет 1. Эффективно распоряжайтесь своим временем
Идеальным способом использования справочных таблиц AP Physics C является просто краткое руководство для тренировки памяти. Вы не хотите тратить драгоценное время на изучение таблиц и символов во время экзамена. Вместо этого быстро перейдите к листу уравнений, чтобы сослаться на значение или уравнение, которое вы не можете вспомнить навскидку.
Совет 2. Быстрые преобразования
Лист уравнений будет особенно полезен для выполнения преобразований и запоминания правильных выражений для общих констант на протяжении всего экзамена. Значения констант и коэффициентов преобразования, включенные в лист уравнений, длинные и сложные, и их может быть трудно запомнить для экзамена. Обращаясь к листу уравнений, чтобы помочь вам в выполнении преобразований, вы сможете эффективно использовать свое время и убедиться, что ваши преобразования правильные.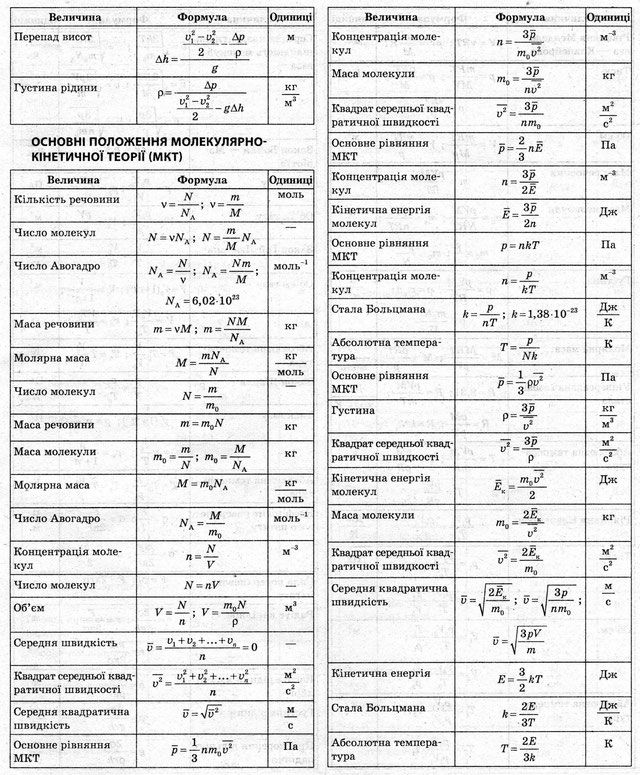
Совет 3. Проверьте свою работу и внесите изменения
Если у вас есть дополнительное время в конце экзамена AP Physics C, используйте это время, чтобы просмотреть свою работу и внести необходимые исправления. Когда вы проверяете свою работу, держите лист уравнений под рукой и проверяйте все значения, формулы и уравнения по листу. Легко случайно пропустить важный показатель степени или символ, который может полностью изменить смысл ваших ответов, особенно в вопросах с бесплатным ответом. Проверка вашей работы на листе уравнений может помочь вам выявить и исправить эти ошибки и максимизировать ваш балл.
Дальнейшие действия
Если вы ищете дополнительные ресурсы, которые помогут изучить некоторые сложные концепции AP Physics C, заметки к курсу IB Physics могут оказаться очень полезными. Они подробно охватывают одни и те же темы и могут помочь пролить свет на идеи и концепции, с которыми вы боретесь. Вы можете найти наш полный список лучших учебных заметок IB Physics здесь.
Вы можете найти наш полный список лучших учебных заметок IB Physics здесь.
Нужна дополнительная информация о том, как пошагово рассчитать ускорение? Здесь мы рассмотрим различные формулы, необходимые для определения различных видов ускорения.
Хотите знать, стоит ли вам сдавать AP Physics C? Ну, все зависит от ваших целей! В этой статье вы узнаете, как выбрать классы AP, которые подходят именно вам.
Хотите улучшить свой результат SAT на 160 баллов или свой результат ACT на 4 балла? Для каждого теста мы составили руководство по 5 основным стратегиям, которые вы должны использовать, чтобы попытаться улучшить свой результат. Загрузите его бесплатно прямо сейчас:
У вас есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделись этой статьей!
Эшли Робинсон
Об авторе
Эшли Саффле Робинсон имеет докторскую степень. в английской литературе XIX века. Как автор контента для PrepScholar, Эшли стремится предоставить учащимся, направляющимся в колледж, подробную информацию, необходимую им для поступления в школу своей мечты.
в английской литературе XIX века. Как автор контента для PrepScholar, Эшли стремится предоставить учащимся, направляющимся в колледж, подробную информацию, необходимую им для поступления в школу своей мечты.
AP Physics C Equations Sheet Later
Оба теста AP Physics (C) включают удобную информационную страницу с экзаменационным пакетом в день экзамена. Этот информационный листок переполнен физическими формулами и уравнениями, что делает его очень ценным для изучения и сдачи экзаменов AP по физике (C).
Трехстраничный лист уравнений, представленный на тестах AP по физике (C), содержит много информации. Крайне важно знать материал на листе и знать, как использовать его в своих интересах во время экзаменов AP.
В этом учебном пособии мы также выполним следующие действия, чтобы помочь вам в изучении деталей справочных таблиц по физике AP (C):
- Приведите три индикатора использования листа уравнений для подготовки к экзаменам по физике AP (C).
- Назовите три показателя использования листа уравнений во время тестов AP.

- По частям объясните, как использовать таблицу уравнений AP Physics (C).
Из-за пандемии коронавируса COVID-19 экзамены AP теперь будут проводиться в три сессии в период с мая по июнь. Даты ваших экзаменов и то, будут ли они онлайн или оффлайн, будут определяться вашей школой.
Экзамен AP Phy (C)
Существует два экзамена AP по физике (C):
● Один посвящен механике
● Другой посвящен магнетизму и электричеству.
Оба теста AP по физике (C) исследуют применение учащимися научных процессов, связанных с великими понятиями изменения, полей, силовых взаимодействий и сохранения. По курсам АП физики (С) студенты сдают ЕГЭ по следующим темам:
| Магнетизм и электричество | Механика |
| Электрические цепи | Кинематика |
| Проводники, диэлектрики, конденсаторы, 9 шт.0053 | Гравитация |
| Электростатика | Энергия, работа и мощность |
| Магнитные поля | Системы импульса и частиц |
| Электромагнетизм | Вращение |
| Колебания | |
| Законы движения Ньютона |
Оба теста по физике AP (C) длятся 1 час 30 минут. Он включает в себя один раздел бесплатных ответов и один вопрос с несколькими вариантами ответов. Часть MCQ состоит из 35 вопросов по обоим тестам и длится 45 минут. Часть со свободным ответом состоит из трех вопросов по обоим тестам AP по физике (C). Он длится 45 минут. Бесплатные ответы и части с несколькими вариантами ответов составляют половину общего балла. Хорошая новость заключается в том, что таблица уравнений магнетизма и электричества AP-физики (C) и таблица уравнений механики AP-физики (C) идентичны. Поэтому вам не придется учиться по двум разным документам.
Он включает в себя один раздел бесплатных ответов и один вопрос с несколькими вариантами ответов. Часть MCQ состоит из 35 вопросов по обоим тестам и длится 45 минут. Часть со свободным ответом состоит из трех вопросов по обоим тестам AP по физике (C). Он длится 45 минут. Бесплатные ответы и части с несколькими вариантами ответов составляют половину общего балла. Хорошая новость заключается в том, что таблица уравнений магнетизма и электричества AP-физики (C) и таблица уравнений механики AP-физики (C) идентичны. Поэтому вам не придется учиться по двум разным документам.
Лист уравнений
Лист формул AP Phy (C) включен в экзаменационный буклет для всех участников экзамена AP Physics (C). Лист уравнений для каждого экзамена одинаков. Лист уравнений, предоставленный во время экзамена, не является полной таблицей физических уравнений. Он содержит уравнения, в основном используемые в константах, физике, коэффициенты преобразования, значения наиболее часто используемых функций, символы и префиксы.
Как пользоваться формулами таблицы уравнений
Таблица формул AP-физики (C) состоит из пяти разделов:
- Префиксы
- Уравнения
- Символы единиц измерения
- Константы и коэффициенты пересчета
- Значения тригонометрических функций для типичных углов
Часть уравнений таблицы формул самая длинная. Он разделен на подразделы на основе формулы. Подразделы уравнений информационного листа включают электричество и магнетизм, механику, геометрию и тригонометрию, а также исчисление. Каждая область листа с формулами также может использоваться для различных целей в тесте.
Коэффициенты пересчета и константы
Коэффициенты пересчета и константы на листе формул физики AP (C) пригодятся при выполнении различных расчетов теста AP. Эти значения, часто называемые «универсальными константами» или «физическими константами», отличаются постоянным значением в природе независимо от ситуации.
Константы, включенные в таблицу формул, следующие:
- Масса протона
- Вакуумная диэлектрическая проницаемость
- Постоянная закона Кулона
- Номер Авогадро
- Универсальная газовая постоянная
- Масса нейтрона
- Масса электрона
- Постоянная Больцмана
- Величина заряда электрона
- Универсальная гравитационная постоянная
- Ускорение силы тяжести на поверхности Земли
- Один электрон-вольт
- Скорость света
- Одна унифицированная атомная единица массы
- постоянная Планка
- Вакуумная проницаемость
- Магнитная постоянная
- Давление в одну атмосферу
Некоторые константы не имеют единиц измерения, но те, у которых они есть, могут нуждаться в преобразовании и представлении в других единицах измерения теста. В тесте будут использоваться коэффициенты преобразования. Коэффициенты преобразования на листе могут изменять константы из одной части в другую путем их деления или умножения.
В тесте будут использоваться коэффициенты преобразования. Коэффициенты преобразования на листе могут изменять константы из одной части в другую путем их деления или умножения.
Уравнения электричества и магнетизма
Следующая таблица таблицы формул содержит 29 типичных уравнений электричества и магнетизма. Во время теста эти уравнения можно использовать для определения, определения, описания и вычисления следующего:
- Емкость и конденсаторы
- Сопротивление, эквивалентное сопротивление и определение мощности или скорости тепловых потерь через резистор
- Электрические поля и свойства электрических полей
- Разность потенциалов, потенциал за счет множественных точечных зарядов и электростатическая потенциальная энергия
- Величина электростатической силы
- Токи и плотность тока
- Магнитные поля, магнитная сила и магнитный поток
Уравнения в механике
Лист уравнений AP-физики (C) содержит 31 широко используемое уравнение механики. На тесте эти уравнения могут использоваться для определения, описания, расчета и определения следующего:
На тесте эти уравнения могут использоваться для определения, описания, расчета и определения следующего:
- Кинематические зависимости и угловые кинематические зависимости
- Потенциальная энергия, потенциальная энергия пружинящего объекта и гравитационная потенциальная энергия
- Мощность
- Импульс, угловой момент для вращающегося объекта, общая скорость и импульс для одного объекта, движущегося с некоторой скоростью
- Импульс
- Работа, совершаемая над объектом силой, силой трения и силой тяжести
- Кинетическая энергия и кинетическая энергия вращающегося объекта,
- Крутящий момент
- Момент инерции
- Простое гармоническое движение
Тригонометрические и геометрические функции
Наконец, таблицу уравнений, содержащую 14 тригонометрических и геометрических функций, можно использовать для вычисления следующего для экзамена по физике AP (C):
- Площадь треугольника
- Площадь, окружность и длина дуги окружности
- Площадь прямоугольника
- Объем и площадь поверхности шара
- Объем прямоугольного твердого тела
- Объем и площадь поверхности цилиндра
- Формулы для определения величины углов прямоугольного треугольника
Формулы, относящиеся к законам
Раздел по электричеству и магнетизму также включает формулы для следующих законов:
- Закон Ома
- Закон Ампера
- Закон Кулона
- Закон Гаусса
- Закон Био-Савара
- Закон Фарадея
Символы общепринятых угловых единиц, префиксы и тригонометрические функции
Таблица символов и префиксов единиц поможет вам подготовиться к экзамену AP по физике (C). При ответе на вопросы теста префикс сочетается с термином для определенной единицы измерения, чтобы описать число или измерение, например, гига (префикс) и ватты (единицы) или кило (префикс) и граммы (единицы). Если вы не можете вспомнить значение определенного префикса, страница формул может помочь вам с приведенной таблицей.
При ответе на вопросы теста префикс сочетается с термином для определенной единицы измерения, чтобы описать число или измерение, например, гига (префикс) и ватты (единицы) или кило (префикс) и граммы (единицы). Если вы не можете вспомнить значение определенного префикса, страница формул может помочь вам с приведенной таблицей.
Таблица префиксов также включает символ для каждого префикса, который может сочетаться со знаком правильной единицы для ответов на вопросы теста. Например, допустимо указывать значение в гигагерцах (ГГц) или миллисекундах (мс). Наконец, таблица префиксов включает коэффициент или научное обозначение для каждого префикса. Они представлены числом 10 плюс показатель степени, 1012 или 109. Вы можете ожидать использования экспоненциальной записи для представления наименьшего и наибольшего измерений в тесте AP-физики (C).
Тригонометрические функции для обычных углов приведены в последнем разделе на первой странице листа уравнений. Они будут полезны для задач AP-тригонометрии, геометрии и исчисления. В таблице представлены значения cos, sin и tan в различных степенях, которые вы можете использовать в качестве быстрой справки при решении задач на экзамене AP по физике (C).
В таблице представлены значения cos, sin и tan в различных степенях, которые вы можете использовать в качестве быстрой справки при решении задач на экзамене AP по физике (C).
Уравнения
Большая часть таблицы формул, которую вы получите во время экзамена по физике AP (C), содержит стандартные физические уравнения. Эти уравнения классифицируются как механика, электричество и магнетизм, геометрия и тригонометрия. Кроме того, каждый раздел уравнений содержит ключ с символами, который поможет вам вспомнить, что представляет каждый символ в конкретном уравнении.
Лист уравнений AP Physics (C) включает в себя множество физических практик и концепций. Следовательно, очень важно ознакомиться с тем, что находится на листе, и определить, как вы эффективно используете его в качестве ресурса при подготовке и сдаче теста.
18.3 Электрическое поле — физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Вычислять напряженность электрического поля
- Создание и интерпретация рисунков электрических полей
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (5) Учащийся знает природу сил в физическом мире.
 Ожидается, что студент:
Ожидается, что студент:- (С) описать и рассчитать, как величина электрической силы между двумя объектами зависит от их зарядов и расстояния между ними.
Основные термины раздела
| электрическое поле | испытательный заряд |
Поддержка учителей
Поддержка учителей
Спросите учащихся, видели ли они фильмы, в которых используется концепция полей как силовых полей . Попросите их описать, как работают такие поля. Опишите, как можно рассматривать гравитацию как поле, которое окружает массу и с которым взаимодействуют другие массы. Объясните, что электрические поля очень похожи на гравитационные поля.
Возможно, вы слышали о силовом поле в научно-фантастических фильмах, где такие поля применяют силы в определенных точках в космосе, чтобы удерживать злодея в ловушке или защищать космический корабль от вражеского огня. Концепция поля очень полезна в физике, хотя она несколько отличается от того, что вы видите в кино.
Концепция поля очень полезна в физике, хотя она несколько отличается от того, что вы видите в кино.
Поле — это способ концептуализации и отображения силы, которая окружает любой объект и действует на другой объект на расстоянии без видимой физической связи. Например, гравитационное поле, окружающее Землю и все другие массы, представляет гравитационную силу, которая возникла бы, если бы в данной точке поля была помещена другая масса. Майкл Фарадей, английский физик девятнадцатого века, предложил концепцию электрического поля. Если вы знаете электрическое поле, то можете легко рассчитать силу (величину и направление), действующую на любой электрический заряд, который вы поместите в поле.
Электрическое поле создается электрическим зарядом и сообщает нам силу на единицу заряда во всех точках пространства вокруг распределения заряда. Распределение заряда может быть одноточечным; распределение заряда, скажем, по плоской пластине; или более сложное распределение заряда. Электрическое поле распространяется в пространстве вокруг распределения заряда. Теперь рассмотрите возможность размещения пробного заряда в поле. Пробный заряд — это положительный электрический заряд, заряд которого настолько мал, что не возмущает существенно заряды, создающие электрическое поле. Электрическое поле действует на пробный заряд в заданном направлении. Приложенная сила пропорциональна заряду пробного заряда. Например, если мы удвоим заряд пробного заряда, сила, действующая на него, удвоится. Математически говоря, что электрическое поле представляет собой силу на единицу заряда, записывается как
Электрическое поле распространяется в пространстве вокруг распределения заряда. Теперь рассмотрите возможность размещения пробного заряда в поле. Пробный заряд — это положительный электрический заряд, заряд которого настолько мал, что не возмущает существенно заряды, создающие электрическое поле. Электрическое поле действует на пробный заряд в заданном направлении. Приложенная сила пропорциональна заряду пробного заряда. Например, если мы удвоим заряд пробного заряда, сила, действующая на него, удвоится. Математически говоря, что электрическое поле представляет собой силу на единицу заряда, записывается как
E→=F→qtestE→=F→qtest
18.15
где мы рассматриваем только электрические силы. Обратите внимание, что электрическое поле представляет собой векторное поле, направленное в том же направлении, что и сила, действующая на положительный пробный заряд. Единицы электрического поля N/C.
Если электрическое поле создается точечным зарядом или сферой с однородным зарядом, то величина силы между этим точечным зарядом Q и пробным зарядом определяется законом Кулона
F=k|Qqtest|r2F =k|Qqtest|r2
, где используется абсолютное значение, потому что мы учитываем только величину силы. Тогда величина электрического поля равна
Тогда величина электрического поля равна
E=Fqtest=k|Q|r2.E=Fqtest=k|Q|r2.
18,16
Это уравнение дает величину электрического поля, создаваемого точечным зарядом Q . Расстояние r в знаменателе — это расстояние от точечного заряда Q или от центра сферического заряда до интересующей точки.
Если тестовый заряд удалить из электрического поля, электрическое поле все еще существует. Чтобы создать трехмерную карту электрического поля, представьте себе размещение пробного заряда в разных местах поля. В каждом месте измерьте силу, действующую на заряд, и используйте векторное уравнение E→=F→/qtestE→=F→/qtest для расчета электрического поля. Нарисуйте стрелку в каждой точке, где вы поместите пробный заряд, чтобы представить силу и направление электрического поля. Длина стрелок должна быть пропорциональна напряженности электрического поля. Если вы соедините эти стрелки вместе, вы получите линии. На рис. 18.17 показано изображение трехмерного электрического поля, создаваемого положительным зарядом.
Если вы соедините эти стрелки вместе, вы получите линии. На рис. 18.17 показано изображение трехмерного электрического поля, создаваемого положительным зарядом.
Рисунок 18.17 Трехмерное представление электрического поля, создаваемого положительным зарядом.
Поддержка учителей
Поддержка учителей
[BL][OL]Укажите, что все силовые линии электрического поля берут начало от заряда.
[AL]Обратите внимание, что количество линий, пересекающих воображаемую сферу, окружающую заряд, одинаково независимо от размера сферы, которую вы выберете. Спросите, могут ли учащиеся использовать это, чтобы показать, что количество силовых линий, пересекающих поверхность на единицу площади, показывает, что напряженность электрического поля уменьшается пропорционально обратному квадрату расстояния.
Простое рисование линий электрического поля в плоскости, пересекающей заряд, дает двумерные карты электрического поля, показанные на рис.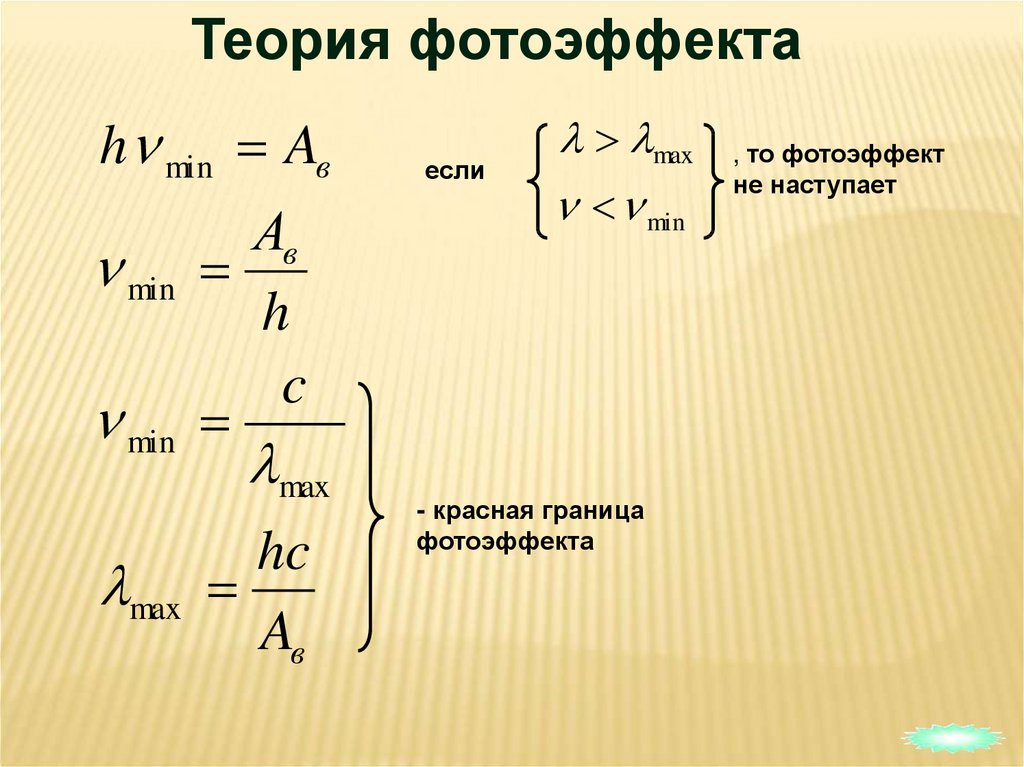 18.18. Слева — электрическое поле, создаваемое положительным зарядом, а справа — электрическое поле, создаваемое отрицательным зарядом.
18.18. Слева — электрическое поле, создаваемое положительным зарядом, а справа — электрическое поле, создаваемое отрицательным зарядом.
Обратите внимание, что силовые линии электрического поля направлены от положительного заряда к отрицательному. Таким образом, положительный пробный заряд, помещенный в электрическое поле положительного заряда, будет отталкиваться. Это согласуется с законом Кулона, согласно которому одноименные заряды отталкиваются друг от друга. Если мы поместим положительный заряд в электрическое поле отрицательного заряда, положительный заряд притянется к отрицательному заряду. Противоположное верно для отрицательных тестовых зарядов. Таким образом, направление линий электрического поля согласуется с тем, что мы находим, используя закон Кулона.
Уравнение E=k|Q|/r2E=k|Q|/r2 говорит о том, что электрическое поле становится сильнее по мере приближения к заряду, который его генерирует. Например, на расстоянии 2 см от заряда Q ( r = 2 см) электрическое поле в четыре раза сильнее, чем на расстоянии 4 см от заряда ( r = 4 см). Снова взглянув на рис. 18.17 и рис. 18.18, мы видим, что линии электрического поля становятся более плотными по мере приближения к заряду, который их генерирует. На самом деле плотность линий электрического поля пропорциональна напряженности электрического поля!
Снова взглянув на рис. 18.17 и рис. 18.18, мы видим, что линии электрического поля становятся более плотными по мере приближения к заряду, который их генерирует. На самом деле плотность линий электрического поля пропорциональна напряженности электрического поля!
Рисунок 18.18 Линии электрического поля от двух точечных зарядов. Красная точка слева несет заряд +1 нКл, а синяя точка справа несет заряд -1 нКл. Стрелки указывают направление, в котором будет двигаться положительный пробный заряд. Линии поля сгущаются по мере приближения к точечному заряду.
Карты электрического поля могут быть составлены для нескольких зарядов или для более сложных распределений зарядов. Электрическое поле от нескольких зарядов можно найти, сложив электрические поля от каждого отдельного заряда. Поскольку эта сумма может быть только одним числом, мы знаем, что только одна линия электрического поля может проходить через любую заданную точку. Другими словами, линии электрического поля не могут пересекаться.
На рис. 18.19(а) показана двумерная карта электрического поля, создаваемого зарядом + q и соседним зарядом — q . Трехмерная версия этой карты получается путем вращения этой карты вокруг оси, проходящей через оба заряда. Положительный пробный заряд, помещенный в это поле, будет испытывать силу в направлении силовых линий в его местоположении. Таким образом, он будет отталкиваться от положительного заряда и притягиваться к отрицательному заряду. Рисунок 18.19(b) показывает электрическое поле, создаваемое двумя зарядами − q . Обратите внимание, как силовые линии отталкиваются друг от друга и не перекрываются. Положительный пробный заряд, помещенный в это поле, будет притягиваться к обоим зарядам. Если вы находитесь далеко от этих двух зарядов, где далеко означает намного дальше, чем расстояние между зарядами, электрическое поле выглядит как электрическое поле от одного заряда -2 q .
Рисунок 18.19 (а) Электрическое поле, создаваемое точечным положительным зарядом (слева) и точечным отрицательным зарядом той же величины (справа). (б) Электрическое поле, создаваемое двумя равными отрицательными зарядами.
Поддержка учителей
Поддержка учителей
Попросите учащихся интерпретировать карты электрического поля. Где поле сильнее? Где поле слабее? В каком направлении поле увеличивается или уменьшается? Где поле наиболее однородно? Могут ли они проверить, что величина заряда одинакова в данной панели? Чем отличается поле двух отрицательных зарядов от поля положительного и отрицательного зарядов?
Виртуальная физика
Исследование электрического поля
Эта симуляция показывает вам электрическое поле из-за зарядов, которые вы размещаете на экране. Начните с установки верхнего флажка на панели параметров с правой стороны, чтобы отобразить электрическое поле. Перетащите заряды из ведер на экран, перемещайте их и наблюдайте за электрическим полем, которое они образуют. Чтобы более точно увидеть величину и направление электрического поля, перетащите датчик электрического поля или датчик электрического поля из нижнего ведра и перемещайте его по экрану.
Перетащите заряды из ведер на экран, перемещайте их и наблюдайте за электрическим полем, которое они образуют. Чтобы более точно увидеть величину и направление электрического поля, перетащите датчик электрического поля или датчик электрического поля из нижнего ведра и перемещайте его по экрану.
Исследования PhET: заряды и поля. Перемещайте точечные заряды по игровому полю, а затем просматривайте электрическое поле, напряжения, эквипотенциальные линии и многое другое.
Нажмите, чтобы просмотреть содержимое
Два положительных заряда размещены на экране. Какое утверждение описывает электрическое поле, создаваемое зарядами?
Постоянно везде.
Рядом с каждым зарядом ноль.

Между зарядками ноль.
Наибольшая сила на полпути между зарядами.
Смотреть физику
Электростатика (часть 2): интерпретация электрического поля
В этом видеоролике объясняется, как рассчитать электрическое поле точечного заряда и как интерпретировать карты электрического поля в целом. Обратите внимание, что лектор использует d для расстояния между частицами вместо r . Обратите внимание, что точечные заряды бесконечно малы, поэтому все их заряды сосредоточены в одной точке. Когда рассматриваются более крупные заряженные объекты, расстояние между объектами должно измеряться между центрами объектов.
Проверка захвата
Верно или неверно — если точечный заряд имеет силовые линии электрического поля, которые указывают на него, заряд должен быть положительным.
- правда
- ложь
Рабочий пример
Какова плата?
Посмотрите на рисунок электрического поля на рис. 18.20. Какова относительная сила и знак трех зарядов?
Рисунок 18.20 Карта электрического поля трех заряженных частиц.
Стратегия
Мы знаем, что электрическое поле простирается от положительного заряда и заканчивается отрицательным зарядом. Мы также знаем, что количество силовых линий электрического поля, которые касаются заряда, пропорционально заряду. Заряд 1 имеет 12 полей, выходящих из него. В заряд 2 входит шесть силовых линий. В заряд 3 входит 12 силовых линий.
Решение
Линии электрического поля выходят из заряда 1, так что это положительный заряд. Линии электрического поля проходят через заряды 2 и 3, поэтому они являются отрицательными зарядами. Отношение зарядов равно q1:q2:q3=+12:-6:-12q1:q2:q3=+12:-6:-12. Таким образом, величина зарядов 1 и 3 вдвое превышает величину заряда 2.
Линии электрического поля проходят через заряды 2 и 3, поэтому они являются отрицательными зарядами. Отношение зарядов равно q1:q2:q3=+12:-6:-12q1:q2:q3=+12:-6:-12. Таким образом, величина зарядов 1 и 3 вдвое превышает величину заряда 2.
Обсуждение
Хотя мы не можем определить точный заряд каждой частицы, мы можем получить много информации из электрического поля относительно величины и знака зарядов. и где сила пробного заряда будет наибольшей (или наименьшей).
Рабочий пример
Электрическое поле от дверной ручки
Дверная ручка, которую можно принять за сферический металлический проводник, приобретает заряд статического электричества q=-1,5 нКл. q=-1,5 нКл. Чему равно электрическое поле на расстоянии 1,0 см от дверной ручки? Диаметр дверной ручки 5,0 см.
Стратегия
Поскольку дверная ручка является проводником, весь заряд распределяется по внешней поверхности металла. Кроме того, поскольку дверная ручка считается идеально сферической, заряд на поверхности распределяется равномерно, поэтому мы можем рассматривать дверную ручку так, как если бы весь заряд был сосредоточен в центре дверной ручки. Справедливость этого упрощения будет доказана в следующем курсе физики. Теперь нарисуйте дверную ручку и определите вашу систему координат. Используйте +x+x, чтобы указать внешнее направление, перпендикулярное двери, с x=0x=0 в центре дверной ручки (как показано на рисунке ниже).
Кроме того, поскольку дверная ручка считается идеально сферической, заряд на поверхности распределяется равномерно, поэтому мы можем рассматривать дверную ручку так, как если бы весь заряд был сосредоточен в центре дверной ручки. Справедливость этого упрощения будет доказана в следующем курсе физики. Теперь нарисуйте дверную ручку и определите вашу систему координат. Используйте +x+x, чтобы указать внешнее направление, перпендикулярное двери, с x=0x=0 в центре дверной ручки (как показано на рисунке ниже).
Если диаметр дверной ручки 5,0 см, ее радиус 2,5 см. Мы хотим знать электрическое поле на расстоянии 1,0 см от поверхности дверной ручки, что составляет расстояние r = 2,5 см + 1,0 см = 3,5 см, r = 2,5 см + 1,0 см = 3,5 см от центра дверной ручки. Мы можем использовать уравнение E=k|Q|r2E=k|Q|r2, чтобы найти величину электрического поля. Направление электрического поля определяется знаком заряда, который в данном случае отрицательный.
Решение
Введение заряда Q=-1,5 нКл=-1,5×10-9.
Обсуждение
Похоже на огромное электрическое поле. К счастью, требуется электрическое поле примерно в 100 раз сильнее (3×106 Н/Кл3×106 Н/Кл), чтобы заставить воздух разлагаться и проводить электричество. Кроме того, вес взрослого человека составляет около 70 кг × 9,8 м/с2 ≈ 700 Н70 кг × 9,8 м/с2 ≈ 700 Н, так почему вы не чувствуете силы, действующей на протоны в вашей руке, когда вы тянетесь к дверной ручке? Причина в том, что ваша рука содержит равное количество отрицательного заряда, который отталкивает отрицательный заряд дверной ручки. Из-за поляризации в вашей руке может развиться очень небольшая сила, но вы никогда этого не заметите.
Практические задачи
15.
Какова величина электрического поля на расстоянии 20 см от точечного заряда q = 33 нКл?
- 7,4 × 10 3 Н/З
- 1,48 × 10 3 Н/З
- 7,4 × 10 12 Н/З
- 0
16.
Заряд -10 нКл находится в начале. В каком направлении электрическое поле от заряда указывает на x + 10 см?
- Электрическое поле направлено в сторону от отрицательных зарядов.
- Электрическое поле указывает на отрицательные заряды.
- Электрическое поле направлено в сторону положительных зарядов.
- Электрическое поле направлено в сторону от положительных зарядов.
Проверьте свое понимание
17.
Когда линии электрического поля сближаются, что это говорит вам об электрическом поле?
- Электрическое поле обратно пропорционально плотности линий электрического поля.
- Электрическое поле прямо пропорционально плотности линий электрического поля.
- Электрическое поле не связано с плотностью линий электрического поля.
- Электрическое поле обратно пропорционально квадратному корню из плотности силовых линий электрического поля.

18.
Если пять линий электрического поля исходят из заряда +5 нКл, сколько линий электрического поля должно исходить из заряда +20 нКл?
- пять строк поля
- 10 строк поля
- 15 строк поля
- 20 строк поля
AP Физика C Уравнения электричества и магнетизма
УРАВНЕНИЯ | ИНФОРМАЦИЯ |
Закон Кулона | |
Напряженность электрического поля | |
Напряженность электрического поля для системы зарядов | |
Напряженность электрического поля при непрерывном заряде | |
Частица в электрическом поле | |
Линейная плотность заряда | |
Поверхностная плотность заряда | |
Объемная плотность заряда | |
Электрический флюс | |
Обобщенный электрический поток | |
Закон Гаусса | |
Потенциальная разница между двумя точками | |
Общая разница потенциалов | |
Изменение потенциальной энергии | |
Электрический потенциал | |
Электрический потенциал из-за непрерывного заряда | |
Электрическая потенциальная энергия | |
Электрический потенциал (в координатах) |
Емкость | |
Емкость параллельных пластин | |
Электрический дипольный момент | |
Параллельная комбинация конденсаторов | |
| Серия Комбинация конденсаторов | |
Энергия, запасенная в конденсаторе | |
Плотность энергии | |
Диэлектрическая проницаемость | |
Крутящий момент, действующий на электрический диполь | |
Потенциальная энергия электрической дипольной системы | |
Средний ток | |
Текущий | |
Плотность тока | |
Закон Ома (обобщенный) | |
Закон Ома |
Сопротивление | |
Удельное сопротивление (металла) | |
Удельное сопротивление (проводника) | |
Средний ток в проводнике | |
Скорость дрейфа | |
Электроэнергия |
Электродвижущая сила (максимальное напряжение, которое может обеспечить батарея) | |
| Цепи серии | |
Параллельные цепи | |
Правило Кирхгофа №1 (правило соединения) | |
Правило Кирхгофа № 2 (правило цикла) | |
Максимальный заряд конденсатора | |
Постоянная времени | |
Зарядка конденсатора от аккумулятора | |
Начальный ток в цепи (с разряжающимся конденсатором) | |
Разрядка конденсатора | |
Магнитный дипольный момент | |
Радиус пути заряженной частицы в магнитном поле | |
Угловая скорость заряженной частицы | |
Магнитная сила | |
Магнитная сила (в проводе произвольной формы) | |
Крутящий момент в токовой петле | |
Потенциальная энергия магнитного диполя в магнитном поле | |
Магнитный поток | |
Биот — Савар Ло | |
Сила магнитного поля (два параллельных провода) | |
Закон Ампера | |
Закон Гаусса для магнетизма | |
Магнитное поле длинного прямого провода | |
Магнитное поле от тороида | |
Магнитное поле соленоида | |
Закон индукции Фарадея | |
Закон индукции Фарадея (обобщенный) | |
ЭДС движения | |
Индуктивность | |
Индуктивность соленоида с воздушным сердечником | |
Собственная индуктивность | |
Постоянная времени цепи RL | |
Ток в цепи RL | |
Начальный ток в цепи разряда RL | |
Затухание тока в цепи RL | |
Энергия, запасенная в магнитном поле индуктора | |
Плотность энергии в месте с магнитным полем | |
Взаимная индуктивность | |
Индуцированная ЭДС | |
Угловая частота в LC-цепи | |
Угловая частота в цепи RLC | |
Заряд конденсатора в цепи RLC | |
Индуктивное сопротивление | |
Емкостное реактивное сопротивление | |
Полное сопротивление цепи переменного тока серии RLC | |
Фазовый угол | |
Среднеквадратичное значение тока | |
Среднеквадратичное значение напряжения | |
Средняя мощность в цепи RLC | |
Средняя мощность в цепи RLC (по сопротивлению) | |
Среднеквадратичное значение тока в последовательной цепи RLC | |
Резонансная частота последовательной цепи RLC | |
Трансформаторы переменного тока | |
Ток смещения | |
Вектор Пойнтинга | |
Закон силы Лоренца | |
Закон Гаусса (первое уравнение Максвелла) | |
Закон Гаусса для магнетизма (второе уравнение Максвелла) | |
Закон индукции Фарадея (обобщенный) | |
Ампер — Закон Максвелла (четвертое уравнение Максвелла) | |
Скорость света | |
Зависимость частоты от длины волны |
Электромагнитные волны (волновые уравнения) | |
Радиационное давление (полное поглощение) | |
Среднее значение вектора Пойнтинга | |
Вернуться в AP Physics C
Веб-сайт физического кабинета
Назначение SE10: электрическое поле
Цели:
- Студент должен уметь определять электрическое поле и распознавать переменные, влияющие (и не влияющие) на напряженность электрического поля в данном месте.
- Студент должен уметь использовать уравнения электрического поля и относительно простые числа для определения величины и направления напряженности электрического поля в заданном месте.
Чтение:
Класс физики — Статическое электричество, урок 4, часть а
Заряд Q создает электрическое поле. Пробным зарядом q измеряют напряженность электрического поля на расстоянии d от Q. На пробный заряд q действует сила F. Напряженность электрического поля в этом месте определяется выражением ___. Перечислите все, что применимо… . | |
Определение Напряженность электрического поля : Любой источник заряда Q будет создавать электрическое поле в окружающем его пространстве. | |
Напряженность электрического поля ( E ) определяется как количество силы, действующей на пробный заряд на единицу заряда пробного заряда ( q ). То есть E = F/q . Электрическая сила ( F ) зависит от ряда переменных, как описано законом Кулона. В приведенном выше уравнении Q 1 может быть исходным зарядом Q , а Q 2 может быть тестовым зарядом q . | |
Какие переменные влияют на напряженность электрического поля заряда? Как можно использовать силу пробного заряда для определения напряженности электрического поля другого заряда? |
Заряд Q создает электрическое поле. Пробный заряд q используется для измерения напряженности электрического поля на расстоянии d от Q. Напряженность электрического поля определяется как ____. | |
Определение Напряженность электрического поля : Любой источник заряда Q будет создавать электрическое поле в окружающем его пространстве. | |
Легко запутаться в математике напряженности электрического поля. Важно помнить, что в любом электрическом взаимодействии всегда участвуют два заряда. В этом случае начисления составляют q и q . Большой Q представляет собой исходный заряд, создающий электрическое поле. Маленький q представляет собой тестовый заряд, который используется для измерения напряженности электрического поля в заданном месте, окружающем заряд источника. Уделите особое внимание количеству заряда — q или q — используемому в каждом уравнении. | |
Как можно использовать силу пробного заряда для определения напряженности электрического поля другого заряда? |
Стандартной метрической единицей напряженности электрического поля является ____. | |
Напряженность электрического поля ( E ) в любом месте, окружающем заряд источника, можно определить путем измерения силы ( E ).4004 F ), воздействующего на испытательный заряд ( q ), размещенный в этом месте. | |
Стандартные метрические единицы количества можно понять, подумав о его формуле. | |
Определение Напряженность электрического поля : Любой источник заряда Q будет создавать электрическое поле в окружающем его пространстве. Напряженность электрического поля ( E ) в любом заданном месте в этом пространстве можно определить, поместив пробный заряд q в пространство и измерив силу ( F ), действующую на него. | |
Напряженность электрического поля ( E ) определяется как величина силы, действующей на испытательный заряд на единицу заряда испытательного заряда ( q ). То есть E = F/q . Электрическая сила ( F ) зависит от ряда переменных, как описано законом Кулона. В приведенном выше уравнении Q 1 может быть зарядом источника Q и Q 2 может быть пробным зарядом q . Если выражение для силы, данное уравнением закона Кулона, заменить F в уравнении напряженности электрического поля, то уравнение для электрического поля примет вид | |
Легко запутаться в математике напряженности электрического поля. | |
Какие переменные влияют на напряженность электрического поля заряда? Как можно использовать силу пробного заряда для определения напряженности электрического поля другого заряда? |
ИСТИНА или ЛОЖЬ : Величина электрического поля является векторной величиной. (Примечание: ваше фактическое утверждение «Верно-ложно» выбирается случайным образом из набора вариантов и может отличаться от приведенного здесь.) | |
Электрическое поле как вектор: Электрическое поле в заданном месте вокруг заряда источника ( Q ) является векторной величиной. То есть имеет направление. Сила, действующая на пробный заряд ( q ), может быть силой притяжения (по направлению к исходному заряду) или силой отталкивания (от исходного заряда) в зависимости от того, являются ли Q и q имеют одинаковый или противоположный заряд. При определении направления электрического поля используется условное обозначение, что направление всегда одно и то же, независимо от типа заряда q . Согласно соглашению, направление электрического поля соответствует направлению, в котором положительный пробный заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q . | |
Является ли электрическое поле скалярной или векторной величиной? |
По соглашению направление электрического поля ____. | |
Электрическое поле как вектор: Электрическое поле ( E ) в данном месте относительно заряда источника ( Q ) является векторной величиной. То есть имеет направление. Сила, действующая на пробный заряд ( q ), может быть силой притяжения (по направлению к исходному заряду) или силой отталкивания (от исходного заряда) в зависимости от того, заряжены ли Q и q одинаково или противоположно. | |
Как определить направление электрического поля? |
Положительный заряд создает электрическое поле. Направление электрического поля будет ____. | |
Электрическое поле как вектор: Электрическое поле ( E ) в заданном месте относительно заряда источника ( Q ) — векторная величина. | |
По соглашению, направление вектора электрического поля в любом данном месте — это направление, в котором положительный пробный заряд будет выталкиваться или тянуться, если его поместить в это место. Сочетая это соглашение с правилом отталкивания одинаково заряженных объектов, можно определить направление электрического поля в пространстве, окружающем источник положительного заряда. | |
Как определить направление электрического поля? |
Отрицательный заряд создает электрическое поле. Направление электрического поля будет ____. | |
Электрическое поле как вектор: Электрическое поле ( E ) в данном месте относительно заряда источника ( Q ) является векторной величиной. То есть имеет направление. | |
По соглашению, направление вектора электрического поля в любом данном месте — это направление, в котором положительный пробный заряд будет выталкиваться или тянуться, если его поместить в это место. Сочетая это соглашение с правилом притяжения противоположно заряженных объектов, можно определить направление электрического поля в пространстве, окружающем источник отрицательного заряда. | |
Как определить направление электрического поля? |
Следуйте за нами
Использование уравнений конденсатора — AP Physics C Electricity
Все ресурсы AP Physics C Electricity
1 Диагностический тест 46 практических тестов Вопрос дня Карточки Учитесь по концепции
AP Физика C Электричество Справка » Экзамен по электричеству и магнетизму » Электрические схемы » конденсаторы » Использование уравнений конденсатора
Вас наняли сделать конденсатор из двух параллельных металлических листов. Если бы кто-то хотел, чтобы вы сделали тонкий конденсатор из этих металлических листов, и листы должны были быть разделены, какой площади должны быть две металлические пластины?
Если бы кто-то хотел, чтобы вы сделали тонкий конденсатор из этих металлических листов, и листы должны были быть разделены, какой площади должны быть две металлические пластины?
Возможные ответы:
Правильный ответ:
Объяснение:
Для конденсаторов с плоскими пластинами уравнение выглядит следующим образом.
Решите для .
Теперь мы можем подставить заданные нами значения.
Сообщить об ошибке
Пластины плоского конденсатора разнесены и находятся на одной площади. К конденсатору приложена разность потенциалов. Найдите емкость.
Возможные ответы:
Правильный ответ:
Объяснение:
Емкость связана с площадью пластины и расстоянием по уравнению .
Зная площадь и расстояние, мы можем найти емкость. Напряжение в данном случае значения не имеет.
Сообщить об ошибке
Пластины плоского конденсатора разнесены и находятся на одной площади. К конденсатору приложена разность потенциалов. Вычислите заряд каждой пластины.
Возможные ответы:
Правильный ответ:
Пояснение:
Заряд конденсатора определяется уравнением . Мы знаем, что напряжение равно , но нам нужно определить емкость, исходя из площади и расстояния между пластинами.
Мы можем подставить это значение в уравнение для заряда.
Сообщить об ошибке
Пластины плоского конденсатора раздвинуты. К конденсатору приложена разность потенциалов. Вычислите величину генерируемого электрического поля.
Возможные ответы:
Правильный ответ:
Пояснение:
Электрическое поле конденсатора определяется формулой . У нас нет этих переменных, поэтому нам придется скорректировать уравнение.
Емкость можно определить по площади пластин и расстоянию между ними.
Это уравнение упрощается до , что позволяет нам решить, используя значения, указанные в вопросе.
Сообщить об ошибке
Если два одинаковых плоскопараллельных конденсатора емкостью соединены последовательно, что верно для эквивалентной емкости, ?
Возможные ответы:
Правильный ответ:
Объяснение:
Соответствующие уравнения:
Используйте уравнение ряда, заменив C1 и C2 данной константой C:
емкость любого из отдельных конденсаторов.
Сообщить об ошибке
Каждая из двух параллельных проводящих пластин имеет площадь и разделена расстоянием, . Одна пластина имеет заряд, равномерно распределенный по ней, а другая имеет заряд . Протон (заряд ) сначала удерживается возле положительной пластины, а затем высвобождается так, что ускоряется по направлению к отрицательной пластине. Какую кинетическую энергию приобрел протон в этом процессе?
Возможные ответы:
Правильный ответ:
Объяснение:
Соответствующие уравнения:
Согласно теореме о работе-энергии работа, совершаемая протоном, равна изменению его кинетической энергии.
1. Найдите выражение для разности потенциалов , через и , приравняв два уравнения емкости:
2. Умножьте разность потенциалов на заряд протона, чтобы найти работу (и, следовательно, кинетическую энергию):
Сообщить об ошибке
А и конденсатор соединены последовательно с батареей.






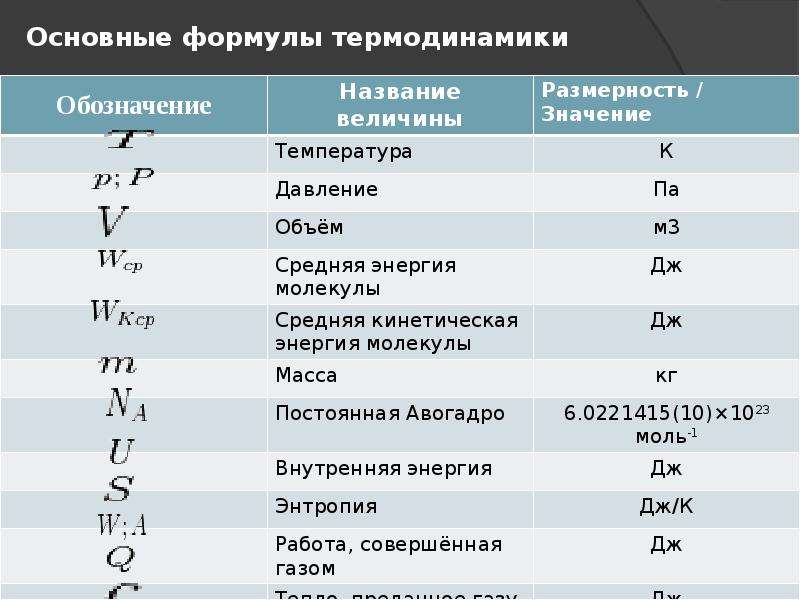

 Ожидается, что студент:
Ожидается, что студент:


 Напряженность электрического поля ( E ) в любом заданном месте в этом пространстве можно определить, поместив пробный заряд q в пространство и измерив силу ( F ), воздействующее на него. Напряженность электрического поля определяется как количество силы на единицу заряда испытательного заряда.
Напряженность электрического поля ( E ) в любом заданном месте в этом пространстве можно определить, поместив пробный заряд q в пространство и измерив силу ( F ), воздействующее на него. Напряженность электрического поля определяется как количество силы на единицу заряда испытательного заряда. Если выражение для силы, данное уравнением закона Кулона, подставить вместо F в уравнении напряженности электрического поля, то уравнение для электрического поля принимает вид
Если выражение для силы, данное уравнением закона Кулона, подставить вместо F в уравнении напряженности электрического поля, то уравнение для электрического поля принимает вид Напряженность электрического поля ( E ) в любом заданном месте в этом пространстве можно определить, поместив пробный заряд q в пространство и измерив силу ( F ), действующую на него. Напряженность электрического поля определяется как количество силы на единицу заряда испытательного заряда.
Напряженность электрического поля ( E ) в любом заданном месте в этом пространстве можно определить, поместив пробный заряд q в пространство и измерив силу ( F ), действующую на него. Напряженность электрического поля определяется как количество силы на единицу заряда испытательного заряда.
 Напряженность электрического поля — это отношение силы к заряду (см. раздел Formula Fix выше). Таким образом, единицы напряженности электрического поля — это единицы силы, деленные на единицы заряда. Стандартной метрической единицей силы является ньютон; стандартной метрической единицей заряда является кулон. Таким образом, стандартной метрической единицей напряженности электрического поля является Ньютон/Кулон, сокращенно N/C. 9-9 Кулоновский пробный заряд. Напряженность электрического поля, создаваемая зарядом в 4 мкК, составляет ____ Н/Кл.
Напряженность электрического поля — это отношение силы к заряду (см. раздел Formula Fix выше). Таким образом, единицы напряженности электрического поля — это единицы силы, деленные на единицы заряда. Стандартной метрической единицей силы является ньютон; стандартной метрической единицей заряда является кулон. Таким образом, стандартной метрической единицей напряженности электрического поля является Ньютон/Кулон, сокращенно N/C. 9-9 Кулоновский пробный заряд. Напряженность электрического поля, создаваемая зарядом в 4 мкК, составляет ____ Н/Кл. Напряженность электрического поля определяется как количество силы на единицу заряда испытательного заряда.
Напряженность электрического поля определяется как количество силы на единицу заряда испытательного заряда. Важно помнить, что в любом электрическом взаимодействии всегда участвуют два заряда. В этом случае начисления составляют q и q . Большой Q представляет собой исходный заряд, создающий электрическое поле. Little q представляет собой тестовый заряд, который используется для измерения напряженности электрического поля в заданном месте, окружающем заряд источника. Уделите большое внимание количеству заряда — Q или q — используется в каждом уравнении.
Важно помнить, что в любом электрическом взаимодействии всегда участвуют два заряда. В этом случае начисления составляют q и q . Большой Q представляет собой исходный заряд, создающий электрическое поле. Little q представляет собой тестовый заряд, который используется для измерения напряженности электрического поля в заданном месте, окружающем заряд источника. Уделите большое внимание количеству заряда — Q или q — используется в каждом уравнении.

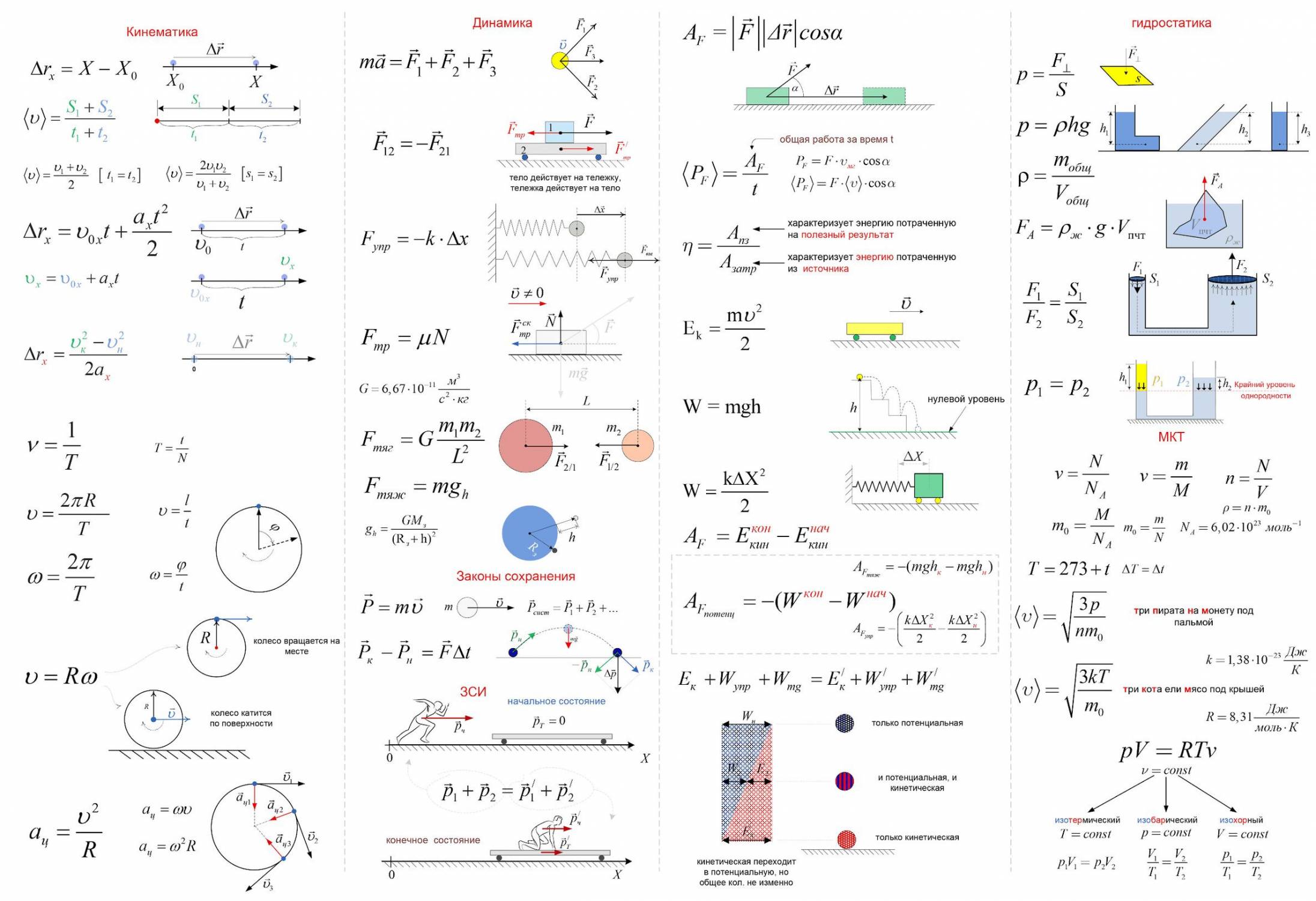 заряжен. При определении направления электрического поля используется условное обозначение, согласно которому направление зависит от типа заряда исходного заряда 9.4004 В . Согласно соглашению, направление электрического поля соответствует направлению, в котором положительный пробный заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q .
заряжен. При определении направления электрического поля используется условное обозначение, согласно которому направление зависит от типа заряда исходного заряда 9.4004 В . Согласно соглашению, направление электрического поля соответствует направлению, в котором положительный пробный заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q . То есть имеет направление. Сила, действующая на пробный заряд ( q ), может быть силой притяжения (по направлению к исходному заряду) или силой отталкивания (от исходного заряда) в зависимости от того, заряжены ли Q и q одинаково или противоположно. заряжен. При определении направления электрического поля используется соглашение, согласно которому направление зависит от типа заряда исходного заряда Q . Согласно соглашению, направление электрического поля совпадает с направлением положительный тестовый заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q .
То есть имеет направление. Сила, действующая на пробный заряд ( q ), может быть силой притяжения (по направлению к исходному заряду) или силой отталкивания (от исходного заряда) в зависимости от того, заряжены ли Q и q одинаково или противоположно. заряжен. При определении направления электрического поля используется соглашение, согласно которому направление зависит от типа заряда исходного заряда Q . Согласно соглашению, направление электрического поля совпадает с направлением положительный тестовый заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q . Положительный заряд источника и положительный пробный заряд будут отталкивать друг друга. То есть положительный пробный заряд будет отталкиваться от положительного исходного заряда во всех точках пространства, окружающего исходный заряд.
Положительный заряд источника и положительный пробный заряд будут отталкивать друг друга. То есть положительный пробный заряд будет отталкиваться от положительного исходного заряда во всех точках пространства, окружающего исходный заряд. Сила, действующая на пробный заряд ( q ), может быть силой притяжения (по направлению к исходному заряду) или силой отталкивания (от исходного заряда) в зависимости от того,4004 Q и q заряжены одинаково или противоположно. При определении направления электрического поля используется соглашение, согласно которому направление зависит от типа заряда исходного заряда Q . Согласно соглашению, направление электрического поля соответствует направлению, в котором положительный пробный заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q .
Сила, действующая на пробный заряд ( q ), может быть силой притяжения (по направлению к исходному заряду) или силой отталкивания (от исходного заряда) в зависимости от того,4004 Q и q заряжены одинаково или противоположно. При определении направления электрического поля используется соглашение, согласно которому направление зависит от типа заряда исходного заряда Q . Согласно соглашению, направление электрического поля соответствует направлению, в котором положительный пробный заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q .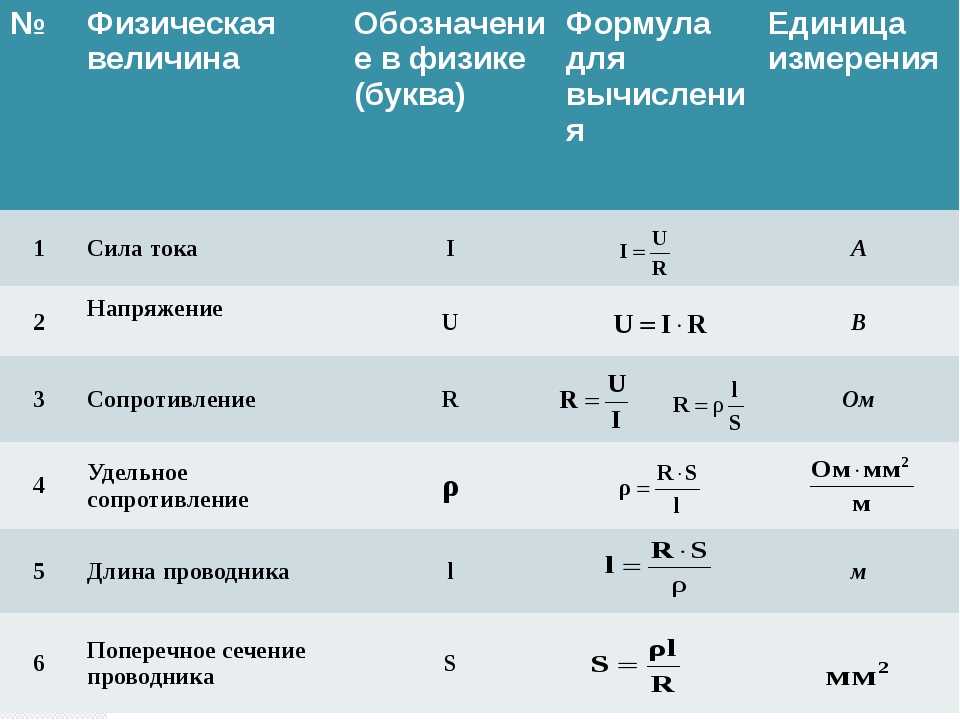 Отрицательный заряд источника и положительный пробный заряд будут притягиваться друг к другу. То есть положительный пробный заряд будет притягиваться к отрицательному исходному заряду во всех точках пространства, окружающего исходный заряд.
Отрицательный заряд источника и положительный пробный заряд будут притягиваться друг к другу. То есть положительный пробный заряд будет притягиваться к отрицательному исходному заряду во всех точках пространства, окружающего исходный заряд.