Линейная функция, ее график и свойства / Функции / Алгебра / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Алгебра
- Функции
- Линейная функция, ее график и свойства
Определение:
| Функцию, которую можно задать формулой вида , и — некоторые числа, — независимая переменная, называют линейной. |
Примеры линейных функций:
Областью определения линейной функции являются все числа.
Графиком линейной функции является прямая.
Построим график функции .
Составим таблицу значений этой функции для некоторых значений аргумента .
| 3 | 2 | 1 | 0 | 1 | 2 | 3 | |
| 9 | 7 | 5 | 3 | 1 | 1 | 3 |
Отметим точки с координатами (3; 9), (2; 7), (1; 5), (0; 3), (1; 1), (2; 1), (3; 3) на координатной плоскости.
Все точки, отмеченные на координатной плоскости, лежат на одной прямой, которая и является графиком функции .
Вспомним, фигура может быть графиком некоторой функции, если любая прямая, перпендикулярная оси абсцисс, имеет с этой фигурой не более одной точки. Следовательно, прямая, которая является графиком линейной функции, не может быть вертикальной.
Прямая однозначно задается любыми двумя точками, поэтому для построения графика линейной функции достаточно выбрать два произвольных значения аргумента и составить таблицу значений функции, имеющую лишь два столбца.
Пример. Постройте график функции .
Решение: Составим таблицу значений этой функции для некоторых значений аргумента .
Отметим на координатной плоскости точки с координатами (0; 5) и (3; 1) и проведем через них прямую, которая является графиком линейной функции .
Частные случаи линейной функции:
1) Если и , то .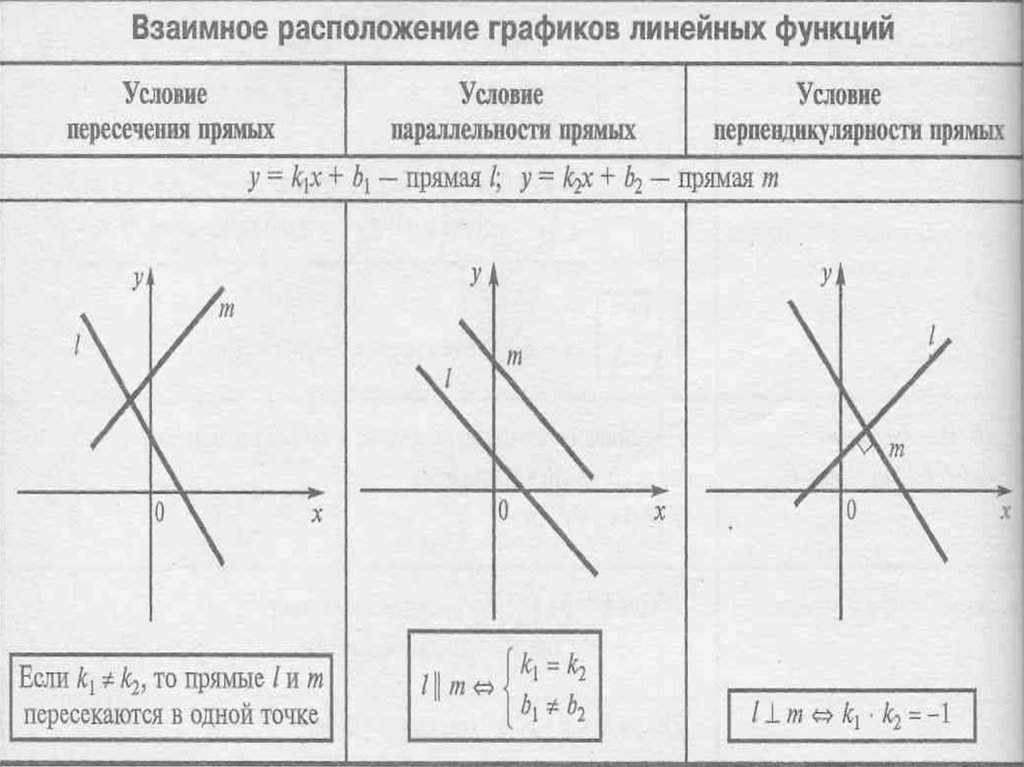
Функцию называют прямой пропорциональностью.
Примеры прямых пропорциональностей:
Графиком функции прямой пропорциональности является прямая, которая проходит через точку О(0; 0), т.к. если = 0, то при любом значении получаем = 0. Поэтому для построения графика прямой пропорциональности достаточно указать какую-нибудь точку графика, отличную от начала координат, и провести прямую через эту точку и точку О(0; 0).
На рисунке ниже изображены графики прямых пропорциональностей, указанных выше.
2) Если , то .
Значения функции остаются неизменными при любых изменениях значений аргумента.
Графиком функции , где является прямая, параллельная оси , т.к. ордината (координата ) для любого значения будет иметь одно и то же значение . Если же = 0, то = 0 и графиком этой функции является ось абсцисс.
На рисунке ниже изображены графики функций
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Связи между величинами. Функция
Функция
Способы задания функции
График функции
Введение в алгебру
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Одночлены
Многочлены
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Функции
Системы линейных уравнений с двумя переменными
Алгебра
Правило встречается в следующих упражнениях:
7 класс
Номер 7, Мерзляк, Полонский, Якир, Учебник
Номер 855, Мерзляк, Полонский, Якир, Учебник
Номер 864, Мерзляк, Полонский, Якир, Учебник
Номер 865, Мерзляк, Полонский, Якир, Учебник
Номер 869, Мерзляк, Полонский, Якир, Учебник
Номер 878, Мерзляк, Полонский, Якир, Учебник
Номер 881, Мерзляк, Полонский, Якир, Учебник
Номер 884, Мерзляк, Полонский, Якир, Учебник
Номер 892, Мерзляк, Полонский, Якир, Учебник
Номер 11, Мерзляк, Полонский, Якир, Учебник
Линейная функция, ее свойства и график
теория по математике 🎲 функции
ОпределениеФункция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией.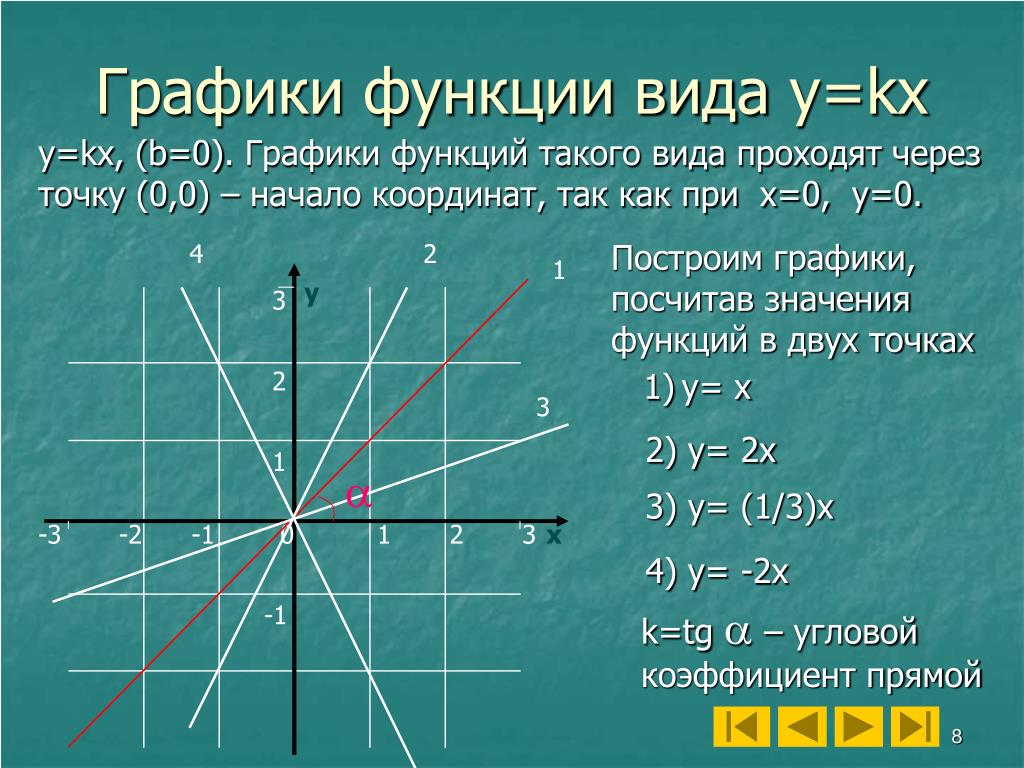 Переменную х называют независимой переменной, переменную у – зависимой переменной.
Переменную х называют независимой переменной, переменную у – зависимой переменной.
Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.
Число k называется угловым коэффициентом прямой.
- Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.
- Областью значений также является множество всех действительных чисел.
- Функция не имеет ни наибольших, ни наименьших значений.
- При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.
- При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.
- При k=0 прямая параллельна оси х.
- Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.

Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.
Пример №1
Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:
Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).
| х | 0 | 3 |
| у |
Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:
у=2х – 1=2×0 – 1= –1;
у=2х – 1=2×3 – 1= 5.
Вписываем в таблицу значения у:
| х | 0 | 3 |
| у | –1 | 5 |
Теперь строим систему координат, отмечаем в ней точки с координатами А(0; –1) и В(3;5), проводим через эти две точки прямую.
Итак, по формуле мы видим, что угловой коэффициент – положительный, значит, график – возрастает, что мы и видим на нашем графике.
Пример №2.
Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.
| х | 0 | 2 |
| у | 4 | –2 |
По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).
Пример №3
Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ:
КОЭФФИЦИЕНТЫ:
1) k>0, b<0 2) k>0, b>0 3) k<0, b<0ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>900) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.
У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<90 0). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1103oУстановите соответствие между функциями и их графиками.
Функции:
A) y = 3x
Б) y = -3x
В) y = (1/3)x
Графики:
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
y = kx + b
График данной функции зависит от k и b.
- если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1
Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.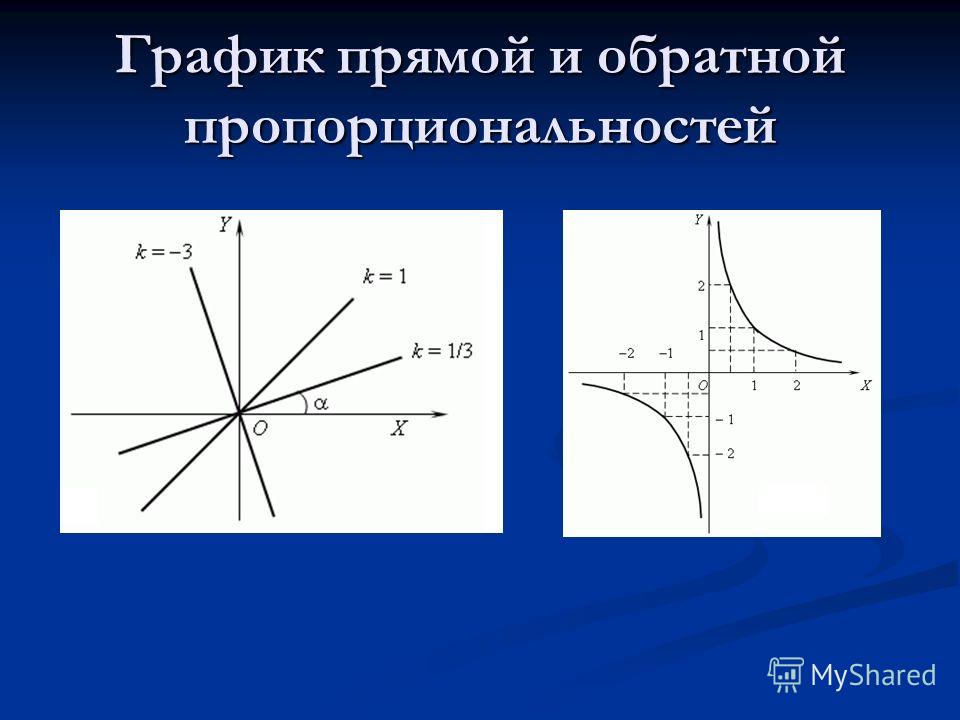
Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231pазбирался: Даниил Романович | обсудить разбор | оценить
Даниил Романович | Просмотров: 3.4k | Оценить:
Линейная функция
Функция называется
линейной, если ее можно записать в виде \(y=kx+b\), где \(k\) и \(b\) -некоторые числа.Примеры:
|
\(y=\frac{1}{3}x-5\) |
\(k=\frac{1}{3}\), \(b=-5\) |
|
|
\(y=2x\) |
\(k=2\), \(b=0\) |
|
|
\(y=8\) |
\(k=0\), \(b=8\) |
Функция не всегда сразу задана в виде \(y=kx+b\), иногда такой вид получится только после преобразований. Например, \(y=6(x-1)+10x\) — это линейная функция, потому что если раскрыть скобки и привести подобные слагаемые мы получим \(y=16x-6\).
Например, \(y=6(x-1)+10x\) — это линейная функция, потому что если раскрыть скобки и привести подобные слагаемые мы получим \(y=16x-6\).
Чтобы в этом убедиться построим графики функций \(y=2x\), \(y=\frac{1}{3}x-5\), \(y=8\).
Если вы вдруг забыли, как строить графики, можете прочитать об этом здесь.
Как меняется график при разных \(k\)?
Чтобы определить, как влияет на график коэффициент \(k\), построим несколько функций разными \(k\): \(\frac{1}{3}\),\(-\frac{1}{3}\),\(2\),\(-2\) и \(0\). При этом во всех функциях сделаем \(b\) одинаковым (равным нулю), чтобы убрать его влияние.
То есть, построим графики для функций: \(y=\frac{1}{3}x\), \(y=-\frac{1}{3}x\), \(y=2x\), \(y=-2x\), \(y=0\).
Заметьте, что при \(k=2\) и \(\frac{1}{3}\) — функция возрастает, а при \(k=-2\) и \(-\frac{1}{3}\) — убывает.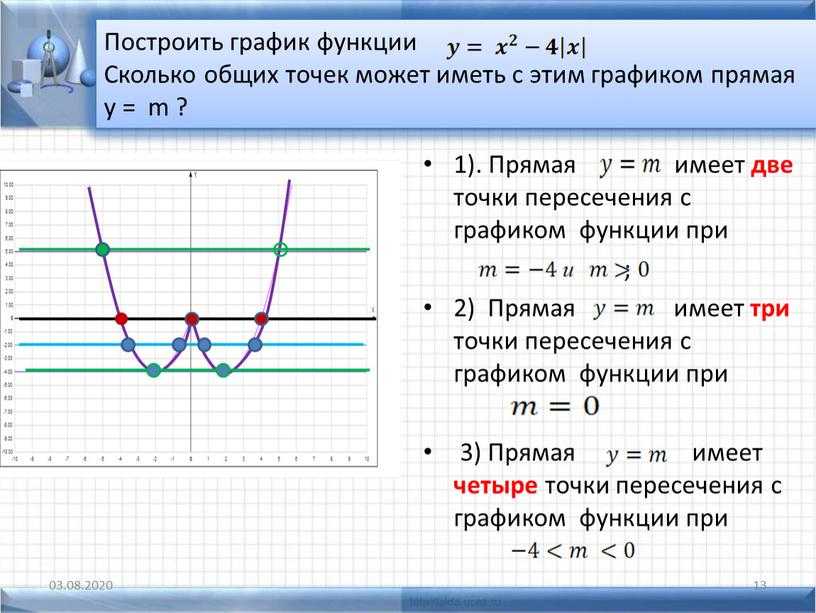 На самом деле:
На самом деле:
При любом \(k>0\) функция возрастает и при любом \(k<0\) — убывает. Когда же \(k=0\) — она не возрастает и не убывает, а идет параллельна оси \(x\) (или совпадает с ней).
Так же можно заметить, чем больше модуль \(k\), тем «круче» график.
Как по графику определить коэффициент k?
- Сначала определим, возрастает или убывает функция. Если возрастает – знак коэффициента \(k\) плюс, если убывает – минус.
- Дальше надо построить на прямой прямоугольный треугольник, так чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Примерно вот так:
Чтобы определить значение \(k\) по модулю (то есть, без учета знака), надо вертикальную сторону треугольника поделить на горизонтальную. Можно использовать правило для запоминания: «стоячий бьет лежачего». В данных случаях \(|k|=\frac{AC}{BC}\). То есть на первом графике \(k=2\),а на втором \(k=-\frac{1}{4}\).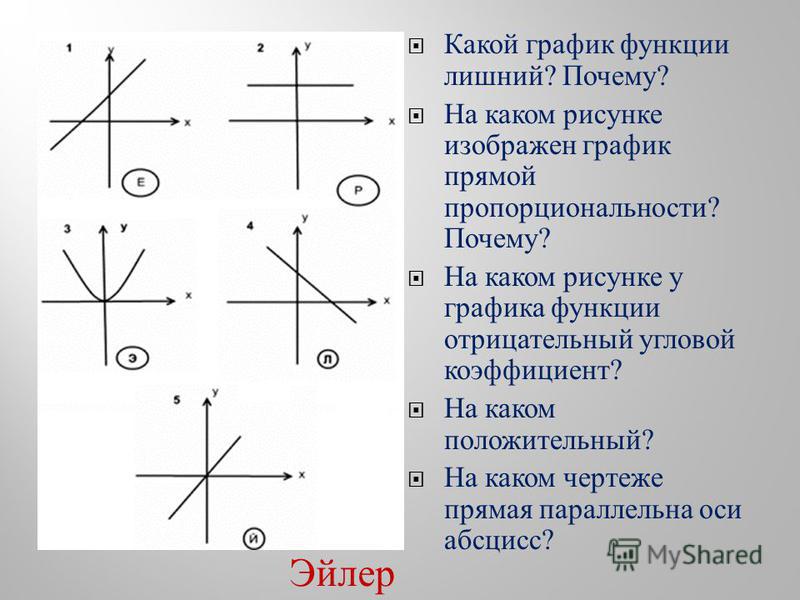
Как меняется график при разных значениях \(b\)?
Чтобы определить, как \(b\) влияет на график, построим несколько функций с разными \(b\): \(6\), \(2\), \(0\), \(-3\) и \(-8\). При этом \(k\) пусть во всех функциях будет равен \(2\).
Не сложно заметить, что прямая либо поднимается на \(b\) (если \(b>0\)) либо опускается на \(|b|\) если
(\(b<0\)).
Как по графику функции определить значение \(b\)?
Очень просто — прямая пересекает ось \(y\) всегда в точке \(b\). Вы можете это увидеть на предыдущем графике.
Пример (ОГЭ): На рисунке изображены графики функций вида \(y=kx+b\). Установите соответствие между графиками функций и знаками коэффициентов \(k\) и \(b\).
A. B.C.
Коэффициенты
| 1) \(k>0\),\(b>0\) | 2) \(k<0\), \(b>0\) | 3) \(k<0\), \(b<0\) | 4) \(k>0\), \(b<0\) |
Решение:
А. – функция убывает, поэтому \(k<0\). Точка пересечения оси \(y\) и прямой находится выше нуля, значит \(b>0\). Подходит вариант под цифрой 2).
– функция убывает, поэтому \(k<0\). Точка пересечения оси \(y\) и прямой находится выше нуля, значит \(b>0\). Подходит вариант под цифрой 2).
B. — функция возрастает — \(k>0\). Точка пересечения оси \(y\) и прямой находится выше нуля, значит \(b>0\). Подходит вариант под цифрой 1).
C. – функция убывает — \(k<0\). Точка пересечения оси \(y\) и прямой находится ниже нуля, значит \(b<0\). Подходит вариант под цифрой 3).
Ответ: 213.
«Читерский» способ строить график линейной функции
Можно конечно строить график линейной функции по точкам, как описано
здесь, но можно и быстрее, буквально в три шага:
-
Отмечаем точку \(b\) на оси игреков.
-
От неё идем вправо на количество клеточек равное знаменателю \(k\), и вверх на количество клеточек равное числителю \(k\) (если \(k>0\)) или вниз на тоже количество (если \(k<0\)).

-
Проводим через эти две точки прямую.
Пример: Построить график функции \(y=3x+1\).
|
Шаг 1. \(b=1\), поэтому отмечаем точку с этим значением на оси \(y\)
|
Шаг 2. \(k=3\), а тройка это тоже самое, что \(\frac{3}{1}\). При этом \(k>0\). Поэтому идем вправо на единицу и вверх на \(3\). Ставим точку. |
Шаг 3. Проводим через эти две точки прямую. |
Пример: Построить график функции \(y=-\frac{1}{4} x-3\).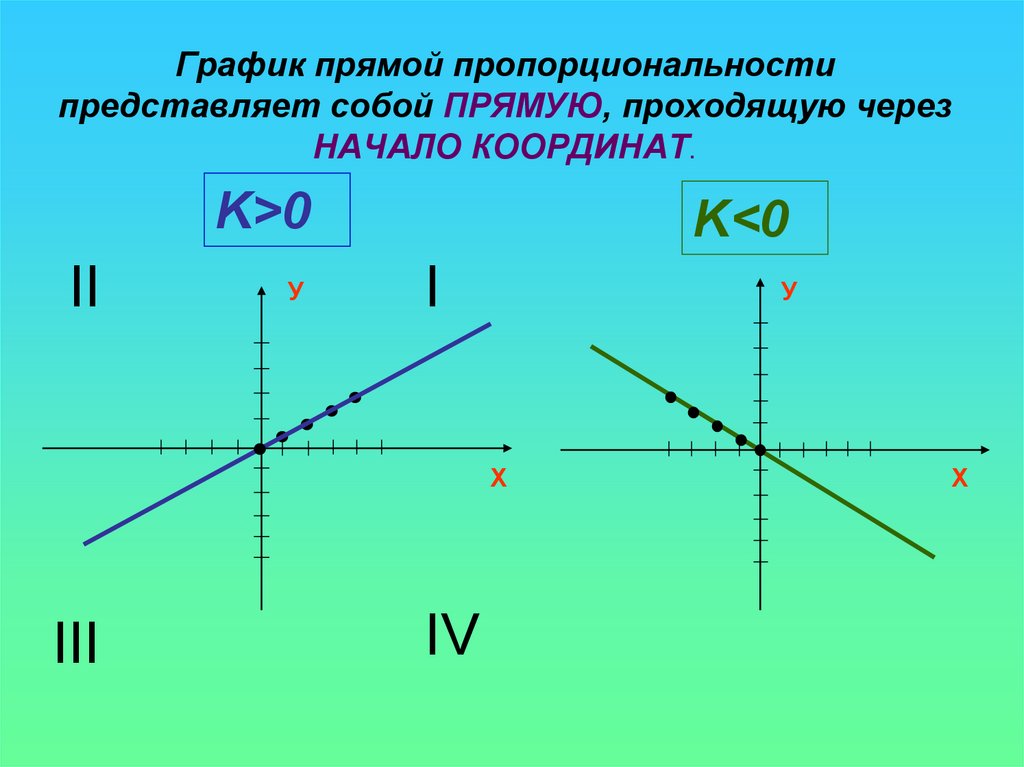
|
Шаг 1. \(b=-3\) отмечаем точку с этим значением на оси \(y\).
|
Шаг 2. \(k=-\frac{1}{4}\), \(k<0\), числитель \(1\), знаменатель \(4\). Значит, идем вправо на \(4\) и вниз на единицу. |
Шаг 3. Проводим через эти две точки прямую. |
Немного потренируйтесь и вы сами поймете, какой это классный способ строить линейную функцию.
Как построить график функций? График функции у 0 5
Здравствуйте, Давид.
График функции представляет собой её геометрический образ. Он показывает, где на координатной плоскости находится точка, координаты которой (Х и У) связаны определенным математическим выражением (функцией).
Он показывает, где на координатной плоскости находится точка, координаты которой (Х и У) связаны определенным математическим выражением (функцией).
Перед тем, как приступить к построению графика функций, сначала необходимо начертить оси координат ОХ и ОУ. Лучше всего для этого использовать масштабно — координатную бумагу. Далее следует определить тип функции, потому что у различных функций графики очень сильно отличаются. К примеру, линейная функция, о которой пойдет речь ниже, имеет график в виде прямой линии. После этого нужно определить область определения функций, т.е. ограничения для значений Х и У. К примеру, если Х находиться в знаменателе дроби, то его значение не может быть равным 0. Далее надо найти нули функции, то есть места пересечения графика функции с осями координат.
Приступим к построению графика функции, указанной в пункте а) вашего вопроса.
Функция у= — 6х + 4 , график которой требуется построить в первой задаче вашего вопроса, является линейной функцией, т. к. линейные функции представлены выражением y = kx + m. Областью определения линейной функции считается вся прямая ОХ. Параметр m в линейной функции определяет точку, в которой график линейной функции пересекает ось OY.
к. линейные функции представлены выражением y = kx + m. Областью определения линейной функции считается вся прямая ОХ. Параметр m в линейной функции определяет точку, в которой график линейной функции пересекает ось OY.
Для того, чтобы построить график линейной функции достаточно определить хотя бы две её точки, потому что графиком функции является прямая. Если найти больше точек, то можно построить более точный график. Вообще, при построении графика линейной функции необходимо определить точки, в каких график пересечет оси координат Х, У.
Итак, в вашем случае точки пересечения графика функции с осями координат будут такими:
При Х=0, У= -6*0+4=4 Таким образом, мы получили значение параметра m в линейной функции.
У=0, то есть 0= -6*Х+4, то есть 6х=4, следовательно Х=4/6=0,667
При Х= -1, У=-6*-1+4=10
При Х=1, У= -6*1+4=-2
При Х=2, У= -6*2+4=-8
Получив все вышеуказанные точки, вам остается только отметить их на координатной плоскости, соединить прямой линией, как показано в примере на рисунке, который прикреплен к данной статье.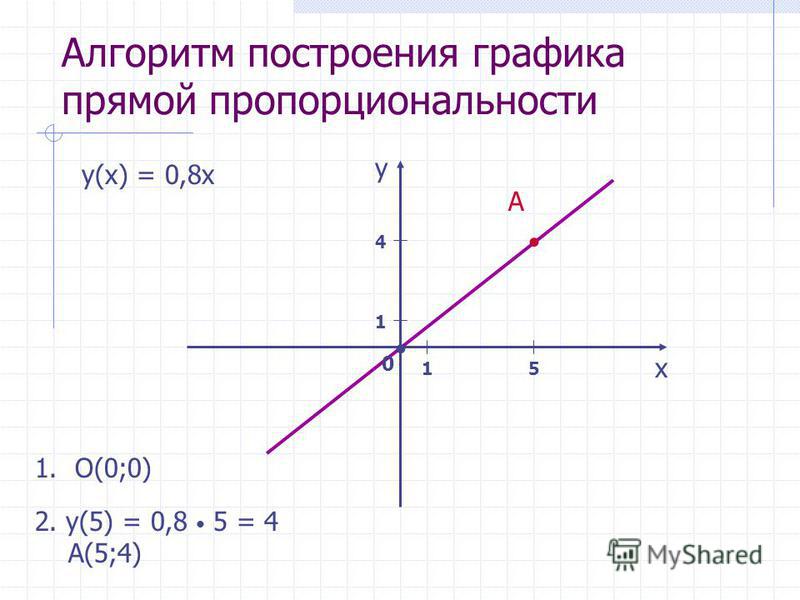
Теперь построим график функции, указанной в пункте б) вашего вопроса.
Сразу видно, что функция у= 0,5х , из второй задачи, также является линейной функцией. В отличие от первого примера, в данном выражении отсутствует значение m, а это говорит о том, что график функции у= 0,5х проходит через начало осей координат, то есть в их нулевой точке.
При Х=0, У= 0,5*0=0
При Х= 1, У=0,5*1=0,5
При Х=2, У= 0,5*2=1
При Х=3, У=0,5*3=1,5
При Х= -1, У=0,5*-1= -0,5
При Х= -2, У= 0,5*-2= -1
При Х= -3, У=0,5*3= -1,5
Теперь, имея все вышеуказанные значения Х и У вы без труда сможете поставить эти точки на координатной плоскости, соединить их прямой линией при помощи линейки, и у вас получится график линейной функции у=0,5х
Ниже я привела ссылку, перейдя по которой, вы можете найти уроки по математике, алгебре, геометрии и русскому языку. Я бы посоветовала вам прочитать несколько тем, которые касаются построения графиков функций. В данном учебном материале очень наглядно показано, как можно построить графики линейных функций, а в темах, которые расположены далее можно увидеть примеры построения графиков других функций. Все написано достаточно подробно, поэтому это будет понятно не только тем, кто давно закончил школу и имеет представление о том, как можно построить график функции, но и тем, кто только начинает постигать азы науки. Я считаю, что увидев наглядно на конкретных примерах, как строятся графики функций, вы потом без проблем сможете решить любую задачу по построению графика функций.
Все написано достаточно подробно, поэтому это будет понятно не только тем, кто давно закончил школу и имеет представление о том, как можно построить график функции, но и тем, кто только начинает постигать азы науки. Я считаю, что увидев наглядно на конкретных примерах, как строятся графики функций, вы потом без проблем сможете решить любую задачу по построению графика функций.
Сегодня мы внимательно изучим функции, графиком которых является прямая линия.
Запиши в тетрадь тему урока
«Линейная функция и прямая пропорциональность».
Внимательно выполняй все задания и
старайся запомнить новые для тебя определения.
Запомни определение:
Линейной функцией называется функция, которую можно задать формулой вида
у = kx + b, где х — независимая переменная, k и b — некоторые числа.
Например: если k = 0,5 и b = -2, то у = 0,5х — 2.
Задание:
Построить график линейной функции у = 0,5х — 2.
Составь таблицу значений пар (х, у).
Отметь их на координатной плоскости.
Соедини точки линией.
Проверь решение:
Построим график линейной функции у = 0,5х — 2.
| х | -4 | 0 | 2 | 4 |
| у | -4 | -2 | -1 | 0 |
Для построения графика у = -х + 3 вычислим координаты двух точек
| х | -2 | 4 |
| у | 5 | -1 |
Отметим их на координатной плоскости две точки и соединим их прямой.
А сможешь ли ты определить:
принадлежит ли точка А(36; 5) графику линейной функции ?
Да
Нет
А теперь сравни эти два графика и увидим, что у линейной функции у = kx + b,
еще до его построения можно «предугадать» расположение прямой линии на координатной плоскости!
Как?
Просто надо внимательно посмотреть на числа k и b.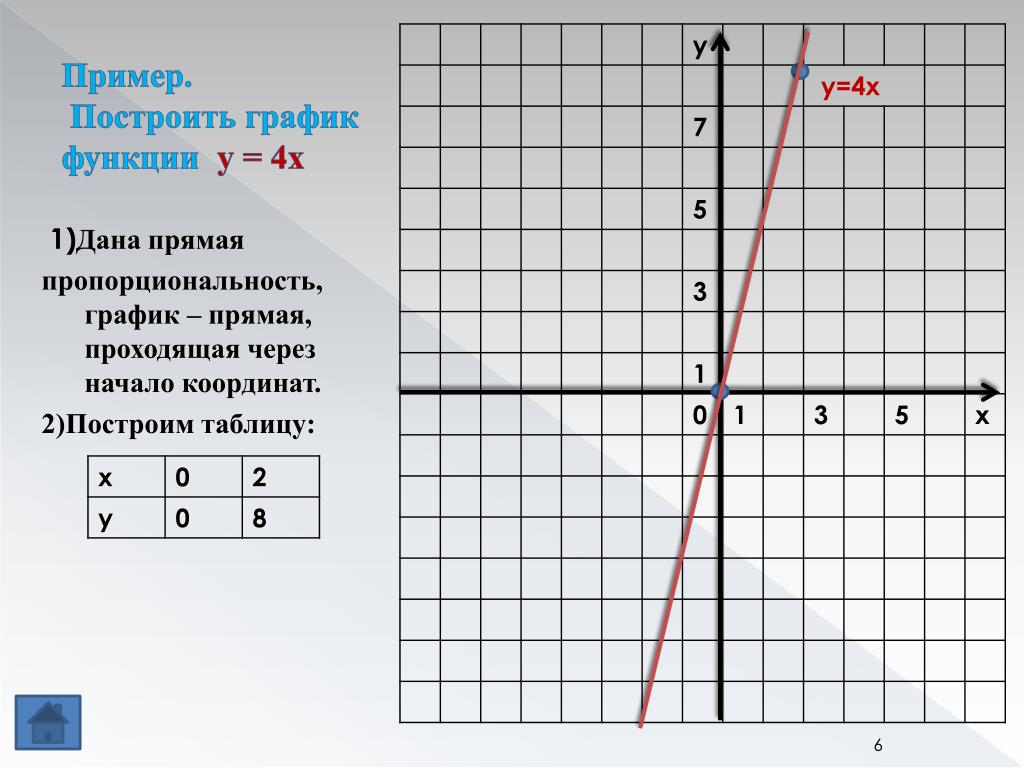 ..
..
И они многое нам расскажут!
Попробуй догадаться…
| Функция у = 0,5х — 2 | Функция у = -х + 3 |
Итак, наблюдаем и делаем выводы:
1) Первый пересекает ось ОУ в точке (0; -2), а второй в (0; 3)
!!! у первого b = -2, а у второго b = 3
Вывод: по числу b в формуле y = kx + b мы определим в какой точке прямая пересечет ось ординат.
2) Первый наклонен к положительному направлению оси ОХ под острым углом, а второй — под тупым углом.
!!! у первого k > 0, а у второй функции k
Вывод: если в формуле y = kx + b мы видим, что число k > 0 значит график наклонен к положительному направлению оси абсцисс под острым углом;
если же число k Число k (коэффициент при х) называют за это — угловым коэффициентом.
Запомни это все! Нам такие знания еще не раз пригодятся
Если в формуле y = kx + b, мы возьмем b = 0, то получим формулу y = kx.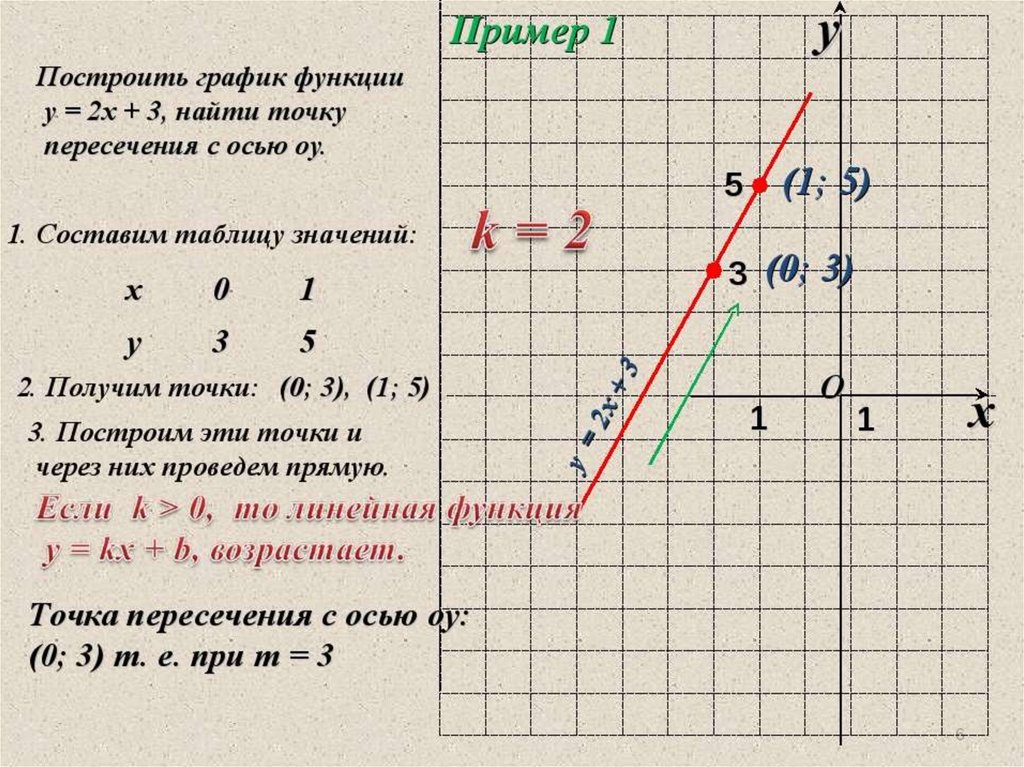
Запомни определение:
Функция, которую можно задать формулой y = kx, где k — некоторое число не равное 0, х — переменная, называется прямой пропорциональностью.
Выполни в своей тетради задание:
Придумай несколько формул прямой пропорциональности с разными коэффициентами k и построй их графики в одной координатной плоскости.
Поскольку у прямой пропорциональности b = 0, то график пересечет ось ОУ в точке (0; 0).
На одной координатной плоскости мы можем нарисовать и несколько графиков!
У линейной функции график — прямая линия.
А прямые могут быть параллельными или пересекаться в одной точке…
Интересно, а до построения графиков, только посмотрев (внимательно!) на их формулы, мы может сделать вывод:
Графики этих функций — пересекутся,
графики этих функций — расположены параллельно.
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации.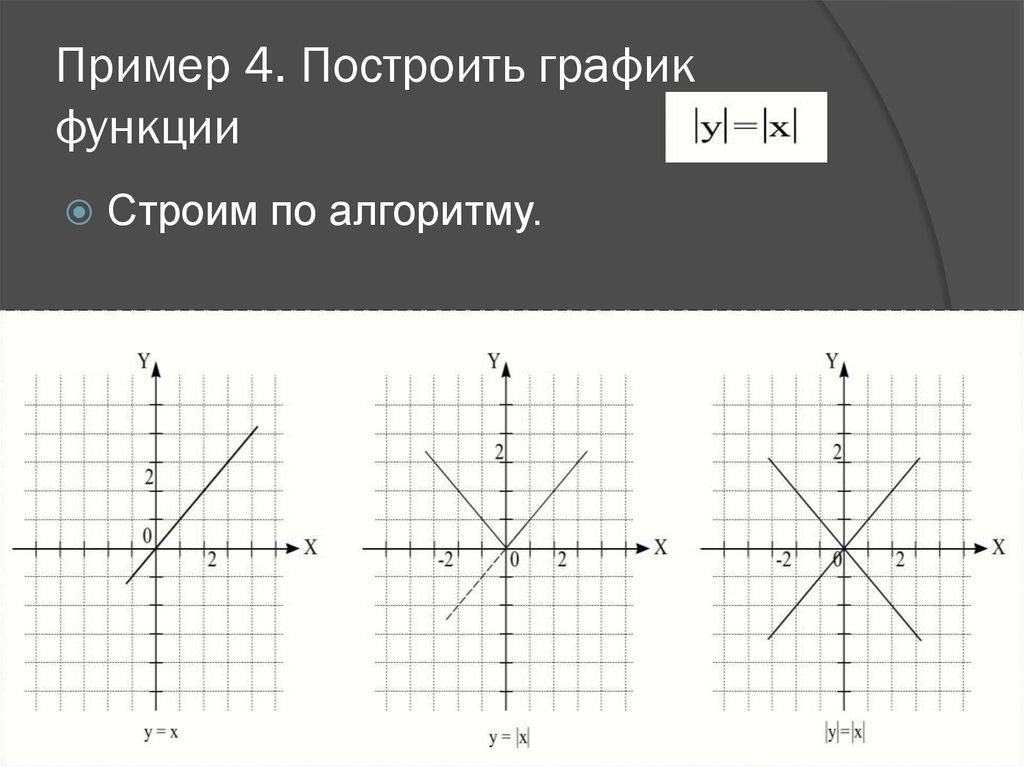 Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Урок алгебры в 9 классе по теме «Построение графиков функции, аналитическое выражение которых содержит знак абсолютной величины» был построен на основе компьютерных технологии, применяя исследовательскую деятельность обучения.
Цели урока: Обучающая: Наглядно продемонстрировать учащимся возможности использования компьютера при построении графиков функции с модулями; для самоконтроля, экономии времени при построении графиков функций вида у=f |(х)| , у = | f (х)| , у=|f |(х)| |.
Развивающая: Развитие интеллектуальных умений и мыслительных операций — анализ и синтез сравнение, обобщение. Формирование ИКТ компетентности учащихся.
Воспитывающая: Воспитание познавательного интереса к предмету путем введения новейших технологий обучения. Воспитание самостоятельности при решении учебных задач.
Оборудование: Оборудование: компьютерный
класс, интерактивная доска, презентация на тему
«Построение графиков функции, аналитическое
выражение которых содержит знак абсолютной
величины», раздаточный материал: карточки для
работы с графической моделью функций, листы для
фиксирования результатов исследования функций,
персональные компьютеры.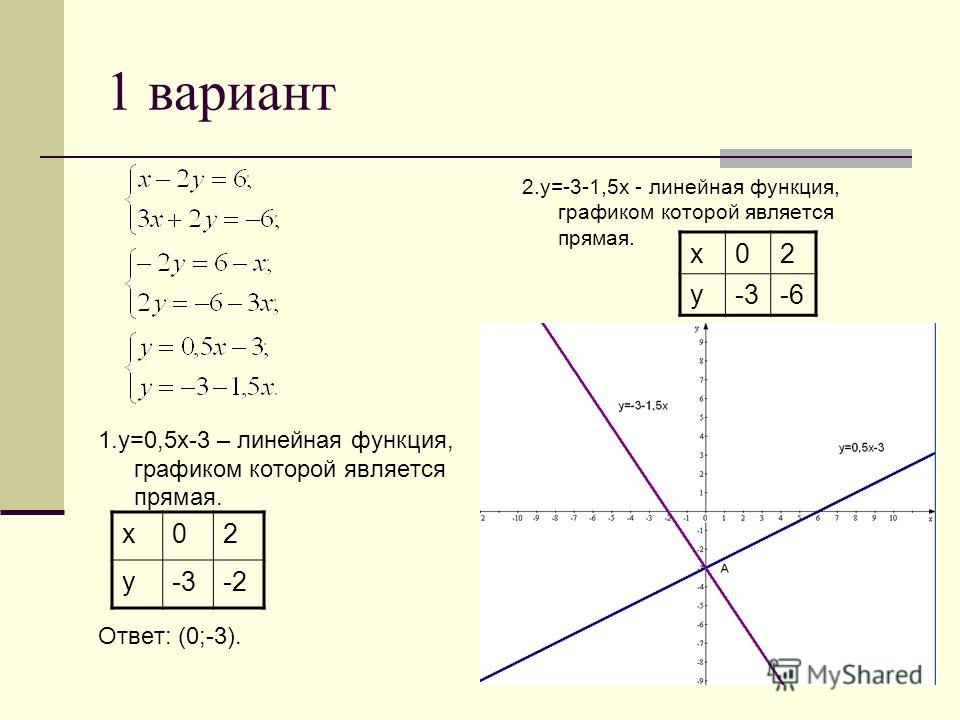 Лист самоконтроля.
Лист самоконтроля.
Программное обеспечение: презентация Microsoft PowerPoint «Построение графиков функции, аналитическое выражение которых содержит знак абсолютной величины»
Ход урока
1. Организационный момент
2. Повторение, обобщение и систематизация. Это этап урока сопровождается компьютерной презентацией.
График функции у=f |(х)|
у=f |(х)| — четная функция, т.к. | х | = | -х |, то f |-х| = f | х |
График этой функции симметричен относительно оси координат.
Следовательно, достаточно построить график функции у=f (х) для х>0,а затем достроить его левую часть, симметрично правой относительно оси координат.
Например, пусть графиком функции у=f (х) является кривая, изображенная на рис.1, тогда графиком функции у=f |(х)| будет кривая, изображенная на рис.2.
1. Исследование графика функции у= |х|
Таким образом, искомый график есть ломанная,
составленная из двух полупрямых. (Рис.3)
(Рис.3)
Из сопоставления двух графиков: у=х и у= |х|, учащиеся сделают вывод, что второй получается из первого зеркальным отображением относительно ОХ той части первого графика, которая лежит под осью абсцисс. Это положение вытекает из определения абсолютной величины.
Из сопоставления двух графиков: у = х и у = -х, сделают вывод: функции у = f(|х|) получается из графика у = f (x) при х 0 симметричным отображением относительно оси ОУ.
Можно ли применять этот метод построения графиков для любой функции, содержащей абсолютную величину?
Слайд 3 и 4.
1. Построите график функции у=0,5 х 2 — 2|х| — 2,5
1) Поскольку |х| = х при х 0, у=0,5 х 2 — 2х — 2,5 . Если ху=0,5 х 2 + 2х — 2,5 .
2) Если рассмотрим график у=0,5 х 2 -2х — 2,5 при х
Можно ли применять этот метод построения графиков дл квадратичной функции, для графиков обратной пропорциональности, содержащие абсолютную величину?
1) Поскольку |х| = х при х 0, требуемый график
совпадает с параболой у=0,25 х 2 — х — 3.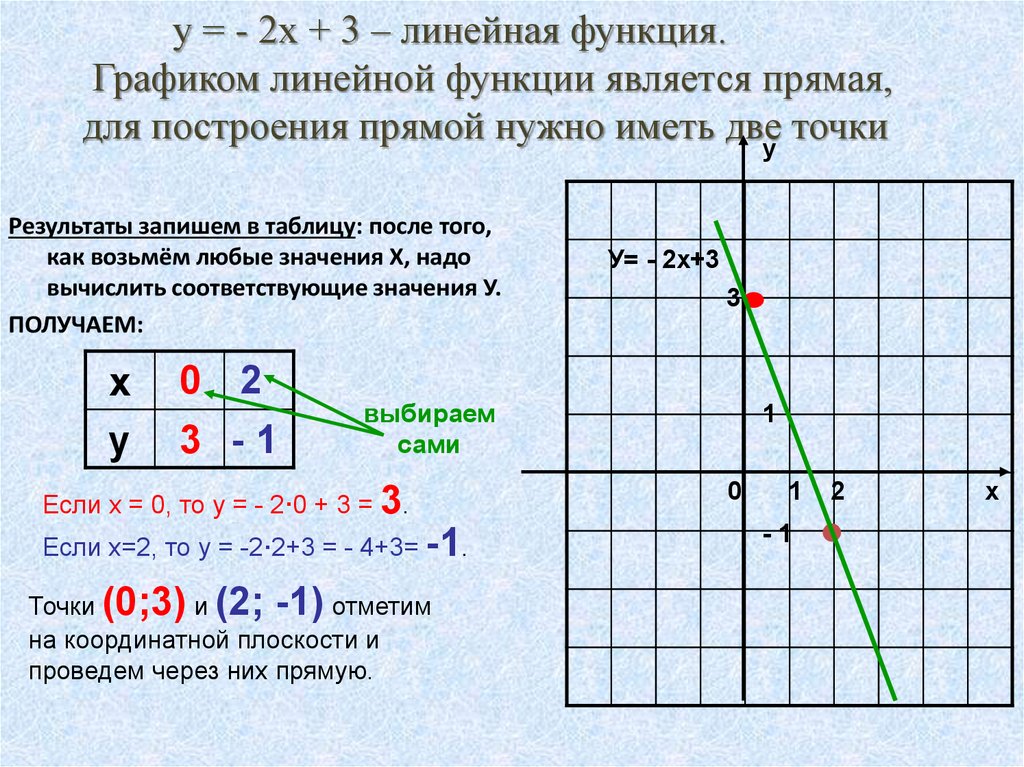 Если
ху=0,25 х 2
+ х — 3.
Если
ху=0,25 х 2
+ х — 3.
2) Если рассмотрим график у=0,25 х 2 — х — 3 при х 0 и отобразить его относительно оси ОУ мы получим тот же самый график.
(0; — 3) координаты точки пересечения графика функции с осью ОУ.
у =0, х 2 -х -3 = 0
х 2 -4х -12 = 0
Имеем, х 1 = — 2; х 2 = 6.
(-2; 0) и (6; 0) — координаты точки пересечения графика функции с осью ОХ.
Если х
Значит, часть требуемого графика, соответствующая значениям х0.
б) Поэтому достраиваю для х
На тетрадях ученики доказывают, что график функции у = f |(х)| совпадает с графиком функции у = f (х) на множестве неотрицательных значений аргумента и симметричен ему относительно оси ОУ на множестве отрицательных значений аргумента.
Доказательство: Если х 0, то f |(х)|= f (х),
т.е. на множестве неотрицательных значений
аргумента графики функции у = f (х) и у = f |(х)|
совпадают. Так как у = f |(х)| — чётная функция, то её
график симметричен относительно ОУ.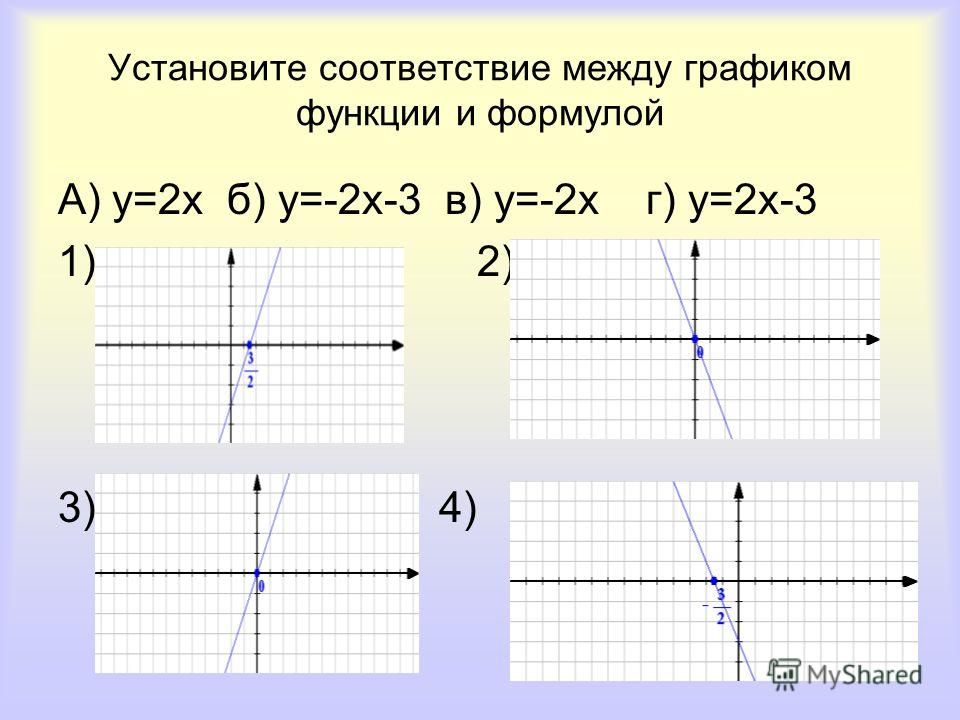
Таким образом, график функции у = f |(х)| можно получить из графика функции у = f (х) следующим образом:
1. построить график функции у = f(х) для х>0;
2. Для х
Вывод: Для построения графика функции у = f |(х)|
1. построить график функции у = f(х) для х>0;
2. Для х отразить построенную часть
относительно оси ОУ.
Слайд 5
4. Исследовательская работа по построению графика функции у = | f (х)|
Построить график функции у = |х 2 — 2х|
Освободимся от знака модуля по определению
Если х 2 — 2х0,
т.е. если х
0 и х2, то |х 2 —
2х|= х 2 — 2х
Если х 2 — 2х
Видим, что на множестве х
0 и х2 графики функции
у = х 2 — 2х и у = |х 2 — 2х|совпадают, а на множестве (0;2)
графики функции у = -х 2 + 2х и у = |х 2 — 2х| совпадают. Построим их.
График функции у = | f (х)| состоит из части графика функции у = f(х) при у?0 и симметрично отражённой части у = f(х) при у
Построить график функции у = |х 2 — х — 6|
1) Если х 2 — х -6 0, т.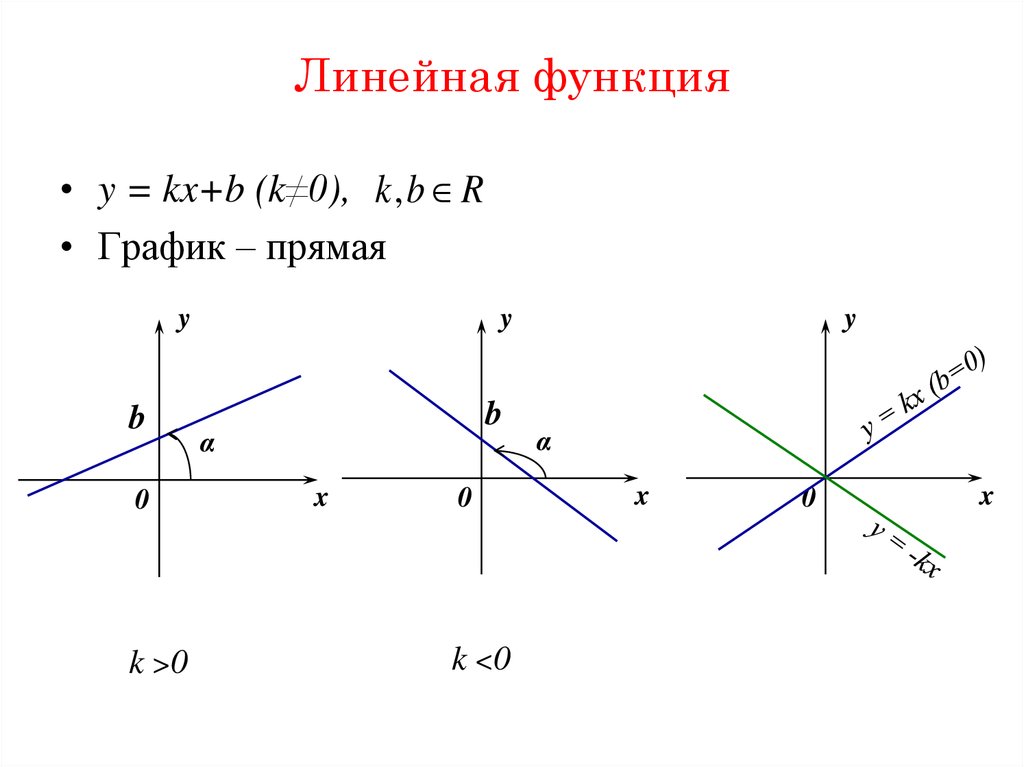 е. если х
е. если х
-2 и х3, то |х 2 — х -6|= х 2 — х -6.
Если х 2 — х -6
Построим их.
2) Построим у = х 2 — х -6 . Нижнюю часть графика
симметрично отбражаем относительно ОХ.
Сравнивая 1) и 2), видим что графики одинаковые.
Работа на тетрадях.
Докажем, что график функции у = | f (х)| совпадает с графиком функции у = f (х) для f(х) >0 и симметрично отражённой частью у = f(х) при у
Действительно, поопределению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий:
у = f(х), если f(х) 0; у = — f(х), если f(х)
Для любой функции у = f(х), если f(х) >0, то
| f (х)| = f(х), значит в этой части график функции
у = | f (х)| совпадает с графиком самой функции
Если же f(х) ) симметричнаточке(х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ «отрицательную» часть графика у = f(х).
Вывод: действительно для построения графика функции у = |f(х) | достаточно:
1. Построить график функции у = f(х) ;
Построить график функции у = f(х) ;
F(х)
Вывод: Для построения графика функции у=|f (х) |
1.Построить график функции у=f (х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f (х)
Слайды 8-13.
5. Исследовательская работа по построению графиков функции у=|f |(х)| |
Применяя определение абсолютной величины и ранее рассмотренные примеры, построим графиков функции:
у = |2|х| — 3|
у = |х 2 — 5|х||
у = | |х 2 | — 2| и сделал выводы.
Для того чтобы построить график функции у = | f |(х)| надо:
1. Строить график функции у = f(х) для х>0.
2. Строить вторую часть графика, т. е. построенный график симметрично отражать относительно ОУ, т.к. данная функция четная.
3. Участки получившегося графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
Построить график функции у = | 2|х | — 3| (1-й способ по определению модуля)
1.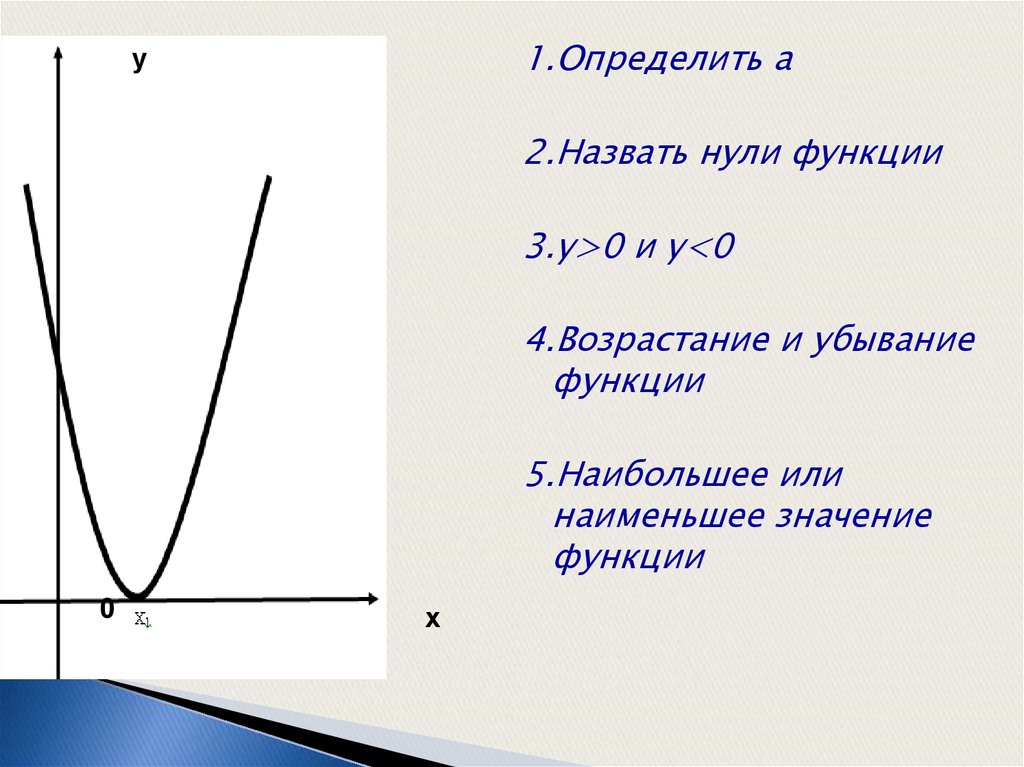 Строим у = 2|х | — 3 , для 2 |х| — 3 > 0 , | х
|>1,5 т.е. х1,5
Строим у = 2|х | — 3 , для 2 |х| — 3 > 0 , | х
|>1,5 т.е. х1,5
а) у = 2х — 3 , для х>0
б) для х
2. Строим у = —2 |х| + 3 , для 2|х | — 3
а) у = —2х + 3 , для х>0
б) для х
У = | 2|х | — 3|
1) Строим у = 2х-3, для х>0.
2) Строим прямую, симметричную построенной относительно оси ОУ.
3) Участки графика, расположенные в нижней полуплоскости, отображаю симметрично относительно оси ОХ.
Сравнивая оба графика, видим, что они одинаковые.
у = | х 2 — 5|х| |
1. Строим у = х 2 — 5 |х|, для х 2 — 5 |х| > 0 т.е. х >5 и х
а) у = х 2 — 5 х, для х>0
б) для х
2. Строим у = — х 2 + 5 |х| , для х 2 — 5 |х|
а) у = — х 2 + 5 х, для х>0
б) для х
У = | х 2 — 5|х| |
а) Строим график функции у = х 2 — 5 х для х>0.
Б) Строим часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней
полуплоскости, преобразовываю на верхнюю
полуплоскость симметрично оси ОХ.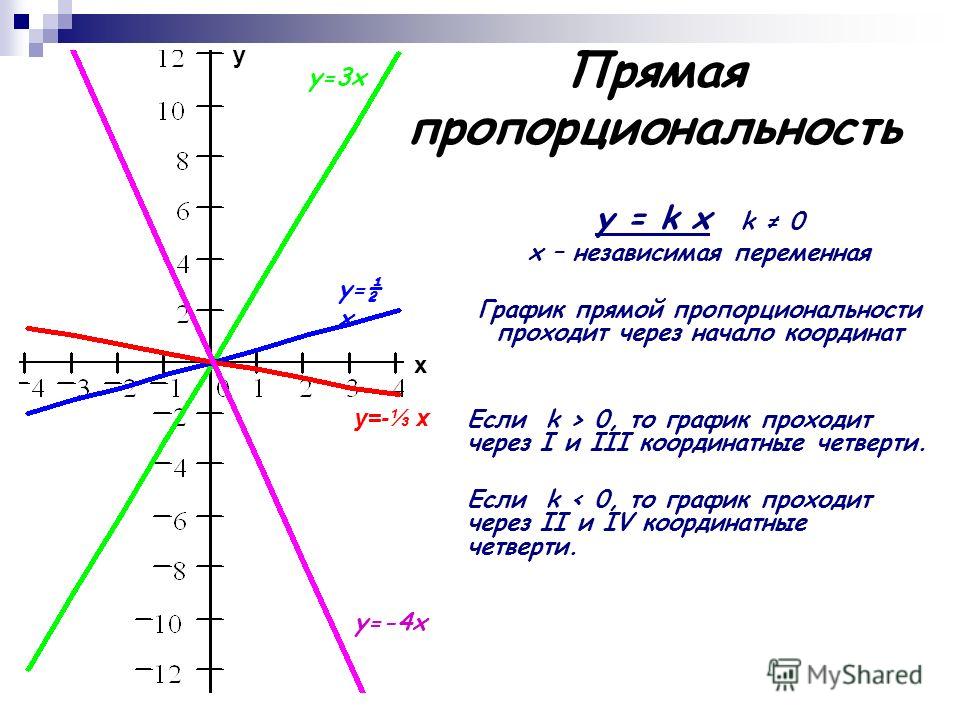
Сравнивая оба графика, видим что они одинаковые. (Рис.10)
3. Подведение итогов урока.
14,15 слайды.
у=f |(х)|
1.Построить график функции у=f (х) для х>0;
2.Построить для х
Алгоритм построения графика функции у=|f (х) |
1.Построить график функции у=f (х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f (х)
Алгоритм построения графика функции у=|f |(х)| |
1. Построить график функции у=f (х) для х>0.
2. Построить кривую графика, симметричную построенной относительно оси ОУ, т.к. данная функция четная.
3. Участки графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
Линейная функция. Виды, свойства, графики.
7 класс.
ГЛАВА 2. Функции.
§ 6. Линейная функция.
Количество функций неограничено.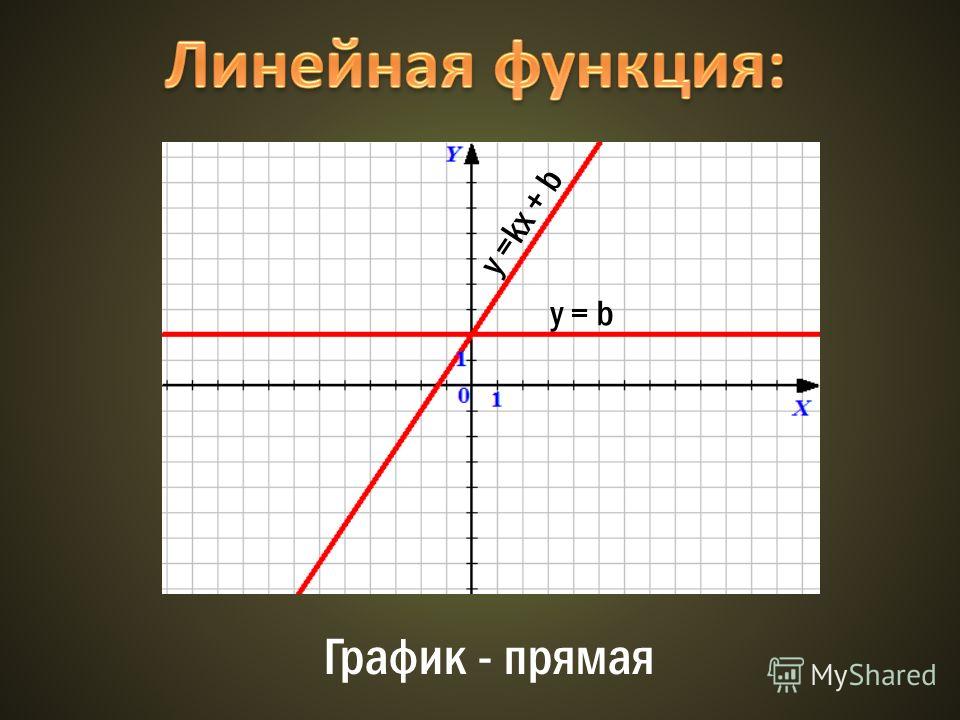 Однако, существуют функции, которые можно объединить в группы. Они имеют общую формулу, схожие свойства, графиком таких функций является одна и та же кривая. Прежде чем начать рассматривать одну из таких групп функций, введём несколько новых понятий.
Однако, существуют функции, которые можно объединить в группы. Они имеют общую формулу, схожие свойства, графиком таких функций является одна и та же кривая. Прежде чем начать рассматривать одну из таких групп функций, введём несколько новых понятий.
Функция называется возрастающей, если большему значению х соответствует большее значение у (т.е. при увеличении х увеличивается у).
Функция называется убывающей, если большему значению х соответствует меньшее значение у (т.е. при увеличении х уменьшается у).
Рассмотрим это на графике.
Фраза «при увеличении х…» означает, что мы рассматриваем график слева направо (также, как пишем и читаем). Если при этом график опускается вниз, то он убывает, если график поднимается вверх, то он возрастает.
На данном рисунке график убывает, если и ; а возрастает, если и .
Это можно записать так:
функция убывает при ;
функция возрастает при .
Теперь введём понятие линейной функции.
Линейной функцией называется функция, вида , где и – некоторые числа.
Например, .
Графиком любой линейной функции является прямая.
В зависимости от значений и , линейная функция разделяется на три вида. Рассмотрим каждый из них.
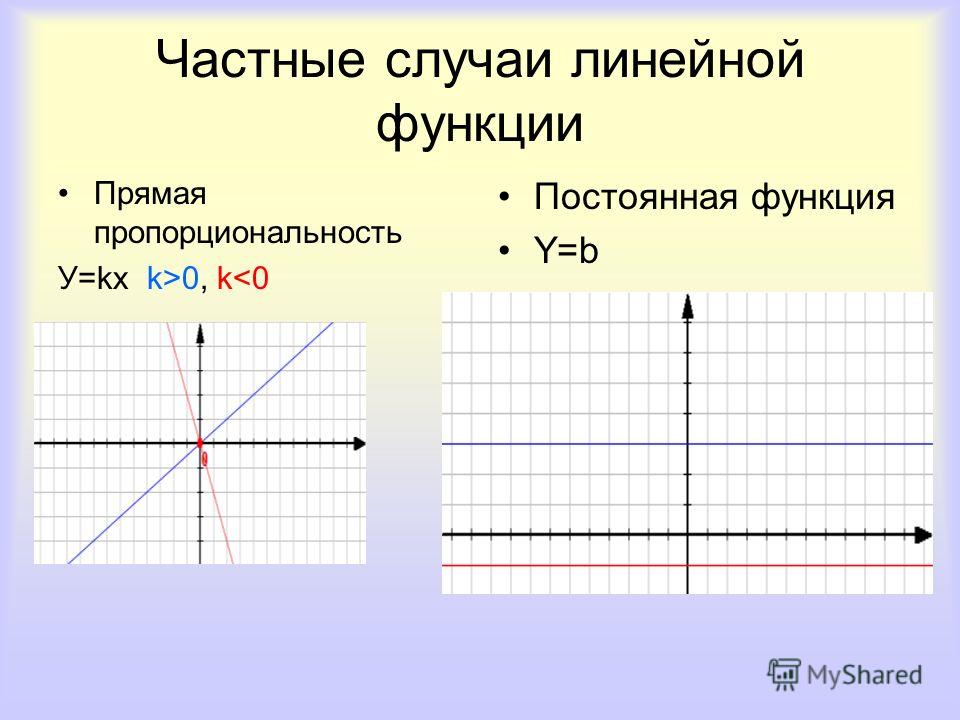
1. Если , то функция приобретает вид y = b. Такую функцию называют постоянной. Её графиком является прямая, параллельная оси Ox, проходящая через точку (0; b).
Область определения —
Область значений —
Функция является постоянной, поэтому промежутков возрастания и убывания у неё нет
Например, – постоянная функция, графиком является прямая, параллельная оси Ох, проходящая через точку .
Промежутков возрастания и убывания нет.
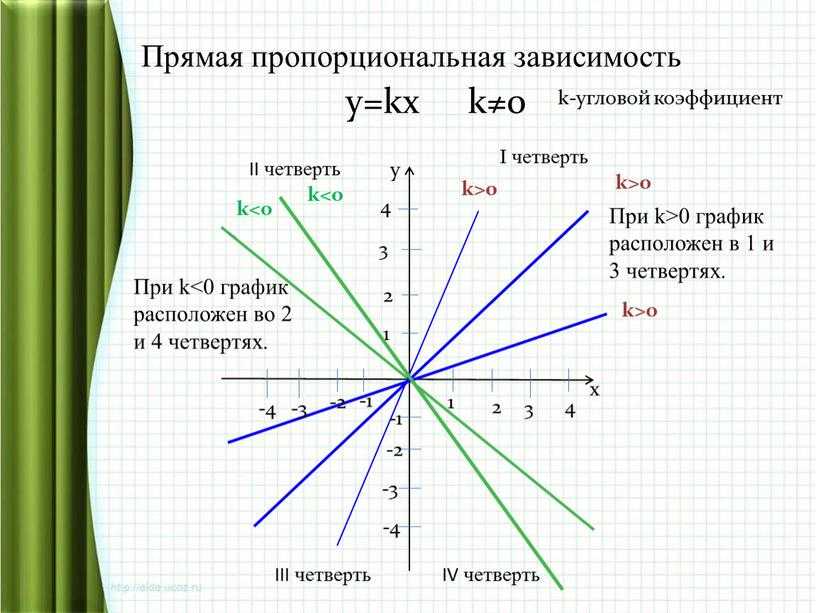
2. Если , то функция приобретает вид y = kx. Такую функцию называют прямой пропорциональностью. Её графиком является прямая, проходящая через начало координат и точку с произвольно выбранным значением аргумента Если , то прямая составляет с положительным направлением оси Ox острый угол. Если , то прямая составляет с положительным направлением оси Ox тупой угол. Поскольку от значения k зависит угол наклона прямой к положительному направлению оси Ох, то его называют угловым коэффициентом.
Область определения —
Область значений —
Если , то функция возрастает при
Если , то функция убывает при .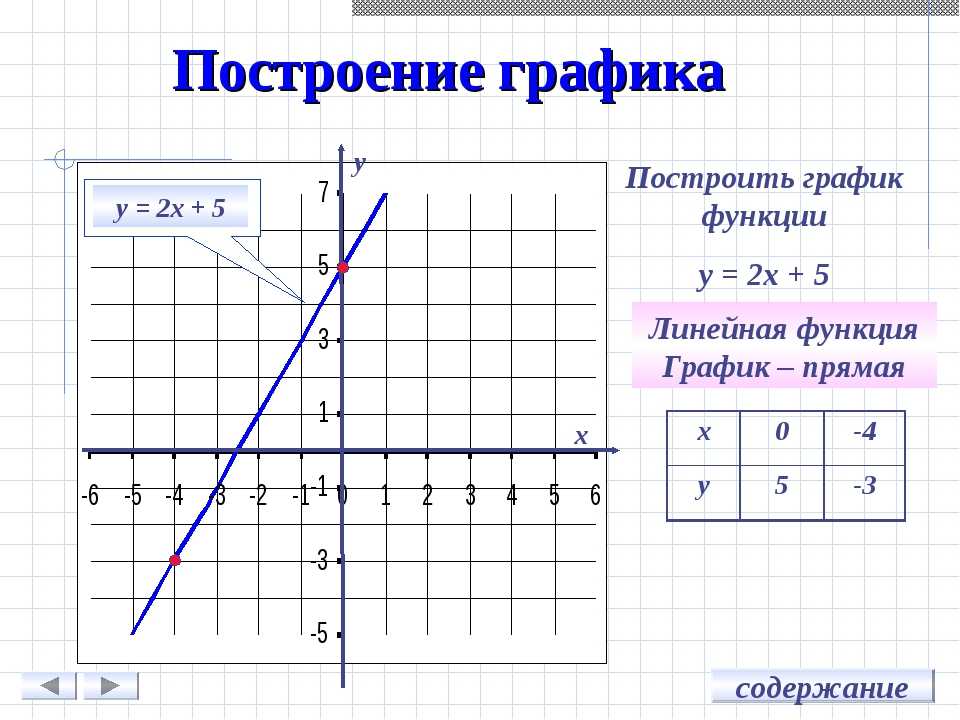
Например, а) – прямая пропорциональность, графиком является прямая, проходящая через начало координат и точку , и составляющая с положительным направлением оси Ох острый угол, т.к. .
Функция возрастает при .
б) – прямая пропорциональность, графиком является прямая, проходящая через начало координат и точку , и составляющая с положительным направлением оси Ох тупой угол, т.к. .
Функция убывает при .
3. Если , то функция не меняет свой вид . Это линейная функция. Её графиком является прямая, проходящая через точку и точку с произвольно выбранным значением аргумента . Коэффициент играет здесь такую же роль, как и в прямой пропорциональности.
Область определения —
Область значений —
Если , то функция возрастает при
Если , то функция убывает при .
Например, а) – линейная функция, графиком является прямая, проходящая через точки и , и составляющая с положительным направлением оси Ох острый угол, т.к. .
Функция возрастает при .
б) – линейная функция, графиком является прямая, проходящая через точки и , и составляющая с положительным направлением оси Ох тупой угол, т.к. .
Функция убывает при .
Рассмотрим теперь взаимное расположение графиков линейных функций.
Пусть даны две линейные функции и .
Если , то графики данных функций совпадают.
Если , то графики функций параллельны.
Если , то графики функций пересекаются в точке (или в точке , что то же самое).
Если , то графики пересекаются. Для нахождения координат точки пересечения необходимо решить уравнение: и найденное значение аргумента (х) подставить в любую из двух формул, посчитать полученное числовое выражение. Это и есть ордината точки пересечения графиков.
Например,
и . Так как у этих функций коэффициенты равны, то их графики параллельны.
и . Так как у этих функций коэффициенты k разные, а значения одинаковые и равны 1, то графики этих функций пересекаются в точке .
и .
 У этих функций k и b имеют разные значения, поэтому, чтобы найти координаты точки пересечения графиков этих функций, решим уравнение (приравниваем правые части):
У этих функций k и b имеют разные значения, поэтому, чтобы найти координаты точки пересечения графиков этих функций, решим уравнение (приравниваем правые части):
Подставляем найденное значение аргумента в любую из двух функций:
Значит, точка пересечения графиков данных функций .
В завершение конкретизируем значение коэффициента k и числа b в формуле линейной функции:
коэффициент k показывает угол наклона прямой к положительному направлению оси Ох. Если , этот угол острый; если , то этот угол тупой;
число b определяет точку пересечения прямой с осью Оу. — точка пересечения.
Из данных функций выбрать линейные:
Назовите коэффициенты k и b линейной функции :
Для функции представлена таблица:
Найдите коэффициент k и заполните таблицу.
Определите вид функции, постройте её график. Найдите область определения и область значений функции, найдите промежутки возрастания и убывания функции.
Не выполняя построения, определить угол наклона прямой к положительному направлению оси Ох и точку пересечения с осью Оу:
Функции заданы формулами . Укажите те из них, графиком которых является прямая, проходящая через начало координат, и постройте эти графики.
Функция задана формулой . Определите:
значение функции, если значение аргумента равно ;
значение аргумента, при котором значение функции равно ;
возрастающей или убывающей является данная функция?
Постройте график функции . Пользуясь графиком, найдите:
значение функции, если значение аргумента равно
значение аргумента, при котором значение функции равно
значения аргумента, при которых функция принимает положительные значения;
промежутки возрастания (или убывания) функции.

Не выполняя построения графика функции , укажите, через какие точки проходит этот график: .
Задайте формулой прямую пропорциональность, если известно, что её график проходит через точку .
Постройте в одной системе координат графики функций и укажите координаты их точки пересечения:
и ;
и .
Не выполняя построения графиков функций ; , определите:
чему равен угловой коэффициент каждой функции;
каково взаимное расположение графиков данных функций;
каковы координаты точек пересечения графиков функций с осями координат.
Не выполняя построения графиков функций , определите:
в какой точке каждый график пересекает ось у; ось х;
чему равен угловой коэффициент каждой функции;
каково взаимное расположение графиков данных функций.

Постройте в одной системе координат графики функций и запишите их область определения и область значений: .
Не выполняя построения, найдите координаты точек пересечения с осями координат графиков функций:
Не выполняя построения графика функции , найдите точку этого графика, у которой:
абсцисса равна ординате;
абсцисса и ордината – противоположные числа.
Найдите , если известно, что график функции проходит через точку .
Найдите , если известно, что график функции проходит через точку .
График функции пересекает оси координат в точках . Найдите значения и .
Все точки графика функции имеют одинаковую ординату, равную . Найдите значения и .
График функции параллелен оси абсцисс и проходит через точку .
 Найдите значения и .
Найдите значения и .Постройте графики функций:
Не выполняя построения, найдите точки пересечения графиков функций:
и
и .
Задайте формулой линейную функцию, график которой изображён на рисунке.
Постройте график функции:
Пересекаются ли графики функций:
и ;
и ?
В том случае, когда графики пересекаются, постройте их. Определите по графику координаты точки пересечения и проверьте результаты вычислением.
Запишите формулу функции, график которой параллелен графику функции и проходит через точку .
Найдите координаты точки пересечения графиков функций
и
При каком значении параметра а графики функций и
параллельны? Постройте графики этих функций.
При каком значении параметра а графики функций и
параллельны? Постройте графики этих функций.
Постройте прямые, координаты точек которых удовлетворяют уравнению .
Постройте прямые, координаты точек которых удовлетворяют уравнению .
При каком значении k графики линейных функций и имеют более одной общей точки?
Найдите наибольшее и наименьшее значение линейной функции на промежутке .
4
Алгебра. Урок 5. Графики функций
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Декартова система координат
- Функция
Прямая
Парабола
Гипербола
Квадратный корень
- Возрастающая/убывающая функция
- Наибольшее/наименьшее значение функции
- Примеры решений заданий из ОГЭ
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.
Линейная функция – функция вида y=ax+b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b:
Если a>0, прямая будет проходить через I и III координатные четверти.
b – точка пересечения прямой с осью y.
Если a<0, прямая будет проходить через II и IV координатные четверти.
b – точка пересечения прямой с осью y.
Если a=0, функция принимает вид y=b.
Отдельно выделим график уравнения x=a.
Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».
Графиком функции y=ax2+bx+c является парабола.
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a,b,c:
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a>0 , ветки параболы направлены вверх.
- Если a<0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y.
- Коэффициент b помогает найти xв – координату вершины параболы.

xв=−b2a
- Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
- Если D>0 – две точки пересечения.
- Если D=0 – одна точка пересечения.
- Если D<0 – нет точек пересечения.
Графиком функции y=kx является гипербола.
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k>0, то ветви гиперолы проходят через I и III четверти.
Если k < 0, ветви гиперболы проходят через II и IV четверти.
Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y.
Функция y = x имеет следующий график:
Функция y = f(x)возрастает на интервале, если большему значению аргумента (большему значению x) соответствует большее значение функции (большее значение y).
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
Функция y = f(x)убывает на интервале, если большему значению аргумента (большему значению x) соответствует меньшее значение функции (большее значение y).
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:
Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y). Это значение и будет являться наибольшим значением функции.
Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y). Это значение и будет являться наименьшим значением функции.
Скачать домашнее задание к уроку 5.
Функции — Линейные функции и уравнения
Наклон линейного уравнения — это число, которое показывает, насколько круто поднимается или опускается линия на нашем графике. Если мы притворимся, что линия представляет собой гору, мы как будто говорим о склоне горы. Если вам это поможет, нарисуйте вверху снежную шапку. Некоторые альпинисты. Подъемник. Впрочем, ничего слишком сложного.
Двигаемся слева направо по оси x , так же, как мы читаем. Если линия становится выше, когда мы движемся вправо, то мы поднимаемся на гору, поэтому линия имеет положительный наклон
Если линия становится ниже, когда мы движемся вправо, то мы спускаемся с горы, поэтому линия имеет отрицательный наклон.
Если мы остаемся на той же высоте, то наклон равен нулю, потому что мы не поднимаемся и не спускаемся. Довольно скучная гора, если вы спросите нас.
Теперь давайте найдем реальные числа для уклонов. Говоря о горах, наклон — это соотношение, которое описывает, насколько быстро меняется наша высота, когда мы движемся вправо. Не наш реальный физический рост, заметьте. Мы не станем ниже или выше на протяжении этих примеров, даже если к концу вы почувствуете, что выросли.
Не наш реальный физический рост, заметьте. Мы не станем ниже или выше на протяжении этих примеров, даже если к концу вы почувствуете, что выросли.
Джули взбирается на гору. На каждые 10 футов, которые проходит Джулия (измеряется по земле), она поднимается на 20 футов выше. Каков наклон горы?
На каждый фут, пройденный Джули (измеряется по земле), она поднимается на 2 фута над землей. Она была бы еще выше над землей, если бы носила каблуки, но мы полагаем, что это был бы странный выбор для альпинизма.
Наклон линии y = x равен 1. Если мы сдвинемся вправо на 1 на x — ось, мы также перемещаемся вверх на единицу по оси y :
Найдите наклон линии, изображенной ниже. Если мы не получим от вас вестей в течение трех часов, мы пошлем за вами смотрителя парка.
Давайте посмотрим, что происходит между парой точек графика:
На этой линии или горе мы поднимаемся на 2 на каждые 3, которые мы преодолеваем. За исключением одного раза, когда мы поднялись на 2, столкнулись с горным львом и побежали обратно на 7.
За исключением одного раза, когда мы поднялись на 2, столкнулись с горным львом и побежали обратно на 7.
Наш склон .
Один из способов представить уклон .
Чтобы использовать эту формулу для определения наклона линии, мы сначала фиксируем две точки на графике, координаты которых мы можем легко вычислить.
Повышение на — это сумма и изменений между этими двумя точками, и это число может быть положительным или отрицательным. Помните, вы можете подняться на или спуститься с горы на . Прогон — это сумма x изменений между этими двумя точками. Обычно мы думаем о перемещении из точки слева в точку справа, что означает, что x увеличивается, а «бег» всегда положителен. Вы можете подняться или опуститься, но вы никогда не побежите назад, верно? Мы имеем в виду, кроме того момента, когда вы пятились от горного льва.
Тогда наклон этой линии:
Будьте осторожны: Это все очень хорошо и полезно запомнить формулу, но для того, чтобы использовать ее правильно, вам нужно знать, что на самом деле означают «подъем» и «бег» , Это не относится к вашему нижнему белью, задирающемуся на вас, или к вашим чулкам, которые в них сползают, хотя и то, и другое было бы чудесно запоминающимся изображением.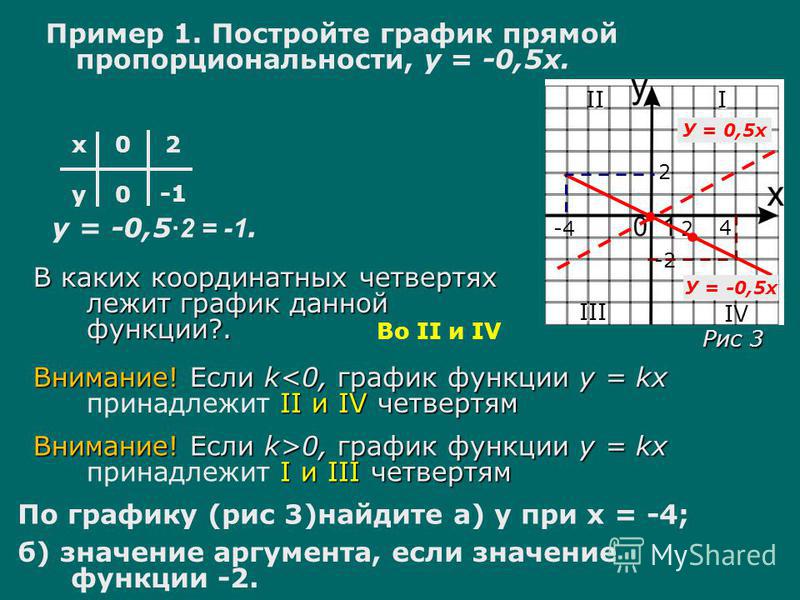 твоя голова:
твоя голова:
Пример задачи
Найдите наклон линии, показанной ниже.
Давайте найдем пару точек, с координатами которых удобно и легко работать, и посмотрим, какой подъем и разбег между этими двумя точками. Используйте изображение нижнего белья, если хотите. Это не поможет вам с этой проблемой, но вас никто не останавливает.
Наклон:
Пример задачи
Найдите наклон линии, показанной ниже.
Если мы попытаемся применить формулу к вертикальной линии, у нас будут проблемы. Поскольку «пробег» между любыми двумя точками на вертикальной линии равен 0, и мы не можем делить на 0, наклон вертикальной линии не определен. Таким образом, наклон линии x = 1 не определен.
Разумно, так как для того, чтобы бежать прямо на отвесную гору, потребуются мощные бедра. Если вы попытаетесь это сделать, вы также скоро потеряете определение.
Пример задачи
Найдите наклон проходящей линии через точки (1, 3) и (2, 7).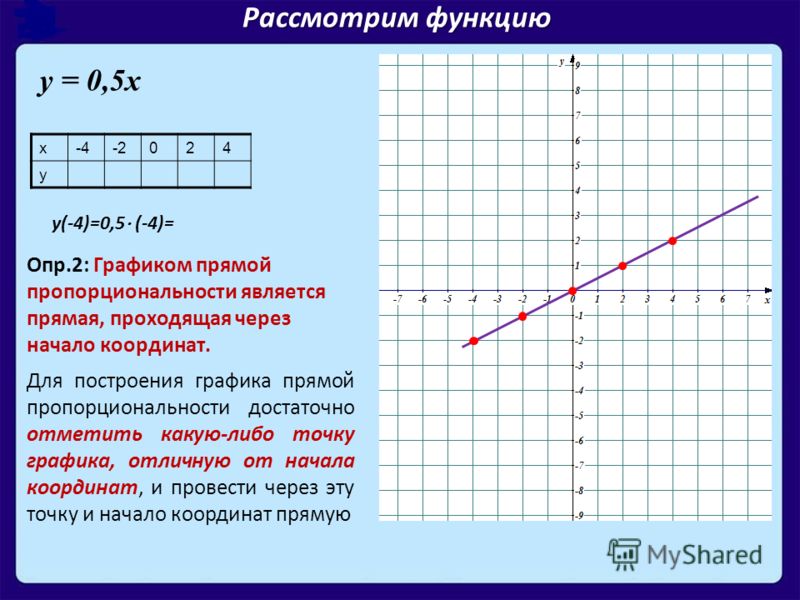
Мы можем найти наклон прямой, если заданы любые две точки на прямой. Мы знаем, что часть линии будет выглядеть так:
Чтобы попасть из точки (1, 3) в точку (2, 7), нам нужно двигаться вправо 1 и вверх 4:
Значит наклон линии . Йоделай-хи-ху!
Пример задачи
Найдите наклон прямой, проходящей через (-3, 1) и (2, -2).
Часть линии выглядит так:
Расстояние, которое мы проходим, чтобы получить от одного значения x в другое равно 3 + 2 = 5, так как сначала мы должны пройти от x = -3 до x = 0, а затем от x = 0 до x = 2. У нас есть остановка на оси y , где мы можем быстро перекусить фаст-фудом по завышенной цене, пока ждем нашей соединительной линии.
Чтобы перейти от одного значения y к другому, сначала мы переходим от y = 1 к y = 0, а затем от y = 0 к г = -2, для общего роста -3.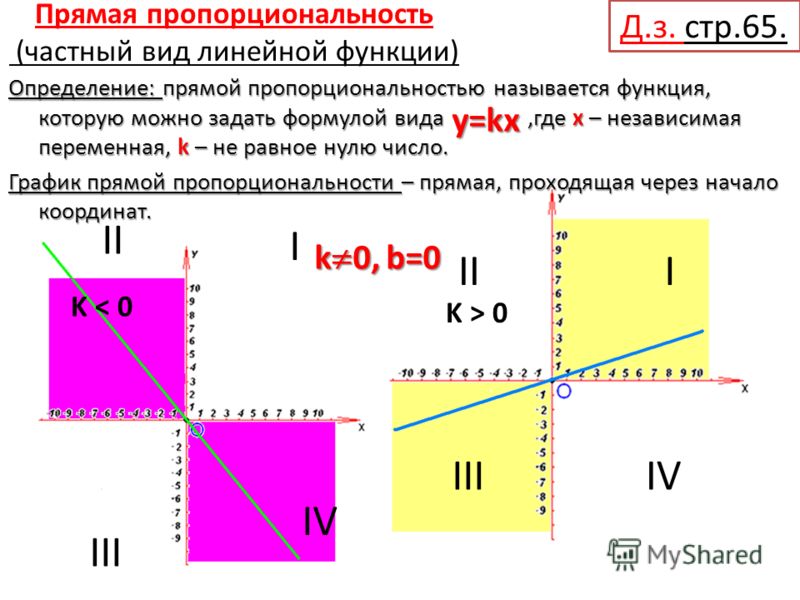 Еще раз, мы не могли получить прямой рейс. Ах хорошо. Это даст нам больше времени, чтобы прочитать книгу, над которой мы работали.
Еще раз, мы не могли получить прямой рейс. Ах хорошо. Это даст нам больше времени, чтобы прочитать книгу, над которой мы работали.
Таким образом, наклон этой линии равен .
Будьте осторожны: Часто делаются ошибки при расчете подъема и разбега, когда используются отрицательные координаты. Чтобы не ошибиться, рекомендуем нарисовать рисунок, который поможет в расчетах. Если искусство вам не по душе, найдите гору или забронируйте билет на самолет, чтобы воплотить в жизнь один из наших предыдущих примеров. Донести мысль таким образом будет дороже и отнять много времени, но это, безусловно, донесет идею до дома.
Итак, теперь мы можем считать наклон линии по графику или по любым двум точкам на линии. Мы хорошо себя чувствуем. Как насчет построения графика линии, если задана одна точка и наклон?
Пример задачи
Изобразите линию, проходящую через (0, 0) и имеющую наклон 2.
Начнем с рисования заданной точки:
Нам сказали, что линия имеет наклон из 2, что означает, что по мере того, как x перемещается на 1, y увеличивается на 2:
Теперь у нас есть две точки, которых достаточно, чтобы провести линию:
Линейные функции и прямые линии
6. 2 — Линейные функции и прямые линии
2 — Линейные функции и прямые линии6.2 — Линейные функции и прямые линии
Линейные функции
Нажмите здесь, чтобы просмотреть функции. Линейные функции — самые простые из всех типов функций. Линейная функция принимает число x в качестве входных данных и возвращает число м x + b в качестве выходных данных: m и b — константы. Другими словами, x умножается на м (это называется масштабированием на коэффициент м ) а затем добавляется b (это называется сдвигом на сумму b ). Используя обозначение функции, линейная функция выглядит следующим образом:f ( x ) = м x + б .Если мы допустим y = f ( x ), то это будет выглядеть так:
y = m x + b .Это называется уравнением 90 200 прямой линии 90 201, потому что, если мы нанесем точки, которые удовлетворить этому уравнению на графике y против x , тогда, как мы увидим ниже, все точки лежат на прямой.
Обычно линейная функция используется для преобразования одного набора единиц измерения в другой. Простой пример: если i — это расстояние, измеряемое в дюймах, а c — то же самое. расстояние измеряется в сантиметрах; тогда c = 2,54 i . Это просто масштабирование. Более сложный пример: если c — это температура измеряется в градусах Цельсия и f одно и то же температура измеряется в градусах Фаренгейта; тогда f = 1,8 c + 32. Это масштабирование и сдвиг.
Уравнение прямой
В разделе 6.1 мы ввели декартову плоскость с осью x , нарисованной горизонтально, и осью y , нарисованной вертикально. Предположим, что m и b — константы. Мы хотим построить график линейной функции:y = м x + б ,на этой плоскости и показать, что график представляет собой прямую линию. Для этого делаем следующую таблицу значений из y (то есть выражения 90 184 м x 90 185 + 90 184 b 90 185 ) по сравнению с 90 184 x 90 185 : 90 287
Обратите внимание на следующее:
- Каждая строка таблицы соответствует точке на графике.

- Одна из строк говорит, что когда x = 0, то y = b . Таким образом, точка (0, b ) является точкой на графике. Поскольку эта точка лежит на оси y , число b называется y перехват .
- При переходе от одной строки таблицы к другой значение x увеличивается на 1, а значение y увеличивается на m . Потому что увеличение устойчиво, точки должны лежать на прямой линии , а не на какой-либо другой кривой.
- Чем больше м есть, тем быстрее у увеличивается. Если м отрицательно, то значение г на самом деле уменьшает . Число м известно как уклон .
- x не обязательно должно быть целым числом — это может быть любое действительное число. Потому что
действительные числа плотны точки на графике
бесконечно близко друг к другу и образуют сплошную линию (т. е. нет промежутков).

| Вывод: Уравнение у = м x + б ,где m и b — константы, — уравнение прямой . м называется склоном, а б называется пересечение и . Эта форма уравнения называется наклоном . форма . Возможны и другие формы; Нажмите здесь, чтобы увидеть их. |
Нахождение уравнения прямой
Учитывая график прямой линии, есть несколько способов найти ее уравнение.
Метод 1: Этот метод работает, только если видна точка пересечения и .
- Найдите любые две точки, ( x 1 , y 1 ) и ( x 2 , y 2 ), на линии и подставьте их координаты в следующую формулу, чтобы получить м :
- Получить б из осмотра и перехват графа.

- Подставьте полученные числа для m и b в уравнение y = m x + b .
Метод 2: Этот метод работает, даже если точка пересечения y не видна.
- Как и в методе 1, найдите любые две точки, ( x 1 , y 1 ) и ( x 2 , y 2 ), на линии и подставьте их координаты в следующую формулу, чтобы получить м :
- Подставьте число, которое вы получили для м , в
уравнение y = m x + b .
Также возьмите одну из точек, скажем ( x 1 , y 1 ),
и подставьте его координаты в уравнение. Это дает:
y 1 = м x 1 + b
- Может показаться, что это не так, но это уравнение имеет только одну переменную, b ,
и вы можете легко решить для него.

- Подставьте полученные числа для m и b в уравнение y = m x + b .
Метод 3: Этот метод имеет то преимущество, что он использует только алгебру, а не геометрию, и может применяться к любому типу функции, а не только к прямой линии:
- Найдите две точки,
( x 1 , y 1 ) и
( x 2 , y 2 ), которые находятся на линии.
Возьмите первую точку ( x 1 , y 1 ) и
подставить его в уравнение прямой линии, y = m x + b .
Это дает:
г 1 = м x 1 + б
Точно так же возьмем вторую точку ( x 2 , y 2 ) и подставить его в уравнение прямой линии, y = m x + b . Это дает:
Это дает:y 2 = м x 2 + b
- Вместе эти два уравнения составляют систему двух уравнений с двумя неизвестными, м и б .
Мы можем решить их для m и b методом исключения.
Если быть точным, если мы вычтем первое уравнение из второго, то b равно
исключаем и получаем уравнение:
y 2 − y 1 = m x 2 − m x 1 ,
что при решении на m , дает то же уравнение, что и в двух других методах, а именно: - Найти b обратной заменой. Чтобы быть точным, подставьте число, которое вы
полученное для м в одно уравнение системы уравнений, скажем в y 1 = m x 1 + b .
 Это может выглядеть не так, но это уравнение имеет только одну переменную, b ,
и вы можете легко решить для него.
Это может выглядеть не так, но это уравнение имеет только одну переменную, b ,
и вы можете легко решить для него.
Пример: Используйте метод 1, чтобы найти уравнение прямой линии на графике справа.
Решение: Две точки на этой прямой равны ( x 1 , y 1 ) = (0, 15) и ( х 2 , у 2 ) = (3, 0). Подстановка этих координат в формулу наклона дает
= −5.По осмотру y перехват
б = 15.Подставляя эти два значения для м и б в уравнение прямой линии, y = m x + b , дает
y = −5 x + 15,
Пример: Используйте метод 3, чтобы найти уравнение прямой линии на графике справа.
Решение: На этой прямой есть две точки (7, 15) и (1, 3).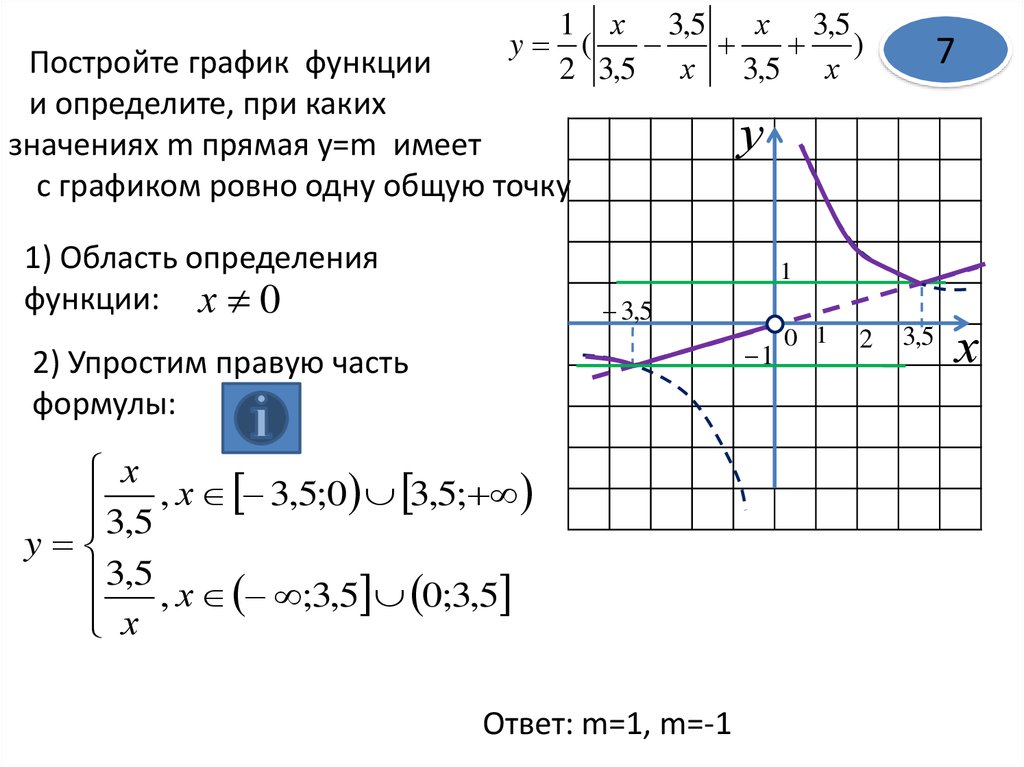 Подставляем координаты точки (7, 15)
в уравнение прямой, г = м x + б ,
а затем сделайте то же самое для точки (1, 3).
Это дает систему двух уравнений с двумя неизвестными, m и b .
Неизвестный b можно исключить, вычитая уравнения:
Подставляем координаты точки (7, 15)
в уравнение прямой, г = м x + б ,
а затем сделайте то же самое для точки (1, 3).
Это дает систему двух уравнений с двумя неизвестными, m и b .
Неизвестный b можно исключить, вычитая уравнения:
y = 2 х + 1.
| Упражнения тренера по алгебре |
Если вы нашли эту страницу в веб-поиске, вы не увидите
Оглавление в рамке слева. 92}$ производить изогнутую линию (график справа: график — кривая линия) вместо прямой линии, как левый график (график — прямая линия) на картинке? С левой стороны я соединил все точки маленькими прямыми линиями.
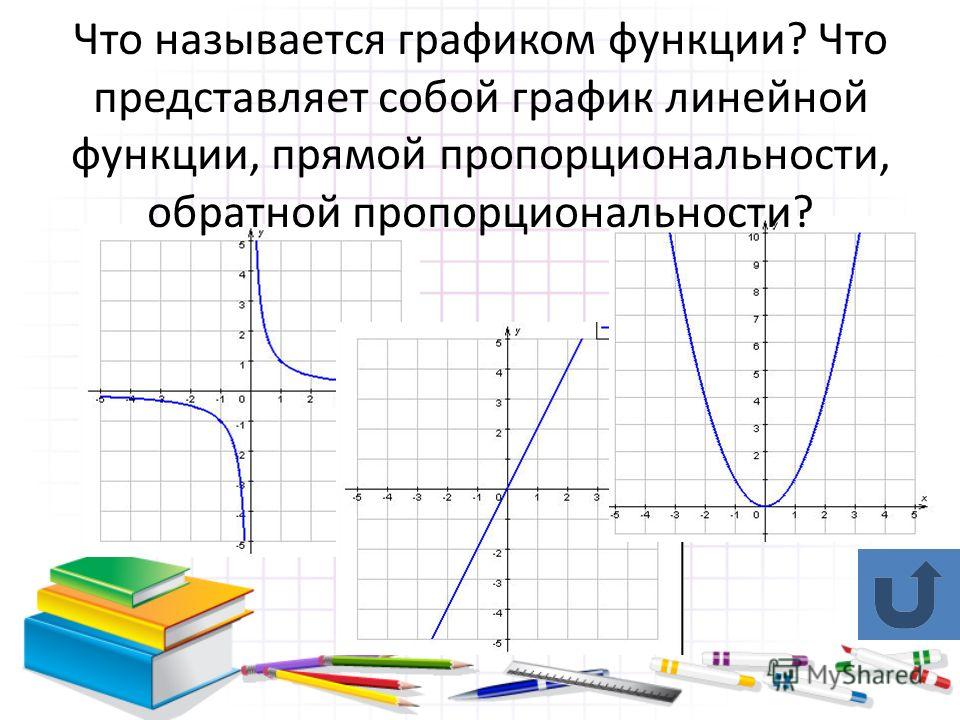 Но по книге это не правильно. Нет смысла обсуждать график изогнутой формы. Пожалуйста, просветите меня своим простым и экспертным мнением. Заранее спасибо!
Но по книге это не правильно. Нет смысла обсуждать график изогнутой формы. Пожалуйста, просветите меня своим простым и экспертным мнением. Заранее спасибо!- функции
- графические функции
$\endgroup$
6
$\begingroup$
Когда вы рисуете график функции, вы можете найти некоторые точки, как вы это делали, выбирая некоторые числа $x$, вычисляя их образы $f(x)$ и рисуя эти точки $(x,f(x)) $.
Вы сделали это с $(0,0),(1,1),(2,4),(-1,1),(-2,4)$.
Чтобы получить правильный график функции, вы должны взять КАЖДЫЙ другой $x \in \mathbb{R}$ и нарисовать каждую точку $(x,f(x))$.
Очевидно, что это невозможно, но чем больше точек вы найдете и нарисуете, тем больше нарисованный вами график будет похож на оригинал.
В этом случае соединять точки, которые вы нарисовали, прямой линией неправильно, потому что, если вы возьмете другие точки, например $(\frac{1}{2},\frac{1}{4})$, вы заметите что эта точка находится не на прямой линии, соединяющей $(0,0)$ и $(1,1)$, а ниже. 2$ является примером гладкой функции в том смысле, что она имеет производную в каждой точке своего графика (эквивалентно, уникальная касательная в точке каждую точку на графике). Таким образом, график, полученный нанесением точек и их соединением отрезками (то, что мы могли бы назвать кусочно-линейными), не имеет касательной в точках, где пересекаются отрезки, поскольку отрезки имеют разные наклоны. В любом случае это суть. Я мог бы быть более точным, но это заняло бы больше времени. Кроме того, я не уверен в вашей математической подготовке. 92}$) направление ВСЕГДА меняется, и у вас никогда не может быть трех или более точек на одной линии. Поэтому, если вы рисуете графики, соединяя точки прямыми линиями, если ваш график не является прямой линией, вы всегда можете делать только приближения к идеальному графику, для чего вам нужно соединить все бесконечные точки. Компьютеры могут соединять множество точек, бесконечных на наш взгляд, поэтому второй график, который вы опубликовали, очень похож на идеальный график.
2$ является примером гладкой функции в том смысле, что она имеет производную в каждой точке своего графика (эквивалентно, уникальная касательная в точке каждую точку на графике). Таким образом, график, полученный нанесением точек и их соединением отрезками (то, что мы могли бы назвать кусочно-линейными), не имеет касательной в точках, где пересекаются отрезки, поскольку отрезки имеют разные наклоны. В любом случае это суть. Я мог бы быть более точным, но это заняло бы больше времени. Кроме того, я не уверен в вашей математической подготовке. 92}$) направление ВСЕГДА меняется, и у вас никогда не может быть трех или более точек на одной линии. Поэтому, если вы рисуете графики, соединяя точки прямыми линиями, если ваш график не является прямой линией, вы всегда можете делать только приближения к идеальному графику, для чего вам нужно соединить все бесконечные точки. Компьютеры могут соединять множество точек, бесконечных на наш взгляд, поэтому второй график, который вы опубликовали, очень похож на идеальный график.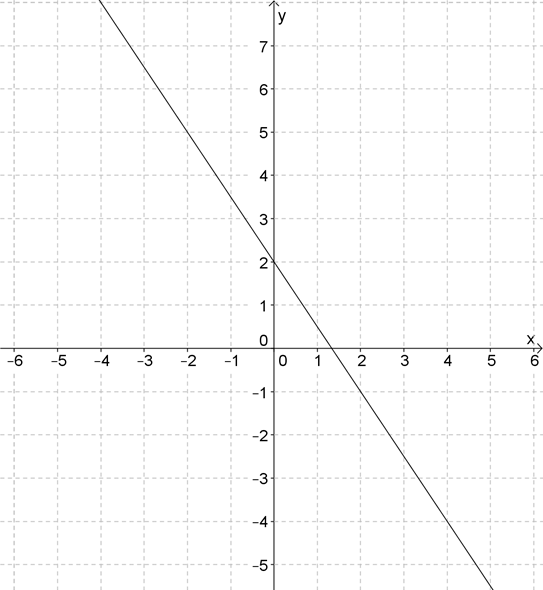
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
алгебраическое предварительное исчисление — Почему график $f(x)=ax+b$ представляет собой прямую линию?
Спросил
Изменено 5 лет, 5 месяцев назад
Просмотрено 591 раз
$\begingroup$
Я впервые буду преподавать ученикам 10-го класса, и при подготовке лекции мне было просто любопытно узнать об этом, чтобы я мог объяснить это своим ученикам
Спасибо
- алгебра-предварительный анализ
$\endgroup$
3
$\begingroup$
Ваш вопрос больше о педагогике, чем о математике. Причина, «почему» этот график представляет собой прямую линию, на самом деле зависит от того, какие предварительные знания по алгебре и геометрии вы привнесли в проблему.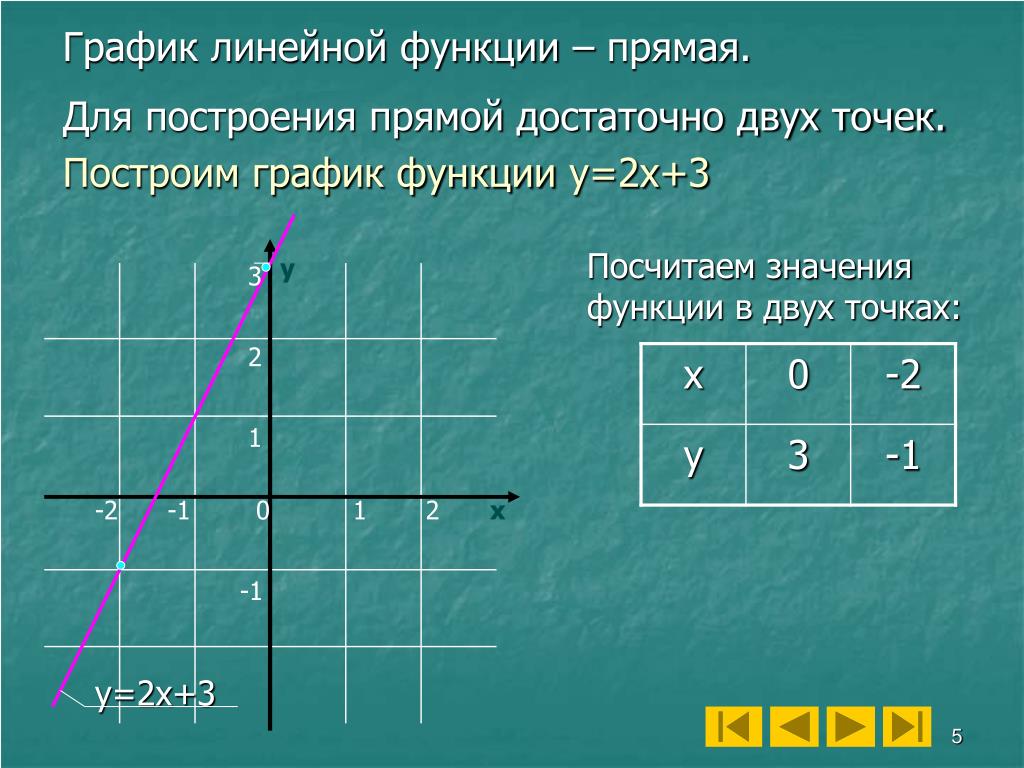 Десятиклассники и профессиональные математики получат ответы разного уровня сложности.
Десятиклассники и профессиональные математики получат ответы разного уровня сложности.
Итак, прежде чем начать урок, я бы посоветовал вам сделать несколько вещей.
Сначала подумайте, почему вы считаете, что график представляет собой прямую линию. Возможно, это не способ убедить десятиклассника, но с этого важно начать.
Тогда подумай о том, что уже знает твой класс. Нарисовали ли они много графиков из таблиц данных, иногда видя прямые линии, иногда нет? Сделали ли они это для данных, сгенерированных путем оценки различных видов функций? Если нет, то вы должны начать там. Они эмпирически обнаружат, что линейные функции имеют линии для графиков. Геометрический смысл $b$ как точки пересечения $y$ должен быть достаточно ясен. Наклон $a$ нам более тонкий. Подобные треугольники помогут. То же самое можно сказать и о приложениях к физическим ситуациям: подумайте о построении графика пройденного расстояния в зависимости от времени, пройденного с постоянной скоростью, банковского баланса с течением времени с простыми процентами, воды, заполняющей бассейн.
Вы не можете сделать это на «лекции». Обучение такого рода «почему» — это процесс, который требует времени и диалога. Кое-что из того, что работает, вы можете узнать от своих учеников.
Работая над преподаванием в десятом классе, задавайте вопросы на https://matheducators.stackexchange.com/ . Возможно, этот вопрос будет лучше там.
Удачи.
Редактировать: здесь есть связанные вопросы, которые могут помочь:
Как бы вы доказали, что график линейного уравнения является прямой линией и наоборот, на уровне «старшей школы»?
Почему мы считаем, что уравнение $ax+by+c=0$ представляет собой прямую?
$\endgroup$
3
$\begingroup$
Если они знают функции как «правила, которые присваивают числа другим числам» или что-то в этом роде, сначала покажите им график $y =x$, взяв числа за $x$ и нанеся их по точкам.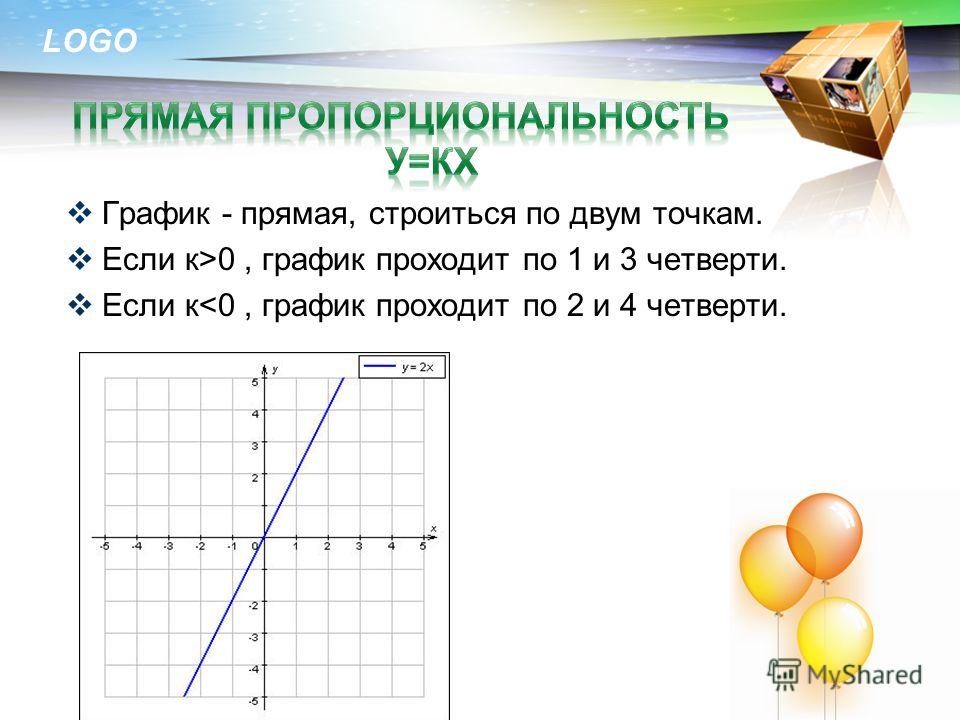 Затем покажите $2x$, $2x+1$ и т. д. и работайте по общей формуле. Как только вы начнете рисовать точки, учащиеся должны легко — и буквально — соединить точки.
Затем покажите $2x$, $2x+1$ и т. д. и работайте по общей формуле. Как только вы начнете рисовать точки, учащиеся должны легко — и буквально — соединить точки.
$\endgroup$
$\begingroup$
Что такое геометрическая линия? Концепция в основном, что это прямо. Что это значит. Значит… ну, значит, имеет постоянную крутизну, если бы она стала круче или помельче, то… бы изгибалась. Что означает постоянная крутизна или уклон? Это означает, что на любое расстояние, которое вы пройдете по горизонтали, вы пройдете пропорциональное расстояние по вертикали.
Следовательно, мы можем говорить о склонах, подъемах и тому подобных вещах. Вывод: каждая линия будет иметь отчетливый наклон, который представляет собой соотношение пропорционального подъема по сравнению с пробегом.
Итак, что означает плоскость x-y. Это означает, что мы можем нанести пары x, y на плоскость, где каждая точка представляет пару чисел, а любая фигура или кривая является визуальным представлением некоторой связи между значениями чисел. Наоборот.
Наоборот.
Итак, два вопроса: 1) если я нарисую физическую линию на плоскости, какое отношение между числами она представляет. 2) Какая кривая описывает отношение $y=mx+b$.
2) ответить проще. Каждое положительное увеличение X приведет к пропорциональному увеличению y. Другими словами, это устойчивый пропорциональный рост для пропорционального пробега; склон. Это линия. $m $ представляет его наклон. ($b $ просто представляет его относительное положение, где он начинается. Это точка пересечения yz, но… это совершенно другой план урока.)
Для полноты ответа следует также ответить 1). Линия имеет наклон. Таким образом, для любого увеличения значения x в большинстве случаев будет пропорциональное увеличение y. Если значение x увеличивается на $x $, то значение $y$ больше всего увеличивается на некоторое $mx $, где $m $ представляет собой увеличение наклона линии. Таким образом, $y=m+b$, где $b$ — просто некоторое постоянное значение, представляющее начальную ориентацию линии.
$\endgroup$
$\begingroup$
$\треугольник f = f(x+\треугольник h)-f(x)=a(x+\треугольник h)+b-(ax+b)=a\треугольник x$.
Таким образом, $\треугольник f = a\треугольник x$, так что для каждого изменения $x$ происходит пропорциональное изменение $a$, соответствующее наклону (постоянно).
$\endgroup$
5
$\begingroup$
Функция y=ax+b является прямой линией, потому что скорость, с которой функция растет, постоянна, т. е. наклон линии всегда постоянен, т. е. угол, который она образует с положительным направлением оси x, всегда постоянен . Надеюсь это поможет.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
прямых графиков: определение и уравнение
Прямые графики — это графическое представление линейных уравнений, где наивысшая степень равна 1. Их форма — прямая линия, а градиент вдоль линии постоянен.
Уравнение для прямых
Все линейные линии могут быть выражены в формате , где:
- y — значение координаты y точки на прямой.
- x — значение координаты x той же точки на прямой.
- м — градиент прямолинейного графика, который можно найти с помощью
Градиент определяется как крутизна линии в заданной точке.
- b — значение координаты y при пересечении прямой с осью y (x = 0).
Найдите уравнение прямой между точками (-1, 2) и (0, 8). Пожалуйста, оставьте свой ответ в форме
Пусть A = (-1, 2) и C = (0, 8). Градиент можно найти с помощью уравнения и точек
А = (-1, 2) и С = (0, 8).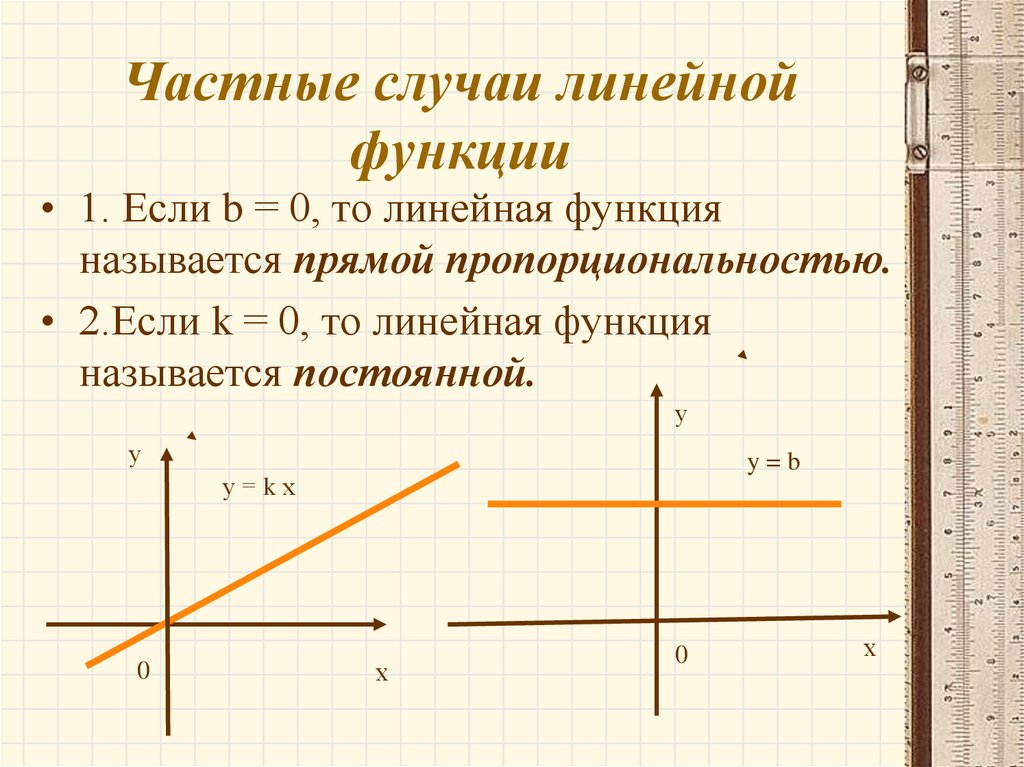
Другой метод расчета градиента — использование уравнения
Это уравнение требует рисования прямоугольного треугольника под линией и его координат, включая точку B = (0, 2), где угол треугольник равен 90°. Мы можем увидеть это графически как:
Графическое представление примера. Хайме Николс, StudySmarter Original
Поскольку точка C (0, 8) находится на оси Y, координата Y становится равной b в уравнении.
Следовательно, уравнение будет
. Вы можете переписать предыдущий пример в форме, используя точку A (-1, 2) и м = 6 следующим образом:
.
Уравнение также можно записать в виде. В отличие от первых двух уравнений, эта форма не может быть получена путем прямой подстановки значений в формулу. Вместо этого вы должны найти уравнение в одном из первых двух уравнений, а затем преобразовать его в форму.
Прямая линия имеет уклон и проходит через точку (0, 10). Запишите уравнение этой прямой в виде .
Запишите уравнение этой прямой в виде .
Сначала запишите уравнение прямой линии в одной из первых двух форм, где
м = и
Далее, A, B и C должны быть целыми числами, поэтому вам нужно умножить обе части уравнение на два, чтобы удалить дробь.
Наконец, вам нужно переместить x на другую сторону, чтобы он был в форме .
Нахождение координат с помощью уравнения прямой линии
Вас могут попросить найти координаты с помощью линейного уравнения. Для этого вы подставляете одно из значений в линейное уравнение, чтобы получить другое.
Линия A имеет линейное уравнение . Какова координата y точки на прямой, когда x = 14?
Зная значение x, вы можете подставить его в уравнение.
Следовательно, ответ (14, 136).
Строка B имеет линейное уравнение. Какова координата x точки на прямой, когда y = 17?
Зная значение y, вы можете подставить его в уравнение.
Следовательно, координата (5, 17)
Важно дать ответ в форме, заданной в вопросе.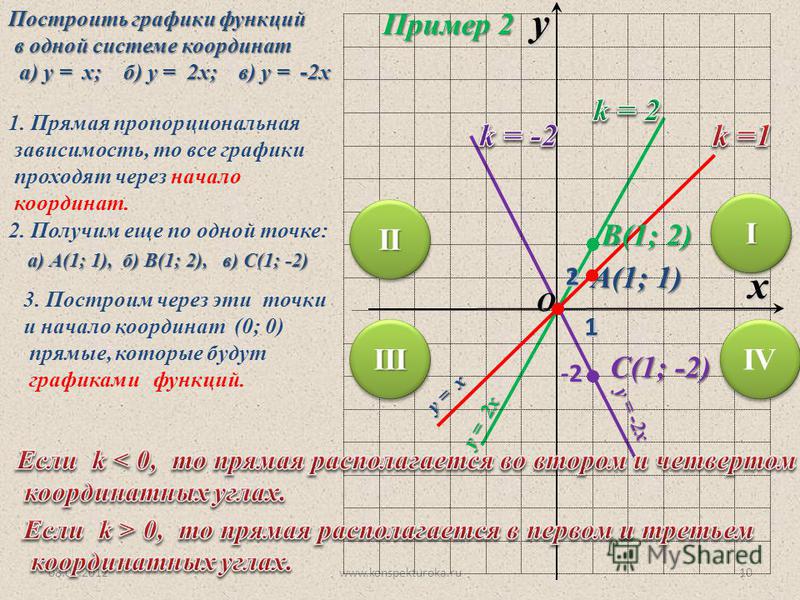 Если вас попросят указать координаты, убедитесь, что вы дали свой ответ в виде координат. Это распространенная ошибка, но ее легко избежать.
Если вас попросят указать координаты, убедитесь, что вы дали свой ответ в виде координат. Это распространенная ошибка, но ее легко избежать.
Как построить линейный график?
Чтобы построить линейный график, вам необходимо:
Построить таблицу значений x и y.
Нарисуйте свою ось на миллиметровой бумаге и подпишите ее, если они относятся к реальной ситуации.
Нанесите заданные точки на график.
Соедините все точки одной прямой с помощью линейки.
Проведите линию
1. Plot a table of the x and y values
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -5 | -3 | -1 | 1 | 3 | 5 |
2. Нарисуйте свой AXIS
Нарисуйте свой AXIS
. 9000.
9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000.. Джейми Николс, StudySmarter Originals4. Соедините все точки прямой линией. вам, чтобы рассчитать более сложное уравнение вопросов прямой линии. Используя предыдущий пример y = 6x + 8, мы пройдемся по характеристикам других типов градиентов.
Отрицательный уклон
На графике показаны линии и .
Отрицательный градиент на графике, Хайме Николс, StudySmarter Originals
Из этого графика мы можем сделать два наблюдения относительно отрицательного градиента: поэтому наличие отрицательного градиента не влияет на точку пересечения по оси y.
По мере того, как мы увеличиваем переменную x, переменная y уменьшается, и поэтому линия движется по диагонали вниз.
Градиент параллельных линий
Параллельные линии — это линии, которые существуют на одном и том же графике, но не пересекаются, постоянно сохраняя одно и то же расстояние друг от друга.
На приведенном ниже графике показаны две параллельные линии и
График параллельных линий, Джейми Николс, StudySmarter Originals
Есть два замечания, которые можно сделать о параллельных линиях:
- Когда две линии параллельны, градиенты одинаковы . В этом примере обе линии имеют градиент 6,9.0291
- Линии имеют разные значения для b и, следовательно, имеют разные точки пересечения с осью Y.
Градиент перпендикулярных линий
Перпендикулярные линии — это линии, которые пересекаются друг с другом в точке
На приведенном ниже графике показаны две перпендикулярные линии: и .
График перпендикулярных линий, Хайме Николс, StudySmarter Originals
Есть два важных замечания, которые можно сделать относительно градиентов перпендикулярных линий.
Чтобы линии пересекались друг с другом, градиенты двух прямых должны быть отрицательными обратными величинами. Отрицательная величина, обратная градиенту, определяется по формуле , где м — исходный градиент. В этом примере градиенты двух линий являются отрицательными обратными значениями друг друга.
Точка пересечения по оси Y одинакова для обеих линий, поскольку точка пересечения лежит на оси Y. Y-пересечение было бы другим для каждой линии, если бы линия пересечения не лежала на оси y. Например, если бы точка пересечения была (1, 14), вы бы подставили ее в формулу:
График перпендикулярных линий, Хайме Николс, StudySmarter Originals
Как найти уравнение графика прямой по набору точек?
Есть несколько различных типов вопросов, которые вам могут задать, и мы рассмотрим их с примерами.
Нахождение уравнения прямой, где точка пересечения с координатой Y неизвестна.
Иногда вам не сообщают точку пересечения по оси y, что означает, что нам нужно вычислить значение для C, если мы используем форму Ax + By = C.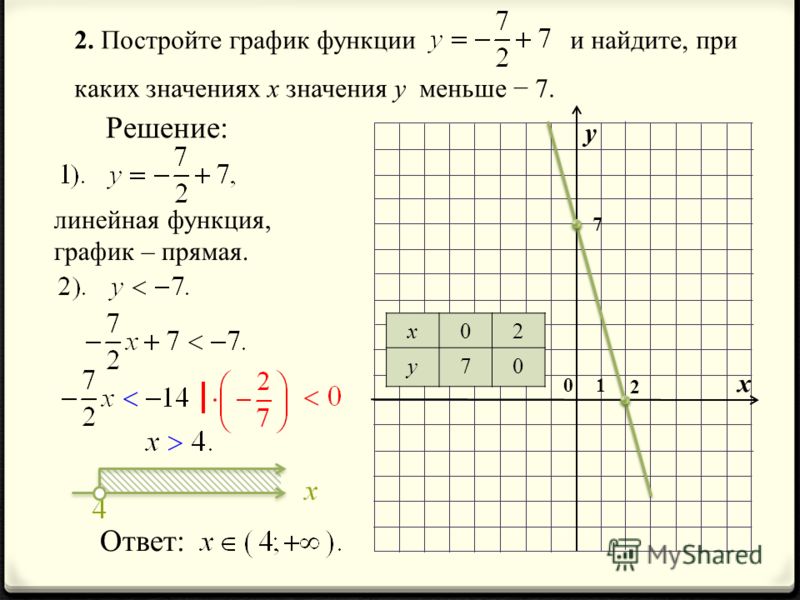 Для этого нам нужны следующие шаги:
Для этого нам нужны следующие шаги:
- Расчет градиента
- Подставьте значения x и y из точки на линии в уравнение.
- Переставьте, чтобы получить значение для
Линия C — это прямая, проходящая через 2 точки (2, 4) и (4,7). Какое уравнение для линии C?
- Рассчитайте градиент:
- Подставьте градиент и одну из точек в уравнение. Мы будем использовать точку (2, 4):
- Переставить, чтобы получить значение для b: Следовательно, ответ: Однако вас могут попросить написать уравнение Ax + By = C. C в этом уравнении не такой же, как b в первом уравнении, поэтому нам нужно продолжать переставлять.
Если у вас возникли трудности с этим шагом и вам не сказали указать конкретную форму, вам может быть проще работать с уравнением, поскольку вам не нужно переставлять, чтобы найти значение для b. Для приведенного выше примера вам нужно найти градиент и подставить точку в уравнение: .
Нахождение уравнения прямой по графикам
Нахождение линейного уравнения по графикам аналогичен вышеописанному методу с небольшими отличиями.
Определите две точки на линии
Рассчитайте градиент, используя эти две точки
Найдите значение b, посмотрев, где линия пересекает точку пересечения оси y
- Сформулируйте уравнение 9000.
Найдите линейное уравнение для графика ниже.
Треугольник, используемый для нахождения градиента, Хайме Николс
- Определите две точки на линии: (0, 2) и (1, 1) лежат на линии.
- Найдите градиент:
- Найдите точку пересечения y: Точка (0, 2) находится на оси y, поэтому b = 2.
- Подставьте значения в формулу:
Горизонтальные линии
Как градиент горизонтальные прямые равны 0, уравнение прямой равно y = b, где b — точка пересечения с осью y.
График y = b, Хайме Николс, StudySmarter Originals
Эта горизонтальная линия имеет уравнение y = 10, поскольку она пересекает ось y в точке (0, 10).
Вертикальные линии
Градиент вертикальных линий равен бесконечности и может быть выражен в уравнении x = d, где d — это точка пересечения линии с осью x.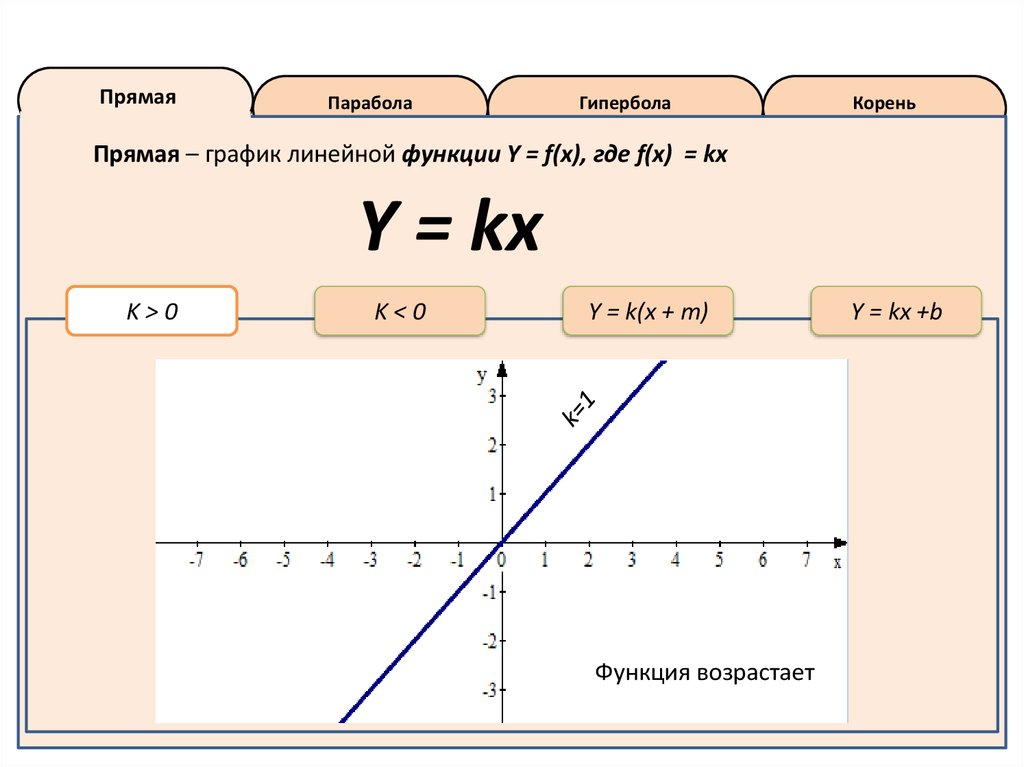
График x = d, Хайме Николс, StudySmarter Originals
Эта вертикальная линия имеет уравнение , потому что она пересекается с осью x в точке (0,5, 0)
Использование прямых графиков для примеров из реальной жизни
Прямые графики можно использовать для представления взаимосвязей между любыми двумя переменными. Например, компании используют его, чтобы показать, сколько продаж они совершают с течением времени.
Ниже вы можете увидеть пример линейного графика, показывающего общее количество продаж с течением времени. В этом примере мы используем (y) как общее количество проданных автомобилей и (x) как количество недель.
Пример линейного графика, Хайме Николс
Чтобы найти скорость изменения, нам нужно определить градиент. Из уравнения мы знаем, что градиент равен 3. Это означает, что норма количества продаж составляет 3 автомобиля в неделю.
Если вас попросят контекстуализировать градиент на экзамене, важно ссылаться на него как на скорость чего-либо для получения оценок.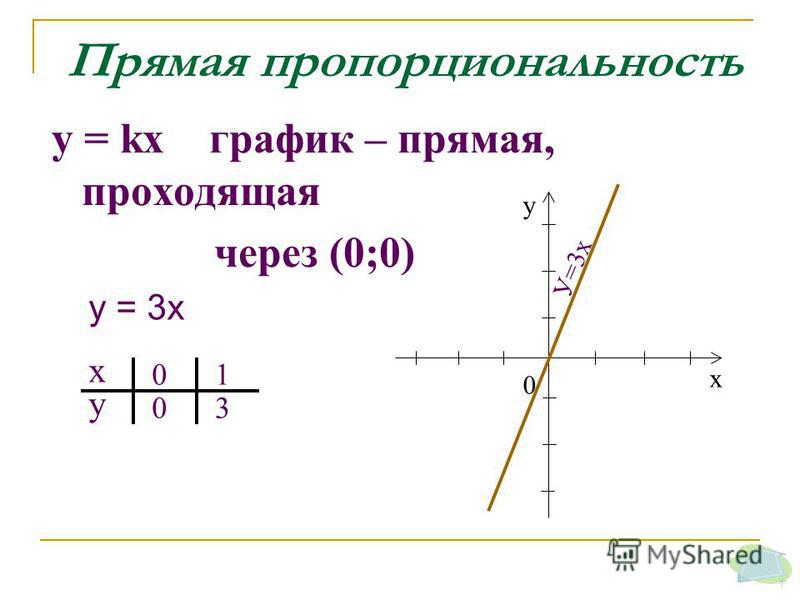
Возможно, вам также придется объяснить положение y-перехвата. В этом примере линия пересекается с началом координат, что имеет смысл, поскольку в 0 недель они еще не начали продавать автомобили.
Иногда, особенно на прямолинейных графиках, связанных с затратами, линия может пересекаться выше начала координат. Обычно это предполагает наличие некоторых фиксированных первоначальных затрат, которые необходимо учитывать. Распространенным примером, используемым на экзаменах, является депозит. Важно отметить, что эта стоимость является фиксированной и, следовательно, не меняется независимо от изменения x и y.
Прямые графики – ключевые выводы
- – основное уравнение прямой линии, но вы также можете использовать и
- В уравнении прямой линии м представляет градиент, который можно найти по формуле: и c представляет собой точку пересечения по оси Y прямолинейного графика
- Параллельные линии имеют одинаковый градиент, в то время как градиенты перпендикулярных линий обратно пропорциональны друг другу.

- Уравнение для вертикальной линии: x = d, где d — пересечение с осью x.
- Уравнение для горизонтальной линии: y = b, где b — пересечение с осью y.
Прямые графики — математика GCSE
Введение
Как построить линейный график
Таблица прямых графиков
Распространенные заблуждения
Практические вопросы по линейным графикам
Прямые графики Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Как построить линейный график
Таблица прямых графиков
Распространенные заблуждения
Практикуйте прямые графики, вопросы
Прямые графики Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем о прямолинейных графиках, в том числе о том, как рисовать прямолинейные графики формы y = mx + c с помощью таблицы и пары координат.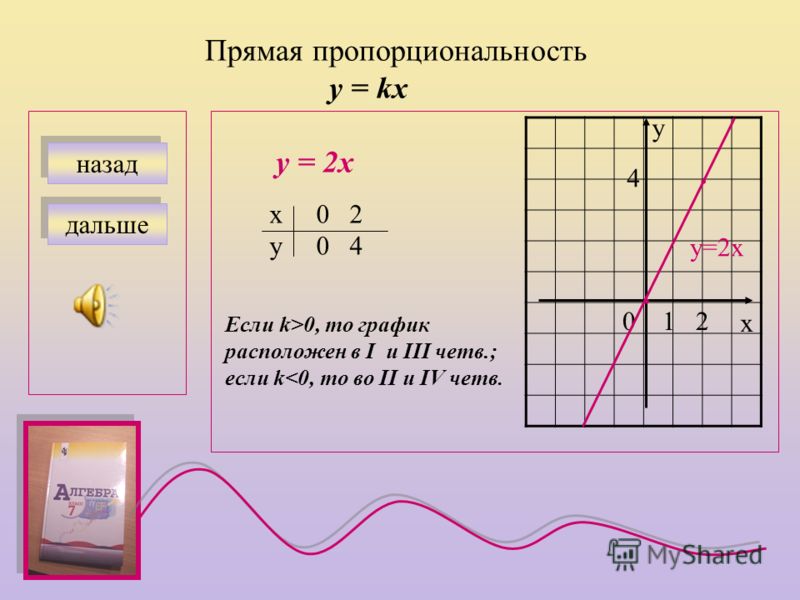 Мы узнаем, как рассчитать градиент прямой линии, включая параллельные и перпендикулярные линии, и как быстро нарисовать линейный график с ограниченной информацией.
Мы узнаем, как рассчитать градиент прямой линии, включая параллельные и перпендикулярные линии, и как быстро нарисовать линейный график с ограниченной информацией.
Существуют также рабочие листы с линейными графиками, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое линейный график?
Прямолинейный график представляет собой визуальное представление линейной функции. Он имеет общее уравнение:
у=мх+с
Где m — уклон линии
А c — точка пересечения у.
у=2х+1
Здесь мы видим, что градиент = 2, а точка пересечения с осью y происходит в точке (0,1).
График этого уравнения выглядит следующим образом:
На графике выделено несколько важных значений, которые вы должны иметь возможность пометить на любом линейном графике.
К ним относятся:
- Помеченные оси для x и y .

- Четко нанесенные координаты.
- Одна прямая линия по всей сетке — необходимо использовать линейку.
- Точка пересечения с осью Y.
- Уравнение прямой.
Что такое линейный график?
1. Построение линейных графиков
Чтобы построить линейные графики , нам нужно подставить значения для x в уравнение для графика и вычислить соответствующие значения для y .
Мы часто помещаем эти значения в таблицу, чтобы сделать нашу работу более понятной. После того, как мы вычислили координаты, мы можем изобразить их в виде графика.
Пример
Заполните таблицу, чтобы построить график уравнения.
у=х+4
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|
| y=x+4 | 5 | 7 | 8 |
- Подставьте каждое заданное значение вместо x в общее уравнение прямой .

Здесь нам нужно подставить значения x в таблицу, чтобы вычислить значения для y .
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|
| y=x+4 | y=-2+4 у=2 | у=-1+4 у=3 | у=0+4 у=4 | 5 | у=2+4 y=6 | 7 | 8 |
2 Нанесите полученные координаты на набор осей с метками .
Поскольку координата записывается как (x,y) , из таблицы у нас теперь есть координаты (-2,2), (-1,3), (0,4), (1,5), (2 ,6), (3,7) и (4,8), которые мы можем построить:
3 Проведите прямую линию через все нанесенные координаты через всю область построения .
Главный совет: не забудьте пометить строку как уравнение в вопросе. Здесь мы обозначили прямую линию y = x + 4 .
Пошаговое руководство: Уравнение прямой
2.
 Набросок графика
Набросок графика Иногда нам нужен только набросок прямолинейного графика – нам не нужно, чтобы он был построен с той же точностью, как если бы мы вычисляли координаты.
Набросанный график должен включать определенную информацию, такую как помеченные оси, помеченная линия и точки, в которых линия пересекает оси.
Сравним плохой набросок с хорошим наброском прямой y=2x+1
Плохой набросок
Хотя линия имеет положительный градиент и пересекает ось y в одной точке, на графике предполагается, что существуют только положительные значения x . Также ничего на графике не помечено.
Хороший эскиз
Ключевые части, которые следует выделить на изображении выше:
- Помеченные оси x и y без масштаба
- Несколько четко нанесенных координат
- Одна прямая линия по всей сетке – необходимо использовать линейку
- Точка пересечения с осью у
- Точка пересечения с осью х
- Уравнение прямой
3.
 Нахождение середины отрезка
Нахождение середины отрезкаСередина отрезка точка, которая лежит точно посередине между двумя точками. Это одинаковое расстояние от каждой конечной точки отрезка прямой.
Мы находим середину отрезка, находя среднее значение координат x и среднее значение координат y двух конечных точек.
Например, для точек (4, 6) и (8, 2):
Среднее значение координат x =\frac{4+8}{2}=\frac{12}{2}=6
Среднее значение координат y =\frac{6+2}{2}=\frac{8}{2}=4
Таким образом, координаты средней точки равны (6, 4).
Пошаговое руководство: Как найти середину
4. Градиент линии
Градиент линии говорит нам, насколько крута линия. Он говорит нам, на сколько шагов поднимается линия при каждом пересечении. Следовательно, чем выше градиент, тем круче линия.
Если градиент отрицательный, линия идет вниз, а не вверх (слева направо).
Пример :
Вычислите уклон прямой линии на диаграмме.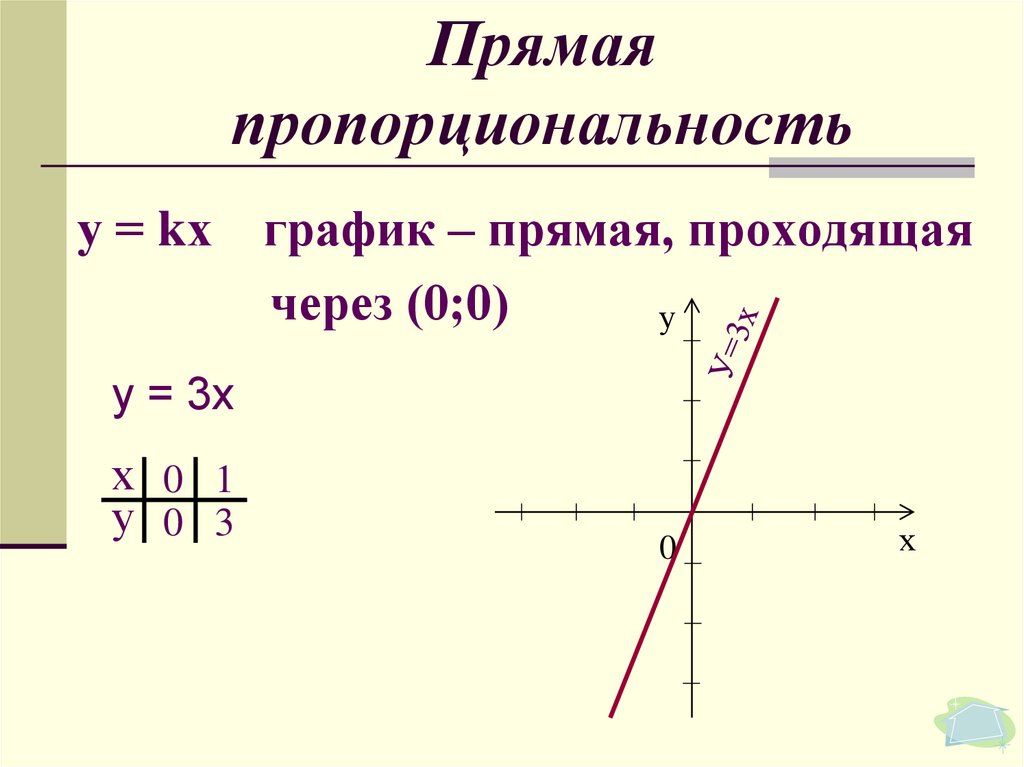
- Укажите две координаты, лежащие на одной прямой.
Найдя две координаты, проходящие через углы квадратов сетки, мы получим координаты (0,1) и (4,7) .
2 Найдите изменение в y и изменение в х .
Изменение y равно y_2 − y_1 = 7 − 1 = 6 .
Изменение x равно x_2 − x_1 = 4 − 0 = 4 .
3Здесь
м=\фракция{6}{4}=\фракция{3}{2}
Итак, градиент линии равен m=\frac{3}{2} .
Пошаговое руководство: Градиент линии
5. y = mx + c
Общее уравнение для прямой линии : y=mx+c , где m — градиент, а c — у перехвата.
Мы можем найти уравнение прямой линии, найдя градиент и точку пересечения y, а затем используя эти значения в уравнении.
Пример :
Две координаты A (3,5) и B (5,11) лежат на одной прямой L. Используйте эти координаты, чтобы найти уравнение прямой L.
- Рассчитайте градиент линии .
m=\frac{y_2-y_1}{x_2-x_1}=\frac{11-5}{5-3}=\frac{6}{2}=3
Итак, градиент m = 3
2 Вычислить точку пересечения прямой линии по оси Y.
Когда y = 3x + c при A (3,5) ,
\begin{выровнено} 5&=3\умножить на 3+с\\\\ 5&=9+с\\\\ с&=-4 \end{выровнено}
Таким образом, точка пересечения y находится в точке (0,−4) .
3 Составьте уравнение прямой.
у=3х-4
Пошаговое руководство: y=mx+c
6. Параллельные и перпендикулярные линии
Параллельные линии 9о друг к другу.
Градиенты перпендикулярных линий умножаются вместе, чтобы получить -1 (они являются отрицательными обратными величинами).
Пример :
Покажите, что две прямые y = 6 — 4x и 4y = x перпендикулярны.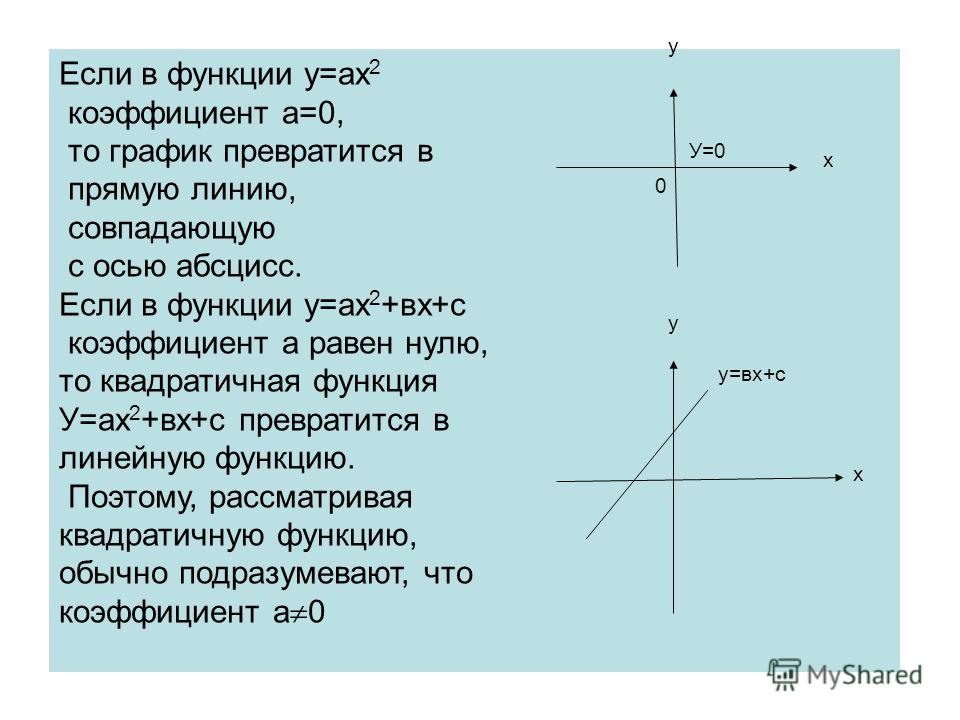
- Преобразуйте оба уравнения в форму y = mx + c .
Здесь мы имеем y = -4x + 6 и y = \frac{1}{4}x .
2 Укажите уклон каждой линии .
{{m}_{1}}=-4 и {{m}_{2}}=\frac{1}{4}
3 Перемножьте градиенты. Если они равны -1, две линии перпендикулярны.
-4\times\frac{1}{4}=\frac{-4}{4}=-1
Да, они перпендикулярны.
Пошаговое руководство: Параллельные и перпендикулярные линии
Изучение прямых графиков
Сводка линейных графиков
- Для линейных графиков есть линейная зависимость между значениями x и y, поэтому линия прямая и должна быть проведена с помощью линейки.
- Градиент определяет насколько крута линия , а точка пересечения y сообщает нам место, где прямая пересекает ось y .

- Каждая прямая может быть нарисована точно путем подстановки значений x в общее уравнение прямой y = mx + c или начерчена с соответствующей маркировкой.
- Мы можем рисовать прямые линии с положительным градиентом, с отрицательным градиентом, горизонтальные или вертикальные, параллельные и перпендикулярные.
Как построить линейный график
Чтобы построить линейный график:
- Подставьте каждое заданное значение x в общее уравнение прямой линии.
- Нанесите полученные координаты на набор осей с метками .
- Проведите прямую через все нанесенные координаты по всей области построения .
Рабочий лист с прямыми графиками
Получите бесплатный рабочий лист с прямыми графиками, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКОРО
ИксРабочий лист с прямыми графиками
Получите бесплатный рабочий лист с прямыми графиками, содержащий более 20 вопросов и ответов.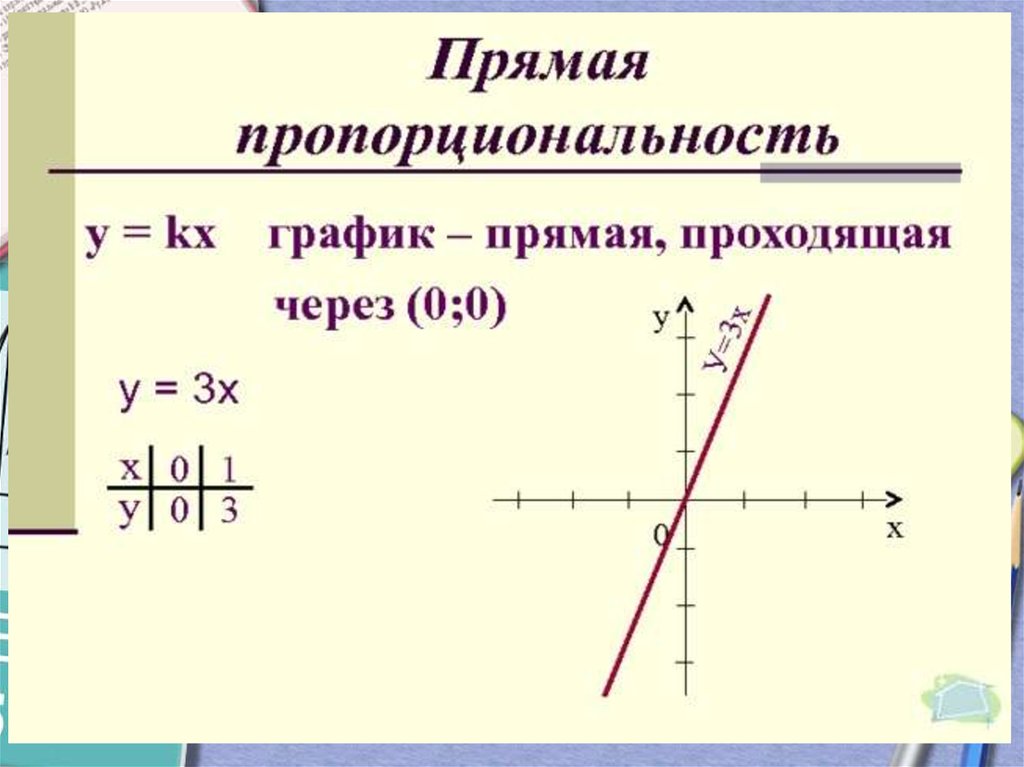 Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.
СКОРО
Примеры линейных графиков
Пример 1: Дан график y = mx + c и таблица
Постройте график уравнения y=2x-3
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y=-x+4 | -5 |
Подставьте каждое заданное значение вместо x в общее уравнение прямой .
| х | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| у=2х-3 | у = (2 × -2) — 3 у = -4 — 3 у = -7 | -5 | у = (2 × 0) — 3 у = 0 — 3 у = — 3 | у = (2 × 1) — 3 у = 2 — 3 у = -1 | у = (2 × 2) — 3 у = 4 — 3 y = 1 |
Нанесите полученные координаты на набор осей с метками .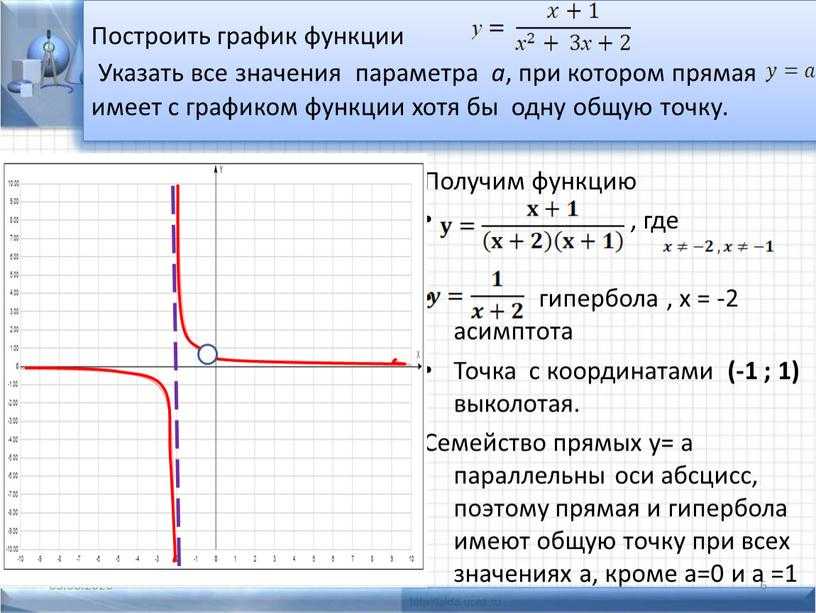
Теперь у нас есть следующие координаты для построения на наборе осей:
(-2,-7), (-1,-5), (0,-3), (1,-1), ( 2,1).
Проведите прямую через все нанесенные координаты по всей области построения .
Пример 2: Различные масштабы осей
Постройте график уравнения на наборе осей ниже.
у=\фракция{1}{2}х-2
Подставьте каждое заданное значение x в общее уравнение прямой линии .
Здесь нам не нужно заполнять таблицу, поэтому нам нужно выбрать значения для x, которые появляются на наборе осей. Помните, что чем больше точек вы сможете нанести, тем больше вероятность того, что ваша прямая линия будет правильной. Здесь мы выберем значения x равными 0, 1 и 2.
Когда x = 0,
\begin{align} &y=(\frac{1}{2}\times{0})-2\\\\ &y=0-2\\\\ &y= -2 \end{aligned}
Итак, у нас есть координата (0,−2) .
Когда x = 1 ,
\begin{aligned} &y=(\frac{1}{2}\times{1})-2\\\\ &y=\frac{1}{2}- 2\\\\ &y=-1\frac{1}{2} \end{aligned}
Итак, у нас есть координата (1, -1\frac{1}{2}).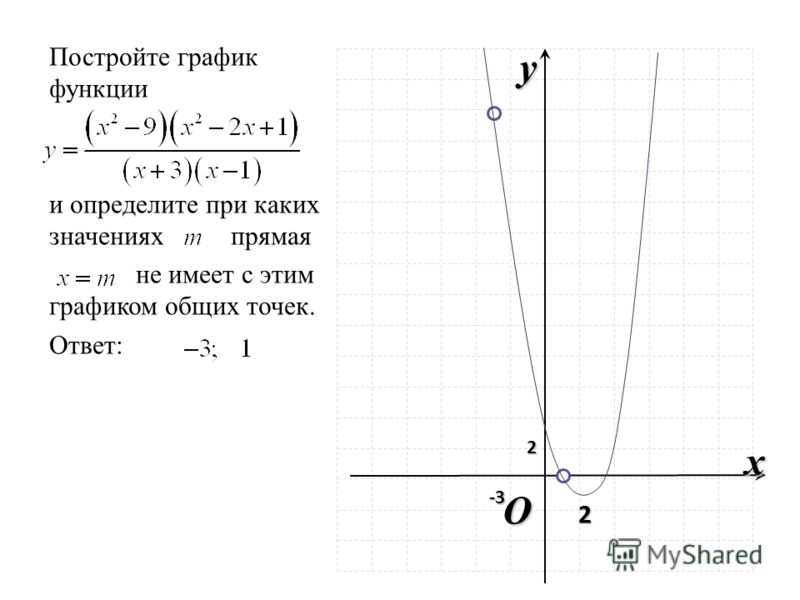
Когда x = 2 ,
\begin{aligned} &y=(\frac{1}{2}\times{2})-2\\\\\ &y=1-2\\\\ &y =-1 \end{выровнено}
Итак, у нас есть координата (2,−1) .
Теперь у нас есть три координаты: (0,−2), (1,−1\frac{1}{2}) и (2,−1) .
Нанесите полученные координаты на набор осей с метками .
Проведите прямую через все нанесенные координаты по всей области построения .
Пример 3: Постройте прямую линию не в форме y = mx + c
Постройте график уравнения ниже на заданном наборе осей для -2\leq{x}\leq2.
2у-6=4х
Подставьте каждое заданное значение x в общее уравнение прямой линии .
Сначала нам нужно изменить уравнение 2y = 4x + 6, чтобы сделать y субъектом. Это упростит вычисление значений y.
Чтобы сделать y субъектом:
Теперь мы можем подставить значения x в y = 2x + 3, чтобы найти соответствующую координату y.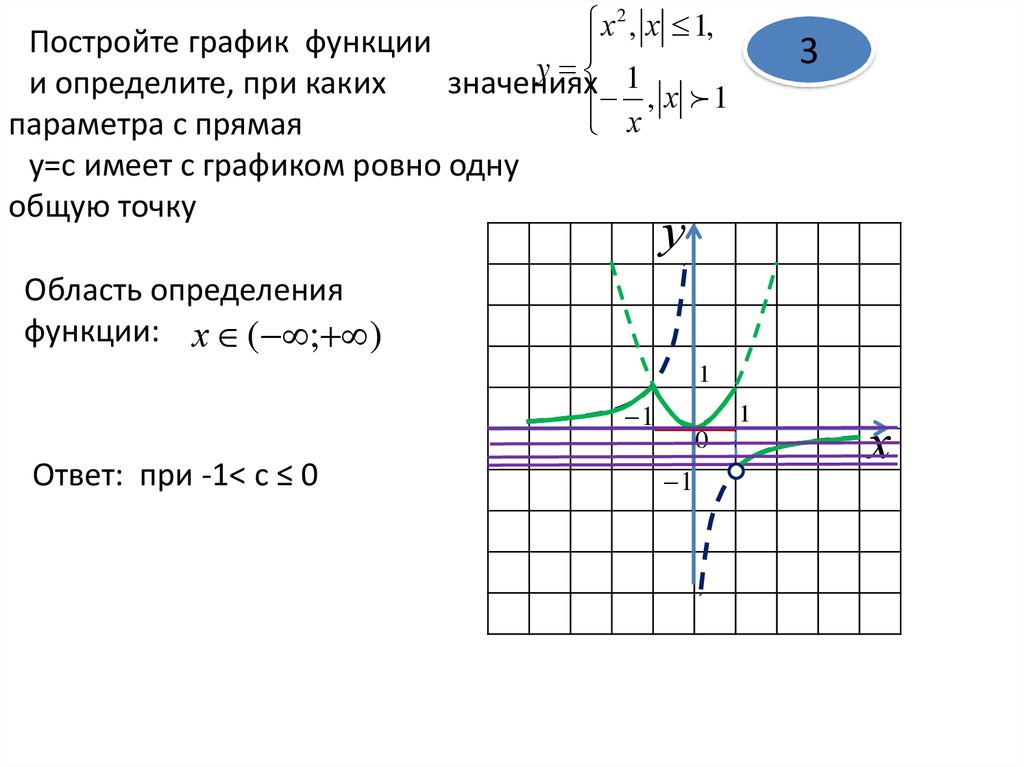
Здесь мы нарисуем таблицу для y = 2x + 3 для диапазона значений -2\leq{x}\leq2.
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | y=(2 × −2) +3 у = -4 + 3 у = -1 | у = (2 × -1) +3 у = -2 + 3 у = 1 | у = (2 × 0) +3 у = 0 + 3 у = 3 | у = (2 × 1) +3 у = 2 + 3 у = 5 | у = (2 × 2) +3 у = 4 + 3 y = 7 |
Нанесите полученные координаты на набор помеченных осей .
Теперь у нас есть координаты: (−2,−1), (−1,1), (0,3), (1,5) и (2,7) .
Проведите прямую через все нанесенные координаты по всей области построения .
Пример 4: Отрицательный градиент в форме y = mx + c
Заполните таблицу, чтобы построить график уравнения.
у=-4х+1
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | 1 |
Подставьте каждое заданное значение вместо x в общее уравнение прямой линии 904.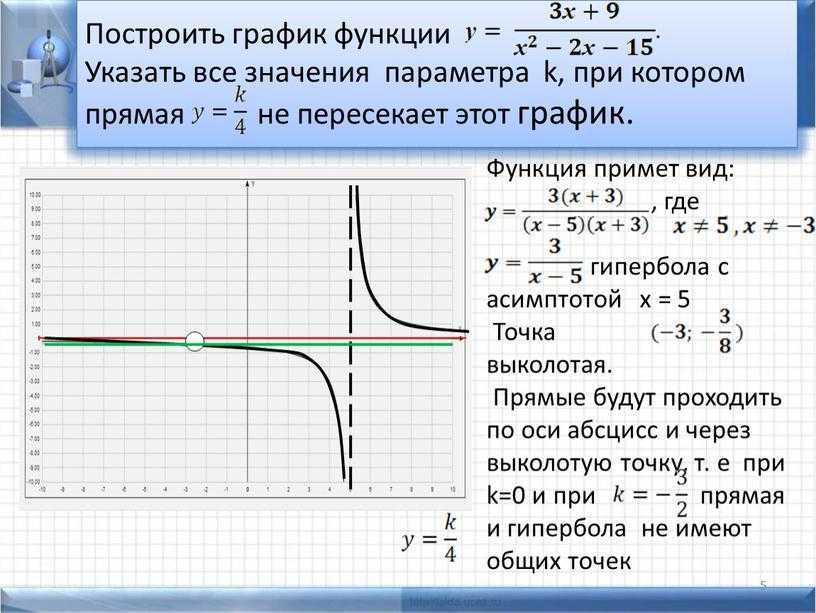
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | |||||
| у = (-4 × -1) + 1 у = 4 + 1 у = 5 | 1 | у = (−4 × 1) + 1 у = -4 + 1 у = -3 | у = -4 × 2) + 1 у = -8 + 1 y = −7 |
Нанесите полученные координаты на набор осей с метками .
Теперь у нас есть координаты: (−2,9), (−1,5), (0,1), (1,−3) и (2,−7) .
Проведите прямую через все нанесенные координаты по всей области построения .
Пример 5: Отрицательный градиент не в форме y = mx + c
Постройте график уравнения для -1\leq{x}\leq3.
3х+у=2
Подставьте каждое заданное значение x в общее уравнение прямой линии .
Сначала нам нужно изменить уравнение 3x + y = 2, чтобы сделать y субъектом.
Чтобы сделать y субъектом:
Теперь мы можем подставить значения x в y = −3x + 2, чтобы найти соответствующую координату y. Здесь мы нарисуем таблицу для y = −3x + 2 для диапазона значений -1\leq{x}\leq3.
| x | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|
| у = + | у = 3 + 2 у = 5у = (-3 × 0) + 2 у = 0 + 2 у = 2 | у = (-3 × 1) + 2 у = -3 + 2 у = -1 | у = (-3 × 2) + 2 у = -6 + 2 у = -4 | у = (-3 × 3) + 2 у = -9 + 2 y = -7 |
Нанесите полученные координаты на набор осей с метками .
Теперь у нас есть следующие координаты линии 3x + y = 2: (-1,5), (0,2), (1,-1), (2,-4), (3,-7)
Проведите прямую через все нанесенные координаты по всей области построения .
Распространенные заблуждения
- Проведите линию через всю сетку
Прямая линия непрерывна.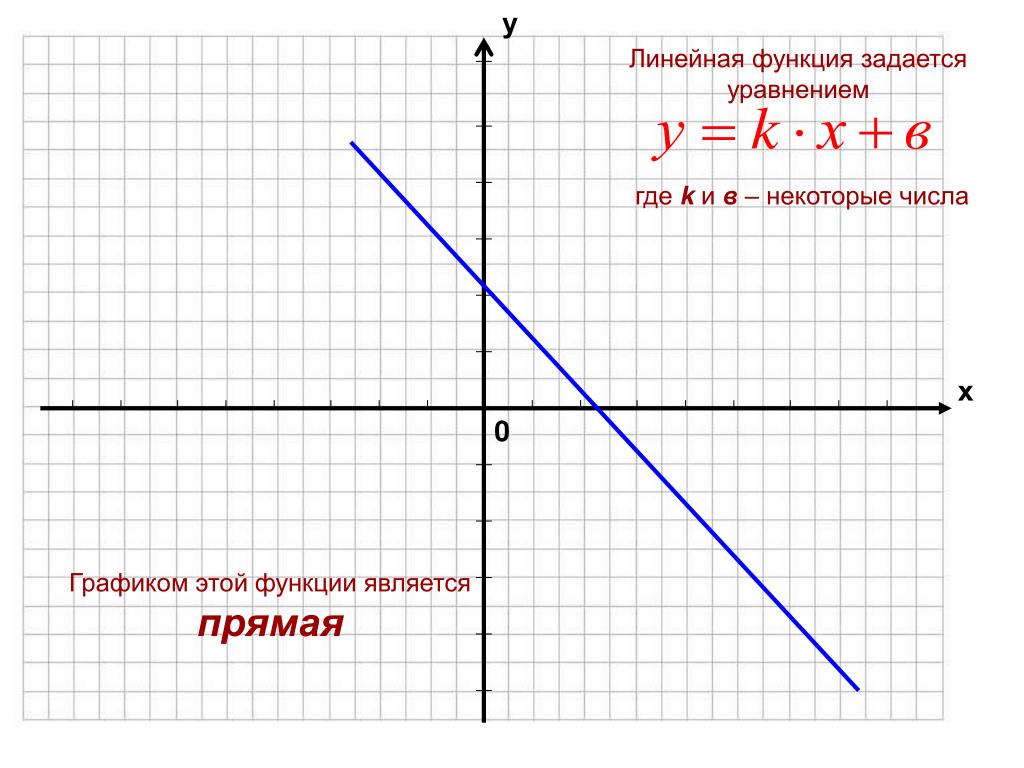 Если вы соединяете координаты только на наборе осей, вы рисуете только часть линии. Убедитесь, что график расширен по всей сетке. Визуальное описание см. ниже:
Если вы соединяете координаты только на наборе осей, вы рисуете только часть линии. Убедитесь, что график расширен по всей сетке. Визуальное описание см. ниже:
- Одинаковая маркировка осей
Шкала на каждой оси является линейной, что означает, что каждая единица имеет заданное расстояние. Когда вы записываете шкалу на набор осей, убедитесь, что каждая единица имеет такое же количество квадратов сетки, что и следующая, это очень важно вокруг начала координат. См. ниже визуальное представление нескольких заблуждений с маркировкой осей:
- Не использовать линейку
Это не обязательно неправильное представление, но причина, по которой вы всегда должны использовать линейку, заключается в том, что вы рисуете одна прямая линия, без разрывов, перегибов или кривых. Прямая линия есть прямая линия!
- Линия не прямая (случайные координаты)
Иногда вы сгенерировали координату, которая не находится в ожидаемом положении на прямой линии.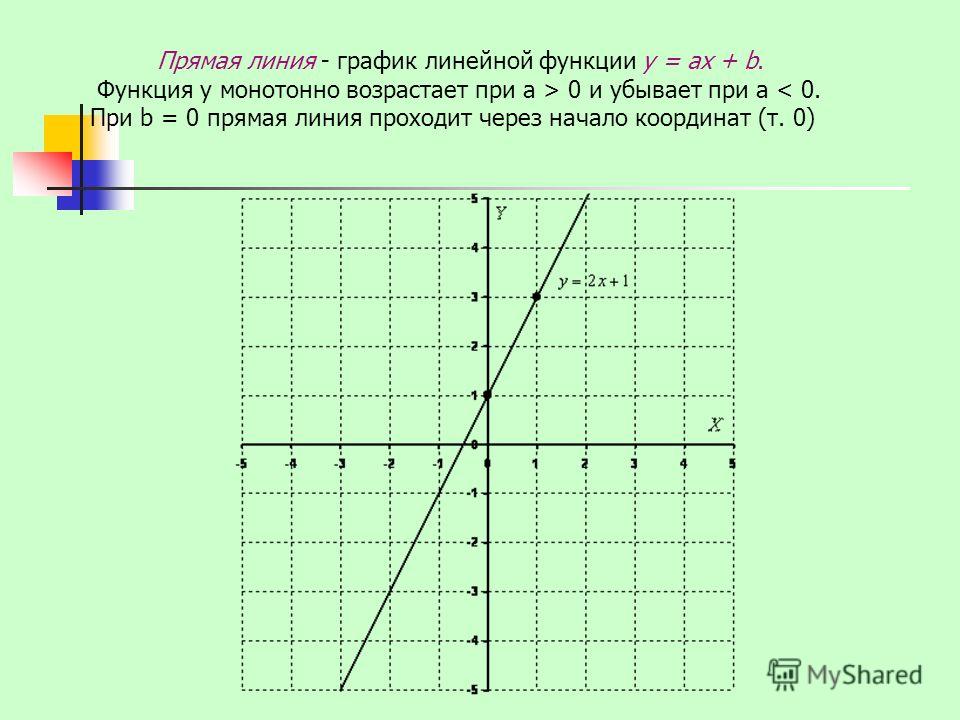 Это может означать одно из двух: а) подстановка рассчитана неправильно, б) координата нанесена неправильно.
Это может означать одно из двух: а) подстановка рассчитана неправильно, б) координата нанесена неправильно.
Чтобы решить эту проблему, посмотрите, где должна лежать координата, используя прямую линию, чтобы помочь вам, и проверьте построение координаты, а затем подстановку.
- Перепутать значения x и y
Координата на декартовой сетке имеет общий вид (x, y) . Убедитесь, что при создании координат значение x отображается первым в скобках, а затем значение y, которое было рассчитано.
Практические вопросы по линейным графикам
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| у = 6х — 8 | −4 | −2 | 0 | −2 | 4 | 10 |
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| у = 6х — 8 | 4 | 2 | 0 | 2 | 4 | 10 |
| х | −2 | −1 | 0 | 1 | 2 | 3 |
| у = 6х — 8 | −20 | −14 | −8 | −2 | 4 | 10 |
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| у = 6х — 8 | −20 | −14 | −6 | −2 | 4 | 10 |
При x=-2
\begin{выровнено} &y=(6\times-2)-8\\ &у=-12-8\\ &у=-20 \end{выровнено}
При x=-1
\begin{выровнено} &y=(6\times-1)-8\\ &у=-6-8\\ &у=-14 \end{выровнено}
Когда x= 0
\begin{выровнено} &y=(6\times0)-8\\ &у=0-8\\ &у=-8 \end{выровнено}
Когда x=1
\begin{выровнено} &y=(6\times1)-8\\ &у=6-8\\ &у=-2 \end{выровнено}
При x= 2
\begin{выровнено} &y=(6\times2)-8\\ &у=12-8\\ &у=4 \end{выровнено}
При x= 3
\begin{выровнено} &y=(6\times3)-8\\ &у=18-8\\ &у=10 \end{выровнено}
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| у = 6х — 8 | −20 | −14 | −8 | −2 | 4 | 10 |
| x | −2 | −1 | 0 | 1 |
| у = 5х + 3 | −7 | −2 | 3 | 8 |
При x=-2
\begin{выровнено} &y=(5\times-2)+3\\ &у=-7 \end{выровнено}
При x=-1
\begin{выровнено} &y=(5\times-1)+3\\ &у=-2 \end{выровнено}
Когда x= 0
\begin{выровнено} &y=(5\times0)+3\\ &у=3 \end{выровнено}
При x=1
\begin{выровнено} &y=(5\times1)+3\\ &у=8 \end{выровнено}
\begin{выровнено} &x \quad \quad \quad \,-8 \quad \quad -4 \quad \quad 0 \quad \quad \;4 \quad \quad \;\,8\\ y=&-\frac{1}{4}x \quad \quad \; 2 \четверка \четверка \;\;\; 1 \quad \quad \, 0 \quad \;\;-1 \quad \;\; -2 \end{выровнено}
Чтобы вычислить координаты некоторых точек на этом графике, мы можем использовать значения x, которые легко делятся на 4 (т.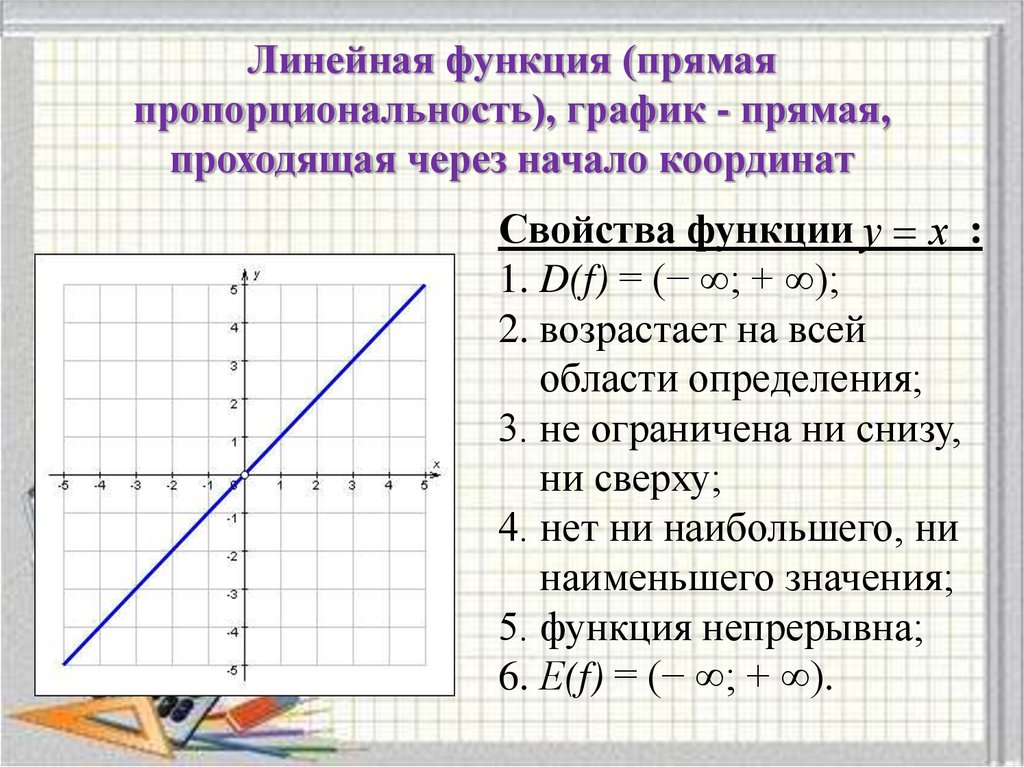 е. числа в таблице умножения на 4).
е. числа в таблице умножения на 4).
При x=-8
\begin{выровнено} &y=(-\frac{1}{4}\times{-8})\\ &у=2 \end{выровнено}
При x=-4
\begin{выровнено} &y=(-\frac{1}{4}\times{-4})\\ &у= 1 \end{выровнено}
Когда x= 0
\begin{выровнено} &y=(-\frac{1}{4}\times{0})\\ &у=0 \end{выровнено}
При x=4
\begin{выровнено} &y=(-\frac{1}{4}\times{4})\\ &у=-1 \end{выровнено}
При x=8
\begin{выровнено} &y=(-\frac{1}{4}\times{8})\\ &у=-2 \end{выровнено}
| x | −2 | −1 | 0 | 1 | 2 |
| 2у + 3х = 12 | 9 | 7,5 | 6 | 4,5 | 3 |
При x=-2
\begin{выровнено}
&y=(-1. 5\times-2)+6\\
&у=3+6\\
&у=9
\end{выровнено}
5\times-2)+6\\
&у=3+6\\
&у=9
\end{выровнено}
При x=-1
\begin{выровнено} &y=(-1.5\times-1)+6\\ &у=1,5+6\\ &у=7,5 \end{выровнено}
Когда x= 0
\begin{выровнено} &y=(-1.5\times0)+6\\ &у=0+6\\ &у=6 \end{выровнено}
Когда х=1
\begin{выровнено} &y=(-1.5\times1)+6\\ &у=-1,5+6\\ &у=4,5 \end{выровнено}
При x=2
\begin{выровнено} &y=(-1.5\times2)+6\\ &у=-3+6\\ &у=3 \end{выровнено}
y=-6x+3
y=6x-3
y=3x+6
y=3x-6
Общее уравнение прямой имеет вид y=mx+c, где m — градиент (так что это будет 3x ), а c — это точка пересечения y (так что это будет -6 ).
y=-4x+5
y=4x-3
y=2x+5
y=\frac{1}{4}x +5
Градиенты параллельных линий равны, поэтому любая линия с градиент 4 будет параллелен y=4x+5.
Прямые графики Вопросы GCSE
1. Обведите координату, лежащую на прямой 6x + 12y = 0
| (12,6) | (18,0) | (2,0) | (2,-1) | (-4,-2) |
(1 отметка)
Показать Ответ
(2, -1)
(1)
2. (a) Две прямые линии пересекаются в точке с.
.
Рассчитайте координату P.
(b) Укажите градиент линии 2y = x+8
(5 баллов)
Показать ответ
(A)
Горизонтальная линия y=2
(1)
Когда Y = 2, 2 × 2 = x+8
(1)
x = -4 и (-4,2)
(1. )
(б)
у=\фракция{1}{2}х+4
(1)
м=\фракция{1}{2}
(1)
3.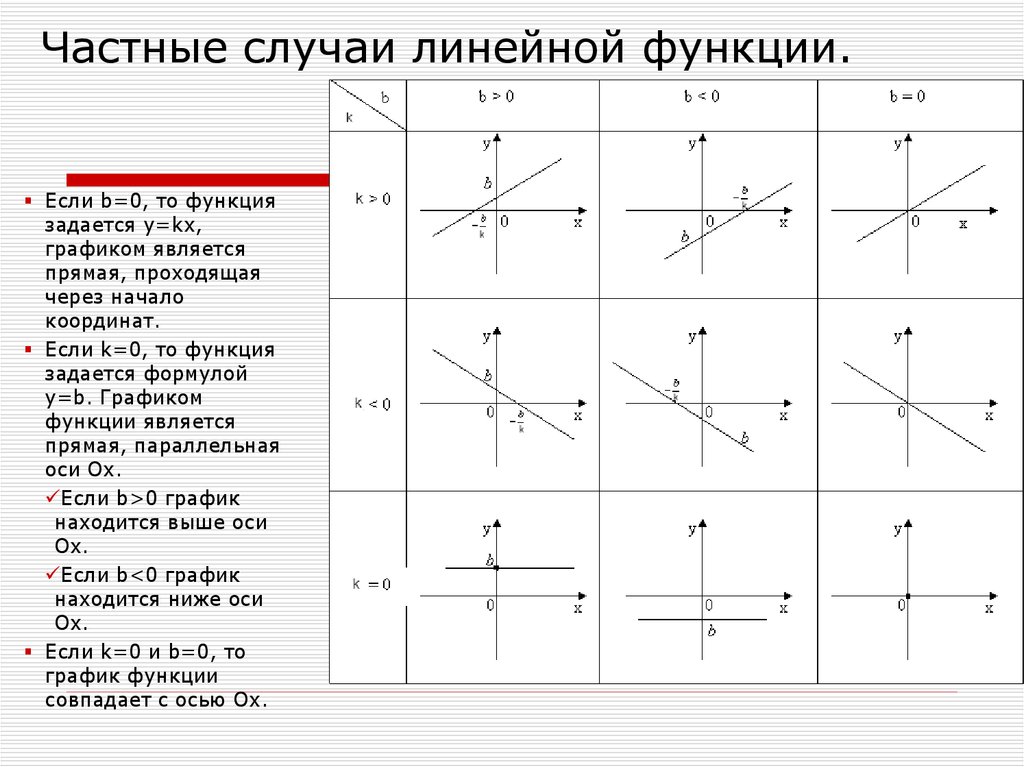 (a) Заполните таблицу для y=-6+4x
(a) Заполните таблицу для y=-6+4x
| x | −3 | −2 | −1 | 0 | 1 | 2 |
| г | −18 | −2 |
(b) Нарисуйте график линии y = -6+4x
( 5 M Arks)
Показать ответ
(а)
| x | −3 | −2 | −1 | 0 | 1 | 2 |
| г | −18 | −14 | −10 | −6 | −2 | 2 |
(2)
(B)
Все координаты, построенные правильно
(1)
One Continuy Straight Line через все очки
2
One Continuy Straight Line через все очки
9000 2 1 (One Continuy Straight Pright Line
9000 2 1 ( One Continuy Straight Pright Line.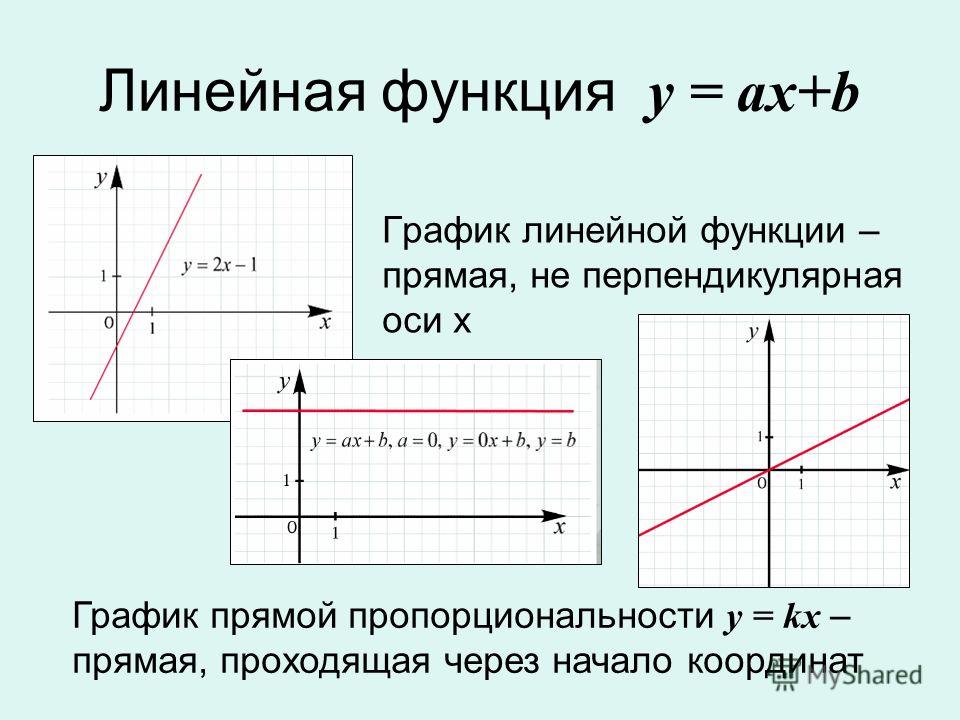
Y-Intercept, четко обозначенная
(1)
Контрольный список обучения
Вы узнали, как:
- Узнавать, нарисов , с помощью уравнений относительно x и y и декартовой плоскости
- привести заданное линейное уравнение с 2 переменными к стандартной форме y = mx + c ; вычислять и интерпретировать градиенты и точки пересечения графиков таких линейных уравнений численно, графически и алгебраически
- свободно перемещаться между различными числовыми, алгебраическими, графическими и диаграммными представлениями, включая линейные функции
- распознавать, чертить и интерпретировать графики линейных функций
- использовать форму y = mx + c для обозначения параллельных {и перпендикулярных} линий; найти уравнение прямой через 2 заданные точки или через 1 точку с заданным уклоном
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning.

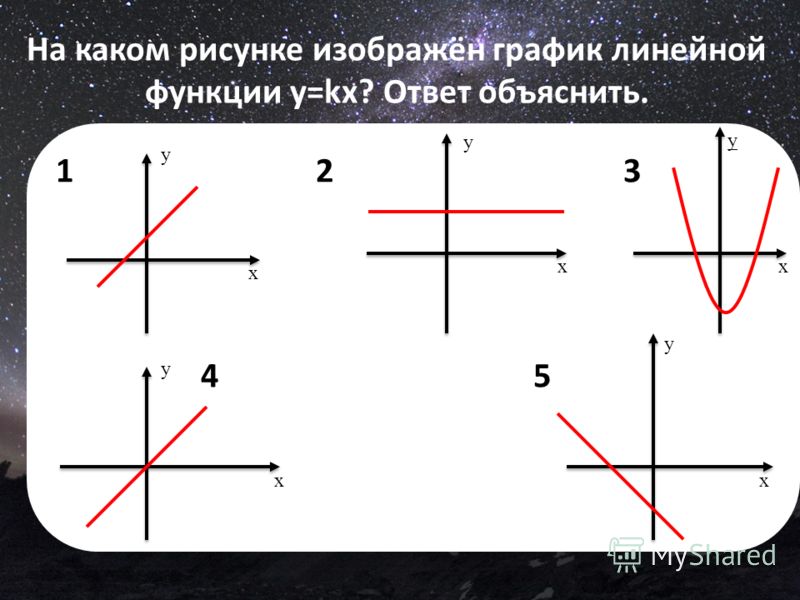
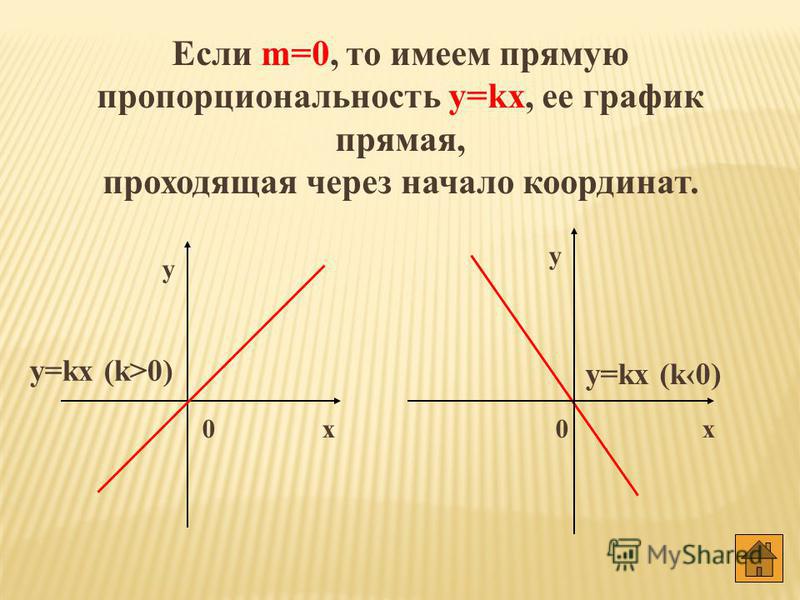
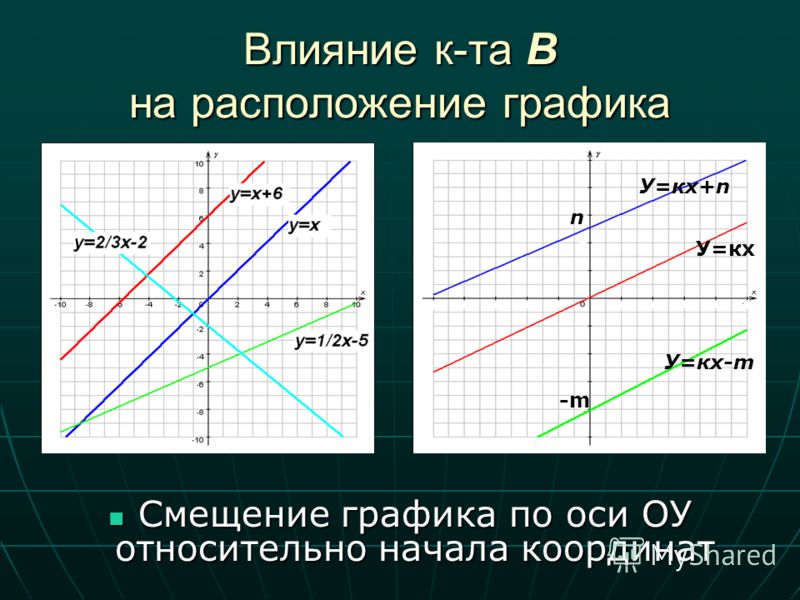 У этих функций k и b имеют разные значения, поэтому, чтобы найти координаты точки пересечения графиков этих функций, решим уравнение (приравниваем правые части):
У этих функций k и b имеют разные значения, поэтому, чтобы найти координаты точки пересечения графиков этих функций, решим уравнение (приравниваем правые части):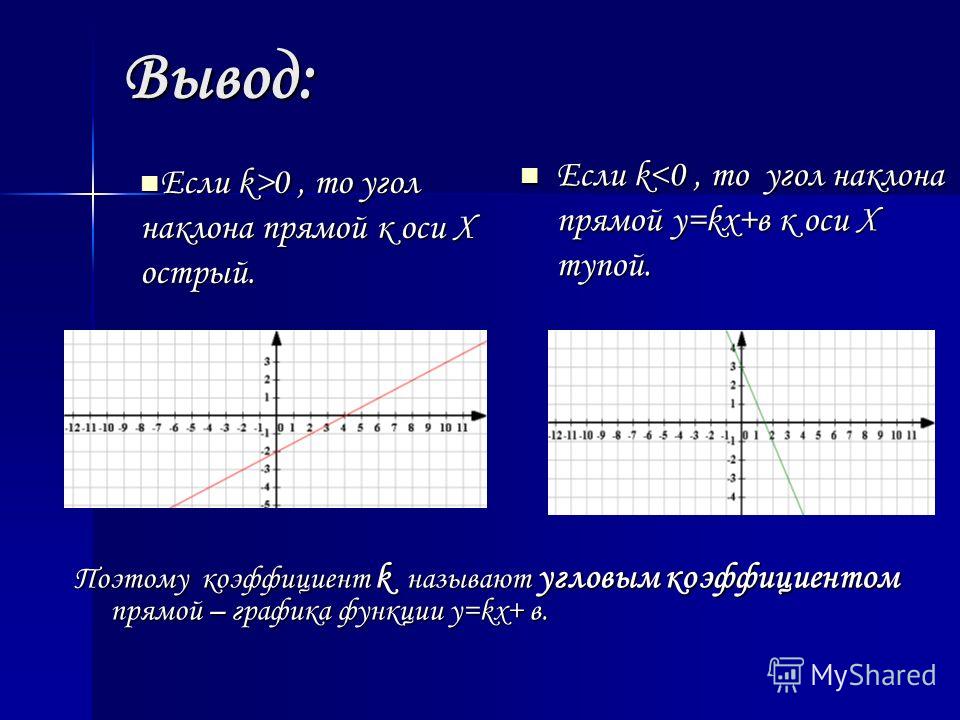
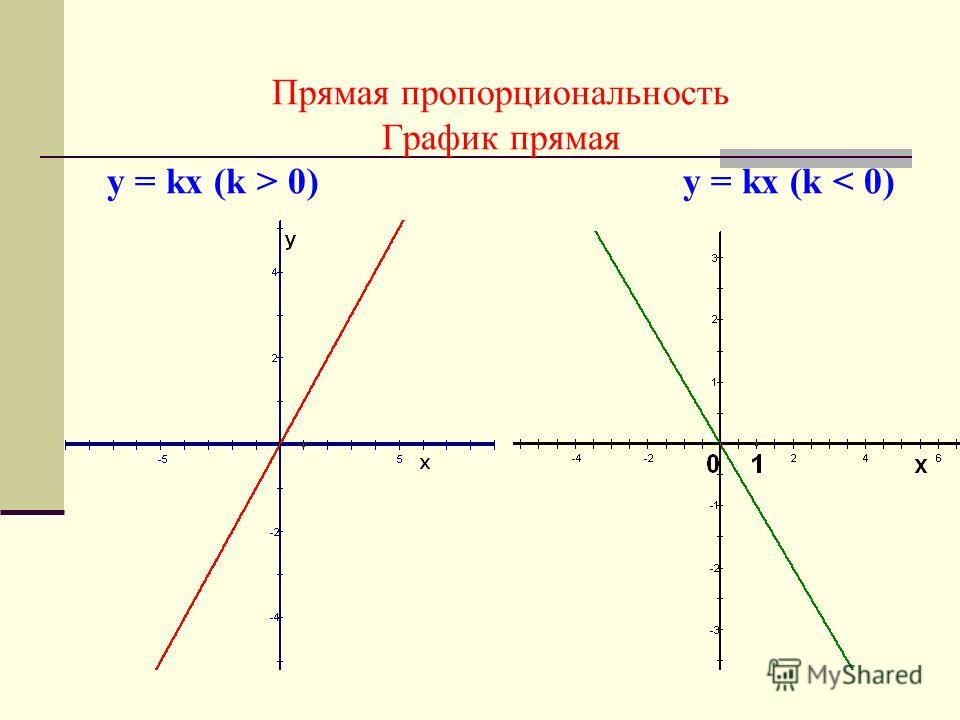
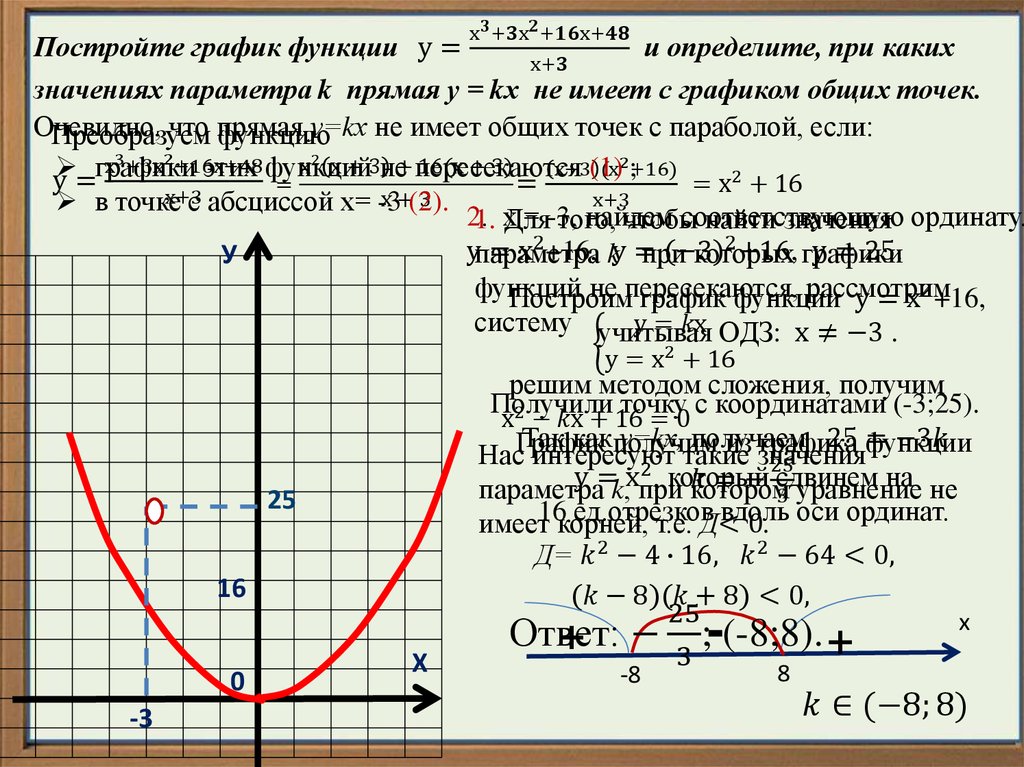 Найдите значения и .
Найдите значения и .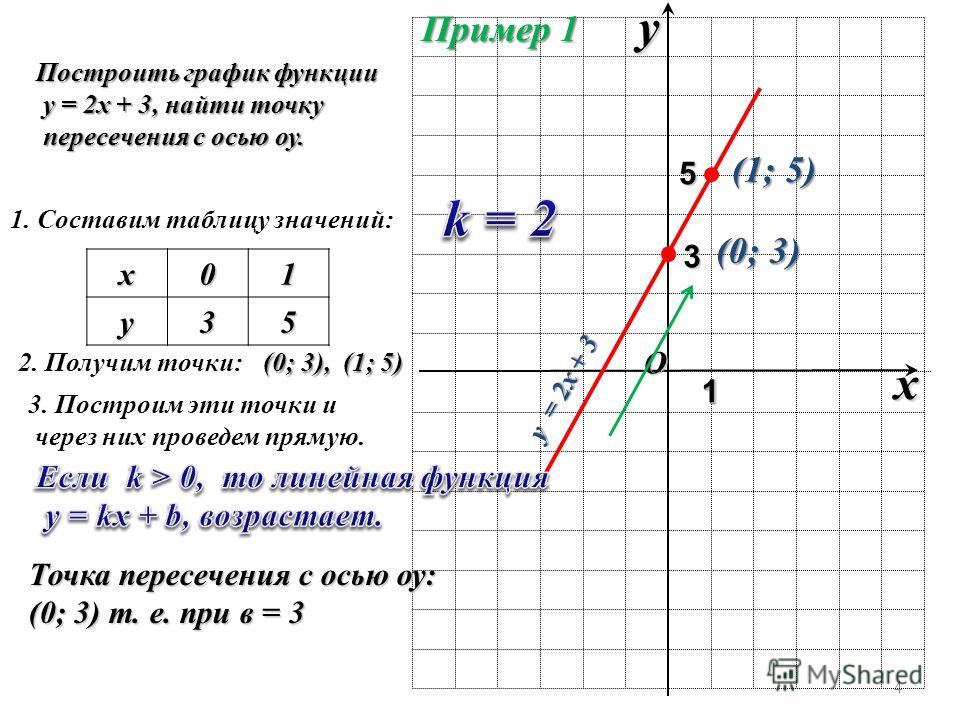
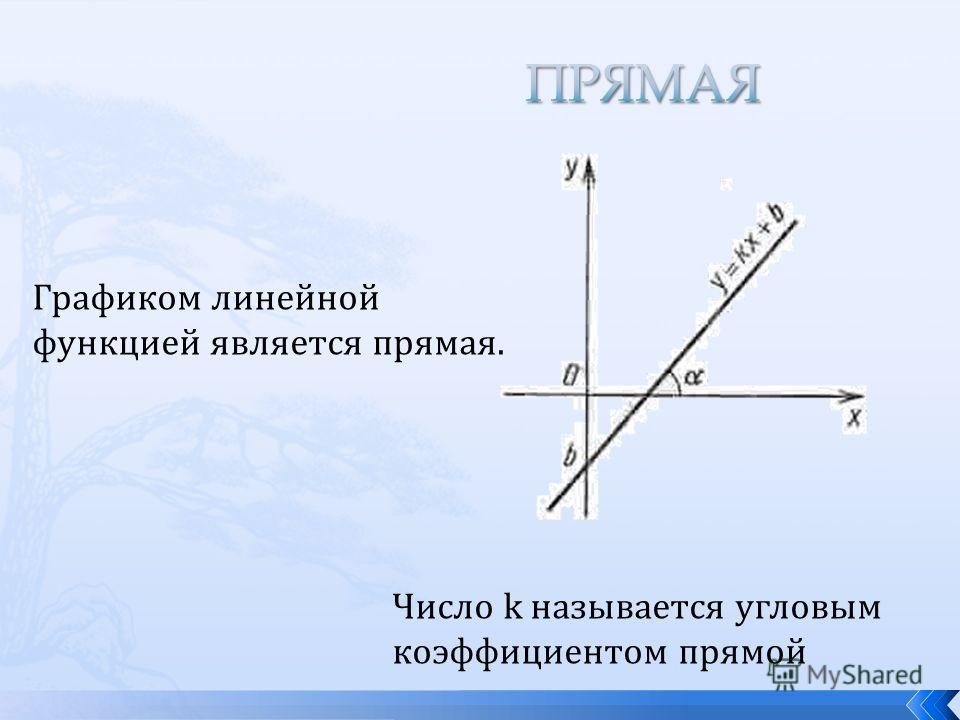

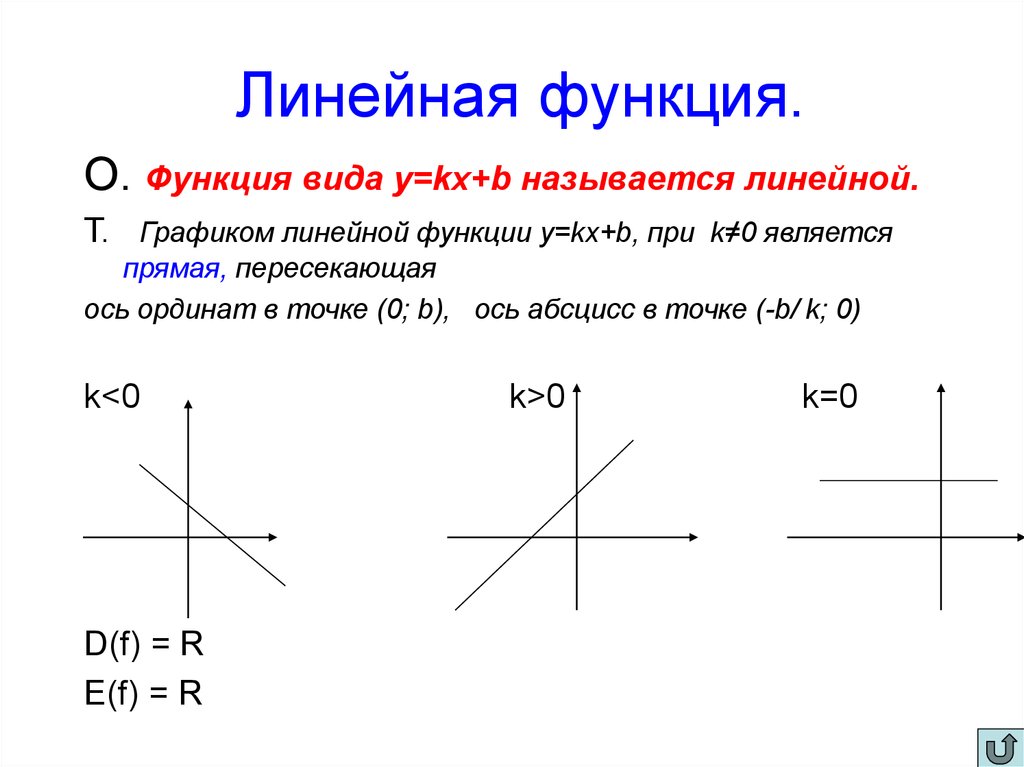

 Это дает:
Это дает: Это может выглядеть не так, но это уравнение имеет только одну переменную, b ,
и вы можете легко решить для него.
Это может выглядеть не так, но это уравнение имеет только одну переменную, b ,
и вы можете легко решить для него.