Скалярные и векторные величины в физике и математике » Kupuk.net
Величиной в физике и математике называют свойства физических тел, измеряемых при помощи выполнения математических операций. Они имеют единицы измерения и зависят от физических законов и аксиом. Выделяют скалярные и векторные величины, обладающие различными характеристиками и параметрами.
Особенности скалярных величин
Скалярные величины характеризуются только одним параметром — числовым значением. Они разделяются на 2 вида:
- Чистые скаляры. Характеризуются числовым значением, не находящимся в зависимости от осей отсчета — линий пересечения плоских поверхностей в единой системе координат.
- Псевдоскаляры. Находятся при помощи расчета числа, знак которого зависит от положительного направления осей в системе координат.
В физике в список скалярных величин входят:
- Масса — определяет величину материи и ее гравитационные свойства.
 Измеряется в килограммах и обозначается буквой латинского алфавита m.
Измеряется в килограммах и обозначается буквой латинского алфавита m. - Температура — средняя кинетическая энергия физического тела. Выражается в кельвинах или градусах Цельсия.
- Работа — мера действия силы на физическое тело или систему тел. Измеряется в Джоулях и обозначается латинской буквой A.
- Длина — величина, определяющая дистанцию между 2 концами тела в продольном направлении. Исчисляется в метрах. Особым видом длины является путь — скаляр, выражающий расстояние между начальным и конечным положением объекта, осуществляющего перемещение по заданной траектории.
- Время — продолжительность действия или события. Рассчитывается в секундах.
- Период — время совершения 1 полного колебания. Обозначается символом T и измеряется в секундах.
- Частота — величина, обратная периоду. Определяет количество полных колебаний в единицу времени. Рассчитывается в Герцах.
- Объем — скаляр, обозначающий размер пространства, ограниченного поверхностями со всех сторон.
 Измеряется в м3.
Измеряется в м3. - Напряжение — измеряет изменение потенциальной энергии тела, приходящейся на единицу заряда. Обозначается буквой U и рассчитывается в Вольтах.
- Сила тока — скаляр, показывающий число электрических зарядов, проходящих через сечение проводника в единицу времени. Обозначается символом I и рассчитывается в Амперах.
- Энергия — обозначает способность тела осуществлять работу.
Если скаляры выражают одно единственное свойство физического тела, то они называются однородными. Величины, описывающие несколько свойств объекта, именуются разнородными. Однородные скаляры сравнимы: они либо равны, либо одна из них больше или меньше другой. Но скалярные величины разного рода не могут сравниваться друг с другом.
Определение положительного скаляра и его измерения
Понятие положительной скалярной величины и ее измерения позволяет сравнивать между собой однородные скаляры. Положительная скалярная величина способна принимать значения строго выше 0. Она обозначается знаком «+». Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-«. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта.
Положительная скалярная величина способна принимать значения строго выше 0. Она обозначается знаком «+». Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-«. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта.
Чтобы получить скалярную величину, достаточно умножить ее числовое значение на ее единицу измерения. Для структуризации и стандартизации вычислений физических параметров тела была разработана Международная система СИ. Она устанавливает единицы измерения для каждой величины. Во время проведения расчетов скалярных величин применяют алгебраические действия — сложение, вычитание, деление и умножение (отдельный подвид — возведение в степень).
Особенности векторных величин
Их определение: «В физике векторными величинами называются свойства материи, характеризующиеся несколькими параметрами: модулем и направлением». Модулем вектора будет являться числовое значение величины, никогда не принимающее отрицательных значений. Он обозначается символом «||». Для обозначения направления используется стрелка, располагающаяся над символом вектора.
Модулем вектора будет являться числовое значение величины, никогда не принимающее отрицательных значений. Он обозначается символом «||». Для обозначения направления используется стрелка, располагающаяся над символом вектора.
В физике и математике примерами векторных величин являются:
- Сила — мера взаимодействия физических веществ. Обозначается латинской буквой F и измеряется в Ньютонах. Три закона Исаака Ньютона составляют основу классической механики. С их помощью можно определить массу тела и его ускорение.
- Скорость — расстояние, пройденное материей за определенный временной промежуток. Маркируется символом V и рассчитывается в м/с. Скорость используется для определения пути и времени движения предмета при помощи формулы: S = V * t. Скорость, с которой тело движется по окружности, называется линейной.
- Ускорение — величина, показывающая изменение показателей скорости физического тела. Ускорение свободного падения действует на все тела, придавая им силу тяжести.
 Оно направлено к ядру Земли и равняется 9,8 м/с2
Оно направлено к ядру Земли и равняется 9,8 м/с2 - Импульс — характеризует величину движения тела. Маркируется буквой латинского алфавита p и рассчитывается в кг*м/с. С помощью этой величины человек может определить массу физического тела и скорость ее передвижения.
На графиках функции векторные величины изображаются в виде прямой линии, имеющей направление и свои собственные координаты в заданном масштабе.
Свойства векторов
Вектор — математический элемент, представляющий собой прямой отрезок с направлением. Он обозначается либо 2 заглавными латинскими буквами, либо одной прописной. Длиной вектора является его модуль. Если длина вектора равняется 0, то он называется нулевым. Вектор, имеющий длину 1 см, именуется единичным. Длина ненулевого вектора выражается в виде расстояния между началом и концом направленного отрезка.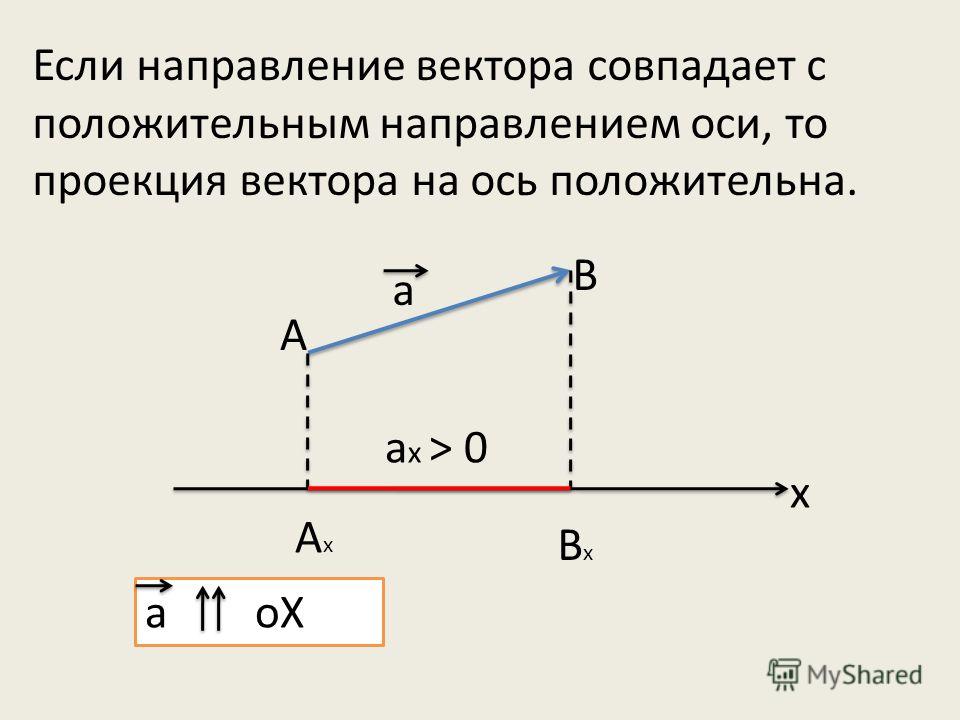 Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции:
Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции:
- Произведение вектора на косинус между осью и направленным отрезком равен проекции вектора.
- Проекция на ось принимает значения меньше 0, если отрезок с осью образует тупой угол.
- Проекция на ось принимает значение больше 0, если отрезок с осью образует острый угол.
Коллинеарные векторы — отрезки, располагающиеся либо на одной прямой, либо на параллельных прямых. Нулевой вектор коллинеарен всегда. Если коллинеарные векторы направлены в одну сторону, то они называются сонаправленными. Если отрезки направлены в диаметрально противоположные стороны, то они называются противоположно направленными. Коллинеарные векторы являются равными, если они одинаковы по модулю и направлению.
Построение отрезков с направлением на плоскости осуществляется при помощи его координат для осей абсцисса и ордината.
Для изображения направленного отрезка необходимо построить точки, координаты которых соответствуют началу и концу вектора, и соединить их.
С векторами также можно производить операции сложения, деления, вычитания и умножения. Чтобы сложить два вектора, необходимо от произвольной точки на плоскости отложить первый направленный отрезок и от него отложить второй вектор. Отрезок, соединяющий начало первого вектора и конец второго, будет считаться их суммой. Этот способ сложения именуется методом треугольника.
Вторым способом нахождения суммы векторов является метод параллелограмма. От произвольной точки откладываются оба направленных отрезка. Полученный рисунок нужно достроить до параллелограмма. Диагональ фигуры будет являться суммой векторов.
Для осуществления вычитания необходимо отложить от произвольной точки первый вектор. От полученного отрезка откладывается следующий вектор. Второй отрезок нужно направить в противоположную сторону. Линия, соединяющая отрезки, будет являться разностью векторов.
С векторами также можно проводить операцию умножения. Произведение длин направленных отрезков на косинус угла между ними называется скалярным. В результате вычислений получается число — скаляр. Скалярное произведение равно 0 в случае, когда отрезки пересекаются под углом 90°. Зная скалярное произведение, человек сможет найти косинус угла между построенными векторами.
Полученные в результате выполнения алгебраических операций выражения применяются для исследования перемещения тел вокруг оси вращения и изучения элементов высшей математики. Также направленные отрезки нашли широкое применение в геометрии и астрономии.
Скалярные и векторные величины и действия над ними в физике с примерами
Содержание:
Скалярные и векторные величины:
В 7-м и 8-м классах мы рассматривали различные физические величины. Для одних величин достаточно знать их числовое значение и единицу измерения.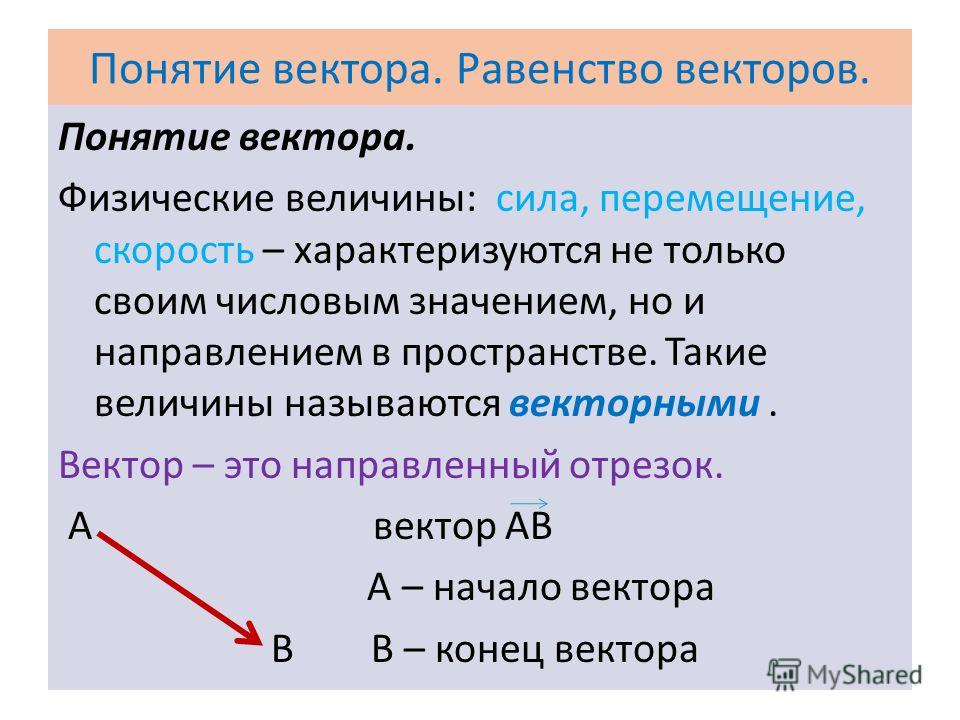 Например, масса
Например, масса
На рисунках 14, а и 14, б девочка действует на санки силой, имеющей одно и то же числовое значение. Но в первом случае санки лишь немного погрузились в снег, а во втором — пришли в движение. Значит, сила определяется не только числовым значением, но и направлением. Сила — величина векторная.
Векторной величиной является и скорость движения тел (рис. 15), и многие другие физические величины.
Что нужно знать о векторных величинах (векторах)
Векторы характеризуются модулем и направлением в пространствеМодулем вектора называется его числовое значение.
Вектор изображают в виде направленного отрезка (стрелки). Стрелка указывает, куда направлен вектор (рис. 14, 15). Длина стрелки характеризует модуль вектора (рис. 16). Над буквенным обозначением вектора ставят стрелку, например:
Модуль вектора обозначают той же буквой, но без стрелки над ней или символом Например, модуль вектора на рисунке 16 равен
Модуль любого (не равного нулю) вектора — число положительное.
Равные векторы лежат на одной и той же прямой или на параллельных прямых и направлены в одну и ту же сторону. На рисунке 17 Однако, несмотря на равенство модулей, так как у векторов различные направления.
Угол между векторамиЧтобы найти угол между векторами (рис. 18, а), нужно совместить их начала (рис. 18, б). Если направления векторов одинаковы, то (рис. 18, в), если противоположны, то (рис. 18, г).
Умножение вектора на число
Произведение вектора на число есть вектор Чему в равен его модуль? Куда направлен вектор
Модуль вектора равен
Если то вектор направлен так же, как вектор а если то противоположно ему.
На рисунке 19 показаны результаты умножения вектора на 2, на 0,5, на (-3) и на (-1) соответственно.
Противоположные векторыВектор называется противоположным вектору если У векторов одинаковые модули, но противоположные направления (рис. 19, а, г).
19, а, г).
В 7-м классе вы складывали силы, направленные или одинаково, или в противоположные стороны. Результатом сложения в первом случае была сила, модуль которой равен а во втором
То же самое получается и при сложении векторов (рис. 20). Если они направлены одинаково (рис. 20, а), то их сумма имеет модуль Если же направления векторов противоположны (рис. 20, б), то модуль их суммы Обратите внимание: в последнем случае вектор направлен так, как вектор с большим модулем (т. е. как вектор ).
А как сложить векторы, направленные под любым углом друг к другу? Для этого можно использовать любое из двух следующих далее правил.
Правило параллелограммаСовместим начала векторов (рис. 21, а), сохраняя их направления (рис. 21, б). Построим параллелограмм ABCD, принимая векторы за его стороны. Сумма векторов есть вектор совпадающий с диагональю АС параллелограмма: (см. рис. 21, б).
Совместим конец вектора с началом вектора сохраняя их направления (рис. 21, в). Вектор проведенный из начала вектора в конец вектора равен сумме (см. рис. 21, в).
Из рисунков 21, б и 21, в ясно, что правило треугольника и правило параллелограмма дают одинаковые результаты. А как найти разность векторов?
Вычитание векторовПусть начала векторов совмещены (рис. 22). Проведем вектор из конца вычитаемого вектора в конец уменьшаемого вектора Вектор есть искомая разность: Докажите с помощью построения, что Такой способ вычитания векторов очень удобен.
Правило многоугольника
Чтобы найти сумму нескольких векторов (например, ), каждый следующий вектор нужно проводить из конца предыдущего (рис. 23). Замыкающий вектор проведенный из начала первого вектора в конец последнего есть сумма данных векторов:
Правило многоугольника следует из правила треугольника.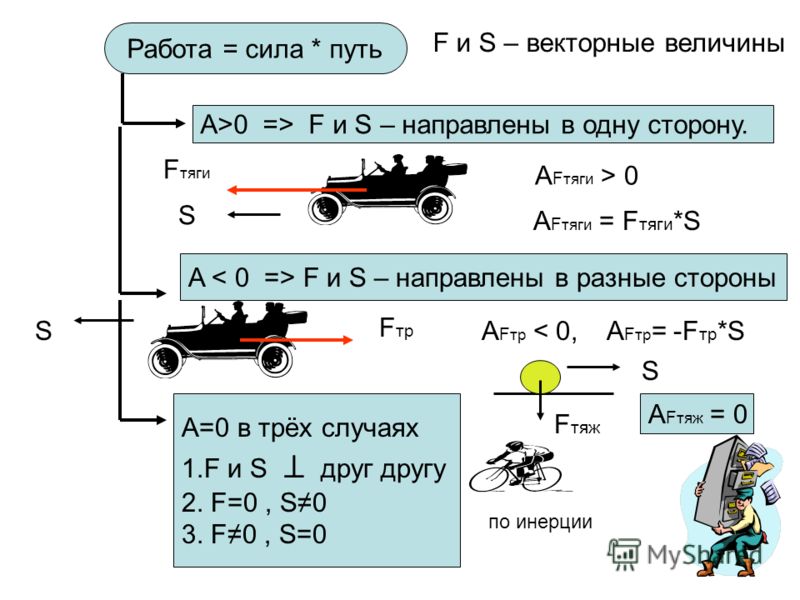
Не путайте модуль суммы векторов, т. е. и сумму их модулей Равенство выполняется только для одинаково направленных векторов (см. рис. 20, а на с. 13). Во всех остальных случаях т. е. модуль суммы векторов меньше суммы их модулей. Так получается потому, что в любом треугольнике (см. рис. 21, в) длина одной стороны меньше суммы длин двух других сторон. Проверьте это на примерах.
Нуль-векторПусть вектор равен вектору Тогда их разность т. е. нуль-вектору.
Главные выводы:
- Векторные величины характеризуются модулем и направлением, скалярные — только числовым значением.
- Сумму двух векторов находят по правилу параллелограмма или треугольника.
- Разность двух векторов находят, проводя вектор из конца вычитаемого вектора в конец уменьшаемого (при совмещенных началах векторов).
- Разность векторов можно найти как сумму
- Произведение вектора на число есть вектор При направления векторов совпадают, а при — противоположны.
 Модуль вектора равен
Модуль вектора равен
Скалярные и векторные величины
К пониманию того, что для описания природы нужно использовать язык математики, ученые пришли давно. Собственно, некоторые разделы математики и были созданы для того, чтобы описывать природу кратким и доступным языком. Так, для определения мгновенной скорости, работы переменной силы, объема тел неправильной формы и т. д. были созданы дифференциальное и интегральное исчисления. Для более наглядного описания физических процессов научились строить графики функций, а для быстрой обработки результатов эксперимента придумали методы приближенных вычислений. Вспомним скалярные и векторные величины, без которых вам не обойтись при изучении курса физики 10 класса.
Физические величины, используемые в физике для количественной характеристики физических явлений и объектов, делятся на два больших класса: скалярные величины и векторные величины.
К скалярным величинам, или скалярам (от лат. scalaris — ступенчатый), относятся величины, которые определяются только значением. Например, масса тела — скалярная величина, и если мы говорим, что масса тела равна двум килограммам (m=2 кг), то полностью определяем эту величину. Сложить две скалярные физические величины означает сложить их значения, представленные в одинаковых единицах. Понятно, что складывать можно только однородные скаляры (например, нельзя складывать массу и время, плотность и работу и т. д.).
Например, масса тела — скалярная величина, и если мы говорим, что масса тела равна двум килограммам (m=2 кг), то полностью определяем эту величину. Сложить две скалярные физические величины означает сложить их значения, представленные в одинаковых единицах. Понятно, что складывать можно только однородные скаляры (например, нельзя складывать массу и время, плотность и работу и т. д.).
Для определения векторных величин важно знать не только их значения, но и направления. Вектор (от лат. vector — носитель) — это направленный отрезок, то есть отрезок, имеющий и длину, и направление. Длину направленного отрезка называют модулем вектора. Обозначают векторные величины буквами греческого и латинского алфавитов, над которыми ставят стрелки, или полужирными буквами. Например, скорость записывают так: v или ; модуль вектора скорости соответственно обозначают как v.
Правила сложения (вычитания) векторов отличаются от правил сложения (вычитания) скалярных величин.
Сумму двух векторов находят по правилу параллелограмма или по правилу треугольника (рис. 3.1, 3.2). Как найти сумму нескольких векторов, показано на рис. 3.3, как найти разность двух векторов, показано на рис. 3.4.
В результате умножения векторной величины на скалярную величину k получается вектор (рис. 3.5).
Обратите внимание! Единица произведения векторной и скалярной величин определяется как произведение единицы одной величины на единицу другой. Например, нужно найти перемещение самолета, который в течение 0,5 ч летит на север со скоростью 500 км/ч. Вектор перемещения: . Поскольку t > 0, то вектор перемещения будет направлен в ту же сторону, что и вектор скорости , а модуль вектора перемещения будет равен: s v = =t 500 км /ч⋅ = 0 5, ч к 250 м.
- Заказать решение задач по физике
Как найти проекции вектора на оси координат
Осуществлять математические операции с векторами гораздо сложнее, чем со скалярами, поэтому, решая задачи, от векторных физических величин переходят к их проекциям на оси координат.
Пусть вектор лежит в плоскости XОY (рис. 3.6). Опустим из точки А (начало вектора ) и точки В (конец вектора ) перпендикуляры на ось ОX. Основания этих перпендикуляров — точки — проекции точек А и В на ось ОX, а отрезок — проекция вектора на ось ОX. Проекцию вектора обозначают той же буквой, что и вектор, с указанием оси в нижнем индексе, например: . Если из начала и конца вектора провести перпендикуляры к оси ОY, получим отрезок — проекцию вектора на ось ОY ( ). Знак проекции вектора зависит от направлений вектора и оси координат. Если от проекции начала вектора до проекции его конца нужно двигаться в направлении оси координат, то проекция вектора на эту ось считается положительной, а если наоборот, то проекция вектора считается отрицательной (см. рис. 3.6).
В общем случае проекцию вектора находят обычными геометрическими методами (рис. 3.7, а). На практике часто приходится иметь дело со случаями, когда вектор параллелен или перпендикулярен оси координат.
Если вектор параллелен оси координат, а его направление совпадает с направлением оси, то его проекция на эту ось положительна и равна модулю вектора (рис. 3.7, б). Если направление вектора противоположно направлению оси координат, то его проекция на эту ось равна модулю вектора, взятому с противоположным знаком (рис. 3.7, в). Если же вектор перпендикулярен оси координат, то его проекция на эту ось равна нулю (рис. 3.7, г). Очень важным свойством проекций является то, что проекция суммы двух векторов (рис. 3.8) или нескольких векторов на координатную ось равна алгебраической сумме проекций этих векторов на данную ось.
Именно это свойств позволяет заменять в уравнении векторные величины их проекциями — скалярными величинами и далее решать полученное уравнение обычными алгебраическими методами.
Тест с ответами: «Векторные величины»
1. Какое правило используется для сложения двух неколлинеарных векторов?
а) Правило Пифагора
б) Правило параллельных прямых
в) Правило параллелограмма +
2. Если два ненулевых вектора лежат на параллельных прямых или на одной прямой, то они называются:
Если два ненулевых вектора лежат на параллельных прямых или на одной прямой, то они называются:
а) сонаправленные
б) коллинеарные +
в) нулевые
3. Отрезок, для которого указано, какая из его граничных точек — начало, а какая – конец это:
а) Прямая
б) Луч
в) Вектор +
4. Выберите векторную физическую величину:
а) время
б) скорость тела +
в) масса тела
5. Нескольких векторов сложили по правилу многоугольника. Начало первого вектора совпало с концом последнего. Чему равна сумма векторов?
а) нулевому вектору +
б) вектору равному разнице первого вектора и последнего
в) единичному вектору
6. Как называются векторы, если они сонаправленные и имеют равные модули?
а) нулевые
б) Коллинеарные
г) Равные +
7. Чем характеризуются векторные величины?
а) численным значением и направлением +
б) только численным значением
в) только направлением
8. Два вектора коллинеарны и направлены в противоположные стороны.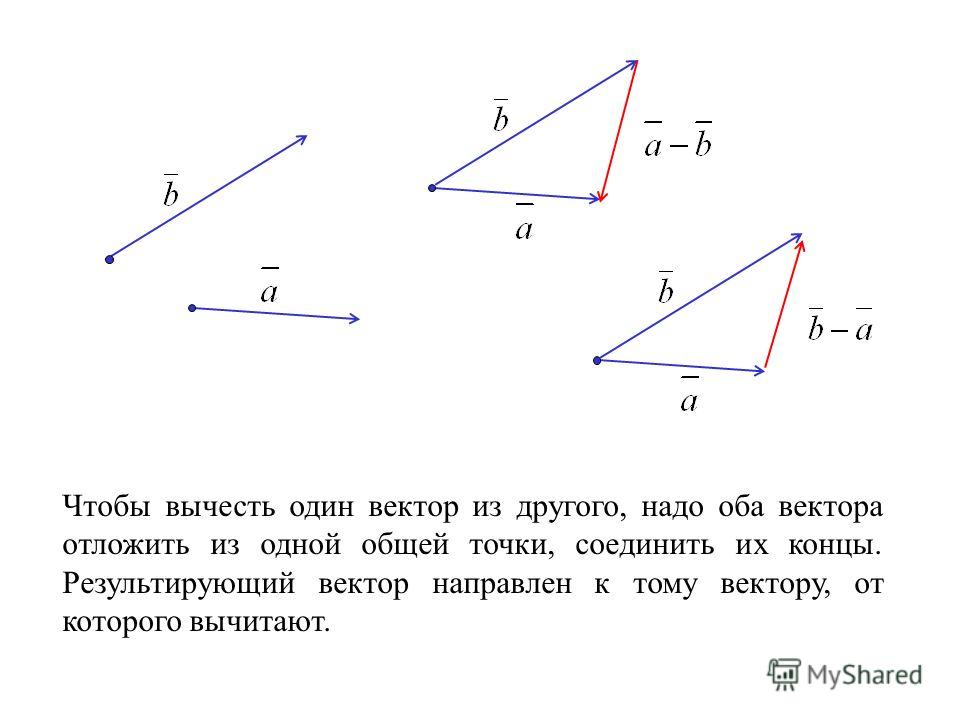 Их модули равны 3 и 4 соответственно. Чему равен модуль суммы этих векторов?
Их модули равны 3 и 4 соответственно. Чему равен модуль суммы этих векторов?
а) 1 +
б) 5
в) 7
9. Если из произвольной точки отложить первый вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало первого с концом второго – это будет:
а) разность первого и второго векторов
б) сумма первого и второго векторов +
в) нулевой вектор
10. Чем характеризуются скалярные величины?
а) численным значением и направлением
б) только численным значением +
в) только направлением
11. В чего изображается на графике нулевой вектор?
б) В виде точки +
а) В виде прямой
в) В виде направленного отрезком
12. Какое правило используется для сложения двух любых векторов?
а) Правило Пифагора
б) Правило треугольника
в) Правило параллелограмма +
13. Как называется вектор, начало которого совпадает с его концом
а) Нулевой +
б) Начальный
в) Точечный
14. Какой вектор направлен вниз к поверхности Земли?
а) вектор скорости свободно падающего тела +
б) вектор скорости автомобиля, движущего по горизонтальной дороге
в) вектор скорости взлетающей вверх ракеты
15. Как называется закон: сумма двух векторов не изменится от порядка слагаемых?
Как называется закон: сумма двух векторов не изменится от порядка слагаемых?
a) Переместительный законом +
б) сочетательный законом
в) правило параллелограмма
16. Автомобиль двигался по прямой дороге со скоростью 60 км/час. После знака ограничения скорости, автомобилист снизил скорость до 40 км час. Как изменился вектор скорости автомобиля.
а) Модуль вектора скорости увеличился в 1,5 раза, направление не изменилось
б) Модуль вектора скорости уменьшился в 1,5 раза, направление не изменилось
в) Модуль вектора скорости уменьшился в 1,5 раза, направление изменилось
17. Выберите скалярную физическую величину:
а) перемещение тела
б) скорость тела
в) масса тела +
18. При умножении векторной величины на скалярную получается:
а) скалярная величина
б) векторная величина +
в) в одних случаях скалярная, а в других векторная величина
19. Что такое модуль вектора?
а) направление вектора
б) числовое значение вектора +
в) координата вектора
20. Ракета вылетает под углом 30 градусов к горизонту со скоростью 300 м/с. Чему равен модуль вертикальной составляющей вектора скорости ракеты?
Ракета вылетает под углом 30 градусов к горизонту со скоростью 300 м/с. Чему равен модуль вертикальной составляющей вектора скорости ракеты?
а) 150 м/с +
б) 260 м/с
в) 300 м/с
21. Как обозначают векторы?
а) буквами со стрелкой над ними +
б) буквами без стрелки над ними
в) цифрами
22. Угол между вектором силы и осью х составляет z. Модуль вектора силы равен F. Чему равен модуль составляющей вектора силы вдоль оси x?
а) F*sin(z)
б) F*cos(z) +
в) F*tg(z)
23. Как обозначают модуль вектора?
а) буквами со стрелкой над ними
б) буквами без стрелки над ними +
в) цифрами
24. Как называются два вектора с равными модулями, лежащие на параллельных прямых, если их направления противоположны?
а) противоположными +
б) коллинеарными
в) сонаправленными
25. Равными считаются векторы, у которых одинаковы:
а) модули
б) и модули, и направления +
в) направления
26.Какой вектор получится в результате умножения любого вектора на ноль?
а) единичный вектор
б) начальный вектор
в) нулевой вектор
27. Два вектора направлены перпендикулярно друг к другу. Их модули равны 3 и 4 соответственно. Чему равен модуль суммы этих векторов?
Два вектора направлены перпендикулярно друг к другу. Их модули равны 3 и 4 соответственно. Чему равен модуль суммы этих векторов?
а) 5 +
б) 6
в) 7
28. Если при равномерном прямолинейном движении тела вектор перемещения разделить на время перемещения, что получится?
а) модуль скорости
б) вектор скорости +
в) модуль перемещения
29. Два вектора сонаправлены. Их модули равны 3 и 4 соответственно. Чему равен модуль суммы этих векторов?
а) 5
б) 6
в) 7 +
30. Если два вектора коллинеарны и их направления совпадают, то они называются:
а) сонаправленные +
б) коллинеарные
в) нулевые
31. Если из произвольной точки отложить первый вектор, а также второй вектор, и построить вектор, соединяющий конец второго вектора с концом первого – это будет:
а) разность первого и второго векторов +
б) сумма первого и второго векторов
в) нулевой вектор
Рис.1 Обозначение векторов. Координаты вектораЛюбой вектор имеет свои координаты. Координатами вектора называются числа x2-x1 и y2-y1. Например, координаты вектора с начальной точкой А (1;1) и конечной точкой В (4;3) будут: Координаты нулевого вектора равны нулю. Абсолютная величина вектора — это его длина. А следовательно, ее можно определить как расстояние между двумя точками, начальной и конечной. Т.е. Два вектора называются равными, если у них соответствующие координаты равны. | Рис.2 Координаты вектора. 2.Сложение векторовПусть заданы два вектора со своими координатами (b1;b2). Тогда суммой двух векторов будет вектор с координатами В векторной форме можно записать так: Для сложения векторов используются два метода: метод треугольника и метод параллелограмма. Для сложения векторов методом треугольника необходимо перенести вектор параллельным переносом так, чтобы конец вектора совпадал с началом вектора . и конец вектора и будет сумма векторов По методу параллелограмма, если два вектора имеют общее начало, то суммой двух векторов будет диагональ параллелограмма, построенного на этих векторах, т.е. вектор Разностью двух векторов называется такой вектор , который нужно прибавить к вектору , чтобы получить вектор Рис.3 Сложение векторов. 3.Умножение вектора на числоЛюбой вектор с координатами (x;y) можно умножить на простое число, например λ. (Рис.3) Тогда произведением вектора на число λ будет называться вектор с координатами (λx;λy). Абсолютная величина вектора будет равна: Для любых двух векторов число λ можно вынести за скобку λ ( Если λ > 0, то направление вектора не изменяется, а если λ 2 и называется скалярным квадратом. Отсюда следует, что Теорема. Скалярное произведение двух векторов равно произведению их абсолютных величин на косинус угла между ними. Доказательство. Пусть даны два вектора а и b и угол между ними α. Тогда квадрат суммы двух векторов равен: Следовательно, скалярное произведение двух векторов не зависит от выбора системы координат, а зависит только от их абсолютных величин. (Рис.5) Так как координаты вектора (b cos α; b sin α), то скалярное произведение двух векторов Рис.5 Скалярное произведение векторов. Отсюда вытекает следующий вывод: если два вектора перпендикулярны, то их скалярное произведение равно нулю. если скалярное произведение двух ненулевых векторов равно нулю, то векторы перпендикулярны. Репетитор: Васильев Алексей АлександровичПредметы: математика, физика, информатика, экономика, программирование. 2000 руб / 120 мин — подготовка к ЕГЭ и ГИА для школьников. 3000 руб / 120 мин — индивидуально (базовый уровень). 2000 руб / 120 мин — студенты. Тел. 8 916 461-50-69, email: alexey-it@ya. 6.Пример 1Четырехугольник ABCD — параллелограмм. Докажите равенство векторов Доказательство: Пусть ABCD данный параллелограмм (Рис.6). Необходимо доказать, что вектора параллельному переносу таким образом, чтобы точка А совпала с точкой D. При таком перемещении точка А смещается по прямой AD и переходит в точку D. Это значит, что точка В переместится по параллельной прямой ВС в точку С. Таким образом, при параллельном переносе прямая АВ переходит в параллельную прямую DC, а вектор переходит в вектор . А это значит, что эти вектора равны. Действительно, так как при перемещении прямая АВ переходит в параллельную прямую DC, а точка А переходит в точку D, то на луче DC можно отложить только один вектор, равный вектору Рис.6 Задача. Четырехугольник ABCD — параллелограмм. Пример 2Даны точки А(1;1), B(3;1), C(2;-2), D(4;-2). Докажите равенство векторов Доказательство: Найдем координаты векторов Таким образом, координаты векторов следующие: А так как равные вектора имеют равные соответствующие координаты и xAB = xCD, yAB = yCD, то вектора Рис. Пример 3В треугольнике АВС проведена медиана AM. Докажите, что Доказательство: , равный и параллельный вектору от точки С. И отложим вектор , равный и параллельный вектору от точки В (Рис.8). Тодга получим параллелограмм, в котором вектор , так же как вектор . А так как диагонали параллелограмма пересекаются в точке М и делятся этой точкой пополам, то |
Что такое скаляр и вектор
Физические величины различной природы могут иметь различную математическую структуру описания.
Из элементарного курса известны простейшие определения скаляра (скалярной величины) и вектора (векторной величины):
¾ скаляром называется величина, которая при определенном выборе единицы измерения однозначно характеризуется числом, ее измеряющим;
¾ вектор определяется своей величиной (модулем) и направлением в пространстве и складывается с другим вектором той же физической размерности по правилу треугольника или параллелограмма.
Для описания вектора в трехмерном пространстве (рис. П.1.1) необходимо одновременно задать три параметра (три проекции, или модуль вектора и углы между направлением вектора и какими-либо двумя из трех координатных направлений). Очевидное различие в математических структурах скалярной и векторной величин приводит к различию в свойствах указанных объектов.
Строгая классификация физических объектов основана на изучении характера изменения их компонент при преобразованиях систем координат (т.е. при переходе от одной координатной системы к другой). В физике чаще всего имеют дело с преобразованиями систем координат в обычном трехмерном пространстве или в четырехмерном пространстве-времени Минковского.
Трансформационные свойства физических величин могут быть различны в этих случаях. К примеру, кинетическая энергия материальной точки — скаляр относительно преобразований системы координат в трехмерном пространстве и одна из компонент 4-вектора относительно преобразований в пространстве Минковского.
Важно отметить, что и вид преобразований системы координат может оказаться существенным. Так “вращения” и “сдвиги” координатных систем отличаются тем, что переводят “правые” координатные системы в “правые”, а «отражение» относительно одной из координатных поверхностей переводит «правую» координатную систему в «левую». Физическая величина может оказаться инвариантной (неизменной) при преобразовании «вращения» и неинвариантной при преобразовании «отражения».
При изучении преобразований систем координат в основной части курса мы ограничимся преобразованиями сдвига и вращения правых декартовых систем координат.
В общем, указание трансформационных свойств физической величины (т.е. ее тензорного характера) имеет смысл только по отношению к определенной группе преобразований координат в данном пространстве. С рассматриваемой точки зрения, скаляр — это величина, инвариантная относительно (разрешенных) преобразований координат, а вектор — совокупность компонент, которые при преобразовании координат трансформируются по определённому правилу, с этим правилом мы познакомимся ниже.
Ниже для описания скалярной величины или функции используются общепринятые обозначения. Векторные величины принято описывать или в символической форме (т.е. без указания конкретной системы координат), например, вектор , или в координатной форме , где упорядоченные величины в фигурных скобках представляют собой проекции вектора на соответствующие координатные линии декартовой системы координат.
Сложение векторных величин по правилу треугольника или параллелограмма (рис. П.1.2)
эквивалентно покоординатному сложению:
Для векторных величин определено умножение на скалярную величину:
Геометрический образ описанной операции очень нагляден: вектор направлен так же как и вектор , но его величина в «l раз больше» (если l>0 и размерности не имеет).
Поскольку вектор определен величиной и направлением в пространстве, его можно представить в форме:
,
где – единичный безразмерный вектор (орт), совпадающий по направлению с исходным вектором ; обозначение используется для записи абсолютной величины (модуля) вектора .
Заметим, что в декартовой системе координат имеет место соотношение:
Для декартовой системы координат в трехмерном пространстве удобно ввести орты координатных линий: (используемые иногда обозначения не всегда удобны). В этом случае вектор можно представить в форме:
Определение операций «сложение» и «умножение на скалярную величину» позволяет ввести операцию «вычитания» векторов (рис. П.1.2) по следующему правилу:
.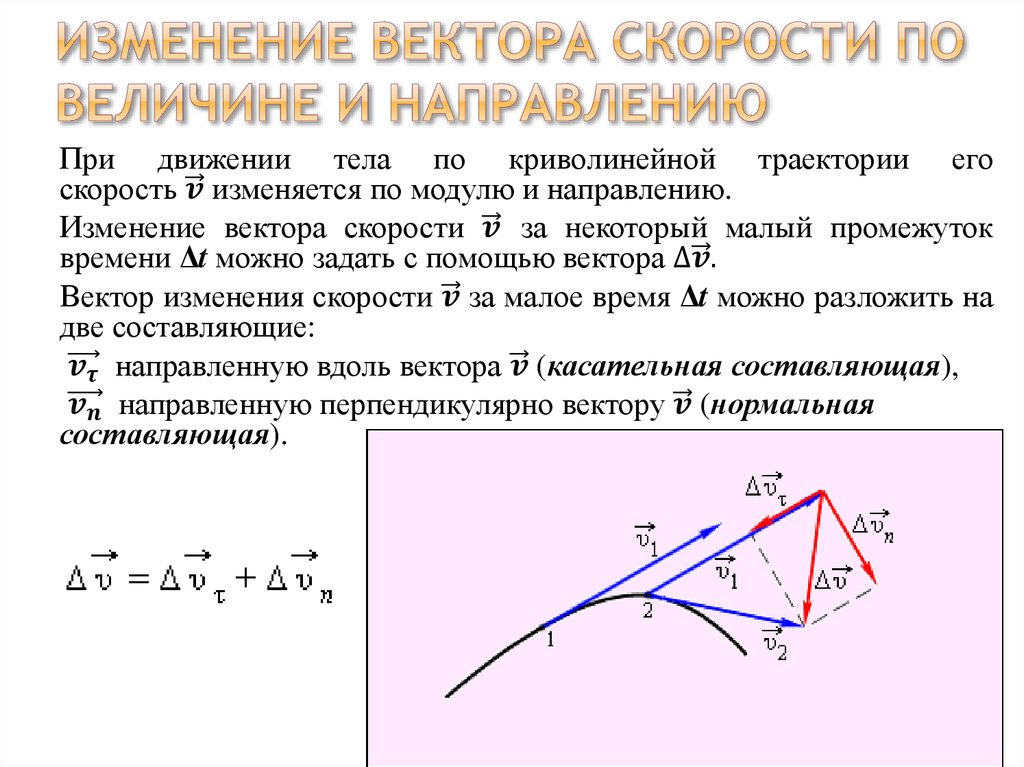
Для векторных величин известны три различные операции умножения. Первая из них, скалярное произведение двух векторов, определена правилом:
где a— угол между направлениями векторов и , результат операции —скалярная величина (рис. П.1.3).
Если для произвольных векторов и , таких, что и , имеет место соотношение , то такие векторы называются ортогональными друг другу. Геометрический смысл скалярного произведения двух векторов становится очевидным, если заметить, что выражение представляет собой либо произведение проекции вектора на направление на модуль вектора , то есть , либо произведение проекции вектора на направление вектора на модуль вектора , то есть . Легко проверить, что .
Векторное произведение векторов и определено правилом:
где – орт, направленный по нормали к плоскости, в которой расположены векторы и , причем система направлений , , является «правой» системой: кратчайшее угловое расстояние между направлениями векторов и (угол a) соответствует движению от к против часовой стрелки, если смотреть с конца орта (или с конца вектора ). Очевидно, что направление орта нормали совпадает с направлением вектора .
Очевидно, что направление орта нормали совпадает с направлением вектора .
Легко видеть, что результатом векторного произведения двух векторов является вектор, причем . В координатной форме записи имеют место соотношения
Если , то векторы и либо параллельны друг другу, т.е. , либо антипараллельны, т.е. .
Геометрический смысл векторного произведения становится наглядным, если векторы и представляют собой направленные отрезки двух прямых, исходящих из одной точки пространства, в этом случае величина представляет собой площадь параллелограмма, построенного на векторах и .
В качестве упражнения рекомендуется проверить соотношения:
Прямое или тензорное произведение двух векторов определено следующим образом. Если имеем вектор , или в координатной форме , и вектор , или в координатной форме {bx,, by, bz}, то можно построить двухиндексный объект – матрицу
=
как результат тензорного произведения = Ä , что в координатной форме имеет вид
Сij = ai bj , i,j=1,2,3.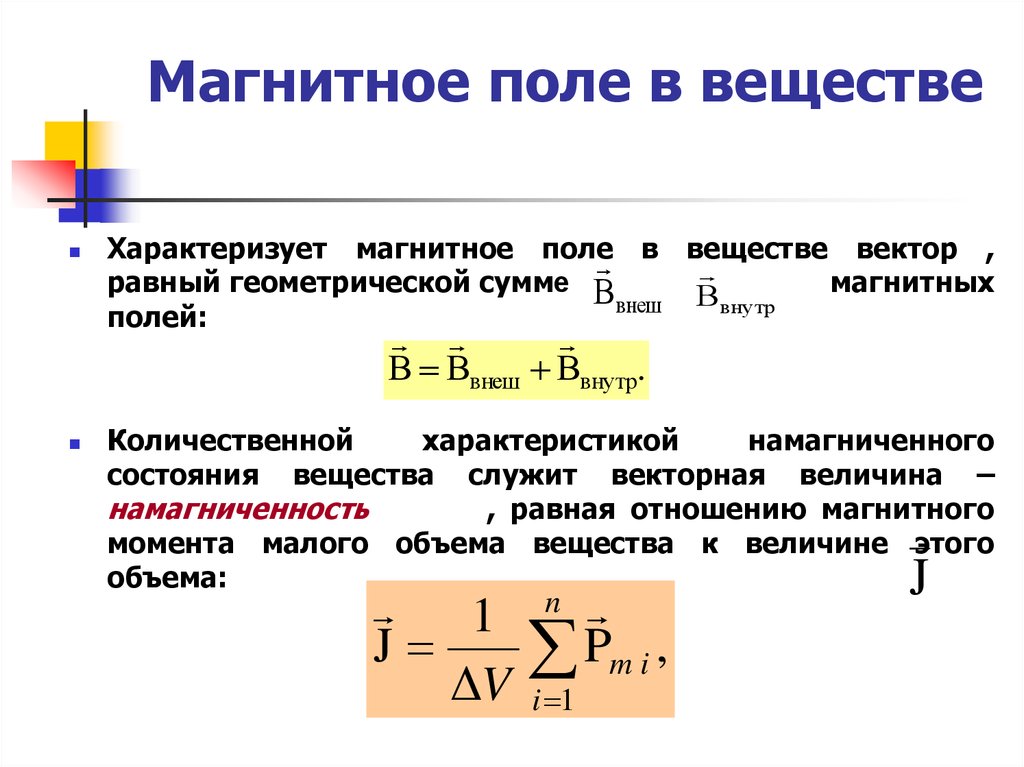
Объект, построенный таким образом, обладает свойствами тензора второго ранга. Тензоры второго и более высокого ранга используются при описании физических явлений в механике сплошных сред, электродинамике, теории относительности и т.д.
Описание алгебраических операций над векторными величинами заключим напоминанием, что операция деления векторных величин не определена.
| | | следующая лекция ==> | |
| Источники векторного поля. | | | Правило преобразования компонент векторов |
Дата добавления: 2017-09-01; просмотров: 7250; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Знакомство с R (молниеносное и поверхностное).
- О курсе
- Презентации и данные
- Полезности
Собственно, сам R
RStudio — среда для разработки (IDE) на R
Онлайн IDE для R — на тот случай, если у вас не установлен R:
- https://rstudio.
 cloud
cloud
- Создайте папку, где будут храниться ВСЕ материалы курса. Например: Мы будем ее называть рабочей директорией. В эту папку помещайте ВСЕ файлы с кодом (с расширением .R).
- Внутри папки
linmodrсоздайте папкуdata, где будут храниться все файлы с данными для анализа.
В итоге у вас должно получиться примерно это:
C:\linmodr\ C:\linmodr\data\
Настройка RStudio
Все настройки RStudio находятся в меню Tools -> Global Options
- Восстановление рабочего пространства из прошлого сеанса — это лучше
отменить, т.к. обычно переменные-призраки очень мешают. На вкладке
Generalубираем галочкуRestore .RData into workspace at startup, и меняемSave workspace to .RData on exit—Never - Перенос длинных строк в окне кода — это удобно. На вкладке
Codeставим галочку рядом с опциейSoft-wrap R source files
Комментарии в текстах программ обозначаются символом #
# это комментарии, они не будут выполняться
Ctrl + Shift + C— закомментировать/раскомментировать выделенный фрагмент кодаCtrl + Enter— отправляет активную строку из текстового редактора в консоль, а если выделить несколько строк, то будет выполнен этот фрагмент кода.
TabилиCtrl + Space— нажмите после того как начали набирать название функции или переменной, и появится список автоподстановки. Это помогает печатать код быстро и с меньшим количеством ошибок.
- В RStudio можно поставить курсор на слово
setwdи нажатьF1 - Перед названием функции можно напечатать знак вопроса и выполнить
эту строку
?setwd - Можно воспользоваться функцией
help()
help("setwd")## [1] 4
1024/2
## [1] 512
## [1] 1 2 3 4 5 6 7 8 9 10
## [1] 136
## [1] 16
sqrt(27)
## [1] 5.196152
Оператор присваивания это символ стрелочки <-. Он
работает справа налево, это значит, что значение выражения в его правой
части присваивается объекту в левой части.
Переменные — это такие контейнеры, в которые можно положить разные
данные и даже функции.
Имена переменных могут содержать латинские буквы обоих регистров, символы точки . и подчеркивания _ , а так же цифры. Имена переменных должны начинаться с латинских букв. Создавайте понятные и “говорящие” имена переменных.
var_1 <- 1024 / 2 1238 * 3 -> var_2 var_2
## [1] 3714
Как выбрать название переменной?
a— плохо, и дажеb,с, илих. Но в некоторых случаях допустимо:)var1— плохо, но уже лучшеvar_1— плохо, но уже лучшеshelllength— говорящее, но плохо читаетсяshell_length,wing_colourилиleg_num— хорошие говорящие и читабельные названия
Данные в R можно хранить в виде разных объектов.
В результате выполнения следующих команд числа. Одно выражение — одно значение.
## [1] 23
sqrt(25)
## [1] 5
На самом деле, эти величины — просто векторы единичной длины
Векторы — один объект, внутри которого несколько
значений.
Некоторые способы создания векторов:
- Оператор: используется для создания целочисленных векторов, где значения следуют одно за другим без пропусков
1:10 # от одного до 10
## [1] 1 2 3 4 5 6 7 8 9 10
-5:3 # от -5 до 3
## [1] -5 -4 -3 -2 -1 0 1 2 3
- Функция
seq()создает последовательности из чисел
seq(from = 1, to = 5, by = 0.5)
## [1] 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
- Функция
c()— от англ. concatenate. Следите, чтобы было английское си, а не русское эс:).
?c # посмотрите хелп к функции
Функция c принимает несколько (произвольное количество)
аргументов, разделенных запятыми. Она собирает из них вектор.
c(2, 4, 6)
## [1] 2 4 6
c(-9.3, 0, 2.17, 21.3)
## [1] -9.30 0.00 2.17 21.30
Векторы можно хранить в переменных для последующего использования
vect_num <- -11:12 # численный вектор от -11 до 12 сохранен в переменной vect_num vect_num_1 <- c(1.3, 1.7, 1.2, 0.9, 1.6, 1.4) # численный вектор, сохранен в переменной vect_num_1
Адресация внутри векторов
При помощи оператора [], можно обратится к некоторым
элементам вектора. В квадратных скобках вам нужно указать один или
несколько порядковых номеров элементов
vect_num[1] # первый элемент в векторе vect_num
## [1] -11
vect_num[10] # 10-й элемент
## [1] -2
vect_num[22]
## [1] 10
Если вам нужно несколько элементов, то их нужно передать квадратным скобкам в виде вектора. Например, нам нужны элементы с 3 по 5. Вот вектор, который содержит значения 3, 4 и 5.
## [1] 3 4 5
Если мы его напишем в квадратных скобках, то добудем элементы с такими порядковыми номерами
vect_num[3:5]
## [1] -9 -8 -7
Аналогично, если вам нужны элементы не подряд, то передайте вектор с номерами элементов, который вы создали при помощи функции c() c(2, 4, 6) # это вектор содержащий 2, 4 и 6, поэтому
vect_num[c(2, 4, 6)] # возвращает 2-й, 4-й и 6-й элементы
## [1] -10 -8 -6
vect_num[c(1, 10, 20)] # возвращает 1-й, 10-й и 20-й элементы
## [1] -11 -2 8
Вектор — одномерный объект. У его элементов только один порядковый
номер (индекс). Поэтому при обращении к элементам вектора нужно
указывать только одно число или один вектор с адресами.
У его элементов только один порядковый
номер (индекс). Поэтому при обращении к элементам вектора нужно
указывать только одно число или один вектор с адресами.
Правильно:
vect_num[c(1, 2, 5)] # возвращает 1-й, 3-й и 5-й элементы
## [1] -11 -10 -7
Но R выдаст ошибку, если при обращении к вектору, вы не создавали вектор, а просто перечислили номера элементов через запятую.
vect_num[1, 3, 5] # ошибка vect_num[15, 9, 1] # ошибка
vect_num[c(15, 9, 1)] # правильно
## [1] 3 -3 -11
При помощи функции c() можно объединять несколько векторов в один вектор
c(1, 1, 5:9)
## [1] 1 1 5 6 7 8 9
c(vect_num, vect_num)
## [1] -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 ## [20] 8 9 10 11 12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 ## [39] 3 4 5 6 7 8 9 10 11 12
c(100, vect_num)
## [1] 100 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 ## [20] 7 8 9 10 11 12
Добываем 1, 3, 5 и с 22 по 24 элементы
vect_num[c(1, 3, 5, 22:24)]
## [1] -11 -9 -7 10 11 12
Числовые данные
Уже видели в прошлом разделе.
Текстовые данные
Каждый текстовый элемент (говорят “строка” — string или character) должен быть окружен кавычками — двойными или одинарными.
"это текст"
## [1] "это текст"
'это тоже текст'
## [1] "это тоже текст"
Текстовые значения можно объединять в вектора.
Это текстовый вектор
rainbow <- c("red", "orange", "yellow", "green", "blue", "violet")
rainbow # весь вектор## [1] "red" "orange" "yellow" "green" "blue" "violet"
Добываем первый и последний элементы
В данном случае я точно знаю, что их 6, мне нужны 1 и 6.
rainbow[c(1, 6)]
## [1] "red" "violet"
Добываем элементы с 3 по 6
Если у вас вдруг слишком короткий вектор в этом задании, то можно склеить новый из двух
double_rainbow <- c(rainbow, rainbow) double_rainbow
## [1] "red" "orange" "yellow" "green" "blue" "violet" "red" "orange" ## [9] "yellow" "green" "blue" "violet"
rainbow[3:6] # элементы с 3 по 6
## [1] "yellow" "green" "blue" "violet"
Логические данные
TRUE # истина
## [1] TRUE
FALSE # ложь
## [1] FALSE
Для ленивых — можно сокращать первыми заглавными буквами. Но
лучше так не делать, чтобы читать программы было легче.
Но
лучше так не делать, чтобы читать программы было легче.
c(T, T, T, T, F, F, T, T)
## [1] TRUE TRUE TRUE TRUE FALSE FALSE TRUE TRUE
Логический вектор
c(TRUE, TRUE, TRUE, FALSE, FALSE, TRUE)
## [1] TRUE TRUE TRUE FALSE FALSE TRUE
Еще логический вектор
short_logical_vector <- c(FALSE, TRUE)
Создаем длинный логический вектор.
Чтобы создавать длинные вектора из повторяющихся элементов, можно использовать функцию rep()
?rep
rep(x = 1, times = 3) # 1 повторяется 3 раза
## [1] 1 1 1
rep(x = "red", times = 5) # "red" повторяется 5 раз
## [1] "red" "red" "red" "red" "red"
rep(x = TRUE, times = 2) # TRUE повторяется 2 раза
## [1] TRUE TRUE
В R названия аргументов функций можно не указывать, если вы используете аргументы в том же порядке, что прописан в help к этой функции.
rep(TRUE, 5) # TRUE повторяется 5 раз, аргументы без названий
## [1] TRUE TRUE TRUE TRUE TRUE
Создаем логический вектор, где TRUE повторяется 3 раза, FALSE 3 раза
и TRUE 4 раза. Результат сохраняем в переменной vect_log
Результат сохраняем в переменной vect_log
vect_log <- c(rep(TRUE, 3), rep(FALSE, 3), rep(TRUE, 4)) vect_log
## [1] TRUE TRUE TRUE FALSE FALSE FALSE TRUE TRUE TRUE TRUE
Применение логических векторов для фильтрации данных
Логические векторы создаются при проверке выполнения каких либо
условий, заданных при помощи логических операторов (>, <, ==, !=, >=, <=, !, &, |).
Такие векторы можно использовать для фильтрации данных
Вспомните, у нас был вот такой текстовый вектор
double_rainbow
## [1] "red" "orange" "yellow" "green" "blue" "violet" "red" "orange" ## [9] "yellow" "green" "blue" "violet"
Задача 1. Допустим, мы хотим из этого вектора извлечь только желтый цвет.
Мы можем создать логический вектор, в котором TRUE будет только для 3-го и 9-го элементов
f_yellow <- double_rainbow == "yellow" f_yellow
## [1] FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE
Этот логический вектор-фильтр мы можем использовать для извлечения
данных из double_rainbow
double_rainbow[f_yellow]
## [1] "yellow" "yellow"
Задача 2. Допустим, мы хотим извлечь из double_rainbow желтый и синий
Желтый фильтр у нас уже есть, поэтому мы создадим фильтр для синего.
Допустим, мы хотим извлечь из double_rainbow желтый и синий
Желтый фильтр у нас уже есть, поэтому мы создадим фильтр для синего.
f_blue <- double_rainbow == "blue"
Выражение “желтый или синий” можно записать при помощи логического
“или” (|)
f_yellow | f_blue
## [1] FALSE FALSE TRUE FALSE TRUE FALSE FALSE FALSE TRUE FALSE TRUE FALSE
Задача решена, мы извлекли желтый и синий цвета.
double_rainbow[f_yellow | f_blue]
## [1] "yellow" "blue" "yellow" "blue"
То же самое можно было бы записать короче.
В одну строку — совершенно нечитабельно:
double_rainbow[double_rainbow == "yellow" | double_rainbow == "blue"]
## [1] "yellow" "blue" "yellow" "blue"
Фильтр отдельно — читается лучше:
f_colours <- double_rainbow == "yellow" | double_rainbow == "blue" double_rainbow[f_colours]
## [1] "yellow" "blue" "yellow" "blue"
У нас был числовой вектор
vect_num
## [1] -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 ## [20] 8 9 10 11 12
Задача 3. Давайте извлечем из числового вектора
Давайте извлечем из числового вектора vect_num только значения больше 0
vect_num[vect_num > 0]
## [1] 1 2 3 4 5 6 7 8 9 10 11 12
Задача 4. Давайте извлечем из вектора vect_num все
числа, которые либо меньше или равны -8, либо больше или равны 8
f_5_8 <- (vect_num <= -8) | (vect_num >= 8) vect_num[f_5_8]
## [1] -11 -10 -9 -8 8 9 10 11 12
Факторы
Факторы — это способ хранения дискретных (=категориальных данных). Например, если вы поймали 10 улиток и посмотрели их цвет. У большого количества улиток небольшое счетное количество возможных цветов.
snail_colours <- c("red", "green", "green", "green", "yellow", "yellow", "yellow", "yellow")
snail_colours # это текстовый вектор.## [1] "red" "green" "green" "green" "yellow" "yellow" "yellow" "yellow"
Но цвет “желтый” обозначает одно и то же для каждой из улиток.
Поэтому в целях экономии места можно записать цвета этих улиток в виде
вектора, в котором численным значениям будут сопоставлены “этикетки”
(называются “уровни” — levels) — названия цветов. Мы можем создать
“фактор” цвет улиток.
Мы можем создать
“фактор” цвет улиток.
factor(snail_colours)
## [1] red green green green yellow yellow yellow yellow ## Levels: green red yellow
уровни этого фактора
- 1 — green,
- 2 — red,
- 3 — yellow
По умолчанию, R назначает порядок уровней по алфавиту. Можно изменить
порядок (см. help("factor")). Нам это пригодится позже
double_rainbow # текстовый вектор
## [1] "red" "orange" "yellow" "green" "blue" "violet" "red" "orange" ## [9] "yellow" "green" "blue" "violet"
Создаем фактор из текстового вектора и складываем его в переменную
f_double_rainbow <- factor(double_rainbow)
Как узнать, что за данные хранятся в переменной?
Чтобы узнать, что за данные хранятся в переменной, используйте
функцию class()
class(f_double_rainbow)
## [1] "factor"
class(vect_log)
## [1] "logical"
class(vect_num)
## [1] "integer"
class(rainbow)
## [1] "character"
Встроенные константы в R: NA, NULL, NAN, Inf
- NA — англ “not available”.
 Когда объект был, но его свойство не
измерили или не записали.
Когда объект был, но его свойство не
измерили или не записали. - NULL — пусто — просто ничего нет
- NaN — “not a number”
- Inf — “infinity” — бесконечность
Вот текстовый вектор с пропущенным значением
rainbow_1 <- c("red", "orange", NA, "green", "blue", "violet")Кстати, если попросили добыть из вектора номер элемента, которого там точно нет, то R выдаст NA, потому, что такого элемента нет
rainbow_1[198]
## [1] NA
Поэкспериментируем с векторами. Проверим, как работают арифметические операции
vect_num + 2
## [1] -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
vect_num * 2
## [1] -22 -20 -18 -16 -14 -12 -10 -8 -6 -4 -2 0 2 4 6 8 10 12 14 ## [20] 16 18 20 22 24
vect_num * (-2)
## [1] 22 20 18 16 14 12 10 8 6 4 2 0 -2 -4 -6 -8 -10 -12 -14 ## [20] -16 -18 -20 -22 -24
vect_num ^2
## [1] 121 100 81 64 49 36 25 16 9 4 1 0 1 4 9 16 25 36 49 ## [20] 64 81 100 121 144
Теперь посмотрим на встроенные константы в действии.
Создаем новый вектор для экспериментов
NAs_NANs <- c(1, 3, NA, 7, 0, 22:24)
Вот так он выглядит
NAs_NANs
## [1] 1 3 NA 7 0 22 23 24
Что произойдет с NA?
NAs_NANs + 2 # останется NA
## [1] 3 5 NA 9 2 24 25 26
NAs_NANs * 0 # останется NA
## [1] 0 0 NA 0 0 0 0 0
NAs_NANs / 0 # останется NA
## [1] Inf Inf NA Inf NaN Inf Inf Inf
Но в последнем случае вы увидите
- Inf при делении чисел на ноль
- NaN при делении нуля на ноль
NaN получится, если взять корень из отрицательного числа
sqrt(-1)
## Warning in sqrt(-1): NaNs produced
## [1] NaN
Вы уже видели массу функций, их легко узнать по скобкам после ключевого слова. Познакомимся еще с несколькими и научимся писать пользовательские функции. Пользовательские функции позволяют автоматизировать повторяющиеся действия и делают код легко читаемым.
Вот наш вектор
NAs_NANs
## [1] 1 3 NA 7 0 22 23 24
Длину вектора можно вычислить при помощи функции length()
length(NAs_NANs)
## [1] 8
Сумму элементов вектора при помощи функции sum()
sum(NAs_NANs)
## [1] NA
Упс! Почему-то получилось NA
Чтобы узнать, почему и как это исправить — посмотрите в help("sum"). Выяснится, что у функции
Выяснится, что у функции sum() есть аргумент na.rm, который по умолчанию принимает
значение FALSE, то есть NA не учитываются при
подсчете суммы.
Если мы передадим функции sum аргумент na.rm = TRUE, то получится правильная сумма
sum(NAs_NANs, na.rm = TRUE)
## [1] 80
Та же история с функцией mean
mean(NAs_NANs, na.rm = TRUE)
## [1] 11.42857
Попробуем написать пользовательскую функцию mmean(),
которая будет по умолчанию считать среднее значение элементов в векторе
с учетом пропущенных значений (NA)
mmean <- function(x){
mean(x, na.rm = TRUE)
}В этом коде: — mmean — переменная, название функции. В эту переменную
мы складываем функцию, которую создает функция function() — function() — функция, которая делает функции. В скобках
перечисляются аргументы (названия переменных, которые мы передаем в
функцию, чтобы она что-то сделала с ними) — { } — в
фигурных скобках тело функции — последовательность действий, которую
нужно сделать с аргументами
У больших функций бывает еще инструкция return(),
которая сообщает, что именно должна возвращать наша функция. Вот как
выглядела бы наша функция с этой инструкцией
Вот как
выглядела бы наша функция с этой инструкцией
mmean <- function(x){
res <- mean(x, na.rm = TRUE)
return(res)
}Проверим нашу функцию при помощи встроенной функции
mean(vect_num, na.rm = TRUE)
## [1] 0.5
mmean(vect_num)
## [1] 0.5
Работает
Датафрейм — один из способов хранения табличных данных в R. Создадим датафрейм.
Для этого, для начала, создадим векторы с данными для переменных.
len <- 1:9 # числовой
col <- c(rep("green", 4), rep("red", 5)) # текстовый
wid <- seq(from = 2, by = 2, to = 18) # числовойТеперь сложим эти векторы в датафрейм
my_worms <- data.frame(Length = len, Width = wid, Colour = col)
Можно проверить, действительно мы создали объект класса data.frame
class(my_worms) # смотрим, действительно датафрейм
## [1] "data.frame"
Содержимое датафрейма можно просмотреть несколькими способами
my_worms # печать датафрейма
## Length Width Colour ## 1 1 2 green ## 2 2 4 green ## 3 3 6 green ## 4 4 8 green ## 5 5 10 red ## 6 6 12 red ## 7 7 14 red ## 8 8 16 red ## 9 9 18 red
View(my_worms) # просмотр в RStudio head(my_worms)
## Length Width Colour ## 1 1 2 green ## 2 2 4 green ## 3 3 6 green ## 4 4 8 green ## 5 5 10 red ## 6 6 12 red
tail(my_worms)
## Length Width Colour ## 4 4 8 green ## 5 5 10 red ## 6 6 12 red ## 7 7 14 red ## 8 8 16 red ## 9 9 18 red
# fix(my_worms) # ручное редактирование.осторожно! избегайте его использовать, никаких документов о нем не останется
Адресация внутри датафреймов
Вывод столбца-переменной при помощи оператора $ и имени переменной
my_worms$Length
## [1] 1 2 3 4 5 6 7 8 9
my_worms$Width
## [1] 2 4 6 8 10 12 14 16 18
У каждой ячейки в датафрейме есть координаты вида [строка, столбец]
my_worms[2, 3] # вторая строка в 3 столбце
## [1] "green"
my_worms[2, ] # вторая строка целиком
## Length Width Colour ## 2 2 4 green
my_worms[1:9, 2] # строки с 1 по 9 во втором столбце
## [1] 2 4 6 8 10 12 14 16 18
my_worms[, 2] # второй столбец целиком
## [1] 2 4 6 8 10 12 14 16 18
Базовые графики
Скаттерплот (точечный график) — по оси х и y непрерывные числовые величины
plot(x = my_worms$Width, y = my_worms$Length)
Боксплот — по оси х дискретная величина, по оси y значение
непрерывной величины. Черта — медиана, коробка — 25 и 75 перцентили, усы
— либо размах варьирования, либо 1.5 интерквартильных расстояния (1.5
высоты коробки), если есть “выбросы”.
Черта — медиана, коробка — 25 и 75 перцентили, усы
— либо размах варьирования, либо 1.5 интерквартильных расстояния (1.5
высоты коробки), если есть “выбросы”.
plot(x = as.factor(my_worms$Colour), y = my_worms$Length)
Для настройки внешнего вида см graphical parameters в help
На самом деле, мы не будем пользоваться этой системой графики, но об этом в следующих сериях
Графики из пакета ggplot2
В R есть более удобный (но, может быть, более многословный) пакет для рисования графиков — ggplot2. Чтобы использовать функции из пакета ggplot2, нужно его сначала установить.
Установка пакета в локальную библиотеку делается один раз. Поэтому
строку с install.packages() не нужно включать в финальную
версию кода.
install.packages('ggplot2')В текущей сессии работы в R пакет нужно активировать перед
использованием. Когда вы в следующий раз начнете работать с R, нужные
пакеты придется снова активировать. Поэтому строки с загрузкой пакетов
при помощи library() обязательно должны остаться в
финальной версии кода.
library(ggplot2)
Нарисуем те же самые графики при помощи пакета ggplot2.
ggplot(data = my_worms) + geom_point(aes(x = Width, y = Length))
ggplot(data = my_worms) + geom_boxplot(aes(x = Colour, y = Length))
Добавляем для точек эстетику цвет (colour) из переменной Colour
ggplot(data = my_worms) + geom_point(aes(x = Width, y = Length, colour = Colour))
Графики можно сохранять в переменных, и использовать потом
gg <- ggplot(data = my_worms) + geom_point(aes(x = Width, y = Length, colour = Colour))
Чтобы вывести график, нужно напечатать название переменной.
Можно менять темы оформления графика. Если тема нужна только один раз, то прибавляем ее к графику
gg + theme_dark()
gg + theme_light()
gg + theme_classic()
Можно установить нужную тему до конца сессии.
theme_set(theme_bw()) gg
Подписи осей и легенд задает функция labs()
gg + labs(x = "Ширина", y = "Длина", colour = "Цвет")
Графики можно делить на фасетки при помощи facet_wrap или facet_grid
gg + facet_wrap(~Colour, nrow = 1)
Чтобы изменить подписи цветов, нужно изменить уровни соотв. фактора.
фактора.
my_worms$col_rus <- factor(my_worms$Colour, levels = c("green", "red"), labels = c("Зеленый", "Красный"))
ggplot(data = my_worms) +
geom_point(aes(x = Width, y = Length, colour = col_rus)) +
labs(x = "Ширина", y = "Длина", colour = "Цвет") +
facet_wrap(~col_rus, nrow = 1)Value Vectors — Apache Drill
В этом документе определяются структуры данных, необходимые для передачи последовательностей столбцовые данные между операторами.
Цели
Поддержка операторов, написанных на нескольких языках
ValueVectors должны поддерживать операторы, написанные на C/C++/Assembly. Поддерживать это, базовый ByteBuffer не потребует модификации при передаче через интерфейс JNI. ValueVector будет считаться неизменным один раз построен. Endianness еще не рассматривался.
Доступ
Чтение случайного элемента из ValueVector должно быть операцией с постоянным временем.
Чтобы приспособиться, элементы идентифицируются по их смещению от начала
буфер. Повторяющиеся, обнуляемые и переменная ширина ValueVectors используются в
дополнительный вектор значений фиксированной ширины для индексации каждого элемента. Доступа для записи нет
поддерживается после создания ValueVector.
Повторяющиеся, обнуляемые и переменная ширина ValueVectors используются в
дополнительный вектор значений фиксированной ширины для индексации каждого элемента. Доступа для записи нет
поддерживается после создания ValueVector.
Эффективные подмножества векторов значений
Когда оператор возвращает подмножество значений из ValueVector, он должен повторно используйте исходный ValueVector. Для этого используется уровень косвенности. введен для пропуска определенных значений в векторе. Этот уровень косвенность — это последовательность смещений, которые ссылаются на смещение в исходном ValueVector и количество последующих значений, которые должны быть включены в подмножество.
Распределение в пуле
ValueVectors использует один или несколько скрытых буферов. Эти буферы будут быть взяты из пула. Векторы ценности сами создаются и уничтожаются как схема изменяется в ходе итерации записи.
Однородные типы значений
Каждое значение в векторе значений относится к одному и тому же типу. Реализация Record Batch отвечает за
создание нового вектора значения каждый раз при изменении схемы.
Реализация Record Batch отвечает за
создание нового вектора значения каждый раз при изменении схемы.
Определения
Типы данных
Каноническим источником определений типов значений является Drill Документ Типы данных. Перечислены отдельные типы на вкладке «Основные типы данных», а типы векторов значений можно найти на вкладке «Векторы значений».
Операторы
Оператор отвечает за преобразование потока полей. Он работает на Запись пакетов или постоянных значений.
Пакет записей
Набор значений полей для некоторого диапазона записей. Партия может состоять из Векторы значений, и в этом случае каждый пакет состоит ровно из одной схемы.
Вектор значений
Вектор значений состоит из одного или нескольких непрерывных буферов; тот, который хранит последовательность значений и ноль или более, которые хранят любые метаданные связанный с ValueVector.
Структура данных
ValueVector хранит значения в ByteBuf, который представляет собой непрерывную область
Память. Дополнительные уровни косвенности используются для поддержки значения переменной.
ширины, значения, допускающие значение NULL, повторяющиеся значения и векторы выбора. Эти уровни
косвенности — это прежде всего таблицы поиска, которые состоят из одного или нескольких фиксированных
width ValueVectors, которые можно комбинировать (например, для обнуляемых, переменной ширины
ценности). Фиксированная ширина ValueVector необнуляемых, неповторяющихся значений делает
не требуют косвенного поиска; элементы могут быть доступны непосредственно через
умножение позиции на шаг.
Дополнительные уровни косвенности используются для поддержки значения переменной.
ширины, значения, допускающие значение NULL, повторяющиеся значения и векторы выбора. Эти уровни
косвенности — это прежде всего таблицы поиска, которые состоят из одного или нескольких фиксированных
width ValueVectors, которые можно комбинировать (например, для обнуляемых, переменной ширины
ценности). Фиксированная ширина ValueVector необнуляемых, неповторяющихся значений делает
не требуют косвенного поиска; элементы могут быть доступны непосредственно через
умножение позиции на шаг.
Значения фиксированной ширины
Векторы значений фиксированной ширины просто содержат упакованную последовательность значений. Случайный доступ поддерживается доступом к элементу n в ByteBuf[0] + Index * Stride, где Индекс отсчитывается от 0. Ниже показан базовый буфер Значения INT4 [1 .. 6]:
Обнуляемые значения
Обнуляемые значения представлены вектором битовых значений. Каждый бит в
вектор соответствует элементу в ValueVector. Если бит не установлен,
значение равно NULL. В противном случае значение извлекается из базового
буфер. Ниже показан NullableValueVector значений INT4 2, 3.
и 6:
Если бит не установлен,
значение равно NULL. В противном случае значение извлекается из базового
буфер. Ниже показан NullableValueVector значений INT4 2, 3.
и 6:
Повторяющиеся значения
Повторяющийся вектор значений используется для элементов, которые могут содержать несколько значений (например, массив JSON). Таблица пар смещения и количества используется для представления каждый повторяющийся элемент в ValueVector. Нулевой счет означает, что элемент не имеет значений (обратите внимание, что поле смещения в этом случае не используется). Следующее иллюстрирует три поля; один с двумя значениями, один без значений и один с одним значением:
ValueVector Представление эквивалентного JSON:
x:[1, 2]
x:[ ]
x:[3]
Значения ширины переменной
Значения ширины переменной хранятся непрерывно в ByteBuf. Каждый элемент
представлен записью в фиксированной ширине ValueVector смещений. Длина
запись выводится путем вычитания смещения следующего поля. Потому что
из этого таблица смещения всегда будет содержать на одну запись больше, чем общее количество
элементы, причем последняя запись указывает на конец буфера.
Потому что
из этого таблица смещения всегда будет содержать на одну запись больше, чем общее количество
элементы, причем последняя запись указывает на конец буфера.
Повторяющиеся векторы карты
Повторяющийся вектор карты содержит одну или несколько карт (аналогично массиву объектов в формате JSON). Значения каждого поля на карте хранятся непрерывно в БайтБуф. Чтобы получить доступ к определенной записи, используйте справочную таблицу пар количества и смещения. используется. Эта таблица поиска указывает на первое повторяющееся поле в каждом столбце, в то время как количество указывает максимальное количество элементов для столбца. следующий пример иллюстрирует RepeatedMap с двумя записями; один с двумя объектов и один с одним объектом:
Представление ValueVector эквивалентного JSON:
x: [ {имя: «Сэм», возраст: 1}, {имя: «Макс», возраст: 2}]
x: [ {имя: «Джо» ‘, age:3} ]
Векторы выбора
Вектор выбора представляет собой подмножество вектора значений. Это реализовано
со списком смещений, которые идентифицируют каждый элемент в ValueVector как
включены в SelectionVector. В случае фиксированной ширины ValueVector,
смещения ссылаются на базовый ByteBuf. В случае обнуляемого повторного
или переменная ширина ValueVector, смещение ссылается на соответствующий поиск
стол. Ниже показан SelectionVector из INT4 (фиксированная ширина).
значения 2, 3 и 5 из исходного вектора [1 .. 6]:
Это реализовано
со списком смещений, которые идентифицируют каждый элемент в ValueVector как
включены в SelectionVector. В случае фиксированной ширины ValueVector,
смещения ссылаются на базовый ByteBuf. В случае обнуляемого повторного
или переменная ширина ValueVector, смещение ссылается на соответствующий поиск
стол. Ниже показан SelectionVector из INT4 (фиксированная ширина).
значения 2, 3 и 5 из исходного вектора [1 .. 6]:
Ниже показан тот же ValueVector с полями, допускающими значение NULL:
← Полезное исследование Компиляция из исходного кода →
2.1 Что такое вектор?
Если вы уже слышали о векторах в математике, вы можете думать о векторе как о чем-то, что имеет величину и направление и может быть представлено последовательностью чисел. В своем понятии вектора R сохраняет идею последовательности, но отбрасывает величину и направление. Понятие «числа» даже не нужно.
Для R вектор — это просто последовательность элементов. Существует два основных типа векторов:
Существует два основных типа векторов:
- атомарные векторы, которые бывают одной из шести форм, называемых типами векторов ; 90 111 неатомарных векторов, называемых 90 112, перечисляют 90 113 , элементы которых вообще могут быть R-объектами любого типа.
Сейчас мы просто будем изучать атомарные векторы. Для примера создадим несколько векторов.
Мы можем создать вектор чисел, используя функцию c() :
numVec <- c(23,2, 45, 631, -273, 0, 48,371, 100000,
85, 92, -236, 8546, 98774, 0, 0, 1, 3)
numVec ## [1] 23.200 45.000 631.000 -273.000 0.000 48.371 100000.000 ## [8] 85.000 92.000 -236.000 8546.000 98774.000 0.000 0.000 ## [15] 1.000 3.000
Вы можете думать, что c означает «комбинировать». c() принимает свои аргументы, разделенные запятыми, и объединяет их в вектор.
Если вы внимательно изучите приведенный выше вывод, то заметите, что R распечатал все числовые значения в векторе с точностью до трех знаков после запятой, что оказалось наибольшим числом знаков после запятой, которое мы присвоили любому из чисел, которые сделали вверх numVec . Вы также заметите числа в скобках в начале строк. Каждое число представляет собой позицию в векторе, занимаемую первым элементом вектора, напечатанным в строке. Положение элемента в векторе называется его индекс . Сообщение об индексах ведущих элементов помогает вам найти определенные элементы в выходных данных.
Вы также заметите числа в скобках в начале строк. Каждое число представляет собой позицию в векторе, занимаемую первым элементом вектора, напечатанным в строке. Положение элемента в векторе называется его индекс . Сообщение об индексах ведущих элементов помогает вам найти определенные элементы в выходных данных.
2.1.1 Типы атомарных векторов
Числа в numVec — это то, что программисты называют числами двойной точности . Вы можете убедиться в этом сами с помощью функции typeof() :
typeof(numVec)
## [1] "double"
Функция typeof() возвращает тип любого объекта в R. Как что касается векторов, то существует шесть возможных типов, из которых мы будем иметь дело только с четырьмя:0003
-
двойной -
целое число -
символов -
логический
Давайте посмотрим на примеры других типов. Вот вектор типа
Вот вектор типа integer :
intVec <- c(3L, 17L, -22L, 45L) intVec
## [1] 3 17 -22 45
L после каждого числа означает для R, что число должно храниться в памяти как целое число, а не в формате двойной точности. Официально тип integer :
typeof(intVec)
## [1] "integer"
Вы должны знать, что если вы пропустите один или несколько из L , то R создаст вектор типа двойной :
numVec2 <- c(3, 17, -22, 45) typeof(numVec2)
## [1] "double"
Мы не будем много работать с векторами целочисленного типа, но вы увидите их в дикой природе.
Мы также можем создавать векторы из фрагментов текста, называемых строками : они называются символов векторов. Как отмечалось в предыдущей главе, мы используем кавычки для разделения строк:
strVec <- c("Мозги", "есть", "не", "самый", "лучший",
«вещи», «в», «в», «мир», «93,2»)
strVec ## [1] "Мозги" "не" "не" "самые лучшие" "вещи" "в" "этом" "мире" ## [10] "93.2"
typeof(strVec)
## [1] "character"
Обратите внимание, что "93.2" создает строку, а не число.
Последний тип векторов, который следует рассмотреть, это логических векторов. Вот пример:
logVec <- c(ИСТИНА, ЛОЖЬ, T, T, F, F, ЛОЖЬ) logVec
## [1] ИСТИНА ЛОЖЬ ИСТИНА ИСТИНА ЛОЖЬ ЛОЖЬ ЛОЖЬ
Для представления логического значения вы можете использовать:
-
ИСТИНАилиTдля представления истины; -
FALSEилиFдля представления ложности.
Вы не можете представить правду или ложь другим способом. Если вы попробуете что-нибудь еще, например следующее, вы получите сообщение об ошибке:
badVec <- c(TRUE, false)
## Ошибка: объект 'false' не найден
Примечание : Хотя R позволяет интерпретировать T как TRUE и F61 FAL как FAL , в некоторых случаях их использование может быть опасным. Лучше привыкнуть всегда использовать
Лучше привыкнуть всегда использовать TRUE и FALSE , а не разрешенные сокращения.
2.1.2 Приведение
Что произойдет, если вы попытаетесь представить ложь строкой "ложь" ?
новыйВектор <- c(ИСТИНА, "ложь") newVector
## [1] "TRUE" "false"
newVector не является логическим вектором. Проверьте это:
typeof(newVector)
## [1] "character"
Чтобы понять, что здесь произошло, вы должны вспомнить, что все элементы атомарного вектора должны быть одного типа. . Если функция c() представлена значениями разных типов, то R следует набору внутренних правил до привести некоторые значения к новому типу таким образом, чтобы все результирующие значения были одного типа. Вам не нужно знать все правила приведения, но стоит отметить, что
-
символпревосходитdouble, - , что, в свою очередь, превосходит целое число
- , который, в свою очередь, превосходит
логических.

Следующие примеры показывают это:
typeof(c("one", 1, 1L, TRUE)) ## [1] "character"
typeof(c(1, 1L, TRUE))
## [1] "double"
typeof(c(1L, TRUE))
## [1] "integer"
Автоматическое приведение может быть удобно в одних обстоятельствах, но в других может дать неожиданные результаты. Лучше всего следить за тем, с какими типами вы имеете дело, и проявлять осторожность при объединении значений для создания новых векторов.
Вы также можете приводить векторы «вручную» с помощью функций:
-
as.numeric(); -
as.integer(); -
as.character(); -
as.logical().
Вот несколько примеров:
numVec <- c(3, 2.5, -7.32, 0) as.character(numVec)
## [1] "3" "2.5" "-7.32" "0"
as.integer(numVec)
## [1] 3 2 -7 0
as.logical(numVec)
## [1] ИСТИНА ИСТИНА ИСТИНА ИСТИНА ЛОЖЬ
Обратите внимание, что при преобразовании числового значения в логическое число 0 становится ЛОЖЬ и все ненулевые числа становятся ИСТИНА .
2.1.3 Объединение векторов
Вы можете комбинировать уже созданные векторы для создания новых, более крупных:
numVec1 <- c(5, 3, 10) numVec2 <- c(1, 2, 3, 4, 5, 6) numCombined <- c(numVec1, numVec2) numCombined
## [1] 5 3 10 1 2 3 4 5 6
Здесь вы можете видеть, что векторы отличаются от наборов: они могут повторять одно и то же значение в разных индексах, как мы видим в случае 3 выше.
2.1.4 NA Values
Рассмотрим следующий вектор, который можно рассматривать как запись роста людей в дюймах:
heights <- c(72, 70, 69, 58, NA, 45)
NA в пятой позиции вектора — это особое значение, которое можно рассматривать как означающее «Не назначено». Это способ R позволить нам указать, что значение не было записано или пропало по какой-то причине.
Это способ R позволить нам указать, что значение не было записано или пропало по какой-то причине.
2.1.5 «Все в R является вектором»
Некоторые говорят, что все в R является вектором. Это небольшое преувеличение, но оно удивительно близко к истине.
И все же это кажется неправдоподобным. Как насчет элементов атомарного вектора, например? Отдельный элемент совсем не похож на вектор: это значение, а не последовательность значений.
По крайней мере, нам так кажется. Но на самом деле в R нет «одиночных значений», которые могут существовать сами по себе. Рассмотрим, например, что мы думаем о числе 17:
## [1] 17
Видите [1] впереди, в выводе выше? Это указывает на то, что строка начинается с первый элемент вектора. Таким образом, число 17 не существует само по себе: оно существует как вектор типа double — вектор длины 1.
Даже NA всегда является вектором длины 1
## [1] NA
Он имеет тип логический :
typeof(NA)
## [1] "логический"
Обратите внимание, что даже тип NA оценивает в R вектор: вектор символов длина 1, единственным элементом которой является строка «logical!»
2.
 1.6 Именованные векторы
1.6 Именованные векторыЭлементы вектора могут иметь имена, если угодно:
возрастов <- c(Беттина = 32, Крис = 64, Рамеш = 101) возраст
## Беттина Крис Рамеш ## 32 64 101
Наличие имен не мешает вектору быть вектором типа double : он должен быть double , потому что его элементами являются double .
typeof(age)
## [1] "double"
Мы можем называть элементы вектора, когда создаем его с помощью c() , или мы можем назвать их позже. Один из способов сделать это с помощью функции имен() :
имен(высот) <- c("Пугало", "Железный человек", "Лев", "Дороти", "Тото", "Бок")
высота ## Пугало Железнодорожник Лев Дороти Тото Бок ## 72 70 69 58 NA 45
2.1.7 Векторы специальных символов
R поставляется с двумя удобными предопределенными векторами символов:
букв
## [1] "a" "b" "c" "d" "е" "ж" "г" "ч" "и" "к" "к" "л" "м" "н" "о" "р" "ц" "р" "с" "т" "у " ## [22] "v" "w" "x" "y" "z"
БУКВЫ
## [1] «А» «В» «С» «Г» «Е» «Ф» «Г» «Н» «И» «Дж» «К» «Л» «М» " Н" "О" "П" "К" "Р" "С" "Т" "У" ## [22] "V" "W" "X" "Y" "Z"
Мы будем использовать их время от времени.
2.1.8 Длина векторов
Функция length() сообщает нам, сколько элементов имеет вектор:
length(heights)
## [1] 6
Рассмотрим следующий вектор:
upperLower <- c(БУКВЫ, буквы)
Какой должна быть длина upperLower ? Проверьте свой ответ, используя функцию length() .
Верно или неверно: c("a", 2, TRUE) дает вектор длины три, состоящий из строки "a" , числа 2 и логического значения TRUE .
Функция as.numeric() пытается привести свой ввод к числам. Насколько хорошо он может выбирать «числа» в строках. Попробуйте следующие вызовы. Когда 9(-2)
as.numeric("31,245")
2.1.10 Решения к практическим упражнениям
Всего 26 букв, поэтому длина
upperlowerдолжна быть \(2 \times 26 = 52\). Проверим:длина (верхний нижний)
## [1] 52
Ложь! Результирующий вектор будет атомарным — все его элементы будут одного типа данных.
 Нестроки будут преобразованы в строки, что даст:
Нестроки будут преобразованы в строки, что даст:с ("а", 2, ИСТИНА)## [1] "а" "2" "ИСТИНА"
as.numeric()не очень умен: он выбрал число в"3.214"и3.25e-3, но в остальных случаях вернулNA.
13.2 Вычисления с векторными функциями
Пример 13.2.2. Вектор скорости для $\langle \cos t,\sin t,\cos t\rangle$ равно $\langle -\sin t,\cos t,-\sin t\rangle$. Как и прежде, первые две координаты означают, что из выше эта кривая выглядит как круг. Координата $z$ теперь также периодический, так что при движении объекта по кривой его высота колеблется вверх и вниз. На самом деле оказывается, что кривая наклонный эллипс, как показано на рисунке 13.2.3. $\квадрат$
Рисунок 13.2.3. Эллипс ${\bf r}=\langle \cos t,\sin t,\cos t\rangle$.
Пример 13.2.3. Вектор скорости для $\langle \cos t,\sin
t,\cos 2t\rangle$ равно $\langle -\sin t,\cos
t,-2\sin 2t\rangle$. 2\rangle$, где они встречаются.
92$, что означает $t=1$. Это вместе с
$u=2$ удовлетворяет всем трем уравнениям. Таким образом, две кривые пересекаются в
$(1,0,4)$, первый при $t=1$ и второй при
$t=2$.
2\rangle$, где они встречаются.
92$, что означает $t=1$. Это вместе с
$u=2$ удовлетворяет всем трем уравнениям. Таким образом, две кривые пересекаются в
$(1,0,4)$, первый при $t=1$ и второй при
$t=2$.
Производные равны $\langle 1,-1,2t\rangle$ и $\langle -1,1,2t\rangle$; в точке пересечения это $\langle 1,-1,2\rangle$ и $\langle -1,1,4\rangle$. косинус угол между ними тогда $$\cos\theta = {-1-1+8\over\sqrt6\sqrt{18}}={1\over\sqrt3},$$ поэтому $\theta=\arccos(1/\sqrt3)\приблизительно0,96$. $\квадрат$
Производные векторных функций подчиняются некоторым знакомым правилам: которые нам иногда будут нужны.
Теорема 13.2.5 Предположим, что ${\bf r}(t)$ и ${\bf s}(t)$ — дифференцируемые функции, $f(t)$ — дифференцируемая функция, а $a$ — вещественное число.
а. $\ds {d\over dt} a{\bf r}(t) = a{\bf r}'(t)$
б. $ \ ds {d \ over dt} ({\ bf r} (t) + {\ bf s} (t)) = {\bf г}'(т) + {\bf s}'(т)$
в. $ \ ds {d \ over dt} f (t) {\ bf r} (t) = f (t) {\ bf r} '(t) + f' (t) {\ bf r} (t) $
д. $ \ ds {d \ over dt} ({\ bf r} (t) \ cdot {\ bf s} (t)) =
{\ bf r} '(t) \ cdot {\ bf s} (t) + {\ bf r} (t) \ cdot {\ bf s} '(t) $
$ \ ds {d \ over dt} ({\ bf r} (t) \ cdot {\ bf s} (t)) =
{\ bf r} '(t) \ cdot {\ bf s} (t) + {\ bf r} (t) \ cdot {\ bf s} '(t) $
эл. $ \ ds {d \ over dt} ({\ bf r} (t) \ times {\ bf s} (t)) = {\bf r}'(t)\times{\bf s}(t) +{\bf r}(t)\times{\bf s}'(t)$
ф. $\ds {d\over dt} {\bf r}(f(t))= {\bf r}'(f(t))f'(t)$
$\qed$
Обратите внимание, что, поскольку векторное произведение не является коммутативным, вы должны не забудьте сделать три перекрестных произведения в формуле (e) в правильном заказ.
Когда производная функции $f(t)$ равна нулю, мы знаем, что
функция имеет горизонтальную касательную и может иметь локальный максимум
или минимальный балл. Если ${\bf r}'(t)={\bf 0}$, геометрическая
интерпретация совершенно иная, хотя интерпретация в терминах
движения аналогично. Конечно, мы знаем, что объект имеет нулевую скорость
в такой точке, и, таким образом, он может резко изменить направление. В
три измерения есть много способов изменить направление;
геометрически это часто означает, что кривая имеет вершину или точку, как в
путь мяча, который отскакивает от пола или стены. 92,1\rangle$ имеет точку возврата в точке $\langle 1,0,1\rangle$.
92,1\rangle$ имеет точку возврата в точке $\langle 1,0,1\rangle$.
Иногда нас будет интересовать направление ${\bf r}'$, но не его длина. В некоторых случаях мы все еще можем работать с ${\bf r}'$, например, когда находим угол между двумя кривыми. В других случаях будет полезно работать с единичным вектором в том же направление как ${\bf r}'$; конечно, мы можем вычислить такой вектор с помощью деля ${\bf r}'$ на собственную длину. Этот стандартный тангенс вектор обычно обозначается ${\bf T}$: $${\bf T}={{\bf r}'\over|{\bf r}'|}.$$ В некотором смысле, когда мы вычисляли угол между двумя касательными векторами, мы уже использовали единичный тангенс, так как $$\cos\theta = {{\bf r}'\cdot{\bf s}'\over|{\bf r}'||{\bf s}'|}= {{\bf r}'\over|{\bf r}'|}\cdot{{\bf s}'\over|{\bf s}'|}$$
Теперь, когда мы знаем, как понимать ${\bf r}'$, мы сразу знаем,
какой должна быть первообразная, а именно
$$\int {\bf r}(t)\,dt = \langle \int f(t)\,dt,\int g(t)\,dt,\int h(t)\,dt
\rangle,$$, если ${\bf r}=\langle f(t),g(t),h(t)\rangle$. t {\bf v}(u)\,du.$$
92,t\rangle$ и $\langle \cos(\pi t/2),\sin(\pi t/2), t\rangle$
где они пересекаются.
(отвечать)
t {\bf v}(u)\,du.$$
92,t\rangle$ и $\langle \cos(\pi t/2),\sin(\pi t/2), t\rangle$
где они пересекаются.
(отвечать)
Пример 13.2.7 Найдите косинус угла между кривыми $\langle \cos t,-\sin(t)/4,\sin t\rangle$ и $\langle \cos t,\sin t, \sin(2t)\rangle$ где они пересекаются. (отвечать)
Пример 13.2.8 Предположим, что $|{\bf r}(t)|=k$ для некоторой константы $k$. Этот означает, что $\bf r$ описывает некоторый путь на сфере радиуса $k$ с центром в начале координат. Покажите, что $\bf r$ перпендикулярно ${\bf r}'$ в каждой точке. Подсказка: используйте теорему 13.2.5, часть (d).
Пример 13.2.9 Жучка ползает по спице колеса, которое лежит вдоль
радиус колеса. Ошибка ползает со скоростью 1 единица в секунду и
колесо вращается со скоростью 1 радиан в секунду. Предположим, что колесо лежит
в плоскости $y$-$z$ с центром в начале координат, а в момент времени $t=0$
спица лежит вдоль положительной оси $y$, а ошибка находится в начале координат. Найдите вектор-функцию ${\bf r}(t)$
для положения жука в момент времени $t$ вектор скорости
${\bf r}'(t)$, единичный тангенс ${\bf T}(t)$ и скорость жука
$|{\bf r}'(t)|$.
(отвечать)
92,
\cos t\rangle$, начиная с $\langle 0,0,0\rangle$, когда $t=0$.
Найдите функцию
${\bf r}$ с указанием его местоположения.
(отвечать)
Найдите вектор-функцию ${\bf r}(t)$
для положения жука в момент времени $t$ вектор скорости
${\bf r}'(t)$, единичный тангенс ${\bf T}(t)$ и скорость жука
$|{\bf r}'(t)|$.
(отвечать)
92,
\cos t\rangle$, начиная с $\langle 0,0,0\rangle$, когда $t=0$.
Найдите функцию
${\bf r}$ с указанием его местоположения.
(отвечать)
Пример 13.2.16 Какова физическая интерпретация скалярного произведения двух векторные функции? Какова физическая интерпретация векторное произведение двух векторных функций?
Пример 13.2.17 Покажите, используя правила перекрестных произведений и дифференцирования,
что
$${d\over dt} ({\bf r}(t) \times {\bf r}'(t))=
{\bf r}(t) \times {\bf r}''(t).$$
93
\rangle$ и ${\bf g}(t) =\langle \cos(t), \cos(2t), t+1 \rangle$
пересекаются, и найти угол между кривыми в этой точке. (Намекать:
Вам нужно настроить это как задачу о пересечении линий,
записав одну в $s$ и одну в $t$.) Если бы эти две функции были
траектории двух самолетов в одном масштабе времени, будет ли
самолеты сталкиваются в точке пересечения? Объяснять. (отвечать)
(отвечать)
Пример 13.2.19 Найдите уравнение плоскости, перпендикулярной кривой ${\bf r}(t) = \langle 2\sin(3t),t,2\cos(3t)\rangle$ в точке $(0,\pi,-2)$. (отвечать) 94\rangle$ это плоскость, перпендикулярная кривой, также параллельна плоскости $6x+6y-8z=1$? (отвечать)
Пример 13.2.22 Найдите уравнение касательной к $\langle \cos t, \sin t, \cos(6t)\rangle$, когда $t=\pi/4$. (отвечать)
ВЕКТОР в R ▷ [СОЗДАТЬ и ИНДЕКСировать элементы ВЕКТОРА]
Что такое вектор в языке программирования R? Векторы — это самая основная структура данных в R . Эти структуры позволяют объединять данные одного типа. Следует отметить, что существует несколько способов создания вектора в R, например, объединение двух или более векторов, использование последовательностей или использование генераторов случайных данных.
- 1 Что такое вектор?
- 2 Создать вектор в R
- 3 Вектор имени в R
- 4 Вектор порядка в R
- 4.
 1 Функция сортировки
1 Функция сортировки - 4.2 Функция порядка
- 4.3 Обратный вектор
- 4.
- 5 Combine .
- 7 Сравнение двух векторов
- 8 Последовательность векторов в R
- 9 Генерация случайного вектора в R
- 10 Длина вектора
- 11 Доступ к элементам векторов в R
- 11.1 Числовой индекс для доступа к элементам вектора
- 11.2 Логический индекс для доступа к элементам вектора
- 12 Добавить элемент в вектор R
- 13 Как удалить вектор в R?
- 13.1 Удалить значение из вектора
Что такое вектор?
Вектор — это просто набор объектов одного и того же типа . Вы можете создавать логические, символьные, числовые, комплексные или даже факторные векторы, среди прочего. Стоит отметить, что различные члены вектора называются компонентами. Кроме того, вы можете проверить класс вектора с помощью class функция и тип элементов с функцией typeof .
Создать вектор в R
Векторы в R можно создать с помощью функции c , которая используется для конкатенации объектов . Вы можете сохранить вектор в памяти, присвоив ему имя с помощью оператора <- .
# Создание векторов R с функцией 'c'
х <- с (12, 6, 67)
у <- с(2, 13)
y 2 13 Векторы также могут быть нечисловыми . Следовательно, вы можете создавать векторы с символами, логическими объектами или другими типами объектов данных.
штат <- c("Нью-Йорк", "Огайо", "Вашингтон", "Алабама")
класс(состояние) # "персонаж"
логика <- c(ИСТИНА, ИСТИНА, ЛОЖЬ, ИСТИНА)
класс(логика) # "логический"
Однако, если вы смешаете данные внутри вектора, компоненты будут принудительно изменены.
смесь <- c(ИСТИНА, "Правильно", 8, 2.2)
смесь # "ИСТИНА" "Правильно" "8" "2.2"
класс(микс) # "персонаж"
typeof(mix) # "персонаж" Назовите вектор в R
Вы также можете назвать элементы вектора. Для этого просто выберите имя для каждого компонента или только для некоторых из них.
Для этого просто выберите имя для каждого компонента или только для некоторых из них.
my_vector <- c(оранжевый = 4, яблоко = 6)
my_vector оранжевое яблоко
4 6 Кроме того, если вы уже создали вектор, вы можете использовать функцию setNames следующим образом:
setNames(y, c("апельсин", "яблоко")) Заказать вектор в R
Функция сортировки
Для упорядочивая или сортируя вектор, вы можете вызвать функцию sort , передав вектор в качестве аргумента. По умолчанию функция сортирует в порядке возрастания .
г <- с(12, 15, 3, 22)
sort(z) 3 12 15 22 Вы также можете отсортировать данные в порядке убывания , установив для аргумента уменьшение значение TRUE . Следовательно, мы можем вызвать следующее:
sort(z, уменьшение = TRUE) 22 15 12 3 Функция порядка
В качестве альтернативы можно использовать скобки и упорядочивать компоненты вектора в виде индекса, используя функцию порядка .
# В порядке возрастания
z[order(z)] # Эквивалент sort(z)
# По убыванию
z[order(-z)] # Эквивалент sort(z, по убыванию = TRUE) Обратный вектор
Вы можете изменить порядок вектора в R, вызвав функцию rev .
# Обратный порядок вектора
об(г) 22 3 15 12 Объединить векторы
Объединить два или более векторов так же просто, как создать один. На самом деле вам просто нужно вызвать функцию c и передать векторы в качестве аргументов, чтобы вы могли добавить (дописать) вектор к другому.
х <- с(1, 2, 3)
у <- с(4, 5, 6)
c(x, y) 1 2 3 4 5 6 Следует отметить, что порядок компонентов имеет значение.
c(y, x) 4 5 6 1 2 3 Создать пустой вектор
Иногда вам нужно инициализировать пустой вектор в R и заполнить его в цикле. Какими бы ни были ваши потребности, вы можете использовать c функция без указания аргументов. Вы также можете использовать функцию
Вы также можете использовать функцию вектор .
# Пустой вектор
мой_вектор <- c()
# Заполнение вектора с помощью цикла for
для (я в 1:10) {
мой_вектор[я] <- я
}
my_vector 1 2 3 4 5 6 7 8 9 10 Если вы хотите заполнить пустой вектор, более эффективно предварительно выделить память , создав вектор (например, с значениями NA ) длины вашего окончательного вектора или используя вектор функция.
# Предварительное выделение памяти
my_vector <- rep(NA, 5)
my_vector <- вектор (длина = 5)
# Заполнение вектора с помощью цикла for
для (я в 1:5) {
мой_вектор[я] <- я
} В этом случае разницы не заметишь, тем не менее, для более дорогих задач сокращение времени выполнения может быть огромным.
Сравнить два вектора
В R есть несколько способов сравнения векторов. Во-первых, вы можете сравнивать элементы один за другим с помощью некоторого логического оператора. Обратите внимание, что если один вектор больше другого, количество элементов должно быть кратным, иначе произойдет ошибка.
Обратите внимание, что если один вектор больше другого, количество элементов должно быть кратным, иначе произойдет ошибка.
х <- с(1, 5)
у <- с(4, 0)
х > у # ЛОЖЬ ИСТИНА
х <- с (1, 5)
у <- с(4, 0, 1, 3)
# Это сравнивает 1 > 4, 5 > 0, 1 > 1 и 5 > 3
x > y # ЛОЖЬ ИСТИНА ЛОЖЬ ИСТИНА
х <- с (1, 5, 1)
у <- с(4, 0, 1, 3)
x > y # Ошибка Во-вторых, вы также можете проверить, содержатся ли элементы первого вектора во втором с помощью %in% .
x %in% y # TRUE FALSE В-третьих, еще один вариант — вернуть общие элементы между первым вектором и вторым:
# Вернуть общие элементы
x[x %in% y] # 1 Наконец, вы можете сравнить, все ли элементы первого вектора находятся во втором, с помощью функции all следующим образом:
x <- c(1, 5)
у <- с(4, 5, 1, 3)
all(x %in% y) # TRUE Векторы последовательности в R
В R числовые последовательности можно создавать разными способами. Среди них вы можете использовать оператор
Среди них вы можете использовать оператор : или функции seq и rep .
1:4
№ 1 2 3 4
последовательность (1, 4, 0,5)
# 1,0 1,5 2,0 2,5 3,0 3,5 4,0
seq(от = 1, до = 5, length.out = 9)
# 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
повтор(1, 5)
# 1 1 1 1 1 Генерировать случайный вектор в R
В R есть несколько функций для работы с генерацией случайных чисел. Функция по образцу позволяет создавать случайные последовательности. В следующем коде мы моделируем 5 бросков (размер выборки: 5) игральной кости (6 возможных результатов).
sample(1:6, size = 5, replace = TRUE) Вы также можете использовать функции runif или rnorm , которые генерируют случайные последовательности чисел посредством равномерного и нормального распределения соответственно.
# Нормальные значения
rnorm(5, среднее = 0, sd = 1)
# -1,5611892 -0,2540665 -1,91 0,3040152 -1,4899171
# Универсальные значения
runif(5, мин. = 2, макс. = 10)
# 8.929246 8.610883 7.686587 7.495158 3.771902
= 2, макс. = 10)
# 8.929246 8.610883 7.686587 7.495158 3.771902
Примечание о генерации случайных чисел. При генерации случайных чисел, вы будете получать разные значения каждый раз, когда вы выполняете команду, поэтому ваши предыдущие результаты будут отличаться от наших. Чтобы установить начальное число генератора случайных чисел для воспроизводимого примера, вам сначала нужно вызвать set.seed функция.
set.seed(1) # Вы можете установить любое другое целое число в качестве начального значения
# Нормальные значения
rnorm(5, среднее = 0, sd = 1)
# -0,6264538 0,1836433 -0,8356286 1,5952808 0,3295078
# Универсальные значения
runif(5, мин. = 2, макс. = 10)
# 3.647797 3.412454 7.496183 5.072830 8.158731 Длина вектора
Вы можете получить длину заданного вектора с помощью функции length . Длина вектора — это количество его компонентов.
my_data <- c("вектор", "последовательность", "rnorm", "runif")
п <- длина (мои_данные)
# Длина вектора
п # 4 Доступ к элементам векторов в R
Доступ к элементам индекса позволяет получить доступ к уникальным элементам, таким как первый или последний элементы, подмножество вектора, замену, изменение или удаление некоторых элементов вектора. Этого можно добиться с помощью числовых или логических индексов.
Этого можно добиться с помощью числовых или логических индексов.
Числовой индекс для доступа к элементам вектора
Для доступа к элементам вектора можно указать в скобках соответствующий субиндекс вектора (целое положительное число).
Рассмотрим, например, буквы, заданные функцией букв .
букв <- буквы
буква "а" "б" "в" "г" "д" "ж" "ж" "ч" "и" "к" "к" "л" "м" "н" "о" "р «к»
"r" "s" "t" "u" "v" "w" "x" "y" "z" В следующем блочном коде приведены некоторые примеры доступа к различным данным.
# Первый элемент
письмо [1]
# Первый элемент, упрощающий выходной класс
письмо[[1]]
# Третий и четвертый элемент
письмо [с (3, 4)]
# Последний элемент вектора
буква [длина (письмо)]
# Четные буквы
пусть [последовательность (2, п, 2)]
# Нечетные буквы
пусть [последовательность (1, п, 2)]
lett[-seq(2, n, 2)] # Эквивалент Логический индекс для доступа к элементам вектора
Другой возможностью является использование логического вектора . В этом случае вы получите доступ к позициям со значением
В этом случае вы получите доступ к позициям со значением TRUE . Рассмотрим пример с максимальной месячной температурой испанского города в 2017 году.
33.16, 36.97, 33.29, 28.98, 24.31, 22.43)
месяц <- c("Январь", "Февраль", "Март", "Апрель", "Май", "Июнь",
«июль», «август», «сентябрь», «октябрь», «ноябрь», «декабрь»)
Например, теперь вы можете искать месяцы со значениями больше 30.
# Месяцы со значениями максимальной температуры больше 30
month[temp > 30] "Июнь" "Июль" "Август" "Сентябрь" Обратите внимание, что вывод temp > 30 является логическим вектором.
ЛОЖЬ ЛОЖЬ ЛОЖЬ ЛОЖЬ ЛОЖЬ ЛОЖЬ ИСТИНА ИСТИНА ИСТИНА ИСТИНА ИСТИНА ЛОЖЬ ЛОЖЬ ЛОЖЬ Также можно комбинировать логические условия.
# Месяцы с максимальной температурой ниже 20 ИЛИ выше 35
месяц[темп < 20 | температура > 35] «Февраль» «Март» «Август» Добавить элемент в вектор R
Теперь можно попробовать добавить букву «с» в вектор, который мы создали ранее. Сначала нужно найти предыдущую (или следующую) букву в алфавите. Мы будем искать букву «н» и ставить «н» сразу после. Вы можете использовать функцию
Сначала нужно найти предыдущую (или следующую) букву в алфавите. Мы будем искать букву «н» и ставить «н» сразу после. Вы можете использовать функцию which , чтобы найти индекс элемента в векторе, который соответствует букве «n».
# Ищем индекс
n1 <- который(lett == "n")
п1 # 14 Имея это в виду, с помощью одной строки кода вы можете объединить символы.
c(lett[1:n1], "ñ", lett[-(1:n1)]) Если вы хотите добавить элемент в начало или в конец вектора, просто используйте c в соответствующем порядке.
# Добавление буквы 'ñ' в начало вектора
с ("ñ", букв.)
# Добавление буквы 'ñ' в конце вектора
c(lett, "ñ") Как удалить вектор в R?
Вы можете удалить вектор в R с помощью rm или присвоение ей другого значения, например NULL .
my_vector <- c(1, 2, 5, 6, 7)
# С функцией rm
гм (мой_вектор)
# Переопределение вектора другим значением
мой_вектор <- 0
# Присвоение NULL
my_vector <- NULL Удалить значение из вектора
Если вы хотите удалить только некоторые определенные значения вектора, вы можете использовать знак - , указывающий индексы, которые вам не нужны. Давайте посмотрим на некоторые примеры.
Давайте посмотрим на некоторые примеры.
вектор <- c("Лондон", "Нью-Йорк", "Париж")
# Удаление "Лондон"
vector[-1] # "Нью-Йорк" "Париж"
vector[который(вектор != "Лондон")] # Эквивалент
vector[-what(vector == "London")] # Эквивалент Векторные функции | Безграничное исчисление |
Вектор-функции
Векторная функция покрывает набор многомерных векторов на пересечении областей
fff
,
ggg
и
hhh
.
Цели обучения
Описать применение векторнозначных функций
Ключевые выводы
Ключевые моменты
- Векторнозначная функция может состоять из векторов и/или скаляров.
- Каждая функция-компонент в функции с векторным значением представляет положение значения в другом измерении.
- Область определения функции значения вектора является пересечением областей определения функции компонента.

- Векторные функции могут вести себя так же, как векторы, и вычисляться аналогично.
Ключевые термины
- домен : множество всех возможных математических объектов (точек), в которых определена данная функция
- вектор : направленная величина, имеющая как величину, так и направление; разница со знаком между двумя точками
- скаляр : величина, имеющая величину, но не направление; сравнить вектор
Что такое векторнозначная функция?
Также называемые векторными функциями, векторные функции позволяют вам выражать положение точки в нескольких измерениях в рамках одной функции. Они могут быть выражены в бесконечном количестве измерений, но чаще всего выражаются в двух или трех измерениях. Вход в векторную функцию может быть вектором или скаляром. В этом атоме мы собираемся представить свойства и использование векторных функций.
Свойства векторнозначных функций
Функция с векторным значением позволяет вам представлять положение частицы в одном или нескольких измерениях. Трехмерная векторнозначная функция требует трех функций, по одной для каждого измерения. В декартовой форме со стандартными единичными векторами (i,j,k) векторную функцию можно представить одним из следующих способов:
r(t)=f(t)i+g(t)j+h( t) kr (t) = ⟨f (t), g (t), h (t) ⟩ \ mathbf {r} (t) = f (t) \ mathbf {i} + g (t) \ mathbf {j } + ч(т)\mathbf{к}\\ \mathbf{r}(t) = \langle f(t), g(t), h(t) \rangler(t)=f(t)i+g(t)j+h(t)kr(t )=⟨f(t),g(t),h(t)⟩
, где
ttt
используется в качестве переменной. Это трехмерная векторнозначная функция. На графике показано визуальное представление
r(t)=⟨2cos(t),4sin(t),t⟩\mathbf{r}(t) = \langle 2 \cos(t), 4 \sin (t), t \rangler(t)=⟨2cos(t),4sin(t),t⟩
.
Вектор-функция : это график параметрической кривой (простая вектор-функция с одним параметром размерности
111
). График кривой:
График кривой:
⟨2cos(t),4sin(t),t⟩\langle 2 \cos(t), 4 \sin(t),t \rangle⟨2cos(t),4sin(t),t⟩
где
ttt
идет от
000
к
8π8 \pi8π
.
Это можно разбить на три отдельные функции, называемые компонентными функциями:
x(t)=2cos(t)y(t)=4sin(t)z(t)=tx(t) = 2 \cos(t) )y(t) = 4 \sin(t)z(t) = tx(t)=2cos(t)y(t)=4sin(t)z(t)=t
.
Если бы вы взяли поперечное сечение перпендикулярно любой из трех осей, вы бы увидели график этой функции. Например, если бы вы разрезали трехмерную фигуру перпендикулярно
zzz
-ось, график, который вы увидите, будет представлять собой график функции
z(t)=tz(t)=tz(t)=t
. выполняет все функции компонента. Его можно найти, взяв пересечение областей функций отдельных компонентов. С векторными функциями можно манипулировать так же, как с вектором; их можно складывать, вычитать, а также можно найти скалярное произведение и перекрестное произведение.
Его можно найти, взяв пересечение областей функций отдельных компонентов. С векторными функциями можно манипулировать так же, как с вектором; их можно складывать, вычитать, а также можно найти скалярное произведение и перекрестное произведение.
Пример
В этом примере мы будем использовать время в качестве параметра. Следующая функция с векторным значением представляет время:
ttt
:
r(t)=f(t)i+g(t)j+h(t)k\mathbf{r}(t) = f(t )\mathbf{i} + g(t)\mathbf{j} + h(t)\mathbf{k}r(t)=f(t)i+g(t)j+h(t)k
Эта функция представляет позицию. Следовательно, если взять производную от этой функции, то получим скорость:
dr(t)dt=f(t)i′+g(t)j′+h(t)k′ =v(t) \ displaystyle {\ frac {d \ mathbf {r} (t)} {dt} = f (t) \ mathbf {i} '+ g (t) \ mathbf {j}' + h (t) \ mathbf {k }' \\ \,\qquad = \mathbf{v}(t)\\ }dtdr(t)=f(t)i′+g(t)j′+h(t)k′=v(t )
Если мы продифференцируем второй раз, то получим ускорение:
dv(t)dt=a(t)\displaystyle{\frac{d\mathbf{v}(t)}{dt}= \mathbf {a}(t)}dtdv(t)=a(t)
Длина дуги и скорость
Длина дуги и скорость являются, соответственно, функцией положения и его производной по времени.
Цели обучения
Различать длину дуги и скорость
Ключевые выводы
Ключевые точки
- Длина дуги определяется путем размещения ряда точек вдоль кривой, соединения их отрезками и последующего сложения длин этих отрезков.
- Начало вывода формулы длины дуги начинается с теоремы Пифагора.
- При нахождении длины дуги интеграл должен использоваться относительно положения,
xxx
. - При нахождении скорости по кривой интеграл должен быть по времени,
ttt
.
Ключевые термины
- производная : мера того, как функция изменяется при изменении ее входных данных
- скорость : векторная величина, которая обозначает скорость изменения положения по отношению ко времени или скорость с компонентом направления
Длина дуги и скорость
Поскольку длина — это величина, включающая положение, легко сделать вывод, что производная длины или положения даст вам скорость — также известную как скорость — функции. Это потому, что производная дает вам скорость изменения параметра. Скорость – это скорость изменения положения во времени. Давайте начнем с этого атома, взглянув на длину дуги с исчислением.
Это потому, что производная дает вам скорость изменения параметра. Скорость – это скорость изменения положения во времени. Давайте начнем с этого атома, взглянув на длину дуги с исчислением.
Длина дуги
Длина дуги — это длина, которую вы получите, если возьмете кривую, выровняете ее, а затем измерите длину этой линии. Длину дуги можно найти с помощью геометрии, но ради этого атома мы собираемся использовать интегрирование. Длина дуги аппроксимируется путем соединения конечного числа точек вдоль и кривой, соединения этих линий для создания цепочки очень маленьких прямых линий и сложения их вместе. Чтобы найти это с помощью интегрирования, мы должны начать с использования теоремы Пифагора для длины различных сторон треугольника: 92*dx}∫ab1+dxdy2∗dx
Кривые и теорема Пифагора : Для небольшого участка кривой ∆s можно аппроксимировать с помощью теоремы Пифагора.
Длина дуги : Длина дуги эквивалентна взятию кривой, ее выпрямлению и измерению, как показано на этой анимации.
Очевидно, что в некоторых случаях требуются полярные координаты вместо декартовых. В полярных координатах:
r=f(θ)r=f(\theta)r=f(θ)
Скорость дуги 92}}v(t)=s′=[X′(t)]2+[Y′(t)]2
Вычисление векторнозначных функций
Векторная функция — это функция, которая может вести себя как группа отдельных векторов и выполнять дифференциальные и интегральные операции.
Цели обучения
Обсудите, как манипулируют векторными функциями
Ключевые выводы
Ключевые моменты
- Векторнозначная функция может состоять из векторов и/или скаляров.
- Каждая функция-компонент в функции с векторным значением представляет положение значения в другом измерении.
- Векторные функции могут вести себя так же, как векторы, и вычисляться аналогично.
- Векторные функции широко используются при изучении электромагнитных полей, гравитационных полей и течений жидкости.

Ключевые термины
- вектор : направленная величина, имеющая как величину, так и направление; разница со знаком между двумя точками
- скаляр : величина, имеющая величину, но не направление; сравнить вектор
Векторнозначная функция, также называемая векторной функцией, представляет собой математическую функцию одной или нескольких переменных, диапазон которых представляет собой набор многомерных векторов или бесконечномерных векторов. Входные данные функции с векторным знаком могут быть скаляром или вектором. Размерность домена не определяется размерностью диапазона.
Типичным примером функции с векторным значением является функция, которая зависит от единственного параметра в виде вещественного числа
ttt
, часто представляющий время, в результате чего получается вектор
v(t)\mathbf{v}(t)v(t)
. В терминах стандартных единичных векторов
В терминах стандартных единичных векторов
i\mathbf{i}i
,
j\mathbf{j}j
,
k\mathbf{k}k
декартова трехмерного пространства эти конкретные тип вектор-функций задается такими выражениями, как:
r(t)=f(t)i+g(t)j+h(t)k\mathbf{r}(t) = f(t) \mathbf{i} + g(t)\mathbf{j} + h(t)\mathbf{k}r(t)=f(t)i+g(t)j+h(t)k
где
f(t)f(t)f(t)
,
g(t)g(t)g(t)
, и
h(t)h(t)h( t)
– координатные функции параметра
ttt
. Вектор
v(t)\mathbf{v}(t)v(t)
имеет хвост в начале координат и голову в координатах, вычисленных функцией.
Векторные функции также можно обозначать в другом обозначении:
r(t)=⟨f(t),g(t),h(t)⟩\mathbf{r}(t)=\langle f( t), g(t), h(t)\rangler(t)=⟨f(t),g(t),h(t)⟩
Векторная функция : Этот график является визуальным представлением трехмерной векторной функции
r(t)=⟨2cos(t),4sin(t),t⟩\mathbf{r} (t) = \langle 2 \cos(t), 4 \sin(t), t \rangler(t)=⟨2cos(t),4sin(t),t⟩
. Это можно разбить на три отдельные функции, называемые компонентными функциями:
Это можно разбить на три отдельные функции, называемые компонентными функциями:
x(t)=2cos(t)y(t)=4sin(t)z(t)=tx(t) = 2 \cos(t) )y(t) = 4 \sin(t)z(t) = tx(t)=2cos(t)y(t)=4sin(t)z(t)=t
.
Векторное исчисление — это раздел математики, который охватывает дифференцирование и интегрирование векторных полей в любом количестве измерений. Поскольку векторные функции ведут себя как отдельные векторы, вы можете манипулировать ими так же, как и вектором. Векторное исчисление широко используется в физике и технике, в основном в отношении электромагнитных полей, гравитационных полей и потоков жидкости. При взятии производной вектор-функции эту функцию следует рассматривать как группу отдельных функций.
Векторные функции используются в ряде дифференциальных операций, таких как градиент (измеряет скорость и направление изменения в скалярном поле), завиток (измеряет тенденцию векторной функции вращаться вокруг точки в векторном поле), и дивергенция (измеряет величину источника в данной точке векторного поля).
Длина дуги и кривизна
Кривизна объекта — это степень, в которой он отклоняется от плоской формы, и может быть определена с помощью длины дуги.
Цели обучения
Объясните взаимосвязь между кривизной объекта и длиной дуги
Ключевые выводы
Ключевые точки
Ключевые термины
- острота : тонкость острия заостренного объекта
- кривизна : степень отклонения объекта от плоскости
- нормаль : линия или вектор, перпендикулярный другой линии, поверхности или плоскости
Кривизна дуги
Кривизна дуги — это значение, которое представляет направление и резкость кривой. На любой кривой есть центр кривизны C. Это точка пересечения двух бесконечно близких нормалей к этой кривой. Радиус R — это расстояние от этой точки пересечения до центра кривизны.
Кривизна : Кривизна — это величина, на которую объект отклоняется от плоскости. Для любой кривой С и точки Р на ней существует единственная окружность или прямая, наиболее точно аппроксимирующая кривую вблизи Р\. Затем кривизна C в P определяется как кривизна этой окружности или линии. Радиус кривизны определяется как величина, обратная кривизне.
Чтобы найти значение кривизны, нам нужно взять параметр времени s и единичный касательный вектор, который в данном случае совпадает с единичным вектором скорости T, который также является функцией времени. кривизна представляет собой величину скорости изменения касательного вектора, T:
κ=∥dTds∥\kappa=\Vert\frac{dT}{ds}\Vertκ=∥dsdT∥
Где
κ\ kappaκ
— кривизна, а
dTds\frac{dT}{ds}dsdT
— вектор ускорения (скорость изменения вектора скорости во времени). 92*dx}\\ ∫ab1+dxdy2∗dx
Планетарное движение согласно Кеплеру и Ньютону
Кеплер объяснил, что планеты движутся по эллипсу вокруг Солнца, которое находится в одном из двух фокусов эллипса.
Цели обучения
Назовите три закона движения планет, сформулированные Иоганном Кеплером
Ключевые выводы
Ключевые моменты
- Первый закон движения планет Кеплера описывает движение их орбиты вокруг Солнца.
- Второй закон движения планет Кеплера объясняет, почему планета движется быстрее по мере приближения к Солнцу и медленнее по мере удаления.
- Третий закон движения планет Кеплера объясняет, как период орбиты связан с большой полуосью ее орбиты.
- Ньютон берет информацию, представленную Кеплером, и использует ее, чтобы объяснить, что значение силы, действующей на объект, является произведением его массы и его орбитального ускорения.
- Ньютон также поясняет, что орбита имеет эллиптическую форму, потому что, хотя каждая планета притягивается к Солнцу, они также притягиваются друг к другу.
Ключевые термины
- гравитационная постоянная : эмпирическая физическая постоянная, используемая при расчете гравитационного притяжения между объектами с массой
- эксцентриситет : отношение — постоянное для любого конкретного конического сечения — расстояния точки от фокуса к ее расстоянию от директрисы
- эллипс : замкнутая кривая; геометрическое место точки, для которой сумма расстояний от этой точки до двух других фиксированных точек (называемых фокусами эллипса) постоянна; эквивалентно коническому сечению, представляющему собой пересечение конуса с плоскостью, не пересекающей основание конуса
Иоганн Кеплер описывает движение планет с помощью трех законов: 1. Орбита каждой планеты имеет эллиптическую форму, при этом Солнце находится в одном из двух фокусов этого эллипса, называемых занятым фокусом; 2. Если провести линию от планеты к Солнцу, то эта линия охватит равное количество площадей за равные промежутки времени; 3. Квадрат периода обращения пропорционален кубу большой полуоси орбиты планеты.
Орбита каждой планеты имеет эллиптическую форму, при этом Солнце находится в одном из двух фокусов этого эллипса, называемых занятым фокусом; 2. Если провести линию от планеты к Солнцу, то эта линия охватит равное количество площадей за равные промежутки времени; 3. Квадрат периода обращения пропорционален кубу большой полуоси орбиты планеты.
Первый закон Кеплера
Как мы уже говорили, первый закон движения планет гласит, что орбита каждой планеты представляет собой эллипс с Солнцем в одном из фокусов. Чтобы обсудить этот закон и следующие за ним законы, нам следует более внимательно изучить компоненты эллипса.
Эксцентриситет эллипса говорит о том, насколько вытянут эллипс. Эксцентриситет может быть от 0 до 1. Если эксцентриситет равен нулю, значит это круг. Во времена Кеплера крайними значениями планетарного эксцентриситета были Венера, 0,007, и Меркурий, 0,2. Эксцентриситет - это то, что отличает эллипс от окружности.
r=p1+Σ⋅cosθ\displaystyle{r=\frac{p}{1+{\Sigma} \cdot \cos{\theta}}}r=1+Σ⋅cosθp
, где
ppp
— полуширота прямой кишки,
Σ\SigmaΣ
— эксцентриситет,
rrr
— расстояние между планетой и солнцем,
θ\theta положение планеты и ее самый прямой путь к Солнцу. Минимальное расстояние возникает, когда угол равен 0. Максимальное расстояние возникает, когда угол составляет 180 градусов. Эти значения важны, потому что уравнение для эксцентриситета: 92}}}b=1−Σ2
Минимальное расстояние возникает, когда угол равен 0. Максимальное расстояние возникает, когда угол составляет 180 градусов. Эти значения важны, потому что уравнение для эксцентриситета: 92}}}b=1−Σ2
p
Площадь эллипса находится следующим образом:
A=π⋅a⋅bA=\pi \cdot a \cdot bA=π⋅a⋅b
Ellipse : The important components of an ellipse are as follows: semi-major axis
aaa
, semi-minor axis
bbb
, semi-latus rectum
ppp
, the center of the эллипс, а два его фокуса отмечены большими точками. Для
θ=0\тета = 0θ=0
градусов,
r=rminr = r_{\text{min}}r=rmin
и для
θ=180\theta = 180θ=180
градусов,
r=rmaxr = r_{\text{max}} r=rmax
. 2\theta=n\cdot a\cdot bπ⋅a⋅b=P⋅21⋅r2⋅θr2θ=n⋅a⋅b
2\theta=n\cdot a\cdot bπ⋅a⋅b=P⋅21⋅r2⋅θr2θ=n⋅a⋅b
, где
θ\thetaθ
— угловая скорость относительно времени, а
nnn
— среднее движение планеты вокруг Солнца.
Второй закон : Иллюстрация второго закона Кеплера. Планета движется быстрее рядом с Солнцем, так что за заданное время сметается та же площадь, что и на больших расстояниях, где планета движется медленнее. Зеленая стрелка представляет скорость планеты, а фиолетовые стрелки представляют силу, действующую на планету. 93}}T24π2=R3GM
, где
TTT
— период,
GGG
— гравитационная постоянная, а
RRR
— расстояние между центрами масс двух тел.
Какое отношение Ньютон имеет к Кеплеру?
Ньютон вывел свою теорию ускорения планеты из первого и второго законов Кеплера. Ньютон предположил, что направление планеты всегда направлено к Солнцу. Кроме того, величина ускорения обратно пропорциональна квадрату его расстояния от Солнца. Исходя из этого, Ньютон определил силу, действующую на планету, как произведение ее массы и ускорения. Следовательно, по закону Ньютона каждая планета притягивается к Солнцу, а сила, действующая на планету, прямо пропорциональна массе и обратно пропорциональна квадрату ее расстояния от Солнца.
Ньютон предположил, что направление планеты всегда направлено к Солнцу. Кроме того, величина ускорения обратно пропорциональна квадрату его расстояния от Солнца. Исходя из этого, Ньютон определил силу, действующую на планету, как произведение ее массы и ускорения. Следовательно, по закону Ньютона каждая планета притягивается к Солнцу, а сила, действующая на планету, прямо пропорциональна массе и обратно пропорциональна квадрату ее расстояния от Солнца.
Касательные векторы и векторы нормали
Вектор нормальен к другому вектору, если их пересечение образует угол 90 градусов в точке касания.
Цели обучения
Различать касательные векторы и векторы нормалей
Ключевые выводы
Ключевые точки
- Чтобы один вектор касался другого вектора, угол пересечения должен составлять ровно 90 градусов. На кривой или неровном объекте каждая точка будет иметь уникальный вектор нормали.

- Если вы хотите проверить, нормальны ли два вектора друг к другу, вы можете найти их скалярное произведение и убедиться, что оно равно нулю.
- Если вы хотите точно определить угол между двумя векторами, вы можете использовать следующее уравнение, в котором также используется скалярное произведение:
a∙b=∣a∣∣b∣cosθ\mathbf{a} \bullet\mathbf{b} = \left|\mathbf{a}\right| \влево|\mathbf{b}\вправо| \cos \thetaa∙b=∣a∣∣b∣cosθ
. - Чтобы найти касательный вектор к другому вектору или объекту, просто возьмите производную от опорного вектора.
Ключевые термины
- касательная : прямая линия, касающаяся кривой в одной точке, не пересекая ее там
- перпендикулярно : под прямым углом или образующим его
Чтобы вектор был нормалью к объекту или вектору, он должен быть перпендикулярен вектору направления точки касания. Пересечение, образованное двумя объектами, должно быть прямым углом.
Векторы нормалей
Объект нормальен к другому объекту, если он перпендикулярен к точке отсчета. Это означает, что пересечение двух объектов образует прямой угол. Обычно эти векторы обозначаются как
n\mathbf{n}n
.
Рис. 1: Вектор нормали : Эти векторы перпендикулярны плоскости, поскольку их пересечение с плоскостью образует прямой угол.
Не только векторы могут быть «нормальными» к объектам, но и плоскости тоже могут быть нормальными.
Рис. 2: Нормальная плоскость : Плоскость может быть определена как нормаль к объекту, если вектор направления плоскости образует прямой угол с объектом в точке касания. Эта плоскость нормальна к точке сферы, к которой она касается. Каждая точка на сфере будет иметь уникальную нормальную плоскость.
Точечный продукт
Как мы рассмотрели в другом атоме, одна из манипуляций с векторами называется скалярным произведением. Когда вы берете скалярное произведение двух векторов, ваш ответ будет в виде одного значения, а не вектора. Чтобы два вектора были нормальны друг к другу, скалярное произведение должно быть равно нулю.
Когда вы берете скалярное произведение двух векторов, ваш ответ будет в виде одного значения, а не вектора. Чтобы два вектора были нормальны друг к другу, скалярное произведение должно быть равно нулю.
a∙b=0 =a1b1+a2b2+a3b3 =∣a∣∣b∣cosθ\mathbf{a} \bullet \mathbf{b} = 0\\ \,\,\,\quad = a_1b_1+a_2b_2+a_3b_3\\ \,\,\,\quad = \left|\mathbf{a}\right| \влево|\mathbf{b}\вправо| \cos \thetaa∙b=0=a1b1+a2b2+a3b3=∣a∣∣b∣cosθ
Касательные векторы
Касательные векторы почти точно такие же, как нормальные векторы, за исключением того, что они касаются, а не нормальны к другому вектору или объекту. Эти векторы можно найти, получив производную опорного вектора,
r(t)\mathbf{r}(t)r(t)
:
r(t)=f(t)i+g( t)j+h(t)k\mathbf{r}(t) = f(t)\mathbf{i}+g(t)\mathbf{j}+h(t)\mathbf{k}r(t )=f(t)i+g(t)j+h(t)k
Лицензии и атрибуты
Контент под лицензией CC, ранее опубликованный
- Курирование и доработка.
 Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензионный контент CC, Особая атрибуция
- Векторнозначная функция. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- скалярная. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- домен. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- вектор. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Функция векторного значения. Предоставлено : WikiPedia. Лицензия : Общественное достояние: Нет данных Авторские права
- Длина дуги. Предоставлено : Википедия.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - производная. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- скорость. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Функция векторного значения. Предоставлено : WikiPedia. Лицензия : Общественное достояние: Нет данных Авторские права
- Длина дуги. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторские права
- Длина дуги – прибл. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Векторное исчисление. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Векторнозначная функция.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - скалярная. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- вектор. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Функция векторного значения. Предоставлено : WikiPedia. Лицензия : Общественное достояние: Нет данных Авторские права
- Длина дуги. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторские права
- Длина дуги – прибл. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Википедия. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Кривизна.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - нормальный. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- резкость. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- кривизна. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Функция векторного значения. Предоставлено : WikiPedia. Лицензия : Общественное достояние: Нет данных Авторские права
- Длина дуги. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторские права
- Длина дуги – прибл. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Википедия.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - Соприкасающийся круг. Предоставлено : Википедия. Лицензия : Общественное достояние: Нет данных Copyright
- Законы Кеплера о движении планет. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Безграничная. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- эллипс. Предоставлено : Викисловарь. Расположен по адресу : https://en.wiktionary.org/wiki/ellipse. Лицензия : CC BY-SA: Attribution-ShareAlike
- гравитационная постоянная. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Функция векторного значения.
 Предоставлено : WikiPedia. Лицензия : Общественное достояние: Нет данных Авторские права
Предоставлено : WikiPedia. Лицензия : Общественное достояние: Нет данных Авторские права - Длина дуги. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторское право
- Длина дуги – прибл. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Википедия. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Соприкасающийся круг. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторское право
- Второй закон Кеплера. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Эллипс широкой прямой кишки. Предоставлено : Википедия. Лицензия : CC BY: Attribution
- Вектор нормали.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - касательная. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- перпендикулярно. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Функция векторного значения. Предоставлено : WikiPedia. Лицензия : Общественное достояние: Нет данных Авторское право
- Длина дуги. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторское право
- Длина дуги – прибл. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Википедия. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Соприкасающийся круг.
 Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторское право
Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторское право - Второй закон Кеплера. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Эллипс широкой прямой кишки. Предоставлено : Википедия. Лицензия : CC BY: Attribution
- Векторы нормалей2. Предоставлено : Википедия. Лицензия : Общественное достояние: Авторские права неизвестны
- Нормальная поверхность. Предоставлено : Википедия. Лицензия : Общественное достояние: Неизвестно Copyright
Добавить или добавить элемент к вектору в R?
- Автор сообщения: NNK
- Категория сообщения: R Программирование
- Последнее изменение сообщения: 31 июля 2022 г.

Как добавить или добавить элемент в вектор в R? Используйте функцию append() , чтобы добавить один или несколько элементов в вектор. Вектор в R — это последовательность элементов данных одного типа. поэтому, когда вы добавляете элемент в вектор, убедитесь, что вы добавляете элемент того же типа.
1. Краткие примеры добавления элемента в вектор
Ниже приведены краткие примеры того, как добавить или добавить один или несколько элементов в вектор в R.
# Быстрые примеры
# Использование базы R append()
vec = c('java','python')
vec2 <- добавить(vec,'r')
печать (vec2)
# Добавляем элемент в вектор в указанной позиции
vec = c('java','python')
vec2 <- добавить (vec, 'r', после = 1)
печать (vec2)
# Добавить несколько элементов в вектор
vec2 <- c(vec,'r','php')
печать (vec2)
# Добавляем к вектору другой вектор
vec = c('java','python')
vec2 = с('r','php')
vec3 <- добавить(vec,vec2)
печать (vec3)
# Добавляем значение к пустому вектору
empVec <- символ()
vec2 = c(empVec,'R')
печать (vec2)
2.
 Синтаксис функции append() для добавления элемента в вектор
Синтаксис функции append() для добавления элемента в вектор Ниже приведены синтаксис и использование функции append() . Функция append() возвращает вектор, содержащий значения в формате 90 125 x 90 126, с элементами из 90 125 значений 90 126, добавленными после указанного элемента в формате 90 125 x . По умолчанию он добавляется в конец вектора x .
# Синтаксис добавления() добавить (х, значения, после = длина (х))
Параметры :
-
x— входной вектор -
значений— строка, список или вектор. -
после– позиция для добавления. По желанию. Если не указано, элемент добавляется в конец вектора.
Возврат :
- Возвращает вектор после добавления элемента.
3. Добавить элемент в вектор с помощью append()
С помощью функции R base append() добавим элемент в существующий вектор в R. По умолчанию он добавляет элемент в конец вектора. В следующем примере добавляется элемент
По умолчанию он добавляет элемент в конец вектора. В следующем примере добавляется элемент r на вектор. Здесь я использовал c() для создания вектора.
# Использование базы R append()
vec = c('java','python')
vec2 <- добавить(vec,'r')
печать (vec2)
# Выход
# [1] "java" "python" "r"
4. Добавить элемент в вектор в указанной позиции
Используйте параметр после , чтобы указать позицию, в которую вы хотите добавить элемент в векторе. В следующем примере элементы добавляются после первой позиции.
# Добавляем элемент в вектор в указанной позиции
vec = c('java','python')
vec2 <- добавить (vec, 'r', после = 1)
печать (vec2)
# Выход
# [1] "java" "r" "python"
5. Добавить несколько элементов в вектор
append() не поддерживает добавление нескольких элементов за раз, поэтому используйте базовую функцию c() R для добавления нескольких элементов в вектор.
# Добавить несколько элементов в вектор vec2 <- c(vec,'r','php') печать (vec2) # Выход # [1] "java" "python" "r" "php"
6.
 Добавление вектора к другому вектору
Добавление вектора к другому векторуЕсли у вас есть два вектора, вы можете добавить один вектор к другому с помощью функции append() в R. В следующем примере второй вектор добавляется в конец первого вектора и возвращается один вектор со всеми элементами.
# Добавляем к вектору другой вектор
vec = c('java','python')
vec2 = с('r','php')
vec3 <- добавить(vec,vec2)
печать (vec3)
# Выход
# [1] "java" "python" "r" "php"
7. Добавление значения к пустому вектору
Функция c() также может использоваться для добавления значения к пустому вектору. Здесь функция символов () используется для создания пустого вектора символов.
# Добавляем значение к пустому вектору empVec <- символ() vec2 = c(empVec,'R') печать (vec2) # Выход [1] «Р»
8. Заключение
В этой статье вы узнали, как добавлять или присоединять элемент к вектору с помощью функций R base append(), c(). Также научились добавлять элемент в указанную позицию, добавлять несколько элементов в вектор и добавлять значение к пустому вектору с примерами.

 Измеряется в м3.
Измеряется в м3. Оно направлено к ядру Земли и равняется 9,8 м/с2
Оно направлено к ядру Земли и равняется 9,8 м/с2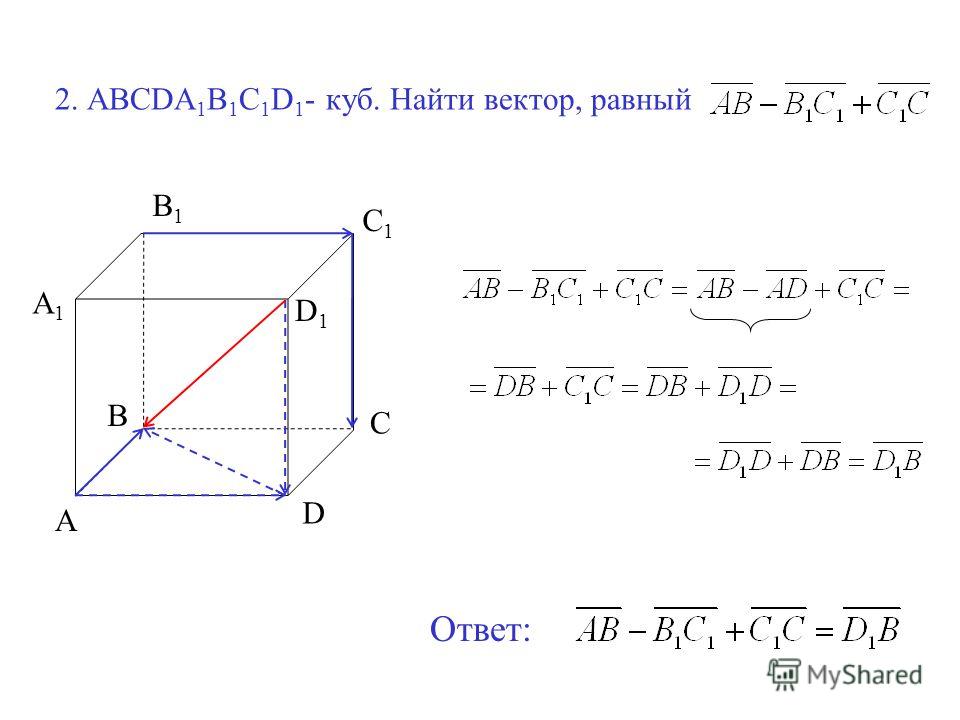 Для изображения направленного отрезка необходимо построить точки, координаты которых соответствуют началу и концу вектора, и соединить их.
Для изображения направленного отрезка необходимо построить точки, координаты которых соответствуют началу и концу вектора, и соединить их. Модуль вектора равен
Модуль вектора равен

 Тогда начало вектора
Тогда начало вектора
 ru
ru 7 Задача. Даны точки А(1;1), B(3;1), C(2;-2), D(4;-2).
7 Задача. Даны точки А(1;1), B(3;1), C(2;-2), D(4;-2).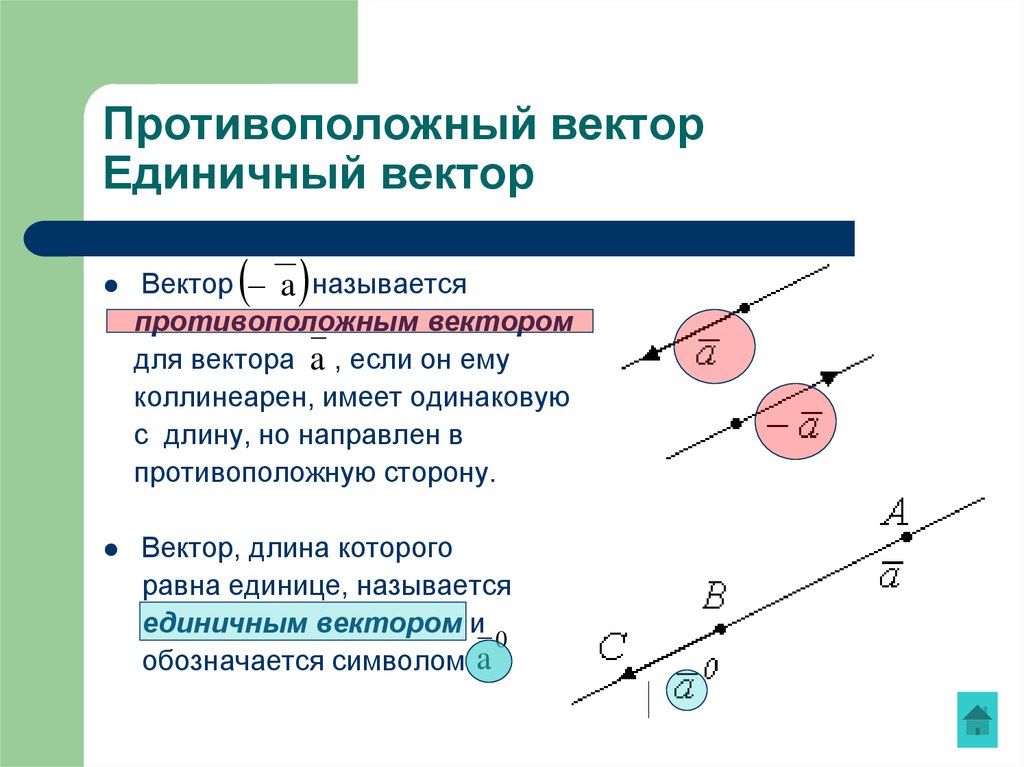 cloud
cloud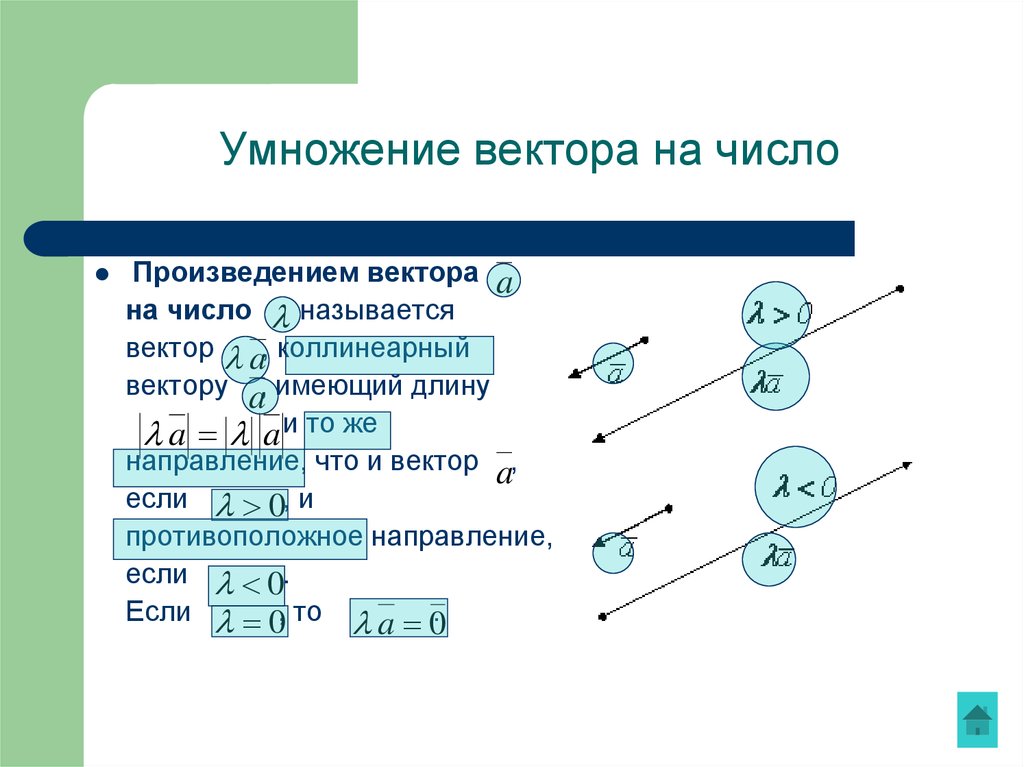
 3, 1.7, 1.2, 0.9, 1.6, 1.4) # численный вектор, сохранен в переменной vect_num_1
3, 1.7, 1.2, 0.9, 1.6, 1.4) # численный вектор, сохранен в переменной vect_num_1 Когда объект был, но его свойство не
измерили или не записали.
Когда объект был, но его свойство не
измерили или не записали. осторожно! избегайте его использовать, никаких документов о нем не останется
осторожно! избегайте его использовать, никаких документов о нем не останется