Урок математики по теме «Деление дробей в уравнениях»
Форма урока: объяснение нового материала.
Цели урока:
- Обучающая: выработать навыки учащихся умножать и делить обыкновенные дроби, решать и оформлять задачи на уравнения.
- Воспитательная: воспитывать самостоятельность, аккуратность
- Развивающая: развивать внимание, математическую речь, вычислительные навыки учащихся, интерес к математике.
Ожидаемые результаты: дети научаться решать задачи и уравнения на дроби.
Этапы урока |
Время (мин) | Слайды |
Организационный момент. |
2 | Слайд 1 |
| Устная работа и повторение ранее изученного | 8 | Слайды 2, 3, 4, 5,6 |
| Формирование новых знаний и умений | 10 | Слайды 7, 8 |
| Физкультминутка | 2 | Слайды 9, 10 |
| Закрепление нового материала | 5 | Слайд 11 |
| Проверка знаний (с/р) | 10 | Слайд 12 |
| Постановка домашнего задания | 1 | Слайд 13 |
| Подведение итогов урока | 2 |
ХОД УРОКА
I. Организационный этап
– Здравствуйте, мы проведем сегодня урок по
теме «Деление дробей в уравнених». Откройте
тетради, запишите число, классная работа и тему
урока.
Откройте
тетради, запишите число, классная работа и тему
урока.
Целью нашего урока является закрепление и
проверка умений умножать и делить обыкновенные
дроби, а также повторить навыки решения задач и
уравнений.
II. Устный опрос учащихся
Чтобы умным в жизни стать
Надо дроби изучать
1) Переведите смешанную дробь в неправильную (Приложение 1, слайд 3)
2) Выделите целую часть (Приложение 1, слайд 4)
3) Умножьте дроби (Приложение 1, слайд 5)
– Повторим правило умножения двух дробей: Чтобы умножить дробь на дробь нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе знаменателем.
4) Выполните деление (в тетрадях с последующей взаимопроверкой, сосед у соседа) (Приложение 1, слайд 6)
– Повторим правило деления двух дробей: Чтобы
разделить одну дробь на другую, нужно первую
дробь умножить на дробь, обратную второй.
III. Формирование новых знаний и умений
– При изучении темы деление большое значение имеет умение решать уравнения. Рассмотрим пример и запишем его в тетрадь. (Приложение 1, слайд 7)
– Чтобы решить уравнение необходимо
определить какой компонент в уравнении является
неизвестным.
– Какой?
– 1 множитель
– Правильно! Чтобы найти неизвестный множитель,
что нужно сделать?
– Находим корень уравнения, выполняя деление. Выполним проверку и запишем ответ.
– А теперь давайте проверим ваше умение решать задачи.
№ 597 (Приложение 1, слайд 7)
– Сколько всего прошел лыжник ? (26 км)
– Сколько километров прошел в первый день?
(неизвестно)
– Сколько километров прошел во второй день?
(неизвестно)
– Какую величину, с какой сравнивают?
– Что возьмем за х?
– Как найти дробь от числа?
– Сколько километров прошел за два дня?
– Как найти?
– Составим уравнение.
– 14 км лыжник прошел во второй день
26 – 14 = 12 км лыжник прошел в первый день.
№ 598 (Приложение 1, слайд 8)
– Вспомним что такое 1% (одна сотая)
– Какой дробью запишем 75% (75/100 = 3/4)
– Сколько грибов собрала белка? (неизвестно)
– Сколько грибов собрал бельчонок? (неизвестно)
– Какую величину, с какой сравнивают?
– Что обозначим за икс?
– Как найти дробь от числа?
– Сколько собрали вместе белка и бельчонок?
– Составим уравнение.
200 грибов собрала белка
350 – 200 = 150 грибов собрал бельчонок
IV. Физкультминутка
– Встаем и выполняем несколько упражнений.
А теперь, ребята, встали,
Быстро руки вверх подняли,
В стороны, вперёд, назад
Повернулись вправо, влево,
Тихо сели, вновь за дело.
V. Закрепление нового материала
№ 594
– Сколько собрал Митя?
– Сколько собрал Коля?
– Какую величину, с какой сравнивают?
– Что обозначим за икс?
– Как найти дробь от числа?
– Сколько собрали вместе мальчики?
28 грибов собрал Митя
64 – 28 = 36 грибов собрал Коля
VI. «Математический выбор»
Уравнения, оцениваемые в 3 балла: Уравнения, оцениваемые в 5 баллов:
1) 1)
2) 2)
3) 3)
4) 4)
Уравнения, оцениваемые в 6 баллов:
1)
2)
3)
4)
Оценки: 5 – 12 баллов; 4 – 9 баллов; 3 – 6 баллов.
Каждый выбирает себе уравнения по «плечу».
Учитель во время работы оценивает учеников.
VII. Итог урока
– С каким настроением вы сегодня работали на
уроке?
– Какая задача для вас была самой интересной?
– Ребята чему мы научились на сегодняшнем уроке?
– Как найти часть от числа?
– Как найти неизвестный множитель?
Оценки за урок.
VIII. Домашнее задание
– С листов решить любые три уравнения, из тех которые не решали в классе.
Презентация «Умножение и деление действия второй степени» (17 слайдов)
Слайд 1
Умножение и деление действия второй степени.
Цель урока: знать определение умножения, деления, название компонентов действий умножения и деления. Уметь производить действие умножения и деления многозначных чисел столбиком.
Слайд 2
1. Устный счет:
1) Составить тройку примеров из чисел:
16;8; ;8;24 16; ;24
+ =24 24- = — =8
2) Cоставить и решить четыре примера на сложение и вычитание:
a) 16;30;46 б) 543;120;
+ = ; + =
— = ; — =
— —
Слайд 3
3) Восстановить пропущенные числа
а) 503+503+503=503х
б) 140+140+140+140= х
в) 58+ + + + = 58 х 5
г) 12х = + +
Слайд 4
Решить уравнения:
a) +120=500 б) х 6=72
500- =120 : 6 = 12
-380=120 72 : = 6
Слайд 5
2. Сравним следующие взаимосвязанные действия:
Сравним следующие взаимосвязанные действия:
Умножение
5 х 2=10
1)Числа, которые
перемножают называются множители
2) Результат умножения называют произведением
5 и 2 – множители
5- первый множитель
2 – второй множитель
10- произведение
Деление
10:5=2
Действие, с помощью которого по известному произведению 10 и известному множителю 5 находят неизвестный множитель– называется делением.
Деление – это действие обратное умножению.
Число, которое делят, называется делимым. Число, на которое делят, называется делителем.
Результат деления называется частным.
10- делимое.
5- делитель.
2- частное.
Слайд 6
10:5= =2
При переходе от умножения к делению происходит следующие изменения компонентов и результата:
5 х 2 = 10 10 : 2 = 5
Множитель Множитель Произведение Делимое Делитель Частное
Умножение и деление – это действия второй ступени.
10
5
Вместо двоеточия (:) в качестве знака деления часто пишут дробную черту:
Слайд 7
Вспомним как решаются уравнения, содержащие действия второй ступени.
Нахождение множителя
Требуется решить уравнение 5 х Х = 350
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. X = 350 : 5
X = 70
Проверка: подставим значение (корня) неизвестного в исходные уравнение: левая часть равенства равна правой части
5 х 70? 350
350 = 350
Слайд 8
Нахождение делителя
Решить следующие уравнение:
350:y=70
. Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Y=350:70
Y=5
Проверка: подставим найденный корень 350 в исходное уравнение: левая часть равна правой части.
350:5 ? 70
70 = 70
Слайд 9
Нахождение делимого
Решить следующие уравнение:
a : 5 = 70
Чтобы найти неизвестный делитель (y) надо делимое (350) разделить на частное.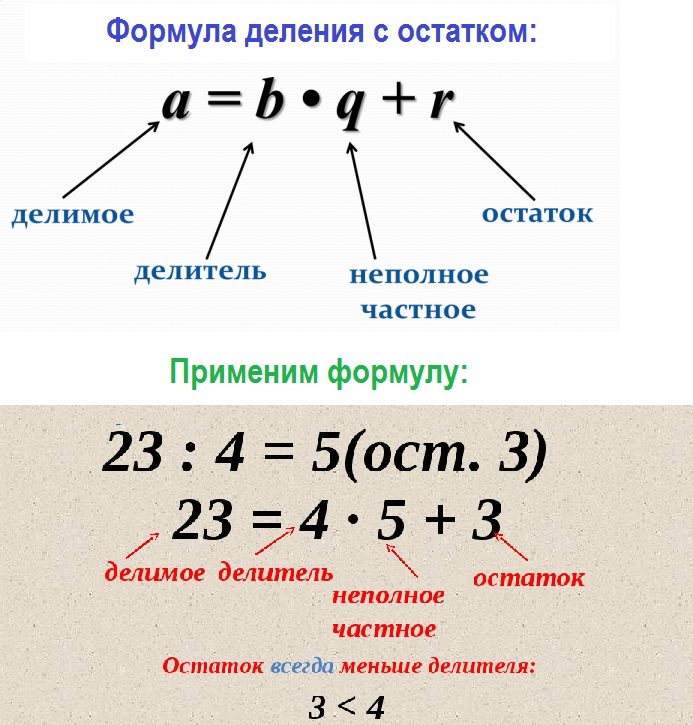 a = 70 х 5
a = 350
a = 70 х 5
a = 350
Проверка: подставим найденный корень в исходное уравнение. Левая часть равенства равна правой
350:5?70
70=70
Слайд 10
3. Решение упражнений.
1) Составить и решить четверки примеров на умножение и деление со следующими числами:
Образец : 20;41;820
41 х 20=820 820:20=41
20 х 41=820 820:41=20
а) 300; 4; б) 60см;4; 2м40см. в) 540кг;3;
Слайд 11
2) Выполнить умножение и проверить ответ делением.
a) 308 х 27 б) 234 х 56 в) 2806 х 17
а) 300х4=1200
4х300=1200
1200:300=4
1200:4=300
б) 60х4=240
4х60=240
240:60=4
240:4=60
в)540х3=1620
3х540=1620
1620:3=540
1620:540=3
Слайд 12
Слайд 13
3) Выполнить умножение и проверить ответ двумя способами (оба делением).
а) 94х58 б) 63х87 в) 591х7
К4) ак найти неизвестное слагаемое ? Неизвестный множитель? Сравнить решения следующих уравнений:
X+20=600 и Yх20=600
Придумать соответствующие задачи и решить их.
Слайд 14
б) Как найти неизвестное уменьшаемое?
Неизвестное делимое?
a-20=80 и b:20=80
в) Как найти неизвестное вычитаемое?
Неизвестный делитель?
Решить уравнения:
80-p=4 и 80:k=4
способами(5)Выполнить деление и проверить ответ двумя умножением и делением).
38088:6 380088:6
Слайд 15
Слайд 16
5) Решить задачи:
a) Длина кита достигает 30 м, а длина змеи анаконды 10 м. Во сколько раз кит длиннее анаконды?.
30м, 10,
б) со 30м, в ставить обратную задачу по схеме:
3 раза,
в) составсхеить вторую обратную задачу по ме :
; в 3 раза ; 10м.
Слайд 17
6. Записать вместо звездочки пропущенную цифру
Простое математическое уравнение взорвало сеть, ученые назвали правильный ответ. А вы сможете? (ФОТО)
09:22
02 Августа 2019
ЕРЕВАН, 2 августа. Новости-Армения. Известные российские математики назвали правильный ответ в примере из школьной математики с делением и умножением, породившем споры в социальных сетях.
Новости-Армения. Известные российские математики назвали правильный ответ в примере из школьной математики с делением и умножением, породившем споры в социальных сетях.
28 июля один из пользователей опубликовал в Twitter пример из школьной программы по математике: «8:2(2+2)=?». Обсуждение примера вызвало широкий резонанс, и перешло на международный уровень, пользователи разных стран получали ответ «16» или «1».
Российский математик, доктор физико-математических наук, первый декан факультета математики Высшей школы экономики Сергей Ландо рассказал ТАСС, что правильный ответ в России будет 16. «На территории Российской Федерации деление и умножение имеют равные приоритеты. В США или Англии может быть другой порядок. В России сначала выполняется операция в скобках, потом деление на эту сумму, а потом результат умножается на следующий множитель. Правильный ответ — 16», — сказал он. Ландо добавил, что в подобных спорных случаях специалисты стараются обозначить порядок операций скобками.
Заведующий кафедры высшей математики Национального исследовательского университета «Московский институт электронной техники» (НИУ МИЭТ) Александр Прокофьев подтвердил ТАСС, что правильный ответ — 16, и объяснил, почему пример вызвал столько споров.
«Ошибаются, как я полагаю, преимущественно взрослые. У школьников вопросов быть не должно. Первой выполняется операция в скобках, затем, согласно приоритету арифметических действий, деление и умножение — они являются равноправными и выполняются слева направо. Студенты привыкают отделять косой чертой числитель от знаменателя, поэтому путаются в данном примере, полагая, что умножение двойки на скобку расположено в знаменателе», — сказал Прокофьев.
С ними согласилась и заведующая кафедры «Математика» Российского университета транспорта Людмила Кочнева. «Если бы стояла скобка после знака деление, то правильным ответом была бы единица. Если бы после восьмерки была горизонтальная черта — знак дробного деления — а внизу 2(2+2), это была бы единица. А раз все это в строчку, вы должны делать операции в том порядке, в котором они написаны. Восемь делим на два, четыре умножаем на 2+2, получается 16. Это просто манера записи, ничего интересного — чисто арифметическая задача, но все-таки более опрятно надо писать сам пример», — пояснила она. —0—
А раз все это в строчку, вы должны делать операции в том порядке, в котором они написаны. Восемь делим на два, четыре умножаем на 2+2, получается 16. Это просто манера записи, ничего интересного — чисто арифметическая задача, но все-таки более опрятно надо писать сам пример», — пояснила она. —0—
Читайте новости первыми и обсуждайте их — в нашем Telegram-канале
#Математика #задача #Twitter
Новости СМИ2
Partners News
Материалы по теме
23:49
28 Сентября 2022
Пашинян призвал разместить международных наблюдателей в районах Армении, пострадавших от азербайджанской оккупации
22:35
28 Сентября 2022
Новый пакет санкций против РФ обсуждается в Еврокомиссии
22:11
28 Сентября 2022
Армянская сторона имеет 3 жертвы в результате провокации Азербайджана – Минобороны РА
21:54
28 Сентября 2022
Третий президент Армении призывает общество к неусыпной борьбе
21:29
28 Сентября 2022
Секретарь Совбеза Армении обсудил с конгрессменом США агрессию Азербайджана
Лента Новостей
23:49
28 Сентября 2022
Пашинян призвал разместить международных наблюдателей в районах Армении, пострадавших от азербайджанской оккупации
22:35
28 Сентября 2022
Новый пакет санкций против РФ обсуждается в Еврокомиссии
22:11
28 Сентября 2022
Армянская сторона имеет 3 жертвы в результате провокации Азербайджана – Минобороны РА
21:54
28 Сентября 2022
Третий президент Армении призывает общество к неусыпной борьбе
21:29
28 Сентября 2022
Секретарь Совбеза Армении обсудил с конгрессменом США агрессию Азербайджана
Вся лента
Популярное
22:53
26 Сентября 2022
Вопрос Арцаха решен – Левон Тер-Петросян
13540
15:47
26 Сентября 2022
В небе над Арменией замечены спутники Starlink компании SpaceX (ФОТО, ВИДЕО)
8755
18:45
27 Сентября 2022
Сильное землетрясение в Турции ощутили жители Еревана и Ширака
8670
11:01
26 Сентября 2022
Азербайджанцы убили армянского военнослужащего и отправили фото его жене — экс-омбудсмен
7130
23:36
26 Сентября 2022
США рассматривают возможность продажи оружия Армении — ANCA
4255
Агентство АРКА
Другие материалы раздела
17:24
28 Сентября 2022
В Армении задумались о расширении преподавания западноармянского языка
«Фонд Гюльбенкян» предложил Минобразования Армении сотрудничество в создании платформ для популяризации западноармянского языка
16:54
28 Сентября 2022
Ереван примет 14-ю международную конференцию по экстремофилам в 2024 году
Очередная, 14-я международная конференция по экстремофилам* пройдет в Ереване в 2024 году
15:47
26 Сентября 2022
В небе над Арменией замечены спутники Starlink компании SpaceX (ФОТО, ВИДЕО)
В небе над Арменией минувшей ночью засекли серию спутников Starlink компании SpaceX Илона Маска
09:55
26 Сентября 2022
Юпитер окажется на самом близком за 59 лет расстоянии от Земли
Планета Юпитер будет находиться в созвездии Рыб вблизи небесного экватора
09:28
26 Сентября 2022
Вирусолог назвал срок окончания пандемии COVID-19
Окончание пандемии коронавируса могут объявить до конца года, считает главный научный сотрудник Института им. Гамалеи
Гамалеи
10:25
23 Сентября 2022
Бизнес-ангел Рэм Дарбинян назвал 3 секрета успеха и три причины провалов стартапов
Бизнес-ангел, инвестор более 60 стартапов Рем Дарбинян в эксклюзивном интервью порталу «АРКА-Телеком» раскрыл три топ-секрета успеха и три главных причины провалов стартапов
21:04
09 Сентября 2022
В Армении — сезон инжира: чем он вреден и полезен
Этот сладкий фотогеничный фрукт давно обзавелся целой армией поклонников
13:13
08 Сентября 2022
Телескоп Джеймса Уэбба обнаружил тысячи новых звезд в туманности Тарантул
Космический телескоп НАСА Джеймс Уэбб обнаружил тысячи новых звезд в туманности Тарантул
18:05
05 Сентября 2022
STARMUS как предчувствие. Превращение Армении в платформу гармонизации науки и искусства
STARMUS как предчувствие. Превращение Армении в платформу гармонизации науки и искусства
11:32
05 Сентября 2022
Лайфхаки: как использовать коричневый шум от стресса
Как бы мы ни пытались оградить себя от стресса в повседневной жизни, сделать это удается далеко не всегда
10:38
05 Сентября 2022
Нарушения сна являются самым явным предиктором смерти — ученые
Ученые из Медицинской школы Стэнфордского университета озвучили влияние сна на продолжительность жизни
21:20
03 Сентября 2022
Ученый спрогнозировал появление в Китае нового штамма коронавируса
Новый штамм коронавируса может зародиться в Китае, считает заведующий лабораторией геномной инженерии МФТИ Павел Волчков
Консультация для преподавателей 6 класса (февраль)
Тема консультации : «РАЦИОНАЛЬНЫЕ ЧИСЛА. УРАВНЕНИЯ»Дидактическая основа
УРАВНЕНИЯ»Дидактическая основаДидактической основой непрерывного курса математики «Учусь учиться» является дидактическая система деятельностного метода обучения «Школа 2000…». Ее главной особенностью является то, что знания не даются учащимся в готовом виде, а организуется их самостоятельное открытие детьми. Такой подход обеспечивает высокий уровень математической подготовки, развивает мышление учащихся, их способности, повышает интерес к изучению математики, обеспечивает личностные и метапредметные результаты образования, соответствующие ФГОС.
Содержание консультацииВ соответствии с планированием учебного материала по курсу математики «Учусь учиться» для 6 класса в феврале продолжается работа с третьей главой «Рациональные числа». Из второго параграфа изучаются П.3.2.3 «Умножение рациональных чисел», П.3.2.4 «Деление рациональных чисел», П.3.2.5 «Какие числа мы знаем и что мы о них не знаем», П.3.2. «О системах счисления*», содержание которых продолжает развитие числовой содержательно-методической линии курса. В феврале изучается и третий параграф «Уравнения», содержание которого относится к алгебраической линии курса. Последний пункт этого параграфа – «Решение задач с помощью уравнений» – развивает линию моделирования.
В феврале изучается и третий параграф «Уравнения», содержание которого относится к алгебраической линии курса. Последний пункт этого параграфа – «Решение задач с помощью уравнений» – развивает линию моделирования.
Вместе с тем, в процессе изучения этих тем параллельно развиваются и все остальные линии курса. Такой подход является общим для данного курса: на каждом этапе его изучения, параллельно с ведущей линией, по которой идет расширение понятийной базы, закрепляются и отрабатываются знания и умения по всем остальным разделам курса.
- сформировать умение умножать и делить рациональные числа, использовать свойства умножения и деления для рационализации вычислений;
- систематизировать знания о числовых множествах, сформировать представление о расширения числовых множеств, поставить проблему недостаточности изученных чисел для измерения длин отрезков;
- сформировать представления о записи чисел в различных системах счисления, переводе из одной системы счисления в другую;
- сформировать умение выполнять простейшие преобразования выражений;
- уточнить понятия уравнения и систематизировать методы решения уравнений; сформировать умение решать линейные уравнения путем переноса слагаемых;
- уточнить алгоритм решения задач методом уравнений.

В соответствии с принципом минимакса дидактической системы деятельностного метода «Школа 2000…» организовать работу по учебнику 5 класса возможно в условиях различных учебных планов образовательных учреждений. Поэтому тематическое планирование по изучению данного курса разработано для 5 ч и для 6 ч в неделю. При 6 ч в неделю добавочные часы идут на выполнение дополнительных заданий и уроки рефлексии, позволяющие учащимся лучше усвоить изучаемый материал.
Тематическое планирование разработано в двух вариантах: для учителей, закончивших ознакомительные курсы по программе «Школа 2000…» и работающих на базовом (содержательном) уровне реализации дидактической системы «Школа 2000…», и для учителей, закончивших углубленные курсы по программе «Школа 2000…» и работающих на технологическом уровне реализации дидактической системы «Школа 2000…».
Мы предлагаем Вам скачать тематическое планирование на III четверть (5 ч в неделю).
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
Методические рекомендации к организации учебного процессаГлава 3. «Рациональные числ໧ 2. Арифметика рациональных чисел. П.3 Умножение рациональных чисел1) При открытии правил умножения учащиеся используют определение умножения чисел, условие, что все известные им свойства чисел выполняются и на множестве рациональных чисел, переместительное и распределительное свойство умножения, правило сложения противоположных чисел. Для этого с учащимися выделяется четыре возможных случая, которые могут возникнуть при умножении рациональных чисел. Для каждого подбираются конкретные примеры, на которых и открываются правила умножения. Чтобы учащиеся могли самостоятельно открыть эти правила нужно подбирать примеры чисел с одинаковыми модулями, например, 4 ∙ 5, – 4 ∙5; 4 ∙ (–5) и –4 ∙ (5) В первом случае перемножаются положительные числа, данное правило известно учащимся. Во втором случае отрицательное число умножается на положительное, данное правило выводится на основании определения произведения, как суммы одинаковых слагаемых. В третьем случае положительное число умножается на отрицательное, правило для него выводится с применением переместительного свойства умножения и сводится к предыдущему случаю. А вот четвертый случай – умножение отрицательного числа на отрицательное – требует более серьезных рассуждений. Для того чтобы найти значение этого произведения учащимся придется сложить его с предыдущим произведением, значение которого уже известно: ( –4) ∙ (5) + 4 ∙ (–5). Применение распределительного свойства приведет к результату, равному нулю. Отсюда делается вывод, что данные произведения имеют противоположные значения. Все четыре случая обобщаются в общеизвестное правило. В менее подготовленном классе для открытия учащимся можно предоставить вывод о знаке произведения второго или третьего случая. А четвертый случай учитель разберет в подводящем диалоге.
Во втором случае отрицательное число умножается на положительное, данное правило выводится на основании определения произведения, как суммы одинаковых слагаемых. В третьем случае положительное число умножается на отрицательное, правило для него выводится с применением переместительного свойства умножения и сводится к предыдущему случаю. А вот четвертый случай – умножение отрицательного числа на отрицательное – требует более серьезных рассуждений. Для того чтобы найти значение этого произведения учащимся придется сложить его с предыдущим произведением, значение которого уже известно: ( –4) ∙ (5) + 4 ∙ (–5). Применение распределительного свойства приведет к результату, равному нулю. Отсюда делается вывод, что данные произведения имеют противоположные значения. Все четыре случая обобщаются в общеизвестное правило. В менее подготовленном классе для открытия учащимся можно предоставить вывод о знаке произведения второго или третьего случая. А четвертый случай учитель разберет в подводящем диалоге. В более подготовленном классе учащиеся могут работать по плану, разработанному совместно с учителем, и разобрать все четыре случая самостоятельно. В этом случае нужно проводить пошаговый взаимный контроль выводов, сделанных группами.
В более подготовленном классе учащиеся могут работать по плану, разработанному совместно с учителем, и разобрать все четыре случая самостоятельно. В этом случае нужно проводить пошаговый взаимный контроль выводов, сделанных группами.
2) № 512 готовит учащихся к открытию правила умножения рациональных чисел, здесь учащиеся должны вспомнить и применить понятие произведения.
3) № 513 служит для отработки нового правила, полученная блок-схема поможет учащимся – визуалам, т.е. тем ученикам, которые воспринимающие большую часть информации с помощью зрения.
4) № 515 используется для первичного закрепления открытого учащимися правила. Из этого же номера учитель может отобрать задания для самостоятельной работы на уроке открытия нового знания.
5) При выполнении № 516 учащиеся вспоминают частный случай умножения с нулем (№ 514 (а)) и решают уравнение, пользуясь правилом: произведение равно нули, когда хотя бы один из множителей равен нулю. Перед выполнением задания можно задать вопросы, что общего в этих уравнениях, чем они отличаются, по какому признаку уравнения можно разбить на три группы. Чтобы ответить на третий вопрос учащимся придется сначала решить уравнения. В уравнениях первого столбика они получат один корень, второго столбика (и в уравнении под буквой (д) – два, в уравнении под буквой (е) – три корня. Можно предложить учащимся составить уравнение, которое имеет три корня, чтобы уравнению под буквой (е) не было «одиноко».
Чтобы ответить на третий вопрос учащимся придется сначала решить уравнения. В уравнениях первого столбика они получат один корень, второго столбика (и в уравнении под буквой (д) – два, в уравнении под буквой (е) – три корня. Можно предложить учащимся составить уравнение, которое имеет три корня, чтобы уравнению под буквой (е) не было «одиноко».
6) Выполнение заданий №№ 517 – 519 направлено на формирование умения сравнивать с нулем произведения рациональных чисел. Учащиеся должны сделать вывод, что для сравнения с нулем нет необходимости вычислять значение произведения, а достаточно выяснить его знак.
7) При выполнении № 522 учащиеся учатся применять законы умножения для рационализации вычислений.
8) Задания №№ 523 – 525 предлагаются в учебнике для опережающей подготовки и должны выполняться с учетом принципа минимакса.
§ 2. Арифметика дробей. П.4 Деление рациональных чисел9) Алгоритм деления рациональных чисел получается на основе того, что деление является операция обратной умножению.
10) № 538 служит для отработки нового правила, полученная блок-схема поможет учащимся – визуалам, т.е. тем ученикам, которые воспринимающие большую часть информации с помощью зрения.
11) Выражения из № 540 используются для первичного закрепления открытого учащимися правила. Из них же учитель может отобрать задания для самостоятельной работы на уроке открытия нового знания.
12) Правило деления рациональных чисел переносится на обыкновенные дроби, с учащимися фиксируется правило знака «минус» для дроби: знак «минус можно перенести из числителя в знаменатель, а можно поставить его перед самой дробью. В связи с этим появляется возможность еще раз вернуться к пройденному материалу на новом этапе развития учащихся. Можно вернуться к вычислению значения дробного выражения (№ 543). Можно повторить условия перевода из обыкновенной в десятичную дробь, правила сравнения дробей, правила сравнения рациональных чисел, понятие периодической дроби (№ 544).
13) При выполнении №№ 546 — 547 учащиеся учатся применять законы деления для рационализации вычислений.
§ 2. Арифметика рациональных чисел. П.5 Какие числа мы знаем, и что мы о них знаем или не знаем14) При изучении данного пункта можно с учащимися зафиксировать эталоны по каждому из известных им числовых множеств, в которых учащиеся отмечают все известные им свойства. Например, для множества натуральных чисел можно построить следующий эталон:
Множество натуральных чисел
N = {1, 2, 3, …}- Натуральные числа служат для счета предметов и измерения величин, когда мерка укладывается в измеряемой величине целое число раз.
- Множество натуральных чисел бесконечно.
- Мы умеем записывать натуральные числа, представлять их в виде суммы разрядных слагаемых, выполнять над ними арифметические действия.
- Мы знаем свойства натуральных чисел, среди которых основными являются переместительный, сочетательный и распределительный законы сложения и умножения.

- В множестве натуральных чисел всегда выполнимы операции сложения и умножения.
15) Устанавливается взаимосвязь между множествами натуральных и рациональных чисел, строится диаграмма Венна этих множеств. Учащиеся получают представление о законе неразрушения: Любое расширение сохраняет свойства своего подмножества. ((№ 562 – 564).
16) В этом же пункте ставится проблема недостаточности изученных чисел для выражения длин отрезков. Например, доказывается, что рациональных чисел недостаточно для выражения длины диагонали квадрата со стороной, равной 1. (№№ 565 – 566).
§ 2. Арифметика рациональных чисел. П.6 О системах счисления*17) Материал, связанный с рассмотрением различных систем счисления, носит ознакомительный характер. Он расширяет представления детей о способах записи чисел и показывает возможности использования математических исследований для практического применения на примере двоичной системы счисления.
§ 3. Уравнения. П.1 Раскрытие скобок
Уравнения. П.1 Раскрытие скобок18) В этом пункте учащиеся открывают общее правило раскрытия скобок в выражениях, содержащих алгебраическую сумму. Для их вывода учащиеся анализируют правила прибавления суммы к числу и вычитания суммы из числа, записанные в буквенном виде.
Для раскрытия скобок, перед которыми стоит числовой множитель, учащиеся будут применять уже известные им правила раскрытия скобок – используя распределительный закон умножения. Такие преобразования и раньше выполнялись учащимися, теперь они рассматриваются на множестве рациональных чисел в обобщенном виде.
19) При выполнении № 2 учащиеся только раскрывают скобки, без дальнейших преобразований. В следующих заданиях полученные после раскрытия скобок выражения уже должны упрощаться.
20) Начиная с задания № 7, учащиеся раскрывают скобки, перед которыми стоит числовой множитель.
21) При выполнении заданий №№ 9 – 10 развивается математическая речь учащихся.
22) Задания №№ 11 – 13 должны выполняться с учетом принципа минимакса, заложенного в данном учебнике. Они предлагаются в учебнике для того, чтобы более подготовленные учащиеся смогли развиваться в зоне своего ближайшего развития.
Они предлагаются в учебнике для того, чтобы более подготовленные учащиеся смогли развиваться в зоне своего ближайшего развития.
23) В этом пункте у учащихся формируется понятия коэффициента и подобных слагаемых. В качестве «открытия», которое могут совершить учащиеся при изучении данного пункта можно предложить несколько вариантов. Первый – само понятие коэффициента (открытие совершается путем работы со справочной литературой или другими источниками информации) Второй – способ определения коэффициента в произведениях, у которых отсутствует числовой множитель (учащиеся применяют свойства умножения на 1 и –1и понятие коэффициента). Третий – способ определения коэффициента в произведениях, которые помимо буквенных содержат несколько числовых множителей. В последнем случае учащимся потребуется переместительное и сочетательное свойства умножения и понятие коэффициента. Для проблематизации можно воспользоваться № 27.
24) В № 30 помимо определения коэффициента учащимся нужно определить и буквенную часть. Выполнение этого задания готовит введение понятия подобных слагаемых, которое , как известно опирается на понятие «буквенная часть».
Выполнение этого задания готовит введение понятия подобных слагаемых, которое , как известно опирается на понятие «буквенная часть».
25) В этом пункте помимо подготовки к изучению курса алгебры в 7 классе учащиеся развивают вычислительные навыки и повторяют понятие степени.
§ 3. Уравнения. П.3 Приведение подобных слагаемых26) В этом пункте учащиеся знакомятся с понятием подобных слагаемых, с понятием приведения подобных слагаемых. Само преобразование ими уже выполнялось, начиная с 5 класса, без введения в их речевую практику соответствующей терминологии. Учащиеся приводили подобные слагаемые, обосновывая это преобразование распределительным свойством умножения: ab +ac = a (b + c).
27) В № 42 учащиеся приводят подобные слагаемые, подробно расписывая данное преобразование с опорой на распределительное свойство. Запись будет выглядеть следующим образом: –4n + n + 2n = –4n + 1n + 2n = (– 4+ 1+ 2)n = –1n = –n.
28) В № 43 учащиеся закрепляют новое для них понятие подобных слагаемых и связывают его с понятием коэффициента.
29) Задания №№ 44 – 46 направлены на закрепление умения приводить подобные слагаемые и новой терминологии. После того как учащиеся приведут подобные слагаемые устно (в № 44), можно разрешить им «сворачивать» запись, подчеркивая подобные слагаемые и производя вычисления с их коэффициентами устно.
30) В № 47 учащиеся выполняют уже известные им преобразования выражений, здесь важно, чтобы учащиеся проговаривали свои действия, используя новую терминологию.
31) В заданиях №№ 48 – 50 учащиеся выполняют преобразования для решения уравнения, рационализации нахождения значения буквенных выражений и для решения задач.
§ 3. Уравнения. П.4 Понятие уравнения32) Данный пункт посвящен уточнению понятия уравнения и связанных с ним понятий. Понятия уравнения, его корня, решения уравнения известны учащимся с начальной школы. Наряду с рассматриваемым в начальной школе понятием уравнения, как равенства с переменной, значение которой надо найти, учащиеся вспоминают и то, что уравнение является предложением с переменной. Интересным для ребят будет знакомство с термином корня уравнения как с примером метафоры в математическом языке. Подобно корню растения, удерживающего его в почве, корень уравнения удерживает его в множестве истинных высказываний.
Наряду с рассматриваемым в начальной школе понятием уравнения, как равенства с переменной, значение которой надо найти, учащиеся вспоминают и то, что уравнение является предложением с переменной. Интересным для ребят будет знакомство с термином корня уравнения как с примером метафоры в математическом языке. Подобно корню растения, удерживающего его в почве, корень уравнения удерживает его в множестве истинных высказываний.
33) При выполнении задания № 69 учащиеся не только выбирают, какая из записей является уравнением, но и обосновывают свой выбор. При этом шестиклассники могут ссылаться на определение уравнения или на два его характеристических свойства. Аналогично строится работа с заданием № 71, при его выполнении учащиеся проговаривают каждый раз определение корня уравнения.
34) Уточняется вопрос о числе корней уравнения. В связи с этим выполняются задания №№ 72 – 75. В них учащимся придется решить уравнения, которые имеют один, два, пять корней, бесконечное число корней или не имеют их вовсе.
35) Кроме понятий, известных учащимся с начальной школы у учащихся формируется представление о множестве значений переменной, входящей в уравнение. Под этим множеством понимается множество значений, при котором уравнение имеет смысл. В связи с этим в задание № 72 включаются уравнения, корни которого не могут принимать значение равное нулю. Это представление формируется и при выполнении задания № 76.
36) Открытия можно организовать на вопросах, связанных с количеством корней уравнения или с множеством значений переменной, входящей в уравнение.
§ 3. Уравнения. П.5 Решение уравнений37) В этом пункте систематизируются все известные учащимся методы решения уравнений.
1) Использование правил нахождения неизвестных компонентов арифметических действий.
2) Упрощение выражений в записи уравнения.
3) Метод «весов» (вычитание из обеих частей равенства одного и того же числа и умножение обеих частей равенства на одно и то же число для приведения коэффициентов к целым числам).
4) Основное свойство пропорции.
Общенаучные методы, когда иного способа решения нет:
5) Метод проб и ошибок.
6) Метод перебора.
38) Для того, чтобы учащиеся самостоятельно «открыли» прием решения уравнений путем переноса слагаемых, можно создать следующую проблемную ситуацию.
Предложить учащимся решить данные уравнения одним способом:
1) 5 + х = 1; 2) – х – 48 = 18; 3) х – 8 = 3х;
На данный момент учащиеся могут решить первые два уравнения, находя неизвестный компонент арифметических действий, третье — методом весов. Учащиеся, выполняют первый шаг в решении уравнений, используя известные им методы. Проанализировав решение с использованием понятия «алгебраическая сумма», и сравнивая полученные равенства с исходными, учащиеся формулируют новое общее правило.
39) Чтобы подготовить изучение следующего пункта можно решить одну из задач №№ 93 – 95. При составлении уравнения в № 93 учащимся в первый раз придется записать на математическом языке, что жидкость из одной емкости «перелили» в другую. При решении задач № 93 и № 95 учащиеся заполняют таблицу, для № 94 учащиеся могут использовать графическую схему, составленное по ней уравнение пока не обосновывается. При нехватке времени решение задач можно опустить, им будет полностью посвящен следующий пункт.
При решении задач № 93 и № 95 учащиеся заполняют таблицу, для № 94 учащиеся могут использовать графическую схему, составленное по ней уравнение пока не обосновывается. При нехватке времени решение задач можно опустить, им будет полностью посвящен следующий пункт.
40) При выполнении № 96 учащиеся применяют все известные им на данный момент методы решения уравнений.
§ 3. Уравнения. П.6 Решение задач с помощью уравнений41) В этом пункте уточняется представление о математическом моделировании, которое начинало формироваться у учащихся с 5 класса. Говоря о моделировании в 5 классе с учащимися обговаривались два его основных этапа – составление математической модели (как перевод с русского языка на математический) и работа с этой моделью для получения ответа на вопрос задачи. Теперь уточняется, что процесс математического моделирования включает в себя три этапа:
1) построение модели;
2) работа с моделью;
3) практический вывод из модели и его анализ.
В соответствии с этими этапами решение задачи с помощью уравнения также разбивается на три этапа. Можно попросить учащихся самостоятельно найти и назвать каждый из них. В данном пункте основное внимание сосредотачивается на первом и третьем этапах, т.к. решению уравнений был посвящен предыдущий пункт.
42) С учащимися строится алгоритм решения задачи с помощью уравнения. С данного момента, учащиеся начинают записывать обоснование составления уравнения (в случае заполнения ими таблицы они уже делали это и ранее). Причем учащиеся знакомятся с четкими указаниями того, что нужно записывать в обоснование: какая величина принята за х; как выражаются через х другие неизвестные величины; условие, на основании которого составлено уравнение.
43) Опыт показывает, что затруднение у учащихся вызывает оптимальный выбор величины, которую следует обозначить за х. То есть такой выбор, который бы обеспечивал простоту составленного ими уравнения и удобство его решения. Здесь им могут помочь «неформальные правила», которыми можно дополнить пятый шаг алгоритма: если задача на дроби за х удобнеевзять целое, если нет – наименьшую из величин. И правило, сформулированное в учебнике: «Пробуй, а если не получится – пробуй еще!»
Здесь им могут помочь «неформальные правила», которыми можно дополнить пятый шаг алгоритма: если задача на дроби за х удобнеевзять целое, если нет – наименьшую из величин. И правило, сформулированное в учебнике: «Пробуй, а если не получится – пробуй еще!»
44) В этом пункте повторяются и систематизируются все изученные учащимися виды текстовых задач, они решаются с помощью уравнения.
45) Следует обратить внимание на задание № 120, при выполнении которого учащиеся фиксируют на математическом языке результат того, что некие объекты «переложили», «перелили» (если учитель не отобрал задание № 93 для предыдущих уроков, то этот вид задач для них будет новым).
Эталоны46) В результате изучения данных тем у учащихся появляются следующие эталоны: правила умножения и деления рациональных чисел, диаграмма Венна, отображающая взаимосвязь между числовыми множествами, известных шестиклассникам; определения уравнения, корня, решения уравнения; список методов решения уравнений, алгоритм решения задач с помощью уравнения. Данные эталоны приведены в учебном пособии Л.Г. Петерсон, Л.А. Грушевской «Построй свою математику», которое предусматривает специальную работу с ними.
Данные эталоны приведены в учебном пособии Л.Г. Петерсон, Л.А. Грушевской «Построй свою математику», которое предусматривает специальную работу с ними.
Приведем пример эталона из указанного пособия:
Методические рекомендации по планированию уроковПри организации учебного процесса необходимо учитывать, что выполнение всех заданий из учебника не является обязательным. Принципы минимакса и вариативности обеспечивают возможность обучения по курсу математики программы «Школа 2000…» детей разного уровня подготовки, в том числе и высокого. Поэтому уровень и количество заданий, включенных в учебник, определялись в соответствии с зоной ближайшего развития более подготовленных учащихся. Предполагается, что учитель выбирает для работы те задания, которые соответствуют уровню подготовки детей и задачам конкретного урока.
Мы предлагаем Вам скачать методические рекомендации по планированию уроков.
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как. ..»)
..»)
С примерами организации уроков по изучению темы «Рациональные числа» Вы можете познакомиться в серии дисков со сценариями уроков в технологии деятельностного метода к учебнику математики для 5 − 6 классов основной школы авторов Г.В. Дорофеева, Л.Г. Петерсон по программе «Учусь учиться».
Предлагаем Вашему вниманию вариант сценария урока по рассматриваемым темам, в котором описан возможный способ организации самостоятельной познавательной деятельности учащихся на основе технологии деятельностного метода обучения «Школа 2000…».
Урок 92
Тема: «Умножение рациональных чисел»
Автор: Сидняева В.М. (школа № 1018, г. Москва), Лотова Н.С.
Основные цели:
1) сформировать умение находить произведение рациональных чисел, использовать свойства умножения для рационализации вычислений;
2) повторить и закрепить совместные действия с обыкновенными и десятичными дробями, прямую и обратную пропорциональную зависимости величин, решение уравнений с модулем.
Мы предлагаем Вам cкачать сценарий урока
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
Уважаемые коллеги! В соответствии с Вашими просьбами предлагаем Вам скачать решение задач на смекалку, которые входят в данные параграфы.
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
Если у Вас возникли какие-либо вопросы, напишите нам, заполнив форму обратной связи.
Мы свяжемся с Вами.
Что такое уравнение? Как решать уравнения?
Уравнение — одно из краеугольных понятий всей математики. Как школьной, так и высшей. Имеет смысл разобраться, правда? Тем более, что это очень простое понятие. Ниже сами убедитесь. 🙂 Так что же такое уравнение?
То, что это слово однокоренное со словами «равный», «равенство», возражений, думаю, ни у кого не вызывает.
Уравнение — это два математических выражения, соединённых между собой знаком «=» (равно).
Но… не каких попало. А таких, в которых (хотя бы в одном) содержится неизвестная величина. Или, по-другому, переменная величина. Или, сокращённо, просто «переменная». Которая обычно обозначается буквой «х».
Переменных может быть одна, может быть несколько. В школьной математике чаще всего рассматриваются уравнения с одной переменной. И мы тоже пока что будем рассматривать уравнения с одной переменной. С двумя переменными или более — в специальных уроках.
Что значит решить уравнение?
Идём дальше.
Переменная, входящая в уравнение, может принимать любые допустимые математикой значения. На то она и переменная. 🙂 При каких-то значениях переменной получается верное числовое равенство, а при каких-то — нет.
Так вот:
Решить уравнение означает найти ВСЕ такие значения переменной, при подстановке которых в исходное уравнение получается верное равенство. Или, более научно, верное тождество. Или доказать, что таких значений переменной не существует.
Что такое верное равенство? Это равенство, не вызывающее сомнений даже у человека, абсолютно не отягощённого глубокими математическими познаниями. Например, 5=5, 0=0, -10=-10. И так далее. 🙂
Значения переменной, при подстановке которых достигается это самое верное равенство, называются очень красиво и научно — корни уравнения.
Корень может быть один, может быть несколько. А может быть и бесконечно много корней — целый интервал или даже вообще вся числовая прямая от –∞ до +∞. Да, такое тоже бывает! Всё от конкретного уравнения зависит.)
А бывает и такое, что нельзя найти такие иксы, которые давали бы нам верное равенство. Принципиально нельзя. По определённым причинам. Нету таких иксов…
Принципиально нельзя. По определённым причинам. Нету таких иксов…
В таких случаях обычно говорят, что уравнение не имеет корней.
Для чего нужны уравнения?
Вопрос смешной. Для жизни! В школе, как правило, уравнения нужны для решения текстовых задач. Это, напоминаю, задачи на движение, на работу, на проценты и многие другие.
А во взрослой жизни без уравнений невозможны было бы ответить даже на самые обычные, но жизненно важные вопросы повседневности: какая будет погода завтра, выдержит ли заданную нагрузку здание. Или лифт. Или самолёт. Куда попадёт ракета… И не было бы сейчас среди нас ни синоптиков, ни инженеров, ни бухгалтеров, ни экономистов, ни программистов… За ненадобностью. Внушает?)
Почему это так? А потому, что уравнениями описываются почти все известные человеку природные явления и процессы. Изменение давления и температуры воздуха с высотой, закон всемирного тяготения, размножение бактерий, радиоактивный распад, химические реакции, электричество, спрос и предложение — в основе всего этого лежат математические уравнения! Простые, сложные — всякие. Какое явление или ситуация, такое и уравнение.)
Какое явление или ситуация, такое и уравнение.)
Итак, запоминаем:
Уравнения — очень мощный и универсальный инструмент для решения самых разных прикладных задач.
А какие бывают уравнения?
Уравнений в математике несметное количество. Самых разных видов. Но всё многообразие уравнений можно условно разделить всего на 4 категории:
1. Линейные,
2. Квадратные,
3. Дробные (или дробно-рациональные),
4. Прочие.
Разные категории уравнений требуют и разного подхода к их решению: линейные уравнения решаются одним способом, квадратные — другим, дробные — третьим, тригонометрические, логарифмические, показательные и прочие — тоже решаются своими методами.
Прочих уравнений, разумеется, больше всего, да…) Это и иррациональные, и тригонометрические, и показательные, и логарифмические, и многие другие уравнения. И даже дифференциальные уравнения (для студентов), где роль неизвестного играет не число, а функция. Или даже семейство функций. 🙂
Или даже семейство функций. 🙂
В соответствующих уроках мы подробно разберём все эти типы уравнений. А здесь у нас — базовые приёмы и правила.
Называются эти правила — тождественные (или — равносильные) преобразования уравнений. Их всего два. И нигде их не обойти. Так что знакомимся!
Как решать уравнения? Тождественные (равносильные) преобразования уравнений.
Решение любого уравнения заключается в поэтапном преобразовании входящих в него выражений. Но преобразований не абы каких, а таких, чтобы от шага к шагу суть всего уравнения не менялась. Несмотря на то, что после каждого преобразования уравнение будет видоизменяться и, в конечном счёте, станет совсем не похоже на исходное.
Такие преобразования в математике называются равносильными или тождественными. Их довольно много, но среди всего многообразия тождественных преобразований уравнений выделяется два базовых. О них и пойдёт речь в этом уроке. Да-да, всего два! Но — крайне важных! И каждое из них заслуживает отдельного внимания.
О них и пойдёт речь в этом уроке. Да-да, всего два! Но — крайне важных! И каждое из них заслуживает отдельного внимания.
Применение этих двух тождественных преобразований в том или ином порядке гарантирует успех в решении 99% уравнений математики. Заманчиво, правда?
Итак, вперёд!
Первое тождественное преобразование:
К обеим частям уравнения можно прибавить (или отнять) любое (но одинаковое!) число или выражение (в том числе и с переменной). Суть уравнения от этого не изменится.
Это преобразование вы применяете всюду, наивно думая, что переносите какие-то члены из одной части уравнения в другую, меняя знаки. 🙂
Например, такое крутое уравнение:
Тут и думать нечего, перебрасываем тройку вправо, меняя минус на плюс:
А что же происходит в действительности? А на самом деле вы… прибавляете к обеим частям уравнения тройку!
Вот что у вас происходит:
И результат получается тем же самым:
Вот и всё. Слева остаётся чистый икс (чего мы, собственно, и добиваемся), а справа — что уж получится. Но самое главное то, что от прибавления тройки к обеим частям суть всего уравнения не изменилась!
Слева остаётся чистый икс (чего мы, собственно, и добиваемся), а справа — что уж получится. Но самое главное то, что от прибавления тройки к обеим частям суть всего уравнения не изменилась!
Дело в том, что привычный нам перенос слагаемых из одной части в другую со сменой знака — это просто сокращённый вариант первого тождественного преобразования.
И зачем нам так глубоко копать? В уравнениях — незачем. Переносите себе спокойно и не парьтесь. Только знаки менять не забывайте.) А вот в неравенствах привычка к переносу может и слегка обескуражить, да…
Это было первое тождественное преобразование. Переходим ко второму.
Второе тождественное преобразование:
Обе части уравнения можно умножить (разделить) на одно и то же отличное от нуля число или выражение.
Это тождественное преобразование мы вы постоянно применяете, когда решаете что-нибудь совсем уж жуткое типа:
Тут каждому ясно, что х=3. А вот как вы получили этот ответ? Подобрали? Угадали?
А вот как вы получили этот ответ? Подобрали? Угадали?
Чтобы не подбирать и не гадать (мы с вами математики, а не гадалки), нужно понять, что вы просто поделили обе части уравнения на четвёрку. Которая нам и мешает.
Вот так:
Эта палка с делением означает, что на четвёрку делятся обе части нашего уравнения. Через дроби эта процедура выглядит так:
Слева четвёрки благополучно сокращаются, остаётся икс в гордом одиночестве. А справа при делении 12 на 4 получается, понятное дело, тройка. 🙂
И все дела.)
Звучит невероятно, но эти два (всего два!) простых преобразования лежат в основе решения всех уравнений математики! Да-да, именно всех, я нисколько не преувеличиваю! От линейных и квадратных в школе до дифференциальных в ВУЗе.)
Ну что, посмотрим на тождественные преобразования уравнений в действии?
Применение тождественных преобразований к решению уравнений.
Начнём с первого тождественного преобразования. Переноса вправо-влево.
Пример для новичков:
1 — х = 3 — 2х
Дело нехитрое. Это линейное уравнение. Работаем прямо по заклинанию: «С иксами влево, без иксов — вправо».
Эта мантра — универсальная инструкция по применению первого тождественного преобразования. Вот и смотрим на уравнение. Какое слагаемое с иксом у нас справа? Что? 2х? Не-а!) Справа у нас -2х (минус два икс)! Поэтому при переносе в левую часть минус поменяется на плюс:
1 — х +2х = 3
Полдела сделано, иксы собрали слева. Осталось все числа собрать справа. Слева в уравнении стоит единичка. Опять вопрос — с каким знаком? Ответ «с никаким» не катит.) Слева перед единицей и вправду ничего не написано. А это значит, что перед ней стоит знак «плюс». Так уж в математике повелось: ничего не написано — значит, плюс.)
Так уж в математике повелось: ничего не написано — значит, плюс.)
И поэтому вправо единичка перенесётся уже с минусом:
-х + 2х = 3 — 1
Вот почти и всё. Слева приводим подобные, а справа — считаем. И получаем:
х = 2
Это было совсем примитивное уравнение.
Теперь пример покруче, для старшеклассников:
Решить уравнение:
Уравнение логарифмическое. Ну и что? Какая разница? Всё равно первым шагом делаем базовое тождественное преобразование («С иксами влево ….»). Для этого слагаемое с иксом (то есть, —log3x) переносим влево. Со сменой знака:
А числовое выражение (log34) переносим вправо. Также со сменой знака, разумеется:
Вот и всё. Справа получилась чистая формула. Кто дружит с логарифмами, тот в уме дорешает уравнение и получит:
Справа получилась чистая формула. Кто дружит с логарифмами, тот в уме дорешает уравнение и получит:
х=3
Что? Хотите синусы? Пожалуйста, вот вам синусы:
И снова всё то же самое! Выполняем первое тождественное преобразование — переносим sin x влево (с минусом), а -0,25 переносим вправо (с плюсом):
Получили простейшее тригонометрическое уравнение с синусом, решить которое (для знающих) также не составляет никакого труда.
Видите, насколько универсально первое равносильное преобразование! Встречается везде и всюду и не обойти его никак… Именно поэтому так важно уметь его делать на автомате и без ошибок.
Собственно, ошибиться здесь можно лишь в одном — забыть сменить знак при переносе. Что и происходит сплошь и рядом. Внимательность никто не отменял, да…)
Ну что, продолжаем наши игры? Развлекаемся теперь со вторым преобразованием!)
Решить уравнение:
7х=28
Крутяк, прямо скажем. ) Ладно, это эмоции…
) Ладно, это эмоции…
Смотрим и соображаем: что нам мешает в этом уравнении? Что-что… Да семёрка мешает! Хорошо бы от неё избавиться. Да так, чтобы исходное уравнение не испортить.)
Но как? Перенести вправо? Ээээ… Стоп! Нельзя.) Семёрка с иксом умножением связана. Коэффициент, видите ли.) Нельзя её оторвать от икса и вправо перенести. Вот всё выражение 7х целиком — пожалуйста (вопрос — зачем?). А семёрку отдельно — никак нет.
Самое время про умножение/деление вспомнить! Нам ведь в ответе чистый икс нужен, не так ли? А семёрка — мешает. Вот и делим левую часть на семь. «Очищаем» икс от коэффициента. Так нам надо. Но тогда и правую часть тоже надо поделить на семь: этого уже математика требует. Что уж там получится, то и получится. Но пример хороший. Я старался.) 28 на 7 замечательно делится. Получится 4.
Ответ: х=4
Или такое уравнение:
Что здесь нам мешает? Дробь 1/6, не так ли? Вот давайте и избавимся от неё. Безопасно для уравнения.) Как? Ну, можно поступить аналогично — поделить обе части на эту самую 1/6. Но в уме это не очень удобно. Кое-кто и запутается…
Безопасно для уравнения.) Как? Ну, можно поступить аналогично — поделить обе части на эту самую 1/6. Но в уме это не очень удобно. Кое-кто и запутается…
Но мы же не только делить, мы ещё и умножать умеем!) Вспоминаем из младших классов, после какого действия у нас пропадает дробь? Правильно! Дробь у нас пропадает при умножении на число, равное (или кратное) её знаменателю. Вот и умножим обе части нашего уравнения на 6. Слева всё равно чистый икс получится, а умножение правой части на 6 — не самая трудная работа.)
Вот и всё.) Умножение обеих частей уравнения на нужное число позволяет сразу избавляться от дробей, минуя промежуточные выкладки, в которых, между прочим, запросто можно и ошибок наляпать. Короче дорога — меньше ошибок!
Теперь снова на машину времени и — в старшие классы:
Решить уравнение:
Чтобы добраться до икса и тем самым решить это крутое тригонометрическое уравнение, нам надо сначала получить слева чистый косинус, безо всяких коэффициентов. А двойка мешает. 🙂 Вот и делим на 2 всю левую часть:
А двойка мешает. 🙂 Вот и делим на 2 всю левую часть:
Но тогда и правую часть тоже придётся разделить на двойку: это уже МАТЕМАТИКЕ надо. Делим:
Получили справа табличное значение косинуса. И теперь уравнение решается за милую душу.)
Вот и вся премудрость. Как видите, тождественные преобразования уравнений — штука полезная. И при этом не самая сложная. Перенос да умножение/деление. Однако далеко не у всех они получаются с первого раза и без ошибок, ох не у всех… Основные проблемы здесь две.
Проблема первая (для малоопытных):
Иногда ученик думает, что упрощение уравнений делается по одному, раз и навсегда установленному правилу. И никак не может уловить и понять это правило: в каких-то примерах начинают с домножения (или деления), в каких-то — с переноса. Где-то три раза переносят и ни разу не домножают…
Например, такое линейное уравнение:
10х + 5 = 5х — 20
С чего начинать? Можно начать с переноса:
10х — 5х = -20 — 5
А можно сначала поделить обе части на пятёрку, а затем уж переносить. Тогда сразу числа попроще станут:
Тогда сразу числа попроще станут:
Как видим, и так и сяк решать можно. И это — в примитивном примере! Вот и возникает у неопытных учеников вопрос: «Как правильно?»
По-всякому правильно! Кому как удобнее. 🙂 Универсального рецепта здесь нет и быть не может. Математика предлагает вам на выбор два вида преобразований уравнений. А порядок этих самых преобразований зависит исключительно от исходного уравнения, а также от личных предпочтений и привычек решающего.
Проблема вторая (для всех…ну… почти):
Ошибки в вычислениях. В преобразованиях постоянно приходится перемножать скобки. Заключать выражения в скобки и раскрывать скобки. Умножать и делить дроби. Работать со степенями… Короче, в наличии весь набор элементарных действий математики. Со всеми вытекающими…
Обе эти проблемы устраняются только одним способом — практикой. Исчезают сомнения и ошибки. Примеры становятся проще, задания — легче. И в итоге не математика командует вами, а вы — математикой. 🙂
Примеры становятся проще, задания — легче. И в итоге не математика командует вами, а вы — математикой. 🙂
Деление натуральных чисел и его свойства, правила и примеры.
Деление натуральных чисел.
Рассмотрим понятие деление на задаче:
В корзине лежало 12 яблок. Шестеро детей разобрали яблоки. У каждого ребенка получилось одинаковое количество яблок. Сколько яблок у каждого ребенка?
Решение:
Нам нужно 12 яблок поделить на шестерых детей. Запишем математически задачу 12:6.
Или по-другому можно сказать. На какое число нужно умножить число 6, чтобы получилось число 12? Запишем в виде уравнения задачу. Количество яблок нам неизвестно, поэтому обозначим их за переменную x.
x⋅6=12
Чтобы найти неизвестное x нам нужно 12:6=2
Ответ: по 2 яблока у каждого ребенка.
Рассмотрим подробно пример 12:6=2:
Число 12 называется делимым. Это число, которое делят.
Число 6 называется делителем. Это число, на которое делят.
И результат деления число 2 называют частным. Частное показывает во сколько раз делимое больше делителя.
В буквенном виде деление выглядит так:
a:b=c
a – делимое,
b – делитель,
c – частное.
Так что же такое деление?
Деление – это действие, обратное умножению. По произведению одного множителя мы можем найти другой множитель.
Деление проверяется умножением, то есть:
a:b=c, проверка с⋅b=a
18:9=2, проверка 2⋅9=18
Неизвестный множитель.
Рассмотрим задачу:
В каждой упаковке по 3 штуки елочных шаров. Чтобы нарядить елку нам нужно 30 шаров. Сколько нам нужно взять упаковок с елочными шарами?
Решение:
x – неизвестное количество упаковок шаров.
3 – штуки в одной упаковки шаров.
30 – всего шаров.
x⋅3=30 нам нужно столько раз взять по 3, чтобы получилось в итоге 30. x – это неизвестный множитель. То есть, чтобы найти неизвестный множитель нужно, произведение поделить на известный множитель.
х=30:3
х=10.
Ответ: 10 упаковок шаров.
Неизвестное делимое.
Рассмотрим задачу:
В каждой упаковке по 6 цветных карандашей. Всего упаковок 3 штуки. Сколько всего карандашей было, до того пока их не разложили по упаковкам?
Решение:
x – всего карандашей,
6 – карандашей в каждой упаковке,
3 – упаковки карандашей.
Запишем уравнение задачи в виде деления.
x:6=3
x – это неизвестное делимое. Чтобы найти неизвестное делимое надо, частное умножить на делитель.
х=3⋅6
х=18
Ответ: 18 карандашей.
Неизвестный делитель.
Разберём задачу:
Было 15 шаров в магазине. За день в магазин пришло 5 покупателей. Покупатели купили равное количество шаров. Сколько шаров купил каждый покупатель?
Решение:
х – количество шаров, которое купил один покупатель,
5 – количество покупателей,
15 – количество шаров.
Запишем уравнение задачи в виде деления:
15:х=5
х – в данном уравнении является неизвестным делителем. Чтобы найти неизвестный делитель, мы делимое делим на частное.
х=15:5
х=3
Ответ: по 3 шара у каждого покупателя.
Свойства деления натурального числа на единицу.
Правило деления:
Любое число, деленное на 1 результатом будет тоже самое число.
7:1=7
a:1=a
Свойства деления натурального числа на нуль.
Рассмотрим пример: 6:2=3, проверить правильно ли мы поделили можно умножением 2⋅3=6.
Если мы 3:0, то сделать проверку мы не сможем, потому что любое число умноженное на нуль будет нуль. Поэтому запись 3:0 не имеет смысла.
Правило деления:
Делить на нуль нельзя.
Свойства деления нуля на натуральное число.
0:3=0 эта запись имеет смысл. Если мы ничего поделим на три части то получим ничего.
0:a=0
Правило деления:
При делении 0 на любое натуральное число не равное нулю, результат всегда будет равен 0.
Свойство деления одинаковых чисел.
3:3=1
a:a=1
Правило деления:
При делении любого числа на себя, не равное нулю, результат будет равен 1.
Вопросы по теме “Деление”:
В записи a:b=c назовите, что здесь является частным?
Ответ: a:b и c.
Что такое частное?
Ответ: частное показывает во сколько раз делимое больше делителя.
При каком значении m запись 0⋅m=5?
Ответ: при умножении на нуль в ответе всегда будет 0. Запись не имеет смысла.
Существует ли такое n, что 0⋅n=0?
Ответ: да, запись имеет смысл. При умножении любого числа на 0 будет 0, поэтому n – любое число.
Пример №1:
Найдите значение выражение: а) 0:41 б) 41:41 в) 41:1
Ответ: а) 0:41=0 б) 41:41=1 в) 41:1=41
Пример №2:
При каких значениях переменных верно равенство: а) х:6=8 б) 54:х=9
а) х – в данном примере является делимым. Чтобы найти делимое нужно частное умножить на делитель.
Чтобы найти делимое нужно частное умножить на делитель.
х – неизвестное делимое,
6 – делитель,
8 – частное.
х=8⋅6
х=48
б) 54 – делимое,
х – делитель,
9 – частное.
Чтобы найти неизвестный делитель, нужно делимое поделить на частное.
х=54:9
х=6
Задача №1:
У Саши 15 марок, а Миши 45 марок. Во сколько раз у Миши марок больше чем у Саши?
Решение:
Можно задачу решить двумя способами. Первый способ:
15+15+15=45
Нужно 3 числа 15, чтобы получить 45, следовательно, в 3 раза у Миши марок больше, чем у Саши.
Второй способ:
45:15=3
Ответ: в 3 раза у Миши марок больше, чем у Саши.
Использование свойств деления и умножения равенства для решения уравнений
Результаты обучения
- Определить, является ли число решением уравнения
- Проверьте свое решение линейного уравнения, чтобы убедиться в его точности
- Решите уравнения, используя свойства деления и умножения равенства
- Решите уравнения, которые необходимо упростить
Решите алгебраические уравнения, используя свойства умножения и деления равенства
Точно так же, как вы можете складывать или вычитать одну и ту же точную величину в обеих частях уравнения, вы также можете умножать или делить обе части уравнения на одну и ту же величину, чтобы написать эквивалентное уравнение. Для начала давайте в качестве примера рассмотрим числовое уравнение [латекс]5\cdot3=15[/латекс]. Если вы умножите обе части этого уравнения на [latex]2[/latex], вы все равно получите верное уравнение.
Для начала давайте в качестве примера рассмотрим числовое уравнение [латекс]5\cdot3=15[/латекс]. Если вы умножите обе части этого уравнения на [latex]2[/latex], вы все равно получите верное уравнение.
[латекс]\begin{array}{r}5\cdot 3=15\,\,\,\,\,\,\, \\ 5\cdot3\cdot2=15\cdot2 \\ 30=30\ ,\,\,\,\,\,\,\end{массив}[/латекс]
Эта характеристика уравнений обобщена в M Свойстве Равенства Умножения .
Давайте рассмотрим свойства деления и умножения равенства, поскольку мы готовимся использовать их для решения одношаговых уравнений.
Свойство равенства деления
Для всех действительных чисел [latex]a,b,c[/latex] и [latex]c\ne 0[/latex], если [latex]a=b[/latex], затем [latex]\Large\frac{a}{c}\normalsize =\Large\frac{b}{c}[/latex].
Если два выражения равны друг другу, и вы разделите обе части на одно и то же число, не равное нулю, полученные выражения также будут эквивалентны.
Свойство равенства умножения
Для всех вещественных чисел [latex]a,b,c[/latex], если [latex]a=b[/latex], то [latex]ac=bc[/latex].
Если два выражения равны друг другу и вы умножаете обе части на одно и то же число, полученные выражения также будут эквивалентны.
Проще говоря, когда вы делите или умножаете обе части уравнения на одну и ту же величину, вы все равно получаете равенство. Когда уравнение включает в себя умножение или деление, вы можете «отменить» эти операции, используя обратную операцию, чтобы изолировать переменную.
В предыдущем примере, чтобы «отменить» умножение, мы разделили. Как вы думаете, как мы «отменяем» деление? Далее мы покажем пример, который требует от нас использования умножения для отмены деления.
пример
Решить: [латекс]\большой\фрак{а}{-7}\нормальный размер =-42[/латекс]
Показать решение
Теперь посмотрите, сможете ли вы решить задачу, требующую умножения для отмены деления. Вспомните правила умножения двух отрицательных чисел — два отрицательных числа при умножении дают положительное.
попробуйте
Еще один способ представить решение уравнения, когда операцией является умножение или деление, заключается в том, что мы хотим умножить коэффициент на обратный мультипликатив (обратный), чтобы изменить коэффициент на [латекс]1[/латекс ].
В следующем примере мы изменим коэффициент на [latex]1[/latex] путем умножения на мультипликативную обратную величину [latex]\frac{1}{2}[/latex].
В видео ниже вы увидите примеры того, как использовать свойства равенства умножения и деления для решения одношаговых уравнений с целыми числами и дробями.
пример
Решите: [латекс]4x=-28[/латекс]
Решение:
Чтобы решить это уравнение, мы используем свойство равенства деления, чтобы разделить обе части на [латекс]4[/латекс ].
| [латекс]4x=-28[/латекс] | |
| Разделите обе части на 4, чтобы отменить умножение. | [латекс]\Large\frac{4x}{\color{red}4}\normalsize =\Large\frac{-28}{\color{red}4}[/latex] |
| Упрощение. | [латекс]х =-7[/латекс] |
Проверьте свой ответ. | [латекс]4x=-28[/латекс] |
| Пусть [латекс]х=-7[/латекс]. Замените x на [латекс]-7[/латекс]. | [латекс]4(\color{red}{-7})\stackrel{\text{?}}{=}-28[/latex] |
| [латекс]-28=-28[/латекс] |
Поскольку это верное утверждение, [латекс]х=-7[/латекс] является решением [латекс]4х=-28[/латекс].
Теперь вы можете попытаться решить уравнение, требующее деления и содержащее отрицательные числа.
попробуйте
Когда вы начнете решать уравнения, требующие нескольких шагов, вы можете обнаружить, что в итоге вы получите уравнение, похожее на уравнение в следующем примере, с отрицательной переменной. Как стандартная практика, хорошо убедиться, что переменные положительны, когда вы решаете уравнения. Следующий пример покажет вам, как это сделать.
пример
Решить: [латекс]-r=2[/латекс]
Показать решение
Теперь можно попробовать решить уравнение с отрицательной переменной.
попробуйте
Следующее видео содержит примеры использования свойств деления и умножения для решения уравнений с переменной справа от знака равенства.
Двухшаговые линейные уравнения
Если уравнение имеет вид [латекс]ах+b=с[/латекс], где [латекс]х[/латекс] — переменная, уравнение можно решить следующим образом: до. Сначала «отменить» сложение и вычитание, а затем «отменить» умножение и деление.
Примеры
Решите: [латекс]4x+6=-14[/латекс]
Решение:
В этом уравнении переменная находится только в левой части. Левую часть имеет смысл называть переменной стороной. Следовательно, правая часть будет постоянной стороной.
Поскольку левая сторона является переменной стороной, цифра 6 неуместна. Мы должны «отменить» добавление [латекс]6[/латекс], вычитая [латекс]6[/латекс], и чтобы сохранить равенство, мы должны вычесть [латекс]6[/латекс] с обеих сторон. Используйте свойство вычитания равенства. Мы должны «отменить» добавление [латекс]6[/латекс], вычитая [латекс]6[/латекс], и чтобы сохранить равенство, мы должны вычесть [латекс]6[/латекс] с обеих сторон. Используйте свойство вычитания равенства. | [латекс]4x+6\цвет{красный}{-6}=-14\цвет{красный}{-6}[/латекс] | |
| Упрощение. | [латекс]4x=-20[/латекс] | |
| Теперь все [latex]x[/latex] слева, а константа справа. | ||
| Используйте Свойство Разделения Равенства. | [латекс]\Large\frac{4x}{\color{red}{4}}\normalsize =\Large\frac{-20}{\color{red}{4}}[/latex] | |
| Упрощение. | [латекс]x=-5[/латекс] | |
| Чек: | [латекс]4x+6=-14[/латекс] | |
| Пусть [латекс]х=-5[/латекс] . | [латекс]4(\цвет{красный}{-5})+6=-14[/латекс] | |
| [латекс]-20+6=-14[/латекс] | ||
| [латекс]-14=-14\четверка\галочка[/латекс] | ||
Решить: [латекс]2y — 7=15[/латекс]
Показать решение
Теперь вы можете попробовать аналогичную задачу.
Попробуй
В следующем видео мы покажем примеры решения двухшаговых линейных уравнений.
Не забудьте проверить решение алгебраического уравнения, подставив значение переменной в исходное уравнение.
В следующем разделе мы узнаем, как решать уравнения, которые необходимо упростить, прежде чем их можно будет решить.
Поддержите!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Переменные в уравнениях умножения и деления — 3-й класс математики
На прошлом уроке вы узнали, как решать уравнения на сложение и вычитание с переменными.
Это было потрясающе! 😺 Давайте повторим, что вы узнали.
Решение уравнений с переменными Обзор
Уравнение показывает, что два выражения равны или сбалансированы.
Чтобы решить уравнение с переменной, возьмите одну переменную с одной стороны уравнения.
Как? 🤔
Это похоже на математическую магию. 🧙♂️
Чтобы получить одну переменную, отмените операции , которые были выполнены с переменной.
Вы можете отменить сложение с вычитанием.
Подсказка: Вот почему сложение и вычитание называются обратными операциями .
Подсказка: Инверсия означает противоположность или реверс.
Вы можете добавить число к как стороны уравнения, и оно останется сбалансированным.
Подсказка: думайте об этом, как о добавлении одинакового количества шариков в две чаши.
Вы можете вычесть число из обеих сторон уравнения, и оно также останется сбалансированным .
Совет : подумайте об этом, как о том, чтобы взять одинаковое количество шариков из двух мисок.
👉 Вы даже можете добавить или вычесть переменная из обе стороны уравнения, и оно останется сбалансированным!
Пока вы выполняете операцию с обеих сторон, уравнение остается сбалансированным.
Отличная работа! 🤓
А что, если у нас есть уравнение умножения с переменной, например:
y × 2 = 10
Чтобы решить его, нам нужно получить y только с одной стороны.
Как мы можем получить и в одиночку? 🤔
👉 Нам нужно отменить операцию умножения.
Чтобы отменить умножение, мы делаем обратную операцию , деление.
Обратные операции
Умножение и деление обратные операции, так же как сложение и вычитание обратные операции.
Деление отменяет умножение, а умножение отменяет деление.
👉 Вот пример того, как деление отменяет умножение.
10 × 2 ÷ 2 = 10
Если мы начнем с 10, затем умножим на 2, а затем разделим на 2, мы вернемся к 10.
Решение переменных в уравнениях умножения
Итак, вернемся к нашей проблеме.
y × 2 = 10
👉 Мы можем отменить умножение, разделив обе части на 2!
Вот как это выглядит, записанное математическими уравнениями:
y × 2 = 10
y × 2 ÷ 2 = 10 ÷ 2
y = 5
Подсказка: Вы только что использовали математические трюки, чтобы переписать уравнения , чтобы их было легче решать, одно под другим.
Вы будете заниматься этим еще много лет, даже в старшей школе и колледже! 👩🏫
Подсказка : Вот некоторые математические приемы, которые вы уже знаете: упростите все, что вы можете, и добавьте или вычтите числа из 9.0022 обе стороны стороны уравнения, чтобы сохранить его сбалансированным, но более легким для решения. 🤯
Ты математический гений!
Итак, решение уравнения равно y = 5!
Проверим правильность нашего ответа, заменив переменную найденным числом:
2y = 10
2 × 5 = 10
10 = 10 6 Так как левая сторона равна 10 6 справа, это означает, что мы нашли правильное значение для y! ✅Переменные в уравнениях деления
Попробуем вместе решить уравнение деления.
Решите для p:
p ÷ 7 = 12👉 p делится на 7.
Как это отменить?
👉 You have to multiply both sides by 7.
p ÷ 7 = 12
p ÷ 7 × 7 = 12 × 7
p = 84The solution в уравнении равно р = 84!
Переменные в делителеРассмотрим пример.
Решите для q:
36 ÷ q = 6Поскольку q использовалось для деления 36, давайте умножим обе части на q и посмотрим, что получится.
36 ÷ Q = 6
36 ÷ Q × Q = 6 × Q
36 = 6QСовет: Q ктд. .
Q’s отменяет каждый другой слева.
Теперь у нас есть уравнение умножения. 😁
Но нам все еще нужно получить переменную q с одной стороны, чтобы увидеть ее значение.
Как мы доберемся в одиночку? Как это:
36 = 6Q
36 ÷ 6 = 6Q ÷ 6
6 = QРаствор по равным — Q =
.
Раствор по равным — Q =
.0022 6!
Отлично! Теперь вы знаете, как найти переменную в умножении или делении. 🎉 Это довольно большое дело.
Готовы к практике? 💪
Решение простых уравнений | Определение, примеры, решения и итоги
ВведениеВ арифметике обычно встречаются утверждения следующего типа –
- 16 + 6 = 22
- 7 x (4 + 6) = 7 x 4 + 7 х 6
Такой оператор, содержащий символ «=», называется оператором равенства или просто равенством .
Ни один из приведенных выше операторов не использует переменную.
Утверждение о равенстве, которое включает одну или несколько переменных, называется уравнением.
Рассмотрим следующие утверждения:
- Число x, увеличенное на 7, равно 15.
- 9 превышает число x на 3
- 4 раза, когда число x равно 24
- Число y, деленное на 5, равно 7
- Сумма числа x и удвоенного числа y равна 12
Вышеприведенные утверждения можно записать следующим образом: –
- x + 7 = 15
- 9 – x = 3
- 4x = 24
6 9 \frac{y}{5}$ = 7
- x + 2y = 12
Каждое из приведенных выше утверждений является выражением равенства, содержащим одну или несколько переменных. Таким образом, каждое из них представляет собой уравнение.
Определение линейного уравненияУравнение, в котором самая высокая степень задействованных переменных равна 1, называется линейным уравнением. Другими словами, линейное уравнение — это математическое уравнение, определяющее линию. Хотя каждое линейное уравнение соответствует ровно одной строке, каждая строка соответствует бесконечному количеству уравнений. Эти уравнения будут иметь переменную, наивысшая степень которой равна 1,9.
0017
Знак равенства делит уравнение на две части, а именно на левую и правую части, которые записываются как L.H.S и R.H.S соответственно.
Линейные уравнения, основанные на количестве переменныхУ нас есть различные линейные уравнения, основанные на количестве переменных. Например,
Уравнение с одной переменнойУравнение может иметь только одну переменную, например –
12x – 10 = 0
18x = 12
Уравнение с двумя переменными. Уравнение может иметь две переменные, такие как
12x +10y — 10 = 0
12x +23y = 20
Уравнение с тремя переменнымиАнти. такие переменные, как
12x +10y -3z – 10 = 0
12x +23y – 12z = 20
Точно так же могут быть уравнения с любым количеством переменных. Существуют различные методы решения линейных уравнений в зависимости от количества переменных, которые они имеют.
Решение линейного уравненияТеперь давайте посмотрим, как решать линейные уравнения с одной переменной.
Число, которое делает L.H.S = R.H.S, когда оно заменяет переменную в уравнении, считается удовлетворяющим уравнению и называется решением или корнем уравнения.
Решение линейных уравнений
Прежде чем изучать методы решения уравнений, важно знать, что существуют определенные правила решения уравнений. Давайте проверим, что это за правила —
Правила решения линейных уравненийНиже приведены правила решения линейных уравнений –
- Мы можем добавить одно и то же число к обеим частям уравнения. Это означает, что если x + 5 = 7, то x + 5 + 2 = 7 + 2
- Мы можем вычесть одно и то же число из обеих частей уравнения. Это означает, что если x + 5 = 7, то x + 5 – 2 = 7 – 2
- Мы можем умножить обе части уравнения на одно и то же ненулевое число.
Это означает, что если х + 5 = 4, то 6 ( х + 5 ) = 6 х 4
- Мы можем разделить обе части уравнения на одно и то же ненулевое число. Это означает, что если 3x = 10, то $\frac{3x}{3} = \frac{10}{3}$
Давайте теперь узнаем, какие существуют методы решения линейных уравнений.
Существует множество методов решения линейных уравнений. Некоторые из них –
Решение уравнений с делением
- Решение уравнений с делением
- Решение уравнений с умножением
- Методом проб и ошибок
- Метод транспонирования
Мы можем использовать ту же идею «делать одно и то же с обеими сторонами», которую мы используем для решения уравнений со сложением и вычитанием, для решения уравнений, включающих умножение и деление. Для этого вспомним, что мы понимаем под делением.
С другой стороны, при делении, когда мы делимся, мы разделяемся на равные группы. Например, 10 ÷ 5 = 2 означает, что 10 делится на 2 группы по 5
Мы можем решить приведенные ниже уравнения, «избавившись» или «отменив» умножение путем деления (выполнив обратную операцию.
)
Давайте разберемся на примере.
Предположим, мы хотим решить уравнение 3 n = 12
Поскольку коэффициент при n равен 3, разделим обе части уравнения на 3. Получим
3 n ÷ 3 = 12 ÷ 3
⇒ n = 4
Ниже приведено графическое представление того же для лучшего понимания.
Возьмем другой пример
Предположим, мы хотим решить уравнение 5 n = 15
Поскольку коэффициент при n равен 5, разделим обе части уравнения на 5. Получим
5 n ÷ 3 = 15 ÷ 5
⇒ n = 3
Ниже приведено графическое представление того же для лучшего понимания.
Решение уравнений с умножениемМы можем решить приведенные ниже уравнения, «избавившись» или «отменив» деление путем умножения (выполняя противоположную операцию). Когда мы умножаем, мы объединяем группу равных чисел. Например, 3 x 4 = 12 означает 3 группы по 4 или 4 группы по 3, что в свою очередь равно 12.
Давайте разберемся на примере.
Предположим, мы хотим решить уравнение $\frac{n}{3}$ = 2
Чтобы решить это уравнение, w умножит обе части на 3, чтобы получить
$\frac{n}{3}$ x 3 = 2 x 3
⇒ n = 6
Ниже приведено графическое представление того же для лучшего понимания.
Возьмем другой пример.
Предположим, мы хотим решить уравнение $\frac{n}{5}$ = 4
Чтобы решить это уравнение, w умножит обе части на 5, чтобы получить
$\frac{n}{5}$ х 5 = 4 х 5
⇒ n = 20
Ниже приведено графическое представление того же самого для лучшего понимания.
Таким образом, сверху мы можем сказать, что мы можем «избавиться» или «отменить» умножение путем деления, и мы можем «избавиться» или «отменить» деление путем умножения.
Метод проб и ошибокВ этом методе мы часто угадываем корень уравнения. Находим значения левой части L.H.S и правой части R.H.S данного уравнения для различных значений переменной. Значение переменной, для которой LHS = RHS, является корнем уравнения.
Давайте разберемся с методом на нескольких примерах.
Пример
Решите следующие уравнения методом проб и ошибок:
- x + 7 = 10
- 5x = 30
Решение
6 9 проверьте значения левой и правой сторон уравнения для некоторых значений x и продолжайте делать это до тех пор, пока левая сторона не станет равной правой стороне
- Данное уравнение имеет вид x + 7 = 10
У нас есть,
L.H.S = x + 7 и R.H.S =10
Мы будем подставлять различные значения x в LHS, пока не получим результат 10, который является нашим R.H.S.
Следующие таблицы показывают наши предположения о пробной и ошибке —
3 3 R. «X» L.H.S R.SH.S 3 R.SH.S 3 R.H.S 3 R.SH.S SH.S
. 1 + 7 = 8 10 № 2 2 + 7 = 10 № 3 3 + 7 = 100074 10 3 + 7 = 100074 10 Да. Имеем, что при замене x на 3 получаем L.H.S = R.H.S Следовательно, x = 3 является решением уравнения, x + 7 = 10
- Данное уравнение имеет вид 5x = 30
. Имеем LHS = 5x и RHS = 30
Мы будем подставлять различные значения x в LHS, пока не получим результат 30, который является нашим RHS.
Value of “x” L.H.S R.H.S Is L.H.S = R.H.S 1 5 x 1 = 5 30 No 2 5 x 2 = 10 30 No 3 5 x 3 = 15 30 No 4 5 x 4 = 20 30 No 5 5 x 5 = 25 30 No 6 5 x 6 = 30 30 Yes From the above table, we have что, когда x заменяется на 6, мы получаем L.
H.S = R.H.S
Следовательно, x = 6 является решением уравнения, 5x = 30
Метод транспонированияПутем транспонирования члена уравнения с помощью простых средних изменив его тон и перенеся в другую часть уравнения, любой член уравнения можно перевести в другую сторону с изменением его знака, не нарушая равенства. Этот процесс называется транспозицией, когда мы переносим член уравнения из левой стороны в правую. и R.H.S на L H.S знак плюс термина меняется на знак минус с другой стороны и наоборот
Метод перестановки включает следующие шаги –
Решение реальных задач с помощью простых линейных уравнений
- Получение линейного уравнения
- Определение неизвестной величины (переменной)
- Упрощение левой и правой сторон путем удаления группирующих символов (если они есть)
- Перенос всех членов, содержащих переменную, в LHS и постоянные члены RHS уравнения. Обратите внимание, что размер терминов будет меняться при переносе их с левой стороны на правую и наоборот
- Упростите левую и правую стороны в простейшей форме, чтобы каждая сторона содержала только один термин
- Решите полученное уравнение по правилам.
Теперь мы узнаем о постановке и решении некоторых практических задач. Эти проблемы связаны с отношениями между неизвестными величинами, которые мы называем переменными, и известными величинами, которые известны как числа и часто формулируются словами. Вот почему мы часто называем эту задачу словесной задачей . Словесная задача сначала переводится в виде уравнения, содержащего неизвестные величины, т.е. переменные, и известные величины, т.е. числа или константы, а затем мы решаем ее любым из изученных нами методов. Процедура перевода текстовой задачи в форму уравнения известна как постановка задачи. Таким образом, процесс решения текстовой задачи состоит из двух частей, а именно формулировки и решения
- Для решения текстовой задачи необходимо выполнить следующие шаги –
- Внимательно прочитать задачу и отметить, что дано и что требуется
- Обозначить неизвестную величину несколькими буквами, скажем, x, y, z и т.
д.
- Переведите условия задачи в математическую формулировку
- Используя условие, данное в задаче, составьте уравнение
- Решите уравнение для неизвестного
- Проверьте, удовлетворяет ли решение уравнению
Давайте теперь разберемся с приведенными выше шагами на нескольких примерах –
Пример 1 Сумма двух последовательных чисел равна 53, найдите числа.
Решение Нам дано, что
Сумма двух последовательных чисел равна 53. Нам нужно найти эти два числа. Итак, следуя шагам, определенным выше, мы сначала даем имя неизвестному значению, которое в данном случае является числом. Следовательно,
Пусть первое число будет x.
Тогда следующим последовательным числом будет x + 1
Известно, что сумма двух последовательных чисел равна 53, поэтому мы можем составить уравнение следующим образом –
x + ( x + 1 ) = 53
Теперь, когда у нас есть уравнение, мы решим его относительно x.
х + ( х + 1 ) = 53
⇒ 2х + 1 = 53
⇒ 2х = 53 – 1
⇒ 2х = 52
⇒ Теперь х = 26
. следующее число является последовательным числом, второе число будет x + 1 = 27,Следовательно, два числа равны 26 и 27
Пример 2 Мать Сары в три раза старше Сары и в четыре раза старше ее сестры; Анна. Энн на три года моложе Сары. Сколько лет Саре, Энн и их маме?
Решение Нам сообщили, что –
Мать Сары в три раза старше Сары и в четыре раза старше сестры Сары; Анна. Энн на три года моложе Сары.
Итак, следуя описанным выше шагам, мы сначала даем имя неизвестному значению, которым в данном случае является возраст Сары и Анны. Следовательно,
Пусть возраст Сары равен x лет
Дано, что Энн на три года моложе Сары.
Следовательно,
Возраст Анны = ( x – 3 ) лет
Кроме того, известно, что мать Сары в три раза старше Сары
Следовательно,
Возраст матери Сары = 3x лет……………… ………….
. (1)
Далее, мать Сары в четыре раза старше Анны
Следовательно,
Возраст матери Сары = 4 ( x – 3 ) года ……………………… (2 )
Из (1) и (2) имеем
3x = 4 ( x – 3 )
⇒ 3x = 4x – 12
⇒ 3x – 4x = -12
⇒ -x = -12
⇒ возраст Сары x = 12
лет, следовательно, x = 12
лет. .
Сейчас
Возраст Анны = (x – 3) лет
Следовательно, возраст Анны = 12 – 3 = 9 лет
Кроме того,
Возраст матери Сары = 3x лет
Возраст матери Сары =
3 х 12 = 36 лет. или более переменных называется уравнением.Следовательно, возраст Сары = 12 лет, возраст Анны = 9 лет и возраст матери Сары = 36 лет
Решенные примерыПример 1 Решение следующего уравнения: 2x + 7 = 19
Решение Мы дали, что
2x + 7 = 1
⇒ 2x = 1
. ⇒ 2x = 12
⇒ x = 6
Следовательно, x = 6 является решением уравнения 2x + 7 = 19
Пример 2 Решить уравнение x -1 7 и проверить результат 90
Раствор У нас есть x -3 = 5
Чтобы решить это уравнение, мы должны пройти проверку в левой части (L.
H.S). Чтобы получить x на LHS сам по себе, нам нужно сдвинуть -3. Это можно сделать, добавив три к обеим частям уравнения.
Имеем
х– 3 = 5
⇒ х – 3 + 3 = 5 + 3
⇒ х + 0 = 8
⇒ х = 8
Следовательно, уравнение x – 3 = 5
Теперь давайте проверим результат.
Подставив x = 8 в данное уравнение, мы получим
Л.С.С = x – 3 = 8 – 3 = 5
Имеем С.С.С = 5
Поскольку С.С.С = С.С.С, мы можем сказать, что наш ответ правильный.
Example 3 Solve 0.3x + 0.4 = 0.28x + 1.16
Solution We have
0.3x + 0.4 = 0.28x + 1.16
⇒ 0.3x – 0.28x = 1.16 – 0.4
⇒ ( 0,3 – 0,28 )x + 1,16 – 0,4
⇒ 0,02x = 0,76
⇒ x = $\frac{0,76}{0,02}$
⇒ x = 38
Следовательно, x = 38 является решением задачи 0,3x + 0,4 = 0,28x + 1,16
Ключевые факты и заключение о равенстве AУравнение, в котором наивысшая степень задействованных переменных равна 1, называется линейным уравнением. У нас есть различные линейные уравнения, основанные на количестве переменных. Мы можем добавить одно и то же число к обеим частям уравнения. Это означает, что если х + 5 = 7, то х + 5 + 2 = 7 + 2 Мы можем вычесть одно и то же число из обеих частей уравнения. Это означает, что если x + 5 = 7, то x + 5 – 2 = 7 – 2 Мы можем умножить обе части уравнения на одно и то же ненулевое число. Это означает, что если x + 5 = 4, то 6 ( x + 5 ) = 6 x 4 Мы можем разделить обе части уравнения на одно и то же ненулевое число. Это означает, что если 3x = 10, то $\frac{3x}{3} = \frac{10}{3}$ Решение уравнений с делением, Решение уравнений с умножением, Методом проб и ошибок и методом транспонирования некоторые из методов, с помощью которых мы можем решать простые линейные уравнения. Уравнения с одной переменной (на тему трудоустройства) Рабочие листы
Построение графиков линейных уравнений (на тему первых афроамериканцев) Рабочие листы по математике
Построение графиков и решение систем линейных уравнений с двумя переменными Рабочие листы по математике для 8-го классаПросмотреть все рабочие листы 90 17 We22 90 17 We22 90 потратить много времени на изучение и сбор информации на этом сайте.
Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Символы умножения и деления, выражения и отношения
Цель
Этот модуль развивает понимание умножения и деления, включая обратную связь между двумя операциями, а также когда и как их использовать в ситуациях решения задач. Учащиеся изучают правила представления операций умножения и деления в виде уравнений.
Цели достижения
NA3-6: Запишите и интерпретируйте аддитивные и простые мультипликативные стратегии, используя слова, диаграммы и символы, с пониманием равенства.
Разработка АО и другие учебные ресурсы
Конкретные результаты обучения
- Читать, писать и понимать символы умножения и деления, знак равенства и язык, связанный с этими символами.
- Напишите контекст рассказа для заданных уравнений умножения и деления.
- Знать, что операция умножения коммутативна.
- Определите связанные факты умножения и деления («семейства фактов»).
- Распознать обратную зависимость операций умножения и деления.
- Признать, что деление не является коммутативным.
- Правильно используйте слова «фактор» и «продукт»
- Определите факторы заданных сумм.
Описание математики
Эта последовательность уроков устанавливает связь между повторяющимся сложением и умножением. Он вводит деление и исследует взаимосвязь между операциями умножения и деления.
В рамках этих уроков развиваются три основных понимания.
- Учащиеся должны понимать отношения между величинами, представленными уравнениями умножения и деления. Например, 4 x 5 = 20 может представлять собой «четыре количества по пять равны 20» или «20 в четыре раза больше, чем 5».
- Учащиеся должны выучить словарный запас, связанный с умножением и делением, а также значение этих слов.
Важная лексика включает множители (числа умножаются), произведение (ответ на умножение), умножение на (умножение одной величины в х раз), равенство (одинаковость количества).
- Умножение также может быть представлено в пространстве. Массивы — это эффективный способ показать структуру и образец нескольких групп и, в данном случае, прочно связать умножение и деление с измерением.
При изучении структуры и модели умножения и деления основное внимание уделяется также развитию раннего понимания числовых свойств . На этих уроках формально исследуется коммутативное свойство умножения (то есть порядок, в котором умножаются числа, не меняет ответ). Распределительное свойство, при котором один или оба фактора разделяются для облегчения вычислений (например, 12 x 55 = 10 x 55 + 2 x 55), является основополагающим для стратегий расчета, включая письменные алгоритмы.
При изучении поведения операций умножения и деления важно, чтобы учащиеся делали обобщения, в которых они могли бы указать, «что всегда происходит», когда предпринимаются определенные действия.
Например, им следует признать, что, хотя правило «перестановки» (коммутативное) всегда верно для умножения, оно неверно для деления.
Эта серия уроков посвящена однозначным множителям и делителям. Он признает, что учащиеся должны иметь много возможностей представить умножение и деление. операции для решения текстовых задач. Это подкрепляется глубоким пониманием использования символов и выражений умножения и деления для математического мышления и выражения отношений. Учащиеся также должны уметь создавать контексты, которые может выражать уравнение. Установление связей между языком и символами необходимо для развития правильного понимания математических идей и концепций.
Возможности для адаптации и дифференциации
Возможности обучения в этом модуле можно дифференцировать, предоставляя или удаляя поддержку учащихся и изменяя требования к заданиям. Способы дифференциации включают:
- предоставление физических материалов, чтобы учащиеся могли предвидеть действия и обосновывать свои решения.
Использование таких материалов, как кубы, квадратные плитки и диаграммы массивов, для моделирования ситуаций и связывания стратегий, используемых учащимися, с представленными величинами.
- , соединяющие символы и математический словарь, особенно символы умножения и деления (x, ÷) и равенства (=). Явное моделирование правильного использования уравнений и алгоритмов и обсуждение значения символов в контексте.
- изменение сложности используемых чисел. Умножение на такие множители, как два, четыре, пять, десять, и деление на одни и те же делители, как правило, проще, чем на такие множители, как три, шесть, семь, восемь и девять. Подумайте, какие факты умножения ваши ученики будут уверенно применять при решении задач.
- побуждает учащихся сотрудничать в малых группах, делиться и обосновывать свои идеи.
- с использованием технологий, особенно калькуляторов, в прогнозирующих, основанных на шаблонах способах оценки произведений и частных, например. Если ответ на 4 x 8 = 32, будет ли ответ на 32 ÷ 5 больше или меньше 8? Откуда вы знаете? разрешить использование калькуляторов там, где вы хотите, чтобы учащиеся больше сосредоточились на процессе получения разумного ответа или на выявлении закономерностей, чем на отработке навыков вычисления.
Контекст, используемый для этого блока, — это стеганые одеяла, тиваевае и ткань тапа. Подумайте, как вы можете использовать знания сообщества в этом контексте. Есть ли члены сообщества, которых вы могли бы пригласить, чтобы поговорить о культурном происхождении тиваев или тапа? В этих контекстах важно обеспечить подлинность, актуальность и цель важных культурных знаний. Вы можете изменить контекст на ситуации, более соответствующие повседневной жизни, интересам или культурной самобытности ваших учащихся. Массивы распространены в разных культурах, и их можно найти в узорах плитки, текстиле, упаковке, стопках домов и игровых досках для игр. Поощряйте учащихся к творчеству, принимая различные стратегии от других и предлагая учащимся создавать свои собственные проблемы, которые должны решать другие, в значимом контексте.
Требуемые ресурсы Материалы
- Не менее двух прямоугольных стеганых одеял, тиваева или тапа
- Цветные пластиковые квадратные плитки (или маленькие квадратики из картона другого цвета)
- Бумага в клетку
- Калькуляторы
- Кубики Unifix
- Игральные карты
- PowerPoint 1
- PowerPoint 2
- Копи-мастер 1
- Копи-мастер 2
- Копи-мастер 3
Деятельность
Занятие 1
Занятие 1
- Покажите учащимся два разных прямоугольных лоскутных одеяла.
Это была бы хорошая возможность взглянуть на любую школьную ткань тапа или панели тукутуку. Кроме того, используйте PowerPoint 1, чтобы показать изображения подходящих стеганых одеял или ткани тапа. Например:
Разработайте контекст для обучения этому разделу. Это может включать изготовление одеяла или тапы (даже гипотетически) для детского отделения в местной больнице или хосписе. Подумайте, как вы можете использовать знания своих учеников и их сообщества. Могут ли взрослые принести tivaevae, siapo или сделанные ими одеяла или фотографии вещей?
Вовлеките учащихся в обсуждение лоскутных одеял, установив, как создаются узоры.- Спросите: «Какая математика содержится в этих стеганых одеялах?» (например, лоскутное одеяло 3 x 3)
Запишите идеи учащихся в карточке класса. (Это могут быть числа, геометрия, измерения: например, 3 + 3 + 3 = 9, 3 x 3 = 9, 9 квадратов, один большой квадрат, стороны одинаковой длины, 9 разделить на 3 и т. д.). Сравните количество квадратов в разных примерах.- Подсветка операции и отношения символов (или слов), которые были записаны. Например:
- Напишите каждый символ на отдельном листе бумаги формата А4. Попросите пары учащихся взять по одному листу (один символ), и каждый по очереди запишет в заданный период времени (например, за 2 минуты) , используя слова и картинки/диаграммы , и проведите мозговой штурм всего, что они знают об этом символе. (или слово). Попросите учащихся привести пример того, где можно использовать их символ.
- Попросите учащихся вернуться на коврик, рассаживаясь двумя отдельными группами: группа с операций символов (+ — x ÷) и группы с связями символов (<> =). Попросите выбранные пары учащихся объяснить, почему они сидят на своих местах и какие идеи они записали для своих символов.
В этом обсуждении подчеркните язык , используемый , разработайте понимание того, что такое числовая операция (математический процесс, который изменяет число или сумму), и повторите значение знака равно .
Сохраните листы мозгового штурма для дальнейшего использования.Мероприятие 2
- Подготовьте пакеты по 12, 18, 20, 24 и 30 пластиковых плиток, маленькие цветные квадратики из картона или квадратики из ткани. Сделайте их, карандаши и бумагу, доступными для пар учащихся.
Поставьте задачу. «Покажите, , используя диаграммы и уравнения , сколькими различными способами можно расположить эти лоскуты, чтобы сделать «мини-лоскутное одеяло»?»
Предложите учащимся поработать в парах, чтобы записать свои идеи.- Предложите учащимся поделиться своими идеями с парой, у которой было одинаковое количество плиток, и записать все варианты расположения, о которых они не подумали.
- Обменивайтесь идеями в классе, изучайте и записывайте основные понятия в классной таблице. Оставьте эту работу учащегося для занятия 2.
Например: из пакета с 18 «заплатками» (плитками).
В ходе обсуждения опирайтесь на идеи, которыми поделились в Упражнении 1 (см.выше), выделяя и записывая словами эти идеи:
- Аранжировки «патчей» могут быть записаны с использованием различных операций .
- Умножение с использованием 9Символ 0021 x может отображать ту же идею как многократное сложение (равных количеств), используя символ + .
- Символ для подразделения или деления на равные группы: ÷ . Он называется символом деления .
- Это расположение с одинаковыми строками и столбцами называется массивом .
- Поза и запись: «9+ 9 = 6 x 3. Вы согласны или не согласны». Попросите пары студентов обсудить это утверждение и обосновать свою позицию (объяснить, почему они согласны или не согласны и откуда они знают, что они правы).
Запишите обоснование ученика, выделив отношения эквивалентности (оба равны 18, всего 18 патчей в обоих массивах).Выделите мультипликативные представления, такие как «9 равно 3 x 3, поэтому 9 + 9 равно 6 x 3».
Упражнение 3
Напишите два уравнения в таблице классов, одно на умножение и одно на деление.
Например: 6 x 5 = 30 28 ÷ 4 = 7. Прочитайте их вместе. Пусть каждый учащийся нарисует схему стеганого одеяла или тапа, которая представляет уравнение. Попросите их написать словесное описание того, как стеганое одеяло/ткань представляет собой уравнение.Упражнение 4
Завершите сеанс просмотром символов операций и отношений и их значений.
Занятие 2
Занятие 1
- Начните с того, что по крайней мере два ученика поделятся своими схемами одеяла/ткани из предыдущего занятия. Попросите других учащихся записать уравнения, представленные на схеме. Подчеркните тот факт, что математику из реальной жизни можно представить с помощью диаграмм, слов и символов.
- Проведите мозговой штурм на диаграмме класса других ситуаций в нашей жизни, где мы видим и используем умножение или деление.
Когда учащиеся будут делиться идеями, попросите их назвать конкретные числа. Запишите эти истории, используя диаграммы и слова.
Например: Мы видим умножение, когда:
- 12 упаковок по 20 мармеладок завернуты вместе в большую упаковку для продажи на школьной ярмарке – четыре упаковки в ряд и три ряда.
- Школа покупает три набора хоккейных клюшек по десять штук в каждом.
- На мараэ мы сидим в четыре ряда по шесть человек.
- Прочитайте сказки еще раз вместе. Попросите учащихся использовать символы для записи уравнений для каждой из историй в своих книгах/на доске/бумаге. Те учащиеся, которые закончат быстро, могут придумать больше контекстных историй. Поощряйте учащихся создавать контекстные истории, отражающие их повседневную жизнь (в отличие от выбора «случайных» чисел).
Предложите парам учащихся поделиться своими уравнениями. Если учащиеся записали, используя многократное сложение, попросите их также записать уравнения умножения.Упражнение 2
- Просмотрите информацию о символах из сеанса 1, выделив символы операций, + — x ÷ , и символы взаимосвязи, равно (=), больше (>) и меньше (<) символы взаимосвязи.
Попросите учащихся поработать в парах, используя ситуации из предыдущего задания. Студенты должны обсудить ситуации и посмотреть, сколько уравнений или неравенств они могут написать. Например:
3 x 4 = 4 x 3
3 x 4 < 2 x 10
4 x 6 > 2 x 10 > 4 x 3
Они должны использовать диаграммы, чтобы показать, как они узнают, что они верны.- Предложите учащимся поделиться своей работой в парах. При этом они должны по очереди читать вслух то, что они написали.
Занятие 3
- Вернитесь к стеганым одеялам/тапа-тканям (изображения). Объясните, что некоторым маленьким детям нравятся лоскутные одеяла с алфавитом, в которых на каждой клеточке изображено что-то, начинающееся с другой буквы алфавита. Поговорите о том, что некоторые из них могут быть.
Например: A может изображать яблоко, B — бабочку, C — кошку и так далее.
- Предоставьте учащимся бумагу, карандаши и фломастеры.
Поставьте задачу: Вы собираетесь сделать лоскутное одеяло/тапа с алфавитом, чтобы подарить кому-нибудь. У вас есть время до конца сегодняшней сессии, чтобы спланировать свой дизайн и то, как вы будете располагать свои «квадратные лоскуты» . Где-то в проблеме может быть вызов. Вы решаете, как лучше решить эту проблему для вашего дизайна стеганого одеяла.
Сколько букв в алфавите? (26)
Почему изготовление одеяла из 26 квадратов может быть проблемой?- Пусть учащиеся поэкспериментируют с 26 квадратами. Они могут нарисовать возможные варианты использования квадратных плиток или кубов. Цифровые инструменты также можно использовать для упорядочивания плиток и представления работ учащихся.
(26 будет состоять только из массивов 1 x 26 или 2 x 13, что нежелательно для лоскутного одеяла такого типа.Учащиеся встретят «остаток» (6 x 4 + 2, 5 x 5 + 1) или найдут некоторые «заплатки» короткие (7 x 4). Примите реалистичные решения для контекста (например, лоскутное одеяло 5 x 5: поместите 2 буквы на одну заплатку, лоскутное одеяло 6 x 4: сделайте его 7 x 4 и включите 2 новых или пустых патчи.)
- Предложение: Если мы добавим патчи для каждой из цифр 0-9, сколько тогда будет патчей? (26 + 10 = 36)
Посмотрите, какие одеяла вы могли бы сделать тогда.
Попросите учащихся найти все возможные варианты:
1 x 36 2 x 18 3 x 12 4 x 9 6 x 6 Почему?Занятие 3
Занятие 1
- Предложите учащимся поделиться своими рисунками стеганых одеял с алфавитом для 36 нашивок. Обсудите «оставшуюся проблему» и оцените творческие решения.
Почему нельзя было сделать одеяло с пятью заплатками подряд?
Запишите 36 ÷5 = 7 r 1 и спросите учащихся, что означает r 1 (остаток от 1).
Укажите, что часто задачи на деление решаются неравномерно. Мы называем то, что осталось, , а остаток .- Представьте, что у нас есть 26 патчей, и мы пытаемся разместить по шесть патчей в каждом ряду. Один из способов записать эту задачу: 26 ÷ 6 = 4 r2.
- На диаграмме классов быстро нарисуйте массивы, которые были разработаны для 26 патчей.
- Обсудите «размеры» массива, вводя слова факторы и произведение . Модель с примером:
Попросите каждого учащегося записать под своим дизайном лоскутного одеяла то, что находится в рамке выше, регулируя числа для своего дизайна.Деятельность 2
Напишите на доске 4 36 9.
Вот еще три числа, которые связаны умножением и делением.
Запишите набор уравнений умножения и деления, используя эти числа.Предложите учащимся работать в парах, чтобы составить уравнения и создать массив, представляющий все четыре уравнения.
Студенты должны быть готовы обосновать свою позицию (объясняя, откуда они знают, что они правы).
4 x 9 = 36 9 x 4 = 36 36 ÷ 4 = 9 36 ÷ 9 = 4
Свяжите каждое уравнение с массивом 9 x 4, который учащиеся должны узнать из предыдущего задания по созданию лоскутного одеяла. Особое внимание обратите на деление. Например, 36 ÷ 4 = 9дает количество строк, созданных из 36 патчей (площадь), если каждый ряд состоит из четырех патчей.- Подведите итоги на классной таблице. Например:
- Есть четыре связанных факта только (семейство фактов) и не более.
4 х 7 = 28 7 х 4 = 28 28 ÷ 4 = 7 28 ÷ 7 = 4- Умножение — это операция «переворота». Вы можете изменить порядок факторов без изменения произведения. (Это как сложение.)
Мы говорим, что умножение (и сложение) равно коммутативный .
4 х 7 = 7 х 4 = 28- Деление не является коммутативным, т.е. 36 ÷ 4 = 9, но 4 ÷ 36 = 0,1111… (1/9). Частные деления не совпадают (ответ).

Мы говорим, что деление (и вычитание) не коммутативно .Задание 3
- Попросите учащихся сыграть в игру Умножение, рисование и запись в парах . Рассмотрите возможность объединения в пары учащихся с одинаковым уровнем знания таблицы умножения, что будет способствовать развитию туакана-тейна и уверенности учащихся в своих навыках.
Им нужны игральные карты (с номерами от 2 до 9), карандаш и бумага.
Победителем становится тот, у кого после десяти раундов окажется больше всего пар карточек с одинаковыми продуктами, но изготовленными с использованием разных факторов.
Например: 6 x 4 = 8 x 3 = 24, или 4 x 4 = 2 x 8 = 16
Как играть:
Карты перемешиваются и кладутся лицевой стороной вниз в стопку между обоими игроками.
Игроки по очереди переворачивают по три карты из стопки. Это факторы. Игрок возвращает одну карту в низ стопки.Игрок должен написать факт(ы) умножения для двух карт. Они также могут нарисовать массив и записать семейство фактов.
Например:- Учащиеся завершают занятие написанием словесных сценариев для своих наборов уравнений (семейство фактов). Вы можете выбрать работу со студентами, которым нужна дополнительная поддержка, в небольшой группе, в то время как другие студенты будут работать самостоятельно. В конечном счете, все учащиеся должны уметь писать словесные сценарии для наборов уравнений. Они могут быть написаны с использованием цифровых инструментов и могут быть смоделированы с использованием материалов (например, счетчиков). Это не обязательно должны быть сценарии квилтинга.
Например: «Было три мешка по пять яблок в каждом. Пятнадцать поделили на три мешка — это пять. Если эти пятнадцать яблок разложить по пяти мешкам, то в каждом окажется по три. Это будет пять лотов по три.Занятие 4
Упражнение 1
Покажите альтернативный набор стеганых одеял или ткани тапа (PowerPoint 2).
Например:
Попросите четырех учащихся записать по одному факту каждого из связанных фактов.
(6 х 5 = 30, 5 х 6 = 30, 30 ÷ 5 = 6, 30 ÷ 6 = 5) и объяснить каждый факт со ссылкой на лоскутное одеяло, включая демонстрацию коммутативного (оборотного) свойства умножения. =Поверните одеяло, чтобы продемонстрировать это.Занятие 2
- Раздайте учащимся соединяющие кубики (или цветные фишки). Пусть пары учеников возьмут по 48 кубиков. Спросите, какие множители могут составить 48. Запишите возможности, используя умножение; 1 х 48, 2 х 24, 3 х 16 и т. д.
- Попросите одного ученика из каждого ученика смоделировать пару 4 x 12, соединив кубики. Затем пусть его партнер использует те же кубики для моделирования 12 x 4. Обсудите, что получится. (Им нужно было перегруппировать их). Повторите с 6 x 8 и 8 x 6. Подчеркните, что коммутативное свойство включает те же множители и произведение, но требует другого взгляда на массив (т. е. либо строки, либо столбцы образуют одинаковые множества).
- Разложите на карточках факты умножения 48 (Переписчик 1). Задержать 5 раз? и 7 х? Соедините пары уравнений, демонстрирующих свойство коммутативности.
Думаете, это все факты умножения на произведение 48? (Вы можете расположить карты в порядке первого множителя.)
Почему нет 5-кратных и 7-кратных фактов? (Используйте карточки. Учащиеся должны понять, что 48 не входит в число кратных 5 и 7. 48 не делится на 5 и 7).
С помощью калькулятора покажите, что 48 ÷ 5 = 9,6 и 48 ÷ 7 = 6,857142857…
Как вы думаете, что показывает десятичная часть произведения? (Остаток, поэтому 48 не делится на 5 и 7)- Попросите учащихся изучить факты умножения с разным количеством кубиков, используя язык тех же множителей и произведений, сосредоточив внимание на перегруппировке. Их исследование может показать, что некоторые числа имеют только два делителя, например 17 и 31. Эти числа являются простыми.
Занятие 3
- Запишите одно знакомое уравнение умножения в таблицу класса.
Например, 6 x 2 = 12. Пусть один из учащихся в каждой паре смоделирует это, составив 6 групп по 2 и , соединив кубики вместе в одну линию из 12.
Запишите 12 ÷ 6 = 2. другой ученик в паре разыгрывает это с кубиками.
Предложите учащимся описать, что произошло, и запишите такие идеи, как: это наоборот, деление не умножение, это наоборот, мы вернулись к тому, с чего начали.
Спросите, Всегда ли так? Как мы можем узнать? Принимайте идеи учеников. Они должны включать студентов, изучающих больше примеров.Сделайте вывод, что невозможно проверить все факты умножения и деления. Скажем, идея «отмены» означает, что умножение и деление являются обратными операциями, как включение и выключение выключателя света. Уничтожение друг друга — это именно то, как ведут себя умножение и деление.
Написать « обратная связь» на диаграмме классов. Обсудите слова, похожие на инверсию, например.
перевернуть, отменить, вернуть, вернуть и их значение. Установите связь с обратной зависимостью между сложением и вычитанием. Подчеркните, что в каждой паре операций одна операция или действие отменяет другое.
Вернитесь к одеялу в Упражнении 1 (выше) и к записанным уравнениям:
(6 x 6 = 30, 5 x 6 = 30, 30 ÷ 5 = 6, 30 ÷ 6 = 5)
Попросите учащихся объяснить «отмену» (снова обратная связь со ссылкой на лоскутное одеяло. (Это немного сложнее увидеть, потому что этот массив физически нельзя «отменить». Однако вы можете составить ряды из шести кубиков и показать 5 x 6, расположив пять рядов по вертикали Сколько у меня лоскутов? Что произойдет, если я теперь разделю на пять? )Напишите в таблице класса:
Знание того, что умножение и деление являются обратными операциями, полезно, потому что……..
Попросите учащихся предложить причины и записать их, в том числе:
Мы можем использовать умножение, чтобы решить задачи на деление.
Мы можем проверить операции деления с помощью умножения. (Как?)Занятие 4
Раздайте Copymaster 2 для работы учащихся. Подчеркните обратные операции и необходимость для учащихся показать или объяснить , как умножение помогает решать задачи на деление.
Занятие 5
Занятие 1
Повторите основные выводы из Занятия 4. Предложите учащимся поработать в парах, чтобы поделиться своими решениями задач квилтинга из Занятия 4, Занятие 4. Предложите им задавать друг другу вопросы.
Упражнение 2
- Покажите несколько примеров лоскутного одеяла или ткани тапа с помощью PowerPoint 1:
- Напишите в таблице классов:
Одно одеяло из шестнадцати заплаток:
Одно одеяло из тридцати заплаток:
Одно лоскутное одеяло из сорока пяти заплаток:
Если бы я переставил заплатки в один ряд, как бы выглядело лоскутное одеяло? (Больше похоже на длинный шарф)- Попросите учащихся записать уравнения умножения для каждого из этих утверждений.

Одно одеяло из шестнадцати заплат: 1 x 16 = 16
Одно одеяло из девяти заплат: 1 x 30 = 30
Одно одеяло из тридцати заплат: 1 x 45 = 45
Если ваши уравнения верны, каковы ответы на 16 ÷ 1 = ☐ , 30 ÷ 1 = ☐ , 45 ÷ 1 = ☐?- Попросите учащихся обсудить свои идеи, а затем объяснить и обосновать свое мнение. Связывают ли они деление с вопросом «Сколько столбцов одного патча составляет в общей сложности 16, 30 или 45 патчей?»
Если ваши уравнения верны, каковы ответы на 16 ÷ 16 = ☐ , 30 ÷ 30 = ☐ , 45 ÷ 45 = ☐?
Связывают ли они деление с вопросом «Сколько рядов по 16 нашивок дает в общей сложности 16 накладок и т. д.?»- Приведите другие примеры деления числа на единицу и само на себя. Для проверки ответов можно использовать калькуляторы.
Занятие 3
Предложите учащимся работать в группах от 2 до 4 над Это правда? (Переписчик 3 (Цель: различать правильные и неправильные уравнения и выражения умножения и деления и уметь объяснить, почему, обосновывая свое решение)
Учащиеся по очереди выбирают утверждение и объясняют его другим в группе, если и почему утверждение является фактом, или если и почему оно неверно (истинно или ложно)
Попросите учащихся создать свои собственные факты или нефакты, связанные с умножением и делением, например.
8 x 9 = 72, поэтому 72 ÷ 18 = 4. Обменяйтесь фактами и не фактами между учащимися.
Занятие 4
Завершите это занятие обзором знаний, полученных за пять занятий.
Домашняя ссылка
Уважаемые родители и whānau,
В алгебре на этой неделе мы изучали числовые операции умножения и деления и взаимосвязь между ними.
Один из способов, с помощью которого учащиеся закрепят изученное, состоит в том, чтобы прочитать верные и ложные утверждения, а также определить и объяснить, какие из них неверны и почему.
Вашему ребенку может понравиться играть в » I s это факт?» игра с тобой. По очереди очень важно, чтобы каждый человек объяснил, почему утверждение верно или нет.
Мы надеемся, что вам понравится эта задача.
Спасибо.
Попробуйте эти примеры:
1 x 25 = 25, поэтому 25 ÷ 25 = 1 Верно или неверно
28 ÷ 4 = 7, поэтому 4 ÷ 28 = 7 Верно или неверно
Вложения
Добавить в план
Третий уровень
Решение уравнений умножения и деления
Семейства четырех фактов
Введение семейств фактов умножения и деления.
В каждой семье всегда есть четыре факта, если только факторы не совпадают, например ; в этом случае в семье есть только два факта. Используйте следующие примеры, чтобы познакомить учащихся с семьями из четырех фактов.
«Тая знает, что . Иеремия говорит, что если Тая знает этот факт, она также может знать три других факта, принадлежащих к тому же семейству фактов. Действительно ли у фактов есть семьи? Что такое настоящая семья?»
Студенты, скорее всего, узнают связанный факт умножения. Не забудьте записать все соответствующие факты на доске. Если учащиеся не могут изложить соответствующие факты деления, напишите на доске
24 ÷ ___ = ___. Спросите учащихся, могут ли они использовать эту подсказку, чтобы написать соответствующие факты деления. Подскажите их по мере необходимости. Убедитесь, что семья из четырех фактов написана на доске, когда вы закончите.Представьте следующий визуальный элемент «семейство фактов»:
«Использование треугольника, подобного этому, для организации ваших семейств фактов может быть хорошим визуальным представлением».

Проработайте хотя бы еще один пример со студентами. «Тая тоже знает . Какие еще факты из семьи этого факта может знать Тая?» Студенты, скорее всего, смогут изложить другие факты, так как это второй пример. Тем не менее, напишите первое число и операцию на доске, если это необходимо, чтобы подсказать учащимся. Например, напишите 7 × ___ = ___, если учащиеся не могут определить конкретный факт в семье. Обязательно покажите треугольник и напишите на доске каждый факт из группы из четырех фактов.
Теперь помогите учащимся изучить семейства из четырех фактов и найти закономерности. «Сколько фактов в каждой семье?» ( 4 ) «Поскольку в каждой семье по 4 факта, их называют четырехфактными семьями. Посмотрите на семейства из четырех фактов из обоих примеров. Что вы заметили в этих семьях из четырех фактов?» Учащиеся могут высказать много наблюдений.
Цель состоит в том, чтобы они заметили, что в каждой семье есть два факта умножения и два факта деления.
Раздайте и ознакомьте с рабочим листом «Семейства из четырех фактов» (M-3-5-2_Семейства из четырех фактов и KEY.docx). «Обратите внимание на обложку рабочего листа: перечислены семейства из четырех фактов, но многие числа отсутствуют. Обязательно заполните пробелы в каждом семействе из четырех фактов. На обратной стороне листа приводится один факт. Пожалуйста, напишите остальные три факта в каждом семействе из четырех фактов».
Пока учащиеся работают, следите за их прогрессом. Помогите учащимся понять, что в каждой семье есть два факта умножения и два факта деления. Обратитесь к обсуждению (с использованием цветных плиток) коммутативного свойства умножения. Это должно помочь учащимся понять, почему в каждой семье есть два факта умножения. Кроме того, используйте обсуждение умножения и деления из Урока 1, чтобы помочь учащимся запомнить, что при умножении общее количество объектов находится во многих равных группах, тогда как деление используется для деления общего числа на множество равных групп.
По этой причине произведением или ответом задачи на умножение является делимое или первое число в задачах на деление.
Когда учащиеся закончат работу, попросите отдельных учащихся написать на доске названия семейств фактов с последней страницы. Опять же, помогите учащимся проверить, что в каждом семействе есть две задачи на умножение и две задачи на деление и что во всех четырех фактах используются одни и те же три числа.
Решение уравнений умножения и деления
Раздайте и покажите Wipe Out! рабочий лист (M-3-5-2_Wipe Out! и KEY.docx) для изучения учащимися. «Что вы заметили в этих проблемах?» ( В каждом числовом предложении или уравнении пропущено число .)
Спросите учащихся, «С человеком, сидящим рядом с вами, попытайтесь определить, какое число отсутствует в первом числовом предложении, . Обсудите, какие стратегии вы использовали, чтобы найти пропущенное число». Дайте учащимся время обсудить это.
Попросите добровольцев поделиться своими идеями. Если учащиеся не обсуждают деление как возможную стратегию решения, объясните, что деление () можно использовать для нахождения пропущенного числа.
Помогите учащимся понять, как записать свой ответ как значение , написав = 3 во втором столбце. Кроме того, помогите учащимся понять, как проверить свой ответ. В третьем столбце запишите числовое предложение или уравнение, заменяющее значение , в результате чего получится 3 × 8, и вычислите, чтобы убедиться, что 3 × 8 = 24.
Теперь спросите учащихся: определить, какое число отсутствует во втором числовом предложении, . Обсудите, какие стратегии вы использовали, чтобы найти пропущенное число». Опять же, дайте студентам время обсудить это. Попросите добровольцев поделиться своими идеями. Если учащиеся не обсуждают умножение как возможную стратегию решения, объясните, что умножение (5 × 6) можно использовать для нахождения пропущенного числа. Напишите на доске как 5 × 6 = 30, так и 30 ÷ 6 = 5.
Помогите учащимся понять связь между этим заданием и заданием, посвященным семьям из четырех фактов. Объясните учащимся, что если в задаче на деление пропущено число, как в этом примере, для определения пропущенного числа можно использовать соответствующий факт умножения.
Убедитесь, что учащиеся записали свой ответ, написав = 30 во втором столбце. Кроме того, помогите учащимся проверить свой ответ, написав 30 ÷ 6 = 5 в третьем столбце, а затем убедитесь, что это правда.
Попросите учащихся продолжить работу в парах, чтобы выполнить задание Wipe Out! Практический рабочий лист.
Введение переменных
«В стирании! Проблемы, в числовом предложении или уравнении отсутствовало число. Было похоже, что кто-то нацарапал число маркером». Напишите на доске один пример: . «Вместо пустого поля математики используют переменные для представления пропущенных чисел в числовых предложениях или уравнениях. Переменная — это буква или символ, который используется для представления отсутствующего числа.
В качестве переменной можно использовать любую букву или символ». Попросите ученика назвать вам его/ее любимую букву алфавита. Перепишите уравнение, используя эту букву в качестве переменной, например: (Попробуйте перейти от языка числового предложения к уравнение. Объясните, что, поскольку эти утверждения включают переменные, а не строго числа, их чаще называют уравнениями. Помогите учащимся, подчеркнув «равно» в уравнении. Уравнения — это утверждения, в которых равны знаков, и обе части уравнения равны по значению.)
Попросите еще как минимум двух учащихся назвать свои любимые буквы алфавита. Перепишите уравнение, используя эти буквы. Попросите учащихся определить значение пропущенного числа. Помогите учащимся понять, что значение пропущенного числа равно 48, независимо от того, используется ли буква в качестве переменной. Помогите учащимся проверить, действительно ли число 48 соответствует уравнению.
Приведите еще два примера.
Напишите и на доске. Попросите учащихся переписать оба уравнения, используя переменные, и найти значения переменных. Не забудьте напомнить учащимся проверить свои ответы. После того, как учащиеся закончат работу, попросите двух добровольцев написать уравнения и решения на доске.
Раздайте копии рабочего листа «Решение уравнений» (M-3-5-2_Решение уравнений и KEY.docx). Студенты должны выполнить это индивидуально. Следите за успеваемостью учащихся.
Если учащиеся затрудняются, помогите им подумать о связанных операциях умножения и деления и полагаться на семейства из четырех фактов. Например, чтобы решить, помогите учащимся вместо того, чтобы думать, поскольку учащиеся лучше запоминают факты умножения, чем факты деления.
Используйте предложения в этом разделе, чтобы адаптировать урок к потребностям учащихся. В разделе «Рутина» представлены предложения по пересмотру концепций урока в течение учебного года. Секция малых групп предназначена для студентов, которым может быть полезна дополнительная практика.
Раздел «Расширение» включает в себя возможности для учащихся, готовых выйти за рамки требований стандарта.
- Подпрограмма: Чтобы помочь учащимся повторить эту концепцию, используйте игру «Соответствие» (M-3-5-2_Игра «Соответствие».docx). Match Game включает в себя уравнения и решения, напечатанные на отдельных карточках. В игру можно играть двумя способами.
- Учащиеся должны перетасовать карточки и положить их на стол лицевой стороной вниз. Учащиеся по очереди переворачивают две карточки. Если карточки соответствуют совпадению, уравнению и его решению, учащийся сохраняет эти карточки и делает еще один ход. Если карты не совпадают, ход переходит к следующему ученику.
- Студенты тянут по 5 карточек. Учащиеся по очереди спрашивают одного из других игроков о соответствующей карточке, например: «Игрок 2, есть ли у вас уравнение, которое имеет решение n = 8?» Или они могут спросить: «У вас есть ответ на 4 × n = 32?» Если у Игрока 2 есть эта карта, он отдает ее запрашивавшему игроку.
Если у Игрока 2 нет этой карты, другой игрок берет карту из стопки, а затем ход переходит к следующему игроку.
- Малая группа: Студенты, которым нужна дополнительная практика, могут быть объединены в небольшие группы для работы над семействами из четырех фактов и использования их для решения уравнений умножения и деления.
Распечатайте семейные карточки фактов с этого сайта: http://www.mathcats.com/explore/factfamilies/multinfo.html
Скройте одну цифру на каждой семейной карточке фактов. Попросите учащихся определить пропущенное число. Раскройте номер, чтобы помочь им определить, верны ли они. Время от времени останавливайтесь на определенной карточке и просите их написать все четыре факта в семействе фактов. Когда учащимся покажется, что они достаточно успешно определили пропущенное число, напишите уравнение для конкретной карточки. Попросите их решить уравнение. Помогите им понять, что определение пропущенного числа действительно решает уравнение.
Например, если 3 и 15 показаны, а 5 скрыто, напишите уравнение 15 ÷ n = 3 или n × 3 = 15. Используя карточки, напишите уравнения умножения и деления, чтобы учащиеся могли попрактиковаться в решении обоих. В конце концов, вы можете попросить учащихся написать уравнения и решить их.
- Расширение: Учащиеся, готовые к более сложной задаче, могут писать свои собственные задачи из реальной жизни. Учащиеся должны работать в парах. Каждый учащийся составляет уравнение умножения или деления, используя переменную. Затем учащиеся в каждой паре обмениваются уравнениями. Каждый учащийся создает реальную задачу для уравнения и решает задачу со словами. Затем учащиеся обмениваются своими словесными задачами со своим партнером, чтобы проверить точность и немедленно дать обратную связь.
3.2 Решение уравнений с использованием свойств деления и умножения равенства – промежуточная алгебра II
К концу этого раздела вы сможете:
- Решать уравнения, используя свойства деления и умножения равенства
- Решите уравнения, которые необходимо упростить
Вы могли заметить, что все уравнения, которые мы до сих пор решали, имели вид или .
Мы смогли изолировать переменную, добавив или вычтя постоянный член на стороне уравнения с переменной. Теперь мы увидим, как решать уравнения, в которых переменная умножается на константу, и поэтому потребуется деление, чтобы изолировать переменную.
Давайте снова посмотрим на нашу головоломку с конвертами и фишками (рис. 1).
Рисунок .1На иллюстрации два одинаковых конверта, содержащих одинаковое количество жетонов. Помните, что левая сторона рабочего пространства должна равняться правой стороне, но счетчики с левой стороны «спрятаны» в конвертах. Итак, сколько фишек в каждом конверте?
Как определить номер? Мы должны разделить жетоны с правой стороны на две группы одинакового размера, чтобы они соответствовали двум конвертам с левой стороны. 6 счетчиков, разделенных на 2 равные группы, дают по 3 счетчика в каждой группе (начиная с ).
Какое уравнение моделирует ситуацию, показанную на (рис. 2)? Есть два конверта, и каждый содержит жетоны. Вместе два конверта должны содержать в общей сложности 6 жетонов.
Рисунок .2
Если мы разделим обе части уравнения на 2, как мы сделали с конвертами и счетчиками, получаем: Мы обнаружили, что каждый конверт содержит 3 фишки. Это проверяет? Мы знаем, так это работает! Три жетона в каждом из двух конвертов равняются шести!
Этот пример ведет к свойству разделения на равенство.
Деление Свойство равенства: Для всех действительных чисел , и , если , то .
Свойство равенства умножения: Для всех действительных чисел , если , то .
Когда вы делите или умножаете обе части уравнения на одну и ту же величину, вы все равно получаете равенство.
Давайте рассмотрим, как эти свойства равенства могут быть применены для решения уравнений. Помните, что цель состоит в том, чтобы «отменить» операцию над переменной. В приведенном ниже примере переменная умножается на , поэтому мы разделим обе части на, чтобы «отменить» умножение.
Решить: .
Решение
Мы используем свойство равенства деления, чтобы разделить обе части на .
Let x equal negative seven.” and shows 4x equals negative 28. The next line shows four times negative seven may be equal to negative twenty-eight. The last line shows that negative twenty-eight equals negative twenty-eight with a check mark.» data-label=»»>
Разделите обе части на 4, чтобы отменить умножение. Упрощение. Проверьте свой ответ. Позволять . Поскольку это верное утверждение, это решение .
Решить: .
Показать ответy = −16
Решить: .
Показать ответz = −13
В предыдущем примере, чтобы «отменить» умножение, мы разделили. Как вы думаете, как мы «отменяем» разделение?
Решить: .
Решение
Здесь делится на . Мы можем умножить обе части на , чтобы изолировать .
Умножьте обе части на . Упрощение. Проверьте свой ответ. Позволять . Решить: .
Показать ответb = 144
Решить: .
Показать ответc = 128
Решить: .
Решение
Помните эквивалентно .
Переписать как . Разделите обе части на . Чек. Заменитель Упрощение. Мы видим, что есть еще два способа решения.
Мы могли бы умножить обе части на .
Мы могли бы принять противоположное обе стороны.
Решить: .
Показать ответk = −8
Решить: .
Показать ответг = −3
Решить: .
Решение
Поскольку произведение числа и его обратного числа равно , наша стратегия будет состоять в том, чтобы изолировать путем умножения на обратное число .
The next line says “Check your answer. Let x equal 27 and shows two-thirds x equals 18. The next line shows two-thirds times 27 may equal 18. The last line shows that 18 equals 18 with a check mark.» data-label=»»>
Умножьте на обратную величину . Обратные числа умножаются на единицу. Умножить. Проверьте свой ответ. Пусть Обратите внимание, что мы могли разделить обе части уравнения на изолировать . Хотя это сработает, умножение на обратное требует меньше шагов.
Решить: .
Показать ответn = 35
Решить: .
Показать ответy = 18
Многие уравнения начинаются сложнее, чем те, которые мы только что решили. Во-первых, нам нужно максимально упростить обе части уравнения
Решить: .
Решение
Начните с объединения одинаковых терминов, чтобы упростить каждую сторону.
Объедините похожие термины. Разделите обе стороны на 12, чтобы выделить x. Упрощение. Проверьте свой ответ. Пусть
Решить: .
Показать ответx = 2
Решить: .
Показать ответn = −5
Решить: .
Решение
Упростите каждую сторону, объединив одинаковые термины.
» data-label=»»>
Упростите каждую сторону. Разделите обе стороны на 3, чтобы выделить у. Упрощение. Проверьте свой ответ. Пусть Обратите внимание, что переменная оказалась справа от знака равенства, когда мы решили уравнение. Вы можете сделать еще один шаг, чтобы записать решение с переменной слева от знака равенства.
Решить: .
Показать ответc = −3
Решить: .
Показать ответРешить: .
Решение
Помните — всегда сначала упрощайте каждую сторону.
The next line says “Simplify” and shows negative 3n equals 21. The next line says “Divide both sides by negative 3 to isolate n” and shows negative 3n over a red negative 3 equals 21 over a red negative 3. The next line says “Divide” and shows n equals negative 7. The next line says “Check your answer. Let n equal negative 7.” and shows negative 3 times parentheses n minus 2 minus 6 equals 21. The next line shows negative 3 times parentheses negative 7 minus 2 minus 6 may equal 21. The next line shows negative 3 times negative 9 minus 6 may equal 21. The next line shows 27 minus 6 may equal 21. The last line shows 21 equals 21 with a check mark.» data-label=»»>
Распределить. Упрощение. Разделите обе части на -3, чтобы изолировать n. Проверьте свой ответ. Позволять . Решить: .
Показать ответn = −6
Решить: .
Показать ответn = −5
- Свойства равенства деления и умножения
- Свойство равенства деления: Для всех действительных чисел a, b, c, и , если , то .
- Свойство равенства умножения: Для всех действительных чисел а, б, в, если , то .
Решите уравнения, используя свойства деления и умножения равенства
В следующих упражнениях решите каждое уравнение для переменной, используя свойство равенства деления, и проверьте решение.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. В следующих упражнениях решите каждое уравнение для переменной, используя свойство равенства умножения, и проверьте решение.
13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. Решение уравнений, которые необходимо упростить
В следующих упражнениях решите уравнение.
27. 28. 29. 30. 31. 32. 33. 34. 35. 36. Математика на каждый день
37. Преподавание В детском саду Конни есть дети. Она хочет, чтобы они попали в равные группы. Найдите количество детей в каждой группе, решив уравнение .
38. Воздушные шары Рамона купила воздушные шары для вечеринки. Она хочет сделать равные пучки. Найдите количество шариков в каждой связке, решив уравнение. 39. Цена за единицу Нишант заплатил за упаковку бутылок сока. Найдите цену каждой бутылки , решив уравнение . 40. Стоимость билетов Дарья оплатила детские билеты на каток. Найдите цену каждого билета , решив уравнение . 41. Ткань Строительная бригада использовала ярды ткани для изготовления флагов для одной трети участников. Найдите, сколько ткани , им потребуется, чтобы сделать флаги для всей команды, решив уравнение . 42. Экономия топлива Внедорожник Тани расходует вдвое меньше миль на галлон (миль на галлон), чем гибридный автомобиль ее мужа. Внедорожник получает. Найдите количество миль на галлон гибридного автомобиля, решив уравнение .
Письменные упражнения
43. Эмилиано считает, что это решение уравнения . Объясните, почему он не прав. 44. Фрида начала решать уравнение, складывая обе части. Объясните, почему метод Фриды дает правильное решение.
1. 9 3. 3 5. −6 7. 7 9. 15 11. 0 13. 28 15. 36 17. −48 19. 80 21. 25 23. −32 25. 5/2 27. у = -1 29. м = −5 31. 33. q = 24 35. р = 56 37. 6 детей 39. 1,08 $ 41. 42 ярда 43. Ответ будет другим. Эта глава была адаптирована из «Решение уравнений с использованием свойств деления и умножения равенства» в Preалгебра (OpenStax) Линн Маречек, МэриЭнн Энтони-Смит и Андреа Ханикатт Матис, которая находится под лицензией CC BY 4.






 Раствор по равным — Q =
Раствор по равным — Q =
 0017
0017 Теперь давайте посмотрим, как решать линейные уравнения с одной переменной.
Теперь давайте посмотрим, как решать линейные уравнения с одной переменной. Это означает, что если х + 5 = 4, то 6 ( х + 5 ) = 6 х 4
Это означает, что если х + 5 = 4, то 6 ( х + 5 ) = 6 х 4 )
) 

 SH.S
SH.S  H.S = R.H.S
H.S = R.H.S
 д.
д. 
 . (1)
. (1) H.S). Чтобы получить x на LHS сам по себе, нам нужно сдвинуть -3. Это можно сделать, добавив три к обеим частям уравнения.
H.S). Чтобы получить x на LHS сам по себе, нам нужно сдвинуть -3. Это можно сделать, добавив три к обеим частям уравнения.
 Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
 Важная лексика включает множители (числа умножаются), произведение (ответ на умножение), умножение на (умножение одной величины в х раз), равенство (одинаковость количества).
Важная лексика включает множители (числа умножаются), произведение (ответ на умножение), умножение на (умножение одной величины в х раз), равенство (одинаковость количества).  Например, им следует признать, что, хотя правило «перестановки» (коммутативное) всегда верно для умножения, оно неверно для деления.
Например, им следует признать, что, хотя правило «перестановки» (коммутативное) всегда верно для умножения, оно неверно для деления. Использование таких материалов, как кубы, квадратные плитки и диаграммы массивов, для моделирования ситуаций и связывания стратегий, используемых учащимися, с представленными величинами.
Использование таких материалов, как кубы, квадратные плитки и диаграммы массивов, для моделирования ситуаций и связывания стратегий, используемых учащимися, с представленными величинами.
 Это была бы хорошая возможность взглянуть на любую школьную ткань тапа или панели тукутуку. Кроме того, используйте PowerPoint 1, чтобы показать изображения подходящих стеганых одеял или ткани тапа. Например:
Это была бы хорошая возможность взглянуть на любую школьную ткань тапа или панели тукутуку. Кроме того, используйте PowerPoint 1, чтобы показать изображения подходящих стеганых одеял или ткани тапа. Например: 

 выше), выделяя и записывая словами эти идеи:
выше), выделяя и записывая словами эти идеи: Выделите мультипликативные представления, такие как «9 равно 3 x 3, поэтому 9 + 9 равно 6 x 3».
Выделите мультипликативные представления, такие как «9 равно 3 x 3, поэтому 9 + 9 равно 6 x 3». Когда учащиеся будут делиться идеями, попросите их назвать конкретные числа. Запишите эти истории, используя диаграммы и слова.
Когда учащиеся будут делиться идеями, попросите их назвать конкретные числа. Запишите эти истории, используя диаграммы и слова. 
 Например: A может изображать яблоко, B — бабочку, C — кошку и так далее.
Например: A может изображать яблоко, B — бабочку, C — кошку и так далее. 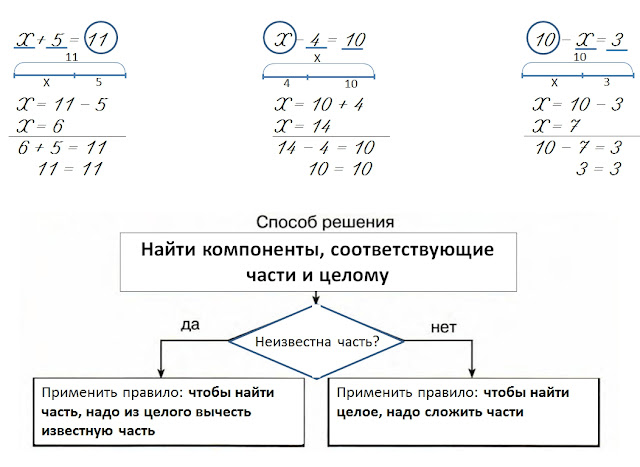 Учащиеся встретят «остаток» (6 x 4 + 2, 5 x 5 + 1) или найдут некоторые «заплатки» короткие (7 x 4). Примите реалистичные решения для контекста (например, лоскутное одеяло 5 x 5: поместите 2 буквы на одну заплатку, лоскутное одеяло 6 x 4: сделайте его 7 x 4 и включите 2 новых или пустых патчи.)
Учащиеся встретят «остаток» (6 x 4 + 2, 5 x 5 + 1) или найдут некоторые «заплатки» короткие (7 x 4). Примите реалистичные решения для контекста (например, лоскутное одеяло 5 x 5: поместите 2 буквы на одну заплатку, лоскутное одеяло 6 x 4: сделайте его 7 x 4 и включите 2 новых или пустых патчи.)
 Студенты должны быть готовы обосновать свою позицию (объясняя, откуда они знают, что они правы).
Студенты должны быть готовы обосновать свою позицию (объясняя, откуда они знают, что они правы). 
 Игрок должен написать факт(ы) умножения для двух карт. Они также могут нарисовать массив и записать семейство фактов.
Игрок должен написать факт(ы) умножения для двух карт. Они также могут нарисовать массив и записать семейство фактов.  Например:
Например: 
 Например, 6 x 2 = 12. Пусть один из учащихся в каждой паре смоделирует это, составив 6 групп по 2 и , соединив кубики вместе в одну линию из 12.
Например, 6 x 2 = 12. Пусть один из учащихся в каждой паре смоделирует это, составив 6 групп по 2 и , соединив кубики вместе в одну линию из 12.  перевернуть, отменить, вернуть, вернуть и их значение. Установите связь с обратной зависимостью между сложением и вычитанием. Подчеркните, что в каждой паре операций одна операция или действие отменяет другое.
перевернуть, отменить, вернуть, вернуть и их значение. Установите связь с обратной зависимостью между сложением и вычитанием. Подчеркните, что в каждой паре операций одна операция или действие отменяет другое.
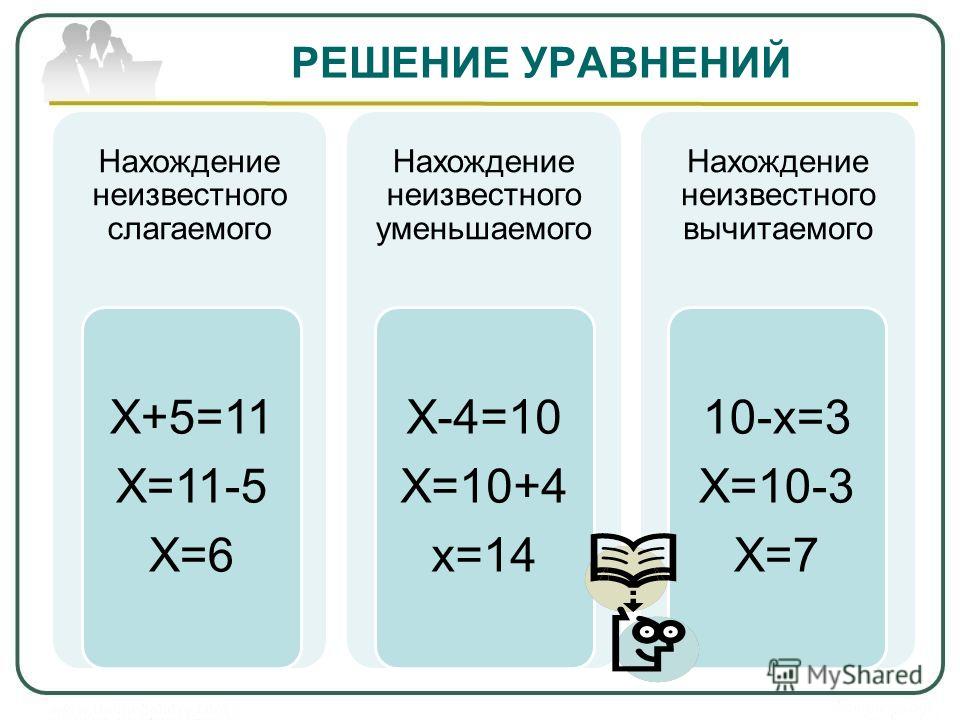
 8 x 9 = 72, поэтому 72 ÷ 18 = 4. Обменяйтесь фактами и не фактами между учащимися.
8 x 9 = 72, поэтому 72 ÷ 18 = 4. Обменяйтесь фактами и не фактами между учащимися. В каждой семье всегда есть четыре факта, если только факторы не совпадают, например ; в этом случае в семье есть только два факта. Используйте следующие примеры, чтобы познакомить учащихся с семьями из четырех фактов.
В каждой семье всегда есть четыре факта, если только факторы не совпадают, например ; в этом случае в семье есть только два факта. Используйте следующие примеры, чтобы познакомить учащихся с семьями из четырех фактов.
 Цель состоит в том, чтобы они заметили, что в каждой семье есть два факта умножения и два факта деления.
Цель состоит в том, чтобы они заметили, что в каждой семье есть два факта умножения и два факта деления. По этой причине произведением или ответом задачи на умножение является делимое или первое число в задачах на деление.
По этой причине произведением или ответом задачи на умножение является делимое или первое число в задачах на деление. Попросите добровольцев поделиться своими идеями. Если учащиеся не обсуждают деление как возможную стратегию решения, объясните, что деление () можно использовать для нахождения пропущенного числа.
Попросите добровольцев поделиться своими идеями. Если учащиеся не обсуждают деление как возможную стратегию решения, объясните, что деление () можно использовать для нахождения пропущенного числа. Помогите учащимся понять связь между этим заданием и заданием, посвященным семьям из четырех фактов. Объясните учащимся, что если в задаче на деление пропущено число, как в этом примере, для определения пропущенного числа можно использовать соответствующий факт умножения.
Помогите учащимся понять связь между этим заданием и заданием, посвященным семьям из четырех фактов. Объясните учащимся, что если в задаче на деление пропущено число, как в этом примере, для определения пропущенного числа можно использовать соответствующий факт умножения.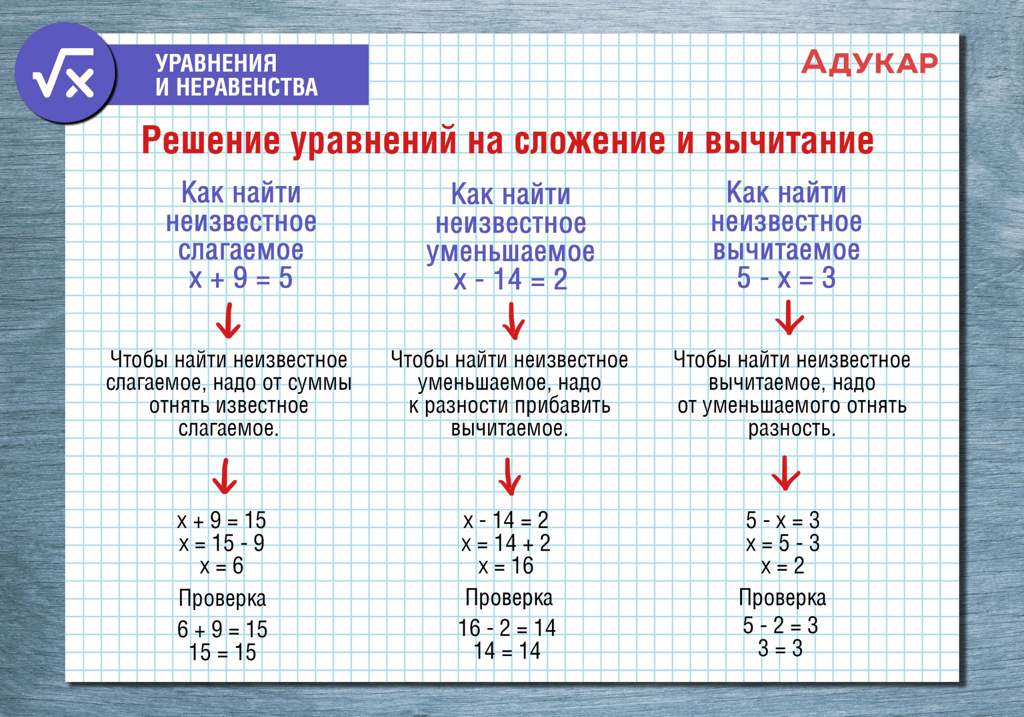 В качестве переменной можно использовать любую букву или символ». Попросите ученика назвать вам его/ее любимую букву алфавита. Перепишите уравнение, используя эту букву в качестве переменной, например: (Попробуйте перейти от языка числового предложения к уравнение. Объясните, что, поскольку эти утверждения включают переменные, а не строго числа, их чаще называют уравнениями. Помогите учащимся, подчеркнув «равно» в уравнении. Уравнения — это утверждения, в которых равны знаков, и обе части уравнения равны по значению.)
В качестве переменной можно использовать любую букву или символ». Попросите ученика назвать вам его/ее любимую букву алфавита. Перепишите уравнение, используя эту букву в качестве переменной, например: (Попробуйте перейти от языка числового предложения к уравнение. Объясните, что, поскольку эти утверждения включают переменные, а не строго числа, их чаще называют уравнениями. Помогите учащимся, подчеркнув «равно» в уравнении. Уравнения — это утверждения, в которых равны знаков, и обе части уравнения равны по значению.) Напишите и на доске. Попросите учащихся переписать оба уравнения, используя переменные, и найти значения переменных. Не забудьте напомнить учащимся проверить свои ответы. После того, как учащиеся закончат работу, попросите двух добровольцев написать уравнения и решения на доске.
Напишите и на доске. Попросите учащихся переписать оба уравнения, используя переменные, и найти значения переменных. Не забудьте напомнить учащимся проверить свои ответы. После того, как учащиеся закончат работу, попросите двух добровольцев написать уравнения и решения на доске. Раздел «Расширение» включает в себя возможности для учащихся, готовых выйти за рамки требований стандарта.
Раздел «Расширение» включает в себя возможности для учащихся, готовых выйти за рамки требований стандарта. Если у Игрока 2 нет этой карты, другой игрок берет карту из стопки, а затем ход переходит к следующему игроку.
Если у Игрока 2 нет этой карты, другой игрок берет карту из стопки, а затем ход переходит к следующему игроку. Например, если 3 и 15 показаны, а 5 скрыто, напишите уравнение 15 ÷ n = 3 или n × 3 = 15. Используя карточки, напишите уравнения умножения и деления, чтобы учащиеся могли попрактиковаться в решении обоих. В конце концов, вы можете попросить учащихся написать уравнения и решить их.
Например, если 3 и 15 показаны, а 5 скрыто, напишите уравнение 15 ÷ n = 3 или n × 3 = 15. Используя карточки, напишите уравнения умножения и деления, чтобы учащиеся могли попрактиковаться в решении обоих. В конце концов, вы можете попросить учащихся написать уравнения и решить их. Мы смогли изолировать переменную, добавив или вычтя постоянный член на стороне уравнения с переменной. Теперь мы увидим, как решать уравнения, в которых переменная умножается на константу, и поэтому потребуется деление, чтобы изолировать переменную.
Мы смогли изолировать переменную, добавив или вычтя постоянный член на стороне уравнения с переменной. Теперь мы увидим, как решать уравнения, в которых переменная умножается на константу, и поэтому потребуется деление, чтобы изолировать переменную.





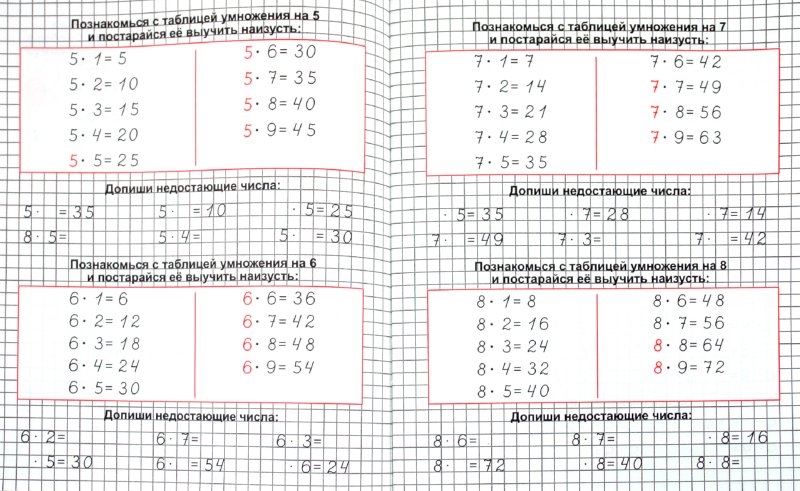 Пусть
Пусть

 Она хочет, чтобы они попали в равные группы. Найдите количество детей в каждой группе, решив уравнение .
Она хочет, чтобы они попали в равные группы. Найдите количество детей в каждой группе, решив уравнение . Внедорожник получает. Найдите количество миль на галлон гибридного автомобиля, решив уравнение .
Внедорожник получает. Найдите количество миль на галлон гибридного автомобиля, решив уравнение .