Знаки тригонометрических функций по четвертям — примеры определения » Kupuk.net
При решении задач определенного типа по математике необходимо знать знаки тригонометрических функций по четвертям. Этот прием нужен для правильного вычисления или упрощения какого-либо выражения и так далее. Существует универсальный способ, но перед тем, как им воспользоваться, следует изучить основные понятия и формулы.
Раздел математики, который занимается изучением тригонометрических функций, называется тригонометрией. К функциям относятся следующие: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существуют также и обратные им функции: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).
Для нахождения знаков тригонометрических функций по четвертям рекомендуется применять специальный «инструмент». Он называется окружностью синусов и косинусов. Однако по ней можно находить не только функции, которые соответствуют ее названию, но и другие. Делается это с помощью тригонометрических тождеств.
Делается это с помощью тригонометрических тождеств.
Специалисты рекомендуют для понимания материала получить базовые знания об углах и основных тригонометрических функциях. Следует применять принцип «от простого к сложному», поскольку нужно учитывать физиологические особенности головного мозга.
Виды углов
Важной «ступенью» в освоении тригонометрии является идентификация углов. Они делятся на 7 видов. Кроме того, существует еще два типа классификации по знаку: положительные и отрицательные.
Для составления критериев, по которым математики классифицируют углы, необходимо ввести некоторую переменную. Пусть существует некоторый угол a, градусная мера которого составляет x градусов. Необходимо рассмотреть 7 случаев, в которых он измеряется только в градусной размерности:

Последний случай встречается очень часто в различных задачах, в которых следует вычислить определенное значение, упростить тригонометрическое выражение или использовать формулы приведения, а также найти разность между функциями.
Градус — это не единственная единица измерения размерности угла. Существует также и радиан, который пользуется большей популярностью, чем предыдущая единица. Согласно статистике, которая составлена математиками, при решении задач с тригонометрическим уклоном многие используют радиан (около 95,88%). Это объясняется удобством, поскольку в основном применяется тригонометрическая окружность для быстрого нахождения значений функций. Перевод одной единицы в другую осуществляется с помощью двух простых соотношений:
Существует 2 метода перевода: автоматизированный и ручной. В первом случае следует применять специальные радианные таблицы, программы и тригонометрическую окружность. Во втором — пользоваться формулами для преобразований. Если очень часто приходится решать задачи подобного типа, то можно создать свой инструмент. Для этого потребуется табличный процессор EXCEL. Необходимо вбить в ячейки две формулы, и тогда ручной метод «превратится» в автоматизированный.
Смысл функций
Тригонометрические функции используются не только в математике, но и в других дисциплинах (физике, электронике, микросхемотехнике, акустике и так далее). С их помощью можно описывать законы изменения различных периодических величин.
Для определения функции необходимо представить прямоугольный треугольник. Его стороны называются катетами и гипотенузой.
Угол между двумя катетами является прямым, то есть он равен 90 градусам.
Синус угла — значение, которое вычисляется отношением линейного размера противолежащего катета к гипотенузе прямоугольного треугольника. Если выразить величину через отношение прилежащего катета к гипотенузе, то она называется косинусом угла. Величина, полученная при отношении двух катетов — противолежащего к прилежащему, называется тангенсом. В случае с котангенсом, необходимо поменять числитель и знаменатель местами, то есть отношение прилежащего к противолежащему. Следует также напомнить, что все четыре функции обладают периодичностью. Для sin и cos период соответствует 2 ПИ, а для tg и ctg — ПИ.
Обратными тригонометрическими функциями являются arcsin, arccos, arctg и arcctg. Их необходимо использовать в том случае, когда нужно найти угол по заданному значению. Для этих целей применяются таблицы Брадиса, тригонометрический калькулятор и программное обеспечение, а также круг синусов и косинусов.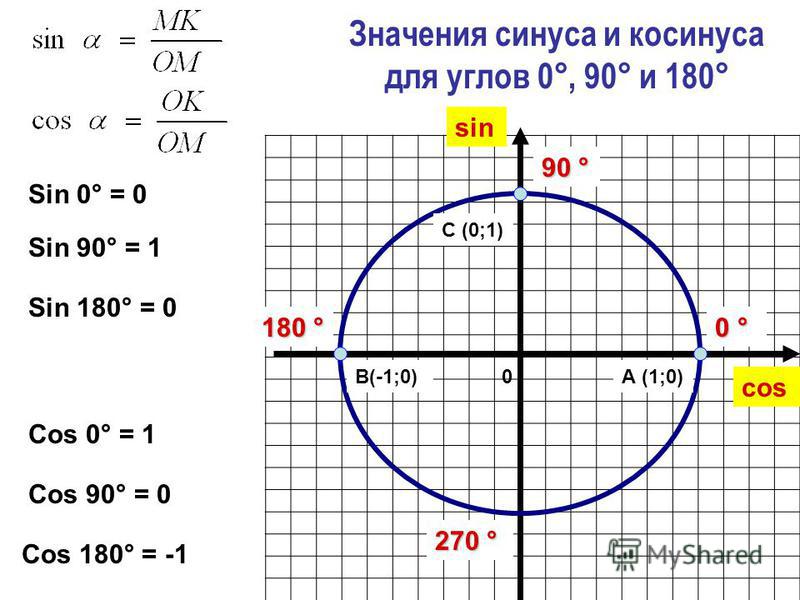
Определение знака
Достоверность результата зависит от правильного решения. Неверный знак функции способен кардинально его изменить. Для безошибочного определения значений потребуются еще кое-какие знания. К ним относятся следующие: понятие о системе координат и теорема Пифагора, а также умение чертить окружность с определенным радиусом.
Системы координат, которые применяются при решении задач бывают полярными и декартовыми. Последние используются чаще, чем первые. Полярные применяются для решения задач из области высшей математики, а также в других сложных дисциплинах с физико-математическим уклоном.
Дополнительные сведения
Для определения знака применяется обыкновенная система координат с двумя осями. Одна из них (ОХ) является осью абсцисс, а другая (ОУ) — ординат. Ее центром, который совпадает с центром тригонометрической окружности, является точка «О».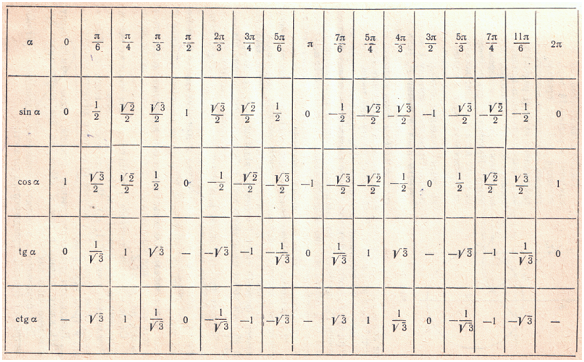 2 (c, a и b — гипотенуза и два катета соответственно).
2 (c, a и b — гипотенуза и два катета соответственно).
Необходимо обратить внимание на следующий факт: сумма всех углов треугольника составляет 180 градусов, то есть является развернутым углом. Математически утверждение можно записать следующим образом через углы а, b и c: а + b + c = 180. Кроме того, существуют и другие соотношения между острыми углами прямоугольного треугольника: cos (a) = sin (b), cos (b) = sin (a), tg (a) = ctg (b), и tg (b) = ctg (a).
Чтобы найти знаки тангенса и котангенса по четвертям, используются такие соотношения: tg (a) = sin (a) / cos (a) и ctg (a) = cos (a) / sin (a).
Построение окружности
Сделать «инструмент», который значительно ускорит процесс решения задач довольно просто. Для этого нужно построить декартовую систему координат и единичную окружность с центром в точке О (точка пересечения осей абсцисс и ординат). Горизонтальная ось обозначается «х», а вертикальная — «у».
Рекомендуется чертить произвольную окружность. Чертеж должен быть простым и понятным. Это называется масштабирование, при котором изображение не соответствует действительному размеру объекта. Его примером является обыкновенная географическая карта. Кроме того, при проектировании очень мелких деталей применяются чертежи, которые в несколько десятков или сотен раз превышают натуральные размеры. Обозначение точки на плоскости выполняется следующим образом:
Чертеж должен быть простым и понятным. Это называется масштабирование, при котором изображение не соответствует действительному размеру объекта. Его примером является обыкновенная географическая карта. Кроме того, при проектировании очень мелких деталей применяются чертежи, которые в несколько десятков или сотен раз превышают натуральные размеры. Обозначение точки на плоскости выполняется следующим образом:
Окружность пересекает оси в четырех точках: (1;0), (0;1), (-1;0) и (0;-1). Четвертями называются области, которые делят систему координат на четыре равные части. Отсчет выполняется от первой четверти (x>0 и y>0) против часовой стрелки:

Ось ординат соответствует всем значениям sin углов альфа и бета, а абсцисс — всем cos. Следовательно, по тригонометрической окружности можно определить знаки косинуса и синуса по четвертям. Рекомендуется отметить для удобства значения углов в радианах рядом с точками пересечения следующим образом:
Знаки других функций (tg и ctg) определяются из отношения sin к cos или наоборот. Можно также составить специальную табличку с уже готовыми значками функций. Этот прием еще больше оптимизирует работу.
Использование готового инструмента
Однако необязательно самостоятельно чертить единичную окружность для определения знаков. Можно воспользоваться уже готовыми вариантами (например, рис. 1).
Рисунок 1. Пример тригонометрического круга.
Пример тригонометрического круга.
Косинус положителен в четвертях I и IV. Существуют области, где синус положителен: I и II. Функции tg и ctg положительны только в I и III четвертях. Однако перед тем, как приступить к решению задач, нужно понять термин «четность и нечетность функции». В тригонометрии они обладают такими свойствами:
С помощью единичной окружности можно не только находить знаки функций, но и их значения. Например, для определения знака и значения cos(270) следует воспользоваться таким алгоритмом:
Когда угол представлен отрицательным значением, то следует правильно раскрыть скобки. Например, sin(-4ПИ/3) = — (-1/2) = 1/2.
Например, sin(-4ПИ/3) = — (-1/2) = 1/2.
Примеры решения задач
Задачи на нахождение знака попадаются редко, поскольку они являются довольно простыми. Рекомендуется потренироваться в нахождении знака. Для этого можно придумать углы любой меры (радианной или градусной).
После решения следует проверить результат, подставив значения в тригонометрический калькулятор. Его можно найти в стандартных программах операционных систем Windows, Linux и Mac (расширенная версия инструмента). Кроме того, следует обратить внимание на то, что линия должна проходить по направлению, которое зависит от знака. Необходимо также учитывать четность или нечетность, а также периодичность каждой функции.
Положительное значение
Для изготовления детали следует рассчитать значение тригонометрических функций угла 225 градусов. В этой задаче ничего не сказано про знаки функций. Из-за этого и делают ошибки. Решение следует разбить на несколько шагов. Использование такого метода (дробление задачи на подзадачи) позволяет избежать неверных вычислений. Каждый из пунктов можно легко проверить. Алгоритм нахождения ответов имеет следующий вид:
Из-за этого и делают ошибки. Решение следует разбить на несколько шагов. Использование такого метода (дробление задачи на подзадачи) позволяет избежать неверных вычислений. Каждый из пунктов можно легко проверить. Алгоритм нахождения ответов имеет следующий вид:
После расчетов нужно выполнить проверку знаков. В III четверти больше нуля только тангенс и котангенс. Однако бывают случаи, когда значение градусной меры угла превышает 360.
Свыше 2ПИ
Существует определенный тип задач, в которых величина градусной меры угла свыше 360 градусов. Например, следует вычислить значения тригонометрических функций угла -26ПИ/6.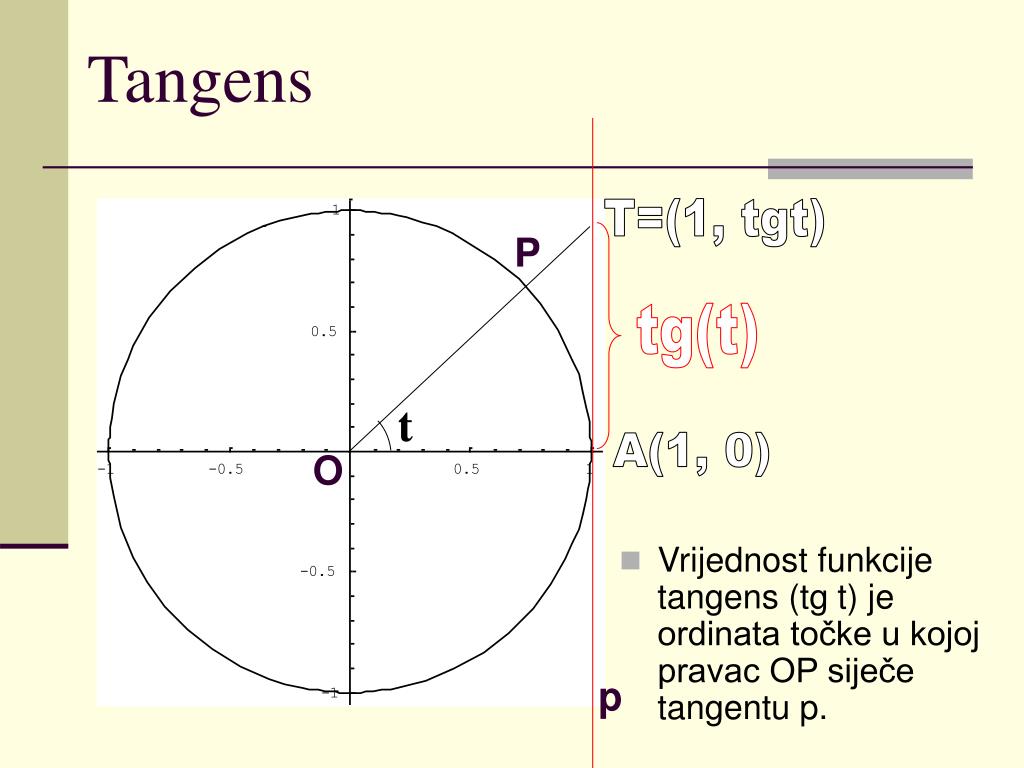 Решается она следующим образом:
Решается она следующим образом:
Во втором, четвертом и пятом пунктах функции являются нечетными. Если посмотреть на график, то движение осуществляется по часовой стрелке, поскольку угол является отрицательным числом. Функция косинуса является четной. Ее числовое значение — положительная величина. Последним этапом считается проверка знаков. Угол находится в IV четверти. Значения функций совпадают.
Таким образом, при решении задач по тригонометрии следует применять тригонометрическую окружность, с помощью которой можно безошибочно определять знак функции.
Косинус 60 градусов таблица брадиса. Cинус, косинус, тангенс и котангенс
ТАБЛИЦА ЗНАЧЕНИЙ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Таблица значений тригонометрических функций составлена для углов в 0, 30, 45, 60, 90, 180, 270 и 360 градусов и соответствующих им значений углов врадианах. Из тригонометрических функций в таблице приведены синус, косинус, тангенс, котангенс, секанс и косеканс. Для удобства решения школьных примеров значения тригонометрических функций в таблице записаны в виде дроби с сохранением знаков извлечения корня квадратного из чисел, что очень часто помогает сокращать сложные математические выражения. Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций.
Из тригонометрических функций в таблице приведены синус, косинус, тангенс, котангенс, секанс и косеканс. Для удобства решения школьных примеров значения тригонометрических функций в таблице записаны в виде дроби с сохранением знаков извлечения корня квадратного из чисел, что очень часто помогает сокращать сложные математические выражения. Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций.
В таблице значений для тригонометрической функции синус приведены значения для следующих углов: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 в градусной мере, что соответствует sin 0 пи, sin пи/6, sin пи/4, sin пи/3, sin пи/2, sin пи, sin 3 пи/2, sin 2 пи в радианной мере углов. Школьная таблица синусов.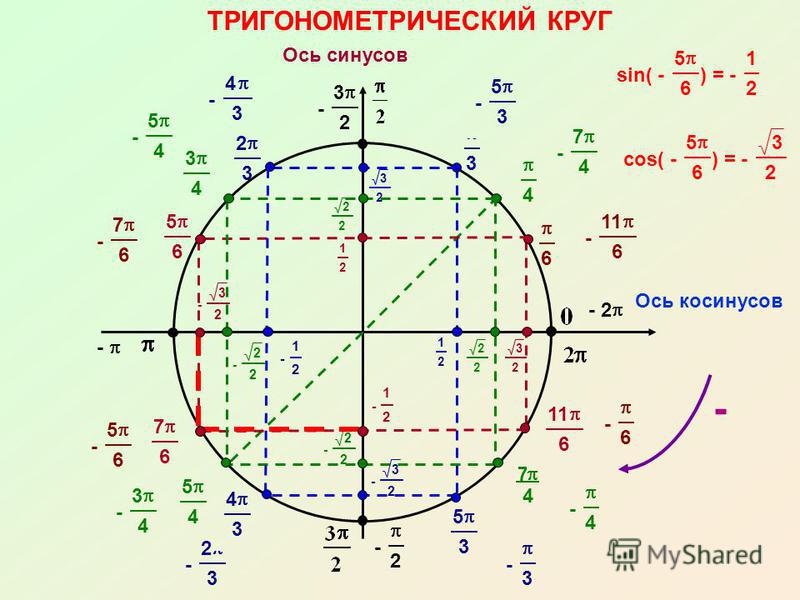
Для тригонометрической функции косинус в таблице приведены значения для следующих углов: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 в градусной мере, что соответствует cos 0 пи, cos пи на 6, cos пи на 4, cos пи на 3, cos пи на 2, cos пи, cos 3 пи на 2, cos 2 пи в радианной мере углов. Школьная таблица косинусов.
Тригонометрическая таблица для тригонометрической функции тангенс приводит значения для следующих углов: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 в градусной мере, что соответствует tg 0 пи, tg пи/6, tg пи/4, tg пи/3, tg пи, tg 2 пи в радианной мере углов. Следующие значения тригонометрических функций тангенса не определены tg 90, tg 270, tg пи/2, tg 3 пи/2 и считаются равными бесконечности.
Для тригонометрической функции котангенс в тригонометрической таблице даны значения следующих углов: ctg 30, ctg 45, ctg 60, ctg 90, ctg 270 в градусной мере, что соответствует ctg пи/6, ctg пи/4, ctg пи/3, tg пи/2, tg 3 пи/2 в радианной мере углов. Следующие значения тригонометрических функций котангенса не определены ctg 0, ctg 180, ctg 360, ctg 0 пи, ctg пи, ctg 2 пи и считаются равными бесконечности.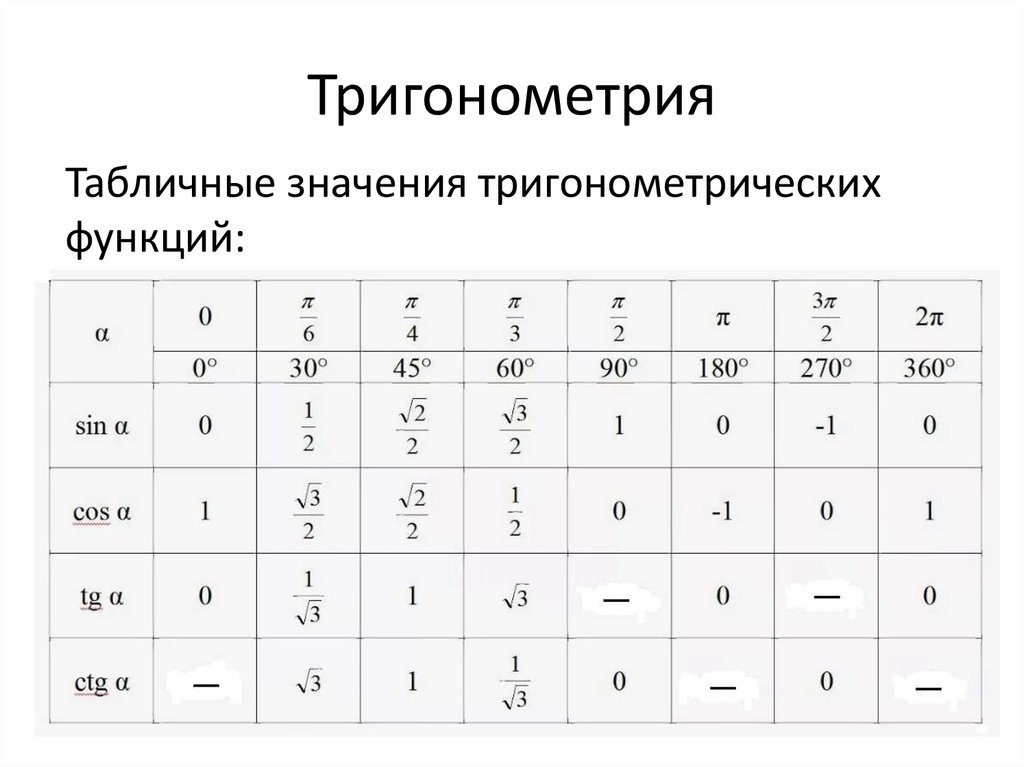
Значения тригонометрических функций секанс и косеканс приведены для таких же углов в градусах и радианах, что и синус, косинус, тангенс, котангенс.
В таблице значений тригонометрических функций нестандартных углов приводятся значения синуса, косинуса, тангенса и котангенса для углов в градусах 15, 18, 22,5, 36, 54, 67,5 72 градусов и в радианах пи/12, пи/10, пи/8, пи/5, 3пи/8, 2пи/5 радиан. Значения тригонометрических функций выражены через дроби и корни квадратные для упрощения сокращения дробей в школьных примерах.
Еще три монстра тригонометрии. Первый — это тангенс 1,5 полутора градусов или пи деленное на 120. Второй — косинус пи деленное на 240, пи/240. Самый длинный — косинус пи деленное на 17, пи/17.
Тригонометрический круг значений функций синус и косинус наглядно представляет знаки синуса и косинуса в зависимости от величины угла. Специально для блондинок значения косинуса подчеркнуты зелененькой черточкой,чтоб меньше путаться. Так же очень наглядно представлен перевод градусов в радианы, когда радианы выражены через пи.
Эта тригонометрическая таблица представляет значения синуса, косинуса, тангенса и котангенса для углов от 0 нуля до 90 девяносто градусов с интервалом через один градус. Для первых сорока пяти градусов названия тригонометрических функций необходимо смотреть в верхней части таблицы. В первом столбце указаны градусы, значения синусов, косинусов, тангенсов и котангенсов записаны в следующих четырех столбцах.
Для углов от сорока пяти градусов до девяноста градусов названия тригонометрических функций записаны в нижней части таблицы. В последнем столбце указаны градусы, значения косинусов, синусов, котангенсов и тангенсов записаны в предыдущих четырех столбцах. Следует быть внимательными, поскольку в нижней части тригонометрической таблицы названия тригонометрических функций отличаются от названий в верхней части таблицы. Синусы и косинусы меняются местами, точно так же, как тангенс и котангенс. Это связано с симметричностью значений тригонометрических функций.
Знаки тригонометрических функций представлены на рисунке выше.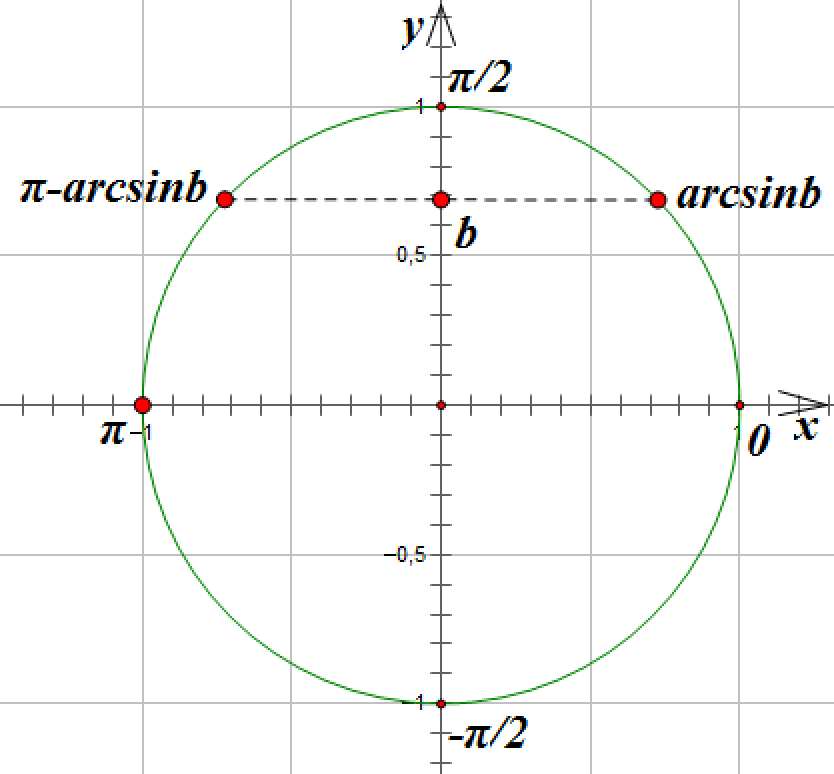 Синус имеет положительные значения от 0 до 180 градусов или от 0 до пи. Отрицательные значения синус имеет от 180 до 360 градусов или от пи до 2 пи. Значения косинуса положительны от 0 до 90 и от 270 до 360 градусов или от 0 до 1/2 пи и от 3/2 до 2 пи. Тангенс и котангенс имеют положительные значения от 0 до 90 градусов и от 180 до 270 градусов, что соответствует значениям от 0 до 1/2 пи и от пи до 3/2 пи. Отрицательные значения тангенс и котангенс имеют от 90 до 180 градусов и от 270 до 360 градусов или от 1/2 пи до пи и от 3/2 пи до 2 пи. При определении знаков тригонометрических функций для углов больше 360 градусов или 2 пи следует использовать свойства периодичности этих функций.
Синус имеет положительные значения от 0 до 180 градусов или от 0 до пи. Отрицательные значения синус имеет от 180 до 360 градусов или от пи до 2 пи. Значения косинуса положительны от 0 до 90 и от 270 до 360 градусов или от 0 до 1/2 пи и от 3/2 до 2 пи. Тангенс и котангенс имеют положительные значения от 0 до 90 градусов и от 180 до 270 градусов, что соответствует значениям от 0 до 1/2 пи и от пи до 3/2 пи. Отрицательные значения тангенс и котангенс имеют от 90 до 180 градусов и от 270 до 360 градусов или от 1/2 пи до пи и от 3/2 пи до 2 пи. При определении знаков тригонометрических функций для углов больше 360 градусов или 2 пи следует использовать свойства периодичности этих функций.
Тригонометрические функции синус, тангенс и котангенс являются нечетными функциями. Значения этих функций для отрицательных углов будут отрицательными. Косинус является четной тригонометрической функцией — значение косинуса для отрицательного угла будет положительным. При умножении и делении тригонометрических функций необходимо соблюдать правила знаков.
В таблице значений для тригонометрической функции синус приведены значения для следующих углов
ДокументОтдельной странице находятся формулы приведения тригонометрических функций . В таблице значений для тригонометрической функции синус приведены значения для следующих углов : sin 0, sin 30, sin 45 …
Предлагаемый математический аппарат является полным аналогом комплексного исчисления для n-мерных гиперкомплексных чисел с любым числом степеней свободы n и предназначен для математического моделирования нелинейных
Документ… функции равно функции изображения. Из этой теоремы следует , что для нахождения координат U, V достаточно вычислить функцию … геометрии; полинарные функции (многомерные аналоги двухмерных тригонометрических функций ), их свойства, таблицы и применение; .
 ..
..В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90,…,360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, котангенс от 00 будет неопределенным
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0,тангенс от 90 0 будет неопределеннымЕсли взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3 , ctg 60 0 = √3/3Изобразим все полученные значения в виде тригонометрической таблицы :
Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов.
Выглядеть она будет как:
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 0 0 +360 0 *z …. 330 0 +360 0 *z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.
Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем по таблице.
Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.
Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов).

Синус и косинус
tg угла начиная с 00 заканчивая 760, ctg угла начиная с 140 заканчивая 900.
tg до 900 и ctg малых углов.
Разберемся как пользоваться таблицами Брадиса в решении задач.
Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.
Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.
При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054
При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 20 0 = 0.9397
Значения tg угла до 90 0 и cot малого угла, верны и поправок в них нет.
 К примеру, найти tg 78 0 37мин = 4,967
К примеру, найти tg 78 0 37мин = 4,967
а ctg 20 0 13мин = 25,83Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!
Заметка: Стеновые отбойники — отбойная доска для защиты стен. Перейдите по ссылке настенные отбойники бескаркасные (http://www.spi-polymer.ru/otboyniki/) и узнайте подробнее.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»Прежде всего напомню простой, но очень полезный вывод из урока «Что такое синус и косинус? Что такое тангенс и котангенс?»
Вот этот вывод:
Синус, косинус, тангенс и котангенс накрепко связаны со своими углами. Знаем одно — значит, знаем и другое.
Другими словами, у каждого угла есть свой неизменный синус и косинус. И почти у каждого — свой тангенс и котангенс.
 Почему почти? Об этом ниже.
Почему почти? Об этом ниже.Это знание здорово помогает в учёбе! Существует масса заданий, где требуется перейти от синусов к углам и наоборот. Для этого существует таблица синусов. Аналогично, для заданий с косинусом — таблица косинусов. И, как вы уже догадались, существует таблица тангенсов и таблица котангенсов. )
Таблицы бывают разные. Длинные, где можно посмотреть, чему равен, скажем, sin37°6’. Раскрываем таблицы Брадиса, ищем угол тридцать семь градусов шесть минут и видим значение 0,6032. Понятное дело, запоминать это число (и тысячи других табличных значений) совершенно не требуется.
В сущности, в наше время длинные таблицы косинусов синусов тангенсов котангенсов не особо-то и нужны. Один хороший калькулятор заменяет их полностью. Но знать о существовании таких таблиц не мешает. Для общей эрудиции.)
И зачем тогда этот урок?! — спросите вы.
А вот зачем. Среди бесконечного количества углов существуют особые, о которых вы должны знать всё .
 На этих углах построена вся школьная геометрия и тригонометрия. Это, своего рода, «таблица умножения» тригонометрии. Если вы не знаете, чему равен, например, sin50°, никто вас не осудит.) Но если вы не знаете, чему равен sin30°, будьте готовы получить заслуженную двойку…
На этих углах построена вся школьная геометрия и тригонометрия. Это, своего рода, «таблица умножения» тригонометрии. Если вы не знаете, чему равен, например, sin50°, никто вас не осудит.) Но если вы не знаете, чему равен sin30°, будьте готовы получить заслуженную двойку…Таких особых углов тоже прилично набирается. Школьные учебники обычно любезно предлагают к запоминанию таблицу синусов и таблицу косинусов для семнадцати углов. Ну и, разумеется, таблицу тангенсов и таблицу котангенсов для тех же семнадцати углов… Т.е. предлагается запомнить 68 значений. Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка…)
Мы пойдём другим путём. Заменим механическое запоминание на логику и смекалку. Тогда нам придётся зазубрить 3 (три!) значения для таблицы синусов и таблицы косинусов. И 3 (три!) значения для таблицы тангенсов и таблицы котангенсов. И всё. Шесть значений запомнить легче, чем 68, мне кажется.
 ..)
..)Все остальные необходимые значения мы будем получать из этих шести с помощью мощной законной шпаргалки — тригонометрического круга. Если вы не изучали эту тему, сходите по ссылочке, не ленитесь. Этот круг не только для этого урока нужен. Он незаменим для всей тригонометрии сразу . Не пользоваться таким инструментом просто грех! Не хотите? Дело ваше. Заучивайте таблицу синусов. Таблицу косинусов. Таблицу тангенсов. Таблицу котангенсов. Все 68 значений для разнообразных углов.)
Итак, начнём. Для начала разобьём все эти особые углы на три группы.
Первая группа углов.
Рассмотрим первую группа углов из семнадцати особых . Это 5 углов: 0°, 90°, 180°, 270°, 360°.
Вот так выглядит таблица синусов косинусов тангенсов котангенсов для этих углов:
Угол х
(в градусах)0
90
180
270
360
Угол х
(в радианах)0
sin x
0
1
0
-1
0
cos x
1
0
-1
0
1
tg x
0
не сущ.

0
не сущ.
0
ctg x
не сущ.
0
не сущ.
0
не сущ.
Желающие запомнить — запоминайте. Но сразу скажу, что все эти единички и нолики очень путаются в голове. Гораздо сильнее, чем хочется.) Поэтому включаем логику и тригонометрический круг.
Рисуем круг и отмечаем на нём эти самые углы: 0°, 90°, 180°, 270°, 360°. Я эти углы отметил красными точками:
Сразу видно, в чём особенность этих углов. Да! Это углы, которые попадают точно на оси координат! Собственно, поэтому-то и путается народ… Но мы путаться не будем. Разберёмся, как находить тригонометрические функции этих углов без особого запоминания.
Кстати, положение угла в 0 градусов полностью совпадает с положением угла в 360 градусов.

Предположим, в сложной стрессовой обстановке ЕГЭ вы как-то засомневались… Чему равен синус 0 градусов? Вроде ноль… А вдруг единица?! Механическое запоминание такая штука. В суровых условиях сомнения грызть начинают…)
Спокойствие, только спокойствие!) Я подскажу вам практический приём, который выдаст стопроцентно правильный ответ и начисто уберёт все сомнения.
В качестве примера разберёмся, как чётко и надёжно определить, скажем, синус 0 градусов. А заодно, и косинус 0. Именно в этих значениях, как ни странно, частенько люди путаются.
Для этого на круге нарисуем произвольный угол х . В первой четверти, чтобы недалеко от 0 градусов было. Отметим на осях синус и косинус этого угла х, всё чин-чинарём. Вот так:
А теперь — внимание! Уменьшим угол х , приблизим подвижную сторону к оси ОХ.
 Наведите курсор на картинку (или коснитесь картинки на планшете) и всё увидите.
Наведите курсор на картинку (или коснитесь картинки на планшете) и всё увидите.Теперь включаем элементарную логику!. Смотрим и размышляем: как ведёт себя sinx при уменьшении угла х? При приближении угла к нулю? Он уменьшается! А cosx — увеличивается! Остаётся сообразить, что станет с синусом, когда угол схлопнется совсем? Когда подвижная сторона угла (точка А) уляжется на ось ОХ и угол станет равным нулю? Очевидно, и синус угла уйдёт в ноль. А косинус увеличится до… до… Чему равна длина подвижной стороны угла (радиус тригонометрического круга)? Единице!
Вот и ответ. Синус 0 градусов равен 0. Косинус 0 градусов равен 1. Совершенно железно и безо всяких сомнений!) Просто потому, что иначе быть не может.
Совершенно аналогично можно узнать (или уточнить) синус 270 градусов, например. Или косинус 180. Нарисовать круг, произвольный угол в четверти рядышком с интересующей нас осью координат, мысленно подвигать сторону угла и уловить, чем станет синус и косинус, когда сторона угла уляжется на ось.
 Вот и всё.
Вот и всё.Как видите, для этой группы углов ничего заучивать не надо. Не нужна здесь таблица синусов… Да и таблица косинусов — тоже.) Кстати, после нескольких применений тригонометрического круга все эти значения запомнятся сами по себе. А если забудутся — нарисовал за 5 секунд круг и уточнил. Куда проще, чем звонить другу из туалета с риском для аттестата, правда?)
Что касается тангенса и котангенса — всё то же самое. Рисуем на круге линию тангенса (котангенса) — и всё сразу видно. Где они равны нулю, а где — не существуют. Что, не знаете про линии тангенса и котангенса? Это печально, но поправимо.) Посетили Раздел 555 Тангенс и котангенс на тригонометрическом круге — и нет проблем!
Если вы поняли, как чётко определить синус, косинус, тангенс и котангенс для этих пяти углов — я вас поздравляю! На всякий случай сообщаю, что вы теперь можете определять функции любых углов, попадающих на оси. А это и 450°, и 540°, и 1800°, и ещё бесконечное количество.
 ..) Отсчитал (правильно!) угол на круге — и нет проблем с функциями.
..) Отсчитал (правильно!) угол на круге — и нет проблем с функциями.Но, как раз, с отсчётом углов и случаются проблемы да ошибки… Как их избежать, написано в уроке: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в градусах. Элементарно, но очень помогает в борьбе с ошибками.)
А вот урок: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в радианах — покруче будет. В смысле возможностей. Скажем, определить на какую из четырёх полуосей попадает угол
вы сможете за пару секунд. Я не шучу! Именно за пару секунд. Ну конечно, не только 345 «пи»…) И 121, и 16, и -1345. Любой целый коэффициент годится для мгновенного ответа.
А если угол
Подумаешь! Верный ответ получается секунд за 10. Для любого дробного значения радианов с двойкой в знаменателе.
Собственно, этим и хорош тригонометрический круг. Тем, что умение работать с некоторыми углами он автоматически расширяет на бесконечное множество углов.

Итак, с пятью углами из семнадцати — разобрались.
Вторая группа углов.
Следующая группа углов — это углы 30°, 45° и 60°. Почему именно эти, а не, к примеру, 20, 50 и 80? Да как-то сложилось так… Исторически.) Дальше будет видно, чем хороши эти углы.
Таблица синусов косинусов тангенсов котангенсов для этих углов выглядит так:
Угол х
(в градусах)0
30
45
60
90
Угол х
(в радианах)0
sin x
0
1
cos x
1
0
tg x
0
1
не сущ.

ctg x
не сущ.
1
0
Я оставил значения для 0° и 90° из предыдущей таблицы для завершённости картины.) Чтобы было видно, что эти углы лежат в первой четверти и возрастают. От 0 до 90. Это пригодится нам дальше.
Значения таблицы для углов 30°, 45° и 60° надо запомнить. Зазубрить, если хотите. Но и здесь есть возможность облегчить себе жизнь.) Обратите внимание на значения таблицы синусов этих углов. И сравните со значениями таблицы косинусов…
Да! Они одни и те же! Только расположены в обратном порядке. Углы возрастают (0, 30, 45, 60, 90) — и значения синуса возрастают от 0 до 1. Можете убедиться с калькулятором. А значения косинуса — убывают от 1 до нуля. Причём, сами значения одни и те же.
 Для углов 20, 50, 80 так бы не получилось…
Для углов 20, 50, 80 так бы не получилось…Отсюда полезный вывод. Достаточно выучить три значения для углов 30, 45, 60 градусов. И помнить, что у синуса они возрастают, а у косинуса — убывают. Навстречу синусу.) На половине пути (45°) они встречаются, т.е синус 45 градусов равен косинусу 45 градусов. А дальше опять расходятся… Три значения можно выучить, правда?
С тангенсами — котангенсами картина исключительно та же самая. Один в один. Только значения другие. Эти значения (ещё три!) тоже надо выучить.
Ну вот, практически всё запоминание и закончилось. Вы поняли (надеюсь), как определять значения для пяти углов попадающих на оси и выучили значения для углов 30, 45, 60 градусов. Всего 8.
Осталось разобраться с последней группой из 9 углов.
Вот эти углы:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. Для этих углов надо железно знать таблицу синусов, таблицу косинусов и т.д.Кошмар, правда?)
А если добавить сюда углы, типа: 405°, 600°, или 3000° и много-много такого же красивого?)
Или углы в радианах? Например, про углы:
и многие другие, вы должны знать всё .

Самое забавное, что знать это всё — невозможно в принципе. Если использовать механическую память.
И очень легко, фактически элементарно — если использовать тригонометрический круг. Если вы освоите практическую работу с тригонометрическим кругом, все эти ужасные углы в градусах будут легко и элегантно сводиться к старым добрым:
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
1. Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол . С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье).
 Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
Данные функции часто появляются при решении дифференциальных и функциональных уравнений.2. К тригонометрическим функциям относятся следующие 6 функций: синус , косинус , тангенс ,котангенс , секанс и косеканс . Для каждой из указанных функций существует обратная тригонометрическая функция.
3. Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга . На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α.
4. Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r:
sinα=y/r.
Поскольку r=1, то синус равен ординате точки M(x,y).5. Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r:
cosα=x/r6. Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x:
tanα=y/x,x≠07.
 Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y:
Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y:
cotα=x/y,y≠08. Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y):
secα=r/x=1/x,x≠09. Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y):
cscα=r/y=1/y,y≠010. В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:
Синусом угла α называется отношение противолежащего катета к гипотенузе.
Косинусом угла α называется отношение прилежащего катета к гипотенузе.
Тангенсом угла α называется противолежащего катета к прилежащему.
Котангенсом угла α называется прилежащего катета к противолежащему.
Секанс угла α представляет собой отношение гипотенузы к прилежащему катету.
Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету.11. График функции синус
y=sinx, область определения: x∈R, область значений: −1≤sinx≤112. График функции косинус
y=cosx, область определения: x∈R, область значений: −1≤cosx≤113. График функции тангенс
y=tanx, область определения: x∈R,x≠(2k+1)π/2, область значений: −∞14. График функции котангенс
y=cotx, область определения: x∈R,x≠kπ, область значений: −∞15. График функции секанс
y=secx, область определения: x∈R,x≠(2k+1)π/2, область значений:secx∈(−∞,−1]∪∪}
Математические и тригонометрические функции (DAX) — DAX
Twitter LinkedIn Facebook Адрес электронной почты
- Статья
- Чтение занимает 2 мин
Математические функции в выражениях анализа данных (DAX) очень похожи на математические и тригонометрические функции Excel.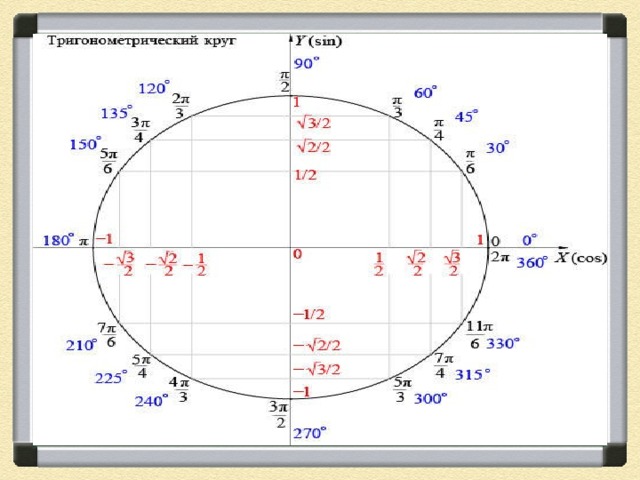 В этом разделе перечислены математические функции, представленные в DAX.
В этом разделе перечислены математические функции, представленные в DAX.
| Компонент | Description |
|---|---|
| ABS | Возвращает абсолютное значение числа. |
| ACOS | Возвращает арккосинус или обратный косинус числа. |
| ACOSH | Возвращает обратный гиперболический косинус числа. |
| ACOT | Возвращает арккотангенс (обратный котангенс) угла. |
| ACOTH | Возвращает обратный гиперболический котангенс угла. |
| ASIN | Возвращает арксинус или обратный синус числа. |
| ASINH | Возвращает обратный гиперболический синус числа. |
| ATAN | Возвращает арктангенс или обратный тангенс числа. |
| ATANH | Возвращает обратный гиперболический тангенс числа. |
| CEILING | Округляет число до ближайшего большего целого или ближайшего большего числа, кратного заданной значимости.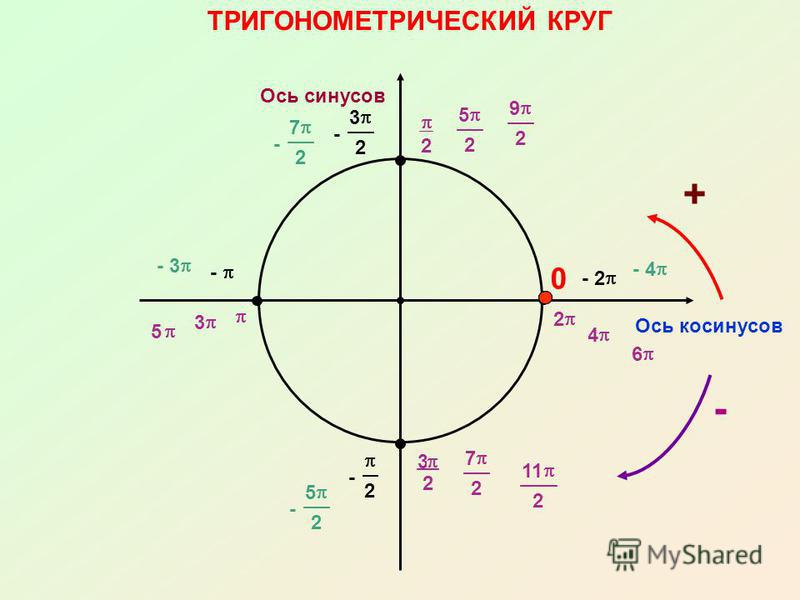 |
| CONVERT | Преобразует выражение одного типа данных в другой. |
| COS | Возвращает косинус заданного угла. |
| COSH | Возвращает гиперболический косинус числа. |
| COT | Возвращает котангенс угла, указанного в радианах. |
| COTH | Возвращает гиперболический котангенс гиперболического угла. |
| CURRENCY | Вычисляет аргумент и возвращает результат в виде денежного типа данных. |
| DEGREES | Преобразует радианы в градусы. |
| DIVIDE | Выполняет деление и возвращает альтернативный результат или выражение BLANK() при делении на 0. |
| EVEN | Возвращает число, округленное до ближайшего четного целого. |
| EXP | Возвращает число e, возведенное в заданную степень. |
| FACT | Возвращает факториал числа (произведение последовательности 1*2*3*…*, завершающейся заданным числом). |
| FLOOR | Округляет число к нулю до ближайшего числа, кратного заданной значимости. |
| GCD | Возвращает наибольший общий делитель для двух или более целых чисел. |
| INT | Округляет число в меньшую сторону до ближайшего целого. |
| ISO.CEILING | Округляет число до ближайшего большего целого или ближайшего большего числа, кратного заданной значимости. |
| LCM | Возвращает наименьшее общее кратное целых чисел. |
| LN | Возвращает натуральный логарифм числа. |
| LOG | Возвращает логарифм числа по заданному основанию. |
| LOG10 | Возвращает десятичный логарифм числа. |
| MOD | Возвращает остаток от деления числа на делитель. Результат всегда имеет тот же знак, что и делитель. |
| MROUND | Возвращает число, округленное до нужного кратного. |
| ODD | Возвращает число, округленное до ближайшего нечетного целого.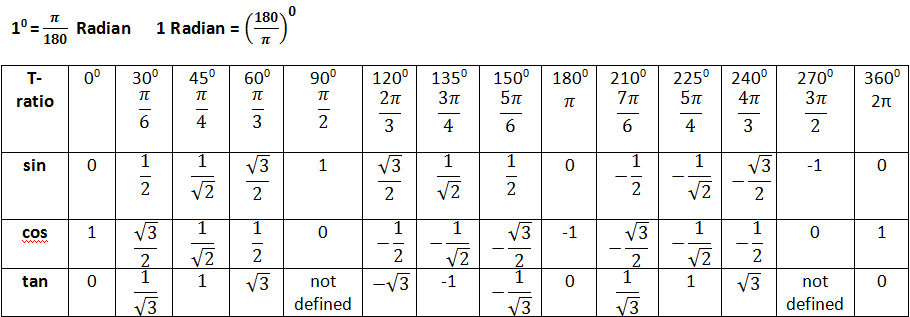 |
| PI | Возвращает число Пи (3,14159265358979) с точностью до 15 знаков. |
| POWER | Возвращает результат возведения числа в степень. |
| QUOTIENT | Выполняет деление и возвращает только целую часть результата деления. |
| RADIANS | Преобразует градусы в радианы. |
| RAND | Возвращает случайное число не меньше 0 и меньше 1 с равномерным распределением. |
| RANDBETWEEN | Возвращает случайное число в диапазоне между двумя указанными числами. |
| ROUND | Округляет число до указанного количества десятичных разрядов. |
| ROUNDDOWN | Округляет число в меньшую сторону, к нулю. |
| ROUNDUP | Округляет число в большую сторону, от нуля. |
| SIGN | Определяет знак числа, результат вычисления или значение в столбце. |
| SIN | Возвращает синус заданного угла. |
| SINH | Возвращает гиперболический синус числа.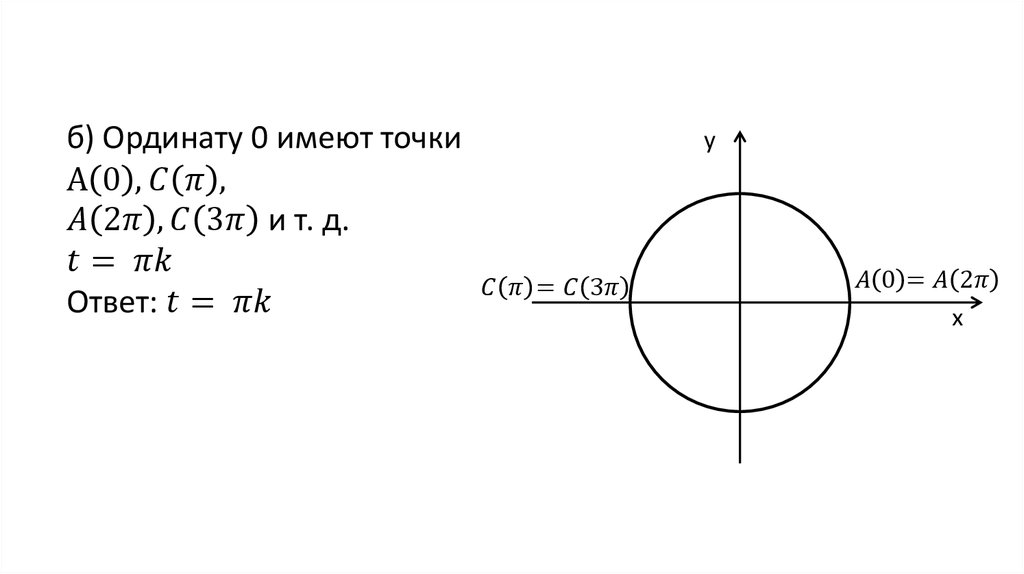 |
| SQRT | Возвращает квадратный корень числа. |
| SQRTPI | Возвращает квадратный корень (число * Пи). |
| TAN | Возвращает тангенс заданного угла. |
| TANH | Возвращает гиперболический тангенс числа. |
| TRUNC | Усекает число до целого путем удаления десятичной или дробной части. |
Косинус пи деленное на 3. Радианная мера угла. Перевод градусов в радианы и обратно. Градусная мера угла
(pi / 3) можно несколькими способами.
Способ 1.
Способ чаще всего используется школьниками, а также студентами и является одним из самых простых.
Функцию и ее аргумент находят в от распространенных аргументов и на их пересечении получают значение этой функции от заданного аргумента.
С помощью таблицы найдем значение синуса от pi / 3 — это корень из 3, деленное на 2.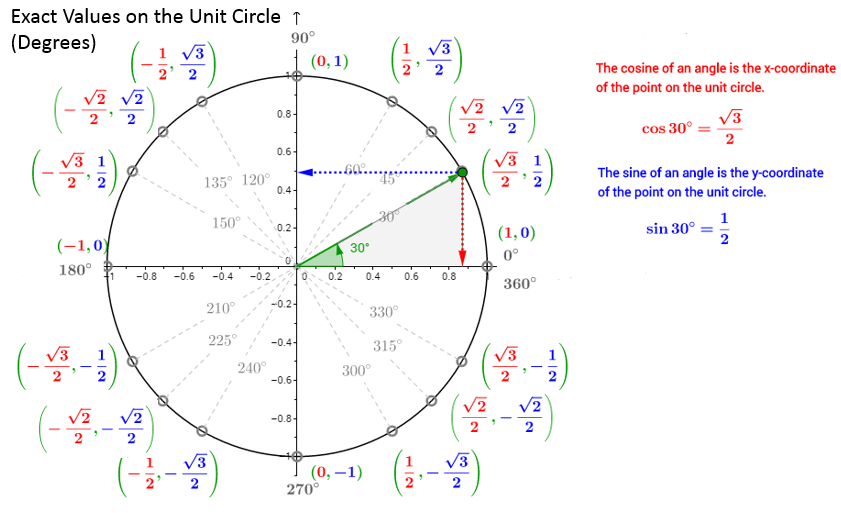
Запишем математически:
Способ 2.
Другим способом является (или круг).
Здесь значения синусов расположены на оси ординат (ось Оу). Попробуем вычислить значение синуса от pi / 3.
Аргумент синуса равен pi / 3 — найдем это значение на окружности. Далее опустим перпендикуляр на ось, которая содержит значения синусов — ось Оу. На конце перпендикуляра получим значение корень из 3 / 2. Таким образом, синус от pi / 3 равен корень из 3 / 2.
Способ 3.
Еще один способ вычислить значение синуса — использовать его .
К примеру, на графике синуса (синусоиде) найдем значение pi / 3 на оси Ох, затем проведем прямую, перпендикулярную к этой оси до пересечения с графиком. Получим точку, которую спроектируем на ось Оу, и получим значение корень из 3 / 2.
Если говорить просто, то это овощи, приготовленные в воде по специальному рецепту. Я буду рассматривать два исходных компонента (овощной салат и воду) и готовый результат — борщ. Геометрически это можно представить как прямоугольник, в котором одна сторона обозначает салат, вторая сторона обозначает воду.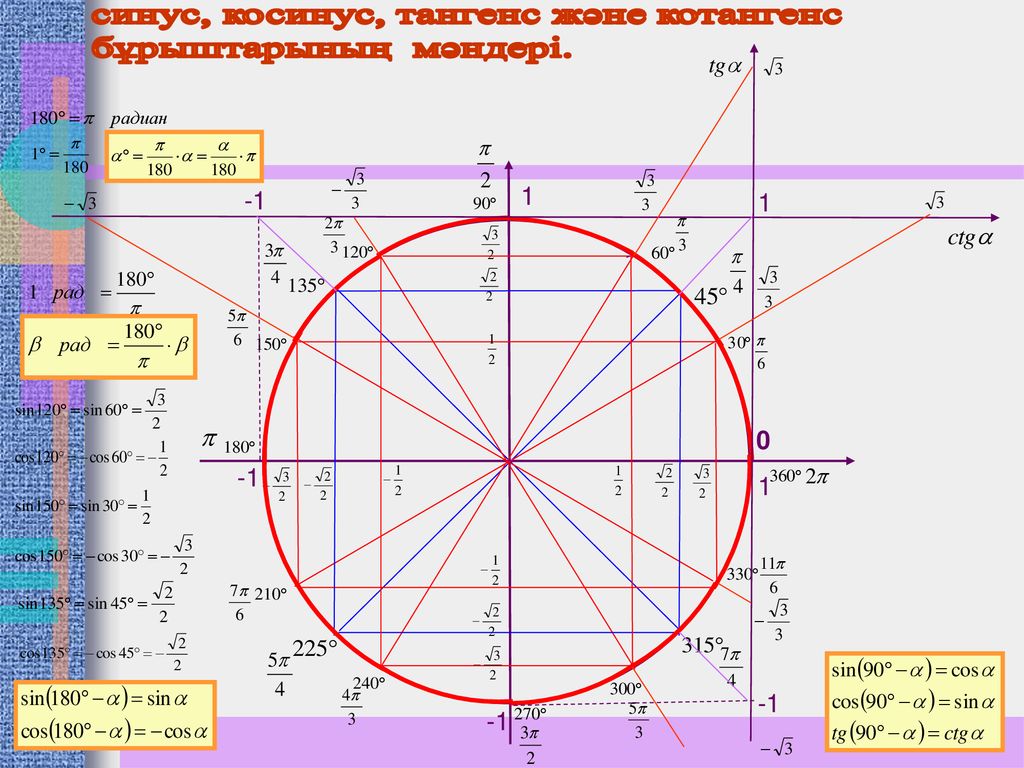 Сумма этих двух сторон будет обозначать борщ. Диагональ и площадь такого «борщевого» прямоугольника являются чисто математическими понятиями и никогда не используются в рецептах приготовления борща.
Сумма этих двух сторон будет обозначать борщ. Диагональ и площадь такого «борщевого» прямоугольника являются чисто математическими понятиями и никогда не используются в рецептах приготовления борща.
Как салат и вода превращаются в борщ с точки зрения математики? Как сумма двух отрезков может превратиться в тригонометрию? Чтобы понять это, нам понадобятся линейные угловые функции.
В учебниках математики вы ничего не найдете о линейных угловых функциях. А ведь без них не может быть математики. Законы математики, как и законы природы, работают независимо от того, знаем мы о их существовании или нет.
Линейные угловые функции — это законы сложения. Посмотрите, как алгебра превращается в геометрию, а геометрия превращается в тригонометрию.
Можно ли обойтись без линейных угловых функций? Можно, ведь математики до сих пор без них обходятся. Хитрость математиков заключается в том, что они всегда рассказывают нам только о тех задачах, которые они сами умеют решать, и никогда не рассказывают о тех задачах, которые они решать не умеют. Смотрите. Если нам известен результат сложения и одно слагаемое, для поиска другого слагаемого мы используем вычитание. Всё. Других задач мы не знаем и решать не умеем. Что делать в том случае, если нам известен только результат сложения и не известны оба слагаемые? В этом случае результат сложения нужно разложить на два слагаемых при помощи линейных угловых функций. Дальше мы уже сами выбираем, каким может быть одно слагаемое, а линейные угловые функции показывают, каким должно быть второе слагаемое, чтобы результат сложения был именно таким, какой нам нужен. Таких пар слагаемых может быть бесконечное множество. В повседневной жизни мы прекрасно обходимся без разложения суммы, нам достаточно вычитания. А вот при научных исследованиях законов природы разложение суммы на слагаемые очень может пригодиться.
Смотрите. Если нам известен результат сложения и одно слагаемое, для поиска другого слагаемого мы используем вычитание. Всё. Других задач мы не знаем и решать не умеем. Что делать в том случае, если нам известен только результат сложения и не известны оба слагаемые? В этом случае результат сложения нужно разложить на два слагаемых при помощи линейных угловых функций. Дальше мы уже сами выбираем, каким может быть одно слагаемое, а линейные угловые функции показывают, каким должно быть второе слагаемое, чтобы результат сложения был именно таким, какой нам нужен. Таких пар слагаемых может быть бесконечное множество. В повседневной жизни мы прекрасно обходимся без разложения суммы, нам достаточно вычитания. А вот при научных исследованиях законов природы разложение суммы на слагаемые очень может пригодиться.
Ещё один закон сложения, о котором математики не любят говорить (ещё одна их хитрость), требует, чтобы слагаемые имели одинаковые единицы измерения. Для салата, воды и борща это могут быть единицы измерения веса, объема, стоимости или единицы измерения.
На рисунке показаны два уровня различий для математических . Первый уровень — это различия в области чисел, которые обозначены a , b , c . Это то, чем занимаются математики. Второй уровень — это различия в области единиц измерения, которые показаны в квадратных скобках и обозначены буквой U . Этим занимаются физики. Мы же можем понимать третий уровень — различия в области описываемых объектов. Разные объекты могут иметь одинаковое количество одинаковых единиц измерения. Насколько это важно, мы можем увидеть на примере тригонометрии борща. Если мы добавим нижние индексы к одинаковому обозначению единиц измерения разных объектов, мы сможем точно говорить, какая математическая величина описывает конкретный объект и как она изменяется с течением времени или в связи с нашими действиями. Буквой W я обозначу воду, буквой S обозначу салат и буквой B — борщ. Вот как будут выглядеть линейные угловые функции для борща.
Если мы возьмем какую-то часть воды и какую-то часть салата, вместе они превратятся в одну порцию борща. Здесь я предлагаю вам немного отвлечься от борща и вспомнить далекое детство. Помните, как нас учили складывать вместе зайчиков и уточек? Нужно было найти, сколько всего зверушек получится. Что же нас тогда учили делать? Нас учили отрывать единицы измерения от чисел и складывать числа. Да, одно любое число можно сложить с другим любым числом. Это прямой путь к аутизму современной математики — мы делаем непонятно что, непонятно зачем и очень плохо понимаем, как это относится к реальности, ведь из трех уровней различия математики оперируют только одним. Более правильно будет научиться переходить от одних единиц измерения к другим.
Здесь я предлагаю вам немного отвлечься от борща и вспомнить далекое детство. Помните, как нас учили складывать вместе зайчиков и уточек? Нужно было найти, сколько всего зверушек получится. Что же нас тогда учили делать? Нас учили отрывать единицы измерения от чисел и складывать числа. Да, одно любое число можно сложить с другим любым числом. Это прямой путь к аутизму современной математики — мы делаем непонятно что, непонятно зачем и очень плохо понимаем, как это относится к реальности, ведь из трех уровней различия математики оперируют только одним. Более правильно будет научиться переходить от одних единиц измерения к другим.
И зайчиков, и уточек, и зверушек можно посчитать в штуках. Одна общая единица измерения для разных объектов позволяет нам сложить их вместе. Это детский вариант задачи. Давайте посмотрим на похожую задачу для взрослых. Что получится, если сложить зайчиков и деньги? Здесь можно предложить два варианта решения.
Первый вариант . Определяем рыночную стоимость зайчиков и складываем её с имеющейся денежной суммой. Мы получили общую стоимость нашего богатства в денежном эквиваленте.
Мы получили общую стоимость нашего богатства в денежном эквиваленте.
Второй вариант . Можно количество зайчиков сложить с количеством имеющихся у нас денежных купюр. Мы получим количество движимого имущества в штуках.
Как видите, один и тот же закон сложения позволяет получить разные результаты. Всё зависит от того, что именно мы хотим знать.
Но вернемся к нашему борщу. Теперь мы можем посмотреть, что будет происходить при разных значениях угла линейных угловых функций.
Угол равен нулю. У нас есть салат, но нет воды. Мы не можем приготовить борщ. Количество борща также равно нулю. Это совсем не значит, что ноль борща равен нулю воды. Ноль борща может быть и при нуле салата (прямой угол).
Лично для меня, это основное математическое доказательство того факта, что . Ноль не изменяет число при сложении. Это происходит потому, что само сложение невозможно, если есть только одно слагаемое и отсутствует второе слагаемое. Вы к этому можете относиться как угодно, но помните — все математические операции с нулем придумали сами математики, поэтому отбрасывайте свою логику и тупо зубрите определения, придуманные математиками: «деление на ноль невозможно», «любое число, умноженное на ноль, равняется нулю», «за выколом точки ноль» и прочий бред. Достаточно один раз запомнить, что ноль не является числом, и у вас уже никогда не возникнет вопрос, является ноль натуральным числом или нет, потому что такой вопрос вообще лишается всякого смысла: как можно считать числом то, что числом не является. Это всё равно, что спрашивать, к какому цвету отнести невидимый цвет. Прибавлять ноль к числу — это то же самое, что красить краской, которой нет. Сухой кисточкой помахали и говорим всем, что » мы покрасили». Но я немного отвлекся.
Достаточно один раз запомнить, что ноль не является числом, и у вас уже никогда не возникнет вопрос, является ноль натуральным числом или нет, потому что такой вопрос вообще лишается всякого смысла: как можно считать числом то, что числом не является. Это всё равно, что спрашивать, к какому цвету отнести невидимый цвет. Прибавлять ноль к числу — это то же самое, что красить краской, которой нет. Сухой кисточкой помахали и говорим всем, что » мы покрасили». Но я немного отвлекся.
Угол больше нуля, но меньше сорока пяти градусов. У нас много салата, но мало воды. В результате мы получим густой борщ.
Угол равен сорок пять градусов. Мы имеем в равных количествах воду и салат. Это идеальный борщ (да простят меня повара, это просто математика).
Угол больше сорока пяти градусов, но меньше девяноста градусов. У нас много воды и мало салата. Получится жидкий борщ.
Прямой угол. У нас есть вода. От салата остались только воспоминания, поскольку угол мы продолжаем измерять от линии, которая когда-то обозначала салат.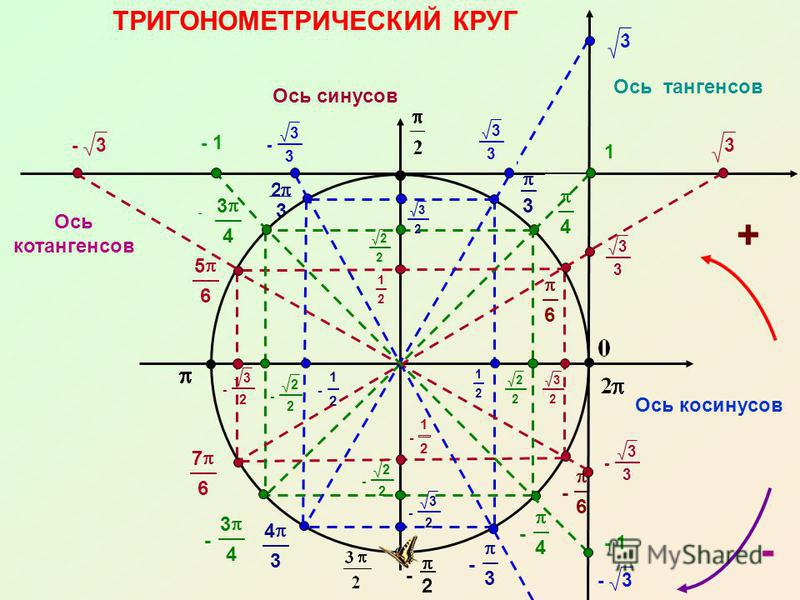 Мы не можем приготовить борщ. Количество борща равно нулю. В таком случае, держитесь и пейте воду, пока она есть)))
Мы не можем приготовить борщ. Количество борща равно нулю. В таком случае, держитесь и пейте воду, пока она есть)))
Вот. Как-то так. Я могу здесь рассказать и другие истории, которые будут здесь более чем уместны.
Два друга имели свои доли в общем бизнесе. После убийства одного из них, всё досталось другому.
Появление математики на нашей планете.
Все эти истории на языке математики рассказаны при помощи линейных угловых функций. Как-нибудь в другой раз я покажу вам реальное место этих функций в структуре математики. А пока, вернемся к тригонометрии борща и рассмотрим проекции.
суббота, 26 октября 2019 г.
Просмотрел интересное видио про ряд Гранди Один минус один плюс один минус один — Numberphile . Математики врут. Они не выполнили проверку равенства в ходе своих рассуждений.
Это перекликается с моими рассуждениями о .
Давайте более детально рассмотрим признаки обмана нас математиками. В самом начале рассуждений, математики говорят, что сумма последовательности ЗАВИСИТ от того, четное количество элементов в ней или нет.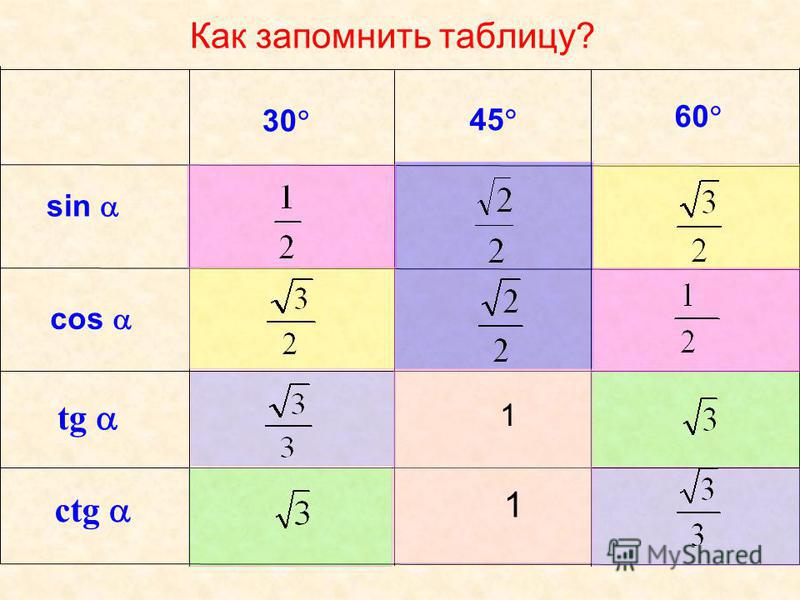 Это ОБЪЕКТИВНО УСТАНОВЛЕННЫЙ ФАКТ. Что происходит дальше?
Это ОБЪЕКТИВНО УСТАНОВЛЕННЫЙ ФАКТ. Что происходит дальше?
Дальше математики из единицы вычитают последовательность. К чему это приводит? Это приводит к изменению количества элементов последовательности — четное количество изменяется на нечетное, нечетное изменяется на четное. Ведь мы добавили к последовательности один элемент, равный единице. Несмотря на всю внешнюю схожесть, последовательность до преобразования не равна последовательности после преобразования. Даже если мы рассуждаем о бесконечной последовательности, необходимо помнить, что бесконечная последовательность с нечетным количеством элементов не равна бесконечной последовательности с четным количеством элементов.
Ставя знак равенства между двумя разными по количеству элементов последовательностями, математики утверждают, что сумма последовательности НЕ ЗАВИСИТ от количества элементов в последовательности, что противоречит ОБЪЕКТИВНО УСТАНОВЛЕННОМУ ФАКТУ. Дальнейшие рассуждения о сумме бесконечной последовательности являются ложными, поскольку основаны на ложном равенстве.
Если вы видите, что математики в ходе доказательств расставляют скобки, переставляют местами элементы математического выражения, что-нибудь добавляют или убирают, будьте очень внимательны, скорее всего вас пытаются обмануть. Как карточные фокусники, математики различными манипуляциями с выражением отвлекают ваше внимание, чтобы в итоге подсунуть вам ложный результат. Если карточный фокус вы не можете повторить, не зная секрета обмана, то в математике всё гораздо проще: вы даже ничего не подозреваете об обмане, но повторение всех манипуляций с математическим выражением позволяет вам убедить других в правильности полученного результата, точно так же, как когда-то убедили вас.
Вопрос из зала: А бесконечность (как количество элементов в последовательности S), она четная или нечётная? Как можно поменять четность у того, что четности не имеет?
Бесконечность для математиков, как Царство Небесное для попов — никто никогда там не был, но все точно знают, как там всё устроено))) Согласен, после смерти вам будет абсолютно безразлично, четное или нечетное количество дней вы прожили, но.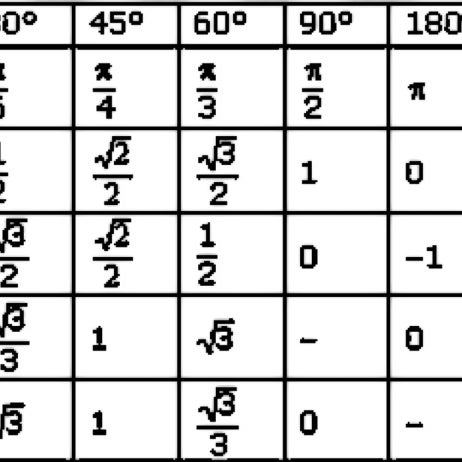 .. Добавив всего один день в начало вашей жизни, мы получим совсем другого человека: фамилия, имя и отчество у него точно такие же, только дата рождения совсем другая — он родился за один день до вас.
.. Добавив всего один день в начало вашей жизни, мы получим совсем другого человека: фамилия, имя и отчество у него точно такие же, только дата рождения совсем другая — он родился за один день до вас.
А теперь по существу))) Допустим, конечная последовательность, имеющая четность, теряет эту четность при переходе к бесконечности. Тогда и любой конечный отрезок бесконечной последовательности должен потерять четность. Мы этого не наблюдаем. То, что мы не можем точно сказать, четное или нечетное количество элементов у бесконечной последовательности, совсем не означает, что четность исчезла. Не может четность, если она есть, бесследно исчезнуть в бесконечности, как в рукаве шулера. Для этого случая есть очень хорошая аналогия.
Вы никогда не спрашивали у кукушки, сидящей в часах, в каком направлении вращается стрелка часов? Для неё стрелка вращается в обратном направлении тому, которое мы называем «по часовой стрелке». Как это не парадоксально звучит, но направление вращения зависит исключительно от того, с какой стороны мы вращение наблюдаем.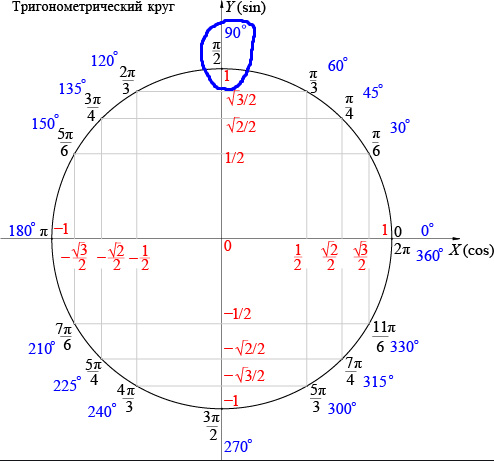 И так, у нас есть одно колесо, которое вращается. Мы не можем сказать, в каком направлении происходит вращение, поскольку мы его можем наблюдать как с одной стороны плоскости вращения, так и с другой. Мы можем только засвидетельствовать факт, что вращение есть. Полная аналогия с четностью бесконечной последовательности S .
И так, у нас есть одно колесо, которое вращается. Мы не можем сказать, в каком направлении происходит вращение, поскольку мы его можем наблюдать как с одной стороны плоскости вращения, так и с другой. Мы можем только засвидетельствовать факт, что вращение есть. Полная аналогия с четностью бесконечной последовательности S .
Теперь добавим второе вращающееся колесо, плоскость вращения которого параллельна плоскости вращения первого вращающегося колеса. Мы по прежнему не можем точно сказать, в каком направлении вращаются эти колеса, но мы абсолютно точно можем сказать, вращаются оба колеса в одну сторону или в противоположные. Сравнивая две бесконечные последовательности S и 1-S , я при помощи математики показал, что у этих последовательностей разная четность и ставить знак равенства между ними — это ошибка. Лично я верю математике, я не доверяю математикам))) Кстати, для полного понимания геометрии преобразований бесконечных последовательностей, необходимо вводить понятие «одновременность» .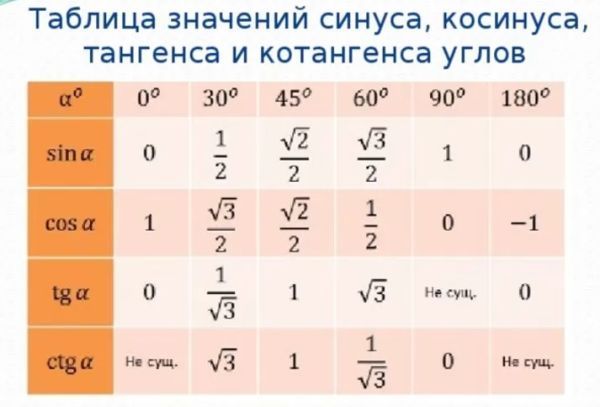 Это нужно будет нарисовать.
Это нужно будет нарисовать.
среда, 7 августа 2019 г.
Завершая разговор о , нужно рассмотреть бесконечное множество. Дало в том, что понятие «бесконечность» действует на математиков, как удав на кролика. Трепетный ужас перед бесконечностью лишает математиков здравого смысла. Вот пример:
Первоисточник находится . Альфа обозначает действительное число. Знак равенства в приведенных выражениях свидетельствует о том, что если к бесконечности прибавить число или бесконечность, ничего не изменится, в результате получится такая же бесконечность. Если в качестве примера взять бесконечное множество натуральных чисел, то рассмотренные примеры можно представить в таком виде:
Для наглядного доказательства своей правоты математики придумали много разных методов . Лично я смотрю на все эти методы, как на пляски шаманов с бубнами. По существу, все они сводятся к тому, что либо часть номеров не занята и в них заселяются новые гости, либо к тому, что часть посетителей вышвыривают в коридор, чтобы освободить место для гостей (очень даже по-человечески). Свой взгляд на подобные решения я изложил в форме фантастического рассказа о Блондинке. На чем основываются мои рассуждения? Переселение бесконечного количества посетителей требует бесконечно много времени. После того, как мы освободили первую комнату для гостя, один из посетителей всегда будет идти по коридору из своего номера в соседний до скончания века. Конечно, фактор времени можно тупо игнорировать, но это уже будет из разряда «дуракам закон не писан». Всё зависит от того, чем мы занимаемся: подгоняем реальность под математические теории или наоборот.
Свой взгляд на подобные решения я изложил в форме фантастического рассказа о Блондинке. На чем основываются мои рассуждения? Переселение бесконечного количества посетителей требует бесконечно много времени. После того, как мы освободили первую комнату для гостя, один из посетителей всегда будет идти по коридору из своего номера в соседний до скончания века. Конечно, фактор времени можно тупо игнорировать, но это уже будет из разряда «дуракам закон не писан». Всё зависит от того, чем мы занимаемся: подгоняем реальность под математические теории или наоборот.
Что же такое «бесконечная гостиница»? Бесконечная гостиница — это гостиница, в которой всегда есть любое количество свободных мест, независимо от того, сколько номеров занято. Если все номера в бесконечном коридоре «для посетителей» заняты, есть другой бесконечный коридор с номерами «для гостей». Таких коридоров будет бесконечное множество. При этом у «бесконечной гостиницы» бесконечное количество этажей в бесконечном количестве корпусов на бесконечном количестве планет в бесконечном количестве вселенных, созданных бесконечным количеством Богов. Математики же не способны отстраниться от банальных бытовых проблем: Бог-Аллах-Будда — всегда только один, гостиница — она одна, коридор — только один. Вот математики и пытаются подтасовывать порядковые номера гостиничных номеров, убеждая нас в том, что можно «впихнуть невпихуемое».
Математики же не способны отстраниться от банальных бытовых проблем: Бог-Аллах-Будда — всегда только один, гостиница — она одна, коридор — только один. Вот математики и пытаются подтасовывать порядковые номера гостиничных номеров, убеждая нас в том, что можно «впихнуть невпихуемое».
Логику своих рассуждений я вам продемонстрирую на примере бесконечного множества натуральных чисел. Для начала нужно ответить на очень простой вопрос: сколько множеств натуральных чисел существует — одно или много? Правильного ответа на это вопрос не существует, поскольку числа придумали мы сами, в Природе чисел не существует. Да, Природа отлично умеет считать, но для этого она использует другие математические инструменты, не привычные для нас. Как Природа считает, я вам расскажу в другой раз. Поскольку числа придумали мы, то мы сами будем решать, сколько множеств натуральных чисел существует. Рассмотрим оба варианта, как и подобает настоящим ученым.
Вариант первый. «Пусть нам дано» одно-единственное множество натуральных чисел, которое безмятежно лежит на полочке.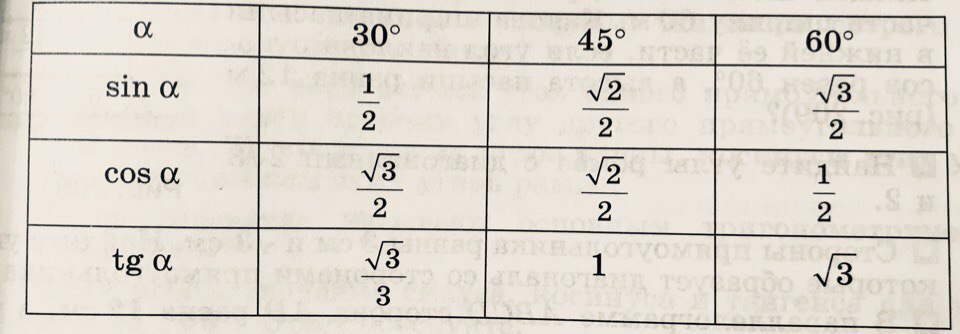 Берем с полочки это множество. Всё, других натуральных чисел на полочке не осталось и взять их негде. Мы не можем к этому множеству прибавить единицу, поскольку она у нас уже есть. А если очень хочется? Без проблем. Мы можем взять единицу из уже взятого нами множества и вернуть её на полочку. После этого мы можем взять с полочки единицу и прибавить её к тому, что у нас осталось. В результате мы снова получим бесконечное множество натуральных чисел. Записать все наши манипуляции можно так:
Берем с полочки это множество. Всё, других натуральных чисел на полочке не осталось и взять их негде. Мы не можем к этому множеству прибавить единицу, поскольку она у нас уже есть. А если очень хочется? Без проблем. Мы можем взять единицу из уже взятого нами множества и вернуть её на полочку. После этого мы можем взять с полочки единицу и прибавить её к тому, что у нас осталось. В результате мы снова получим бесконечное множество натуральных чисел. Записать все наши манипуляции можно так:
Я записал действия в алгебраической системе обозначений и в системе обозначений, принятой в теории множеств, с детальным перечислением элементов множества. Нижний индекс указывает на то, что множество натуральных чисел у нас одно и единственное. Получается, что множество натуральных чисел останется неизменным только в том случае, если из него вычесть единицу и прибавить эту же единицу.
Вариант второй. У нас на полочке лежит много разных бесконечных множеств натуральных чисел. Подчеркиваю — РАЗНЫХ, не смотря на то, что они практически не отличимы. Берем одно из этих множеств. Потом из другого множества натуральных чисел берем единицу и прибавляем к уже взятому нами множеству. Мы можем даже сложить два множества натуральных чисел. Вот что у нас получится:
Берем одно из этих множеств. Потом из другого множества натуральных чисел берем единицу и прибавляем к уже взятому нами множеству. Мы можем даже сложить два множества натуральных чисел. Вот что у нас получится:
Нижние индексы «один» и «два» указывают на то, что эти элементы принадлежали разным множествам. Да, если к бесконечному множеству прибавить единицу, в результате получится тоже бесконечное множество, но оно не будет таким же, как первоначальное множество. Если к одному бесконечному множеству прибавить другое бесконечное множество, в результате получится новое бесконечное множество, состоящее из элементов первых двух множеств.
Множество натуральных чисел используется для счета так же, как линейка для измерений. Теперь представьте, что к линейке вы добавили один сантиметр. Это уже будет другая линейка, не равная первоначальной.
Вы можете принимать или не принимать мои рассуждения — это ваше личное дело. Но если когда-то вы столкнетесь с математическими проблемами, задумайтесь, не идете ли вы по тропе ложных рассуждений, протоптанной поколениями математиков. Ведь занятия математикой, прежде всего, формируют у нас устойчивый стереотип мышления, а уже потом добавляют нам умственных способностей (или наоборот, лишают нас свободомыслия).
Ведь занятия математикой, прежде всего, формируют у нас устойчивый стереотип мышления, а уже потом добавляют нам умственных способностей (или наоборот, лишают нас свободомыслия).
pozg.ru
воскресенье, 4 августа 2019 г.
Дописывал постскриптум к статье о и увидел в Википедии этот замечательный текст:
Читаем: «… богатая теоретическая основа математики Вавилона не имела целостного характера и сводилась к набору разрозненных приемов, лишенных общей системы и доказательной базы.»
Вау! Какие мы умные и как хорошо можем видеть недостатки других. А слабо нам посмотреть на современную математику в таком же разрезе? Слегка перефразируя приведенный текст, лично у меня получилось следующее:
Богатая теоретическая основа современной математики не имеет целостного характера и сводится к набору разрозненных разделов, лишенных общей системы и доказательной базы.
За подтверждением своих слов я далеко ходить не буду — имеет язык и условные обозначения, отличные от языка и условных обозначений многих других разделов математики.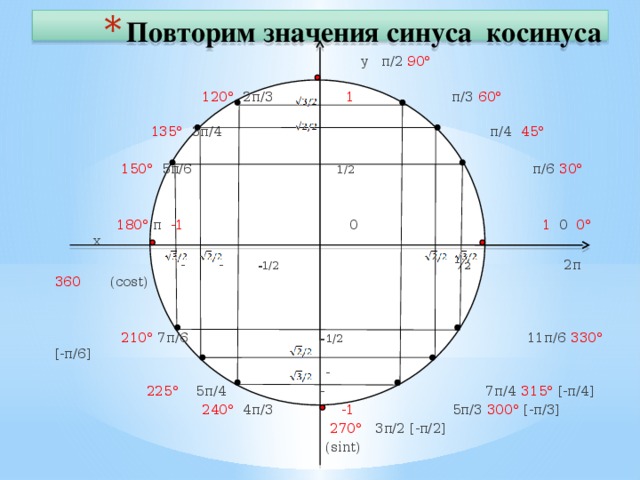 Одни и те же названия в разных разделах математики могут иметь разный смысл. Наиболее очевидным ляпам современной математики я хочу посвятить целый цикл публикаций. До скорой встречи.
Одни и те же названия в разных разделах математики могут иметь разный смысл. Наиболее очевидным ляпам современной математики я хочу посвятить целый цикл публикаций. До скорой встречи.
суббота, 3 августа 2019 г.
Как разделить множество на подмножества? Для этого необходимо ввести новую единицу измерения, присутствующую у части элементов выбранного множества. Рассмотрим пример.
Пусть у нас есть множество А , состоящее из четырех человек. Сформировано это множество по признаку «люди» Обозначим элементы этого множества через букву а , нижний индекс с цифрой будет указывать на порядковый номер каждого человека в этом множестве. Введем новую единицу измерения «половой признак» и обозначим её буквой b . Поскольку половые признаки присущи всем людям, умножаем каждый элемент множества А на половой признак b . Обратите внимание, что теперь наше множество «люди» превратилось в множество «люди с половыми признаками». После этого мы можем разделить половые признаки на мужские bm и женские bw половые признаки.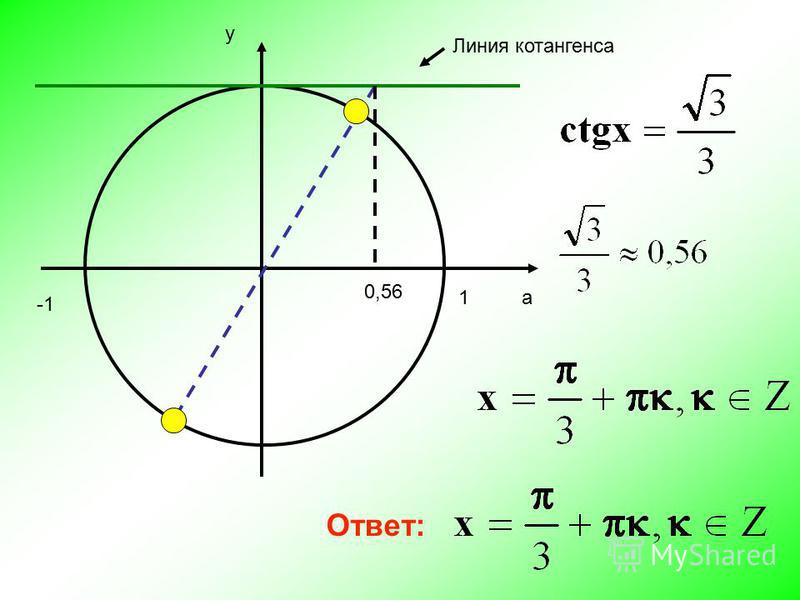 Вот теперь мы можем применить математический фильтр: выбираем один из этих половых признаков, безразлично какой — мужской или женский. Если он присутствует у человека, тогда умножаем его на единицу, если такого признака нет — умножаем его на ноль. А дальше применяем обычную школьную математику. Смотрите, что получилось.
Вот теперь мы можем применить математический фильтр: выбираем один из этих половых признаков, безразлично какой — мужской или женский. Если он присутствует у человека, тогда умножаем его на единицу, если такого признака нет — умножаем его на ноль. А дальше применяем обычную школьную математику. Смотрите, что получилось.
После умножения, сокращений и перегруппировок, мы получили два подмножества: подмножество мужчин Bm и подмножество женщин Bw . Приблизительно так же рассуждают математики, когда применяют теорию множеств на практике. Но в детали они нас не посвящают, а выдают готовый результат — «множество людей состоит из подмножества мужчин и подмножества женщин». Естественно, у вас может возникнуть вопрос, насколько правильно применена математика в изложенных выше преобразованиях? Смею вас заверить, по сути преобразований сделано всё правильно, достаточно знать математическое обоснование арифметики, булевой алгебры и других разделов математики. Что это такое? Как-нибудь в другой раз я вам об этом расскажу.
Что касается надмножеств, то объединить два множества в одно надмножество можно, подобрав единицу измерения, присутствующую у элементов этих двух множеств.
Как видите, единицы измерения и обычная математика превращают теорию множеств в пережиток прошлого. Признаком того, что с теорией множеств не всё в порядке, является то, что для теории множеств математики придумали собственный язык и собственные обозначения. Математики поступили так, как когда-то поступали шаманы. Только шаманы знают, как «правильно» применять их «знания». Этим «знаниям» они обучают нас.
В заключение, я хочу показать вам, как математики манипулируют с
Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.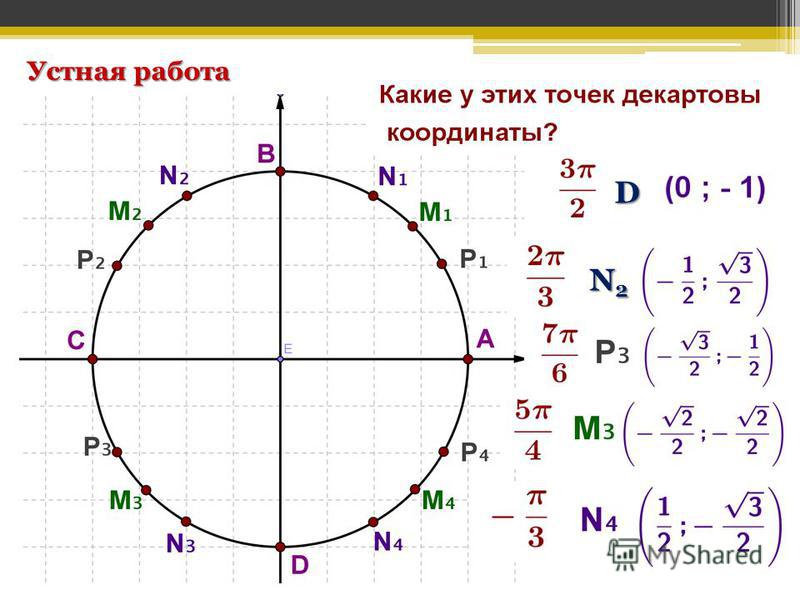
Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку.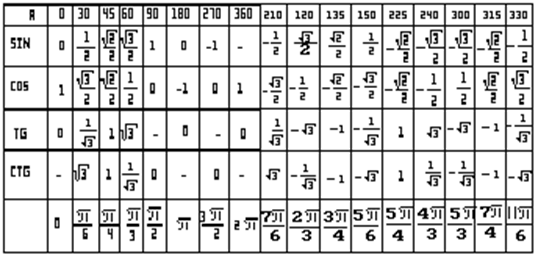 Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».
Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:
За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
Теперь Ахиллес на восемьсот шагов опережает черепаху.
Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Другая интересная апория Зенона повествует о летящей стреле:
Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.
В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Покажу процесс на примере. Отбираем «красное твердое в пупырышку» — это наше «целое». При этом мы видим, что эти штучки есть с бантиком, а есть без бантика. После этого мы отбираем часть «целого» и формируем множество «с бантиком». Вот так шаманы добывают себе корм, привязывая свою теорию множеств к реальности.
А теперь сделаем маленькую пакость. Возьмем «твердое в пупырышку с бантиком» и объединим эти «целые» по цветовому признаку, отобрав красные элементы. Мы получили множество «красное». Теперь вопрос на засыпку: полученные множества «с бантиком» и «красное» — это одно и то же множество или два разных множества? Ответ знают только шаманы. Точнее, сами они ничего не знают, но как скажут, так и будет.
Мы получили множество «красное». Теперь вопрос на засыпку: полученные множества «с бантиком» и «красное» — это одно и то же множество или два разных множества? Ответ знают только шаманы. Точнее, сами они ничего не знают, но как скажут, так и будет.
Этот простой пример показывает, что теория множеств совершенно бесполезна, когда речь заходит о реальности. В чем секрет? Мы сформировали множество «красное твердое в пупырышку с бантиком». Формирование происходило по четырем разным единицам измерения: цвет (красное), прочность (твердое), шероховатость (в пупырышку), украшения (с бантиком). Только совокупность единиц измерения позволяет адекватно описывать реальные объекты на языке математики . Вот как это выглядит.
Буква «а» с разными индексами обозначает разные единицы измерения. В скобках выделены единицы измерения, по которым выделяется «целое» на предварительном этапе. За скобки вынесена единица измерения, по которой формируется множество. Последняя строчка показывает окончательный результат — элемент множества.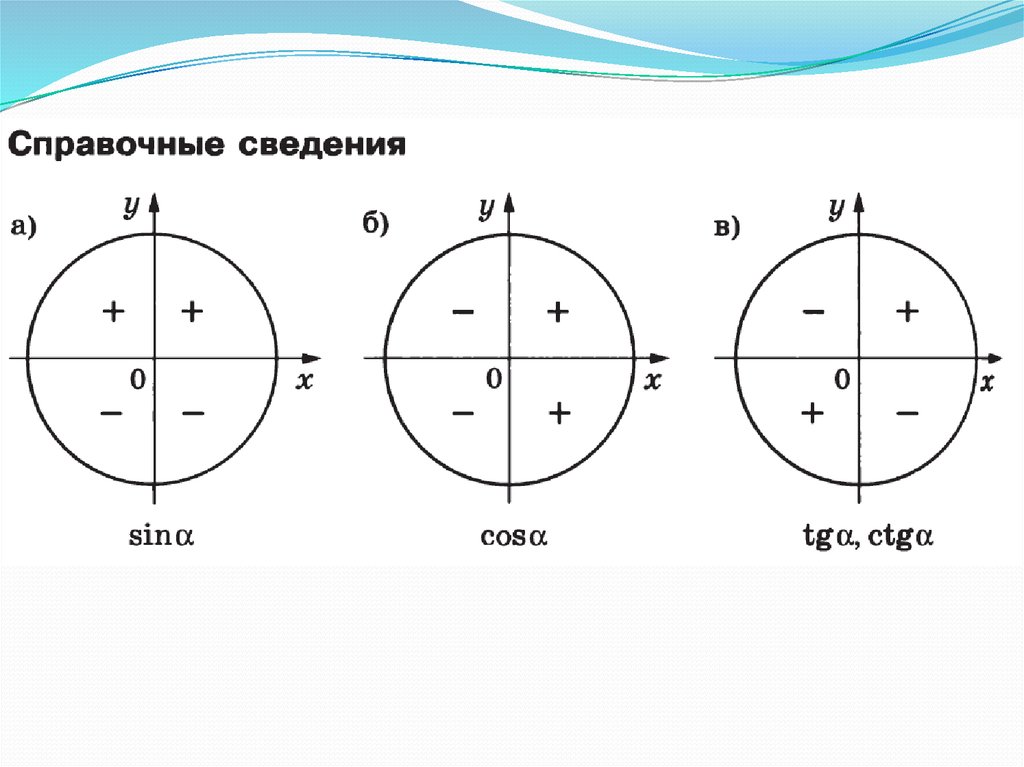 Как видите, если применять единицы измерения для формирования множества, тогда результат не зависит от порядка наших действий. А это уже математика, а не пляски шаманов с бубнами. Шаманы могут «интуитивно» придти к такому же результату, аргументируя его «очевидностью», ведь единицы измерения не входят в их «научный» арсенал.
Как видите, если применять единицы измерения для формирования множества, тогда результат не зависит от порядка наших действий. А это уже математика, а не пляски шаманов с бубнами. Шаманы могут «интуитивно» придти к такому же результату, аргументируя его «очевидностью», ведь единицы измерения не входят в их «научный» арсенал.
При помощи единиц измерения очень легко разбить одно или объединить несколько множеств в одно надмножество. Давайте более внимательно рассмотрим алгебру этого процесса.
Таблица значений тригонометрических функций составлена для углов в 0, 30, 45, 60, 90, 180, 270 и 360 градусов и соответствующих им значений углов врадианах . Из тригонометрических функций в таблице приведены синус, косинус, тангенс, котангенс, секанс и косеканс . Для удобства решения школьных примеров значения тригонометрических функций в таблице записаны в виде дроби с сохранением знаков извлечения корня квадратного из чисел, что очень часто помогает сокращать сложные математические выражения.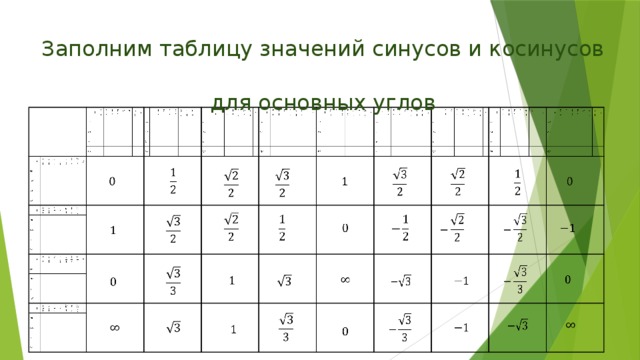 Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций.
Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций.
В таблице значений для тригонометрической функции синус приведены значения для следующих углов: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 в градусной мере, что соответствует sin 0 пи, sin пи/6, sin пи/4, sin пи/3, sin пи/2, sin пи, sin 3 пи/2, sin 2 пи в радианной мере углов. Школьная таблица синусов.
Для тригонометрической функции косинус в таблице приведены значения для следующих углов: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 в градусной мере, что соответствует cos 0 пи, cos пи на 6, cos пи на 4, cos пи на 3, cos пи на 2, cos пи, cos 3 пи на 2, cos 2 пи в радианной мере углов. Школьная таблица косинусов.
Школьная таблица косинусов.
Тригонометрическая таблица для тригонометрической функции тангенс приводит значения для следующих углов: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 в градусной мере, что соответствует tg 0 пи, tg пи/6, tg пи/4, tg пи/3, tg пи, tg 2 пи в радианной мере углов. Следующие значения тригонометрических функций тангенса не определены tg 90, tg 270, tg пи/2, tg 3 пи/2 и считаются равными бесконечности.
Для тригонометрической функции котангенс в тригонометрической таблице даны значения следующих углов: ctg 30, ctg 45, ctg 60, ctg 90, ctg 270 в градусной мере, что соответствует ctg пи/6, ctg пи/4, ctg пи/3, tg пи/2, tg 3 пи/2 в радианной мере углов. Следующие значения тригонометрических функций котангенса не определены ctg 0, ctg 180, ctg 360, ctg 0 пи, ctg пи, ctg 2 пи и считаются равными бесконечности.
Значения тригонометрических функций секанс и косеканс приведены для таких же углов в градусах и радианах, что и синус, косинус, тангенс, котангенс.
В таблице значений тригонометрических функций нестандартных углов приводятся значения синуса, косинуса, тангенса и котангенса для углов в градусах 15, 18, 22,5, 36, 54, 67,5 72 градусов и в радианах пи/12, пи/10, пи/8, пи/5, 3пи/8, 2пи/5 радиан.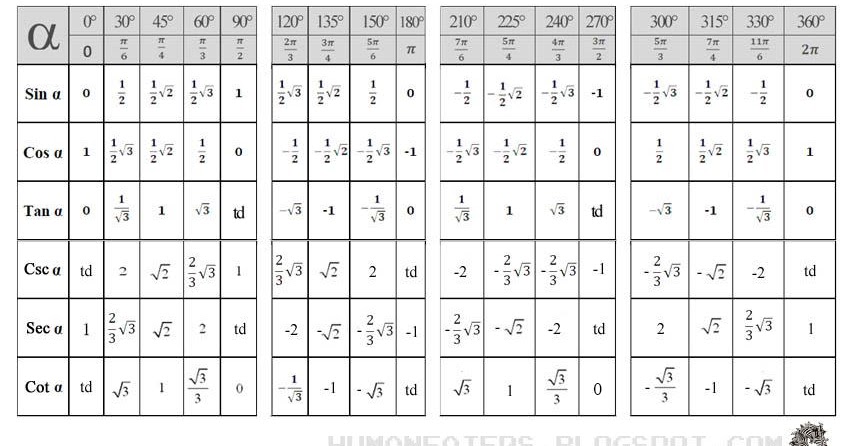 Значения тригонометрических функций выражены через дроби и корни квадратные для упрощения сокращения дробей в школьных примерах.
Значения тригонометрических функций выражены через дроби и корни квадратные для упрощения сокращения дробей в школьных примерах.
Еще три монстра тригонометрии. Первый — это тангенс 1,5 полутора градусов или пи деленное на 120. Второй — косинус пи деленное на 240, пи/240. Самый длинный — косинус пи деленное на 17, пи/17.
Тригонометрический круг значений функций синус и косинус наглядно представляет знаки синуса и косинуса в зависимости от величины угла. Специально для блондинок значения косинуса подчеркнуты зелененькой черточкой,чтоб меньше путаться. Так же очень наглядно представлен перевод градусов в радианы, когда радианы выражены через пи.
Эта тригонометрическая таблица представляет значения синуса, косинуса, тангенса и котангенса для углов от 0 нуля до 90 девяносто градусов с интервалом через один градус. Для первых сорока пяти градусов названия тригонометрических функций необходимо смотреть в верхней части таблицы. В первом столбце указаны градусы, значения синусов, косинусов, тангенсов и котангенсов записаны в следующих четырех столбцах.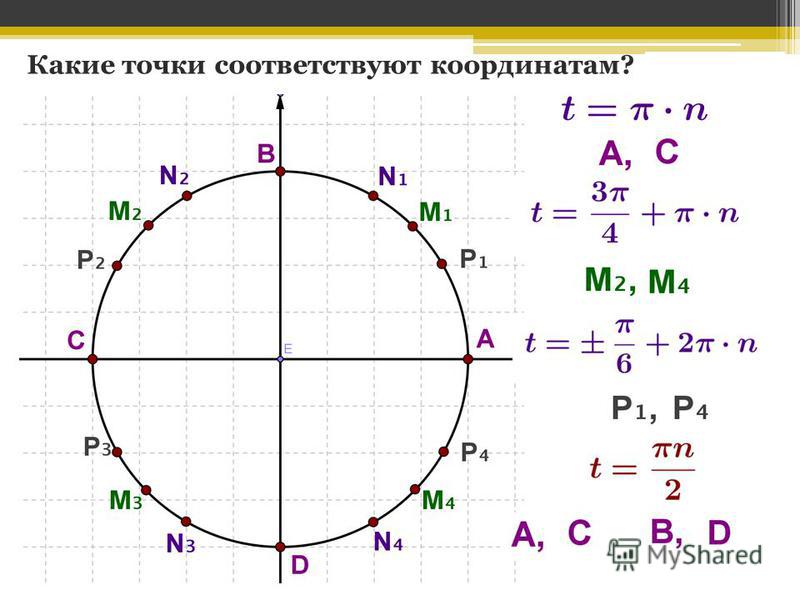
Для углов от сорока пяти градусов до девяноста градусов названия тригонометрических функций записаны в нижней части таблицы. В последнем столбце указаны градусы, значения косинусов, синусов, котангенсов и тангенсов записаны в предыдущих четырех столбцах. Следует быть внимательными, поскольку в нижней части тригонометрической таблицы названия тригонометрических функций отличаются от названий в верхней части таблицы. Синусы и косинусы меняются местами, точно так же, как тангенс и котангенс. Это связано с симметричностью значений тригонометрических функций.
Знаки тригонометрических функций представлены на рисунке выше. Синус имеет положительные значения от 0 до 180 градусов или от 0 до пи. Отрицательные значения синус имеет от 180 до 360 градусов или от пи до 2 пи. Значения косинуса положительны от 0 до 90 и от 270 до 360 градусов или от 0 до 1/2 пи и от 3/2 до 2 пи. Тангенс и котангенс имеют положительные значения от 0 до 90 градусов и от 180 до 270 градусов, что соответствует значениям от 0 до 1/2 пи и от пи до 3/2 пи.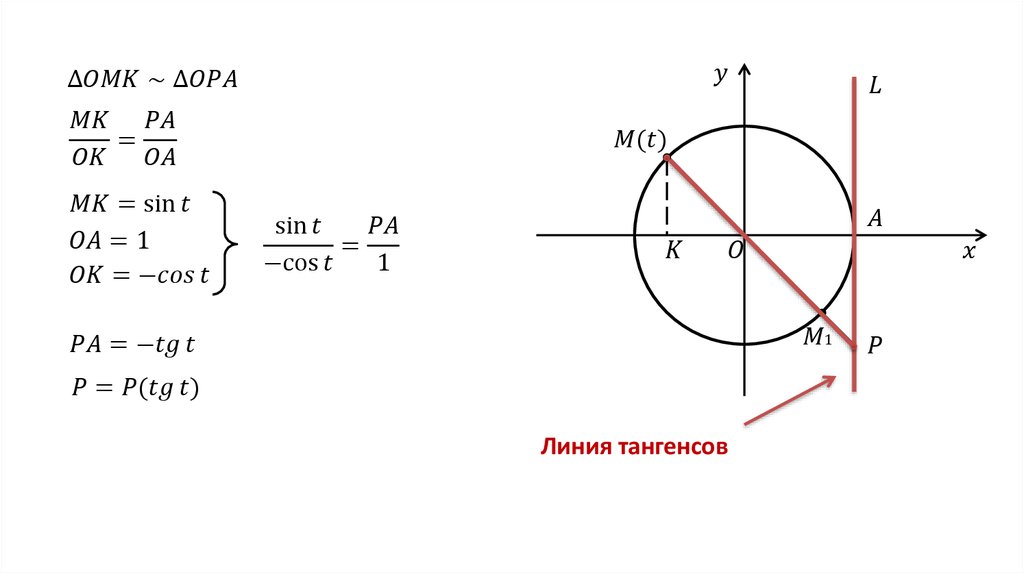 Отрицательные значения тангенс и котангенс имеют от 90 до 180 градусов и от 270 до 360 градусов или от 1/2 пи до пи и от 3/2 пи до 2 пи. При определении знаков тригонометрических функций для углов больше 360 градусов или 2 пи следует использовать свойства периодичности этих функций.
Отрицательные значения тангенс и котангенс имеют от 90 до 180 градусов и от 270 до 360 градусов или от 1/2 пи до пи и от 3/2 пи до 2 пи. При определении знаков тригонометрических функций для углов больше 360 градусов или 2 пи следует использовать свойства периодичности этих функций.
Тригонометрические функции синус, тангенс и котангенс являются нечетными функциями. Значения этих функций для отрицательных углов будут отрицательными. Косинус является четной тригонометрической функцией — значение косинуса для отрицательного угла будет положительным. При умножении и делении тригонометрических функций необходимо соблюдать правила знаков.
Корень 2/2 это сколько пи? — Это по-разному бывает (смотрите картинку). Нужно знать, какая именно тригонометрическая функция равна корню из двух, деленному на два.
Если вам понравилась публикация и вы хотите знать больше, мне в работе над другими материалами.
cos pi делённый на 2
Главная > Справочник > Математические формулы.
Математические формулы.
Перевод радиан в градусы.
A d = A r * 180 / пи
Перевод градусов в радианы.
A r = A d * пи / 180
Где A d — угол в градусах, A r — угол в радианах.
Длина окружности.
L = 2 * пи * R
Длина дуги окружности.
L = A * R
Площадь треугольника.
p=(a+b+c)/2 — полупериметр.
Площадь круга.
S = пи * R 2
Площадь сектора.
S = L d * R/2 = (A * R 2)/2
Площадь поверхности шара.
S = 4 * пи * R 2
S = 2 * пи * R * H
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
S = пи * R * L
S = пи * R * L + пи * R 2
Объем шара.
V = 4 / 3 * пи * R 3
Объем цилиндра.
V = пи * R 2 * H
Объем конуса.
Размещено: 15.01.13
Обновлено: 15.11.14
Просмотров всего: 10754
сегодня: 1
Главная > Справочник > Математические формулы.
Егор
Доброй вечер! Вы задали очень интересный вопрос, надеюсь, мы сможем Вам помочь.
Как решать С1. Урок 2. ЕГЭ по математике 2014
Нам с вами нужно решить такую задачку: найти cos pi делённый на 2.
Чаще всего для решения таких задач нужно определить показатели косинуса либо же синуса. Для углов от 0 до 360 градусов практически любое значение cos или sin можно с лёгкостью найти в соответствующих табличках, которые существуют и распространены, как например такие:
Но у нас с Вами не синус (sin), а косинус. Давайте сначала разберёмся, что такое косинус. Cos (косинус) — это одна из тригонометрических функцией. Для того, чтоб высчитать косинус острого прямоугольного треугольника Вам нужно будет знать отношение катета прилежащего угла к гипотенузе. Косинус pi делённый на 2 можно легко высчитать по тригонометрической формуле, которая относится к стандартным формулам тригонометрии. Но а если мы с Вами говорим о значении косинуса pi делённый на 2, то для этого мы воспользуемся таблицей, о которой уже вспоминали и не раз:
Но а если мы с Вами говорим о значении косинуса pi делённый на 2, то для этого мы воспользуемся таблицей, о которой уже вспоминали и не раз:
Удачи Вам в дальнейших решениях подобных заданий!
Ответ:
Главная > Справочник > Математические формулы.
Математические формулы.
Перевод радиан в градусы.
A d = A r * 180 / пи
Перевод градусов в радианы.
A r = A d * пи / 180
Где A d — угол в градусах, A r — угол в радианах.
Длина окружности.
L = 2 * пи * R
Где L — длина окружности, R — радиус окружности.
Длина дуги окружности.
L = A * R
Где L — длина дуги окружности, R — радиус окружности, A — центральный угол, выраженный в радианах
Для окружности A = 2*пи (360 градусов), получим L = 2*пи*R.
Площадь треугольника.
S = (p * (p-a) * (p-b) * (p-c)) 1/2
Где S — площадь треугольника, a, b, c — длины сторон,
p=(a+b+c)/2 — полупериметр.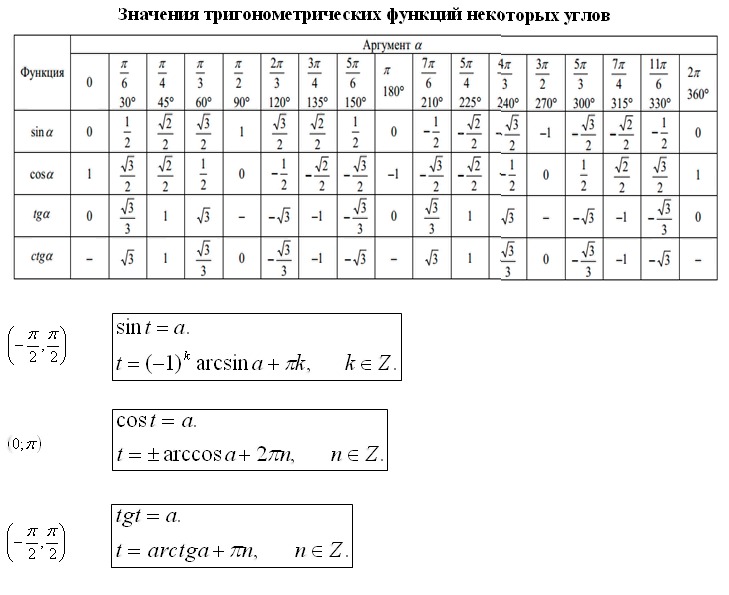
Площадь круга.
S = пи * R 2
Где S — площадь круга, R — радиус круга.
Площадь сектора.
S = L d * R/2 = (A * R 2)/2
Где S — площадь сектора, R — радиус круга, L d — длина дуги.
Площадь поверхности шара.
S = 4 * пи * R 2
Где S — площадь поверхности шара, R — радиус шара.
Площадь боковой поверхности цилиндра.
S = 2 * пи * R * H
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
Площадь полной поверхности цилиндра.
S = 2 * пи * R * H + 2 * пи * R 2
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
Площадь боковой поверхности конуса.
S = пи * R * L
Где S — площадь боковой поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.
Площадь полной поверхности конуса.
S = пи * R * L + пи * R 2
Где S — площадь полной поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.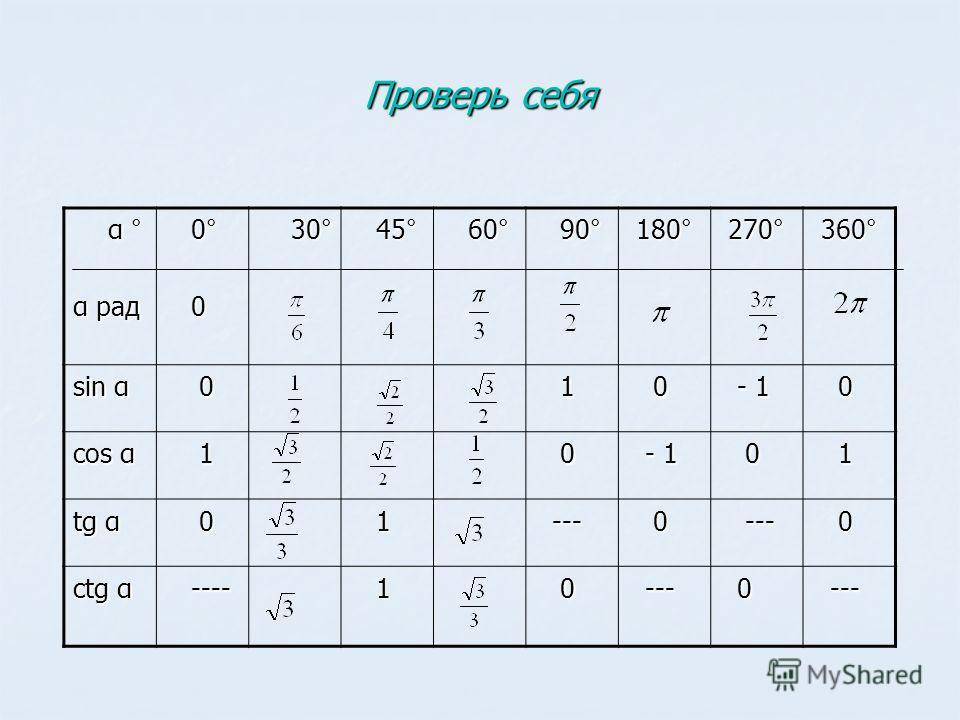
Объем шара.
V = 4 / 3 * пи * R 3
Где V — объем шара, R — радиус шара.
Объем цилиндра.
V = пи * R 2 * H
Где V — объем цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
Объем конуса.
V = пи * R * L = пи * R * H/cos (A/2) = пи * R * R/sin (A/2)
Где V — объем конуса, R — радиус основания конуса, L — длина образующей конуса, A — угол при вершине конуса.
Размещено: 15.01.13
Обновлено: 15.11.14
Просмотров всего: 10742
сегодня: 1
Главная > Справочник > Математические формулы.
Егор
Закрепить провод на клеммах батарейки Крона можно трубочкой, отрезанной от колпачка медицинской иголки.
Существует несколько вариантов вычисления значения выражения cos (3 / 2 Пи).
Первый вариант. Использование
Этот вариант самый легкий и простой и заключается в том, что в таблице нужно найти соответствующие значения.
Существует много разновидностей таблицы, в некоторых из них аргументы представлены только в виде радиан, в других — в градусах, а некоторые содержат значения и радиан, и градусов.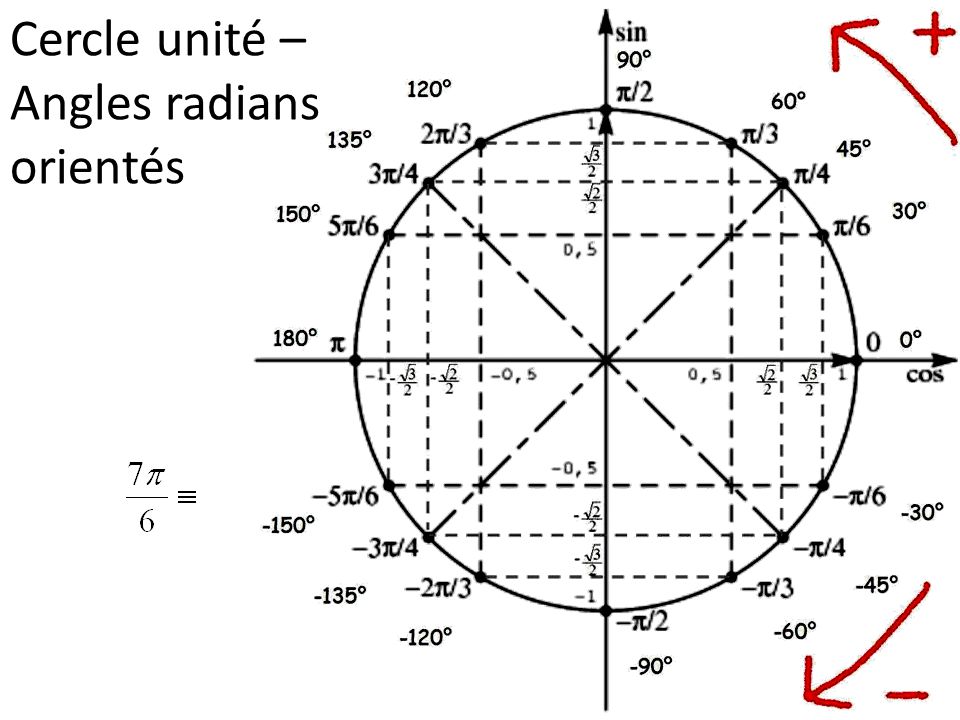
Иногда все же полезно перевести значение угла в градусы, чтобы легче воспринять значение косинуса. Но не запрещается использовать таблицу с градусами и радианами)).
Из таблицы определим значение косинуса от 3 Пи / 2 — это 0.
Математическая запись:
Второй вариант. .
Удобный вариант, если недоступна таблица тригонометрических функций. Здесь значение тригонометрической функции можно определить с помощью тригонометрической окружности.
На тригонометрической окружности (или круге) на оси абсцисс расположены значения функции косинус.
Согласно заданию аргумент функции равен 3 Пи / 2. На окружности это значение находится на оси ординат в самом низу. Чтобы вычислить значение заданной функции нужно опустить перпендикуляр на ось Ох, после чего получим значение 0. Таким образом, косинус от 3 Пи / 2 равен 0.
Третий вариант. Использование .
Если нет таблицы, а по тригонометрической окружности ориентироваться сложно, то полезно использовать график косинуса, по которому также можно определить значение.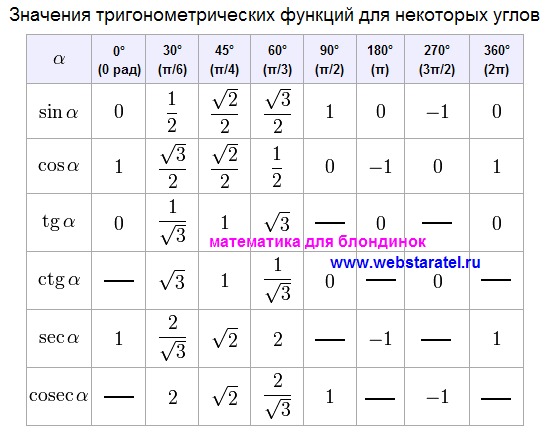
Примечание . В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. См. также полезные материалы: Для определения значения тригонометрической функции , найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов. Синус пи, косинус пи, тангенс пи и других углов в радианахПриведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах . Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам. Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180 . Примеры : 2. Косинус пи . 3. Тангенс пи Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)
Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов0, 15, 30, 45, 60, 90 … 360 градусов (цифровые значения «как по таблицам Брадиса»)
|
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы 92 | ||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Детская кроватка пи/3 — Найти значение Детская кроватка пи/3
LearnPracticeDownload
Значение cot pi/3 равно 0,5773502. . . . Раскладушка пи/3 радиана в градусах записывается как раскладушка ((π/3) × 180°/π), т. е. раскладушка (60°). В этой статье мы обсудим методы нахождения значения cot pi/3 на примерах.
. . . Раскладушка пи/3 радиана в градусах записывается как раскладушка ((π/3) × 180°/π), т. е. раскладушка (60°). В этой статье мы обсудим методы нахождения значения cot pi/3 на примерах.
- Колыбель пи/3: 1/√3
- Кот пи/3 в десятичном виде: 0,5773502. . .
- Детская кроватка (-pi/3): -0,5773502. . . или -(1/√3)
- Cot pi/3 в градусах: детская кроватка (60°)
Каково значение Cot pi/3?
Значение cot pi/3 в десятичном виде равно 0,577350269. . .. Cot pi/3 также можно выразить с помощью эквивалента заданного угла (pi/3) в градусах (60°).
Мы знаем, используя преобразование радиан в градусы, θ в градусах = θ в радианах × (180°/pi)
⇒ пи/3 радиана = пи/3 × (180°/пи) = 60° или 60 градусов
∴ кроватка пи/3 = кроватка π/3 = кроватка (60°) = 1/√3 или 0,5773502. . .
Объяснение:
Для кроватки pi/3 угол pi/3 лежит между 0 и pi/2 (первый квадрант). Поскольку функция котангенса положительна в первом квадранте, значение cot pi/3 = 1/√3 или 0,5773502. . .
Поскольку функция котангенса положительна в первом квадранте, значение cot pi/3 = 1/√3 или 0,5773502. . .
Поскольку функция котангенса является периодической функцией, мы можем представить cot pi/3 как cot pi/3 = cot(pi/3 + n × pi), n ∈ Z.
⇒ раскладушка пи/3 = раскладушка 4пи/3 = раскладушка 7пи/3 и так далее.
Примечание: Поскольку котангенс является нечетной функцией, значение cot(-pi/3) = -cot(pi/3).
Методы определения значения Cot pi/3
Функция котангенса положительна в 1-м квадранте. Значение cot pi/3 равно 0,57735. . .. Мы можем найти значение кроватки пи/3 по:
- Используя тригонометрические функции
- Использование единичного круга
Cot pi/3 в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить cot pi/3 как:
- cos(pi/3)/sin(pi/3)
- ± cos(pi/3)/√(1 — cos²(pi/3))
- ± √(1 — sin²(pi/3))/sin(pi/3) г.
- ± 1/√(сек²(пи/3) — 1)
- ± √(cosec²(pi/3) — 1)
- 1/тангенс (пи/3)
Примечание: Поскольку pi/3 лежит в 1-м квадранте, окончательное значение cot pi/3 будет положительным.
Мы можем использовать тригонометрические тождества, чтобы представить cot pi/3 как
- tan (pi/2 — pi/3) = tan pi/6
- -тангенс (пи/2 + пи/3) = -тангенс 5пи/6
- -кроватка (пи — пи/3) = -кроватка 2пи/3
Детская кроватка пи/3 с использованием единичного круга
Чтобы найти значение cot π/3 с помощью единичной окружности:
- Поверните «r» против часовой стрелки, чтобы образовать угол пи/3 с положительной осью x.
- Раскладушка pi/3 равна координате x (0,5), деленной на координату y (0,866) точки пересечения (0,5, 0,866) единичной окружности и r.
Отсюда значение cot pi/3 = x/y = 0,5774 (приблизительно)
☛ Также проверьте:
- cos 3pi
- , потому что 5pi/8
- , потому что 2pi/8
- желтовато-коричневый 5pi/2
- грех 5pi/8
- рыжевато-коричневый 2pi/3
Примеры использования Cot pi/3
Пример 1: Используя значение cot pi/3, найдите: (cosec²(pi/3) — 1).

Решение:
Мы знаем, (cosec²(pi/3) — 1) = (cot²(pi/3)) = 0,3333
⇒ (косек²(пи/3) — 1) = 0,3333Пример 2: Упрощение: 9(cot(pi/3)/tan(pi/6))
Решение:
Мы знаем cot pi/3 = tan pi/6
⇒ 9 раскладушка(пи/3)/танг(пи/6) = 9 (раскладушка(пи/3)/раскладушка(пи/3))
= 9(1) = 9Пример 3. Найдите значение (cos (pi/3) cosec (pi/6) sec (pi/6))/2. [Подсказка: используйте cot pi/3 = 0,5774]
Решение:
Используя формулы тригонометрии,
(cos (pi/3) cosec (pi/6) sec (pi/6))/2 = cos (pi/3)/(2 sin (pi/6) cos (pi/6))
г. Используя формулу sin 2a,
2 sin (pi/6) cos (pi/6) = sin (2 × pi/6) = sin pi/3
⇒ cos (pi/3) / sin (pi/3) = кроватка pi/3
⇒ (cos (pi/3) cosec (pi/6) sec (pi/6))/2 = 0,5774
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о Cot pi/3
Что такое Cot pi/3?
Cot pi/3 — значение котангенса тригонометрической функции для угла, равного π/3 радиан. Значение cot pi/3 равно 1/√3 или 0,5774 (приблизительно).
Как найти значение Ct pi/3?
Значение cot pi/3 можно рассчитать, построив угол π/3 радиан с осью x, а затем найдя координаты соответствующей точки (0,5, 0,866) на единичной окружности. Значение cot pi/3 равно координате x (0,5), деленной на координату y (0,866). ∴ ctg пи/3 = 0,5774
Как найти число пи/3 в терминах других тригонометрических функций?
Используя формулу тригонометрии, значение cot pi/3 может быть выражено через другие тригонометрические функции следующим образом:
- cos(pi/3)/sin(pi/3)
- ± cos(pi/3)/√(1 — cos²(pi/3))
- ± √(1 — sin²(pi/3))/sin(pi/3)
- ± 1/√(сек²(пи/3) — 1)
- ± √(cosec²(pi/3) — 1)
- 1/тангенс (пи/3)
☛ Также проверьте: таблицу тригонометрии
Каково значение Cot pi/3 в пересчете на Sin pi/3?
Используя тригонометрические тождества, мы можем записать кроватку pi/3 через sin pi/3 как кроватка(pi/3) = √(1 — sin²(pi/3))/sin pi/3 . Здесь значение sin pi/3 равно √3/2.
Здесь значение sin pi/3 равно √3/2.
Каково значение Cot pi/3 в пересчете на Cosec pi/3?
Поскольку функцию котангенса можно представить с помощью функции косеканса, мы можем записать cot pi/3 как √(cosec²(pi/3) — 1). Значение cosec pi/3 равно 1,15470.
Загрузить БЕСПЛАТНЫЕ учебные материалы
Тригонометрия
Рабочие листы по математике и
визуальный учебный план
Решения Бальбхарати по математике и статистике 1 (Искусство и наука) 11-й Стандарт Государственного совета Махараштры, глава 3 — Тригонометрия — 2 [Последнее издание]
919 решения по математике и статистике 1 (Искусство и наука) 11-й Стандартный совет штата Махараштра Глава 3 Тригонометрия — 2 Разное Упражнение 3 [Страницы 56 — 58]Разное Упражнение 3 | Вопрос I. (1) | Страница 56
Выберите правильный вариант из предложенных вариантов:
Значение sin(n + 1) A sin (n + 2) A + cos(n + 1) A cos(n + 2) A равно
SIN A
COS A
— COS A
SIN 2A
Взгляд Раствор
MISCELLENEGNARY 3 | Q I. (2) | Страница 56
(2) | Страница 56
Выберите правильный вариант из предложенных вариантов:
Если tan A – tan B = x и cot B – cot A = y, то cot (A – B) = _____
`1/y — 1/x`
`1/x — 1/y`
`1/x + 1/y`
x
17 17 ` — y)`
ПРОСМОТР РЕШЕНИЯ
Разное Упражнение 3 | Вопрос I. (3) |
Выберите правильный вариант из предложенных вариантов:
Если sin θ = n sin (θ + 2α), то tan (θ + α) равен
`(1 + n)/(2 — n) tan alpha`
`(1 — n)/(1 + n) tan alpha`
tan α
`(1 + n)/(1 — n) tan alpha`
ПРОСМОТР РЕШЕНИЯ
Разное Упражнение 3 | Вопрос I. (iv) | Страница 57
Выберите правильный вариант из предложенных вариантов:
Значение `costheta/(1 + sin theta)` равно ……
`tan(theta/2 — pi/4)`
`tan(-pi/4 — theta/2)`
`tan(pi/4 — theta/2)`
`tan(pi/4 + theta/2)`
ПРОСМОТР РЕШЕНИЯ
Разное Упражнение 3 | Вопрос I. (v) | Страница 57
(v) | Страница 57
Выберите правильный вариант из предложенных вариантов:
Значение cos A cos (60° – A) cos (60° + A) равно ……
`1/ 2Cos3 «a» `
COS 3A
` 1/4COS3 «A» `
4 COS 3A
Просмотр
1811. Вопрос I. (vi) | Страница 57
Выберите правильный вариант из предложенных:
Значение `sin pi/14sin (3pi)/14sin (5pi)/14sin (7pi)/14sin (9pi)/14sin (11pi)/14sin (13pi)/14 ` is ….
`1/16`
`1/64`
`1/128`
`1/256`
VIEW SOLUTION
Разное Упражнение 3 | Вопрос I. (vii) | Страница 57
Выберите правильный вариант из предложенных вариантов:
Если α + β + γ = π, то значение sin 2 α + sin 2 β – sin 2 γ равно ………
2 sin α
7 27
2 sin α cos β sin γ
2 sin α sin β cos γ
2 sin α sin β sin γ
ПРОСМОТР Упражнение 3 Разное
1
Вопрос I. (viii) | Страница 57
(viii) | Страница 57
Выберите правильный вариант из предложенных вариантов:
Пусть 0 < A, B < `pi/2` удовлетворяет уравнению 3 sin 2 A + 2 sin 2 B = 1 и 3 sin 2A − 2 sin 2B = 0, тогда A + 2B равно ______
π
`pi/2`
12π
1 pi/4`
ПРОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Q I, (ix) | Страница 57
Выберите правильный вариант из предложенных вариантов:
В ∆ABC, если cot A cot B cot C > 0, то треугольник равен _________
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Q I. (х) |
Выберите правильный вариант из предложенных вариантов:
Числовое значение tan 20° tan 80° cot 50° равно ______.
`sqrt(3)`
`1/sqrt(3)`
`2sqrt(3)`
`1/(2sqrt(3)`
VIEW РЕШЕНИЕ
Разное Упражнение 3 Q II (1) Страница 57
Докажите следующее:
tan 20° tan 80° cot 50° = `sqrt(3)`
ПРОСМОТР РЕШЕНИЯ
Разное Упражнение 3 | Вопрос II. (2) |
(2) |
Докажите следующее:
Если sin α sin β − cos α cos β + 1 = 0, то докажите cot α tan β = −1
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос II. (3) |
Докажите следующее:
`cos (2pi)/15 cos (4pi)/15cos (8pi)/15cos (16pi)/15 = 1/16`
ПРОСМОТР РЕШЕНИЯ
Разное Упражнение 3 | Вопрос II. (4) | Страница 57
Докажите следующее:
`(1 + cos pi/8)(1 + cos (3pi)/8)(1 + cos (5pi)/8)(1 + cos (7pi)/8) = 1/ 8`
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос II. (5) |
Докажите следующее:
cos 12°+ cos 84° + cos 156° + cos 132° = `-1/2`
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос II. (6) |
Докажите следующее:
`cos(pi/4 + x) + cos(pi/4 — x) = sqrt(2)cosx`
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос II. (7) |
Докажите следующее:
`(sin5x — 2sin3x + sinx)/(cos5x — cosx)` = tanx
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос II. (8) |
(8) |
Докажите следующее:
sin 2 6x − sin 2 4x = sin2x sin10x
ПРОСМОТР РЕШЕНИЯ
Разное Упражнение 3 | Вопрос II. (9) | Страница 57
Докажите следующее:
cos 2 2x − cos 2 6x = sin4x sin8x
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос II. (10) |
Докажите следующее:
cot4x (sin5x + sin3x) = cotx (sin5x − sin3x)
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос II. (11) |
Докажите следующее:
`(cos9x — cos5x)/(sin17x — sin3x) = — (sin2x)/(cos10x)`
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос II. (12) | Страница 57
Докажите следующее:
Если sin 2A = λsin 2B, то докажите, что `(tan(«A» + «B»))/(tan(«A» — «B»)) = (lambda + 1)/(lambda — 1)`
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос II. (13) |
Докажите следующее:
`(2cos2″A» + 1)/(2cos2″A» — 1)` = tan(60° + A) tan(60° − A)
ПРОСМОТР РЕШЕНИЯ
Разное Упражнение 3 | Вопрос II. (14) | Страница 57
(14) | Страница 57
Докажите следующее:
tanA + tan(60° + A) + tan(120° + A) = 3 tan 3A
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос II. (15) | Страница 57
Докажите следующее:
3tan 6 10° – 27 tan 4 10° + 33tan 2 10° = 1
VIEW Разное | Вопрос II. (16) |
Докажите следующее:
cosec 48° + cosec 96° + cosec 192° + cosec 384° = 0
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос II. (17) | Страница 58
Докажите следующее:
3(sin x – cos x) 4 + 6(sin x + cos x) 2 + 4(sin 6 x + cos 6 x) = 13
ПРОСМОТР РЕШЕНИЯ
1 Разное
| Вопрос II. (18) |
Докажите следующее:
tan A + 2 tan 2A + 4 tan 4A + 8 cot 8A = cot A
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос II. (19) |
Докажите следующее:
Если A + B + C = `(3pi)/2`, то cos 2A + cos 2B + cos 2C = 1 − 4 sin A sin B sin C 92x)` = secx cosecx − 2sinx cosx
ПОСМОТРЕТЬ РЕШЕНИЕ
Разное Упражнение 3 | Вопрос II.

 Угол между двумя катетами является прямым, то есть он равен 90 градусам.
Угол между двумя катетами является прямым, то есть он равен 90 градусам.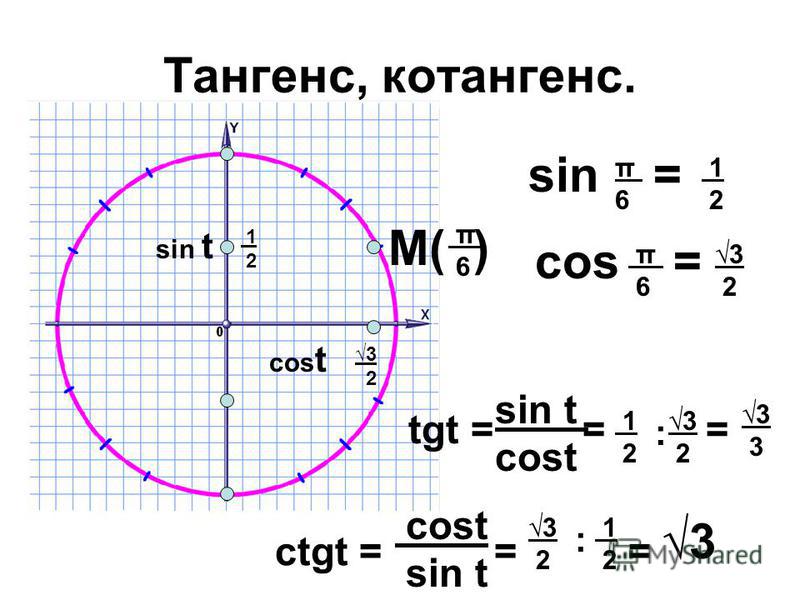 ..
..
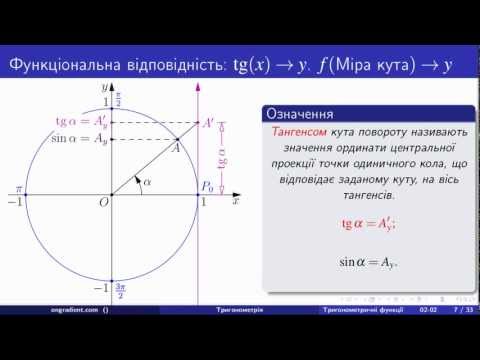
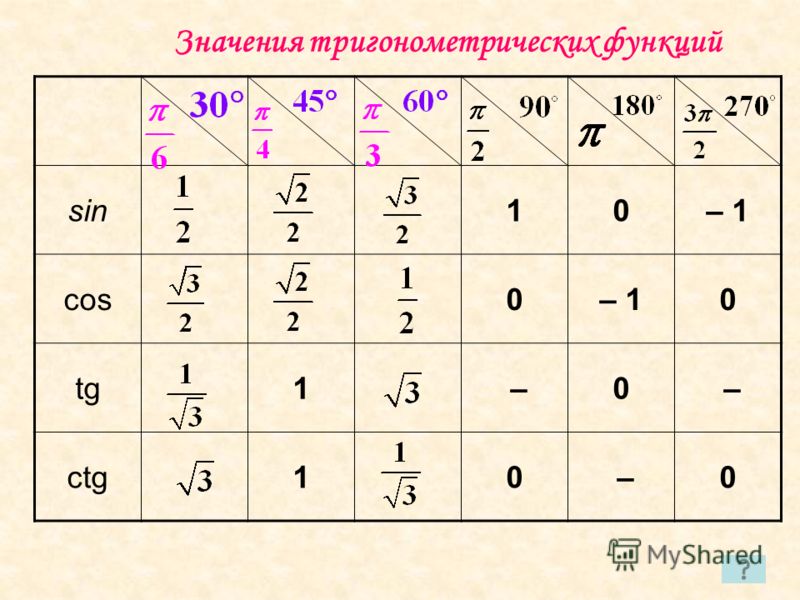 К примеру, найти tg 78 0 37мин = 4,967
К примеру, найти tg 78 0 37мин = 4,967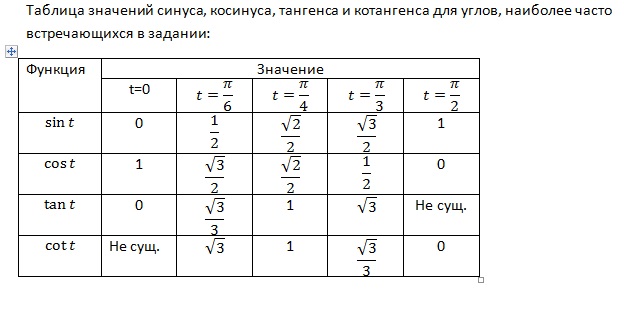 Почему почти? Об этом ниже.
Почему почти? Об этом ниже. На этих углах построена вся школьная геометрия и тригонометрия. Это, своего рода, «таблица умножения» тригонометрии. Если вы не знаете, чему равен, например, sin50°, никто вас не осудит.) Но если вы не знаете, чему равен sin30°, будьте готовы получить заслуженную двойку…
На этих углах построена вся школьная геометрия и тригонометрия. Это, своего рода, «таблица умножения» тригонометрии. Если вы не знаете, чему равен, например, sin50°, никто вас не осудит.) Но если вы не знаете, чему равен sin30°, будьте готовы получить заслуженную двойку…
 Наведите курсор на картинку (или коснитесь картинки на планшете) и всё увидите.
Наведите курсор на картинку (или коснитесь картинки на планшете) и всё увидите.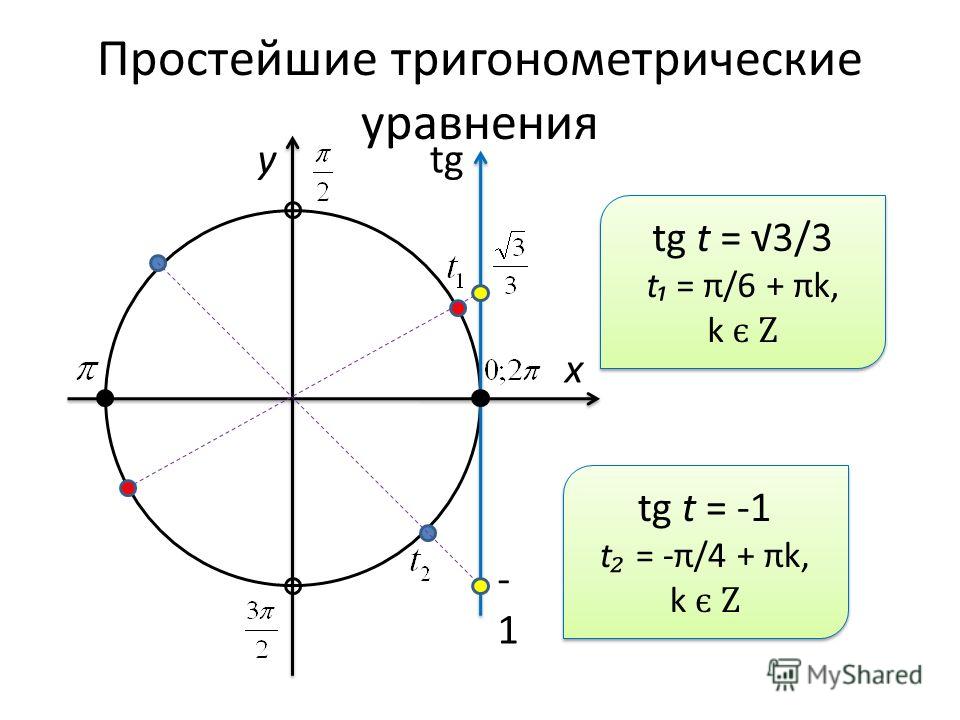 Вот и всё.
Вот и всё.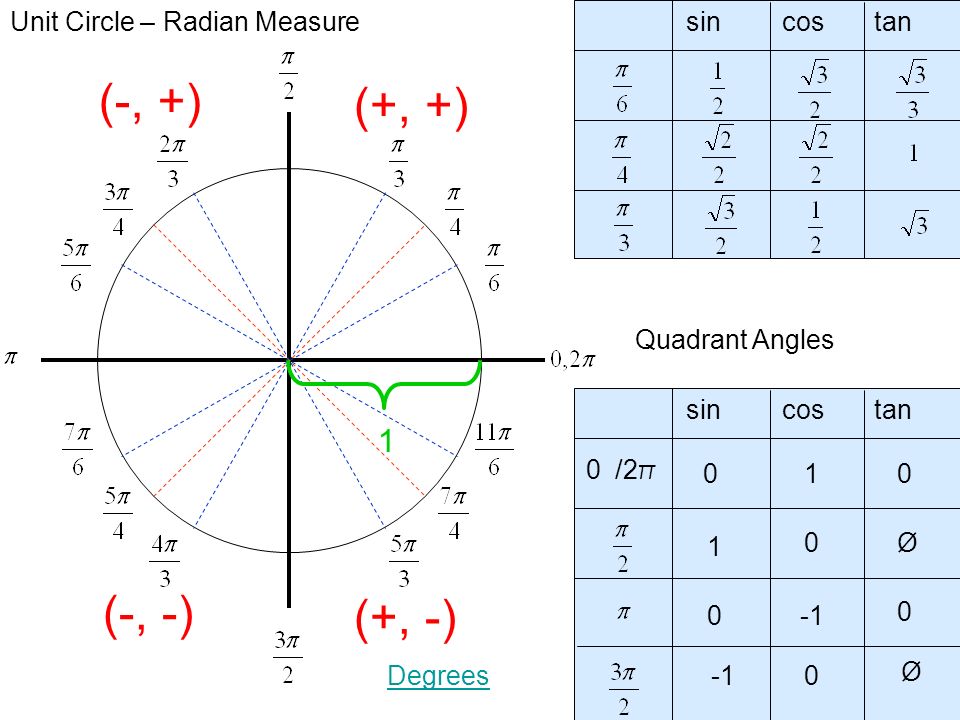 ..) Отсчитал (правильно!) угол на круге — и нет проблем с функциями.
..) Отсчитал (правильно!) угол на круге — и нет проблем с функциями.
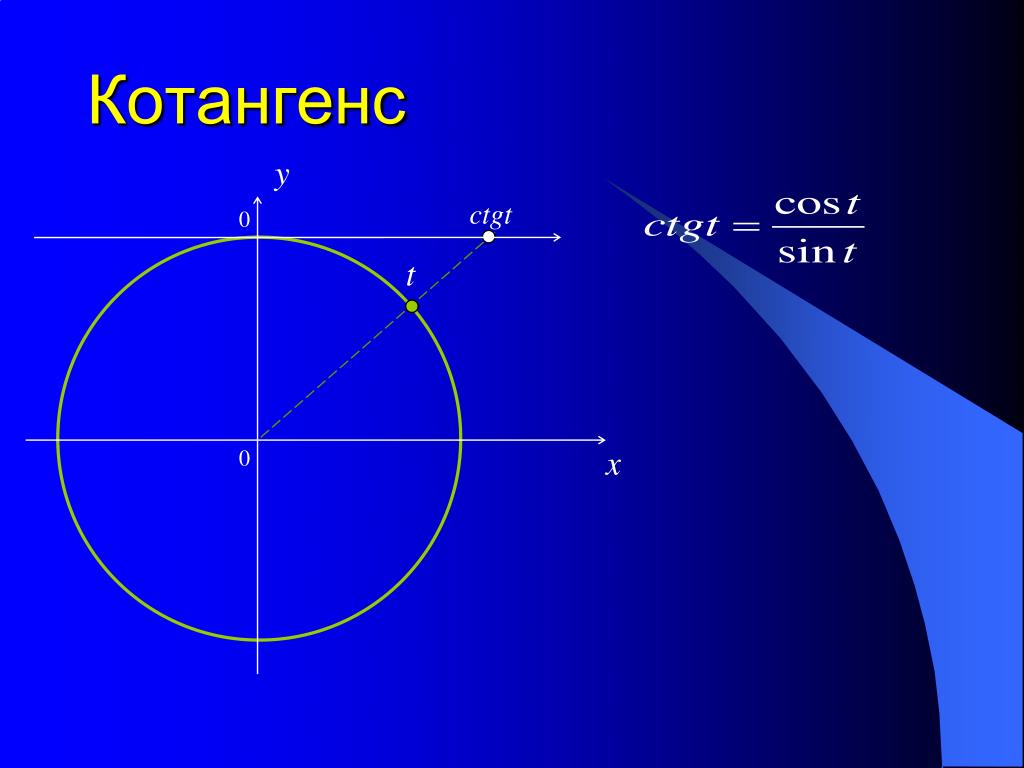
 Для углов 20, 50, 80 так бы не получилось…
Для углов 20, 50, 80 так бы не получилось…
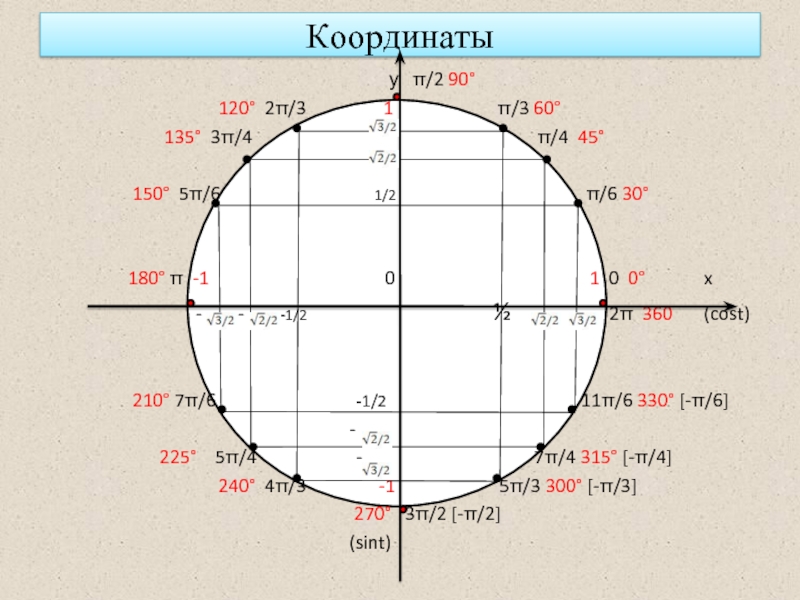 Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
Данные функции часто появляются при решении дифференциальных и функциональных уравнений. Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y:
Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y: 
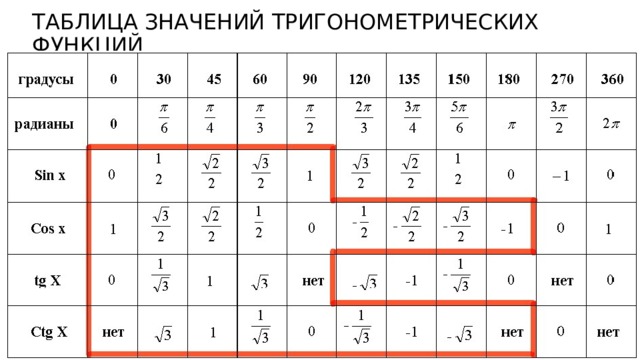
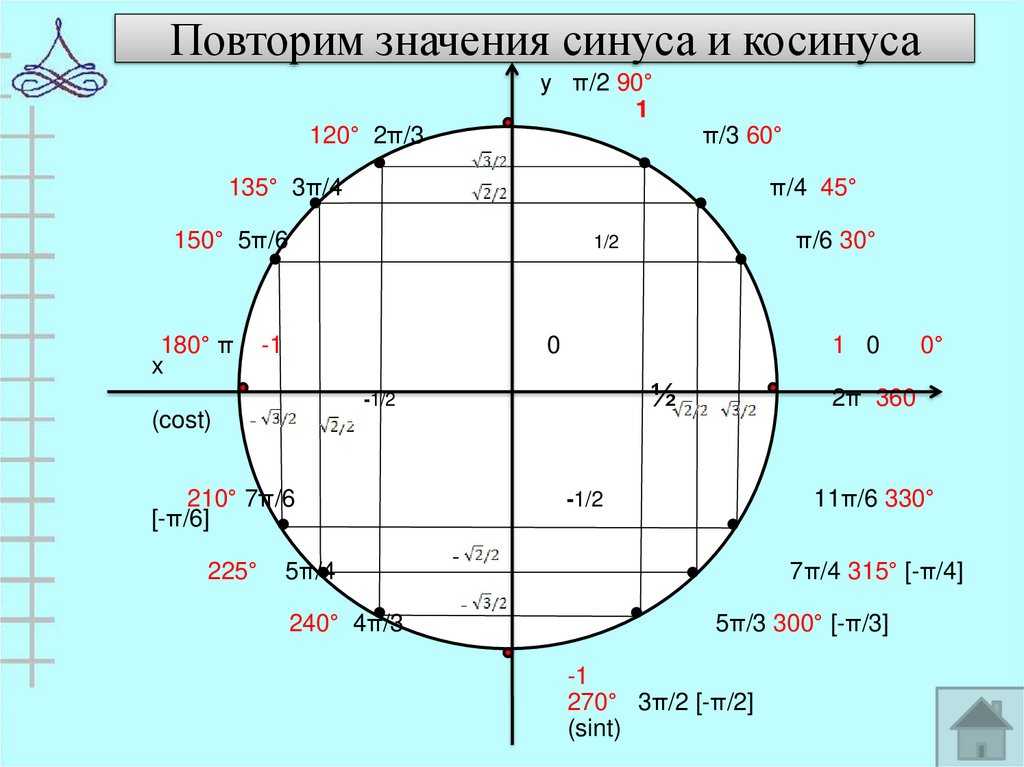 Градус, короче, штука простая…
Градус, короче, штука простая…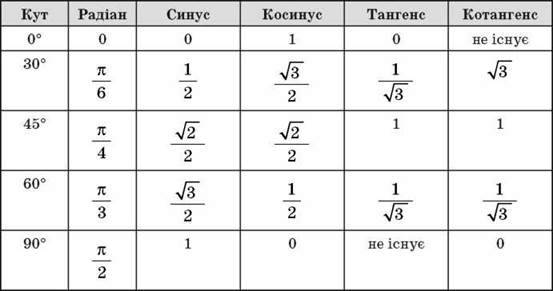 В принципе нельзя. Ну, во сколько раз окружность больше диаметра установили, конечно. Примерно. В 3,1415926… раз.
В принципе нельзя. Ну, во сколько раз окружность больше диаметра установили, конечно. Примерно. В 3,1415926… раз. Выскажу версию. У древних вавилонян не спросишь… Для строительства, или, скажем, астрономии, круг удобно делить на равные части. А теперь прикиньте, на какие числа делится нацело 100, и на какие — 360? И в каком варианте этих делителей нацело — больше? Людям такое деление очень удобно. Но…
Выскажу версию. У древних вавилонян не спросишь… Для строительства, или, скажем, астрономии, круг удобно делить на равные части. А теперь прикиньте, на какие числа делится нацело 100, и на какие — 360? И в каком варианте этих делителей нацело — больше? Людям такое деление очень удобно. Но… Смотрим картинки.
Смотрим картинки. Как? Легко! Если в 3,14 радианах 180° градусов, то в 1 радиане в 3,14 раз меньше! То есть, мы делим первое уравнение (формула — это тоже уравнение!) на 3,14:
Как? Легко! Если в 3,14 радианах 180° градусов, то в 1 радиане в 3,14 раз меньше! То есть, мы делим первое уравнение (формула — это тоже уравнение!) на 3,14: