Чем отличается арифметическая от геометрической прогрессия: Арифметическая и геометрическая прогрессии — урок. Основной государственный экзамен 9 класс, Математика.

Разница между арифметической и геометрической последовательностью

• 2019

Последовательность описывается как систематический набор чисел или событий, называемых терминами, которые расположены в определенном порядке. Арифметические и геометрические последовательности — это два типа последовательностей, которые следуют шаблону, описывая, как вещи следуют друг за другом. Когда существует постоянная разница между последовательными членами, последовательность называется арифметической последовательностью

Меры предосторожно…

Please enable JavaScript

Меры предосторожности при обмене личной информацией в Интернете

,

С другой стороны, если последовательные члены находятся в постоянном соотношении, последовательность является геометрической . В арифметической последовательности термины могут быть получены путем добавления или вычитания константы к предыдущему члену, причем в случае геометрической прогрессии каждый член получается путем умножения или деления константы на предыдущий член.

Здесь, в этой статье, мы собираемся обсудить существенные различия между арифметической и геометрической последовательностью.

Сравнительная таблица

Основа для сравнения	Арифметическая последовательность	Геометрическая последовательность
Имея в виду	Арифметическая последовательность описывается как список чисел, в котором каждый новый термин отличается от предыдущего термина постоянной величиной.	Геометрическая последовательность — это набор чисел, в котором каждый элемент после первого получается путем умножения предыдущего числа на постоянный коэффициент.
Удостоверение личности	Общая разница между последовательными терминами.	Общее соотношение между последовательными сроками.
Продвинутый	Сложение или вычитание	Умножение или деление
Вариация условий	линейный	экспоненциальный
Бесконечные последовательности	расходящийся	Расходящиеся или сходящиеся

Определение арифметической последовательности

Арифметическая последовательность относится к списку чисел, в которых разница между последовательными членами постоянна. Проще говоря, в арифметической прогрессии мы добавляем или вычитаем фиксированное ненулевое число, каждый раз бесконечно. Если a является первым членом последовательности, то это может быть записано как:

a, a + d, a + 2d, a + 3d, a + 4d ..

где а = первый член
d = общая разница между терминами

Пример : 1, 3, 5, 7, 9…
5, 8, 11, 14, 17…

Определение геометрической последовательности

В математике геометрическая последовательность представляет собой набор чисел, в которых каждый член последовательности является постоянным кратным предыдущего члена. В более тонких терминах, последовательность, в которой мы умножаем или делим фиксированное ненулевое число, каждый раз бесконечно, тогда прогрессия называется геометрической. Кроме того, если a является первым элементом последовательности, то это можно выразить как:

a, ar, ar2, ar3, ar 4…

где а = первый член
d = общая разница между терминами

Пример : 3, 9, 27, 81…
4, 16, 64, 256 . .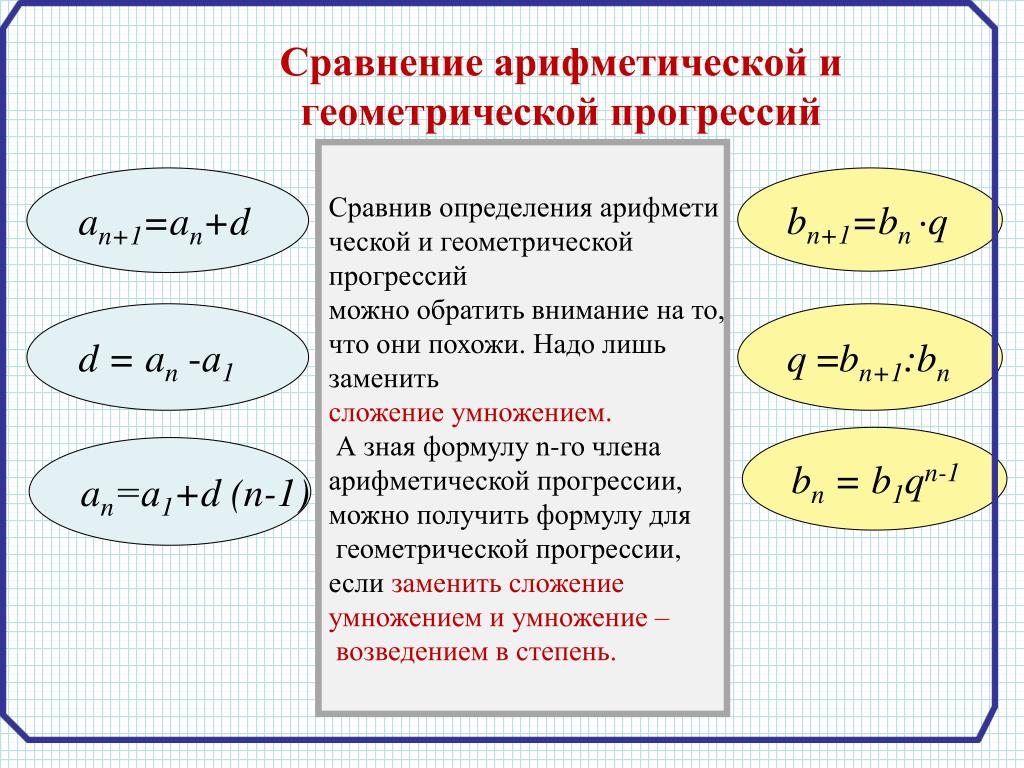

Следующие пункты заслуживают внимания, поскольку речь идет о разнице между арифметической и геометрической последовательностями:

1. В качестве списка чисел, в котором каждый новый термин отличается от предыдущего термина на постоянную величину, является арифметическая последовательность. Набор чисел, в котором каждый элемент после первого получается путем умножения предыдущего числа на постоянный коэффициент, называется геометрической последовательностью.
2. Последовательность может быть арифметической, когда есть общая разница между последовательными членами, обозначенными как «d». Напротив, когда существует общее соотношение между последовательными членами, представленными как «r», последовательность называется геометрической.
3. В арифметической последовательности новый член получается путем добавления или вычитания фиксированного значения к / из предыдущего члена. В отличие от геометрической последовательности, в которой новый термин определяется путем умножения или деления фиксированного значения от предыдущего.
4. В арифметической последовательности изменение членов последовательности является линейным. В отличие от этого, изменение в элементах последовательности является экспоненциальным.
5. Бесконечные арифметические последовательности расходятся, в то время как бесконечные геометрические последовательности сходятся или расходятся, в зависимости от обстоятельств.

Заключение

Следовательно, с учетом приведенного выше обсуждения было бы ясно, что существует огромная разница между двумя типами последовательностей. Кроме того, можно использовать арифметическую последовательность для определения сбережений, затрат, конечного прироста и т. Д. С другой стороны, практическое применение геометрической последовательности заключается в определении прироста населения, интереса и т. Д.

Все о геометрической прогрессии

1. Что такое геометрическая прогрессия?
2. Формулы и свойства геометрической прогрессии
3. Калькуляторы геометрической прогрессии
4. Примеры решения заданий с геометрической прогрессией

 

Ученикам может показаться, что изучение геометрической прогрессии – это нечто абстрактное и оторванное от жизни. На самом деле множество экономических процессов построены именно на основе геометрической прогрессии.

 

Например, если вы положите деньги на банковский депозит и захотите посчитать сколько процентов заработаете за три года, самым удобным способом провести вычисления будет именно через формулу геометрической прогрессии. Этот инструмент также применяется в проектировании, архитектуре и строительстве.

 

В этом тексте вы сможете узнать базовую информацию о формулах и свойства геометрической прогрессии, а также понять принцип, по которому она действует.

 

Что такое геометрическая прогрессия?

 

3, 12, 48, 192, 768, 3072 – это пример геометрической прогрессии. Все эти объединенные единым общим множителем. В теории геометрической прогрессии он называется знаменателем и обозначается как q. В этом случае q = 4. Чтобы создать геометрическую прогрессию, нам нужно сначала три умножить на четыре, затем 12 – снова на 4, потом 48 на 4 и так далее.

Читайте также: Плюсы и минусы образования за рубежом

 

Определение геометрической прогрессии

Геометрическая прогрессия – это прежде всего последовательность чисел. Каждый пункт этой последовательности, начиная со второго, равен предыдущему числу, умноженному на одинаковый множитель.

 

Устойчивое число множитель, которое собственно и образует последовательность под названием геометрическая прогрессия, называется знаменателем прогрессии и обозначается, как мы уже отметили выше, буквой q.

 

Члены прогрессии обозначаются как , где под индикатором n имеется в виду порядковый номер члена в прогрессии. Соответственно, первый член прогрессии (в нашем первом примере равен 3 – это b1, а второй (12) – это b2.

 

Предполагается, что ни первый член, ни знаменатель прогрессии не равен нулю.

Свойства геометрической прогрессии

Геометрическая прогрессия становится удобным инструментом вычислений, когда вы понимаете, что с помощью ее свойств и связанных с ней формул можно легко вычислить, чему равно 

 

 

И действительно – если попробуем вручную умножать каждое число ряда на 4, в конце концов восьмым числом этой геометрической прогрессии станет 49152.

 

После усвоения главного принципа, лежащего в основе геометрической прогрессии, можем закрепить знания, проверив на практике первый пример с банковским депозитом. 

 

Допустим, вы кладете на свой счет $ 100 под 6% годовых, и хотите узнать, какую сумму получите за 3 года. В таком случае вы будете использовать в своих расчетах геометрическую прогрессию, ведь ежегодно вы будете умножать все большую сумму на один и тот же множитель (в данном примере он равен 6%, то есть – 1,06)

 

Чтобы вычислить сумму вклада в момент завершения действия депозита, используем уже знакомую формулу для нахождения значения любого члена прогрессии: 

 

 

 

В чем разница между геометрической и арифметической прогрессией?

 

В геометрической прогрессии члены прогрессии умножаются на постоянное число, тогда как арифметическая прогрессия воплощает последовательность чисел, в которой к каждому предыдущему члена добавляется одно и то же постоянное число.

 

Представим это на примерах.

 

Предположим, что знаменатель (q) в случае геометрической прогрессии составит 3 и так же в арифметической прогрессии устойчивое слагаемое будет равно 3. И стартовый член прогрессии в обоих случаях также составит одно и то же число – 4.

 

Арифметическая прогрессия тогда будет выглядеть как последовательность 4, 7 (= 4 + 3), 10 (= 7 + 3) .., 13 .., 16 .., 19 …

А геометрическая прогрессия – как последовательность 4, 12 (= 4 * 3), 36 (= 12 * 3), 108 .., 324 …

 

Читайте также: Учимся играя. Что такое геймификация
 

Формулы и свойства геометрической прогрессии

 

Свойства членов геометрической прогрессии – это формулы, упрощающие расчеты. Вот некоторые из них:

 

Чтобы найти знаменатель геометрической прогрессии, следует использовать следующую формулу:

Произведение членов, равноудаленных от краев геометрической прогрессии, то есть, соседних, всегда является постоянной величиной, то есть:

С формулой расчета любого члена геометрической прогрессии мы уже знакомы. Она выглядит так:

А формула нахождения суммы п первых членов геометрической прогрессии выглядит так:

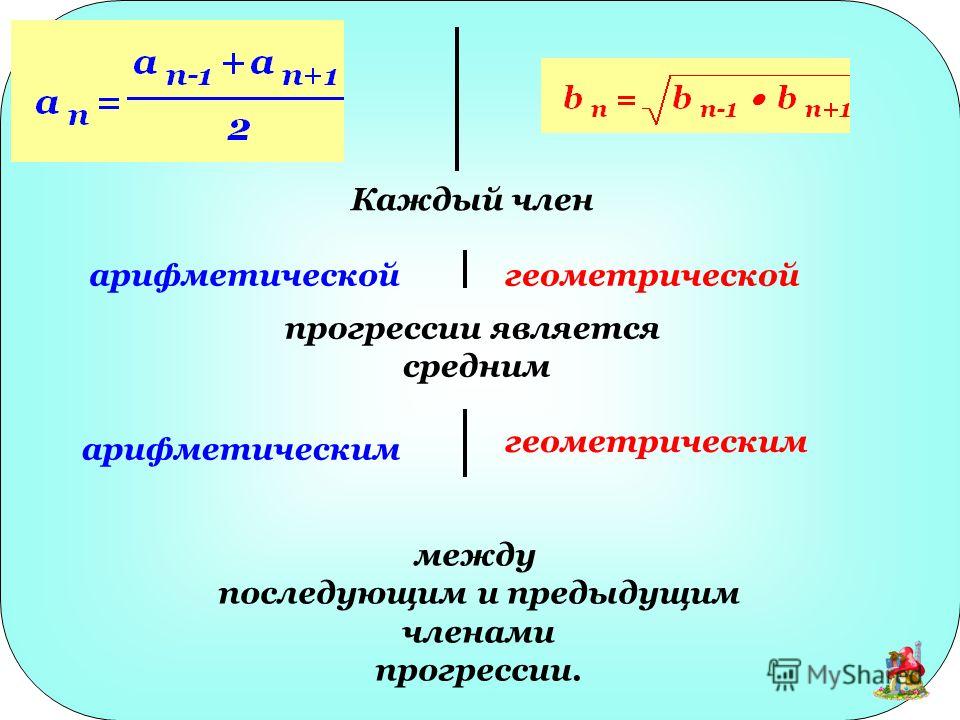
Любой член геометрической прогрессии, начиная со второго, будет равняться среднему арифметическому соседних с ним членов, то есть при , 

Калькуляторы геометрической прогрессии

 

В сети есть множество калькуляторов как арифметической, так и геометрической прогрессии. Некоторые из них могут не только посчитать сумму прогрессии или найти знаменатель, но и отразить пошаговое решение того или иного примера. Пользуясь ими вы не только найдете ответ, но и сможете понять принцип действий и запомнить некоторые из формул.

 

Однако если вы переживаете сложности с пониманием геометрической прогрессии, эффективным решением может быть работа с репетитором по алгебре. На сайте БУКИ вы можете найти репетитора по любому предмету.

 

Что касается онлайн-калькуляторов прогрессии, то в Keisan Online Calculator вы можете вычислить или сумму геометрической прогрессии, а также значение любого ее члена с пошаговым решением вашего примера. А в Geometric Sequence Calculator вы сможете вычислить любой составляющая прогрессии: и знаменатель геометрической прогрессии (q), и сумму бесконечный прогрессии (Sn), и сумму первых членов (Sn).

 

Примеры решения заданий с геометрической прогрессией

 

2. Вычислим знаменатель геометрической прогрессии, если b1=5,5; b2=11.

Решение: 

Вычислим знаменатель прогрессии, поделив друг на друга соседние члены:

q = b2/b1 = 11/5,5 = 2.

Ответ: 

Знаменатель прогрессии (q) равен 2.

3. Вычислим знаменатель геометрической прогрессии, если b1=0,3; b2= -30.

Решение:

Вычислим знаментель прогрессии, поделив друг на друга соседние члены: 

q = b2/b1= -30/0,3= -100.

Ответ:

Знаменатель прогрессии (q) равен -100.


Читайте также: Самые популярные специальности в мире: выбор студентов 2021

6.2: Арифметические и геометрические последовательности

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

40929

• Ричард В. Беверидж
• Общественный колледж Клэтсопа

Двумя распространенными типами математических последовательностей являются арифметические последовательности и геометрические последовательности. Арифметическая последовательность имеет постоянную разницу между каждой последовательной парой членов. Это похоже на линейные функции, которые имеют вид \(y=m x+b .\) Геометрическая последовательность имеет постоянное отношение между каждой парой последовательных членов. Это создаст эффект постоянного множителя.

Примеры

Арифметическая последовательность:
\(\{5,11,17,23,29,35, \dots\}\)
Обратите внимание, здесь постоянная разность равна 6. Если мы хотим написать общий термин для этой последовательности, есть несколько подходов. Один из подходов состоит в том, чтобы взять постоянную разность в качестве коэффициента для члена \(n\): \(a_{n}=6 n+?\). Тогда нам просто нужно заполнить вопросительный знак значением, которое соответствует последовательности. Мы могли бы сказать для последовательности:

\(\{5,11,17,23,29,35, \dots\}\)
\(a_{n}=6 n-1\)
Существует также формула который вы можете запомнить, в котором говорится, что любая арифметическая последовательность с постоянной разностью \(d\) выражается как:
\(a_{n}=a_{1}+(n-1) d\)
Обратите внимание, что если мы подставим значения из нашего примера, мы получим тот же ответ, что и раньше:
\(a_{n}= a_{1}+(n-1) d\)
\(a_{1}=5, d=6\)
Итак, \(a_{1}+(n-1) d=5+(n- 1) * 6=5+6 n-6=6 n-1\)
или \(a_{n}=6 n-1\)
Если члены арифметической прогрессии становятся меньше, то постоянная разность равна отрицательное число.
\(\{24,19,14,9,4,-1,-6, \dots\}\)
\(a_{n}=-5 n+29\)

Геометрическая последовательность
In геометрическая последовательность всегда имеет постоянный множитель. Если множитель больше, чем \(1,\), то условия будут увеличиваться. Если множитель меньше \(1,\), то члены будут становиться меньше. 9{n-1}\) и т. д.

Упражнения 6.2
Определите, является ли каждая последовательность арифметической, геометрической или ни той, ни другой.
Если это арифметика, определить постоянную разницу.
Если оно геометрическое, определите постоянный коэффициент.
1) \(\quad\{18,22,26,30,34, \dots\}\)
2) \(\quad\{9,19,199,1999, \dots\}\)
3) \ (\quad\{8,12,18,27, \dots\}\)
4) \(\quad\{15,7,-1,-9,-17, \dots\}\)
5) \(\ четырехъядерный \ левый \ {\ гидроразрыва {1} {2}, \ гидроразрыва {2} {3}, \ гидроразрыва {3} {4}, \ гидроразрыва {4} {5}, \ гидроразрыва {5} 6}, \точки\справа\}\)
6) \(\quad\{100,-50,25,-12. 5,\dots\}\)
7) \(\quad\{-8,12,32,52,\dots\}\)
8) \(\quad\{1,4,9,16,25,\dots\}\)
9) \(\quad\{11,101,1001,10001,\ldots\}\)
10) \( \quad\{12,15,18,21,24, \dots\}\)
11) \(\quad\{80,20,5,1.25, \dots\}\)
12) \(\quad \{5,15,45,135,405, \dots\}\)
13) \(\quad\{1,3,6,10,15, \dots\}\)
\(\begin{array}{ll} \text { 14) } & \{2,4,6,8,10, \dots\}\end{массив}\)
15) \(\quad\{-1,-2,-4,-8 ,-16, \dots\}\)
16) \(\quad\{1,1,2,3,5,8,13,21, \dots\}\)

---

Эта страница под названием 6.2: Арифметические и геометрические последовательности распространяется под лицензией CC BY-NC-SA и была создана, изменена и/или курирована Ричардом В. Бевериджем.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   Ричард В. Беверидж

   Лицензия

   CC BY-NC-SA

   Показать страницу TOC

   нет

2. Теги

   1. источник[1]-math-37270

Разница между арифметической и геометрической последовательностями (со сравнительной таблицей)

Последовательность описывается как систематический набор чисел или событий, называемых терминами, расположенных в определенном порядке. Арифметические и геометрические последовательности — это два типа последовательностей, которые следуют шаблону, описывая, как вещи следуют друг за другом. Когда существует постоянная разница между последовательными членами, последовательность называется арифметической последовательностью ,

. С другой стороны, если последовательные члены находятся в постоянном соотношении, последовательность равна геометрический . В арифметической последовательности члены могут быть получены путем прибавления или вычитания константы к предыдущему члену, при этом в случае геометрической прогрессии каждый член получается путем умножения или деления константы на предыдущий член.

Здесь, в этой статье, мы собираемся обсудить существенные различия между арифметической и геометрической последовательностями.

Содержание: арифметическая последовательность и геометрическая последовательность

1. Сравнительная таблица
2. Определение
3. Ключевые отличия
4. Заключение

Сравнительная таблица

Основание для сравнения	Арифметическая последовательность	Геометрическая последовательность
Значение	Арифметика Последовательность описывается как список чисел, в котором каждый новый член отличается от предыдущего на постоянную величину.	Геометрическая последовательность — это набор чисел, в котором каждый элемент после первого получается путем умножения предыдущего числа на постоянный коэффициент.
Идентификация	Общий Разница между последовательными терминами.	Обыкновенное соотношение между последовательными терминами.
Расширенный на	Сложение или вычитание	Умножение или деление
Варианты терминов	Линейная	Экспоненциальная
Бесконечные последовательности	Расходящиеся	Расходящиеся или сходящиеся

Определение арифметической последовательности

Арифметическая последовательность относится к списку чисел, в котором разница между последовательными элементами постоянна. Проще говоря, в арифметической прогрессии мы прибавляем или вычитаем фиксированное, отличное от нуля число, каждый раз бесконечно. Если a является первым членом последовательности, то это можно записать как:

a, a+d, a+2d, a+3d, a+4d..

где, a = первый термин
d = общая разница между терминами

Пример : 1, 3, 5, 7, 9…
5, 8, 11, 14, 17…

Определение геометрической последовательности

В математике геометрическая последовательность — это набор чисел, в котором каждый член прогрессия постоянно кратна предыдущему члену. Говоря более точно, последовательность, в которой мы умножаем или делим фиксированное, отличное от нуля число, каждый раз до бесконечности, называется геометрической прогрессией. Далее, если a является первым элементом последовательности, то это можно выразить так:

a, ar, ar ² , ar ³ , ar ⁴ …

где, a = первый член
d = общая разница между членами

90 Пример: , 27, 81…
4, 16, 64, 256..

Основные различия между арифметической и геометрической последовательностями

Следующие пункты заслуживают внимания, поскольку речь идет о разнице между арифметической и геометрической последовательностями:

1. В виде списка чисел , в котором каждый новый член отличается от предыдущего на постоянную величину, является арифметической последовательностью. Набор чисел, в котором каждый элемент после первого получается путем умножения предыдущего числа на постоянный коэффициент, известен как геометрическая последовательность.
2. Последовательность может быть арифметической, когда существует общая разница между последовательными элементами, обозначенная как «d». Напротив, когда существует общее отношение между последовательными элементами, представленными буквой «r», последовательность называется геометрической.
3. В арифметической последовательности новый член получается путем прибавления или вычитания фиксированного значения к/из предыдущего члена.

   No related posts.