Чему равен косинус в прямоугольном треугольнике: Косинус одного из острых углов прямоугольного треугольника равен 0,6. Чему равен другой острый угол? Ответ:…

Синус, косинус, тангенс острого угла прямоугольного треугольника

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Синус, косинус, тангенс острого угла прямоугольного треугольника

1.Закончи предложение: «Треугольник, у
которого один угол прямой
называется…»
А) остроугольный
Б) равнобедренный
В) равносторонний
Г) прямоугольный
2. Отметь прямоугольный
треугольник:
3. Как называются стороны в
прямоугольном треугольнике?
А) боковые стороны
Б) основания
В) катеты и гипотенуза
Г) параллельные стороны
4. Один из острых углов
прямоугольного треугольника равен
30°, чему равен другой острый угол?
А) 90°
Б) 60°
В) 30°
С) 180°
5. Выберите формулу площади
прямоугольного треугольника:
1
А) S =2 a·b
1
Б) S =2 a·h
1
B) S = 2 a·b·sin α
Г) S = √ٕp(p-a)(p-b)(p-c)
6. Катет прямоугольного
треугольника, лежащий напротив
угла в 30°, равен 15см. Чему равна
гипотенуза?
А) 15см
Б) 7,5см
В) 20см
Г) 30см
Оценка «5» — все верные ответы.
Оценка «4» — 5 верных ответов.
Оценка «3» — 4 верных ответа.
«Надо ещё повторить» — менее 4
верных ответов.
B
Назвать катет, прилежащий к
углу А.
Назвать катет, прилежащий к
углу В.
Назвать катет,
противолежащий углу А.
Назвать катет,
противолежащий углу В.
C
A
Синусом острого угла
прямоугольного
треугольника
называется
отношение
противолежащего
катета к гипотенузе.
В
С
А
BC
sin A
AB
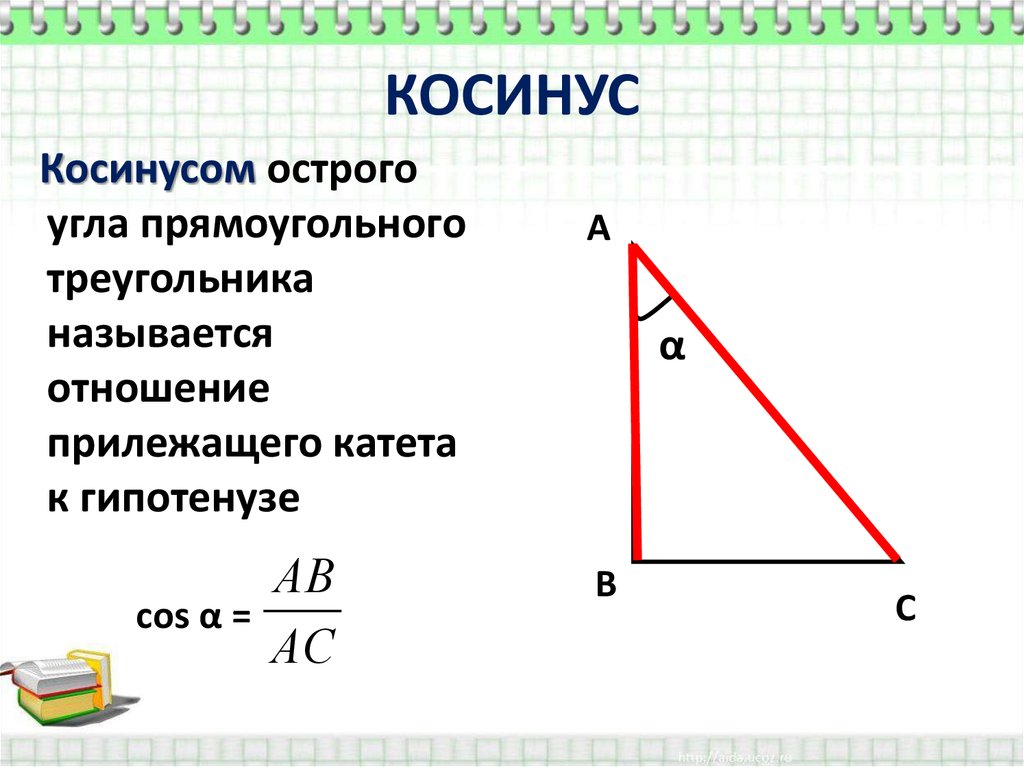
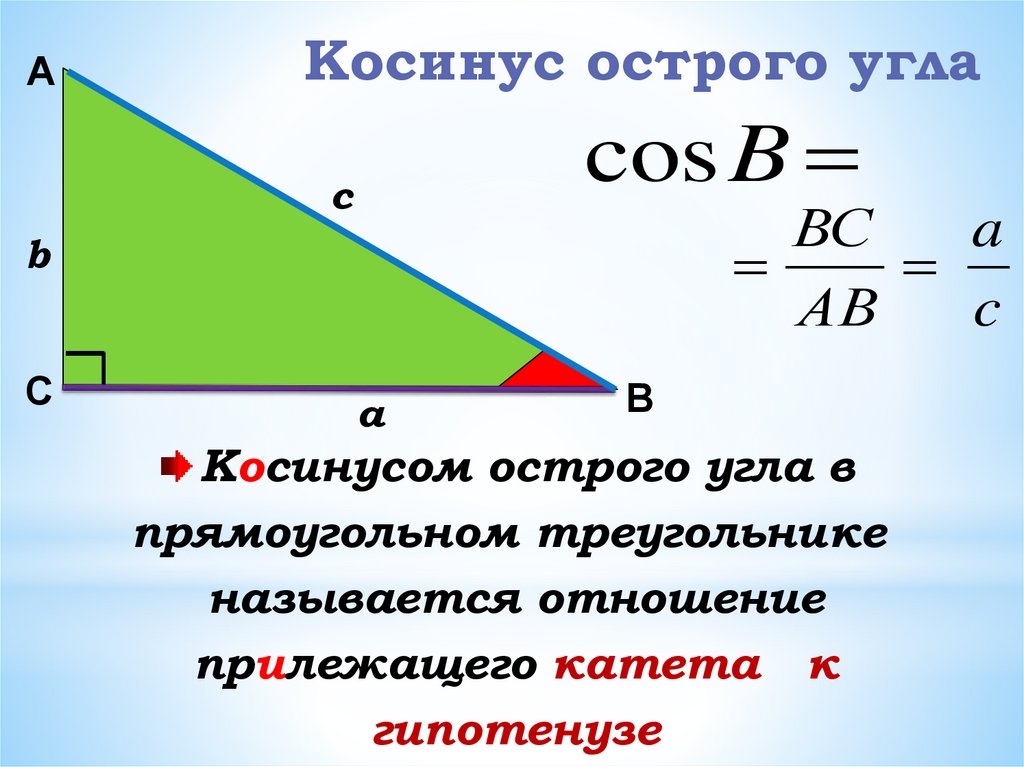
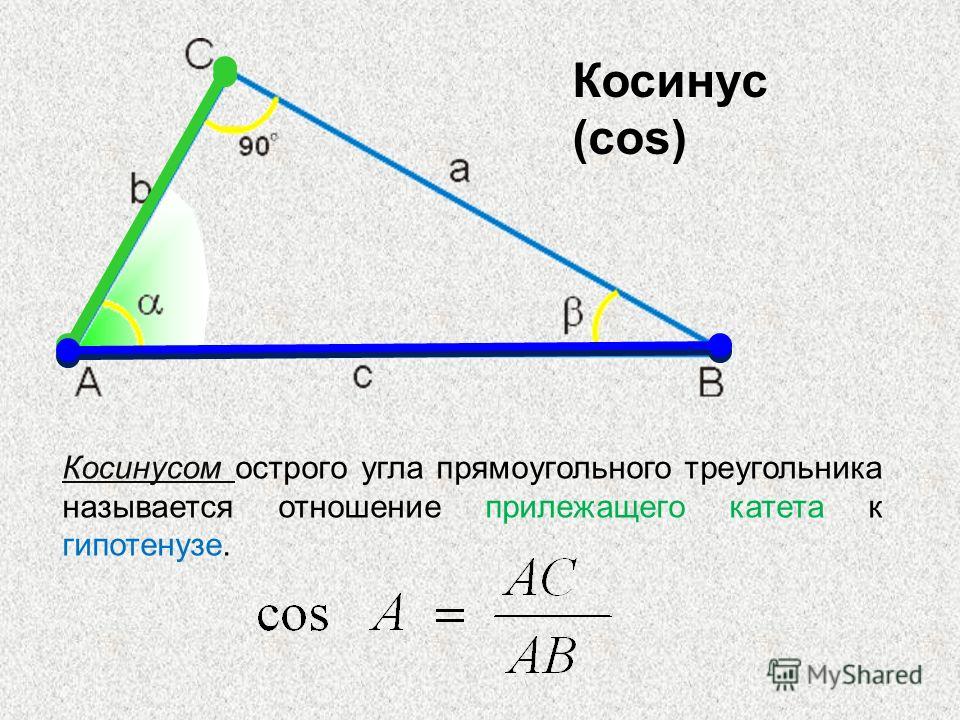
Косинусом острого
угла прямоугольного
треугольника
называется
отношение
прилежащего катета
к гипотенузе.
В
С
А
AC
cos A
AB
Тангенсом острого
угла прямоугольного
треугольника
называется
отношение
противолежащего
катета к
прилежащему.
В
С
А
BC
tg A
AC
B
BC
sin A
AB
AC
cos A
AB
BC
tg A
AC
C
A
sin B ?
cos B ?
tg B ?
cos A
cos BAC
Значение косинуса
острого угла
прямоугольного
треугольника не
зависит от величины и
положения
прямоугольного
треугольника.
Найти: 1) sin A, 2) cоs A, 3) tg A, 4) сtg A,
Ответ:
В
tg
A=
sin
соs A=
сtg A=
A=
13 см
5
12
12
5
13
512
13
5см
С
А
1.Выполнение домашнего задания начни с изучения
§ 4 пункта 66.
2. Повтори определения синуса, косинуса, тангенса и
котангенса острого угла прямоугольного
треугольника.
3. Реши следующие задачи из учебника:
№ 591(а), № 592 (а).

English     Русский Правила

Геометрия 7-9 класс.

\circ }.\) Найдите угол D, если \(AB = 7\sqrt 3 .\) Ответ дайте в градусах.

Ответ

ОТВЕТ: 60.

Задача 25. В равнобедренном треугольнике АВС с основанием АВ проведены высоты AN и СМ. Найдите отношение AN : СМ, если \(\cos B = \frac{1}{5}.\)

Ответ

ОТВЕТ: 2 : 5.

Задача 26. В равнобедренном треугольнике АВС с основанием АВ проведены высоты AN и СМ. Найдите отношение AN : СМ, если \(\sin B = \frac{3}{5}.\)

Ответ

ОТВЕТ: 8 : 5.

Задача 27. Дан прямоугольник ABCD со сторонами АВ = 6 и ВС = 8 диагонали которого пересекаются в точке О. Найдите \(\sin \,\angle \,AOB.\)

Ответ

ОТВЕТ: 0,96.

Задача 28. В прямоугольном треугольнике АВС \(\left( {\angle \,C = {{90}^ \circ }} \right)\) проведена медиана СМ = 17. \circ }\) проведена медиана СМ и высота СН. Найдите sin A, если AВ = 12 и \(MH = 3\sqrt 3 .\)

Ответ

ОТВЕТ: \(\frac{{\sqrt {2 — \sqrt 3 } }}{2}.\)

Задача 30. В трапеции ABCD с основаниями AD = 10 и ВС проведена высота ВН треугольника АВС. Найдите \(\cos \,\angle \,HBC,\) если CD = 6  и АС = 8.

Ответ

ОТВЕТ: 0,6.

Реклама

Поддержать нас

8.2: Неправильные треугольники — Закон косинусов

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

1376

• OpenStax
• OpenStax

Цели обучения

В этом разделе вы:

• Используйте закон косинусов для решения косоугольных треугольников.
• Решение прикладных задач с использованием закона косинусов.
• Используйте формулу Герона, чтобы найти площадь треугольника.

Предположим, что лодка выходит из порта, проходит \(10\) миль, поворачивает на \(20\) градусов и проходит еще 8 миль, как показано на рисунке \(\PageIndex{1}\). Как далеко от порта находится лодка?

Рисунок \(\PageIndex{1}\)

К сожалению, хотя закон синусов позволяет нам рассматривать многие случаи непрямоугольных треугольников, он не помогает нам с треугольниками, в которых известный угол находится между двумя известными сторонами, треугольником SAS (сторона-угол-сторона), или когда известны все три стороны, но не известны углы, треугольник SSS (сторона-сторона-сторона). В этом разделе мы исследуем еще один инструмент для решения косоугольных треугольников, описываемых этими двумя последними случаями.

Использование закона косинусов для решения косоугольных треугольников

Инструмент, который нам нужен для решения проблемы расстояния лодки от порта, — это Закон косинусов , который определяет взаимосвязь между измерениями углов и длинами сторон в косоугольных треугольниках. Три формулы составляют закон косинусов. На первый взгляд формулы могут показаться сложными, поскольку они включают много переменных. Однако, как только закономерность понята, с законом косинусов работать легче, чем с большинством формул на этом математическом уровне.

Понимание того, как выводится закон косинусов, будет полезно при использовании формул. Вывод начинается с обобщенной теоремы Пифагора, которая является расширением теоремы Пифагора на непрямоугольные треугольники. Вот как это работает: Произвольный непрямоугольный треугольник \(ABC\) помещен в координатную плоскость с вершиной \(A\) в начале координат, сторона \(c\) проведена по x -ось, а вершина \(C\) расположена в некоторой точке \((x,y)\) на плоскости, как показано на рисунке \(\PageIndex{2}\). Как правило, треугольники существуют где угодно на плоскости, но для этого объяснения мы поместим треугольник, как указано выше.

Рисунок \(\PageIndex{2}\)

Мы можем опустить перпендикуляр из \(C\) на ось x- (это высота или высота).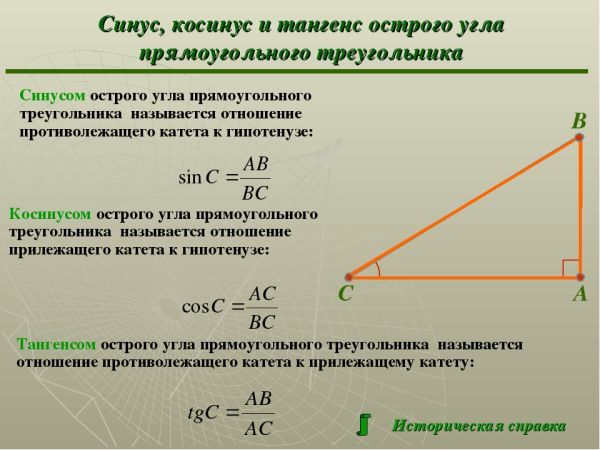 Вспоминая основные тригонометрические тождества, мы знаем, что

\(\cos \theta=\dfrac{x(adjacent)}{b(гипотенуза)}\) и \(\sin \theta=\dfrac{y(противоположный)} {b(гипотенуза)}\) 92−2bc \cos \theta \end{array}\)

Полученная формула является одним из трех уравнений закона косинусов. Аналогично находятся остальные уравнения.

Имейте в виду, что всегда полезно делать набросок треугольника при вычислении углов или сторон. В реальном сценарии попробуйте нарисовать схему ситуации. По мере появления дополнительной информации диаграмму, возможно, придется изменить. Внесите эти изменения в диаграмму, и, в конце концов, проблему будет легче решить.

ЗАКОН КОСИНУСОВ

Закон косинусов гласит, что квадрат любой стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения двух других сторон и косинуса прилежащей стороны треугольника. угол.

Рисунок \(\PageIndex{3}\)

Для треугольников, обозначенных как на рисунке \(\PageIndex{3}\), с углами \(\alpha\), \(\beta\ ) и \(\gamma\) и противоположных соответствующих сторон \(a\), \(b\) и \(c\) соответственно, закон косинусов задается в виде трех уравнений.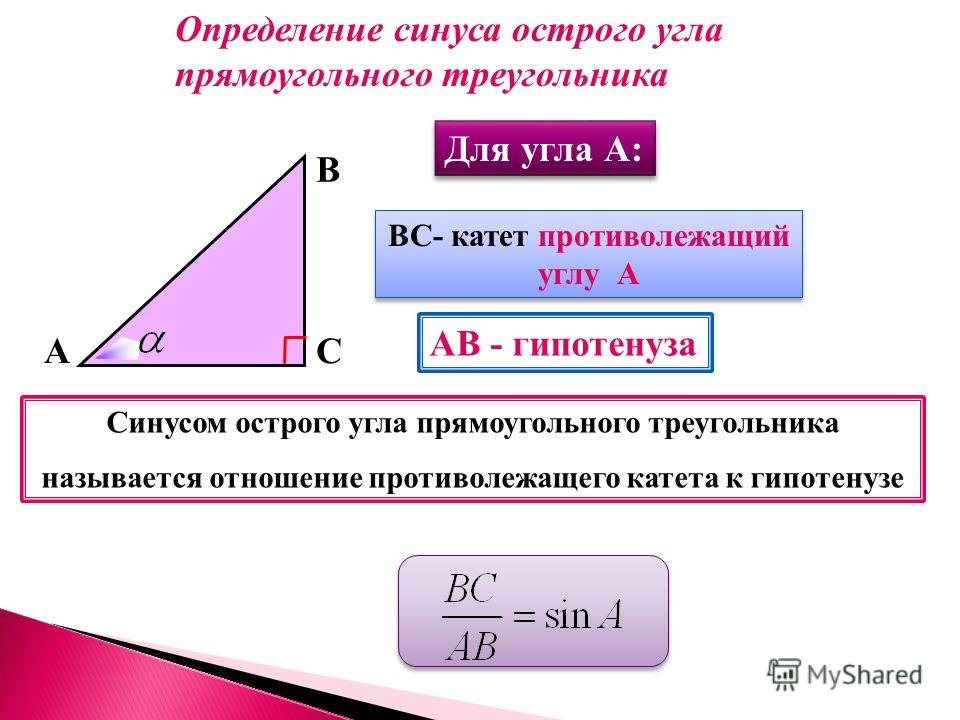 92}{2аб}\]

Как: Зная две стороны и угол между ними (SAS), найти размеры оставшейся стороны и углов треугольника

1. Начертить треугольник. Найдите величины известных сторон и углов. Используйте переменные для представления мер неизвестных сторон и углов.
2. Примените закон косинусов, чтобы найти длину неизвестной стороны или угла.
3. Примените закон синусов или косинусов, чтобы найти величину второго угла.
4. Вычислите величину остаточного угла.

Пример \(\PageIndex{1}\): нахождение неизвестной стороны и углов треугольника SAS

Найдите неизвестную сторону и углы треугольника на рисунке \(\PageIndex{4}\).

Рисунок \(\PageIndex{4}\)

Решение

Сначала обратите внимание на то, что дано: две стороны и угол между ними. Это устройство классифицируется как SAS и предоставляет данные, необходимые для применения закона косинусов. {−1}\left(\dfrac{10\sin(30°)}{6,013}\ right) & \text{Найдите арксинус } \dfrac{10\sin(30°)}{6,013}. \\[4pt] \alpha≈56,3° \end{array}\)

Другая возможность для \(\альфа\) была бы \(\альфа=180°-56,3°≈123,7°\). На исходной диаграмме \(\альфа\) примыкает к самой длинной стороне, поэтому угол \(\альфа\) острый и, следовательно, \(123,7°\) не имеет смысла. Обратите внимание, что если мы решим применить закон косинусов, мы получим уникальный ответ. Нам не нужно рассматривать другие возможности, поскольку косинус уникален для углов между \(0°\) и \(180°\). Используя \(\alpha≈56,3°\), мы можем найти третий угол треугольника. 9{\circ} \end{align*}\]

Полный набор углов и сторон

\(\alpha≈56.3°\) \(a=10\)

\(\beta=30°\ ) \(b≈6,013\)

\(\gamma≈93,7°\) \(c=12\)

Упражнение \(\PageIndex{1}\)

Найдите недостающую сторону и углы данного треугольника : \(\alpha=30°\), \(b=12\), \(c=24\).

Ответить

\(a≈14,9\), \(\beta≈23,8°\), \(\gamma≈126,2°\).

Пример \(\PageIndex{2}\): Нахождение угла треугольника SSS 92−2(25)(18)\cos \alpha & \text{Подставьте соответствующие измерения.} \\[4pt] 400=625+324−900 \cos \alpha & \text{ Упрощайте каждый шаг.} \ \[4pt] 400=949−900 \cos \alpha \\[4pt] −549=−900 \cos \alpha & \text{Изолировать}\cos \alpha. \\[4pt] 0,61≈\cos \alpha & \text{Найти арккосинус.} \\[4pt] \alpha≈52,4° \end{массив}\)

См. рисунок \(\PageIndex{5}\ ).

Рисунок \(\PageIndex{5}\)

Анализ

Поскольку арккосинус может возвращать любой угол между \(0\) и \(180\) градусами, при использовании этого метода не будет неоднозначных случаев.

Упражнение \(\PageIndex{2}\)

Учитывая \(a=5\), \(b=7\) и \(c=10\), найдите недостающие углы.

Ответить

\(\альфа≈27,7°\), \(\бета≈40,5°\), \(\гамма≈111,8°\)

Решение прикладных задач с использованием закона косинусов

Так же, как закон синусов обеспечивает соответствующие уравнения для решения ряда приложений, закон косинусов применим к ситуациям, в которых данные соответствуют косинусным моделям.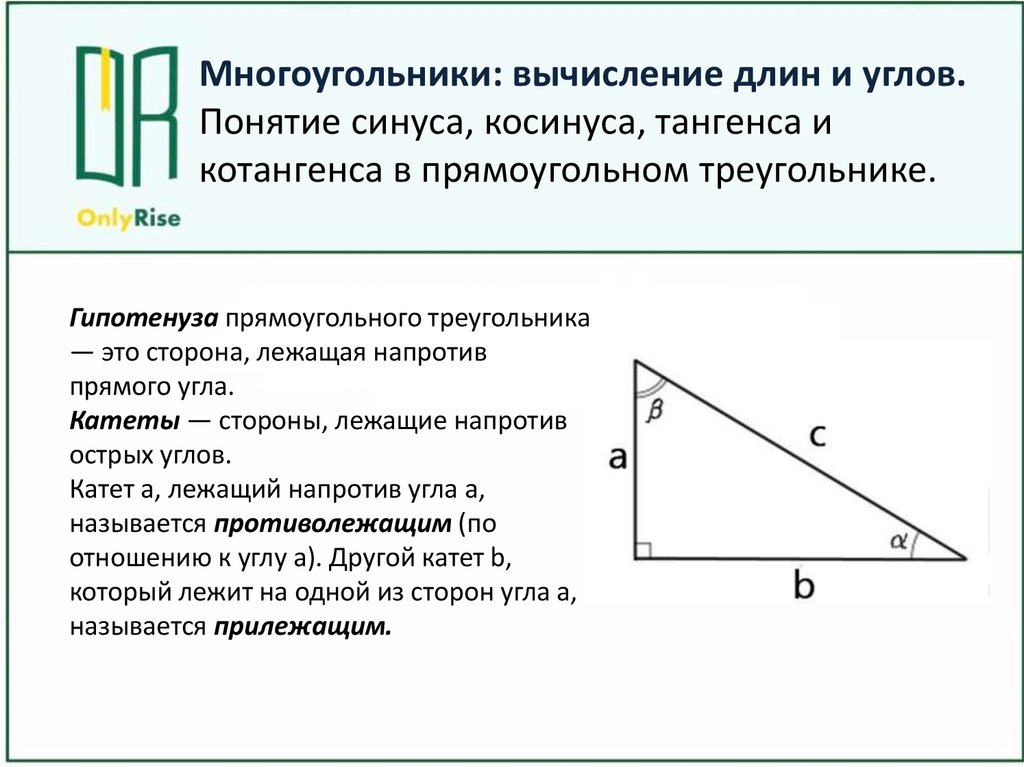 Мы можем увидеть их в области навигации, геодезии, астрономии и геометрии, и это лишь некоторые из них.

Пример \(\PageIndex{3A}\): Использование закона косинусов для решения задачи связи

На многих сотовых телефонах с GPS приблизительное местоположение может быть указано до получения сигнала GPS. Это достигается с помощью процесса, называемого триангуляцией, который работает с использованием расстояний от двух известных точек. Предположим, что в радиусе действия сотового телефона есть две вышки сотовой связи. Две башни расположены в \(6000\) футов друг от друга на прямом шоссе, идущем с востока на запад, а сотовый телефон находится к северу от шоссе. Основываясь на задержке сигнала, можно определить, что сигнал находится в \(5050\) футов от первой башни и в \(2420\) футов от второй башни. Определите положение сотового телефона к северу и востоку от первой башни и определите, насколько далеко он находится от шоссе.

Решение

Для простоты мы начнем с рисования схемы, подобной рисунку \(\PageIndex{6}\), и пометки полученной информации.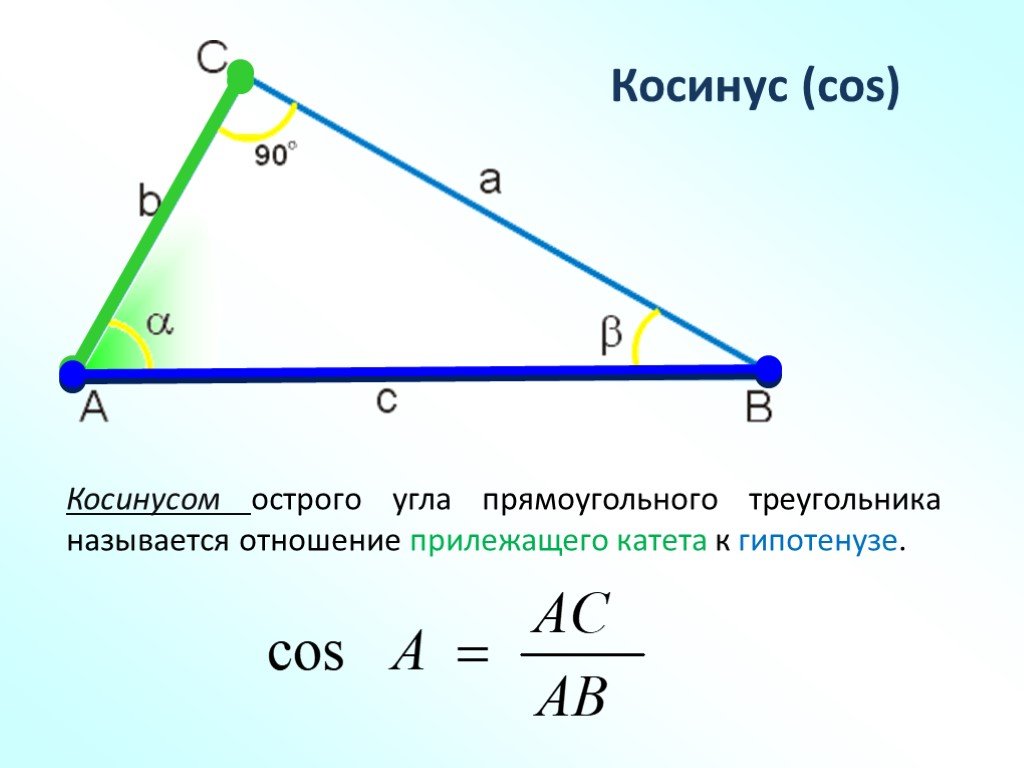

Рисунок \(\PageIndex{6}\)

Используя закон косинусов, мы можем найти угол \(\theta\). Помните, что закон косинусов использует квадрат одной стороны, чтобы найти косинус противоположного угла. Для этого примера пусть \(a=2420\), \(b=5050\) и \(c=6000\). Таким образом, \(\theta\) соответствует противоположной стороне \(a=2420\). 9{−1}(0,9183) \\[4pt] \theta &≈ 23,3° \end{align*}\]

Чтобы ответить на вопросы о положении телефона к северу и востоку от башни и расстоянии до шоссе, отпустите перпендикуляр от положения сотового телефона, как показано на рисунке \(\PageIndex{7}\). Это образует два прямоугольных треугольника, хотя для этой задачи нам нужен только прямоугольный треугольник, включающий первую башню.

Рисунок \(\PageIndex{7}\)

Используя угол \(\theta=23,3\)° и основные тригонометрические тождества, мы можем найти решения. Таким образом

\[\begin{align*} \cos(23,3°) &= \dfrac{x}{5050} \\[4pt] x &= 5050\cos(23,3°) \\[4pt] x &≈ 4638,15 \, футы\\[4pt] \sin(23,3°) &= \dfrac{y}{5050} \\[4pt] y &= 5050\sin(23,3°) \\[4pt] y &≈1997,5 \, футов \end{align*}\]

Сотовый телефон находится примерно в \(4638\) футах к востоку и \(1998\) футах к северу от первой башни и \(1998\) футах от шоссе.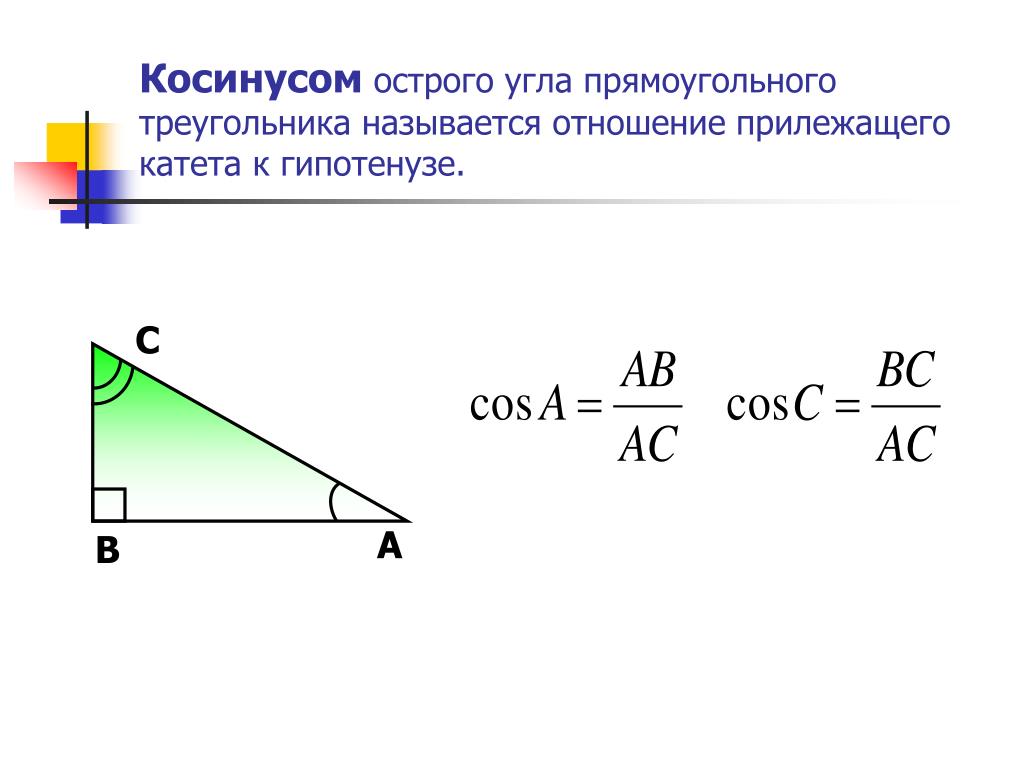

Пример \(\PageIndex{3B}\): расчет пройденного расстояния с использованием треугольника SAS

Возвращаясь к нашей задаче в начале этого раздела, предположим, что судно выходит из порта, проходит \(10\) миль, поворачивает \( 20\) градусов и проходит еще \(8\) миль. Как далеко от порта лодка? Диаграмма повторяется здесь на рисунке \(\PageIndex{8}\). 92 &= 314,35 \\[4pt] x &= \sqrt{314,35} \\[4pt] x&≈17,7\, миль \end{align*}\]

Судно находится примерно в \(17,7\) милях от порта .

Использование формулы Герона для нахождения площади треугольника

Мы уже научились находить площадь косоугольного треугольника, зная две стороны и угол. Мы также знаем формулу нахождения площади треугольника через основание и высоту. Однако, когда мы знаем три стороны, мы можем использовать формулу Герона вместо нахождения высоты. Герон Александрийский был геометром, жившим в первом веке нашей эры. Он открыл формулу для нахождения площади косоугольного треугольника, когда известны три стороны.

ФОРМУЛА ГЕРОНА

Формула Герона находит площади косоугольных треугольников, у которых известны стороны \(a\), \(b\) и \(c\).

\[Площадь=\sqrt{s(s−a)(s−b)(s−c)}\]

, где \(s=\dfrac{(a+b+c)}{2}\ ) составляет половину периметра треугольника, иногда называемого полупериметром.

Пример \(\PageIndex{4}\): использование формулы Герона для нахождения площади заданного треугольника

Найдите площадь треугольника на рисунке \(\PageIndex{9}\) с помощью формулы Герона.

Рисунок \(\PageIndex{9}\)

Решение

Сначала мы вычисляем \(s\).

\[\begin{align*} s&= \dfrac{(a+b+c)}{2}\\ s&= \dfrac{(10+15+7)}{2}\\ &= 16 \ end{align*}\]

Затем применяем формулу.

\[\begin{align*} Area&= \sqrt{s(s-a)(sb)(s-c)}\\ Area&= \sqrt{16(16-10)(16-15)(16-7)}\ \ Area&\ приблизительно 29,4 \end{align*}\]

Площадь приблизительно равна \(29,4\) квадратных единиц.

Упражнение \(\PageIndex{3}\)

Используйте формулу Герона, чтобы найти площадь треугольника со сторонами длиной \(a=29,7\) футов, \(b=42,3\) футов и \(c= 38,4 фута

Ответ

Площадь = \(552\) квадратных футов

Пример \(\PageIndex{5}\): Применение формулы Герона к реальной задаче

Городской застройщик из Чикаго хочет построить здание, состоящее из лофтов для художников, на треугольном участке, граничащем с Раш-стрит, Вабаш-авеню и Пирсон-стрит.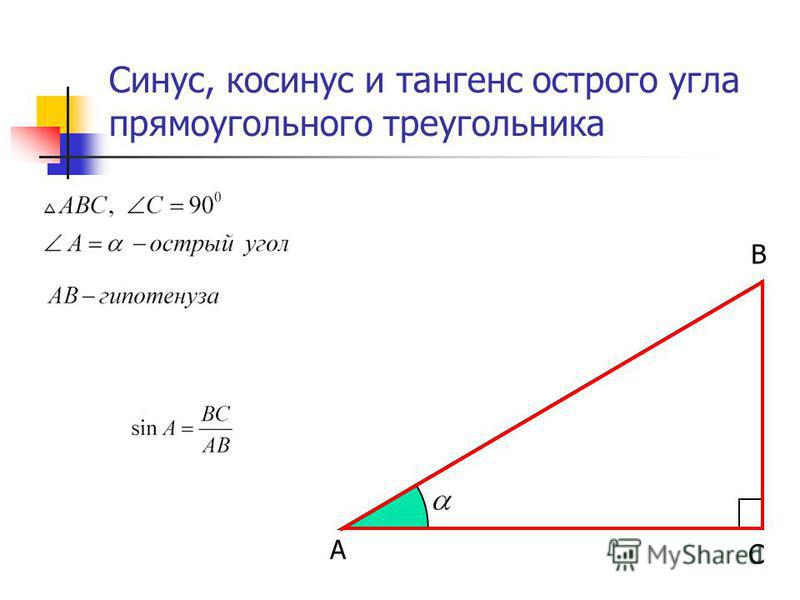 Фасад по Раш-стрит составляет примерно \(62,4\) метра, по Вабаш-авеню — примерно \(43,5\) метра, а по Пирсон-стрит — примерно \(34,1\) метра. Сколько квадратных метров доступно застройщику? См. рисунок \(\PageIndex{10}\) для просмотра городской собственности.

Рисунок \(\PageIndex{10}\)

Решение

Найдите размер \(s\), равный половине периметра.

\[\begin{align*} s&= \dfrac{(62,4+43,5+34,1)}{2}\\ s&= 70\; м\\ \text {Применить формулу Герона.}\\ Area&= \sqrt{70(70-62,4)(70-43,5)(70-34,1)}\\ Area&= \sqrt{506 118,2}\\ Area&\приблизительно 711,4 \end{align*}\]

У застройщика около \(711,4\) квадратных метров.

Упражнение \(\PageIndex{4}\)

Найдите площадь треугольника по данным \(a=4,38\) фута, \(b=3,79\) фута и \(c=5,22\) фута.

Ответ

около \(8,15\) квадратных футов

СМИ

Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с законом косинусов.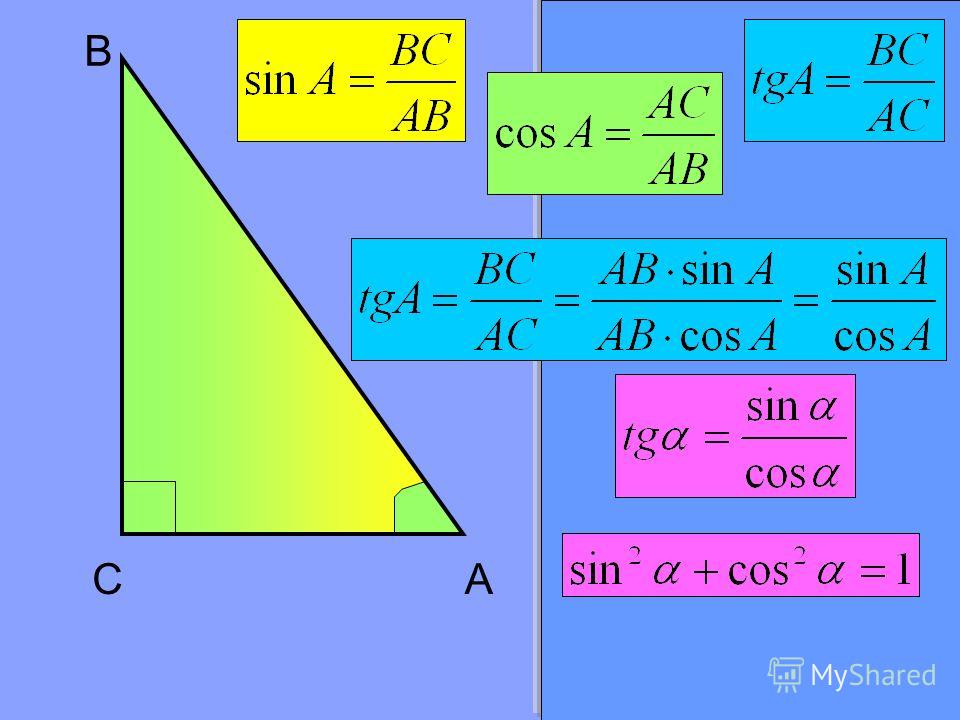

• Закон косинусов
• Закон косинусов: приложения
• Закон косинусов: Приложения 2

Ключевые уравнения 92−2ab \cos\gamma\)

Формула Герона

\(Площадь=\sqrt{s(s−a)(s−b)(s−c)}\)

, где \(s=\dfrac{(a+b+c)}{2}\)

Ключевые понятия

• Закон косинусов определяет взаимосвязь между измерениями углов и длинами сторон в косоугольных треугольниках.
• Обобщенная теорема Пифагора — это закон косинусов для двух случаев косоугольных треугольников: SAS и SSS. Удаление воображаемого перпендикуляра разбивает косой треугольник на два прямоугольных треугольника или образует один прямоугольный треугольник, что позволяет связать стороны и вычислить измерения. См. Пример \(\PageIndex{1}\) и Пример \(\PageIndex{2}\).
• Закон косинусов полезен для многих типов прикладных задач. Первым шагом в решении таких задач обычно является набросок представленной проблемы. Если предоставленная информация соответствует одной из трех моделей (трем уравнениям), примените закон косинусов, чтобы найти решение. См. Пример \(\PageIndex{3}\) и Пример \(\PageIndex{4}\).
• Формула Герона позволяет вычислить площадь в косоугольных треугольниках. Все три стороны должны быть известны, чтобы применить формулу Герона. См. пример \(\PageIndex{5}\) и см. пример \(\PageIndex{6}\).

Авторы и авторство

---

Эта страница под заголовком 8.2: Неправильные треугольники — закон косинусов распространяется по лицензии CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать страницу TOC

   нет

   Включено

   да

2. Теги

   1. Формула Герона
   2. Закон косинусов
   3. источник@https://openstax. org/details/books/precalculus

Правый треугольник Тригонометрический калькулятор

, созданный Давиде Борчиа

, рассмотрено Luis Hoyos

Последнее обновление: MAR 01, 2023

Table of Socults:

• Основы тригонометрии
9003 с шагами
• Другие калькуляторы тригонометрии и прямоугольных треугольников (и не только)
• Часто задаваемые вопросы

Калькулятор тригонометрии прямоугольного треугольника может помочь вам с проблемами, где встречаются углы и треугольники: продолжайте читать, чтобы узнать:

• Основы тригонометрии;
• Как вычислить прямоугольный треугольник с помощью тригонометрии;
• Рабочий пример того, как использовать тригонометрию для расчета прямоугольного треугольника с шагами;

И многое другое!

Основы тригонометрии

Тригонометрия — раздел математики, который связывает углов с длиной определенных отрезков . Мы определяем несколько тригонометрических функций: например, синус, косинус и тангенс. Все они принимают угол в качестве аргумента, возвращая меру длины, связанную с самим углом. Использование тригонометрический круг мы можем определить некоторые тригонометрические функции и их связь с углами.

Как видно из рисунка, синус и косинус равны проекции радиуса на ось, а касательная лежит вне окружности. Если вы присмотритесь, то сможете идентифицировать прямоугольный треугольник, используя элементы, которые мы ввели выше: давайте обнаружим взаимосвязь между тригонометрическими функциями и этой фигурой.

Тригонометрические расчеты прямоугольных треугольников

Рассмотрим острый угол в тригонометрическом круге выше: обратите внимание, как можно построить прямоугольный треугольник где:

• Радиус — это гипотенуза; и
• Синус и косинус являются катетами треугольника.

α\alphaα является одним из острых углов, а прямой угол лежит на пересечении катетов (синуса и косинуса)

Запомните на мгновение: длина катета, противоположного углу α\alphaα — его синус

, sin⁡(α)\sin(\alpha)sin(α)! Вы только что нашли простой и быстрый способ вычисления углов и сторон прямоугольного треугольника с помощью тригонометрии.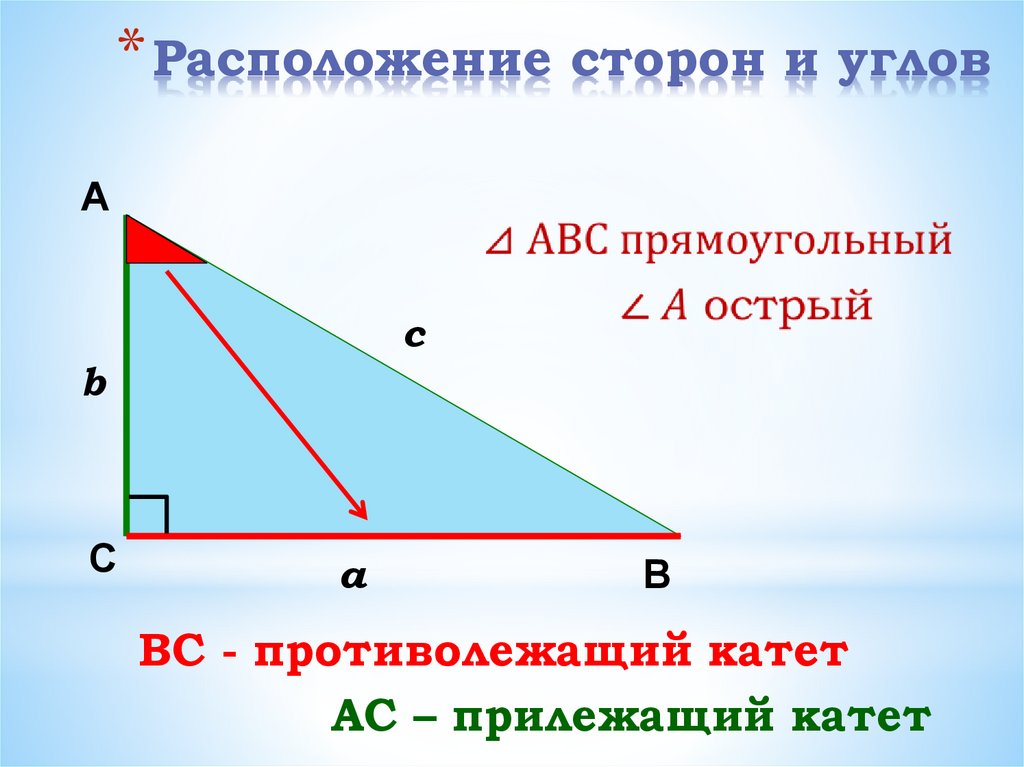

Полные соотношения между углами и сторонами прямоугольного треугольника должны содержать коэффициент масштабирования, обычно радиус (гипотенузу). Определите напротив и рядом с . Тогда мы можем написать:

sin⁡(α)=противоположный гипотенузаcos⁡(α)=смежный гипотенузаtan⁡(α)=противоположныйсмежный\begin{split} \ sin (\ alpha) & = \ frac {\ mathrm {напротив}} {\ mathrm {гипотенуза}} \\ [1em] \cos(\alpha)&= \frac{\mathrm{смежный}}{\mathrm{гипотенуза}}\\[1em] \ tan (\ alpha) & = \ frac {\ mathrm {напротив}} {\ mathrm {смежный}} \\ [1em] \end{split}sin(α)cos(α)tan(α)​=hypotenuseopposite​=hypotenuseadjacent​=adjacentopposite​​

Поменяв катеты ролями, можно найти значения тригонометрических функций для другого угла.

Взяв обратную тригонометрическую функцию , можно найти значения острых углов любого прямоугольного треугольника.

Используя три приведенных выше уравнения и комбинацию сторон, углов или других величин, вы можете решить любой прямоугольный треугольник .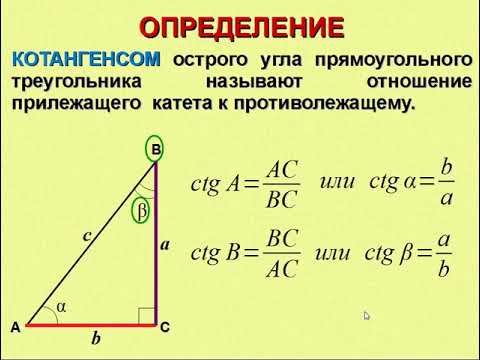 Случаи, которые мы реализовали в нашем калькуляторе:

• Решение треугольника, зная две стороны ;
• Решение треугольника, зная один угол и одну сторону ; и
• Решение треугольника, зная площадь и одну сторону .

Пример вычисления тригонометрии прямоугольного треугольника с шагами

Возьмем прямоугольный треугольник с гипотенузой c=5c = 5c=5 и углом α=38°\alpha=38\gradeα=38°. Удивительно, но этих данных достаточно, чтобы полностью решить прямоугольный треугольник! Выполните следующие шаги:

1. Вычислите третий угол: β=180°−α\beta = 180\градус — \alphaβ=180°−α.
2. Вычислите синус α\alphaα и используйте его значение, чтобы найти длину противоположного катета:
   • sin⁡(α)=0,61567\sin(\alpha) = 0,61567sin(α)=0,61567.
   • напротив=sin⁡(α)⋅гипотенуза=0,61567⋅5=3,078\mathrm{противоположный} = \sin(\alpha)\cdot\mathrm{гипотенуза} = 0,61567 \cdot 5 = 3,078противоположный=sin(α)⋅гипотенуза =0,61567⋅5=3,078.
3. Найдите длину последней стороны либо с помощью теоремы Пифагора, либо с помощью косинусных соотношений cos⁡(α)=adjacent/hypotenuse\cos(\alpha) = \mathrm{adjacent}/\mathrm{hypotenuse}cos(α)= смежная/гипотенуза. Учитывая cos⁡(α)=0,788\cos(\alpha) =0,788cos(α)=0,788:
   • смежный=0,788⋅5=3,94\mathrm{соседний} = 0,788\cdot 5 = 3,94соседний=0,788⋅5=3,94.

Вот оно!

Другие калькуляторы тригонометрии и прямоугольных треугольников (и не только)

Если вам понравился наш калькулятор тригонометрии прямоугольного треугольника, почему бы не попробовать другие наши похожие инструменты? Вот они:

• Тригонометрический калькулятор;
• Калькулятор косинуса треугольника;
• Калькулятор синуса треугольника;
• Калькулятор триггерного треугольника;
• Калькулятор триггеров;
• Калькулятор синус-косинус-тангенса;
• Калькулятор соотношения тангенсов; и
• Калькулятор угла касательной.

Часто задаваемые вопросы

Как применить тригонометрию к прямоугольному треугольнику?

Чтобы применить тригонометрию к прямоугольному треугольнику, помните, что синус и косинус соответствуют сторонам прямоугольного треугольника . Чтобы решить прямоугольный треугольник с помощью тригонометрии:

1. Определить острый угол в треугольнике α . Для этого угла:
   • sin(α) = напротив/гипотенуза ; и
   • cos(α) = смежный/гипотенуза .
2. Взяв обратных тригонометрических функций , мы можем найти значение угла α .
3. Вы можете повторить процедуру для другого угла.

Чему равна гипотенуза треугольника с углом α = 30° и противоположным катетом a = 3?

Длина гипотенузы 6 . Чтобы найти этот результат:

1. Вычислите синус α : sin(α) = sin(30°) = 1/2 .

   No related posts.