Задачи на сложение и вычитание дробей
Лёгкий
Задача 1
Вычислите сумму дробей: [tex]\frac{1}{5}+\frac{2}{5}[/tex]
[tex]\frac{2}{5}[/tex]
[tex]\frac{1}{5}[/tex]
[tex]\frac{3}{10}[/tex]
[tex]\frac{3}{5}[/tex]
Задача 2
Найдите значение [tex]\frac{3}{7}+\frac{2}{7}[/tex]
[tex]\frac{5}{14}[/tex]
[tex]\frac{5}{7}[/tex]
[tex]\frac{1}{7}[/tex]
[tex]\frac{6}{7}[/tex]
Задача 3
Вычислите [tex]\frac{1}{3}+\frac{2}{3}[/tex]
$\frac{4}{3}$
$\frac{2}{3}$
$1$
$3$
Задача 4
Посчитайте значение: [tex]\frac{2}{15}+\frac{5}{15}[/tex]
$\frac{7}{30}$
$\frac{7}{15}$
$\frac{10}{15}$
$\frac{1}{3}$
Задача 5
Найдите сумму дробей: [tex]\frac{8}{11}+\frac{4}{11}[/tex]
[tex]\frac{12}{22}[/tex]
[tex]\frac{13}{11}[/tex]
[tex]\frac{10}{11}[/tex]
[tex]\frac{12}{11}[/tex]
Задача 6
Вычислите [tex]\frac{2}{187}-\frac{2}{187}[/tex]
$0$
$1$
$2$
$\frac{1}{187}$
Задача 7
Вычислите [tex]\frac{13}{39}-\frac{8}{39}[/tex]
$\frac{5}{39}$
$5$
$\frac{4}{39}$
$\frac{21}{39}$
Задача 8
Найдите значение [tex]\frac{18}{19}-\frac{11}{19}[/tex]
$\frac{7}{9}$
$\frac{29}{19}$
$\frac{6}{19}$
$\frac{7}{19}$
Задача 9
Найдите значение [tex]\frac{15}{8}-\frac{14}{8}[/tex]
[tex]\frac{1}{8}[/tex]
[tex]8[/tex]
[tex]\frac{2}{8}[/tex]
[tex]\frac{13}{8}[/tex]
Задача 10
Найдите значение [tex]\frac{19}{27}-\frac{6}{27}[/tex]
[tex]\frac{1}{3}[/tex]
[tex]\frac{12}{27}[/tex]
[tex]\frac{14}{27}[/tex]
[tex]\frac{13}{27}[/tex]
Задача 11
Найдите сумму дробей [tex]\frac{2}{5}[/tex] и [tex]\frac{1}{5}[/tex]
[tex]\frac{1}{5}[/tex]
[tex]\frac{2}{5}[/tex]
[tex]\frac{3}{5}[/tex]
[tex]\frac{4}{5}[/tex]
Задача 12
Вычислите [tex]\frac{5}{6}+\frac{10}{6}[/tex]
$\frac{15}{3}$
$\frac{50}{36}$
$\frac{5}{3}$
$\frac{5}{2}$
Задача 13
Определите значение [tex]\frac{6}{7}-\frac{4}{7}[/tex]
[tex]\frac{1}{7}[/tex]
[tex]\frac{2}{7}[/tex]
[tex]\frac{3}{7}[/tex]
[tex]2[/tex]
Задача 14
Вычтите [tex]\frac{5}{13}[/tex] из [tex]\frac{14}{13}[/tex]
[tex]\frac{19}{13}[/tex]
[tex]\frac{9}{13}[/tex]
[tex]1\frac{9}{13}[/tex]
[tex]\frac{8}{13}[/tex]
Задача 15
Вычислите [tex]\frac{3}{18}+\frac{15}{18}[/tex]
[tex]1[/tex]
[tex]\frac{1}{18}[/tex]
[tex]\frac{17}{18}[/tex]
[tex]\frac{19}{18}[/tex]
Задача 16
Найдите значение [tex]\frac{2}{7}+\frac{3}{7}-\frac{5}{7}[/tex]
[tex]\frac{1}{7}[/tex]
[tex]1[/tex]
[tex]\frac{6}{7}[/tex]
[tex]0[/tex]
Задача 17
Выполните сложение дробей: [tex]\frac{8}{91}+\frac{13}{91}[/tex]
[tex]\frac{20}{91}[/tex]
[tex]\frac{21}{91}[/tex]
[tex]\frac{22}{91}[/tex]
[tex]\frac{23}{91}[/tex]
Задача 18
Вычтите дроби: [tex]\frac{15}{45}-\frac{5}{45}[/tex]
[tex]\frac{3}{5}[/tex]
[tex]\frac{3}{9}[/tex]
[tex]\frac{20}{45}[/tex]
[tex]\frac{2}{9}[/tex]
Задача 19
Сложите дроби: [tex]\frac{5}{6}+\frac{4}{6}[/tex]
[tex]\frac{4}{3}[/tex]
[tex]1\frac{1}{2}[/tex]
[tex]\frac{9}{12}[/tex]
[tex]\frac{5}{3}[/tex]
Задача 20
Сложите дроби: [tex]\frac{43}{56}+\frac{13}{56}[/tex]
[tex]\frac{54}{56}[/tex]
[tex]\frac{55}{56}[/tex]
$1$
$2$
Задача 21
Найдите сумму дробей: [tex]\frac{1}{10}+\frac{7}{10}[/tex]
[tex]\frac{4}{5}[/tex]
[tex]\frac{3}{5}[/tex]
[tex]\frac{7}{10}[/tex]
[tex]\frac{9}{10}[/tex]
Задача 22
Выполните вычитание дробей: [tex]\frac{5}{18}-\frac{1}{18}[/tex]
[tex]\frac{1}{9}[/tex]
[tex]\frac{1}{4}[/tex]
[tex]\frac{3}{9}[/tex]
[tex]\frac{2}{9}[/tex]
Задача 23
Сложите дроби: [tex]\frac{5}{18}[/tex] и [tex]\frac{16}{18}[/tex]
[tex]1\frac{5}{6}[/tex]
[tex]\frac{8}{6}[/tex]
[tex]1\frac{1}{6}[/tex]
[tex]\frac{5}{6}[/tex]
Задача 24
Вычтите дроби: [tex]\frac{6}{10}-\frac{1}{10}[/tex]
[tex]\frac{1}{5}[/tex]
[tex]\frac{1}{2}[/tex]
[tex]\frac{2}{5}[/tex]
[tex]\frac{7}{10}[/tex]
Лёгкий
Прислать задачу
Правильный:
Неверный:
Неразрешенные задачи:
6 класс.
 Виленкин § 2. Сложение и вычитание дробей
Виленкин § 2. Сложение и вычитание дробей
Админ
Математика 6 класс УЧЕБНИК 2021 в 2-х частях (УМК Виленкин и др.) §2. Сложение и вычитание дробей с разными знаменателями (Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел).
Перейти в ОГЛАВЛЕНИЕ
Ознакомительная версия перед покупкой. Цитаты из учебного пособия использованы в учебных целях.
Математика 6 класс (УМК Виленкин)
§ 2. Сложение и вычитание дробей с разными знаменателями
8. Основное свойство дроби.
9. Сокращение дробей.
10. Приведение дробей к общему знаменателю.
11. Сравнение, сложение и вычитание дробей с разными знаменателями.
12. Сложение и вычитание смешанных чисел.
Задания для самопроверки.
Проектные задачи.
§
2. Сложение и вычитание дробейс разными знаменателями
8. Основное свойство дроби.
Задачи 216 — 246 с ответами ОГЛАВЛЕНИЕ
9. Сокращение дробей.
Задачи 247 — 279 с ответами ОГЛАВЛЕНИЕ
10. Приведение дробей к общему знаменателю.
Задачи 280 — 308 с ответами ОГЛАВЛЕНИЕ
11. Сравнение, сложение и вычитание дробей с разными знаменателями.
Мы умеем сравнивать, складывать и вычитать дроби с одинаковыми знаменателями.
Чтобы сравнить (сложить, вычесть) дроби с разными знаменателями, надо: 1) привести данные дроби к наименьшему общему знаменателю; 2) сравнить (сложить, вычесть) полученные дроби.
Задачи 309 — 340 с ответами Задачи 341 — 380 с ответами
в ОГЛАВЛЕНИЕ УЧЕБНИКА
12. Сложение и вычитание смешанных чисел.
Переместительное и сочетательное свойства сложения позволяют привести сложение смешанных чисел к сложению их целых частей и к сложению их дробных частей.
Задания для самопроверки.
Проектные задачи.
- Задача для будущего изобретателя робототехники.
База геологов и научно-исследовательский центр расположены по одну сторону реки. Геологи должны выйти с базы, дойти до реки, взять пробы воды и доставить полученные данные в исследовательский центр.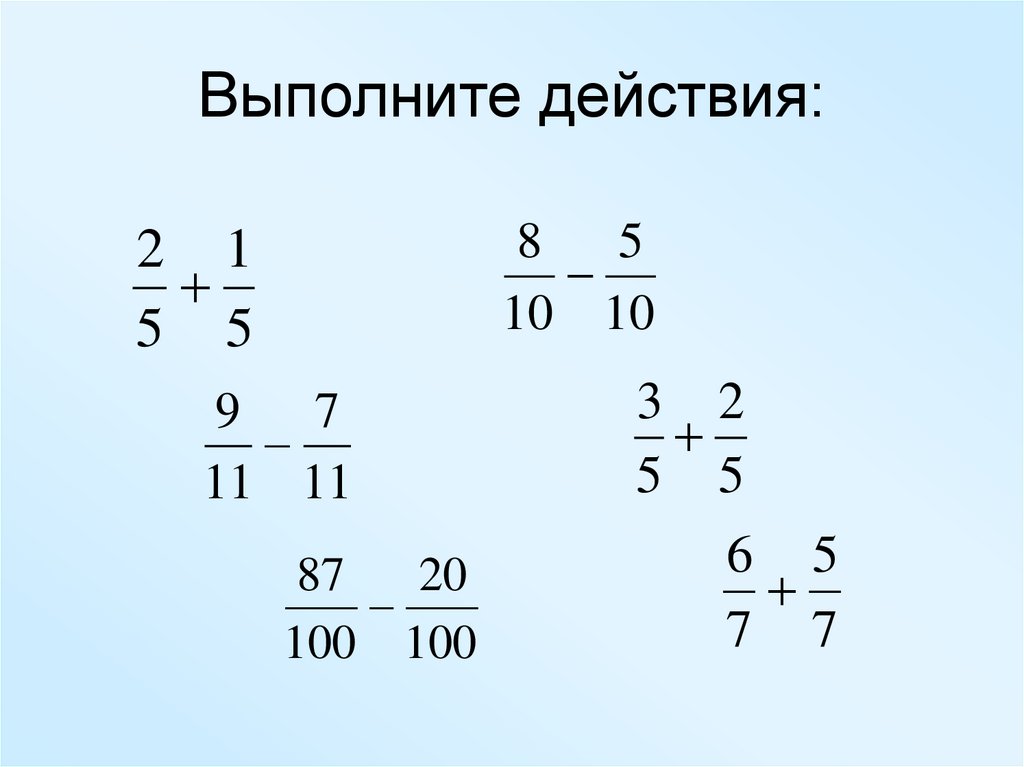 Найдите кратчайший путь геологов. Считать реку прямой линией.
Найдите кратчайший путь геологов. Считать реку прямой линией.
- Задача для будущего финансиста.
Двое имеют по некоторой сумме каждый. Первый даёт из своих денег другому столько, сколько у другого было. Затем второй отдаёт первому столько, сколько теперь осталось у первого. После этого у каждого оказывается по 12 монет. Сколько денег было у каждого вначале?
Вы смотрели: Математика 6 класс УЧЕБНИК 2021 в 2-х частях (УМК Виленкин и др.) §2. Сложение и вычитание дробей с разными знаменателями
(Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел).Перейти в ОГЛАВЛЕНИЕ
Просмотров: 37 616
Математика_УчебникиПохожие записи
Структуры задач на сложение и вычитание
Донна была учителем, тренером по математике, интервенционистом и координатором учебных программ. Часто выступая на государственных и национальных конференциях, она делится своей любовью к математике с мировой аудиторией через свой веб-сайт Math Coach’s Corner. Донна также является соавтором Guided Math Workshop.
Часто выступая на государственных и национальных конференциях, она делится своей любовью к математике с мировой аудиторией через свой веб-сайт Math Coach’s Corner. Донна также является соавтором Guided Math Workshop.
Быстрая викторина. Сколько структур задач существует для задач на сложение и вычитание?
Если вы сказали где-то около 15 строений, вы находитесь в правильном приближении. К сожалению, учащиеся часто знакомятся только с простейшими структурами. Как преподаватели, мы должны иметь представление обо всех структурах и методично преподавать их нашим ученикам.
Этот пост содержит партнерские ссылки, что просто означает, что когда вы используете мою ссылку и покупаете продукт, я получаю небольшую комиссию. С вас не взимается дополнительная плата, и я ссылаюсь только на книги и продукты, которые лично использую и рекомендую.
«…учителя, которые не осведомлены о разнообразии ситуаций и соответствующих структур, могут случайным образом предлагать ученикам задачи без надлежащей последовательности, чтобы поддержать учащихся; полное понимание смысла операций».
(Ван де Валле и др.)
Таблицы ниже были адаптированы из Математика в начальной и средней школе: обучение развитию (Ван де Валле и др.), феноменальной книги для развития вашего собственного понимания математики.
Структуры сложения/вычитания сгруппированы в три основных типа: Изменение, Часть/Часть/Целое и Сравнение. Для каждого типа существует несколько структур, в зависимости от того, какая информация известна, а какая неизвестна.
Проблемы с изменением
Первое, что вы можете заметить, это то, что структуры не обозначаются как сложение или вычитание. Хотя мы обычно думаем о соединении с как о сложении, а о , отделяющем , как о вычитании, из диаграммы видно, что это не всегда так. Результат неизвестен — самая простая и знакомая структура. Вы можете думать об этом как о классических задачах на сложение и вычитание. По мере того, как мы перемещаемся по графику, проблемы становятся все более сложными, и мы видим, что 9Структуры 0019 Change Unknown и Start Unknown можно интерпретировать как сложение или вычитание.
Надлежащий способ представить задачи — начать с самых простых, Результат неизвестен , проблем. Начните с «Объединить задачи» и позвольте учащимся попрактиковаться в решении именно этого типа задач. Помогите учащимся сосредоточиться на значении каждого числа в задаче с точки зрения Изменить , Старт или Результат . Рисование моделей — хорошая стратегия, помогающая учащимся анализировать и визуализировать каждую проблему. Затем введите отдельные задачи, снова давая им возможность попрактиковаться только с этим типом. Затем пришло время их смешать, поэтому учащиеся должны определить подходящую структуру, исходя из проблемы.
Теперь начните перемещаться по графику, используя тот же процесс. Представьте следующую структуру (Присоединиться, Изменить Неизвестно ), попрактиковаться в этой структуре, а затем смешать ее с другими, которые они уже знают. Имейте в виду, что этот процесс требует времени. Если вы учитель второго класса, составьте график введения структур в течение учебного года. Используйте числа, соответствующие вычислительным навыкам учащихся.
Если вы учитель второго класса, составьте график введения структур в течение учебного года. Используйте числа, соответствующие вычислительным навыкам учащихся.
Часть-Часть-Целое
Задачи Часть-Часть-Целое очень похожи на Изменение. Тонкое отличие состоит в том, что в этих задачах часто нет действия, что делает их немного более абстрактными для учащихся. Структура Whole Unknown — очень простая задача на сложение. В структуре One Part Unknown мы знаем общее количество и одну из частей, но упускаем другую часть. Это также обычно называют проблемой отсутствующих дополнений. Мы часто решаем задачи такого типа с помощью вычитания, но также хорошо работает стратегия подсчета. Действительно интересная структура — Both Parts Unknown. Это приложение для решения задач на знание все комбинации для числа !
По мере того, как учащиеся знакомятся со структурами, помните, что создавать задач так же важно, как и решать их. Я люблю деятельность, которую я называю Вы пишете историю . Дайте учащимся уравнение и попросите их написать рассказ по нему и нарисовать модель для своего рассказа.
Дайте учащимся уравнение и попросите их написать рассказ по нему и нарисовать модель для своего рассказа.
Еще одно замечание о задачах «Изменение» и «Часть-Часть-Целое». Хотя все эти примеры имеют два дополнения, вы также можете использовать более двух дополнений, чтобы усложнить задачу. Подумайте: В столовой 425 студентов. 127 учеников — пятиклассники, 146 — четвероклассники, остальные — третьеклассники. Сколько 3-классников в столовой?
Сравнение
Наконец, у нас есть задачи на сравнение, которые включают сравнение двух величин — большей и меньшей. Их также можно записать, используя на больше или на меньше. Меньше намного сложнее для учащихся. Мы хотим убедиться, что мы вводим вычитание сравнения с использованием манипуляций, чтобы помочь учащимся понять структуру. См. этот поз. t для получения дополнительной информации.
Вот оно! Все структуры для задач на сложение и вычитание. Вы можете загрузить собственную копию таблиц, показывающих структуры, используя кнопку ниже.
Вы можете загрузить собственную копию таблиц, показывающих структуры, используя кнопку ниже.
Я с нетерпением жду информации о том, как вы будете учить эти структуры в своем классе, поэтому обязательно оставьте комментарий!
Ресурсы для проблемных структур
Морроу-Леонг, К., Мур, С.Д., и Годжак, Л. (2021). Математизируйте это!: выходя за рамки ключевых слов, чтобы понять смысл словесных задач , классы K-2 или классы 3-5 . Тысяча дубов, Калифорния: Корвин.
Карпентер, Томас П. и др. (2015) Математика для детей: когнитивно-ориентированное обучение . Хайнеманн.
Типы задач на сложение и вычитание В примерах используются целые числа
Обзор
- Проблемы соединения
- Отдельные проблемы
- Проблемы части-части-целого
- Сравните или уравняйте задачи
- Образцы для классификации
Проблемы соединения
(начальный номер + номер изменения = сумма или результат)
Отсутствует сумма или результат неизвестен
(начальный номер + номер изменения = ____________)
- У Пита было 3 яблока.

- У Санди было 7 монет. Майк дал ей еще 4. Сколько всего десятицентовиков у Сэнди?
Добавление отсутствующих изменений неизвестно
(начальный номер + ____________ = сумма или результат)
- У Кэти было 5 карандашей. Сколько еще карандашей она должна положить с собой, чтобы всего у нее было 7 карандашей?
- У Сэнди есть 7 монет. Майк дал ей еще немного. Теперь у Санди 11 десятицентовиков. Сколько ей дал Майк?
Отсутствует начало или начальное дополнение неизвестно
(____________ + номер изменения = сумма или результат)
- Боб получил 2 печенья. Теперь у него 5 печений. Сколько печенья было у Боба вначале?
- У Сэнди есть десять центов. Майк дал ей еще 4. Теперь у Санди 11 десятицентовиков. Сколько десятицентовиков было у Сэнди для начала?
Отдельные задачи
(начало — изменение = разница или сумма или результат)
Результирующая разница или сумма неизвестна
(начальный номер + номер изменения = ____________)
- У Сэнди 11 десятицентовиков.
 Она дала Майку 4 цента. Сколько десятицентовиков сейчас у Сэнди?
Она дала Майку 4 цента. Сколько десятицентовиков сейчас у Сэнди? - У Джо было 8 шариков. Затем он дал 5 шариков Тому. Сколько шариков сейчас у Джо?
Отсутствует изменение сложения/вычитания Неизвестно
(начальный номер + ____________ = разность или сумма)
- У Сэнди было 11 десятицентовиков. Она дала немного Майку. Теперь у нее 7 копеек. Сколько она дала Майку?
- У Фреда было 11 конфет. Он потерял некоторые части. Теперь у него 4 конфеты. Сколько конфет потерял Фред?
Начальное добавление/уменьшение неизвестно
(____________ + номер изменения = разница или сумма)
- У Сэнди было несколько десятицентовиков. Она дала 4 Майку. Теперь у Сэнди осталось 7 десятицентовиков. Сколько десятицентовиков было у Сэнди для начала?
- У Карен были проблемы со словами. Она решила 2 из них. У нее все еще проблемы с тремя словами. Со сколькими словесными задачками она должна была начать?
Часть — Часть — Целое Проблемы
(часть + часть = целое)
Отсутствует целое или сумма Неизвестно
(часть + часть = ____________
- В волейбольной команде 6 мальчиков и 8 девочек.

- У Бобби 3 монеты, а у Аззи 5. Если их сложить, сколько у них будет?
- У Майка 5 пенни и 10 десятицентовиков. Сколько у него монет?
- У Майка 5 монет, а у Сэнди 10 монет. Они кладут туда копейки в копилку. Сколько монет они положили в банк?
- У Сары есть 6 сахарных пончиков и 9 обычных пончиков. Затем она кладет их все на тарелку. Сколько пончиков на тарелке?
Отсутствующая часть неизвестна
(часть + ____________ = целиком) или
(____________ + часть = целиком)
- У Карлоса в кармане было 8 четвертаков. Он протягивает руку и вытаскивает четыре. Сколько еще у него в кармане?
- У Брайана 14 цветов. Восемь из них красные, а остальные желтые. Сколько желтых цветов у Брайана?
- Бобби и Сэнди положили 12 десятицентовиков в кошелек для мелочи. Сэнди поставила 8. Сколько поставила Бобби? или Майк и Сэнди положили 11 центов в копилку.
 Майк положил 7 центов. Сколько десятицентовиков положила Сэнди?
Майк положил 7 центов. Сколько десятицентовиков положила Сэнди? - У Майка 10 монет. 7 его монет — десятицентовики, а остальные — пенни. Сколько копеек?
- У Джо и Тома 8 шариков, когда они сложили все свои шарики вместе. У Джо 3 шарика. Сколько шариков у Тома?
Проблемы сравнения или выравнивания
(одно значение + или — разница = второе значение)
Разница неизвестна
(одно значение + или — разница = второе значение)
(одно значение — второе значение = разница)
- У Джо 3 воздушных шарика. У его сестры Конни 5 воздушных шаров. На сколько больше шариков у Конни, чем у Джо?
- У Дженис есть 8 жевательных резинок. У Тома 2 палочки жевательной резинки. На сколько палочек у Тома меньше, чем у Дженис?
- У Майка 11 десятицентовых монет, а у Сэнди 5. На сколько десятицентовых монет у Майка больше, чем у Сэнди?
- У Майка 11 монет.
 У Санди 5 центов. На сколько монет у Сэнди меньше, чем у Майка?
У Санди 5 центов. На сколько монет у Сэнди меньше, чем у Майка?
Большее неизвестное
(одно значение + разница = второе значение)
(второе значение — разница = первое значение)
- У Луиса 6 золотых рыбок. У Карлы на 2 золотых больше, чем у Луиса. Сколько золотых рыбок у Карлы?
- Папа купил в воскресенье 18 бутылок молока, а в понедельник принес на 6 бутылок меньше. Сколько бутылок он принес в понедельник?
- У Майка на 4 монеты больше, чем у Сэнди. У Санди 7 центов. Сколько монет у Майка?
- У Сэнди на 4 монеты меньше, чем у Майка. У Санди 7 центов. Сколько монет у Майка?
- У Джейн 7 кукол. У Ани 3 куклы. Сколько кукол нужно потерять Джейн, чтобы их было столько же, сколько Энн?
- У Конни 13 шариков. Если Джим выиграет 5 шариков, у него будет столько же шариков, сколько у Конни. Сколько шариков у Джима?
Меньшее неизвестное
(одно значение + разница = второе значение)
(второе значение — разница = первое значение)
- У Максин 9 свитеров.
 У нее на 5 свитеров больше, чем у Сью. Сколько свитеров у Сью?
У нее на 5 свитеров больше, чем у Сью. Сколько свитеров у Сью? - У Джима 5 шариков. У него на 8 шариков меньше, чем у Конни. Сколько шариков у Конни?
- У Сэнди на 4 монеты меньше, чем у Майка. У Майка 11 центов. Сколько монет у Сэнди?
- У Майка на 4 монеты больше, чем у Сэнди. У Майка 11 центов. Сколько монет у Сэнди? У Сьюзен 8 шариков.
- У Фреда 5 шариков. Сколько еще шариков нужно Фреду, чтобы у него было столько же шариков, сколько у Сьюзан?
Куда бы вы их положили?
- В футбольной команде было 6 мальчиков. К команде присоединились еще два мальчика. Сейчас в команде столько же мальчиков, сколько и девочек. Сколько девушек в команде?
- На столе стояло 11 стаканов. Я убрал 4 из них, чтобы на столе было столько же стаканов, сколько тарелок. Сколько тарелок стояло на столе?
- В танцевальной группе было несколько девушек. Четверо из них сели так, чтобы у каждого мальчика был партнер.


 (Ван де Валле и др.)
(Ван де Валле и др.) 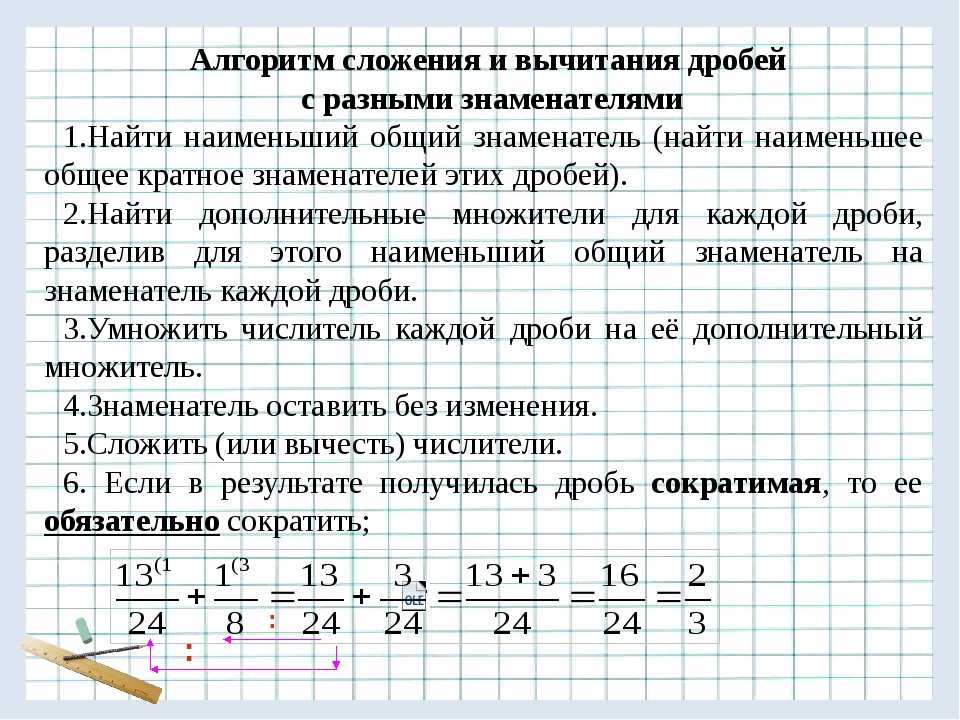
 Она дала Майку 4 цента. Сколько десятицентовиков сейчас у Сэнди?
Она дала Майку 4 цента. Сколько десятицентовиков сейчас у Сэнди?
 Майк положил 7 центов. Сколько десятицентовиков положила Сэнди?
Майк положил 7 центов. Сколько десятицентовиков положила Сэнди? У Санди 5 центов. На сколько монет у Сэнди меньше, чем у Майка?
У Санди 5 центов. На сколько монет у Сэнди меньше, чем у Майка? У нее на 5 свитеров больше, чем у Сью. Сколько свитеров у Сью?
У нее на 5 свитеров больше, чем у Сью. Сколько свитеров у Сью?