Чему равен котангенс угла если его тангенс равен минус одному: Чему равен котангенс угла, если его тангенс равен: 1) -1 2) 3 ???

Чему равен котангенс угла, если его тангенс равен: 1) -1 2) 3 ??? — Знания.site

Последние вопросы

• Геометрия

  7 минут назад

  Знайдіть висоту трикутника, проведенудо середньої за довжиною сторони, якщо сторони трикутника до рівнюють 9 см, 10 см 17 см

• Геометрия

  13 минут назад

  Очень срочно пожалуста даю 40 балів

• Геометрия

  43 минут назад

  Вписанный и описанный шестиугольник

• Геометрия

  58 минут назад

  Геометрія 2. ……………………………….

• Геометрия

  1 час назад

  Допоможіть будь ласочка, дуже вас прошу / Помогите пожалуйста, очень сильно вас прошу.( Если что 8 класс) Срочно! Даю 60 баллов ​

• Геометрия

  2 часа назад

  дано дві сторони трикутника й кут між ними. знайдіть інші два кути і третю сторону, якщо b=4, c=5, a(альфа) = 60°ДОПОМОЖІТЬ БУДЬ ЛАСКА​

• Геометрия

  2 часа назад

  в трикутнику ABC AC = 8 см BC = 15 см Чи може sin A =3/5?
• Геометрия

  2 часа назад

  100 баллов! срочно! ​

• Геометрия

  3 часа назад

  геометрия 9 клас многокутник Дано коло, радіус якого дорівнює 16 см. Знайди: сторону правильного трикутника, вписаного в це коло; см сторону правильного трикутника, описаного навколо цьо­го кола; см сторону правильного чотирикутника, описаного навколо цього кола; см сторону правильного чотирикутника, вписаного в дане коло; см сторону правильного шестикутника, вписаного в дане коло; см

• Геометрия

  3 часа назад

  Знайди радіус, вписаного в правильний многокутник кола, внутрішній кут якого дорівнює 162°, а периметр дорівнює 40 см. Результат округли до одиниць

• Геометрия

  3 часа назад

  Каков меньший диаметр усечённого конуса

• Геометрия

  3 часа назад

  чим небезпечні кислотні дощі

• Геометрия

  4 часа назад

  Как на треугольнике найти высоту АН?

• Геометрия

  4 часа назад

  Помогите решить пожалуйста

• Геометрия

  4 часа назад

  Бісектриса прямого і гострого кутів прямокутного трикутника врезультаті перетину утворюють кути один з яких дорівнює 112 градусів знайдіть гострі кути трикутника? Даю 91 бал.

Все предметы

English

United States

Polski

Polska

Bahasa Indonesia

Indonesia

English

India

Türkçe

Türkiye

English

Philippines

Español

España

Русский

Россия

How much to ban the user?

1 hour 1 day

10 класс. Алгебра. Тригонометрические функции. Формулы приведения. — Формулы приведения.

Комментарии преподавателя

Фор­му­лы при­ве­де­ния

Фор­му­лы при­ве­де­ния пред­на­зна­че­ны для того, чтобы при­ве­сти три­го­но­мет­ри­че­скую функ­цию про­из­воль­но­го угла  к три­го­но­мет­ри­че­ской функ­ции наи­мень­ше­го из углов.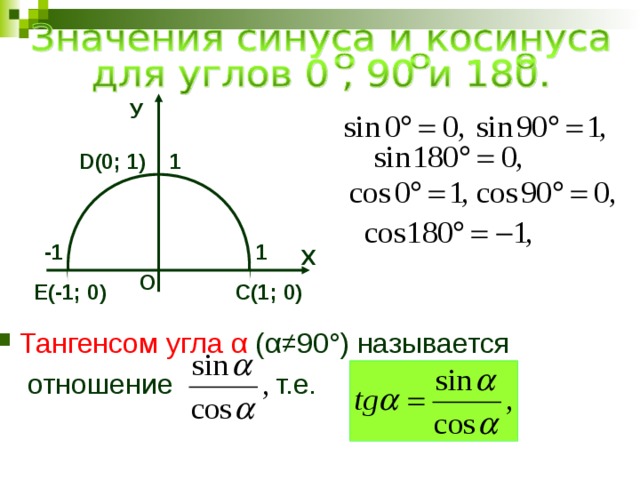

Рас­смот­рим кон­крет­ный при­мер. Рас­смот­рим дуги в  и, со­от­вет­ствен­но, (рис. 1).

 как пря­мо­уголь­ные по ги­по­те­ну­зе и остро­му углу 

Из ра­вен­ства тре­уголь­ни­ков сле­ду­ет ра­вен­ство со­от­вет­ству­ю­щих сто­рон.

Функ­ции боль­ше­го угла при­ве­де­ны к функ­ци­ям мень­ше­го угла. В этом суть фор­мул при­ве­де­ния.

Для при­ме­не­ния фор­мул при­ве­де­ния три­го­но­мет­ри­че­скую функ­цию лю­бо­го угла нужно при­ве­сти к од­но­му из видов: .

Фор­мул при­ве­де­ния много, но все они под­чи­ня­ют­ся двум пра­ви­лам:

Пер­вое пра­ви­ло:

Для ар­гу­мен­тов  функ­ция ме­ня­ет­ся на ко­функ­цию, т.е. синус на ко­си­нус и на­о­бо­рот, тан­генс на ко­тан­генс и на­о­бо­рот.

Для ар­гу­мен­тов  функ­ция не ме­ня­ет­ся.

При­ме­ры на пер­вое пра­ви­ло:

Знак пока не учи­ты­ва­ем, он опре­де­ля­ет­ся вто­рым пра­ви­лом, пока важно по­нять, в каких слу­ча­ях функ­ция ме­ня­ет­ся на ко­функ­цию, а в каких не ме­ня­ет­ся.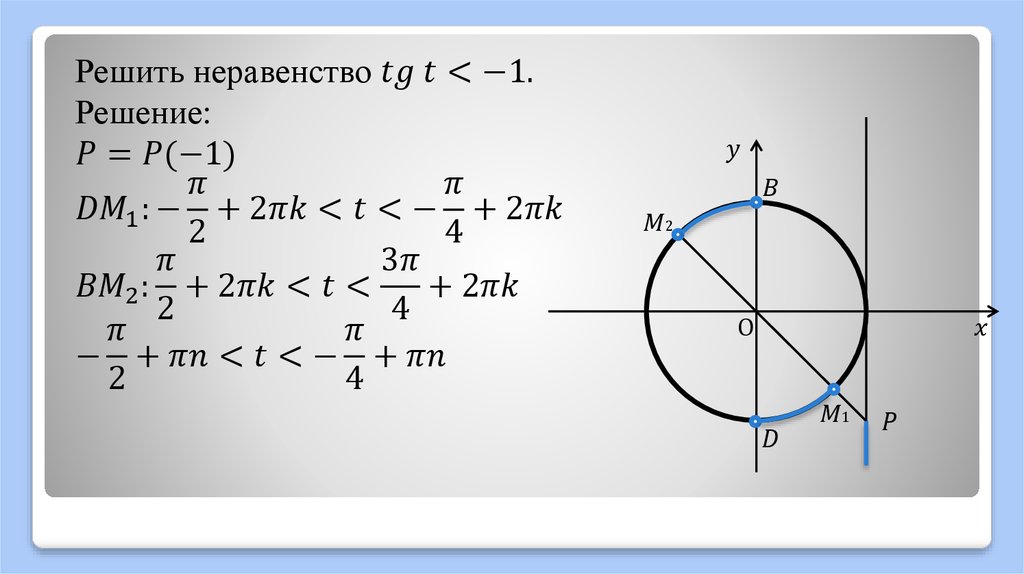

1) 

2) 

3) 

4) 

Для ар­гу­мен­тов вида на­име­но­ва­ние функ­ции сле­ду­ет из­ме­нить на ко­функ­цию.

5) 

6) 

7) 

8) 

Для ар­гу­мен­тов вида на­име­но­ва­ние функ­ции не ме­ня­ет­ся.

Вто­рое пра­ви­ло (для знака при­ве­ден­ной функ­ции, функ­ции угла ).

1) Счи­та­ем угол  ост­рым, 

2) Опре­де­ля­ем чет­верть и знак в ней при­во­ди­мой функ­ции (функ­ции слева).

3) Ста­вим этот знак перед при­ве­ден­ной к углу  функ­ци­ей (функ­ци­ей спра­ва).

При­ме­ча­ние: Угол  может быть любым, ост­рым мы его счи­та­ем услов­но, для при­ме­не­ния пра­ви­ла.

При­ме­ры на вто­рое пра­ви­ло:

1)  

Рис. 2.

Угол  на­хо­дит­ся во вто­рой чет­вер­ти. Во вто­рой чет­вер­ти , ста­вим знак плюс.

2) 

Рис

Угол  на­хо­дит­ся в тре­тьей чет­вер­ти. В тре­тьей чет­вер­ти  ста­вим знак минус.

3) 

Рис. 4.

Угол  на­хо­дит­ся во вто­рой чет­вер­ти.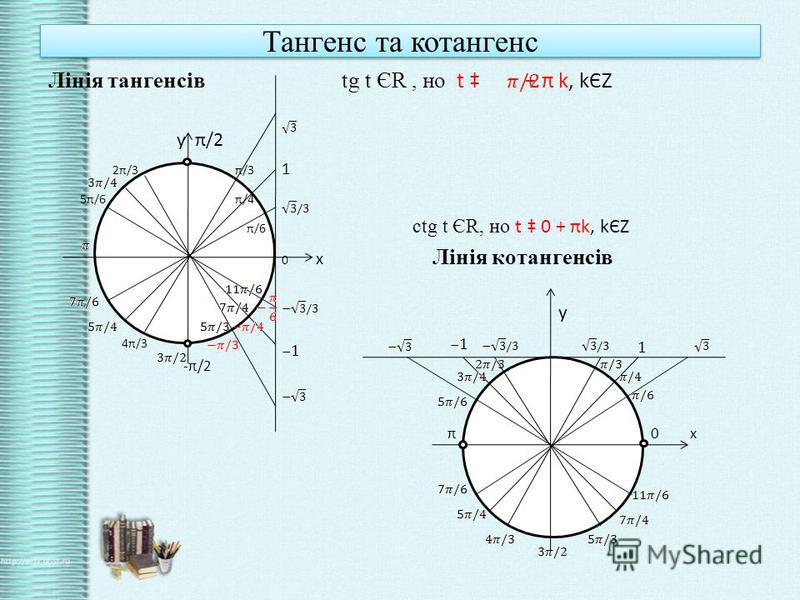 Во вто­рой чет­вер­ти  ста­вим знак минус.

4) 

Рис. 5.

Угол  на­хо­дит­ся в чет­вёр­той чет­вер­ти. В чет­вёр­той чет­вер­ти  ста­вим знак минус.

5) 

Рис. 6.

Угол  на­хо­дит­ся в тре­тьей чет­вер­ти. В тре­тьей чет­вер­ти  ста­вим знак минус.

6) 

Рис. 7.

Угол  на­хо­дит­ся во вто­рой чет­вер­ти, во вто­рой чет­вер­ти  ста­вим знак минус.

7) 

Рис. 8.

Угол  на­хо­дит­ся во вто­рой чет­вер­ти. Во вто­рой чет­вер­ти  ста­вим знак минус.

8) 

Рис. 9.

Угол  на­хо­дит­ся в чет­вёр­той чет­вер­ти. В чет­вёр­той чет­вер­ти  ста­вим знак минус.

Итак, мы рас­смот­ре­ли раз­лич­ные при­ме­ры при­ме­не­ния пер­во­го и вто­ро­го пра­вил фор­мул при­ве­де­ния.

Рас­смот­рим при­е­мы, об­лег­ча­ю­щие за­по­ми­на­ние фор­мул при­ве­де­ния.

1. «Пра­ви­ло ло­ша­ди». Глядя на чис­ло­вую окруж­ность легко от­ве­тить на во­прос, ме­ня­ет­ся ли функ­ция на ко­функ­цию.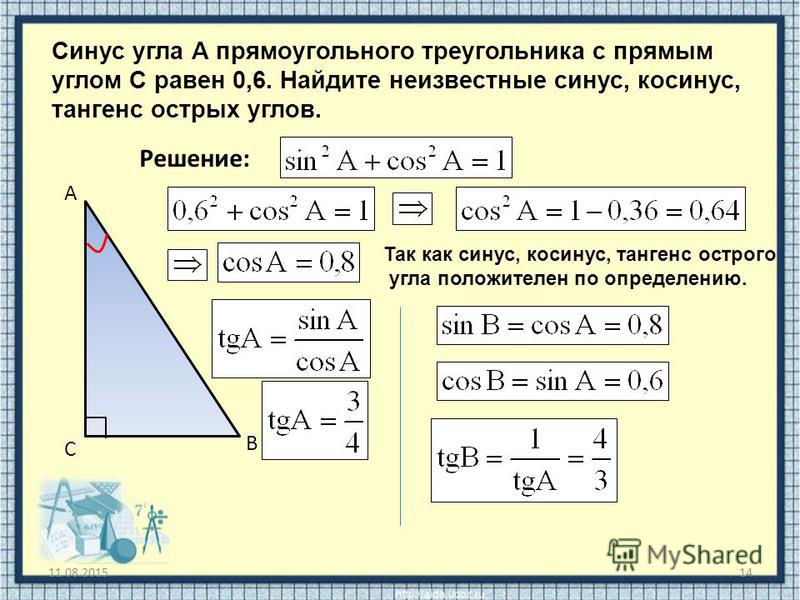

Для ар­гу­мен­тов , т.е. ар­гу­мен­тов, от­ло­жен­ных от вер­ти­каль­ной оси, на во­прос, ме­ня­ет­ся ли функ­ция  на ко­функ­цию, ло­шадь, глядя на точки , будет утвер­ди­тель­но ки­вать – функ­ция ме­ня­ет­ся на ко­функ­цию (рис. 10)  .

Для ар­гу­мен­тов  , т.е. ар­гу­мен­тов, от­ло­жен­ных от го­ри­зон­таль­ной оси, ло­шадь, глядя на точки  будет от­ри­ца­тель­но мо­тать го­ло­вой – функ­ция не ме­ня­ет­ся (рис. 10)  .

2. Ис­поль­зу­ем пе­ри­о­дич­ность и чет­ность.

Вспом­ним, что наи­мень­ший по­ло­жи­тель­ный пе­ри­од у тан­ген­са и ко­тан­ген­са равен  Это зна­чит, что

На­при­мер, 

У си­ну­са и ко­си­ну­са наи­мень­ший по­ло­жи­тель­ный пе­ри­од равен 

На­при­мер,

Рас­смот­рим при­ме­ры на ис­поль­зо­ва­ние фор­мул при­ве­де­ния.

1) Вы­чис­лить зна­че­ния всех три­го­но­мет­ри­че­ских функ­ций для 

Ре­ше­ние (рис. 11).

Угол  на­хо­дит­ся во вто­рой чет­вер­ти, синус в этой чет­вер­ти по­ло­жи­те­лен, ко­си­нус, тан­генс и ко­тан­генс от­ри­ца­тель­ны.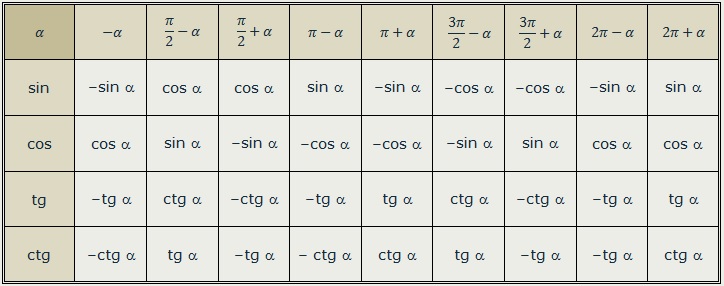

2) Вы­чис­лить зна­че­ния всех три­го­но­мет­ри­че­ских функ­ций угла 

Ре­ше­ние (рис. 12).

Угол  на­хо­дит­ся в тре­тьей чет­вер­ти, в тре­тьей чет­вер­ти синус и ко­си­нус от­ри­ца­тель­ны, тан­генс и ко­тан­генс по­ло­жи­тель­ны.

 

Мы рас­смот­ре­ли фор­му­лы при­ве­де­ния и по­яс­ни­ли их на кон­крет­ных при­ме­рах. В даль­ней­шем мы будем ак­тив­но ис­поль­зо­вать фор­му­лы при­ве­де­ния для пре­об­ра­зо­ва­ния три­го­но­мет­ри­че­ских вы­ра­же­ний.

ИСТОЧНИК

http://interneturok.ru/ru/school/algebra/10-klass/trigonometricheskie-funkcii/formuly-privedeniya

http://www.youtube.com/watch?v=n89ZZG_-5Rk

http://11book.ru/images/shcoolbook_ru/10/10_a_mord_baz.pdf

http://vklasse.org/10-klass/reshebniki/algebra/ag-mordkovich-2009-zadachnik

http://mathematics-tests.com/matematika/10-klass/algebra-10-klass-formuly-privedeniya. pdf

http://mathematics-tests.com/matematika/10-klass/algebra-10-klass-formuly-privedeniya.pptx

Формулы сложения и вычитания для тангенса и котангенса

Щелкните или коснитесь проблемы, чтобы увидеть решение.

Пример 1

Рассчитать тангенс (5 π /12).

Пример 2

Рассчитать кроватку 15°.

Пример 3

Найдите значение \(\tan \left( {\frac{\pi }{3} + \alpha } \right)\), если \(\cos \alpha = 0,6\) и угол \(\alpha\) лежит в квадранте \(4\text{th}\).

Пример 4

Найдите значение \(\cot \left( {\frac{\pi }{4} — \beta } \right)\), если \(\sin \beta = -0,8\) и угол \(\beta\) лежит в квадранте \(3\text{rd}\). 92}.\)

Пример 1.

Вычислить \(\tan \frac{{5\pi }}{{12}}.\)

Раствор.

Запишем угол \(\frac{{5\pi }}{{12}}\) как сумму двух специальных углов:

\[\frac{{5\pi }}{{12}} = \frac{{3\pi + 2\pi }}{{12}} = \frac{{3\pi }}{{12} } + \frac{{2\pi}}{{12}} = \frac{\pi }{4} + \frac{\pi }{6}.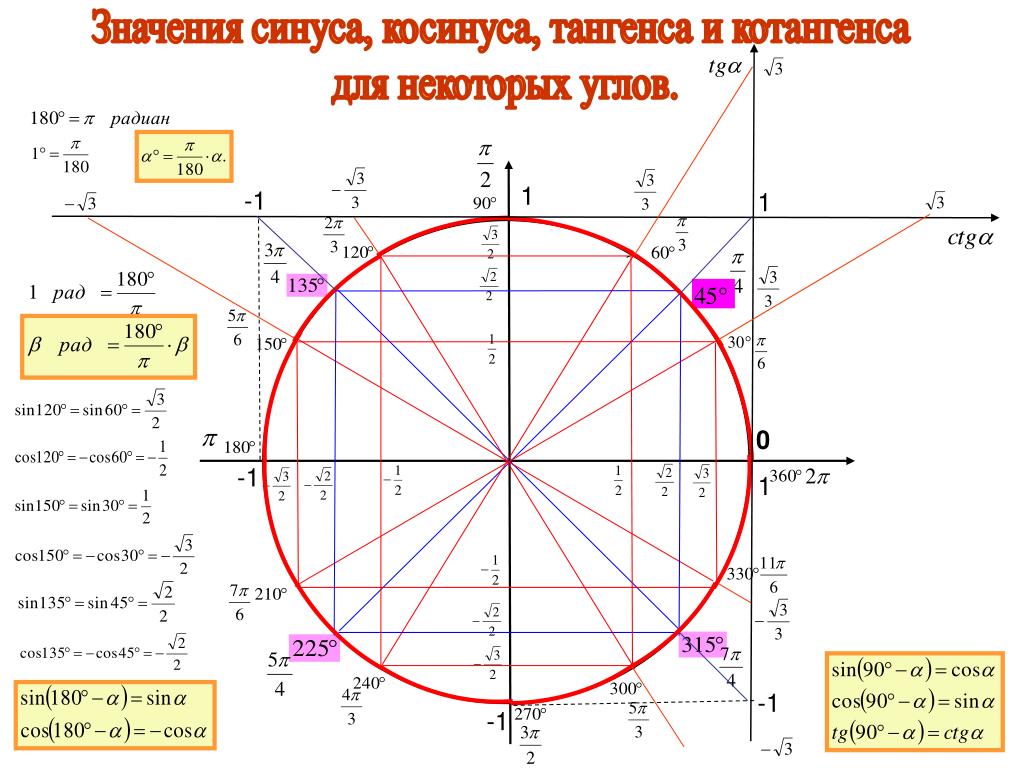 2}}}{{\left ( {\ sqrt 3 — 1} \ right) \ left ( {\ sqrt 3 + 1} \ right)}} = \ frac {{3 + 2 \ sqrt 3 + 1}} {{3 — 1}} = \ frac{{4 + 2\sqrt 3 }}{2} = 2 + \sqrt 3 .\] 92}}}{{\left({\sqrt 3 — 1} \right)\left({\sqrt 3 + 1} \right)}} = \frac{{3 + 2\sqrt 3 + 1}}{ {3 — 1}} = \frac{{4 + 2\sqrt 3 }}{2} = 2 + \sqrt 3 .\]

Пример 3.

Найдите значение \(\tan \left( {\frac{\pi }{3} + \alpha } \right)\), если \(\cos \alpha = 0,6\) и угол \(\alpha\) лежит в квадранте \(4\text{th}\).

Раствор.

Сначала мы определяем \(\sin\alpha\), используя тригонометрическое тождество Пифагора. Синус имеет отрицательное значение, потому что \(\alpha\) находится в квадранте \(4\text{th}\). 92}} = — \sqrt {1 — 0,36} = — \sqrt {0,64} = — 0,8\]

Следовательно, тангенс равен

\[\ tan \ alpha = \ frac {{\ sin \ alpha}} {{\ cos \ alpha}} = \ frac {{ — 0,8}} {{0,6}} = — \ frac {4} {3} .\]

Теперь мы можем вычислить \(\tan \left( {\frac{\pi }{3} + \alpha } \right):\)

\[\ tan \left( {\ frac {\ pi} {3} + \ alpha } \right) = \ frac {{\ tan \ frac {\ pi} {3} + \ tan \ alpha}} {{ 1 — \tan \frac{\pi }{3}\tan \alpha}} = \frac{{\sqrt 3 — \frac{4}{3}}}{{1 — \sqrt 3 \cdot \left( { — \frac{4}{3}} \right)}} = \frac{{3\sqrt 3 — 4}}{{4\sqrt 3 + 3}} = \frac{{\left( {3\ sqrt 3 — 4} \right)\left( {4\sqrt 3 — 3} \right)}}{{\left( {4\sqrt 3 + 3} \right)\left( {4\sqrt 3 — 3 } \right)}} = \frac{{36 — 16\sqrt 3 — 92}} = — \sqrt {1 — 0,64} = — \sqrt {0,36} = — 0,6\]

Следовательно,

\[\cot \beta = \frac{{\cos \beta}}{{\sin \beta}} = \frac{{ — 0,6}}{{ — 0,8}} = \frac{3}{4} . \]

По формуле вычитания котангенса,

\[\ раскладушка \ влево ( {\ гидроразрыва {\ пи} {4} — \ бета} \ справа) = \ гидроразрыва {{\ раскладушка \ гидроразрыва {\ пи} {4} \ раскладушка \ бета + 1}} { {\ cot \ beta — \ cot \ frac {\ pi} {4}}} = \ frac {{1 \ cdot \ frac {3} {4} + 1}} {\ frac {3} {4} — 1}} = \frac{{\frac{7}{4}}}{{ — \frac{1}{4}}} = — 7.\]

92}\alpha}}\cos 2\alpha — \sin 2\alpha = \tan 2\alpha \cos 2\alpha — \sin 2\alpha = \frac{{\sin 2\alpha \cancel{\cos 2 \alpha} }}{\cancel{\cos 2\alpha}} — \sin 2\alpha = \sin 2\alpha — \sin 2\alpha = 0.\]

При делении на \(\cos2\alpha\) мы предполагаем, что

\[\cos 2\alpha \ne 0,\;\; \Rightarrow 2\alpha \ne \frac{\pi }{2} + \pi n,\;\; \Rightarrow \alpha \ne \frac{\pi }{4} + \frac{{\pi n}}{2},\;n \in \mathbb{Z}.\]

Пример 6.

Упростите выражение \[\frac{{\tan \frac{{31\pi }}{{36}} — \tan \frac{\pi }{9}}}{{1 — \tan \frac{{5\pi}}{{36}}\tan \frac{\pi }{9}}}.\]

Раствор.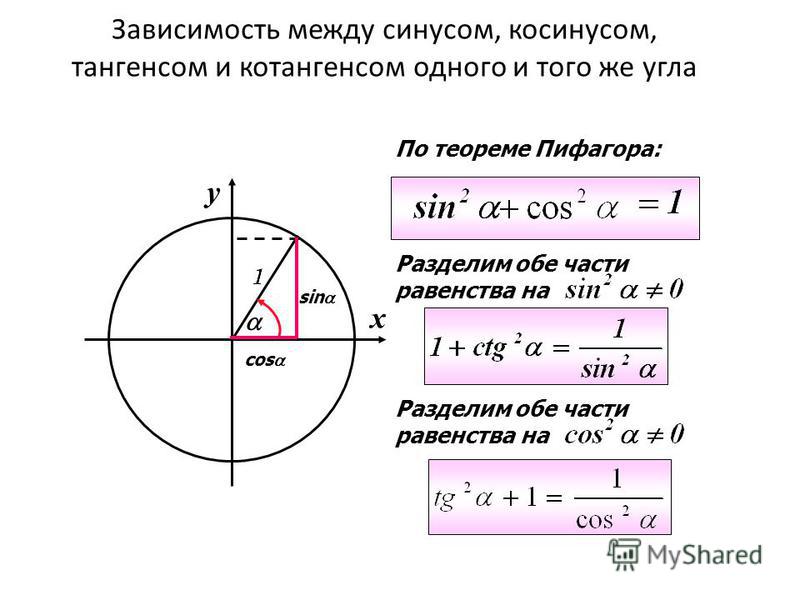

Перепишем первый член в числителе в виде

\[\tan \frac{{31\pi}}{{36}} = \tan \frac{{36\pi — 5\pi}}}{{36}} = \tan \left( {\pi — \frac{{5\pi }}{{36}}} \right).\]

Тангенс — нечетная функция с периодом \(\pi.\). Поэтому

\[\tan \frac{{31\pi}}{{36}} = \tan \left( {\pi — \frac{{5\pi}}}{{36}}} \right) = \tan \left( { — \frac{{5\pi }}{{36}}} \right) = — \tan \frac{{5\pi }}{{36}}.\]

Подставьте этот результат в исходное выражение и упростите, используя формулу сложения тангенсов:

\[\ frac {{\ tan \ frac {{31 \ pi}} {{36}} — \ tan \ frac {\ pi {9}}} {{1 — \ tan \ frac {{5 \ pi }}{{36}}\tan \frac{\pi }{9}}} = \frac{{ — \tan \frac{{5\pi}}}{{36}} — \tan \frac{\pi {9}}}{{1 — \tan \frac{{5\pi}}{{36}}\tan \frac{\pi }{9}}} = — \frac{{\tan \frac{ {5\pi }}{{36}} + \tan \frac{\pi }{9}}}{{1 — \tan \frac{{5\pi}}}{{36}}\tan \frac{ \ pi {9}}} = — \ tan \ left ( {\ frac {{5 \ pi}} {{36}} + \ frac {\ pi} {92}\frac{\pi }{{24}}}} = \frac{{\left( {\tan \frac{{7\pi}}}{{24}} — \tan \frac{\pi}}{ {24}}} \right)\left( {\tan \frac{{7\pi}}{{24}} + \tan \frac{\pi}{{24}}} \right)}}{{ \left( {1 — \tan \frac{{7\pi}}}{{24}}\tan \frac{\pi }{{24}}} \right)\left( {1 + \tan \frac{ {7\pi}}{{24}}\tan \frac{\pi}{{24}}} \right)}} = \frac{{\tan \frac{{7\pi}}}{{24} } — \tan \frac{\pi }{{24}}}}{{1 + \tan \frac{{7\pi}}}{{24}}\tan \frac{\pi }{{24}} }} \cdot \frac{{\tan \frac{{7\pi}}}{{24}} + \tan \frac{\pi }{{24}}}}{{1 — \tan \frac{{ 7\pi}}{{24}}\tan \frac{\pi}{{24}}}} = \tan\left( {\frac{{7\pi}}}{{24}} — \frac{ \pi }{{24}}} \right)\tan \left( {\frac{{7\pi}}}{{24}} + \frac{\pi}{{24}}} \right) = \ tan \ frac {{6 \ pi}} {{24}} \ tan \ frac {{8 \ pi}} {{24}} = \ tan \ frac {\ pi} {4} \ tan \ frac {\ pi }{3} = 1 \cdot \sqrt 3 = \sqrt 3 .

\]

Пример 8.

Докажите, что \[\tan \left( {\alpha + \beta } \right) \gt \tan \alpha + \tan \beta \], если \(0 \lt \alpha \lt \frac {\pi }{4}\) и \(0 \lt \beta \lt \frac{\pi }{4}.\)

Раствор.

По формуле сложения тангенсов,

\[\tan \left( {\alpha + \beta} \right) = \frac{{\tan \alpha + \tan \beta}}{{1 — \tan \alpha \tan \beta}}.\ ]

Касательная функция возрастает в своей области определения. Итак, если \(0 \lt \alpha \lt \frac{\pi }{4},\), то \(0 \lt \tan\alpha \lt 1.\) Аналогично, если \(0 \lt \beta \lt \frac{\pi }{4},\), затем \(0 \lt \tan\beta \lt 1.\)

Это означает, что произведение \(\tan\alpha\tan\beta\) меньше, чем \(1.\) Следовательно, мы имеем

\[0 \лт\тангенс \альфа\тангенс \бета \лт 1,\]

\[\Стрелка вправо — 1 \lt — \tan \alpha \tan \beta \lt 0,\]

\[\Стрелка вправо 0 \lt 1 — \tan \alpha \tan \beta \lt 1.\]

Мы видим, что знаменатель положителен, но меньше \(1.\) Тогда

\[\frac{{\tan \alpha + \tan \beta}}{{1 — \tan \alpha \tan \beta}} \gt \tan \alpha + \tan \beta,\] 92\) и \(y_2 = \frac{1}{x}\) пересекаются.