Чему равен синус 180 градусов: Чему равен синус 180° градусов

Sin 180 градусов — Найдите значение Sin 180 градусов

LearnPracticeDownload

Значение sin 180 градусов равно 0 . Sin 180 градусов в радианах записывается как sin (180° × π/180°), т. е. sin (π) или sin (3,141592…). В этой статье мы обсудим способы нахождения значения sin 180 градусов на примерах.

• Sin 180°: 0
• Грех (-180 градусов): 0
• Sin 180° в радианах: грех (π) или грех (3,1415926 . . . .)

Каково значение греха 180 градусов?

Значение sin 180 градусов равно 0. Sin 180 градусов можно также выразить с помощью эквивалента заданного угла (180 градусов) в радианах (3,14159 . . .).

Используя преобразование градусов в радианы, мы знаем, что θ в радианах = θ в градусах × (pi/180°)
⇒ 180 градусов = 180° × (π/180°) рад = π или 3,1415 . . .
∴ sin 180° = sin(3.1415) = 0

Объяснение:

Для sin 180 градусов угол 180° лежит на отрицательной оси x.

Таким образом, значение sin 180° = 0
Поскольку функция синуса является периодической функцией, мы можем представить sin 180° как sin 180 градусов = sin(180° + n × 360°), n ∈ Z.
⇒ sin 180° = sin 540° = sin 900° и так далее.
Примечание: Поскольку синус является нечетной функцией, значение sin(-180°) = -sin(180°) = 0.

Методы определения значения Sin 180 градусов задается как 0. Мы можем найти значение sin 180 градусов по формуле:

• Использование единичного круга
• Использование тригонометрических функций

Sin 180 градусов с помощью единичной окружности

Чтобы найти значение sin 180 градусов с помощью единичной окружности:

• Поверните ‘r’ против часовой стрелки, чтобы образовать угол 180° с положительной осью x.
• Грех 180 градусов равен координате y(0) точки пересечения (-1, 0) единичной окружности и r.

Отсюда значение sin 180° = y = 0

Sin 180° в терминах тригонометрических функций

Используя формулы тригонометрии, мы можем представить sin 180 градусов как:

• ± √(1-cos²(180°))
• ± тангенс 180°/√(1 + тангенс²(180°))
• ± 1/√(1 + раскладушка²(180°))
• ± √(сек²(180°) — 1)/сек 180°
• 1/косек 180°

Примечание. Поскольку 180° лежит на отрицательной оси x, конечное значение sin 180° будет равно 0.

Мы можем использовать тригонометрические тождества, чтобы представить sin 180° как

• sin(180° — 180°) = sin 0°
• -sin(180° + 180°) = -sin 360°
• cos(90° — 180°) = cos(-90°)
• -cos(90° + 180°) = -cos 270°

☛ Также проверьте:

• sin 45 градусов
• грех 20 градусов
• грех 135 градусов
• грех 144 градуса
• грех 44 градуса
• грех 16 градусов

Примеры использования Sin 180 градусов

1. Пример 1: Найдите значение (1 — cos²(180°), если sin 180° = 0.

   Решение:

   Так как (1 — cos²(180°)) = sin²(180°)
   ⇒ (1 — cos²(180°)) = 0

2. Пример 2: Найдите значение 2 × (sin 90° cos 90°). [Подсказка: используйте sin 180° = 0]

   Решение:

   Используя формулу sin 2a,
   2 sin 90° cos 90° = sin(2 × 90°) = sin 180°
   ∵ sin 180° = 0
   ⇒ 2 × (sin 90° cos 90°) = 0

3. Пример 3: Упростить: 2 (sin 180°/sin 90°)

   Решение:

   Мы знаем sin 180° = 0 и sin 90° = 1
   ⇒ 2 sin 180°/sin 90° = 2(0) = 0

перейти к слайдуперейти к слайдуперейти к слайду

 

Готовы увидеть мир глазами математика?

Математика лежит в основе всего, что мы делаем.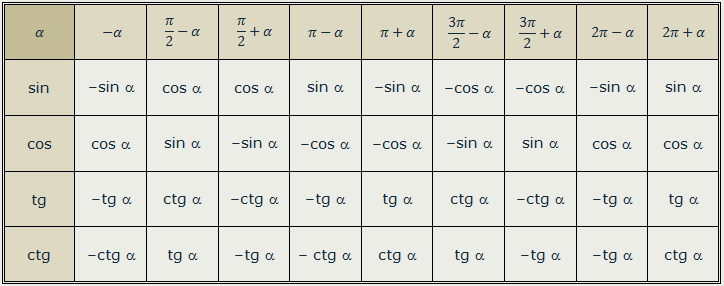 Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.

Запишитесь на бесплатный пробный урок

Часто задаваемые вопросы о Sin 180 Degrees

Что такое Sin 180 Degrees?

Sin 180 градусов — значение тригонометрической функции синуса для угла, равного 180 градусам. Значение sin 180° равно 0.

Как найти Sin 180° с точки зрения других тригонометрических функций?

Используя формулу тригонометрии, значение sin 180° может быть выражено через другие тригонометрические функции следующим образом:

• ± √(1-cos²(180°))
• ± тангенс 180°/√(1 + тангенс²(180°))
• ± 1/√(1 + раскладушка²(180°))
• ± √(сек²(180°) — 1)/сек 180°
• 1/косек 180°

☛ Также проверьте: тригонометрическую таблицу

Каково значение Sin 180 градусов в пересчете на Cosec 180°?

Мы можем представить функцию синуса в терминах функции косеканса, используя тригонометрические тождества, sin 180° можно записать как 1/cosec(180°).

Каково значение Sin 180° в пересчете на Sec 180°?

Поскольку функцию синуса можно представить с помощью функции секанса, мы можем записать sin 180° как -√(sec²(180°) — 1)/sec 180°. Значение sec 180° равно -1.

Как найти значение греха 180 градусов?

Значение sin 180 градусов можно вычислить, построив угол 180° с осью x и затем найдя координаты соответствующей точки (-1, 0) на единичной окружности. Значение sin 180° равно координате y (0). ∴ sin 180° = 0,

 

Скачать БЕСПЛАТНЫЕ учебные материалы

Тригонометрия

Рабочие листы по математике и
наглядный учебный план

Значение Sin 180 – Формула, Таблица значений синуса, Sine 180 Degree и часто задаваемые вопросы

Нуль является точным значением sin 180. Известно, что синус является одной из основных тригонометрических функций, которые помогают определить угол или стороны прямоугольного треугольника. Его еще называют тригонометрическим отношением.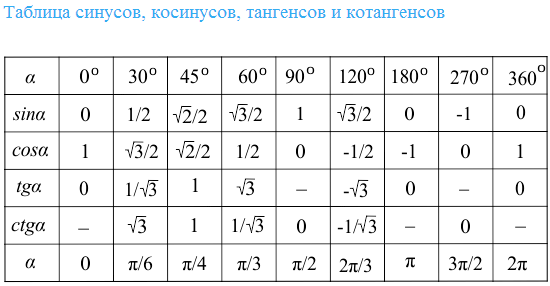 Если тета — это угол в прямоугольном треугольнике, то синус тета равен отношению перпендикуляра к гипотенузе прямоугольного треугольника. Следует отметить, что значение sin 0 также равно 0,9.0003

В математике тригонометрия — это исследование измерений треугольников, которое касается длины, высоты и углов треугольника. Тригонометрия имеет огромное применение в различных областях, таких как технологии, наука, спутниковая навигация и т. д., для вычисления различных измерений с использованием функций косинуса и синуса. В этой статье мы собираемся обсудить значение sin 180 градусов или подробно обсудить значение sin pi.

Синус и его функция

Всего в тригонометрии существует шесть тригонометрических функций: синус, кос, тангенс, секанс, косеканс и котангенс. Из всех этих шести тригонометрических функций три считаются первичными функциями, и функция синуса является одной из них. Остальные двое — загар и кос. Обычно мы определяем синус тета как отношение противоположной стороны прямоугольного треугольника к его гипотенузе. Если рассматривать треугольник с ABC как угол альфа, функция синуса будет: 

(изображение будет обновлено в ближайшее время)

Sin α= Противоположность/Гипотенуза

Теперь мы все знаем, как запутанно запоминать отношения тригонометрических функций, но у нас есть техника или, скорее, уловка, чтобы сделать процесс запоминания легким и интересным. Вы можете запомнить тригонометрические функции с помощью мнемоники SOH-CAH-TOA.

Где SOH означает «синус противоположен гипотенузе», CAH означает «косинус примыкает к гипотенузе», а TOA означает «тангенс прилегает к гипотенузе».

Что такое тригонометрические отношения?

В соответствии с тригонометрическими соотношениями в математике существует три основных или основных тригонометрических соотношения, также известных как тригонометрические тождества.

Формула функции синуса

Диаграмма, приведенная ниже, показывает, что Sin α = BC/AB.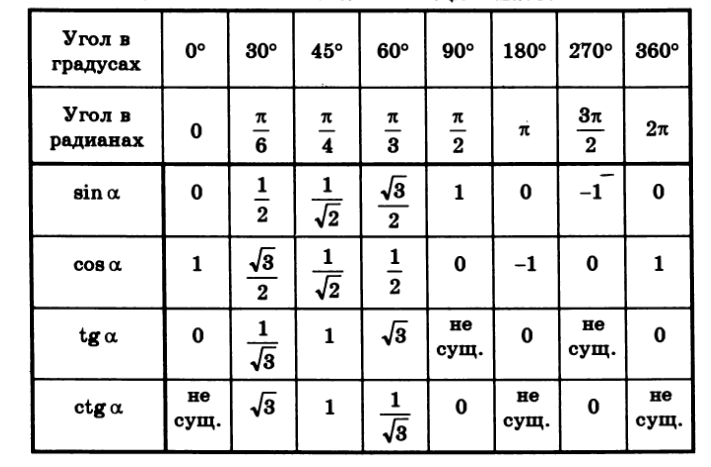

Следовательно, мы можем записать формулу в следующем виде: . Сторона, противоположная углу θ, называется противоположной (O). А сторона, лежащая рядом с углом, называется примыкающей (А).

Теорема Пифагора утверждает, что 

В прямоугольном треугольнике (противоположная)2+(прилежащая)2= (гипотенуза)2

Таблица значений синусов

Ниже приведена таблица синусов от 0 до 360 градусов. с их соответствующими значениями.

Sine Value Table

Sine Degree	Sine Function Values ​​
sin 0	0
sin 30	1/2
sin 45	1/2
sin 60	3/2
sin 90	1
sin 120	3/2
sin 150	1/2
sin 180	0
sin 270	−1
sin 360	0

Apart from these main sin values, there are few more values ​​of sine function:

sin 1 = 0,84                                                                    sin 2 = 0,91 

SIN 5 = −0,96 SIN 10 = −0,54

SIN 20 = 0,91 SIN 30 = −0,99

SIN 40 = 0,75 SIN 50 = −0,26

SIN 70 = 0,77 SIN 80 = −0,99

SIN 100 = 0,77 SIN 80 = −0,99

1 SIN 100 = 0,77.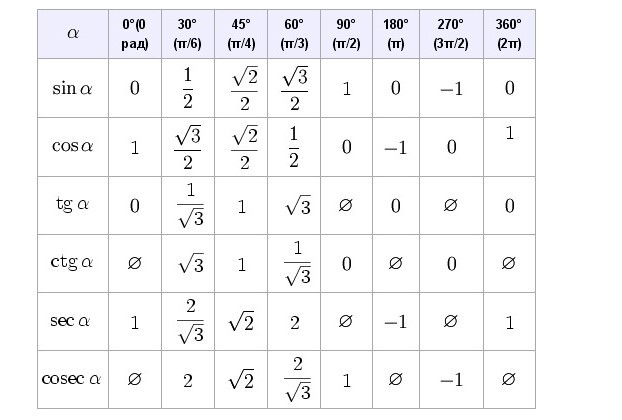 −0,50                                                                sin 105 = −0,97

sin 210= 0.47                                                                      sin 240= 0.95

sin 330= −0.13                                                                    sin 350= 0.95      

Sine 180 Degree Derivation

From the supplementary angle identity,

Sin A = Sin (180° – A )

Следовательно,

Sin ( 180° – A ) равно Sin A

Sin ( 180° – 0° ) равно Sin 0°

Sin 180° равно 0 (поскольку значение Sin 0° равно 0).

Таблица значений каждого соотношения по отношению к различным углам (таблица тригонометрических соотношений стандартных углов).

1191898

\ [\ Infty \]

111868

\ [\ infty \]

111868

\ [\ infty \]

111868

\ [\ infty \]

1918

\ [\ infty \]

1918

.

Angle	0 Degrees	30 Degrees	45 Degrees	60 Degrees	90 Градусов	180 Degrees	270 Degrees	360 Degrees
Sin	0	\[\frac{1}{2} \]	\[\frac{1}{\sqrt{2}}\]	\[\frac{\sqrt{3}}{2}\]	1
8 0	−1	0
Cos	1	]	\[\frac{1}{2}\]	0	−1	0	1
Tan	0	\[\frac{1}{\sqrt{3}}\]	1	\ [\ sqrt {3} \]	\ [\ infty \]	0	\ [\ Infty \]	\. 0	\[\infty \]	0	\[\infty \]
COSEC	\ [\ infty \]	2	\ [\ SQRT {2 \]	. 3}}\]	1	\[\infty \]	−1	\[\infty \]
Sec	1	\[\frac{2}{\sqrt{3}}\]		2	\[\infty \]	−1	\[\infty \]	1

Properties of Sine as Per Quadrants

We может определять значения функции синуса как положительные или отрицательные в зависимости от квадрантов. Вот таблица, где мы видим, что с одной стороны синус 270 отрицателен, а с другой стороны синус 90 положителен. В основном, для первого и второго квадрантов оно положительное, а для третьего и четвертого квадрантов отрицательное.

The four quadrants in the Trigonometry diagram are shown below: 

(Image will be Updated soon)

9199199919910218

(

10218

90268

Range of the Degrees	Quadrant	Sign of the Синусная функция	Диапазон значения SIN
0–90	1 -й квадрант	положительный
1919919	9021
9021
9027
0221 0
90–180	2 -й квадрат	положительный				(			. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт