Пример решения квадратного уравнения через дискриминант: Решение квадратных уравнений: формула корней, примеры

Содержание

Формула расчета решения квадратных уравнений и примеры ее использования

После изучения уравнений первого порядка в школах проходят тему квадратных равенств. Существует несколько методов их решения, однако применение формулы с дискриминантом является самым распространенным и универсальным. Рассмотрим в статье эту формулу решения уравнений квадратных.

Какие уравнения называются квадратными?

Ниже приведен рисунок, на котором изображено равенство, состоящее из трех слагаемых. Переменная x является неизвестной. Поскольку первый член содержит ее во второй степени, то данное выражение получило название квадратного. Латинскими буквами a, b и c в нем обозначены числовые коэффициенты.

Это уравнение называют полным, поскольку в нем присутствуют все слагаемые, содержащие переменную во 2-й, 1-й и 0-й степенях (член c, называемый свободным, можно представить в виде c * x⁰).

Если один из коэффициентов b или c будет нулевым, тогда уравнение станет неполным. Заметим, что равенство нуля числа a автоматически преобразует рассматриваемое выражение в линейное уравнение.

Как для полных, так и для неполных равенств второго порядка можно использовать формулу решения уравнения квадратного через дискриминант.

Универсальная формула

Как было упомянуто выше, через дискриминант формула решения уравнения квадратного может использоваться для нахождения корней равенства второго порядка совершенно любого типа. Эта формула изображена на рисунке ниже.

Из нее видно, что уравнение максимум может иметь два решения (знак ±), однако если подкоренное выражение в знаменателе будет равно нулю, тогда неизвестный x, удовлетворяющий равенству, будет представлен единственным действительным числом. Формула решения уравнения квадратного демонстрирует также, что ее использование возможно в случае знания всех трех (или меньше для неполного уравнения) его коэффициентов.

Рассматриваемую формулу можно получить самостоятельно, для этого достаточно решить уравнение в общем виде с помощью метода дополнения до полного квадрата.

Отметим, что эту формулу для определения корней неполных уравнений нет необходимости использовать, поскольку существуют более простые методы решения (факторизация с помощью вынесения за скобки икса или простой перенос свободного члена в правую часть равенства и взятие корня из него).

Понятие дискриминанта и его значение

Если посмотреть еще раз на формулу решения уравнения квадратного через дискриминант, то последним будет называться разность, заключенная под знак корня в знаменателе, то есть b²— 4 * a *c.

Какую роль он играет? Не зная об уравнении совершенно ничего, а имея только его дискриминант, можно с уверенностью сказать, сколько решений оно имеет, и какого они типа. Так, положительному значению дискриминанта соответствует 2 действительных решения, отрицательное его значение говорит также о 2-х решениях, но они уже будут комплексными числами. Наконец, если дискриминант равен нулю, что выполняется, когда b * b = 4 * a * c, то уравнение будет обладать лишь одним действительным корнем x.

Примеры решения равенств второго порядка

Используя формулу корней квадратного уравнения, решение уравнений квадратных приведем в задачах разного характера.

Задача № 1. Произведение некоторых 2-х чисел равно -84, а их сумма составляет 5. Нужно определить эти числа.

Составляем систему уравнений согласно заданному условию, получаем:

x₁* x₂ = -84

x₁+ x₂ = 5

Выражаем из второго уравнения x₁, подставляем его в первое:

(5 — x₂) *x₂ = -84 = -(x₂)²+ 5 * x₂

Теперь следует перенести члены с иксом и иксом в квадрате в левую часть и вычислить дискриминант:

(x₂)²— 5 * x₂— 84 = 0; D = 25 — 4 *1 * (-84) = 361

Воспользовавшись универсальной формулой, получаем значение корней уравнения:

x₂ = (5 ± 19) / 2 = > x₂ = (12; -7)

Чтобы получить x₁, можно воспользоваться любым из уравнений системы. Подставляя известные значения x₂, мы получим аналогичные числа для x₁. Этот факт означает, что условию задачи удовлетворяет всего одна пара чисел, то есть -7 и 12.

Задача № 2. Теперь решим несколько необычную задачу. Ниже дано уравнение:

x² − k * x + 36 = 0

Необходимо найти все значения k, которые приводили бы к единственному решению равенства.

Чтобы понять, как ответить на поставленный вопрос, следует вспомнить, что уравнения рассматриваемого типа имеет 1 корень только в том случае, если его дискриминант нулевой. То есть нам нужно найти этот дискриминант, откуда можно получить число k. Имеем:

D = k²— 4 * 1 * 36 = 0

Полученное равенство называется чистым уравнением второго порядка (в нем нет коэффициента b). Решаем его:

k = ±√144 = ±12

Таким образом, если число k примет значение +12 или -12, то корень уравнения будет один.

Примеры решения квадратных уравнений с ответами

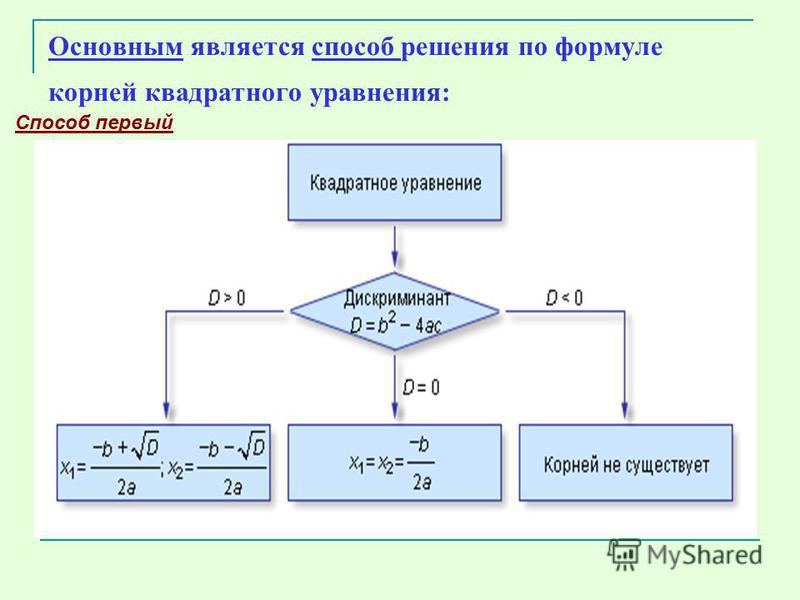
Алгоритм решения квадратных уравнений

Теорема

Квадратным уравнением называется уравнение вида:

Для решения квадратного уравнения необходимо вычислить дискриминант: .

Квадратное уравнение имеет 2 корня, если , один корень, если и не имеет корней, если .

Формулы нахождения корней квадратного уравнения.

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Цена работы

Примеры решений квадратных уравнений

Пример 1

Задача

Решить уравнение:

Решение

Найдём дискриминант:

Ответ

Пример 2

Задача

Решить уравнение:

Решение

Найдём дискриминант:

Ответ

Пример 3

Задача

Решить уравнение:

Решение

ОДЗ:

Ответ

Пример 4

Задача

Решить уравнение:

Решение

ОДЗ:

Ответ

Пример 5

Задача

Решить уравнение:

Решение

ОДЗ:

Обозначим:

Тогда:

Ответ

Пример 6

Задача

Решить уравнение:

Решение

ОДЗ:

Обозначим:

Тогда:

Ответ

Пример 7

Задача

Решить уравнение:

Решение

ОДЗ:

Обозначим:

Тогда:

– корней нет

Ответ

Пример 8

Задача

Решить уравнение:

Решение

ОДЗ:

Ответ

Пример 9

Задача

Решить уравнение:

Решение

ОДЗ:

Отсюда

Ответ

Пример 10

Задача

Решить уравнение:

Решение

– корней нет

Ответ

Средняя оценка 1.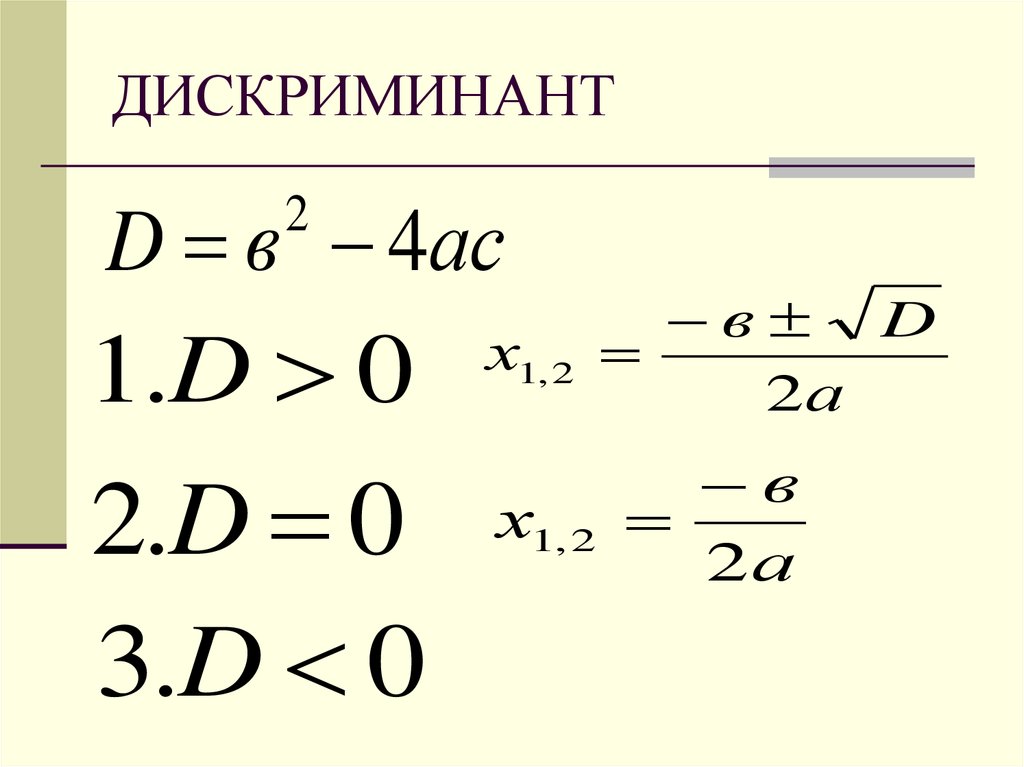 7 / 5. Количество оценок: 7

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

22553

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

Реальные примеры квадратных уравнений

Квадратное уравнение выглядит так:

Квадратные уравнения всплывают во многих реальных ситуациях!

Здесь мы собрали для вас несколько примеров и решаем каждый из них разными методами:

Факторинг Квадратичные уравнения
Завершение квадрата
Графики квадратных уравнений
Квадратичная формула
Онлайн-решатель квадратных уравнений

Каждый пример следует трем основным этапам:

Возьмите описание реального мира и составьте некоторые уравнения
Решить!
Используйте здравый смысл, чтобы интерпретировать результаты

Мячи, стрелы, ракеты и камни

Когда вы бросаете мяч (или стреляете стрелой, стреляете ракетой или бросаете камень), он поднимается в воздух, замедляется по мере движения, затем снова падает быстрее и быстрее. ..

… и квадратное уравнение всегда подскажет вам свое положение!

Пример: метание мяча

Мяч брошен прямо вверх с высоты 3 м над землей со скоростью 14 м/с. Когда он упадет на землю?

Пренебрегая сопротивлением воздуха, мы можем вычислить его высоту, сложив следующие три вещи:
(Примечание:

t — это время в секундах)

Высота начинается с 3 м:		3
Он движется вверх со скоростью 14 метров в секунду (14 м/с):		14т
Гравитация тянет его вниз, изменяя его положение на около 5 м в секунду в квадрате:		−5 т ²
(Примечание для энтузиастов: -5t ² упрощено из -(½)at ² с a=9,8 м/с ² )

Сложите их и получите высоту h в любое время t равно:

h = 3 + 14t − 5t ²

3 + 14t − 5t ² = 0

Какое квадратное уравнение!

В «Стандартной форме» это выглядит так:

−5t

2 + 14t + 3 = 0

Это выглядит еще лучше, если мы умножим все члены на −1:

5t ² − 14t − 3 = 0

Давайте решим это. ..

Есть много способов решить это, здесь мы факторизуем его, используя «Найдите два числа, которые умножьте, чтобы получить a×c , и сложите, чтобы получить b «метод квадратичного факторинга:

a×c = −15 , и b = −14 .

Коэффициенты −15 равны: −15, −5, −3, −1, 1, 3, 5, 15

Пробуя несколько комбинаций, мы находим, что −15 и 1 работают (-15×1 = -15, и −15+1 = −14)

Переписать середину с −15 и 1:5t ² − 15t + t − 3 = 0

Умножить первые два и последние два: 5t(t − 3) + 1(t − 3) = 0

Общий множитель равен (t − 3):(5t + 1)(t − 3) = 0

. Два решения: 5t + 1 = 0 или t − 3 = 0

t =

−0,2 или t = 3

«t = −0,2» — отрицательное время, невозможное в нашем случае.

«t = 3» — это ответ, который нам нужен:

Мяч падает на землю через 3 секунды!

Вот график параболы h = −5t ² + 14t + 3

Он показывает высоту мяча против времени

Некоторые интересные точки:

) При t=0 (в начале) мяч находится на высоте 3 м.

(−0,2,0) говорит о том, что −0,2 секунды ДО того, как мы бросили мяч, он находился на уровне земли. Этого никогда не было! Так что наш здравый смысл говорит игнорировать это.

(3,0) говорит, что через 3 секунды мяч находится на уровне земли.

Также обратите внимание, что мяч летит почти на 13 метров в высоту.

Примечание: Вы можете точно определить, где находится верхняя точка!

Метод объясняется в разделе «Графические квадратные уравнения» и состоит из двух шагов:

Найдите, где (вдоль горизонтальной оси) находится вершина, используя −b/2a :

t = −b/2a = −(− 14)/(2 × 5) = 14/10 = 1,4 секунды

Затем найдите высоту, используя это значение (1.4)

h = −5t ² + 14t + 3 = −5(1,4) ² + 14 × 1,4 + 3 = 12,8 метра

Итак, мяч достигает высшей точки 12,8 метра через 1,4 секунды.

Пример: новый спортивный велосипед

Вы разработали новый стиль спортивного велосипеда!

Теперь вы хотите сделать их много и продать с прибылью.

Ваш стоит будет:

700 000 долларов на производственные затраты, рекламу и т. д.
110 долларов за каждый велосипед

Исходя из похожих велосипедов, вы можете ожидать, что

продаж будут следовать этой «Кривой спроса»:

Продажи в единицах = 70 000 − 200P

Где «P» — цена.

Например, если вы установите цену:

на уровне 0 долларов, вы просто раздадите 70 000 велосипедов
за 350 долларов, вы вообще не будете продавать велосипеды
за 300 долларов вы можете продать 70 000 − 200 × 300 = 10 000 велосипеда

Итак… какая лучшая цена? А сколько надо сделать?

Давайте составим уравнения!

Сколько вы продаете, зависит от цены, поэтому используйте «P» для цены в качестве переменной

Единицы продаж = 70 000 − 200P
Продажи в долларах = Единицы × Цена = (70 000 − 200 пенсов) × P = 70 000 пенсов − 200 пенсов ²
Затраты = 700 000 + 110 x (70 000 — 200 пенсов) = 700 000 + 7 700 000 — 22 000 пенсов = 8 400 000 — 22 000 пенсов
Прибыль = Затраты на продажу = 70 000 пенсов — 200 пенсов ² — (8 400 000 — 22 000 пенсов) = -200 пенсов ² + 92 000 пенсов — 8 400 000

Прибыль = −200P ² + 92 000P − 8 400 000

Да, квадратное уравнение. Давайте решим это, заполнив квадрат.

Решение: −200p

² + 92 000p -8 400 000 = 0

Шаг 1 Разделите все термины на -200

P ² -460p + 42000 = 0

Шаг 2 -460p + 42000 = 0 0005

.0004 Переместите числовой член в правую часть уравнения:

P ² – 460P = -42000

Шаг 3 правая часть уравнения:

(b/2) ² = (−460/2) ² = (−230) ² = 52900

P ² – 460P + 42000 52900

(P – 230) ² = 10900

Шаг 4 Извлеките квадратный корень из обеих частей уравнения:

P – 230 = ±√10900 = ±104 (до ближайшего целого числа)

Шаг 5 Вычтите (-230) из обеих частей (другими словами, прибавьте 230):
P = 230 ± 104 = 126 или 334
Что это нам говорит? В нем говорится, что прибыль равна НУЛЮ, когда Цена равна $126 или $334
Но мы хотим знать максимальную прибыль, не так ли?
Это ровно половина пути между ними! По $230
А вот и график:

Прибыль = -200p ² + 92 000p — 8 400 000
Цена лучшей продажи — $ 230 , и вы можете ожидать:
Продажи единицы = 70 000 — 200 x 230 = 24 000
Продажи в долларах = 230 х 24 000 = 5 520 000 долларов
Затраты = 700 000 + 110 х 24 000 = 3 340 000 долларов
Прибыль = 5 520 000 долл. США − 3 340 000 долл. США = 2 180 000 долл. США
Очень выгодное предприятие.
Пример: малая стальная рама
Ваша компания собирается производить оправы в рамках запуска нового продукта.
Рама будет вырезана из куска стали, и для уменьшения веса окончательная площадь должна быть 28 см ²
Внутренняя часть рамы должна быть 11 см на 6 см
Какой должна быть ширина х металла?
Площадь стали перед резкой:
Площадь = (11 + 2x) × (6 + 2x) см ²
Площадь = 66 + 22х + 12х + 4х ²
Площадь = 4х ² + 34х + 66 + 66 − 66
Площадь = 4x ² + 34x
Давайте решим это графически!
Вот график 4x ² + 34x :
Желаемая площадь 28 показана горизонтальной линией.
Площадь равна 28 см ² Когда:
x составляет около −9,3 или 0,8
Отрицательное значение x не имеет смысла, поэтому ответ:
x = 0,8 см (ок. ) Пример: Речной круиз
3-часовой речной круиз проходит 15 км вверх по течению, а затем обратно. Река имеет скорость 2 км в час. Какова скорость лодки и какое время она плыла вверх по течению?
Есть две скорости, о которых следует подумать: скорость лодки в воде и скорость относительно суши:

Пусть x = скорость лодки на воде (км/ч)
Пусть v = скорость относительно земли (км/ч)
Поскольку река течет вниз по течению со скоростью 2 км/ч:
при движении вверх по течению, v = x−2 (ее скорость уменьшается на 2 км/ч)
при движении вниз по течению, v = x+2 (его скорость увеличивается на 2 км/ч)
Мы можем преобразовать эти скорости во времена, используя:
время = расстояние / скорость
(чтобы проехать 8 км со скоростью 4 км/ч, нужно 8/4 = 2 часа, верно?)
И мы знаем, что общее время равно 3 часам:
общее время = время вверх по течению + время вниз по течению = 3 часа
Соедините все это вместе:
общее время = 15/(x−2) + 15/(x+2) = 3 часа
Теперь мы используем наши навыки алгебры, чтобы найти «x».
Сначала избавьтесь от дробей, умножив на (x-2) (x+2) :
3(x-2)(x+2) = 15(x+2) + 15 (х-2)
Развернуть все:
3(x ² −4) = 15x+30 + 15x−30
Перенести все влево и упростить:
3x ² − 30×0 = 900 − 9020 это квадратное уравнение! Давайте решим это с помощью квадратичной формулы:
Где a , b и c из квадратного уравнения
в «стандартной форме»: x ² + bx + c = 0
Решите 3x
² — 30x — 12 = 0
Коэффициенты: a = 3 , b = −30 и c = −12
Квадратичная формула: 1 √b 4 x 9000 2 −4ac) ] / 2a
Подставь a, b и c: x = [ −(−30) ± √((−30) ² −4×3×(−12)) ] / (2×3)
Решить 😡 = [ 30 ± √(900+144) ] / 6
x = [ 30 ± √(1044) ] / 6
x = ( 30 ± 32,31 ) / 6
х = −0,39 или 10,39

Ответ: x = -0,39 или 10,39 (с точностью до 2 знаков после запятой)
x = -0,39 не имеет смысла для этого реального вопроса, но x = 10,39 просто идеален!
Ответ: Скорость лодки = 10,39 км/ч (с точностью до 2 знаков после запятой)
Итак, путь вверх по течению = 15 / (10,39−2) = 1,79 часа = 1 час 47 минут
И путь вниз по течению = 15 / (10,39 +2) = 1,21 часа = 1 час 13 минут

Пример: резисторы в параллели
Два резистора соединены параллельно, как показано на этой диаграмме:
Общее сопротивление было измерено при 2 Ом, и известно, что один из резисторов на 3 Ом больше, чем другой.
Каковы номиналы двух резисторов?
Формула для расчета полного сопротивления «R _T«:
1 R _T знак равно 1 Р ₁ + 1 Р ₂
В этом случае имеем R _T = 2 и R ₂ = R ₁ + 3
1 2 знак равно 1 Р ₁ + 1 Чт ₁ +3
Чтобы избавиться от дробей, мы можно умножить все члены на 2R ₁ (R ₁ + 3), а затем упростить:
Умножить все члены на 2R ₁ (R ₁ + 3): 2R ₁ (R ₁ +3) 2 = 2R ₁ (R ₁ +3) R ₁ + 2R ₁ (R ₁ + 3) R ₁ +3
Затем упростите: R ₁ (R ₁ + 3) = 2 (R ₁ + 3) + 2R ₁
6 2). ² + 3R ₁ = 2R ₁ + 6 + 2R ₁
Перенести все члены влево:R ₁ ² + 3R ₁ — 2R ₁ — 6 — 2R ₁ = 0
Упрощение: R ₁ ² — R ₁ ² – R _{1 _{— R ₁ ² — R ₁ ^{. Квадратное уравнение!}}}
Давайте решим это с помощью нашего Решателя квадратных уравнений.
Введите 1, -1 и -6
И вы должны получить ответы −2 и 3
R ₁ не может быть отрицательным, поэтому ответ R ₁ = 3 Ом .
Два резистора на 3 Ом и 6 Ом.

Другие
Квадратные уравнения полезны во многих других областях:
Форма параболического зеркала, телескопа-рефлектора или спутниковой антенны определяется квадратным уравнением.
Квадратные уравнения также необходимы при изучении линз и изогнутых зеркал.
И многие вопросы, связанные со временем, расстоянием и скоростью, требуют квадратных уравнений.

Квадратичная формула | Уравнение, как использовать и примеры
Определение квадратичной формулы
Квадратная формула — это алгебраическая формула, используемая для решения квадратных уравнений.
Квадратичная формула — это веха на пути к полному пониманию алгебры. Чтобы понять его, оценить и правильно применить, вам нужно немного узнать его предысторию, а затем оценить каждый термин в нем.
Содержание
Определение квадратичной формулы
Квадратное уравнение в стандартной форме
Что такое квадратичная формула?
Как использовать квадратичную формулу
Шаги решения квадратных уравнений
Поиск пересечений X
Примеры квадратичных формул
Когда использовать квадратичные формулы
Полиномы (выражения со многими членами) могут иметь линейные, квадратные и кубические значения. Путаница возникает, когда мы смотрим на слово «квадратный», потому что оно подразумевает четыре чего-то, например четырехугольник. Но происхождение слова означает «сделать квадратным», так как длина умножается на ширину. В математике значение квадрата — это показатель степени во второй степени. Эти показатели степени 2:
x2
22
б2
Таким образом, квадратичный полином имеет наивысшее значение второй степени; нечто квадратное.
Квадратное уравнение в стандартной форме
Квадратная формула используется для решения квадратных уравнений. Рассмотрим квадратное уравнение в стандартной форме:
ax2 + bx + c = 0
Вы также можете увидеть стандартную форму, называемую общим квадратным уравнением, или общей формой.
Пока ≠ 0, вы сможете разложить квадратное уравнение на множители. Иногда, однако, это становится запутанным или беспорядочным, или вы не можете это учесть.
Что такое квадратичная формула?
Вы всегда можете найти решение любого квадратного уравнения, используя квадратную формулу. Квадратная формула:
x = -b ± b2 — 4ac2a
Эту формулу можно использовать для решения квадратных уравнений. Или, если ваше уравнение факторизовано, вы можете использовать квадратную формулу, чтобы проверить правильность ваших решений квадратного уравнения.
Выражение b2 — 4ac, которое находится под знаком (sqrt) внутри квадратичной формулы, называется дискриминантом. Дискриминант используется для определения количества решений квадратного уравнения.
если b2 — 4ac = 0 → 1 решение
, если b2 – 4ac > 0 → 2 решения
если b2 — 4ac < 0 → нет реального решения
Как использовать квадратную формулу
Давайте начнем с простого квадратного уравнения:
x2 + 5x + 6 = 0
Чтобы квадратичная формула применялась, уравнение, которое вы распутываете, должно быть в форме, в которой все переменные помещаются по одну сторону от знака равенства, а 0 — по другую:
(квадратичное) = 0
Шаги решения квадратных уравнений
Наше квадратное уравнение будет учитывать фактор, так что это отличное место для начала.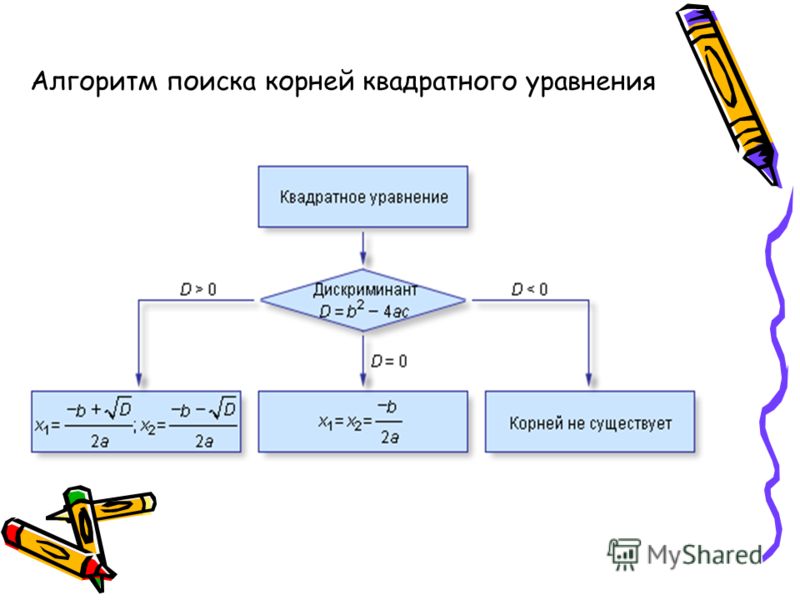 Сначала факторизуем уравнение. Мы ищем два числа, которые умножаются на 6 и добавляются к 5:
x2 + 5x + 6 = 0
(x + 2)(x + 3) = 0
Мы можем видеть, что любое выражение равно 0 (поскольку умножение умноженное на другое выражение дает 0). Мы можем установить каждое выражение равным 0, а затем найти x:
(x + 2) = 0
x = -2
(x + 3) = 0
x = -3
Наши два значения для x равны -2 и -3.
Сравнивая наш пример, x2 + 5x + 6 = 0, со стандартной формой квадратного уравнения (которое также можно просто назвать «квадратным»), мы получаем следующие значения:
a = 1
б = 5
с = 6
Теперь мы можем использовать их в квадратичной формуле и проверить, так как мы уже знаем, что наши ответы -2 и -3:
Всегда надежная квадратичная формула подтверждает значения x как -2 и -3.
Поиск пересечений по оси X
В уравнении типа ax2 + bx + c = y установите y = 0 и вычислите уравнение. Возможные значения x будут точками пересечения x; где ваша линия пересекает ось x.
Подумайте, как много мы знаем о нашем графическом решении еще до того, как проведем какие-либо алгебраические вычисления:
Поскольку уравнение дает два решения для x, у нас есть два x-отрезка
У нас будет парабола
Мы можем начать строить параболу с двух упорядоченных пар (x1, 0) и (x2, 0)
Вершина параболы будет между двумя точками пересечения х
Решив алгебраическое уравнение, вы получили преимущество при построении графика уравнения.
Графические калькуляторы, вероятно, , а не будут равны точности квадратичной формулы. Используйте калькулятор, чтобы проверить округленные результаты, но ожидайте, что они будут немного отличаться.
Например, предположим, что у вас есть ответ из Квадратной формулы, содержащий в себе. Оставьте как есть, а не записывайте его в виде десятичного эквивалента (3,16227766) для большей точности.
Примеры квадратичных формул
Решая квадратные уравнения, вы помогаете себе, зная несколько способов решения любого уравнения. Начните решать квадратное уравнение, наблюдая, будет ли оно множиться (какие два множителя умножаются, чтобы дать c, которые также дают в сумме b?).
Вы также можете попробовать заполнить квадрат. Вы все еще боретесь? Затем примените квадратную формулу.
Используйте любой из этих методов и график, чтобы проверить ответ, полученный любым другим методом. Используйте квадратичную формулу, например, для проверки факторинга.
Давайте попробуем другой пример, используя следующее уравнение:
2×2 — 5x — 7 = 0
Сначала мы можем разложить его на множители:
(2x — 7)(x + 1) = 0
x = 72 = 3,5
x + 1 = 0
x = -1
Затем мы можем проверить это с помощью квадратичной формулы, используя следующие значения:
а = 2
б = -5
с = -7
Если вы затем начертите эту квадратичную функцию на графическом калькуляторе, ваша парабола будет иметь вершину (1,25, -10,125) с точками пересечения по оси x, равными -1 и 3,5.
Вот квадратное число, которое будет множить , а не : x2 — 7x — 3 = 0
Никакие множители -3 не добавляются к -7, поэтому вы не можете использовать факторинг. Что делать? Если бы все, что вы знали, было факторингом, вы бы застряли. Но вы знаете, как попробовать квадратичную формулу со следующими значениями:
а = 1
б = -7
с = -3
Когда использовать квадратную формулу
Квадратные уравнения используются каждый день. Их можно использовать для расчета площадей, формулирования скорости объекта и даже для определения прибыли продукта. Важно, чтобы вы знали, как находить решения квадратных уравнений, используя квадратную формулу.
При использовании квадратичной формулы необходимо быть внимательным к мельчайшим деталям. Например, поставить весь числитель над 2a является , а не необязательным. Все, от -b до квадратного корня, больше 2а.
Алс, обратите внимание на знак ± перед квадратным корнем, который напоминает вам, что нужно найти два значения для x.
Надоедливая буква b в самом начале тоже сложна, поскольку квадратичная формула заставляет вас использовать -b. Старайтесь думать о -b не как об «отрицательном b», а как о 90 629, противоположном 90 630 любого значения «b». Предположим, что ваше b положительно; наоборот отрицательно. Что делать, если ваше исходное b равно уже отрицательный? Подумайте: негатив негатива есть позитив; так что -b положительно!
Под скобкой квадратного корня вы также должны работать с осторожностью. Иногда b2 предшествует отрицательный знак, что означает, что вы возводите в квадрат все b, даже если оно отрицательное. Квадрат отрицательного является положительным, поэтому b2 всегда будет положительным значением.
Суть: работа очень внимательно. Следите за своими знаками, работайте методично и ничего не пропускайте. Затем используйте другой метод, чтобы проверить свою работу. Независимо от того, какой метод вы используете, квадратичная формула доступна вам каждый раз.
No related posts.