Чему равна градусная мера угла: Что такое градусная мера угла? Ответ на webmath.ru

Содержание

Градусная мера угла / Начальные геометрические сведения / Справочник по геометрии 7-9 класс

Главная
Справочники
Справочник по геометрии 7-9 класс
Начальные геометрические сведения
Градусная мера угла

Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения. Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения — с градусом.

Градус — это угол, который равен части развернутого угла,обозначается знаком

часть градуса называется минутой, обозначается знаком

часть минуты называется секундой, обозначается знаком

Пример: (двадцать градусов пятнадцать минут сорок семь секунд)

Градусная мера угла — это положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле.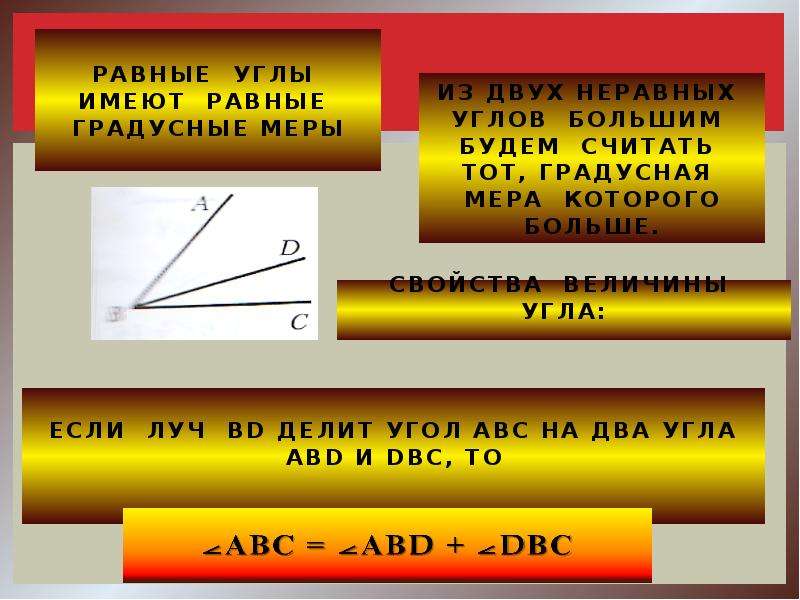

Пример:

Градусная мера угла ABC равна . Говорят: «Угол ABC равен 120 градусам». Пишут: .

Транспортир — это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .

Для того чтобы

измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.

Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).

Вторая сторона при этом, как мы видим,

проходит через деление шкалы 120, значит: .

Свойства:

Равные углы имеют равные градусные меры.
Меньший угол имеет меньшую градусную меру.
Развернутый угол равен .
Неразвернутый угол меньше .
Если луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.

Основные типы углов:

Острый угол — угол, градусная мера которого меньше 90°.

Прямой угол — угол, градусная мера которого равна 90°.

Тупой угол — угол, градусная мера которого больше 90°, но меньше 180°.

Развернутый угол — угол, градусная мера которого равна 180°.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Точки, прямые, отрезки

Провешивание прямой на местности

Луч

Угол

Равенство геометрических фигур

Сравнение отрезков

Сравнение углов

Длина отрезка

Единицы измерения длины, расстояний

Измерение углов на местности

Смежные углы

Вертикальные углы

Перпендикулярные прямые

Построение прямых углов на местности

Начальные геометрические сведения

Правило встречается в следующих упражнениях:

7 класс

Задание 42, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 55, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 80, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 223, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 226, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 4, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 299, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 336, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 379, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 391, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Пользовательское соглашение

Градусная мера угла. Определение

Основные понятия

В рамках вопроса измерения углов, в данном разделе рассмотрим несколько понятий, относящихся к начальным геометрическим сведениям:

угол;

развёрнутый и неразвёрнутый угол;
градус, минута и секунда;
градусная мера угла;
прямой, острый и тупой углы.

Углом называют такую геометрическую фигуру, которая представляет собой точку (вершину) и исходящие из неё два луча (стороны). Угол называют развёрнутым, если оба луча лежат на одной прямой.

Рисунок 1. Угол. Автор24 — интернет-биржа студенческих работ

Помощь со студенческой работой на тему

Градусная мера угла. Определение

Благодаря градусной мере угла можно произвести измерение углов.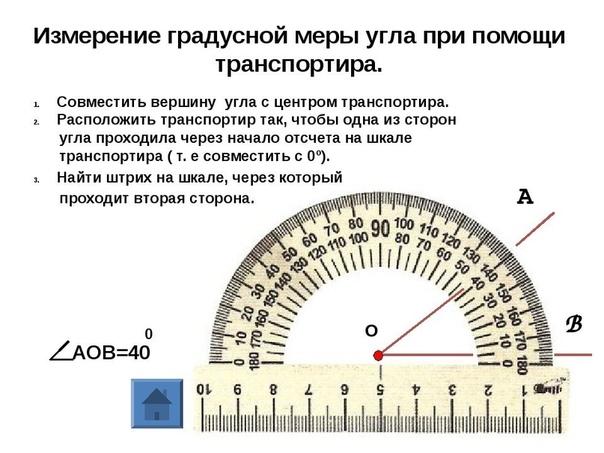 {\circ}$.

Рисунок 4. Прямой, острый и тупой углы. Автор24 — интернет-биржа студенческих работ

В повседневной жизни есть примеры необходимости и важности умения измерять углы и понимать градусную меру. Измерение углов необходимо в различных исследованиях, в том числе в астрономии при определении положения небесных тел.

Для практики, попробуйте начертить хотя бы три неразвёрнутых угла и один развёрнутый разными способами, измерьте с помощью транспортира углы и запишите эти результаты. Можно задать случайные числа и попрактиковаться в точности черчения углов с помощью транспортира, деления их с помощью биссектрисы (биссектриса — это луч, исходящий из вершины данного угла и делящий угол пополам).

Примеры задач

Пример 1

Задача. Есть рисунок:

Рисунок 5. Задача. Автор24 — интернет-биржа студенческих работ

Лучи $DE$ и $DF$ — биссектрисы соответствующих углов $ADB$ и $BDC$. {\circ}$

В данной статье мы раскрыли полностью вопрос о градусной мере угла и как измерять углы.

Что такое градусная мера угла?

☰

Углы измеряют в разных единицах измерениях. Это могут быть градусы, радианы. Чаще всего углы измеряют в градусах. (Не следует путать этот градус с мерой измерения температуры, где также используется слово «градус).

1 градус — это угол, который равен 1/180 части развернутого угла. Другими словами, если взять развернутый угол и поделить его на 180 равных между собой частей-углов, то каждый такой маленький угол будет равен 1 градусу. Размер всех других углов определяется тем, сколько таких маленьких углов можно внутри измеряемого угла уложить.

Обозначается градус знаком °. Это не ноль и не буква О. Это такой специальный, введенный для обозначения градуса, символ.

Таким образом, развернутый угол равен 180°, прямой угол равен 90°, острые углы имеют размер меньший, чем 90°, а тупые — больший, чем 90°.

В метрической системой для измерения расстояния используется метр. Однако используются и более крупные и мелкие единицы. Например, сантиметр, миллиметр, километр, дециметр. По аналогии с этим в градусной мере углов также выделяют минуты и секунды.

Одна градусная минута равна 1/60 градуса. Обозначается она одним знаком ‘.

Одна градусная секунда равна 1/60 минуты или 1/3600 градуса. Обозначается секунда двумя знаками ‘, то есть ».

В школьной геометрии градусные минуты и секунды используются редко, однако надо уметь понимать, например, такую запись: 35°21’45». Это значит, что угол равен 35 градусов + 21 минута + 45 секунд.

С другой стороны, если угол нельзя измерить точно лишь в целых градусах, то не обязательно вводить минуты и секунды. Достаточно использовать дробные значения градуса. Например, 96,5°.

Понятно, что минуты и секунды можно перевести в градусы, выразив их в долях градуса. Например, 30′ равно (30/60)° или 0,5°. А 0,3° равно (0,3 * 60)’ или 18′. Таким образом, использование минут и секунд — это лишь вопрос удобства.

Зачеты по геометрии 7 класс

Зачет по теме: «Начальные геометрические сведения»

Вариант 1.

Обязательная часть

Начертите прямую с. Отметьте точки A, B и D, которые не принадлежат прямой с, так, чтобы отрезок АВ пересекал ее, а отрезок BD не пересекал ее. Пересекает ли отрезок AD прямую с?
Точка М лежит между точками D и К, причем MD = 7см, МК = 11см. Найти расстояние DК.
Начертите угол АВС, равный 80^о. Постройте угол, смежный с ним. Чему равна градусная мера построенного угла?

Проведите биссектрису ВМ построенного угла АВС. Чему равна

градусная мера угла МВС?

Найти градусные меры углов KNP и TNP

Найти длины отрезков BD и DC, если ВС = 24см, а длина отрезка BD на 8см больше длины отрезка DC.

Дополнительная часть.

Отрезки MN и КС пересекаются в точке О, причем сумма градусных мер углов МОС и КОN равна 140^о. Найти величину угла MOD, если OD – биссектриса угла МОС.
Чему равна величина угла, если два смежных с ним угла составляют в сумме 110^о?
Угол MEN, равный 120^о, разделен лучом EF на два угла. Градусная мера одного из них в 3 раза меньше градусной меры другого. Найти градусные меры полученных углов.

Вариант 2.

Обязательная часть

Начертите прямую m. Отметьте точки E, F и P, которые не принадлежат прямой m, так, чтобы отрезки EF и EP пересекали ее. Пересекает ли отрезок FP прямую m?
Точка C лежит между точками A и B, причем AB = 15см, BC = 8см. Найти расстояние AC.
Начертите угол АDС, равный 130^о. Постройте угол, смежный с ним. Чему равна градусная мера построенного угла?

Проведите биссектрису DK построенного угла АDС. Чему равна

градусная мера угла KDA?

Найти градусные меры углов MNK и TNM

Найти длины отрезков BD и DC, если ВС = 30см, а длина отрезка DC на 4см меньше длины отрезка DВ.

Дополнительная часть.

Отрезки MP и DB пересекаются в точке О, причем сумма градусных мер углов PОD и BОM равна 220^о. Найти величину угла POA, если OA – биссектриса угла PОD.
Чему равна величина угла, если два смежных с ним угла составляют в сумме 200^о?
Угол ACB, равный 155^о, разделен лучом CE на два угла. Градусная мера одного из них на ^{25^о меньше градусной меры другого. Найти градусные меры полученных углов.}

Зачет по теме «Признаки равенства треугольников»

Вариант 1

Обязательная часть

Задайте еще один элемент треугольника KNM так, чтобы венным стало равенство:  АВС =  KNM

 BAD = 40^o. Чему равна величина угла BCD?

EF = 15см. Чему равен отрезок СК?

Периметр равнобедренного треугольника равен 84см. Длина боковой стороны – 35см. Найти основание этого треугольника.
CD пересекает АВ в точке О так, что СО = OD, АО = ОВ. Докажите, что

 АСО =  BDO.

MN пересекает DC в точке Р, СМР = DNP. Докажите, что

 МСР =  NDP.

АВ = ВС, AD = DC. Докажите, что  ABD =  CBD.

Дополнительная часть.

Периметр равнобедренного треугольника равен 44см. Длина его боковой стороны больше длины основания на 4см. Найти длины сторон треугольника.
Внутри равнобедренного треугольника АВС с основанием АВ взята точка М так, что АМ = МВ. Докажите, что луч СМ – биссектриса угла АСВ.
В равностороннем треугольнике DCB проведены медианы ВК и DN, пересекающиеся в точке О. Докажите, что  BON =  DOK.

Зачет по теме «Признаки равенства треугольников»

Вариант 2.

Обязательная часть

З адайте еще один элемент треугольника KNM так, чтобы венным стало равенство:  АВС =  KNM

 BAD = 50^o. Чему равна величина угла BCD?

E F = 10см. Чему равен отрезок СК?

Периметр равнобедренного треугольника равен 95см. Длина основания – 35см Найти боковую сторону этого треугольника.
CD пересекает АВ в точке О так, что СО = OD, АО = ОВ. Докажите, что

 АСО =  BDO.

MN пересекает DC в точке Р, СМР = DNP. Докажите, что

 МСР =  NDP.

АВ = ВС, AD = DC. Докажите, что  ABD =  CBD.

Дополнительная часть.

Периметр равнобедренного треугольника равен 20см.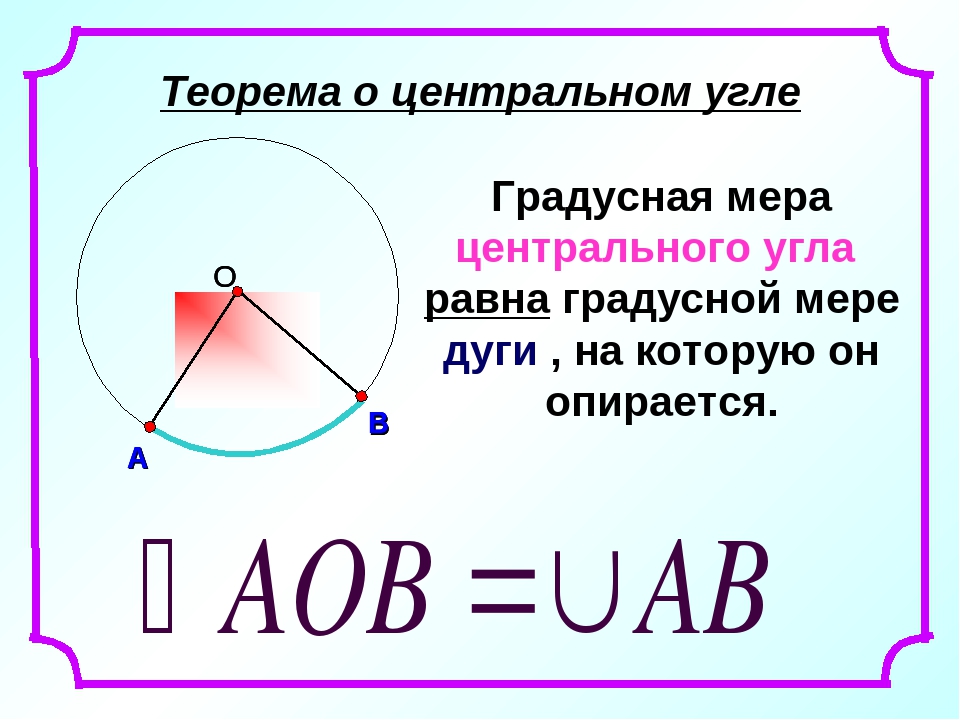 Длина его основания меньше длины боковой стороны в 2 раза. Найти длины сторон треугольника.
Внутри равнобедренного треугольника MNP с основанием MP взята точка C так, что МC = CP. Докажите, что  MCN =  NCP
В равностороннем треугольнике DEC проведены биссектрисы CК и DN, пересекающиеся в точке О. Докажите, что  CON =  DOK.

Зачет по теме «Параллельные прямые»

В ариант 1. Вариант 2.

 1 =  2,  3   4. 1.  1 =  2,  3  4

Какие из прямых c, d, e – параллельны?

BC ||AD, BCA = 34^o 2. BC || AD, CBD = 23^o

Н айти DAC Найти BDA

a || b,  1 = 60^o 3. a || b,  1 = 120^o

Вычислить градусные меры углов 3, 4, 5

OP = OK, OT = OM 4. PT = MK, MP = KT

Д окажите, что a || b

B C = NK, AC = MK,  1 =  2 5. MK = AB, NK =AC, 1 = 2

Доказать: AB || MN Доказать: MN || CB

Тема: «Сумма углов треугольника»

Вариант 1.

Обязательная часть

Какова градусная мера угла С? 2. Треугольник АВС – равнобедренный.

Вычислить углы В и С.

3.Треугольник АВС прямоугольный. 4. ab, 1 = 60⁰. Вычислить градусные

Вычислите угол А меры углов 3, 4, 5.

5 .Вычислите градусные меры углов

АВС и АСВ

6.Вычислите градусные меры остальных углов прямоугольного треугольника, если известно, что один из них на 20⁰ больше другого.

Дополнительная часть.

7.Дано: АО = ОВ, АС  а, BD  a. 8. Дано: DC AD, BС = AD.

Доказать:  АСО = BDO Доказать: AB = CD

9.В треугольнике MDK угол D = 76⁰, а угол М в три раза меньше внешнего угла при вершине К.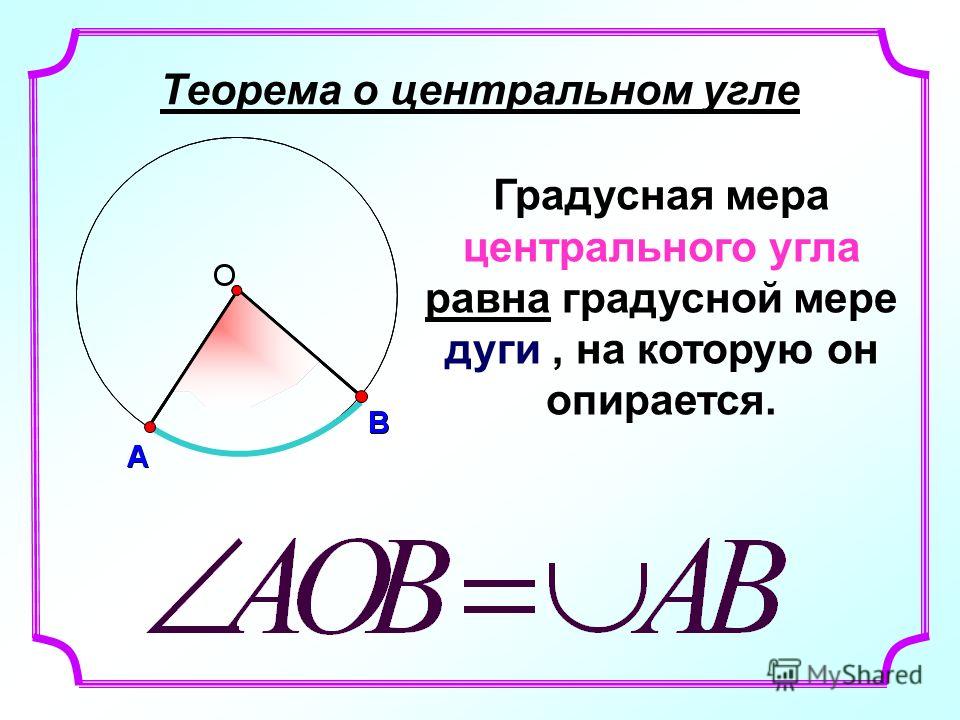 Найдите неизвестные углы треугольника.

Тема: «Сумма углов треугольника»

Вариант 2.

Обязательная часть

1.Какова градусная мера угла С? 2. Треугольник АВС – равнобедренный.

Вычислить углы В и С.

3.Треугольник АВС прямоугольный. 4. ab, 1 = 50⁰. Вычислить градусные

Вычислите угол А углов 3, 4, 5.

5 .Вычислите градусные меры углов

АВС и АСВ

6.Вычислите градусные меры остальных углов прямоугольного треугольника, если известно, что один из них в 5 раз меньше другого.

Дополнительная часть.

7.Дано: АО = ОВ, АС  а, BD  a. 8. Дано: DC AD, BС = AD

Доказать:  АСО = BDO Доказать: AB = CD

9.В треугольнике MDK угол D = 84⁰, а угол М в четыре раза меньше внешнего угла при вершине К. Найдите неизвестные углы треугольника.

Градусная мера дуги окружности

Рассмотрим окружность. Отметим на ней две точки А и B. Эти точки разделяют окружность на две дуги.

Возникает вопрос, а как узнать про какую дугу говорить? Ведь и одна и вторая дуги стягивается хордой АB. Именно для того, чтобы различать дуги, берутся дополнительные точки на этих дугах. Дуги обозначаются специальным знаком и тремя заглавными буквами. Запишем дуги, которые у нас получились: ᴗ, ᴗ. Иногда дуга может обозначаться двумя буквами, но только в том случае, когда точно ясно о какой дуге идет речь. Например, если дуга стягивается диаметром ᴗ. Такая дуга носит особое название – полуокружность.

Давайте введем еще одно определение. Угол с вершиной в центре этой окружности называется центральным углом.

По рисунку видно, что центральный угол может быть любым: как меньше развернутого, так и больше развернутого. Давайте попробуем на рисунке указать центральные углы.

Центральными углами будут углы AOB и EOF. Пусть стороны центрального угла окружности пересекают ее в точках А и B. Центральному углу AOB соответствуют две дуги с концами А и B. Если этот угол развернутый, то ему соответствуют две полуокружности. Если угол не развёрнутый, то говорят, что дуга АB, расположенная внутри этого угла, меньше полуокружности. Про другую дугу говорят, что она больше полуокружности.

Мы помним, что длина окружности вычисляется по формуле . И измеряется длина только в единицах измерения длины. А дуга может измеряться, как в единицах измерения длины, так и в градусах.

, , ; , , ,

Если дуга AB окружности меньше полуокружности или является полуокружностью, то ее градусная мера равна градусной мере центрального угла АОB. Мы знаем, что градусная мера круга равна 360º, поэтому если дуга AB больше полуокружности, то ее градусная мера .

Решим задачу. Найти градусную меру дуг по рисункам.

На первом рисунке дуга BMA меньше полуокружности: .

На втором рисунке изображены две полуокружности, их градусные меры равны .

На третьем рисунке дуга BMA меньше полуокружности и, значит, ее градусная мера равна ,

Решим несколько задач.

Задача. Начертить окружность с центром и отметить на ней точку . Построить хорду так, чтобы:

а) , б) , в) , г)

Решение.

Построим окружность, с центром в точке О. Отметим на окружности точку А. Соединим точки А и О.

Возьмем циркуль и померяем получившийся отрезок ОА. И таким же радиусом проведем окружность, центром которой будет точка А. Эта окружность пересечет исходную окружность в двух точках. Обозначим одну из нах буквой B. Рассмотрим треугольник AOB. Поскольку точка B лежит на окружности, то ОА и ОB равны как радиусы, поскольку из точки А мы проводили окружность с таким же радиусом, то ОА равно AB. Таким образом, треугольник АОВ – равносторонний. Углы равностороннего треугольника равны по 60 градусов, то есть угол АОВ =60º.

Таким образом, мы построили хорду АB так, чтобы угол АОB был равен 60 º.

Теперь давайте построим хорду АБ так, чтобы угол АОB= 90º.

Проведем через точки А и О диаметр окружности. Из точки О проведем перпендикуляр к построенному диаметру, полученный перпендикуляр пересекает окружность в двух точках. Обозначим одну из них за B. Хорда АB и будет искомая.

Теперь давайте построим хорду АB так, чтобы угол АОB=120º.

Для этого проведем через точки О и А диаметр окружности. Он делит окружность на две полуокружности, градусная мера которых равна 180º.

Построим хорду АB, так, чтобы один из центральных углов был равен 60º.

Обозначим вторую точку диаметра C и проведем окружность с радиусом равным радиусу исходной окружности и центром в точке C. Обозначим одну из точек пересечения окружностей за B и получим, что угол COB= 60º, (мы уже выяснили почему), тогда угол АОB= 180-60= 120º. То есть хорда АB – искомая.

Теперь нам надо построить хорду Аб так, чтобы угол АОБ был бы равен ста восьмидесяти градусам. Такой хордой, будет диаметр проведенный через точку А.

Обозначим второй конец диаметра буквой Б и получим искомую хорду.

Задача. Хорды и окружности с центром равны. Доказать, что две дуги с концами и соответственно равны двум дугам с концами и . Найти градусные меры дуг с концами и , если .

Решение. Выполним чертеж.

и по условию

Ответ:.

Задача. На полуокружности взяты точки и так, что , . Найдите хорду , если .

Решение. Выполним чертеж.

− равносторонний

(см)

Ответ: см.

Итак, давайте повторим главное: Дуга – часть окружности. Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности.

Угол с вершиной в центре окружности называется центральным углом этой окружности. Если дуга АB окружности меньше полуокружности или является полуокружностью, то ее градусная мера равна градусной мере центрального угла АОB. Мы знаем, что градусная мера круга равна 360º, поэтому если дуга AB больше полуокружности, то ее градусная мера считается равной .

Центральные и Вписанные углы. Как найти?

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, что и вписанный угол.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

Угол AOC и угол ABC, вписанный в окружность, опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол угол ABC равен половине угла AOC.

Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

ㄥAOB = ◡ AB

Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB угол равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается и половине градусной меры центрального угла, опирающегося на эту же дугу.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Хорда — отрезок, соединяющий две точки на окружности.

Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.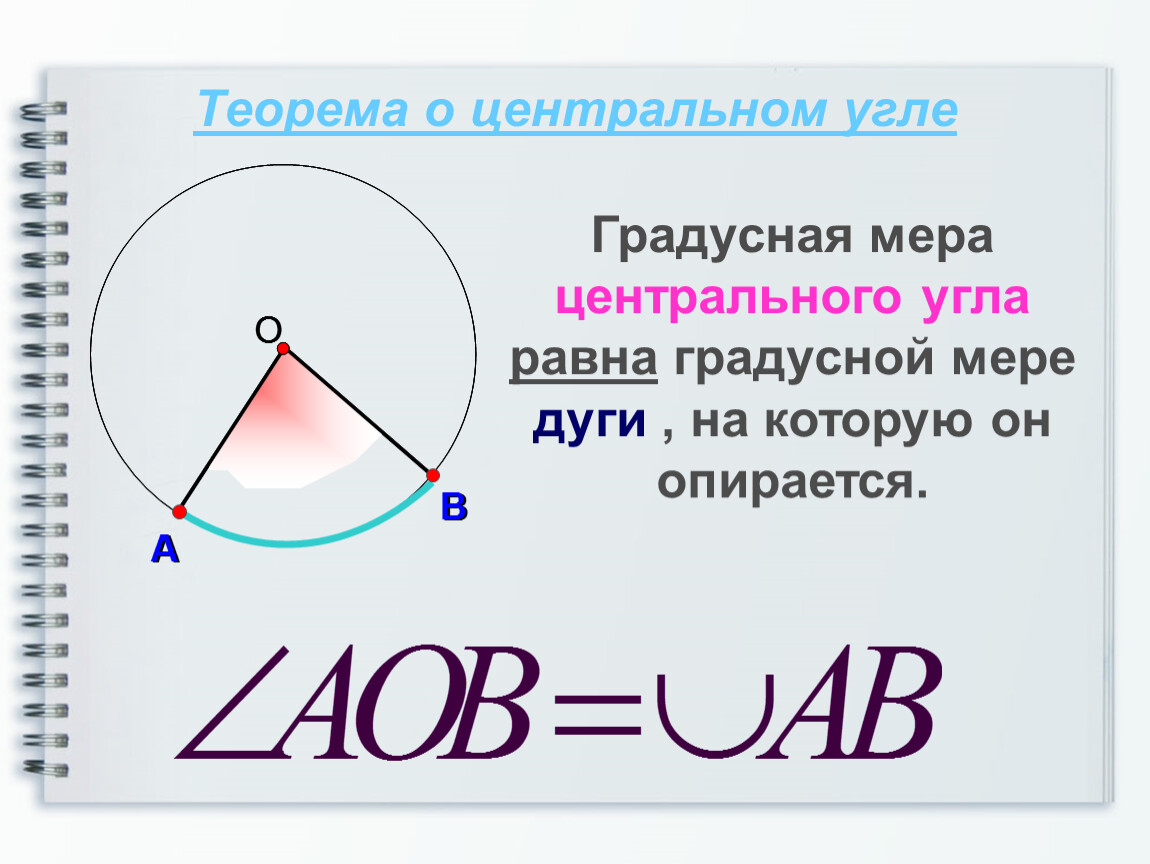

Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу. ㄥACB = ?

Как решаем: окружность 360° — AC — CB = 360 — 200 — 80 = 80
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.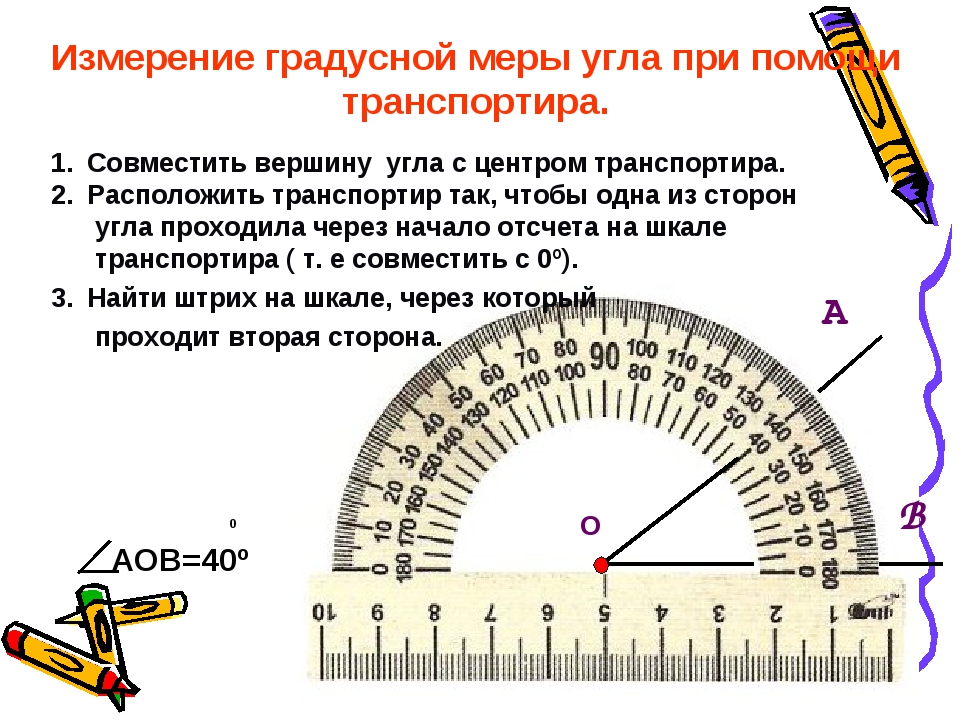
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360 = 72°
Вписанный угол равен половине дуги, поэтому CAB = ½ от CB = 72/36 = 36°

Градусная мера — угло — Большая Энциклопедия Нефти и Газа, статья, страница 1

Градусная мера — угло

Cтраница 1

Градусная мера угла, образованного хордой и касательной, имеющими общую точку на окружности, равна половине градусной меры дуги, заключенной между его сторонами. [1]

Градусная мера угла находится: при помощи транспортира. [2]

Градусная мера угла между параллельными прямыми, считается равной нулю. [3]

Градусная мера угла между параллельными плоскостями считается равной нулю.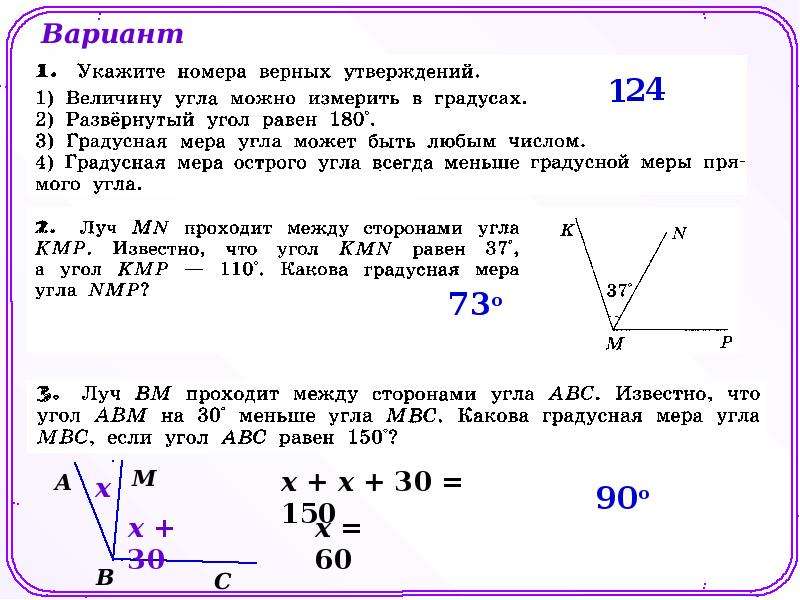 [4]

Градусная мера угла, образованного хордой и касательной, имеющими общую точку на окружности, равна половине градусной меры дуги, заключенной между его сторонами. [5]

Градусная мера угла поворота может быть равной любому действительному числу. [6]

Таблицы перехода от градусной меры угла к радианной и обратно. [7]

Таблицы для перехода от градусной меры угла к радианной и обратно помещены в конце книги ( стр. [8]

По каким формулам переводят градусную меру угла в ра-дианную и наоборот. [9]

Косинус угла зависит только от градусной меры угла. [10]

Формула ( 2) дает градусную меру угла по радианной.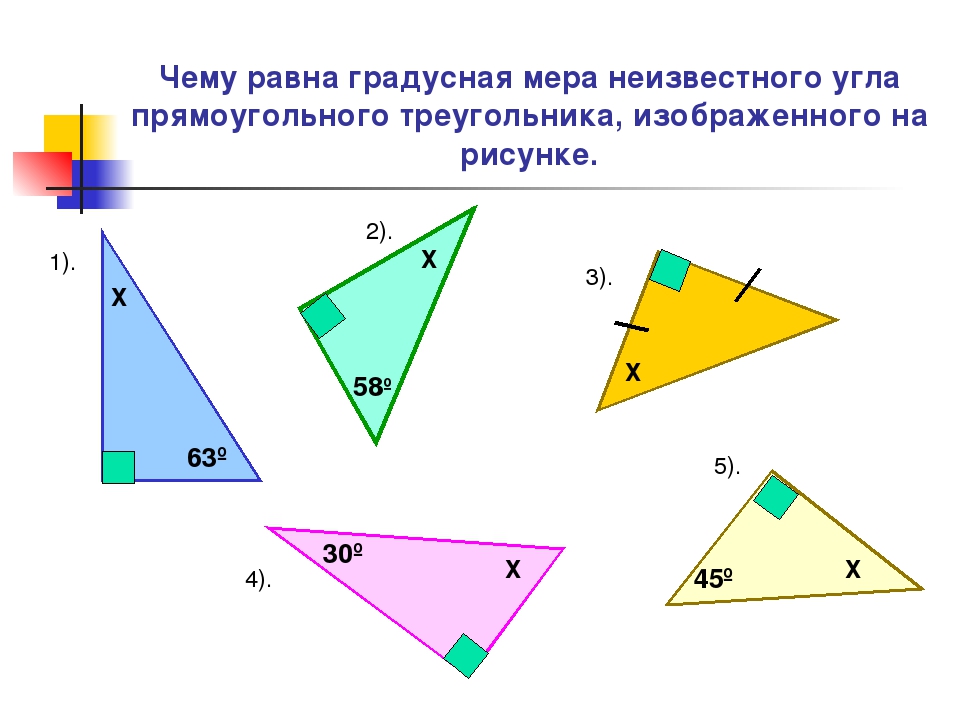 [11]

Последний множитель введен для перехода от градусной меры угла 7 к радианной. [12]

Во многих оптических приборах также используют градусную меру угла. [13]

Градусная мера дуги АВ на рисунке 22 равна градусной мере угла АОВ. Градусная мера дуги АВ обозначается АВ. [14]

Если плоский угол является частью полуплоскости, то его градусной мерой является градусная мера обычного угла с теми же сторонами. Если плоский угол содержит полуплоскость, то его градусная мера равна 360 — а, где а — градусная мера дополнительного плоского угла. [15]

Страницы: 1 2

Найдите градус измерения угла

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Измерение углов

Понятие угла

Понятие угла — одно из важнейших понятий в геометрии.Понятия равенства, сумм и разностей углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов и углов.

Есть две обычно используемые единицы измерения углов. Более знакомая единица измерения — это градусы. Круг делится на 360 равных градусов, так что прямой угол равен 90 °. Пока мы будем рассматривать только углы от 0 ° до 360 °, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360 ° и отрицательные углы.

Градусы можно разделить на минуты и секунды, но это деление не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых минут. Итак, семь с половиной градусов можно назвать 7 градусами и 30 минутами, записанными как 7 ° 30 ‘. Каждая минута далее делится на 60 равных частей, называемых секунд, и, например, 2 градуса 5 минут 30 секунд записывается как 2 ° 5 ’30 дюймов. Деление градусов на минуты и угловые секунды аналогично делению на часы в минуты и секунды.

Части степени теперь обычно обозначаются десятичной дробью. Например, семь с половиной градусов теперь обычно пишут как 7,5 & deg.

Когда один угол нарисован на плоскости xy для анализа, мы нарисуем его в стандартной позиции с вершиной в начале координат (0,0), одна сторона угла вдоль x — ось, а другая сторона — над осью x .

Радианы

Другое распространенное измерение углов — радианы.Для этого измерения рассмотрим единичный круг (круг радиуса 1), центр которого является вершиной рассматриваемого угла. Затем угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко переходить между градусами и радианами. Длина окружности всего круга равна 2 π , следовательно, 360 ° равняется 2 π радиан. Следовательно,

1 ° равен π /180 радиан

а также

1 радиан равен 180/ π градусов

Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах.Убедитесь, что вы знаете, в каком режиме работает ваш калькулятор.

Краткая заметка по истории радианов

Хотя слово «радиан» было придумано Томасом Мьюиром и / или Джеймсом Томпсоном около 1870 года, математики долгое время измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своей книге Elements of Algebra явно сказал, что углы измеряются длиной дуги, отрезанной в единичной окружности.Это было необходимо, чтобы дать его знаменитую формулу, включающую комплексные числа, которая связывает функции знака и косинуса с экспоненциальной функцией. e ^iθ = cos θ + i sin θ

где θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. Мой Краткий курс комплексных чисел.

Радианы и длина дуги

Альтернативное определение радианов иногда дается в виде отношения.

Вместо того, чтобы брать единичную окружность с центром в вершине угла θ , возьмите любую окружность с центром в вершине угла. Тогда радианная мера угла — это отношение длины вытянутой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус окружности равен 2, тогда мера в радианах равна 1.5.

Причина, по которой это определение работает, заключается в том, что длина вытянутой дуги пропорциональна радиусу круга. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку вы можете использовать его для соотнесения длин дуг с углами. Длина дуги равна радиусу r, умноженному на угол θ , где угол измеряется в радианах.

Например, дуга θ = 0,3 радиана в окружности радиуса r = 4 имеет длину 0,3 умноженную на 4, то есть 1,2.

Радианы и площадь сектора

Сектор круга — это часть круга, ограниченная двумя радиусами и дугой круга, соединяющей их концы.

Площадь этого сектора легко вычислить по радиусу r окружности и углу θ между радиусами, когда он измеряется в радианах.Так как площадь всего круга составляет πr ², а сектор относится ко всей окружности, так как угол θ равен 2 π , поэтому

Общие углы

Ниже приведена таблица общих углов для измерения в градусах и радианах. Обратите внимание, что измерение в радианах дано в единицах π . Его, конечно, можно было бы указать в десятичной дроби, но радианы часто появляются с коэффициентом π . .

Уголок	Градусов	Радианы
	90 °	π /2
	60 °	π /3
	45 °	π /4
	30 °	π /6

Упражнения

Эдвин С.

Кроули написал книгу « Тысяча упражнений в плоской и сферической тригонометрии», Университет Пенсильвании, Филадельфия, 1914. Задачи этого короткого курса взяты из этого текста (но не все 1000 из них!). пять знаков точности, поэтому студентам пришлось потрудиться, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синус-косинусов, таблицей касательных, таблицей логарифмов, таблицей log-sin-cos и таблицей log-tan.Теперь мы можем пользоваться калькуляторами! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.

Кроули использовал не десятичные дроби для дробей градуса, а минуты и секунды.

Каждый комплекс упражнений включает в себя, во-первых, формулировку упражнений, во-вторых, некоторые подсказки для решения упражнений, а в-третьих, ответы на упражнения.

1. Выразите следующие углы в радианах.
(а). 12 градусов, 28 минут, то есть 12 ° 28 ‘.
(б). 36 ° 12 ‘.

2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.

3. Учитывая угол a и радиус r, , чтобы найти длину проходящей дуги.
(а). a = 0 ° 17 ’48 дюймов, r = 6,2935.
(б). a = 121 ° 6 ’18 дюймов, r = 0,2163.

4. Учитывая длину дуги l и радиус r, , чтобы найти угол, стянутый в центре.
(а). л = 0,16296, л = 12,587.
(б). l = 1,3672, r = 1,2978.

5. Зная длину дуги l и угол a , который она проходит в центре, найти радиус.
(а). a = 0 ° 44 ’30 дюймов, l = 0,032592.
(б). a = 60 ° 21 ‘6 дюймов, l = 0,4572.

6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус составляет 3200 футов.

7. Кривая железной дороги образует дугу окружности 9 градусов 36,7 минут, радиус до центральной линии пути составляет 2100 футов. Если калибр 5 футов, найдите разницу в длине двух рельсов с точностью до полудюйма.

9. На сколько можно изменить широту, идя на север на одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?

10. Вычислите длину в футах одной угловой минуты на большом круге Земли. Какова длина дуги в одну секунду?

14. На окружности радиусом 5,782 метра длина дуги составляет 1,742 метра. Какой угол он образует в центре?

23. Воздушный шар, известный как 50 футов в диаметре, сужается к глазу под углом 8 1/2 минут.Как далеко это?

Подсказки

1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов.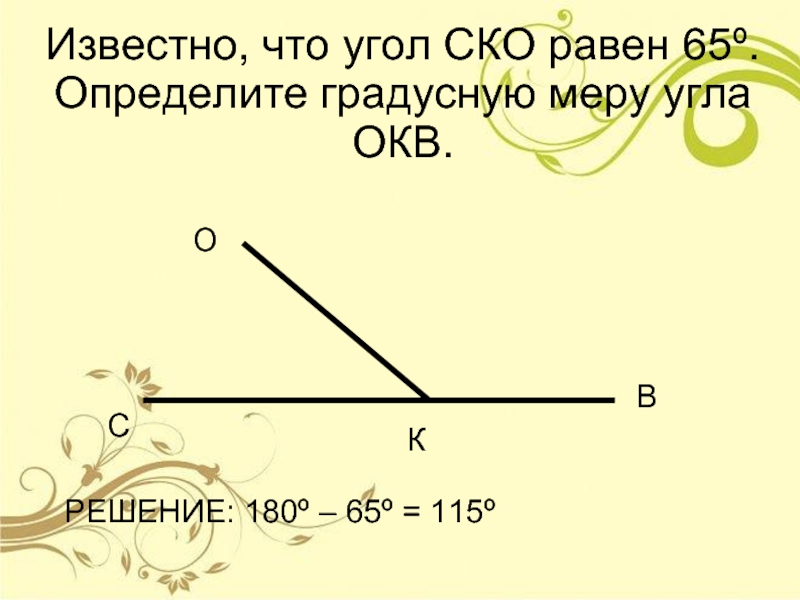 Так, например, 12 ° 28 ‘равно 12 + 28/60, что равно 12,467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.

2. И наоборот, чтобы преобразовать радианы в градусы, разделите на π и умножьте на 180.Таким образом, 0,47623 разделить на π и умножить на 180 дает 27,286 °. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27 ° 17,16 ‘. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 равно примерно 10, поэтому угол также можно записать как 27 ° 17 ’10 дюймов.

3. Чтобы найти длину дуги, сначала преобразуйте угол в радианы. Для 3 (a) 0 ° 17’48 «составляет 0,0051778 радиана. Затем умножьте его на радиус, чтобы найти длину дуги.

4. Чтобы найти угол, разделите его на радиус.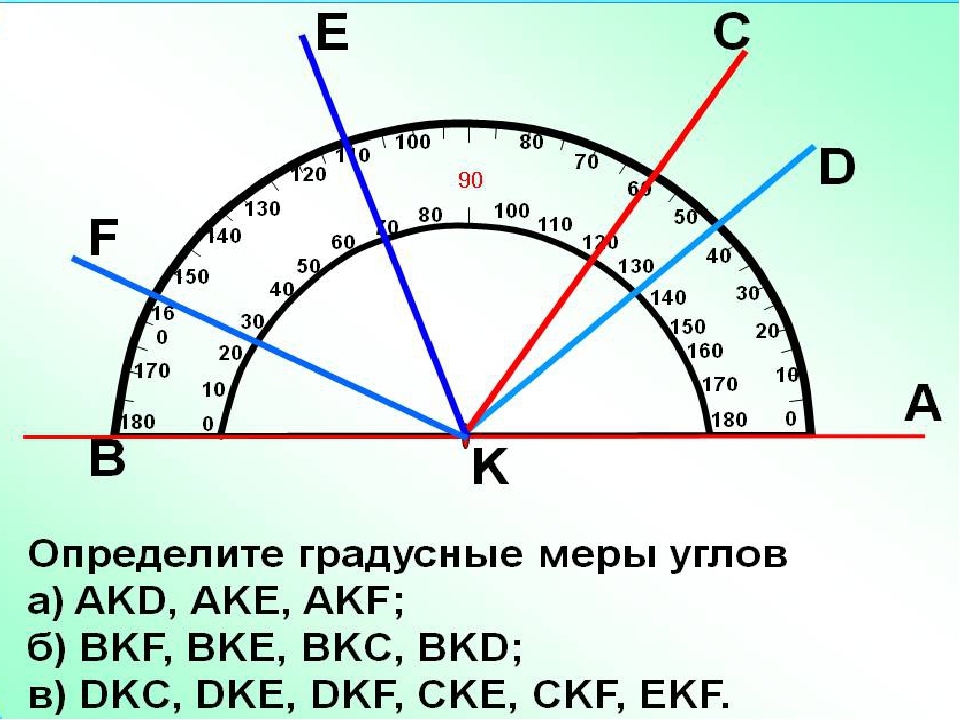 Это дает вам угол в радианах. Это можно преобразовать в градусы, чтобы получить ответы Кроули.

5. Как упоминалось выше, радиан умноженный на радиус = длина дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градусного измерения в радиан. .Итак, чтобы найти радиус r, сначала преобразует угол a в радианы, а затем разделит его на длину l дуги.

6. Длина дуги равна радиусу, умноженному на угол в радианах.

7. Помогает нарисовать фигуру. Радиус внешнего рельса равен 2102,5, а радиус внутреннего рельса — 2097,5.

9. У вас есть круг радиусом 3956 миль и дуга этого круга длиной 1 милю.Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрим, сможете ли вы узнать, каким, по мнению Эратосфена, был радиус Земли, еще в III веке до н. Э.)

10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус — 3956. Какова длина дуги?

14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус.Радианы легко преобразовать в градусы.

23. Представьте, что диаметр воздушного шара является частью дуги окружности с вами в центре. (Это не совсем часть дуги, но довольно близко). Длина дуги составляет 50 футов. Вы знаете угол, так каков радиус этого круга?

Ответы

1. (а). 0,2176. (б). 0,6318.

2. (а). 27 ° 17 ’10 «. (B). 14,56 ° = 14 ° 33,6′ = 14 ° 33’36».

3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.

4. (а). 0,16296 / 12,587 = 0,012947 радиан = 0 ° 44 ’30 дюймов.
(б). 1,3672 / 1,2978 = 1,0535 радианы = 60,360 ° = 60 ° 21,6 ‘= 60 ° 21’ 35 «.

5. (а). л / год = 0,032592 / 0,01294 = 2,518.
(б). л / год = 0,4572 / 1,0533 = 0,4340.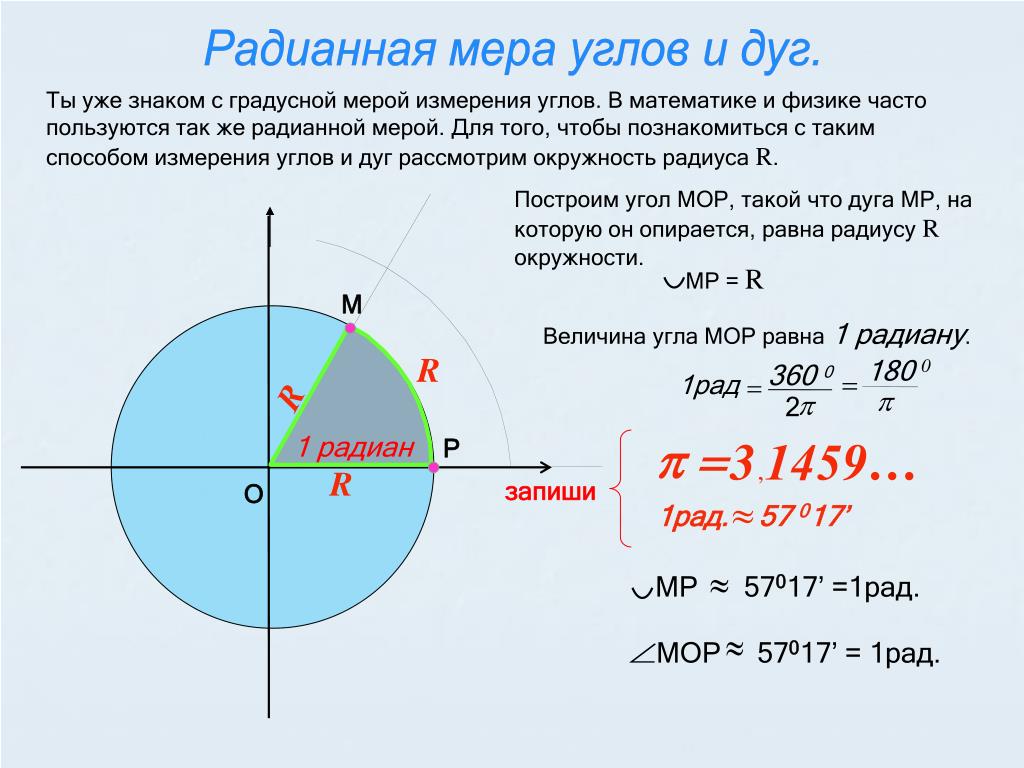

6. ra = (3200 ‘) (0.20604) = 659,31 ‘= 659’ 4 дюйма.

7. Угол a = 0,16776 радиана. Разница в длине составляет 2102,5 a — 1997,5 a , что составляет 5 a. Таким образом, ответ составляет 0,84 фута, что с точностью до дюйма составляет 10 дюймов.

9. Угол = 1/3956 = 0,0002528 радиан = 0,01448 ° = 0,8690 ‘= 52,14 дюйма.

10. Одна минута = 0,0002909 радиан. 1.15075 миль = 6076 футов.Следовательно, одна секунда будет соответствовать 101,3 фута.

14. a = л / об = 1,742 / 5,782 = 0,3013 радиан = 17,26 ° = 17 ° 16 ‘.

23. Угол a равен 8,5 ‘, что составляет 0,00247 радиана. Таким образом, радиус составляет r = л / год = 50 / 0,00247 = 20222 ‘= 3,83 мили, почти четыре мили.

Насчет цифр точности.

Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах.

Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 точка отсчета равна 12 ° 28 ‘, что соответствует примерно четырем знакам точности, поэтому ответ 0,2176 также должен быть дан только с точностью до четырех знаков. (Обратите внимание, что ведущие нули не учитываются при вычислении цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.

Другой пример см. В задаче 3 (a). Данные 0 ° 17’48 «и 6.2935, с точностью до 4 и 5 знаков соответственно. Следовательно, ответ должен быть дан только с точностью до 4 цифр, так как ответ не может быть более точным, чем наименее точные данные. Таким образом, ответ, который может дать калькулятор, а именно 0,032586547, следует округлить до четырех цифр (не включая ведущие нули) до 0,03259.

Хотя окончательные ответы должны быть выражены с соответствующим числом цифр точности, вы все равно должны сохранять все цифры для промежуточных вычислений.

Измерение углов

При изучении геометрии угловые меры часто рассматриваются как степень разделения между двумя лучами с общей конечной точкой, или, возможно, связан с размером данного сектора круга. Обе эти интерпретации неявно накладывают ограничения на допустимые углы измерения. Например, в этих контекстах углы никогда не имеют отрицательных значений.{\ circ} $. В конце концов, как можно иметь сектор круга, превышающий сам круг? Следующее обсуждение обеспечивает переинтерпретацию углов как поворотов на , что позволяет нам обобщить углы так, чтобы их меры могли принимать любое реальное значение, независимо от его знака или величины.

Угол образован двумя половинками, имеющими общую конечную точку, называемую вершиной . Одна половинная линия обозначена как начальная сторона , а другая — клеммная сторона .Мы можем считать, что угол образован поворотом от начальной стороны к конечной. {\ circ} $.{\ circ} $.

Знак меры указывает направление вращения и определяется по формуле:

$ (+) $, если вращение против часовой стрелки

$ (-) $, если вращение по часовой стрелке

Угол
в стандартном положении

Примеры

Практика

Терминальные уголки

Когда два угла имеют одинаковую начальную и конечную стороны, они называются концевыми углами.2 = 1 \} $$ Мы измеряем угол расстоянием $ t $, пройденным по окружности единичной окружности, поскольку угол образуется при повороте от начальной стороны к конечной стороне в стандартном положении.

Условные обозначения знаков остались прежними:

$ (+) $, если вращение против часовой стрелки
$ (-) $, если вращение по часовой стрелке

Радианная мера угла, образованного одним полным поворотом против часовой стрелки, равна длине окружности единичной окружности, которая равна $ 2 \ pi $.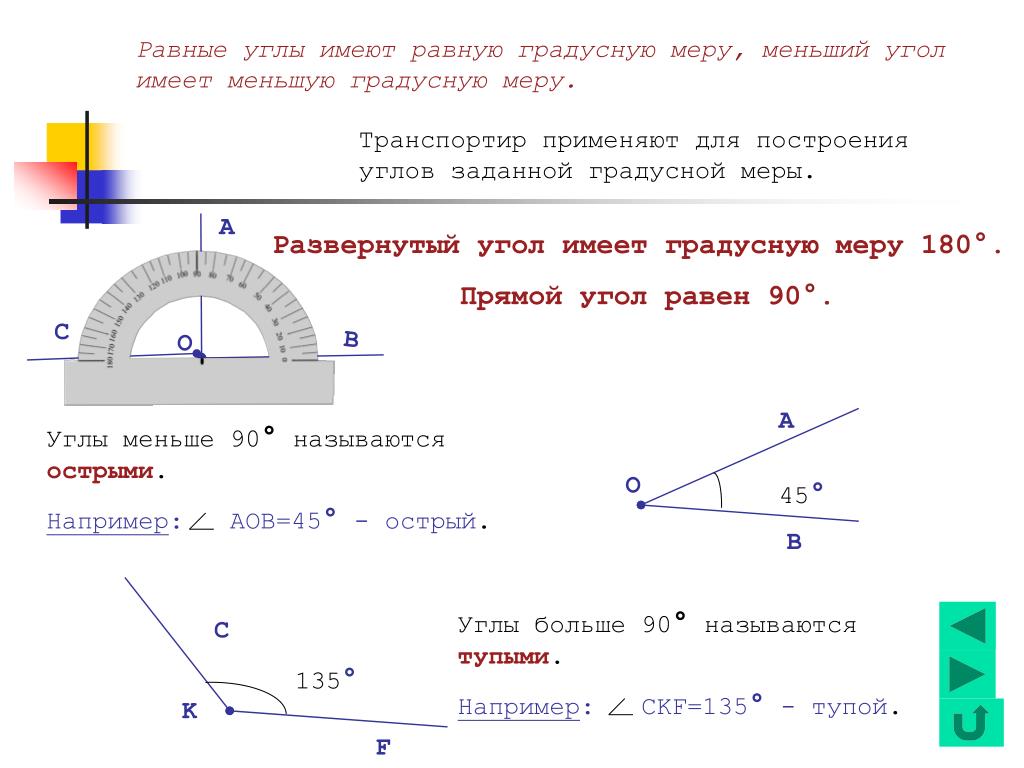 {\ circ}}

долл. США

1.3: Дуги, углы и калькуляторы

Основные вопросы

Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и уметь писать точные, последовательные ответы на эти вопросы.

Как мы измеряем углы в градусах?
Что мы подразумеваем под радианной мерой угла? Как радианная мера угла связана с длиной дуги единичной окружности?
Почему важна мера в радианах?
Как преобразовать радианы в градусы и из градусов в радианы?
Как мы можем использовать калькулятор для приближения значений функций косинуса и синуса?

Древняя цивилизация, известная как Вавилония, была культурным регионом, базирующимся на юге Месопотамии, на территории современного Ирака.Вавилония возникла как независимое государство около 1894 г. до н. Э. Вавилоняне разработали математическую систему, основанную на шестнадцатеричной системе счисления (с основанием 60). Это было началом современного использования 60 минут в час, 60 секунд в минуту и 360 градусов по кругу.

Многие историки теперь считают, что для древних вавилонян год состоял из 360 дней, что является неплохим приближением, учитывая грубость древних астрономических инструментов. Как следствие, они разделили круг на 360 дуг равной длины, что дало им единичный угол, составляющий 1/360 круга или то, что мы теперь знаем как градус.Несмотря на то, что в году 365,24 дня, вавилонская единица угла по-прежнему используется в качестве основы для измерения углов в круге. На рисунке \ (\ PageIndex {1} \) показан круг, разделенный на 6 углов по 60 градусов каждый, что также хорошо сочетается с вавилонской системой счисления с основанием 60.

Рисунок \ (\ PageIndex {1} \): круг с шестью углами в 60 градусов.

Мы часто обозначаем линию, проведенную через 2 точки A и B, как \ (\ overleftrightarrow {AB} \).Часть прямой \ (\ overleftrightarrow {AB} \), которая начинается в точке A и продолжается бесконечно в направлении точки B, называется лучом AB и обозначается \ (\ overrightarrow {AB} \). Точка A — это начальная точка луча \ (\ overrightarrow {AB} \). Угол образуется путем поворота луча вокруг его конечной точки. Луч в его начальном положении называется начальной стороной угла, а положение луча после его поворота называется конечной стороной луча.Конечная точка луча называется вершиной угла .

Рисунок \ (\ PageIndex {2} \): угол с некоторыми обозначениями.

На рисунке \ (\ PageIndex {2} \) показан луч \ (\ overrightarrow {AB} \), повернутый вокруг точки A, образуя угол. Конечной стороной угла является луч \ (\ overrightarrow {AC} \). Мы часто называем это углом ВАС, сокращенно \ (\ angle {BAC} \). Мы также можем называть этот угол углом \ (CAB \) или \ (\ angle {CAB} \). Если мы хотим использовать одну букву для этого угла, мы часто используем греческую букву, такую как \ (\ alpha \) (alpha).Затем мы просто говорим угол ̨. Другие часто используемые греческие буквы: \ (\ beta \) (бета), \ (\ gamma \) (гамма), \ (\ theta \) (theta), \ (\ phi \) (phi) и \ (\ ро \) (ро).

Дуги и уголки

Чтобы определить тригонометрические функции в терминах углов, мы сделаем простую связь между углами и дугами, используя так называемое стандартное положение угла. Когда вершина угла находится в начале координат плоскости \ (xy \), а начальная сторона лежит вдоль положительной оси x, мы видим, что угол находится в стандартной позиции .Конечная сторона угла тогда находится в одном из четырех квадрантов или лежит вдоль одной из осей. Когда сторона вывода находится в одном из четырех квадрантов, сторона вывода определяет так называемое обозначение квадранта угла. См. Рисунок \ (\ PageIndex {3} \).

Рисунок \ (\ PageIndex {3} \): Стандартное положение угла во втором квадранте.

Упражнение \ (\ PageIndex {1} \)

Нарисуйте угол в стандартном положении в

первый квадрант;
третий квадрант; и
четвертый квадрант.

Ответ

На этих графиках показаны положительные углы в стандартном положении. Конечная точка левой точки находится в первом квадранте, точка посередине — в третьем квадранте, а точка справа — в четвертом квадранте.

Если угол находится в стандартном положении, то точка, в которой конечная сторона угла пересекает единичный круг, отмечает конечную точку дуги, как показано на рисунке 1.11. Точно так же конечная точка дуги на единичной окружности определяет луч, проходящий через начало координат и эту точку, которая, в свою очередь, определяет угол в стандартном положении. В этом случае мы говорим, что угол равен , стянутому дугой на градусов. Таким образом, существует естественное соответствие между дугами единичной окружности и углами в стандартном положении. Из-за этого соответствия мы также можем определить тригонометрические терминальные боковые функции в терминах углов, а также дуг. Однако, прежде чем мы это сделаем, нам нужно обсудить два разных способа измерения углов.\ circ \) — это измерение, как и длина. Итак, чтобы сравнить угол, измеренный в градусах, с дугой, измеренной с некоторой длиной, нам нужно соединить размеры. Мы можем сделать это с помощью радианной меры угла.

Радианы будут полезны в том смысле, что радиан — это безразмерная единица измерения. Мы хотим связать угловые измерения с измерениями дуги, и для этого мы напрямую определим угол в 1 радиан как угол, образованный дугой длиной 1 (длина радиуса) на единичной окружности, как показано на рисунке \ (\ PageIndex {5} \).

Рисунок \ (\ PageIndex {5} \): один радиан.

Определение: Radian

Угол один радиан — это угол в стандартном положении на единичной окружности, который образует дуга длиной 1 (в положительном направлении).

Это напрямую связывает углы, измеренные в радианах, с дугами, поскольку мы связываем действительное число как с дугой, так и с углом. Таким образом, угол в 2 радиана отсекает дугу длины 2 на единичной окружности, угол в 3 радиана отсекает дугу длины 3 на единичной окружности и так далее. На рисунке 1.13 показаны конечные стороны углов с размерами 0 радиан, 1 радиан, 2 радиана, 3 радиана, 4 радиана, 5 радиан и 6 радиан. Обратите внимание, что \ (2 \ pi \ приблизительно 6.2832 \) и поэтому \ (6 <2 \ pi \), как показано на рисунке \ (\ PageIndex {6} \).

Рисунок \ (\ PageIndex {6} \): углы с радианной мерой 1, 2, 3, 4, 5 и 6

У нас также могут быть углы с отрицательной радианной мерой, точно так же, как у нас есть дуги с отрицательной длиной. Идея состоит в простом измерении в отрицательном (по часовой стрелке) направлении вокруг единичной окружности.Таким образом, угол, размер которого равен \ (- 1 \) радиан, — это угол в стандартном положении на единичной окружности, который образует дуга длиной 1 в отрицательном (по часовой стрелке) направлении.

Итак, в общем случае угол (в стандартном положении) в t радиан будет соответствовать дуге длины t на единичной окружности. Это позволяет нам обсуждать синус и косинус угла, измеренного в радианах. То есть, когда мы думаем о sin \ ((t) \) и cos \ ((t) \), мы можем рассматривать \ (t \) как:

действительное число;
длина дуги с начальной точкой \ ((1, 0) \) на единичной окружности;
радианная мера угла в стандартном положении.

Когда мы рисуем угол в стандартном положении, мы часто рисуем небольшую дугу возле вершины от начальной стороны до конечной стороны, как показано на рисунке \ (\ PageIndex {7} \), который показывает угол, мера равна \ (\ dfrac {3} {4} \ pi \) радианам.

Упражнение \ (\ PageIndex {2} \)

1. Начертите угол в стандартном положении в радианах:

Рисунок \ (\ PageIndex {7} \): угол с размером \ (\ dfrac {3} {4} \ pi \) в стандартном положении

\ (\ dfrac {\ pi} {2} \) радиан.\ circ \]

Преобразование радианов в градусы

Радиан является предпочтительной мерой углов в математике по многим причинам, главная из которых состоит в том, что радиан не имеет размеров. Однако, чтобы эффективно использовать радианы, нам нужно иметь возможность преобразовывать угловые измерения между радианами и градусами.

Напомним, что один виток единичной окружности соответствует дуге длины \ (2 \ pi \), а дуга длины \ (2 \ pi \) на единичной окружности соответствует углу \ (2 \ pi \ ) радианы.\ circ \), поэтому радиан довольно велик по сравнению с градусом. Эти отношения позволяют быстро переводить градусы в радианы.

Пример \ (\ PageIndex {1} \)

Если угол имеет градусную меру 35 градусов, его радиан может быть рассчитан следующим образом:

\ [35 \ пробел в градусах \ times \ dfrac {\ pi \ пробел радиан} {180 \ пробел в градусах} = \ dfrac {35 \ pi} {180} \ пробел в радианах \]

Переписывая эту дробь, мы видим, что угол с мерой 35 градусов имеет радианную меру \ (\ dfrac {7 \ pi} {36} \) радиан.\ circ \)

Калькуляторы и тригонометрические функции

Теперь мы увидели, что когда мы думаем о \ (\ sin (t) \) или \ (\ cos (t) \), мы можем думать о \ ((t) \) как о действительном числе, длине arc, или радианная мера угла. В разделе 1.5 мы увидим, как определить точные значения функций косинуса и синуса для нескольких специальных дуг (или углов). Например, мы увидим, что \ (\ cos (\ dfrac {\ pi} {6}) = \ dfrac {\ sqrt {3}} {2} \).Однако определение косинуса и синуса как координат точек на единичной окружности затрудняет поиск точных значений для этих функций, за исключением очень специальных дуг. Хотя точные значения всегда лучше, технологии играют важную роль, позволяя нам аппроксимировать значения круговых (или тригонометрических) функций. Большинство портативных калькуляторов, калькуляторов в приложениях для телефонов и планшетов, а также онлайн-калькуляторов имеют ключ косинуса и ключ синуса, которые вы можете использовать для приближения значений этих функций, но мы должны помнить, что калькулятор предоставляет только приближение значения, а не точного значения (за исключением небольшого набора дуг).\ circ \)

Таблица 1.1: Преобразование радианов в градусы.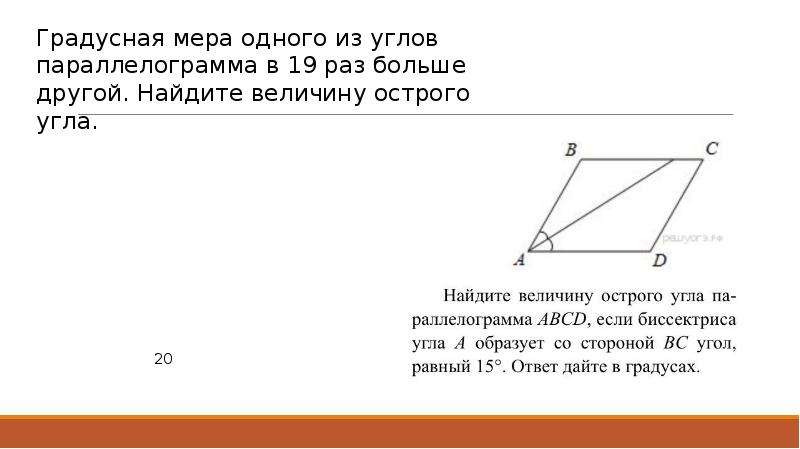

Для этого в калькуляторе есть два режима для углов: радиан и градус. Из-за соответствия между действительными числами, длиной дуг и радианами углов, на данный момент мы всегда будем переводить наши калькуляторы в радианный режим. Фактически, мы видели, что угол, измеренный в радианах, образует дугу этой радианной меры вдоль единичной окружности. Таким образом, косинус или синус угловой меры в радианах — это то же самое, что косинус или синус действительного числа, когда это действительное число интерпретируется как длина дуги вдоль единичной окружности. (Когда мы изучаем тригонометрию треугольников в главе 3, мы будем использовать режим градусов. Вводное обсуждение тригонометрических функций угловой меры в градусах см. В упражнении (4)).

Упражнение \ (\ PageIndex {4} \)

В упражнении 1.6 мы использовали апплет Geogebra под названием Конечные точки дуг на единичной окружности на http://gvsu.edu/s/JY, чтобы аппроксимировать значения функций косинуса и синуса при определенных значениях. Например, мы обнаружили, что

\ (\ cos (1) \ приблизительно 0.5403 \), \ (\ sin (1) \ приблизительно 0,8415 \).
\ (\ cos (2) \ приблизительно -0,4161 \), \ (\ sin (2) \ приблизительно 0,9093 \).
\ (\ cos (-4) \ приблизительно -0,6536 \), \ (\ sin (-4) \ приблизительно 0,7568 \).
\ (\ cos (-15) \ приблизительно -0,7597 \), \ (\ sin (-15) \ приблизительно -0,6503 \).

Используйте калькулятор, чтобы определить эти значения функций косинуса и синуса, и сравните их с указанными выше. Они одинаковы? Насколько они разные?

Ответ

Используя калькулятор, мы получаем следующие результаты с точностью до десяти знаков после запятой.

\ (\ cos (1) \ приблизительно 0,5403023059, \ sin (1) \ приблизительно 0,8414709848 \). \ (\ cos (1) \ приблизительно 0: 4161468365, \ sin (1) \ приблизительно 0,74268 \).

Разница между этими значениями и значениями, полученными в ходе проверки выполнения 1. 6, состоит в том, что эти значения верны с точностью до 10 десятичных знаков (а остальные верны с точностью до 4 десятичных знаков). Если мы округлим каждое из приведенных выше значений до 4 десятичных знаков, мы получим те же результаты, что и в Progress Check 1.6.

\ (\ cos (1) \ приблизительно 0: 6536436209, \ sin (1) \ приблизительно 0.7568024953 \).
\ (\ cos (1) \ приблизительно 0: 7596879129, \ sin (1) \ приблизительно 0,6502878402 \).

Краткое содержание раздела 1.3

В этом разделе мы изучили следующие важные концепции и идеи:

Угол образуется путем поворота луча вокруг его конечной точки. Луч в его начальном положении называется начальной стороной угла, а положение луча после его поворота называется конечной стороной луча.\ circ \) — это угол, равный 1 = 360 центральному углу окружности. Угол один радиан — это угол в стандартном положении на единичной окружности, который образуется дугой длиной 1 (в положительном направлении).
Мы преобразуем величину угла из градусов в радианы, используя тот факт, что каждый градус — это радианы. Мы конвертируем величину угла из 180 радиан в градусы, используя тот факт, что каждый радиан равен 180 градусам.

Тригонометрия: радианы и градусы

Мы определяем угол как объединение двух неколлинеарных лучей, имеющих общую начальную точку.Два луча называются ответвлениями угла и общего начальная точка называется его вершиной.

Мы можем интерпретировать угол, вращая луч из одного положения в другое. Когда мы используем эту интерпретацию угла, луч, с которого начинается, называется начальным сторона, а конечное положение луча называется конечной стороной, как показано на рисунке.

Если мы повернем луч против часовой стрелки, полученный таким образом угол называется положительным.Угол, образованный вращением луча по часовой стрелке, называется как отрицательный угол.

Углы обычно измеряются двумя способами: в градусах и радианах. Мы обсуждаем оба этих метода по очереди.

Измерение угла в шестнадцатеричной системе счисления (градусы, минуты, секунды)

В этом методе мы измеряем угол в градусах, минутах и секундах.\ circ` (Маленький кружок обозначает градус). Аналогично 1 ‘обозначает минуту, а 1’ ‘обозначает секунда в шестнадцатеричной системе измерения углов.

Следующие уравнения показывают взаимосвязь градуса, минуты и секунды.

1 минута = 60 секунд (60 дюймов)

1 градус = 60 минут (60 ‘)

Один полный оборот = `360 ^ \ circ`

Мы представляем несколько примеров преобразования угла, заданного в шестнадцатеричной форме, в десятичную и наоборот.\ circ`21 ’36’

Измерьте угол в круговой системе (радианы)

» Радиан — это мера угла, образуемого в центре окружности дугой, длина которой равна радиусу этой окружности ».

Угол m` \ angle`XOY на рисунке равен одному радиану, поскольку длина дуги XY равна радиусу окружности.

=> m` \ angle`XOY = 1 радиан

Примечание: Длина l дуги, которая образует угол \ theta в центре окружности радиуса r, определяется выражением

l = r` \ theta`

, т.е.длина дуги равна углу, умноженному на радиус окружности. (Здесь `\ theta` выражается в радианах, а не в градусах)

Связь между радианами и градусами

Мы знаем, что для окружности радиуса r длина окружности C равна C = 2` \ pi`r.\ circ`

`\ pi` радианы

`(\ pi) / 6` радиан

Пример 9:

Найдите часто используемые углы единичной окружности в градусах и радианах.

Градус

Градус — это единица измерения, обозначаемая символом °, используемая для обозначения угла на плоскости.Угол, равный 1 °, считывается 1 градус, равен одному полному обороту угла вокруг его вершины. Из диаграммы ниже видно, что вращение конечной стороны угла против часовой стрелки образует круговую траекторию для угла.

Один полный оборот эквивалентен 360 °. Четверть оборота дает угол в 90 °, а половина оборота дает угол 180 °. Хотя углы могут иметь размеры больше, чем показано, выполняя несколько вращений, при изучении геометрии мы в основном будем смотреть только на углы до 360 °.

Знаете ли вы?

Углы могут иметь и другие единицы измерения. Углы могут быть измерены в радианах, что позволяет сравнить длину дуги, полученную при повороте угла, с радиусом окружности. Угол, который составляет 180 °, имеет размер π радиан. Еще одна единица измерения угла называется уклоном. Это также может называться уклон, уклон, уклон, главный спуск, тангаж или подъем. Наклон угла измеряет отношение вертикального расстояния к горизонтальному расстоянию на конечном конце угла.Наклон часто представлен в процентах. У вас может быть опыт использования этой единицы измерения при восхождении или подъеме на гору. Крутизну холма или горы часто описывают в терминах уклона или уклона. Например, уклон холма может составлять 5%.

При использовании символа градуса будьте осторожны и не используйте его для названия угла, а только для его меры.

Имя угла, показанного ниже, — A, а не A °. При указании его меры используйте m∠A = 80 ° или просто ∠A = 80 °, где ∠ — это символ, используемый для обозначения угла.

Уголки специальные

Некоторые углы чаще используются в геометрии из-за их размеров:

Обратите внимание, что угол 90 ° имеет небольшой квадрат в вершине. Это обозначение указывает угол, который составляет 90 °, и нет необходимости указывать размер угла в числовом выражении.

Измерительные углы

Транспортир — это распространенный инструмент, используемый для измерения углов. Большинство транспортиров измеряют углы в градусах.

Транспортиры обычно имеют два набора чисел.Оба набора можно использовать для измерения угла в градусах. Внешний набор изменяется от 0 до 180 градусов, где 0 находится на левой стороне транспортира. Внутренний набор идет от 180 до 0 градусов, где 0 находится с правой стороны транспортира. Какая бы сторона вы ни совпадала с линией нулевого градуса, определяет, какой набор чисел использовать. Посмотрите, как измерить угол в градусах с помощью транспортира.

Знаете ли вы?

Углы с десятичным градусом, например 15,66 °, могут быть преобразованы в единицы измерения в градусах-минутах-секундах, где десятичная часть градусной меры выражается в минутах и секундах.1 ° = 60 ‘= 3600 «, где символ’ представляет минуты, а» означает секунды. Итак, 15,66 ° = 15 ° 39’36 «, что читается как 15 градусов 39 минут 36 секунд.

Уголки | Алгебра и тригонометрия

Игрок в гольф замахивается, чтобы отбить мяч через песчаную ловушку на лужайку. Пилот авиалинии ведет самолет к узкой взлетно-посадочной полосе. Дизайнер платьев создает последнюю моду. Что у них общего? Все они работают с углами, как и все мы в то или иное время. Иногда нам нужно точно измерить углы инструментами.В других случаях мы оцениваем их или судим на глаз. В любом случае правильный угол может иметь значение для успеха или неудачи во многих начинаниях. В этом разделе мы рассмотрим свойства углов.

Углы чертежа в стандартном положении

Для правильного определения угла сначала необходимо определить луч. Луч — это направленный отрезок прямой. Он состоит из одной точки на линии и всех точек, идущих в одном направлении от этой точки. Первая точка называется конечной точкой луча.Мы можем ссылаться на конкретный луч, указав его конечную точку и любую другую точку на нем. Луч на (Рисунок) может быть назван как луч EF или в виде символа [latex] \, \ stackrel {⟶} {EF}. [/ Latex]

Рисунок 1.

Угол — это объединение двух лучей, имеющих общий конец. Конечная точка называется вершиной угла, а два луча — сторонами угла. Угол на (Рисунок) образован из [латекса] \, \ stackrel {⟶} {ED} \, [/ latex] и [latex] \, \ stackrel {⟶} {EF} \, [/ latex]. Углы могут быть названы с использованием точки на каждом луче и вершине, например, angle DEF , или в виде символа [latex] \, \ angle DEF.[/ латекс]

Рисунок 2.

Греческие буквы часто используются в качестве переменных для измерения угла. (Рисунок) — это список греческих букв, обычно используемых для обозначения углов, а примерный угол показан на (Рисунок).


[латекс] \ theta [/ латекс]	[латекс] \ phi \, [/ latex] или [латекс] \, \ varphi [/ latex]	[латекс] \ alpha [/ латекс]	[латекс] \ beta [/ латекс]	[латекс] \ гамма [/ латекс]
тета	фи	альфа	бета	гамма

Рисунок 3. Угол тета, обозначенный как [латекс] \, \ угол \ тета [/ латекс]

Создание угла — это динамический процесс. Начнем с двух лучей, лежащих один на другом. Один оставляем на месте, а другой вращаем. Фиксированный луч — это начальная сторона , , а повернутый луч — конечная сторона. Чтобы идентифицировать разные стороны, мы указываем вращение маленькой стрелкой рядом с вершиной, как на (Рисунок).

Рисунок 4.

Как мы обсуждали в начале раздела, существует множество применений углов, но для того, чтобы использовать их правильно, мы должны уметь их измерять.Мера угла — это величина поворота от начальной стороны к конечной стороне. Вероятно, самая известная единица измерения угла — это градус. Один градус — это [latex] \, \ frac {1} {360} \, [/ latex] кругового вращения, поэтому полное круговое вращение содержит [latex] \, 360 \, [/ latex] градусов. Угол, измеренный в градусах, всегда должен включать единицу измерения «градусы» после числа или включать символ градуса [латекс] °. \, [/ Латекс] Например, [латекс] \, 90 \ text {градусы} = 90 ° . [/ латекс]

Чтобы формализовать нашу работу, мы начнем с рисования углов на координатной плоскости x — y .Углы могут встречаться в любом положении на координатной плоскости, но в целях сравнения принято их изображать в одном и том же положении, когда это возможно. Угол находится в стандартном положении, если его вершина расположена в начале координат, а его начальная сторона проходит вдоль положительной оси x . См. (Рисунок).

Рисунок 5.

Если угол измеряется против часовой стрелки от начальной стороны к конечной стороне, угол считается положительным.Если угол измеряется по часовой стрелке, угол считается отрицательным.

Рисование угла в стандартном положении всегда начинается одинаково — начертите начальную сторону вдоль положительной оси x . Чтобы разместить конечную сторону угла, мы должны вычислить долю полного поворота, которую представляет угол. Мы делаем это, разделив угол в градусах на [латекс] \, 360 °. \, [/ Латекс] Например, чтобы нарисовать угол [латекс] \, 90 ° \, [/ латекс], мы вычисляем, что [ латекс] \, \ frac {90 °} {360 °} = \ frac {1} {4}.\, [/ latex] Таким образом, сторона вывода будет на четверть пути по окружности, двигаясь против часовой стрелки от положительной оси x . Чтобы нарисовать угол [латекс] \, 360 ° [/ латекс], мы вычисляем, что [latex] \, \ frac {360 °} {360 °} = 1. \, [/ Latex] Таким образом, сторона вывода будет равна 1 полное вращение по окружности, двигаясь против часовой стрелки от положительной оси x . В этом случае начальная сторона и конечная сторона перекрываются. См. (Рисунок).

Рисунок 6.

Поскольку мы определяем угол в стандартном положении по его конечной стороне, у нас есть специальный тип угла, конечная сторона которого лежит на оси, квадрантный угол .Этот тип угла может иметь размер [латекс] \ text {0 °,} \, \ text {90 °,} \, \ text {180 °,} \, \ text {270 °,} [/ latex] или [латекс] \, \ text {360 °}. \, [/ latex] См. (рисунок).

Рис. 7. Квадрантные углы имеют концевую сторону, которая лежит вдоль оси. Показаны примеры.

Углы квадранта

Угол — это квадрантный угол, если его конечная сторона лежит на оси, включая [latex] \ text {0 °,} \, \ text {90 °,} \, \ text {180 °,} \, \ text { 270 °,} [/ latex] или [latex] \, \ text {360 °}. [/ Latex]

Как сделать

Если угол измеряется в градусах, начертите угол в стандартном положении.

Выразите угловую меру как долю от [latex] \, \ text {360 °}. [/ Latex]
Уменьшите дробь до простейшего вида.
Нарисуйте угол, содержащий ту же часть круга, начиная с положительной оси x и двигаясь против часовой стрелки для положительных углов и по часовой стрелке для отрицательных углов.

Построение угла в стандартном положении, измеренного в градусах

Нарисуйте угол [латекс] \, 30 ° \, [/ латекс] в стандартном положении.
Нарисуйте угол [латекс] \, — 135 ° \, [/ латекс] в стандартном положении.

Показать решение

Разделите размер угла на [латекс] \, 360 °. [/ Латекс]
[латекс] \ frac {30 °} {360 °} = \ frac {1} {12} [/ латекс]
Чтобы переписать дробь в более знакомую дробь, мы можем распознать, что
[латекс] \ frac {1} {12} = \ frac {1} {3} \ left (\ frac {1} {4} \ right) [/ latex]
Одна двенадцатая равняется одной трети четверти, поэтому, разделив четверть поворота на трети, мы можем нарисовать линию в точках [латекс] \, 30 °, [/ латекс], как показано на (Рисунок).
Рисунок 8.
Разделите размер угла на [латекс] \, 360 °. [/ Латекс]
[латекс] \ frac {-135 °} {360 °} = — \ frac {3} {8} [/ латекс]
В этом случае мы можем распознать, что
[латекс] — \ frac {3} {8} = — \ frac {3} {2} \ left (\ frac {1} {4} \ right) [/ latex]
Отрицательные три восьмых — это полторы раза в четверть, поэтому мы размещаем линию, перемещая по часовой стрелке одну полную четверть и половину другой четверти, как на (Рисунок).
Рисунок 9.

Попробуй

Покажите угол [латекс] \, 240 ° \, [/ латекс] на окружности в стандартном положении.

Показать решение

Преобразование между градусами и радианами

Разделение круга на 360 частей — выбор произвольный, хотя при этом создается знакомая величина в градусах. Мы можем выбрать другие способы разделить круг. Чтобы найти другую единицу, представьте себе процесс рисования круга. Представьте, что вы остановились до того, как круг замкнулся.Нарисованная вами часть называется дугой. Дуга может быть частью полного круга, полного круга или более чем полного круга, представленного более чем одним полным оборотом. Длина дуги вокруг всего круга называется окружностью этого круга.

Окружность круга равна [латекс] \, C = 2 \ pi r. \, [/ Latex]. Если мы разделим обе части этого уравнения на [латекс] \, r, [/ латекс], мы получим соотношение окружность, которая всегда равна [латексу] \, 2 \ pi, [/ латексу] к радиусу, независимо от длины радиуса.Таким образом, длина окружности любого круга равна [латексу] \, 2 \ пи \ приблизительно 6,28 \, [/ латексу] умноженным на длину радиуса. Это означает, что если мы возьмем струну такой же длины, как радиус, и будем использовать ее для измерения последовательных длин по окружности, то будет место для шести полных длин струны и чуть больше четверти седьмой, как показано на (Рис. ).

Рисунок 10.

Это подводит нас к нашей новой угловой мере. Один радиан — это мера центрального угла круга, который пересекает дугу, равную по длине радиусу этого круга.Центральный угол — это угол, образованный в центре круга двумя радиусами. Поскольку общая длина окружности равна [латексу] \, 2 \ pi \, [/ latex], умноженным на радиус, полный круговой поворот равен [latex] \, 2 \ pi \, [/ latex] радианам.

[латекс] \ begin {array} {ccc} \ hfill 2 \ pi \ text {radians} & = & 360 ° \ hfill \\ \ hfill \ pi \ text {radians} & = & \ frac {360 °} { 2} = 180 ° \ hfill \\ \ hfill 1 \ text {radian} & = & \ frac {180 °} {\ pi} \ приблизительно 57,3 ° \ hfill \ end {array} [/ latex]

См. (Рисунок). Обратите внимание, что когда угол описывается без конкретной единицы измерения, он относится к радианам.Например, величина угла 3 означает 3 радиана. Фактически, радиан безразмерен, так как это частное от деления длины (окружности) на длину (радиус) и сокращения единиц длины.

Рис. 11. Угол [латекс] \, t \, [/ latex] составляет величину в один радиан. Обратите внимание, что длина перехваченной дуги равна длине радиуса круга.

Отношение длины дуги к радиусу

Длина дуги [латекс] \, s \, [/ латекс] — это длина кривой вдоль дуги.Так же, как полная длина окружности всегда имеет постоянное отношение к радиусу, длина дуги, образованная любым заданным углом, также имеет постоянную связь с радиусом, независимо от длины радиуса.

Это отношение, называемое радианной мерой, одинаково независимо от радиуса круга — оно зависит только от угла. Это свойство позволяет нам определить меру любого угла как отношение длины дуги [latex] \, s \, [/ latex] к радиусу r . См. (Рисунок).

[латекс] \ begin {array} {ccc} s & = & r \ theta \\ \ theta & = & \ frac {s} {r} \ end {array} [/ latex]

Если [латекс] \, s = r, [/ latex], то [латекс] \, \ theta = \ frac {r} {r} = \ text {1 радиан} \ text {.} [/ латекс]

Рис. 12. (a) Под углом в 1 радиан длина дуги [латекс] \, s \, [/ latex] равна радиусу [латекс] \, r. \, [/ Латекс] (b) Угол в 2 радиана имеет длину дуги [латекс] \, s = 2r. \, [/ Latex] (c) Полный оборот составляет [латекс] \, 2 \ pi, [/ latex] или около 6,28 радиана.

Чтобы развить эту идею, рассмотрим две окружности, одну с радиусом 2, а другую с радиусом 3. Напомним, что длина окружности [латекс] \, C = 2 \ pi r, [/ latex], где [латекс] \ , г \, [/ латекс] — радиус.Тогда меньший круг имеет окружность [латекс] \, 2 \ pi \ left (2 \ right) = 4 \ pi \, [/ latex], а больший круг имеет окружность [латекс] \, 2 \ pi \ left (3 \ right ) = 6 \ pi. \, [/ Latex] Теперь нарисуем угол [латекс] \, 45 ° \, [/ latex] на двух окружностях, как на (Рисунок).

Рис. 13. Угол [латекс] \, 45 ° \, [/ латекс] содержит одну восьмую окружности окружности, независимо от радиуса.

Обратите внимание, что произойдет, если мы найдем отношение длины дуги к радиусу круга.

[латекс] \ begin {array} {ccc} \ text {Меньший круг:} \ frac {\ frac {1} {2} \ pi} {2} & = & \ frac {1} {4} \ pi \ \ \ text {Большой круг:} \ frac {\ frac {3} {4} \ pi} {3} & = & \ frac {1} {4} \ pi \ end {array} [/ latex]

Поскольку оба соотношения равны [latex] \, \ frac {1} {4} \ pi, [/ latex], угловые размеры обеих окружностей одинаковы, даже несмотря на то, что длина и радиус дуги различаются.

Радианы

Один радиан — это мера центрального угла окружности, при которой длина дуги между начальной и конечной сторонами равна радиусу окружности. Полный оборот [латекс] \, \ влево (360 ° \ вправо) \, [/ латекс] равен [латексу] \, 2 \ pi \, [/ latex] радианам. Половина оборота [латекс] \, \ влево (180 ° \ вправо) \, [/ латекс] эквивалентна [латексу] \, \ pi \, [/ latex] радианам.

Радианная мера угла — это отношение длины дуги, образуемой этим углом, к радиусу окружности.Другими словами, если [латекс] \, s \, [/ латекс] — длина дуги круга, а [латекс] \, r \, [/ латекс] — радиус круга, то центральный Угол, содержащий эту дугу, измеряет [latex] \, \ frac {s} {r} \, [/ latex] радианы. В круге радиуса 1 радианная мера соответствует длине дуги.

Измерение в 1 радиан выглядит примерно [латекс] \, 60 °. \, [/ Латекс] Верно?

Да. Это примерно [латекс] \, 57,3 °. \, [/ Latex] Потому что [латекс] \, 2 \ pi \, [/ latex] радиан равны [латекс] 360 °, 1 [/ латекс] радиан равняется [латекс] \, \ frac {360 °} {2 \ pi} \ приблизительно 57.3 °. [/ Латекс]

Использование радианов

Поскольку радиан представляет собой отношение двух длин, это безразмерная мера. Например, на (Рисунок) предположим, что радиус составляет 2 дюйма, а расстояние по дуге также составляет 2 дюйма. Когда мы вычисляем радианную меру угла, «дюймы» отменяются, и мы получаем результат без единиц измерения. Следовательно, нет необходимости писать метку «радианы» после радианной меры, и если мы видим угол, который не отмечен «градусами» или символом градуса, мы можем предположить, что это радианная мера.

Рассматривая самый простой случай, единичный круг (круг с радиусом 1), мы знаем, что 1 поворот равен 360 градусов, [латекс] \, 360 °. [/ Latex] Мы также можем отследить один поворот вокруг круга, найдя окружность, [латекс] \, C = 2 \ pi r, [/ latex] и для единичного круга [латекс] \, C = 2 \ pi. \, [/ latex] Эти два разных способа вращения вокруг круга дайте нам возможность конвертировать градусы в радианы.

[латекс] \ begin {array} {ccccc} \ hfill \ text {1 вращение} & = & 360 ° \ hfill & = & 2 \ pi \ text {радианы} \ hfill \\ \ hfill \ frac {1} { 2} \ text {вращение} & = & 180 ° \ hfill & = & \ pi \ text {радианы} \ hfill \\ \ hfill \ frac {1} {4} \ text {вращение} & = & 90 ° \ hfill & = & \ frac {\ pi} {2} \ text {радианы} \ hfill \ end {array} [/ latex]

Определение особых углов, измеренных в радианах

Помимо знания измерений в градусах и радианах четверти оборота, половины оборота и полного оборота, есть и другие часто встречающиеся углы в одном обороте окружности, с которыми мы должны быть знакомы.Часто встречаются кратные 30, 45, 60 и 90 градусов. Эти значения показаны на (Рисунок). Запоминание этих углов будет очень полезно при изучении свойств, связанных с углами.

Рисунок 14. Часто встречающиеся углы, измеряемые в градусах

Теперь мы можем перечислить соответствующие значения в радианах для общих мер круга, соответствующие тем, которые перечислены на (Рисунок), которые показаны на (Рисунок). Убедитесь, что вы можете проверить каждую из этих мер.

Рисунок 15. Часто встречающиеся углы, измеряемые в радианах

Нахождение радианной меры

Найдите одну треть полного оборота в радианах.

Показать решение

Для любой окружности длина дуги при таком повороте составляла бы одну треть окружности. Мы знаем, что

[латекс] 1 \ text {вращение} = 2 \ pi r [/ латекс]

Итак,

[латекс] \ begin {array} {ccc} \ hfill s & = & \ frac {1} {3} \ left (2 \ pi r \ right) \ hfill \\ & = \ hfill & \ frac {2 \ pi r} {3} \ hfill \ end {array} [/ latex]

Радиан представляет собой длину дуги, деленную на радиус.

[латекс] \ begin {array} {ccc} \ hfill \ text {радианная мера} & = & \ frac {\ frac {2 \ pi r} {3}} {r} \ hfill \\ & = & \ frac {2 \ pi r} {3r} \ hfill \\ & = & \ frac {2 \ pi} {3} \ end {array} [/ latex]

Попробуй

Найдите три четверти полного оборота в радианах.

Показать решение

[латекс] \ frac {3 \ pi} {2} [/ латекс]

Преобразование радианов в градусы

Поскольку градусы и радианы измеряют углы, нам нужно иметь возможность конвертировать между ними.{R}}} {\ pi} [/ латекс]

Эта пропорция показывает, что величина угла [латекс] \, \ theta \, [/ latex] в градусах, деленная на 180, равна измерению угла [latex] \, \ theta \, [/ latex] в радианах, деленному на [ latex] \, \ pi. \, [/ latex] Другими словами, градусы равны 180, а радианы — [latex] \, \ pi. [/ latex]

[латекс] \ frac {\ text {Degrees}} {180} = \ frac {\ text {Radians}} {\ pi} [/ latex]

Преобразование из радианов в градусы

Чтобы преобразовать градусы в радианы, используйте пропорцию

[латекс] \ frac {\ theta} {180} = \ frac {{\ theta} _ {R}} {\ pi} [/ латекс]

Преобразование радианов в градусы

Преобразование радианов в градусы.

[латекс] \ frac {\ pi} {6} [/ латекс]
3

Показать решение

Поскольку нам даны радианы и нам нужны градусы, мы должны установить пропорцию и решить ее.

Используем пропорции, подставляя данную информацию.
[латекс] \ begin {array} {ccc} \ hfill \ frac {\ theta} {180} & = & \ frac {{\ theta} _ {R}} {\ pi} \ hfill \\ \ hfill \ frac {\ theta} {180} & = & \ frac {\ frac {\ pi} {6}} {\ pi} \ hfill \\ \ hfill \ theta & = & \ frac {180} {6} \ hfill \\ \ hfill \ theta & = & 30 ° \ hfill \ end {array} [/ latex]
Используем пропорции, подставляя данную информацию.{R}}} {\ pi} \ hfill \\ \ hfill \ frac {\ theta} {180} & = & \ frac {3} {\ pi} \ hfill \\ \ hfill \ theta & = & \ frac { 3 \ left (180 \ right)} {\ pi} \ hfill \\ \ hfill \ theta & \ приблизительно & 172 ° \ hfill \ end {array} [/ latex]

Попробуй

Преобразовать [латекс] \, — \ frac {3 \ pi} {4} \, [/ latex] радианы в градусы.

Преобразование градусов в радианы

Преобразование [латексных] \, 15 \, [/ латексных] градусов в радианы.

Показать решение

В этом примере мы начинаем с градусов и хотим радиан, поэтому мы снова устанавливаем пропорцию, но подставляем данную информацию в другую часть пропорции.

[латекс] \ begin {array} {ccc} \ hfill \ frac {\ theta} {180} & = & \ frac {{\ theta} _ {R}} {\ pi} \ hfill \\ \ hfill \ frac {15} {180} & = & \ frac {{\ theta} _ {R}} {\ pi} \ hfill \\ \ hfill \ frac {15 \ pi} {180} & = & {\ theta} _ { R} \ hfill \\ \ hfill \ frac {\ pi} {12} & = & {\ theta} _ {R} \ hfill \ end {array} [/ latex]

Анализ

Другой способ подумать об этой проблеме — вспомнить, что [latex] \, 30 ° = \ frac {\ pi} {6}. \, [/ Latex], потому что [latex] \, 15 ° = \ frac {1} {2} \ left (30 ° \ right), [/ latex] мы можем найти, что [latex] \, \ frac {1} {2} \ left (\ frac {\ pi} {6} \ right) \, [/ latex] — это [latex] \, \ frac {\ pi} {12}.[/ латекс]

Попробуй

Преобразовать [латекс] \, 126 ° \, [/ латекс] в радианы.

Показать решение

[латекс] \ frac {7 \ pi} {10} [/ латекс]

Нахождение концевых углов

Преобразование между градусами и радианами может упростить работу с углами в некоторых приложениях. Для других приложений нам может потребоваться другой тип преобразования. Отрицательные углы и углы, превышающие полный оборот, труднее работать, чем углы в диапазоне от [латекс] \, 0 ° \, [/ латекс] до [латекс] \, 360 °, [/ латекс] или [латекс] ] \, 0 \, [/ латекс] в [латекс] \, 2 \ пи.\, [/ latex] Было бы удобно заменить эти углы вне диапазона на соответствующий угол в пределах одного оборота.

Может быть более одного угла иметь одну и ту же сторону вывода. Посмотрите на (рисунок). Угол [латекса] \, 140 ° \, [/ латекса] — положительный угол, измеренный против часовой стрелки. Угол [латекса] \, — 220 ° \, [/ латекса] — отрицательный угол, измеренный по часовой стрелке. Но оба угла имеют одинаковую конечную сторону. Если два угла в стандартном положении имеют одну и ту же конечную сторону, они являются концевыми углами.Каждый угол больше, чем [латекс] \, 360 ° \, [/ латекс] или меньше, чем [латекс] \, 0 ° \, [/ латекс], совпадает с углом между [латексом] \, 0 ° \, [/ латекс] и [латекс] \, 360 °, [/ латекс], и часто удобнее найти угол котерминала в диапазоне от [латекс] \, 0 ° \, [/ латекс] до [латекс] \, 360 ° \, [/ latex], чем работать с углом, выходящим за пределы этого диапазона.

Рис. 16. Угол [латекс] \, 140 ° \, [/ латекс] и угол [латекс] \, — 220 ° \, [/ латекс] являются котерминальными углами.

Любой угол имеет бесконечно много котерминальных углов, потому что каждый раз, когда мы добавляем [латекс] \, 360 ° \, [/ латекс] к этому углу — или вычитаем из него [латекс] \, 360 ° \, [/ латекс] — в результате value имеет терминальную сторону в том же месте.Например, по этой причине [латекс] \, \ text {100 °} \, [/ latex] и [latex] \, \ text {460 °} \, [/ latex] являются концевыми, как и [латекс] \ , -260 °. \, [/ Латекс]

Базовый угол угла — это мера наименьшего положительного острого угла [латекс] \, t \, [/ латекс], образованного конечной стороной угла [латекс] \, t \, [/ латекс] и Горизонтальная ось. Таким образом, положительные опорные углы имеют концевые стороны, которые лежат в первом квадранте, и могут использоваться в качестве моделей для углов в других квадрантах. См. (Рисунок) примеры исходных углов для углов в различных квадрантах.{\ prime}, [/ latex] образованы конечной стороной угла [latex] \, t \, [/ latex] и горизонтальной осью.

Как сделать

Дан угол больше, чем [латекс] \, 360 °, [/ латекс] найдите угол на конце между [латексом] \, 0 ° \, [/ латексом] и [латексом] \, 360 ° [/ латекс]

Вычтите [латекс] \, 360 ° \, [/ латекс] из заданного угла.
Если результат все еще больше [латекс] \, 360 °, [/ латекс], вычтите [латекс] \, 360 ° \, [/ латекс] еще раз, пока результат не окажется между [латекс] \, 0 ° \, [ / латекс] и [латекс] \, 360 °.[/ латекс]
Полученный угол совпадает с исходным углом.

Определение угла на одном конце с углом измерения больше, чем [латекс] \, 360 ° [/ латекс]

Найдите наименьший положительный угол [латекс] \, \ theta \, [/ latex], который совпадает с углом измерения [латекс] \, 800 °, [/ latex], где [latex] \, 0 ° \ le \ theta <360 °. [/ Латекс]

Показать решение

Угол с мерой [латекс] \, 800 ° \, [/ латекс] совпадает с углом с размером [латекс] \, 800-360 = 440 °, [/ латекс] но [латекс] \, 440 ° \ , [/ latex] по-прежнему больше, чем [latex] \, 360 °, [/ latex], поэтому мы снова вычитаем [latex] \, 360 ° \, [/ latex], чтобы найти другой котерминальный угол: [latex] \, 440 -360 = 80 °.[/ латекс]

Угол [латекс] \, \ theta = 80 ° \, [/ latex] совпадает с [латексом] \, 800 °. \, [/ Latex] Другими словами, [латекс] \, 800 ° \ , [/ latex] равно [latex] \, 80 ° \, [/ latex] плюс два полных поворота, как показано на (Рисунок).

Рисунок 18.

Попробуй

Найдите угол [латекс] \, \ альфа \, [/ латекс], который совпадает с углом измерения [латекс] \, 870 °, [/ латекс], где [латекс] \, 0 ° \ le \ alpha <360 °. [/ Латекс]

Показать решение

[латекс] \ альфа = 150 ° [/ латекс]

Как сделать

Для заданного угла с мерой меньше [латекс] \, 0 °, [/ latex] найдите внутренний угол, имеющий меру между [латексом] \, 0 ° \, [/ latex] и [латексом] \, 360 °. .[/ латекс]

Добавьте [латекс] \, 360 ° \, [/ латекс] к заданному углу.
Если результат по-прежнему меньше [латекс] \, 0 °, [/ latex], добавьте [latex] \, 360 ° \, [/ latex] еще раз, пока результат не окажется между [latex] \, 0 ° \, [ /latex impressionand[latex impression\ 360 ° ./latex]
Полученный угол совпадает с исходным углом.

Определение угла на одном конце с углом менее [латекс] \, 0 ° [/ латекс]

Покажите угол с мерой [latex] \, — 45 ° \, [/ latex] на окружности и найдите положительный угол на конце [латекс] \, \ alpha \, [/ latex], такой, что [latex] \, 0 ° \ le \ alpha <360 °.[/ латекс]

Показать решение

Поскольку [латекс] \, 45 ° \, [/ latex] составляет половину [латекса] \, 90 °, [/ latex], мы можем начать с положительной горизонтальной оси и измерить по часовой стрелке половину [латекса] \, 90 ° \, угол [/ латекс].

Поскольку мы можем найти концевые углы путем добавления или вычитания полного поворота [latex] \, 360 °, [/ latex], мы можем найти здесь положительный котерминальный угол, добавив [latex] \, 360 °. [/ Latex]

[латекс] -45 ° + 360 ° = 315 ° [/ латекс]

Затем мы можем показать угол на окружности, как на (Рисунок).

Рисунок 19.

Попробуй

Найдите угол [латекс] \, \ beta \, [/ латекс], который совпадает с углом измерения [латекс] \, — 300 ° \, [/ латекс], такой, что [латекс] \, 0 ° \ le \ бета <360 °. [/ латекс]

Показать решение

[латекс] \ beta = 60 ° [/ латекс]

Нахождение концевых углов, измеренных в радианах

Мы можем найти концевые углы, измеренные в радианах, почти так же, как мы нашли их в градусах. В обоих случаях мы находим концевые углы, добавляя или вычитая один или несколько полных оборотов.

Как сделать

Дан угол больше, чем [latex] \, 2 \ pi, [/ latex], найдите внутренний угол между 0 и [latex] \, 2 \ pi. [/ Latex]

Вычтите [latex] \, 2 \ pi \, [/ latex] из заданного угла.
Если результат все еще больше, чем [latex] \, 2 \ pi, [/ latex], вычтите [latex] \, 2 \ pi \, [/ latex] еще раз, пока результат не окажется между [latex] \, 0 \, [/ латекс] и [латекс] \, 2 \ пи. [/ латекс]
Полученный угол совпадает с исходным углом.

Нахождение концевых углов с помощью радианов

Найдите угол [латекс] \, \ beta \, [/ latex], который совпадает с [latex] \, \ frac {19 \ pi} {4}, [/ latex], где [latex] \, 0 \ le \ бета <2 \ пи.[/ латекс]

Показать решение

При работе в градусах мы нашли концевые углы путем добавления или вычитания 360 градусов, полного поворота. Точно так же в радианах мы можем найти концевые углы, добавляя или вычитая полные обороты [latex] \, 2 \ pi \, [/ latex] радиан:

[латекс] \ begin {array} {ccc} \ hfill \ frac {19 \ pi} {4} -2 \ pi & = & \ frac {19 \ pi} {4} — \ frac {8 \ pi} { 4} \ hfill \\ & = & \ frac {11 \ pi} {4} \ hfill \ end {array} [/ latex]

Угол [латекс] \, \ frac {11 \ pi} {4} \, [/ latex] на одном конце, но не меньше, чем [latex] \, 2 \ pi, [/ latex], поэтому мы вычитаем другое вращение.

[латекс] \ begin {array} {ccc} \ hfill \ frac {11 \ pi} {4} -2 \ pi & = & \ frac {11 \ pi} {4} — \ frac {8 \ pi} { 4} \ hfill \\ & = & \ frac {3 \ pi} {4} \ hfill \ end {array} [/ latex]

Угол [латекс] \, \ frac {3 \ pi} {4} \, [/ latex] совпадает с [латексом] \, \ frac {19 \ pi} {4}, [/ latex], как показано на (Фигура).

Рисунок 20.

Попробуй

Найдите угол измерения [латекс] \, \ theta \, [/ latex], который совпадает с углом измерения [латекс] \, — \ frac {17 \ pi} {6} \, [/ latex] где [латекс] \, 0 \ ле \ тета <2 \ пи.[/ латекс]

Показать решение

[латекс] \, \ frac {7 \ pi} {6} \, [/ латекс]

Определение длины дуги

Напомним, что радианная мера [латекс] \, \ theta \, [/ latex] угла была определена как отношение длины дуги [латекс] \, s \, [/ latex] дуги окружности к радиусу [latex] \, r \, [/ latex] круга, [latex] \, \ theta = \ frac {s} {r}. \, [/ latex] Из этого соотношения мы можем найти длину дуги вдоль круг, заданный под углом.

Длина дуги на окружности

В круге радиусом r показана длина дуги [латекс] \, s \, [/ latex], образуемая углом с размером [латекс] \, \ theta \, [/ latex] в радианах. в (рисунок) —

[латекс] s = r \ theta [/ латекс]

Рисунок 21.

Как сделать

Дан круг радиуса [латекс] \, r, [/ латекс] вычислить длину [латекс] \, s \, [/ латекс] дуги, образованной заданным углом измерения [латекс] \, \ theta . [/ латекс]

При необходимости преобразуйте [латекс] \, \ theta \, [/ latex] в радианы.
Умножьте радиус [латекс] \, r \, \, \ theta: s = r \ theta. [/ Latex]

Определение длины дуги

Предположим, что орбита Меркурия вокруг Солнца представляет собой идеальный круг.Меркурий находится примерно в 36 миллионах миль от Солнца.

За один земной день Меркурий совершает 0,0114 своего полного обращения. Сколько миль он преодолевает за день?
Используйте свой ответ из части (а), чтобы определить радиан движения Меркурия за один земной день.

Показать решение

Начнем с определения окружности орбиты Меркурия.
[латекс] \ begin {array} {ccc} \ hfill C & = & 2 \ pi r \ hfill \\ & = & 2 \ pi \ left (\ text {36 миллионов миль} \ right) \ hfill \\ & \ приблизительно & \ text {226 миллионов миль} \ hfill \ end {array} [/ latex]
Поскольку Меркурий завершает 0.0114 его полного обращения за один земной день, теперь мы можем найти пройденное расстояние.
[латекс] \ left (0,0114 \ right) 226 \ text {миллион миль = 2} \ text {0,58 миллиона миль} [/ latex]
Теперь конвертируем в радианы.
[латекс] \ begin {массив} {ccc} \ hfill \ text {radian} & = & \ frac {\ text {arclength}} {\ text {radius}} \ hfill \\ & = & \ frac {2. \ text {58 миллионов миль}} {36 \ text {миллионов миль}} \ hfill \\ & = & 0,0717 \ hfill \ end {array} [/ latex]

Попробуй

Найдите длину дуги вдоль круга радиусом 10 единиц, ограниченного углом [латекс] \, 215 °.{2}. \, [/ Latex] Если два радиуса образуют угол [латекс] \, \ theta, [/ latex], измеренный в радианах, то [latex] \, \ frac {\ theta} {2 \ pi } \, [/ latex] — это отношение угловой меры к величине полного поворота, а также, следовательно, отношение площади сектора к площади круга. Таким образом, площадь сектора представляет собой долю [latex] \, \ frac {\ theta} {2 \ pi} \, [/ latex], умноженную на всю площадь. (Всегда помните, что эта формула применима, только если [latex] \, \ theta \, [/ latex] выражено в радианах.{2} [/ латекс]

См. (Рисунок).

Рисунок 22. {2} \ hfill \\ & \ приблизительно & 104.{2}. [/ Латекс]

Попробуй

При центральном круговом орошении большая оросительная труба на колесах вращается вокруг центральной точки. У фермера есть центральная система поворота с радиусом 400 метров. Если водные ограничения позволяют ей поливать только 150 тысяч квадратных метров в день, под каким углом она должна установить систему для покрытия? Запишите ответ в радианах с точностью до двух десятичных знаков.

Использование линейной и угловой скорости для описания движения по круговой траектории

Помимо определения площади сектора, мы можем использовать углы для описания скорости движущегося объекта.У объекта, движущегося по круговой траектории, есть два типа скорости. Линейная скорость — это скорость по прямой траектории, которая может определяться расстоянием, по которому она движется (ее перемещением) в заданный интервал времени. Например, если колесо с радиусом 5 дюймов вращается один раз в секунду, точка на краю колеса перемещается на расстояние, равное окружности, или [латекс] \, 10 \ pi \, [/ латекс] дюймов, каждую секунду. . Таким образом, линейная скорость точки составляет [латекс] \, 10 \ пи \, [/ латекс] дюйм / с. Уравнение для линейной скорости выглядит следующим образом, где [латекс] \, v \, [/ латекс] — линейная скорость, [латекс] \, s \, [/ латекс] — смещение, а [латекс] \, t \, [ / латекс] — время.

[латекс] v = \ frac {s} {t} [/ латекс]

Угловая скорость является результатом кругового движения и может быть определена углом, на который точка вращается в заданный интервал времени. Другими словами, угловая скорость — это угловое вращение в единицу времени. Так, например, если шестерня совершает полный оборот каждые 4 секунды, мы можем вычислить ее угловую скорость как [latex] \, \ frac {360 \ text {градусы}} {4 \ text {секунды}} = [/ latex ] 90 градусов в секунду. Угловая скорость может быть выражена, например, в радианах в секунду, оборотах в минуту или градусах в час.Уравнение для угловой скорости выглядит следующим образом, где [латекс] \, \ omega \, [/ latex] (читается как omega) — угловая скорость, [latex] \, \ theta \, [/ latex] — пройденный угол, и [латекс] \, t \, [/ latex] — время.

[латекс] \ omega = \ frac {\ theta} {t} [/ латекс]

Комбинируя определение угловой скорости с уравнением длины дуги, [латекс] \, s = r \ theta, [/ latex], мы можем найти взаимосвязь между угловой и линейной скоростями. Уравнение угловой скорости может быть решено для [latex] \, \ theta, [/ latex], давая [latex] \, \ theta = \ omega t.[/ latex] Подставляя это в уравнение длины дуги, получаем:

[латекс] \ begin {array} {ccc} \ hfill s & = & r \ theta \ hfill \\ & = & r \ omega t \ hfill \ end {array} [/ latex]

Подставляя это в уравнение линейной скорости, получаем:

[латекс] \ begin {array} {ccc} \ hfill v & = & \ frac {s} {t} \ hfill \\ & = & \ frac {r \ omega t} {t} \ hfill \\ & = & r \ omega \ hfill \ end {array} [/ latex]

Угловая и линейная скорость

Когда точка движется по окружности радиуса [латекс] \, r, [/ латекс], ее угловая скорость, [латекс] \, \ omega, [/ latex] — это угловое вращение [латекс] \, \ theta \, [/ латекс] в единицу времени, [латекс] \, т.е.[/ латекс]

[латекс] \ omega = \ frac {\ theta} {t} [/ латекс]

Линейная скорость [latex] \, v, [/ latex] точки может быть найдена как пройденное расстояние, длина дуги [latex] \, s, [/ latex] в единицу времени, [latex] \, t . [/ латекс]

[латекс] v = \ frac {s} {t} [/ латекс]

Когда угловая скорость измеряется в радианах в единицу времени, линейная скорость и угловая скорость связаны уравнением

[латекс] v = r \ omega [/ латекс]

Это уравнение утверждает, что угловая скорость в радианах, [латекс] \, \ omega, [/ latex], представляющая величину вращения, происходящего в единицу времени, может быть умножена на радиус [латекс] \, r \, [ / latex] для расчета общей длины дуги, пройденной за единицу времени, что является определением линейной скорости.

Как сделать

Зная угол поворота и прошедшее время, вычислите угловую скорость.

При необходимости преобразуйте угловую меру в радианы.
Разделите угол в радианах на количество прошедших единиц времени: [latex] \, \ omega = \ frac {\ theta} {t}. [/ Latex]
Результирующая скорость будет в радианах за единицу времени.

Определение угловой скорости

Гидравлическое колесо, показанное на (Рисунок), совершает 1 оборот каждые 5 секунд.Найдите угловую скорость в радианах в секунду.

Рисунок 24.

Показать решение
Колесо совершает 1 оборот или проходит под углом [latex] \, 2 \ pi \, [/ latex] радиан за 5 секунд, поэтому угловая скорость будет [latex] \, \ omega = \ frac {2 \ pi} {5} \ приблизительно 1,257 \, [/ latex] радиан в секунду.
Попробуй
Старая виниловая пластинка проигрывается на проигрывателе, вращающемся по часовой стрелке со скоростью 45 оборотов в минуту. Найдите угловую скорость в радианах в секунду.
Показать решение
[латекс] \ frac {-3 \ pi} {2} \, [/ latex] рад / с
Как сделать
Зная радиус круга, угол поворота и продолжительность прошедшего времени, определите линейную скорость.

При необходимости преобразуйте общее вращение в радианы.
Разделите общее вращение в радианах на прошедшее время, чтобы найти угловую скорость: apply [latex] \, \ omega = \ frac {\ theta} {t}. [/ Latex]
Умножьте угловую скорость на длину радиуса, чтобы найти линейную скорость, выраженную в единицах длины, используемых для радиуса, и единицах времени, используемых для истекшего времени: apply [latex] \, v = r \ omega.[/ латекс]
Поиск линейной скорости
Велосипед имеет колеса диаметром 28 дюймов. Тахометр определяет, что колеса вращаются со скоростью 180 об / мин (оборотов в минуту). Найдите скорость, с которой велосипед движется по дороге.
Показать решение
Здесь у нас есть угловая скорость, и нам нужно найти соответствующую линейную скорость, поскольку линейная скорость внешней стороны шин — это скорость, с которой велосипед движется по дороге.
Начнем с преобразования числа оборотов в минуту в радианы в минуту.Для этого преобразования может быть полезно использовать единицы измерения:
[латекс] 180 \ frac {\ overline {) \ text {rotations}}} {\ text {minute}} \ cdot \ frac {2 \ pi \, \ text {радианы}} {\ overline {) \ text { вращение}}} = 360 \ pi \ frac {\ text {радианы}} {\ text {minute}} [/ latex]
Используя приведенную выше формулу вместе с радиусом колес, мы можем найти линейную скорость:
[латекс] \ begin {array} {ccc} \ hfill v & = & \ left (\ text {14 дюймов} \ right) \ left (360 \ pi \ frac {\ text {радианы}} {\ text {minute} } \ right) \ hfill \\ & = & 5040 \ pi \ frac {\ text {дюймы}} {\ text {minute}} \ hfill \ end {array} [/ latex]
Помните, что радианы — это безразмерная мера, поэтому включать их не обязательно.
Наконец, мы можем захотеть преобразовать эту линейную скорость в более привычное измерение, например мили в час.
[латекс] 5040 \ pi \ frac {\ overline {) \ text {дюймы}}} {\ overline {) \ text {minute}}} \ cdot \ frac {\ text {1} \ overline {) \ text { футов}}} {\ text {12} \ overline {) \ text {дюймы}}} \ cdot \ frac {\ text {1 миля}} {\ text {5280} \ overline {) \ text {ft}}} \ cdot \ frac {\ text {60} \ overline {) \ text {minutes}}} {\ text {1 час}} \ приблизительно 14,99 \ text {миль в час (миль в час)} [/ latex]
Попробуй
Спутник вращается вокруг Земли в 0.{2} [/ латекс] угловая скорость [латекс] \ omega = \ frac {\ theta} {t} [/ латекс] линейная скорость [латекс] v = \ frac {s} {t} [/ латекс] линейная скорость, связанная с угловой скоростью [латекс] v = r \ omega [/ латекс]
Ключевые понятия
Угол образуется из объединения двух лучей, если начальная сторона остается неподвижной, а конечная сторона вращается. Величина поворота определяет меру угла.
Угол находится в стандартном положении, если его вершина находится в начале координат, а его начальная сторона лежит вдоль положительной оси x . Положительный угол измеряется против часовой стрелки от начальной стороны, а отрицательный угол — по часовой стрелке.
Чтобы нарисовать угол в стандартном положении, начертите начальную сторону вдоль положительной оси x , а затем поместите конечную сторону в соответствии с долей полного поворота, которую представляет угол. См. (Рисунок).
Угол может быть измерен не только в градусах, но и в радианах.См. (Рисунок).
Чтобы преобразовать градусы в радианы, используйте пропорцию [latex] \, \ frac {\ theta} {180} = \ frac {{\ theta} _ {R}} {\ pi}. \, [/ Latex] См. (Рисунок) и (Рисунок).
Два угла с одной и той же конечной стороной называются концевыми углами.
Мы можем найти концевые углы, добавляя или вычитая [латекс] \, 360 ° \, [/ латекс] или [латекс] \, 2 \ пи. \, [/ Латекс] См. (Рисунок) и (Рисунок).
Coterminal углы можно найти в радианах так же, как и в градусах.См. (Рисунок).
Длина дуги окружности составляет часть длины окружности всей окружности. См. (Рисунок).
Площадь сектора — это часть площади всего круга. См. (Рисунок).
Объект, движущийся по круговой траектории, имеет как линейную, так и угловую скорость.
Угловая скорость объекта, движущегося по круговой траектории, является мерой угла, на который он поворачивается за единицу времени. См. (Рисунок).
Линейная скорость объекта, движущегося по круговой траектории, — это расстояние, которое он проходит за единицу времени.См. (Рисунок).
Упражнения по разделам
Устный
Начертите угол в стандартном положении. Обозначьте вершину, начальную и конечную стороны.
Показать решение
Объясните, почему существует бесконечное количество углов, которые совпадают с определенным углом.
Укажите, что означает положительный или отрицательный угол, и объясните, как их рисовать.
Показать решение
Направление определяется положительным или отрицательным углом.Положительный угол рисуется против часовой стрелки, а отрицательный угол — по часовой стрелке.
Как соотносится угол в радианах с градусами? Включите в свой абзац объяснение 1 радиан.
Объясните разницу между линейной скоростью и угловой скоростью при описании движения по круговой траектории.
Показать решение
Линейная скорость — это величина, полученная путем вычисления расстояния дуги по сравнению со временем.Угловая скорость — это величина, которая определяется путем вычисления угла дуги по сравнению со временем.
Графический
Для следующих упражнений нарисуйте угол в стандартном положении с заданной мерой.
Показать решение
Показать решение
[латекс] \ frac {2 \ pi} {3} [/ латекс]
Показать решение
[латекс] \ frac {7 \ pi} {4} [/ латекс]
[латекс] \ frac {5 \ pi} {6} [/ латекс]
Показать решение
[латекс] \ frac {\ pi} {2} [/ латекс]
[латекс] — \ frac {\ pi} {10} [/ латекс]
Показать решение
Показать решение
[латекс] 240 ° [/ латекс]
[латекс] \ frac {22 \ pi} {3} [/ латекс]
Показать решение
[латекс] \ frac {4 \ pi} {3} [/ латекс]
[латекс] — \ frac {\ pi} {6} [/ латекс]
[латекс] — \ frac {4 \ pi} {3} [/ латекс]
Показать решение
[латекс] \ frac {2 \ pi} {3} [/ латекс]
Для следующих упражнений см. (Рисунок).{2} [/ латекс]
Алгебраические
Для следующих упражнений преобразуйте углы из радиан в градусы.
[латекс] \ frac {3 \ pi} {4} \, [/ latex] радиан
[латекс] \ frac {\ pi} {9} \, [/ latex] радиан
[латекс] — \ frac {5 \ pi} {4} \, [/ latex] радианы
[латекс] \ frac {\ pi} {3} \, [/ latex] радиан
[латекс] — \ frac {7 \ pi} {3} \, [/ latex] радианы
[латекс] — \ frac {5 \ pi} {12} \, [/ latex] радианы
[латекс] \ frac {11 \ pi} {6} \, [/ latex] радиан
Для следующих упражнений преобразуйте углы из градусов в радианы.
Показать решение
[латекс] \ frac {\ pi} {2} \, [/ latex] радиан
Показать решение
[латекс] -3 \ pi \, [/ latex] радиан
Показать решение
[латекс] \ пи \, [/ латекс] радиан
Показать решение
[латекс] \ frac {5 \ pi} {6} [/ latex] радиан
Для следующих упражнений используйте данную информацию, чтобы найти длину дуги окружности. Округлить до двух десятичных знаков.
Найдите длину дуги круга радиусом 12 дюймов, ограниченного центральным углом [латекс] \, \ frac {\ pi} {4}.\, [/ latex] радианы.
Найдите длину дуги окружности радиусом 5,02 мили, образуемой центральным углом [latex] \, \ frac {\ pi} {3}. [/ Latex]
Показать решение
[латекс] \ frac {5.02 \ pi} {3} \ приблизительно 5,26 \, [/ латекс] миль
Найдите длину дуги окружности диаметром 14 метров, образуемой центральным углом [latex] \, \ frac {5 \ pi} {6}. [/ Latex]
Найдите длину дуги круга радиусом 10 сантиметров, ограниченного центральным углом [латекса] \, 50 °.[/ латекс]
Показать решение
[латекс] \ frac {25 \ pi} {9} \ приблизительно 8,73 \, [/ латекс] сантиметра
Найдите длину дуги окружности радиусом 5 дюймов, ограниченной центральным углом [латекс] \, 220 °. [/ Латекс]
Найдите длину дуги окружности диаметром 12 метров, образуемой центральным углом [латекс] \, 63 °. [/ Латекс]
Показать решение
[латекс] \ frac {21 \ pi} {10} \ приблизительно 6,60 \, [/ латекс] метров
Для следующих упражнений используйте данную информацию, чтобы найти площадь сектора.Округлить до четырех знаков после запятой.
Сектор круга имеет центральный угол [латекс] \, 45 ° \, [/ латекс] и радиус 6 см.
Сектор круга имеет центральный угол [латекс] \, 30 ° \, [/ латекс] и радиус 20 см.
Сектор круга диаметром 10 футов и углом [latex] \, \ frac {\ pi} {2} \, [/ latex] радиан.
Сектор круга радиусом 0,7 дюйма и углом [латекс] \, \ пи \, [/ латекс] радиан.
Для следующих упражнений найдите угол между [латексом] \, 0 ° \, [/ латексом] и [латексом] \, 360 ° \, [/ латексом], лежащий на одном конце с заданным углом.
Для следующих упражнений найдите угол между 0 и [latex] \, 2 \ pi \, [/ latex] в радианах, который является на конце заданным углом.
[латекс] — \ frac {\ pi} {9} [/ латекс]
[латекс] \ frac {10 \ pi} {3} [/ латекс]
Показать решение
[латекс] \ frac {4 \ pi} {3} [/ латекс]
[латекс] \ frac {13 \ pi} {6} [/ латекс]
[латекс] \ frac {44 \ pi} {9} [/ латекс]
Показать решение
[латекс] \ frac {8 \ pi} {9} [/ латекс]
Реальные приложения
Грузовик с колесами диаметром 32 дюйма движется со скоростью 60 миль / ч.Найдите угловую скорость колес в рад / мин. Сколько оборотов в минуту делают колеса?
Велосипед с колесами диаметром 24 дюйма движется со скоростью 15 миль / ч. Найдите угловую скорость колес в рад / мин. Сколько оборотов в минуту делают колеса?
Показать решение
[латекс] 1320 \, [/ латекс] рад / мин [латекс] \, 210.085 \, [/ латекс] об / мин
Колесо радиусом 8 дюймов вращается со скоростью 15 ° / с. Что такое линейная скорость [latex] \, v, [/ latex], угловая скорость в об / мин и угловая скорость в рад / с?
Колесо радиусом [латекс] \, 14 \, [/ латекс] дюймов вращается [латекс] \, 0.5 \, [/ латекс] рад / с. Что такое линейная скорость [latex] \, v, [/ latex], угловая скорость в об / мин и угловая скорость в град / с?
Показать решение
[латекс] 7 \, [/ латекс] дюйм / с, 4,77 об / мин, [латекс] \, 28,65 \, [/ латекс] град / с
CD имеет диаметр 120 миллиметров. При воспроизведении звука угловая скорость изменяется, чтобы поддерживать постоянную линейную скорость в том месте, где читается диск. При чтении по внешнему краю диска угловая скорость составляет около 200 об / мин (оборотов в минуту). Найдите линейную скорость.
При записи на записываемый привод CD-R угловая скорость компакт-диска часто намного выше, чем при воспроизведении звука, но угловая скорость по-прежнему изменяется, чтобы поддерживать постоянную линейную скорость в том месте, где записывается диск. При записи по внешнему краю диска угловая скорость одного привода составляет около 4800 об / мин (оборотов в минуту). Найдите линейную скорость, если диаметр компакт-диска составляет 120 миллиметров.
Показать решение
[латекс] 1 809 557,37 \ text {мм / мин} = 30,16 \ text {м / с} [/ латекс]
Человек стоит на экваторе Земли (радиус 3960 миль).Каковы его линейная и угловая скорости?
Найдите расстояние по дуге на поверхности Земли, которая образует центральный угол 5 минут
[латекс] \ left (1 \ text {minute} = \ frac {1} {60} \ text {степень} \ right) [/ latex]. Радиус Земли составляет 3960 миль.
Показать решение
[латекс] 5,76 \, [/ латекс] миль
Найдите расстояние по дуге на поверхности Земли, которая образует центральный угол 7 минут
[латекс] \ left (1 \ text {minute} = \ frac {1} {60} \ text {степень} \ right) [/ latex].Радиус Земли составляет [латекс] \, 3960 \, [/ латекс] миль.
Рассмотрим часы с часовой и минутной стрелками. Какова мера угла, под которым минутная стрелка показывает в [латексных] \, 20 \, [/ латексных] минутах?
Расширения
Два города имеют одинаковую долготу. Широта города A составляет 9 градусов северной широты, а широта города B — 30 градусов северной широты. Предположим, что радиус Земли составляет 3960 миль. Найдите расстояние между двумя городами.
Город расположен на 40 градусе северной широты.Предположим, что радиус Земли составляет 3960 миль, а Земля вращается каждые 24 часа. Найдите линейную скорость человека, проживающего в этом городе.
Город расположен на 75 градусе северной широты. Предположим, что радиус Земли составляет 3960 миль, а Земля вращается каждые 24 часа. Найдите линейную скорость человека, проживающего в этом городе.
Найдите линейную скорость Луны, если среднее расстояние между Землей и Луной составляет 239 000 миль, предполагая, что орбита Луны круговая и требует около 28 дней.Экспресс-ответ в милях в час.
Велосипед имеет колеса диаметром 28 дюймов. Тахометр определяет, что колеса вращаются со скоростью 180 об / мин (оборотов в минуту). Найдите скорость, с которой велосипед движется по дороге.
Автомобиль проезжает 3 мили. Его шины совершают 2640 оборотов. Какой радиус шины в дюймах?
Колесо трактора имеет диаметр 24 дюйма. Сколько оборотов делает колесо, если трактор проезжает 4 мили?
.
No related posts.