Уравнения перпендикулярных прямых: Перпендикулярные прямые, условие перпендикулярности прямых

Содержание

Перпендикулярные прямые, условие перпендикулярности прямых

В статье рассматривается вопрос о перпендикулярных прямых на плоскости и трехмерном пространстве. Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.

Перпендикулярные прямые – основные сведения

Угол между пересекающимися прямыми в пространстве может быть прямым. Тогда говорят, что данные прямые перпендикулярные. Когда угол между скрещивающимися прямыми прямой, тогда прямые также являются перпендикулярными. Отсюда следует, что перпендикулярные прямые на плоскости пересекающиеся, а перпендикулярные прямые пространства могут быть пересекающимися и скрещивающимися.

То есть понятия «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» считаются равноправными.

Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение.

Определение 1

Две прямые называют перпендикулярными, если угол при их пересечении дает 90 градусов.

Перпендикулярность обозначается «⊥», а запись принимает вид a⊥b, что значит, прямая a перпендикулярна прямой b.

Например, перпендикулярными прямыми на плоскости могут быть стороны квадрата с общей вершиной. В трехмерном пространстве прямые Ox, Oz, Oy перпендикулярны попарно: Ox и Oz, Ox и Oy, Oy и Oz.

Перпендикулярность прямых – условия перпендикулярности

Свойства перпендикулярности необходимо знать, так как большинство задач сводится к его проверке для последующего решения. Бывают случаи, когда о перпендикулярности идет речь еще в условии задания или когда необходимо пользоваться доказательством. Для того, чтобы доказать перпендикулярность достаточно, чтобы угол между прямыми был прямым.

Для того, чтобы определить их перпендикулярность при известных уравнениях прямоугольной системы координат, необходимо применить необходимое и достаточное условие перпендикулярности прямых.

Рассмотрим формулировку.

Теорема 1

Для того, чтобы прямые a и b были перпендикулярными, необходимо и достаточно, чтобы направляющий вектор прямой обладал перпендикулярностью относительно направляющего вектора заданной прямой b.

Само доказательство основывается на определении направляющего вектора прямой и на определении перпендикулярности прямых.

Доказательство 1

Пусть введена прямоугольная декартова система координат Оху с заданными уравнениями прямой на плоскости, которые определяют прямые a и b. Направляющие векторы прямых a и b обозначим a→ и b→. Из уравнения прямых a и b необходимым и достаточным условием является перпендикулярность векторов a→ и b→. Это возможно только при скалярном произведении векторов a→=(ax, ay) и b→=(bx, by) равном нулю, а запись имеет вид a→, b→=ax·bx+ay·by=0. Получим, что необходимым и достаточным условием перпендикулярности прямых a и b, находящихся в прямоугольной системе координат Оху на плоскости, является a→, b→=ax·bx+ay·by=0, где a→=(ax, ay) и b→=bx, by — это направляющие векторы прямых a и b.

Условие применимо, когда необходимо найти координаты направляющих векторов или при наличии канонических или параметрических уравнений прямых на плоскости заданных прямых a и b.

Пример 1

Заданы три точки A (8, 6), B(6, 3), C(2, 10) в прямоугольной системе координат Оху. Определить, прямые АВ и АС перпендикулярны или нет.

Решение

Прямые АВ и АС имеют направляющие векторы AB→ и AC→ соответственно. Для начала вычислим AB→=(-2, -3), AC→=(-6, 4). Получим, что векторы AB→ и AC→ перпендикулярны из свойства о скалярном произведении векторов, равном нулю.

AB→, AC→=(-2)·(-6)+(-3)·4=0

Очевидно, что необходимое и достаточное условие выполнимо, значит, АВ и АС перпендикулярны.

Ответ: прямые перпендикулярны.

Пример 2

Определить, заданные прямые x-12=y-73 и x=1+λy=2-2·λ перпендикулярны или нет.

Решение

a→=(2, 3) является направляющим вектором заданной прямой x-12=y-73,

b→=(1, -2) является направляющим вектором прямой x=1+λy=2-2·λ.

Перейдем к вычислению скалярного произведения векторов a→ и b→. Выражение будет записано:

a→,b→=2·1+3·-2=2-6≠0

Результат произведения не равен нулю, можно сделать вывод, что векторы не перпендикулярны, значит и прямые также не перпендикулярны.

Ответ: прямые не перпендикулярны.

Необходимое и достаточное условие перпендикулярности прямых a и b применяется для трехмерного пространства, записывается в виде a→, b→=ax·bx+ay·by+az·bz=0, где a→=(ax, ay, az) и b→=(bx, by, bz) являются направляющими векторами прямых a и b.

Пример 3

Проверить перпендикулярность прямых в прямоугольной системе координат трехмерного пространства, заданные уравнениями x2=y-1=z+10 и x=λy=1+2·λz=4·λ

Решение

Знаменатели из канонических уравнений прямых считаются координатами направляющего вектора прямой. Координаты направляющего вектора из параметрического уравнения – коэффициенты. Отсюда следует, что a→=(2, -1, 0) и b→=(1, 2, 4) являются направляющими векторами заданных прямых. Для выявления их перпендикулярности найдем скалярное произведение векторов.

Выражение примет вид a→,b→=2·1+(-1)·2+0·4=0.

Векторы перпендикулярны, так как произведение равно нулю. Необходимое и достаточное условие выполнено, значит прямые также перпендикулярны.

Ответ:

прямые перпендикулярны.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Проверка перпендикулярности может проводится, исходя из других необходимых и достаточных условий перпендикулярности.

Теорема 2

Прямые a и b на плоскости считаются перпендикулярными при перпендикулярности нормального вектора прямой a с вектором b, это и есть необходимое и достаточное условие.

Доказательство 2

Данное условие применимо, когда уравнения прямых дают быстрое нахождение координат нормальных векторов заданных прямых. То есть при наличии общего уравнения прямой вида Ax+By+C=0, уравнения прямой в отрезках вида xa+yb=1, уравнения прямой с угловым коэффициентом вида y=kx+b координаты векторов возможно найти.

Пример 4

Выяснить, перпендикулярны ли прямые 3x-y+2=0 и x32+y12=1.

Решение

Исходя их уравнений, необходимо найти координаты нормальных векторов прямых. Получим, что nα→=(3, -1) — это нормальный вектор для прямой 3x-y+2=0.

Упростим уравнение x32+y12=1 до вида 23x+2y-1=0. Теперь четко видны координаты нормального вектора, которые запишем в такой форме nb→=23, 2.

Векторы na→=(3, -1) и nb→=23, 2 будут перпендикулярными, так как их скалярное произведение даст в итоге значение равное 0. Получим na→, nb→=3·23+(-1)·2=0.

Необходимое и достаточное условие было выполнено.

Ответ: прямые перпендикулярны.

Когда прямая a на плоскости определена при помощи уравнения с угловым коэффициентом y=k1x+b1, а прямая b — y=k2x+b2, отсюда следует, что нормальные векторы будут иметь координаты (k1, -1) и (k2, -1). Само условие перпендикулярности сводится к k1·k2+(-1)·(-1)=0⇔k1·k2=-1.

Пример 5

Выяснить, перпендикулярны ли прямые y=-37x и y=73x-12.

Решение

Прямая y=-37x имеет угловой коэффициент, равный -37, а прямая y=73x-12- 73.

Произведение угловых коэффициентов дает значение -1, -37·73=-1, то есть прямые являются перпендикулярными.

Ответ: заданные прямые перпендикулярны.

Имеется еще одно условие, используемое для определения перпендикулярности прямых на плоскости.

Теорема 3

Для перпендикулярности прямых a и b на плоскости необходимым и достаточным условием является коллинеарность направляющего вектора одной из прямых с нормальным вектором второй прямой.

Доказательство 3

Условие применимо, когда есть возможность нахождения направляющего вектора одной прямой и координат нормального вектора другой. Иначе говоря, одна прямая задается каноническим или параметрическим уравнением, а другая общим уравнением прямой, уравнением в отрезках или уравнением прямой с угловым коэффициентом.

Пример 6

Определить, являются ли заданные прямые x-y-1=0 и x0=y-42 перпендикулярными.

Решение

Получаем, что нормальный вектор прямой x-y-1=0 имеет координаты na→=(1, -1), а b→=(0, 2) — направляющий вектор прямой x0=y-42.

Отсюда видно, что векторы na→=(1, -1) и b→=(0, 2) не коллинеарны, потому что условие коллинеарности не выполняется. Не существует такого числа t, чтобы выполнялось равенство na→=t·b→. Отсюда вывод, что прямые не являются перпендикулярными.

Ответ: прямые не перпендикулярны.

Автор: Ирина

Преподаватель математики и информатики.

Кафедра бизнес-информатики Российского университета транспорта

Уравнение двух перпендикулярных прямых

Условием перпендикулярности двух прямых, заданных уравнениями

т.е. две прямые перпендикулярны, если произведение их угловых коэффициентов равно -1 , и не перпендикулярны, если оно не равно -1 .

перпендикулярны, так как

не перпендикулярны, так как

Если уравнение одной из двух прямых не содержит ординаты (т.е. прямая праллельная оси OY), то эта прямая перпендикулярна к другой прямой при условии, что уравнение последней не содержит абсциссы (тогда вторая прямая параллельная оси абсцисс). В противном случае прямые не перпендикулярны. Например прямые х=5 и у=2х не перпендикулярны.

Перпендикулярные прямые – основные сведения

То есть понятия «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» считаются равноправными. Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение.

Две прямые называют перпендикулярными, если угол при их пересечении дает 90 градусов.

Перпендикулярность обозначается « ⊥ », а запись принимает вид a ⊥ b , что значит, прямая a перпендикулярна прямой b .

Например, перпендикулярными прямыми на плоскости могут быть стороны квадрата с общей вершиной. В трехмерном пространстве прямые O x , O z , O y перпендикулярны попарно: O x и O z , O x и O y , O y и O z .

Перпендикулярность прямых – условия перпендикулярности

Пусть введена прямоугольная декартова система координат О х у с заданными уравнениями прямой на плоскости, которые определяют прямые a и b . Направляющие векторы прямых a и b обозначим a → и b → . Из уравнения прямых a и b необходимым и достаточным условием является перпендикулярность векторов a → и b → . Это возможно только при скалярном произведении векторов a → = ( a x , a y ) и b → = ( b x , b y ) равном нулю, а запись имеет вид a → , b → = a x · b x + a y · b y = 0 . Получим, что необходимым и достаточным условием перпендикулярности прямых a и b , находящихся в прямоугольной системе координат О х у на плоскости, является a → , b → = a x · b x + a y · b y = 0 , где a → = ( a x , a y ) и b → = b x , b y — это направляющие векторы прямых a и b .

Заданы три точки A ( 8 , 6 ) , B ( 6 , 3 ) , C ( 2 , 10 ) в прямоугольной системе координат О х у . Определить, прямые А В и А С перпендикулярны или нет.

Прямые А В и А С имеют направляющие векторы A B → и A C → соответственно. Для начала вычислим A B → = ( — 2 , — 3 ) , A C → = ( — 6 , 4 ) . Получим, что векторы A B → и A C → перпендикулярны из свойства о скалярном произведении векторов, равном нулю.

A B → , A C → = ( — 2 ) · ( — 6 ) + ( — 3 ) · 4 = 0

Очевидно, что необходимое и достаточное условие выполнимо, значит, А В и А С перпендикулярны.

Ответ: прямые перпендикулярны.

Определить, заданные прямые x — 1 2 = y — 7 3 и x = 1 + λ y = 2 — 2 · λ перпендикулярны или нет.

Решение

a → = ( 2 , 3 ) является направляющим вектором заданной прямой x — 1 2 = y — 7 3 ,

b → = ( 1 , — 2 ) является направляющим вектором прямой x = 1 + λ y = 2 — 2 · λ .

Перейдем к вычислению скалярного произведения векторов a → и b → . Выражение будет записано:

a → , b → = 2 · 1 + 3 · — 2 = 2 — 6 ≠ 0

Ответ: прямые не перпендикулярны.

Необходимое и достаточное условие перпендикулярности прямых a и b применяется для трехмерного пространства, записывается в виде a → , b → = a x · b x + a y · b y + a z · b z = 0 , где a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) являются направляющими векторами прямых a и b .

Проверить перпендикулярность прямых в прямоугольной системе координат трехмерного пространства, заданные уравнениями x 2 = y — 1 = z + 1 0 и x = λ y = 1 + 2 · λ z = 4 · λ

Знаменатели из канонических уравнений прямых считаются координатами направляющего вектора прямой. Координаты направляющего вектора из параметрического уравнения – коэффициенты. Отсюда следует, что a → = ( 2 , — 1 , 0 ) и b → = ( 1 , 2 , 4 ) являются направляющими векторами заданных прямых. Для выявления их перпендикулярности найдем скалярное произведение векторов.

Выражение примет вид a → , b → = 2 · 1 + ( — 1 ) · 2 + 0 · 4 = 0 .

Ответ: прямые перпендикулярны.

Прямые a и b на плоскости считаются перпендикулярными при перпендикулярности нормального вектора прямой a с вектором b , это и есть необходимое и достаточное условие.

Данное условие применимо, когда уравнения прямых дают быстрое нахождение координат нормальных векторов заданных прямых. То есть при наличии общего уравнения прямой вида A x + B y + C = 0 , уравнения прямой в отрезках вида x a + y b = 1 , уравнения прямой с угловым коэффициентом вида y = k x + b координаты векторов возможно найти.

Выяснить, перпендикулярны ли прямые 3 x — y + 2 = 0 и x 3 2 + y 1 2 = 1 .

Исходя их уравнений, необходимо найти координаты нормальных векторов прямых. Получим, что n α → = ( 3 , — 1 ) — это нормальный вектор для прямой 3 x — y + 2 = 0 .

Упростим уравнение x 3 2 + y 1 2 = 1 до вида 2 3 x + 2 y — 1 = 0 . Теперь четко видны координаты нормального вектора, которые запишем в такой форме n b → = 2 3 , 2 .

Векторы n a → = ( 3 , — 1 ) и n b → = 2 3 , 2 будут перпендикулярными, так как их скалярное произведение даст в итоге значение равное 0 . Получим n a → , n b → = 3 · 2 3 + ( — 1 ) · 2 = 0 .

Необходимое и достаточное условие было выполнено.

Ответ: прямые перпендикулярны.

Когда прямая a на плоскости определена при помощи уравнения с угловым коэффициентом y = k 1 x + b 1 , а прямая b — y = k 2 x + b 2 , отсюда следует, что нормальные векторы будут иметь координаты ( k 1 , — 1 ) и ( k 2 , — 1 ) . Само условие перпендикулярности сводится к k 1 · k 2 + ( — 1 ) · ( — 1 ) = 0 ⇔ k 1 · k 2 = — 1 .

Выяснить, перпендикулярны ли прямые y = — 3 7 x и y = 7 3 x — 1 2 .

Прямая y = — 3 7 x имеет угловой коэффициент, равный — 3 7 , а прямая y = 7 3 x — 1 2 — 7 3 .

Произведение угловых коэффициентов дает значение — 1 , — 3 7 · 7 3 = — 1 , то есть прямые являются перпендикулярными.

Ответ: заданные прямые перпендикулярны.

Имеется еще одно условие, используемое для определения перпендикулярности прямых на плоскости.

Определить, являются ли заданные прямые x — y — 1 = 0 и x 0 = y — 4 2 перпендикулярными.

Получаем, что нормальный вектор прямой x — y — 1 = 0 имеет координаты n a → = ( 1 , — 1 ) , а b → = ( 0 , 2 ) — направляющий вектор прямой x 0 = y — 4 2 .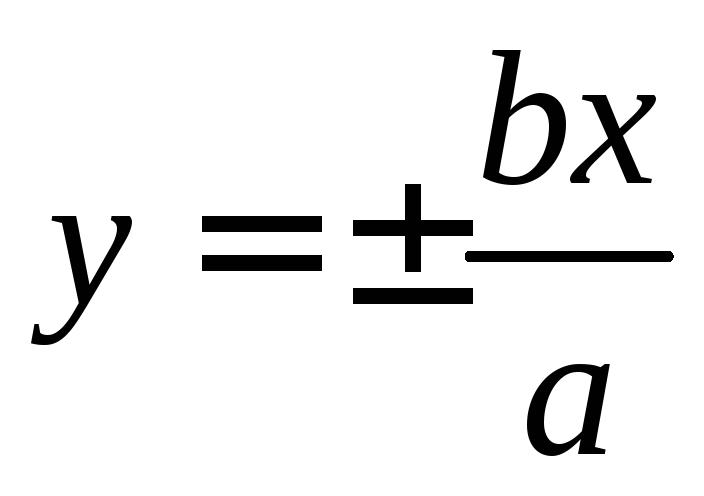

Отсюда видно, что векторы n a → = ( 1 , — 1 ) и b → = ( 0 , 2 ) не коллинеарны, потому что условие коллинеарности не выполняется. Не существует такого числа t , чтобы выполнялось равенство n a → = t · b → . Отсюда вывод, что прямые не являются перпендикулярными.

Уравнение перпендикуляра к двум прямым — это уравнение прямой, перпендикулярной к каждой из прямых, задаётся системой равенств нулю смешанных произведений соответствующего вектора-разности радиусов-векторов точек, направляющего вектора и векторного произведения направляющих векторов.

Содержание

[править] Обозначения

[math]ar r=(x,y,z)[/math] — радиус-вектор точки перпендикуляра;

[math]ar r_1=(x_1,y_1,z_1)[/math] — радиус-вектор точки первой прямой;

[math]ar r_2=(x_2,y_2,z_2)[/math] — радиус-вектор точки второй прямой;

[math]ar s_1=(l_1,m_1,n_1)[/math] — направляющий вектор первой прямой;

[math]ar s_2=(l_2,m_2,n_2)[/math] — направляющий вектор второй прямой;

[править] Формулы:

Векторная форма:

Заметим, что формулы верны только для скрещивающихся прямых.

[править] Пример

Даны две прямые:

Найти уравнение перпендикуляра к этим прямым.

[править] Уравнения прямой:

уравнение прямой, проходящей через две точки;
уравнение прямой, равноудалённой от трёх точек;
уравнение прямой, проходящей через точку в направлении вектора;
уравнение прямой, проходящей через точку параллельно прямой;
уравнение прямой, проходящей через точку перпендикулярно плоскости;
уравнение прямой, образованной пересечением двух плоскостей;
уравнение проекции прямой на плоскость;
уравнение перпендикуляра из точки к прямой в трёхмерном пространстве;
уравнение перпендикуляра из точки к плоскости;
уравнение перпендикуляра к двум прямым.

[править] Ссылки

Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
Выгодский М. Я. Справочник по высшей математике. М.: Наука, 1964, стр. 192.
Участник:Logic-samara

Персональные инструменты

Пространства имён

Варианты

Просмотры

Действия

Поиск

Инструменты

Последнее изменение этой страницы: 23:36, 18 октября 2016.
К этой странице обращались 6355 раз.

Текст страницы доступен по условиям лицензии GNU Free Documentation License. Материалы могут быть скопированы при условии указания активной ссылки на источник копирования в теле статьи (на той же странице). В отдельных случаях могут действовать условия лицензии Creative Commons Attribution-ShareAlike (CC BY-SA 3.0), информацию об этом можно просмотреть на странице обсуждения или в истории правок. В частности, условия лицензии CC BY-SA 3.0 действуют в отношении статей, перенесенных из Википедии (указание на факт переноса всегда есть в истории правок статьи).

Политика конфиденциальности
Описание Циклопедии
Отказ от ответственности

Перпендикулярность прямых — условия перпендикулярности.

— КиберПедия

Перпендикулярные прямые фигурируют чуть ли не в каждой геометрической задаче. Иногда перпендикулярность прямых известна из условия, а в других случаях перпендикулярность прямых приходится доказывать. Для доказательства перпендикулярности двух прямых достаточно показать, используя любые геометрические методы, что угол между прямыми равен девяноста градусам.

А как ответить на вопрос «перпендикулярны ли прямые», если известны уравнения, задающие эти прямые в прямоугольной системе координат на плоскости или в трехмерном пространстве?

Для этого следует воспользоваться необходимым и достаточным условием перпендикулярности двух прямых. Сформулируем его в виде теоремы.

Теорема.

Для перпендикулярности прямых a и b необходимо и достаточно, чтобы направляющий вектор прямой a был перпендикулярен направляющему вектору прямой b.

Доказательство этого условия перпендикулярности прямых основано на определении направляющего вектора прямой и на определении перпендикулярных прямых.

Добавим конкретики.

Пусть на плоскости введена прямоугольная декартова система координат Oxy и заданыуравнения прямой на плоскости некоторого вида, определяющие прямые a и b. Обозначим направляющие векторы прямых а и b как и соответственно. По уравнениям прямых a и bможно определить координаты направляющих векторов этих прямых – получаем и . Тогда, для перпендикулярности прямых a и b необходимо и достаточно, чтобы выполнялось условие перпендикулярности векторов и , то есть, чтобы скалярное произведение векторов и равнялось нулю: .

Итак, необходимое и достаточное условие перпендикулярности прямых a и b в прямоугольной системе координат Oxy на плоскости имеет вид , где и — направляющие векторы прямых a и b соответственно.

Это условие удобно использовать, когда легко находятся координаты направляющих векторов прямых, а также когда прямым a и b соответствуют канонические уравнения прямой на плоскости или параметрические уравнения прямой на плоскости.

Пример.

В прямоугольной системе координат Oxy заданы три точки . Перпендикулярны ли прямые АВ и АС?

Решение.

Векторы и являются направляющими векторами прямых АВ и АС. Обратившись к статье координаты вектора по координатам точек его начала и конца, вычисляем . Векторы и перпендикулярны, так как . Таким образом, выполняется необходимое и достаточное условие перпендикулярности прямых АВ и АС. Следовательно, прямые АВи АС перпендикулярны.

Ответ:

да, прямые перпендикулярны.

Пример.

Являются ли прямые и перпендикулярными?

Решение.

— направляющий вектор прямой , а — направляющий вектор прямой . Вычислим скалярное произведение векторов и : . Оно отлично от нуля, следовательно, направляющие векторы прямых не перпендикулярны. То есть, не выполняется условие перпендикулярности прямых, поэтому, исходные прямые не перпендикулярны.

Ответ:

нет, прямые не перпендикулярны.

Аналогично, необходимое и достаточное условие перпендикулярности прямых a и b в прямоугольной системе координат Oxyz в трехмерном пространстве имеет вид , где и — направляющие векторы прямых a и b соответственно.

Пример.

Перпендикулярны ли прямые, заданные в прямоугольной системе координат Oxyz в трехмерном пространстве уравнениями и ?

Решение.

Числа, стоящие в знаменателях канонических уравнений прямой в пространстве, являются соответствующими координатами направляющего вектора прямой. А координатами направляющего вектора прямой, которая задана параметрическими уравнениями прямой в пространстве, являются коэффициенты при параметре. Таким образом, и — направляющие векторы заданных прямых. Выясним, перпендикулярны ли они: . Так как скалярное произведение равно нулю, то эти векторы перпендикулярны. Значит, выполняется условие перпендикулярности заданных прямых.

Ответ:

прямые перпендикулярны.

Для проверки перпендикулярности двух прямых на плоскости существуют другие необходимые и достаточные условия перпендикулярности.

Теорема.

Для перпендикулярности прямых a и b на плоскости необходимо и достаточно, чтобы нормальный вектор прямой a был перпендикулярен нормальному вектору прямой b.

Озвученное условие перпендикулярности прямых удобно использовать, если по заданным уравнениям прямых легко находятся координаты нормальных векторов прямых. Этому утверждению отвечает общее уравнение прямой вида , уравнение прямой в отрезках и уравнение прямой с угловым коэффициентом .

Пример.

Убедитесь, что прямые и перпендикулярны.

Решение.

По заданным уравнениям прямых легко найти координаты нормальных векторов этих прямых. – нормальный вектор прямой . Перепишем уравнение в виде , откуда видны координаты нормального вектора этой прямой: .

Векторы и перпендикулярны, так как их скалярное произведение равно нулю: . Таким образом, выполняется необходимое и достаточное условие перпендикулярности заданных прямых, то есть, они действительно перпендикулярны.

В частности, если прямую a на плоскости определяет уравнение прямой с угловым коэффициентом вида , а прямую b – вида , то нормальные векторы этих прямых имеют координаты и соответственно, а условие перпендикулярности этих прямых сводится к следующему соотношению между угловыми коэффициентами .

Пример.

Перпендикулярны ли прямые и ?

Решение.

Угловой коэффициент прямой равен , а угловой коэффициент прямой равен . Произведение угловых коэффициентов равно минус единице , следовательно, прямые перпендикулярны.

Ответ:

заданные прямые перпендикулярны.

Можно озвучить еще одно условие перпендикулярности прямых на плоскости.

Теорема.

Для перпендикулярности прямых a и b на плоскости необходимо и достаточно, чтобы направляющий вектор одной прямой и нормальный вектор второй прямой были коллинеарны.

Этим условием, очевидно, удобно пользоваться, когда легко находятся координаты направляющего вектора одной прямой и координаты нормального вектора второй прямой, то есть, когда одна прямая задана каноническим уравнением или параметрическими уравнениями прямой на плоскости, а вторая – или общим уравнением прямой, или уравнением прямой в отрезках, или уравнением прямой с угловым коэффициентом.

Пример.

Являются ли прямые и перпендикулярными?

Решение.

Очевидно, — нормальный вектор прямой , а — направляющий вектор прямой . Векторы и не коллинеарны, так как для них не выполняется условие коллинеарности двух векторов(не существует такого действительного числа t, при котором ). Следовательно, заданные прямые не перпендикулярны.

Ответ:

прямые не перпендикулярны.

21. Расстояние от точки до прямой.

Расстояние от точки до прямой определяется через расстояние от точки до точки. Покажем как это делается.

Пусть на плоскости или в трехмерном пространстве задана прямая a и точка M₁, не лежащая на прямой a. Проведем через точку M₁ прямую b, перпендикулярную прямой a. Обозначим точку пересечения прямых a и b как H₁. Отрезок M₁H₁ называется перпендикуляром, проведенным из точки M₁ к прямой a.

Определение.

Расстоянием от точки M₁ до прямой a называют расстояние между точками M₁ и H₁.

Однако чаще встречается определение расстояния от точки до прямой, в котором фигурирует длина перпендикуляра.

Определение.

Расстояние от точки до прямой – это длина перпендикуляра, проведенного из данной точки к данной прямой.

Это определение эквивалентно первому определению расстояния от точки до прямой.

Обратите внимание на то, что расстояние от точки до прямой – это наименьшее из расстояний от этой точки до точек заданной прямой. Покажем это.

Возьмем на прямой a точку Q, не совпадающую с точкой M₁. Отрезок M₁Q называютнаклонной, проведенной из точки M₁ к прямой a. Нам нужно показать, что перпендикуляр, проведенный из точки M₁ к прямой a, меньше любой наклонной, проведенной из точки M₁ к прямой a. Это действительно так: треугольник M₁QH₁ прямоугольный с гипотенузой M₁Q, а длина гипотенузы всегда больше длины любого из катетов, следовательно, .

22. Плоскость в пространстве R3. Уравнение плоскости.

Плоскость в декартовой прямоугольной системе координат может быть задана уравнением, которое называется общим уравнениемплоскости.

Определение.Вектор перпендикулярен плоскости и называется ее нормальным вектором.

Если в прямоугольной системе координат известны координаты трех точек , не лежащих на одной прямой, то уравнение плоскости записывается в виде: .

Вычислив данный определитель, получим общее уравнение плоскости.

Пример.Написать уравнение плоскости, проходящей через точки .

Решение:

Уравнение плоскости: .

23. Исследование общего уравнения плоскости.

О п р е д е л е н и е 1. Общим уравнением плоскости называется линейное уравнение первой степени относительно трех переменных: х, у и z, т. е. уравнение вида Ax + By + Cz + D = 0. (3.21) Коэффициенты при х, у и z являются координатами вектора, который перпендикулярен плоскости (рис. 57).

Рис. 57

О п р е д е л е н и е 2. Всякий вектор, перпендикулярный плоскости, называется нормальным вектором этой плоскости.

Если известна фиксированная точка M₀ (x₀, y₀, z₀), лежащая в данной плоскости, и вектор , перпендикулярный данной плоскости, то уравнение плоскости, проходящей через точкуM₀ (x₀, y₀, z₀), перпендикулярно вектору , имеет вид

A(x-x₀)+ B(y-y₀) + C(z-z₀)= 0. (3.22)

Покажем, что уравнение (3.22) является общим уравнением плоскости (3.21). Для этого раскроем скобки и соберем в скобки свободный член:

. Ax + By+ Cz + (-Ax₀ — By -Cz₀)= 0

ОбозначивD = -Ax₀ — By -Cz₀ , получим уравнение Ax + By + Cz + D = 0.

Задача 1. Составить уравнение плоскости, проходящей через точку А, перпендикулярно вектору , если A(4, -3, 1), B(1, 2, 3).

Решение. Найдем нормальный вектор плоскости :

Для нахождения уравнения плоскости используем уравнение (3.22):

Ответ: -3x + 5y + 2z + 25 = 0.

Задача 2. Составить уравнение плоскости, проходящей через точку M₀ (-1, 2, -1), перпендикулярно оси OZ.

Решение. В качестве нормального вектора искомой плоскости можно взять любой вектор, лежащий на оси OZ, например, , тогда уравнение плоскости

Ответ: z + 1 = 0.

24. Расстояние от точки до плоскости.

Расстояние от точки до плоскости определяется через расстояние от точки до точки, одна из которых заданная точка, а другая – проекция заданной точки на заданную плоскость.

Пусть в трехмерном пространстве задана точка М₁ и плоскость . Проведем через точку М₁прямую a, перпендикулярную к плоскости . Обозначим точку пересечения прямой a и плоскости как H₁. Отрезок M₁H₁ называют перпендикуляром, опущенным из точки М₁ на плоскость , а точку H₁ – основанием перпендикуляра.

Определение.

Расстояние от точки до плоскости – это расстояние от данной точки до основания перпендикуляра, проведенного из заданной точки к заданной плоскости.

Чаще встречается определение расстояние от точки до плоскости в следующем виде.

Определение.

Расстояние от точки до плоскости – это длина перпендикуляра, опущенного из заданной точки к заданной плоскости.

Следует отметить, что расстояние от точки М₁ до плоскости , определенное таким образом, является наименьшим из расстояний от заданной точки М₁ до любой точки плоскости . Действительно, пусть точка H₂ лежит в плоскости и отлична от точки H₁. Очевидно, треугольник М₂H₁H₂ является прямоугольным, в нем М₁H₁ – катет, а M₁H₂ – гипотенуза, следовательно, . Кстати, отрезок M₁H₂ называется наклонной, проведенной из точки М₁ к плоскости . Итак, перпендикуляр, опущенный из заданной точки на заданную плоскость, всегда меньше наклонной, проведенной из этой же точки к заданной плоскости.

25. Прямая в пространстве R3.

Если прямая проходит через две заданные точки ,то ее уравнениезаписывают в виде: .

Определение. Вектор называется направляющим вектором прямой, если он параллелен или принадлежит ей.

Пример.Написать уравнение прямой, проходящей через две заданные точки .

Решение: Используем общую формулу прямой, проходящей через две заданные точки: — каноническое уравнение прямой, проходящей через точки и . Вектор — направляющий вектор прямой.

26. Взаимное расположение прямых в пространстве R3.

Перейдем к вариантам взаимного расположения двух прямых в пространстве.

Во-первых, две прямые могут совпадать, то есть, иметь бесконечно много общих точек (по крайней мере две общие точки).

Во-вторых, две прямые в пространстве могут пересекаться, то есть, иметь одну общую точку. В этом случае эти две прямые лежат в некоторой плоскости трехмерного пространства. Если две прямые в пространстве пересекаются, то мы приходим к понятию угла между пересекающимися прямыми.

В-третьих, две прямые в пространстве могут быть параллельными. В этом случае они лежат в одной плоскости и не имеют общих точек. Рекомендуем к изучению статью параллельные прямые, параллельность прямых.

После того как мы дали определение параллельных прямых в пространстве, следует сказать онаправляющих векторах прямой линии в силу их важности. Любой ненулевой вектор, лежащий на этой прямой или на прямой, которая параллельна данной, будем называть направляющим вектором прямой. Направляющий вектор прямой очень часто используется при решении задач, связанных с прямой линией в пространстве.

Наконец, две прямые в трехмерном пространстве могут быть скрещивающимися. Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости. Такое взаимное расположение двух прямых в пространстве приводит нас к понятию угла между скрещивающимися прямыми.

Особое практическое значение имеет случай, когда угол между пересекающимися или скрещивающимися прямыми в трехмерном пространстве равен девяноста градусам. Такие прямые называют перпендикулярными (смотрите статью перпендикулярные прямые, перпендикулярность прямых).

27. Взаимное расположение прямой и плоскости в пространстве R3.

Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.

рис.6.

рис.7.

рис.8.

Теорема. Пусть плоскость задана общим уравнением

а прямая L задана каноническими уравнениями

или параметрическими уравнениями

, ,

в которых – координаты нормального вектора плоскости , – координаты произвольной фиксированной точки прямой L, –

координаты направляющего вектора прямой L. Тогда:

1) если , то прямая L пересекает плоскость в точке,координаты которой можно найти из системы уравнений

; (7)

2) если и , то прямая лежит на плоскости;

3) если и , то прямая параллельна плоскости.

Доказательство. Условие говорит о том, что вектроры и не ортогональны, а значит прямая не параллельна плоскости и не лежит в плоскости, а значит пересекает ее в некоторой точке М. Координаты точки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальныеуравнения системы, находим координаты искомой точки.

Если , то это означает, что . А такое возможно лишь тогда, когда прямая лежит на плоскости или параллельна ей. Если прямая лежит на плоскости, то любая точка прямой является точкой плоскости икоординаты любой точки прямой удовлетворяют уравнению плоскости. Поэтому достаточно проверить, лежит ли на плоскости точка . Если , то точка – лежит на плоскости, а это означает, что и сама прямая лежит на плоскости.

Если , а , то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.

Теорема доказана.

Перпендикулярные прямые и их свойства. Перпендикулярные прямые Что называют перпендикулярной прямой

Определение 1

Две прямые называют перпендикулярными, если угол при их пересечении дает 90 градусов.

Перпендикулярность обозначается « ⊥ », а запись принимает вид a ⊥ b , что значит, прямая a перпендикулярна прямой b .

Например, перпендикулярными прямыми на плоскости могут быть стороны квадрата с общей вершиной. В трехмерном пространстве прямые O x , O z , O y перпендикулярны попарно: O x и O z , O x и O y , O y и O z .

Перпендикулярность прямых – условия перпендикулярности

Теорема 1

Доказательство 1

Пусть введена прямоугольная декартова система координат О х у с заданными уравнениями прямой на плоскости, которые определяют прямые a и b . Направляющие векторы прямых a и b обозначим a → и b → . Из уравнения прямых a и b необходимым и достаточным условием является перпендикулярность векторов a → и b → . Это возможно только при скалярном произведении векторов a → = (a x , a y) и b → = (b x , b y) равном нулю, а запись имеет вид a → , b → = a x · b x + a y · b y = 0 . Получим, что необходимым и достаточным условием перпендикулярности прямых a и b , находящихся в прямоугольной системе координат О х у на плоскости, является a → , b → = a x · b x + a y · b y = 0 , где a → = (a x , a y) и b → = b x , b y — это направляющие векторы прямых a и b .

Пример 1

Заданы три точки A (8 , 6) , B (6 , 3) , C (2 , 10) в прямоугольной системе координат О х у. Определить, прямые А В и А С перпендикулярны или нет.

Решение

Прямые А В и А С имеют направляющие векторы A B → и A C → соответственно. Для начала вычислим A B → = (- 2 , — 3) , A C → = (- 6 , 4) . Получим, что векторы A B → и A C → перпендикулярны из свойства о скалярном произведении векторов, равном нулю.

A B → , A C → = (- 2) · (- 6) + (- 3) · 4 = 0

Очевидно, что необходимое и достаточное условие выполнимо, значит, А В и А С перпендикулярны.

Ответ: прямые перпендикулярны.

Пример 2

Определить, заданные прямые x — 1 2 = y — 7 3 и x = 1 + λ y = 2 — 2 · λ перпендикулярны или нет.

Решение

a → = (2 , 3) является направляющим вектором заданной прямой x — 1 2 = y — 7 3 ,

b → = (1 , — 2) является направляющим вектором прямой x = 1 + λ y = 2 — 2 · λ .

Перейдем к вычислению скалярного произведения векторов a → и b → .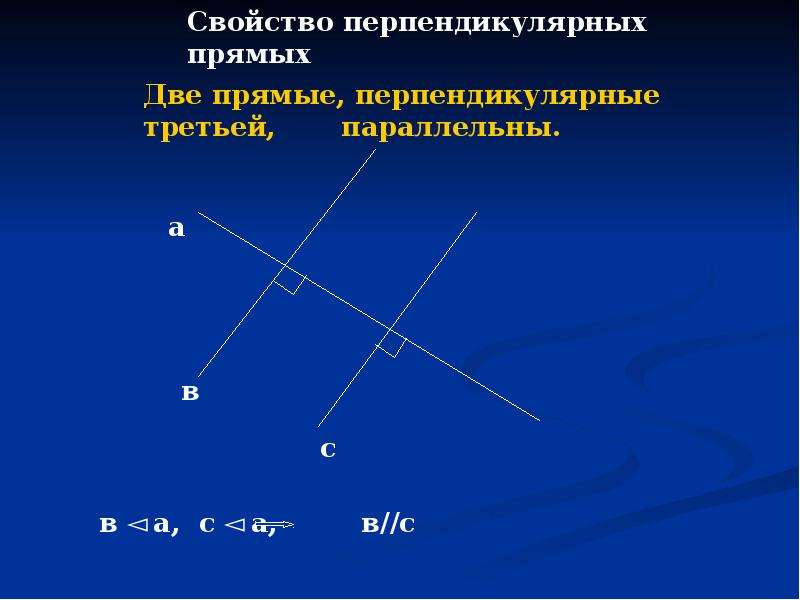 Выражение будет записано:

a → , b → = 2 · 1 + 3 · — 2 = 2 — 6 ≠ 0

Ответ: прямые не перпендикулярны.

Необходимое и достаточное условие перпендикулярности прямых a и b применяется для трехмерного пространства, записывается в виде a → , b → = a x · b x + a y · b y + a z · b z = 0 , где a → = (a x , a y , a z) и b → = (b x , b y , b z) являются направляющими векторами прямых a и b .

Пример 3

Решение

Знаменатели из канонических уравнений прямых считаются координатами направляющего вектора прямой. Координаты направляющего вектора из параметрического уравнения – коэффициенты. Отсюда следует, что a → = (2 , — 1 , 0) и b → = (1 , 2 , 4) являются направляющими векторами заданных прямых.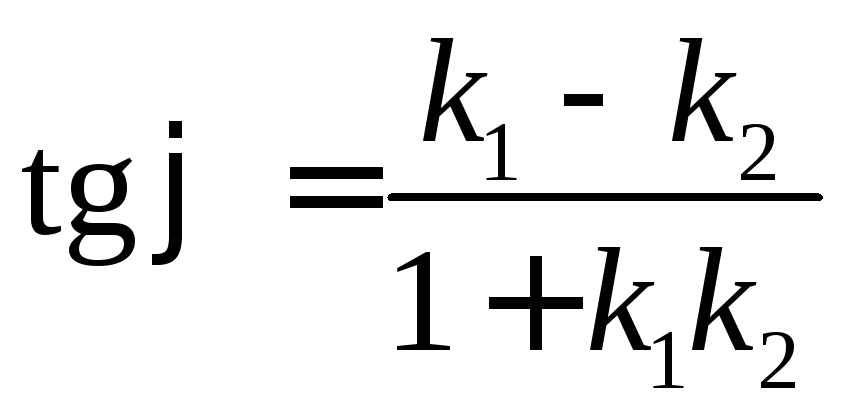 Для выявления их перпендикулярности найдем скалярное произведение векторов.

Выражение примет вид a → , b → = 2 · 1 + (- 1) · 2 + 0 · 4 = 0 .

Ответ: прямые перпендикулярны.

Теорема 2

Прямые a и b на плоскости считаются перпендикулярными при перпендикулярности нормального вектора прямой a с вектором b , это и есть необходимое и достаточное условие.

Доказательство 2

Данное условие применимо, когда уравнения прямых дают быстрое нахождение координат нормальных векторов заданных прямых. То есть при наличии общего уравнения прямой вида A x + B y + C = 0 , уравнения прямой в отрезках вида x a + y b = 1 , уравнения прямой с угловым коэффициентом вида y = k x + b координаты векторов возможно найти.

Пример 4

Выяснить, перпендикулярны ли прямые 3 x — y + 2 = 0 и x 3 2 + y 1 2 = 1 .

Решение

Исходя их уравнений, необходимо найти координаты нормальных векторов прямых. Получим, что n α → = (3 , — 1) — это нормальный вектор для прямой 3 x — y + 2 = 0 .

Векторы n a → = (3 , — 1) и n b → = 2 3 , 2 будут перпендикулярными, так как их скалярное произведение даст в итоге значение равное 0 . Получим n a → , n b → = 3 · 2 3 + (- 1) · 2 = 0 .

Необходимое и достаточное условие было выполнено.

Ответ: прямые перпендикулярны.

Когда прямая a на плоскости определена при помощи уравнения с угловым коэффициентом y = k 1 x + b 1 , а прямая b — y = k 2 x + b 2 , отсюда следует, что нормальные векторы будут иметь координаты (k 1 , — 1) и (k 2 , — 1) . Само условие перпендикулярности сводится к k 1 · k 2 + (- 1) · (- 1) = 0 ⇔ k 1 · k 2 = — 1 .

Пример 5

Выяснить, перпендикулярны ли прямые y = — 3 7 x и y = 7 3 x — 1 2 .

Решение

Прямая y = — 3 7 x имеет угловой коэффициент, равный — 3 7 , а прямая y = 7 3 x — 1 2 — 7 3 .

Ответ: заданные прямые перпендикулярны.

Имеется еще одно условие, используемое для определения перпендикулярности прямых на плоскости.

Теорема 3

Доказательство 3

Пример 6

Определить, являются ли заданные прямые x — y — 1 = 0 и x 0 = y — 4 2 перпендикулярными.

Решение

Получаем, что нормальный вектор прямой x — y — 1 = 0 имеет координаты n a → = (1 , — 1) , а b → = (0 , 2) — направляющий вектор прямой x 0 = y — 4 2 .

Отсюда видно, что векторы n a → = (1 , — 1) и b → = (0 , 2) не коллинеарны, потому что условие коллинеарности не выполняется. Не существует такого числа t , чтобы выполнялось равенство n a → = t · b → . Отсюда вывод, что прямые не являются перпендикулярными.

Ответ: прямые не перпендикулярны.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Перпендикулярные прямые образуют собой целый пласт фигур, построений и вычислений в геометрии. Без понимания перпендикулярных прямых не получится решать такие фигуры, как прямоугольный треугольник, прямоугольник, квадрат или прямоугольная трапеция. Поэтому стоит особенное внимание уделить этим понятиям.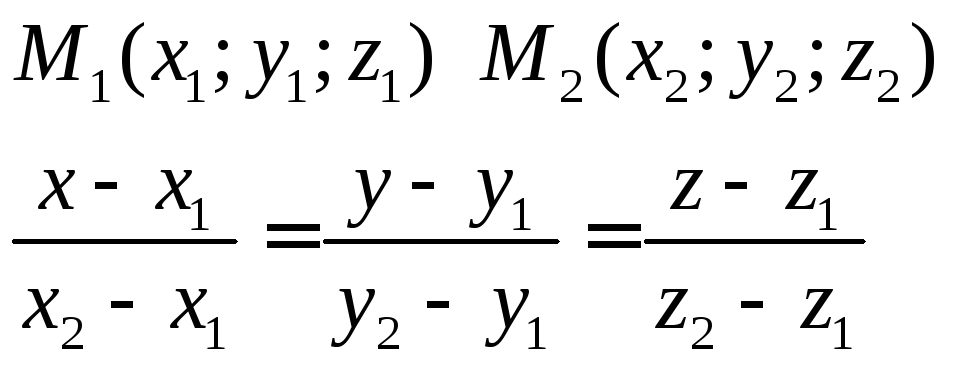

Что такое перпендикулярные прямые

При пересечении двух прямых образуется 4 угла. Определение перпендикулярных прямых звучит так: это прямые, угол между которыми равен 90 градусам. Углов всего 4, полный угол это 360 градусов. Если один из углов равен 90 градусам, то и 3 других будут по 90.

Чтобы отрезки назывались перпендикулярными, так же должно выполняться два условия: отрезки должны пересекаться, а угол пересечения между ними должен равняться 90 градусам.

Рис. 1. Перпендикулярные линии.

Свойства

У перпендикулярных прямых не так много свойств. Все они не требуют доказательств, так как исходят из определения перпендикулярности.

Если каждая из двух прямых перпендикулярны третьей, то эти прямые параллельны. А параллельны они в силу того, что получившиеся односторонние углы будут в сумме давать 180 градусов. А значит, прямые параллельны по 3 признаку параллельности. Это свойство можно доказать по любому из трех признаков параллельности.
Перпендикулярный отрезок от точки до прямой или отрезка будет называться расстоянием от точки до прямой.
Расстояние от прямой до прямой так же является перпендикуляром, опущенным из любой точки одной прямой на другую прямую.
Если на протяжении всей длинны двух прямых расстояние между ними не меняется, то прямые будут параллельными.

Фигуры с перпендикулярными прямыми

Одной из первых фигур, с которыми знакомится человек, являются квадрат и прямоугольник.

Прямые углы приятны человеческому взгляду, поэтому очень часто квадрат или прямоугольник используют как форму для столешниц, стульев, тумбочек и других предметов. Весь окружающий человека мир составлен из параллельных и перпендикулярных линий.

Рис. 2. Квадрат.

Еще со времен Древней Греции известен прямоугольный треугольник. Форму прямоугольного треугольника принимали различные приборы для навигации, кроме того много времени изучению свойств прямоугольного треугольника уделил Пифагор. Именно его авторству принадлежит Теорема Пифагора, которая крайне востребована в решениях задач.

Существует прямоугольная трапеция, у которой одна из сторон прямоугольна обоим основанием. А планометрия и вовсе пестрит перпендикулярами в пространстве: правильная призма, прямоугольная пирамида и самый обычный куб.

К тому же, в любом треугольнике можно провести высоту, что необходимо для нахождения площади фигуры. Перпендикуляр для нахождения площади пригодится и в параллелограмме, а прямоугольный треугольник и квадрат имеют высоту в составе своих сторон, из-за чего площадь этих фигур гораздо проще найти.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Перпендикулярностью называют соотношение между разнообразными объектами в евклидовом пространстве — прямыми, плоскостями, векторами, подпространствами и так далее. В настоящем материале мы более внимательно рассмотрим перпендикулярные прямые и характерные черты, к ним относящиеся. Две прямые могут быть названы перпендикулярными (или взаимоперпендикулярными), если все четыре угла, которые образованы их пересечением, составляют строго по девяносто градусов.

Существуют определенные свойства перпендикулярных прямых, реализованных на плоскости:

Построение перпендикулярных прямых

Перпендикулярные прямые строятся на плоскости с помощью угольника. Любой чертежник должен иметь в виду, что важной особенностью каждого угольника является то, что он обязательно имеет прямой угол. Чтобы создать две перпендикулярные прямые, нам необходимо совместить одну из двух сторон прямого угла нашего

чертежного угольника с данной прямой и провести вторую прямую вдоль второй стороны этого прямого угла. Таким образом будут созданы две перпендикулярные прямые.

Трехмерное пространство

Интересен тот факт, что перпендикулярные прямые могут быть реализованы и в В этом случае такими будут называться две прямые, если они параллельны соответственно каким-либо двух иным прямым, лежащим в той же плоскости и тоже перпендикулярным в ней. Кроме того, если на плоскости перпендикулярными могут быть лишь две прямые, то в трехмерном пространстве — уже три. Более того, в количество перпендикулярных линий (или же плоскостей) может быть еще больше увеличено.

Прямая (отрезок прямой) обозначается двумя большими буквами латинского алфавита или одной маленькой буквой. Точка обозначается только большой латинской буквой.

Прямые могут не пересекаться, пересекаться или совпадать. Пересекающиеся прямые имеют только одну общую точку, непересекающиеся прямые — ни одной общей точки, у совпадающих прямых все точки общие.

Определение. Две прямые, пересекающиеся под прямым углом, называются перпендикулярными. Перпендикулярность прямых (или их отрезков) обозначают знаком перпендикулярности «⊥».

Например:

Ваш AB и CD (рис. 1) пересекаются в точке О и ∠АОС = ∠ВОС = ∠АОD = ∠BOD = 90°, то AB ⊥ CD .

Если AB ⊥ CD (рис. 2) и пересекаются в точке В , то ∠АBC = ∠ABD = 90°

Свойства перпендикулярных прямых

1. Через точку А (рис. 3) можно провести только одну перпендикулярную прямую АВ к прямой СD; остальные прямые, проходящие через точку А и пересекающие СD , называются наклонными прямыми (рис. 3, прямые АЕ и АF ).

2. Из точки A можно опустить перпендикуляр на прямую CD ; длина перпендикуляра (длина отрезка АВ ), проведенного из точки А на прямую CD ,- это самое короткое расстояние от A до CD (рис. 3).

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Линейная функция

Линейной функцией называют функцию, заданную формулой

где k и b – произвольные (вещественные) числа.

При любых значениях k и b графиком линейной функции является прямая линия.

Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом.

График линейной функции

При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график (прямая линия) имеет вид, изображенный на рис. 1, 2 и 3.

k > 0

Рис.

Рис.2

Рис.3

При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.

k = 0

Рис.4

Рис.5

Рис.6

При k < 0 линейная функция (1) убывает на всей числовой прямой, а её график (прямая линия) имеет вид, изображенный на рис. 7, 8 и 9.

k < 0

Рис.

Рис.8

Рис.9

Прямые линии

y = kx + b₁ и y = kx + b₂,

имеющие одинаковые угловые коэффициенты и разные свободные члены , параллельны.

Прямые линии

y = k₁x + b₁ и y = k₂x + b₂ ,

имеющие разные угловые коэффициенты , пересекаются при любых значениях свободных членов.

Прямые линии

y = kx + b₁ и

перпендикулярны при любых значениях свободных членов.

Угловой коэффициент прямой линии

равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).

Рис.10

Рис.11

Рис.12

Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b .

При прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле

Прямые, параллельные оси ординат

Прямые, параллельные оси Oy, задаются формулой

где c – произвольное число, и изображены на рис. 13, 14, 15.

Рис.13

Рис.14

Рис.15

Замечание 1. Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .;

Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые

Рассмотрим уравнение

где p, q, r – произвольные числа.

В случае, когда уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию.

Действительно,

что и требовалось.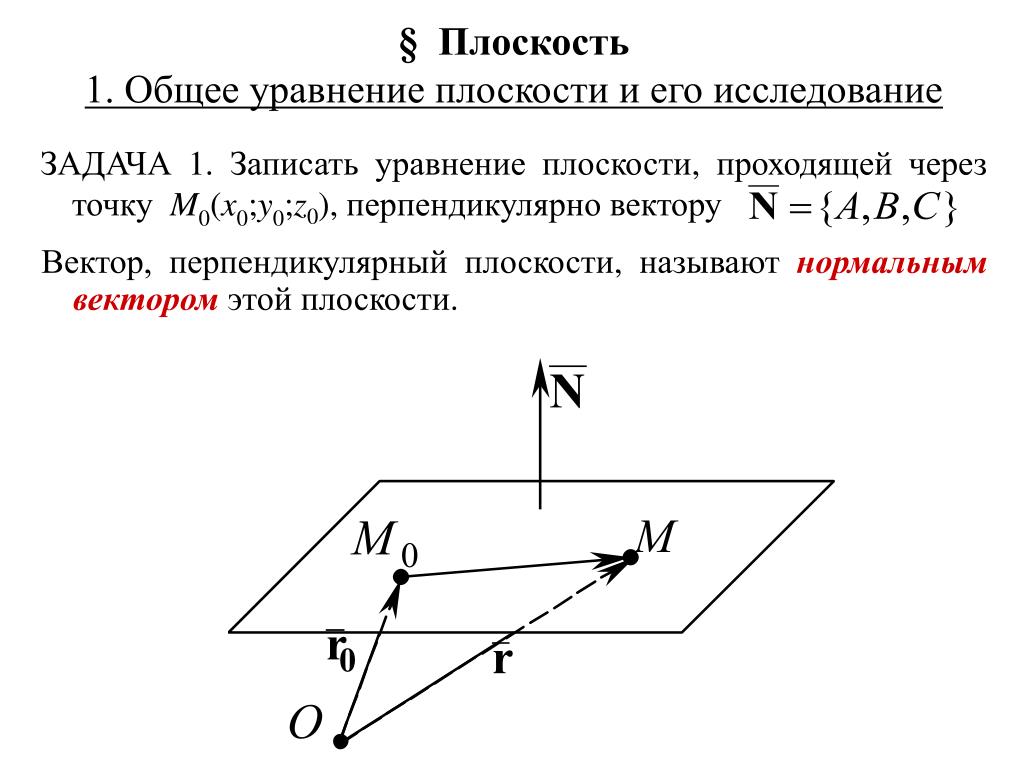

В случае, когда получаем:

откуда вытекает, что уравнение (4) задает прямую линию вида (3).

В случае, когда q = 0, p = 0, уравнение (4) имеет вид

и при r = 0 его решением являются точки всей плоскости:

В случае, когда уравнение (5) решений вообще не имеет.

Замечание 2. При любом значении r₁, не совпадающем с r прямая линия, заданная уравнением

параллельна прямой, заданной уравнением (4).

Замечание 3. При любом значении r₂ прямая линия, заданная уравнением

перпендикулярна прямой, заданной уравнением (4).

Пример. Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и

параллельной к прямой
перпендикулярной к прямой (8).

Решение.

В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
где r₁ – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство
Итак, уравнение прямой, параллельной к прямой
4x + 5y = 7,
задаётся уравнением
4x + 5y = – 7 .
В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
где r₂ – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство
Итак, прямая, перпендикулярная к прямой
4x + 5y = 7 ,
задаётся уравнением
– 5x + 4y = – 22 .

03.03. Общее уравнение прямой | Контрольные работы по математике и други

Общее уравнение прямой

Опишем аналитически геометрическое место точек, лежащих на прямой, следующим образом. Пусть в системе координат Оху дана прямая (рис. 4.4).

Рис. 4.4. Задание прямой общим уравнением

Назовем ненулевой вектор , перпендикулярный к ней, нормальным вектором прямой. Будем считать известными координаты точки , лежащей на прямой. Задание нормального вектора И этой точки M0 однозначно определяет положение прямой на плоскости. Пусть – произвольная точка, лежащая на прямой. Свяжем с точками M0 и M радиус-векторы и . Введем в рассмотрение вектор

Для точек прямой и только для них будет выполняться условие:

Его мы и положим в основу вывода общего уравнения прямой. Необходимым и достаточным условием взаимной перпендикулярности двух векторов является равенство нулю их скалярного произведения:

Или

Раскрывая скобки, получим:

(4. 9)

Это есть уравнение прямой в векторной форме. Оно включает в себя известные векторы и , а также вектор , который характеризует положение произвольной точки, лежащей на данной прямой. Другие точки плоскости ему удовлетворять не будут.

Так как

То в координатной форме уравнение прямой примет вид:

(4.10)

Или

(4.11)

Где

Уравнение (4.11) называется общим уравнением прямой.

Таким образом, мы доказали теорему:

Теорема. Всякой прямой на плоскости соответствует линейное уравнение относительно координат ее точек.

Будет ли справедливо обратное утверждение?

Теорема. Любое уравнение первой степени (4.11) относительно переменных x и y в декартовой прямоугольной системе координат Охy определяет прямую.

ДОКАЗАТЕЛЬСТВО

Пусть в уравнении (4.11) хотя бы один из коэффициентов А или В отличен от нуля. В прямоугольной системе координат Оху возьмем какую либо точку , координаты которой удовлетворяют уравнению (4.11)

. (4.12)

Таких пар чисел существует бесконечно много.

Вычитая из уравнения (4.11) равенство (4.12), получим уравнение (4.10), эквивалентное (4.11). Оно означает, как уже известно, равенство нулю скалярного произведения вектора и вектора , что возможно только тогда, когда переменные x и y являются координатами точки прямой. Это и доказывает теорему.

Общее уравнение прямой без труда приводится к виду (4.1), если :

При этом и .

Коэффициенты A и B являются координатами нормального вектора к прямой, а потому они позволяют получить представление о ее расположении на плоскости. Если A = 0 и , то нормальный вектор , а прямая параллельна оси абсцисс. Уравнение такой прямой имеет вид:

Если , , то нормальный вектор и данная прямая параллельна оси ординат. Ее уравнение приобретает вид:

Именно такая прямая не охватывается множеством прямых, определяемых уравнением (4.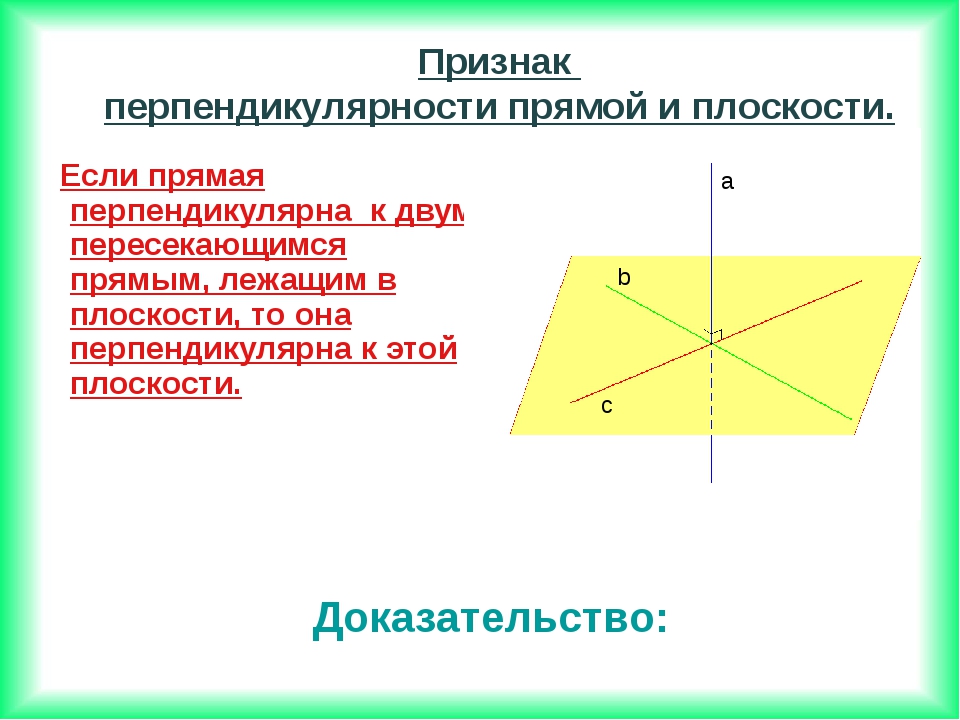 1).

Рис. 4.5. Нахождение угла между прямыми, заданными общим уравнением.

Найдем угол между двумя прямыми (рис. 4.5), заданными общими уравнениями:

(4.13)

(4.14)

По виду уравнений определяем координаты нормальных векторов данных прямых: , . Угол между двумя данными прямыми будет равен углу между их нормальными векторами, как углы со взаимно перпендикулярными сторонами, поэтому решение задачи имеет вид:

. (4.15)

В координатной форме эти выражения записываются следующим образом:

. (4.16)

Если прямые параллельны, то их нормальные векторы и будут коллинеарны, поэтому

. (4.17)

Это равенство определяет условие параллельности прямых в векторном виде. В координатной форме оно будет следующим:

(4.18)

Если прямые взаимно перпендикулярны, то и соответствующие нормальные векторы также перпендикулярны, следовательно, скалярное произведение этих векторов будет равно нулю:

Или в координатной форме:

(4. 19)

Как расположены прямые, у которых

Очевидно, что если в уравнениях (4.13) и (4.14) имеет место пропорциональность

(4.20)

То они определяют одну и ту же прямую.

< Предыдущая		Следующая >

1. Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости.

Рис. 1.

Рассмотрим прямые а и b. Прямые могут пересекаться, скрещиваться, быть параллельными. Для того, чтобы построить угол между ними нужно выбрать точку и через нее провести прямую , параллельную прямой а, и прямую , параллельную прямойb. Прямые и пересекаются. Угол между ними и есть угол между прямыми а и b. Если угол равен 90°, то прямые а и b перпендикулярны.

Лемма: Если одна из двух прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.

Доказательство:

Пусть даны две параллельные прямые а и b, и прямая с,причем . Нужно доказать, что .Возьмем произвольную точку М. Через точку М проведем прямую , параллельную прямой а и прямую , параллельную прямой c (рис. 2). Тогда угол АМС равен 90°.

Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

Обозначение. .

Рис. 3.

Свойство: Если прямая перпендикулярна к плоскости, то она пересекает эту плоскость. (Если , то . )

Доказательство:

Теорема: Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

Доказательство:

Пусть прямая а параллельна прямой а1. Прямая а перпендикулярна плоскости. Докажем, что и прямая а1 перепендикулярна плоскости.

Прямая а перпендикулярна плоскости . Значит, она перпендикулярна любой прямой, лежащей в этой плоскости. Прямая х лежит в плоскости , значит, (см. рис. 6).

Рис 6.

Прямая а перпендикулярна прямой х, а прямая а1 параллельна прямой а. Значит, прямая а1 перпендикулярна прямой х по лемме. Прямую х мы выбирали произвольно. Значит, прямая а1 перпендикулярна любой прямой в плоскости , то есть прямая х перпендикулярна плоскости , что и требовалось доказать.

Теорема: Если две прямые перпендикулярны к плоскости, то они параллельны.

Доказательство:

Пусть прямая а перепендикулярна плоскости и прямая b перепендикулярна плоскости. Докажем, что прямая а параллельна прямой b.

Рис. 7.

Предположим, что прямая b не параллельна прямой а. Через точку М прямой b проведем прямую , параллельно прямой а (рис. 8).

Прямые и а параллельны, прямая а перпендикулярна плоскости . По теореме, прямая также перпендикулярна плоскости .

Прямые b и пересекаются, а значит через них проходит некоторая плоскость. Пусть эта плоскость пересекает плоскость по прямой с. Тогда прямая перпендикулярна прямой с, так как прямая с лежит в плоскости , а прямая ей перпендикулярна.

Но тогда в плоскости, определенной пересекающимися прямыми b и через точку М проходят два перпендикуляра b и к прямой с. Получаем противоречие. Значит, прямая b параллельна прямой а, что и требовалось доказать.

Рис. 8.

Как найти уравнение перпендикулярной прямой

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Поиск параллельных и перпендикулярных прямых

Как использовать алгебру для поиска параллельных и перпендикулярных прямых.

Параллельные линии

Как мы узнаем, что две прямые параллельны ?

Их склоны одинаковые!

Пример:

Найдите уравнение прямой:

параллельно y = 2x + 1
и проходит через точку (5,4)

Наклон y = 2x + 1 равен: 2

У параллельной прямой должен быть одинаковый наклон, равный 2.

Мы можем решить это, используя уравнение «точка-наклон» прямой:

y — y ₁ = 2 (x — x ₁)

И затем ставим точку (5,4):

у — 4 = 2 (х — 5)

И этот ответ в порядке, но давайте также запишем его в форме y = mx + b:

г — 4 = 2х — 10

г = 2х — 6

Вертикальные линии

Но это не работает для вертикальных линий… Объясняю почему в конце.

Не та же строка

Будьте осторожны! Они могут быть той же линией (но с другим уравнением), и поэтому не параллельны .

Как мы узнаем, действительно ли это одна и та же линия? Проверьте их точки пересечения оси Y (где они пересекают ось Y), а также их наклон:

Пример: y = 3x + 2 параллельно y — 2 = 3x?

Для y = 3x + 2 : наклон равен 3, а пересечение оси Y равно 2

Для y — 2 = 3x : наклон равен 3, а пересечение оси Y равно 2

На самом деле это одна и та же линия, поэтому они не параллельны

Перпендикулярные линии

Две прямые перпендикулярны, когда они встречаются под прямым углом (90 °).

Чтобы найти перпендикулярный уклон:

Когда одна линия имеет наклон м, перпендикулярная линия имеет наклон −1 м

Другими словами, отрицательная обратная величина

Пример:

Найдите уравнение прямой, равной

перпендикулярно y = −4x + 10
и проходит через точку (7,2)

Наклон y = −4x + 10 равен: −4

Отрицательное значение , обратное этого наклона:

м = −1 −4 = 1 4

Таким образом, перпендикулярная линия будет иметь наклон 1/4:

y — y ₁ = (1/4) (x — x ₁)

А теперь ставим точку (7,2):

у — 2 = (1/4) (х — 7)

И этот ответ нормальный, но давайте также запишем его в форме «y = mx + b»:

у — 2 = х / 4 — 7/4

у = х / 4 + 1/4

Быстрая проверка перпендикуляра

Когда мы умножаем наклон m на его перпендикулярный наклон −1 m , мы получаем просто −1.

Итак, чтобы быстро проверить, перпендикулярны ли две линии:

Когда мы умножаем их наклон, получаем −1

Как это:

Эти две прямые перпендикулярны?

Линия	Наклон
y = 2x + 1	2
y = −0,5x + 4	-0,5

Когда мы умножаем два угла наклона, получаем:

2 × (−0.5) = −1

Да, мы получили −1, поэтому они перпендикулярны.

Вертикальные линии

Предыдущие методы работают нормально, за исключением вертикальной линии :

В данном случае градиент равен undefined (так как мы не можем делить на 0):

м = y _A — y _B x _A — x _B = 4 — 1 2 — 2 = 3 0 = не определено

Так что просто положитесь на тот факт, что:

одна вертикальная линия параллельна другой вертикальной линии.
: вертикальная линия перпендикулярна горизонтальной линии (и наоборот).

Сводка

параллельных прямых: то же наклон
перпендикулярных линий: отрицательный обратный угол наклон (-1 / м)

параллельных и перпендикулярных линий | Колледж алгебры

Результаты обучения

Определить, параллельны ли прямые или перпендикулярны по их уравнениям
Найдите уравнения прямых, параллельных или перпендикулярных данной прямой

Две линии на графике ниже — это параллельные линии : они никогда не пересекаются.Обратите внимание, что они имеют одинаковую крутизну, что означает, что их уклоны одинаковы. Единственное различие между двумя линиями — перехват y . Если бы мы сместили одну линию по вертикали в сторону пересечения y другой, они стали бы той же линией.

Параллельные линии.

Мы можем определить из их уравнений, параллельны ли две прямые, сравнив их наклоны. Если уклоны одинаковы и точки пересечения y разные, линии параллельны.Если уклоны разные, линии не параллельны.

В отличие от параллельных прямых, перпендикулярные линии пересекаются. Их пересечение образует прямой или 90-градусный угол. Две линии ниже перпендикулярны.

Перпендикулярные линии.

Перпендикулярные линии не имеют одинакового наклона. Наклоны перпендикулярных линий определенным образом отличаются друг от друга. Наклон одной линии является обратной величиной наклона другой линии. Произведение числа на обратную единицу.Если [latex] {m} _ {1} \ text {и} {m} _ {2} [/ latex] являются отрицательными обратными друг другу, их можно умножить вместе, чтобы получить [latex] -1 [/ latex] .

[латекс] {m} _ {1} * {m} _ {2} = — 1 [/ латекс]

Чтобы найти обратное число, разделите 1 на число. Таким образом, величина, обратная 8, равна [latex] \ frac {1} {8} [/ latex], а обратная величина [latex] \ frac {1} {8} [/ latex] — 8. Чтобы найти обратную обратную величину, сначала найдите обратное, а затем измените знак.

Как и в случае с параллельными линиями, мы можем определить, являются ли две прямые перпендикулярными, сравнивая их наклон.Наклон каждой линии ниже отрицателен, обратный другой, поэтому линии перпендикулярны.

[латекс] \ begin {array} {ll} f \ left (x \ right) = \ frac {1} {4} x + 2 \ hfill & \ text {отрицательная обратная величина} \ frac {1} {4} \ text {is} -4 \ hfill \\ f \ left (x \ right) = — 4x + 3 \ hfill & \ text {отрицательная обратная величина} -4 \ text {is} \ frac {1} {4} \ hfill \ end {array} [/ latex]

Произведение наклонов равно –1.

[латекс] -4 \ влево (\ frac {1} {4} \ right) = — 1 [/ латекс]

Общее примечание: параллельные и перпендикулярные линии

Две прямые являются параллельными линиями , если они не пересекаются.Наклоны линий такие же.

[латекс] f \ left (x \ right) = {m} _ {1} x + {b} _ {1} \ text {and} g \ left (x \ right) = {m} _ {2} x + {b} _ {2} \ text {параллельны, если} {m} _ {1} = {m} _ {2} [/ latex].

Если и только если [латекс] {b} _ {1} = {b} _ {2} [/ latex] и [latex] {m} _ {1} = {m} _ {2} [/ latex] , мы говорим, что линии совпадают. Совпадающие линии — это одна и та же линия.

Две прямые — это перпендикулярные линии , если они пересекаются под прямым углом.

[латекс] f \ left (x \ right) = {m} _ {1} x + {b} _ {1} \ text {and} g \ left (x \ right) = {m} _ {2} x + {b} _ {2} \ text {перпендикулярны, если} {m} _ {1} * {m} _ {2} = — 1, \ text {и} {m} _ {2} = — \ frac { 1} {{m} _ {1}} [/ latex].

Пример: определение параллельных и перпендикулярных линий

Для указанных ниже функций определите функции, графики которых представляют собой пару параллельных линий и пару перпендикулярных линий.

[латекс] \ begin {array} {l} f \ left (x \ right) = 2x + 3 \ hfill & \ hfill & h \ left (x \ right) = — 2x + 2 \ hfill \\ g \ left (x \ right) = \ frac {1} {2} x — 4 \ hfill & \ hfill & j \ left (x \ right) = 2x — 6 \ hfill \ end {array} [/ latex]

Показать решение

Параллельные прямые имеют одинаковый наклон. Поскольку функции [latex] f \ left (x \ right) = 2x + 3 [/ latex] и [latex] j \ left (x \ right) = 2x — 6 [/ latex] имеют наклон 2, они представляют собой параллельные линии.Перпендикулярные линии имеют обратный отрицательный наклон. Поскольку −2 и [latex] \ frac {1} {2} [/ latex] являются обратными отрицательными числами, уравнения [latex] g \ left (x \ right) = \ frac {1} {2} x — 4 [ / latex] и [latex] h \ left (x \ right) = — 2x + 2 [/ latex] представляют собой перпендикулярные линии.

Анализ решения

График линий показан ниже.

График показывает, что линии [латекс] f \ left (x \ right) = 2x + 3 [/ latex] и [latex] j \ left (x \ right) = 2x — 6 [/ latex] параллельны, и линии [латекс] g \ left (x \ right) = \ frac {1} {2} x — 4 [/ latex] и [latex] h \ left (x \ right) = — 2x + 2 [/ latex] перпендикулярны.

Написание уравнений параллельных линий

Если мы знаем уравнение прямой, мы можем использовать то, что мы знаем о наклоне, чтобы написать уравнение прямой, параллельной или перпендикулярной данной прямой.

Предположим, нам дана следующая функция:

[латекс] f \ left (x \ right) = 3x + 1 [/ латекс]

Мы знаем, что наклон линии равен 3. Мы также знаем, что точка пересечения y- равна (0, 1). Любая другая линия с наклоном 3 будет параллельна f ( x ).Линии, образованные всеми следующими функциями, будут параллельны f ( x ).

[латекс] \ begin {array} {l} g \ left (x \ right) = 3x + 6 \ hfill \\ h \ left (x \ right) = 3x + 1 \ hfill \\ p \ left (x \ справа) = 3x + \ frac {2} {3} \ hfill \ end {array} [/ latex]

Предположим, мы хотим написать уравнение прямой, параллельной f и проходящей через точку (1, 7). Мы уже знаем, что наклон равен 3. Нам просто нужно определить, какое значение для b даст правильную линию.Мы можем начать с использования формы точечного уклона уравнения для прямой. Затем мы можем переписать его в форме пересечения наклона.

[латекс] \ begin {array} {l} y- {y} _ {1} = m \ left (x- {x} _ {1} \ right) \ hfill \\ y — 7 = 3 \ left ( x — 1 \ right) \ hfill \\ y — 7 = 3x — 3 \ hfill \\ \ text {} y = 3x + 4 \ hfill \ end {array} [/ latex]

Итак, [латекс] g \ left (x \ right) = 3x + 4 [/ latex] параллелен [latex] f \ left (x \ right) = 3x + 1 [/ latex] и проходит через точку (1 , 7).

Как сделать: учитывая уравнение линейной функции, напишите уравнение линии, КОТОРАЯ проходит через данную точку и параллельна данной прямой.

Найдите наклон функции.
Подставляет уклон и заданную точку в форму «точка-уклон» или «пересечение уклона».
Упростить.

Пример: поиск прямой, параллельной заданной прямой

Найдите прямую, параллельную графику [латекса] f \ left (x \ right) = 3x + 6 [/ latex], которая проходит через точку (3, 0).

Показать решение

Наклон данной линии равен 3. Если мы выберем форму пересечения наклона, мы можем заменить [латекс] m = 3 [/ латекс], [латекс] x = 3 [/ латекс] и [латекс] f (x ) = 0 [/ latex] в форму пересечения наклона, чтобы найти точку пересечения y- .

[латекс] \ begin {array} {l} g \ left (x \ right) = 3x + b \ hfill \\ \ text {} 0 = 3 \ left (3 \ right) + b \ hfill \\ \ text {} b = -9 \ hfill \ end {array} [/ latex]

Линия, параллельная f ( x ), которая проходит через (3, 0), равна [latex] g \ left (x \ right) = 3x — 9 [/ latex].

Анализ решения

Мы можем подтвердить, что две линии параллельны, построив их график. На рисунке ниже показано, что две линии никогда не пересекутся.

Написание уравнений перпендикулярных прямых

Мы можем использовать очень похожий процесс, чтобы написать уравнение линии, перпендикулярной данной линии.Однако вместо того, чтобы использовать один и тот же наклон, мы используем отрицательную величину, обратную данному наклону. Предположим, нам дана следующая функция:

[латекс] f \ left (x \ right) = 2x + 4 [/ латекс]

Наклон линии равен 2, и его отрицательная обратная величина равна [латекс] — \ frac {1} {2} [/ latex]. Любая функция с наклоном [латекс] — \ frac {1} {2} [/ latex] будет перпендикулярна f ( x ). Линии, образованные всеми следующими функциями, будут перпендикулярны f ( x ).

[латекс] \ begin {array} {l} g \ left (x \ right) = — \ frac {1} {2} x + 4 \ hfill \\ h \ left (x \ right) = — \ frac { 1} {2} x + 2 \ hfill \\ p \ left (x \ right) = — \ frac {1} {2} x- \ frac {1} {2} \ hfill \ end {array} [/ latex ]

Как и раньше, мы можем сузить наш выбор для конкретной перпендикулярной линии, если знаем, что она проходит через данную точку. Предположим, что мы хотим написать уравнение прямой, которая перпендикулярна f ( x ) и проходит через точку (4, 0). Мы уже знаем, что наклон [латекс] — \ frac {1} {2} [/ latex].Теперь мы можем использовать точку, чтобы найти точку пересечения y , подставив заданные значения в форму пересечения угла наклона линии и решив для b .

[латекс] \ begin {array} {l} g \ left (x \ right) = mx + b \ hfill \\ 0 = — \ frac {1} {2} \ left (4 \ right) + b \ hfill \\ 0 = -2 + b \ hfill \\ 2 = b \ hfill \\ b = 2 \ hfill \ end {array} [/ latex]

Уравнение для функции с наклоном [латекс] — \ frac {1} {2} [/ latex] и точкой пересечения y- 2 равно

[латекс] g \ left (x \ right) = — \ frac {1} {2} x + 2 [/ latex].

Итак, [латекс] g \ left (x \ right) = — \ frac {1} {2} x + 2 [/ latex] перпендикулярен [латексу] f \ left (x \ right) = 2x + 4 [/ латекс] и проходит через точку (4, 0). Имейте в виду, что перпендикулярные линии могут не выглядеть явно перпендикулярными на графическом калькуляторе, если мы не используем функцию квадратного масштабирования.

Вопросы и ответы

Горизонтальная линия имеет нулевой наклон, а вертикальная линия имеет неопределенный наклон. Эти две линии перпендикулярны, но произведение их наклонов не равно –1. Не противоречит ли этот факт определению перпендикулярных линий?

№Для двух перпендикулярных линейных функций произведение их угловых коэффициентов равно –1. Однако вертикальная линия не является функцией, поэтому определение не противоречит.

Как сделать: учитывая уравнение линейной функции, напишите уравнение линии, КОТОРАЯ проходит через данную точку и перпендикулярна данной линии.

Найдите наклон заданной функции.
Определите отрицательную обратную величину уклона.
Подставьте новый наклон и значения для x и y из данной точки в [latex] g \ left (x \ right) = mx + b [/ latex].
Решите относительно b .
Напишите уравнение прямой.

Пример: поиск уравнения перпендикулярной прямой

Найдите уравнение линии, перпендикулярной [латексу] f \ left (x \ right) = 3x + 3 [/ latex], которая проходит через точку (3, 0).

Показать решение

Исходная линия имеет наклон [латекс] m = 3 [/ latex], поэтому наклон перпендикулярной линии будет обратной обратной величиной [латекс] — \ frac {1} {3} [/ latex]. Используя этот наклон и данную точку, мы можем найти уравнение для прямой.

[латекс] \ begin {array} {l} g \ left (x \ right) = — \ frac {1} {3} x + b \ hfill \\ 0 = — \ frac {1} {3} \ left (3 \ right) + b \ hfill \\ \ text {} 1 = b \ hfill \\ b = 1 \ hfill \ end {array} [/ latex]

Линия, перпендикулярная к f ( x ), которая проходит через (3, 0), равна [latex] g \ left (x \ right) = — \ frac {1} {3} x + 1 [/ latex] .

Анализ решения

График из двух линий показан ниже.

Как сделать: даны две точки на линии и третья точка, запишите уравнение перпендикулярной линии, проходящей через точку.

Определите наклон линии, проходящей через точки.
Найдите отрицательное значение, обратное наклону.
Используйте форму пересечения наклона или форму точки-наклона, чтобы написать уравнение, подставляя известные значения.
Упростить.

Пример: поиск уравнения прямой, проходящей через точку и перпендикулярной заданной прямой

Линия проходит через точки (–2, 6) и (4, 5). Найдите уравнение прямой, перпендикулярной и проходящей через точку (4, 5).

Показать решение

По двум точкам данной линии мы можем вычислить наклон этой линии.

[латекс] \ begin {array} {l} {m} _ {1} = \ frac {5 — 6} {4- \ left (-2 \ right)} \ hfill \\ {m} _ {1} = \ frac {-1} {6} \ hfill \\ {m} _ {1} = — \ frac {1} {6} \ hfill \ end {array} [/ latex]

Найдите отрицательное значение, обратное наклону.

[латекс] \ begin {array} {l} {m} _ {2} = \ frac {-1} {- \ frac {1} {6}} \ hfill \\ {m} _ {2} = — 1 \ left (- \ frac {6} {1} \ right) \ hfill \\ {m} _ {2} = 6 \ hfill \ end {array} [/ latex]

Затем мы можем найти точку пересечения y- прямой, проходящей через точку (4, 5).

[латекс] \ begin {array} {l} g \ left (x \ right) = 6x + b \ hfill \\ 5 = 6 \ left (4 \ right) + b \ hfill \\ 5 = 24 + b \ hfill \\ -19 = b \ hfill \\ b = -19 \ hfill \ end {array} [/ latex]

Уравнение линии, проходящей через точку (4, 5) и перпендикулярной линии, проходящей через две заданные точки, есть [латекс] y = 6x — 19 [/ латекс].

Попробуйте

Линия проходит через точки (–2, –15) и (2, –3). Найдите уравнение перпендикулярной линии, проходящей через точку (6, 4).Угол \ circ90∘. Даны две невертикальные линии в форме пересечения наклона

y = m1x + b1y = m2x + b2, \ begin {выровнено} y & = m_1 x + b_1 \\ у & = m_2 x + b_2, \ end {align} yy = m1 x + b1 = m2 x + b2,

две прямые перпендикулярны, если m1 = −1m2m_1 = — \ frac {1} {m_2} m1 = −m2 1, то есть, если наклоны являются отрицательными, обратными друг другу:

На приведенном выше изображении форма пересечения наклона двух линий равна

y = 12x + 3y = −2x − 2, \ begin {align} y & = \ frac {1} {2} x + 3 \\ y & = -2x -2, \ end {align} yy = 21 x + 3 = −2x − 2,

, и поскольку два наклона противоположны друг другу, линии перпендикулярны.

Каково уравнение прямой, проходящей через точку (−7,3) (- 7, 3) (- 7,3) и перпендикулярной прямой y = 15x − 2? Y = \ frac {1} {5} x-2? Y = 51 x − 2?
Пусть y = ax + by = ax + by = ax + b будет уравнением интересующей линии. Тогда, поскольку эта прямая перпендикулярна прямой y = 15x − 2y = \ frac {1} {5} x-2y = 51 x − 2, наклон которой равен 15, \ frac {1} {5}, 51 , должно быть верно, что a = −5.a = -5.a = −5. Итак, уравнение теперь принимает вид y = −5x + b.y = -5x + b.y = −5x + b. Подставляя в координаты (−7,3), (- 7, 3), (- 7,3), получаем 3 = −5 × (−7) + b ⟹ b = −32.3 = -5 \ times (-7) + b \ подразумевает b = -32,3 = −5 × (−7) + b⟹b = −32. Следовательно, уравнение интересующей линии имеет вид y = −5x − 32. □ у = -5x-32. \ _ \ квадрат = −5x − 32. □

Какова сумма всех констант kkk таких, что две строки (k + 1) x − 3y + 2 = 0, (k − 2) x + 4y − 1 = 0 \ begin {array} {c} & ( k + 1) x-3y + 2 = 0, & (k-2) x + 4y-1 = 0 \ end {array} (k + 1) x − 3y + 2 = 0, (k − 2) x + 4y − 1 = 0 перпендикулярны друг другу?
Чтобы две прямые были перпендикулярными, должно быть верно, что (k + 1) × (k − 2) + (- 3) × 4 = 0.2-к-14 & = 0. \ end {выровнены} (k + 1) × (k − 2) + (- 3) × 4k2 − k − 2−12k2 − k − 14 = 0 = 0 = 0. Следовательно, по формуле Виета сумма всех возможных значений kkk равна 1.1.1. □ _ \ квадрат □

параллельных и перпендикулярных линий — концепция

Работа с параллельными и перпендикулярными
линиями действительно важна не только в алгебре, но и в геометрии
.
Итак,
вы захотите повторить эту концепцию в конце
курса алгебры, прежде чем переходить
к геометрии.

Во-первых, две прямые параллельны, если они никогда не пересекаются. Их наклоны одинаковые.
Многие люди думают о
железнодорожных путях, когда думают о
параллельных линиях. Если в своем мозгу
вы представляете себе, как железнодорожные шпалы
— так они называются?
Галстуки? Я думаю так. Они всегда параллельны
. Они никогда, никогда не пересекаются
, и они идут вечно
через землю. Думаю, не
навсегда. Это идея
параллельных линий.

Если вы посмотрите на уравнения,
вы узнаете, что две прямые параллельны, а
не построил их график, если их наклоны
одинаковы. Позвольте мне быстро нарисовать
изображений этого. Помните, что уклоны
означают крутизну линии
. Таким образом, уклоны одинаковы, это означает, что
эти две линии одинаково крутые.
Это то, что может помочь вам
запомнить.

Это другая концепция.
Две прямые называются перпендикулярными
, если они пересекаются под прямым углом
, их наклоны противоположны знакам
, обратным знакам.

Итак, давайте посмотрим на картинку.
Это опять же не идеально,
, а изображение двух перпендикулярных
линий. Перпендикулярные линии означают
, что они пересекаются под прямым углом. Итак,
, если я проведу эту линию прямо здесь, перпендикулярная линия
будет выглядеть как
. Это не здорово. Вы могли бы сказать, что
перпендикулярно
, если бы вы взяли бумагу и воткнули
ее прямо в угол, она
идеально подошла бы, все четыре угла.
Моя не отличная.Вы уловили идею.

Перпендикулярные линии означают, что они пересекают
под прямым углом, который составляет 90 градусов, и с
вы будете много работать с этим в геометрии.

Поговорим подробнее о встречных обратных наклонах
. Например, если бы я дал вам число
-2, обратная величина 2 будет
1/2. Также обратите внимание, как вместо
-2 я написал положительное 1/2. Эти
— противоположные знаки, означающие положительный знак,
— отрицательный, и это
взаимных знаков. Другой пример:
будет, например, 3/4, а противоположный знак
будет равен -4/3.

Это те виды склонов, которые
мы ищем, когда говорим о
перпендикулярных линиях. Эти
— это вещи, которые вам просто нужно запомнить:
: параллель никогда не пересекается,
— тот же уклон; перпендикулярно означает, что они
пересекаются под прямым углом, напротив знака
обратные. На самом деле ярлыков для
нет. Но эти
действительно, очень важные определения
, которые вам понадобятся в алгебре, а
— также в геометрии.

Параллельные и перпендикулярные линии

Определение параллельности и перпендикуляра

Параллельные линии Линии в одной плоскости, которые не пересекаются; их наклоны одинаковы.линии в одной плоскости, которые никогда не пересекаются. Две невертикальные прямые в одной плоскости с наклонами m1 и m2 параллельны, если их наклоны одинаковы, m1 = m2. Рассмотрим следующие две строки:

Рассмотрим соответствующие им графики:

Обе прямые имеют наклон m = 34 и поэтому параллельны.

Перпендикулярные линии Линии в одной плоскости, пересекающиеся под прямым углом; их наклоны противоположны друг другу.- это прямые в одной плоскости, пересекающиеся под прямым углом (90 градусов). Две невертикальные прямые в одной плоскости с наклонами m1 и m2 перпендикулярны, если произведение их наклонов равно −1: m1⋅m2 = −1. Мы можем решить относительно m1 и получить m1 = −1m2. В этой форме мы видим, что перпендикулярные линии имеют наклон, равный отрицательным обратным величинам или противоположным обратным величинам. Два действительных числа, произведение которых равно -1. Для действительного числа ab обратная величина равна -ba .. Например, если задан наклон

, то наклон перпендикулярной прямой противоположен обратной величине:

Математическое обозначение m⊥ означает « м, перпендикуляр.«Мы можем проверить, что два склона образуют перпендикулярные линии, если их произведение равно −1.

С геометрической точки зрения отметим, что если прямая имеет положительный наклон, то любая перпендикулярная линия будет иметь отрицательный наклон. Кроме того, подъем и спуск между двумя перпендикулярными линиями меняются местами.

Перпендикулярные линии имеют наклон, противоположный обратному, поэтому не забудьте найти обратный и изменить знак. Другими словами,

Определение наклона перпендикулярной прямой можно выполнить мысленно.Ниже приведены некоторые примеры.

Заданный уклон	Наклон перпендикулярной линии
м = 12	м⊥ = −2
м = −34	м⊥ = 43
м = 3	м⊥ = −13
м = −4	м⊥ = 14

Пример 1: Определите наклон прямой, параллельной y = −5x + 3.

Решение: Поскольку данная линия находится в форме пересечения наклона, мы можем видеть, что ее наклон равен m = −5. Таким образом, наклон любой прямой, параллельной данной прямой, должен быть одинаковым, m∥ = −5. Математическое обозначение m∥ читается как « м, параллель».

Ответ: m∥ = −5

Пример 2: Определите наклон прямой, перпендикулярной 3x − 7y = 21.

Решение: Сначала найдите y и выразите прямую в форме пересечения наклона.

В этой форме мы видим, что наклон данной прямой равен m = 37, и, следовательно, m − = −73.

Ответ: m⊥ = −73

Попробуй! Найдите наклон прямой, перпендикулярной к 15x + 5y = 20.

Ответ: m⊥ = 13

Нахождение уравнений параллельных и перпендикулярных прямых

Мы видели, что график линии полностью определяется двумя точками или одной точкой и ее наклоном.Часто вас просят найти уравнение линии при некотором геометрическом соотношении — например, параллельна ли линия другой линии или перпендикулярна ей.

Пример 3: Найдите уравнение прямой, проходящей через (6, −1) и параллельной y = 12x + 2.

Решение: Здесь заданная прямая имеет наклон m = 12, а наклон параллельной прямой равен m∥ = 12. Поскольку вам даны точка и наклон, используйте форму линии «точка-наклон» для определения уравнения.

Ответ: y = 12x − 4

Важно иметь геометрическое понимание этого вопроса. Нас попросили найти уравнение прямой, параллельной другой прямой, проходящей через определенную точку.

Через точку (6, −1) мы нашли параллельную линию y = 12x − 4, показанную пунктиром. Обратите внимание, что наклон такой же, как у данной линии, но пересечение y другое. Если иметь в виду геометрическую интерпретацию, тогда будет легче запомнить процесс, необходимый для решения задачи.

Пример 4: Найдите уравнение прямой, проходящей через (−1, −5) и перпендикулярной y = −14x + 2.

Решение: Данная прямая имеет наклон m = −14, следовательно, m⊥ = + 41 = 4. Подставьте этот уклон и данную точку в форму «точка-уклон».

Ответ: y = 4x − 1

Геометрически мы видим, что прямая y = 4x − 1, показанная ниже пунктирной линией, проходит через (−1, −5) и перпендикулярна данной прямой.

Это не всегда тот случай, когда данная линия имеет форму пересечения уклона. Часто для определения уклона приходится выполнять дополнительные действия. Общие шаги по поиску уравнения линии описаны в следующем примере.

Пример 5: Найдите уравнение прямой, проходящей через (8, −2) и перпендикулярной 6x + 3y = 1.

Решение:

Шаг 1: Найдите уклон м .Сначала найдите наклон данной линии. Для этого найдите y , чтобы изменить стандартную форму на форму с пересечением наклона, y = mx + b.

В этой форме вы можете видеть, что наклон равен m = −2 = −21, и, следовательно, m⊥ = −1−2 = + 12.

Шаг 2: Подставьте найденный угол наклона и заданную точку в форму уравнения для прямой. В этом случае наклон равен m⊥ = 12, а заданная точка равна (8, −2).

Шаг 3: Решите относительно y .

Ответ: y = 12x − 6

Пример 6: Найдите уравнение прямой, проходящей через (72, 1) и параллельной 2x + 14y = 7.

Решение: Найдите уклон м , решив для y .

Данная прямая имеет наклон m = −17, поэтому m∥ = −17. Мы используем это и точку (72, 1) в форме точечного наклона.

Ответ: y = −17x + 32

Попробуй! Найдите уравнение прямой, перпендикулярной x − 3y = 9 и проходящей через (−12, 2).

Ответ: y = −3x + 12

При нахождении уравнения линии, перпендикулярной горизонтальной или вертикальной линии, лучше всего учитывать геометрическую интерпретацию.

Пример 7: Найдите уравнение прямой, проходящей через (−3, −2) и перпендикулярной y = 4.

Решение: Мы понимаем, что y = 4 является горизонтальной линией, и мы хотим найти перпендикулярную линию, проходящую через (−3, −2).

Если мы проведем линию перпендикулярно заданной горизонтальной линии, в результате получится вертикальная линия.

Уравнения вертикальных линий имеют вид x = k. Поскольку он должен проходить через (−3, −2), мы заключаем, что x = −3 — это уравнение. Все упорядоченные парные решения вертикальной линии должны иметь одну и ту же координату x .

Ответ: x = −3

Мы можем переписать уравнение любой горизонтальной линии y = k в форме пересечения наклона следующим образом:

Записав в таком виде, мы видим, что наклон m = 0 = 01.Если мы попытаемся найти наклон перпендикулярной линии, найдя обратную обратную величину, мы столкнемся с проблемой: m⊥ = −10, что не определено. Вот почему мы постарались ограничить определение двумя невертикальными линиями. Помните, что горизонтальные линии перпендикулярны вертикальным линиям.

Основные выводы

Параллельные прямые имеют одинаковый наклон.
Перпендикулярные линии имеют наклон, противоположный обратному. Другими словами, если m = ab, то m⊥ = −ba.
Чтобы найти уравнение прямой, сначала используйте данную информацию для определения наклона. Затем используйте наклон и точку на линии, чтобы найти уравнение, используя форму «точка-наклон».
Горизонтальные и вертикальные линии перпендикулярны друг другу.

Тематические упражнения

Часть A: Параллельные и перпендикулярные линии

Определите наклон параллельных и перпендикулярных прямых.

1. y = −34x + 8

2. y = 12x − 3

3. y = 4x + 4

4. y = −3x + 7

5. y = −58x − 12

6. y = 73x + 32

7. y = 9x − 25

8. y = −10x + 15

9. y = 5

10. х = −12

11. х-у = 0

12. х + у = 0

13. 4x + 3y = 0

14.3х − 5у = 10

15. −2x + 7y = 14

16. −x − y = 15

17. 12x − 13y = −1

18. −23x + 45y = 8

19. 2x − 15y = 110

20. −45x − 2y = 7

Определите, параллельны ли линии, перпендикулярны или нет.

21. {y = 23x + 3y = 23x − 3

22. {y = 34x − 1y = 43x + 3

23. {y = −2x + 1y = 12x + 8

24.{y = 3x − 12y = 3x + 2

25. {y = 5x = −2

26. {y = 7y = −17

27. {3x − 5y = 155x + 3y = 9

28. {x − y = 73x + 3y = 2

29. {2x − 6y = 4 − x + 3y = −2

30. {−4x + 2y = 36x − 3y = −3

31. {x + 3y = 92x + 3y = 6

32. {y − 10 = 0x − 10 = 0

33. {y + 2 = 02y − 10 = 0

34. {3x + 2y = 62x + 3y = 6

35. {−5x + 4y = 2010x − 8y = 16

36.{12x − 13y = 116x + 14y = −2

Часть B: Уравнения в форме точечного уклона

Найдите уравнение прямой.

37. Параллельно y = 12x + 2 и проходит через (6, −1).

38. Параллельно y = −34x − 3 и проходит через (−8, 2).

39. Перпендикулярно y = 3x − 1 и проходит через (−3, 2).

40. Перпендикулярно y = −13x + 2 и проходит через (4, −3).

41.Перпендикулярно y = −2 и проходит через (−1, 5).

42. Перпендикулярно x = 15 и проходит через (5, −3).

43. Параллельно y = 3 и проходит через (2, 4).

44. Параллельно x = 2 и проходит через (7, −3).

45. Перпендикулярно y = x и проходит через (7, −13).

46. Перпендикулярно y = 2x + 9 и проходит через (3, −1).

47. Параллельно y = 14x − 5 и проходит через (−2, 1).

48. Параллельно y = −34x + 1 и проходит через (4, 1/4).

49. Параллельно 2x − 3y = 6 и проходит через (6, −2).

50. Параллельно −x + y = 4 и проходит через (9, 7).

51. Перпендикулярно 5x − 3y = 18 и проходит через (−9, 10).

52. Перпендикулярно x − y = 11 и проходит через (6, −8).

53. Параллельно 15x − 13y = 2 и проходит через (−15, 6).

54.Параллельно −10x − 57y = 12 и проходит через (−1, 1/2).

55. Перпендикулярно 12x − 13y = 1 и проходит через (−10, 3).

56. Перпендикулярно −5x + y = −1 и проходит через (−4, 0).

57. Параллельно x + 4y = 8 и проходит через (−1, −2).

58. Параллельно 7x − 5y = 35 и проходит через (2, −3).

59. Перпендикулярно 6x + 3y = 1 и проходит через (8, −2).

60. Перпендикулярно −4x − 5y = 1 и проходит через (−1, −1).

61. Параллельно −5x − 2y = 4 и проходит через (15, −14).

62. Параллельно 6x − 32y = 9 и проходит через (13, 23).

63. Перпендикулярно y − 3 = 0 и проходит через (−6, 12).

64. Перпендикулярно x + 7 = 0 и проходит через (5, −10).

ответы

1: m∥ = −34 и m⊥ = 43

3: m∥ = 4 и m⊥ = −14

5: m∥ = −58 и m⊥ = 85

7: m∥ = 9 и m⊥ = −19

9: m∥ = 0 и m⊥ не определено

11: m∥ = 1 и m⊥ = −1

13: m∥ = −43 и m⊥ = 34

15: m∥ = 27 и m⊥ = −72

17: m∥ = 32 и m⊥ = −23

19: m∥ = 10 и m⊥ = −110

21: параллельный

23: перпендикуляр

25: перпендикуляр

27: перпендикуляр

29: параллельный

31: Ни то, ни другое

33: параллельный

35: параллельный

37: y = 12x − 4

39: y = −13x + 1

41: х = -1

43: y = 4

45: у = −x − 6

47: y = 14x + 32

49: y = 23x − 6

51: y = −35x + 235

53: y = 35x + 15

55: y = −23x − 113

57: y = −14x − 94

59: y = 12x − 6

61: y = −52x + 14

63: х = −6

Как записывать уравнения перпендикулярных и параллельных линий

Параллельные прямые — это прямые, которые простираются до бесконечности, не касаясь ни одной точки.Перпендикулярные линии пересекаются под углом 90 градусов. Оба набора линий важны для многих геометрических доказательств, поэтому важно распознавать их графически и алгебраически. Вы должны знать структуру уравнения прямой линии, прежде чем сможете писать уравнения для параллельных или перпендикулярных линий. Стандартная форма уравнения — «y = mx + b», в котором «m» — наклон линии, а «b» — точка, в которой линия пересекает ось y.

Параллельные линии

Напишите уравнение для первой линии и определите наклон и точку пересечения по оси Y.

Пример: y = 4x + 3 m = slope = 4 b = y-intercept = 3

Скопируйте первую половину уравнения для параллельной прямой. Одна линия параллельна другой, если их наклоны одинаковы.

Пример: Исходная линия: y = 4x + 3 Параллельная линия: y = 4x

Выберите точку пересечения оси Y, отличную от исходной линии. Независимо от величины нового пересечения по оси Y, если наклон одинаков, две линии будут параллельны.

Пример: Исходная линия: y = 4x + 3 Параллельная линия 1: y = 4x + 7 Параллельная линия 2: y = 4x — 6 Параллельная линия 3: y = 4x + 15,328.35

Перпендикулярные линии

Напишите уравнение для первой линии и определите наклон и точку пересечения по оси Y, как в случае с параллельными линиями.

Пример: y = 4x + 3 m = slope = 4 b = y-intercept = 3

Преобразование для переменных «x» и «y». Угол поворота составляет 90 градусов, поскольку перпендикулярная линия пересекает исходную линию под углом 90 градусов.

Пример: x ‘= x_cos (90) — y_sin (90) y’ = x_sin (90) + y_cos (90)

Замените «y» и «x» вместо «x» и «y», а затем запишите уравнение в стандартной форме.

Пример: Исходная строка: y = 4x + 3 Заменитель: -x ‘= 4y’ + 3 Стандартная форма: y ‘= — (1/4) * x — 3/4

Исходная строка, y = 4x + b, перпендикулярно новой строке, y ‘= — (1/4) _x — 3/4, и любой прямой, параллельной новой строке, например y’ = — (1/4) _x — 10.

Перпендикулярные прямые, условие перпендикулярности прямых

Перпендикулярные прямые – основные сведения

Перпендикулярность прямых – условия перпендикулярности

Уравнение двух перпендикулярных прямых

Перпендикулярные прямые – основные сведения

Перпендикулярность прямых – условия перпендикулярности

Содержание

[править] Обозначения

[править] Формулы:

[править] Пример

[править] Уравнения прямой:

[править] Ссылки

Персональные инструменты

Пространства имён

Варианты

Просмотры

Действия

Поиск

Навигация

Инструменты

Перпендикулярность прямых — условия перпендикулярности.

Перпендикулярные прямые и их свойства. Перпендикулярные прямые Что называют перпендикулярной прямой

Перпендикулярность прямых – условия перпендикулярности

Что такое перпендикулярные прямые

Свойства

Фигуры с перпендикулярными прямыми

Сбор и использование персональной информации

Раскрытие информации третьим лицам

Защита персональной информации

Соблюдение вашей конфиденциальности на уровне компании

Свойства перпендикулярных прямых

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Линейная функция

График линейной функции

Прямые, параллельные оси ординат

Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые

03.03. Общее уравнение прямой | Контрольные работы по математике и други

Общее уравнение прямой

ДОКАЗАТЕЛЬСТВО

1. Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости.

Как найти уравнение перпендикулярной прямой

Поиск параллельных и перпендикулярных прямых

Параллельные линии

Пример:

Вертикальные линии

Не та же строка

Пример: y = 3x + 2 параллельно y — 2 = 3x?

Перпендикулярные линии

Пример:

Быстрая проверка перпендикуляра

Вертикальные линии

Сводка

параллельных и перпендикулярных линий | Колледж алгебры

Результаты обучения

Общее примечание: параллельные и перпендикулярные линии

Пример: определение параллельных и перпендикулярных линий

Анализ решения

Написание уравнений параллельных линий

Как сделать: учитывая уравнение линейной функции, напишите уравнение линии, КОТОРАЯ проходит через данную точку и параллельна данной прямой.

Пример: поиск прямой, параллельной заданной прямой

Анализ решения

Написание уравнений перпендикулярных прямых

Вопросы и ответы

Как сделать: учитывая уравнение линейной функции, напишите уравнение линии, КОТОРАЯ проходит через данную точку и перпендикулярна данной линии.

Пример: поиск уравнения перпендикулярной прямой

Анализ решения

Как сделать: даны две точки на линии и третья точка, запишите уравнение перпендикулярной линии, проходящей через точку.

Пример: поиск уравнения прямой, проходящей через точку и перпендикулярной заданной прямой

Попробуйте

Каково уравнение прямой, проходящей через точку (−7,3) (- 7, 3) (- 7,3) и перпендикулярной прямой y = 15x − 2? Y = \ frac {1} {5} x-2? Y = 51 x − 2?

параллельных и перпендикулярных линий — концепция

Параллельные и перпендикулярные линии

Определение параллельности и перпендикуляра

Нахождение уравнений параллельных и перпендикулярных прямых

Основные выводы

Тематические упражнения

ответы

Как записывать уравнения перпендикулярных и параллельных линий

Параллельные линии

Перпендикулярные линии