Второй закон Ньютона
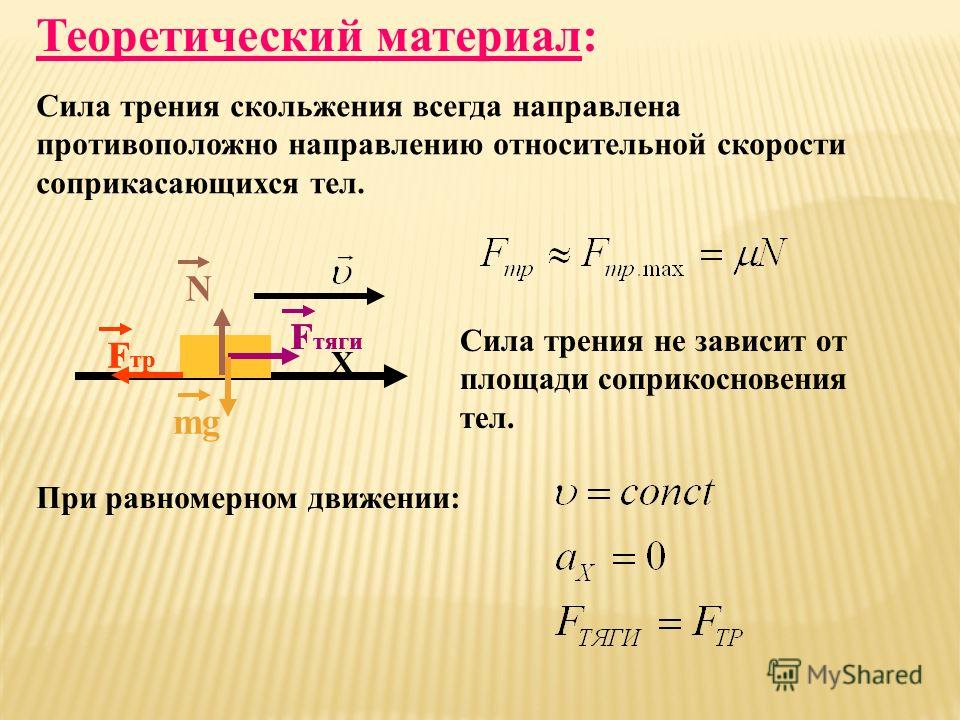
Сила – физическая величина, измеряемоя прибором динамометром и характеризующей действие одного тела на другое. Если на тело действует неуравновешенная сила, то такое тело обязательно изменяет свою скорость или направление движения. Другими словами, действие на тело неуравновешенной силы приводит к появлению ускорения.
Возникает вопрос: каким образом сила и вызываемое ей ускорение связаны друг с другом? Какова формула, выражающая связь этих величин?
Ответ на этот вопрос дает второй закон Ньютона: вектор силы, действующей на тело, в инерциальной системе отсчета равен произведению массы на вектор ускорения этого тела.
Чтобы убедиться в справедливости этой формулы, нужно измерить величины F и ma по отдельности, а затем сравнить их численные значения и направления векторов. Сделаем это. Возьмем прибор, представляющий из себя легко вращающийся диск (1). На нем укреплены указатель частоты вращения (2) и толстая линейка (3), одновременно служащая «рельсом» для ролика (4). При помощи нити ролик привязан к динамометру (5). При вращении ролик натянет нить, и динамометр покажет некую силу F, тем бо’льшую, чем быстрее вращается диск.
При помощи нити ролик привязан к динамометру (5). При вращении ролик натянет нить, и динамометр покажет некую силу F, тем бо’льшую, чем быстрее вращается диск.
Вращая диск, мы получим, например, такие данные:
| Ролик массой 0,25 кг | Ролик массой 0,5 кг | |||
| радиус (R), м | 0.2 | 0.2 | 0.2 | 0.2 |
| период (T), с | 1 | 2 | 1 | 2 |
| ускорение (а) | » 8 м/с2 | » 2 м/с2 | » 8 м/с2 | » 4 м/с2 |
| сила (F) | »2 H | »0.5 H | »4 H | »1 H |
Рассмотрим, как получились эти числа. Радиус R – это расстояние от ролика до центра диска. Во время вращения диска ролик откатывается по линейке до отметки 20 см. Значит, R = 0.2 м. Период T – это время, за которое диск совершает один оборот. Указатель частоты вращения на рисунке показывает 1 об/с. То есть за секунду совершается один оборот. Следовательно, период T = 1 с. Вычисляя центростремительное ускорение ролика по формуле a = 4p2R/T2, получим: 4 · 3.142 · 0.2 / 12 » 8 м/с2. Именно это число и записано в клетке «ускорение».
То есть за секунду совершается один оборот. Следовательно, период T = 1 с. Вычисляя центростремительное ускорение ролика по формуле a = 4p2R/T2, получим: 4 · 3.142 · 0.2 / 12 » 8 м/с2. Именно это число и записано в клетке «ускорение».
Итак, справедливо ли равенство F=ma? Перемножим подчеркнутые числа верхней таблицы. Имеем: 2 Н » 0.25 кг · 8 м/с2. Другими словами, F » ma.
Теперь убедимся, что векторы F и ma сонаправлены. Вспомним, что вектор центростремительного ускорения тела при его равномерном движении по окружности всегда направлен к центру этой окружности. Выясним, куда направлен вектор силы, придающей ролику это ускорение. Вообразим на мгновение, что нить, связывающая ролик и динамометр, вдруг оборвалась. Что произойдет с роликом? Он покатится по линейке и соскочит с диска. Следовательно, нить тянула ролик к оси вращения, не позволяя ему откатиться дальше. Другими словами, вектор F сонаправлен с вектором ускорения.
Таким образом мы подтвердили истинность векторного равенства: F = ma.
Масса покоя или инертная масса?
Масса покоя или инертная масса?УДК. 12:531.18+51]
Масса покоя или инертная масса?
Р. И. Храпко
Исключение из современных учебников физики инертной массы и замена ее массой покоя представляется ошибкой. Эта тема была поднята автором в статье [1,2]. Здесь приведены дополнительные рассуждения в подтверждение такого тезиса.
Конец 20-го века ознаменовался великой путаницей с физическим понятием «масса тела».
1. Масса покоя
В начале века, до создания теории относительности, было все ясно. Массой тела, m, называлось количество вещества тела, и в то же время масса являлась мерой инертности тела. Инертность тела определяет его «количество движения» при заданной скорости v движения, то есть коэффициент пропорциональности в формуле
P = mv.
P — количество движения или, по-научному, импульс тела, а коэффициент m называется инертной массой.
Но массу как меру инертности тела можно определять и с помощью формулы
F = ma: (2)
чем больше масса, тем меньше ускорение тела при заданной силе. Значение массы по формулам (1) и (2) получалось одно и то же, потому что формула (2) является следствием формулы (1), если инертная масса не зависит от времени и скорости.
То же значение массы можно было получить, взвесив тело, то есть измерив силу притяжения к земле или к любому другому заданному телу (масса которого обозначена M). В законе тяготения Ньютона фигурирует та же самая масса m,
, (3)
но тут она называется гравитационной (пассивной) массой. В этом выражается эквивалентность инертной и гравитационной массы. Благодаря этой эквивалентности ускорение свободного падения, как известно, не зависит от природы и массы тела:
(4)
2. Инертная масса
Инертная масса
Однако при создании теории относительности выяснилось, что никакое тело нельзя разогнать до скорости света, потому что при приближении скорости тела к скорости света ускорение тела уменьшается до нуля, как бы ни была велика ускоряющая сила. Другими словами, выяснилось, что инертность тела возрастает до бесконечности при приближении его скорости к скорости света, хотя «количество вещества» тела, очевидно, остается при этом неизменным.
Выскажемся точнее по поводу увеличения инертности тела. Теория относительности показала, что импульс тела P при любых скоростях остается параллелен скорости v. Поэтому формулу P
, (5)
то есть для импульса тела справедливо выражение
. (6)
В этих формулах m0 — это то значение массы
рассматриваемого тела, о котором говорилось
вначале, то есть значение, которое можно получить
после того, как тело затормозят до достаточно
малой скорости. Его называют массой покоя тела.
Поэтому формулы (1), (2), (3) следовало бы записать
так: P = m0v, F = m0a,
.
Однако для малых скоростей, как видно из формулы
(5), инертная масса равна массе покоя, m = m0, и поэтому запись (1), (2), (3) в разделе
«до теории относительности» корректна.
Его называют массой покоя тела.
Поэтому формулы (1), (2), (3) следовало бы записать
так: P = m0v, F = m0a,
.
Однако для малых скоростей, как видно из формулы
(5), инертная масса равна массе покоя, m = m0, и поэтому запись (1), (2), (3) в разделе
«до теории относительности» корректна.
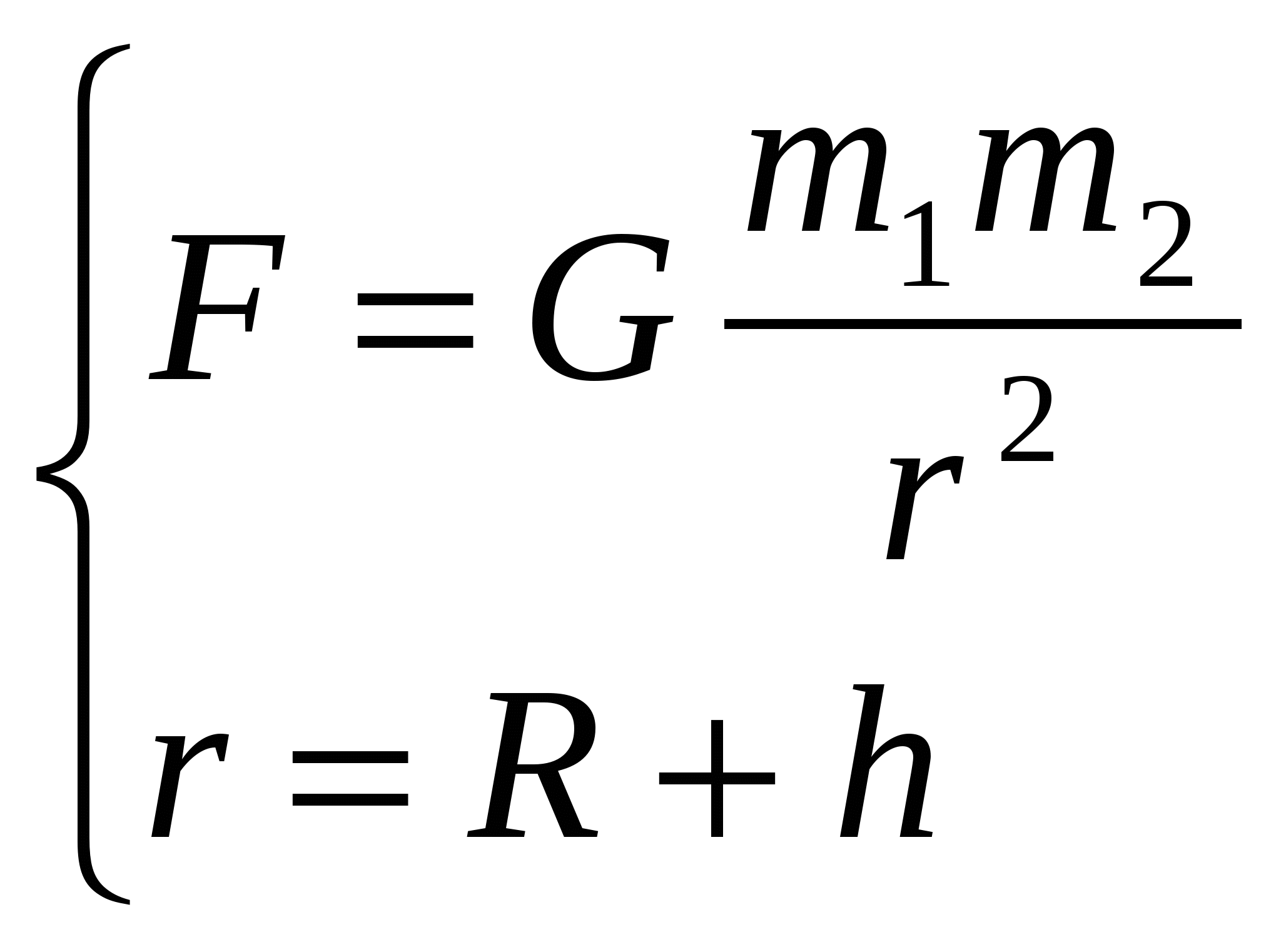 Однако существует собственная
скорость хода часов.
Однако существует собственная
скорость хода часов.При желании проверить формулу (6) вы должны измерить скорость v тела, а потом измерить импульс тела. Для этого следует затормозить тело некоторой преградой, все время замеряя силу F(t), с которой при торможении тело будет действовать на преграду, а потом проинтегрировать. Импульс, как известно, равен
(7)
Эта процедура, по сути, задает операционное определение инертной массы.
Заметим, что формулы (5) и (6) остаются
справедливыми и для объекта, у которого нет массы
покоя, m0 = 0,
например, для фотона или нейтрино (если
предположить, что масса покоя нейтрино равна
нулю). Такие объекты обладают инертной массой и
импульсом, но должны двигаться со скоростью
света, их нельзя остановить, они исчезают при
остановке. Тем не менее, несмотря на постоянство
скорости движения, величина их
инертной массы оказывается различной с точки
зрения различных наблюдателей. Однако в этом
случае не существует какого либо выделенного
значения инертной массы. Либо, можно сказать,
выделенное значение равно нулю.
Однако в этом
случае не существует какого либо выделенного
значения инертной массы. Либо, можно сказать,
выделенное значение равно нулю.
, (5)
она должна обеспечить возрастание самой массы:
. (8)
Коэффициент
называют иногда продольной массой [3] .
Если сила перпендикулярна скорости и, значит, не изменяет величину скорости и инертной массы, то формула F = ma сохраняет свой вид:
. (9)
Последнее обстоятельство позволило Р.
При произвольном направлении силы относительно скорости тела коэффициент пропорциональности в формуле (2) следует рассматривать как некий оператор (тензор), превращающий вектор a в вектор F: F = a. Оператор зависит от величины и направления скорости тела и, вообще говоря, изменяет направление вектора. Это нетрудно принять. Ведь скорость v тела является его свойством, а сила F, действующая на тело — это внешний по отношению к телу фактор. Понятно, что результат воздействия силы, то есть ускорение a тела, может зависеть от соотношения направлений векторов F и v.
3. Гравитационная масса
Гравитационная масса
Одновременно теория относительности показала, что не только инертность тела, но и его вес увеличивается с ростом скорости, причем по тому же закону (5) в соответствии с эквивалентностью инертной и гравитационной массы. Поэтому формула (8) для тела, падающего вниз со скоростью v, выглядит, грубо говоря, так:
= .
Точная формула для ускорения может быть получена в рамках общей теории относительности, как показано в конце статьи:
, . (10)
Эта формула является релятивистским аналогом формулы (4).
4. Энергия
Теория относительности показала далее, что прирост инертной массы, m — m0, умноженный на квадрат скорости света, равен как раз кинетической энергии тела:
(m √ m0)c
Поэтому, если приписать покоящемуся телу энергию покоя E0 = m0c2, то полная энергия E = E0 + Ek тела оказывается пропорциональной инертной массе:
E = mc2 (12)
Эта знаменитая формула Эйнштейна
провозглашает эквивалентность инертной массы и
энергии. Два, доселе различных понятия,
соединяются в одно.
Два, доселе различных понятия,
соединяются в одно.
Заметим, что формула (12), как и формулы (5) и (6) остается справедлива и для объекта, у которого нет массы и энергии покоя, m0 = 0.
При желании проверить формулу (11) и одновременно убедиться в справедливости теории относительности вы должны измерить инертную массу и массу покоя тела как было объяснено выше, и, кроме того, измерить кинетическую энергию тела. Для этого следует при торможении тела упомянутой преградой все время замерять силу, с которой тело будет действовать на преграду в процессе торможения в функции перемещения l преграды, F(l), а потом проинтегрировать. Кинетическая энергия, равная, как известно, в данном случае работе, вычисляется по формуле
.
Здесь F(l)dl — скалярное произведение силы на
инфинитезимальный вектор смещения преграды. Все
это рассказано в [5] .
Формула (11) связывает инертную массу, массу покоя и кинетическую энергию. Используя формулу (6) для вычисления разности m2 √ P2/c2, легко связать инертную массу, массу покоя и импульс:
. (13)
Для частиц с нулевой массой покоя получаем mc = P или E = Pc.
5.
При объединении нескольких тел в систему тел, как известно, их импульсы и их инертные массы складываются. Для двух тел это выглядит так:
P = P1 + P2, m = m1 + m2. (14)
Другими словами, импульс и инертная масса аддитивны. Не так обстоит дело с массой покоя. Из формул (13), (14) следует, что масса покоя пары тел с массами покоя m01, m02 равна не сумме m01 + m02, а сложному выражению, зависящему от импульсов P1, P2:
. (15)
(15)
Таким образом, масса покоя, вообще говоря, не аддитивна. Например, пара фотонов, не имеющих массу покоя, имеет массу покоя, если фотоны летят в разные стороны, и не имеет массу покоя, если фотоны летят в одну и ту же сторону.
Тем не менее, все три величины, P, m, m0, подчиняются закону сохранения, то есть не изменяются со временем для замкнутой системы.
Однако ввиду неаддитивности массы
покоя, на наш взгляд, нецелесообразно
рассматривать массу покоя системы тел. Имеет
смысл говорить лишь о сумме масс покоя отдельных
тел системы. В действительности именно так
поступают на практике. Когда говорят, что при
неупругих соударениях увеличивается масса
покоя, имеют ввиду не массу покоя системы,
которая удивительным образом сохраняется
неизменной при соударениях благодаря
неаддитивности, а сравнивают именно сумму масс
покоя тел до столкновения и массу покоя после
столкновения. Точно так же, когда говорят о
дефекте массы покоя при ядерных реакциях, имеют в
виду не массу покоя, определяемую формулой (15), а
сумму масс покоя частей системы.
Точно так же, когда говорят о
дефекте массы покоя при ядерных реакциях, имеют в
виду не массу покоя, определяемую формулой (15), а
сумму масс покоя частей системы.
6. Сравнение масс
Теперь уместно задать вопрос. Какую из двух масс, массу покоя или инертную массу следует назвать простым словом масса, обозначить буквой m без индексов и тем самым признать «главной» массой. Это — не терминологическая проблема. Здесь имеется серьезная психологическая подоплека.
Чтобы решить, какая из масс — главная, перечислим еще раз свойства обеих масс.
Масса покоя является постоянной
величиной для данного тела и выражает
«количество вещества тела». Она
соответствует привычному дорелятивисткому
ньютоновскому представлению о массе. Но она не
эквивалентна энергии, не эквивалентна
гравитационной массе, она не аддитивна и поэтому
не используется как характеристика системы тел или частиц. Это последнее обстоятельство
вызывает путаницу (см.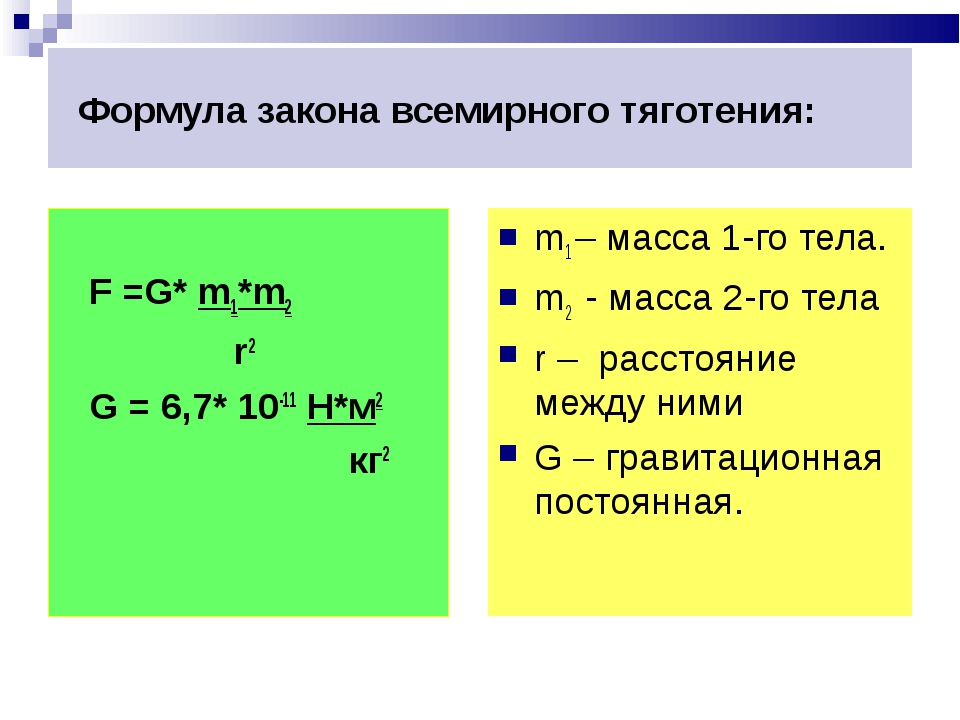 [1] , стр. 1365) и мешает
проявлению закона сохранения массы покоя. Фотоны
и частицы, движущиеся со скоростью света, не
обладают массой покоя. Операционное определение
массы покоя частицы предполагает торможение ее
до малой скорости без использования информации о
текущем состоянии частицы.
[1] , стр. 1365) и мешает
проявлению закона сохранения массы покоя. Фотоны
и частицы, движущиеся со скоростью света, не
обладают массой покоя. Операционное определение
массы покоя частицы предполагает торможение ее
до малой скорости без использования информации о
текущем состоянии частицы.
Инертная масса это — релятивистская масса. Она принимает различное значение для различных наблюдателей, аналогично тому, как скорость хода часов оказывается различной относительно различных наблюдателей. Инертная масса эквивалентна энергии и гравитационной массе, она аддитивна и подчиняется закону сохранения. Инертной массой обладают частицы, не имеющие массы покоя. Операционное определение инертной массы основано на простой формуле P = mv.
На наш взгляд, инертную массу следует называть массой и обозначать m, как это и делалось в настоящей статье.
7. Психологическая подоплека
К сожалению, большое количество
физиков считает массу покоя главной и обозначает
ее m а не m0, а инертную массу дискриминирует и
оставляет без обозначения, что вносит
дополнительную путаницу, поскольку из-за этого
порой бывает трудно понять, о какой массе идет
речь.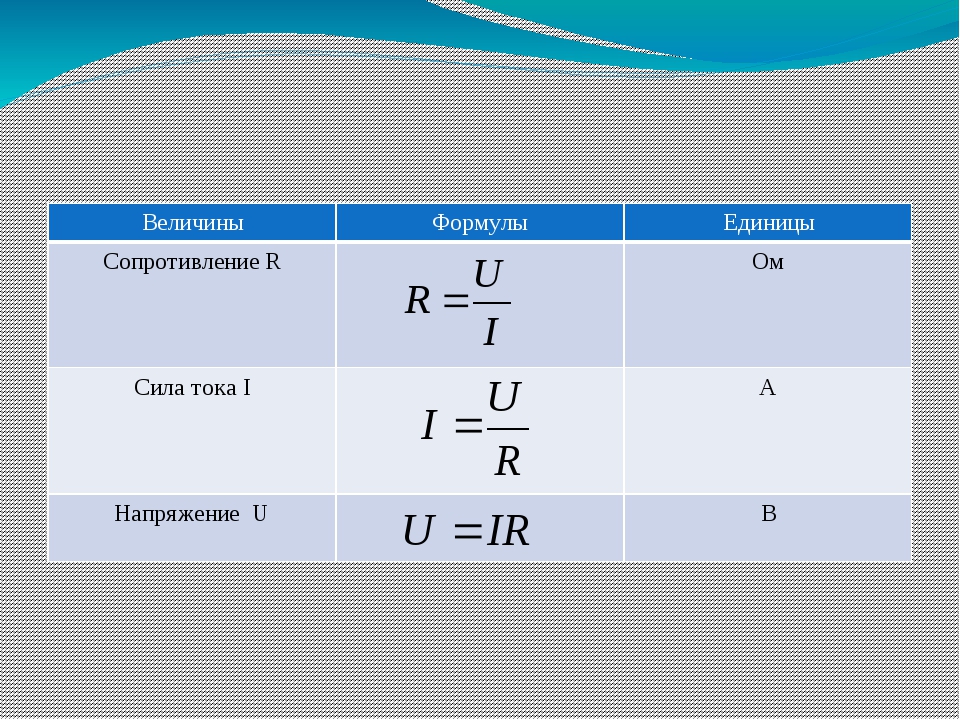
Эти физики соглашаются, например, с тем, что масса газа увеличивается при нагревании, потому что увеличивается содержащаяся в нем энергия, но психологический барьер мешает им попросту объяснить это увеличение ростом массы отдельных молекул вследствие увеличения их тепловой скорости.
Эти физики жертвуют представлением о массе как мере инертности в пользу ярлыка, прикрепляемого к каждой частице с информацией о неизменном «количестве вещества», потому что ярлык соответствует их привычному ньютоновскому представлению о массе. Они считают, например, что излучение, которое, согласно Эйнштейну [6] , «переносит инерцию между излучающими и поглощающими телами», не имеет массы, поскольку к излучению невозможно прикрепить ярлык.
Инертная масса отсутствует в издаваемых сейчас
стандартных учебниках физики в России
(И.В.Савельев) и за рубежом [7,8], а также в
популярной литературе [9] . Этот факт, однако, скрыт
тем обстоятельством, что сторонники массы покоя
настойчиво называют массу покоя не массой покоя,
а просто массой, словом, которое ассоциируется с
мерой инерции.
Главная психологическая трудность заключается в том, чтобы отождествить массу и энергию (которая изменяется), чтобы принять эти две сущности, как одну. Легко принять формулу E0 = m0c2 для покоящегося тела. Труднее принять справедливость формулы E = mc2 для любой скорости. Замечательная формула E= mc2 представляется, например, Л.Б. Окуню «безобразной» [10] .
Сторонники массы покоя, видимо, не в состоянии
принять идею инертной, релятивистской массы так
же, как ранее противники теории относительности
не могли принять относительность времени. Ведь
время жизни астронавта или нестабильной частицы
изменяется так же, как изменяется их инертная
масса: . Здесь уместно процитировать М.
Планка: «Великая научная идея редко внедряется
путем постепенного убеждения и обращения своих
противников, редко бывает, что Савл становится
Павлом. В действительности дело происходит так,
что оппоненты постепенно вымирают, а растущее
поколение с самого начала осваивается с новой
идеей. » [11] К сожалению, великая идея
релятивистской массы тщательно изолируется от молодежи. На данный момент статья
[1, 2] отклонена редакциями следующих журналов:
«Известия вузов. Физика», «Квант», «American Journal of Physics»,
«Physics Education» (Bristol), «Physics Today».
» [11] К сожалению, великая идея
релятивистской массы тщательно изолируется от молодежи. На данный момент статья
[1, 2] отклонена редакциями следующих журналов:
«Известия вузов. Физика», «Квант», «American Journal of Physics»,
«Physics Education» (Bristol), «Physics Today».
8. Шварцшильдовское пространство
Мы получим здесь формулу (10), рассмотрев пространство-время Шварцшильда общей теории относительности с выражением для интервала s [12] :
.
Уравнения радиальной геодезической линии могут быть получены по общей формуле, использующей коэффициенты связности :
, (16)
. (17)
Первый интеграл уравнения (16) легко находится:
. (18)
Запишем теперь выражение для ускорения a, учитывая (18) и то, что соотношения между расстоянием l и временем , с одной стороны, и координатами r, t, с другой, даются формулами
, :
.
Выразив таким образом ускорение a через , мы можем теперь воспользоваться уравнением (17), а затем, вернувшись к l и , получить окончательно
, . (10)
Список литературы
1. Храпко Р. И. Что есть масса? // Успехи физических наук. — 2000, N12. √ с.1363-1366.
2. Храпко Р. И. Что есть масса? — http://www.mai.ru. Труды МАИ, Вып.2.
3. Фриш С. Э., Тиморева А. В. Курс общей физики. Т. 3. — М.: ГИТТЛ, 1951.- 547 с.
4. Фейнман Р. и др. Фейнмановские лекции по физике. Т. 1. — М.: Мир, 1965. √ 232 с.
5. Храпко Р. И., Спирин Г.Г., Разоренов В. М. Механика. — М.: МАИ, 1993. √ 89 с.
6. Эйнштейн А. Зависит ли инерция тела от содержащейся в нем энергии. // Принцип относительности. — ОНТИ, 1935.- с.175-178.
7. Resnick R., Halliday D., Krane K. S. Physics. V.1 — N.Y.: J. Wiley, 1992.-592p.
8. Alonso M., Finn E. J. Physics — N.Y.: Addison-Wesley, 1995. -496p.
-496p.
9. Taylor E. F., Wheeler J. A. Spacetime Physics. √ San Francisco: Freeman, 1966.- 631c. Русский перевод: Тейлор Э. Ф., Уилер Дж. А. Физика пространства-времени. √ М.: Мир, 1971.- 612c.
10. Окунь Л. Б. Понятие массы. // Успехи физических наук. — 1989, т. 158. — с.512-530.
11. Планк М. Происхождение научных идей и влияние их на развитие науки./ М. Планк.// Сборник статей к столетию со дня рождения Макса Планка. — М.: АНСССР, 1958.- с.52.
12. Ландау Л.Д., Лифшиц Е.М. Теория поля. — М.: Наука, 1973.- 504с.
Урок 7. законы динамики ньютона — Физика — 10 класс
Физика, 10 класс
Урок 7. Законы динамики Ньютона
Перечень вопросов, рассматриваемых на уроке: основные характеристики массы и силы; взаимодействие тел; законы динамики Ньютона и их особенности; экспериментальная проверка справедливости законов Ньютона.
Глоссарий по теме.
Масса – одна из основных характеристик материи, определяющая ее инерциальные и гравитационные свойства.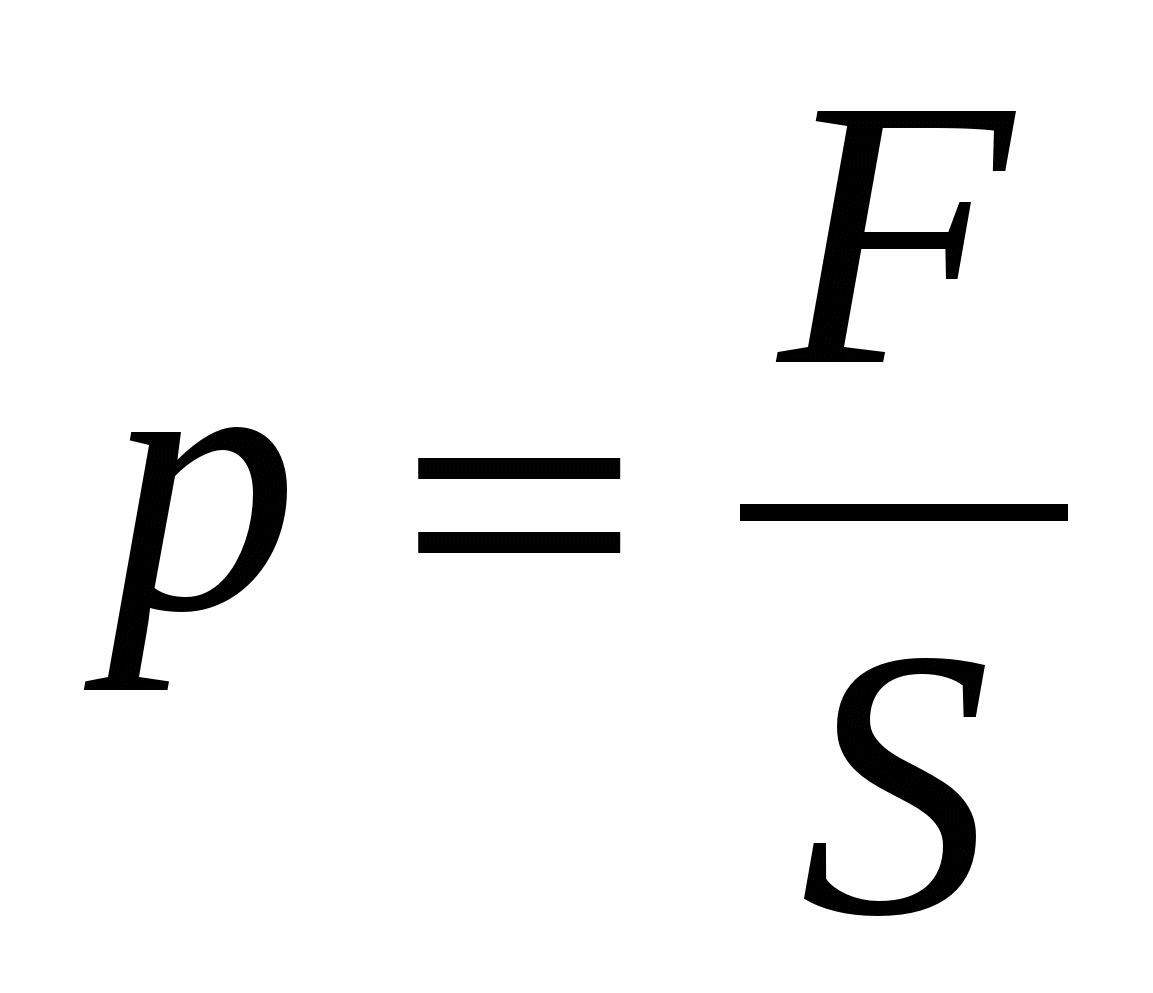
Сила – векторная физическая величина, являющаяся мерой взаимодействия тел.
Взаимодействие – одновременное влияние (действие) тел друг на друга.
Равнодействующая сила производит на тело такое же действие (вызывает такое же действие), как несколько сил, одновременно приложенных к телу.
Инерция – явление сохранения скорости тела при отсутствии (или компенсации) действия на него других тел.
Инерциальная система отсчета – система отсчета, в которой тело, не взаимодействующее с другими телами, сохраняет состояние равномерного прямолинейного движения или покоя.
Неинерциальные системы отсчета — система отсчета, которая двигается с ускорением относительно инерциальной системы отсчета.
Список литературы:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 64 – 87.
О. Ф. Кабардин, В. А. Орлов, А. В. Паномарева. Факультативный курс физики. М.: Просвещение, 1987. – С. 188 – 200.
– С. 188 – 200.
Открытые электронные ресурсы:
http://kvant.mccme.ru/1971/05/zadachi_na_zakony_nyutona.htm
Основное содержание урока
Масса (лат. « massa» — ком, кусочек, глыба) — физическая величина, одна из основных характеристик материи, определяющая ее инерциальные и гравитационные свойства.
Способы измерения массы:1) сравнение с эталоном; 2) взвешивание на весах. В классической механике масса — аддитивная величина; не зависит от рода взаимодействия и скорости движения тела.
Сила — мера взаимодействия тел. Атрибуты силы: точка приложения силы, линия действия силы, модуль силы.
Первый закон Ньютона (закон инерции): если на тело не действуют другие тела, то тело движется прямолинейно и равномерно.
Особенности первого закона Ньютона: указывает на существование инерциальных систем отсчета; равнодействующая всех сил равна нулю: F = 0.
Если есть одна инерциальная система отсчета, то любая другая система, движущаяся относительно неё прямолинейно и равномерно, также является инерциальной.
Второй закон Ньютон: ускорение тела прямо пропорционально силе, действующей на него, и обратно пропорционально его массе: a =F/m.
Другая запись формулы второго закона Ньютона (основное уравнение динамики): F =ma.
Формулировка второго закона Ньютона для системы тел: приращение импульса ∆Pсистемы тел равно по величине и по направлению импульсу внешних сил Fвн, действующих на тело, за то же время: ∆p =(F∆ Pсист).
Особенности второго закона Ньютона: выполняется в инерциальных системах отсчета; скорость тела мала по сравнению со скоростью света; макрообъекты; постоянная масса; справедлив для любых сил; сила — причина, ускорение – следствие; вектор ускорения а сонаправлен с вектором F.
Согласно третьему закону Ньютона тела действуют друг на друга с силами, равными по модулю и противоположными по направлению:
F12 =-F 21
Особенности третьего закона Ньютона: выполняется в инерциальных системах отсчета; силы всегда действуют парами; силы являются силами одной природы; силы не уравновешивают друг друга; выполняется для всех сил в природе
Разбор тренировочных заданий
1. Вставьте в текст пропущенные слова из следующего ряда: действие, скорость, направление, деформация, нагревание.
Вставьте в текст пропущенные слова из следующего ряда: действие, скорость, направление, деформация, нагревание.
Сила характеризует (_____________) одного тела на другое, в результате которого изменяется (___________) тела или происходит (______________) тел.
Правильный ответ: действие; скорость, деформация
2. Автомобиль массой 0,5 т. разгоняется с места равноускоренно и достигает скорости 40 м/с за 20 с. Равнодействующая всех сил, действующих на автомобиль равна __ кН.
Решение:
При V0=0 ускорение автомобиля равно:
a =v /∆t
Следовательно, равнодействующая сила по второму закону Ньютона равна:
F = ma = mv/∆t
Проверка размерностей: F = кг × м/с × с (-1)= [ Н ]
F= 500 кг × (40 м/с)/(20 с)= 1000 Н = 1 кН
Ответ: F= 1 кН.
| |||||
Равномерное движение | Равноускоренное движение | Тело движется вертикально | Тело брошено горизонтально | Тело брошено под углом к горизонту |
|
| Движение вниз
Движение вверх
|
|
| Тело движется по окружности 1. 2. 3. v 4. 5. 6. а – центрострем. ускорение, — угловая скорость, — угол поворота, — угловое ускорение, — частота вращения, Т – период, R — радиус | Механические колебания и волны 1. 3. ускорение a = -A2sin(t + 0), amax = A2 4. период пруж. маят. 5. период мат. маят. 6. 7. 8. 9. 10. v = А –амплитуда, t – время колебаний, N – число колебаний, v скорость, с – скорость света, λ – длина волны, ν – частота, l – длина маятника, Т — период |
Центробежная сила • Джеймс Трефил, энциклопедия «Двести законов мироздания»
Во вращающейся системе отсчета наблюдатель испытывает на себе действие силы, уводящей его от оси вращения.
Вам, наверное, доводилось испытывать неприятные ощущения, когда машина, в которой вы едете, входила в крутой вираж. Казалось, что сейчас вас так и выбросит на обочину. И если вспомнить законы механики Ньютона, то получается, что раз вас буквально вдавливало в дверцу, значит на вас действовала некая сила. Ее обычно называют «центробежная сила». Именно из-за центробежной силы так захватывает дух на крутых поворотах, когда эта сила прижимает вас к бортику автомобиля. (Между прочим, этот термин, происходящий от латинских слов centrum («центр») и fugus («бег»), ввел в научный обиход в 1689 году Исаак Ньютон.)
Казалось, что сейчас вас так и выбросит на обочину. И если вспомнить законы механики Ньютона, то получается, что раз вас буквально вдавливало в дверцу, значит на вас действовала некая сила. Ее обычно называют «центробежная сила». Именно из-за центробежной силы так захватывает дух на крутых поворотах, когда эта сила прижимает вас к бортику автомобиля. (Между прочим, этот термин, происходящий от латинских слов centrum («центр») и fugus («бег»), ввел в научный обиход в 1689 году Исаак Ньютон.)
Стороннему наблюдателю, однако, всё будет представляться иначе. Когда машина закладывает вираж, наблюдатель сочтет, что вы просто продолжаете прямолинейное движение, как это и делало бы любое тело, на которое не оказывает действия никакая внешняя сила; а автомобиль отклоняется от прямолинейной траектории. Такому наблюдателю покажется, что это не вас прижимает к дверце машины, а, наоборот, дверца машины начинает давить на вас.
Впрочем, никаких противоречий между этими двумя точками зрения нет. В обеих системах отсчета события описываются одинаково и для этого описания используются одни и те же уравнения. Единственным отличием будет интерпретация происходящего внешним и внутренним наблюдателем. В этом смысле центробежная сила напоминает силу Кориолиса (см. Эффект Кориолиса), которая также действует во вращающихся системах отсчета.
В обеих системах отсчета события описываются одинаково и для этого описания используются одни и те же уравнения. Единственным отличием будет интерпретация происходящего внешним и внутренним наблюдателем. В этом смысле центробежная сила напоминает силу Кориолиса (см. Эффект Кориолиса), которая также действует во вращающихся системах отсчета.
Поскольку не все наблюдатели видят действие этой силы, физики часто называют центробежную силу фиктивной силой или псевдосилой. Однако мне кажется, что такая интерпретация может вводить в заблуждение. В конце концов, едва ли можно назвать фиктивной силу, которая ощутимо придавливает вас к дверце автомобиля. Просто всё дело в том, что, продолжая двигаться по инерции, ваше тело стремится сохранить прямолинейное направление движения, в то время как автомобиль от него уклоняется и из-за этого давит на вас.
Чтобы проиллюстрировать эквивалентность двух описаний центробежной силы, давайте немного поупражняемся в математике. Тело, движущееся с постоянной скоростью по окружности, движется с ускорением, поскольку оно всё время меняет направление. Это ускорение равно v2/r, где v — скорость, а r — радиус окружности. Соответственно, наблюдатель, находящийся в движущейся по окружности системе отсчета, будет испытывать центробежную силу, равную mv2/r.
Тело, движущееся с постоянной скоростью по окружности, движется с ускорением, поскольку оно всё время меняет направление. Это ускорение равно v2/r, где v — скорость, а r — радиус окружности. Соответственно, наблюдатель, находящийся в движущейся по окружности системе отсчета, будет испытывать центробежную силу, равную mv2/r.
Теперь обобщим сказанное: любое тело, движущееся по криволинейной траектории, — будь то пассажир в машине на вираже, мяч на веревочке, который вы раскручиваете над головой, или Земля на орбите вокруг Солнца — испытывает на себе действие силы, которая обусловлена давлением дверцы автомобиля, натяжением веревки или гравитационным притяжением Солнца. Назовем эту силу F. С точки зрения того, кто находится во вращающейся системе отсчета, тело не движется. Это означает, что внутренняя сила F уравновешивается внешней центробежной силой:
F = mv2/r
Однако с точки зрения наблюдателя, находящегося вне вращающейся системы отсчета, тело (вы, мяч, Земля) движется равноускоренно под воздействием внешней силы. Согласно второму закону механики Ньютона, отношение между силой и ускорением в этом случае F = ma. Подставив в это уравнение формулу ускорения для тела, движущегося по окружности, получим:
Согласно второму закону механики Ньютона, отношение между силой и ускорением в этом случае F = ma. Подставив в это уравнение формулу ускорения для тела, движущегося по окружности, получим:
F = ma = mv2/r
Но тем самым мы получили в точности уравнение для наблюдателя, находящегося во вращающейся системе отсчета. Значит, оба наблюдателя приходят к идентичным результатам относительно величины действующей силы, хотя и исходят из разных предпосылок.
Это очень важная иллюстрация того, что представляет собою механика как наука. Наблюдатели, находящиеся в различных системах отсчета, могут описывать происходящие явления совершенно по-разному. Однако, сколь бы принципиальными ни были различия в подходах к описанию наблюдаемых ими явлений, уравнения, их описывающие, окажутся идентичными. А это — не что иное, как принцип инвариантности законов природы, лежащий в основе теории относительности.
Механика на ЕГЭ по физике
Механика — раздел физики, изучающий виды, законы движения. На ЕГЭ встречается в номерах 1-7, 27-29. Примерно половина экзамена! Неудивительно, ведь механика в физике включает понятия скорости, ускорения, силы, массы, энергии, колебаний, волн. Хотите полностью освоить тему? Подумайте о курсах подготовки к ЕГЭ. Там дают много полезного материала, он пригодится на итоговой аттестации, для учебы в университете. В статье изучим основы механики в физике, рассмотрим главные формулы для ЕГЭ.
На ЕГЭ встречается в номерах 1-7, 27-29. Примерно половина экзамена! Неудивительно, ведь механика в физике включает понятия скорости, ускорения, силы, массы, энергии, колебаний, волн. Хотите полностью освоить тему? Подумайте о курсах подготовки к ЕГЭ. Там дают много полезного материала, он пригодится на итоговой аттестации, для учебы в университете. В статье изучим основы механики в физике, рассмотрим главные формулы для ЕГЭ.
Теория
Изучение механики начнем с теории. Важнейшим понятием является материальная точка — объект с пренебрежимо малыми размерами. Сохраняется только масса. Тело обозначают материальной точкой, когда оно движется поступательно, а расстояния, изучаемые в задаче, много больше размеров. В механике рассматриваются также абсолютно твердые тела. Расстояние между двумя любыми точками таких объектов остается постоянным.
Следующее определение для задач ЕГЭ — перемещение, т.е. вектор, проведенный из точки начала движения в точку его окончания. Не путайте перемещение и путь. Путь — участок траектории, пройденный материальной точкой за определенный промежуток времени. Отношение перемещения ко времени называется скоростью: v = s / t. Задачи по механике в физике иногда рассматривают две скорости, связанные с разными системами координат. Применяется закон сложения скоростей v2 = v1 + v. Здесь v2, v1 — скорости точки в двух системах отсчета, v — скорость системы 1, движущейся относительно системы 2.
Путь — участок траектории, пройденный материальной точкой за определенный промежуток времени. Отношение перемещения ко времени называется скоростью: v = s / t. Задачи по механике в физике иногда рассматривают две скорости, связанные с разными системами координат. Применяется закон сложения скоростей v2 = v1 + v. Здесь v2, v1 — скорости точки в двух системах отсчета, v — скорость системы 1, движущейся относительно системы 2.
В заданиях по механике из ЕГЭ по физике встречается понятие ускорения — величина, отражающая быстроту изменения скорости. Она представляет собой отношение скорости к пройденному времени: a = v / t. Как и скорость, является векторной величиной. Если траектория вогнутая, ускорение делится на две составляющие. Тангенциальная направлена по касательной к траектории, нормальная перпендикулярно к ней. Далее рассмотрим виды движения:
|
Название |
Определение |
Уравнение |
|
Равномерное прямолинейное |
Тело перемещается с постоянной скоростью, за равные промежутки времени проходит равные отрезки пути |
s = s0 + vt или x = x0 + vxt |
|
Равноускоренное прямолинейное |
Тело движется с постоянным ускорением |
x = x0 + v0t + at2 / 2 или vx = v0x + axt |
|
Движение под углом к горизонту |
Тело брошено под углом к горизонту с начальной скоростью, движется по криволинейной траектории |
x = v0cosαt и h = v0sinαt − gt2 / 2 |
|
Равномерное движение по окружности |
Материальная точка имеет круговую траекторию, скорость в каждой точке траектории направлена по касательной к окружности. |
Период: T = 2πr / v Частота: υ = 1 / T Угловая скорость: ω = φ / t = 2πυ, где φ — угол поворота Ускорение: a=4π2Rv2 |
Следующий раздел для подготовки к ЕГЭ — динамика. Описывает законы движения тел, рассматривает инерциальные системы отсчета. Они определяются следующим образом: если на тело не воздействуют никакие силы (или они уравновешены), то тело находится в состоянии покоя или движется равномерно, прямолинейно. Количество систем в природе не ограничено, законы механики в них одинаковы. Неинерциальные системы — движущиеся относительно инерциальных с ускорением. Условие существования инерциальных систем обнаружил Ньютон, оно называется первым законом Ньютона.
Важные формулы касаются массы. Под термином понимают величину, определяющую гравитационные, инертные свойства. Чем тяжелее тело, тем оно инертнее, тем большее ускорение придает при взаимодействии. Второй закон Ньютона выражает соотношение F = ma. В формуле появляется понятие силы — меры взаимодействия (влияния друг на друга) тел. В механике различают силы трения, упругости, гравитационные силы. В задачах иногда встречается принцип суперпозиции: если на тело действует сразу несколько сил, их складывают, представив в виде одной, называемой равнодействующей. С силой связан третий закон Ньютона: для каждого действия есть противодействие, равное по модулю, противоположное по направлению. Запишем в виде F1 = -F2 или m1a1 = -m2a2. Еще несколько важных сил:
Второй закон Ньютона выражает соотношение F = ma. В формуле появляется понятие силы — меры взаимодействия (влияния друг на друга) тел. В механике различают силы трения, упругости, гравитационные силы. В задачах иногда встречается принцип суперпозиции: если на тело действует сразу несколько сил, их складывают, представив в виде одной, называемой равнодействующей. С силой связан третий закон Ньютона: для каждого действия есть противодействие, равное по модулю, противоположное по направлению. Запишем в виде F1 = -F2 или m1a1 = -m2a2. Еще несколько важных сил:
- упругости. Возникает в результате деформации, направлена на возвращение тела в изначальную форму. Определяется законом Гука Fупр = -kx, k — жесткость тела, x — модуль удлинения;
- трение покоя. Два тела соприкасаются, не двигаясь относительно друг друга. Fпок = μпN, N — сила реакции опоры, а μ — коэффициент трения;
- трение скольжения. Соприкасающиеся тела движутся. Сила направлена противоположно движению.
 Fтр = μN;
Fтр = μN; - трение качения. Возникает, когда тело катится подобно колесу. Трение качения намного меньше скольжения. Fкач = μN.
Задания из ЕГЭ
Теорию разобрали, теперь попробуем решить задачи из ЕГЭ.
Задание 1. На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 20 Н. Чему равна сила трения скольжения, если коэффициент трения уменьшится в 4 раза при неизменной массе?
Решение. Формула для трения скольжения: Fтр = μN. Движение горизонтальное, по второму закону Ньютона N = mg. Масса не меняется, следовательно, при уменьшении коэффициента сила уменьшается в 4 раза. 20 Н / 4 = 5 Н.
Ответ: 5
Задание 2. В каком случае Земля считается материальной точкой?
1) рассчитывается длина экватора;
2) изучается земная атмосфера;
3) измеряется расстояние от Земли до Луны;
4) рассчитывается скорость движения Земли относительно Солнца.
Решение. В номерах 1, 2 изучаются свойства Земли, важны форма и размер. В номерах 3, 4 изучаемые расстояния намного больше радиуса Земли, ее можно считать материальной точкой.
В номерах 3, 4 изучаемые расстояния намного больше радиуса Земли, ее можно считать материальной точкой.
Ответ: 34
Задание 3. Тело равномерно движется по окружности радиусом 2 м. По графику определите модуль линейной скорости тела в интервале 0 < t < π.
Решение. Найдем связь угловой и линейной скорости: v = Rω = Rφ / t. В указанном интервале t изменяется в промежутке от -π / 4 до π / 4, следовательно, φ = π / 4 — (-π / 4) = π / 2. v = 2 • π / 2 : π = 1.
Ответ: 1.
Задание 4. Математический маятник колеблется с угловой амплитудой 1 градус. Уменьшили длину нити маятника и массу привязанной дробинки, оставив угловую амплитуду прежней. Определите изменение величин.
А) период колебаний
Б) запас полной механической энергии
1) увеличится
2) уменьшится
3) не изменится
Решение. Период колебаний определяется выражением T=2lg. При уменьшении длины нити уменьшается период колебаний.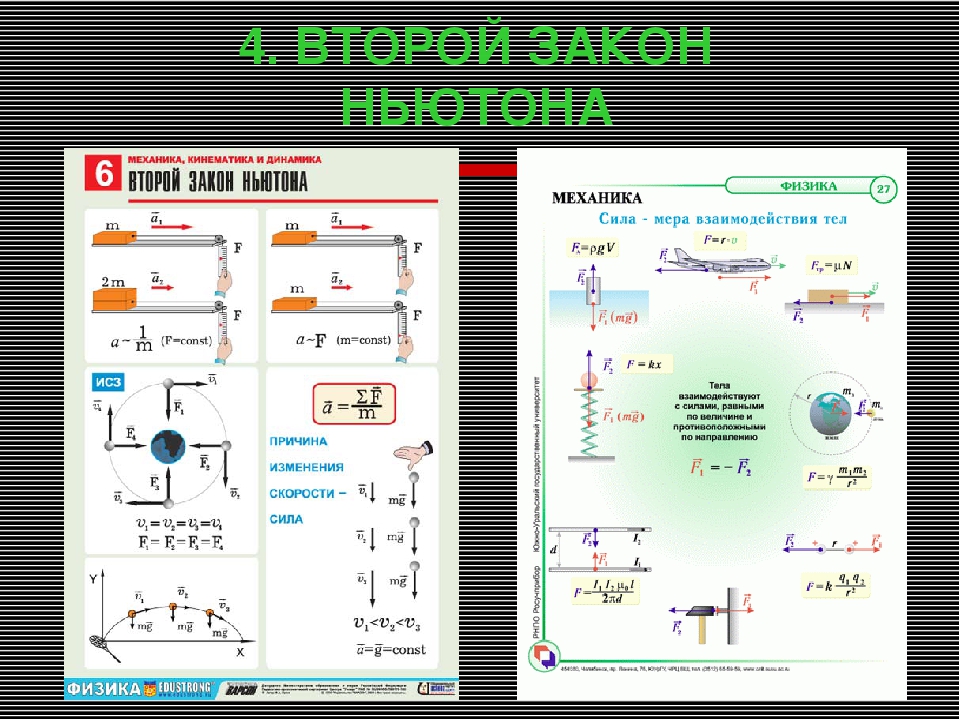 Кроме того, уменьшится потенциальная энергия, общая механическая также станет меньше.
Кроме того, уменьшится потенциальная энергия, общая механическая также станет меньше.
Ответ: 22
Задание 5. Используя рисунок, определите, чему равна проекция ускорения на ось Х через 2 секунды.
Решение. Ускорение — отношение изменения скорости к изменению t. Скорость в первую секунду была равна нулю, в точке v1 стала 1 м/с. Δv = 1 — 0 = 1. Вычисляем ускорение: 1 / 2 = 0,5 м/с2.
Ответ: 0,5.
Мы изучили теорию по механике, разобрались, как решать задания из ЕГЭ по физике. Материал будет полезен при подготовке к экзамену, поэтому сохраните его, повторяйте. Не забывайте практиковаться, решать тематические задачи. Желаем вам удачи на итоговой аттестации!
Dynamics | Безграничная физика
Инерция вращения
Инерция вращения — это тенденция вращающегося объекта оставаться во вращении, если к нему не приложен крутящий момент.
Цели обучения
Объясните взаимосвязь между силой, массой, радиусом и угловым ускорением
Основные выводы
Ключевые моменты
- Чем дальше от оси приложена сила, тем больше угловое ускорение.

- Угловое ускорение обратно пропорционально массе.2) α — вращательный аналог второго закона Ньютона (F = ma), где крутящий момент аналогичен силе, угловое ускорение аналогично поступательному ускорению, а mr2 аналогично массе (или инерции).
Ключевые термины
- инерция вращения : Тенденция вращающегося объекта оставаться вращающимся, если к нему не приложен крутящий момент.
- крутящий момент : вращательное или скручивающее действие силы; (Единица СИ ньютон-метр или Нм; британская единица измерения фут-фунт или фут-фунт)
Если вы когда-либо крутили колесо велосипеда или катали карусель, вы испытали силу, необходимую для изменения угловой скорости.Наша интуиция надежно предсказывает многие из вовлеченных факторов. Например, мы знаем, что дверь открывается медленно, если мы нажимаем слишком близко к ее петлям. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше от оси приложена сила, тем больше угловое ускорение; другое значение состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона.На самом деле существуют точные вращательные аналоги как силы, так и массы.
Первый пример подразумевает, что чем дальше от оси приложена сила, тем больше угловое ускорение; другое значение состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона.На самом деле существуют точные вращательные аналоги как силы, так и массы.
Инерция вращения, как показано на рисунке, — это сопротивление объектов изменениям в их вращении. Другими словами, вращающийся объект будет продолжать вращаться, а невращающийся объект останется неподвижным, если на него не будет действовать крутящий момент. Это должно напомнить вам о Первом законе Ньютона.
Инерция вращения : Для вращения колеса велосипеда требуется сила. Чем больше сила, тем больше угловое ускорение.Чем массивнее колесо, тем меньше угловое ускорение. Если вы надавите на спицу ближе к оси, угловое ускорение будет меньше.
Чтобы установить точное соотношение между силой, массой, радиусом и угловым ускорением, рассмотрим, что произойдет, если мы приложим силу F к точечной массе m, находящейся на расстоянии r от точки поворота.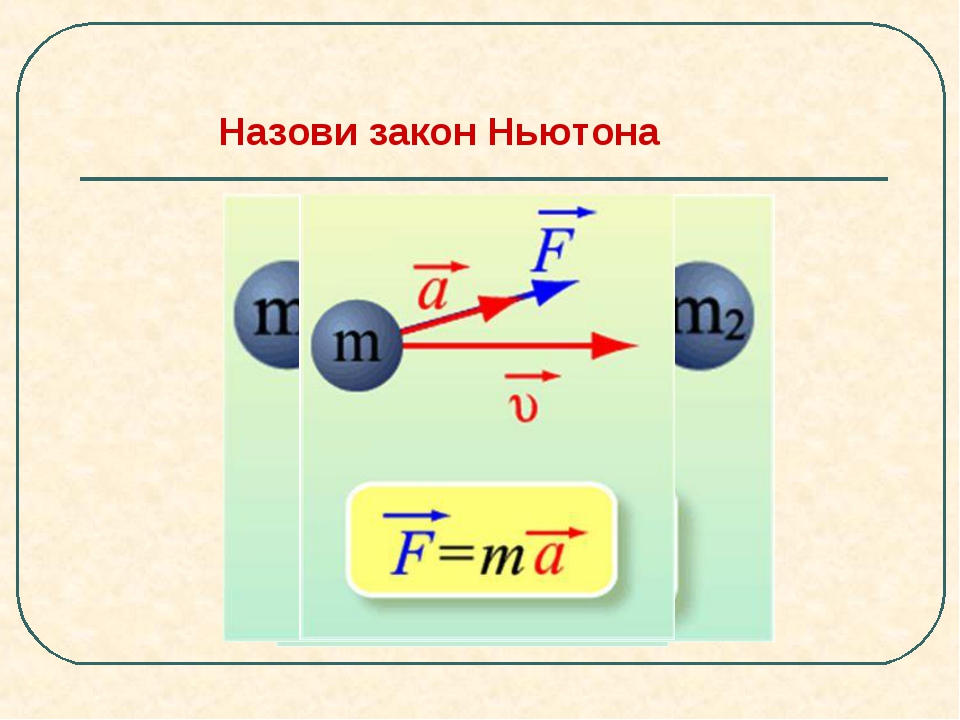 Поскольку сила перпендикулярна r, ускорение [latex] \ text {a} = \ text {F} / \ text {m} [/ latex] получается в направлении F. Мы можем изменить это уравнение так, чтобы F = ma, а затем поищите способы связать это выражение с выражениями для вращательных величин.Заметим, что a = rα, и подставляем это выражение в F = ma, получая:
Поскольку сила перпендикулярна r, ускорение [latex] \ text {a} = \ text {F} / \ text {m} [/ latex] получается в направлении F. Мы можем изменить это уравнение так, чтобы F = ma, а затем поищите способы связать это выражение с выражениями для вращательных величин.Заметим, что a = rα, и подставляем это выражение в F = ma, получая:
[латекс] \ text {F} = \ text {mr} \ alpha [/ latex].
Напомним, что крутящий момент — это эффективность силы при повороте. В этом случае, поскольку F перпендикулярно r, крутящий момент просто равен τ = Fr. Итак, если мы умножим обе части приведенного выше уравнения на r, мы получим крутящий момент в левой части. То есть rF = mr 2 α, или
τ = mr 2 α.
Это уравнение является вращательным аналогом второго закона Ньютона (F = ma), где крутящий момент аналогичен силе, угловое ускорение аналогично поступательному ускорению, а mr 2 аналогично массе (или инерции).Величина mr 2 называется инерцией вращения или моментом инерции точечной массы m на расстоянии r от центра вращения.
Объекты различной формы имеют разную инерцию вращения, которая зависит от распределения их массы.
Веб-сайт класса физики
Законы движения Ньютона: обзор набора задач
Этот набор из 30 задач нацелен на вашу способность различать массу и вес, определять чистую силу по значениям отдельных сил, связывать ускорение с чистой силой и массой, анализировать физические ситуации, чтобы нарисовать диаграмму свободного тела и решить ее. неизвестная величина (ускорение или индивидуальное значение силы) и объединить анализ второго закона Ньютона с кинематикой для определения неизвестной величины (кинематической величины или значения силы).Проблемы варьируются по сложности от очень простых и простых до очень сложных и сложных. Более сложные задачи имеют цветовую кодировку , синие задачи .
Масса против веса
Этот набор из 30 задач нацелен на вашу способность различать массу и вес, определять чистую силу по значениям отдельных сил, связывать ускорение с чистой силой и массой, анализировать физические ситуации, чтобы нарисовать диаграмму свободного тела и решить неизвестная величина (ускорение или индивидуальное значение силы), масса — это величина, которая зависит от количества вещества, присутствующего в объекте; обычно выражается в килограммах. Масса материи, которой обладает объект, не зависит от его местоположения во Вселенной. С другой стороны, вес — это сила тяжести, с которой Земля притягивает к себе объект. Поскольку гравитационные силы меняются в зависимости от местоположения, вес объекта на поверхности Земли отличается от его веса на Луне. Вес, как сила, чаще всего выражается в метрических единицах измерения в ньютонах. Каждое место во Вселенной характеризуется постоянной гравитационного поля, представленной символом g (иногда называемое ускорением свободного падения).Вес (или F grav ) и масса ( м ) связаны уравнением:
Масса материи, которой обладает объект, не зависит от его местоположения во Вселенной. С другой стороны, вес — это сила тяжести, с которой Земля притягивает к себе объект. Поскольку гравитационные силы меняются в зависимости от местоположения, вес объекта на поверхности Земли отличается от его веса на Луне. Вес, как сила, чаще всего выражается в метрических единицах измерения в ньютонах. Каждое место во Вселенной характеризуется постоянной гравитационного поля, представленной символом g (иногда называемое ускорением свободного падения).Вес (или F grav ) и масса ( м ) связаны уравнением:
F грав = m • g
Второй закон движения Ньютона
Второй закон движения Ньютона гласит, что ускорение ( a ), испытываемое объектом, прямо пропорционально чистой силе ( F net ), испытываемой объектом, и обратно пропорционально массе объекта. В форме уравнения можно сказать, что a = F net / m . Чистая сила — это векторная сумма всех индивидуальных значений силы. Если величина и направление отдельных сил известны, то эти силы могут быть добавлены как векторы для определения результирующей силы. Следует обратить внимание на векторную природу силы. Направление важно. Поднимающую силу и прижимающую силу можно добавить, присвоив прижимной силе отрицательное значение, а восходящей силе положительное значение. Аналогичным образом, сила, направленная вправо, и сила, направленная влево, могут быть добавлены путем присвоения левой силе отрицательного значения и правой силы положительного значения.
В форме уравнения можно сказать, что a = F net / m . Чистая сила — это векторная сумма всех индивидуальных значений силы. Если величина и направление отдельных сил известны, то эти силы могут быть добавлены как векторы для определения результирующей силы. Следует обратить внимание на векторную природу силы. Направление важно. Поднимающую силу и прижимающую силу можно добавить, присвоив прижимной силе отрицательное значение, а восходящей силе положительное значение. Аналогичным образом, сила, направленная вправо, и сила, направленная влево, могут быть добавлены путем присвоения левой силе отрицательного значения и правой силы положительного значения.
Уравнение a = F net / m может использоваться как формула для решения проблем, так и как руководство к размышлениям. При использовании уравнения в качестве формулы для решения проблемы важно, чтобы числовые значения двух из трех переменных в уравнении были известны, чтобы найти неизвестную величину.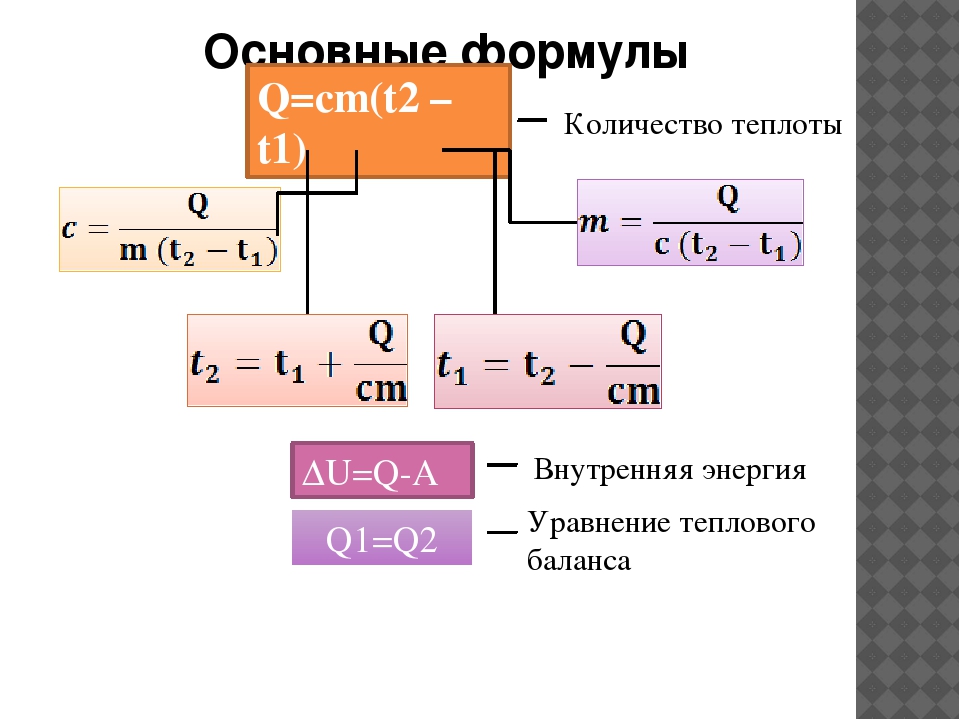 При использовании уравнения в качестве руководства к размышлениям необходимо учитывать прямые и обратные отношения между ускорением и чистой силой и массой. Двукратное или трёхкратное увеличение чистой силы вызовет такое же изменение ускорения, удвоение или утроение его значения.Увеличение массы в два или три раза вызовет обратное изменение ускорения, уменьшив его значение в два или три раза.
При использовании уравнения в качестве руководства к размышлениям необходимо учитывать прямые и обратные отношения между ускорением и чистой силой и массой. Двукратное или трёхкратное увеличение чистой силы вызовет такое же изменение ускорения, удвоение или утроение его значения.Увеличение массы в два или три раза вызовет обратное изменение ускорения, уменьшив его значение в два или три раза.
Диаграммы свободного тела
Диаграммы свободного тела представляют силы, которые действуют на объект в данный момент времени. Отдельные силы, действующие на объект, представлены векторными стрелками. Направление стрелок указывает направление силы, а приблизительная длина стрелки представляет относительную величину силы.Силы обозначены в соответствии с их типом. Схема свободного тела может оказаться полезным подспорьем в процессе решения проблем. Он обеспечивает визуальное представление сил, действующих на объект.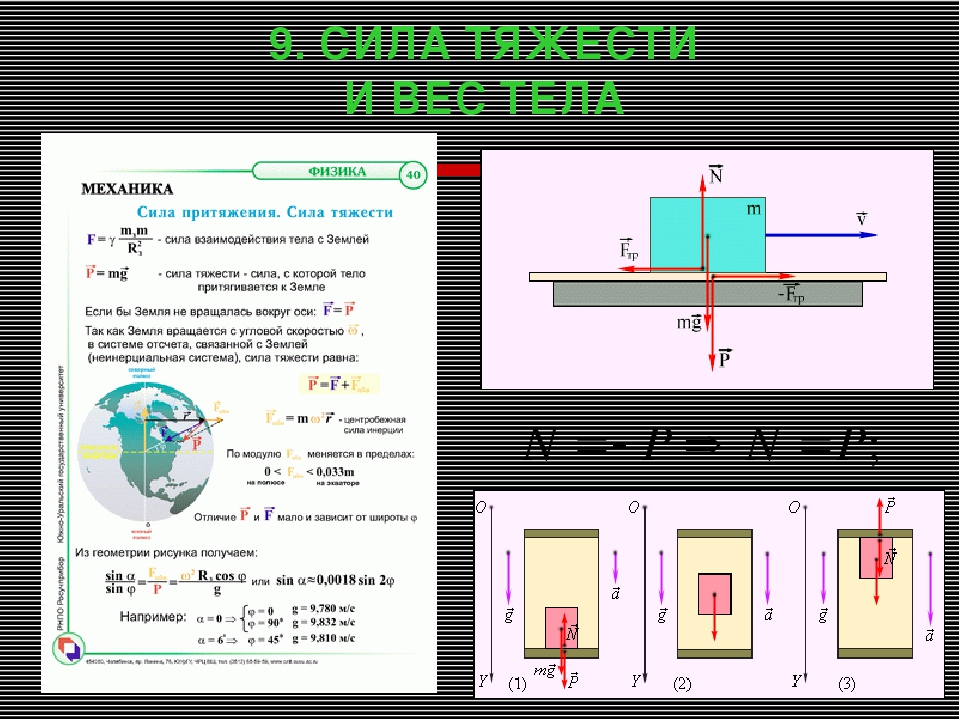 Если величины всех отдельных сил известны, диаграмму можно использовать для определения чистой силы. И если ускорение и масса известны, то можно рассчитать чистую силу, и диаграмму можно использовать для определения значения единственной неизвестной силы.
Если величины всех отдельных сил известны, диаграмму можно использовать для определения чистой силы. И если ускорение и масса известны, то можно рассчитать чистую силу, и диаграмму можно использовать для определения значения единственной неизвестной силы.
Коэффициент трения
Объект, который движется (или событие, пытающееся двигаться) по поверхности, встречает силу трения.Сила трения возникает из-за того, что две поверхности плотно прижимаются друг к другу, вызывая межмолекулярные силы притяжения между молекулами разных поверхностей. Таким образом, трение зависит от природы двух поверхностей и от степени их прижатия друг к другу. Силу трения можно рассчитать по формуле:
F frict = µ • F norm
Символ µ (произносится как «мью») представляет коэффициент трения и будет отличаться для разных поверхностей.
Смешение законов Ньютона и кинематических уравнений
Кинематика относится к описанию движения объекта и фокусируется на вопросах, как далеко?, Как быстро?, Сколько времени? а с каким ускорением? Чтобы помочь ответить на такие вопросы, в модуле «Одномерная кинематика» были представлены четыре кинематических уравнения.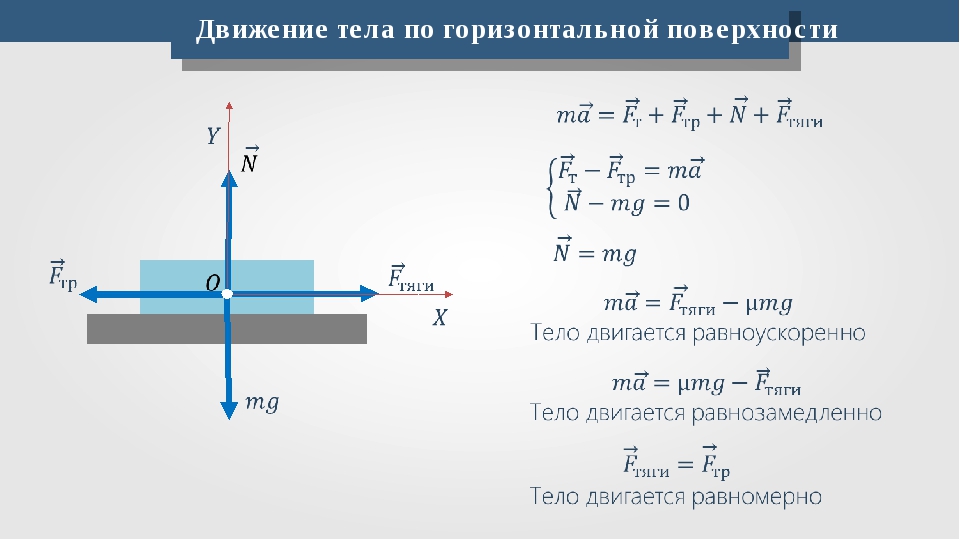 Четыре уравнения перечислены ниже.
Четыре уравнения перечислены ниже.
- d = v o • t + 0.5 • а • т 2
- v f = v o + a • t
- v f 2 = v o 2 + 2 • a • d
- d = (v o + v f ) / 2 • t
где
- d = рабочий объем
- t = время
- a = ускорение
- v o = исходная или начальная скорость
- v f = конечная скорость
Законы Ньютона и кинематика разделяют один из этих общих вопросов: с каким ускорением? Ускорение (a) F net = m • a уравнение — это то же ускорение, что и в кинематических уравнениях.Таким образом, общие задачи включают:
- использование кинематической информации для определения ускорения, а затем использование ускорения в анализе законов Ньютона, или
- использование информации о силе и массе для определения значения ускорения, а затем использование ускорения в кинематическом анализе.

При анализе словесной проблемы физики целесообразно идентифицировать известные величины и систематизировать их либо как кинематические, либо как величины типа F-m-a.
Привычки эффективно решать проблемы
Эффективный решатель проблем по привычке подходит к физической проблеме таким образом, который отражает набор дисциплинированных привычек. Хотя не все эффективные специалисты по решению проблем используют один и тот же подход, все они имеют общие привычки. Эти привычки кратко описаны здесь. Эффективное решение проблем …
- …. внимательно читает задачу и создает мысленную картину физической ситуации. При необходимости они набрасывают простую схему физической ситуации, чтобы помочь визуализировать ее.
- … определяет известные и неизвестные величины в организованном порядке, часто записывая их на диаграмме. Они приравнивают заданные значения к символам, используемым для представления соответствующей величины (например, v o = 0 м / с, a = 2,67 м / с / с, v f = ???).

- …построит стратегию решения неизвестной величины; стратегия, как правило, сосредоточена вокруг использования физических уравнений и во многом зависит от понимания физических принципов.
- … определяет подходящую (ые) формулу (ы) для использования, часто записывая их. При необходимости они выполняют необходимое преобразование количеств в правильные единицы.
- … выполняет подстановки и алгебраические манипуляции, чтобы найти неизвестную величину.
Подробнее …
Дополнительная литература / Учебные пособия:
Следующие страницы из учебного пособия по физике могут быть полезны для понимания концепций и математики, связанных с этими проблемами.
Набор задач о законах движения Ньютона
Просмотреть набор задач
Законы Ньютона о движении Решения с аудиосистемой
Ознакомьтесь с аудиогидом решения проблемы:1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30
F = ma — EWT
Описание
, опубликованный сэром Исааком Ньютоном в 1687 году, Второй закон Ньютона (F = ma) — это один из трех законов движения, которые заложили основу классической механики в Principia . Второй закон гласит, что сумма сил (F) на объекте равна его массе (m), умноженной на ускорение объекта (a).
Второй закон гласит, что сумма сил (F) на объекте равна его массе (m), умноженной на ускорение объекта (a).
В теории энергетических волн второй закон представляет собой совокупность частиц, испытывающих электромагнитные силы, когда они находятся в непосредственной близости. Закон Кулона может быть использован для силы частиц, за исключением того, что это сила, действующая на сумму частиц, измеренную по заряду (q), а не по массе частицы (m). В современной физике трудно согласовать законы движения Ньютона и закон Кулона, потому что заряд и масса — это отдельные свойства (объясняемые здесь отдельно).Как и все силы, движение частиц является результатом конструктивной или деструктивной интерференции волн, вызывающей изменение амплитуды. Частицы движутся, чтобы минимизировать амплитуду. Это движение становится силой. Большая разница в амплитуде вызывает большую силу.
Вывод
Классический вывод и вывод волновой постоянной одинаковы, поскольку в основе лежит соотношение энергии-импульса (E = pc).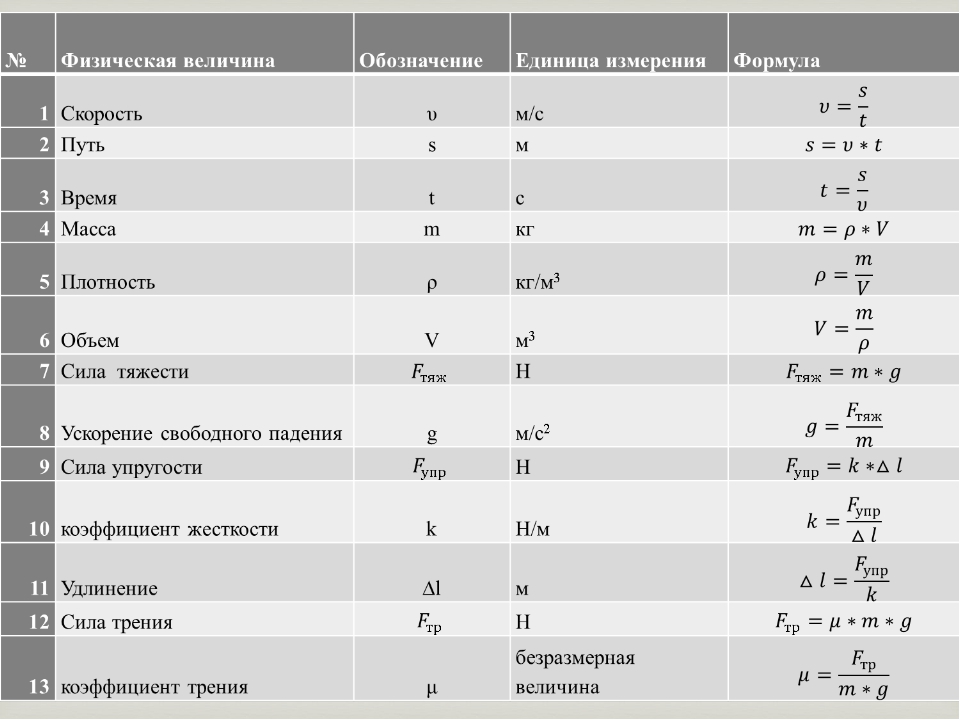 Первые шаги уже были проверены на странице энергии-импульса и здесь не повторяются.Посетите страницу E = pc, чтобы узнать о первых шагах вывода. Более подробную информацию можно найти в статье Key Physics Equations and Experiments . .
Первые шаги уже были проверены на странице энергии-импульса и здесь не повторяются.Посетите страницу E = pc, чтобы узнать о первых шагах вывода. Более подробную информацию можно найти в статье Key Physics Equations and Experiments . .
Проба
Значения ускорения (a) были рассчитаны в разделе «Силы» для различных значений силы тяжести / ускорения на поверхности планеты, включая Землю, которое оказалось равным 9,81 м / с. 2 . Расчеты требуют объяснения для получения количества частиц (Q) на основе оценки нуклонов для планет, которые здесь не рассматриваются.
.
Второй закон движения Ньютона
Первый закон движения Ньютона предсказывает поведение объектов, для которых все существующие силы уравновешены. Первый закон — иногда называемый законом инерции — гласит, что если силы, действующие на объект, уравновешены, то ускорение этого объекта будет 0 м / с / с. Объекты в состоянии равновесия (состояние, при котором все силы уравновешены) не будут ускоряться.Согласно Ньютону, объект будет ускоряться только в том случае, если на него действует чистая или неуравновешенная сила. Присутствие неуравновешенной силы ускоряет объект, изменяя его скорость, направление или одновременно скорость и направление.
Объекты в состоянии равновесия (состояние, при котором все силы уравновешены) не будут ускоряться.Согласно Ньютону, объект будет ускоряться только в том случае, если на него действует чистая или неуравновешенная сила. Присутствие неуравновешенной силы ускоряет объект, изменяя его скорость, направление или одновременно скорость и направление.
Второй закон движения Ньютона относится к поведению объектов, для которых все существующие силы не сбалансированы. Второй закон гласит, что ускорение объекта зависит от двух переменных — чистой силы, действующей на объект, и массы объекта.Ускорение объекта напрямую зависит от чистой силы, действующей на объект, и обратно — от массы объекта. По мере увеличения силы, действующей на объект, ускорение объекта увеличивается. По мере увеличения массы объекта ускорение объекта уменьшается.
Большое уравнениеВторой закон движения Ньютона можно формально сформулировать следующим образом:
Ускорение объекта, создаваемое чистой силой, прямо пропорционально величине чистой силы в том же направлении, что и чистая сила, и обратно пропорционально массе объекта.
Это словесное утверждение можно выразить в виде уравнения следующим образом:
a = F нетто / мПриведенное выше уравнение часто преобразовывается в более знакомую форму, как показано ниже. Чистая сила равна произведению массы на ускорение.
F net = m • a Во всем этом обсуждении упор был сделан на чистую силу .Ускорение прямо пропорционально чистой силе ; чистая сила равна массе, умноженной на ускорение; ускорение в том же направлении, что и чистая сила ; ускорение создается чистой силой . СЕТЕВАЯ СИЛА. Важно помнить об этом различии. Не используйте значение просто «какой-либо одной силы» в приведенном выше уравнении. Это чистая сила, связанная с ускорением. Как обсуждалось в предыдущем уроке, результирующая сила — это векторная сумма всех сил.Если известны все индивидуальные силы, действующие на объект, то можно определить результирующую силу. При необходимости просмотрите этот принцип, вернувшись к практическим вопросам в Уроке 2.
При необходимости просмотрите этот принцип, вернувшись к практическим вопросам в Уроке 2.
В соответствии с приведенным выше уравнением единица силы равна единице массы, умноженной на единицу ускорения. Подставив стандартные метрические единицы для силы, массы и ускорения в приведенное выше уравнение, можно записать следующую эквивалентность единиц.
1 Ньютон = 1 кг • м / с 2Определение стандартной метрической единицы силы определяется приведенным выше уравнением.Один Ньютон определяется как количество силы, необходимое для придания 1 кг массы ускорения 1 м / с / с.
Ваша очередь практиковаться Сеть F = m • уравнение часто используется при решении алгебраических задач. Приведенную ниже таблицу можно заполнить, подставив в уравнение и решив неизвестную величину. Попробуйте сами, а затем используйте кнопки, чтобы просмотреть ответы.
Чистая сила (н. ) ) | Масса (кг) | Разгон (м / с / с) | |
| 1. | 10 | 2 | |
| 2. | 20 | 2 | |
| 3. | 20 | 4 | |
| 4. | 2 | 5 | |
| 5. | 10 | 10 |
Числовая информация в таблице выше демонстрирует некоторые важные качественные отношения между силой, массой и ускорением.Сравнивая значения в строках 1 и 2, можно увидеть, что удвоение чистой силы приводит к удвоению ускорения (если масса остается постоянной). Точно так же сравнение значений в строках 2 и 4 показывает, что уменьшение вдвое чистой силы на приводит к уменьшению вдвое ускорения (если масса остается постоянной). Ускорение прямо пропорционально чистой силе.
Ускорение прямо пропорционально чистой силе.
Кроме того, качественную взаимосвязь между массой и ускорением можно увидеть, сравнив числовые значения в приведенной выше таблице.Обратите внимание на строки 2 и 3, что удвоение массы приводит к уменьшению вдвое ускорения (если сила остается постоянной). Точно так же строки 4 и 5 показывают, что уменьшение массы на на вдвое приводит к удвоению ускорения (если сила остается постоянной). Ускорение обратно пропорционально массе.
Анализ табличных данных показывает, что такое уравнение, как F net = m * a, может быть руководством к размышлениям о том, как изменение одной величины может повлиять на другую величину.Какое бы изменение ни производилось в чистой силе, такое же изменение произойдет и с ускорением. Удвойте, утроите или учетверите чистую силу, и ускорение будет делать то же самое. С другой стороны, какое бы изменение массы ни производилось, с ускорением будет происходить противоположное или обратное изменение. Удвойте, утроите или учетверите массу, и ускорение составит половину, одну треть или одну четвертую от первоначального значения.
Удвойте, утроите или учетверите массу, и ускорение составит половину, одну треть или одну четвертую от первоначального значения.
Направление чистой силы и ускорения
Как указано выше, направление результирующей силы совпадает с направлением ускорения.Таким образом, если известно направление ускорения, то известно и направление результирующей силы. Рассмотрим две диаграммы падения масла ниже для ускорения автомобиля. По диаграмме определите направление чистой силы, действующей на автомобиль. Затем нажмите кнопки, чтобы просмотреть ответы. (При необходимости проверьте ускорение предыдущего блока.)
В заключение, второй закон Ньютона дает объяснение поведения объектов, на которых силы не уравновешиваются.Закон гласит, что несбалансированные силы заставляют объекты ускоряться с ускорением, которое прямо пропорционально чистой силе и обратно пропорционально массе.
 Проверьте свое понимание
Проверьте свое понимание 1. Определите ускорения, возникающие при приложении чистой силы 12 Н к объекту массой 3 кг, а затем к объекту массой 6 кг.
2. К энциклопедии прилагается чистая сила 15 Н, которая заставляет ее ускоряться со скоростью 5 м / с. 2 .Определите массу энциклопедии.
3. Предположим, что салазки ускоряются со скоростью 2 м / с. 2 . Если чистая сила утроится, а масса — вдвое, то каково новое ускорение салазок?
4. Предположим, что салазки ускоряются со скоростью 2 м / с. 2 . Если чистая сила утроится, а масса уменьшится вдвое, то каково новое ускорение салазок?
Второй закон Ньютона
Второй закон НьютонаСамое важное Уравнение в физике
Почти все слышали уравнения E = mc 2 .А также действительно, это самое известное уравнение в физике, устанавливающее эквивалентность энергии и массы. Но это это самое важное уравнение в физике? Знающие ученые скажу нет. Самое важное уравнение в физике — F = ma , также известен как второй закон механики Ньютона. Это управляет поведение всего видимого и невидимого на Земле и в космосе — от траектория бейсбольного мяча к движению планеты.студентов факультетов естествознания и инженерии посвящают половина времени изучения курса классической механики и научимся применять это уравнение. Таким образом, если вы понимаете, что F = ma , вы хорошо разбираетесь в физике.
Сэр Исаак Ньютон (1642-1727)
Ученый, ответственный за важнейшее уравнение по физике * сноска
Так что же уравнение означает? Его можно переписать в эквиваленте и более интуитивно понятная форма как a = F / m .Таким образом, второй закон Ньютона дает ответ тела массой м до силы F . Силы вещи, которые вызывают изменения в движении. Такое изменение называется ускорением и обозначается символом a . Тело претерпевает ускорение, если изменяется его скорость или меняет направление движения.
Когда вы что-то толкаете, вы наносят силу на него. Следовательно, если вы ударите по вазе рукой, все кончено, ваза ощущает силу и претерпевает изменение движения.Ясно, что ваза лежа на боку претерпел изменение состояния.
Множество уравнений во всевозможных полях иметь форму
(реакция) = (эффект движения) / (эффект сопротивления)и второй Ньютона закон имеет такую структуру. Сравнивая приведенное выше с a = F / m , можно увидеть что эффект сопротивления масса объекта, которую иногда называют инерция означает «тенденция оставаться по-прежнему.»Действительно, очень сложно изменить движение тяжелого предмета. Представить пять человек пытаются толкнуть машину. С другой стороны, свет объекты легко разгоняются. Ты не нужно пять физиков, чтобы вкрутить лампочку.
В форме F = ma , Ньютон-секунда закон сообщает нам силу F , необходимую для ускорения a на кузов массой м . Как объяснялось выше, сила движущий импульс, который заставляет тела ускоряться.Примеры сил гравитация, которая, например, заставляет вещи упасть на землю и вызвать планеты для движения вокруг Солнца; трение, которое замедляет предметы поскольку они трутся о другое вещество; то электрическая сила, которая заставляет заряженные тела отталкивать или притягивать друг друга и несет ответственность для подачи электроэнергии; магнитная сила, который, например, отклоняет иглу компаса; плавучесть, которая делает вещи плавать; и так далее.В природе бесчисленное количество сил, все создание изменений в движении.
Первый закон механики Ньютона гласит: что, если на него не действуют силы, покоящееся тело останется в покое или движущееся тело останется в движении движется с той же скоростью и направлением. Этот первый закон фактически следует из второго: Если F = 0 , то a = F / m = 0 тоже , а если объект не ускоряется, значит, не меняет своего движения.
Мир без сил было бы действительно очень скучно. Все тела в покое останется в покое; все движущиеся объекты будут путешествовать с постоянной скоростью в фиксированных направлениях вечно. Там не было бы никаких изменений в движениях. Все было бы предсказуемо, но скучно.
Таким образом, второй закон Ньютона обеспечивает механические средства определения движений предметов. Чтобы определить будущее движение тела, нужно знать его масса м , действующая на него сила F и его текущее состояние движения.Тогда один может определить изменение движения, которое должно произойти, также известное в качестве текущего ускорения a , от a = F / m .
Это обсуждение является интуитивным введением. к самому важному уравнению в физике. Если вы хотите увидеть числовые примеры, нажмите здесь.
————
* сноска Исаак
Ньютон явно не записал второй закон.
в форме F = ma : Это было на самом деле
Леонард Эйлер, выразивший это таким образом.
В начало этого файла.
Эта веб-страница была подготовлена доктором Стюартом Сэмюэлем, который предоставил Jupiter Scientific Publishing разрешение использовать эту страницу а также кто является представителем Библия по Эйнштейну: A Опубликовано научное дополнение к Библии компании Jupiter Scientific, организация, занимающаяся продвижением наука через книги, Интернет и другие средства связи.
Эту веб-страницу НЕЛЬЗЯ копировать на другой веб-сайт. сайты, но другие сайты могут ссылаться на эту страницу.
Авторские права © 2000 Стюарт Самуэль
К информационной странице Jupiter Scientific
Kinetic Energy — The Physics Hypertextbook
Обсуждение
Кинетическая энергия — это простое понятие с простым уравнением, которое легко вывести. Сделаем это дважды.
Вывод с использованием только алгебры (и в предположении постоянного ускорения).Начните с теоремы о работе-энергии, затем добавьте второй закон движения Ньютона.
∆ K = W = F ∆ s = ma ∆ s
Возьмите соответствующее уравнение кинематики и немного измените его.
| v 2 = v 0 2 + 2 a ∆ s | |
| a ∆ с = | v 2 — v 0 2 |
| 2 |
Объедините два выражения.
| ∆ K = м | ⎛ ⎜ ⎝ | v 2 — v 0 2 | ⎞ ⎟ ⎠ |
| 2 |
А теперь кое-что необычное. Расширять.
| ∆ К = | 1 | мв 2 — | 1 | мв 0 2 |
| 2 | 2 |
Если кинетическая энергия — это энергия движения, то, естественно, кинетическая энергия покоящегося объекта должна быть равна нулю.Следовательно, второй член нам не нужен, и кинетическая энергия объекта составляет всего…
K = ½ мв 2
Вывод с использованием исчисления (но теперь нам не нужно ничего предполагать об ускорении). Опять же, начните с теоремы о работе-энергии и добавьте второй закон движения Ньютона (расчетная версия).
| |||||
| |||||
|
Переставьте дифференциальные члены, чтобы получить интеграл и функцию в соглашение.
| |||||
| |||||
|
Интеграл которого довольно просто вычислить за пределы начальной скорости ( v ) до конечной скорости ( v 0 ).
| ∆ К = | 1 | мв 2 — | 1 | мв 0 2 |
| 2 | 2 |
Естественно, кинетическая энергия покоящегося объекта должна быть равна нулю. Таким образом, кинетическая энергия объекта математически определяется следующим уравнением…
K = ½ мв 2
Томас Янг (1773–1829) вывел аналогичную формулу в 1807 году, хотя он пренебрегал добавлением ½ в начале и не использовал слова масса и вес с той же точностью, что и сейчас.Он также был первым, кто использовал слово энергия в его нынешнем значении в лекции о столкновениях, прочитанной перед Королевским институтом.
Термин «энергия» может быть применен с большой долей уместности к произведению массы или веса тела на квадрат числа, выражающего его скорость. Таким образом, если вес в одну унцию движется со скоростью ноги в секунду, мы можем назвать его энергию 1; если второе тело весом в две унции имеет скорость три фута в секунду, его энергия будет вдвое больше квадрата трех, или 18.
Томас Янг, 1807
Янг просто назвал это энергией. Уильям Томсон, лорд Кельвин (1824–1907) добавил прилагательное «кинетическая», чтобы отделить ее от «потенциальной энергии», названной Уильямом Рэнкином (1820–1872) в 1853 году.
Кинетическая энергия иногда обозначается буквой T . Вероятно, это происходит от французского travail mécanique (механическая работа) или Quantité de travail (количество работы).
Сила, масса и ускорение: второй закон движения Ньютона
Первый закон движения Исаака Ньютона гласит: «Покоящееся тело будет оставаться в покое, а тело в движении будет оставаться в движении, если на него не действует внешняя сила.«Что же тогда происходит с телом, когда к нему прикладывается внешняя сила? Эта ситуация описывается вторым законом движения Ньютона.
Согласно НАСА, этот закон гласит:« Сила равна изменению количества движения за одно изменение. во время. Для постоянной массы сила равна массе, умноженной на ускорение ». Это записывается в математической форме как F = м a
F — сила, m — масса и a — ускорение. математика, стоящая за этим, довольно проста.Если вы удвоите силу, вы удвоите ускорение, но если вы удвоите массу, вы уменьшите ускорение вдвое.
Ньютон опубликовал свои законы движения в 1687 году в своей основополагающей работе «Philosophiæ Naturalis Principia Mathematica» («Математические принципы естественной философии»), в которой он формализовал описание того, как массивные тела движутся под действием внешних сил.
Ньютон расширил более раннюю работу Галилео Галилея, который разработал первые точные законы движения масс, по словам Грега Ботуна, профессора физики в Университете Орегона.Эксперименты Галилея показали, что все тела ускоряются с одинаковой скоростью, независимо от размера и массы. Ньютон также раскритиковал и расширил работы Рене Декарта, который также опубликовал свод законов природы в 1644 году, через два года после рождения Ньютона. Законы Декарта очень похожи на первый закон движения Ньютона.
Ускорение и скорость
Второй закон Ньютона гласит, что когда на массивное тело действует постоянная сила, она заставляет его ускоряться, то есть изменять его скорость с постоянной скоростью.В простейшем случае сила, приложенная к неподвижному объекту, заставляет его ускоряться в направлении силы. Однако, если объект уже находится в движении или если эта ситуация рассматривается из движущейся инерциальной системы отсчета, это тело может казаться ускоряющимся, замедляющимся или меняющим направление в зависимости от направления силы и направлений, в которых объект и система отсчета движутся относительно друг друга.
Жирные буквы F и a в уравнении указывают, что сила и ускорение являются векторными величинами , что означает, что они имеют как величину, так и направление.Сила может быть одной силой или сочетанием более чем одной силы. В этом случае мы бы записали уравнение как ∑ F = м a
Большой Σ (греческая буква сигма) представляет векторную сумму всех сил, или чистую силу, действующую на тело.
Довольно сложно представить приложение постоянной силы к телу в течение неопределенного промежутка времени. В большинстве случаев силы могут применяться только в течение ограниченного времени, создавая так называемый импульс .Для массивного тела, движущегося в инерциальной системе отсчета без каких-либо других сил, таких как трение, действующих на него, определенный импульс вызовет определенное изменение его скорости. Тело может ускориться, замедлиться или изменить направление, после чего оно продолжит движение с новой постоянной скоростью (если, конечно, импульс не заставит тело остановиться).
Однако есть одна ситуация, в которой мы действительно сталкиваемся с постоянной силой — силой, вызванной гравитационным ускорением, которая заставляет массивные тела оказывать на Землю нисходящую силу.В этом случае постоянное ускорение свободного падения записывается как g , а Второй закон Ньютона становится F = mg . Обратите внимание, что в этом случае F и g обычно не записываются как векторы, потому что они всегда указывают в одном направлении, вниз.
Произведение массы на гравитационное ускорение, мг , известно как вес , что представляет собой просто еще один вид силы. Без гравитации массивное тело не имеет веса, а без массивного тела гравитация не может создавать силу.Чтобы преодолеть гравитацию и поднять массивное тело, вы должны создать направленную вверх силу м a , которая больше, чем сила тяжести, направленная вниз мг .
Второй закон Ньютона в действии
Ракеты, путешествующие в космосе, охватывают все три закона движения Ньютона.
Если ракете необходимо замедлить, ускориться или изменить направление, для ее толчка используется сила, обычно исходящая от двигателя. Величина силы и место, в котором она обеспечивает толчок, могут изменять либо скорость (часть величины ускорения), либо направление, либо и то, и другое.
Теперь, когда мы знаем, как массивное тело в инерциальной системе отсчета ведет себя, когда на него действует внешняя сила, например, как двигатели, создающие толкающий маневр, маневрируют ракетой, что происходит с телом, которое проявляет эту силу? Эта ситуация описывается третьим законом движения Ньютона.

 : Сила. Второй закон Ньютона :.
: Сила. Второй закон Ньютона :. Если, к примеру, ми изучаем движение автомобиля, то знаем, что он взаимодействует с поверхностью Земли. Нас интересует движение автомобиля, а не Земли.
Как известно, числовые значения ускорений двух взаимодействующих тел обратно пропорциональны их массам:
Если, к примеру, ми изучаем движение автомобиля, то знаем, что он взаимодействует с поверхностью Земли. Нас интересует движение автомобиля, а не Земли.
Как известно, числовые значения ускорений двух взаимодействующих тел обратно пропорциональны их массам:
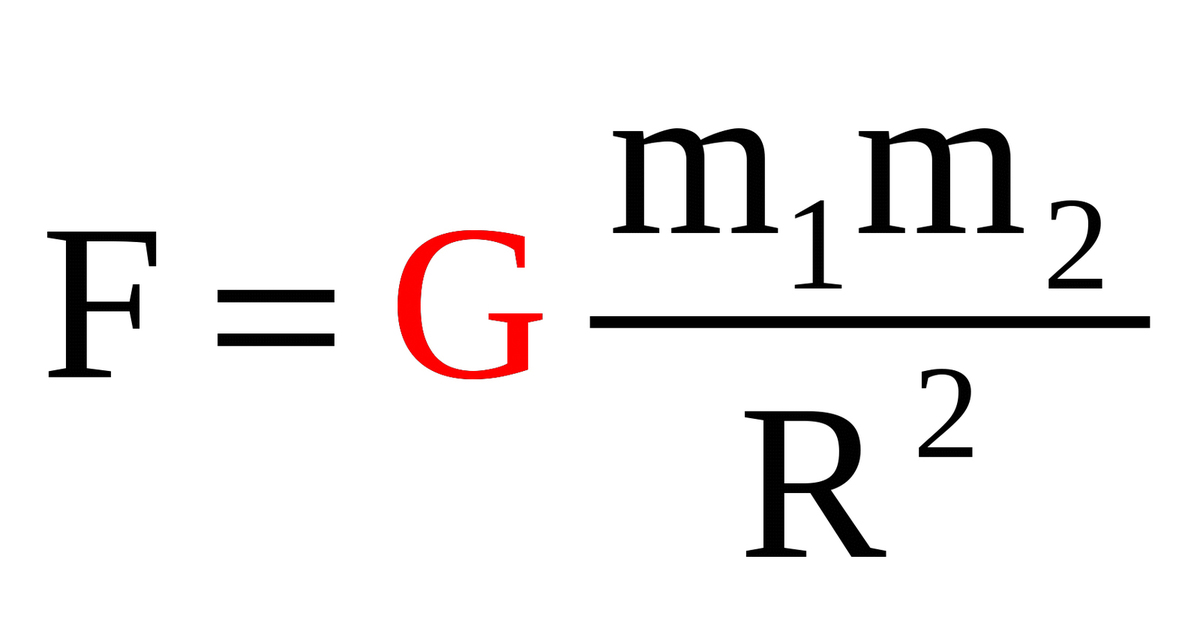 А при умножении вектора на скаляр получаем вектор того же направления, изменяется только его значение.
А при умножении вектора на скаляр получаем вектор того же направления, изменяется только его значение. Эти силы можно сложить по правилу параллелограмма и найти равнодействующею всех приложенных сил. Ускорение, которое телу сообщают все силы вместе равно ускорению, которое получило бы тело под действием равнодействующей силы.
Эти силы можно сложить по правилу параллелограмма и найти равнодействующею всех приложенных сил. Ускорение, которое телу сообщают все силы вместе равно ускорению, которое получило бы тело под действием равнодействующей силы.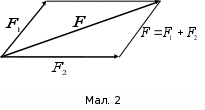 В соответствии со вторым законом Ньютона это значит, что к телу приложена постоянная сила Fx, направленная вдоль оси и равная по модулю max.
В соответствии со вторым законом Ньютона это значит, что к телу приложена постоянная сила Fx, направленная вдоль оси и равная по модулю max.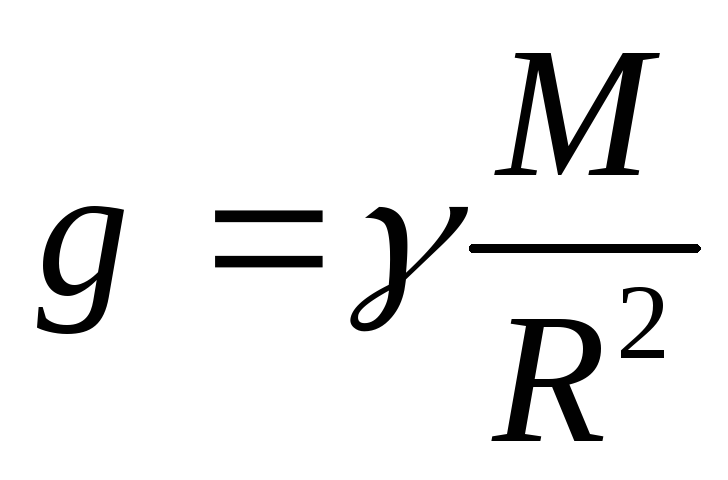 Груз m1 взаимодействует с наклонной плоскостью, нитью и Землёй. Данные тела являются источниками четырёх си: силы реакции опоры N, силы трения скольжения µ N, сила натяжения нити Т, и сила тяжести m1g. Груз m2 взаимодействует лишь с Землёй и нитью, поэтому к нему приложены только две силы – сила тяжести m2g,и сила натяжения нити Т.(Пример №1).
Если приложенных к грузам сил отлична от нуля, то грузы начнут двигаться с ускорением, которое можно найти с помощью второго закона Ньютона. Направления движения тел в общем случае зависят от масс тел, угла наклона плоскости и коэффициента трения.
Если перетягивая груз m2,то сила трения, приложенная к телу m1, оказывается направленной вниз. Применительно к телу m1 второй закон Ньютона, записывается в проекциях на оси X и Y, даёт:
m1a= T-m1gsina- µ N,
0=N-m1gcosa,
Применяя тот же закон к телу m2, получаем:
m2а= m2п-Т,
Из этих уравнений находим ускорение:
а=((m2-m1sina- µm1cosa)/m2+m1)g,
Если предположить, что перетягивает тело m1(сила трения изменяется на противоположную), получаем другой ответ:
а=((msina-m2-µm1cosa)/m2+m1)g,
Так как модули ускорения а>0, то заданных значениях а(угол) и µ, первое из получившихся уравнений справедливо при условии:
m2>=m1(sina+µcosa),
а второе:
m2,
Следовательно второй закон Ньютона позволяет добить массу информации о рассматриемай системе.
Груз m1 взаимодействует с наклонной плоскостью, нитью и Землёй. Данные тела являются источниками четырёх си: силы реакции опоры N, силы трения скольжения µ N, сила натяжения нити Т, и сила тяжести m1g. Груз m2 взаимодействует лишь с Землёй и нитью, поэтому к нему приложены только две силы – сила тяжести m2g,и сила натяжения нити Т.(Пример №1).
Если приложенных к грузам сил отлична от нуля, то грузы начнут двигаться с ускорением, которое можно найти с помощью второго закона Ньютона. Направления движения тел в общем случае зависят от масс тел, угла наклона плоскости и коэффициента трения.
Если перетягивая груз m2,то сила трения, приложенная к телу m1, оказывается направленной вниз. Применительно к телу m1 второй закон Ньютона, записывается в проекциях на оси X и Y, даёт:
m1a= T-m1gsina- µ N,
0=N-m1gcosa,
Применяя тот же закон к телу m2, получаем:
m2а= m2п-Т,
Из этих уравнений находим ускорение:
а=((m2-m1sina- µm1cosa)/m2+m1)g,
Если предположить, что перетягивает тело m1(сила трения изменяется на противоположную), получаем другой ответ:
а=((msina-m2-µm1cosa)/m2+m1)g,
Так как модули ускорения а>0, то заданных значениях а(угол) и µ, первое из получившихся уравнений справедливо при условии:
m2>=m1(sina+µcosa),
а второе:
m2,
Следовательно второй закон Ньютона позволяет добить массу информации о рассматриемай системе.
 время подъема
время подъема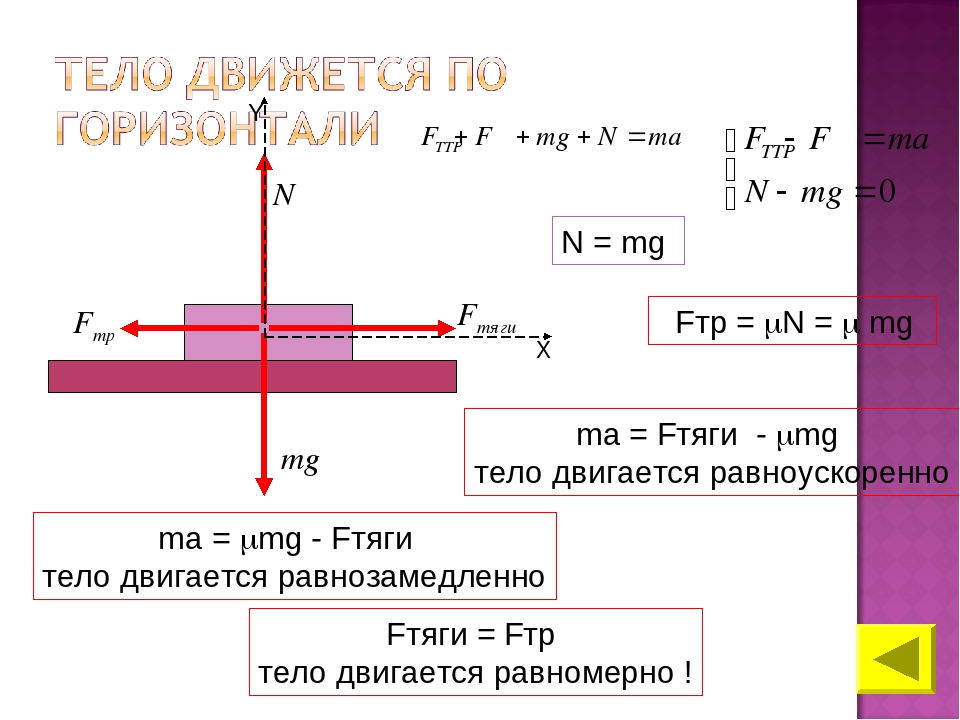 смещение x = Asin(t
+ 0),
2. скорость v = Acos(t
+ 0),
vmax = A
смещение x = Asin(t
+ 0),
2. скорость v = Acos(t
+ 0),
vmax = A  Ускорение — быстрота изменения направления
Ускорение — быстрота изменения направления Fтр = μN;
Fтр = μN;