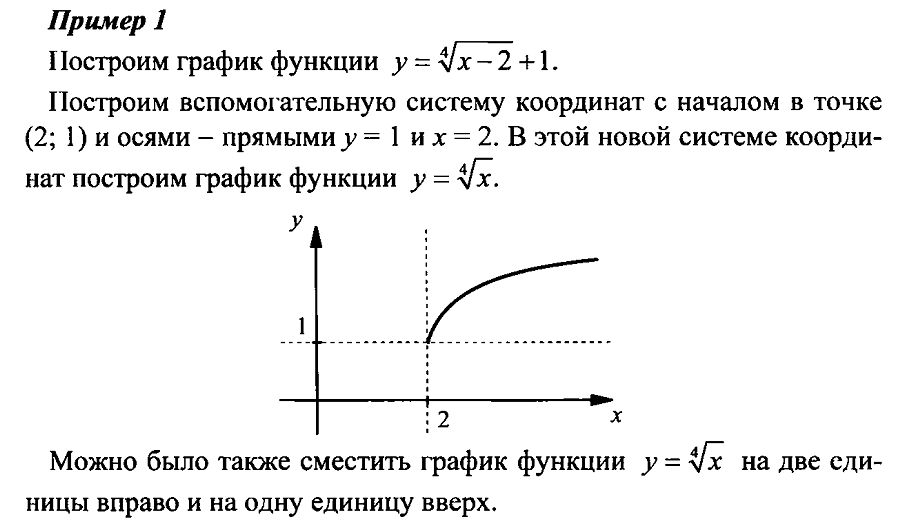
1.2. Корень n-й степени
1.2. Корень n-й степени
В 8-м классе изучались квадратные корни из действительных чисел (их называют также корнями 2-й степени).
Перейдем к изучению корней степени n для произвольного натурального числа n≥2.
Определение. Пусть n≥2 и n∈N. Корнем n-й степени из числа a называется такое число t, n-я степень которого равна a .
Таким образом, утверждение «t — корень n-й степени из a» означает, что tn=a.
Корень 3-й степени называется также кубическим.
Например, кубический корень из числа 125 — это число 5, так как 53=125. Кубический корень из числа −125 — это число −5, так как (−5)3=−125.
Корень 7-й степени из числа 128 — это число 2, так как 27=128. Корень 7-й степени из числа −128 — это число −2, так как (−2)7=−128. Корень 7-й степени из числа 0 — это 0, так как 07=0.
Во множестве действительных чисел существует единственный корень нечетной степени n из любого числа a. Этот корень обозначается
Например, 1253=5,−1287=−2,07=0.
Стр. 11Утверждение о существовании корня нечетной степени из любого числа мы принимаем без доказательства.
Согласно определению, когда n нечетное, то при любом значении а верно равенство
Например, ⎛⎝927⎞⎠7=92,⎛⎝1237⎞⎠7=123,⎛⎝−1237⎞⎠7=−123.
Заметим, что 0 — это единственное число, n-я степень которого равна 0. Поэтому
при любом натуральном n≥2 существует единственный корень n-й степени из 0 — это число 0, т. е. 0n=0.
Примерами корней четной степени могут служить квадратные корни: −7 и 7 — квадратные корни из 49, а −15 и 15 — из 225. Рассмотрим еще несколько примеров. Корни 4-й степени из числа 81 — это числа 3 и −3, так как 34=81 и (−3)4=81. Корни 6-й степени из числа 64 — это числа 2 и −2, так как 26=64 и (−2)6=64.
Во множестве действительных чисел существует ровно два корня четной степени n из любого положительного числа а, их модули равны, а знаки противоположны. Положительный корень обозначается
Например, 814=3,646=2.
Утверждение о существовании корня четной степени из любого положительного
числа мы принимаем без доказательства.
Согласно определению, когда n четное, то при любом положительном значении а верно
равенство
Например, ⎛⎝514⎞⎠4=51,⎛⎝874⎞⎠4=87.
Не существует такого числа, 4-я степень которого равна −81. Поэтому корня 4-й степени из числа −81 не существует. И вообще, поскольку не существует такого числа, четная степень которого была бы отрицательной, то
Стр. 12не существует корня четной степени из отрицательного числа.
Определение. Неотрицательный корень n-й степени из числа a называется арифметическим корнем n-й степени из a .
При четном n символом an обозначается только арифметический корень n-й степени из числа a (при чтении
записи an слово «арифметический» обычно пропускают).
Выражение, стоящее под знаком корня, называется подкоренным выражением.
Извлечь корень n-й степени из числа a — это значит найти значение выражения an.
Так как корня четной степени из отрицательного числа не существует, то выражение an при четном n и отрицательном а не имеет смысла.
Например, не имеют смысла выражения −814 и −646.
Как мы установили, при любом значении а, при котором выражение an имеет смысл, верно равенство
Поэтому равенство (1) является тождеством.
В конце XV в. бакалавр Парижского университета Н. Шюке внес усовершенствования
в алгебраическую символику.
В частности, знаком корня служил символ Rx (от латинского слова radix — корень). Так,
выражение 24+374 в символике Шюке имело вид R¯x424p¯R¯x237.
Знак корня в современном виде был предложен в 1525 г. чешским математиком К. Рудольфом. Его учебник алгебры переиздавался до 1615 г., и по нему учился знаменитый математик Л. Эйлер.
Знак еще называют радикалом.
Стр. 13Пример 1. Верно ли, что:
а) (−2)44=−2;
б) (−2)77=−2?
Решение. а) По определению арифметический корень n-й степени из неотрицательного числа a (n — четное число) является неотрицательным числом, n-я степень которого равна подкоренному выражению a.
Поскольку −2<0, то равенство (−2)44=−2 неверное. Верно равенство (−2)44=2.
б) По определению корень n-й степени из числа а (n — нечетное число) является числом, n-я степень которого равна подкоренному выражению а.
Поскольку (−2)7=−27 — верное равенство, то равенство (−2)77=−2 − верное.
Пример 2. Решить уравнение:
а) x3=7;
б) x4=5.
Решение. а) Решением этого уравнения является такое значение х, 3-я степень которого равна 7, т. е. по определению кубического корня имеем:
б) Решением этого уравнения является такое значение х, 4-я степень которого равна 5, т. е. (по определению) х — это корень 4-й степени из числа 5. Но из положительного
числа 5 существуют два корня четвертой степени, которые равны по модулю и имеют
противоположные знаки. Поскольку положительный корень обозначают 54, то второй корень равен −54, т.
Ответ: а) 73; б) ±54.
В тетради решение уравнения б) (аналогично и а)) можно записать так:
Решение: x4=5 ⇔ x=±54.
Ответ: ±54.
Пример 3. Решить уравнение:
а) (x8)8=x;
б) (x13)13=x.
Стр. 14Решение. а) Число 8 — четное, значит, данное равенство является тождеством при x≥0, поэтому каждое неотрицательное значение х является решением (корнем) уравнения (x8)8=x.
б) Число 13 — нечетное, значит, данное равенство является тождеством при любом значении х, поэтому решением уравнения (x13)13=x является любое действительное число, а R — множество всех его корней.
Ответ: а) [0;+∞); б) R.
Пример 4.
Решить
уравнение
Решение. Обозначим x6=t, тогда получим уравнение
Корни этого уравнения
Таким образом, имеем
откуда x=±2 (поясните, почему уравнение x6=−1 не имеет корней).
Ответ: ±2.
1
1Какое число называется корнем n-й степени из числа а?
1
2
2Сколько существует корней четной степени n из положительного числа а?
2
3
3Корень какой степени существует из любого числа а?
3
4
4Какой корень n-й степени из числа а называется арифметическим?
4
5
5При каких значениях а верно равенство (an)n=a, если:
а) n — нечетное число;
б) n — четное число?
5
Упражнения
1.
24°
1.24°Используя определение арифметического корня n-й степени, докажите, что:
1) 2564=4;
2) 102410=2;
3) 7296=3;
4) 65618=3;
5) 409612=2;
6) 14 6414=11.
1.24°
1.25°
1.25°Верно ли, что:
1) число −4 является корнем четвертой степени из числа 256;
2) число −0,3 является корнем четвертой степени из числа −0,0081?
1.25°
1.26°
1.26°Верно ли, что:
1) −17283=−12;
2) −33753=15;
3) −16 8075=7;
4) −77765=−6?
1.26°
1.27°
1.27°Найдите арифметический квадратный корень из числа:
1) 16;
2) 49;
3) 0;
4) 1;
5) 0,81;
6) 0,25;
7) 2,25;
8) 1,21;
9) 36169;
10) 144289;
11) 169100;
12) 81256.
1.27°
1.28°
1.28°Найдите кубический корень из числа:
1) 1;
2) 0;
3) 343;
4) 8;
5) 127;
6) 0,027;
7) 0,001;
8) 64125.
1.28°
1.29°
1.29°Найдите арифметический корень четвертой степени из числа:
1) 0;
2) 1;
3) 16;
4) 0,0016;
5) 1681;
6) 256625;
7) 0,0001;
8) 0,1296.
1.29°
Вычислите (1.30—1.42).
1.30°
1.30°1) 9,16,25,49,81,100;
2) 0,16,0,09,0,01,0,04,0,0025,0,0001;
3) 273,643,−1253,0,0083,0,0002163,−1 000 0003;
4) 164,6254,10 0004,0,00814,0,000000164,24014;
5) 325,10245,2435,0,031255,100 0005,0,000015;
6) 646,7296,15 6256,40966,0,0466566,1 000 0006.
1.30°
1.31°
1.31°1) −10003;
2) −115;
3) −643;
4) −10245;
5) −1273;
6) −3433;
7) −272163;
8) −31255;
9) −0,000325.
1.31°
Стр. 161.32
1.321) ⎛⎝−33⎞⎠3;
2) ⎛⎝−145⎞⎠5;
3) ⎛⎝−307⎞⎠7;
4) ⎛⎝−1511⎞⎠11;
5) ⎛⎝−69⎞⎠9;
6) ⎛⎝−9915⎞⎠15.
1.32
1.33
1.331) ⎛⎝−22113⎞⎠3·⎛⎝−6195⎞⎠5·⎛⎝−9513⎞⎠13·⎛⎝−1134017⎞⎠17;
2) ⎛⎝−34159⎞⎠9·⎛⎝−1587⎞⎠7·⎛⎝−11145⎞⎠5·⎛⎝−125393⎞⎠3.
1.33
1.34
1.341) ⎛⎝53⎞⎠6;
2) ⎛⎝0,14⎞⎠12;
3) ⎛⎝1125⎞⎠10;
4) ⎛⎝2136⎞⎠18;
5) ⎛⎝567⎞⎠21;
6) ⎛⎝239⎞⎠36.
1.34
1.35
1.351) ⎛⎝35⎞⎠10;
2) ⎛⎝534⎞⎠48;
3) ⎛⎝7610⎞⎠120;
4) ⎛⎝643⎞⎠12;
5) ⎛⎝108⎞⎠16;
6) ⎛⎝1294⎞⎠36.
1.35
1.36°
1.36°1) ⎛⎝10⎞⎠2;
2) ⎛⎝53⎞⎠3;
3) ⎛⎝−124⎞⎠4;
4) −1244;
5) ⎛⎝−35⎞⎠5;
6) ⎛⎝323⎞⎠3;
7) ⎛⎝−444⎞⎠4;
8) ⎛⎝−157⎞⎠7;
9) −5555;
10) ⎛⎝−36⎞⎠6;
11) ⎛⎝−229⎞⎠9;
12) −488.
1.36°
1.37°
1.37°1) 325+−83;
2) 6254−−1253;
3) 12−60,1253;
4) 1+100,00814;
5) 3164−4273;
6) −3383+2,25;
7) 83−643;
8) 164−643.
1.
37°
1.38°
1.38°1) 9+4;
2) 36−164;
3) 0,81+0,0013;
4) 0,0273−0,04;
5) 5−2564;
6) 7+83;
7) −325+164;
8) −273+814.
1.38°
1.39°
1.39°1) (1−2)⎛⎝1+2⎞⎠;
2) ⎛⎝3−2⎞⎠⎛⎝3+2⎞⎠;
3) ⎛⎝23+4⎞⎠⎛⎝23−4⎞⎠;
4) ⎛⎝35−2⎞⎠⎛⎝35+2⎞⎠;
5) ⎛⎝10−6⎞⎠⎛⎝6+10⎞⎠;
6) ⎛⎝7+3⎞⎠⎛⎝3−7⎞⎠.
1.39°
Стр. 171.40
1.401) 1225244⋅15−1382−2323;
2) 58+442−26235;
3) 90+31⎛⎝572−262⎞⎠83;
4) 2364+⎛⎝482−3225⎞⎠−13.
1.40
1.41
1.411) ⎛⎝⎜⎛⎝⎛⎝23⎞⎠33⎞⎠−3−⎛⎝⎛⎝43⎞⎠−55⎞⎠5⎞⎠⎟−1·⎛⎝−277⎞⎠7;
2) ⎛⎝⎜⎛⎝175⎞⎠−10+⎛⎝−409⎞⎠9·⎛⎝537⎞⎠0⎞⎠⎟−1:⎛⎝95⎞⎠−10;
3) ⎛⎝⎜⎛⎝⎜⎛⎝34⎞⎠23⎞⎠⎟6+⎛⎝−4−27⎞⎠7⎞⎠⎟:⎛⎝⎜⎛⎝⎜⎛⎝56⎞⎠05⎞⎠⎟10−⎛⎝−⎛⎝32⎞⎠−19⎞⎠9⎞⎠⎟;
4) ((((−45)3)3)0−(−0,111)−22):(((38)−15)5·((32)37)7+(−129)−9).
1.41
1.42
1.421) ⎛⎝a77⎞⎠7⎛⎝a55⎞⎠5;
2) ⎛⎝a33⎞⎠3⎛⎝a99⎞⎠9;
3) ⎛⎝⎜213⎛⎝a33⎞⎠3·⎛⎝b77⎞⎠7⎞⎠⎟2·⎛⎝⎜−127⎛⎝a55⎞⎠5·⎛⎝b1111⎞⎠11⎞⎠⎟;
4) 337⎛⎝a55⎞⎠5·⎛⎝b99⎞⎠9·⎛⎝⎜−213⎛⎝a77⎞⎠7·⎛⎝b1313⎞⎠13⎞⎠⎟2.
1.42
Найдите естественную область определения выражения (1.43—1.44).
1.43
1.431) x+4;
2) −9+2×4;
3) 5×2−6×10;
4) 8x−4×212;
5) x+33;
6) x−75;
7) x2−47;
8) 2×2−329.
1.43
1.44
1.441) 34x−112;
2) −48x−314;
3) 2−59−5×8;
4) 3−1016−7×6;
5) 2+x4−2(8−6x)3;
6) 12−6×2−7x+(3x−1)·25;
7) −x22(x−2)−5⎛⎝1−3x)−24;
8) 3(x+4)−6(2−x)+9×428.
1.44
Стр. 181.45
1.45Найдите длину ребра куба, если его объем равен:
1) 27 см3;
2) 64 мм3;
3) 0,125 дм3;
4) 0,216 м3.
1.45
Решите уравнение (1.46—1.54).
1.46°
1.46°1) x2=0,49;
2) x2=121;
3) x3=0,008;
4) x3=1000;
5) x3=−64 000;
6) x3=216;
7) x4=0,0625;
8) x4=−16.
1.46°
1.47
1.471) x3=−27;
2) x5=−132;
3) x7=−1;
4) x9=−512;
5) x3=−0,027;
6) x11=0.
1.47
1.48°
1.48°1) x2=11;
2) x4=19;
3) x8=27;
4) x3=25;
5) x7=38;
6) x9=−2;
7) x15=−6;
8) x17=4;
9) x13=−13.
1.48°
1.49
1.491) x2=25 600;
2) x2=0,0196;
3) x2+1=1,0016;
4) 5×2−20=0;
5) x2+25=0;
6) x2+179=0;
7) x2·4=0;
8) −6×2=0;
9) 113×2−12=0;
10) 13×2−1=0.
1.49
1.50
1.501) 4×3+4125=0;
2) 8×3+27=0;
3) −0,1×4=−0,00001;
4) 16×4−81=0;
5) 12×5+16=0;
6) 132×6−2=0.
1.50
1.51
1.511) x4+2=7;
2) x5−3=30;
3) x6−7=19;
4) x3+5=5.
1.51
1.52
1.521) (x+1)4=16;
2) (x−2)6=64;
3) (2x+1)3=27;
4) (3x−1)5=32.
1.52
1.
53
1.531) x10−31×5−32=0;
2) x8−15×4−16=0;
3) x4−12×2+27=0;
4) x6−7×3−8=0;
5) x8−82×4+81=0;
6) x4+2×2−15=0.
1.53
Стр. 191.54
1.541)° (x6)6=x;
2)° (x10)10=x;
3)° (x3)3=x;
4)° (x5)5=x;
5) ⎛⎝x−14⎞⎠4=x−1;
6) ⎛⎝x+212⎞⎠12=x+2;
7) ⎛⎝1×7⎞⎠7=1x;
8) ⎛⎝1x−211⎞⎠11=1x−2.
1.54
3 корень 3 степени из х производная
Вы искали 3 корень 3 степени из х производная? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и x корень x производная, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «3 корень 3 степени из х производная».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 3 корень 3 степени из х производная,x корень x производная,как найти производную корня,корень x производная,корень из x производная,корень из икс производная,корень из х производная,корень кубический из х производная,корень производная,корень х производная,кубический корень из х производная,найти производную x корень из x,под корнем производная,производная x корень x,производная из квадратного корня,производная из корень из икс,производная из корня,производная из корня 3 степени,производная из корня 3 степени из х,производная из корня из 3,производная из корня квадратного,производная из корня х,производная из кубического корня из х,производная из х в степени корень из х,производная квадратного корня,производная квадратного корня из,производная корень,производная корень x,производная корень из x,производная корень из икс,производная корень из х,производная корень из х в степени корень из х,производная корень из х в степени х,производная корень из х в степени х в,производная корень кубический из х,производная корень х,производная корней,производная корня,производная корня 3 степени,производная корня 4 степени,производная корня из 3 степени,производная корня из x,производная корня из х,производная корня из х 3 степени,производная корня квадратного,производная корня кубического,производная корня кубического из x,производная кубический корень из х,производная кубического корня,производная кубического корня из x,производная от x корень из x,производная от квадратного корня,производная от корень из x,производная от корня,производная от корня 3 степени,производная от корня из х,производная от корня квадратного,производная от корня кубического,производная от корня кубического из х,производная от кубического корня,производная от кубического корня из х,производная под корнем,производная с корнем,производная х в степени корень из х,производная х корень,производные с корнями,х под корнем производная,чему равна производная корня из х.
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 3 корень 3 степени из х производная. Просто введите задачу в окошко и нажмите
«решить» здесь (например, как найти производную корня).
Где можно решить любую задачу по математике, а так же 3 корень 3 степени из х производная Онлайн?
Решить задачу 3 корень 3 степени из х производная вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
| 1 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata — d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) относительно x | |
| 5 | Trovare la Derivata — d/dx | 1/x | |
| 6 | Trovare la Derivata — d/dx | x^2 | |
| 7 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata — d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x относительно x | |
| 11 | Вычислим интеграл | интеграл x^2 относительно x | |
| 12 | Вычислим интеграл | интеграл квадратного корня x по x | |
| 13 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x относительно x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 относительно x | |
| 16 | Trovare la Derivata — d/dx | x^3 | |
| 17 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 относительно x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 относительно x | |
| 20 | Trovare la Derivata — d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 22 | Trovare la Derivata — d/dx | sin(2x) | |
| 23 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) относительно x | |
| 25 | Trovare la Derivata — d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata — d/dx | cos(2x) | |
| 28 | Trovare la Derivata — d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x относительно x | |
| 30 | Trovare la Derivata — d/dx | ( натуральный логарифм x)^2 | |
| 31 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata — d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) относительно x | |
| 34 | Trovare la Derivata — d/dx | 2e^x | |
| 35 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata — d/dx | -sin(x) | |
| 37 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata — d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 39 | Trovare la Derivata — d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) относительно x | |
| 41 | Вычислим интеграл | интеграл cos(2x) относительно x | |
| 42 | Trovare la Derivata — d/dx | 1/( квадратный корень x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) относительно x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata — d/dx | x/2 | |
| 46 | Trovare la Derivata — d/dx | -cos(x) | |
| 47 | Trovare la Derivata — d/dx | sin(3x) | |
| 48 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 относительно x | |
| 50 | Вычислим интеграл | интеграл 1 относительно x | |
| 51 | Trovare la Derivata — d/dx | x^x | |
| 52 | Trovare la Derivata — d/dx | x натуральный логарифм x | |
| 53 | Trovare la Derivata — d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл от x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) относительно x | |
| 59 | Trovare la Derivata — d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x относительно x | |
| 61 | Trovare la Derivata — d/dx | y=x^2 | |
| 62 | Trovare la Derivata — d/dx | квадратный корень x^2+1 | |
| 63 | Trovare la Derivata — d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) относительно x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня x по x | |
| 66 | Trovare la Derivata — d/dx | e^2 | |
| 67 | Trovare la Derivata — d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) относительно x | |
| 69 | Trovare la Derivata — d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) относительно x | |
| 72 | Trovare la Derivata — d/dx | x^5 | |
| 73 | Trovare la Derivata — d/dx | 2/x | |
| 74 | Trovare la Derivata — d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata — d/dx | x^(1/2) | |
| 76 | Trovare la Derivata — d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata — d/dx | cos(x^2) | |
| 78 | Trovare la Derivata — d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata — d/dx | кубический корень x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) относительно x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) относительно x | |
| 82 | Trovare la Derivata — d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 от 0 до 10 относительно x | |
| 84 | Вычислим интеграл | интеграл от ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata — d/dx | логарифм x | |
| 86 | Trovare la Derivata — d/dx | arctan(x) | |
| 87 | Trovare la Derivata — d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata — d/dx | 5e^x | |
| 89 | Trovare la Derivata — d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 относительно x | |
| 91 | Вычислим интеграл | интеграл x^2e^x относительно x | |
| 92 | Trovare la Derivata — d/dx | 16 корень четвертой степени 4x^4+4 | |
| 93 | Trovare la Derivata — d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) относительно x | |
| 96 | Trovare la Derivata — d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) относительно x | |
| 98 | Trovare la Derivata — d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata — d/dx | натуральный логарифм x^2 |
Перевод корней в степени и обратно: объяснение, примеры
Часто преобразование и упрощение математических выражений требует перехода от корней к степеням и наоборот.
Данная статья рассказывает о том, как осуществлять перевод корня в степень и обратно. Рассматривается теория, практические примеры и наиболее распространенные ошибки.
Переход от степеней с дробными показателями к корням
Допустим, мы имеем число с показателем степени в виде обыкновенной дроби — amn. Как записать такое выражение в виде корня?
Ответ вытекает из самого определения степени!
ОпределениеПоложительное число a в степени mn — это корень степени n из числа am.
amn=amn.
При этом, обязательно должно выполнятся условие:
a>0; m∈ℤ; n∈ℕ.
Дробная степень числа нуль определяется аналогично, однако в этом случае число m принимается не целым, а натуральным, чтобы не возникло деления на 0:
0mn=0mn=0.
В соответствии с определением, степень amn можно представить в виде корня amn.
Например: 325=325, 123-34=123-34.
Однако, как уже было сказано, не следует забывать про условия: a > 0 ; m ∈ ℤ ; n ∈ ℕ .
Так, выражение -813 нельзя представить в виде -813, так как запись -813 попросту не имеет смысла — степень отрицательных чисел на определена.При этом, сам корень -813 имеет смысл.
Переход от степеней с выражениями в основании и дробными показателями осуществляется аналогично на всей области допустимых значений (далее — ОДЗ) исходных выражений в основании степени.
Например, выражение x2+2x+1-412 можно представить в виде квадратного корня x2+2x+1-4.Выражение в степени x2+x·y·z-z3-73 переходит в выражение x2+x·y·z-z3-73 для всех x, y, z из ОДЗ данного выражения.
Как представить корень в виде степени?
Обратная замена корней степенями, когда вместо выражения с корнем записывается выражения со степенью, также возможна. Просто перевернем равенство из предыдущего пункта и получим:
amn=amn
Опять же, переход очевиден для положительных чисел a. Например, 764=764, или27-53=27-53.
Для отрицательных a корни имеют смысл. Например -426, -23. Однако, представить эти корни в виде степеней -426 и -213 нельзя.
Можно ли вообще преобразовать такие выражения со степенями? Да, если произвести некоторые предварительные преобразования. Рассмотрим, какие.
Используя свойства степеней, можно выполнить преобразования выражения -426.
-426=-12·426=426.
Так как 4>0, можно записать:
426=426.
В случае с корнем нечетной степени из отрицательного числа, можно записать:
-a2m+1=-a2m+1.
Тогда выражение -23 примет вид:
-23=-23=-213.
Разберемся теперь, как корни, под которыми содержатся выражения, заменяются на степени, содержащие эти выражения в основании.
Обозначим буквой A некоторое выражение. Однако не будем спешить с представлением Amn в виде Amn. Поясним, что здесь имеется в виду. Например, выражение х-323, основываясь на равенстве из первого пункта, хочется представить в виде x-323. Такая замена возможна только при x-3≥0, а для остальных икс из ОДЗ она не подходит, так как для отрицательных a формула amn=amn не имеет смысла.
Таким образом, в рассмотренном примере преобразование вида Amn=Amn является преобразованием, сужающим ОДЗ, а из-за неаккуратного применения формулы Amn=Amn нередко возникают ошибки.
Чтобы правильно перейти от корня Amn к степени Amn, необходимо соблюдать несколько пунктов:
- В случае, если число m — целое и нечетное, а n — натуральное и четное, то формула Amn=Amn справедлива на всей ОДЗ переменных.
- Если m — целое и нечетное, а n — натуральное и нечетное,то выражение Amn можно заменить:
— на Amn для всех значений переменных, при которых A≥0;
— на —Amn для для всех значений переменных, при которых A<0; - Если m — целое и четное, а n — любое натуральное число, то Amn можно заменить на Amn.
Сведем все эти правила в таблицу и приведем несколько примеров их использования.
Вернемся к выражению х-323. Здесь m=2 — целое и четное число, а n=3 — натуральное число. Значит, выражение х-323 правильно будет записать в виде:
х-323=x-323.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеПриведем еще один пример с корнями и степенями.
Пример. Перевод корня в степеньx+5-35=x+5-35, x>-5—x-5-35, x<-5
Обоснуем результаты, приведенные в таблице. Если число m — целое и нечетное, а n — натуральное и четное, для всех переменных из ОДЗ в выражении Amn значение A положительно или неотрицательно (при m>0). Именно поэтому Amn=Amn.
Во втором варианте, когда m — целое, положительное и нечетное, а n — натуральное и нечетное, значения Amn разделяются. Для переменных из ОДЗ, при которых A неотрицательно, Amn=Amn=Amn. Для переменных, при которых A отрицательно, получаем Amn=-Amn=-1m·Amn=-Amn=-Amn=-Amn.
Аналогично рассмотрим и следующий случай, когда m — целое и четное, а n — любое натуральное число. Если значение Aположительно или неотрицательно, то для таких значений переменных из ОДЗ Amn=Amn=Amn. Для отрицательных A получаем Amn=-Amn=-1m·Amn=Amn=Amn.
Таким образом, в третьем случае для всех переменных из ОДЗ можно записать Amn=Amn.
Оператор |
Описание |
Простейшие математические операции |
|
+ — * / () |
Сложение, вычитание, умножение, деление и группирующие символы. Знак умножения * — необязателен: выражение 2sin(3 x ) эквивалентно 2*sin(3*x ). x |
Тригонометрические функции |
|
| Синус от x |
|
| Косинус от x |
|
| Тангенс от x . Можно вводить tg(x ) или tan(x ) |
|
| Котангенс от x . Можно вводить ctg(x ) или cot(x ) |
|
| Секанс от x , определяется как 1/cos(x ) |
|
| Косеканс от x , определяется как 1/sin(x ) |
|
| Арксинус от x . Можно вводить arcsin(x ) или asin(x ) |
|
| Арккосинус от x . Можно вводить arccos(x ) или acos(x ) |
|
| Арктангенс от x . Можно вводить arctg(x ) или atan(x ) |
|
| Арккотангенс от x . Можно вводить arcctg(x ) или acot(x ) |
|
| Арксеканс от x |
|
| Арккосеканс от x |
|
Некоторые константы |
|
| Число Эйлера e = 2.718281828459045… |
|
| Число π = 3.141592653589793… |
|
Корень и его свойства. Подробная теория с примерами (ЕГЭ — 2021)
Как умножать корни? На этот вопрос помогает ответить самое простое и базовое свойство: \( \sqrt[n]{ab}=\sqrt[n]{a}\cdot \sqrt[n]{b}\)
Начнем с простенького:
\( \sqrt{5}\cdot \sqrt{2}=\sqrt{10}\)
\( \sqrt{2}\cdot \sqrt{3}=\sqrt{6}\)
Корни из получившихся чисел ровно не извлекаются? Не беда – вот вам такие примеры:
\( \sqrt{2}\cdot \sqrt{8}=\sqrt{16}=4\)
\( \sqrt{12,5}\cdot \sqrt{2}=\sqrt{25}=5\)
А что, если множителей не два, а больше? То же самое! Формула умножения корней работает с любым количеством множителей:
\( \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{10}=\sqrt{100}=10\)
С этим вроде все ясно.
Едем дальше. А если перед нами такое выражение:
\( 3\sqrt{5}\)
Что мы можем с ним сделать? Ну конечно, спрятать тройку под корнем, помня при этом, что тройка – корень квадратный из \( 9\)!
\( 3\sqrt{5}=\sqrt{9}\cdot \sqrt{5}=\sqrt{45}\).
Зачем нам это нужно? Да просто, чтобы расширить наши возможности при решении примеров:
\( 3\sqrt{10}-\sqrt{45}\cdot \sqrt{2}=\sqrt{90}-\sqrt{90}=0\).
Как тебе такое свойство корней? Существенно упрощает жизнь? По мне, так точно!
Только надо помнить, что вносить под знак корня четной степени мы можем только положительные числа.
Посмотрим, где это еще может пригодиться. Например, в задаче требуют сравнить два числа:
Что больше: \( 3\sqrt{7}\ или\ 2\sqrt{17}\)?
Сходу и не скажешь. Ну что, воспользуемся разобранным свойством внесения числа под знак корня? Тогда вперед:
\( 3\sqrt{7}=\sqrt{9\cdot 7}=\sqrt{63}\)
\( 2\sqrt{17}=\sqrt{4\cdot 17}=\sqrt{68}\)
Ну и, зная, что чем больше число под знаком корня, тем больше сам корень! Т.
{2}}\cdot 2}=7\sqrt{2}\)
Неплохо, да? Любой из этих подходов верен, решай как тебе удобно.
Разложение на множители очень пригодится при решении таких нестандартных заданий, как вот это:
\( \sqrt{15}\cdot \sqrt{180}\cdot \sqrt{12}\)
Не пугаемся, а действуем! Разложим каждый множитель под корнем на отдельные множители:
\( \sqrt{15}\cdot \sqrt{180}\cdot \sqrt{12}=\sqrt{5\cdot 3}\cdot \sqrt{36\cdot 5}\cdot \sqrt{2\cdot 6}\)
Разве это конец? Не останавливаемся на полпути!
\( \begin{array}{l}\sqrt{5\cdot 3}\cdot \sqrt{36\cdot 5}\cdot \sqrt{2\cdot 6}=\sqrt{5\cdot 3}\cdot \sqrt{3\cdot 12\cdot 5}\cdot \sqrt{2\cdot 3\cdot 2}=\\=\sqrt{5\cdot 3}\cdot \sqrt{3\cdot 2\cdot 2\cdot 3\cdot 5}\cdot \sqrt{2\cdot 3\cdot 2}\end{array}\)
На простые множители разложили. Что дальше?
А дальше пользуемся свойством умножение корней и записываем все под одним знаком корня:
\( \begin{array}{l}\sqrt{5\cdot 3\cdot 3\cdot 2\cdot 2\cdot 3\cdot 5\cdot 2\cdot 3\cdot 2}=\sqrt{5\cdot 5\cdot 3\cdot 3\cdot 3\cdot 3\cdot 2\cdot 2\cdot 2\cdot 2}=\\=\sqrt{25}\cdot \sqrt{81}\cdot \sqrt{16}=5\cdot 9\cdot 4=180\end{array}\)
Вот и все, не так все и страшно, правда?
А теперь попробуй самостоятельно (без калькулятора! его на экзамене не будет):
\( \sqrt{15}\cdot \sqrt{54}\cdot \sqrt{10}=?\)
Получилось \( 90\)? Молодец, все верно!
А теперь попробуй вот такой пример решить:
\( \sqrt{4225}=?\)
А пример-то – крепкий орешек, так сходу и не разберешься, как к нему подступиться.
Но нам он, конечно, по зубам. Ну что, начнем раскладывать \( 4225\) на множители?
Сразу заметим, что поделить число на \( 5\) (вспоминаем признаки делимости):
\( \sqrt{4225}=\sqrt{845\cdot 5}=\sqrt{169\cdot 5\cdot 5}=\sqrt{13\cdot 13\cdot 5\cdot 5}=5\cdot 13=65\)
А теперь попробуй сам (опять же, без калькулятора!):
\( \sqrt{2304}=?\)
Ну что, получилось \( 48\)? Молодец, все верно!
Квадратный корень в Python 3 — Извлечение кубических и n-ой степени
Под извлечением корня из какого-либо числа чаще всего подразумевают нахождение решение уравнения x в степени n = value, соответственно для квадратного корня, число n — это два, для кубического — 3. Чаще всего под результатом и числом подразумеваются вещественные числа.
В программировании нахождение корней используется очень часто. Разберемся, как и какими методами можно эффективно извлекать корни из числа. Вначале рассмотрим, какие способы есть в Python, и определим самый эффективный. Потом более подробно разберём, как можно найти не только квадратный корень из числа, но и кубический, и потом корень n степени.
Способы извлечения корня
В языке программирования Python 3 существует три способа извлечения корней:
- Использование функции sqrt из стандартной математической библиотеки math.
- Операция возведения в степень **
- Применение функции pow(x, n)
Чтобы воспользоваться первым способом, необходимо вначале импортировать sqrt из модуля math. Это делается с помощью ключевого слова import: from math import sqrt. При помощи этой функции можно извлекать только квадратный корень из числа. Приведем пример:
from math import sqrt x = sqrt(4) print(x) 2.0
Если же нам нужно вычислить в Python корень квадратный из суммы квадратов, то можно воспользоваться функцией hypot из модуля math. Берется сумма квадратов аргументов функции, из нее получается корень. Аргументов у функции два.
from math import hypot x = hypot(4,3) print(x) 5.0
Еще одним, чуть более универсальным методом, будет использование возведения в степень.
Известно, что для того, чтобы взять корень n из числа, необходимо возвести его в степень 1/n. Соответственно, извлечение квадратного корня из числа 4 будет выглядеть так:
n = 2 x = 4**(1./n) print(x) 2.0
Обратите внимание, что в Python 2 необходимо ставить точку после единицы, иначе произойдет целочисленное деление, и 1/n == 0, а не нужной нам дроби. В Python 3 можно не ставить точку.
Последний метод использует функцию pow(value, n). Эта функция в качестве аргумента value возьмет число, которое необходимо возвести в степень, а второй аргумент будет отвечать за степень числа. Как и в предыдущем методе, необходимо использовать дробь, для того, чтобы получить корень числа.
x = pow(4, 0.5) print(x) 2.0
Какой метод быстрее?
Для того, чтобы определить какой же метод предпочтительнее использовать, напишем программу. Замерять время выполнения будем с помощью метода monotonic библиотеки time.
from time import monotonic
from math import sqrt
iterations = 1000000
start = monotonic()
for a in range(iterations):
x = sqrt(4)
print("sqrt time: {:>.
3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
x = 4 ** 0.5
print("** time: {:>.3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
x = pow(4, 0.5)
print("pow time: {:>.3f}".format(monotonic() - start) + " seconds")
sqrt time: 0.266 seconds
** time: 0.109 seconds
pow time: 0.453 seconds
3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
x = 4 ** 0.5
print("** time: {:>.3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
x = pow(4, 0.5)
print("pow time: {:>.3f}".format(monotonic() - start) + " seconds")
sqrt time: 0.266 seconds
** time: 0.109 seconds
pow time: 0.453 secondsКак видно, самое быстрое решение — использовать **. На втором месте метод sqrt, а pow — самый медленный. Правда, метод sqrt наиболее нагляден при вычислении в Python квадратных корней.
Таким образом, если критична скорость, то используем **. Если скорость не критична, а важна читаемость кода, то следует использовать sqrt.
Квадратный корень
Для извлечения квадратного корня самым наглядным способом, правда не самым быстрым, будет использование sqrt из модуля math.
from math import sqrt x = sqrt (value)
Но можно использовать и трюки с возведением в степень 1/2, что тоже будет приводить к нужному результату.
x = value ** (0.5) или x = pow(value, 0.5).
Кубический корень
Для извлечения кубического корня в Python 3 метод sqrt не подойдет, поэтому воспользуйтесь возведением в степень 1/3:
x = value ** (1./3) или x=pow(value, 1/3).
Корень n-степени
Корень n-степени из числа в Python извлекается можно получить двумя способами с помощью возведения в степень 1.0/n:
- С помощью оператора **.
- Используя функцию pow.
Как было проверено выше, оператор ** быстрее. Поэтому его использовать более целесообразно. Приведем пример вычисления кубических корней в Python 3 с помощью этих двух методов:
n = 4. x = 16.0 ** (1./n) print(x) x = pow(16.0, 1./n) print(x) 2.0 2.0
Корень отрицательного числа
Рассмотрим, как поведут себя функции, если будем брать корень из отрицательного числа.
from math import sqrt x = sqrt(-4) File "main.
py", line 2, in
x = sqrt(-4)
ValueError: math domain errorКак видим, функция sqrt выдаёт исключение.
Теперь посмотрим, что будет при использовании других методов.
x = -4 ** 0.5 print(x) x = pow(-4, 0.5) print(x) -2.0 (1.2246467991473532e-16+2j)
Как видно из результата, оператор ** не выдает исключения и возвращает некорректный результат. Функция pow работает корректно. В результате получаем комплексное число 2j, что является верным.
Вывод
В Python существуют два универсальных способа для извлечения корня из числа. Это возведение в необходимую степень 1/n. Кроме того, можно воспользоваться функцией из математического модуля языка, если необходимо извлечь квадратный корень числа.
Все эти методы имеют свои преимущества и недостатки. Самый наглядный это sqrt, но подходит только для квадратный корней из числа. Остальные методы не такие элегантные, но легко могут извлечь корень нужной степени из числа.
Кроме того оператор ** оказался наиболее быстрым при тестировании.
Необходимо также помнить про целочисленное деление, неправильное использование которого может приводить к ошибке в вычислении.
N-й корень и рациональные экспоненты
Результаты обучения
- Упростите корни N-й степени.
- Запишите радикалы как рациональные экспоненты.
Использование рациональных корней
Хотя квадратные корни являются наиболее распространенными рациональными корнями, мы также можем найти кубические корни, корни четвертой степени, корни пятой степени и многое другое. Так же, как функция квадратного корня является обратной функцией возведения в квадрат, эти корни являются обратными функциями соответствующих степенных функций. Эти функции могут быть полезны, когда нам нужно определить число, которое при возведении в определенную степень дает определенное число.{5} = — 243 [/ латекс]. Если [latex] a [/ latex] является действительным числом с хотя бы одним n -м корнем, то основной n -й корень [latex] a [/ latex] — это число с тем же знаком, что и [latex] a [/ latex], который при увеличении до n в -й степени равен [latex] a [/ latex].
Главный n -й корень [латекса] a [/ latex] записывается как [latex] \ sqrt [n] {a} [/ latex], где [latex] n [/ latex] является положительным целым числом больше чем или равно 2. В радикальном выражении [латекс] n [/ латекс] называется индексом и радикала.
A Общее примечание: основной
n -й кореньЕсли [latex] a [/ latex] является действительным числом с по крайней мере одним n -й корень, то основной n -й корень [latex] a [/ latex], записанный как [latex] \ sqrt [n] {a} [/ latex] — это число с тем же знаком, что и [latex] a [/ latex], которое при увеличении до n в -й степени равно [latex] a [/ latex]. Индекс , индекс радикала — [латекс] n [/ латекс].
Пример: упрощение
n -го корняУпростите каждое из следующих действий:
- [латекс] \ sqrt [5] {- 32} [/ латекс]
- [латекс] \ sqrt [4] {4} \ cdot \ sqrt [4] {1,024} [/ латекс]
- [латекс] — \ sqrt [3] {\ dfrac {8 {x} ^ {6}} {125}} [/ латекс]
- [латекс] 8 \ sqrt [4] {3} — \ sqrt [4] {48} [/ латекс]
- [латекс] \ sqrt [5] {- 32} = — 2 [/ латекс], потому что [латекс] {\ left (-2 \ right)} ^ {5} = — 32 \\ \ text {} [/ латекс]
- Во-первых, выразите произведение как одно радикальное выражение. {2}} {5} && \ text {Упростить}. \\ \ end {align} [/ latex]
- [латекс] \ begin {align} \\ & 8 \ sqrt [4] {3} -2 \ sqrt [4] {3} && \ text {Упростите, чтобы получить одинаковые подкоренные выражения}. \\ & 6 \ sqrt [4] {3} && \ text {Добавить}. \ end {align} [/ latex]
{2}} {5} && \ text {Упростить}. \\ \ end {align} [/ latex]Попробуйте
Упростить.
- [латекс] \ sqrt [3] {- 216} [/ латекс]
- [латекс] \ dfrac {3 \ sqrt [4] {80}} {\ sqrt [4] {5}} [/ латекс]
- [латекс] 6 \ sqrt [3] {9000} +7 \ sqrt [3] {576} [/ латекс]
- [латекс] -6 [/ латекс]
- [латекс] 6 [/ латекс]
- [латекс] 88 \ sqrt [3] {9} [/ латекс]
Использование рациональных экспонентов
Радикальные выражения также можно записывать без использования радикального символа.{m}} \ end {align} [/ latex]
Как: дано выражение с рациональной экспонентой, запишите выражение как радикал.
- Определите степень, посмотрев на числитель экспоненты. {\ frac {2} {3}} [/ латекс] как радикал.{\ frac {23} {15}} [/ латекс]
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
дробных (рациональных) экспонентов | Purplemath
Purplemath
Вам уже известна одна взаимосвязь между сторонниками и радикалами: соответствующий радикал «отменит» показатель, а правая сила «отменит» корень.Например:
Но есть еще одно соотношение, которое, кстати, может значительно упростить вычисления, подобные приведенным выше.
MathHelp.com
Для квадратного (или «второго») корня мы можем записать его как половинную степень, например:
.
..или:Кубический (или «третий») корень — это степень одной трети:
Корень четвертой степени равен одной четвертой степени:
Корень пятой степени равен одной пятой степени; и так далее.
Глядя на первые примеры выше, мы можем переписать их так:
Вы можете ввести дробные показатели на вашем калькуляторе для оценки, но не забудьте использовать круглые скобки.Если вы пытаетесь вычислить, скажем, 15 (4/5) , вы должны заключить в скобки «4/5», потому что в противном случае ваш калькулятор будет думать, что вы имеете в виду «(15 4 ) ÷ 5».
Дробные показатели обеспечивают большую гибкость (вы часто это увидите в исчислении), их часто проще написать, чем эквивалентный радикальный формат, и они позволяют выполнять вычисления, которые вы не могли раньше.
Например:Всякий раз, когда вы видите дробную экспоненту, помните, что верхнее число — это степень, а нижнее число — это корень (если вы конвертируете обратно в радикальный формат).Например:
Кстати, некоторые десятичные степени могут быть записаны и в виде дробных показателей. Если вам дано что-то вроде «3 5,5 », вспомните, что 5,5 = 11/2, поэтому:
Однако, как правило, когда вы получаете десятичную степень (что-то другое, кроме дроби или целого числа), вы должны просто оставить ее как есть или, если необходимо, вычислить ее в своем калькуляторе. Например, 3 π , где π — это число, которое вы узнали в геометрии, и примерно равно 3.14159, нельзя упростить или преобразовать в радикал.
Технический момент: когда вы имеете дело с этими показателями с переменными, вам, возможно, придется принять во внимание тот факт, что вы иногда получаете ровные корни.
Подумайте об этом: предположим, вы начали с числа –2. Тогда:Другими словами, вы вводите отрицательное число и получаете положительное число! Это официальное определение абсолютной величины:
.Да, я знаю: они никогда не говорили вам этого, но они ожидают, что вы каким-то образом узнаете, поэтому я говорю вам сейчас.
Итак, если они дадут вам, скажем, x 3/6 , тогда x лучше не быть отрицательным, потому что x 3 все равно будет отрицательным, и вы попытаетесь извлечь шестой корень отрицательного числа. Если они дадут вам x 4/6 , тогда отрицательное значение x станет положительным (из-за четвертой степени) и тогда будет корень шестой степени, поэтому он станет | x | 2/3 (за счет уменьшения дробной мощности).
С другой стороны, если они дадут вам что-то вроде x 4/5 , вам не нужно заботиться о том, является ли x положительным или отрицательным, потому что пятый корень не имеет проблем с отрицательными. (Между прочим, эти соображения не имеют значения, если в вашей книге указано, что вы должны «предполагать, что все переменные неотрицательны».)Технологический момент: калькуляторы и другое программное обеспечение не вычисляют вещи так, как это делают люди; они используют заранее запрограммированные алгоритмы.Иногда конкретный метод, используемый калькулятором, может создать трудности в контексте дробных показателей.
Например, вы знаете, что кубический корень из –8 равен –2, а квадрат –2 равен 4, поэтому (–8) (2/3) = 4. Но некоторые калькуляторы возвращают комплексное значение или сообщение об ошибке, как в случае с одним из моих графических калькуляторов:
Очевидно, это не ожидаемый результат, особенно если вы еще не изучали комплексные числа.
(2/3) «в ячейку, электронная таблица Microsoft» Excel «возвращает ошибку» # ЧИСЛО! «, Еще один бесполезный ответ.Некоторые калькуляторы и программы будут выполнять вычисления, как ожидалось, как показано справа от моего другого графического калькулятора:
Разница связана с заранее запрограммированными вычислительными алгоритмами. Эти алгоритмы обычно пытаются выполнять вычисления способами, требующими наименьшего количества «операций», чтобы обработать введенные вами данные как можно быстрее.
Но иногда самый быстрый метод не всегда самый полезный, и ваш калькулятор «давится».
К счастью, проблему можно обойти. Разделив числитель и знаменатель дробной степени, вы можете ввести выражение, чтобы ваш калькулятор получил правильное значение. Получив бесполезный ответ в моем первом калькуляторе, я повторно ввел число с разбитой на части степенью:
Как вы можете видеть выше, не имело значения, возьму ли я сначала кубический корень из отрицательной восьмерки, а затем возведу в квадрат или сначала возведу в квадрат, а затем получу кубический корень; в любом случае, подавая числитель и знаменатель в калькулятор по отдельности, я смог заставить калькулятор возвращать правильное значение «4».
URL: https://www.purplemath.com/modules/exponent5.htm
степеней и корней — формулы, примеры, викторины | Учебник по математике
В этом учебном пособии по математике мы вводим экспоненты / степени и корни с использованием формул, решаемых примеров и практических вопросов.
Полномочия и корни | Формулы, решенные примеры, практические задачи
Показатели, также называемые степенями, представляют собой способ выражения числа, умноженного на само себя в определенное количество раз.
Когда мы пишем число a , на самом деле это 1 , выраженное как a в степени 1.
а 2 = а * а
a 3 = a * a * a
:
:
a n = a * a * a * a *. . . п раз.Основные формулы в Powers and Roots
Некоторые основные формулы, используемые для решения вопросов об экспонентах:
- ( м ) n = ( n ) м = м
- а м . a n = a m + n
- a -м = 1 / a м
- a м / a n = a m-n = 1 / a n-m
- (ab) n = a n b n
- (a / b) n = a n / b n
- а 0 = 1
2 2 = 4. 2 3 = 8. Это то, что мы узнаем в экспонентах.
√4 = 2. 3 √8 = 2.Это то, что мы узнаем в корнях.
Здесь √ называется квадратным корнем или порядка 2 nd .
3 √ называется кубическим корнем или порядка 3 rd .
Точно так же мы можем получить корень числа любого порядка.
n √a называется surd порядка n.
Обозначение n √ называется радикальным знаком,
n называется порядком сурда и
a называется подкоренным.
Некоторые основные формулы, используемые для решения вопросов о корнях:
- n √a = a 1 / n
- n √ab = n √a * n √b
- n √ (a / b) = n √a / n √b
- ( n √a) n = a
Решенные примеры в Powers & Roots
Рассмотрим несколько примеров:
Задача 1.
Упростить (7.5 * 10 5 ) / (25 * 10 -4 )Решение :
(7,5 * 10 5 ) / (25 * 10 -4 )
→ (75 * 10 4 ) / (25 * 10 -4 )
Отмена 75 с 3 умножением на 25 и применение формулы м / a n = a m-n
→ 3 * 10 4 — (- 4)
→ 3 * 10 8
Задача 2. Найти x, если 3 2x-1 + 3 2x + 1 = 270.
Решение :
Вычитая обыкновенный термин, получаем
→ 3 2х-1 (1 + 3 2 )
Обратите внимание, что здесь мы применили формулу a m + n = a m .a n в письменном виде 3 2x + 1 как произведение 3 2x-1 и 3 2 .
→ 3 2х-1 (10) = 270
→ 3 2х-1 = 27
→ 3 2x-1 = 3 3
→ 2х-1 = 3
→ х = 2.
Задача 3. Упростить [10 [(216) 1/3 + (64) 1/3 ] 3 ] 3/4
Решение :
[10 [(6 3 ) 1/3 + (4 3 ) 1/3 ] 3 ] 3/4
→ [10 [6 + 4] 3 ] 3/4
→ [10 (10) 3 ] 3/4
→ (10 4 ) 3/4
→ 10 3 = 1000.
Задача 4. Упростить [4 0,08 * (2 0,22 ) 2 ] 10 / [16 0,16 * (2 4 ) 0,74 * (4 2 ) 0,1 ]
Решение :
[4 0,08 * (2 0,22 ) 2 ] 10 / [16 0,16 * (2 4 ) 0,74 * (4 2 ) 0,1 ]
Применяя формулу (a m ) n = (a n ) m к подчеркнутой части,
→ [4 0.
08 * (2 2 ) 0,22 ] 10 / [16 0,16 * (2 4 ) 0,74 * (4 2 ) 0,1 ]→ [4 0,08 * 4 0,22 ] 10 / [16 0,16 * (2 4 ) 0,74 * (4 2 ) 0,1 ]
Применяя формулу a m .a n = a m + n к числителю,
→ [4 0,08 + 0,22 ] 10 / [16 0.16 * (2 4 ) 0,74 * (4 2 ) 0,1 ]
Упрощение знаменателя,
→ [4 0,3 ] 10 / [(4 2 ) 0,16 * (4 2 ) 0,74 * (4 2 ) 0,1 ]
Применяя формулу a m .a n = a m + n
→ 4 3 / [(4 2 ) 0,16 + 0,74 + 0,1 ]
→ 4 3 / (4 2 ) 1
Применяя формулу a m / a n = a m-n ,
= 4.
Задача 5. Упростить √ (5 + 3√2) + [1 / √ (5 + 3√2)]
Решение :
Упрощение такого выражения также означает, что знаменатель следует рационализировать. Рационализация выражения означает удаление всех имеющихся квадратных корней.
Термин, который рационализирует, называется сопряженным. В этом примере, чтобы рационализировать 5 + 3√2, мы используем 5-3√2. Следовательно, 5-3√2 называется сопряженным с 5 + 3√2 и наоборот.
Рассмотрим 5 + 3√2 = x.
[√x + (1 / √x)] 2 = x + 1 / x + 2 * √x * 1 / √x
→ (5 + 3√2) + (1 / (5 + 3√2)) + 2
В знаменателе 5 + 3√2. Чтобы удалить квадратный корень, умножим 1 / (5 + 3√2) на (5-3√2) / (5-3√2). Умножение на это никоим образом не меняет значения термина, но помогает рационализировать знаменатель и упростить выражение.
→ (5 + 3√2) + ((5-3√2) / (5 + 3√2) (5-3√2) ) + 2
Применение формулы (a + b) (a-b) = a 2 — b 2 к подчеркнутой части,
→ (5 + 3√2) + [(5-3√2) / (5 2 — (3√2) 2 ] + 2
→ (5 + 3√2) + [(5-3√2) / (25 — (9 * 2)] + 2
→ (5 + 3√2) + [(5-3√2) / 7] + 2
→ [7 (5 + 3√2) + (5-3√2) + 2 (7)] / 7
→ [35 + 21√2 + 5 — 3√2 + 14] / 7
→ [54 + 18√2] / 7
Поскольку исходное выражение было возведено в квадрат для исключения корней, нам нужно применить квадратный корень к этому выражению.
→ √ ([54 + 18√2] / 7)
Примечание. Поскольку мы знали, что результат выражения будет положительным, мы смогли возвести в квадрат, а затем извлечь квадратный корень из выражения. Если есть сомнения в том, что это может быть отрицательно, мы воздержимся от этого.
Задача 6. Если a 2 + b 2 + c 2 = ab + bc + ca, упростите [x a / x b ] ab * [x b / x c ] bc * [x c / x a ] ca
Решение :
Применяя m / a n = a m-n , получаем
→ (x a-b ) a-b * (x b-c ) b-c * (x c-a ) c-a
Применяя формулу (a-b) 2 = a 2 + b 2 -2ab в экспоненте,
→ x (a 2 + b 2 — 2ab) * x (b 2 + c 2 — 2bc) * x (c 2 + a 2 — 2ca )
Применение м .a n = a m + n
→ x (a 2 + b 2 — 2ab + b 2 + c 2 — 2bc + c 2 + a 2 — 2ca)
→ x (2 (a 2 + b 2 + c 2 — (ab + bc + ca)))
→ х (2 (0))
→ x 0 = 1.
Задача 7. Что больше: 4 √3 или 3 √4?
Решение :
Чтобы сравнить два сюрда, они должны быть похожими i.е., они должны быть одного порядка.
4 √3 — это сюрд из 4 -го порядка и 3 √4 — это сюрд из 3 -го порядка .
4 √3 можно записать как 3 1/4 и 3 √4 как 4 1/3 .
Пока еще нет возможности сравнить. Для этого нам нужно взять НОК двух заказов и выразить их как сурды одного заказа.
НОК 3 и 4 равно 12.
1/4 можно записать как (1/4) * (3/3) = 3/12 И 1/3 можно записать как (1/3) * (4/4) = 4/12.
3 1/4 можно записать как 3 3/12 4 1/3 можно записать как 4 4/12 .
3 3/12 = (3 3 ) 1/12 = 12 √27 4 4/12 = (4 4 ) 1/12 = 12 √256
Теперь сравнение между 12 √27 и 12 √256.
Очевидно, 12 √256 больше, чем 256> 27.
Следовательно, 3 √4> 4 √3
Тест на полномочия и корни: решите следующие проблемы :
Проблема 1
Если (2 10 ,2 n ,4 3 ) / (8 n ,16) = 16, найдите n.A. 3
B. 2
C. 5
D. 4Ответ 1
Д.
Пояснение
(2 10 .2 n . (2 2 ) 3 ) / (2 3 ) n ,2 4 = 2 4
Применяя формулу a m / a n = a m-n и принимая только показатели степени,
→ 16 + п — (3n + 4) = 4
→ 12 + п — 3n — 4 = 4
Проблема 2
Если x a + b + c = 3, найдите значение (x 2a — b / x -b ). (x 2b — c / x -c ).(x 2c — a / x -a )A. 3
B. 6
C. 9
D. НетОтвет 2
С.
Пояснение :
Применение m / a n = a m-n ,
→ х 2a — b + b . х 2б — с + с . х 2c — а + а
Применение m .a n = a m + n ,
→ х 2a + 2b + 2c
→ (х a + b + c ) 2
→ 3 2 = 9
Функция, обратная квадратному корню
Чтобы найти обратную функцию квадратного корня, важно сначала набросать или изобразить данную проблему, чтобы четко определить, что такое область и диапазон.Я буду использовать домен и диапазон исходной функции, чтобы описать область и диапазон обратной функции, меняя их местами. Если вам нужна дополнительная информация о том, что я имел в виду под «обменом доменов и диапазонов» между функцией и ее обратной, см. Мой предыдущий урок об этом.
Примеры того, как найти обратную функцию квадратного корня
Пример 1: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.
Каждый раз, когда я сталкиваюсь с функцией извлечения квадратного корня с линейным членом внутри радикального символа, я всегда думаю о ней как о «половине параболы», нарисованной сбоку.Поскольку это положительный случай функции квадратного корня, я уверен, что ее диапазон будет становиться все более положительным, проще говоря, стремительно увеличиваясь до положительной бесконечности.
Эта конкретная функция извлечения квадратного корня имеет этот график с указанием области и диапазона.
С этого момента мне нужно будет решить обратную алгебру, выполнив предложенные шаги. По сути, замените \ color {red} f \ left (x \ right) на \ color {red} y, поменяйте местами x и y в уравнении, решите для y, которое вскоре будет заменено соответствующей обратной записью, и, наконец, укажите домен и диапазон.
Не забудьте использовать методы решения радикальных уравнений для решения обратной задачи. Возведение квадратного корня в квадрат или во вторую степень должно устранить радикал. Однако вы должны сделать это с обеими сторонами уравнения, чтобы сохранить баланс.
Убедитесь, что вы проверили домен и диапазон обратной функции из исходной функции. Они должны быть «противоположны друг другу».
Размещение графиков исходной функции и обратной к ней по одной координатной оси.2} = 1. Его домен и диапазон будут замененной «версией» исходной функции.
Пример 3: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.
Это график исходной функции, показывающий ее домен и диапазон.
Определение диапазона обычно является сложной задачей. Лучший способ найти это — использовать график данной функции с ее областью определения. Проанализируйте, как функция ведет себя по оси Y, учитывая значения x из области.
Вот шаги, чтобы решить или найти обратное значение данной функции квадратного корня.
Как видите, все очень просто. Убедитесь, что вы делаете это осторожно, чтобы избежать ненужных алгебраических ошибок.
Пример 4: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.
Эта функция составляет 1/4 (четверть) окружности с радиусом 3, расположенной в Квадранте II. С другой стороны, это половина полукруга, расположенная над горизонтальной осью.
Я знаю, что он пройдет проверку горизонтальной линии, потому что ни одна горизонтальная линия не пересечет ее более одного раза. Это хороший кандидат на обратную функцию.
Опять же, я могу легко описать диапазон, потому что потратил время на его построение. Что ж, я надеюсь, что вы понимаете важность наличия наглядного пособия, которое поможет определить этот «неуловимый» диапазон.
Присутствие члена в квадрате внутри радикального символа говорит мне, что я буду применять операцию извлечения квадратного корня к обеим сторонам уравнения, чтобы найти обратное.Поступая так, у меня будет положительный или отрицательный результат. Это ситуация, когда я приму решение, какую из них выбрать в качестве правильной обратной функции. Помните, что обратная функция уникальна, поэтому я не могу позволить получить два ответа.
Как мне решить, какой выбрать? Ключевым моментом является рассмотрение домена и диапазона исходной функции. Я поменяю их местами, чтобы получить домен и диапазон обратной функции. Используйте эту информацию, чтобы определить, какая из двух функций-кандидатов удовлетворяет требуемым условиям.
Хотя у них один и тот же домен, диапазон здесь — решающий фактор! Диапазон говорит нам, что обратная функция имеет минимальное значение y = -3 и максимальное значение y = 0.
Случай положительного квадратного корня не соответствует этому условию, так как он имеет минимум при y = 0 и максимум при y = 3. Отрицательный случай должен быть очевидным выбором, даже после дальнейшего анализа.
Пример 5: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.
Полезно увидеть график исходной функции, потому что мы можем легко определить ее домен и диапазон.
Отрицательный знак функции квадратного корня означает, что он находится ниже горизонтальной оси. Обратите внимание, что это похоже на Пример 4. Это также одна четверть круга, но с радиусом 5. Область вынуждает четверть круга оставаться в Квадранте IV.
Вот как мы находим его алгебраически обратный.
Вы выбрали правильную обратную функцию из двух возможных? Ответ — случай с положительным знаком.
Практика с рабочими листамиВозможно, вас заинтересует:
Инверсия матрицы 2 × 2
Функция, обратная абсолютному значению
Функция, обратная постоянной
Функция, обратная экспоненте
Функция, обратная линейной функции
Обратная логарифмическая функция
Обратная квадратичная функция
Обращение рациональной функции
Корень (числа) — определение математического слова
Корень (числа) — определение математического слова — Открытый справочник по математикеКорень числа x — это другое число, которое при умножении само на себя заданное количество раз равно x.
Например, третий корень (также называемый кубическим корнем) из 64 равен 4, потому что если вы умножите три четверки вместе, вы получите 64:
4 × 4 × 4 = 64
Это было бы записано как Вышеупомянутое будет означать «третий корень из 64 равен 4» или «кубический корень из 64 равен 4» .- Второй корень обычно называют «квадратным корнем».
- Третий корень числа обычно называют «кубическим корнем»,
- После этого они называются корнем n, например корень 5, корень 7 и т. Д.
Иногда бывает два корня
Для каждого корня четной степени (например, 2-го, 4-го, 6-го….) есть два корня. Это потому, что умножение двух положительных или двух отрицательных чисел дает положительный результат. Например, рассмотрим квадратный корень из 9.
Какое число, умноженное на само себя, даст 9?
Очевидно 3 будут работать:3 × 3 = 9
Но так будет -3:-3 × -3 = 9
Когда таких корней два, если не указано иное, мы имеем в виду положительный. Строго говоря, когда мы пишем √ 4, мы имеем в виду положительный корень +2.Это называется «главный корень».
Корни отрицательных чисел
У отрицательных чисел нет реальных корней четного порядка. Например, квадратного корня из -9 не существует, потому что -3 × -3 = + 9, а также +3 × +3 = + 9. Это относится ко всем корням четного порядка, 2-му (квадратному) корню, 4-му корню, 6-му корню и так далее.
Однако — это корней нечетного порядка отрицательных чисел. Например, –3 — это кубический корень из –27. Это потому что –3 × –3 × –3 = –27.Первые два члена при умножении дают +9, затем следующее умножение дает
+9 × –3 = –27. Это относится ко всем корням нечетного порядка, таким как 3-й (кубический) корень, 5-й корень, 7-й корень и т. Д.Мнимые числа
Выше сказано, что действительного квадратного корня из отрицательного числа не существует. Обратите внимание на слово «настоящий». Это говорит о том, что нет настоящий номер это квадратный корень отрицательного числа.
Однако в математике и инженерии нам часто нужно найти квадратный корень из отрицательного числа.Чтобы решить эту проблему, мы вводим понятие «мнимого» числа. Он включает в себя символ i , который обозначает квадратный корень из отрицательного числа. Или, другими словами, i 2 = –1
На практике мы можем использовать его для выражения квадратного корня из любого отрицательного числа. Например Это означает, что квадратный корень из –25 — это квадратный корень из +25, умноженный на квадратный корень из отрицательной единицы.
Подробнее о мнимых числах см. Мнимые числа.
Символы
Радиканд
Вещь, корень которой вы находите.Радикальный символ
Символ √ , означающий «корень из». Длина турника важна. См. Примечание ниже.Степень
Сколько раз подкоренное выражение умножается само на себя. 2 означает квадратный корень, 3 означает кубический корень. После этого они называются корень 4-й, 5-й и так далее. Если он отсутствует, предполагается, что это 2 — квадратный корень.Другой способ записи
Корни также можно записать в экспоненциальной форме. В общем Так, например, кубический корень x будет записан Что будет произноситься как «х в степени одной трети».
Другие экспоненты и основные темы
(C) Открытый справочник по математике, 2011 г.
Все права защищены.Как преобразовать корни в дробные экспоненты — стенограмма видео и урока
Запись корня в виде экспоненты
Любое радикальное выражение можно записать в виде экспоненциального выражения. Результат будет иметь показатель степени, который является дробью. Следующие шаги описывают, как должно быть записано экспоненциальное выражение:
- Индекс радикала, который является корнем, становится знаменателем дроби
- Подкоренное выражение становится основой экспоненциального выражения, а
- Если подкоренное выражение радикального выражения имеет показатель степени, это число становится числителем дроби; в противном случае цифра 1 записывается как числитель
Пример 1 В этом первом примере подкоренное выражение равно 28 и становится основанием экспоненциального выражения.Корень радикала равен 5 и становится знаменателем показателя степени. Поскольку подкоренное выражение не имеет показателя степени, числитель дробной степени равен 1.
Пример 2 Во втором примере нет числа, записанного в качестве индекса радикала. Следовательно, корень равен 2. Подкоренное выражение равно 7 с показателем степени 3. 7 становится основанием экспоненциального выражения, а 3 становится числителем показателя степени.Знаменатель показателя степени равен 2, потому что корень равен 2.
Преобразование корня использует
При выполнении операций с радикальными выражениями, таких как умножение или деление, может быть очень трудно решить, если они имеют разные корни. Преобразуя их в экспоненциальные выражения, можно применять свойства экспонент, что упрощает умножение и деление выражений.
В следующем примере показано, как перемножить два радикала, которые имеют одно и то же подкоренное выражение, но разные корни.Во-первых, они преобразуются в экспоненциальные выражения. Затем они умножаются, применяя свойство произведения экспоненты. Свойство продукта экспоненты позволяет вам просто добавлять показатели, когда основания совпадают.
Итоги урока
Хорошо, давайте сделаем обзор. Сначала мы узнали о различных частях радикальных выражений; в основном то, что часть выражения, записанная внутри радикального символа, называется подкоренным элементом и , а индекс — это число, записанное за пределами радикального символа меньшим размером шрифта.
Затем мы узнали, как радикальные выражения имеют корни, которые можно переписать как дроби в экспоненциальных выражениях. Корень радикала определяется индексом и становится знаменателем показателя степени в экспоненциальном выражении. Подкормка становится основой.
Если подкоренное выражение имеет показатель степени, это число становится числителем дробной степени. В противном случае в числителе записывается 1.
Поиск корней — Бесплатная справка по математике
Что такое «рут»?
Корень — это значение, для которого заданная функция равна нулю.Когда эта функция отображается на графике, корнями являются точки, в которых функция пересекает ось x.
Для функции \ (f (x) \) корнями являются значения x, для которых \ (f (x) = 0 \). Например, с функцией \ (f (x) = 2-x \) единственный корень будет \ (x = 2 \), потому что это значение дает \ (f (x) = 0 \).
Конечно, легко найти корни такой тривиальной проблемы, но как насчет чего-то безумного вроде этого:
$$ f (x) = \ frac {(2x-3) (x + 3)} {x (x-2)} $$Шаги по поиску корней рациональных функций
Установить каждый множитель в числителе равным нулю.
Решите этот множитель относительно x.
Проверьте множители знаменателя, чтобы убедиться, что вы не делите на ноль!
Числитель Коэффициенты
Помните, что коэффициент — это что-то умножаемое или делимое, например \ ((2x-3) \) в приведенном выше примере. Итак, два множителя в числителе — это \ ((2x-3) \) и \ ((x + 3) \). Если или из этих факторов могут быть равны нулю, тогда вся функция будет равна нулю.Не имеет значения (ну, есть исключение), что говорит остальная часть функции, потому что вы умножаете на член, равный нулю.
Итак, суть в том, чтобы выяснить, как сделать числитель нулевым, и вы нашли свои корни (также известные как нули по понятным причинам!). В этом примере у нас есть два множителя в числителе, поэтому любой из них может быть равен нулю. Давайте установим их (по отдельности) равными нулю, а затем решим для значений x:
$$ 2x — 3 = 0 $$ $$ 2x = 3 $$ $$ x = \ frac {3} {2} $$И
$$ x + 3 = 0 $$ $$ x = -3 $$Итак, \ (x = \ frac {3} {2} \) и \ (x = -3 \) становятся нашими корнями для этой функции.Они также являются пересечениями по оси x при нанесении на график, потому что y будет равно 0, когда x равен 3/2 или -3.
Факторы знаменателя
Как и в случае с числителем, знаменатели умножаются на два множителя. Это \ (x \) и \ (x-2 \). Приравняем их к нулю и решим:
$$ x = 0 $$И
$$ x — 2 = 0 $$ $$ x = 2 $$Это , а не корней этой функции. Посмотрите, что происходит, когда мы подставляем 0 или 2 для x. В знаменателе получаем ноль, что означает деление на ноль.Это означает, что на данный момент функции не существует. Фактически, x = 0 и x = 2 становятся нашими вертикальными асимптотами (нулями в знаменателе). Итак, существует вертикальная асимптота при x = 0 и x = 2 для указанной выше функции.
Вот геометрическое изображение того, как выглядит приведенная выше функция, включая ОБЕ х-пересечения и ОБЕИ вертикальные асимптоты:
Сводка
Корни функции — это значения x, для которых функция равна нулю. Их также называют нулями. Когда дана рациональная функция, обнулить числитель путем обнуления факторов по отдельности.Убедитесь, что ваши нули не превращают знаменатель в ноль, потому что тогда у вас будет не корень, а вертикальная асимптота.
Найдите корни данного уравнения ниже:
.
{\ frac {2} {3}} [/ латекс] как радикал.{\ frac {23} {15}} [/ латекс]
..или:
Например:
Подумайте об этом: предположим, вы начали с числа –2. Тогда:
С другой стороны, если они дадут вам что-то вроде x 4/5 , вам не нужно заботиться о том, является ли x положительным или отрицательным, потому что пятый корень не имеет проблем с отрицательными. (Между прочим, эти соображения не имеют значения, если в вашей книге указано, что вы должны «предполагать, что все переменные неотрицательны».)
(2/3) «в ячейку, электронная таблица Microsoft» Excel «возвращает ошибку» # ЧИСЛО! «, Еще один бесполезный ответ.
a n = a m + n 
Упростить (7.5 * 10 5 ) / (25 * 10 -4 )
08 * (2 2 ) 0,22 ] 10 / [16 0,16 * (2 4 ) 0,74 * (4 2 ) 0,1 ]