Факт 3.
\(\bullet\) Если \(y=f(x)\) – некоторая функция, то касательная к ней в точке с абсциссой \(x_0\) имеет вид: \[y=f(x_0)+f'(x_0)\cdot (x-x_0)\] \(\bullet\) Следовательно, \(k=f'(x_0)=\mathrm{tg}\,\alpha\) – тангенс угла наклона касательной к положительному направлению оси \(Ox\), он же угловой коэффициент касательной, если ее уравнение записать как \(y=kx+b\).
Факт 4.
\(\bullet\) Если \(f'(x)>0\) на \((a;b)\), то \(f(x)\) возрастает на \((a;b)\).
\(\bullet\) Если \(f'(x)<0\) на \((a;b)\), то \(f(x)\) убывает на \((a;b)\).
\(\bullet\) Если \(f'(x_0)=0\) и в точке \(x_0\) производная меняет свой знак, то \(x_0\) — функции \(f(x)\):
— если производная меняет знак с “\(-\)” на “\(+\)” (считая слева направо), то \(x_0\) — ;
— если производная меняет знак с “\(+\)” на “\(-\)” (считая слева направо), то \(x_0\) — .
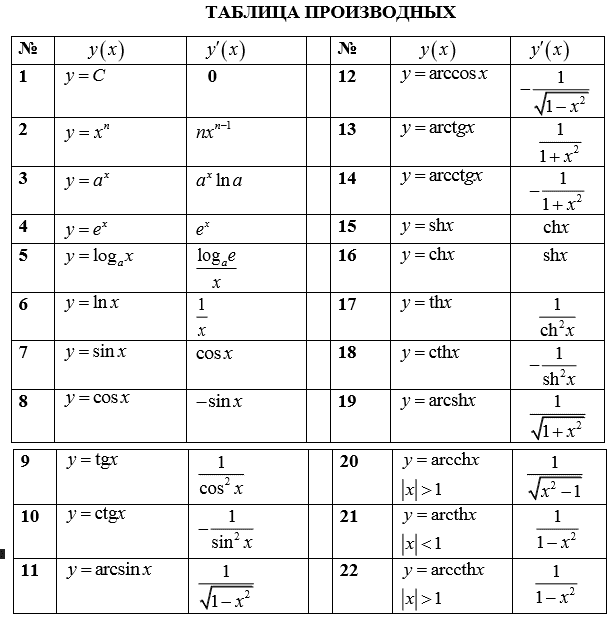
Производные гиперболических функций
Для производных гиперболических функций справедливы соотношения:
|
|
|
|
|
|
|
|
|
| ′ |
|
|
|
|
|
|
|
|
|
|
| ′ |
|
|
|
| ′ |
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ′ |
|
|
|
|
| 1 |
|
|
| |||||
|
| (sh x) |
|
| = ch x; | (ch x) = sh x; | (th x) |
| = |
|
|
|
|
| ; |
|
|
|
| (cth x) |
|
| = − |
|
| . |
| |||||||||||||||||||||||||||||||||||
|
|
| ch 2 x |
| sh 2 x |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Доказательство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||
|
|
|
|
| ′ |
|
|
| ex | −e−x | ′ | ex +e−x |
|
|
|
| ′ |
| ex + e−x | ′ |
| ex −e−x |
|
|
|
| ||||||||||||||||||||||||||||||||||||
(sh x) | = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| = ch x ; (ch x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| = |
|
|
|
|
|
|
| = sh x . | |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||
|
|
|
| 2 |
|
| = |
|
| 2 |
| = |
|
|
|
| 2 |
|
|
|
|
|
|
|
|
|
| 2 |
|
| ||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||
|
|
|
|
|
|
|
|
| ′ |
|
| sh x ′ |
| sh′x ch x −ch′x sh x |
|
| ch3 x −sh3 | x |
|
|
|
|
| 1 |
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||
(th x) | = |
|
|
|
| = |
|
|
|
|
|
|
|
|
|
| = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| = |
|
|
|
|
| , так как | |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| ch x |
|
|
|
|
| ch3 x |
|
|
|
|
|
|
|
|
| ch3 x |
|
|
|
|
|
|
|
|
|
| ch3 | x |
|
|
|
|
| |||||||||||||||||
|
|
|
|
|
|
|
|
| 1 ′ |
|
|
|
|
|
|
|
| ch 2 x −sh 2 x =1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||
′ |
|
|
|
|
|
|
|
|
|
| 1 |
|
|
| 1 |
|
| ch 2 x |
|
| 1 |
|
|
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
(cth x) |
| = |
|
|
|
|
|
|
|
|
| = − |
|
|
|
|
|
|
| = − |
|
|
|
|
|
|
|
| = − |
|
|
|
|
|
|
|
|
|
|
| . |
|
|
|
|
|
|
|
|
|
|
| ||||||||||
|
|
|
|
|
|
| th 2 |
|
| ch 2 |
| sh 2 x | ch | 2 x |
| sh 2 | x |
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||
|
|
|
|
| th x |
|
| x | x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||
Полученные результаты запишем в таблицу 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Таблица 3. | |||||||||||||||||||||||||||||||||||||||||||
(xα )′ = α xα−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (arcsin x)′ = |
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 | − x2 |
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
(e x )′ = ex |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (arccos x)′ = − |
|
| 1 |
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 − x2 |
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
(a x )′ = a x ln a |
|
|
|
|
|
|
|
|
|
|
|
|
| (arctg x)′ = |
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| + x2 |
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
| ||||||||||||||
′ |
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ′ |
|
|
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
| |||||||
(ln x) | = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (arcctg x) | = − |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||
| x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1+ x2 |
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||
(loga x)′ = |
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (sh x)′ | = ch x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||
|
| x ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||
(sin x)′ = cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (ch x)′ | = sh x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||
(cos x)′ = −sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ′ |
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (th x) = | ch 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||
′ |
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ′ |
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
(tg x) | = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (cth x) |
| = − |
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||
cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| sh 2 x |
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||
′ |
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
(ctg x) |
| = − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||
| sin2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||
Пример 3. 1.2 1.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
Вычислите производную функции y = | cos(3x − 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заданная функция является суперпозицией трех функций |
| y = (cos(3x − | 1 | . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2))2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
дифференцировать эту функцию, используя правила дифференцирования, начиная с внешней, степенной функции:
y′ = (cos(3x − 2))12 ′ (cos(3x − 2))′ (3x − 2)′.
15
Производные математические функции — Visual Basic
- Чтение занимает 2 мин
В этой статье
В следующей таблице показаны невстроенные математические функции, которые могут быть производными от встроенных математических функций System.Math объекта. Доступ к встроенным математическим функциям можно получить, добавив Imports System.Math в файл или проект.
| Компонент | Производные эквиваленты |
|---|---|
| Секанс (с (x)) | 1/cos (x) |
| Косеканс (CSC (x)) | 1/Sin (x) |
| Котангенс (Ктан (x)) | 1/Tan (x) |
| Обратный Синус (ASIN (x)) | ATAN (x/Sqrt (-x * x + 1)) |
| Обратный косинус (ACOS (x)) | ATAN (-x/Sqrt (-x * x + 1)) + 2 * ATAN (1) |
| Обратный секанс (АСЕК (x)) | 2 * ATAN (1) — ATAN (Sign (x)/SQRT (x * x – 1)) |
| Обратный косеканс (ACSC (x)) | ATAN (Sign (x)/SQRT (x * x – 1)) |
| Обратная котангенс (Акот (x)) | 2 * ATAN (1) — ATAN (x) |
| Гиперболический синус (SINH (x)) | (Exp (x) – EXP (-x))/2 |
| Гиперболический косинус (COSH (x)) | (Exp (x) + EXP (-x))/2 |
| Гиперболический тангенс (TANH (x)) | (Exp (x) – EXP (-x))/(exp (x) + EXP (-x)) |
| Гиперболический секанс (Сеч (x)) | 2/(exp (x) + EXP (-x)) |
| Гиперболический косеканс (Ксч (x)) | 2/(exp (x) — EXP (-x)) |
| Гиперболический котангенс (КОС (x)) | (Exp (x) + EXP (-x))/(exp (x) – EXP (-x)) |
| Обратный гиперболический синус (Asinh (x)) | Log (x + Sqrt (x * x + 1)) |
| Обратный гиперболический косинус (ACOSH (x)) | Log (x + Sqrt (x * x – 1)) |
| Обратный гиперболический тангенс (ATANH (x)) | Журнал ((1 + x)/(1 – x))/2 |
| Обратный гиперболический секанс (Асеч (x)) | Log ((sqrt (-x * x + 1) + 1)/x) |
| Обратный гиперболический косеканс (Аксч (x)) | Log ((знак (x) * SQRT (x * x + 1) + 1)/x) |
| Обратный гиперболический котангенс (Акос (x)) | Log ((x + 1)/(x – 1))/2 |
См.
 также
такжеПроизводные правила | Математическое исчисление
Производные правила и законы. Таблица производных функций.
Производное определение
Производная функции — это отношение разности значений функции f (x) в точках x + Δx и x к Δx, когда Δx бесконечно мало. Производная — это наклон функции или наклон касательной в точке x.
Вторая производная
Вторая производная определяется по формуле:
Или просто выведите первую производную:
N-я производная
Производная n вычисляется путем вычисления f (x) n раз.
В п — е производная равна производной от (п-1) производное:
f ( n ) ( x ) = [ f ( n -1) ( x )] ‘
Пример:
Найдите четвертую производную от
е ( х ) = 2 х 5
f (4) ( x ) = [2 x 5 ] » » = [10 x 4 ] » ‘= [40 x 3 ]’ ‘= [120 x 2 ]’ = 240 x
Производная на графике функции
Производная функции — это наклон касательной прямой.
Производные правила
Правило производной суммы
Когда a и b постоянные.
( af ( x ) + bg ( x )) ‘= af’ ( x ) + bg ‘ ( x )
Пример:
Найдите производную от:
3 х 2 + 4 х.
Согласно правилу сумм:
а = 3, б = 4
е ( х ) = х 2 , g ( х ) = х
f ‘ ( x ) = 2 x , g’ ( x ) = 1
(3 х 2 + 4 х ) ‘= 3⋅2 х + 4⋅1 = 6 х + 4
Правило производного продукта
( f ( x ) ∙ g ( x )) ‘= f’ ( x ) g ( x ) + f ( x ) g ‘ ( x )
Правило производного частного
Правило производной цепочки
f ( g ( x )) ‘= f’ ( g ( x )) ∙ g ‘ ( x )
Это правило можно лучше понять с помощью обозначений Лагранжа:
Функция линейной аппроксимации
Для малых Δx мы можем получить приближение к f (x 0 + Δx), когда мы знаем f (x 0 ) и f ‘(x 0 ):
f ( x 0 + Δ x ) ≈ f ( x 0 ) + f ‘( x 0 ) ⋅Δ x
Таблица производных функций
| Название функции | Функция | Производная |
|---|---|---|
f ( x ) | f ‘( x ) | |
| Постоянный | const | 0 |
| Линейный | х | 1 |
| Сила | х а | топор а- 1 |
| Экспоненциальный | e x | e x |
| Экспоненциальный | а х | a x ln a |
| Натуральный логарифм | ln ( x ) | |
| Логарифм | журнал b ( x ) | |
| Синус | грех х | cos x |
| Косинус | cos x | -sin x |
| Касательная | загар х | |
| Арксинус | arcsin x | |
| Арккосин | arccos x | |
| Арктангенс | arctan x | |
| Гиперболический синус | зп х | cosh x |
| Гиперболический косинус | cosh x | зп х |
| Гиперболический тангенс | tanh x | |
| Обратный гиперболический синус | sh -1 x | |
| Обратный гиперболический косинус | cosh -1 x | |
| Обратный гиперболический тангенс | танх -1 х |
Производные примеры
Пример # 1
е ( х ) = х 3 +5 х 2 + х +8
f ‘ ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1
Пример # 2
е ( х ) = грех (3 х 2 )
При применении цепного правила:
f ‘ ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]’ = cos (3 x 2 ) ⋅ 6 x
Тест второй производной
Когда первая производная функции равна нулю в точке x 0 .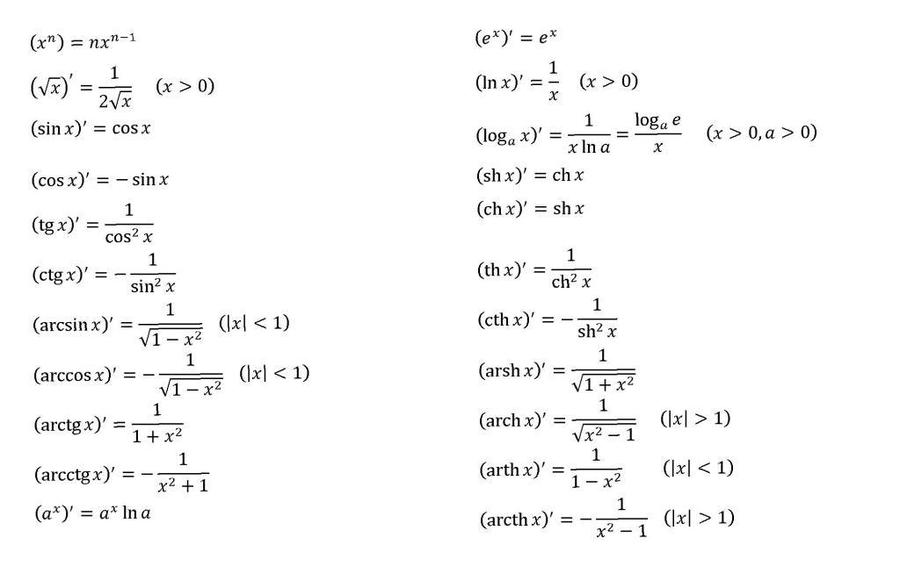 2x = 1$
2x = 1$
ФУНКЦИИ ОТРИЦАТЕЛЬНЫХ АРГУМЕНТОВ
sh(-x) = -sh x
ch(-x) = ch x
th(-x) = -th x
csch(-x) = -csch x
sech(-x) = sech x
cth(-x) = -cth x
ФОРМУЛЫ СЛОЖЕНИЯ
sh (x ± y) = sh x ch y ± ch x sh y
ch (x ± y) = ch x ch y ± sh x sh y
th(x ± y) = (th x ± th y)/(1 ± th x.th y)
cth(x ± y) = (cth x cth y ± l)/(cth y ± cth x)
ФОРМУЛЫ ДВОЙНЫХ УГЛОВ
sh 2x = 2 sh x ch x
ch 2x = ch2x + sh2x = 2 ch2x — 1 = 1 + 2 sh2x
th 2x = (2th x)/(1 + th2x)
ФОРМУЛЫ ПОЛОВИННЫХ УГЛОВ
$\text{sh} \frac{x}{2} = \pm \sqrt{\frac{\text{ch} x — 1}{2}}$ [+ если x > 0, — если x
$\text{ch} \frac{x}{2} = \sqrt{\frac{\text{ch} x + 1}{2}}$
$\text{th} \frac{x}{2} = \pm \sqrt{\frac{\text{ch} x — 1}{\text{ch} x + 1}}$ [+ если x > 0, — если x
$= \frac{\text{sh} x}{\text{ch} x — 1} = \frac{\text{ch} x + 1}{\text{sh} x}$
ФОРМУЛЫ КРАТНОСТИ УГЛОВ
sh 3x = 3 sh x + 4 sh3 x
ch 3x = 4 ch3 x — 3 ch x
th 3x = (3 th x + th3 x)/(1 + 3 th2x)
sh 4x = 8 sh3 x ch x + 4 sh x ch x
ch 4x = 8 ch4 x — 8 ch2 x + 1
th 4x = (4 th x + 4 th3 x)/(1 + 6 th2 x + th4 x)
СТЕПЕНИ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
sh2x = ½ch 2x — ½
ch2 x = ½ch 2x + ½
sh3x = ¼sh 3x — ¾sh x
ch3 x = ¼ch 3x + ¾ch x
sh4x = 3/8 — ½ch 2x + 1/8ch 4x
ch4 x = 3/8 + ½ch 2x + 1/8ch 4x
СУММА, РАЗНИЦА И УМНОЖЕНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
sh x + sh y = 2 sh ½(x + y) ch ½(x — y)
sh x — sh y = 2 ch ½(x + y) sh ½(x — y)
ch x + ch y = 2 ch ½(x + y) ch ½(x — y)
ch x — ch y = 2 sh ½(x + y) sh ½(x — y)
sh x sh y = ½(ch (x + y) — ch (x — y))
ch x ch y = ½(ch (x + y) + ch (x — y))
sh x ch y = ½(sh (x + y) + sh (x — y))
ВЫРАЖЕНИЕ ГИПЕРБОЛТЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ДРУГИЕ
В следующем мы принимаем, что x > 0. 2} + 1})$ $x \neq 0$
2} + 1})$ $x \neq 0$
ОТНОШЕНИЯ МЕЖДУ ОБРАТНЫМИ ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ
csch-1 x = sh-1 (1/x)
sech-1 x = ch-1 (1/x)
cth-1 x = th-1 (1/x)
sh-1(-x) = -sh-1x
th-1(-x) = -th-1x
cth-1 (-x) = -cth-1x
csch-1 (-x) = -csch-1x
ГРАФИКИ ОБРАТНЫХ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
y = sh-1xy = ch-1x
y = th-1x
y = cth-1x
y = sech-1x
y = csch-1x
ОТНОШЕНИЯ МЕЖДУ ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ и ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ
| sin(ix) = i sh x | cos(ix) = ch x | tan(ix) = i th x |
| csc(ix) = -i csch x | sec(ix) = sech x | cot(ix) = -i cth x |
| sh(ix) = i sin x | ch(ix) = cos x | th(ix) = i tan x |
| csch(ix) = -i csc x | sech(ix) = sec x | cth(ix) = -i cot x |
ПЕРИОДИЧНОСТЬ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
In the following k is any integer.
sh (x + 2kπi) = sh x csch (x + 2kπi) = csch x
ch (x + 2kπi) = ch x sech (x + 2kπi) = sech x
th (x + kπi) = th x cth (x + kπi) = cth x
ОТНОШЕНИЕ МЕЖДУ ОБРАТНЫМИ ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ И ОБРАТНЫМИ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ
| sin-1 (ix) = ish-1x | sh-1(ix) = i sin-1x |
| cos-1 x = ±i ch-1 x | ch-1x = ±i cos-1x |
| tan-1(ix) = i th-1x | th-1(ix) = i tan-1x |
| cot-1(ix) = -i cth-1x | cth-1 (ix) = -i cot-1x |
| sec-1 x = ±i sech-1x | sech-1 x = ±i sec-1x |
| csc-1(ix) = -i csch-1x | csch-1(ix) = -i csc-1x |
Производная функции в точке — презентация онлайн
Дифференциальное исчислениеАвтор: И.
 В. Дайняк, к.т.н., доцент
В. Дайняк, к.т.н., доцентКафедра высшей математики БГУИР
Лекция 2
ПРОИЗВОДНАЯ ФУНКЦИИ
В ТОЧКЕ
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производная обратной функции
Пусть для функции f (x) существует обратная функция f –1.
Имеем:
f 1 f ( x) f 1( y) x;
f f 1( y) f ( x) y.
По теореме о производной сложной функции:
f
1
f ( x) f
f ( x) f ( x) f ( y) f ( x)
1
1
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производная обратной функции
Так как
Отсюда:
или
f 1 f ( x) x ,
то
f
1
1
f ( x) f
f
1
( y)
f ( x)
(f
( y) f ( x) ( x) 1
1
,
f ( x)
y f ( x)
1
y f ( x)
1
( y ))
,
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производные элементарных функций
Обратные тригонометрические функции
y arcsin x, x [ 1;1]
Имеем:
f 1( y ) sin y x,
(arcsin x)
y ;
2 2
1
1
1
( f ( y )) (sin y )
1
1
1
cos y
1 sin 2 y
1 x2
Дифференциальное исчисление
Автор: И.
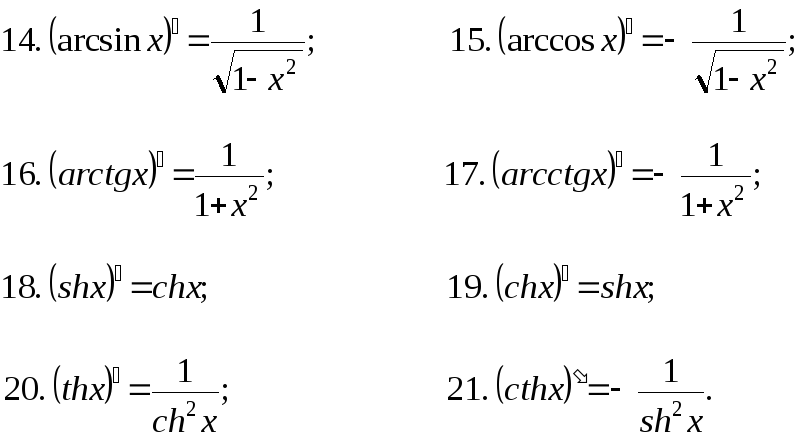 В. Дайняк, к.т.н., доцент
В. Дайняк, к.т.н., доцентКафедра высшей математики БГУИР
Производные элементарных функций
Обратные тригонометрические функции
y arccos x, x [ 1;1]
Имеем:
f 1( y) cos y x,
(arccos x)
y [0; ]
1
1
1
( f ( y )) (cos y )
1
1
1
sin y
1 cos2 y
1 x2
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производные элементарных функций
Обратные тригонометрические функции
y arctg x, x R
Имеем:
f 1( y ) tg y x,
1
1
y ;
2 2
1
1
(arctg x) 1
( f ( y )) (tg y )
cos y
2
1 tg y
2
1 x2
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производные элементарных функций
Обратные тригонометрические функции
y arcctg x, x R
Имеем:
f 1( y) ctg y x,
y [0; ]
1
1
(arcctg x) 1
( f ( y )) (ctg y )
sin y
2
1
1 ctg y
2
1
1 x2
Дифференциальное исчисление
Автор: И.
 В. Дайняк, к.т.н., доцент
В. Дайняк, к.т.н., доцентКафедра высшей математики БГУИР
Таблица производных
(a x ) a x ln a
(e x ) e x
( x ) x 1
1
(log a x) log a e
x
(ln x)
x 2
(c) 0
1
x
1
(arcsin x)
x
(sin x) cos x
1
1 x2
1
(arccos x)
1 x2
(cos x) sin x
(arctg x)
1
(tg x)
2
cos x
(ctg x)
1
2
sin x
1
1 x2
(arcctg x)
1
1 x2
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Таблица производных сложной функции
Пусть
u u(x)
(au ) au ln a u
(eu ) eu u
(u ) u 1 u
u
(log a u ) log a e
u
1
(ln u ) u
u
u 2
1
u
(arcsin u )
u
(sin u ) cos u u
u
1 u2
u
(arccosu )
1 u2
(cos u ) sin u u
1
(tg u )
u
2
cos u
(ctg u )
1
2
sin u
(arctg u )
u
1 u2
u (arcctg u )
u
1 u2
Дифференциальное исчисление
Автор: И.
 В. Дайняк, к.т.н., доцент
В. Дайняк, к.т.н., доцентКафедра высшей математики БГУИР
Гиперболические функции
1) гиперболический косинус
e x e x
ch x
2
2) гиперболический синус
e x e x
sh x
2
3) гиперболический тангенс
sh x e x e x
th x
x x
ch x e e
4) гиперболический котангенс
ch x e x e x
cth x
x x
sh x e e
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Графики гиперболических функций
ch x чётная функция
sh x, th x, cth x нечётные функции
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Гиперболические функции
Основные соотношения:
Производные:
ch3 x sh3 x 1
(ch x) sh x
ch 2 x ch3 x sh3 x
(sh x) ch x
sh 2 x 2 sh x ch x
(th x)
sh( x y) sh x ch y ch x sh y
ch( x y) ch x ch y sh x sh y
th x th y
th( x y)
1 th x th y
1
ch3 x
(cth x)
1
sh 2 x
Дифференциальное исчисление
Автор: И.
 В. Дайняк, к.т.н., доцент
В. Дайняк, к.т.н., доцентКафедра высшей математики БГУИР
Основные правила дифференцирования (повторение)
1) константу можно выносить за знак производной
(c u ) c u
2) формула производной суммы
(u v) u v
3) формула производной произведения
(u v) u v u v
4) формула производной частного
u u v u v
v
v2
(v( x) 0)
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производная сложной функции (повторение)
Пусть функция g(x) имеет производную в точке x0, а
функция f (y) имеет производную в точке y0 = g(x0). Тогда
сложная функция f (g(x)) имеет производную в точке x0,
вычисляемую по формуле
f ( x0 ) f ( y0 ) g ( x0 ),
y g ( x)
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Нахождение производной функции
Пример:
Найти производную функции
x2
3
x2
y ln
sin e 2 x
3x 1
Решение:
Воспользуемся основными правилами дифференцирования:
Дифференциальное исчисление
Автор: И.
 В. Дайняк, к.т.н., доцент
В. Дайняк, к.т.н., доцентКафедра высшей математики БГУИР
Логарифмическое дифференцирование
Пусть функция f (x) > 0.
По теореме о производной сложной функции:
1
ln f ( x)
f ( x)
f ( x)
Выразим отсюда производную:
f ( x) f ( x) ln f ( x)
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Логарифмическое дифференцирование
Пример 1:
Найти производную функции
Решение:
y xn , n N.
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Логарифмическое дифференцирование
Логарифмическое дифференцирование применяется для
нахождения производной сложной функции вида
y f ( x) g (x) ,
представляющей собой «функцию в степени функция».
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Логарифмическое дифференцирование
Пример 2:
Найти производную функции
Решение:
y
x
cos x
.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производная функции, заданной параметрически
Пусть функция у переменной х задана параметрически:
x j (t ),
y y (t ), t T
где функции j(t), y(t) определены в некоторой окрестности
точки t0.
Предположим, что функция x = x (t) имеет обратную функцию
t = t (x), определённую в некоторой окрестности точки x0 = x (t0),
а также существуют производные x’(t0) и y’(t0).
Тогда:
1 yt
y x y x t ( x) yt t x yt
xt xt
yt (t0 )
y x ( x0 )
xt (t0 )
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производная функции, заданной параметрически
Пример:
dy
Найти производную
функции, заданной уравнениями
dx
x 2 sin 2t ,
Решение:
y cos2 t.
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производная функции, заданной неявно
Пусть функция у переменной х задана неявно уравнением
F ( x, y) 0
Для нахождения у’х :
1.
 Дифференцируем тождество по переменной х как
Дифференцируем тождество по переменной х каксложную функцию, предполагая, что у = f (х).
2. Из полученного уравнения пытаемся выразить у’х = f‘ (х).
Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производная функции, заданной неявно
Пример:
Найти производную неявной функции, заданной уравнением
e y x y e,
в точке х0 = 0.
Решение:
Высшая математика
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
math.mmts-it.org
У этого термина существуют и другие значения, см. Производная. Иллюстрация понятия производной
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке
).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование
.В классическом дифференциальном исчислении производная чаще всего определяется через понятия теории пределов, однако исторически теория пределов появилась позже дифференциального исчисления
.Русский термин «производная функции» впервые употребил В. И. Висковатов.[1]
Пусть в некоторой окрестности точки определена функция Производной функции называется такое число , что функцию в окрестности можно представить в виде
если существует
.Определение производной функции через предел
Пусть в некоторой окрестности точки определена функция Производной функции в точке называется предел, если он существует
,Общепринятые обозначения производной функции в точке
Заметим, что последнее обычно обозначает производную по времени (в теоретической механике
).
Производная функции в точке , будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция является дифференцируемой в точке тогда и только тогда, когда её производная в этой точке существует и конечна
:Для дифференцируемой в функции в окрестности справедливо представление
- при
Тангенс угла наклона касательной прямой
Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точки x0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C5 — C1). Тангенс угла α наклона этой касательной — и есть производная в точке x0.
Если функция имеет конечную производную в точке то в окрестности её можно приблизить линейной функцией
Функция называется касательной к в точке Число является угловым коэффициентом или тангенсом угла наклона касательной прямой
.Скорость изменения функции
Пусть — закон прямолинейного движения. Тогда выражает мгновенную скорость движения в момент времени Вторая производная выражает мгновенное ускорение в момент времени
Вообще производная функции в точке выражает скорость изменения функции в точке , то есть скорость протекания процесса, описанного зависимостью
Понятие производной произвольного порядка задаётся рекуррентно. Полагаем
Если функция дифференцируема в , то производная первого порядка определяется соотношением
Пусть теперь производная -го порядка определена в некоторой окрестности точки и дифференцируема. Тогда
Если функция имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от может иметь в некоторой точке частные производные по той же или по любой другой переменной. Для исходной функции эти производные будут частными производными второго порядка (или вторыми частными производными
Для исходной функции эти производные будут частными производными второго порядка (или вторыми частными производными
- или
- или
Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например
,В зависимости от целей, области применения и используемого математического аппарата используют различные способы записи производных. Так, производная n-го порядка может быть записана в нотациях
:- Лагранжа , при этом для малых n часто используют штрихи и римские цифры:
- и т. д.
Такая запись удобна своей краткостью и широко распространена; однако штрихами разрешается обозначать не выше третьей производной
.- — производная первого порядка по при , или — вторая производная по в точке и т. д.
- , или иногда .
- В вариационном исчислении и математической физике часто применяется обозначение , ; для значения производной в точке — .
 Для частных производных обозначение то же, поэтому смысл обозначения определяют из контекста.
Для частных производных обозначение то же, поэтому смысл обозначения определяют из контекста.
Конечно, при этом необходимо не забывать, что служат все они для обозначения одних и тех же объектов
:- Пусть . Тогда
- Пусть . Тогда если то
где обозначает функцию знака. Если то а следовательно не существует
.Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования
:, то
- Формулы производной произведения и отношения обобщаются на случай n-кратного дифференцирования (формула Лейбница):
- где — биномиальные коэффициенты.

Следующие свойства производной служат дополнением к правилам дифференцирования
:Доказательство
Определим производную вектор-функции по параметру
:- .
Если производная в точке существует, вектор-функция называется дифференцируемой в этой точке. Координатными функциями для производной будут
.Свойства производной вектор-функции (всюду предполагается, что производные существуют
):- В. Г. Болтянский, Что такое дифференцирование?, «Популярные лекции по математике», Выпуск 17, Гостехиздат 1955 г., 64 стр.
- В. А. Гусев, А. Г. Мордкович «Математика»
- Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1
- В. М. Бородихин, Высшая математика, учеб. пособие, ISBN 5-7782-0422-1
08-0184 577..587
% PDF-1.5
%
127 0 объект
>
эндобдж
129 0 объект
> поток
2008-11-19T01: 39: 34ZArbortext Advanced Print Publisher 9. 0.114 / W Unicode2021-06-18T03: 00: 26-07: 002021-06-18T03: 00: 26-07: 00Acrobat Distiller 4.05 для Windowsapplication / pdf
0.114 / W Unicode2021-06-18T03: 00: 26-07: 002021-06-18T03: 00: 26-07: 00Acrobat Distiller 4.05 для Windowsapplication / pdf
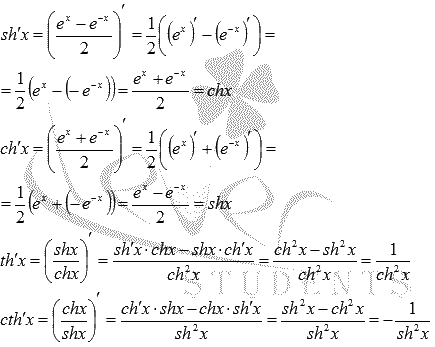 S
BT
/ T1_0 1 Тс
11 0 0 11 120,94 202 504.99997 Тм
(\ 240) Tj
/ T1_3 1 Тс
-7,55696 1 тд
(Обновленная версия) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 141 496,99994 тм
(\ 240) Tj
/ T1_0 1 Тс
28.68094 1 тд
() Tj
0 0 1 рг
-28.68094 0 Тд
(http://cancerpreventionresearch.aacrjournals.org/content/1/7/577)Tj
0 г
0 1.00001 TD
(Последнюю версию этой статьи можно найти по адресу:) Tj
ET
BT
/ T1_0 1 Тс
11 0 0 11 120.94202 463.99994 тм
(\ 240) Tj
/ T1_3 1 Тс
-3.50099 1 тд
(Материал) Tj
-3,44499 1,00001 тд
(Дополнительно) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 141 466,99994 тм
(\ 240) Tj
/ T1_0 1 Тс
38.
S
BT
/ T1_0 1 Тс
11 0 0 11 120,94 202 504.99997 Тм
(\ 240) Tj
/ T1_3 1 Тс
-7,55696 1 тд
(Обновленная версия) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 141 496,99994 тм
(\ 240) Tj
/ T1_0 1 Тс
28.68094 1 тд
() Tj
0 0 1 рг
-28.68094 0 Тд
(http://cancerpreventionresearch.aacrjournals.org/content/1/7/577)Tj
0 г
0 1.00001 TD
(Последнюю версию этой статьи можно найти по адресу:) Tj
ET
BT
/ T1_0 1 Тс
11 0 0 11 120.94202 463.99994 тм
(\ 240) Tj
/ T1_3 1 Тс
-3.50099 1 тд
(Материал) Tj
-3,44499 1,00001 тд
(Дополнительно) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 141 466,99994 тм
(\ 240) Tj
/ T1_0 1 Тс
38.1 тд () Tj 0 0 1 рг -38.
0 Тд
(http://cancerpreventionresearch.aacrjournals.org/content/suppl/2008/12/1 \
0 / 1.7.577.DC1) Tj
0 г
Т *
(Доступ к самым последним дополнительным материалам по адресу:) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 30 443,99997 тм
(\ 240) Tj
0 1 ТД
(\ 240) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 30 423,99997 тм
(\ 240) Tj
Т *
(\ 240) Tj
ET
30 354 525 70 рэ
0 0 мес.
S
BT
/ T1_0 1 Тс
11 0 0 11 120.94202 391. 99997 тм
(\ 240) Tj
/ T1_3 1 Тс
-6.00198 1 тд
(Цитированные статьи) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 141 383,99994 тм
(\ 240) Tj
/ T1_0 1 Тс
34.40392 1 тд
() Tj
0 0 1 рг
-34,40392 0 Тд
(http: //cancerpreventionresearch.aacrjournals.org/content/1/7/577.full#re \
f-list-1) Tj
0 г
0 1.00001 TD
(Эта статья содержит 48 статей, 15 из которых вы можете получить бесплатно по адресу:) Tj
ET
BT
/ T1_0 1 Тс
11 0 0 11 120,94 202 361,99997 тм
(\ 240) Tj
/ T1_3 1 Тс
-6,33498 1 тд
(Цитирование статей) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 141 353,99994 тм
(\ 240) Tj
/ T1_0 1 Тс
35.79392 1 тд
() Tj
0 0 1 рг
-35.79392 0 Тд
(http://cancerpreventionresearch.aacrjournals.org/content/1/7/577.полный # re \
lated-urls) Tj
0 г
Т *
(Эта статья процитирована в 2 статьях, размещенных на HighWire. Перейдите к ar \
ticles at:) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 30 333,99997 тм
(\ 240) Tj
0 1 ТД
(\ 240) Tj
ET
30 209 525 125 рэ
0 0 мес.
S
BT
/ T1_0 1 Тс
11 0 0 11 120.94202 301.99997 тм
(\ 240) Tj
/ T1_3 1 Тс
-5.66901 1 тд
(Оповещения по электронной почте) Tj
ET
BT
/ T1_0 1 Тс
10 0 0 10 295,49973 314 тм
(относится к этой статье или журналу.
99997 тм
(\ 240) Tj
/ T1_3 1 Тс
-6.00198 1 тд
(Цитированные статьи) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 141 383,99994 тм
(\ 240) Tj
/ T1_0 1 Тс
34.40392 1 тд
() Tj
0 0 1 рг
-34,40392 0 Тд
(http: //cancerpreventionresearch.aacrjournals.org/content/1/7/577.full#re \
f-list-1) Tj
0 г
0 1.00001 TD
(Эта статья содержит 48 статей, 15 из которых вы можете получить бесплатно по адресу:) Tj
ET
BT
/ T1_0 1 Тс
11 0 0 11 120,94 202 361,99997 тм
(\ 240) Tj
/ T1_3 1 Тс
-6,33498 1 тд
(Цитирование статей) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 141 353,99994 тм
(\ 240) Tj
/ T1_0 1 Тс
35.79392 1 тд
() Tj
0 0 1 рг
-35.79392 0 Тд
(http://cancerpreventionresearch.aacrjournals.org/content/1/7/577.полный # re \
lated-urls) Tj
0 г
Т *
(Эта статья процитирована в 2 статьях, размещенных на HighWire. Перейдите к ar \
ticles at:) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 30 333,99997 тм
(\ 240) Tj
0 1 ТД
(\ 240) Tj
ET
30 209 525 125 рэ
0 0 мес.
S
BT
/ T1_0 1 Тс
11 0 0 11 120.94202 301.99997 тм
(\ 240) Tj
/ T1_3 1 Тс
-5.66901 1 тд
(Оповещения по электронной почте) Tj
ET
BT
/ T1_0 1 Тс
10 0 0 10 295,49973 314 тм
(относится к этой статье или журналу. ) Tj
0 0 1 рг
-15.44997 0 Тд
(Подпишитесь, чтобы получать бесплатные уведомления по электронной почте) Tj
ET
BT
0 г
/ T1_0 1 Тс
11 0 0 11 120.94202 268,99994 тм
(\ 240) Tj
/ T1_3 1 Тс
-6.38997 1 тд
(Подписки) Tj
0,556 1,00001 тд
(Отпечатки и) Tj
ET
BT
/ T1_0 1 Тс
10 0 0 10 141 271,99994 тм
(\ 240) Tj
13.46497 1 тд
(.) Tj
0 0 1 рг
-6.85098 0 Тд
([email protected]) Tj
0 г
-6.61399 0 Тд
(Отделение) Tj
0 1.00001 TD
(Чтобы заказать перепечатку статьи или подписаться на журнал, свяжитесь с нами \
t Публикации AACR) Tj
ET
BT
/ T1_0 1 Тс
11 0 0 11 120.94202 246.99997 тм
(\ 240) Tj
/ T1_3 1 Тс
-5.66901 1 тд
(Разрешения) Tj
ET
BT
/ T1_0 1 Тс
10 0 0 10 141 208.99985 тм
(\ 240) Tj
0 1 ТД
(Сайт с правами.) Tj
0 1.00001 TD
(\ (CCC \)) Tj
0 1 ТД
(Нажмите «Запросить разрешения», чтобы перейти на страницу защиты авторских прав \
Рэнс Центр) Tj
28.68094 1 тд
(.) Tj
0 0 1 рг
-28.68094 0 Тд
(http://cancerpreventionresearch.aacrjournals.org/content/1/7/577)Tj
0 г
0 1.00001 TD
(Чтобы запросить разрешение на повторное использование всей или части этой статьи, используйте это li \
nk) Tj
ET
BT
/ T1_0 1 Тс
9 0 0 9 247.
) Tj
0 0 1 рг
-15.44997 0 Тд
(Подпишитесь, чтобы получать бесплатные уведомления по электронной почте) Tj
ET
BT
0 г
/ T1_0 1 Тс
11 0 0 11 120.94202 268,99994 тм
(\ 240) Tj
/ T1_3 1 Тс
-6.38997 1 тд
(Подписки) Tj
0,556 1,00001 тд
(Отпечатки и) Tj
ET
BT
/ T1_0 1 Тс
10 0 0 10 141 271,99994 тм
(\ 240) Tj
13.46497 1 тд
(.) Tj
0 0 1 рг
-6.85098 0 Тд
([email protected]) Tj
0 г
-6.61399 0 Тд
(Отделение) Tj
0 1.00001 TD
(Чтобы заказать перепечатку статьи или подписаться на журнал, свяжитесь с нами \
t Публикации AACR) Tj
ET
BT
/ T1_0 1 Тс
11 0 0 11 120.94202 246.99997 тм
(\ 240) Tj
/ T1_3 1 Тс
-5.66901 1 тд
(Разрешения) Tj
ET
BT
/ T1_0 1 Тс
10 0 0 10 141 208.99985 тм
(\ 240) Tj
0 1 ТД
(Сайт с правами.) Tj
0 1.00001 TD
(\ (CCC \)) Tj
0 1 ТД
(Нажмите «Запросить разрешения», чтобы перейти на страницу защиты авторских прав \
Рэнс Центр) Tj
28.68094 1 тд
(.) Tj
0 0 1 рг
-28.68094 0 Тд
(http://cancerpreventionresearch.aacrjournals.org/content/1/7/577)Tj
0 г
0 1.00001 TD
(Чтобы запросить разрешение на повторное использование всей или части этой статьи, используйте это li \
nk) Tj
ET
BT
/ T1_0 1 Тс
9 0 0 9 247. 48564 1.99997 тм
(для исследования рака.) Tj
7,88245 1 тд
(18 июня 2021 г. \ 251 Американская ассоциация 2008 г.) Tj
0 0 1 рг
-19.28495 0 тд
(Cancepreventionresearch.aacrjournals.org) Tj
0 г
-8.11397 0 Td
(Скачано с) Tj
ET конечный поток
эндобдж
140 0 объект
> / Filter / FlateDecode / Height 242 / Length 73940 / Name / X / Subtype / Image / Type / XObject / Width 1539 >> stream
HoXHxQr
48564 1.99997 тм
(для исследования рака.) Tj
7,88245 1 тд
(18 июня 2021 г. \ 251 Американская ассоциация 2008 г.) Tj
0 0 1 рг
-19.28495 0 тд
(Cancepreventionresearch.aacrjournals.org) Tj
0 г
-8.11397 0 Td
(Скачано с) Tj
ET конечный поток
эндобдж
140 0 объект
> / Filter / FlateDecode / Height 242 / Length 73940 / Name / X / Subtype / Image / Type / XObject / Width 1539 >> stream
HoXHxQr Границы | AMI, производное индазола, лечит болезнь Паркинсона, ингибируя фосфорилирование тау-белка
Введение
Болезнь Паркинсона (БП) — распространенное нейродегенеративное заболевание. Апоптоз дофаминергических нейронов черной субстанции играет ключевую роль в патогенезе БП (Del Rey et al., 2018). Тельца Леви или нейриты (Power et al., 2017; Liu et al., 2019a) были обнаружены при продвинутой стадии БП. Поэтому мы исследуем сигнальные пути, которые регулируют апоптоз нейронов, как новую терапевтическую мишень для БП.
Тау-белок — важный белок, связанный с микротрубочками в центральной нервной системе, который в основном регулируется путем фосфорилирования. Он индуцирует и способствует агрегации микротрубочек (Lee et al., 2019). Гиперфосфорилированный тау взаимодействует с α-синуклеином, способствуя агрегации и фиброзу, вызывая образование телец Леви и дисфункцию аксонального транспорта (Singh et al., 2019). Более того, гиперфосфорилирование и агрегация приводят к образованию парных спиральных филаментов (PHFs; Zhou et al., 2018). Талтирелин, аналог TRH длительного действия, подавлял уровни p-тау (S396), проявляя нейропротекторный эффект как на клеточных, так и на животных моделях БП (Zheng et al., 2018). Формула китайской медицины Shaoyao Gancao Tang снижает агрегацию тау и оказывает нейрозащитное действие (Chen et al., 2018). Вместе фосфорилирование тау-белка опосредует патологический процесс болезни Альцгеймера (БА) или БП, которая является потенциальной терапевтической мишенью для лечения нейродегенеративного заболевания (Winer et al., 2018; Chen et al., 2019).
Он индуцирует и способствует агрегации микротрубочек (Lee et al., 2019). Гиперфосфорилированный тау взаимодействует с α-синуклеином, способствуя агрегации и фиброзу, вызывая образование телец Леви и дисфункцию аксонального транспорта (Singh et al., 2019). Более того, гиперфосфорилирование и агрегация приводят к образованию парных спиральных филаментов (PHFs; Zhou et al., 2018). Талтирелин, аналог TRH длительного действия, подавлял уровни p-тау (S396), проявляя нейропротекторный эффект как на клеточных, так и на животных моделях БП (Zheng et al., 2018). Формула китайской медицины Shaoyao Gancao Tang снижает агрегацию тау и оказывает нейрозащитное действие (Chen et al., 2018). Вместе фосфорилирование тау-белка опосредует патологический процесс болезни Альцгеймера (БА) или БП, которая является потенциальной терапевтической мишенью для лечения нейродегенеративного заболевания (Winer et al., 2018; Chen et al., 2019).
Производные индазола обладают мультифармакологической активностью, например противовоспалительной, антибактериальной и противоопухолевой (Denya et al. , 2018; Liu et al., 2019b). Наши предыдущие исследования показали, что 6-гидрокси-1H-индазол, 5-гидрокси-1H-индазол и 6-нитро-1H-индазол ингибируют фосфорилирование тау-белка и оказывают защитное действие на MPP + -индуцированный апоптоз SH. -SY5Y клетки. В частности, 6-гидрокси-1H-индазол продемонстрировал нейрозащитный эффект на 100 мкм MPP + -индуцированный апоптоз клеток SH-SY5Y (Liang et al., 2016). В этом исследовании 6-нитро-1H-индазол использовался в качестве материнского ядра для дальнейшей оптимизации структуры лекарства и изучения производных индазола, которые могут специфически ингибировать фосфорилирование тау-белка. Поскольку лекарство должно попасть в мозг для лечения БП, наша группа ввела 1-положение метила в 6-нитро-1H-индазол для увеличения жирорастворимости соединения, и, наконец, новую небольшую молекулу 6-амино-1-метил -индазол (AMI) был получен.
, 2018; Liu et al., 2019b). Наши предыдущие исследования показали, что 6-гидрокси-1H-индазол, 5-гидрокси-1H-индазол и 6-нитро-1H-индазол ингибируют фосфорилирование тау-белка и оказывают защитное действие на MPP + -индуцированный апоптоз SH. -SY5Y клетки. В частности, 6-гидрокси-1H-индазол продемонстрировал нейрозащитный эффект на 100 мкм MPP + -индуцированный апоптоз клеток SH-SY5Y (Liang et al., 2016). В этом исследовании 6-нитро-1H-индазол использовался в качестве материнского ядра для дальнейшей оптимизации структуры лекарства и изучения производных индазола, которые могут специфически ингибировать фосфорилирование тау-белка. Поскольку лекарство должно попасть в мозг для лечения БП, наша группа ввела 1-положение метила в 6-нитро-1H-индазол для увеличения жирорастворимости соединения, и, наконец, новую небольшую молекулу 6-амино-1-метил -индазол (AMI) был получен.
В этом исследовании мы изучили влияние AMI на модели PD.Тесты MTT и окрашивание Hoechst 33258 использовали для оценки защитного действия AMI на клетки SH-SY5Y после обработки MPP + . Между тем, для обнаружения эффектов AMI in vivo использовали модели на животных ПД, индуцированные МРТР. Леводопа (L-ДОПА) является препаратом первой линии для лечения БП, в наших экспериментах мы выбрали L-ДОФА в качестве контрольного препарата.
Между тем, для обнаружения эффектов AMI in vivo использовали модели на животных ПД, индуцированные МРТР. Леводопа (L-ДОПА) является препаратом первой линии для лечения БП, в наших экспериментах мы выбрали L-ДОФА в качестве контрольного препарата.
Материалы и методы
Материал и антитела
Метил-4-фенилпиридин (MPP + ; # D048), 1-метил-4-фенил-1,2,3,6-тетрагидропиридин (MPTP; # M0896) и леводопа (# D9628) были получены из Сигма (св.Луис, Миссури, США). Коробка с реагентами ABC (Vector PK-6101 Rabbit IgG) и набор для окрашивания по Гольджи (PK401) были получены от FD NeuroTechnologes (Колумбия, Мэриленд, США). P-тау (Ser396; # ab109390) и t-тау (# ab32057) были приобретены у Abcam (Кембридж, Массачусетс), тогда как GSK-3β (# 12456) и фосфорилированный GSK-3β (p-GSK-3β, ser9, # 9323) были приобретены у Cell Signaling Technology (Данверс, Массачусетс, США). Анти-тирозингидроксилаза (TH) была получена от Santa Cruz (Даллас, Техас, США). Мембраны Immoblilon PVDF (# ISEQ00010) и Immobilon Western Chemiluminescent HRP Substrate (# WBKLS0100) были приобретены у Merck Co. (Дармштадт, Германия).
(Дармштадт, Германия).
Мышей C57BL / 6 класса SPF, самцы 6–7 недель, вес 22–27 г, были приобретены в Центре экспериментальных животных провинции Гуандун, номер лицензии: SYXK (Yue) 2016–0167, затем бесплатная питьевая вода, кормление до 10–11 недель. . Все экспериментальные протоколы были одобрены Комитетом по уходу и использованию животных Южного медицинского университета (Гуанчжоу, Гуандун, Китай).
Синтез AMI
6-нитро-1H-индазол растворяли в диметилформамиде, а затем добавляли метилиодид и цианид натрия в соответствии с молярным соотношением 6-нитро-1H-индазол: иодметан: гидрид натрия = 1: 2: 2.Реакционную смесь перемешивали в течение 24 часов, затем фильтровали и трижды экстрагировали этилацетатом, сушили над безводным сульфатом натрия и упаривали с получением 6-нитро-1-метилиндазола. Затем 6-нитро-1-метилиндазол растворяли в метаноле, добавляли палладий на угле в качестве катализатора, проводили реакцию водорода через 4 ч и, наконец, фильтровали и разделяли колоночной хроматографией с получением AMI.
МТТ
Анализ МТТ использовали для определения жизнеспособности клеток SH-SY5Y.Клетки SH-SY5Y высевали с плотностью 1 × 10 4 клеток / лунку в 96-луночные планшеты и инкубировали в течение ночи. Во-первых, различные концентрации MPP + действуют на клетки SH-SY5Y и подтверждают оптимальную концентрацию MPP + на клетках. Добавление MPP + к культурам SH-SY5Y проводили при 300 мкМ. После этого клетки предварительно обрабатывали различными концентрациями AMI в течение 2 часов, а затем добавляли MPP + в конечной концентрации 300 мкМ в течение 48 часов.Добавьте 100 мкл 0,5 мг / мл рабочего раствора МТТ в каждую лунку и инкубируйте в течение 4 ч при 5% CO 2 при 37 ° C. Супернатант сливали, в каждую лунку добавляли 100 мкл ДМСО и встряхивали на низкой скорости в течение 10 мин для полного растворения кристаллов. Оптическую плотность каждой группы образцов измеряли с помощью считывающего устройства для микропланшетов (Bio-Rad Model 680) при длине волны 570 нм. Необработанные клетки представляли 100% жизнеспособность.
Необработанные клетки представляли 100% жизнеспособность.
Hoechst 33258 Окрашивание
Клеточную линию SH-SY5Y предварительно обрабатывали AMI в течение 2 часов, а затем апоптоз, индуцированный MPP + , в течение 48 часов.Клетки фиксировали фиксатором 10 мин. После удаления фиксатора его дважды промывали PBS по 3 мин каждый раз, а затем добавляли 0,5 мл окрашивающего раствора Hoechst 33258, окрашивая линию клеток в течение 5 мин. После удаления окрашивающего раствора культуральный раствор дважды промывали PBS в течение 3 мин. На предметное стекло наносили каплю антифлуоресцентного герметика. Предметное стекло было покрыто покровным стеклом, покрытым клетками, и синие ядра были обнаружены с помощью флуоресцентного микроскопа.Длина волны возбуждения составляла около 350 нм, а длина волны излучения составляла около 460 нм.
Вестерн-блоттинг
Вестерн-блоттинг использовали для определения экспрессии GSK-3β, p-GSK-3β (ser9), Tau, p-Tau (ser396) и TH. После обработки лекарством клетки или ткани быстро собирали и лизировали буфером RIPA, содержащим 1% протеазы и 1% ингибитор фосфатазы, и встряхивали на льду в течение 40 минут. Затем лизат центрифугировали при 12000 об / мин в течение 20 минут при 4 ° C и 10 минут при 12000 об / мин.Супернатант собирали и концентрацию белка определяли с использованием набора для анализа белка BCA. Равное количество белка отделяли электрофорезом в SDS-полиакриламидном геле и переносили на гидрофильную PVDF-мембрану с размером пор 0,4 мкм. Неспецифическое связывание блокировали 5% BSA (вес / объем), а затем мембраны инкубировали в молоке, растворенном в TBST, в течение 2 часов при комнатной температуре. Мембрану трижды промывали TBST в течение 10 мин, а затем инкубировали с первичными антителами при 4 ° C в течение ночи.После промывки и инкубации со вторичными антителами сигналы блоттинга детектировали с помощью системы визуализации в ультрафиолетовом свете Bio-Rad, а иммуноблоттинг количественно определяли с помощью программного обеспечения ImageJ.
После обработки лекарством клетки или ткани быстро собирали и лизировали буфером RIPA, содержащим 1% протеазы и 1% ингибитор фосфатазы, и встряхивали на льду в течение 40 минут. Затем лизат центрифугировали при 12000 об / мин в течение 20 минут при 4 ° C и 10 минут при 12000 об / мин.Супернатант собирали и концентрацию белка определяли с использованием набора для анализа белка BCA. Равное количество белка отделяли электрофорезом в SDS-полиакриламидном геле и переносили на гидрофильную PVDF-мембрану с размером пор 0,4 мкм. Неспецифическое связывание блокировали 5% BSA (вес / объем), а затем мембраны инкубировали в молоке, растворенном в TBST, в течение 2 часов при комнатной температуре. Мембрану трижды промывали TBST в течение 10 мин, а затем инкубировали с первичными антителами при 4 ° C в течение ночи.После промывки и инкубации со вторичными антителами сигналы блоттинга детектировали с помощью системы визуализации в ультрафиолетовом свете Bio-Rad, а иммуноблоттинг количественно определяли с помощью программного обеспечения ImageJ.
Приготовление и введение животной модели Паркинсона
Самцов мышей C57BL / 6 разделили на пять групп (по 12 в каждой группе). Контрольная группа получала физиологический раствор. Группу модели PD вводили 30 мг / кг MPTP (растворенного в физиологическом растворе) путем внутрибрюшинной (i.p.) инъекции ежедневно в течение 5 дней подряд (Schildknecht et al., 2017). Мышей лечили AMI (2 и 4 мг / кг / день, растворенные в физиологическом растворе, содержащем 3% ДМСО) за полчаса до лечения MPTP. Группе L-DOPA давали 10 мг / кг / день (растворяли в физиологическом растворе, содержащем 3% ДМСО + 0,5% CMC-Na, внутрибрюшинно) через 2 часа после обработки MPTP. Между тем, мы записали инкубационный период и продолжительность мышей после введения. Латентный период начинался с внутрибрюшинных инъекций МФТП мышам до наступления паралича. Через десять дней после последней инъекции МРТР мыши проводили поведенческие эксперименты и затем умерщвляли (рис. 3А).
Рисунок 1. (A) Синтетический путь 6-амино-1-метилиндазол (AMI). (B) Спектр водорода AMI. (C) Масс-спектр AMI.
(A) Синтетический путь 6-амино-1-метилиндазол (AMI). (B) Спектр водорода AMI. (C) Масс-спектр AMI.
Рисунок 2 . AMI подавляет апоптоз клеток SH-SY5Y, индуцированный MPP + . (A) Анализ МТТ проводили для оценки эффекта MPP + на пролиферацию клеток SH-SY5Y. (B) Анализ МТТ проводили для оценки влияния AMI на пролиферацию клеток SH-SY5Y.Репрезентативные изображения (D) и количественные данные (C) ядерного окрашивания Hoechst 33258 в клетках SH-SY5Y, столбик = 50 мкМ. (E) AMI увеличивал внутриклеточные уровни p-GSK-3β (Ser9) в клетках SH-SY5Y, обработанных MPP + . (F) Денситометрическое количественное определение уровней белка p-GSK3β (ser-9) / t-GSK-3β. (G) MPP + увеличивал внутриклеточные уровни p-tau (Ser396) в клетках SH-SY5Y. (H) Денситометрическое количественное определение уровней белка p-tau (ser396) / t-tau в разное время. (I) AMI снижал внутриклеточные уровни белка p-tau (ser396) / t-tau через 8 часов. (J) Денситометрическое количественное определение уровней белка p-tau (ser396) / t-tau через 8 часов после обработки AMI. * p <0,05, ** p <0,01, *** p <0,001 по сравнению с группой MPP + . # p <0,05, ## p <0,01 по сравнению с группой носителя (контроль).
(I) AMI снижал внутриклеточные уровни белка p-tau (ser396) / t-tau через 8 часов. (J) Денситометрическое количественное определение уровней белка p-tau (ser396) / t-tau через 8 часов после обработки AMI. * p <0,05, ** p <0,01, *** p <0,001 по сравнению с группой MPP + . # p <0,05, ## p <0,01 по сравнению с группой носителя (контроль).
Рисунок 3. (A) Экспериментальный режим дозирования. (B) Типичные изображения и количественные данные окрашивания TH в черной субстанции среднего мозга. Увеличение: 40 × (a — контроль; b — MPTP; c — AMI 2 мг / кг; d — AMI 4 мг / кг; e — L-DOPA 10 мг / кг; f — количество TH-иммунопозитивных клеток в веществе. нигра). (C) Экспрессию белка TH исследовали с помощью вестерн-блоттинга. (D) Уровни белка TH определяли количественно с помощью денситометрии. Толщина среза: 35 мкм. ## p <0,01 по сравнению с контролем; * p <0.01, ** p <0,001 по сравнению с MPTP.
Толщина среза: 35 мкм. ## p <0,01 по сравнению с контролем; * p <0.01, ** p <0,001 по сравнению с MPTP.
TH Иммуногистохимия
Через семь дней после последней инъекции МРТР вентральный средний мозг был изолирован и содержание TH было определено с помощью иммуногистохимии. Срезы головного мозга (35 мкм) промывали 0,3% тритоном в течение 30 минут, а затем обрабатывали свежеприготовленным 3% H 2 O 2 в течение 1 часа. Срезы головного мозга дважды промывали PBS по 10 мин каждый и 1 час сывороткой, затем инкубировали в течение ночи с кроличьими антителами к TH (1: 10 000, 3% BSA с PSB) при 4 ° C.Затем срезы головного мозга трижды промывали PBS в течение 10 мин при комнатной температуре и инкубировали с вторичным антителом из набора в течение 1 ч при комнатной температуре. Затем срезы мозга инкубировали в течение 1 ч в наборе ABC (Vector PK-6101 Rabbit IgG) и трижды промывали PBS. Наконец, окраска проявлялась в DAB в течение 2–5 мин, срезы головного мозга промывались PBS и срезы сушились. После того, как пятна были обезвожены и стали прозрачными, их сфотографировали под световым микроскопом при увеличении × 400.Подсчитывали количество TH-положительных дофаминергических нейронов в черной субстанции каждой мыши. Среднее количество правой и левой сторон считалось количеством нейронных клеток каждой мыши (Wang et al., 2007).
После того, как пятна были обезвожены и стали прозрачными, их сфотографировали под световым микроскопом при увеличении × 400.Подсчитывали количество TH-положительных дофаминергических нейронов в черной субстанции каждой мыши. Среднее количество правой и левой сторон считалось количеством нейронных клеток каждой мыши (Wang et al., 2007).
Окрашивание по Гольджи
Изучить морфологические изменения дендритов нервов и дендритных шипов в головном мозге животных после медикаментозной обработки окрашиванием по Гольджи (Zhong et al., 2019). Через семь дней после последней инъекции МРТР срезы черной субстанции получали для окрашивания по Гольджи.Согласно инструкции производителя по окрашиванию по Гольджи (FD Neuro Technologes), мы смешивали жидкость A и жидкость B в течение 24 часов и хранили в темноте. Весь мозг помещали в приготовленный окрашивающий раствор в темноте на 3 недели при нормальной температуре и переносили в раствор С, выдерживаемый в темноте не менее 72 часов. Затем средний мозг фиксировали раствором для заливки, нарезали на замороженном слайсере (100 мкм), прикрепляли к предметному стеклу, погружали в раствор C и сушили для получения срезов. Срезы дважды промывали бидистиллированной водой по 4 мин каждый раз.Затем срезы инкубировали в течение 10 мин в рабочем растворе, состоящем из раствора D, раствора E и бидистиллированной воды = 1: 1: 2. Морфология нейронов наблюдалась под микроскопом.
Срезы дважды промывали бидистиллированной водой по 4 мин каждый раз.Затем срезы инкубировали в течение 10 мин в рабочем растворе, состоящем из раствора D, раствора E и бидистиллированной воды = 1: 1: 2. Морфология нейронов наблюдалась под микроскопом.
Для анализа дендритных ветвей неаксональные синапсы длиной более 10 мкм, непосредственно выходящие из тела клетки, определяются как первичные дендриты. Все выступы, выходящие из первичного дерева, называются вторичными дендритами, а все выступы на средних концах ниже 10 мкм называются кончиками аксонов. При выполнении анализа Шолла учитываются несколько концентрических окружностей с центром на теле клетки, которые отличаются друг от друга диаметром на 15 мкм, и все выступы в концентрических кругах.
Поведенческий эксперимент
Подъем на полюс, испытание на вращающемся стержне и испытание на тягу были выполнены через 10 дней после последней инъекции МФТП (Wang et al., 2007). В группе 6–8 мышей, все поведенческие тесты проводились двойным слепым методом.
В тесте на тягу тест на тягу измеряет силу мышц. Шнур диаметром 0,5 см помещался на 70 см по горизонтали. Передние лапы каждой мыши подвешивались на веревке, и мышь отпускалась. Регистрировали время падения, а также то, тянула ли мышь задние конечности за веревку.Кал и моча мышей смывали перед экспериментом.
В тесте с вращающимся стержнем тест на вращающийся стержень является распространенным методом оценки нервно-мышечной координации. Сначала мышей помещали на вращающийся стержень (диаметром 6 см) на 30 с, а затем тренировали с постоянной скоростью 12 об / мин в течение 180 с. Через шестьдесят минут после последней тренировки мышь помещали на стержень, и инкубационный период ее падения регистрировали как конечную точку измерения. Среднее время трех испытаний было рассчитано для статистического анализа.
В тесте лазанья по шесту мышей помещали возле верхней части деревянной палки с шероховатой поверхностью (диаметром 10 мм и высотой 55 см) так, чтобы их головы были обращены вверх. Регистрировали общее время, за которое каждое животное достигло пола, с максимальной продолжительностью 120 с. Каждую мышь тестировали трижды с 10-минутными интервалами, и для статистического анализа рассчитывали среднее время.
Регистрировали общее время, за которое каждое животное достигло пола, с максимальной продолжительностью 120 с. Каждую мышь тестировали трижды с 10-минутными интервалами, и для статистического анализа рассчитывали среднее время.
Статистический анализ
Статистический анализ был выполнен с использованием SPSS 13.0. Результаты выражали как среднее ± стандартное отклонение.Односторонний дисперсионный анализ ANOVA был использован для множественных сравнений групп. Статистическая значимость была установлена на уровне P <0,05.
Результат
Описание AMI
AMI был получен в результате двухэтапной реакции (рис. 1A), а спектр водорода (рис. 1B) и масс-спектр (рис. 1C) показали характерный пик поглощения как AMI.
AMI улучшает апоптоз в клетках SH-SY5Y после лечения MPP
+
 Он индуцирует и способствует агрегации микротрубочек (Lee et al., 2019). Гиперфосфорилированный тау взаимодействует с α-синуклеином, способствуя агрегации и фиброзу, вызывая образование телец Леви и дисфункцию аксонального транспорта (Singh et al., 2019). Более того, гиперфосфорилирование и агрегация приводят к образованию парных спиральных филаментов (PHFs; Zhou et al., 2018). Талтирелин, аналог TRH длительного действия, подавлял уровни p-тау (S396), проявляя нейропротекторный эффект как на клеточных, так и на животных моделях БП (Zheng et al., 2018). Формула китайской медицины Shaoyao Gancao Tang снижает агрегацию тау и оказывает нейрозащитное действие (Chen et al., 2018). Вместе фосфорилирование тау-белка опосредует патологический процесс болезни Альцгеймера (БА) или БП, которая является потенциальной терапевтической мишенью для лечения нейродегенеративного заболевания (Winer et al., 2018; Chen et al., 2019).
Он индуцирует и способствует агрегации микротрубочек (Lee et al., 2019). Гиперфосфорилированный тау взаимодействует с α-синуклеином, способствуя агрегации и фиброзу, вызывая образование телец Леви и дисфункцию аксонального транспорта (Singh et al., 2019). Более того, гиперфосфорилирование и агрегация приводят к образованию парных спиральных филаментов (PHFs; Zhou et al., 2018). Талтирелин, аналог TRH длительного действия, подавлял уровни p-тау (S396), проявляя нейропротекторный эффект как на клеточных, так и на животных моделях БП (Zheng et al., 2018). Формула китайской медицины Shaoyao Gancao Tang снижает агрегацию тау и оказывает нейрозащитное действие (Chen et al., 2018). Вместе фосфорилирование тау-белка опосредует патологический процесс болезни Альцгеймера (БА) или БП, которая является потенциальной терапевтической мишенью для лечения нейродегенеративного заболевания (Winer et al., 2018; Chen et al., 2019). , 2018; Liu et al., 2019b). Наши предыдущие исследования показали, что 6-гидрокси-1H-индазол, 5-гидрокси-1H-индазол и 6-нитро-1H-индазол ингибируют фосфорилирование тау-белка и оказывают защитное действие на MPP + -индуцированный апоптоз SH. -SY5Y клетки. В частности, 6-гидрокси-1H-индазол продемонстрировал нейрозащитный эффект на 100 мкм MPP + -индуцированный апоптоз клеток SH-SY5Y (Liang et al., 2016). В этом исследовании 6-нитро-1H-индазол использовался в качестве материнского ядра для дальнейшей оптимизации структуры лекарства и изучения производных индазола, которые могут специфически ингибировать фосфорилирование тау-белка. Поскольку лекарство должно попасть в мозг для лечения БП, наша группа ввела 1-положение метила в 6-нитро-1H-индазол для увеличения жирорастворимости соединения, и, наконец, новую небольшую молекулу 6-амино-1-метил -индазол (AMI) был получен.
, 2018; Liu et al., 2019b). Наши предыдущие исследования показали, что 6-гидрокси-1H-индазол, 5-гидрокси-1H-индазол и 6-нитро-1H-индазол ингибируют фосфорилирование тау-белка и оказывают защитное действие на MPP + -индуцированный апоптоз SH. -SY5Y клетки. В частности, 6-гидрокси-1H-индазол продемонстрировал нейрозащитный эффект на 100 мкм MPP + -индуцированный апоптоз клеток SH-SY5Y (Liang et al., 2016). В этом исследовании 6-нитро-1H-индазол использовался в качестве материнского ядра для дальнейшей оптимизации структуры лекарства и изучения производных индазола, которые могут специфически ингибировать фосфорилирование тау-белка. Поскольку лекарство должно попасть в мозг для лечения БП, наша группа ввела 1-положение метила в 6-нитро-1H-индазол для увеличения жирорастворимости соединения, и, наконец, новую небольшую молекулу 6-амино-1-метил -индазол (AMI) был получен. Между тем, для обнаружения эффектов AMI in vivo использовали модели на животных ПД, индуцированные МРТР. Леводопа (L-ДОПА) является препаратом первой линии для лечения БП, в наших экспериментах мы выбрали L-ДОФА в качестве контрольного препарата.
Между тем, для обнаружения эффектов AMI in vivo использовали модели на животных ПД, индуцированные МРТР. Леводопа (L-ДОПА) является препаратом первой линии для лечения БП, в наших экспериментах мы выбрали L-ДОФА в качестве контрольного препарата. (Дармштадт, Германия).
(Дармштадт, Германия).
 Необработанные клетки представляли 100% жизнеспособность.
Необработанные клетки представляли 100% жизнеспособность. После обработки лекарством клетки или ткани быстро собирали и лизировали буфером RIPA, содержащим 1% протеазы и 1% ингибитор фосфатазы, и встряхивали на льду в течение 40 минут. Затем лизат центрифугировали при 12000 об / мин в течение 20 минут при 4 ° C и 10 минут при 12000 об / мин.Супернатант собирали и концентрацию белка определяли с использованием набора для анализа белка BCA. Равное количество белка отделяли электрофорезом в SDS-полиакриламидном геле и переносили на гидрофильную PVDF-мембрану с размером пор 0,4 мкм. Неспецифическое связывание блокировали 5% BSA (вес / объем), а затем мембраны инкубировали в молоке, растворенном в TBST, в течение 2 часов при комнатной температуре. Мембрану трижды промывали TBST в течение 10 мин, а затем инкубировали с первичными антителами при 4 ° C в течение ночи.После промывки и инкубации со вторичными антителами сигналы блоттинга детектировали с помощью системы визуализации в ультрафиолетовом свете Bio-Rad, а иммуноблоттинг количественно определяли с помощью программного обеспечения ImageJ.
После обработки лекарством клетки или ткани быстро собирали и лизировали буфером RIPA, содержащим 1% протеазы и 1% ингибитор фосфатазы, и встряхивали на льду в течение 40 минут. Затем лизат центрифугировали при 12000 об / мин в течение 20 минут при 4 ° C и 10 минут при 12000 об / мин.Супернатант собирали и концентрацию белка определяли с использованием набора для анализа белка BCA. Равное количество белка отделяли электрофорезом в SDS-полиакриламидном геле и переносили на гидрофильную PVDF-мембрану с размером пор 0,4 мкм. Неспецифическое связывание блокировали 5% BSA (вес / объем), а затем мембраны инкубировали в молоке, растворенном в TBST, в течение 2 часов при комнатной температуре. Мембрану трижды промывали TBST в течение 10 мин, а затем инкубировали с первичными антителами при 4 ° C в течение ночи.После промывки и инкубации со вторичными антителами сигналы блоттинга детектировали с помощью системы визуализации в ультрафиолетовом свете Bio-Rad, а иммуноблоттинг количественно определяли с помощью программного обеспечения ImageJ.
 (A) Синтетический путь 6-амино-1-метилиндазол (AMI). (B) Спектр водорода AMI. (C) Масс-спектр AMI.
(A) Синтетический путь 6-амино-1-метилиндазол (AMI). (B) Спектр водорода AMI. (C) Масс-спектр AMI. (I) AMI снижал внутриклеточные уровни белка p-tau (ser396) / t-tau через 8 часов. (J) Денситометрическое количественное определение уровней белка p-tau (ser396) / t-tau через 8 часов после обработки AMI. * p <0,05, ** p <0,01, *** p <0,001 по сравнению с группой MPP + . # p <0,05, ## p <0,01 по сравнению с группой носителя (контроль).
(I) AMI снижал внутриклеточные уровни белка p-tau (ser396) / t-tau через 8 часов. (J) Денситометрическое количественное определение уровней белка p-tau (ser396) / t-tau через 8 часов после обработки AMI. * p <0,05, ** p <0,01, *** p <0,001 по сравнению с группой MPP + . # p <0,05, ## p <0,01 по сравнению с группой носителя (контроль). Толщина среза: 35 мкм. ## p <0,01 по сравнению с контролем; * p <0.01, ** p <0,001 по сравнению с MPTP.
Толщина среза: 35 мкм. ## p <0,01 по сравнению с контролем; * p <0.01, ** p <0,001 по сравнению с MPTP. После того, как пятна были обезвожены и стали прозрачными, их сфотографировали под световым микроскопом при увеличении × 400.Подсчитывали количество TH-положительных дофаминергических нейронов в черной субстанции каждой мыши. Среднее количество правой и левой сторон считалось количеством нейронных клеток каждой мыши (Wang et al., 2007).
После того, как пятна были обезвожены и стали прозрачными, их сфотографировали под световым микроскопом при увеличении × 400.Подсчитывали количество TH-положительных дофаминергических нейронов в черной субстанции каждой мыши. Среднее количество правой и левой сторон считалось количеством нейронных клеток каждой мыши (Wang et al., 2007). Срезы дважды промывали бидистиллированной водой по 4 мин каждый раз.Затем срезы инкубировали в течение 10 мин в рабочем растворе, состоящем из раствора D, раствора E и бидистиллированной воды = 1: 1: 2. Морфология нейронов наблюдалась под микроскопом.
Срезы дважды промывали бидистиллированной водой по 4 мин каждый раз.Затем срезы инкубировали в течение 10 мин в рабочем растворе, состоящем из раствора D, раствора E и бидистиллированной воды = 1: 1: 2. Морфология нейронов наблюдалась под микроскопом.
 Регистрировали общее время, за которое каждое животное достигло пола, с максимальной продолжительностью 120 с. Каждую мышь тестировали трижды с 10-минутными интервалами, и для статистического анализа рассчитывали среднее время.
Регистрировали общее время, за которое каждое животное достигло пола, с максимальной продолжительностью 120 с. Каждую мышь тестировали трижды с 10-минутными интервалами, и для статистического анализа рассчитывали среднее время. Цитотоксичность in vitro MPP + против клеток SH-SY5Y человека была определена с использованием анализа МТТ.Как показано в результатах на фиг. 2A, MPP + может ингибировать рост клеток SH-SY5Y человека дозозависимым образом. Мы выбрали 300 мкМ MPP + для клеточного эксперимента. Клетки SH-SY5Y предварительно обрабатывали 10 и 100 мкМ AMI в течение 2 часов и обрабатывали 300 мкМ MPP + в течение 48 часов. Анализ МТТ показал, что AMI ослабляет цитотоксичность MPP + клеток SH-SY5Y (рис. 2B). Кроме того, MPP + снижает количество TH-положительных клеток и вызывает сокращение объема ядра.Однако ядерный пикноз был значительно уменьшен при предварительной обработке ОИМ в течение 2 часов (рисунки 2C, D). Эти результаты показывают, что AMI имеет защитное вмешательство в индуцированный MPP + апоптоз клеток SH-SY5Y.
2A, MPP + может ингибировать рост клеток SH-SY5Y человека дозозависимым образом. Мы выбрали 300 мкМ MPP + для клеточного эксперимента. Клетки SH-SY5Y предварительно обрабатывали 10 и 100 мкМ AMI в течение 2 часов и обрабатывали 300 мкМ MPP + в течение 48 часов. Анализ МТТ показал, что AMI ослабляет цитотоксичность MPP + клеток SH-SY5Y (рис. 2B). Кроме того, MPP + снижает количество TH-положительных клеток и вызывает сокращение объема ядра.Однако ядерный пикноз был значительно уменьшен при предварительной обработке ОИМ в течение 2 часов (рисунки 2C, D). Эти результаты показывают, что AMI имеет защитное вмешательство в индуцированный MPP + апоптоз клеток SH-SY5Y.
ингибирует индуцированное MPP
+ гиперфосфорилирование тау-белка (Ser396) в клетках SH-SY5Y MPP + -индуцированное гиперфосфорилирование тау в клетках SH-SY5Y и 300 мкМ MPP + -обработанные клетки SH-SY5Y в течение 8 ч показали, что экспрессия p-тау (Ser396) была самой высокой, а затем постепенно снижалась. (Рисунки 2E, F).Поэтому мы выбрали 8 часов для выявления влияния AMI на уровень фосфорилирования тау-белка. Как показано на фиг. 2I, J, 10 мкМ и 100 мкМ AMI, по-видимому, снижали уровень p-тау (Ser396) после обработки MPP + , общая экспрессия тау не изменилась. Кроме того, обработка MPP + заметно ингибировала экспрессию p-GSK3β (Ser9). Однако предварительная обработка AMI увеличивала фосфорилирование GSK3β в клетках SH-SY5Y (Фигуры 2G, H). В целом мы обнаружили, что AMI, снижающий гиперфосфорилирование тау-белка, может быть связан с его ингибированием активности GSK-3β.
(Рисунки 2E, F).Поэтому мы выбрали 8 часов для выявления влияния AMI на уровень фосфорилирования тау-белка. Как показано на фиг. 2I, J, 10 мкМ и 100 мкМ AMI, по-видимому, снижали уровень p-тау (Ser396) после обработки MPP + , общая экспрессия тау не изменилась. Кроме того, обработка MPP + заметно ингибировала экспрессию p-GSK3β (Ser9). Однако предварительная обработка AMI увеличивала фосфорилирование GSK3β в клетках SH-SY5Y (Фигуры 2G, H). В целом мы обнаружили, что AMI, снижающий гиперфосфорилирование тау-белка, может быть связан с его ингибированием активности GSK-3β.
AMI улучшает симптомы у мышей C57 / BL после лечения MPTP
Симптомы у мышей наблюдались после введения MPTP и AMI. Группа MPTP показала симптомы тремора всего тела, вертикальных волос, изогнутой спины, вертикального хвоста и медленных движений. Тем не менее, симптомы группы ОИМ 2,0 мг / кг и 4,0 мг / кг были значительно облегчены, с легким тремором, вертикальными волосами, изогнутой спиной и вертикальным хвостом. В то же время наблюдали и регистрировали латентный период от инъекции МРТР до вышеуказанных симптомов и продолжительность симптомов БП.Как показано в таблице 1, латентный период симптомов БП в группах ОИМ 2,0 мг / кг и 4,0 мг / кг был значительно больше, чем в группе МРТР, и продолжительность была сокращена. Кроме того, продолжительность симптомов БП у мышей, очевидно, сократилась, но латентный период не изменился после лечения леводопой по сравнению с группой МРТР.
В то же время наблюдали и регистрировали латентный период от инъекции МРТР до вышеуказанных симптомов и продолжительность симптомов БП.Как показано в таблице 1, латентный период симптомов БП в группах ОИМ 2,0 мг / кг и 4,0 мг / кг был значительно больше, чем в группе МРТР, и продолжительность была сокращена. Кроме того, продолжительность симптомов БП у мышей, очевидно, сократилась, но латентный период не изменился после лечения леводопой по сравнению с группой МРТР.
Таблица 1 . Влияние 6-амино-1-метилиндазола (AMI) на латентный период и продолжительность МРТР-модели симптомов БП у мышей ( n = 11–12, × ± с).
AMI увеличивает DA нейроны у мышей C57 / BL после лечения MPTP
TH представляет собой важный и специфический фермент, ограничивающий скорость синтеза DA, который имеет эффект метки на нейроны DA. Чем больше количество TH-положительных клеток, тем больше содержание DA. Мы использовали иммуногистохимию и вестерн-блоттинг для обнаружения экспрессии TH в черной субстанции среднего мозга. Как показано на фиг. 3В, выживаемость нейронов в группе МРТР, очевидно, снизилась по сравнению с контрольной группой, что доказывает, что модель животного PD была успешно создана.Однако количество нейронов у мышей, которым предварительно вводили 2,0 мг / кг AMI (65,80 ± 12,8%, p <0,001) и 4,0 мг / кг AMI (64,13 ± 5,7%, p <0,001), было выше. чем в группе MPTP (34,84 ± 2,7%; Рисунки 3B – F). Кроме того, TH-положительные нейроны в группе L-DOPA (34,86 ± 4,9%) были аналогичны модельной группе. Эти результаты показали, что AMI восстанавливает потерю дофаминовых нейронов у мышей и обладает нейропротекторным эффектом, в то время как леводопа не оказывает защитного действия на нейроны.
Как показано на фиг. 3В, выживаемость нейронов в группе МРТР, очевидно, снизилась по сравнению с контрольной группой, что доказывает, что модель животного PD была успешно создана.Однако количество нейронов у мышей, которым предварительно вводили 2,0 мг / кг AMI (65,80 ± 12,8%, p <0,001) и 4,0 мг / кг AMI (64,13 ± 5,7%, p <0,001), было выше. чем в группе MPTP (34,84 ± 2,7%; Рисунки 3B – F). Кроме того, TH-положительные нейроны в группе L-DOPA (34,86 ± 4,9%) были аналогичны модельной группе. Эти результаты показали, что AMI восстанавливает потерю дофаминовых нейронов у мышей и обладает нейропротекторным эффектом, в то время как леводопа не оказывает защитного действия на нейроны.
Для дальнейшего изучения того, оказывает ли AMI защитный эффект на нейроны DA, использовали вестерн-блоттинг для определения экспрессии TH в среднем мозге. Экспрессия белка TH в группе МРТР была маркерно ниже, чем в контрольной группе. По сравнению с группой MPTP, группы вмешательства с 2 мг / кг и 4 мг / кг AMI увеличивали экспрессию белка TH. Эти результаты также предполагают, что AMI может улучшать вызванную МРТР потерю TH в полосатом теле мышей и оказывает защитное действие на дегенерацию DA нейронов (Фигуры 3C, D).
Эти результаты также предполагают, что AMI может улучшать вызванную МРТР потерю TH в полосатом теле мышей и оказывает защитное действие на дегенерацию DA нейронов (Фигуры 3C, D).
AMI усиливает дендриты черной субстанции у мышей C57 / BL после лечения MPTP
Чтобы изучить влияние AMI на дендриты черной субстанции, использовали окрашивание по Гольджи для определения плотности и длины нейрональных дендритов в черной субстанции. Как показано на рисунках 4A – E, общее количество точек ветвления дендритов в черной субстанции среднего мозга было уменьшено в группе MPTP (3,75 ± 0,89, p <0,01) по сравнению с контрольной группой (9,62 ± 0,52).Однако 4,0 мг / кг AMI (8,25 ± 0,89, p <0,01) значительно увеличили общее количество точек ветвления дендритов и длину дендритов. Группа 2,0 мг / кг ОИМ (4,25 ± 0,89) может быть связана с недостаточной дозой, не демонстрирующей очевидного защитного эффекта. Мы также обнаружили, что группа in L-DOPA (2,37 ± 0,74) оказывает слабое влияние на плотность нейрональных дендритов в черной субстанции мышей (рисунки 4F, G).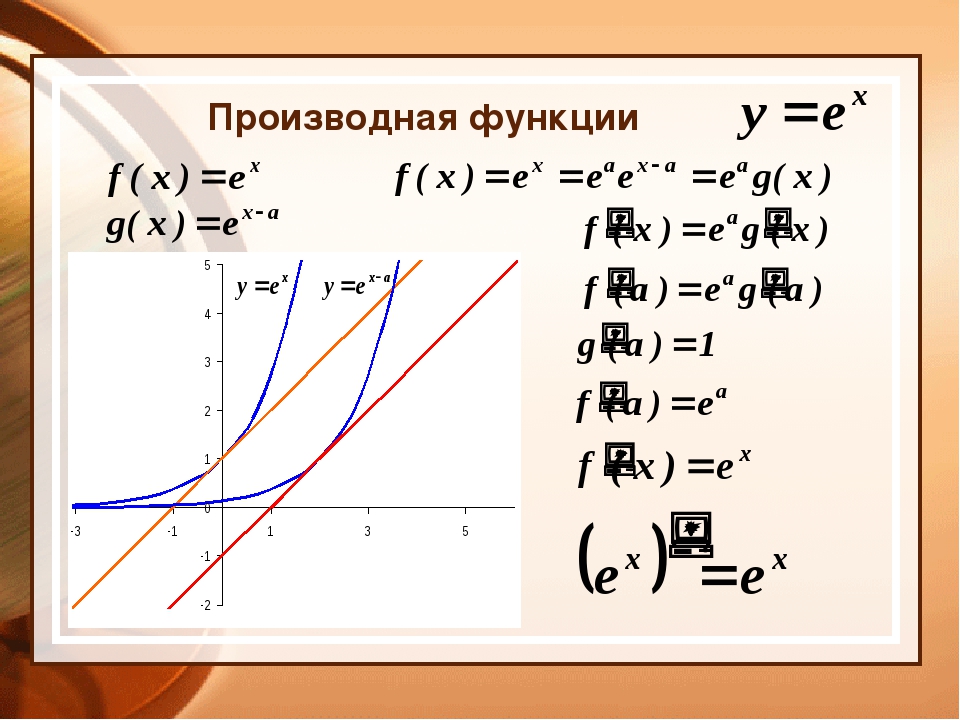 Эти результаты показали, что AMI может эффективно улучшить снижение плотности дендритных шипов, вызванное MPTP.
Эти результаты показали, что AMI может эффективно улучшить снижение плотности дендритных шипов, вызванное MPTP.
Рисунок 4 . Окрашивание по Гольджи для определения плотности и длины нейрональных дендритов в черной субстанции головного мозга (A) Контроль; (B) MPTP; (C) AMI 2 мг / кг; (D) AMI 4 мг / кг; (E) L-ДОПА 10 мг / кг. (F) Общее количество точек ветвления дендритов. (G) Длина дендрита. Увеличение: 40 ×, толщина среза: 100 мкм. ## p <0,01 по сравнению с контролем; ** p <0.001 против MPTP.
AMI улучшает поведенческие аномалии у мышей C57 / BL после лечения MPTP
Мы использовали тест тяги, тест вращающегося стержня и тест лазанья с шестом, чтобы исследовать поведенческие способности в различных группах лечения. Как показано на фиг. 5A, было замечено, что задние лапы группы МРТР были слабыми, и лапы не могли удерживать проволоку, но мыши в других группах могли удерживать проволоку одной или двумя лапами.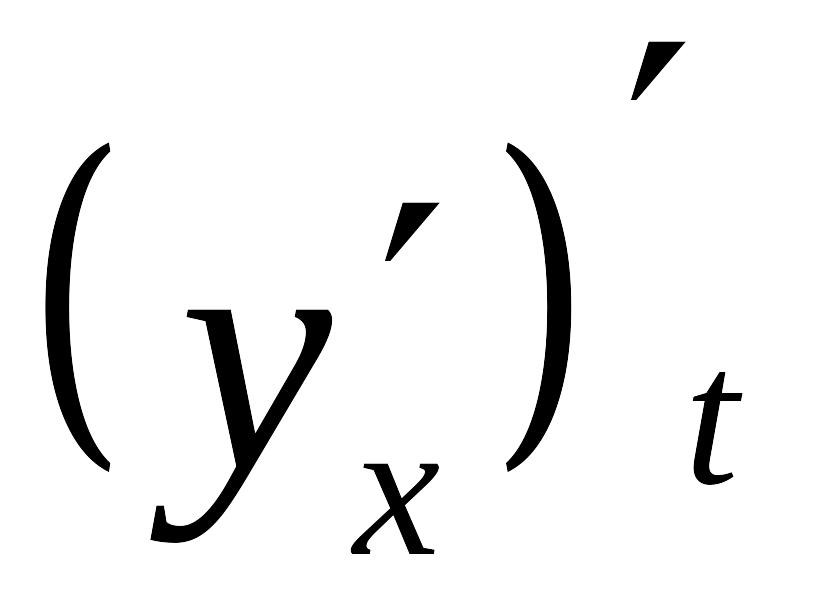 Баллы показали, что группа с ОИМ 2,0 мг / кг (2,50 ± 0,53), группа ОИМ 4,0 мг / кг (2.38 ± 0,52), группа L-ДОФА (2,71 ± 0,49) и контрольная группа (2,86 ± 0,38) не имели значимых различий, однако оценки в группе MPTP (1,40 ± 0,55, p <0,001) были ниже, чем в контрольной группе. . В тесте с вращающимся стержнем AMI и L-DOPA могут улучшить вызванную MPTP постуральную подвижность и медленную реакцию (рис. 5B). Наконец, мыши в группе МРТР оставались дольше в каждой секции стержня, результаты тестов с лазанием по шесту показывают, что оценки в группе 2,0 мг / кг AMI (8,0 ± 1,22), 4.Группа 0 мг / кг AMI (7,60 ± 1,14) и группа L-DOPA (7,60 ± 0,55) были выше, чем в группе MPTP (5,20 ± 1,64, p <0,05; Рисунок 5C).
Баллы показали, что группа с ОИМ 2,0 мг / кг (2,50 ± 0,53), группа ОИМ 4,0 мг / кг (2.38 ± 0,52), группа L-ДОФА (2,71 ± 0,49) и контрольная группа (2,86 ± 0,38) не имели значимых различий, однако оценки в группе MPTP (1,40 ± 0,55, p <0,001) были ниже, чем в контрольной группе. . В тесте с вращающимся стержнем AMI и L-DOPA могут улучшить вызванную MPTP постуральную подвижность и медленную реакцию (рис. 5B). Наконец, мыши в группе МРТР оставались дольше в каждой секции стержня, результаты тестов с лазанием по шесту показывают, что оценки в группе 2,0 мг / кг AMI (8,0 ± 1,22), 4.Группа 0 мг / кг AMI (7,60 ± 1,14) и группа L-DOPA (7,60 ± 0,55) были выше, чем в группе MPTP (5,20 ± 1,64, p <0,05; Рисунок 5C).
Рисунок 5 . ОИМ улучшил поведенческие расстройства у мышей с моделью БП, вызванной МРТР. (A) Тест Rotarod. (B) Испытание на тягу. (C) Тест на восхождение на шест. ## p <0,01 по сравнению с контролем; * p <0,01, ** p <0,001 по сравнению с MPTP, n = 6–8.
В совокупности эти результаты свидетельствуют о том, что мыши в группе МРТР испытывали трудности при выполнении движений из-за слабости задних конечностей. Сравнение групп AMI 2,0 мг / кг и 4,0 мг / кг. Статистическая значимость значительно улучшила препятствие, демонстрируя более плавные движения и более высокие оценки поведения.
Обсуждение
Наиболее заметным патологическим признаком БП является потеря дофаминергических нейронов в черной субстанции. Следовательно, разработка нового препарата, ингибирующего дофаминергический апоптоз, может значительно улучшить лечебный эффект БП (Yang et al., 2018а; Гейбл и др., 2019). Это исследование показало, что AMI оказывает защитное действие на индуцированный MPP + апоптоз клеток SH-SY5Y, и этот эффект сопровождается снижением уровня фосфорилирования тау-белка.
Аномальное фосфорилирование тау-белка в основном связано с дисбалансом регуляции протеинкиназы и фосфатазы (Lee et al., 2019; Singh et al., 2019). Когда активность киназы увеличивается, а активность фосфатазы снижается, тау-белок гиперфосфорилируется.Протеинкиназы включают GSK-3 и циклин-зависимую киназу 5 (CDK5), в которой GSK-3β фосфорилирует множество сайтов тау-белка. Важно отметить, что GSK-3β является одной из вышестоящих тау-киназ, которая участвует в образовании фосфорилирования тау и нейрофибриллярных клубков при БА, а также является ключом к множеству сигналов выживания нейронов, препятствующих апоптозу нейронов (Yang et al. , 2018b; Chang et al., 2019; Shi et al., 2019). Недавние исследования идентифицировали GSK-3β как потенциальную терапевтическую мишень при болезни Альцгеймера (Shi et al., 2019). Кизил иридоид гликозид, многообещающий агент для терапии БА, ингибирует гиперфосфорилирование тау-белка через , регулируя перекрестную связь между передачей сигналов GSK-3β и PP2A (Yang et al., 2018a). Osthole снижает фосфорилирование тау-белка посредством сигнального пути PI3K / AKT / GSK-3β при AD (Yao et al., 2019). В соответствии с предыдущими исследованиями, наши результаты показали, что AMI подавляет экспрессию тау-киназы GSK-3β, расположенной выше по течению. Кроме того, тау-протеинкиназа II (TPKII), образованная комплексом, содержащим две субъединицы циклин-зависимой киназы 5 (CDK5) и p35, может синергетически повышать эффективность фосфорилирования GSK-3β тау-белка (Xiao et al., 2018; Giannopoulos et al., 2019). Следовательно, нам необходимо исследовать экспрессию тау-протеинкиназы II (TPKII) в следующем эксперименте.
Это исследование также показало, что AMI оказывает терапевтическое действие на модель PD животных in vivo . Для приготовления модели мышей PD использовали непрерывную инъекцию высоких доз MPTP в течение 5 дней, а леводопу использовали в качестве положительного контроля. Дофаминовые нейроны были разрушены МРТР, и уровни дофамина были снижены у мышей. Дофамин не восполнялся за короткое время, поэтому поведенческие аномалии группы MPTP стали серьезными, но AMI защищал дофаминовые нейроны мышей от повреждения MPTP, в то время как L-DOPA был дополнен дофамином, который также улучшил поведенческие аномалии Паркинсона (Thomas et al. ., 2019). Напротив, результаты иммуногистохимии TH показали, что количество нейронов DA в группе L-DOPA не было значительно выше, чем в группе MPTP, что дополнительно иллюстрирует текущие основные недостатки лечения L-DOPA с PD, эти препараты могут только улучшают симптомы, но не могут эффективно отсрочить прогрессирование заболевания и предотвратить апоптоз дофаминовых нейронов. Кроме того, при длительном применении L-DOPA его эффективность постепенно снижалась, большинство пациентов переносили такие осложнения, как дискинезия или психические расстройства (Wichmann, 2019).
Поддержание плотности дендритных шипов полосатого тела может отсрочить обострение БП, продлить время использования леводопы и улучшить его терапевтический эффект (Deutch et al., 2007). Окрашивание по Гольджи использовали для наблюдения за морфологией нейронов (Chechowska et al., 2019). AMI значительно увеличивает плотность нейрональных дендритов в черной субстанции мышей. Следует отметить, что увеличение плотности дендритных шипов полосатого тела может компенсировать снижение уровня DA в полосатом теле животных при БП и способствовать восстановлению их поведенческой функции (Kim et al., 2013). Результаты нашего поведенческого эксперимента согласуются с литературными сообщениями. В целом ОИМ оказывает нейропротекторное и нейротрофическое действие. С одной стороны, он защищает целостность дендритных шипов, с другой стороны, AMI сохраняет потерю дофаминовых нейронов и эффективно улучшает поведенческие аномалии мышей C57 / BL.
Заявление о доступности данных
Наборы данных, созданные для этого исследования, доступны по запросу соответствующему автору.
Заявление об этике
Исследование на животных было рассмотрено и одобрено Комитетом по уходу и использованию животных Южного медицинского университета (Гуанчжоу, Гуандун, Китай).
Взносы авторов
ЗМ провел экспериментальные работы, анализ и интерпретацию данных. ZW-t задумал и подготовил рукопись. WW-y, XJ-p и WH-t разработали исследование и критически отредактировали рукопись. Другие авторы принимали участие в сборе данных и проверяли рукопись. Все авторы внесли свой вклад в статью и одобрили представленную версию.
Финансирование
Работа поддержана ключевым проектом Фонда естественных наук провинции Гуандун (No.2017A030313884).
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Список литературы
Chang, H., Di, T., Wang, Y., Zeng, X., Li, G., Wan, Q., et al. (2019). Делеция сейпина у мышей усиливает фосфорилирование и агрегацию тау-белка за счет снижения нейронального PPARγ и инсулинорезистентности. Neurobiol.Дис. 127, 350–361. DOI: 10.1016 / j.nbd.2019.03.023
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Chen, I.-C., Lin, T.-H., Hsieh, Y.-H., Chao, C.-Y., Wu, Y.-R., Chang, K.-H., et al. (2018). Сформулированный китайской медициной шаояо ганьцао тан уменьшает агрегацию тау и оказывает нейрозащитное действие за счет антиоксидантного и противовоспалительного действия. Оксид. Med. Клетка. Longev. 2018: 9595741. DOI: 10.1155 / 2018/9595741
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Чен, X., Кордич, Дж. К., Уильямс, Э. Т., Левин, Н., Коул-Стросс, А., Маршалл, Л. и др. (2019). Связанные с болезнью Паркинсона мыши с ноккином D620N VPS35 проявляют тау-невропатологию и дофаминергическую нейродегенерацию. Proc. Natl. Акад. Sci. U S A 116, 5765–5774. DOI: 10.1073 / pnas.1814
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Чеховска, Н., ван Ринен, А., Ланг, Ф., Эйбергер, Б., и Баадер, С. Л. (2019). Обновленная методика окрашивания по Гольджи, улучшающая специфичность клеток мозжечка. Histochem. Cell Biol. 151, 327–341. DOI: 10.1007 / s00418-018-01766-0
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Del Rey, N. L.-G., Quiroga-Varela, A., Garbayo, E., Carballo-Carbajal, I., Fernandez-Santiago, R., Monje, M., et al. (2018). Успехи в лечении болезни Паркинсона: 200 лет спустя. Фронт. Нейроанат. 12: 113. DOI: 10.3389 / fnana.2018.00113
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Деня, И., Малан, С. Ф., и Жубер, Дж. (2018). Производные индазола и их терапевтические применения: патентный обзор (2013-2017). Мнение эксперта. Ther. Пат. 28, 441–453. DOI: 10.1080 / 13543776.2018.1472240
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Дойч, А. Ю., Колбран, Р. Дж., И Уиндер, Д. Дж. (2007). Пластичность полосатого тела и дендритное ремоделирование средних шиповидных нейронов при паркинсонизме. Parkinsonism Relat. Disord. 13, S251 – S258. DOI: 10.1016 / S1353-8020 (08) 70012-9
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Гейбл, Ф.Ф., Хенрих, М. Т., и Ортель, В. Х. (2019). Мезенцефальная и экстрамезэнцефальная дофаминергические системы при болезни Паркинсона. J. Neural. Трансм. 126, 377–396. DOI: 10.1007 / s00702-019-01970-9
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Яннопулос П. Ф., Чиу Дж. И Пратико Д. (2019). Нарушения обучения, дефицит памяти и невропатология у старых трансгенных мышей с тау-белком зависят от биосинтеза лейкотриенов: роли пути киназы cdk5. Мол. Neurobiol. 56, 1211–1220. DOI: 10.1007 / s12035-018-1124-7
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ким, В., Им, М. Дж., Пак, К. Х., Ли, К. Дж., Чой, С., и Юн, Б. Дж. (2013). Ремоделирование дендритной структуры шиповидных нейронов полосатого тела сопровождает восстановление поведения на мышиной модели болезни Паркинсона. Neurosci. Lett. 557, 95–100. DOI: 10.1016 / j.neulet.2013.10.049
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ли, С., Mankhong, S., и Kang, J.-H. (2019). Внеклеточные пузырьки как источник биомаркеров Альцгеймера: возможности и проблемы. Внутр. J. Mol. Sci. 20: 1728. DOI: 10.3390 / ijms20071728
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Лян, X., Чжу, W., Xu, Y., Lai, C., Rao, J., and Wang, W. (2016). Защитная роль 6-гидрокси-1-h-индазола на мышиной модели болезни Паркинсона, индуцированной МРТР. Eur. J. Pharmacol. 791, 348–354. DOI: 10.1016 / j.ejphar.2016.08.011
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Лю Дж., Купер К. А., Вайнтрауб Д. и Даходвала Н. (2019a). Фармакологическое лечение апатии при расстройствах непристойного тела: систематический обзор. Parkinsonism Relat. Disord. 60, 14–24. DOI: 10.1016 / j.parkreldis.2018.11.002
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Лю, З., Чен, Л., Ю, П., Чжан, Ю., Фанг, Б., Ву, К. и др. (2019b).Открытие производных 3- (индол-5-ил) -индазола в качестве новых антагонистов белка 2 миелоидной дифференцировки / толл-подобного рецептора 4 для лечения острого повреждения легких. J. Med. Chem. 62, 5453–5469. DOI: 10.1021 / acs.jmedchem.9b00316
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Пауэр, Дж. Х. Т., Барнс, О. Л., и Чегини, Ф. (2017). Тельца Леви и механизмы гибели нейрональных клеток при болезни Паркинсона и деменции с непристойными тельцами. Brain Pathol. 27, 3–12. DOI: 10.1111 / bpa.12344
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Шильдкнехт, С., Ди Монте, Д. А., Папе, Р., Тье, К., и Лейст, М. (2017). Переломные моменты и эндогенные детерминанты нигростриатальной дегенерации МФТП. Trends Pharmacol. Sci. 38, 541–555. DOI: 10.1016 / j.tips.2017.03.010
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ши, X. Л., Ву, Дж. Д., Лю, П., и Лю, З. П. (2019).Синтез и оценка новых ингибиторов GSK-3β как многофункциональных агентов против болезни Альцгеймера. Eur. J. Med. Chem. 167, 211–225. DOI: 10.1016 / j.ejmech.2019.02.001
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Сингх Б., Ковело А., Мартелл-Мартинес Х., Нанкларес К., Шерман М. А., Окематти Э. и др. (2019). Тау необходим для прогрессирующего дефицита синапсов и памяти в модели альфа-синуклеинопатии у трансгенных мышей. Acta Neuropathol. 138, 551–574. DOI: 10.1007 / s00401-019-02032-w
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Thomas, I., Alam, M., Bergquist, F., Johansson, D., Memedi, M., Nyholm, D., et al. (2019). Сенсорные алгоритмы дозирования для перорального приема микротаблеток леводопы / карбидопы при болезни Паркинсона: первый опыт. J. Neurol. 266, 651–658. DOI: 10.1007 / s00415-019-09183-6
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ван, В., Yang, Y., Ying, C., Li, W., Ruan, H., Zhu, X., et al. (2007). Ингибирование киназы-3β гликогенсинтазы защищает дофаминергические нейроны от токсичности МРТР. Нейрофармакология. 52, 1678–1684. DOI: 10.1016 / j.neuropharm.2007.03.017
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Винер, Дж. Р., Маасс, А., Прессман, П., Стивер, Дж., Шонхаут, Д. Р., Бейкер, С. Л. и др. (2018). Связь между тау, β-амилоидом и познанием при болезни Паркинсона. JAMA Neurol. 75, 227–235. DOI: 10.1001 / jamaneurol.2017.3713
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Xiao, N., Zhang, F., Zhu, B., Liu, C., Lin, Z., Wang, H., et al. (2018). Накопление тау-белка, опосредованное CDK5, запускает индуцированный метамфетамином апоптоз нейронов через путь деградации, связанный с эндоплазматическим ретикулумом. Toxicol. Lett. 292, 97–107. DOI: 10.1016 / j.toxlet.2018.04.027
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ян, К., Ли, X., Гао, W., Wang, Q., Zhang, L., Li, Y., et al. (2018a). Иридоидный гликозид кизила ингибирует гиперфосфорилирование тау-белка через , регулируя перекрестную связь между передачей сигналов GSK-3β и PP2A. Фронт. Pharmacol. 9: 682. DOI: 10.3389 / fphar.2018.00682
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ян Л., Ван Х., Лю Л. и Се А. (2018b). Роль передачи сигналов инсулин / IGF-1 / PI3K / Akt / GSK3β в деменции при болезни Паркинсона. Фронт. Neurosci. 12:73. DOI: 10.3389 / fnins.2018.00073
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Яо Ю., Ван Ю., Конг Л., Чен Ю. и Ян Дж. (2019). Остхол снижает фосфорилирование тау-белка через сигнальный путь PI3K / AKT / GSK-3β при болезни Альцгеймера. Life Sci. 217, 16–24. DOI: 10.1016 / j.lfs.2018.11.038
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Чжэн, К., Чен, Г., Тан, Ю., Цзэн, В., Пэн, К., Wang, J., et al. (2018). Аналог TRH талтирелин защищает дофаминергические нейроны от нейротоксичности MPTP и ротенона. Фронт. Клетка. Neurosci. 12: 485. DOI: 10.3389 / fncel.2018.00485
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Zhou, Y., Shi, J., Chu, D., Hu, W., Guan, Z., Gong, C.X., et al. (2018). Значение фосфорилирования и усечения тау-белка в этиопатогенезе болезни Альцгеймера. .
Вы можете использовать следующие стандартные функции: sqrt — квадратный корень, exp — степень экспоненты, lb — логарифм по основанию 2, lg — логарифм по основанию 10, ln — логарифм по основанию e, sin — синус, cos — косинус, tg — тангенс, ctg — котангенс, sec — секанс, косеканс — косеканс, arcsin — arcsine, arccos — arccosine, arctg — арктангенс, arcctg — арккотангенс, arcsec — arcsecant, arccosec — arccosecant, versin — versien, vercos — vercosine, haversin — гаверсинус, exsec — exsecant — excsc excosecant, sh — гиперболический синус, ch — гиперболический косинус, th — гиперболический тангенс, cth — гиперболический котангенс, sech — гиперболический секанс, csch — гиперболический косеканс, abs — модуль, sgn — signum (знак), logP — логарифм по основанию P , f.е. log7 (x) — логарифм по основанию 7, _ rootP — корень P-й степени, т.е. root3 (x) — кубический корень
Нахождение производной
Получить производную легко, используя правила дифференцирования и таблицу производных элементарных функций. Сложная задача — интерпретировать введенное выражение и упростить полученную формулу производной. Я изо всех сил пытаюсь ее решить, но это уже другая история.
Правила дифференциации
1) правило сумм:
2) правило произведения:
3) правило частного:
4) правило цепочки:
Производные общих функций
Полином или элементарная степень:
Показательная функция:
Логарифмическая функция:
Тригонометрические функции:
,
,
,
Обратные тригонометрические функции:
,
,
,
:
| ; | Функционально-дифференциальные включения типа Хейла с дробным порядком производной в банаховом пространстве Илолов М.И. , Гульжонов Д.Н. , Ж.Ш. Рахматов Аннотация: За последние десятилетия существенное развитие получила теория функционально-дифференциальных включений, в первую очередь отложенного функционально-дифференциального включения. Ученые из разных стран проводят исследования по теории начально-краевых задач для различных классов дифференциальных, интегро-дифференциальных и функционально-дифференциальных включений в частные производные с целыми и дробными порядками производных.Настоящая работа посвящена дробным функционально-дифференциальным и интегро-дифференциальным включениям типа Хейла, занимающим промежуточное место между функционально-дифференциальными включениями с запаздыванием и включениями нейтрального типа. Установлены достаточные условия существования слабых решений включений типа Хейла с дробным порядком производной. В основе исследования лежат методы дробного интегро-дифференциального исчисления и теория неподвижных точек многозначных отображений.Известно, что динамика экономических, социальных и экологических макросистем — это многозначный динамический процесс, а дробно-дифференциальные и интегро-дифференциальные включения — естественные модели динамики макросистем. Такие включения также используются для описания некоторых физико-механических систем с гистерезисом. В конце статьи приведен пример, иллюстрирующий абстрактные результаты. Ключевые слова: функционально-дифференциальное включение, дробная производная Капуто, многозначное отображение, неподвижная точка. DOI: https://doi.org/10.22405/2226-8383-2018-20-4-208-225 Полный текст: PDF-файл (591 kB) УДК: 511.5 Образец цитирования: Илолов М.И., Гульжонов Д.Н., Ж.Ш. А. Рахматов, “Функционально-дифференциальные включения типа Хейла с дробным порядком производной в банаховом пространстве”, Чебышевский сб., 20: 4 (2019), 208–225 Цитирование в формате AMSBIB Варианты соединения: Цитирующие статьи в Google Scholar: Русские цитаты,
Цитаты на английском языке |
|
Производное изофталата, нацеленное на домен C1, HMI-1b11 способствует разрастанию нейритов и экспрессии GAP-43 посредством активации PKC в клетках SH-SY5Y
TY — JOUR
T1 — Производное изофталата, нацеленное на домен C1, HMI-1b11 способствует разрастанию нейритов и экспрессия GAP-43 посредством активации PKC в клетках SH-SY5Y
AU — Talman, Virpi
AU — Amadio, Marialaura
AU — Osera, Cecilia
AU — Sorvari, Salla
AU — Boije af Gennavnav
AU — Yli-Kauhaluoma, Jari
AU — Rossi, Daniela
AU — Govoni, Stefano
AU — Collina, Simona
AU — Ekokoski, Elina
AU — Tuominen, Raimo
AU — Pascale, Alessia
PY — 2013
Y1 — 2013
N2 — Протеинкиназа C (PKC) представляет собой семейство серин / треонинфосфотрансфераз, повсеместно экспрессируемых и участвующих во многих клеточных функциях, таких как пролиферация и апоптоз дифференциация. Домен C1 PKC представляет собой привлекательную лекарственную мишень, особенно для разработки активаторов PKC. Диалкил-5- (гидроксиметил) изофталаты представляют собой новую группу синтетических лигандов С1-домена, которые проявляют антипролиферативный эффект в клетках карциномы шейки матки HeLa.Здесь мы выбрали два изофталата, HMI-1a3 и HMI-1b11, и охарактеризовали их действие на линию клеток нейробластомы человека SH-SY5Y. Оба активных изофталата проявляли значительные антипролиферативные и индуцирующие дифференцировку эффекты. Поскольку HMI-1b11 не ухудшал выживаемость клеток даже при самой высокой протестированной концентрации (20 мкМ) и поддерживал рост нейритов и дифференцировку клеток SH-SY5Y, мы сосредоточились на изучении его сигнальных каскадов ниже по течению и влиянии на экспрессию генов. Соответственно, микроматрица экспрессии генов по всему геному и анализ обогащения набора генов показали, что HMI-1b11 (10 мкМ) индуцировал изменения в генах, в основном связанные с дифференцировкой клеток.В частности, дальнейшие исследования показали, что воздействие HMI-1b11 индуцировало повышающую регуляцию GAP-43, маркера прорастания нейритов и дифференцировки нейронов. Эти эффекты вызывались 7-минутной обработкой HMI-1b11 и специфически зависели от активации PKC, поскольку предварительная обработка селективным ингибитором Gö6976 отменяла повышающую регуляцию белка GAP-43, наблюдаемую через 12 часов. Параллельно мы обнаружили, что 7-минутное воздействие HMI-1b11 индуцировало накопление PKC в цитоскелете, эффект, который снова был предотвращен предварительной обработкой Gö6976.Несмотря на схожую аффинность связывания с PKC, изофталаты по-разному влияли на PKC-зависимую передачу сигналов ERK1 / 2: индуцированное HMI-1a3 фосфорилирование ERK1 / 2 было временным, тогда как HMI-1b11 индуцировало быстрое, но продолжительное фосфорилирование ERK1 / 2. В целом наши данные согласуются с предыдущими исследованиями, показывающими, что активация путей PKCα и ERK1 / 2 участвует в регуляции дифференцировки нейронов. Кроме того, поскольку PKC классифицируется как одна из когнитивных киназ, а активация PKC считается потенциальной терапевтической стратегией для лечения когнитивных расстройств, наши результаты показывают, что HMI-1b11 представляет собой многообещающее ведущее соединение в исследованиях, направленных на предотвращение или противодействие нарушение памяти.
AB — Протеинкиназа C (PKC) представляет собой семейство сериновых / треониновых фосфотрансфераз, которые повсеместно экспрессируются и участвуют во многих клеточных функциях, таких как пролиферация, апоптоз и дифференцировка. Домен C1 PKC представляет собой привлекательную лекарственную мишень, особенно для разработки активаторов PKC. Диалкил-5- (гидроксиметил) изофталаты представляют собой новую группу синтетических лигандов С1-домена, которые проявляют антипролиферативный эффект в клетках карциномы шейки матки HeLa. Здесь мы выбрали два изофталата, HMI-1a3 и HMI-1b11, и охарактеризовали их действие на линию клеток нейробластомы человека SH-SY5Y.Оба активных изофталата проявляли значительные антипролиферативные и индуцирующие дифференцировку эффекты. Поскольку HMI-1b11 не ухудшал выживаемость клеток даже при самой высокой протестированной концентрации (20 мкМ) и поддерживал рост нейритов и дифференцировку клеток SH-SY5Y, мы сосредоточились на изучении его сигнальных каскадов ниже по течению и влиянии на экспрессию генов. Соответственно, микроматрица экспрессии генов по всему геному и анализ обогащения набора генов показали, что HMI-1b11 (10 мкМ) индуцировал изменения в генах, в основном связанные с дифференцировкой клеток.В частности, дальнейшие исследования показали, что воздействие HMI-1b11 индуцировало повышающую регуляцию GAP-43, маркера прорастания нейритов и дифференцировки нейронов. Эти эффекты вызывались 7-минутной обработкой HMI-1b11 и специфически зависели от активации PKC, поскольку предварительная обработка селективным ингибитором Gö6976 отменяла повышающую регуляцию белка GAP-43, наблюдаемую через 12 часов. Параллельно мы обнаружили, что 7-минутное воздействие HMI-1b11 индуцировало накопление PKC в цитоскелете, эффект, который снова был предотвращен предварительной обработкой Gö6976.Несмотря на схожую аффинность связывания с PKC, изофталаты по-разному влияли на PKC-зависимую передачу сигналов ERK1 / 2: индуцированное HMI-1a3 фосфорилирование ERK1 / 2 было временным, тогда как HMI-1b11 индуцировало быстрое, но продолжительное фосфорилирование ERK1 / 2. В целом наши данные согласуются с предыдущими исследованиями, показывающими, что активация путей PKCα и ERK1 / 2 участвует в регуляции дифференцировки нейронов. Кроме того, поскольку PKC классифицируется как одна из когнитивных киназ, а активация PKC считается потенциальной терапевтической стратегией для лечения когнитивных расстройств, наши результаты показывают, что HMI-1b11 представляет собой многообещающее ведущее соединение в исследованиях, направленных на предотвращение или противодействие нарушение памяти.
KW — 317 Аптека
U2 — 10.1016 / j.phrs.2013.04.008
DO — 10.1016 / j.phrs.2013.04.008
M3 — Артикул
VL — 73
SP — 44
EP — 54
JO — Фармакологические исследования
JF — Фармакологические исследования
SN — 1043-6618
ER —
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки вашего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Обработчик производного потока копирования PDF-файлов
Общего назначения
Некоторые учреждения хранят очень большие мастер-файлы PDF.Для доставки конечным пользователям необходимо создать версию более низкого качества.
В этом примере показано, как использовать интерфейс обработчика потока для создания производных копий.
Версия продукта Совместимость
3.x.
Тип интерфейса
Обработчик потока.
Поток
- Создайте сценарий преобразования.
- Создайте новый обработчик потока.
- Создайте правило задачи общего представления.
- Настройте правило как часть обогащения.
Создайте сценарий преобразования
В /exlibris/dps/d4_1/system.dir/bin создайте следующий исполняемый сценарий run_pdf_deriv_copy.sh:
#! / Bin / sh
для ARG сделать
T_ARG = "\" $ ARG \ ""
ARGS = "$ ARGS $ ARG"
T_ARGS = "$ T_ARGS $ T_ARG"
LAST_ARG = "$ ARG"
Выполнено
eval /exlibris/product/ghostscript-8.70/bin/ps2pdf -dPDFSETTINGS = / screen $ T_ARGS
выход $? Примечание :
версия ghostscript может время от времени обновляться Ex Libris. Последняя версия связана с $ dps_product / bin / gs.
Клиенты с многосерверной средой могут предпочесть разместить сценарий в разделе operating_shared. В этом случае программные ссылки должны быть созданы из /exlibris/dps/d4_1/system.dir/bin каждого сервера в общий каталог.
Создание обработчика потока
В разделе «Администрирование» откройте таблицу сопоставления Stream Handler Util. Добавьте новую строку со следующими параметрами:
type = external_program worker = run_pdf_deriv_copy (= имя скрипта без расширения файла) file_ext = pdf params_pattern = '$ 1' '$ 2' event_id = 188 name = pdf_deriv description = Создать производную копию PDF
Нажмите «Создать» и сохраните.





 1.1.
1.1. 1.1. Производные основных элементарных функций.
1.1. Производные основных элементарных функций.
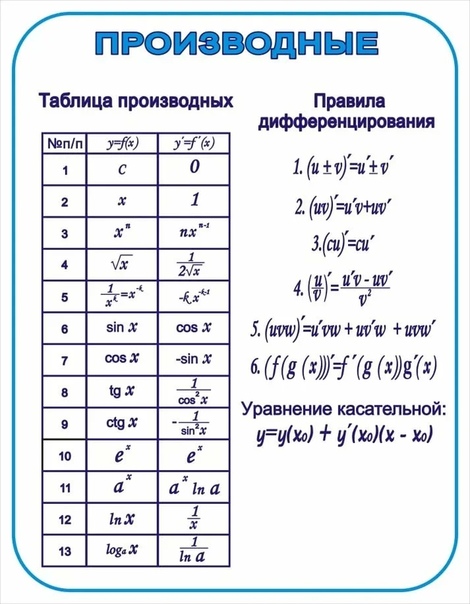 Будем
Будем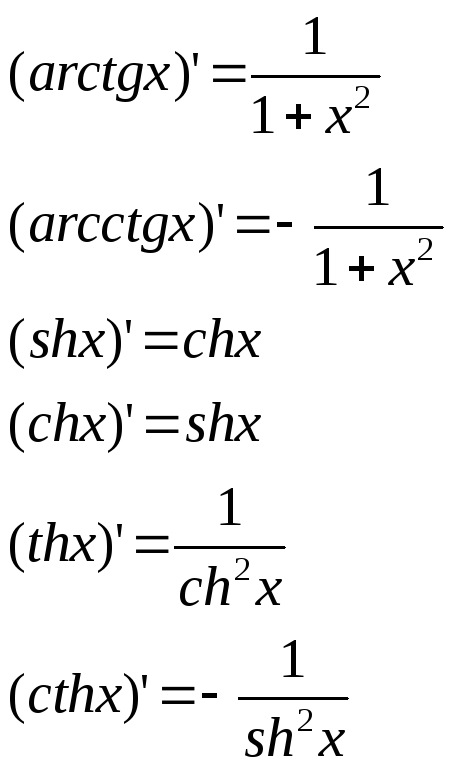 Для частных производных обозначение то же, поэтому смысл обозначения определяют из контекста.
Для частных производных обозначение то же, поэтому смысл обозначения определяют из контекста.
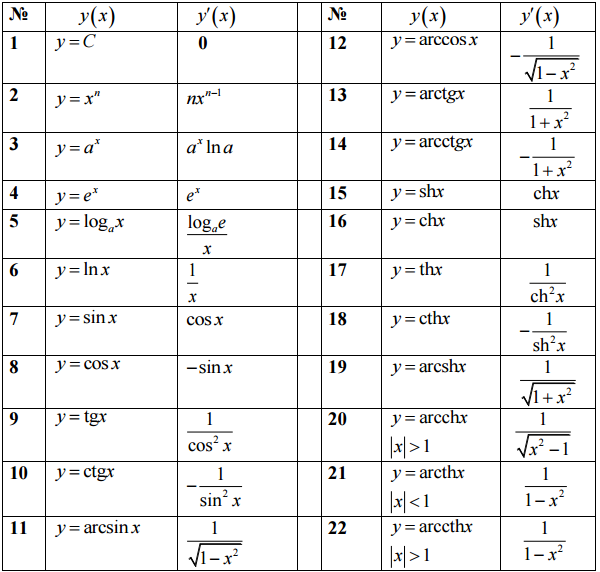 99997 тм
(\ 240) Tj
/ T1_3 1 Тс
-6.00198 1 тд
(Цитированные статьи) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 141 383,99994 тм
(\ 240) Tj
/ T1_0 1 Тс
34.40392 1 тд
() Tj
0 0 1 рг
-34,40392 0 Тд
(http: //cancerpreventionresearch.aacrjournals.org/content/1/7/577.full#re \
f-list-1) Tj
0 г
0 1.00001 TD
(Эта статья содержит 48 статей, 15 из которых вы можете получить бесплатно по адресу:) Tj
ET
BT
/ T1_0 1 Тс
11 0 0 11 120,94 202 361,99997 тм
(\ 240) Tj
/ T1_3 1 Тс
-6,33498 1 тд
(Цитирование статей) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 141 353,99994 тм
(\ 240) Tj
/ T1_0 1 Тс
35.79392 1 тд
() Tj
0 0 1 рг
-35.79392 0 Тд
(http://cancerpreventionresearch.aacrjournals.org/content/1/7/577.полный # re \
lated-urls) Tj
0 г
Т *
(Эта статья процитирована в 2 статьях, размещенных на HighWire. Перейдите к ar \
ticles at:) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 30 333,99997 тм
(\ 240) Tj
0 1 ТД
(\ 240) Tj
ET
30 209 525 125 рэ
0 0 мес.
S
BT
/ T1_0 1 Тс
11 0 0 11 120.94202 301.99997 тм
(\ 240) Tj
/ T1_3 1 Тс
-5.66901 1 тд
(Оповещения по электронной почте) Tj
ET
BT
/ T1_0 1 Тс
10 0 0 10 295,49973 314 тм
(относится к этой статье или журналу.
99997 тм
(\ 240) Tj
/ T1_3 1 Тс
-6.00198 1 тд
(Цитированные статьи) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 141 383,99994 тм
(\ 240) Tj
/ T1_0 1 Тс
34.40392 1 тд
() Tj
0 0 1 рг
-34,40392 0 Тд
(http: //cancerpreventionresearch.aacrjournals.org/content/1/7/577.full#re \
f-list-1) Tj
0 г
0 1.00001 TD
(Эта статья содержит 48 статей, 15 из которых вы можете получить бесплатно по адресу:) Tj
ET
BT
/ T1_0 1 Тс
11 0 0 11 120,94 202 361,99997 тм
(\ 240) Tj
/ T1_3 1 Тс
-6,33498 1 тд
(Цитирование статей) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 141 353,99994 тм
(\ 240) Tj
/ T1_0 1 Тс
35.79392 1 тд
() Tj
0 0 1 рг
-35.79392 0 Тд
(http://cancerpreventionresearch.aacrjournals.org/content/1/7/577.полный # re \
lated-urls) Tj
0 г
Т *
(Эта статья процитирована в 2 статьях, размещенных на HighWire. Перейдите к ar \
ticles at:) Tj
ET
BT
/ T1_2 1 Тс
10 0 0 10 30 333,99997 тм
(\ 240) Tj
0 1 ТД
(\ 240) Tj
ET
30 209 525 125 рэ
0 0 мес.
S
BT
/ T1_0 1 Тс
11 0 0 11 120.94202 301.99997 тм
(\ 240) Tj
/ T1_3 1 Тс
-5.66901 1 тд
(Оповещения по электронной почте) Tj
ET
BT
/ T1_0 1 Тс
10 0 0 10 295,49973 314 тм
(относится к этой статье или журналу. ) Tj
0 0 1 рг
-15.44997 0 Тд
(Подпишитесь, чтобы получать бесплатные уведомления по электронной почте) Tj
ET
BT
0 г
/ T1_0 1 Тс
11 0 0 11 120.94202 268,99994 тм
(\ 240) Tj
/ T1_3 1 Тс
-6.38997 1 тд
(Подписки) Tj
0,556 1,00001 тд
(Отпечатки и) Tj
ET
BT
/ T1_0 1 Тс
10 0 0 10 141 271,99994 тм
(\ 240) Tj
13.46497 1 тд
(.) Tj
0 0 1 рг
-6.85098 0 Тд
(
) Tj
0 0 1 рг
-15.44997 0 Тд
(Подпишитесь, чтобы получать бесплатные уведомления по электронной почте) Tj
ET
BT
0 г
/ T1_0 1 Тс
11 0 0 11 120.94202 268,99994 тм
(\ 240) Tj
/ T1_3 1 Тс
-6.38997 1 тд
(Подписки) Tj
0,556 1,00001 тд
(Отпечатки и) Tj
ET
BT
/ T1_0 1 Тс
10 0 0 10 141 271,99994 тм
(\ 240) Tj
13.46497 1 тд
(.) Tj
0 0 1 рг
-6.85098 0 Тд
( 48564 1.99997 тм
(для исследования рака.) Tj
7,88245 1 тд
(18 июня 2021 г. \ 251 Американская ассоциация 2008 г.) Tj
0 0 1 рг
-19.28495 0 тд
(Cancepreventionresearch.aacrjournals.org) Tj
0 г
-8.11397 0 Td
(Скачано с) Tj
ET конечный поток
эндобдж
140 0 объект
> / Filter / FlateDecode / Height 242 / Length 73940 / Name / X / Subtype / Image / Type / XObject / Width 1539 >> stream
HoXHxQr
48564 1.99997 тм
(для исследования рака.) Tj
7,88245 1 тд
(18 июня 2021 г. \ 251 Американская ассоциация 2008 г.) Tj
0 0 1 рг
-19.28495 0 тд
(Cancepreventionresearch.aacrjournals.org) Tj
0 г
-8.11397 0 Td
(Скачано с) Tj
ET конечный поток
эндобдж
140 0 объект
> / Filter / FlateDecode / Height 242 / Length 73940 / Name / X / Subtype / Image / Type / XObject / Width 1539 >> stream
HoXHxQr