3. Степень числа. Арифметический корень
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯСтепень числаСтепенью числа а с показателем k, где k принадлежит множеству натуральных чисел, называется произведение k множителей, каждый из которых равен а:
Число а называется основанием степени, а число k — показателем степени.
Свойства1. Четная степень отрицательного числа есть число положительное.
2. Нечетная степень отрицательного числа есть число отрицательное.
3. Любая степень положительного числа — положительное число.
4. При возведении нуля в любую натуральную степень получим нуль. Нуль в нулевой степени не определен.
5. При возведении единицы в любую натуральную степень получим единицу.
6. При возведении числа в отрицательную степень заменяем его на частное 1 и этого числа в положительной степени:
7. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остается прежним:
8.
При делении степеней с одинаковыми основаниями показатели степеней вычитаются, а основание остается прежним:
9. При возведении степени в степень показатели степеней перемножаются, а основание остается прежним:
10. Степень произведения равна произведению степеней множителей:
11. Степень частного равна частному степеней делимого и делителя:
Арифметический корень
Арифметическим корнем n-ой степени из положительного действительного числа а называется неотрицательное число b, n-ая степень которого равна а.
Корень 2-ой степени из числа а обозначается:
Свойства1. Корень степени n из числа в степени n равен самому числу, если n нечетно, или модулю числа, если n четно.
2. Корень из произведения чисел равен произведение корней из этих чисел.
3. Корень из частного чисел равен частному корней из этих чисел.
4. Чтобы внести число под знак корня нужно возвести его в степень корня.
УПРАЖНЕНИЯ
1. Выпишите верные равенства:
Решение:
Не подходят:
2. Сравните с единицей числа:
Решение:
3. Вычислите:
Решение:
4. а) Запишите числовое выражение (83 · 85)2 в виде степени с основанием 2.
б) Запишите числовое выражение (94 · 96)3 в виде степени с основанием 3.
Решение:
5. Найдите значения выражения:
Решение:
6.
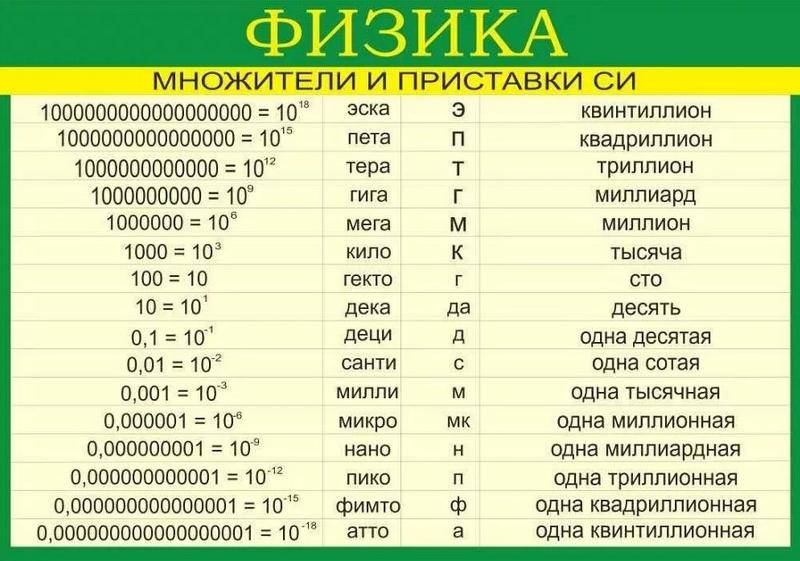Определите знак выражения:
Решение:
Ответ: выражение положительно.
7. Упростите выражение:
Решение:
а)
Ответ: -9
8. Упростите выражение:
Решение:
9. Вычислите:
Решение:
а)
Ответ: 0,01.
10. Упростите выражение:
Решение:
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Укажите два последовательных целых числа, между которыми заключено число:
2. Имеет ли смысл выражение:
3. Найдите значение выражения:
4.
Найдите значения выражения: а) 411 · 4-9; б) 6-5 : 6-3.
5. Выполните действия:
6. Вычислите:
7. Вычислите:
8. Выполните действия:
9. Найдите значение выражения:
10. Упростите выражение:
ПРОВЕРЬТЕ СЕБЯ
Запишите следующие числа как степень 2 i 8 ii 128 iii 1024…
Перейти к
- Целые числа
- Дроби и десятичные дроби
- Рациональное число
- Показатели и силы
- Наборы
- Соотношение и пропорция
- Процент и его применение
- Алгебраические выражения
- Линейные уравнения и неравенства
- Линии и углы
- Треугольники и их свойства
- Конгруэнтность треугольников
- Практическая геометрия
- Симметрия
- Визуализация твердых фигур
- Периметр и площадь
- Обработка данных
Главная > ML Aggarwal Solutions Класс 7 Математика >
Глава 4 — Экспоненты и полномочия > Показатели и степени.
Упражнение 4.
>
Вопрос 7 9{10} Связанные вопросы
Заполните пропуски: (i) В выражении основание = …. И показатель степени = …..(ii) В выражении основание…
Найдите значение следующего: (i) (ii) (iii) (iv) (v) (vi)
Выразите следующее в экспоненциальной форме: (i) 6 x 6 x 6 x 6 x 6 (ii) t x t x t (iii) 2 x 2 x a x …
Упростите следующее (i) 7 x (ii) (iii)
Упростите следующее (i) (ii) (iii) (iv) (v) (vi)
Определите большее число в каждом из следующих: (i) (ii) (iii) (iv)
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Exercises
Exponents and Powers Exercise 4
Chapters
Integers
Fractions and Decimals
Rational Numbers
Exponents and Powers
Sets
Ratio and Proportion
Percentage and Its applications
Algebraic Expressions
Линейные уравнения и неравенства
Линии и углы
Треугольники и их свойства
Конгруэнтность треугольников
Практическая геометрия
Симметрия
Визуализация объемных фигур
Периметр и площадь 900 Обработка данных 3 90
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
Десятичная система, экспоненты и совершенные числа | Бретт Берри | Математические лайфхаки
У каждой системы счисления есть основание.
Это базовая структура, на которой строится система. В предыдущем разделе мы уже видели два примера базовых систем: вавилонскую шестидесятеричную систему и индийско-арабскую десятичную систему.
по основанию системы счисления равно количеству уникальных числовых символов. Чтобы определить основание системы счисления, спросите себя: «
Начнем с десятичной системы.
Десятичная система названа так потому, что в ней 10 уникальных символов. Эти символы, конечно же, 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Поскольку каждое место может занимать только 9, нам нужно увеличить каждую позицию в нашей системе разрядности в множитель. 10.
Наше первое разрядное значение — это разряд единиц или единиц. Мы можем заполнить эту позицию любыми числами от 0 до 9.
Как только мы дойдем до 9, нам нужно начать новую колонку слева.
Когда мы размещаем числа в этой колонке, мы больше не имеем в виду, сколько отдельных единиц у нас есть.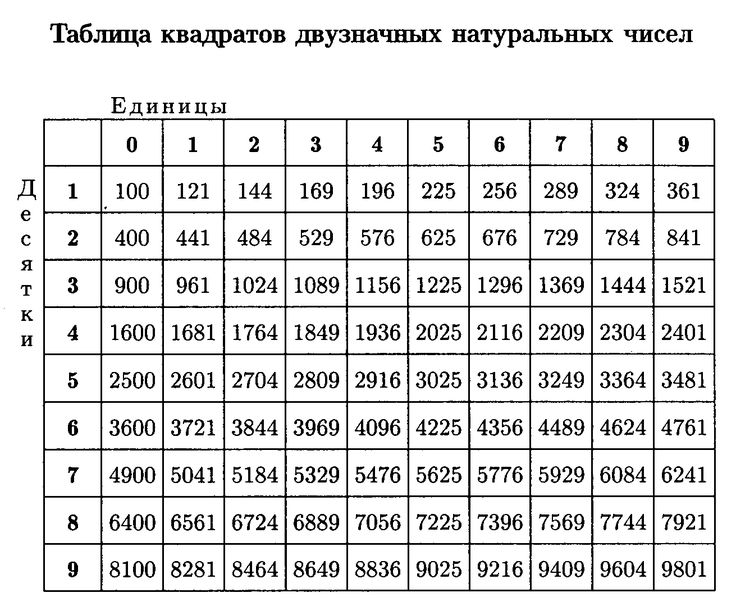
Этот новый столбец показывает, сколько десятков у нас есть. Имея всего два столбца, мы можем посчитать целые числа до 9.9.
Но как только мы туда добираемся, мы снова застреваем. Теперь нам нужен столбец, чтобы выразить, сколько сотен у нас есть.
Добавьте столбец сотен, чтобы выразить все числа до 999.
Как вы уже догадались, нам понадобится столбец для выражения тысяч. Этот процесс может продолжаться столько, сколько нам нужно, добавляя новые столбцы слева, каждый из которых в десять раз больше по значению, чем предыдущий.
Теперь мы можем легко препарировать любое заданное нам число.
Например, предположим, что нам дано число 273. В десятичной системе счисления 273 состоит из 2 сотен, 7 десятков и 3 единиц.
Следовательно, мы можем выразить число 273 в расширенной форме как:
Теперь давайте пофантазируем, используя показатели степени в наших десятичных разложениях. Что такое показатель? Рад, что вы спросили.
Экспоненты — это сокращенная запись для многократного умножения.
Давайте взглянем на наиболее распространенный показатель степени: степень 2 или 90 143 в квадрате 90 144 числа.
- Чему равно число в квадрате ?
- Сколько стоит два в квадрате ?
- Чему равно три в квадрате ?
Видите образец?
Чтобы возвести число в квадрат, возьмите число и умножьте его само на себя. Почему это называется квадратурой? Верный своему названию, мы создаем квадрат с заданным числом сторон.
Например, я буду использовать точки для обозначения длин сторон обычных квадратов.
Хорошо, так что нужно немного воображения, чтобы увидеть площадь. А как насчет два в квадрате?
И три в квадрате:
Четыре, пять и шесть в квадрате:
… и так далее.
Мы наткнулись на еще один математический термин: совершенных квадратных числа . Это набор чисел, которые получаются в результате возведения в квадрат натуральных чисел: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 и т. д.
Угадайте, как поведет себя показатель степени 3?
Я дам вам ответы на первые пять чисел в кубе и вы поймете как я получил ответы.
Подумай об этом. Ты понял?
Число справа получается путем взятия числа слева, называемого основанием , , и умножения его на само трижды .
Как вы уже догадались, это начало другого особого набора чисел, называемого совершенных кубических чисел.
Если бы мы собирали трехмерный куб, используя базовое число в качестве длины стороны, нам потребовалось бы количество точек, эквивалентное числу справа, чтобы построить куб.
(Например, нам потребуется 8 точек, чтобы построить куб со стороной, равной двум, 27 точек, чтобы построить куб со стороной, равной трем, 64 точки, чтобы построить куб со стороной, равной четырем, и так далее.)
Показатель степени представляет количество раз, когда основание умножается само на себя.