Правило разности деления на число: Свойства деления. Деление произведения, суммы и разности на число

Содержание

Свойства деления. Деление произведения, суммы и разности на число

Деление произведения на число
Деление числа на произведение
Деление суммы на число
Деление разности на число
Общие формулы свойств деления

Деление произведения на число

Произведение можно разделить на число двумя способами:

1) Чтобы разделить произведение на какое-нибудь число, можно сначала вычислить значение произведения (выполнить умножение) и полученный результат разделить.

Например, чтобы найти значение выражения:

(12 · 5) : 3,

можно сначала умножить 12 на 5:

12 · 5 = 60

и полученное произведение разделить на 3:

60 : 3 = 20,

значит (12 · 5) : 3 = 60 : 3 = 20.

Если один из сомножителей делится на число, на которое надо разделить произведение, то можно воспользоваться вторым способом нахождения частного от деления произведения на число.

2) Чтобы разделить произведение на какое-нибудь число, можно разделить на это число один любой сомножитель, оставив другие без изменений.

Например, чтобы найти значение выражения:

(8 · 20) : 4,

можно сначала разделить любой из сомножителей (8 или 20) на 4:

8 : 4 = 2

и полученное частное умножить на другой сомножитель:

2 · 20 = 40,

значит (8 · 20) : 4 = (8 : 4) · 20 = 2 · 20 = 40.

Данное выражение можно решить ещё так:

(8 · 20) : 4 = 8 · (20 : 4) = 8 · 5 = 40.

Деление числа на произведение

Число можно разделить на произведение двумя способами:

1) Чтобы разделить какое-нибудь число на произведение, можно сначала вычислить значение произведения (выполнить умножение), а затем разделить число на полученный результат.

Например, чтобы найти значение выражения:

60 : (3 · 2),

можно сначала умножить 3 на 2:

3 · 2 = 6

и разделить 60 на полученный результат:

60 : 6 = 10,

значит 60 : (3 · 2) = 60 : 6 = 10.

Если число, которое нужно разделить на произведение, делится на каждый сомножитель, из которого состоит данное произведение, то можно воспользоваться вторым способом нахождения частного от деления числа на произведение.

2) Чтобы разделить какое-нибудь число на произведение, можно разделить это число на первый сомножитель, полученное частное разделить на второй сомножитель, это частное на третий и т. д.

Например, чтобы найти значение выражения:

120 : (5 · 3),

можно сначала разделить 120 на 5:

120 : 5 = 24,

а теперь, полученное частное 24 разделить на 3:

24 : 3 = 8,

значит 120 : (5 · 3) = (120 : 5) : 3 = 24 : 3 = 8.

Так как от перестановки множителей произведение не изменится, то множители можно поменять местами:

120 : (3 · 5)

и разделить 120 сначала на 3, а затем полученный результат разделить на 5:

120 : (3 · 5) = (120 : 3) : 5 = 40 : 5 = 8.

Получается, что не важно на какой множитель сначала делить число, результат будет одинаковым:

120 : (5 · 3) = (120 : 5) : 3 = 24 : 3 = 8

тоже самое, что и

120 : (5 · 3) = (120 : 3) : 5 = 40 : 5 = 8.

Из данного примера можно сделать вывод, что значение частного не изменится от порядка выполнения действий.

Деление суммы на число

Сумму можно разделить на число двумя способами:

1) Чтобы разделить сумму на какое-нибудь число, можно сначала вычислить значение суммы (выполнить сложение) и полученный результат разделить.

Например, чтобы найти значение выражения:

(15 + 12) : 3,

можно сначала сложить числа 15 и 12:

15 + 12 = 27

и полученную сумму разделить на 3:

27 : 3 = 9,

значит (15 + 12) : 3 = 27 : 3 = 9.

Если все слагаемые в записи суммы делятся на число, на которое надо разделить сумму, то можно воспользоваться вторым способом нахождения частного от деления суммы на число.

2) Чтобы разделить сумму на какое-нибудь число, можно разделить на это число каждое слагаемое отдельно и полученные частные сложить.

Например, чтобы найти значение выражения:

(42 + 28 + 70) : 7,

можно каждое слагаемое разделить на число 7:

42 : 7 = 6, 28 : 7 = 4 и 70 : 7 = 10;

и полученные частные (6, 4 и 10) сложить:

6 + 4 + 10 = 20,

значит (42 + 28 + 70) : 7 = 42 : 7 + 28 : 7 + 70 : 7 = 6 + 4 + 10 = 20.

Деление разности на число

Разность можно разделить на число двумя способами:

1) Чтобы разделить разность на какое-нибудь число, можно сначала вычислить значение разности (выполнить вычитание) и полученный результат разделить.

Например, чтобы найти значение выражения:

(24 — 8) : 2,

можно сначала вычесть из 24 число 8:

24 — 8 = 16,

и полученную разность разделить на 2:

16 : 2 = 8,

значит (24 — 8) : 2 = 16 : 2 = 8.

Если и уменьшаемое и вычитаемое в записи разности делятся на число, на которое надо разделить разность, то можно воспользоваться вторым способом нахождения частного от деления разности на число.

2) Чтобы разделить разность на какое-нибудь число, можно разделить на это число отдельно уменьшаемое и вычитаемое, а потом из первого частного вычесть второе.

Например, чтобы найти значение выражения:

(42 — 28) : 7,

можно отдельно уменьшаемое и вычитаемое разделить на число 7:

42 : 7 = 6, 28 : 7 = 4

и найти разность полученных частных:

6 — 4 = 2,

значит (42 — 28) : 7 = 42 : 7 — 28 : 7 = 6 — 4 = 2.

Общие формулы свойств деления

Все свойства деления можно представить в виде формул:

Распределительные свойства
(a + b) : c = a : c + b : c
(a — b) : c = a : c — b : c
(a · b) : c = (a : c) · b = (b : c) · a
a : (b · c) = (a : b) : c = (a : c) : b
Действия с единицей и нулём
a : 1 = a
a : a = 1
0 : a = 0 (a ≠ 0)
На нуль делить нельзя

Деление разности на число | План-конспект урока по математике (3 класс):

ДЕЛЕНИЕ РАЗНОСТИ НА ЧИСЛО

Цель: организация усвоения учащимися распределительного закона деления относительно вычитания; применение правила деления разности на число; совершенствовать вычислительные навыки.

Планируемые результаты:

Предметные: формирование УУД: поиск путей рациональных вычислений, самоконтроль; развивать умение самостоятельно выделять и формулировать познавательную цель; строить речевое высказывание в устной форме; учить ставить новую учебную задачу, в сотрудничестве с учителем; принимать и сохранять учебную задачу;

Личностные: формировать внутреннюю позицию школьника на уроке положительного отношения к школе; учебно–познавательный интерес к новому материалу; способность к самооценке на основе критерия успешности учебной деятельности.

Тип урока: изучение нового материала

Ход урока

Организационный момент

Здравствуйте, ребята.

Долгожданный дан звонок – начинается урок.
Все друг к другу повернёмся – и тихонько улыбнёмся.

Проверка домашней работы

Т.стр.32 №70

3. Устный счет.

— Реши устно (дети по одному выходят к доске и записывают ответ)

25:5=5 12:2=6 28:7=4

8:2=4 45:5=9 40:5=8

81:9=9 32:8=4 15:3=5

14:2=7 72:8=9 9:3=3

54:6=9 63:9=7 50:10=5

49:7=6 18:6=3

48:8=6 35:7=5

10:5=2

2) Сколько треугольников на чертеже? (11)

4. Сообщение темы урока.

Какое выражение лишнее?

(12 + 4) : 2 (14 + 21) :7

(45 + 30) : 5 (30 – 15) : 3

Как вы думаете, как будет звучать наша новая тема? («Деление разности на число»).

5. Работа по теме урока.

1. Задание 122.

– Вычислите значения данных выражений (решают у доски по одному)

(35 – 25) : 5 = 2 56 : 7 – 14 : 7 = 6

(56 – 14) : 7 = 6 35 : 5 – 25 : 5 = 2

(64 – 40) : 8 = 3 64 : 8 – 40 : 8 = 3

– Составьте из них три верных равенства.

(35 – 25) : 8 = 35 : 5 – 25 : 5

(64 – 40) : 8 = 64 : 8 – 40 : 8

(56 – 14) : 7 = 56 : 7 – 14 : 7

– Чем похожи и чем отличаются выражения, которые образуют верное равенство?

– В каждом равенстве подчеркните те выражения, в которых записано деление разности на число.

— Неподчеркнутые выражения можно рассматривать как разность двух частных, каждое из которых получено в результате деления разности на число.

2. Задание 123.

– Чем похожи и чем отличаются данные равенства?

(54 + 18) : 9 = 54 : 9 + 18 : 9

(54 – 18) : 9 = 54 : 9 – 18 : 9

– Докажите, что они являются верными.

– Какое правило можно привести для обоснования первого равенства? (Правило деления суммы на число.)

– Сформулируйте правило деления разности на число. (Если уменьшаемое и вычитаемое можно разделить на данное число, то, выполнив это деление и вычтя из первого полученного значения частного второй, мы найдем результат деления данной разности на это число.)

3. Задание 124.

– Используя только числа 45, 27 и 9, составьте верное равенство, которое подтверждало бы правило деления разности на число.

(45 – 27) : 9 = 45 : 9 – 27 : 9.

4. Задание 125. ( выполняют самостоятельно, затем меняемся тетрадями и проверяем)

– Воспользуйтесь правилом деления разности на число для вычисления значения данных выражений.

(80 – 8) : 8 = 80 : 8 – 8 : 8 = 10 – 1 = 9

(50 – 5) : 5 = 50 : 5 – 5 : 5 = 10 – 1 = 9

(90 – 18): 9 = 90 : 9 – 18 – 9 = 10 – 2 = 8

(60 – 12) : 6 = 60 : 6 – 12 : 6 = 10 – 2 = 8

(70 – 21) : 7 = 70 : 7 – 21 : 7 = 10 – 3 = 7

– 32) : 8 = 80 : 8 – 32 : 8 = 10 – 4 = 6

6. Физкультминутка

Вновь у нас физкультминутка,

Наклонились, ну-ка, ну-ка!

Распрямились, потянулись,

А теперь назад прогнулись.

Голова устала тоже.

Так давайте ей поможем!

Вправо-влево, раз и два

Думай, думай, голова (вращение головой)

Хоть зарядка хороша,

Отдохнули мы слегка.

7. Продолжение работы по теме урока.

1. Задание 127.

– Используя данную запись, объясните, как вычислили значение частного.

114 : 6 = (120 – 6) : 6 = 120 : 6 – 6 : 6 = (60 + 60) : 6 – 6 : 6 = (60 : 6 + 60 : 6) – 6 : 6 = (10 + 10) – 1 = 19

– Вычислите таким же способом значение частного 133 : 7.

133 : 7 = (140 – 7) : 7 = 140 : 7 – 7 : 7 = (70 + 70) : 7 – 7 : 7 = (70 : 7 + 70 : 7) – 7 : 7 = (10 + 10) – 1 = 19

2. Задание 128. (таблицу заполняем на доске)

– Прочитайте задачу.

– Что известно?

– Что требуется узнать?

– Решите данную задачу двумя способами. Каждый вариант решения запишите в виде одного выражения. В каждом случае вычислите и запишите ответ.

Решение:

I способ.

(42 – 24) : 6 = 18 : 6 = 3 (гв.) – белых гвоздик в одном букете.

II способ.

42 : 6 – 24 : 6 = 7 – 4 = 3 (гв.) – белых гвоздик в одном букете.

Ответ: 3 гвоздики.

3. Задание 129.

– Сформулируйте задачу, решением которой является выражение (56 – 32) : 8.

Задача. Было 56 кг яблок. Из них 32 кг – красных яблок, остальные – зеленые. Все яблоки разложили в 8 одинаковых ящиков поровну.

Сколько килограммов зеленых яблок было в одном ящике?

– Вычислите и запишите решение этой задачи.

Решение:

(56 – 32) : 8 = 24 : 8 = 3 (кг) – зеленых яблок.

Ответ: 3 кг.

4. Задание 130.

– Сформулируйте задачу, решением которой является выражение 56 : 8 – 32 : 8.

– Можно ли здесь использовать задачу из задания 129? (Можно.)

– Докажите.

(56 – 32) : 8 = 56 : 8 – 32 : 8.

8. Итог урока.

– Что нового узнали на уроке?

– Как выполнить деление разности на число?

Домашнее задание. № 126.

Оценки.

Карточки:(Работают в парах, затем меняются карточками с другой парой и проверяют)

1. Сторона квадрата равна 8 см. Чему равен его периметр?

Решение:

8 • 4 = 32 (см) – периметр

Ответ: 32 см.

Периметр квадрата 28 см. Чему равна его сторона?

Решение: 28 : 4 = 7 (см)

Ответ: 7 см.

3. Длина прямоугольника 14 см. Чему равна ширина, если периметр 44 см? Решение:

1)44 : 2 = 22 (см) – половина периметра

2)22 – 14 = 8 (см) – ширина

Ответ: 8 см.

4)В вазе лежало 15 яблок и 10 мандаринов. Эти фрукты раздали 5 детям поровну каждому. Сколько всего фруктов получил каждый ребенок?

Решение: (15+10) : 5= 15 : 5 +10 : 5= 3+2= 5 (по фр.)

Ответ: по 5 фруктов.

5) Разность 140 и 35 разделить на 7.

Решение: (140 – 35) : 7 =140 : 7 – 35 : 7 = 20 – 5 = 15

Правила делимости (тесты)

Легко проверить, можно ли точно разделить одно число на другое

делится на

«Делится на» означает «при делении одного числа на другое получается целое число»

Примеры:

14 — делится на 7, потому что 14 ÷ 7 = 2 ровно

15 IS Не делится на 7, потому что 15 ÷ 7 = 2 1 7 (результат не целое число)

0 равно кратному 7, потому что 0 ÷ 7 = 0 ровно (0 — целое число)

«делится на» и «можно точно разделить на» означают одно и то же

Правила делимости

Эти правила позволяют проверить, делится ли одно число на другое, без необходимости выполнять слишком много вычислений!

Пример: 723 делится на 3?

Можно попробовать разделить 723 на 3

Или использовать правило «3»: 7+2+3=12, а 12 ÷ 3 = 4 ровно Да

Примечание. Ноль делится на любым числом (кроме самого себя), поэтому на все эти тесты ставится «да».

Любое целое число (не дробь) делится на 1

Последняя цифра четная (0,2,4,6,8)

12 8 Да

12 9 Нет

Сумма цифр делится на 3

381 (3+8+1=12 и 12÷3 = 4) Да

217 (2+1+7=10 и 10÷3 = 3 ¹ / ₃ ) Нет

При необходимости это правило можно повторить:

99996 (9+9+9+9+6 = 42, тогда 4+2=6) Да

Последние 2 цифры делится на 4

13 12 IS (12 ÷ 4 = 3) Да

70 19 не (19 ÷ 4 = 4

3 /₄ ) №

Мы также можем вычесть 20 столько раз, сколько захотим перед проверкой:

68: вычесть 3 лота из 20, и мы получим 8 Да

102: вычесть 5 лотов из 20, и мы получим 2 Нет

Другой Метод состоит в том, чтобы дважды разделить число пополам и посмотреть, останется ли результат целым числом:

124/2 = 62, 62/2 = 31, а 31 — целое число. Да

30/2 = 15, 15/2 = 7,5, что не является целым числом. №

Последняя цифра 0 или 5

17 5 Да

80 9 Нет

Является четным и делится на 3 (выполняет как правило 2, так и правило 3 выше)

114 (четное число, и 1+1+4=6 и 6÷3 = 2) Да

308 (четно, но 3+0+8=11 и 11÷3 = 3 ²

/ ₃ ) Нет

Удвойте последнюю цифру и вычтите ее из числа, образованного другими цифрами. Результат должен делиться на 7. (Мы можем снова применить это правило к этому ответу)

672 (Двойная 2 равна 4, 67−4=63 и 63÷7=9) Да

105 (Двойная 5 равна 10, 10−10=0 и 0 делится на 7) Да

905 (Двойная 5 равна 10, 90−10=80 и 80÷7=11 ³ / ₇ ) №

Последние три цифры делятся на 8

109 816 (816 ÷ 8 = 102).0002 Быстрая проверка состоит в том, чтобы разделить три раза пополам, и результат все равно будет целым числом:

816/2 = 408, 408/2 = 204, 204/2 = 102 Да

302/2 = 151, 151/ 2 = 75,5 Нет

Сумма цифр делится на 9

(Примечание. При необходимости это правило можно повторить)

1629 (1+6+2+9=18 и снова 1+8=9) Да

2013 (2+0+1+3=6) Нет

Номер заканчивается на 0

22 0 Да

22 1 Нет

Сложение и вычитание цифр в чередующемся порядке (добавление цифры, вычитание следующей цифры, добавление следующей цифры и т. д.). Затем проверьте, делится ли этот ответ на 11.

1 3 6 4 (+1−3+6−4 = 0 ) Да

90 1 1+3 = 11 ) Да

3 7 2 9 (+3−7+2−9 = −11 ) Да

9 8 7 (+9−8+7 = 8 ) Нет

4

Число делится на 3 и 4 (он проходит как правило 3, так и правило 4 выше)

648
( По 3? 6+4+8=18 и 18÷3=6 Да)
(По 4? 48÷4=12 Да)
Оба проходят, поэтому Да

520002
( На 3? 5+2+4=11, 11÷3= 3 ² / ₃ Нет)
(Не нужно проверять по 4) Нет
И многое другое! Существуют не только тесты на делимость для больших чисел, но и другие тесты для показанных нами чисел.
Факторы могут быть полезными
Факторы — это числа, которые вы умножаете, чтобы получить другое число:
Это может быть полезно, потому что:
Когда одно число делится на другое число…
… тогда это также делится на каждый из множителей этого числа.

Пример: если число делится на 6, оно также делится на 2 и 3
Пример: если число делится на 12, оно также делится на 2, 3, 4 и 6
Еще одно правило для 11
Вычесть последнюю цифру из числа, состоящего из остальных цифр.
Если это число делится на 11, то и исходное число тоже делится.

При необходимости можно повторить,
Пример: 286
28 − 6 равно 22, где равно , кратному 11, поэтому 286 делится на 11
Пример: 14641
1464 − 1 равно 1463
146 − 3 равно 143
14 − 3 равно 11, где равно , которое делится на 11, поэтому 14641 делится на 11

1625, 1626, 1627, 1628, 2689, 3599, 3600, 3601, 3602, 5007
Отдел ÷ | Основы арифметики
На этой странице рассказывается об основах Подразделения (÷) .
См. другие наши арифметические страницы для обсуждения и примеров: сложение ( + ), вычитание (-) и умножение ( × ).
Деление
Обычный письменный символ деления (÷). В электронных таблицах и других компьютерных приложениях используется символ «/» (косая черта).
Деление — это противоположность умножения в математике.
Деление часто считается самой сложной из четырех основных арифметических функций. На этой странице объясняется, как выполнять вычисления деления. Как только мы хорошо разберемся в методе и правилах, мы сможем использовать калькулятор для более сложных вычислений, не делая ошибок.
Разделение позволяет нам разделить или «поделиться» числами, чтобы найти ответ. Например, давайте подумаем, как найти ответ на 10 ÷ 2 (десять разделить на два). Это то же самое, что «делить» 10 конфет между двумя детьми. У обоих детей должно получиться одинаковое количество конфет. В этом примере ответ равен 5.
Некоторые краткие правила деления:
Когда вы делите 0 на другое число, ответ всегда равен 0. Например: 0 ÷ 2 = 0. То есть 0 конфет делятся поровну. среди 2 детей — каждому ребенку по 0 конфет.
Когда вы делите число на 0, вы вообще не делите (это серьезная проблема в математике). 2 ÷ 0 невозможно. У вас есть 2 конфеты, но нет детей, чтобы разделить их между собой. На 0 делить нельзя.
При делении на 1 ответ совпадает с числом, которое вы делили. 2 ÷ 1 = 2. Две конфеты разделить на одного ребенка.

При делении на 2 число уменьшается пополам. 2 ÷ 2 = 1.
Любое число, деленное на одно и то же число, равно 1. 20 ÷ 20 = 1. Двадцать конфет разделить на двадцать детей — каждый ребенок получает по одной конфете.
Числа должны быть разделены в правильном порядке. 10 ÷ 2 = 5, тогда как 2 ÷ 10 = 0,2. Десять конфет, разделенных на двоих детей, сильно отличаются от 2 конфет, разделенных на 10 детей.
Все дроби, такие как ½, ¼ и ¾, являются суммами деления. ½ равно 1 ÷ 2. Одна конфета делится на двоих детей. См. нашу страницу Дроби для получения дополнительной информации.
Множественные вычитания
Точно так же, как умножение — это быстрый способ вычисления множественных сложений, деление — это быстрый способ выполнения множественных вычитаний.

Например:
Если у Джона в машине 10 галлонов топлива, и он использует 2 галлона в день, сколько дней до того, как у него закончится топливо?
Мы можем решить эту задачу, выполнив серию вычитаний или посчитав в обратном порядке с шагом 2.
В день 1 Джон начинается с 10 галлонов и заканчивается 8 галлонов. 10 — 2 = 8
В день 2 Джон начинает с 8 галлонов и заканчивает 6 галлонов. 8 — 2 = 6
В день 3 Джон начинает с 6 галлонов и заканчивает 4 галлонов. 6 — 2 = 4
В день 4 Джон начинает с 4 галлонов и заканчивает 2 галлонов. 4 — 2 = 2
В день 5 Джон начинает с 2 галлонов и заканчивает 0 галлонов. 2 — 2 = 0
У Джона закончилось топливо на 5-й день.
Более быстрый способ выполнить это вычисление — разделить 10 на 2. То есть, сколько раз 2 делится на 10 или сколько партий по два галлона содержится в десять галлонов? 10 ÷ 2 = 5.
Таблица умножения (см. умножение) может помочь нам найти ответ на простые вычисления деления.
В приведенном выше примере нам нужно было вычислить 10 ÷ 2 . Для этого с помощью таблицы умножения найдите столбец для 2 (красный заштрихованный заголовок). Двигайтесь вниз по столбцу, пока не найдете нужный номер: 10 .
Переместитесь по строке влево, чтобы увидеть ответ (красный заштрихованный заголовок) 5 .
Таблица умножения
× 1 2 3 4 5 6 7 8 9 10
1 1 2 3 4 5 6 7 8 9 10
2 2 4 6 8 10 12 14 16 18 20
3 3 6 9 12 15 18 21 24 27 30
4 4 8 12 16 20 24 28 32 36 40
5 5 10 15 20 25 30 35 40 45 50
6 6 12 18 24 30 36 42 48 54 60
7 7 14 21 28 35 42 49 56 63 70
8 8 16 24 32 40 48 56 64 72 80
9 9 18 27 36 45 54 63 72 81 90
10 10 20 30 40 50 60 70 80 90 100
Мы можем выполнить другие простые вычисления деления, используя тот же метод.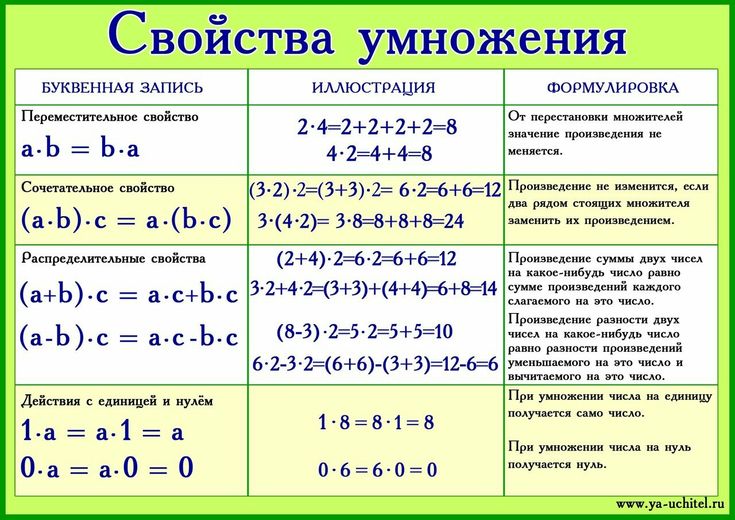 56 ÷ 8 = 7 например. Найдите 7 в верхней строке, посмотрите вниз по столбцу, пока не найдете 56 , затем найдите соответствующий номер строки, 8 .
Если возможно, вы должны попытаться запомнить приведенную выше таблицу умножения, потому что она значительно ускоряет выполнение простых вычислений на умножение и деление.
Деление больших чисел
Вы можете использовать калькулятор для выполнения вычислений деления, особенно когда вы делите большие числа, которые труднее вычислить в уме. Однако важно понимать, как выполнять вычисления деления вручную. Это полезно, когда у вас нет калькулятора под рукой, но также необходимо, чтобы убедиться, что вы правильно используете калькулятор и не делаете ошибок. Деление может показаться пугающим, но на самом деле, как и в большинстве арифметических операций, оно логично.
Как и со всей математикой, проще всего это понять, если мы рассмотрим пример:
Машине Дейва нужны новые шины. Ему нужно заменить все четыре шины на машине плюс запаску.
Дэйв получил предложение от местного гаража на 480 фунтов стерлингов, включая шины, установку и утилизацию старых шин. Сколько стоит каждая шина?
Задача, которую нам нужно вычислить, это 480 ÷ 5 . Это то же самое, что сказать, сколько раз 5 будет входить в 480?
Условно запишем так:
5 4 8 0
Работаем слева направо в логической системе.
Начнем с деления 4 на 5 и сразу наткнемся на проблему. 4 не делится на 5, чтобы получить целое число, так как 5 больше 4.
Язык, который мы используем в математике, может сбивать с толку. Другой способ взглянуть на это — спросить: «Сколько раз 5 входит в 4?».
Мы знаем, что 2 дважды входит в число 4 (4 ÷ 2 = 2), и мы знаем, что 1 входит в число 4 четыре раза (4 ÷ 1 = 4), но 5 не входит в число 4, потому что 5 больше 4.
Число, на которое мы делим (в данном случае 5), должно входить в число, на которое мы делим (в данном случае 4), целое число раз. Как вы увидите, это не обязательно должно быть точное целое число.
Так как 5 не входит в 4, мы ставим 0 в первую колонку (сотни). Для получения справки о столбцах сотен, десятков и единиц см. нашу страницу о числах .
Сотни Десятки Единицы
0
5 4 8 0
Далее мы движемся вправо, чтобы включить столбец десятков. Теперь мы можем увидеть, сколько раз 5 входит в число 48.
5 входит в число 48, поскольку 48 больше 5. Однако нам нужно выяснить, сколько раз оно входит в число 48.
Если мы обратимся к нашей таблице умножения, то увидим, что 9 × 5 = 45 и 10 × 5 = 50 .
48 число, которое мы ищем, находится между этими двумя значениями. Помните, нас интересует целое количество раз , которое 5 входит в 48. Десять раз — это слишком много.
Мы видим, что 5 входит в число 48 целое число (9) раз, но не точно, с оставшимися 3.
9 × 5 = 45
48 – 45 = 3
Теперь мы можем сказать, что 5 входит в число 48 девять раз, но с остатком 3. нашли из числа, на которое мы делим: 48 — 45 = 3 .
Таким образом, 5 × 9 = 45, + 3, чтобы получить 48.
Мы можем ввести 9 в столбце десятков в качестве ответа для второй части вычисления и поставить наш остаток перед нашим последним числом в единицах измерения. столбец. Наше последнее число становится 30.
Сотни Десятки Единицы
0 9
5 4 8 30
Теперь разделим 30 на 5 (или узнаем, сколько раз 5 входит в 30). Используя нашу таблицу умножения, мы видим, что ответ равен ровно 6 без остатка. 5 × 6 = 30. Мы пишем 6 в столбце единиц нашего ответа.
Сотни Десятки Единицы
0 9 6
5 4 8 30
Поскольку остатка нет, мы закончили расчет и получили ответ 96 .
Новые шины Дейва будут стоить £96 каждая. 480 ÷ 5 = 96 и 96 × 5 = 480 .
Раздел рецептов
Наш последний пример разделения основан на рецепте. Часто при приготовлении пищи рецепты сообщают вам, сколько еды они собираются приготовить, например, достаточно, чтобы накормить 6 человек.
Ингредиенты, указанные ниже, необходимы для приготовления 24 волшебных тортов, однако нам нужно сделать только 8 волшебных тортов. Мы немного изменили ингредиенты для этого примера (оригинальный рецепт: BBC Food).
Первое, что нам нужно установить, это сколько восьмерок в числе 24. Воспользуйтесь таблицей умножения выше или своей памятью. 3 × 8 = 24 — если мы разделим 24 на 8, мы получим 3. Поэтому нам нужно разделить каждый ингредиент ниже на 3, чтобы получить нужное количество смеси для приготовления 8 сказочных пирожных.
Ингредиенты
120 г сливочного масла, размягченного при комнатной температуре
120 г сахарной пудры
3 куриных яйца, слегка взбитых
1 чайная ложка ванильного экстракта
120 г самоподнимающейся муки
1-2 столовые ложки молока
Количество масла, сахара и муки одинаковое, 120г. Следовательно, необходимо вычислить 120 ÷ 3 только один раз, так как ответ будет одинаковым для этих трех ингредиентов.
3 1 2 0
Как и раньше, мы начинаем с левого столбца (сотни) и делим 1 на 3. Однако 3 ÷ 1 не идет, так как 3 больше 1. Далее мы смотрим, сколько раз 3 входит в 12. Используя таблицу умножения, если нужно, мы можем увидеть, что 3 входит в число 12 ровно 4 раза по без остатка.
0 4 0
3 1 2 0
120 г ÷ 3 равно 40 г. Теперь мы знаем, что нам понадобится 40 г сливочного масла, сахара и муки.
В исходном рецепте указано 3 яйца, и мы снова делим на 3. Таким образом, 3 ÷ 3 = 1, значит, нужно одно яйцо.
Далее по рецепту требуется 1 чайная ложка ванильного экстракта. Нам нужно разделить одну чайную ложку на 3. Мы знаем, что деление можно записать в виде дроби, поэтому 1 ÷ 3 — это то же самое, что ⅓ (одна треть). Вам понадобится ⅓ чайной ложки ванильного экстракта, хотя на самом деле может быть сложно точно отмерить ⅓ чайной ложки!
Оценка может быть полезна, и единицы измерения можно изменить!
Мы можем посмотреть на это по-другому, если мы знаем, что одна чайная ложка равна 5 мл или 5 миллилитрам. (Если вам нужна помощь с единицами измерения, см. нашу страницу Системы измерения .) Если мы хотим быть более точными, мы можем попробовать разделить 5 мл на 3. 3 входит в 5 один раз (3) с 2 в остатке. 2 ÷ 3 равно ⅔, поэтому 5 мл, разделенные на 3, дают нам 1⅔ мл, что в десятичных дробях равно 1,666 мл. Мы можем использовать наши навыки оценки и сказать, что одна чайная ложка, разделенная на три, чуть больше, чем полтора мл. Если у вас на кухне есть несколько таких крошечных мерных ложек, вы можете быть очень точны!
Мы можем оценить ответ, чтобы убедиться, что мы правы. Три партии по 1,5 мл дают нам 4,5 мл. Таким образом, три партии «чуть больше 1,5 мл» дают нам около 5 мл. Рецепты редко являются точной наукой, поэтому небольшая оценка может быть забавой и хорошей практикой для нашей ментальной арифметики.
Далее по рецепту требуется 1–2 ст.л. молока. Это от 1 до 2 столовых ложек молока. У нас нет определенного количества, и то, сколько молока вы добавите, будет зависеть от консистенции вашей смеси.
No related posts.