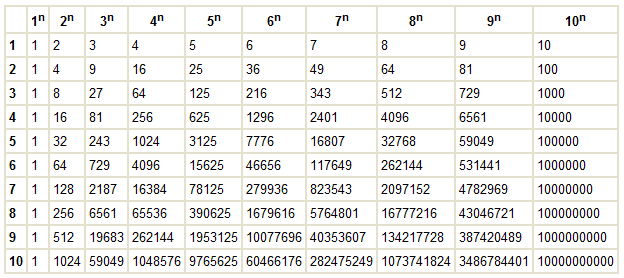
Что дает число в нулевой степени: Степень с показателем 0 — урок. Алгебра, 7 класс.

Содержание

Робокуб с балансиром и маховиком удержался на единственной точке опоры

Швейцарские инженеры разработали новую версию роботизированного куба Cubli, теперь он может балансировать на одной точке опоры, используя пассивный балансир и всего один маховик. О том, как это работает, создатели рассказали журналу IEEE Spectrum.

В робототехнике существует множество конструкций, которые вдохновлены животным миром и способны сохранять баланс. Например, человекоподобный робот Atlas, который умеет бегать, делать обратное сальто и заниматься паркуром и вставать на руки или LOLA, который помогает себе руками для стабильной ходьбы по сложному рельефу.

Однако простые роботы, которые имеют нестабильное строение и минимальное число степеней свободы, тоже могут сохранять равновесие. Нередко в таких устройствах используются маховики. Например, мы рассказывали о роботе с симметричной нестабильной конструкцией и двумя колесами-маховиками: на одном он ездит, а другое использует для поддержания баланса. Еще один пример — самосборные робокубы, которые могут не только удерживать равновесие, но и самостоятельно передвигаться.

Подобными разработками занимаются инженеры Института динамических систем и управления Швейцарской высшей технической школы Цюриха. Сначала они создали роботизированную скульптуру The Balancing Cube, которая могла балансировать на любом из своих краев. Она состояла из не зависимых друг от друга модулей и работала за счет обмена информацией между ними. Затем представили Cubli, который умел не только балансировать, в том числе, на наклонной плоскости, но и перемещаться в заданном направлении. Внутри него было три маховика, необходимые скорости вращения которых рассчитывались автоматически исходя из положения куба в пространстве.

Теперь команда инженеров из того же института под руководством Маттиаса Хофера (Matthias Hofer) решила пойти дальше. Они создали новую версию Cubli, который, как и предшественник, может балансировать на одной точке. Однако для этого использует только один маховик — для выравнивания и по тангажу (по поперечной оси), и по крену (по продольной оси). Как и в случае с предшественником, инерционные датчики с его корпуса подают информацию о положении куба в пространстве на электрический мотор, который регулирует скорость вращения маховика. Реактивный момент действует на корпус конструкции и стабилизирует систему. Однако у нового робота две степени свободы (вращения вокруг вертикальной оси не происходит из-за трения) и всего один маховик. Поэтому баланс он сохраняет за счет разницы моментов инерции.

Для этого вдоль продольной оси корпуса нового Cubli разместили балансир (перекладину с утяжелителями). Такая конструкция сделала разницу в моменте инерции между двумя осями максимальной и увеличила его по оси крена. Маховик необходимо вращать быстрее, чтобы компенсировать тангаж, и медленнее — крен. Микроконтроллер куба использует это свойство и стабилизирует оба направления одновременно, рассчитывая необходимый для электрического мотора крутящий момент для поддержания баланса.

Эксперименты показали, что система работает — при выводе куба из равновесия он восстанавливается. Однако на видео-демонстрации он компенсировал только совсем слабое касание.

Как отмечают инженеры, у разработки есть потенциал для применения в космосе, а именно в управлении ориентацией спутников. Многие из них удерживаются в правильном положении именно за счет маховиков. Так, Cubli может стать примером управления спутниками вытянутой формы в случае их множественного отказа.

Ранее мы рассказывали о роботе, который также имеет конструкцию обратного маятника и способен передвигаться в любом направлении. Однако для сохранения баланса он использует другую технологию — две пары колес Илона, которые позволяю ему двигаться в любом направлении без поворота колес.

Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.

Нефть снова в районе $80.

Что говорит в пользу роста

Итоги предыдущих торгов

Февральские фьючерсы на нефть Brent: $79,04 (-2,67%)
Январские фьючерсы на нефть WTI: $74,29 (-2,39%)
Спред между актуальными контрактами на марки Brent и WTI составляет около $4,7 в пользу Brent.

В фокусе

В пятницу цены на нефть продолжали корректироваться и закрыли торги ниже $80 за баррель. Снижение сдерживало заявление Минэнерго США о начале восполнения запасов нефти в SPR. Между тем на фоне постепенного снятия антиковидных ограничений в Китае растет число заболеваний, создавая риски для новой политики смягчения. Буровая активность в США продолжает стагнировать, а в Канаде начался сезонный спад.

Фьючерсы на Brent сегодня с утра пытаются вернуться выше $80 за баррель. После двух дней снижения коррекционный потенциал выглядит реализованным, не исключается возвращение к росту. Формально котировки находятся в нисходящем тренде, так что до момента преодоления $84 за баррель рост может быть неустойчивым и возможны новые волны распродаж.

Покупка нефти в SPR

Минэнерго США объявило о покупке пробной партии в 3 млн барр. по новой схеме с использованием контрактов с фиксированной ценой. Контракты будут заключены не позднее 13 января, фактические поставки планируются в феврале 2023 г.

Это первая покупка после рекордного выпуска из SPR, который с начала года составил 211 млн барр. Администрация Байдена реализовала масштабные продажи резервов в попытках сдержать рост цен на топливо и сбалансировать рынок. В отдельные недели продажи из SPR превышали 1 млн б/с. В результате уровень стратегических запасов упал до минимума с 1984 г.

Партия 3 млн барр. некритична для рыночного баланса, но сам по себе факт покупки дает сигнал в пользу роста цен. Оператор SPR из крупного продавца превращается в крупного покупателя.

Покупки в SPR выглядят несколько преждевременными. Ранее Байден заявлял, что восполнение запасов планируется при цене $67–72 за баррель WTI. Котировки опустились в этот коридор в четверг 8 декабря, но уже в понедельник 12 декабря вернулись выше. Вероятно, власти не рассчитывают на дальнейшее устойчивое снижение цен и готовы покупать уже сейчас.

Всплеск инфекции в Китае

Смягчение карантинов обернулось всплеском инфекции в стране. По словам главного эпидемиолога страны, в ближайшие три месяца стране предстоит пройти через три волны заболеваемости, первая из которых уже началась. Пиковые показатели ожидаются во время и после празднования китайского Нового года с 21 по 27 января.

Рост заболеваемости ухудшает перспективы отмены ограничений и полноценного восстановления деловой активности. Например, на этой неделе власти многих крупных городов уже заявили о запуске или продлении дистанционного режима в школах. Однако смягчение политики «нулевой терпимости» уже назрело и, скорее всего, вопрос только в сроках реализации.

Ситуация с COVID-19 в Китае и реакция на нее местных властей остается важным фактором неопределенности в части мирового спроса на нефть. Являясь вторым по величине потребителем нефти в мире с долей около 14%, Китай в значительной степени влияет на баланс на мировых площадках. Чем меньше ограничений в Китае, тем выше спрос на топливо и тем выше поддержка для нефтяных цен.

Буровая активность в США

По подсчетам Baker Hughes, число активных буровых нефтяных установок в США на прошлой неделе сократилось на 5 уст., до 620 уст. Весь прирост с начала ноября обнулился. В Канаде число активных установок по нефти также снизилось на 7 уст., до 124 уст. в рамках сезонного снижения активности перед рождественскими праздниками.

Рост бурения на американском континенте остается сдержанным, что не дает поводов для существенного пересмотра прогнозов по добыче на 2023 г. По оценке EIA, добыча в США вырастет до 12,6 млн б/с к декабрю 2023 г. и в среднем за год составит 12,34 млн б/с.

Сегодня с утра фьючерсы на Brent растут на 1% и торгуются в районе $79,9 за баррель.

БКС Мир инвестиций

Почему ноль, возведенный в нулевую степень, определяется как единица « Математическая наука и технологии

Обновлено! 5 февраля 2017 г. 0=1, по причинам, выходящим за рамки согласованности с биномиальной теоремой (аргумент Кнута).

Контекст дебатов: непрерывная математика

Три варианта значения появляются потому, что , как функция двух непрерывных переменных, имеет разрыв в точке (0,0) и принимает три разных значения в зависимости от направления приближения к разрыву:

Зафиксировав y=0, для всех имеем . (Доказательство: каждое утверждение выполняется для всех ). Действительно, как , приближаясь слева или справа, при y=0. (Это была причина Эйлера.)
Зафиксировав x=0, имеем для . (Когда y < 0, у нас есть деление на ноль, которое не определено в действительных числах и в расширенных действительных числах). Беря пределы, как , приближаясь только сверху, при x=0.
Фиксируя x=0, мы имеем неопределенное значение, когда y < 0 из-за деления на ноль.

Обратите внимание, что разрыв не является простым (точечным) разрывом, а скорее полюсным разрывом из-за подхода снизу. (Упражнение: что происходит при подходе к началу координат под углом 45 градусов?)

Принципы принятия решения в математике: расширение и непротиворечивость

В математике, когда существует более одного выбора, решение обычно принимается путем расширения существующего прецедента поддерживать согласованность с уже накопленными и принятыми доказательствами.

Элементарным примером является то, как обычное умножение распространяется с двух положительных чисел на положительное и отрицательное число, а затем на два отрицательных числа, т. е. .

«Минус умножить на минус — это плюс.
Причину этого нам не нужно обсуждать!
— Б.Х. Оден

Эмпирически умножение двух положительных чисел имеет четко определенный, осязаемый смысл как многократное сложение. Это значение сохраняется, когда одно из чисел отрицательное. Но когда оба отрицательны, эмпирическое значение терпит неудачу.

Для математика объявление чего-то неопределенным (выдача ошибки) означает потерю эффективности, потому что теперь каждый экземпляр должен проверяться на случай неопределенности, и это нужно рассматривать отдельно. Если бы можно было найти определение, которое остается совместимым со всеми другими эмпирически полученными правилами, и если это определение означает, что вычисления могут продолжаться независимо от решения, то это большая победа.

Непротиворечивость в данном конкретном случае — это дистрибутивность умножения над сложением, закон, который для положительных чисел может быть принят на полностью эмпирических основаниях. (Полный аргумент см. в сноске. ¹ .)

Обращение к дискретной математике – Согласованность с биномиальной теоремой

В дискретной математике нет понятия «приближение» — человек находится либо в , либо вдали от него, и в этом случае или .

Случай может быть решен на основании непротиворечивости в отношении биномиальной теоремы, т. е. потери вычислительной эффективности, чтобы рассматривать этот случай отдельно. Это аргумент Кнута (из «Искусства компьютерного программирования» и славы TeX), основанный на сохранении согласованности с биномиальной теоремой, когда x = 0, из-за ее фундаментального места как в дискретной, так и в непрерывной математике:

«Некоторые учебники оставляют количество неопределенным, потому что функции и имеют разные предельные значения при уменьшении до 0. Но это ошибка. Мы должны определить для всех , должна ли биномиальная теорема быть справедливой, когда , и/или . Теорема слишком важна, чтобы ее произвольно ограничивать! Напротив, функция совершенно не важна».
— из Concrete Mathematics, стр. 162, Р. Грэм, Д. Кнут, О. Паташник, Addison-Wesley, 1988.

Различные обозначения математических вычислительных платформ

Учитывая универсальность соглашения среди математиков, удивительно обнаружить, что различные вычислительные платформы реализовали разные значения:

Значение один: Калькулятор Google, R, Octave, Ruby и калькулятор Microsoft дают .
Нулевое значение: Hexalon Max (калькулятор) и физический ручной калькулятор TI-36 дают .
Неопределенное значение: Максима и Microsoft Excel (2000) дают неопределенное значение, т. е. возникает ошибка.

Альтернативный критерий принятия решения – осязаемое вычисление с поддающимся проверке подсчетом, требующее ответа

В то время как аргумент Кнута об удобном расширении работает, конечное суммирование целых степеней дает нам реальный, осязаемый результат (конечную сумму), значение которого (эмпирически определимый факт) неизбежно зависит от выбранного значения . Итак, здесь у нас есть аргумент согласованности, который не опирается на эффективность.

Решающий шаг в этом рассуждении происходит при выводе (*1b) из (*1a) в Конечное суммирование целых степеней, часть 2 .

Извлекая соответствующую часть этого вывода, мы имеем:

После расширения биномиальной степени с использованием биномиальной формулы и дальнейших манипуляций мы получаем:

(Вытяните член из обеих сумм. Примечание: )

(что после дополнительных манипуляций дает)

Ключевой шаг происходит в (***) выше: мы отделяем член внутренней суммы, чтобы получить: . Чтобы исключить это из внешнего суммирования, необходимо рассмотреть выражение для все . Теперь 0, возведенный в любую положительную степень , равен 0, поэтому мы можем развеять случай . Но что? Необходимо принять решение: или или . Неопределенность не вариант, так как ситуация реальная и требуется продолжение упрощения.

Аргумент в пользу

Каковы последствия выбора другого определения, т.е. ? В этом случае окончательная формула для отличается от линейной константы , а выбор приводит к точной формуле и вычисляемому значению, которое соответствует суммированию грубой силы. 90=1 требуется:

Ссылки
The Math Forum

( Если вы разработчик программного обеспечения математического пакета, мне было бы интересно узнать, как вы пришли к своему решению. Вы можете отправить мне электронное письмо, используя ссылку для комментариев ниже. )

Если вам понравилась эта статья, не стесняйтесь щелкнуть здесь, чтобы подписаться на мою RSS-ленту.

Сноски

Принимая во внимание, что любое количество, умноженное на ноль, равно нулю, и что одно, умноженное на любое количество, является количеством, мы без колебаний предоставляем . Но затем обратите внимание, что мы пишем , что означает, что, объединяя два выражения, мы имеем . Если мы примем закон распределения умножения над сложением для положительных целых чисел исключительно на эмпирических основаниях и если мы хотим, чтобы отрицательные числа вели себя так же, как наши
эмпирически принимает положительных целых чисел, тогда мы хотим, чтобы закон распределения также выполнялся. И, следовательно, у нас есть Что означает, что должно быть противоположным (аддитивным обратным) , и, следовательно, ↩
Последствия для непрерывной математики являются предметом отдельного обсуждения. Утверждения, что разрыв существует в начале координат, недостаточно. ↩

Число нулей в конце | Brilliant Math & Science Wiki

Содержание

Теория замыкающих нулей
Факториалы в базе десяти
Завершающие нули в других базах

Прежде чем приступить к вычислению конечных нулей факториала, сначала подумайте, откуда берутся конечные нули.

Сколько нулей в конце этих чисел? На какую наибольшую степень десяти делятся эти числа? 9b \times k2a×5b×k, где kkk — целое число, такое что 2∤k2 \nmid k2∤k и 5∤k,5 \nmid k,5∤k, то количество нулей в конце этого числа равно min⁡ (а,б).\мин(а,б).мин(а,б).

Это понимание становится важным для эффективного определения количества конечных нулей в факториалах. Достаточно найти меньшую из степеней 2 или 5, так что нет необходимости считать большую из этих степеней.

В свете приведенной выше теоремы стратегия нахождения конечных нулей факториала будет вращаться вокруг простой факторизации факториала. 92. \end{выровнено} 7!8!9!===7×6!=24×32×5×78×7!=24×32×5×7×239×8!=24×32×5 ×7×23×32.

Потому что высшая степень числа 5, которая делит 6!,7!,8!,9!6!,7!,8!,9!6!,7!,8!,9! равен 1, все они имеют одинаковое количество конечных нулей. □_\квадрат □

Стратегия теперь состоит в том, чтобы подсчитать количество кратных 5 в факторном произведении.

Однако следует также учитывать, что число в факторном произведении может давать степень 5 больше 1.

Найдите количество конечных нулей в 30!.30!.30!. 9151 фактор. Следовательно, количество нулей в конце 30!30!30! 7.\в коробке{7}.7. □_\квадрат□

Обратите внимание, что каждое число, кратное 5 в факторном произведении, будет вносить 111 в число конечных нулей. Кроме того, каждое число, кратное 25, добавляет 111 дополнительных нулей к числу конечных нулей. Затем каждое число, кратное 125, будет вносить еще 111 в число конечных нулей и так далее.

Найдите количество завершающих нулей в 500!500!500!.
Количество кратных 5, которые меньше или равны 500, составляет 500÷5=100,500 \дел 5 =100,500÷5=100.
Тогда число кратное 25 равно 500÷25=20.500 \дел 25 = 20.500÷25=20.

Тогда число кратное 125 равно 500÷125=4,500 \дел 125 = 4,500÷125=4.
Следующая степень числа 5 равна 625, что больше 500.
Следовательно, количество нулей в конце 500!500!500! равно 100+20+4=124,100+20+4=\в коробках{124}. 100+20+4=124. □_\квадрат□

Как вы, наверное, уже поняли, мы можем определить количество нулей в конце N!N!N! для любого положительного целого числа NNN. Попробуйте следующий пример и посмотрите, сможете ли вы найти хороший способ выразить его.

1000!=4023872600770…4720000000…0⏟Много 0 из 1000! = 4023872600770 \ldots 472 \underbrace{0000000 \ldots 0}_{\text{Много нулей}} 1000!=4023872600770…472Много 0’s0000000…0
Приведенные выше некоторые цифры 1000!1000!1000!. Сколько (конечных) нулей стоит в конце этого числа?
Способ решения точно такой же, как и в предыдущем примере:

Количество кратных 5, которые меньше или равны 1000, равно 1000÷5=2001000\div5 = 200 1000÷5=200.
Количество кратных 25, которые меньше или равны 1000, равно 1000÷25=401000\div25 = 40 1000÷25=40.
Количество кратных 125, которые меньше или равны 1000, равно 1000÷125=81000\div125 = 8 1000÷125=8.
Единственным числом, кратным 625, которое меньше или равно 1000, является само число 625. 9k}}\right\rfloor=0,0 < 5kn < 1 ⟺ ⌊5kn⌋=0, поэтому на основную сумму это не влияет.
Первый член подсчитывает, сколько раз число, кратное 5, появляется в факторном произведении, второе подсчитывает число, кратное 25, и так далее.
Определите количество нулей в конце числа 777!777!777!.
Подставляем 777 в формулу и получаем
⌊7775⌋+⌊77725⌋+⌊777125⌋+⌊777625⌋=155+31+6+1=193. □\begin{align} \left\lfloor{\frac{777}{5}}\right\rfloor+\left\lfloor{\frac{777}{25}}\right\rfloor+\left\lfloor{\frac{ 777}{125}}\right\rfloor+\left\lfloor{\frac{777}{625}}\right\rfloor &= & 155+31+6+1 \\ &=&193. \ _\square \end{выровнено} ⌊5777⌋+⌊25777⌋+⌊125777⌋+⌊625777⌋==155+31+6+1193. □

Обратите внимание, что последовательность останавливается после ⌊777625⌋\left\lfloor{\frac{777}{625}}\right\rfloor⌊625777⌋, потому что все после этого будет равно 0. Вам не нужно запоминать сложные формулы для решайте подобные задачи постоянно, но просто знайте, как и почему это работает.
10 14 15 16
Найдите количество нулей в конце числа 60!60!60!.
2015! умножается на себя в 2015 раз следующим образом:

2015!×2015!×⋯×2015!⏟2015.\underbrace { 2015!\times 2015!\times\cdots\times 2015! }_{ 2015 }.20152015!×2015!×⋯×2015!.
Подсчитайте, сколько нулей в конце!
Определите количество конечных нулей 10005!10005!10005!.
Подставляем 10005 в формулу и получаем
⌊100055⌋+⌊1000525⌋+⌊10005125⌋+⌊10005625⌋+⌊100053125⌋=2001+400+80+16+3=2500.\begin{align} \left\lfloor { \frac { 105005}{ } } \right\rfloor +\left\lfloor { \frac { 10005 }{ 25 } } \right\rfloor +\left\lfloor { \frac { 10005 }{ 125 } } \right\rfloor +\left\lfloor { \frac { 10005 }{ 625 } } \right\rfloor +\left\lfloor { \frac { 10005 }{ 3125 } } \right\rfloor & = & 2001+400+80+16+3 \\ & = & 2500 . \end{выровнено} ⌊510005⌋+⌊2510005⌋+⌊12510005⌋+⌊62510005⌋+⌊312510005⌋==2001+400+80+16+32500.
Обратите внимание, что последовательность остановится после ⌊100053125⌋\left\lfloor{\frac{10005}{3125}}\right\rfloor⌊312510005⌋, потому что все после этого будет равно 0. Таким образом, ответ 250025002500. □_\square □

000 333 444 555
Для скольких положительных целых значений nnn n!n!n! заканчиваются ровно 23 нулями в конце?
92}(1001!)22002!
Сколько нулей в конце числа выше?
Альтернативный способ вычисления конечных нулей факториала дается путем анализа числа в другом простом основании.
Для заданного целого числа nnn и простого числа p,p,p пусть Sp(n){ S }_{ p }(n)Sp(n) будет суммой цифр числа nnn по основанию p,p,p, и пусть vp(n)v_p(n)vp(n) — наивысшая степень ppp в n!. n!.n!. Тогда
vp(n)=n−Sp(n)p−1. {v}_{p}(n) = \frac{n-{S}_{p}(n)}{p-1}. vp(n)=p−1n−Sp(n).
Найдите количество конечных нулей в 452!.452!.452!.
Для приведенной выше формулы n=452.n=452.n=452. Учитывая, что этот факториал находится в десятичной системе счисления, цель состоит в том, чтобы найти наивысшую степень числа 555 в 452!.452!.452!. Следовательно, p=5.p=5.p=5.
Сначала необходимо вычислить число по основанию 5:
⌊452125⌋=3452−3⋅125=77⌊7725⌋=377−3⋅25=2⌊25⌋=0.\begin{выровнено} \left\lfloor \frac{452}{125} \right\rfloor &= 3 \\ 452 — 3 \cdot 125 &= 77 \\ \\ \left\lfloor \frac{77}{25} \right\rfloor &= 3 \\ 77 — 3 \cdot 25 &= 2 \\ \\ \left\lfloor \frac{2}{5} \right\rfloor &= 0. \end{выровнено}⌊125452⌋452−3⋅125⌊2577⌋77−3⋅25⌊52⌋=3=77=3=2=0.
Тогда 45210=33025.452_{10}=3302_{5}.45210=33025.
Сумма цифр числа 452 по основанию 5 равна
.
S5(452)=3+3+0+2=8.S_5(452)=3+3+0+2=8.S5(452)=3+3+0+2=8.
Используя приведенную выше формулу, наибольшая степень числа 5 в 452!452!452!
v5(452)=452−85−1=111.\begin{выровнено} v_5(452) &= \frac{452-8}{5-1} \\\\ &= 111. \end{выровнено}v5(452)=5−1452−8=111.
Таким образом, в 452!.452!.452! есть 111\упакованные{111}111 нулей в конце. □_\квадрат□
Процесс определения количества конечных нулей в других простых основаниях аналогичен процессу в десятичной системе счисления. Во-первых, подумайте, что вызывает конечный нуль в другой системе счисления.
Сколько нулей в конце у этих чисел с основанием 10 в основании 6?
200
756
864
Преобразование каждого числа в основание 6,
20010=5326:0 нули в конце75610=33006:2 нули в конце86410=40006:3 нули в конце.\begin{align} 200_{10} &= 532_{6}&: &\quad 0 \text{конечные нули} \\ 756_{10} &= 3300_{6}&: &\quad 2 \text{конечные нули} \\ 864_{10} &= 4000_{6}&: &\quad 3 \text{конечные нули}. \end{align}200107561086410=5326=33006=40006:::0 нули в конце2 нули в конце 3 нули в конце. 9a \times k,ba×k, где a, b,a,\ b,a, b и kkk — целые числа, такие что bbb положительно, aaa неотрицательно и b∤k,b \nmid k,b ∤k, то количество нулей в конце числа nnn в базе bbb равно а.а.а.
Этот метод делает ненужным полное преобразование числа в новое основание для подсчета конечных нулей. Это особенно важно для вычисления конечных нулей факториала.
Найдите количество нулей в конце числа 10!10!10! в базе 12.
91,10!=124×52×71.
Следовательно, число нулей в конце 10!10!10! в базе 12 это 4.\boxed{4}.4. □_\квадрат□
Обратите внимание, что существует «узкое место» степеней 5 в базе 10, но не обязательно постоянное «узкое место» в других системах счисления. При вычислении конечных нулей необходимо учитывать каждую степень простого числа в базе. Метод вычисления степени простого факториала очень похож на метод вычисления основания 10:
. Пусть vp(n)v_p(n)vp(n) дает наивысшую степень ppp в n!n!n!. Затем 92 х 5,45=32×5.
Найдите степень числа 333 в 100!:100!:100!:
v3(100)=⌊1003⌋+⌊1009⌋+⌊10027⌋+⌊10081⌋=33+11+3+1=48.\begin{выровнено} v_3(100) &= \left\lfloor \frac{100}{3} \right\rfloor + \left\lfloor \frac{100}{9} \right\rfloor + \left\lfloor \frac{100}{ 27} \право\rпол + \лево\lпол \frac{100}{81} \право\rпол \\ &= 33+11+3+1 \\ &= 48. \end{выровнено}v3(100)=⌊3100⌋+⌊9100⌋+⌊27100⌋+⌊81100⌋=33+11+3+1=48.
Сила 3 в 100!100!100! равно 48, значит степень 92 \nmid l32∤l и 5∤l.5 \nmid l.5∤l.
Следовательно, 100!100!100! имеет 24\упакованных{24}24 конечных нуля в базе 45. □_\квадрат□
Найдите количество конечных нулей в представлении числа 2017!.2017!.2017! по основанию 17.
Уточнение : 2017, как здесь написано, находится в системе счисления по основанию 10.
Найдите наименьшее целое число NNN такое, что когда N!N!N! записывается в по основанию 12 , имеет 121 конечный нуль.
No related posts.