Что первое умножение или вычитание: Порядок действий в Математике

Содержание

Порядок действий в математике. Действия первой, второй ступеней в выражениях. Что первое умножение или деление в 2022 году

Действия первой и второй ступени с натуральными числами. Порядок действий

Мы уже рассмотрели арифметические действия сложения и вычитания. Эти действия называются действиями первой ступени. Умножение и деление принято считать действиями второй ступени. Если в математическом выражении есть несколько действий, включая действия и первой, и второй ступени, есть разные числа, соответственно результат зависит от порядка совершенных действий. Поэтому при решении примеров следует соблюдать правильный порядок действий.

Если в выражении нет скобок и присутствуют только действия второй ступени, то действия выполняются в том порядке, в котором они написаны, слева направо.

Например, 80 : 4 ⋅ 2 : 10 = 20 ⋅ 2 : 10 = 40 : 10 = 4

Если в выражении нет скобок и присутствуют только действия первой ступени, то действия выполняются в том порядке, в котором они написаны, слева направо.

Например, 56 + 10 – 25 + 30 = 66 – 25 + 30 = 41 + 30 = 71

Если в выражении нет скобок и случаются действия разных степеней, то сначала выполняют действия второй ступени, а затем действия первой ступени. Напомним, умножение и деление считаются действиями второй ступени, сложение и вычитание – действиями первой ступени.

Например, 43 + 25 ⋅ 4 – 10. Сначала выполним умножение 25 ⋅ 4 = 100, 43 + 100 – 10 = 133.

Если в выражении есть скобки, сначала выполняем действия в скобках, а затем все остальные согласно порядку действий. Если в скобках записано выражение из нескольких действий первой и второй ступеней, то в скобках также сначала выполняем действия второй ступени.

То есть порядок действий в выражении будет следующим:
действия в скобках
умножение и деление,
сложение и вычитание.
Действия в пределах одной ступени выполняются поочередно слева направо.

Сначала сложение или вычитание?

Сложение и вычитание являются действиями первой ступени, если нет скобок, то они выполняются поочередно слева направо.

Какое первое действие – умножение или деление?

И умножение, и деление – это действия второй степени, они «равноправны». Поэтому, если нет скобок, действия выполняются поочередно слева направо.

Сначала умножение или сложение?

Поскольку умножение является действием высшей степени, а сложение – действием низшей степени, если нет скобок, то сначала выполняем умножение.

Что сначала – деление или вычитание?

Поскольку деление является действием высшей степени, а вычитание – действием низшей степени, если нет скобок, сначала выполняем деление.

Алгоритм вычисления числового выражения

Перед вычислением числового выражения следует определить порядок действий и только после этого приступать к расчетам.

Рассмотрим выражение с несколькими действиями и скобками.

(53 – 42 : 7) ⋅ (22 ⋅ 2 +36 — 12) + 30

Первоочередность действий в данном выражении будет такой:

42 разделить на 7 (42 : 7 = 6)
Из 53 вычесть результат первого действия: 53 – 6 = 47
Во вторых скобках сначала нужно выполнить умножение 22 на 2: 22 ⋅ 2 = 44
К результату умножения прибавляем 36: 44 + 36 = 80
Из полученной суммы вычитаем 12: 80 – 12 = 68
Умножим множители, которые являются результатами выполнения действий в первых и вторых скобках: 47 ⋅ 68 = 3196
К произведению прибавляем 30: 3196 + 30 = 3226

Ответ: (53 – 42 : 7) ⋅ (22 ⋅ 2 +36 -12) + 30 = 3226

Порядок действий с круглыми, квадратными и фигурными скобками

В математических выражениях встречаются не только круглые () скобки, но и квадратные — [ ] и фигурные { }. Фигурные и квадратные скобки используют тогда, когда у скобки необходимо взять выражение в скобках. Порядок действий со скобками следующий: сначала выполняем действия внутри круглых скобок согласно правилам последовательности, второй этап – действия в квадратных скобках, третий этап – действия в фигурных скобках согласно правилам последовательности.

Рассмотрим выражение с круглыми и квадратными скобками

100 — 4 ⋅ [14 + 45 : (10 + 5)] + 6 ⋅ (30 + 4 ⋅ 5 + 10).

Выполним действия в круглых скобках:

10 + 5 = 15

30 + 4 ⋅ 5 + 10 = 30 + 20 + 10 = 60

Выполним действия в квадратных скобках: 14 + 45 : 15 = 17
Выполним остальные действия: 100 – 4 ⋅ 17 + 6 ⋅ 60 = 100 – 68 + 360 = 32 + 360 = 392

Арифметические действия над числами

Советы → Полезные сведения → Арифметика → Арифметические действия

Нахождение по нескольким данным числам одного нового числа называется арифметическим действием. В арифметике рассматривается шесть действий:

сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.

1. Сложение. Это действие состоит в том, что по нескольким числам, называемым слагаемыми, находится число, называемое их суммой.

Пример: 4+3=7, где 4 и 3 – слагаемые, а 7 – их сумма.

2. Вычитание – действие, посредством которого по данной сумме (уменьшаемое) и данному слагаемому (вычитаемое) находят искомое слагаемое (разность).
Это действие обратно сложению.

Пример: 7 – 3 = 4, где 7 – уменьшаемое, 3 – вычитаемое, а 4 – разность.

3. Умножение. Умножить некоторое число (множимое) на целое число (множитель) – значит повторить множимое слагаемым столько раз, сколько единиц содержится в множителе. Результат умножения называется произведением.

Пример: 2 ∙ 3 = 6, где 2 – множимое, 3 – множитель, а 6 – произведение. (2 ∙ 3 = 2 + 2+ 2 = 6)

Если множитель и множимое меняются ролями, то произведение остается тем же. Поэтому множитель и множимое также называются сомножителями.

Пример: 2 ∙ 3 = 3 ∙ 2, то есть (2 + 2 + 2 = 3 + 3)

Полагают, что если множителем является 1, то a ∙ 1 = a.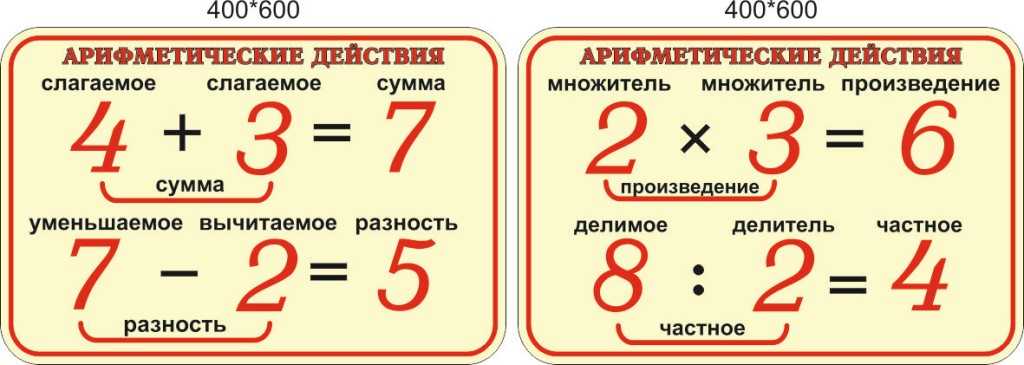

Например: 2 ∙ 1 = 2, 44 ∙ 1 = 44, 13 ∙ 1 = 13.

4. Деление. Посредством деления по данному произведению (делимое) и данному сомножителю (делитель) находят искомый сомножитель (частное).
Это действие обратно умножению.

Пример: 8 : 2 = 4, где 8 – делимое, 2 – делитель, а 4 – частное.

Проверка деления: произведение делителя 2 и частного 4 дает делимое 8. 2 ∙ 4 = 8

Деление с остатком

Если при делении целого числа на целое число в частном получается целое число, то такое деление целых чисел называется точным, или, что первое число нацело делится (или просто – делится) на второе.

Например: 35 делится (нацело) на 5, частное есть целое число 7.

Второе число при этом называется делителем первого, первое же – кратным второго.

Во многих случаях можно, не выполняя деления, узнать, делится ли нацело одно целое число на другое (см. признаки делимости).

Точное деление возможно далеко не всегда. В таком случае выполняют так называемое деление с остатком. В этом случае находят такое наибольшее число, которое при умножении на делитель даст произведение, не превосходящее делимого. Это число называется неполным частным. Разность между делимым и произведением делителя на неполное частное называется остатком от деления.

Делимое равно делителю, умноженное на неполное частное, плюс остаток. Остаток всегда меньше делителя.

Пример: Неполное частное от деления числа 27 на 4 равно 6, а остаток равен 3. Очевидно, 27 = 4∙6 + 3 и 3˂4.

5. Возведение в степень. Возвести некоторое число в целую степень (во вторую, в третью и т.д.) – значит взять это число сомножителем два, три раза и т.д. Иначе говоря, возведение в степень выполняется повторным умножением.
Число, которое берётся сомножителем, называется основанием степени; число, показывающее, сколько раз повторяется основание, называется показателем степени; результат возведения числа в степень называется степенью этого числа.

Пример: 2∙2∙2 = 2³ = 8; где 2 – основание степени, 3 – показатель степени, 8 – степень.

Вторую степень числа иначе называют квадратом, третью степень – кубом. Первой степенью числа называют само это число.

6. Извлечение корня есть действие, посредством которого по данной степени (подкоренное число) и данному показателю степени (показатель корня) находят искомое основание (корень).
Это действие обратно возведению в степень.

Пример: ³√64 = 4; где 64 – подкоренное число, 3 – показатель корня, 4 – корень.

Проверка извлечения корня: 4³=64. Возведение числа 4 в 3-ю степень даёт 64.

Корень второй степени иначе называют квадратным; корень третьей степени – кубическим.
При знаке квадратного корня показатель корня принято опускать: √36 = 6 означает ²√36 = 6.

Использованная лит-ра:
Справочник по элементарной математике — Выгодский М.

Я., «Наука», 1974 г.
Справочник по математике. Пособие для учащихся 9—11 кл. — Шахно К. У., «Учпедгиз», 1961 г.

→ Читайте по теме: Признаки делимости

→ Арифметика

→ В раздел Советы

При полной или частичной публикации статьи в Интернете обязательно указание активной гиперссылки на источник http://programmistan.narod.ru

Что такое порядок операций? – определение, правила и примеры

Порядок операций – это набор правил, которым необходимо следовать в определенном порядке при решении уравнения.

Все мы хорошо знаем четыре основных математических действия: сложение, умножение, деление и вычитание. С детства мы постоянно репетируем задачи, связанные с этими четырьмя операциями. Эти операции используются, от добавления счета за вашу покупку в торговом центре до разделения пиццы на четыре равные части. Но до сих пор мы решали проблемы, связанные с каждой операцией в отдельности.

Что, если у нас есть выражение, в котором все четыре операции работают вместе? Мы сначала умножаем или сначала вычитаем? Это может быть проблематично, если вы будете следовать неправильному подходу. Это может привести к неправильным ответам. Поэтому порядок действий вступил в действие.

Анализ любого математического утверждения с использованием арифметических операций, таких как деление, умножение, сложение и вычитание, в математике называется операциями. Давайте посмотрим на законы порядка операций и посмотрим, насколько хорошо мы можем их вспомнить, используя простые стратегии. В этой статье вы узнаете порядок операций, правила порядка операций, математический порядок операций и решите задачи на порядок операций.

Почему выполняется Порядок операций?

При оценке уравнений в арифметике может потребоваться выполнение множества операций, и упрощение, в конце концов, дает разные результаты. Однако на каждую фразу может быть только один правильный ответ. Мы используем принципы, чтобы упростить любое данное математическое выражение, чтобы найти правильный ответ. Эти принципы основаны на всех основных математических операторах.

С единственной целью всегда получать правильные ответы на любое математическое уравнение, был реализован порядок операций.

Каков порядок действий?

В математике такие операторы, как сложение (+), вычитание (-), умножение (×) и деление (÷), имеют приоритет друг над другом. Мы не можем самостоятельно решить выражение, содержащее любой из двух операторов. Мы должны следовать правилам порядка операций, которые гласят, что в любом выражении, как арифметическом, так и алгебраическом, первыми будут оцениваться скобки. Заказ будет рассчитываться во вторую очередь. Умножение и деление будут оцениваться третьими и, наконец, сложение и вычитание будут упрощены.

Приоритет решения любого выражения упоминается в таблице ниже:

Приоритет	Операция
Первые	Блинга	Порядки (Экспоненты, Квадратный корень, Кубический корень, Логарифмический и т. д.)
Третьи	Деление или умножение (Операция, расположенная слева от выражения, будет оцениваться первой)
Четвертая	Сложение или вычитание (в зависимости от того, какая операция находится в левой части выражения, будет оцениваться первой)

Определение порядка операций принципы приоритета, которые мы используем при решении любого математического уравнения, включающего множество операций.

Когда между двумя операторами существует подвыражение, должен быть реализован оператор, который появляется первым в таблице, упомянутой в предыдущем разделе.

Давайте теперь разберемся с порядком операций, правило за правилом, в соответствии с установленным приоритетом: операторы, применяемые к выражению. При решении любого выражения всегда двигайтесь от левой стороны к правой. Это поможет вам облегчить упрощение этого выражения. Теперь прочитайте правила, упомянутые ниже, чтобы полностью понять концепцию порядка операций:

Правило 1: Необходимо всегда проверять наличие скобок или круглых скобок в выражении. Чаще всего в математических выражениях встречаются скобки «()», «{}» и «[]». Когда терм содержит все три скобки, решите уравнение следующим образом:

Сначала решите термины внутри круглой скобки «()» или круглых скобок.
Решите условия внутри фигурных скобок «{}» секунды.
Наконец, решите условия в квадратных скобках «[ ]».

Кроме того, помните, что если в любой из скобок есть несколько операций, обязательно используйте порядок операций для их решения.

Правило 2: После того, как вы решите числа в скобках, найдите любые термины в следующем порядке, такие как возведенные в степень термины, корневые термины, логарифмические термины, тригонометрические термины и т. д., и решите их.

Правило 3: Осталось расставить четыре основных оператора в правильном порядке. Вы можете выполнять умножение или деление в зависимости от того, какой оператор стоит первым с левой стороны выражения.

Правило 4: Последним шагом является добавление или вычитание элементов в том же порядке слева направо.

Если вы помните эти пять правил, значит, вы усвоили порядок действий. Каким бы длинным ни было выражение, вы легко сможете решить его, не задумываясь. Если вы не уверены, что запомните эти правила, есть два простых способа их запомнить. Они известны как BODMAS и PEMDAS. В следующих разделах вы узнаете об этих двух аббревиатурах для порядка операций.

Способы запоминания порядка операций – BODMAS и PEMDAS

Существует два очень важных способа запоминания порядка действий. Они сокращенно называются правилом PEMDAS и правилом BODMAS. Буквы в этих аббревиатурах определяют математические операции. Буква, которая присутствует первой, применяется первой к любому уравнению.

Давайте теперь узнаем, что означает каждая из букв в этих аббревиатурах:

Порядок операций BODMAS

BODMAS — наиболее распространенная аббревиатура для порядка операций. Многие из вас наверняка слышали об этом где-то в своей жизни. В развернутом виде это означает:

B – Скобки ( ), { }, [ ]
О – Заказ
D – Отдел (÷)
M – Умножение (×)
А – Дополнение (+)
S – Вычитание (-)

Порядок работы PEMDAS

PEMDAS также является аббревиатурой от порядка работы. Тем не менее, его меньше слышно в нашей повседневной жизни, но он столь же эффективен, как и БОДМАС.

P – Скобки (), {}, [].
E – Показатель степени (a2) (Например, здесь a – это число с показателем степени 2 )
М – Умножение (×)
Д – Отдел (÷)
A – означает Дополнение (+)
S – означает вычитание (-)

Это самый эффективный метод запоминания последовательности событий. Забавная фраза « Пожалуйста, извините, моя дорогая тетя Салли »- хороший способ запомнить PEMDAS.

Оба эти метода используются для упрощения нашего понимания порядка операций. Мы увидим пример порядка операций, чтобы прояснить эту тему.

Каков порядок операций в математике?

Порядок операций — это правило, определяющее правильную последовательность шагов для вычисления математического выражения. Если у вас есть выражение только с одной операцией (например, только сложение, только вычитание, только умножение или только деление), правильный способ его решения — слева направо. Однако для выражений с несколькими операциями необходимо соблюдать порядок операций.

Пример порядка операций

Давайте рассмотрим различные примеры, упомянутые ниже, чтобы понять точность правил, используемых в порядке операций.

Для вычисления арифметических операторов

Выражение 1: 2 + 3 x 5

Правильный способ: Правильный способ решить это выражение — сначала умножить 3 x 5 = 15, а затем добавить 2 к результату. 15 + 2 = 17.
Неверный путь: Если сначала добавить 2 + 3. Получаем 6 х 5 = 30, что неверно при решении этого выражения.

Выражение 2: 15 ÷ 3 x 2 – 6

Правильный способ: Правильный способ решить это выражение – сначала разделить 15 и 3 = 5, потому что оно ближе к левой части выражения. Затем умножьте 5 на 2 = 10 и вычтите из этого 6, что дает 10 – 6 = 4.
Неверный способ: Если умножить 3 х 2 = 6, то вычесть из него 6, то получим 15 ÷ 0 = не определено. Это неправильный способ решения этого выражения.

Для оценки заказов

Выражение 1: 6 x 32

Правильный способ: Правильный способ решить это выражение — сначала решить порядок, то есть 32 = 9. Теперь умножьте это на 6. 9 x 6 = 54
Неверный путь: Если умножить 6 х 3 = 18, то возведем в квадрат ответ, получим 182 = 324, что неверно.

Выражение 2: 2 x sin 30

Правильный способ: Сначала оцените порядок sin 30 = ½. Теперь умножаем 2 на ответ. 2 х ½ = 1
Неверный способ: Если умножить 30 на 2 = 60 и решить порядок, то получим sin 60 = 3/2. Какой ответ неверный

Для оценки кронштейнов

Выражение 1: (12 + 3) x 4

Решение: В этом выражении мы видим, что скобки присутствуют; следовательно, мы сначала решим содержимое в скобках. Следовательно, 12 + 3 = 15. Теперь умножаем 15 на 4 = 60.

Выражение 2: 4 – 32 ÷ 8

4 – 32 ÷ 8 = 8 – 8 = 0 – это решение. (Это правильно. Это правильный способ.)

Рассмотрим другой подход к тому же выражению.

4 – 32 ÷ 8 = (-28) ÷ 8 = -3,5 (Неверно (это неправильный метод).

Выражение 3: 8 x (6 + 6)

8 x (12) = 96 (Это правильный способ решения скобок.)

Рассмотрим другой метод для того же выражения.

8 x (6 + 6) = 48 + 6 = 54 (Это неправильный способ решения скобок.)

Примечание: Мы должны соблюдать шаблон операторов при выполнении порядка операций над любой данной фразой.

Из вышеупомянутых правил мы узнаем, как выполнять несколько операций, если они входят в одно уравнение. Очень важно изучить эти понятия, чтобы исключить все возможные ошибки при выполнении расчетов. Более того, освоение порядка действий поможет получить больше баллов на экзаменах.

Порядок действий — Бесплатная помощь по математике

Введение

Порядок операций — очень простая концепция, необходимая для правильного понимания математики. В отличие от чтения, где мы всегда работаем слева направо, иногда с математикой нам нужно решить одну часть задачи перед другой, иначе окончательный ответ может быть неверным! Мы используем термин «порядок операций», чтобы описать, над какой частью проблемы нужно работать в первую очередь. Возьмите это уравнение в качестве примера:

$$ 4+6 \дел 2 * 11 = ? $$

Если бы вы просто решали слева направо, ответ был бы неверным. Давайте сделаем это сейчас: 4 + 6 = 10. Разделите это на 2, чтобы получить 5. Умножьте 5 на 11, чтобы получить 55. К сожалению, хотя это казалось правильным, этот ответ неверен.

Правильный порядок действий

Порядок действий позволит вам правильно решить эту задачу. Порядок такой: скобки , экспоненты , умножение и деление и, наконец, Сложение и вычитание . Всегда сначала выполняйте операции внутри круглых скобок, а затем выполняйте операции с показателями степени. После этого выполните все умножение и деление слева направо, и, наконец, выполните все сложение и вычитание слева направо.

Популярным способом запоминания заказа является аббревиатура PEMDAS. Скобки, экспоненты, умножение и деление, сложение и вычитание. Вы также можете создать небольшую фразу, например « P аренда E извините M y D ear A unt S ally.» Что бы вы ни выбрали, убедитесь, что вы очень хорошо знаете все шесть шагов порядка операций.

Давайте попробуем решить это уравнение еще раз, на этот раз с помощью PEMDAS.