Что первым делают умножение или деление: Порядок действий в Математике

Содержание

Порядок выполнения действий | Математика | 5 класс

На уроке вы узнаете о роли скобок в выражениях и о правилах, по которым выполняются действия. А также решите несколько интересных примеров.

Введение

В любом языке есть правила грамотной записи. Кроме самих слов, который несут основной смысл, мы используем знаки препинания. Они тоже крайне важны.

Вспомним всем известное «казнить нельзя помиловать». От того, где поставить запятую, смысл выражения меняется на противоположный (см. рис. 1).

Рис. 1. Как меняется смысл фразы от запятой

В этом предложении есть слова, которые несут смысл, а есть знак препинания – запятая, который очень сильно на этот смысл влияет.

В математическом языке тоже есть такой знак препинания, это скобки.

Пример 1

Если выполнять действия, как они записаны, то получаем 6: .

Но если поставить скобки вокруг суммы , то сразу смысл выражения меняется: .

Роль скобок. Порядок операций

В математике есть простые правила, указывающие, какие действия в каком порядке надо совершать. Скобки нужны, если мы хотим влиять на этот порядок действий. Зная эти правила, ошибиться в порядке действий практически невозможно. Их мы сейчас и обсудим.

Сложение и вычитание равноправны

В этом примере у нас есть и сложение, и вычитание. Эти действия равноправны. Мы делаем их все подряд слева направо. Расставим последовательность действий.

Умножение и деление тоже равноправны

Если у нас только умножение и деление, то мы опять делаем все действия подряд слева направо:

Сначала умножение и деление, потом сложение и вычитание

Если у нас разные действия в одном примере, то сначала нужно сделать все умножения и деления, слева направо, а потом все сложения и вычитания, тоже слева направо.

Действия в скобках раньше всего

Действия в скобках делаются в первую очередь. Сначала вспомним еще раз нашу задачку, с которой начали урок.

Умножение идет первым, поэтому сначала умножение, потом сложение.

Но если поставить сложение в скобки, то начинаем мы с него, а умножение делаем вторым.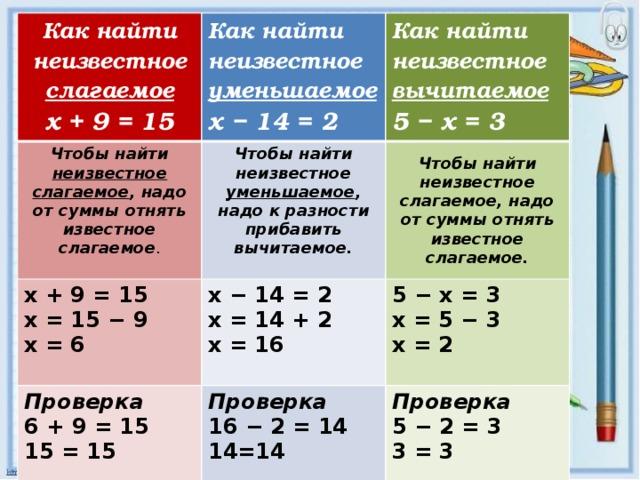

Очень простая задача, но здесь видно, что последовательность действий важна, меняем последовательность, получаем разные ответы.

Пример 2

Сначала действия в скобках. Их две. Значит, расставляем последовательность действий над скобками слева направо. Потом идут умножение и деление слева направо, и последнее вычитание:

Порядок выполнения действий

действия в скобках
умножение и деление
сложение и вычитание

Пример 3

Внутри скобок может оказаться несколько действий. Тогда они выполняются по обычным правилам: сначала действия в скобках – сначала умножение, потом вычитание. Остались снаружи от скобок деление и последнее сложение.

Пример 4

Внутри скобок могут оказаться еще скобки. Значит, смотрим на весь пример, сначала нужно сделать все действия внутри больших скобок, пользуясь правилом, то есть сначала действия в скобках, затем деление, затем сложение. Снаружи больших скобок сначала умножение, потом сложение.

Пример 5

Рассмотрим еще один прием вычислений, который иллюстрирует, как можно сократить количество действий.

Расставим последовательность действий.

Получилось восемь действий. Делая по одному действию, мы должны будем переписать этот пример восемь раз и только потом получим ответ. Это будет выглядеть так:

Запись можно сократить. Расставим последовательность действий. 1 и 2 действие не влияют на третье. Его можно сделать одновременно с первым. А то, что мы делаем в первых скобках, не влияет на то, что делаем во вторых. Действия в первых больших и последних скобках тоже можно делать одновременно.

За один раз выполнены три действия. Далее одновременно можно сделать по одному действию в первых и вторых скобках: деление и вычитание.

Заканчиваем решение:

Запись получилась короче.

Заключение

Этот прием одновременных вычислений требует тренировки. Навык сам появится, когда вы выполните достаточное количество примеров.

Список рекомендованной литературы

Математика. 5 класс. Зубарева И. И., Мордкович А. Г. 14-е изд., испр. и доп. — М.: 2013. – 270 с.
Математика. 5 класс. Виленкин Н. Я., Жохов В. И. и др. 24-е изд., испр. — М.: 2008. — 280 с.
Математика. 5 класс. Учебник в 2 ч. Дорофеев Г. В., Петерсон Л. Г. 2-е изд., перераб. — М.: 2011; Ч. 1 — 176 с, Ч. 2 — 240 с.

Рекомендованные ссылки на ресурсы сети Интернет

Интернет-портал «matematika-na.ru» (Источник)
Интернет-портал «school-assistant.ru» (Источник)
Интернет-портал «urokimatematiki.ru» (Источник)

Домашнее задание

Решите примеры:

Что будет первым умножение или деление? – Обзоры Вики

Порядок операций можно запомнить по аббревиатуре PEMDAS, которая означает: круглые скобки, показатели степени, умножение и деление слева направо, а сложение и вычитание слева направо. Здесь нет круглых скобок или показателей степени, поэтому начните с умножения и деления слева направо.

Итак, каков порядок операций в математике? Чтобы помочь учащимся в Соединенных Штатах запомнить этот порядок операций, учителя вставляют в них аббревиатуру PEMDAS: круглые скобки, показатели, умножение, деление, сложение, вычитание.

Имеет ли значение порядок умножения и деления? Умножение и деление можно делать вместе. Другими словами, не имеет значения, выполняете ли вы сначала деление или умножение, но они должны выполняться после круглых скобок и показателей степени, а также перед сложением и вычитанием.

Дополнительно Можно ли выполнять умножение и деление в любом порядке? Оформить заказ операций говорит вам сначала выполнить умножение и деление слева направо, прежде чем выполнять сложение и вычитание. Продолжайте выполнять умножение и деление слева направо. Далее складываем и вычитаем слева направо.

Можно ли выучить деление перед умножением? дети начинают учить умножение во втором классе, и деление в третьем классе.

Каковы 5 порядка операций?

Она выступает за Круглые скобки, экспоненты, умножение / деление, сложение / вычитание. В школах PEMDAS часто расширяется до мнемоники «Пожалуйста, извините, моя дорогая тетя Салли». Канада и Новая Зеландия используют BEDMAS, что означает скобки, экспоненты, деление/умножение, сложение/вычитание.

Почему вы делаете сначала умножение и деление? Учащиеся должны были своими словами ответить на вопрос, который передает концепцию: Умножение и деление делается до сложения и вычитания чтобы преобразовать группы элементов в промежуточные итоги похожих элементов, которые можно объединить для получения общей суммы.

Что такое правило MDAS в математике? MDAS означает Умножение, деление, сложение и вычитание. Это часть Порядка операций, набора правил, определяющих последовательность упрощения математических операций. Он используется, когда выражение или уравнение имеют более одной операции.

Имеет ли деление преимущество перед умножением?

Умножение имеет тот же приоритет, что и деление, но умножение и деление имеют более высокий приоритет, чем сложение и вычитание.

Также Каковы четыре правила математики? Четыре правила математики сложение, вычитание, умножение и деление. На следующих веб-страницах вы можете узнать, как это сделать вручную (без калькулятора), а также другую важную информацию о порядке приоритета этих операций.

Что такое правило DMAS?

правило DMAS следует, когда в данной задаче присутствует несколько арифметических операций, таких как сложение, вычитание, умножение и деление. В нем говорится, что они должны выполняться в порядке деления, умножения, сложения и вычитания.

Почему студенты борются с разделением? Ребенку, которому не хватает фундаментального навыка, будет трудно разделить потому что это связано с предыдущими концепциями. Деление — это повторное вычитание и противоположность умножения. Это связано со счетом, целым и частями и пропорциональным мышлением.

Верно ли правило Бодмаса?

Его буквы обозначают скобки, порядок (значение полномочий), деление, умножение, сложение, вычитание. … Он не содержит скобок, степеней, деления или умножения, поэтому мы будем следовать BODMAS и делать сложение с последующим вычитанием: это ошибочно. Правильное значение 3.

В Бодмасе деление предшествует умножению?

PEMDAS («круглые скобки, показатели степени…») и BEDMAS также используются в США и Австралии. Возвращаясь к приведенному выше примеру, правильным ответом будет первый ответ, поскольку он следует правилам BODMAS: деление можно сделать перед умножением и должно быть сделано до сложения, а умножение предшествует сложению.

Что правильно MDAS или DMAS? Это не MDAS. На самом деле это DMAS, что означает деление, умножение, сложение и вычитание. В математике это правило соблюдается, что означает, что в уравнении или задаче порядок упрощения будет в указанном выше формате.

Как решить порядок действий? Порядок операций сообщает нам порядок решения шагов в выражениях с более чем одной операцией. Первый, решаем любые операции внутри скобок или скобок. Во-вторых, решаем любые показатели. В-третьих, мы решаем все умножение и деление слева направо.

Как вы оцениваете MDAS?

Чем отличается деление умножения? Умножение и деление тесно связаны между собой, поскольку деление — это обратная операция умножения. Когда мы делим, мы пытаемся разделить на равные группы, в то время как умножение предполагает объединение равных групп. … Если мы разделим этот продукт на один из множителей, то в результате получим другой множитель.

Каковы 4 порядка операций?

Порядок операций — это правило, указывающее правильную последовательность шагов для вычисления математического выражения. Мы можем запомнить порядок с помощью PEMDAS: Круглые скобки, экспоненты, умножение и деление (слева направо), сложение и вычитание (слева направо). Создал Сал Хан.

Почему умножение и деление имеют одинаковый приоритет? Сказать, что умножение и деление имеют одинаковый приоритет, значит сказать, что в выражении без скобок они оба должны выполняться до операций с более низким приоритетом, такие как сложение и вычитание, и что они оба должны выполняться после операций более высокого приоритета, таких как возведение в степень.

Какую скобку вы решите в первую очередь?

Согласно правилу BODMAS, если выражение содержит скобки ((), {}, []) мы должны сначала решить или упростить скобку, за которой следует «порядок» (что означает степени и корни и т. д.), затем деление, умножение, сложение и вычитание слева направо.

Каковы основные математические формулы? Некоторые примеры основных математических формул:

Периметр прямоугольника = 2 (длина + ширина)
Площадь прямоугольника = длина × ширина.
Периметр квадрата = 4 × длина стороны.
Площадь квадрата = длина стороны × длина стороны.
Объем прямоугольного параллелепипеда = длина × ширина × высота.
Прибыль = Цена продажи – Себестоимость.

Чем сложение и вычитание отличаются от умножения и деления?

Хотя операций четыре, они влекут за собой только два действия: объединение или разделение. Сложение и умножение объединяют действия и вычитание и деление являются разделяющими действиями.

Может ли MDAS быть DMSA? Это в равной степени может быть DMAS, DMSA и MDAS.. Дело в том, что умножение и деление всегда имеют более высокий приоритет, чем сложение и вычитание, за исключением скобок.

В чем разница между правилом Пемдаса и Бодмаса?

PEMDAS и BODMAS абсолютно идентичны; это разные названия одного и того же набора правил. В BODMAS вы не всегда делаете «деление перед умножением», а в PEMDAS вы не всегда делаете «умножение перед делением».

1.3 Порядок действий (обзор) — Алгебра среднего уровня

Глава 1: Обзор алгебры

При упрощении выражений важно делать это в правильном порядке. Рассмотрим задачу 2 + 5 ⋅ 3, решенную двумя разными способами:

Метод 1: добавьте сначала	Метод 2: сначала умножить
Добавить: 2 + 5 ⋅ 3	Умножить: 2 + 5 ⋅ 3
Умножить: 7 ⋅ 3	Добавить: 2 + 15
Решение: 21	Решение: 17

Предыдущий пример показывает, что если одну и ту же задачу решить двумя разными способами, она приведет к двум разным решениям. Однако только один метод может быть правильным. Получается, что второй способ правильный. Порядок операций заканчивается самой простой операцией — сложением (или вычитанием). Прежде чем сложение будет завершено, выполните все повторные сложения, также известные как умножение (или деление). Прежде чем умножение будет завершено, выполните все повторные умножения, также известные как показатели степени. Когда что-то должно быть сделано не по порядку, чтобы это было на первом месте, заключайте это в скобки (или объединяйте символы). Таким образом, этот список представляет собой порядок операций, используемых для упрощения выражений.

1-й Скобки (группировка)

2-й Экспоненты

3-й Умножение и деление (слева направо)

4-й Сложение и вычитание (слева направо)

Умножение и деление находятся на одном уровне, потому что это одна и та же операция (деление — это просто умножение на обратное). Это означает, что умножение и деление должны выполняться слева направо. Поэтому в одних задачах на первом месте стоит деление, а в других — умножение. То же самое верно для сложения и вычитания (вычитание — это просто сложение противоположного). 92 & \text{Экспоненты} \\ \\ 2+3(25)&\text{Умножение} \\ \\ 2+75 & \text{Добавить} \\ \\ 77&\text{Решение} \end{массив }[/латекс]

Очень важно не забывать умножать и делить слева направо!

Оцените [latex]30\div 3 \cdot 2[/latex], используя порядок операций.

[латекс]\begin{array}{rl} 30 \div 3 \cdot 2 & \text{Разделить сначала (слева направо)} \\ \\ 10\cdot 2 & \text{Умножить} \\ \\ 20 & \text{Решение} \end{массив}[/latex]

92-7\влево[-8\вправо](-1) \} & \text{Экспоненты след.} \\ \\ 2 \{64 — 7\влево[-8\вправо](-1) \} &\ text{Умножить слева направо} \\ \\ 2 \{64 + 56(-1) \}& \text{Завершить умножение в скобках} \\ \\ 2 \{64 — 56 \} & \text{Вычесть в скобках} \\ \\ 2 \{8 \} & \text{Умножение} \\ \\ 16 & \text{Решение} \end{массив}[/latex]

Как показано в примере 1.3.3, для решения проблемы может потребоваться несколько шагов.

Ключ к успешному решению проблем с порядком операций — найти время, чтобы показать свою работу и выполнять по одному шагу за раз. Это снизит вероятность ошибиться в пути. 94-(-8)\cdot 3}{15\div 5-1} & \text{Вычислить показатель степени в числителе и разделить в знаменателе} \\ \\ \dfrac{16-(-8)\cdot 3 }{3-1} & \text{Умножить в числителе, вычесть в знаменателе} \\ \\ \dfrac{16-(-24)}{2} & \text{Добавить в числителе} \\ \\ \dfrac{40}{2} & \text{Разделить} \\ \\ 20 & \text{Решение} \end{массив}[/latex]

Другим типом группирующего символа является абсолютное значение. Все, что находится внутри набора скобок абсолютного значения, должно оцениваться, как если бы это был обычный набор скобок. Затем, как только внутренняя часть завершена, возьмите абсолютное значение — или расстояние от нуля — чтобы сделать число положительным. 92| & \text{Вычисление показателей} \\ \\ 1+3|-16-(-8)| + 2|3+25| & \text{Добавить внутри абсолютных значений} \\ \\ 1+3|-8| + 2|28| & \text{Вычисление абсолютных значений} \\ \\ 1+3(8)+2(28) & \text{Умножение слева направо} \\ \\ 1+24+56 & \text{Сложение слева направо} \\ \\ 81 & \text{Решение} \end{массив}[/latex]

Приведенный выше пример также иллюстрирует важный момент, касающийся показателей степени:

Показатели считаются относящимися только к числу, к которому они присоединены. 92(4 — 3) — 8]\} + 12}[/латекс]

Ключ ответа 1.3

Математика на основе запросов: зачем умножать перед сложением?

Продолжая наше исследование того, почему у нас есть правила для порядка операций, мы начали с того, что вспомнили, что мы узнали и задались вопросом о вчера используя нашу аналогию со сверхспособностями:

Одним из наших вопросов было: «Зачем нам нужны правила для порядка операций в математике?»

Это отличный вопрос, и сегодня мы его рассмотрели.

Когда дети узнают ПОЧЕМУ в математике (а не только КАК), они глубже узнают и ценят математику.

Конечно, гораздо проще просто объяснить правила БОДМАС/порядок работы, но мы должны хотеть, чтобы дети понимали, почему это так.

Мы начали с того, что использовали наши калькуляторы, чтобы ответить:

Некоторые из наших калькуляторов сказали, что ответ будет 19, а другие сказали 35.

Как это может быть?!?!?

Это нас озадачило.

Поделились некоторыми теориями.

Так какой же правильный ответ? / Есть ли правильный ответ?

Чтобы выяснить это, мы подумали о том, как мы могли бы интерпретировать числовое предложение, если бы не было правил.

Вспомнив, что умножение — это многократное сложение, мы обнаружили, что более разумно умножать перед сложением, потому что умножение — это многократное сложение. Чтобы разобраться в числовом предложении, мы можем разбить его на сложение:

Ученик предложил попробовать еще одно числовое предложение, и одноклассник предложил это числовое предложение:

Нам показалось интересным, как мы нашли столько разных возможных ответов.

Что это говорит нам о математике?

— Должны быть специальные правила, иначе есть более одного ответа, и это не работает с математикой.

— Представьте, если бы эти числа представляли деньги. Мы бы закончили с разными суммами!

— В математике должна быть какая-то грамматика, как в языках. Мы можем путать слова, но нам нужно следовать правилам грамматики, иначе нас могут неправильно понять. Я думаю, что в математике должны быть правила, чтобы мы все могли понять, что делаем.

Что мы должны сделать в первую очередь?

— кронштейны

Зачем?

— Потому что мы не знаем его стоимости. Нам нужно сначала выяснить это, прежде чем мы сможем что-то сделать с числовым предложением.

Итак, после скобок, что нам делать дальше?

— Вычислить 3 в квадрате.

Почему?

Потому что это тоже неизвестное значение. Нам нужно знать его значение.

Но почему бы не решить это перед раскрытием скобок?

— я думаю, это потому, что когда мы смотрим на 3 в квадрате, мы можем получить представление о его значении, но со скобками нам действительно нужно больше думать о том, какое значение оно представляет.

Эта теория нам понятна.

Итак, что нам делать дальше?

— Умножить 4 на 7