$\frac12 \sin x < \frac12 x < \frac12 \mathop {\rm tg}\nolimits x$.
Таким образом, $\sin x < x < \frac{\sin x}{\cos x}$.
$\cos x < \frac{\sin x}x < 1$. $\forall x\colon 0 < |x| < \frac\pi 2$.
Т.к. $y = \cos x$ непрерывна в точке $x=0$, то $\lim \limits _{x\to 0} \cos x = \cos 0 = 1$.
По теореме о зажатой функции $\lim \limits _{x\to 0} \frac{\sin x}x = 1$. $\blacksquare $
Следствие. $\lim \limits _{x\to 0} \frac{\arcsin x}x = 1$.
$\blacktriangle $ Рассмотрим $y = \arcsin x$. Тогда $\lim \limits _{x\to 0} y(x) = \arcsin 0 = 0$, $y(x) \neq 0$ при $x \neq 0$.
Т.к. $\lim \limits _{y\to 0} \frac{y}{\sin y} = 1$, то по теореме о замене переменной в пределе $\lim \limits _{x\to 0} \frac{\arcsin x}{x} = \lim \limits _{y\to 0} \frac{y}{\sin y} = 1$. $\blacksquare $
Лемма 5.3. Если $\{ K_ n\} , K_ n \in \mathbb {N}, K_ n\to +\infty $, то $\lim \limits _{n\to \infty }(1 + \frac1{K_ n})^{K_ n} = e$.
Арксинус, формула, график функции арксинус, урок и презентация
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:Тригонометрические уравнения. Арксинус (PPTX)
Что будем изучать:
1. Что такое арксинус?
2. Обозначение арксинуса.
3. Немного истории.
4. Определение.
5. Таблица значений арксинуса.
6. Примеры.
Что такое арксинус?
Ребята, мы с вами уже научились решать уравнения для косинуса, давайте теперь научимся решать подобные уравнения и для синуса. Рассмотрим sin(x)= √3/2. Для решения этого уравнения требуется построить прямую y= √3/2 и посмотреть: в каких точках она пересекает числовую окружность. Видно, что прямая пересекает окружность в двух точках F и G.
Эти точки и будут решением нашего уравнения. Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk,
а x2= 2π/3 + 2πk.
Решить данное уравнение довольно просто, но как решить, например, уравнение
sin(x)= 5/6. Очевидно, что это уравнение будет иметь также два корня, но какие значения будут соответствовать решению на числовой окружности? Давайте внимательно посмотрим на наше уравнение sin(x)= 5/6.
Решением нашего уравнения будут две точки: F= x1 + 2πk и G= x2 + 2πk,
где x1 – длина дуги AF, x2 – длина дуги AG.
Заметим: x2= π — x1, т.к. AF= AC — FC, но FC= AG, AF= AC — AG= π — x1.
Но, что это за точки?
Столкнувшись с подобной ситуацией, математики придумали новый символ – arcsin(x). Читается, как арксинус.
Тогда решение нашего уравнения запишется так: x1= arcsin(5/6), x2= π -arcsin(5/6).
И решение в общем виде: x= arcsin(5/6) + 2πk и x= π — arcsin(5/6) + 2πk.
Арксинус — это угол (длина дуги AF, AG) синус, которого равен 5/6.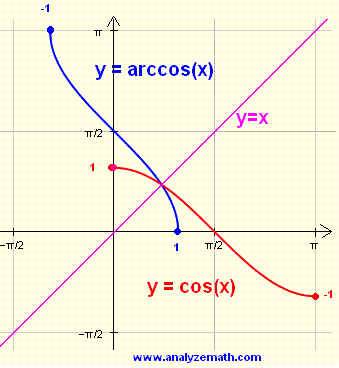
Немного истории арксинуса
История происхождения нашего символа совершенно такая же, как и у arccos. Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами.
Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга). Это вполне согласуется со смыслом понятия: arcsin x — это угол (а можно сказать и дуга), синус которого равен x.
Определение арксинуса
Если |а|≤ 1, то arcsin(a) – это такое число из отрезка [- π/2; π/2], синус которого равен а.
Если |а|≤ 1, то уравнение sin(x)= a имеет решение: x= arcsin(a) + 2πk и
Перепишем:
x= π — arcsin(a) + 2πk = -arcsin(a) + π(1 + 2k).
Ребята, посмотрите внимательно на два наших решения.
Как думаете: можно ли их записать общей формулой? Заметим, что если перед арксинусом стоит знак «плюс», то π умножается на четное число 2πk, а если знак «минус», то множитель — нечетный 2k+1.
С учётом этого, запишем общую формула решения для уравнения sin(x)=a:
Есть три случая, в которых предпочитают записывать решения более простым способом:
sin(x)=0, то x= πk,
sin(x)=1, то x= π/2 + 2πk,
sin(x)=-1, то x= -π/2 + 2πk.
Для любого -1 ≤ а ≤ 1 выполняется равенство: arcsin(-a)=-arcsin(a).
Таблица значений арксинуса
Таблица значений синуса
Таблица значений арксинуса
Напишем таблицу значений косинуса наоборот и получим таблицу для арксинуса.
Примеры
1. Вычислить: arcsin(√3/2).
Решение: Пусть arcsin(√3/2)= x, тогда sin(x)= √3/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= π/3, т.к. sin(π/3)= √3/2 и –π/2 ≤ π/3 ≤ π/2.
Ответ: arcsin(√3/2)= π/3.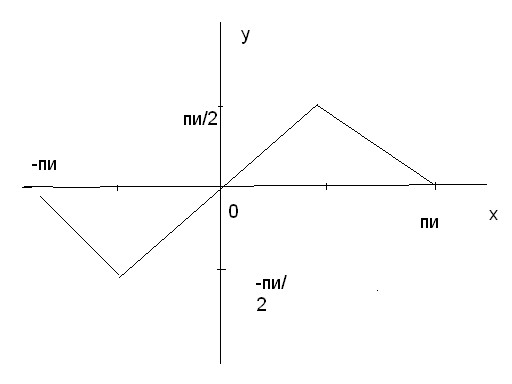
2. Вычислить: arcsin(-1/2).
Решение: Пусть arcsin(-1/2)= x, тогда sin(x)= -1/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= -π/6, т.к. sin(-π/6)= -1/2 и -π/2 ≤-π/6≤ π/2.
Ответ: arcsin(-1/2)=-π/6.
3. Вычислить: arcsin(0).
Решение: Пусть arcsin(0)= x, тогда sin(x)= 0. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0.
4. Решить уравнение: sin(x) = -√2/2.
Решение: Воспользуемся определением, тогда решение запишется в виде:
Посмотрим в таблице значение: arcsin (-√2/2 )= -π/4.
Ответ: x= -π/4 + 2πk и x= 5π/4 + 2πk.
5. Решить уравнение: sin(x) = 0.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(0) + 2πk и x= π — arcsin(0) + 2πk. Посмотрим в таблице значение: arcsin(0)= 0.
Ответ: x= 2πk и x= π + 2πk
6. Решить уравнение: sin(x) = 3/5.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(3/5) + 2πk и x= π — arcsin(3/5) + 2πk.
Ответ: x= (-1)n — arcsin(3/5) + πk.
7. Решить неравенство sin(x)
Решение: Синус — это ордината точки числовой окружности. Значит: нам надо найти такие точки, ордината которых меньше 0.7. Нарисуем прямую y=0.7. Она пересекает числовую окружность в двух точках. Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk
Задачи на арксинус для самостоятельного решения
1) Вычислить: а) arcsin(√2/2), б) arcsin(1/2), в) arcsin(1), г) arcsin(-0.8).
2) Решить уравнение: а) sin(x) = 1/2, б) sin(x) = 1, в) sin(x) = √3/2, г) sin(x) = 0.25,
д) sin(x) = -1.2.
3) Решить неравенство: а) sin (x)> 0.6, б) sin (x)≤ 1/2.
тригонометрия — Почему $\arcsin(\sin(x))$ равно $x$?
$\begingroup$
Почему $\arcsin(\sin(x))$ равно $x$?
В большинстве видеороликов только говорится об этом, но не дается никаких объяснений, кроме: «Они отменяются».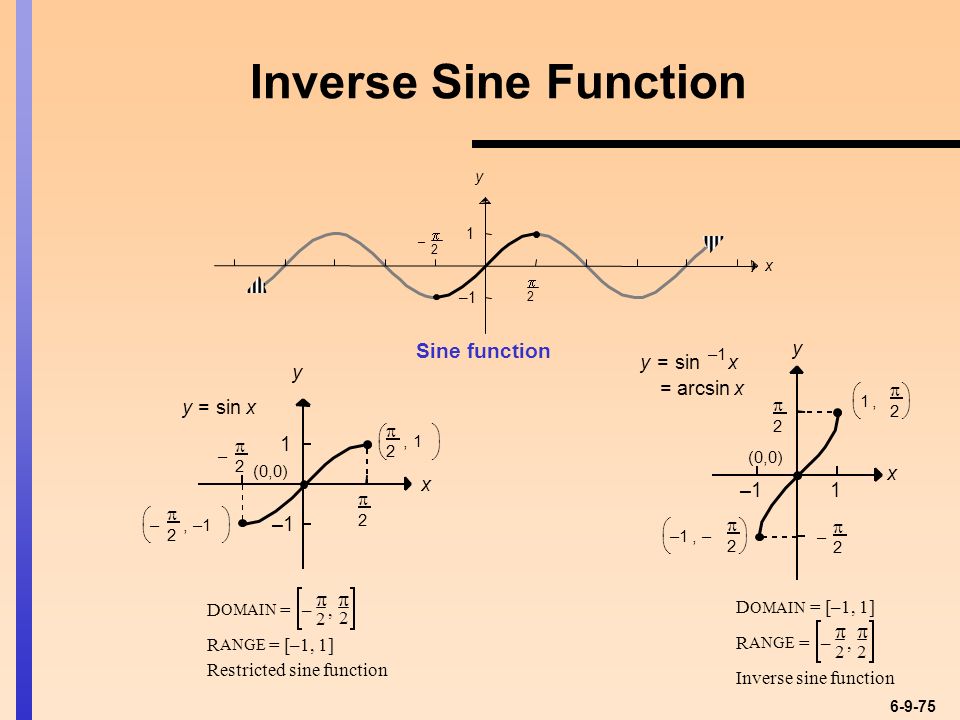
Поскольку это не взаимно, как они «отменяются»?
- тригонометрия
- обратная функция
$\endgroup$
$\begingroup$
По определению, $\arcsin\colon[-1,1]\longrightarrow\left[-\frac\pi2,\frac\pi2\right]$ является обратным сужению на $\left[-\frac\ pi2,\frac\pi2\right]$ функции синуса. Следовательно, для каждого $x\in\left[-\frac\pi2,\frac\pi2\right]$ мы имеем $\arcsin\bigl(\sin(x)\bigr)=x$, потому что это часть определения обратных функций. Другая часть определения говорит, что если $x\in[-1,1]$, то $\sin\bigl(\arcsin(x)\bigr)=x$.
$\endgroup$
1
$\begingroup$
Это , а не действительно для всех $x$! Например.
$\arcsin(\sin(10\tfrac{\pi}{4})) = \arcsin(1) = \tfrac{\pi}{2}.$
Поскольку $\sin(x)$ является периодическим, вы должны ограничить $x$ до $[- \tfrac{\pi}{2}, \tfrac{\pi}{2}].$ Для других $x$ вы получить пилообразную функцию для $\arcsin(\sin(x))$
$\endgroup$
1 9{-1}(f(x))=x$ для всех $x \in A$.
Это означает «отмена».
$\endgroup$
1
$\begingroup$
Возможно, это поможет увидеть это графически.
Ограничение $x \in [-\pi/2, \pi/2]$ для того, чтобы существовало уникальное значение для $\arcsin(x)$. Черные стрелки на графике ниже показывают влияние $x\to \sin(x) = y$. Затем красные стрелки показывают эффект $y \to \arcsin(y)=\arcsin(\sin(x)) = x$, и вы возвращаетесь к тому, с чего начали.
Вы можете вообразить расширение графика за пределы $x \in [-\pi/2, \pi/2]$, чтобы понять, почему не существует уникального значения $\arcsin(x)$.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | загар (30 градусов) | ||
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | соз(пи/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc (45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек (30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найдите точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | соз(пи/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc (60 градусов) | |
| 25 | Найти точное значение | сек (45 градусов) | |
| 26 | Найти точное значение | csc (30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | 92|
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.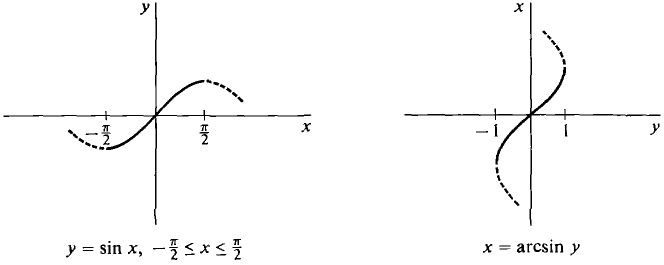 |