Для производства 4-х видов продукции используется 3 вида сырья.
Пример 1:
Для производства 4-х видов продукции используется 3 вида сырья. Нормы расхода сырья (кг) запасы (кг) его ценность от реализации единицы продукции заданы таблицей.
Составить план выпуска продукции, обеспечивающий получение максимальной прибыли, используя симплексный метод.
| Нормы расхода ресурсов на единичное изделие | Запас | |||
изделие 1 | изделие 2 | изделие 3 | изделие 4 | ||
Ресурс 1 | 5 | 10 | 15 | 20 | 150 |
Ресурс 2 | 20 | 15 | 10 | 5 | 170 |
Ресурс 3 | 15 | 9 | 4 | 17 | 190 |
Ценность | 6,5 | 8 | 14 | 10 |
|
Решение от преподавателя:
при следующих условиях-ограничений.
Составим математическую модель. Обозначим:
х1 – выпуск изделий вида А;
х2 – выпуск изделий вида В;
х3 – выпуск изделий вида С.
Запишем систему ограничений:
5x1+10x2+15x3+20x4≤150
20x1+15x2+10x3+5x4≤170
15x1+9x2+4x3+17x4≤190
Определим максимальное значение целевой функции
F(X) = 6.5x1+8x2+14x3+10x4
По экономическому содержанию переменные х1, х2, х3 могут принимать только неотрицательные значения:
х1, х2, х3 ≥0.
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
5x1+10x2+15x3+20x4+x5 = 150
20x1+15x2+10x3+5x4+x6 = 170
15x1+9x2+4x3+17x4+x7 = 190
Решим систему уравнений относительно базисных переменных: x5, x6, x7
Полагая, что свободные переменные равны 0, получим первый опорный план:
X0 = (0,0,0,0,150,170,190)
Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
x5 | 150 | 5 | 10 | 15 | 20 | 1 | 0 | 0 |
x6 | 170 | 20 | 15 | 10 | 5 | 0 | 1 | 0 |
x7 | 190 | 15 | 9 | 4 | 17 | 0 | 0 | 1 |
F(X0) | 0 | -6. | -8 | -14 | -10 | 0 | 0 | 0 |
5
Переходим к основному алгоритму симплекс-метода.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной x3, так как это наибольший коэффициент по модулю.
Вычислим значения Di по строкам как частное от деления: bi / ai3
и из них выберем наименьшее:
min (150 : 15 , 170 : 10 , 190 : 4 ) = 10
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (15) и находится на пересечении ведущего столбца и ведущей строки.
Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 | min |
x5 | 150 | 5 | 10 | 15 | 20 | 1 | 0 | 0 | 10 |
x6 | 170 | 20 | 15 | 10 | 5 | 0 | 1 | 0 | 17 |
x7 | 190 | 15 | 9 | 4 | 17 | 0 | 0 | 1 | 47. |
F(X1) | 0 | -6.5 | -8 | -14 | -10 | 0 | 0 | 0 |
5
Формируем следующую часть симплексной таблицы. Вместо переменной x5 в план 1 войдет переменная x3.
Получаем новую симплекс-таблицу:
Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
x3 | 10 | 0. | 0.667 | 1 | 1.333 | 0.067 | 0 | 0 |
x6 | 70 | 16.667 | 8.333 | 0 | -8.333 | -0.667 | 1 | 0 |
x7 | 150 | 13.667 | 6.333 | 0 | 11. | -0.267 | 0 | 1 |
F(X1) | 140 | -1.833 | 1.333 | 0 | 8.667 | 0.933 | 0 | 0 |
333
667Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю.
Вычислим значения Di по строкам как частное от деления: bi / ai1
и из них выберем наименьшее:
min (10 : 0.333 , 70 : 16.
667 , 150 : 13.667 ) = 4.2
Следовательно, 2-ая строка является ведущей.
Разрешающий элемент равен (16.667) и находится на пересечении ведущего столбца и ведущей строки.
Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 | min |
x3 | 10 | 0.333 | 0.667 | 1 | 1. | 0.067 | 0 | 0 | 30 |
x6 | 70 | 16.667 | 8.333 | 0 | -8.333 | -0.667 | 1 | 0 | 4.2 |
x7 | 150 | 13.667 | 6.333 | 0 | 11. | -0.267 | 0 | 1 | 10.976 |
F(X2) | 140 | -1.833 | 1.333 | 0 | 8.667 | 0.933 | 0 | 0 |
333
667Формируем следующую часть симплексной таблицы. Вместо переменной x6 в план 2 войдет переменная x1.
Получаем новую симплекс-таблицу:
Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
x3 | 8. | 0 | 0.5 | 1 | 1.5 | 0.08 | -0.02 | 0 |
x1 | 4.2 | 1 | 0.5 | 0 | -0.5 | -0.04 | 0.06 | 0 |
x7 | 92.6 | 0 | -0.5 | 0 | 18. | 0.28 | -0.82 | 1 |
F(X2) | 147.7 | 0 | 2.25 | 0 | 7.75 | 0.86 | 0.11 | 0 |
6
5
Конец итераций: индексная строка не содержит отрицательных элементов — найден оптимальный план
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:
Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
x3 | 8. | 0 | 0.5 | 1 | 1.5 | 0.08 | -0.02 | 0 |
x1 | 4.2 | 1 | 0.5 | 0 | -0.5 | -0.04 | 0.06 | 0 |
x7 | 92.6 | 0 | -0.5 | 0 | 18. | 0.28 | -0.82 | 1 |
F(X3) | 147.7 | 0 | 2.25 | 0 | 7.75 | 0.86 | 0.11 | 0 |
6
5
Оптимальный план можно записать так:
x1 = 4.2, x2 = 0, x3 = 8.6, x4 = 0
F(X) = 6.5•4.2 + 8•0 + 14•8.6 + 10•0 = 147.7
Работа вам нужна срочно. Не волнуйтесь, уложимся!
Заполните, пожалуйста, данные для автора:
- 22423 авторов готовы помочь тебе.
- 2402 онлайн
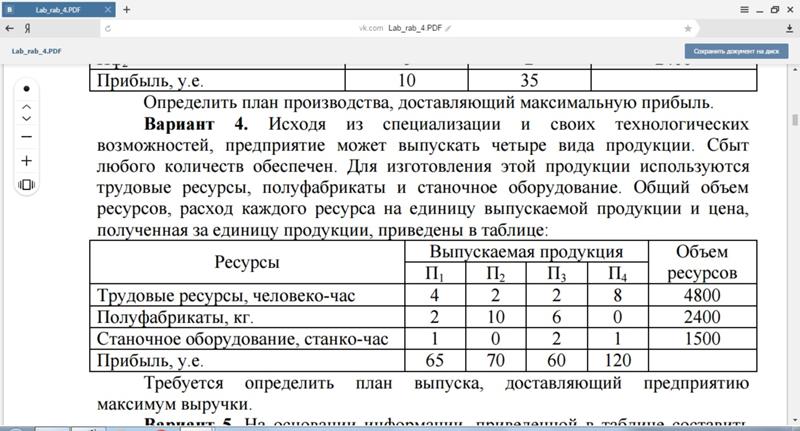
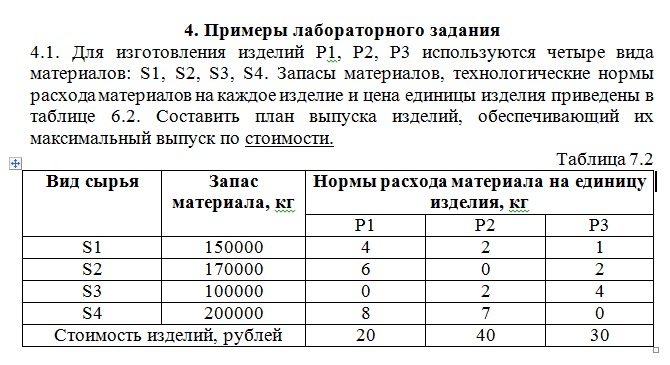
2. Для изготовления четырех видов продукции используют три вида сырья.
Запасы сырья, нормы его расхода и цена каждого продукта приведены в таблице.Тип | Нормы расхода сырья на одно изделие | Запасы | ||||
Сырья | А | Б | В | Г | сырья | |
I | 1 | 2 | 1 | 0 | 18 | |
II | 1 | 1 | 2 | 1 | 30 | |
III | 1 | 3 | 3 | 2 | 40 | |
Цена изделия | 12 | 7 | 18 | 10 | ||
При решении задачи на максимум общей стоимости выпускаемой продукции были получены следующие результаты:
Х1=18, Х2 = 0, Х3 = 0, Х4=11;
Требуется:
1)Сформулировать прямую оптимизационную задачу на максимум общей стоимости и двойственную задачу, найти ее оптимальный план;
2)Определить,
как изменятся общая стоимость продукции
и план ее выпуска при увеличении запасов
сырья I и II вида на 4 и 3 единицы соответственно
и уменьшении на 3 единицы сырья III вида.
3) Определить целесообразность включения в план изделия «Д» ценой 10 ед., на изготовление которого расходуется по две единицы каждого вида сырья ед.
3. Пусть r(t) – стоимость продукции, производимой за год на единице оборудования, возраст которого t лет; l(t) – ежегодные затраты на обслуживание этого оборудования; s(t) – остаточная стоимость оборудования; p(t) – стоимость нового оборудования через t лет от начала планового периода. Определить оптимальный цикл замены оборудования в период времени N=8 лет, чтобы прибыль от использования оборудования была максимальной.
t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
r(t) | 24 | 22 | 21 | 18 | 15 | 12 | 8 | 6 | 4 |
l(t) | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
s(t) | 22 | 18 | 15 | 11 | 7 | 3 | 0 | 0 | 0 |
p(t) | 15 | 15 | 15 | 16 | 16 | 16 | 17 | 17 | 17 |
4.
Предприятие
производит 3 вида продукции: А1,
А 2, А3, используя сырьё двух
видов: В1 и В2. Известны
затраты сырья i—го вида aij,
количества сырья каждого вида bi (i=1,2), а также
прибыль, полученная от единицы изделия j-го вида cj (j=1,2,3).
Сформулировать прямую оптимизационную задачу на максимум прибыли. и двойственную задачу, найти оптимальный план двойственной задач, используя теоремы двойственности;
Определить, как изменятся прибыль при увеличении запасов сырья I и II вида на 20 и 60 ед. соответственно.
На сколько уменьшится прибыль при принудительном выпуске единицы нерентабельной продукции.
Определить целесообразность включения в план изделия «Д» , на изготовление которого расходуется по две единицы каждого вида сырья, прибыль от которого равна 2 .
Н иже в таблице приведена матрица затрат A=(aij), справа от таблицы значение bi(i=1,2) и внизу – cj (j=1,2,3).
2 1 3
5. Решить целочисленную ЗЛП (ЦЗЛП):
Max f ( x ) = 2х1+ 5 х2
х1 + х2 61
-1/3 х1 +2/3 х2 1
х1 0, х 2 0, х1, х2 – целые.
6. Найти решение
транспортной задачи, исходные данные
которой приведены в табл., при дополнительных
условиях: из А2 в В4 и из А3 в В1 перевозки
не могут быть осуществлены, а из А4 в В2
будет завезено 40 единиц груза.
Поставщики
Потребители
В1 В2 В3 В4 В5
Запасы
А1
10
5
3
1
4
170
А2
7
3
4
5
2
230
А3
8
4
1
9
3
100
Потребности
120
80
160
90
50
7.
Найти решение
транспортной задачи, исходные данные
которой приведены в табл., при дополнительных
условиях: из А1 в В1 и из А2 в В5 перевозки
не могут быть осуществлены, а из А2 в В1
будет завезено 50 единиц груза.
Поставщики
Потребители
В1 В2 В3 В4 В5
Запасы
А1
1
2
3
1
4
200
А2
6
3
4
5
2
230
А3
8
2
1
9
3
100
Потребности
120
80
160
90
50
8.
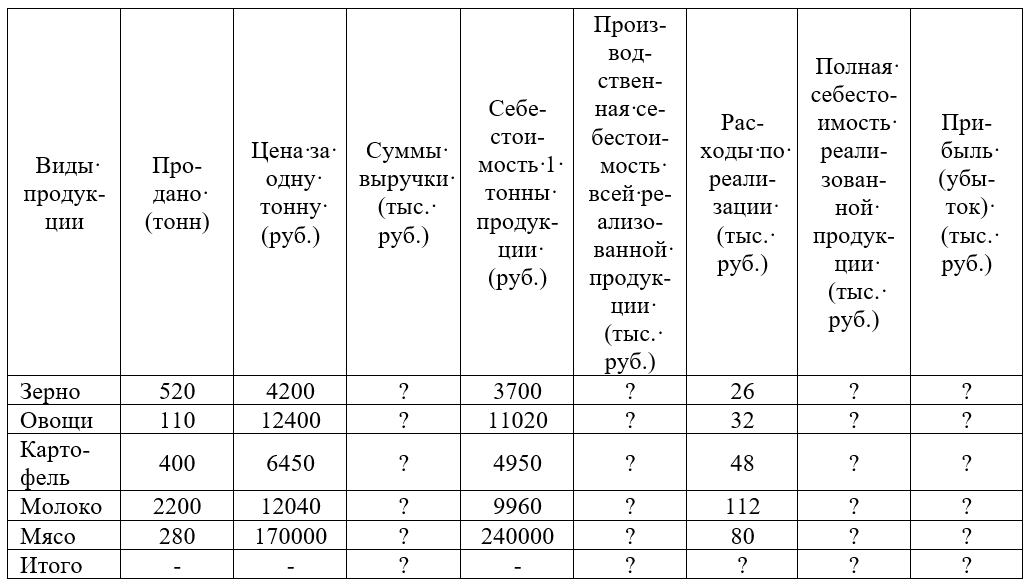Для
изготовления трех видов продукции
используют три вида сырья. Запасы
сырья, нормы его расхода и цена каждого
продукта приведены в таблице.
Тип | Нормы расхода сырья на одно изделие | Запасы | ||
Сырья | А | Б | В | сырья |
I | 4 | 2 | 1 | 180 |
II | 3 | 1 | 3 | 210 |
III | 1 | 2 | 5 | 244 |
Цена | 10 | 14 | 12 | |
При решении задачи на максимум общей стоимости выпускаемой продукции были получены следующие результаты:
Х1
= 0, Х2 =82, Х3 = 16.
Требуется:
1).Сформулировать прямую оптимизационную задачу на максимум общей стоимости, сформулировать двойственную задачу, найти оптимальный план двойственной задач, используя теоремы двойственности;
2).Определить, как изменится общая стоимость продукции и план выпуска при увеличении запасов сырья I и III вида на 4 ед. каждого;
3).Определить целесообразность включения в план изделия «Г», на изготовление которого расходуется соответственно 1, 3 и 2 ед. каждого вида сырья ценой 13 ед. и изделия «Д» на изготовление которого расходуется по две единицы каждого вида сырья ценой 12 ед.
9. Решить целочисленную ЗЛП (ЦЗЛП):
Max f ( x ) = 2х1+ 5 х2
х1 + х2 51
-1/3 х1 +2/3 х2 2
х1
0, х2 0, х1,
х2 – целые.
10. Решить графическим и симплекс-методом задачу линейного программирования. Сформулировать двойственную задачу и найти ее оптимальный план ( 2 способа)
Max f ( x ) = 3х1+ 2х2
2х1 + х2 50
5х1 + 3х2 15
х1 0, х2 0
11. Решить целочисленную ЗЛП (ЦЗЛП):
Max f ( x ) = 3х1+ 2х2
х1 + 2х2 10
х1 + х2 6.4
х1 0, х2 0, х1, х2 – целые.
12. На предприятии выпускается три вида изделий, используется при этом три вида сырья:
Сырье | Нормы затрат ресурсов на единицу продукции | Запасы | ||||
А | Б | В | сырья | |||
I | 18 | 15 | 12 | 360 | ||
II | 6 | 4 | 8 | 192 | ||
III | 5 | 3 | 3 | 180 | ||
Цена | 9 | 10 | 16 | |||
При решении задачи на максимум общей стоимости выпускаемой продукции были получены следующие результаты:
Х1 = 0; Х2 = 8; Х3 = 20;
Требуется :
Сформулировать прямую оптимизационную задачу на максимум общей стоимости продукции, сформулировать двойственную задачу, найти оптимальный план двойственной задач, используя теоремы двойственности;
Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если запас сырья I вида увеличить на 45 кг.
, а II —
уменьшить на 9кг.?Целесообразно ли выпускать изделие Г ценой 11 единиц, если нормы затрат сырья 9, 4 и 6 кг.?
, а II —
уменьшить на 9кг.?13. Решить целочисленную ЗЛП (ЦЗЛП):
Max f ( x ) = х1+ 2х2
5х1 + 9х2 45
х1 +3 х2 12
х1 0, х2 0, х1, х2 – целы
Тренировочные задачи 2
Сырье – значение, типы, примеры, учет
Сырье относится к необработанным веществам или неочищенным природным ресурсам, используемым для производства готовых товаров. Эти материалы подвергаются обработке и преобразованию в промежуточные вещества, которые в дальнейшем используются для изготовления конечных продуктов для продажи.
Примеры включают хлопок, сырую нефть, уголь, сырую биомассу, резиновые заготовки, минеральные руды, древесину и т. д.Эти необработанные или менее обработанные материалы, иногда называемые сырьевыми товарами, являются важнейшими компонентами первичного производства. Могут быть прямые или косвенные материалы, в зависимости от их использования в производстве конечной продукции. Эти факторы производстваФакторы производстваФакторы производства определяют ресурсы, используемые для производства или создания готовых товаров и услуг, продажа и покупка которых поддерживает рыночную экономику на плаву.Читать далее торговля на товарных биржах. Они также играют решающую роль в экономическом росте. Экономический рост. Экономический рост относится к увеличению совокупного производства и рыночной стоимости экономических товаров и услуг в экономике за определенный период.
СОДЕРЖАНИЕ
- Определение сырья
- Понимание сырья
- Источники сырья
- Практические примеры
- Пример № 1
- Пример № 2
- Учтение сырого материала
- Зачасто часто часто задаваемые (
- 111111 (Зачатая частопито. Часто задаваемые вопросы)
- Рекомендуемые статьи
Часто задаваемые вопросы) Вы можете свободно использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Сырье (wallstreetmojo.com)
- Сырье означает необработанные вещества или природные ресурсы, используемые для производства готовой продукции для продажи. Они составляют неотъемлемую часть управления запасами и факторами производства.
- Сырьевые товары могут быть растительными (кукуруза, пиломатериалы и сахар), животными (например, кожа, шерсть и шелк) и минеральными (железная руда, природный газ, уголь и драгоценные металлы).
- Многие страны зависят от своих запасов полезных ископаемых, которые служат незавершенным сырьем для других стран. Эти факторы производства играют решающую роль в их экономическом росте.
- Классификация незавершенных материалов на прямые (используемые непосредственно в конечном продукте) и косвенные (используемые только в процессе производства конечного продукта) упростит их учет.
Сырье является важным аспектом управления запасамиУправление запасамиУправление запасами в бизнесе относится к управлению обработкой заказов, производством, хранением и продажей сырья и готовой продукции. Это гарантирует, что нужный тип товаров будет доставлен в нужное место в нужном количестве в нужное время и по правильной цене. Таким образом, поддерживается доступность продукции на складах, в магазинах розничной торговли и у дистрибьюторов. Подробнее для производственных предприятий. Следовательно, отслеживание этих поставок становится критически важным, чтобы избежать каких-либо производственных проблем. Почти все, что производится и продается, происходит от переработки необработанных материалов, выкопанных из земли. Например, сталь является сырьем для автомобильной промышленности.
Естественно доступные в различных формах, эти ресурсы выступают в качестве основных ресурсов в массовом производстве. Массовое производство.
Массовое производство определяется как производство товаров в больших масштабах без ущерба для качества. Подробнее о некоторых продуктах. С другой стороны, перерабатываемые отходы становятся второстепенным товаром при производстве готовой продукции.
Многие страны полагаются на свои запасы полезных ископаемых, которые служат необработанным сырьем для других. Кроме того, страна с богатыми природными ресурсами может стать самодостаточной экономикой.
Экспорт — это идеальный способ получения доходов для улучшения внутреннего производства и создания новых рабочих мест. Однако экспорт сырья или незавершенных материалов может нанести ущерб экономике страны. Например, импортеры отказываются от такого соглашения из-за экспортных налогов и ограничений, налагаемых экспортером, что влияет на выручку первого Доход Доход — это сумма денег, которую бизнес может заработать в ходе своей обычной деятельности, продавая свои товары и услуги. В случае федерального правительства это относится к общей сумме доходов, полученных от налогов, которые остаются неотфильтрованными от каких-либо вычетов.
читать далее.
Эти материалы можно разделить на три категории, в зависимости от того, как они получены:
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылка атрибуцииКак указать авторство?Ссылка на статью должна быть гиперссылкой
Например:
Источник: Сырье (wallstreetmojo.com)
- Животноводство : Агропромышленность является наиболее распространенным потребителем этих товаров. Текстильная, кожевенная, молочная и другие отрасли промышленности перерабатывают такие вещества, как кожа, шерсть, шелк и т. д., для производства готовой продукции.
- На растительной основе : Это материалы, полученные из лесного и сельскохозяйственного производства. Эта категория необработанных веществ, иногда называемая нерафинированными ресурсами на растительной основе, включает сахар, целлюлозу, растительное масло, кукурузу, пиломатериалы, пробку, хлопок и т. д.
- , мрамор, железная руда, бензин, природный газ, уголь, драгоценные металлы и т. д. Вещества из этой категории используются в промышленных условиях или для изготовления красивых ювелирных изделий.
д.Для более глубокого понимания концепции рассмотрим следующие примеры сырья:
Пример №1Исследование, проведенное Организацией экономического сотрудничества и развития ОЭСР) исследовали, как экспорт полезных ископаемых может способствовать общему экономическому росту. В нем проанализированы экспортные ограничения на металлы и полезные ископаемые, введенные четырьмя африканскими странами.
Габон, Южная Африка, Замбия и Зимбабве запретили экспорт меди, марганца, свинца и хромита, соответственно, для поощрения отечественной перерабатывающей промышленности. ОЭСР изучила их меры экспортного контроля, такие как экспортные тарифы, прямые запреты на экспорт и требования о неавтоматических экспортных лицензиях.
Исследование показало, что эти ограничения не принесли никакой пользы перерабатывающей промышленности. Наоборот, результаты нанесли ущерб горнодобывающему сектору. В нем также указано, что экономическое воздействие экспортных ограничений зависит от того, какие полезные ископаемые экспортирует конкретная страна.
Явление, при котором нация обладает большим количеством природных ресурсов, но при этом страдает от отсутствия экономического роста и развития, называется «голландской болезнью» или «проклятием ресурсов». ОЭСР пришла к выводу, что сокращение препятствий для экспорта полезных ископаемых может оказать благоприятное влияние на глобальное экономическое процветание.
Пример № 2 Недавно Европейский Союз и Украина подписали Меморандум о взаимопониманииМеморандум о взаимопониманииМеморандум о взаимопонимании (МОВ) – это первоначальный уровень согласия, продемонстрированный заинтересованными сторонами в документе, для достижения определенных взаимно согласованных целей.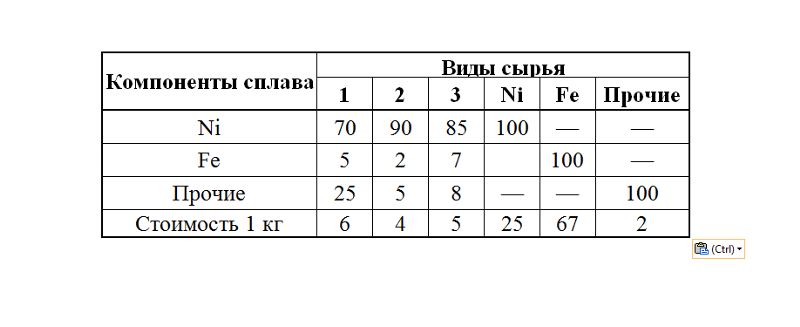
. Например, две страны подписывают Меморандум о взаимопонимании, в котором излагаются условия их предстоящего торгового партнерства.Подробнее (МоВ) для увеличения поставок сырья после негативного воздействия COVID-19.по различным отраслям. Эти поставки помогут поддержать зеленые и цифровые проекты в оборонной, аэрокосмической, автомобильной, возобновляемой энергетике, здравоохранении, электронике и других отраслях.
Это произошло после введения Европейской комиссией в сентябре 2020 года Плана действий по критически важным видам сырья. В 2020 году ЕС объявил об увеличении поставок бокситов, стронция, титана и лития для укрепления цепочек поставок полезных ископаемых после пандемии экономики восстановление.
Учет сырья Бюджетирование и учет запасов сырья Запасы сырьяЗапасы сырья — это стоимость продукции в запасах компании, которая не была использована для запасов готовой продукции и незавершенного производства. Запасы сырья – это часть стоимости запасов, которая отражается в балансе в разделе оборотных средств.
Подробнее на балансе имеют решающее значение для производственных подразделений. В балансовом отчетеБалансовый отчетБалансовый отчет — это один из финансовых отчетов компании, который представляет акционерный капитал, обязательства и активы компании в определенный момент времени. Он основан на уравнении бухгалтерского учета, которое гласит, что сумма общих обязательств и капитала владельца равна общим активам компании. Более того, в инвентарной этикетке необработанные товары указаны как оборотные активы. В поле debitDebitDebit делается запись либо об увеличении расходов компании, либо об уменьшении ее доходов. дополнительная сторона инвентарного учета при документировании неочищенного ресурса. С другой стороны, кредиторская задолженностьСчета к оплатеСчета к оплате — это сумма, причитающаяся бизнесу своим поставщикам или поставщикам за покупку продуктов или услуг. Он классифицируется как текущие обязательства в балансе и должен быть погашен в течение отчетного периода. Читать далее счет показывает покупку этих материалов как кредит.
После завершения производства запас готовой продукции Запас готовой продукции Запас готовой продукции относится к готовой продукции, полученной в процессе производства или через товары. Это конечный продукт компании, готовый к продаже на рынке. Читать далее дебетуется, а счет незавершенного производства кредитуется. Кроме того, если производственный процесс короткий, работа в технологической части опускается.
Вы можете свободно использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку на авторство. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Сырье (wallstreetmojo.com)
Разделение сырья или незавершенных материалов на прямые и косвенные упростит процесс учета.
- Прямые материалы – Это первичные входящие товары или необработанные ресурсы, такие как древесина, хлопок и т. д., используемые непосредственно компаниями для производства готовой продукции. Для прямых материалов счет незавершенного производства дебетуется необработанными материалами, использованными в производственном процессе. Наоборот, этот же счет зачисляется, когда нет инвентаря.
- Непрямые материалы — Это необработанные материалы, которые не являются непосредственно частью конечного продукта. Вместо этого они способствуют только его производству. Примеры этих долгосрочных фабричных поставок включают клей, ленту, масло и т. д. Кроме того, учет непрямых материалов, используемых в производственном процессе, учитывает их характер и тип.
Для прямых материалов счет незавершенного производства дебетуется необработанными материалами, использованными в производственном процессе. Наоборот, этот же счет зачисляется, когда нет инвентаря. На отдельном счете запасов отслеживается историческая стоимость прямых материалов. Стоимость прямых материалов. Стоимость прямых материалов — это общие затраты, понесенные компанией при покупке сырья, наряду со стоимостью других компонентов, включая расходы на упаковку, транспортировку и хранение, налоги и т. д. , которые связаны непосредственно с изготовлением и выпуском различных продуктов компании.
читать дальше. Когда товары продаются, цены на сырье отражаются в себестоимости проданных товаровСтоимость проданных товаровСебестоимость проданных товаров (COGS) представляет собой совокупную сумму прямых затрат, понесенных в связи с проданными товарами или услугами, включая прямые расходы, такие как сырье, прямые затраты на рабочую силу и другие прямые расходы. Однако он исключает все косвенные расходы, понесенные компанией.
читать далее (COGS) счет. По косвенным материалам дебетуется счет накладных расходов, а по кредиту актива запасов сырья. Остаток впоследствии распределяется между себестоимостью проданных товаров и ликвидационными запасами после отчетного периода.
Часто задаваемые вопросы (FAQ)
Что такое сырье?
Сырье – это необработанные материалы или природные ресурсы, используемые для производства или производства готовой продукции для продажи. Эти материалы могут быть использованы в их необработанном или обработанном виде, если это будет сочтено подходящим.
Примеры включают хлопок, сырую нефть, уголь, резиновые заготовки, минеральные руды, древесину и т. д.
Какие существуют два типа сырья?
Прямые материалы — это вещества, используемые непосредственно компаниями для производства готовой продукции. К ним относятся неочищенные природные ресурсы, такие как древесина, хлопок и т. д.
Косвенные материалы не являются непосредственно частью готового продукта, но способствуют его производству. Примеры этих долгосрочных активов включают клей, скотч, масло и т. д.
Каково основное правило учета сырья?
В балансовой ведомости инвентарная метка ставит незавершенные материалы в качестве оборотных средств. Запись делается по дебету счета инвентаризации при учете необработанного материала. Приобретение сырьевых товаров отражается кредитом на счете кредиторской задолженности.
Рекомендуемые статьи
Это руководство по сырью и его значению.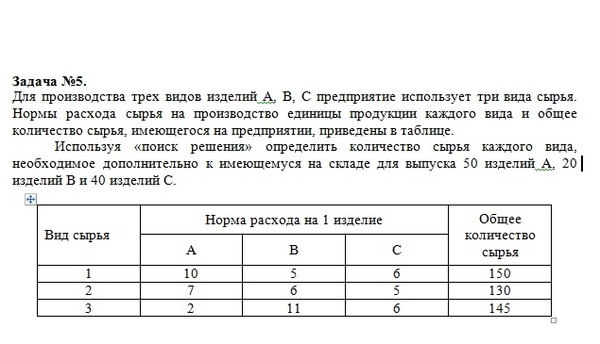
Здесь мы обсуждаем учет сырья вместе с источниками, типами и примерами. Вы можете узнать больше из следующих статей –
- Ведомость материалов
- Прямые материалы
- Глобализация
Каковы 4 типа запасов?
Если что-то и верно для товарно-материальных запасов, так это то, что они перемещаются по множеству каналов, прежде чем попасть к потребителю. Чтобы вести свой бизнес с наименьшими затратами, важно понимать четыре различных типа часто используемых запасов и этапы, через которые они проходят. Но сначала давайте определим «инвентарь».
Что такое запасы?Запасы — это все, что компания использует для продажи или производства продукции, от готовой продукции и деталей до сырья. И в зависимости от того, какие товары или услуги предоставляет ваш бизнес, инвентарь может быть чем угодно: от бананов и гвоздей до шелка-сырца и бесценных произведений искусства.
Обычно управление запасами осуществляется с помощью системы управления запасами: лист бумаги или блокнот, электронная таблица или программное обеспечение для управления запасами.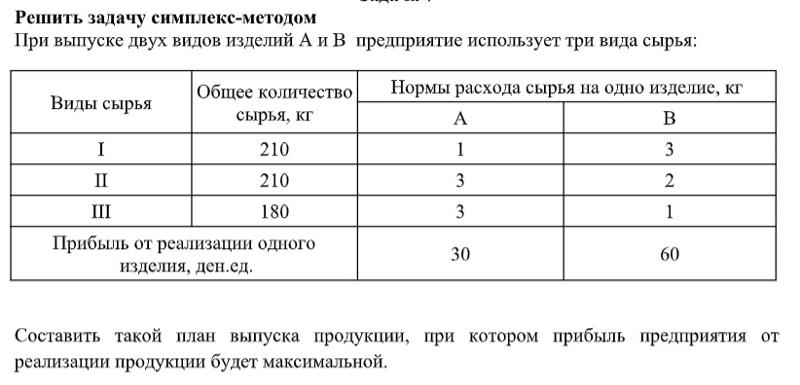
Правильно управляя своими запасами, ваш бизнес будет знать, достаточно ли у вас запасов, чтобы удовлетворить спрос клиентов, и точно знать, когда пришло время разместить новый заказ.
В компаниях практикуется жесткий контроль запасов, поскольку это влияет на производительность и прибыльность. И даже если бизнес не продает и не потребляет каждый день, почти каждая компания может извлечь выгоду из управления такими активами, как компьютеры и мебель.
Какие существуют 4 типа запасов?
Наиболее часто используются четыре типа запасов: сырье, незавершенное производство (WIP), готовая продукция и техническое обслуживание, ремонт и капитальный ремонт (MRO). Вы можете практиковать лучший контроль запасов и более разумное управление запасами, когда знаете тип запасов, которые у вас есть. Это включает в себя выбор лучшего программного обеспечения для управления запасами, чтобы отслеживать все эти запасы.
1. Сырье
Материалы, необходимые для превращения вашего инвентаря в готовый продукт, являются сырьем.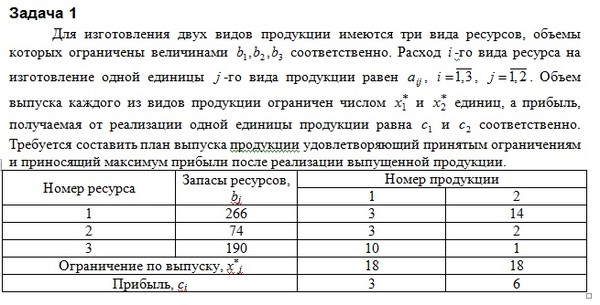
Эти товарно-материальные ценности представляют собой фрагменты составных частей, которые в настоящее время находятся на складе, но еще не использовались ни в незавершенном производстве, ни в запасах готовой продукции.
Существует два типа сырья: прямые материалы, которые используются непосредственно в готовой продукции, и косвенные материалы, которые являются частью накладных или производственных затрат.
Пример инвентаризации: Например, прямым сырьем может быть кожа для изготовления ремней для вашей компании, подпадающая под эту категорию. Или, если вы продаете искусственные цветы для своего бизнеса по дизайну интерьера, используемый хлопок также будет считаться прямым сырьем.
Косвенным сырьем могут быть лампочки, батарейки или что-либо еще, что косвенно способствует поддержанию работы вашего магазина.
Статья по теме: Что такое спецификация (BOM)?
2. Незавершенное производство Инвентарь, над которым ведется работа, является незавершенным производством (WIP), как и звучит название.
С точки зрения затрат незавершенное производство включает в себя сырье (плюс, иногда затраты на оплату труда), которые все еще находятся «в производстве» на момент окончания отчетного периода.
Другими словами, любое прямое и непрямое сырье, которое ваш бизнес использует для создания готовой продукции, является незавершенным производством.
Пример инвентаризации: Если вы продаете медицинское оборудование, упаковка будет считаться НЗП. Это потому, что лекарство не может быть продано потребителю, пока оно не будет храниться в надлежащей упаковке. Это буквально работа в процессе.
Другим примером может служить свадебное платье на заказ, которое еще не готово к концу финансового года. Кружево, шелк и тафта больше не сырье, но и не совсем готовое свадебное платье.
Готовы ли вы изменить методы инвентаризации вашего бизнеса?
Начать бесплатную пробную версию
3.
Готовая продукция Пожалуй, самым простым из всех типов инвентаризации является инвентаризация готовой продукции. Этот инвентарь вы выставили на продажу на своем веб-сайте? Это готовая продукция. Любой продукт, готовый к продаже вашим клиентам, подпадает под эту категорию.
Пример инвентаризации: Готовой продукцией может быть предварительно упакованный фруктовый салат, банный халат с монограммой или сделанный на заказ ноутбук, готовый для использования сотрудником.
4. Капитальный ремонт / ТОиРИнвентарь ТОиР, также известный как материалы для технического обслуживания, ремонта и эксплуатации, состоит из мелких деталей. Это запасы, необходимые для сборки и продажи готового продукта, но не встроенные в сам продукт.
В зависимости от специфики вашего бизнеса этот инвентарь может находиться на складе, у поставщика или в пути для доставки.
Пример инвентаризации: Например, перчатки для работы с упаковкой продукта будут считаться ТОиР.
Основные офисные принадлежности, такие как ручки, маркеры и бумага, также относятся к этой категории.
Чем может помочь программное обеспечение для управления запасами
Отслеживание всех этих запасов может показаться утомительным, особенно если ваши продукты хранятся повсюду. Это особенно верно, если вы все еще используете устаревшие системы, такие как электронные таблицы.
Но с правильным программным обеспечением для управления запасами вы можете держать все в порядке. Программное обеспечение для инвентаризации точно показывает в режиме реального времени, сколько товара у вас есть на складе, и предупреждает вас, когда вам нужно больше. Это также простой способ отслеживать, на каком этапе процесса находится весь ваш инвентарь. Настраиваемые функции делают его еще более интуитивно понятным.
С помощью программного обеспечения для управления запасами вы можете:
- Следить за текущим уровнем запасов, чтобы знать, когда заказать дополнительные запасы, которые вам нужны.
