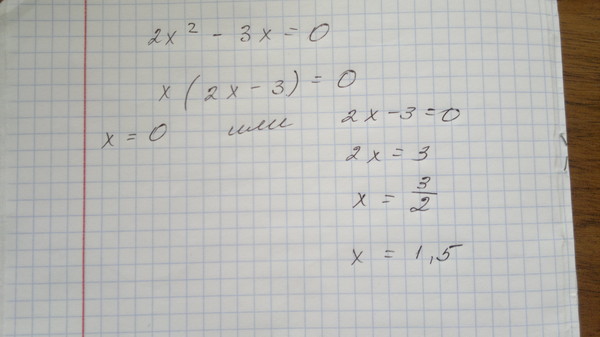( 10 в квадрате + 11 в квадрате + 12 в квадрате + 13 в квадрате + 14 в квадрате) / 365 =???
Картина русского художника Н. П. Богданова-Бельского (1868—1945), написанная в 1895 году. Отрывки истории картины и школы из https://story.dirty.ru/bogdanov-belskii-ustnyi-schet-v-narodnoi-shkole-chto-na-samom-dele-izobrazheno-na-kartine-882108/ -нужно посмотреть ссылку, чтобы увидеть картину или http://mathemlib.ru/books/item/f00/s00/z0000003/st083.shtml (видна доска)
«Многие видели картину «Устный счет в народной школе». Конец 19 века, народная школа, доска, интеллигентный учитель, бедно одетые дети, 9−10 лет, с энтузиазмом пытаются решить в уме задачу написанную на доске. Первый решивший сообщает ответ учителю на ухо, шепотом, чтобы другие не потеряли интерес.
Теперь посмотрим на задачу: (10 в квадрате 11 в квадрате 12 в квадрате 13 в квадрате 14 в квадрате) / 365 ???
… Наши дети в возрасте 9 лет не решат такую задачу, уж во всяком случае в уме! Почему чумазых и босоногих деревенских детей в деревянной школе из одной комнаты учили так хорошо, а наших детей учат так плохо?!
Не спешите возмущаться. Приглядитесь к картине. Вам не кажется, что учитель выглядит слишком интеллигентно, как-то по-профессорски, и одет с явной претензией? Почему в школьном классе такой высокий потолок и дорогущая печь с белыми кафельными изразцами? Неужели так выглядели деревенские школы и учителя в них?
Приглядитесь к картине. Вам не кажется, что учитель выглядит слишком интеллигентно, как-то по-профессорски, и одет с явной претензией? Почему в школьном классе такой высокий потолок и дорогущая печь с белыми кафельными изразцами? Неужели так выглядели деревенские школы и учителя в них?
Разумеется, выглядели они не так. .Картина называется «Устный счет в народной школе С.А.Рачинского». Сергей Рачинский — профессор ботаники Московского университета, человек с определенными правительственными связями (например, приятель обер-прокурора Синода Победоносцева), помещик — в середине жизни бросил все дела, уехал в свое имение (Татево в Смоленской губернии) и завел там (разумеется, за свой счет) экспериментальную народную школу.
Школа была одноклассной, что отнюдь не значило, что в ней учат один год. В такой школе учили тогда 3−4 года (а в двухклассных школах — 4−5 лет, в трехклассных — 6 лет). Слово одноклассный означало то, что дети трех лет обучения составляют единый класс, и один учитель занимается с ними со всеми в пределах одного урока.
Педагогическая теория Рачинского была весьма оригинальной, и разные ее части как-то плохо сходились друг с другом. Во-первых, основой образования для народа Рачинский считал обучение церковно-славянскому языку и Закон Божий, причем не столько объяснительный, сколько состоящий в заучивании молитв. Рачинский твердо верил, что знающий наизусть определенное количество молитв ребенок непременно вырастет высоконравственным человеком, причем сами звуки церковно-славянского языка уже окажут улучшающее нравственность воздействие. Для практики в языке Рачинский рекомендовал детям наниматься читать Псалтирь над покойниками (sic!).
Во-вторых, Рачинский считал, что крестьянам полезно и нужно быстро считать в уме. Преподаванием математической теории Рачинский интересовался мало, а вот устный счет в своей школе он поставил очень хорошо. Ученики твердо и быстро отвечали, сколько сдачи с рубля надо дать тому, кто покупает 6 ¾ фунта моркови по 8 ½ копейки за фунт. Возведение в квадрат, изображенное на картине, было самой сложной математической операцией, изучавшейся в его школе.
Ученики твердо и быстро отвечали, сколько сдачи с рубля надо дать тому, кто покупает 6 ¾ фунта моркови по 8 ½ копейки за фунт. Возведение в квадрат, изображенное на картине, было самой сложной математической операцией, изучавшейся в его школе.
И наконец, Рачинский был сторонником очень практичного преподавания русского языка — от учеников не требовалось ни особенных навыков правописания, ни хорошего почерка, теоретической грамматике их вообще не учили. Главное было научиться бегло читать и писать, пусть корявым почерком и не слишком грамотно, но понятно, то, что может пригодиться крестьянину в быту: простые письма, прошения и пр. Еще в школе Рачинского преподавался кой-какой ручной труд, дети пели хором, и на этом всё образование и заканчивалось.
Рачинский был настоящим энтузиастом. Школа стала всей его жизнью. Дети у Рачинского жили в общежитии и были организованы в коммуну: они выполняли все работы по хозяйственному обслуживанию самих себя и школы. Рачинский, не имевший семьи, проводил с детьми всё время с раннего утра до позднего вечера, а так как он был очень добрый, благородный и искренне привязанный к детям человек, его влияние на учеников было огромным. Кстати, первому решившему задачу ребенку Рачинский выдавал пряник (в буквальном смысле слова, кнута же у него не было).
Кстати, первому решившему задачу ребенку Рачинский выдавал пряник (в буквальном смысле слова, кнута же у него не было).
Сами школьные занятия занимали 5−6 месяцев в году, а в остальное время Рачинский индивидуально занимался с детьми постарше, готовя их к поступлению в различные учебные заведения следующей ступени; начальная народная школа не была прямо связана с другими учебными заведениями и после нее нельзя было продолжить обучение без добавочной подготовки. Рачинский желал видеть наиболее продвинутых из своих учеников учителями начальной школы и священниками, так что готовил он детей преимущественно в духовные и учительские семинарии. Бывали и значительные исключения — прежде всего, это сам автор картины, Николай Богданов-Бельский, которому Рачинский помог попасть в Московское училище живописи, ваяния и зодчества. Но, как ни странно, вести крестьянских детей по магистральному пути образованного человека — гимназия / университет / государственная служба — Рачинский не желал.
Рачинский писал популярные педагогические статьи и продолжал пользоваться определенным влиянием в столичных интеллектуальных кругах.
…Картина изображает не типичную, а уникальную школу. Это памятник Сергею Рачинскому, уникальной личности и педагогу, последнему представителю той когорты консерваторов и патриотов, к которой еще нельзя было отнести известное выражение «патриотизм — последнее прибежище негодяя». Массовая народная школа была в хозяйственном отношении обустроена значительно беднее, курс математики в ней был короче и проще, а преподавание слабее. И, конечно же, ученики обыкновенной начальной школы не могли не только решить, но и понять задачу, воспроизведенную на картине.
Кстати, а каким методом школьники решают задачу на доске? Только прямым, в лоб: умножить 10 на 10, запомнить результат, умножить 11 на 11, сложить оба результата, и так далее.
Или (вторая нижняя ссылка — школа СССР):
«Надо было сложить 121, 144, 169 и 196. Я попарно сложил числа первое и третье, второе и четвертое. Так удобнее. Получилось 290 плюс 340. Общая сумма, включая первую сотню — 730. Делим на 365 — получаем 2.
— в ряду двузначных чисел — у первых пяти его представителей — есть удивительное свойство. Сумма квадратов первых трех чисел ряда (10, 11 и 12) равна сумме квадратов следующих двух (13 и 14). И равняется эта сумма 365. Легко запомнить! Столько дней в году. Если год не високосный. Зная это свойство, ответ можно получить за секунду. Без всякой интуиции…»
Полностью можно прочитать по упомянутой ссылке. Варианты счета:https://ru.wikipedia.org/wiki/%D0%A3%D1%81%D1%82%D0%BD%D1%8B%D0%B9_%D1%81%D1%87%D1%91%D1%82. _%D0%92_%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%BD%D0%BE%D0%B9_%D1%88%D0%BA%D0%BE%D0%BB%D0%B5_%D0%A1._%D0%90._%D0%A0%D0%B0%D1%87%D0%B8%D0%BD%D1%81%D0%BA%D0%BE%D0%B3%D0%BE
или школа СССР:
http://www.viskra.ru/2013/06/blog-post_28.html
_%D0%92_%D0%BD%D0%B0%D1%80%D0%BE%D0%B4%D0%BD%D0%BE%D0%B9_%D1%88%D0%BA%D0%BE%D0%BB%D0%B5_%D0%A1._%D0%90._%D0%A0%D0%B0%D1%87%D0%B8%D0%BD%D1%81%D0%BA%D0%BE%D0%B3%D0%BE
или школа СССР:
http://www.viskra.ru/2013/06/blog-post_28.html