✅ Гиперболические функции — poznanie-21vek.ru
Содержание
- 1 Гиперболические функции
- 1.1 Гиперболические функции — sh, ch, th, cth, sech, csch
- 1.2 Введение
- 1.3 Гиперболические функции
Гиперболические функции — sh, ch, th, cth, sech, csch
ОПРЕДЕЛЕНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
Гиперболический синус
sh x = (e x — e -x )/2
Гиперболический косинус
ch x = (e x + e -x )/2
Гиперболический тангенс
th x = (e x — e -x )/(e x + e -x )
Гиперболический котангенс
cth x = (e x + e -x )/(e x — e -x )
Гиперболический секанс
sech x = 2/(e x + e -x )
Гиперболический косеканс
csch x = 2/(e x — e -x )
ОТНОШЕНИЯ МЕЖДУ ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ
cth x = 1/th x = ch x/sh x
ch 2 x — sh 2 x = 1
sech 2 x + th 2 x = 1
cth 2 x — csch 2 x = 1
ФУНКЦИИ ОТРИЦАТЕЛЬНЫХ АРГУМЕНТОВ
ФОРМУЛЫ СЛОЖЕНИЯ
ch (x ± y) = ch x ch y ± sh x sh y
th(x ± y) = (th x ± th y)/(1 ± th x. th y)
th y)
cth(x ± y) = (cth x cth y ± l)/(cth y ± cth x)
ФОРМУЛЫ ДВОЙНЫХ УГЛОВ
sh 2x = 2 sh x ch x
ch 2x = ch 2 x + sh 2 x = 2 ch 2 x — 1 = 1 + 2 sh 2 x
th 2x = (2th x)/(1 + th 2 x)
ФОРМУЛЫ ПОЛОВИННЫХ УГЛОВ
$text frac= pm sqrt x — 1>>$ [+ если x > 0, — если x 0, — если x 3 x
ch 3x = 4 ch 3 x — 3 ch x
th 3x = (3 th x + th 3 x)/(1 + 3 th 2 x)
sh 4x = 8 sh 3 x ch x + 4 sh x ch x
ch 4x = 8 ch 4 x — 8 ch 2 x + 1
th 4x = (4 th x + 4 th 3 x)/(1 + 6 th 2 x + th 4 x)
СТЕПЕНИ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
sh 3 x = ¼sh 3x — ¾sh x
ch 3 x = ¼ch 3x + ¾ch x
sh 4 x = 3/8 — ½ch 2x + 1/8ch 4x
ch 4 x = 3/8 + ½ch 2x + 1/8ch 4x
СУММА, РАЗНИЦА И УМНОЖЕНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
sh x + sh y = 2 sh ½(x + y) ch ½(x — y)
sh x — sh y = 2 ch ½(x + y) sh ½(x — y)
ch x + ch y = 2 ch ½(x + y) ch ½(x — y)
ch x — ch y = 2 sh ½(x + y) sh ½(x — y)
sh x sh y = ½(ch (x + y) — ch (x — y))
ch x ch y = ½(ch (x + y) + ch (x — y))
sh x ch y = ½(sh (x + y) + sh (x — y))
ВЫРАЖЕНИЕ ГИПЕРБОЛТЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ДРУГИЕ
В следующем мы принимаем, что x > 0. Если x -1 a называется обратным гиперболическим синусом of x. Аналогично определяются и другие обратные гиперболические функции. Обратные гиперболические функции являются многозначными, но в случае обратных тригонометрических функций мы ограничимся основными значениями, при которых их можно рассматривать как однозначные.
Если x -1 a называется обратным гиперболическим синусом of x. Аналогично определяются и другие обратные гиперболические функции. Обратные гиперболические функции являются многозначными, но в случае обратных тригонометрических функций мы ограничимся основными значениями, при которых их можно рассматривать как однозначные.
Ниже приведен список основных значений [если не указано иное] обратных гиперболических функций, выраженных через логарифмические функции, которые принимаются в качестве вещественных.
Функция sh x = e x — e — x 2 называется гиперболическим синусом. Функция ch x = e x + e — x 2 н азывается гиперболическим косинусом.
Подобно тому, как тригонометрические синус и косинус являются координатами точки на координатной окружности, гиперболические синус и косинус являются координатами точки на гиперболе.
Эти функции определены и непрерывны на всей числовой оси. Гиперболический синус является нечетной функцией, возрастающей на всей числовой оси. Гиперболический косинус является четной функцией, убывающей на промежутке (–∞; 0) и возрастающей на промежутке (0; +∞) . Точка (0; 1) является минимумом этой функции.
Гиперболический косинус является четной функцией, убывающей на промежутке (–∞; 0) и возрастающей на промежутке (0; +∞) . Точка (0; 1) является минимумом этой функции.
Графики функций y = sh x и y = ch x
По аналогии с тригонометрическими функциями определены гиперболические тангенс и котангенс: th x = sh x ch x , cth x = ch x sh x .
Тангенс определён на всей числовой оси, котангенс – при всех x ≠ 0 ( lim x → ± 0 cth x = ± ∞ ). Обе функции непрерывны на всей области определения, нечетны и имеют горизонтальные асимптоты y = –1 ( при x → –∞) и y = 1 ( при x → +∞).
Графики функций y = th x и y = сth x
Приведём некоторые формулы, связанные с гиперболическими функциями.
sh x + ch x = e x
ch 2 x – sh 2 x = 1 ch 2x = ch 2 x + sh 2 x sh 2x = 2 sh x ch x sh (x + y) = sh x ch y + ch x sh y ch (x + y) = ch x ch y + sh x sh y
Функции, обратные гиперболическим синусу и тангенсу, определены и непрерывны на всей числовой оси. Они обозначаются соответственно arsh x и arth x. У гиперболического косинуса определены сразу две обратные функции: arch–x при x ≤ 0 и arch+x при x ≥ 0.
Они обозначаются соответственно arsh x и arth x. У гиперболического косинуса определены сразу две обратные функции: arch–x при x ≤ 0 и arch+x при x ≥ 0.
Графики функций y = arsh x и y = arth x. Графики функции y = arch– x и y = arch+ x.
В заключение приведём формулы для обратных гиперболических функций: arsh x = ln x + 1 + x 2 , x ∈ ℝ arth x = 1 2 ln 1 + x 1 — x , |x| arch — x = ln x — x 2 — 1 , x ≥ 1, arch + x = ln x + x 2 — 1 , x ≥ 1.
Введение
В математике и её приложениях к естествознанию и технике находят широкое применение показательные функции. Это, в частности, объясняется тем , что многие изучаемые в естествознании явления относятся к числу так называемых процессов органического роста, в которых скорости изменения участвующих в них функций пропорциональны величинам самих функций.
Если обозначить через функцию, а через аргумент, то дифференциальный закон процесса органического роста может быть записан в виде где некоторый постоянный коэффициент пропорциональности.
Интегрирование этого уравнения приводит к общему решению в виде показательной функции
Если задать начальное условие при , то можно определить произвольную постоянную и, таким образом, найти частное решение которое представляет собой интегральный закон рассматриваемого процесса.
К процессам органического роста относятся при некоторых упрощающих предположениях такие явления, как, например, изменение атмосферного давления в зависимости от высоты над поверхностью Земли, радиоактивный распад, охлаждение или нагревание тела в окружающей среде постоянной температуры, унимолекулярная химическая реакция (например, растворение вещества в воде), при которой имеет место закон действия масс ( скорость реакции пропорциональна наличному количеству реагирующего вещества ), размножение микроорганизмов и многие другие.
Возрастание денежной суммы вследствие начисления на неё сложных процентов (проценты на проценты) также представляет собой процесс органического роста.
Эти примеры можно было бы продолжать.
Наряду с отдельными показательными функциями в математике и её приложениях находят применение различные комбинации показательных функций, среди которых особое значение имеют некоторые линейные и дробно-линейные комбинации функций и так называемые гиперболические функции. Этих функций шесть, для них введены следующие специальные наименования и обозначения:
Возникает вопрос, почему даны именно такие названия, причём здесь гипербола и известные из тригонометрии названия функций: синус, косинус, и т. д.? Оказывается, что соотношения, связывающие тригонометрические функции с координатами точек окружности единичного радиуса, аналогичны соотношениям, связывающим гиперболические функции с координатами точек равносторонней гиперболы с единичной полуосью. Этим как раз и оправдывается наименование гиперболических функций.
Гиперболические функции
Функции, заданные формулами называют соответственно гиперболическим косинусом и гиперболическим синусом.
Эти функции определены и непрерывны на , причем — четная функция, а — нечетная функция.
Рисунок 1.1 — Графики функций
Из определения гиперболических функций и следует, что:
По аналогии с тригонометрическими функциями гиперболические тангенс и котангенс определяются соответственно формулами
Функция определена и непрерывна на , а функция определена и непрерывна на множестве с выколотой точкой ; обе функции — нечетные, их графики представлены на рисунках ниже.
Рисунок 1.2 — График функции
Рисунок 1.3 — График функции
Можно показать, что функции и — строго возрастающие, а функция — строго убывающая. Поэтому указанные функции обратимы. Обозначим обратные к ним функции соответственно через .
Рассмотрим функцию, обратную к функции , т.е. функцию . Выразим ее через элементарные. Решая уравнение относительно , получаем Так как , то , откуда
Заменяя на , а на , находим формулу для функции, обратной для гиперболического синуса:
Замечание. Название “гиперболические функции” объясняется тем, что уравнения можно рассматривать как параметрические уравнения гиперболы . Параметр в уравнениях гиперболы равен удвоенной площади гиперболического сектора. Это отражено в обозначениях и названиях обратных гиперболических функций, где частица есть сокращение латинского (и английского) слова “” — площадь.
Параметр в уравнениях гиперболы равен удвоенной площади гиперболического сектора. Это отражено в обозначениях и названиях обратных гиперболических функций, где частица есть сокращение латинского (и английского) слова “” — площадь.
Упражнение. Доказать формулы:
Выразим ее через элементарные. Решая уравнение относительно , получаем так как , то , откуда Заменяя на , а на получим
Источники:
http://www.math20.com/ru/vysshaya-matematika/giperbolicheskie-funktsii/giperbolicheskie-funktsii.html
http://mathematics.ru/textbook4/chapter2/section4/paragraph5/
http://studbooks.net/2398279/matematika_himiya_fizika/giperbolicheskie_funktsii
Почему Швейцария называется «Швейцарией»? — SWI swissinfo.ch
Фреска «Fundamentum» художника Генриха Даниота (Heinrich Danioth. 1896-1953) на фасаде «Музея Союзной грамоты» («Bundesbriefmuseum») в городе Швиц, столице одноименного кантона. На ней изображена мифологическая клятва первых швейцарцев, образовавших, якобы, Швейцарию в 1291 году.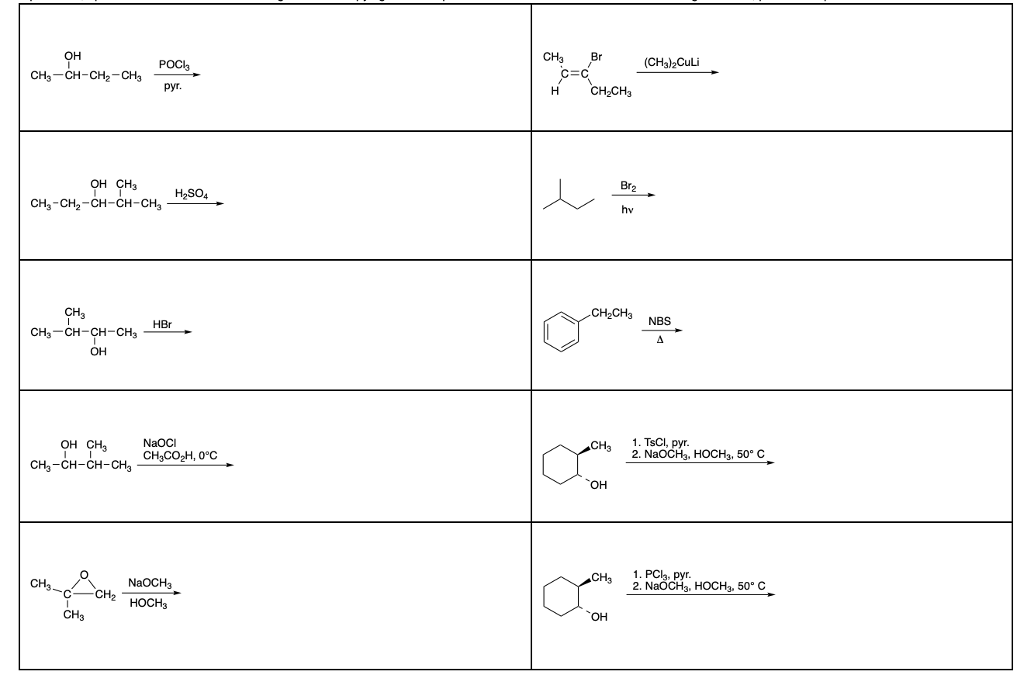 В действительности эта история выглядит совершенно иначе. Keystone
В действительности эта история выглядит совершенно иначе. KeystoneКаждая страна имеет свое название, и у этого названия есть своя история. Давайте посмотрим, откуда взялось название «Швейцария»?
Этот контент был опубликован 01 августа 2019 года — 07:00Для начала уточним, что слово «Швейцария» является русскоязычным адаптированным вариантом немецкого общепринятого названия страны «Die Schweiz» в современном написании. Почему мы отталкиваемся от немецкого названия? Швейцария как страна и нация начинает складываться в немецкоязычном пространстве, а потому немецкие названия в соответствии с принципом старшинства являются более «аутентичными».
Итак, откуда пошло название страны? Для начала уточним, однако, какое именно. Официальное немецкое название Швейцарии звучит следующим образом: «Schweizerische Eidgenossenschaft». Как это перевести на русский? С первым словом все понятно, но что такое «Eidgenossenschaft»? Немецкие обозначения «Eidgenonssenschaft» / «eidgenössisch» носят официально-бюрократический характер. В основе этих обозначений находится понятие «Eid», или «клятва», а также «Genossenschaft», или «товарищество».
Как это перевести на русский? С первым словом все понятно, но что такое «Eidgenossenschaft»? Немецкие обозначения «Eidgenonssenschaft» / «eidgenössisch» носят официально-бюрократический характер. В основе этих обозначений находится понятие «Eid», или «клятва», а также «Genossenschaft», или «товарищество».
Таким образом, «Schweizerische Eidgenossenschaft» следует переводить как «Швейцарское товарищество по клятве». Понятно? Ничего не понятно. Какая «клятва» и какое «товарищество»? Уточним, что речь идет о «Союзной грамоте» 1291 года и о механизме взаимного обеспечения гарантий безопасности отдельных регионов в условиях отсутствия устойчивых институтов имперской власти в альпийских областях будущей Швейцарии в период раннего средневековья. Подробнее — в этом материале.
Показать больше
Так или иначе, наименование «Швейцарское товарищество по клятве» применяется только в Швейцарии и только на немецком языке, а за рубеж, в том числе и в русский язык, попал и закрепился франкоязычный вариант Confédération suissе, или Швейцарская Конфедерация. И это название тоже многих приводит в недоумение, особенно, когда читаешь, что «Швейцарская Конфедерация является федерацией». Так чем же все-таки является страна, с учетом того, что федерация и конфедерация — это две взаимоисключающие формы государственного устройства?
И это название тоже многих приводит в недоумение, особенно, когда читаешь, что «Швейцарская Конфедерация является федерацией». Так чем же все-таки является страна, с учетом того, что федерация и конфедерация — это две взаимоисключающие формы государственного устройства?
Показать больше
Если совсем коротко, то ситуация выглядит довольно просто: латинское «Confoederatio» является по смыслу прямым переводом понятия «Eidgenossenschaft», а по сути — как раз-таки «федерацией» в той форме, как ее понимали в средневековье. Еще короче: то, что в средние века называли «конфедерацией», означает форму государственного устройства, которая в современном мире называется «федерацией». И тогда, если учитывать этот смысловой сдвиг, все более или менее становится на свои места: современная Швейцария является классической федерацией.
Изначальный регион
Куда более распространено, разумеется, название «Швейцария», которая является прямой адаптацией локального топонима «Schwyz».
Еще одно название Швейцарии — «Confoederatio Helvetica». Это латинское словосочетание ссылается на одно из племен, населявших территорию нынешней Швейцарии. Звалось это племя «гельветы». Оно было первым племенем, упомянутым в письменных источниках по истории Швейцарии. Краткий вариант этого имени, понятие «Helvetia», до сего дня используется на почтовых марках и монетах. Кроме того, «гельветикой» называется один из самых популярных шрифтов, о чем подробнее можно прочитать ниже.
Начальные буквы слов «Confoederatio» и «Helvetica» образуют также сокращения:
CH: используется в качестве обозначения швейцарского доменного имени в сети интернет и на автомобильных номерах;
CHF: международное обозначение швейцарской валюты «швейцарский франк»;
HB: национальный код, используемый в гражданской авиации;
HB9: национальный код, используемый радиолюбителями.
Старое название «Helvetia» часто неофициально используется внутри Швейцарии, с тем чтобы сгладить противоречия немецко- и франкоязычных регионов страны. Швейцарские франкофоны, обычно либерально настроенные, не очень довольны тем, что название страны выводится из наименования немецкого, да еще и консервативного региона Швиц. Поэтому название «Helvetia» призвано играть роль своего рода символического моста между двумя важнейшими лингвистическими ареалами страны, разделенными так называемым «Картофельным рвом», подробнее о котором можно прочитать в этом материале.
Показать больше
Показать больше
В соответствии со стандартами JTI
Показать больше: Сертификат по нормам JTI для портала SWI swissinfo.ch
Показать больше
Поделиться этой историей
XC70 I — что это за номер CH- ???? — Клуб Вольво
Интересно !
x
JavaScript is disabled. For a better experience, please enable JavaScript in your browser before proceeding.
- Thread starter Romeo
- Start date
- Replies 3
- Views 12K
- Status
- Not open for further replies.

Ответить
Romeo
Постоянный участник
- Joined
- Mar 15, 2013
- Messages
- 45
- Имя
- YV1BZ985681014289
- #1
Езжу на Вольво месяц и вот при поиске запчастей в каталоге exist постоянно натыкаюсь на какой то номер с буквами CH- далее идут шесть цифр. судя по всему это какой то инд.номер автомобиля. Никак не могу определить какой у меня этот номер, те где его искать и что это??
Хелп пжл!!
Sort by date Sort by votes
little
- Joined
- Dec 20, 2010
- Messages
- 18,229
- Модель
- Пешеход
- Регион
- Санкт-Петербург
- #2
Это последние 6 цифр вин кода
Добавлено через 56 секунд
СН- это от вин кода
-СН это до вин кода
Upvote 0 Downvote
Евгений_
- Joined
- Jan 17, 2010
- Messages
- 2,450
- Марка машины
- Volvo
- Модель Volvo
- XC70 II P2
- Регион
- Московская область
- Имя
- Евгений
- #3
CH — это от слова «chassis» — № шасси. Как уже сказали, последние цифры VIN.
Как уже сказали, последние цифры VIN.
Upvote 0 Downvote
Leo_Spb
- Joined
- Jul 31, 2006
- Messages
- 18,961
- Марка машины
- Volvo
- Имя
- Леонид
- #4
Romeo said:
Езжу на Вольво месяц и вот при поиске запчастей в каталоге exist постоянно натыкаюсь на какой то номер с буквами CH- далее идут шесть цифр. судя по всему это какой то инд.номер автомобиля. Никак не могу определить какой у меня этот номер, те где его искать и что это??
Хелп пжл!!Click to expand.
..
лучше спросите вольвовские номера тут на форуме, можете для общего развития почитать сборник тем по S80II — там много идентичного с XC70II — они на одной платформе
Upvote 0 Downvote
- Status
- Not open for further replies.
Беларусь Чтиво на минуту S40 продали без переоформления. Эпопея поисков машины
- liner
- Вольво в Беларуси
2
Последнее сообщение: blackkasper
- Replies
- 24
- Views
- 2K
blackkasper
F. A.Q. Проверка автомобиля перед покупкой. Подробно от просмотра объявлений до оформления.
A.Q. Проверка автомобиля перед покупкой. Подробно от просмотра объявлений до оформления.
- РосАвтоПодбор
- Хочу VOLVO. Нужны советы
Последнее сообщение: РосАвтоПодбор
- Replies
- 6
- Views
- 10K
РосАвтоПодбор
XC70 I Бензин Творится что-то неладное
- AlexandrV
- Двигатель, ECM
Последнее сообщение: AlexandrV
- Replies
- 10
- Views
- 2K
AlexandrV
Москва Не актуально СТО Вольво МосАвтоШина. Опыт работы.
Опыт работы.
- VNeal
- Архив
23
Последнее сообщение: РАФ
- Replies
- 49
- Views
- 4K
РАФ
XC90 I Итог неизвестен Троит, проблемы с двигателем
- Дмитрий001
- Архив
Последнее сообщение: Kertman
- Replies
- 4
- Views
- 4K
Kertman
S60 I F. A.Q. Жидкости во все узлы S60R, достало, запутался полностью.
A.Q. Жидкости во все узлы S60R, достало, запутался полностью.
- RedAngel
- Масла, тех. жидкости
Последнее сообщение: RedAngel
- Replies
- 2
- Views
- 566
RedAngel
Все модели F.A.Q. Всё об источниках воды в салоне.
- Vicc67
- Общие вопросы
Последнее сообщение: skydriver
- Replies
- 2
- Views
- 12K
skydriver
Share:
Vkontakte Odnoklassniki Mail. ru Liveinternet Livejournal Facebook WhatsApp Telegram Viber Skype Email Share Link
ru Liveinternet Livejournal Facebook WhatsApp Telegram Viber Skype Email Share Link
Что означает CH? Бесплатный словарь
Также найдено в: Словарь, Тезаурус, Медицинский, Финансовый, Энциклопедия, Википедия.
Фильтр категорий: Показать все (104)Наиболее распространенные (1)Технологии (6)Правительство и военные (16)Наука и медицина (29)Бизнес (12)Организации (19)Сленг / жаргон (15)
| Акроним | Определение |
|---|---|
| CH | Confoederatio Helvetica (Швейцарская Конфедерация; Швейцария) |
| CH | Change |
| CH | China |
| CH | Child |
| CH | Channel |
| CH | Church |
| CH | Chapter |
| CH | История церкви |
| CH | Возвращение домой |
| CH | Цепочка | 9 CH0014 Chief |
| CH | Community Health (various organizations) |
| CH | Switzerland (country code, top level domain) |
| CH | Credit Hours |
| CH | Мэрия |
| CH | Чемпион |
| CH | Club House (карты Великобритании) |
| Chestry0015 | |
| CH | Children’s Hospital |
| CH | Central Heating |
| CH | Cultural Heritage |
| CH | Chester (postcode, United Kingdom) |
| CH | Chemin (французский: Path; обозначение улицы Canada Post) |
| CH | Холестерин |
| CH | Chorus |
| CH | College Humor (online website) |
| CH | |
| CH | Courthouse |
| CH | Clearinghouse |
| CH | Carolina Herrera |
| CH | Chennai (столица Тамилнаду, Индия) |
| CH | Шиншилла (порода кроликов) |
| CH | Campbell Hausfeld (Cincinnati, OH) |
| CH | Chronic Hepatitis |
| CH | Centre Hospitalier (French: general hospital) |
| CH | Chaplain |
| CH | Come Home |
| CH | Грузовой вертолет |
| CH | Columbia House (клуб звукозаписи) | Critical Habitat |
| CH | Cluster Headache |
| CH | Ciudad de La Habana (postcode for Havana, Cuba) |
| CH | Carolina Hurricanes (NHL) |
| CH | Орден Почетных товарищей (осн. 1917; Великобритания) 1917; Великобритания) |
| CH | Голова управления |
| CH | Городской охотник 0018 |
| CH | Peoples Republic of China (including Tibet) |
| CH | Cerebral Hemisphere |
| CH | Crack-Head |
| CH | Customs House |
| CH | Ручка для переноски |
| CH | Confoederatio Helvetica (Швейцария, международная автоматическая идентификация) |
| CH | Continuum Hypothesis |
| CH | Crown Hill (cemetery) |
| CH | Cargo Hold |
| CH | Center Hall (real estate) |
| CH | Дом Завета |
| CH | Обычное оборудование |
| CH | Благотворительный госпиталь |
| Товарищ чести | 0015 |
| CH | Cambridge Heart, Inc. (Bedford, MA) (Bedford, MA) |
| CH | Call Hold |
| CH | Chieti, Abruzzo (Italian province) |
| CH | Завоевание Героя |
| Ch | Синдром Чедиак-Хигаши |
| Ch | House Height |
| CH | КРИСТАЯ (BLU School), BLU).0018 |
| CH | Compass Heading |
| CH | Controlled Humidity |
| CH | Contingency Hospital (US DoD) |
| CH | Correspondent Host |
| CH | Рукоятка для зарядки (огнестрельное оружие) |
| CH | Критические часы |
| CH | Контактная рукоятка |
| CH0015 | Clone High (cartoon) |
| CH | Component Handling |
| CH | Communications House (light rail, Dallas, Texas) |
| CH | Certified Hydrographer (surveying) |
| CH | Корона-пятка (длина плода) |
| CH | Каскадная головка | 9014 90 Ручка Crazy0015
| CH | Cardboard Heroes (gaming) |
| CH | Code Holder |
| CH | Chartered Herbalist |
| CH | Calico Hills |
| CH | Capital Height |
| CH | Работа с пострадавшими (Скорая помощь Св. Иоанна, Великобритания) Иоанна, Великобритания) |
| CH | Обработчик существ (Звездные войны: Галактики) |
| CH | Clarion Health |
| CH | Complete Heal (Everquest gaming) |
| CH | Chairman/Chairperson |
| CH | Congenital Hyperthyroidism |
| CH | Подсчет сердечных сокращений (диапазон) |
| CH | Сравнить Halfword (IBM) |
| CH | Cochrane Hill |
| CH | Callitrichid Hepatitis |
| CH | Clack House (Clay Aiken fan message board) |
| CH | Cossacks Heaven (gaming site) |
| CH | Clay Высокая пластичность (тип почвы) |
| CH | Неоднородность конституции |
| CH | Модуляция несущей/гула | Candle-Hour |
| CH | Coeficiente Honorário (Spanish: conorary coefficient, Brazil) |
| CH | Charriere Unit (French catheter scale) |
Copyright 1988-2018 AcronymFinder. ком, Все права защищены.
ком, Все права защищены.
Предложите новое определение
Что означает CH?
Аббревиатура » Термин
Термин » Аббревиатура
Слово в термине
#ABCDEFGHIJKLMNOPQRSTUVWXYZ НОВЫЙ
Сокр. » Срок
Срок » Сокр.
Word in Term
Фильтровать по: Выберите категорию из списка…──────────ВсеГосударственные (1)Интернет (3)Медицинские (3)Разное (3)Региональные (1)Спортивные (2)Архитектурные (2) )Электроника (1)Генеалогия (1)Геология (1)Физика (2)Университеты (4)Бухгалтерский учет (1)Банковское дело (1)Карьера (1)Компании и фирмы (1)Общий бизнес (1)Символы NYSE (1)Род занятий и позиции (2)Продукты (1)Конференции (1)Охрана природы (1)Образовательные (1)Известные и знаменитости (4)Музыка (2)Школы (1)Ассемблирование (1)Расширения файлов (2)Игры (1)Общие вычисления (2) Аппаратное обеспечение (1) Сеть (1) Программное обеспечение (4) Органы власти (1) Окружающая среда (1) Файлы ФБР (1) Управление по санитарному надзору за качеством пищевых продуктов и медикаментов (1) Юридические и юридические вопросы (3) Государственные и местные органы (1) Военные (7) НАСА ( 1)Военно-морской флот (1)Поставщики (2)Транспорт (1)Правительство США (3)Французский (1)Итальянский (2)Доменные имена (1)Веб-сайты (1)Британская медицина (2)Клиническая медицина (1)Заболевания (1) Здравоохранение (1)Лаборатория (1)Неврология (1)Физиология (4)Награды и медали (1)Шахматы (1)Строительство (2)Собаки (1)Фермерство и сельское хозяйство (1)Продовольствие и питание (1)Приколы (1) )Хобби (1)Имена и Псевдонимы (1)Доставка и парусный спорт (1)Сленг (1)Неклассифицированный (10)Единицы измерения (3)USPS (1)Канадский (1)Страны (1)Штаты Индии (1)Коды языков (2 буквы) (2)Гольф (1)Хоккей (1)Охота (1)Гонки (1) Сортировать по: ПопулярностиВ алфавитном порядкеКатегории
Термин | Определение | Опции | Рейтинг |
| CH | Проверить! Разное » Шахматы | Rate it: | |||||||
| CH | Channel Governmental » Military — and more. | Rate it: | |||||||
| Ch | Главный Бизнес ».0015 | Characteristic Medical » Physiology | Rate it: | ||||||
| CH | CHronic Medical » Physiology | Rate it: | |||||||
| CH | Чемпион Спорт и многое другое. | 5 | 0807 | ||||||
| CH | Chest Medical » Physiology | Rate it: | |||||||
| CH | Chaplain Governmental » Military | Оценить: | |||||||
| CH | Кредитные часы Академические и научные » Университеты | Rate it: | |||||||
| CH | Central Heating Business » Products | Rate it: | |||||||
| CH | Court House Правительственный » Юридический | Оценить: | |||||||
| CH | 40 Дом Совета400004 Academic & Science » Universities | Rate it: | |||||||
| CH | Contact Hours Miscellaneous » Unit Measures | Rate it: | |||||||
| CH | Канализованный Правительственный » Файлы ФБР | 7 | Оценить:0015 | ||||||
| Ch | Контроль H Вычисления »Программное обеспечение | . .. .. | Оценить: | ||||||
| CH | Континуум Гипотеза 9 Академический 40003 | Rate it: | |||||||
| CH | Common Hardware Governmental » Military — and more… | Rate it: | |||||||
| CH | Счетчик Вычисления ». | .0014 Complementary Health Medical » Physiology | Rate it: | ||||||
| CH | Cargo Helicopter Governmental » Military | Rate it : | |||||||
| CH | Время контакта Разное » Единица измерения | Rate it: | |||||||
| CH | Contact Handled Academic & Science » Electronics | Rate it: | |||||||
| CH | Certified Hypnotherapist Business » Род занятий и должности | Оценить: | |||||||
| CH | Контролируемая влажность0003 Правительство »военные — и больше . | Оценка ИТ: |
12345All
9000 1234539393. 9073
9074.- CH
подробнее »
Знаете что такое
CH ? Есть еще одно хорошее объяснение для CH ? Не держите это в себе! Все еще не можете найти искомое определение аббревиатуры? Используйте нашу технологию Power Search , чтобы искать более уникальные определения в Интернете!Цитата
Используйте приведенные ниже параметры цитирования, чтобы добавить эти сокращения в свою библиографию.
Самый большой ресурс в Интернете для
Акронимы и сокращения
Член сети STANDS4
Изображение или иллюстрация
Ч.

Крючок
CH
Кредит »
Просмотреть Abbreviations.com
#ABCDEFGHIJKLMNOPQRSTUVWXYZ
Бесплатно, регистрация не требуется:
Добавить в Chrome
Получите мгновенное объяснение любой аббревиатуры или аббревиатуры, которая попадется вам в любом месте в Интернете!
Бесплатно, регистрация не требуется:
Добавить в Firefox
Получите мгновенное объяснение любой аббревиатуры или аббревиатуры, которая попадется вам в любом месте в Интернете!
Викторина
Окончательный тест аббревиатуры
»
АИ
A. Инопланетный интеллект
B. Искусственный интеллект
C. Искусственное безумие
D.
 Произвольная информация
Произвольная информация
Вставить
Поделитесь изображением CH
»Нажмите, чтобы просмотреть:
ch — Викисловарь
См. также: Приложение: Варианты «ch»
Содержание
- 1 Translingual
- 1.1 Письмо
- 1.2 Символ
- 2 английский
- 2.1 Этимология 1
- 2.1.1 Существительное
- 2.2 Этимология 2
- 2.2.1 Существительное
- 2.3 Этимология 3
- 2.3.1 Произношение
- 2.3.2 Местоимение
- 2.4 Анаграммы
- 2.1 Этимология 1
- 3 Чехия
- 3.1 Письмо
- 3.1.1 Замечания по использованию
- 3.1 Письмо
- 4 эсперанто
- 4.1 Письмо
- 4.1.1 См. также
- 4.1 Письмо
- 5 французский
- 5.1 Альтернативные формы
- 5.2 Этимология 1
- 5.
 2.1 Прилагательное
2.1 Прилагательное
- 5.
- 5.3 Этимология 2
- 5.3.1 Существительное
- 6 Венгерский
- 6.1 Произношение
- 6.2 Письмо
- 6.2.1 Замечания по использованию
- 6.2.2 Склонение
- 6.3 См. также
- 6.4 Каталожные номера
- 7 латышский
- 7.1 Письмо
- 7.1.1 Замечания по использованию
- 7.1 Письмо
- 8 Словацкий
- 8.1 Произношение
- 8.2 Письмо
- 8.3 См. также
- 8.4 Дополнительная литература
- 9 испанский
- 9.1 Письмо
- 9.1.1 Замечания по использованию
- 9.2 Дополнительная литература
- 9.1 Письмо
- 10 узбекский
- 10.1 Произношение
- 10.2 Письмо
- 10.3 См. также
- 11 валлийский
- 11.1 Произношение
- 11.2 Письмо
- 11.2.1 Замечания по использованию
- 11.
 3 Мутация
3 Мутация- 11.3.1 См. также
- 11.4 Дополнительная литература
Translingual [EDIT]
Английская Википедия имеет статью:
Ch
Wikipedia
За буква [править]
CH (. )
- Диграф от c и h, который в некоторых языках считается отдельной буквой.
Символ[править]
ch
- Альтернативная форма cosh («гиперболический косинус»)
- (международные стандарты) Код языка ISO 639-1 для Чаморро .
Английский[править]
Этимология 1[править]
Существительное[править]
ч.
- Аббревиатура цепи — единица измерения, равная 22 ярдам
Этимология 2
Существительное[править]
ч
- (Япония) Аббревиатура канала
Этимология 3 Сравните голландский
‘k , афетический вариант ik («I»). Еще у ич, И.
Еще у ич, И.Произношение[править]
- МФА (ключ) : /t͡ʃ/
Местоимение[править]
ch
- (obsolete, dialectal) Alternative form of I
Anagrams[edit]
- H&C, H.C., H/C, HC, h/c
Letter[edit]
ch ( нижний регистр , верхний регистр CH , смешанный регистр Ch )
- Орграф, четырнадцатая буква чешского алфавита, после h и до i .
Замечания по употреблению
Эсперанто[править]
Письмо[править]
ч.
- Орграф, используемый в h-системе для представления ĉ.
См. также[править]
- gh, hh, jh, sh
- cx, gx, hx, jx, sx, ux
Альтернативные формы[править]
- гл.

Этимология 1[править]
Сокращение от чак («каждый»).
Прилагательное
- шт. (каждый)
Этимология 2[править]
Сокращение от cheval-vapeur («лошадиная сила»).
Существительное0017 множественное число
ч )- л.с. (лошадиная сила)
Венгерский [править]
CH (Digráf) на Венгерской Википедии
[EDIT]
Буква[ редактировать]
ch ( нижний регистр , верхний регистр Ch )
- Диграф, используемый в нескольких венгерских словах, а также в некоторых фамилиях, именах и географических названиях.
Замечания по использованию[править]
Он используется (среди прочего) в следующих словах вместе с их производными и составными частями: Achilles-in, allochton, acháj, achát, akrosztichon, almanach, anarchia/anarchikus/ анархист/анархизм, архаикус/архаизал/архаизм, археология/археолог, архимандрита, архитектура, архив/архив/архивум, автохтон, вакханалия, вакхия, балдахин, бархес, баркохба/баркохбазик, бронхит, цефалгия chanti, чарльстон, чарта, хартия, чартизмус, чата, кьянти, хориамбус, хрипка, кушетка, дистишон, дурчмарс, эхо, ехт, эвхаристия/ hierarchikus, hipochonder/hipochondria, ichtioszaurusz, jacht, kapitälchen, [ krach, lichthóf, macher, machiavellizmus, machináció/machinál, malachit, mannlicher, matriarchátus, mazochista/mazochizmus, mechanika/mechanikus/mechanisztikus/механизал /механизмус, метал ачи, молох, монархия/монархикус/монархиста, олигарха/олигархия/олигарчикус, орхидея, патриарха/патриархалис/патриархатус, печ/печес, пончо, понцихтер, псзиче/псзихиатер/псзихиатрия/псзичикай/ pszichikum/pszicho-/pszichózis, richtig, rizskoch, sarlach, stich, strichel, szacharin, szinekdoche, sztrichnin, technika/technikum/technikus/technokrácia/technokrata/technológia/technológus, трахома, трохеус, влах, винчестер .
Официально признанные имена: Ахиллес, Ахиллес, Ахим, Арчибальд, Иоахим, Мельхиор, Орхидея, Психе, Рахель, Ричард . [1]
Фамилии (выборка из известных людей [2] ): Аулич, Дамьянич, Форгач, Кеглевич, Кнезич, Ковач, Лачкович, Мадач, Мадершпах, Орлай Петрич, Сечени, Сечени, Зак, Зичи .
Географические названия (вместе с их производными, например, chilei ): Charlestown, Chatham-szigetek, Chile, Chișinau, Déli-Georgia és Déli-Sandwich-szigetek, Liechtenstein, Nouakchott, Seychelle-szigetek , а также два населенных пункта в Венгрии, Chernelházadamonya и Zichyújfalu, холм в Будапеште Széchenyi-hegy (назван в честь Иштвана Сечени) и район в Будапеште, Széchenyihegy (назван в честь холма).
Склонение
притяжательное — единственное число
притяжательное — множественное число
| Притяжательные формы ch | ||
|---|---|---|
| владелец | одиночное владение | множественное владение |
| 1-е лицо поет. | ч-м | ч-им |
| 2-е лицо поет. | ч-д | ch-id |
| 3-е лицо поет. | ч-я | ч-и |
| 1-е лицо множественного числа | ч-нк | ч-чернила |
| 2-е лицо множественного числа | ч-ток | ч-иток |
| 3-е лицо множественного числа | ч-жук | ч-ик |
См.
 также[править]
также[править]- (буквы латинского алфавита) betű ; А а, А а, В б, С в, Cs cs, D d, Dz dz, Dzs dzs, E e, É é, F f, G g, Gy gy, H h, I i, Í í, J j , К к, Л л, Лы лы, М м, Н н, Ны ны, О, О, О, О, О, П р, Р р, С с, Сз сз, Т т, Ты ты, У u, Ú ú, Ü ü, Ű ű, V v, Z z, Zs zs. Только в расширенном алфавите: Q q W w X x Y y . Обычно используется: ch . Также определено: 9Személyekről elnevezett budapesti utcanevek évfordulók tükrében («Названия улиц в Будапеште, названные в честь людей, отраженные в юбилеях») Дьёрдя Месароша
- (устарело) буква, использовавшаяся в старом, довоенном латышском написании, но теперь везде замененная на h (верхний регистр H)
- (фонема) МФА (ключ) : /x/
- Шестнадцатая буква словацкого алфавита, написанная латиницей.
- (буквы латинского алфавита) písmeno ; А а, Б а, Д а, Б б, С в, Ч ч, Д д, Д д, Дз дз, Дж дж, Е д, Э э, Ф ф, Г г, Ч з, Ч ч , I i, í, J j, K k, L l, Ĺ ĺ, Ľ ľ, M м, N n, Ň ň, O o, Óó, Ô ô, P p, Q q, R r, Ŕ ŕ , S s, Š š, T t, Ť ť, U u, Ú ú, V v, W w, X x, Y y, Ý ý, Z z, Ž ž
- Ch в Словацких словарях по адресу slovnik.juls.savba.sk
- che , бывшая четвертая буква испанского алфавита, после c и до d
- “ch”, in Diccionario de la lengua española, Vigésima tercera edición , Real Academia Española, 2014
- (phoneme) IPA (key ) : / тʃ /
- Двадцать восьмая буква узбекского алфавита, написанная латиницей.
- (буквы латинского алфавита) harf ; A a, B b, D d, E e, F f, G g, H h, I i, J j, K k, L l, M m, N n, O o, P p, Q q, R r , S s, T t, U u, V v, X x, Y y, Z z, Oʻ oʻ, Gʻgʻ, Sh sh, Ch ch , Ng ng
- (стандартный) IPA (ключ) : /ɛχ/
- (неофициальный) IPA (ключ) : /χ/
- Четвертая буква валлийского алфавита, называемая èch и написанная латинским шрифтом.

Латышский[править]
Буква[править]
ch ( нижний регистр , верхний регистр CH , смешанный регистр7 9 9)
Заметки об использовании[править]
Это письмо все еще можно найти в старых книгах или в книгах, написанных латышской диаспорой до распада Советского Союза. Раньше он обозначал звук символа IPA / x /, в отличие от / h /; но поскольку в современном латышском произношении эти звуки слились как /x/,
Раньше он обозначал звук символа IPA / x /, в отличие от / h /; но поскольку в современном латышском произношении эти звуки слились как /x/,
Произношение[править]
Буква[править]
ch ( верхний регистр ch )
См. также[править]
Дополнительное чтение [РЕДАКТИРОВАТЬ]
Испанский [EDIT]
Letter.
 кейс CH , смешанный кейс Ch )
кейс CH , смешанный кейс Ch )Примечания по использованию
С 1994 года это письмо обрабатывается как c , за которым следует h только для целей сопоставления (сортировки). В 2010 году эта буква была официально удалена RAE из испанского алфавита.
Further reading[edit]
Pronunciation[edit]
Письмо
См. также[править]
Произношение[править]
Letter[edit]
ch ( нижний регистр , верхний регистр)


 ..
.. ..
.. ..
.. Gaming
Gaming ..
.. Произвольная информация
Произвольная информация 2.1 Прилагательное
2.1 Прилагательное 3 Мутация
3 Мутация