Виды двоичных кодов
В микропроцессорах двоичные коды используются для представления любой обрабатываемой информации. При этом разрядность обрабатываемых чисел может превышать разрядность самого процессора и используемой в нЈм памяти. В этом случае длинное число может занимать несколько ячеек памяти и обрабатываться несколькими командами процессора. При обработке все ячейки памяти, выделенные под многобайтное число, рассматриваются как одно число.
Для представления числовой информации могут использоваться знаковые и беззнаковые коды. Для определЈнности примем длину слова процессора равной восьми битам.
Беззнаковые двоичные коды.
Первый вид двоичных кодов, который мы рассмотрим — это целые беззнаковые коды. В этих кодах каждый двоичный разряд представляет собой степень цифры 2:
При этом минимально возможное число, которое можно записать таким двоичным кодом, равно 0. Максимально возможное число, которое можно записать таким двоичным кодом, можно определить как:
Этими двумя числами полностью можно определить
диапазон, чисел которые можно представить таким
двоичным кодом. В случае двоичного
восьмиразрядного беззнакового целого числа
диапазон будет: диапазон чисел, которые можно
записать таким кодом: 0 .. 255. Для
шестнадцатиразрядного кода этот 0 .. 65535. В
восьмиразрядном процессоре для хранения такого
числа используется две ячейки памяти,
расположенные в соседних адресах. Для работы с
такими числами используются специальные
команды.
В случае двоичного
восьмиразрядного беззнакового целого числа
диапазон будет: диапазон чисел, которые можно
записать таким кодом: 0 .. 255. Для
шестнадцатиразрядного кода этот 0 .. 65535. В
восьмиразрядном процессоре для хранения такого
числа используется две ячейки памяти,
расположенные в соседних адресах. Для работы с
такими числами используются специальные
команды.
Второй вид двоичных кодов, который мы рассмотрим — это прямые целые знаковые коды. В этих кодах старший разряд в слове используется для представления знака числа. В прямом знаковом коде нулем обозначается знак ‘+’, а единицей — знак ‘-‘. В результате введения знакового разряда диапазон чисел смещается в сторону отрицательных чисел:
В случае двоичного восьмиразрядного знакового
целого числа диапазон чисел, которые можно
записать таким кодом: -127 .. +127. Для
шестнадцатиразрядного кода этот диапазон будет:
-32767 .. +32767. В восьмиразрядном процессоре для
хранения такого числа тоже используется две
ячейки памяти, расположенные в соседних адресах.
Недостатком такого кода является то, что знаковый разряд и цифровые разряды приходится обрабатывать раздельно. Алгоритм программ, работающий с такими кодами получается сложный. Для выделения и изменения знакового разряда приходится применять механизм маскирования разрядов, что резко увеличивает размер программы и уменьшает ее быстродействие. Для того, чтобы алгоритм обработки знакового и цифровых разрядов не различался, были введены обратные двоичные коды.
Знаковые обратные двоичные коды.
Обратные двоичные коды отличаются от прямых только тем, что отрицательные числа в них получаются инвертированием всех разрядов числа. При этом знаковый и цифровые разряды не различаются. Алгоритм работы с такими кодами резко упрощается.
Тем не менее при работе с обратными кодами
требуется специальный алгоритм распознавания
знака, вычисления абсолютного значения числа,
восстановления знака результата числа. Кроме
того, в прямом и обратном коде числа для
запоминания числа 0 используется два кода, тогда
как известно, что число 0 положительное и
отрицательным не может быть никогда.
Знаковые дополнительные двоичные коды.
От перечисленных недостатков свободны дополнительные коды. Эти коды позволяют непосредственно суммировать положительные и отрицательные числа не анализируя знаковый разряд и при этом получать правильный результат. Все это становится возможным благодаря тому, что дополнительные числа являются естественным кольцом чисел, а не исскуственным образованием как прямые и обратные коды. Кроме того немаловажным является то, что вычислять дополнение в двоичном коде чрезвычайно легко. Для этого достаточно к обратному коду добавить 1:
Диапазон чисел, которые можно записать таким кодом: -128 .. +127. Для шестнадцатиразрядного кода этот диапазон будет: -32768 .. +32767. В восьмиразрядном процессоре для хранения такого числа используется две ячейки памяти, расположенные в соседних адресах.
В обратных и дополнительных кодах наблюдается
интересный эффект, который называется эффект
распространения знака. Он заключается в том, что
при преобразовании однобайтного числа в
двухбайтное достаточно всем битам старшего
байта присвоить значение знакового бита
младшего байта.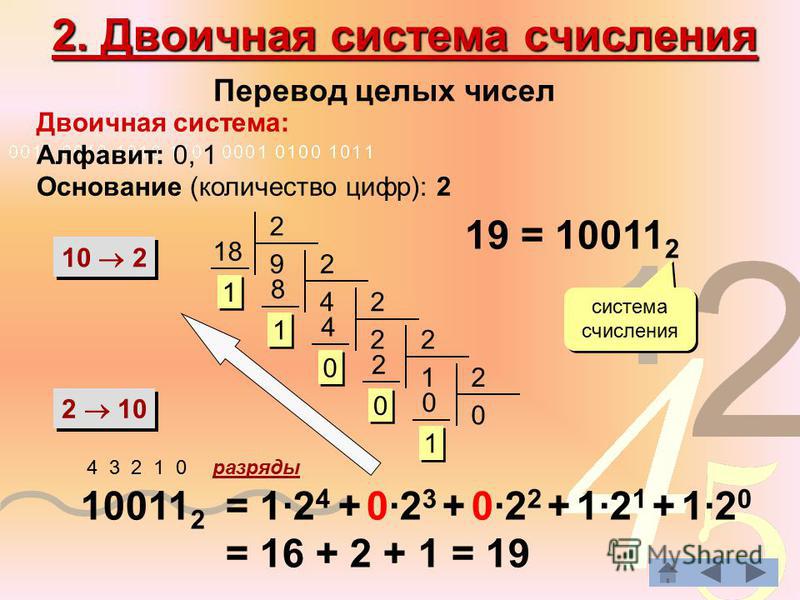 То есть для хранения знака числа
можно использовать сколько угодно старших бит.
При этом значение кода совершенно не изменяется.
То есть для хранения знака числа
можно использовать сколько угодно старших бит.
При этом значение кода совершенно не изменяется.
Использование для представления знака числа двух бит предоставляет интересную возможность контролировать переполнения при выполнении арифметических операций. Рассмотрим несколько примеров.
1) Просуммируем числа 12 и 5
В этом примере видно, что в результате суммирования получается правильный результат. Это можно проконтролировать по флагу переноса C, который совпадает со знаком результата (действует эффект распространения знака).
2) Просуммируем два отрицательных числа -12 и -5
В этом примере флаг переноса C тоже совпадает со знаком результата, то есть переполнения не произошло и в этом случае
3) Просуммируем положительное и отрицательное число -12 и +5
В этом примере при суммировании положительного
и отрицательного числа автоматически получается
правильный знак результата. В данном случае знак
результата отрицательный.
4) Просуммируем положительное и отрицательное число +12 и -5
В данном примере знак результата положительный. Флаг переноса совпадает со знаком результата, поэтому переполнения не было и в этом случае.
5)Просуммируем числа 100 и 31
В этом примере видно, что в результате суммирования произошло переполнение восьмибитовой переменной, т.к. в результате операции над положительными числами получился отрицательный результат. Однако если рассмотреть флаг переноса, то он не совпадает со знаком результата. Эта ситуации является признаком переполнения результата и легко обнаруживается при помощи операции «исключающее ИЛИ» над старшим битом результата и флагом переноса C. Большинство процессоров осуществляют эту операцию аппаратно и помещают результат во флаг переполнения OV.
В этом примере результате операции над
отрицательными числами в результате
суммирования произошло переполнение
восьмибитовой переменной, т.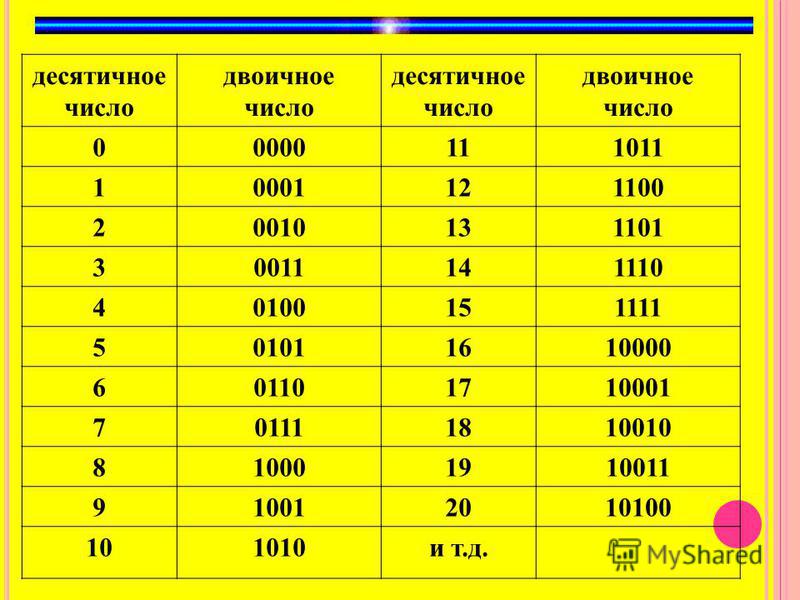
Представление дробных чисел в двоичном коде с фиксированной запятой.
Кроме целых чисел часто требуется работать с дробными числами. Следующий вид двоичных кодов, который мы рассмотрим — это дробные коды. Как и в случае целых чисел, дробные числа могут быть беззнаковые и знаковые. Для записи знаковых чисел могут быть использованы прямые, обратные и дополнительные коды. Принцип их построения точно такой же, как и в случае целых чисел.
Рассмотрим, как можно записать дробное число. До сих пор мы предполагали, что двоичная запятая находится правее самого младшего разряда. Но кто сказал, что она должна всегда находиться в этом месте? Мы можем договориться, что запятая находится слева от самого старшего разряда, и тогда в такой переменной можно будет записывать только дробные числа:
Или договоримся, что она находится точно посередине переменной, и тогда мы сможем записывать смешанные числа:
Остальные случаи рассматривать не будем. Они
строятся точно так же как и для целых чисел.
Они
строятся точно так же как и для целых чисел.
Представление чисел в двоичном коде с плавающей запятой.
Часто приходится обрабатывать очень большие числа (например, расстояние между звЈздами) или наоборот очень маленькие числа (например, размеры атомов или электронов). При таких вычислениях пришлось бы использовать числа с очень большой разрядностью. В то же время нам не нужно знать расстояние между звЈздами с точностью до миллиметра. Для вычислений с такими величинами числа с фиксированной запятой неэффективны.
В десятичной арифметике для записи таких чисел используется алгебраическая форма. При этом число записывается в виде мантиссы, умноженной на 10 в степени, отображающей порядок числа, Например:
0,2*105; 0,16*10-38
Для записи двоичных чисел тоже используется
такая форма записи. Эта форма записи называется
запись числа с плавающей точкой. Напомним, что
мантисса не может быть больше единицы и после
запятой в мантиссе не может записываться ноль.
А теперь рассмотрим промышленные стандарты, используемые для представления чисел в компьютерах. Существует стандарт IEEE 754 для представления чисел с одинарной точностью (float) и с двойной точностью (double). Для записи числа в формате с плавающей запятой одинарной точности требуется тридцатидвухбитовое слово. Для записи чисел с двойной точностью требуется шестидесятичетырЈхбитовое слово. Чаще всего числа хранятся в нескольких соседних ячейках памяти процессора. Форматы числа в формате с плавающей запятой одинарной точности и числа в формате с плавающей запятой удвоенной точности приведены на рисунке
На рисунке буквой S обозначен знак числа, 0 — это
положительное число, 1 — отрицательное число. e
обозначает смещЈнный порядок числа. Смещение
требуется, чтобы не вводить в число еще один знак.
СмещЈнный порядок всегда положительное число.
Для одинарной точности для порядка выделено
восемь бит. Для смещЈнного порядка двойной
точности отводится 11 бит. Для одинарной точности
смещение принято 127, а для двойной точности — 1023. В
десятичной мантиссе после запятой могут
присутствовать цифры 1:9, а в двоичной — только 1.
Поэтому для хранения единицы после двоичной
запятой не выделяется отдельный бит в числе с
плавающей запятой. Единица подразумевается, как
и двоичная запятая. Кроме того, в формате чисел с
плавающей запятой принято, что мантисса всегда
больше 1. То есть диапазон значений мантиссы
лежит в диапазоне от 1 до 2.
В
десятичной мантиссе после запятой могут
присутствовать цифры 1:9, а в двоичной — только 1.
Поэтому для хранения единицы после двоичной
запятой не выделяется отдельный бит в числе с
плавающей запятой. Единица подразумевается, как
и двоичная запятая. Кроме того, в формате чисел с
плавающей запятой принято, что мантисса всегда
больше 1. То есть диапазон значений мантиссы
лежит в диапазоне от 1 до 2.
Рассмотрим несколько примеров:
1) Определить число с плавающей запятой, лежащее в четырЈх соседних байтах:
11000001 01001000 00000000 00000000
— Знаковый бит, равный 1 показывает, что число отрицательное.
— Экспонента 10000010 в десятичном виде соответствует числу 130. Вычтя число 127 из 130, получим число 3.
— Теперь запишем мантиссу: 1,100 1000 0000 0000 0000 0000
— И, наконец, определим десятичное число: 1100,1b = 12,5d
2) Определить число с плавающей запятой, лежащее в четырЈх соседних байтах:
11000011 00110100 00000000 00000000
— Знаковый бит, равный 1 показывает, что число
отрицательное.
— Экспонента 10000110 в десятичном виде соответствует числу 134. Вычтя число 127 из 134, получим число 7.
— Теперь запишем мантиссу: 1,011 0100 0000 0000 0000 0000
— И, наконец, определим десятичное число: 10110100b=180d
Для того чтобы записать ноль, достаточно записать в смещенный порядок число 00000000b. Значение мантиссы при этом не имеет значения. Число, в котором все байты равны 0, тоже попадает в этот диапазон значений.
Бесконечность соответствует смещенному порядку 11111111b и мантиссе, равной 1,0. При этом существует минус бесконечность и плюс бесконечность (переполнение и антипереполнение), которые часто отображаются на экран монитора как +INF и -INF.
Все остальные комбинации битов (в том числе и все единицы) воспринимаются как не числа и отображаются на экран: NaN.
Запись десятичных чисел.
Иногда бывает удобно хранить числа в памяти
процессора в десятичном виде (Например, для
вывода на экран дисплея). Для записи таких чисел
используются двоично-десятичные коды. Для записи
одного десятичного разряда используется четыре
двоичных бита. Эти четыре бита называются
тетрадой. Иногда встречается название, пришедшее
из англоязычной литературы: нибл. При помощи
четырех бит можно закодировать шестнадцать цифр.
Лишние комбинации в двоично-десятичном коде
являются запрещенными. Таблица соответствия
двоично-десятичного кода и десятичных цифр
приведена ниже:
Для записи
одного десятичного разряда используется четыре
двоичных бита. Эти четыре бита называются
тетрадой. Иногда встречается название, пришедшее
из англоязычной литературы: нибл. При помощи
четырех бит можно закодировать шестнадцать цифр.
Лишние комбинации в двоично-десятичном коде
являются запрещенными. Таблица соответствия
двоично-десятичного кода и десятичных цифр
приведена ниже:
Остальные комбинации двоичного кода в тетраде являются запрещенными. Запишем пример двоично-десятичного кода:
1258 = 0001 0010 0101 1000
589 = 0000 0101 1000 1001
Достаточно часто в памяти процессора для хранения одной десятичной цифры выделяется одна ячейка памяти (восьми, шестнадцати или тридцатидвухразрядная). Это делается для повышения скорости работы программы. Для того, чтобы отличить такой способ записи двоично-десятичного числа от стандартного, способ записи десятичного числа, как это показано в примере, называется упакованной формой двоично-десятичного числа.
Суммирование двоично-десятичных чисел.
Суммирование двоично-десяичных чисел можно производить по правилам обычной двоичной арифметики, а затем производить двоично-десятичную коррекцию. Двоично-десятичная коррекция заключается в проверке каждой тетрады на допустимые коды. Если в какой либо тетраде обнаруживается запрещенная комбинация , то это говорит о переполнении. В этом случае необходимо произвести двоично-десятичную коррекцию. Двоично-десятичная коррекция заключается в дополнительном суммировании числа шесть (число запрещенных комбинаций) с тетрадой, в которой произошло переполнение или произошЈл перенос в старшую тетраду. ПриведЈм два примера:
Запись текстов в памяти процессора.
Все символы и буквы могут быть закодированы при
помощи восьми двоичных символов. Наиболее
распространенными таблицами являются таблицы
ASCII с национальными расширениями, применяющиеся
в DOS (и которые можно использовать для записи
текстов в микропроцессорах), и таблицы ANSI,
применяющиеся в WINDOWS. В таблицах ASCII и ANSI первые 128
символов совпадают. В этой части таблицы
содержатся символы цифр, знаков препинания,
латинские буквы верхнего и нижнего регистров и
управляющие символы. Национальные расширения
символьных таблиц и символы псевдографики
содержатся в последних 128 кодах этих таблиц,
поэтому русские тексты в операционных системах
DOS и WINDOWS не совпадают.
В таблицах ASCII и ANSI первые 128
символов совпадают. В этой части таблицы
содержатся символы цифр, знаков препинания,
латинские буквы верхнего и нижнего регистров и
управляющие символы. Национальные расширения
символьных таблиц и символы псевдографики
содержатся в последних 128 кодах этих таблиц,
поэтому русские тексты в операционных системах
DOS и WINDOWS не совпадают.
[Назад] [Содержание] [Вперёд]
Двоичное счисление — SBP-Program
Автор: Субботин Б.П.
- Перевод двоичного числа в десятичное
- Двоичные дроби
- Перевод дробного двоичного числа в десятичное
- Двоичная система счисления: как сравнить два числа?
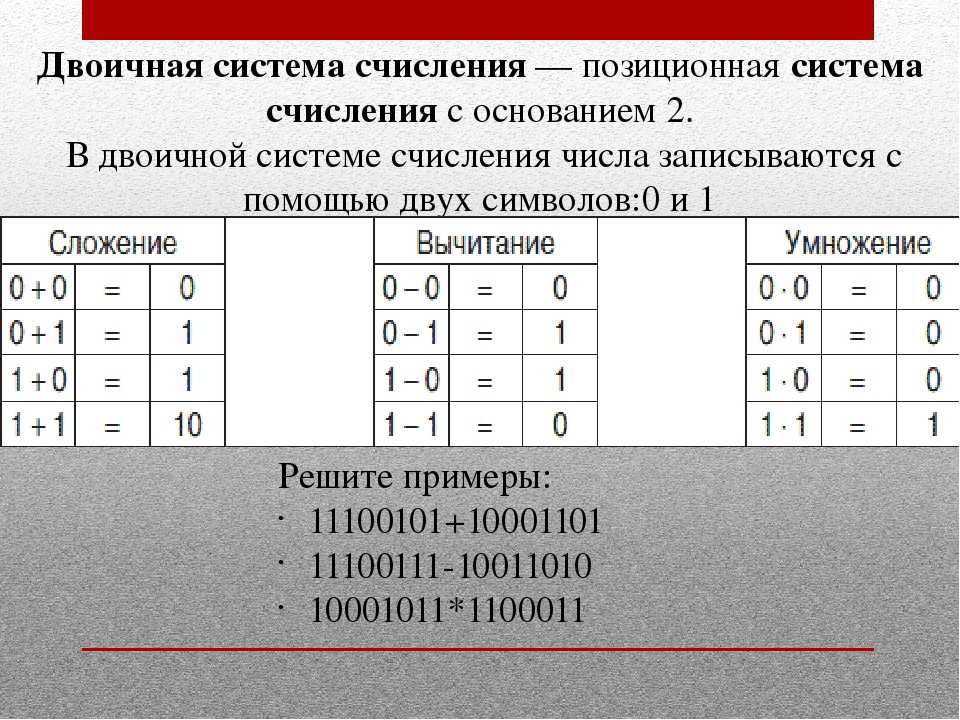
- Двоичная система счисления: сложение
- Двоичная система счисления: вычитание
- Двоичная система счисления: умножение
- Двоичная система счисления: деление
Двоичное счисление имеет в своей основе только две цифры: 0 и 1. Все числа записывают с помощью этих двух цифр. Основание двоичной системы счисления равно двум.
Основание двоичной системы счисления равно двум.
Двоичная система счисления применяется в компьютерной технике. Бит — это наименьшая единица информации. Слово «бит», по-английски bit, происходит от «binary digit», что значит «двоичная цифра». Бит может быть единицей или нулём, ведь в двоичной системе счисления имеются только две цифры: 0 и 1.
Двоичное счисление относится к позиционным системам счисления. Это значит, что значение двоичного числа связано с позициями цифр в нём. Пример: двоичные числа 1101 и 1011 составлены из одинакового количества единиц и нулей, но позиции их различны, значит и числа различны.
Вот таблица позиций числа 1101:
Теперь таблица позиций числа 1011:
Номера позиций начинаются с нуля.
Перевод двоичного числа в десятичное
Основание двоичной системы счисления равно двум, это мы будем использовать. Каждую двоичниую цифру в двоичном числе умножим на два в степени, равной номеру позиции двоичной цифры в числе. Для примера возьмём числа из предыдущего раздела: 1101 и 1011 и найдём их десятичные эквиваленты.
Вот таблица позиций числа 1101:
Степени 2 равны номеру позиции.
Итак, двоичное число 1101 равно 13 в десятичной системе счисления.
Теперь число 1011. Его таблица позиций:
Степени 2 равны номеру позиции.
Итак, двоичное число 1011 равно 11 в десятичной системе счисления.
Наверх
Двоичные дроби
Дроби в двоичной системе счисления записывают как и в десятичной:
1101,1101
Таблица позиций числа 1101,1101
Позиции дробной части начинаются с -1.
Наверх
Перевод дробного двоичного числа в десятичное
Переведём двоичное дробное число 1101,1101 в десятичную дробь.
Таблица позиций числа 1101,1101
Степени 2 равны номеру позиции.
Итак, двоичное число 1101,1101 равно 13,8125 в десятичной системе счисления.
Наверх
Двоичная система счисления: как сравнить два числа?
Двоичные числа сравнивают также, как и в десятичной системе счисления, примеры:
100 > 10
100 < 110
111 < 1111
111 < 1000
Наверх
Двоичная система счисления: сложение
Правила сложения двоичных чисел аналогичны правилам в десятичной системе счисления.
Таблица сложения в двоичной системе счисления:
1 + 1 = 10
1 + 0 = 1 и 0 + 1 = 1
0 + 0 = 0
Здесь все числа двоичные.
Пример в двоичной системе счисления:
1 + 0 = 1
Переведём левую и правую части этого равенства в десятичную систему:
1 * 20 + 0 * 20 = 1 * 20
получаем в десятичной системе:
1 + 0 = 1
Пример:
Сложим числа 1001 и 10. Складывать будем «столбиком», как и в десятичной системе счисления:
Пример:
Сложим 100 и 100:
Пример:
Сложим 101 и 101:
Наверх
Двоичная система счисления: вычитание
Таблица вычитания двоичных чисел:
10 — 1 = 1
1 — 0 = 1
1 — 1 = 0
0 — 0 = 0
Здесь все числа двоичные.
Пример в двоичной системе счисления:
10 — 1 = 1
Переведём левую и правую части этого равенства в десятичную систему:
1 * 21 + 0 * 20 — 1 * 20 = 1 * 20
получаем в десятичной системе:
2 + 0 — 1 = 1
Пример. Вычтем из числа 100 число 10. Вычетать будем «столбиком», как и в десятичной системе счисления:
Вычтем из числа 100 число 10. Вычетать будем «столбиком», как и в десятичной системе счисления:
Здесь сначала из правого нуля в 100 вычли ноль, а после, чтоб из среднего нуля в 100 вычесть 1, мы заняли 1 из позиции 3. Всё как в десятичной системе, но в нашем распоряжении только 0 и 1 и таблица вычитания.
Пример. Вычтем из числа 1001 число 10.
Пример. Вычтем из числа 1000 число 1.
Наверх
Двоичная система счисления: умножение
Таблица умножения двоичных чисел:
1 * 1 = 1
1 * 0 = 0 и 0 * 1 = 0
0 * 0 = 0
Здесь все числа двоичные.
Пример. Умножать будем «столбиком», как и в десятичной системе счисления:
Пример:
Наверх
Двоичная система счисления: деление
Используя таблицу вычитания и таблицу умножения для двоичных чисел, делим подобно тому, как мы делим десятичные числа.
Пример деления двоичных чисел:
| ]]> | ]]> |
Наверх
Объяснение двоичных чисел для программистов
Всем известно, что компьютеры работают с единицами и нулями. Это связано с тем, что процессоры состоят из миллиардов транзисторов, которые по сути являются просто переключателями.
Это связано с тем, что процессоры состоят из миллиардов транзисторов, которые по сути являются просто переключателями.
Любой код, который вы пишете, должен быть обработан компьютером и, следовательно, должен быть преобразован в двоичные инструкции для работы.
Это не просто выполнение кода, который использует двоичный код, он также используется для хранения всего в памяти и любых файлов, которые вы записываете на диск. Все хранится как единицы и нули.
Прежде чем мы перейдем к тому, как именно работает двоичная система, нам нужно взглянуть на существующую систему счисления.
Подпишитесь на дополнительные видеоматериалыТекущая система счисления
Все наши числа представлены цифрами от 0 до 9. Итак, всего 10 символов, которые мы используем для представления каждого числа от 0 до бесконечности.
Вы, наверное, помните, как в школе числа представляли числовые столбцы.
Мы можем поместить только до 9 в каждый столбец, и как только нам нужно подняться выше, мы должны перейти к следующему столбцу.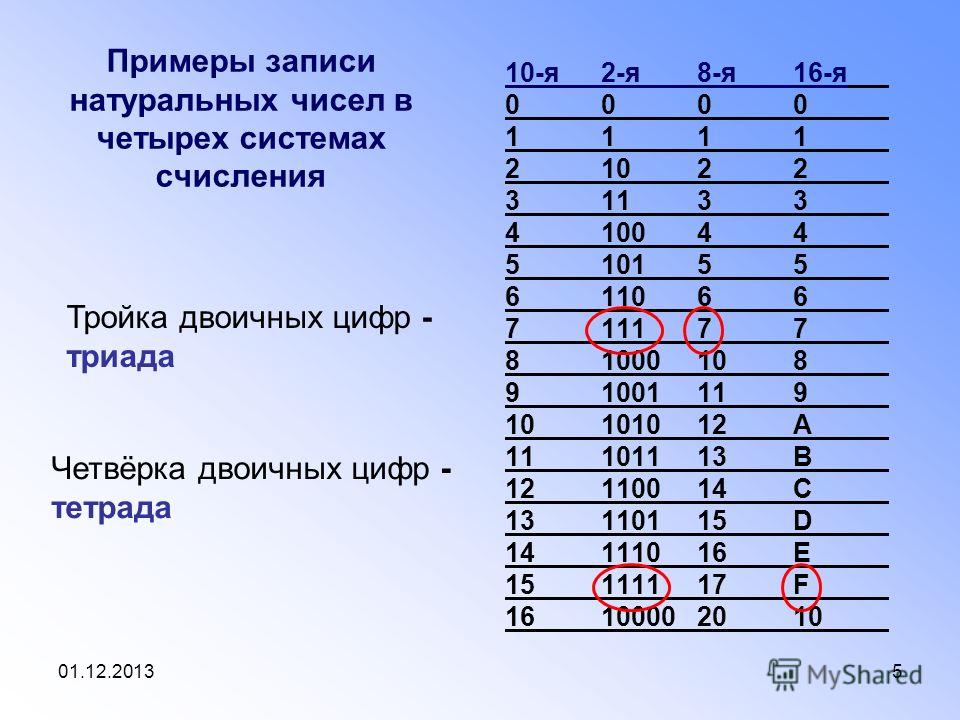
Это то, что мы называем системой счисления с основанием 10 . Каждый столбец представляет собой степень числа 10.
Все знают систему счисления с основанием 10, и, вероятно, все используют ее, поскольку у нас 10 пальцев.
Двоичная система счисления
Что, если вместо использования 10 символов для представления всех чисел мы будем использовать только 2.
Тогда это будет система счисления с основанием 2, если эти 2 символа равны 0 и 1, тогда это то, что мы называем двоичным.
Если мы вернемся к нашим 4 столбцам. Если в системе счисления с основанием 10 каждый столбец представляет степень числа 10, то в системе счисления с основанием 2 каждый столбец представляет степень числа 2. каждый столбец, что получается как 8 + 4 + 2 + 1 = 15. Если вы добавите 0, то всего будет 16 чисел, от 0 до 15.
Двоичные числа также можно использовать для представления букв. В базовом наборе символов ASCII первые 7 цифр, используемых для представления, используются для представления 128 различных символов.
А = 0100 0001 Б = 0100 0010 С = 0100 0011 Д = 0100 0100 E = 0100 0101
Затем добавляется 8-я цифра, чтобы учесть все остальные специальные символы, всего 256 символов.
Å = 1100 0101 Æ = 1100 0110 Ö = 1101 0110
Другие системы счисления
В программировании используются не только двоичные числа, мы часто кодируем данные в другие системы счисления.
Электронные письма кодируются с использованием base64. Таким образом, в отличие от двоичного кода, в котором используются 0 и 1, в базе 64 используются заглавные буквы от A до Z, строчные буквы от a до z, числа от 0 до 9.и символы +, / и =.
ABCDEFGHIJKLMNOPQRSTUVWXYZ АБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЫЭЮЯ 0123456789 +/=
Base 32 также часто используется. Преимущество base32 заключается в том, что он использует только прописные буквы от A до Z и числа от 0 до 7. Поскольку в нем нет специальных символов, он отлично подходит для таких вещей, как имена файлов или для использования в URL-адресах.
ABCDEFGHIJKLMNOPQRSTUVWXYZ01234567
И, конечно же, нельзя забывать о базе 16, в которой используются цифры от 0 до 9 и буквы от A до F.
0 = 0 1 = 1 2 = 2 3 = 3 4 = 4 5 = 5 6 = 6 7 = 7 8 = 8 9 = 9 А = 10 В = 11 С = 12 Д = 13 Э = 14 F = 15
База 16 также известна как шестнадцатеричная и чаще всего используется для представления цветов в CSS.
Цвета в шестнадцатеричном формате записываются как 3 набора по 2 символа.
Каждый набор представляет красный, зеленый и синий соответственно.
Поскольку у нас есть 2 символа и число с основанием 16, первый символ справа равен 16 в степени 0, что равно 1, а второй символ равен 16 в степени 1, что равно 16.
Таким образом, наибольшее число, которое мы можем представить двумя символами в шестнадцатеричном формате, — это FF, что будет равно 15 x 16 + 15 x 1 = 255. был бы синий.
Это дает нам в общей сложности 256 x 256 x 256 = 16 777 216 цветов, которые могут быть представлены в шестнадцатеричном виде.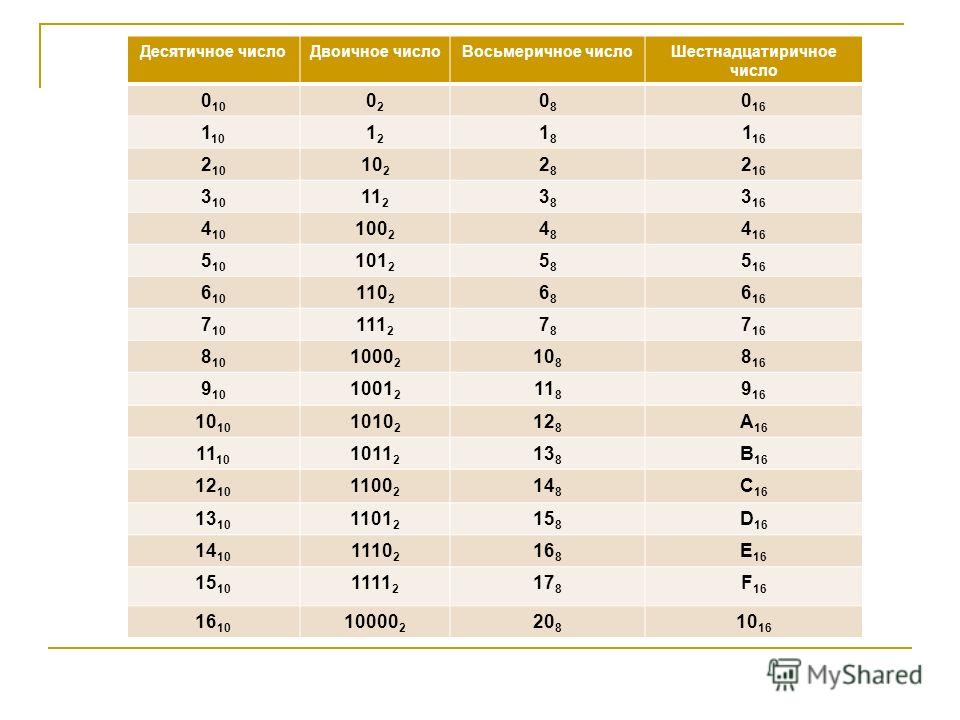 7. 90 = 255
7. 90 = 255
А как насчет отрицательных чисел?
Байт со знаком может хранить только от -128 до 127. Причина этого в том, что нам нужно использовать один из битов для хранения знака числа.
Для этой цели мы используем самый левый бит. Если самый левый бит равен 1, число отрицательное, а если это 0, число положительное.
0000 0000 = 0 1000 0000 = -128
Числа со знаком используют представление, известное как дополнение до двух.
Числа от 0 до 127 представлены так же, как мы делали выше. Однако для отрицательных чисел мы считаем от -128.
1000 0000 = -128 1000 0001 = -127 1111 1111 = -1
Есть еще 256 чисел, которые могут быть представлены этим 8-битным двоичным числом.
- -128 до -1 = 128 номеров,
- от 1 до 127 = 127 номеров
- и 0
Чем больше цифр в двоичном числе, тем большее число можно сохранить. Итак, int обычно занимает 32 бита, что означает, что это 32-значное двоичное число:
0000 0000 0000 0000 0000 0000 0000 0000
это беззнаковое целое число , мы можем хранить чуть более 4 миллиардов.
ДВОИЧНОЕ ЧИСЛО | Английский означает
Примеры двоичного числа
двоичное число
Двоичное число представлено списком двоичных цифр, причем младшая значащая цифра идет первой.
Из Кембриджского корпуса английского языка
Тогда состояние можно представить с помощью двоичный число , например двоичный 10011 для первого состояния на пространственно-временной диаграмме выше.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.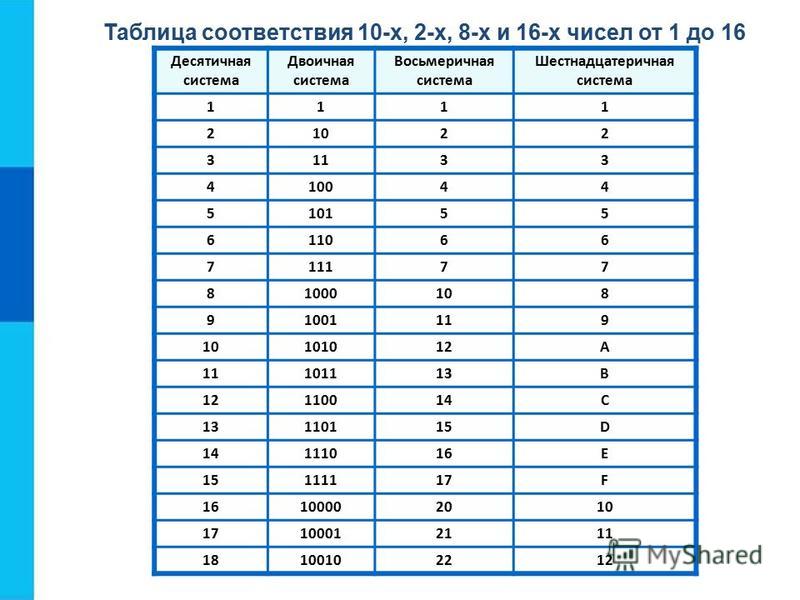
Его можно считать первым ученым-компьютерщиком и теоретиком информации, среди прочего, за то, что он задокументировал двоичный номер система.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
В начале моделирования уникальное двоичное число от 1 до 46 было случайным образом присвоено каждому слову в качестве его представления.
Из Кембриджского корпуса английского языка
На самом деле, кроме двоичной системы чисел , ничто не может быть однозначно принято в качестве действительного строительного блока для нашей системы.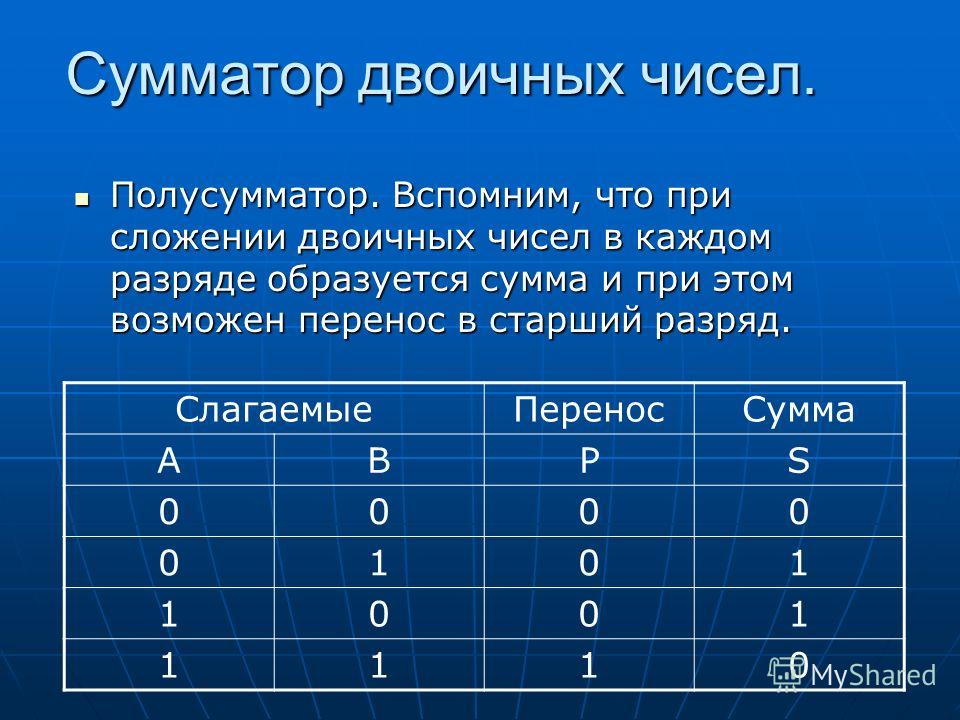
Из Кембриджского корпуса английского языка
Напряжения двух проводов и напряжение записывающего устройства регистрировались последовательно каждые 48 мс, преобразовывались в 12-битное двоичное число и записывались на магнитную ленту.
Из Кембриджского корпуса английского языка
Длина двоичного числа может называться его битовой длиной.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
При преобразовании двоичного числа числа в base85 (85 «не» является степенью двойки) старшие биты действительно влияют на младшие цифры base85 и наоборот.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
Приложения, использующие арифметические схемы, часто выигрывают от использования альтернатив двоичным числовым системам.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
Битовая строка, интерпретируемая как двоичное число , может быть преобразована в десятичное число.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
Таким образом, очевидно, что к нашему результату переноса-сохранения можно добавить еще одно двоичное число число , не переполнив нашу емкость памяти: но что тогда?
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
Ранние компьютеры использовали два разных подхода к адресации памяти, представляя адрес либо как двоичное число , либо как десятичное число.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
Конечным результатом является (полный) список двоичных числовых систем в фиксированном измерении.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.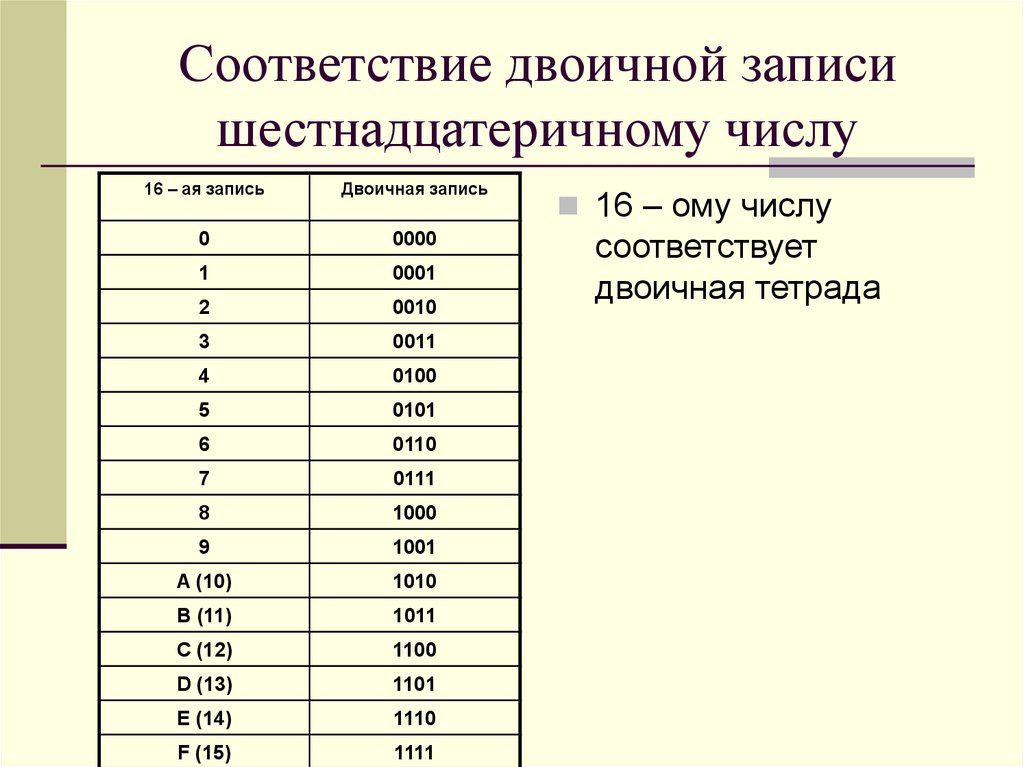
Каждая коллоидная частица обладает способностью хранить информацию, известную как , двоичное число , , число , 0 и 1, после приложения к ней сильного магнитного поля.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
Набор битов может иметь состояния: подробности см. в binary number .
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.