Диагональ четырехугольника Калькулятор | Вычислить Диагональ четырехугольника
✖Площадь четырехугольника — это количество двумерного пространства, занимаемого четырехугольником.ⓘ Площадь четырехугольника [A] | акрАкко (служба США)НаходятсяАрпентамбарКарроКруговая дюймаКруговая MilCuerdaарамДунамРаздел электрон КрестаГаусадьбаMuпингплощадьPyongклочок землиСабинРазделКвадратный АнгстремПлощадь СантиметрПлощадь цепи Площадь декаметровойквадратный дециметрКвадратный футКвадратный фут (служба США)Площадь гектометровыеКвадратный дюймквадратный километрКвадратный метрПлощадь микрометраПлощадь MilКвадратная миляКвадратная миля (римская)Квадратная миля (Статут)Квадратная миля (служба США)Площадь МиллиметрПлощадь NanometreМера площадиПлощадь полюсаПлощадь РодКвадратный Rod (служба США)Квадратный дворрастяжениегородокВарас Castellanas CuadВарас Conuqueras Cuad | +10% -10% | |
✖Высота столбца 1 четырехугольника — это высота треугольника, образованного диагональю четырехугольника. | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% | |
✖Высота второго столбца четырехугольника — это высота треугольника, образованного диагональю четырехугольника. | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
|
✖Диагональ четырехугольника – это прямая линия, соединяющая два противоположных угла четырехугольника. |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
⎘ копия |
👎
Формула
сбросить
👍
Диагональ четырехугольника Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Преобразование входов в базовый блок
Площадь четырехугольника: 60 Квадратный метр —> 60 Квадратный метр Конверсия не требуется
Высота второй колонны четырехугольника: 8 метр —> 8 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
10 метр —> Конверсия не требуется
< 4 Четырехугольник Калькуляторы
Диагональ четырехугольника формула
Диагональ четырехугольника = 2*Площадь четырехугольника/(Высота столбца 1 четырехугольника+Высота второй колонны четырехугольника)
d = 2*A/(h1+h2)
Что такое Четырехугольник?
Четырехугольник — это плоская фигура, имеющая четыре стороны или ребра, а также четыре угла или вершины.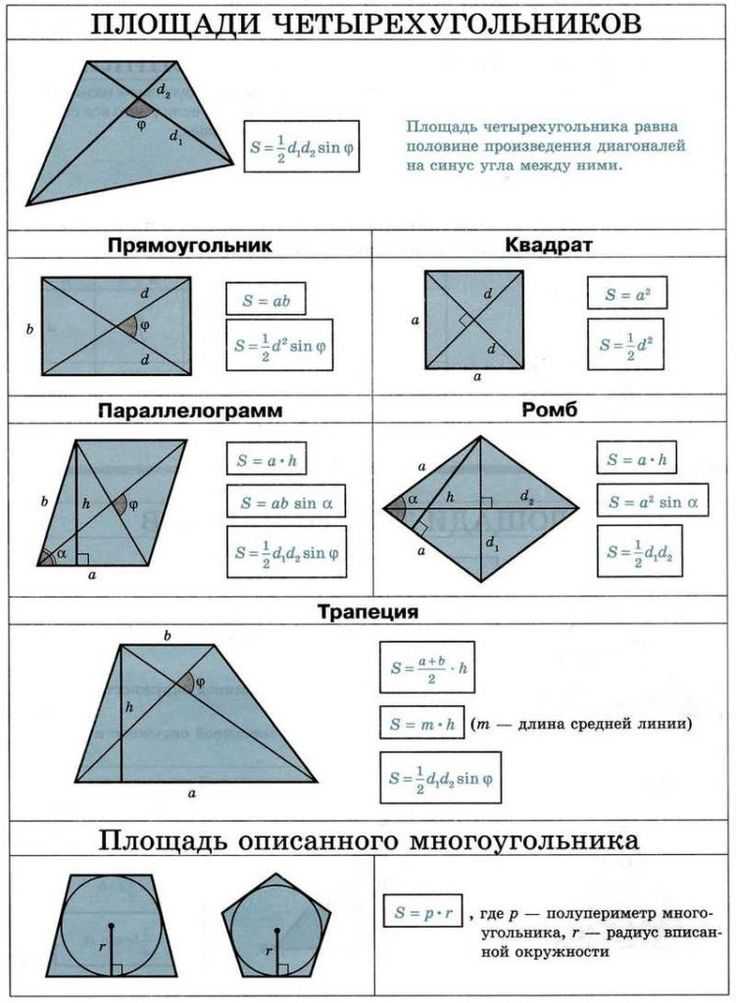
Share
Copied!
Урок по теме «Решение задач на вычисление площади четырехугольников»
Урок рассчитан на один академический час и проводится после того, как изучены формулы для вычисления площадей треугольников, прямоугольника, квадрата, параллелограмма и трапеции.
Цели урока:
- Образовательные: повторить ранее изученные формулы для вычисления площадей выпуклых фигур, вывести и научиться пользоваться формулами для вычисления площадей выпуклых четырехугольников, имеющих перпендикулярные диагонали;
- Развивающие: развитие логического мышления, памяти, внимания, выработка математической зоркости;
- Воспитательные: воспитание трудолюбия,
интереса к предмету, умение внимательно
выслушивать ответы одноклассников.

Необходимое оборудование:
-
компьютер,
-
проектор.
Ход урока.
- Организационный момент.
- Устная работа.
Проводится по чертежам, выведенным с проектора на экран.
Задание. Для каждой из геометрических фигур найти площадь, назвав используемую формулу. Опрос ведется фронтально, учащиеся могут отвечать по желанию.
- Введение новых знаний.
Учитель обращает внимание учащихся на то, что до сих пор, в основном, площади фигур вычислялись по двум элементам: основанию и высоте, проведенной к основанию. Однако, в случае, если в четырехугольнике диагонали взаимно перпендикулярны, его площадь можно вычислить, зная длины диагоналей.
Учитель просит учащихся
сформулировать тему урока. Учащиеся
предлагают свои варианты темы урока. Принимается такая: «Вычисление площади
выпуклого четырехугольника, имеющего
взаимно перпендикулярные диагонали».
Принимается такая: «Вычисление площади
выпуклого четырехугольника, имеющего
взаимно перпендикулярные диагонали».
Задача. Доказать, что площадь выпуклого четырехугольника, имеющего взаимно перпендикулярные диагонали, равна половине произведения его диагоналей.
Запись на доске.
Дано:
ABCD – вып. четырехугольник,
AC ┴ BD.
Доказать:
SABCD=1/2 ACBD.
Доказательство:
- пусть AC ∩ BD = O, тогда
SABC
=1/2 ACBО, т.к. BO является высотой в ABC,SABC=1/2 ACDO, т.к. DO является высотой в ADC.
- SABCD= SABC+ SADC = 1/2 ACBО + 1/2 ACDO = 1/2 AC(BO+DO)= 1/2 ACBD, ч.т.д.
Учитель. Какие вы знаете четырехугольники с взаимно-перпендикулярными диагоналями?
Ученик. Ромб и квадрат.
Ромб и квадрат.
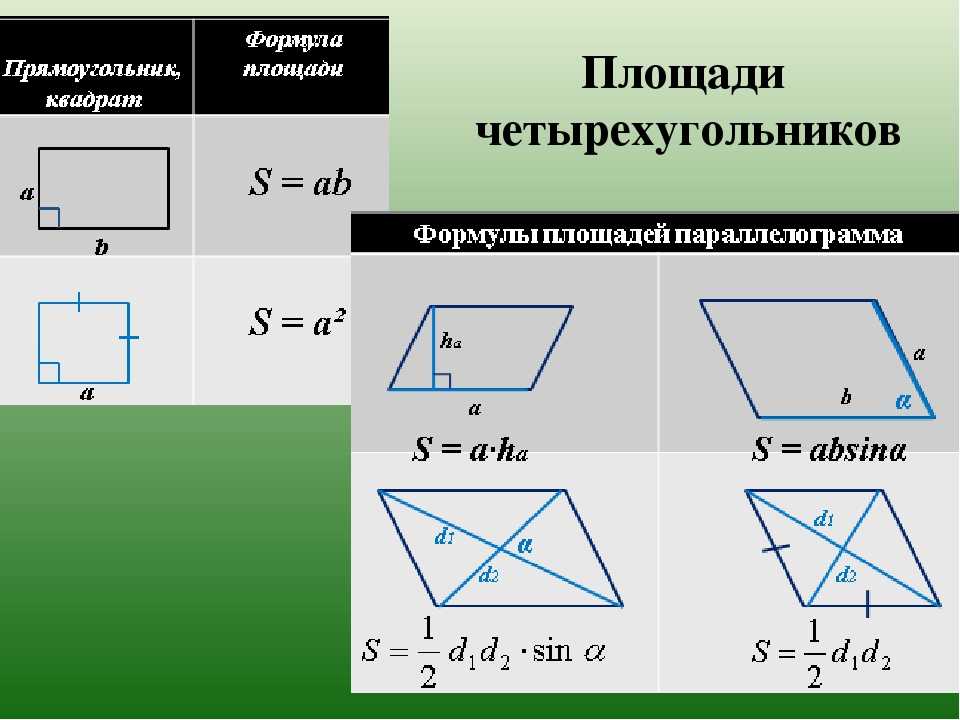
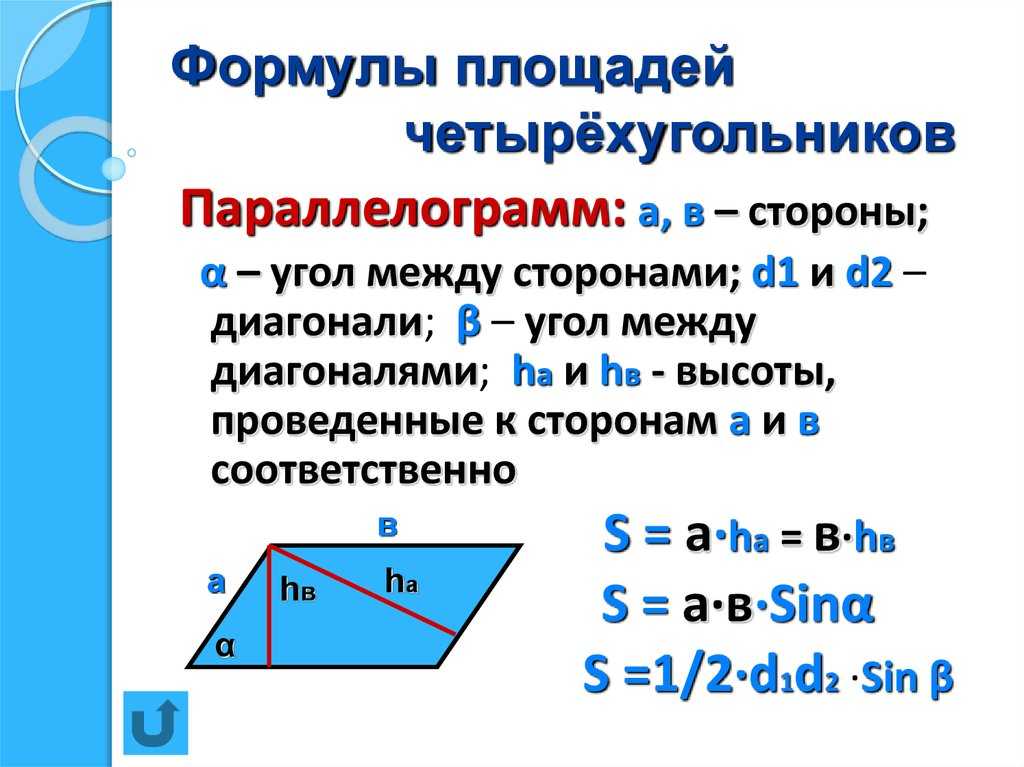
Учитель. Давайте запишем формулы в общем виде для вычисления площадей ромба и квадрата для их диагоналей.
Запись на доске:
Sромба=1/2d1d2, где d1, d2 – диагонали ромба.
Учитель. Что можно сказать о диагоналях квадрата, кроме того, что они взаимно перпендикулярны?
Ученик. Диагонали квадрата равны, то есть d1 = d2.
Учитель проситученика записать формулу для вычисления площади квадрата по его диагонали.
Ученик пишет на доске:
Sквадрата = ½ d2, где d – диагональ квадрата.
- Закрепление выведенных формул.
Учитель. Приведите свои примеры использования выведенных формул.
Ученик. Найти площадь ромба, если его диагонали равны 3см и 6см.
Решение: S=1/2 36
= 9 (см2).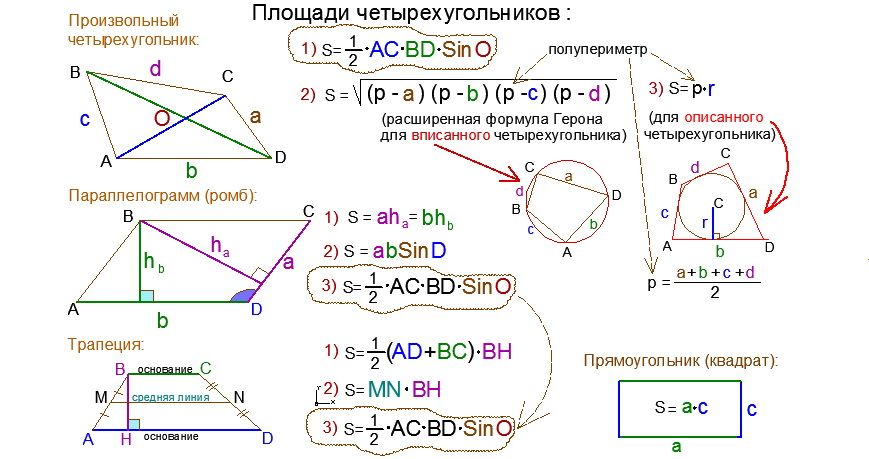
Ученик. Найти площадь квадратного участка земли, если его диагональ равна 10м.
Решение: S=1/2 102=50 (м2).
Учитель. Придумайте обратные задачи.
Ученик. Найти одну из диагоналей ромба, если его площадь равна 20 см2, а вторая диагональ 8 см.
Решение: d1= 2S/d2, d1= 220/8 = 5 (см)
Ученик. Найти диагональ квадрата, если его площадь равна 18 см2.
Решение: d2=2S, d2=36, d=6(см).
Учитель. Давайте теперь решим более сложную задачу, в которой известны площадь ромба, а также соотношение между длинами диагоналей, а требуется найти диагонали.
(На эту задачу лучше вызвать
сильного ученика, т.к. она решается с
помощью уравнения и является сложной для
слабых учеников). Во время обдумывания
решения предложенной задачи средними и
сильными учениками класса, слабые получают
карточки-задания на отработку выведенных
формул.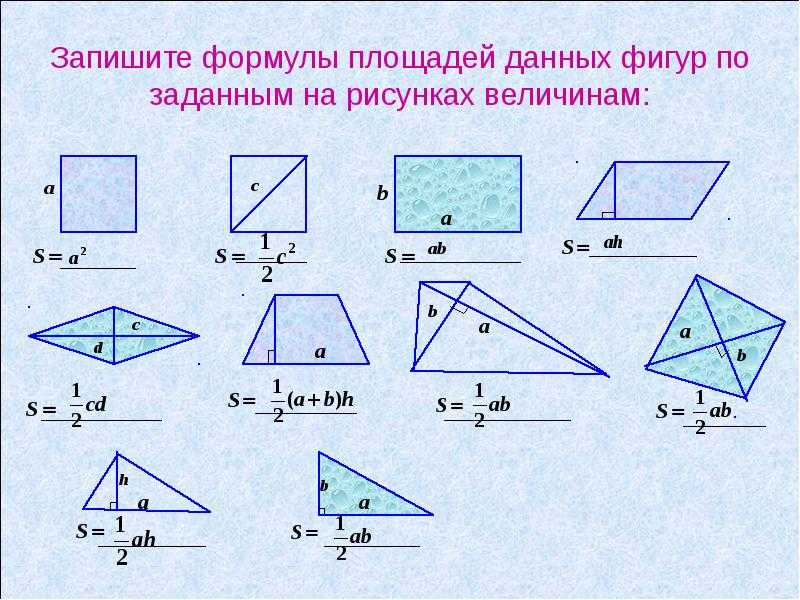 Каждая карточка содержит по 2
простые задачи типа:
Каждая карточка содержит по 2
простые задачи типа:
-
Вычислить площадь ромба, если одна из его диагоналей равна 5 см, а другая в 4 раза больше.
-
Вычислить диагональ квадрата, если его площадь равна 32 см2.
Задача (для средних и сильных учеников).
Одна из диагоналей ромба, площадь которого равна 27 см2, в 1,5 раза больше другой диагонали. Найти диагонали этого ромба.
Ученик записывает на доске:
Дано:
ABCD – ромб,
AC = 1,5 BD,
SABCD = 27 см2.
Найти:
AC, BD.
Решение:
- SABCD = 1/2 ACBD.
Пусть BD = x см, тогда AC = 1,5x см. Т.к. по условию задачи SABCD = 27 см2, то получаем уравнение:
1/21,5xx = 27,
1,5x2=54,
x2=36,
x=6 ( x=-6 не подходит по смыслу
задачи).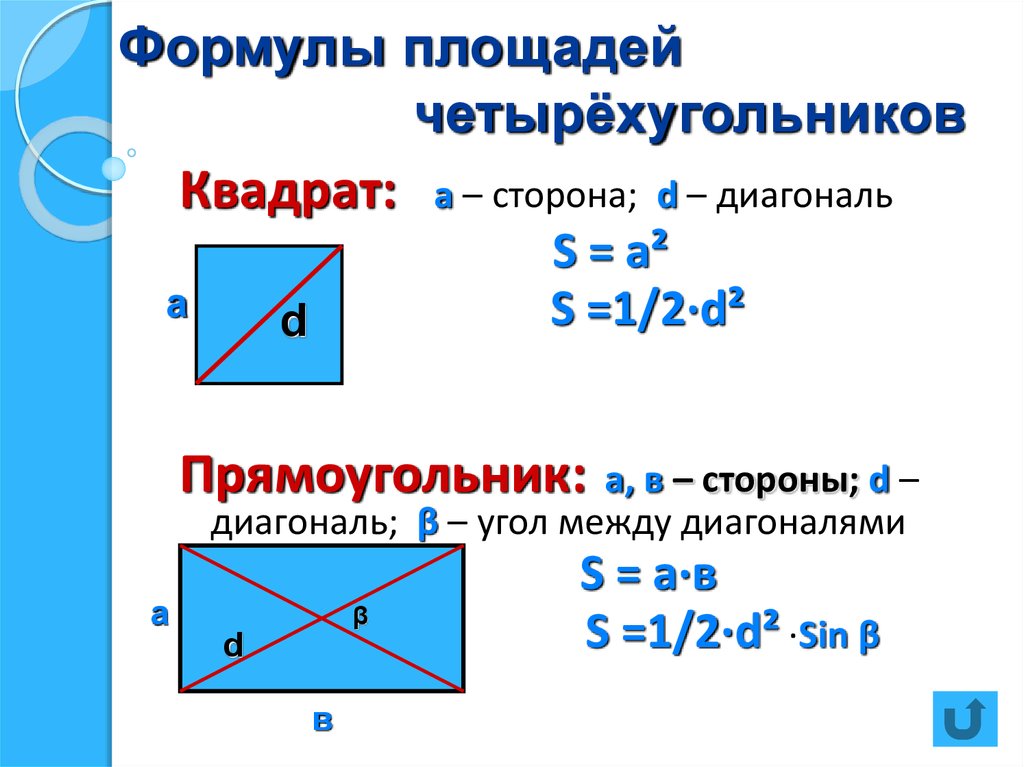
- BD = 6 см, AC = 1,56= 9 см.
Ответ : 6 см и 9 см.
- Итог урока.
Учитель. Какие новые формулы мы сегодня узнали?
Ученик. Формулы для вычисления площадей выпуклых четырехугольников, имеющих взаимно-перпендикулярные диагонали, в частности, для ромба и квадрата.
Учитель. Какая еще из известных вам геометрических фигур может иметь взаимно-перпендикулярные диагонали?
Ученик. Трапеция.
Учитель. Верно, значит можно вычислить и площадь трапеции, если у нее взаимно-перпендикулярные диагонали. Этими формулами можно пользоваться наряду с ранее изученными.
- Домашнее задание (творческое).
- Придумать по 2 задачи (2 прямые и 2
обратные) на применение изученных формул
и записать их с решениями.
 Чем сложнее
задача, тем выше оценка.
Чем сложнее
задача, тем выше оценка. - Для слабых учеников (у кого не получится придумать задачи):
Задача. Найти площадь трапеции, если ее диагонали взаимно перпендикулярны, а их длины равны 10 см и 16 см.
Вопрос Видео: Вычисление площади четырехугольника с помощью тригонометрии
Стенограмма видео
𝐴𝐵𝐶𝐷 – четырехугольник, угол 𝐴𝐵𝐶 равен 90 градусам, мера угла 𝐵𝐴𝐷 равна 41 градусу, 𝐐 до 30,9 см, а 𝐵𝐷 равно 𝐵𝐶. Найдите площадь 𝐴𝐵𝐶𝐷, давая ответ с точностью до двух знаков после запятой.
Начнем с рисования четырехугольника. Нам говорят, что угол 𝐴𝐵𝐶 прямой, а также говорят, что угол 𝐵𝐴𝐷 равен 41 градусу. Длины 𝐴𝐵 и 𝐴𝐷 равны 30,9.сантиметры. Нам также говорят, что длины 𝐵𝐷 и 𝐵𝐶 равны. Это означает, что у нас есть два равнобедренных треугольника. Первый, треугольник 𝐴𝐵𝐷, имеет две стороны по 30,9 см.
Мы знаем, что сумма углов любого треугольника равна 180 градусам. И что в равнобедренном треугольнике два угла равны. Угол 𝐴𝐷𝐵 равен углу 𝐴𝐵𝐷. Чтобы вычислить эти углы, мы можем вычесть 41 из 180, а затем разделить на два. Это дает нам 69,5. Углы 𝐴𝐷𝐵 и 𝐴𝐵𝐷 равны 69.5 градусов. Вспоминая, что угол 𝐴𝐵𝐶 равен 90 градусам, мы можем вычислить угол 𝐷𝐵𝐶, вычитая 69,5 из 90. Это равно 20,5 градусам.
Угол 𝐴𝐷𝐵 равен углу 𝐴𝐵𝐷. Чтобы вычислить эти углы, мы можем вычесть 41 из 180, а затем разделить на два. Это дает нам 69,5. Углы 𝐴𝐷𝐵 и 𝐴𝐵𝐷 равны 69.5 градусов. Вспоминая, что угол 𝐴𝐵𝐶 равен 90 градусам, мы можем вычислить угол 𝐷𝐵𝐶, вычитая 69,5 из 90. Это равно 20,5 градусам.
Мы знаем, что можем вычислить площадь любого треугольника по формуле: половина 𝑎𝑏 умножается на грех 𝐶, где угол 𝐶 лежит между двумя сторонами 𝑎 и 𝑏. Для первого треугольника у нас достаточно информации. Однако в треугольнике 𝐵𝐶𝐷 нам нужно сначала вычислить длину 𝐵𝐶 и 𝐵𝐷. Нам говорят, что эти длины равны, поэтому мы будем использовать правило косинусов для треугольника один, чтобы вычислить длину 𝐵𝐷.
Правило косинуса гласит, что 𝑎 в квадрате равно 𝑏 в квадрате плюс 𝑐 в квадрате минус два 𝑏𝑐, умноженное на cos 𝐴, где угол 𝐴 противоположен длине стороны 𝑎, которую мы пытаемся вычислить. Это означает, что 𝐵𝐷 в квадрате равно 30,9 в квадрате плюс 30,9 в квадрате минус два, умноженное на 30,9, умноженное на 30,9, умноженное на косинус 41 градуса.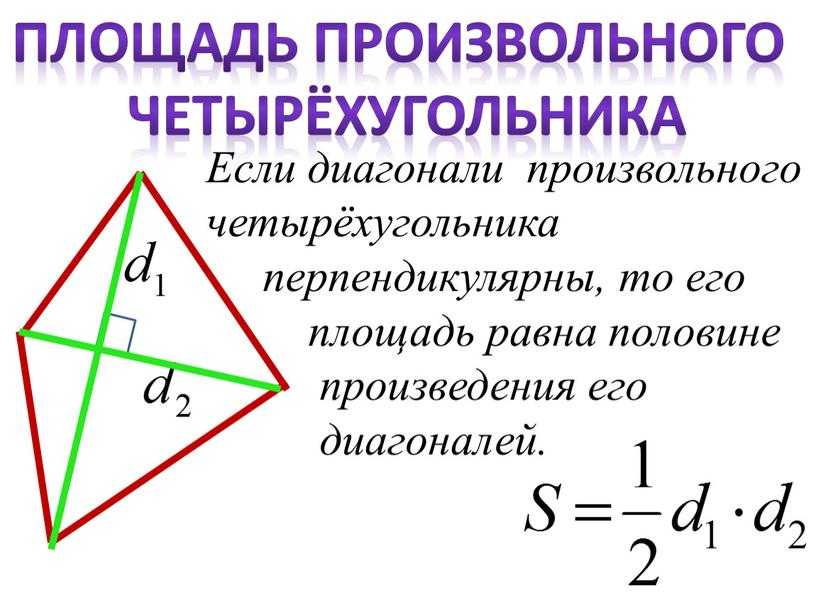 Ввод правой части в наш калькулятор дает нам 468,411 и так далее. Затем мы можем извлечь корень из обеих частей этого уравнения, чтобы 𝐵𝐷 было равно 21,642 и так далее.
Ввод правой части в наш калькулятор дает нам 468,411 и так далее. Затем мы можем извлечь корень из обеих частей этого уравнения, чтобы 𝐵𝐷 было равно 21,642 и так далее.
При выполнении остальных расчетов мы будем использовать неокругленный ответ. Однако мы видим, что 𝐵𝐷 и 𝐵𝐶 равны 21,6 сантиметра с точностью до одной десятой. Теперь мы можем определить площади треугольника один и треугольника два. Площадь треугольника 𝐴𝐵𝐷 равна половине, умноженной на 30,9, умноженной на 30,9, умноженной на 41 градус. Это равно 313,20586 и так далее.
Таким же образом мы можем вычислить площадь треугольника 𝐵𝐶𝐷, где длины сторон равны 𝐵𝐶 и 𝐵𝐷, а угол равен 20,5 градуса. Это дает нам ответ 82.02058 и так далее. Сложение площадей этих двух треугольников даст нам площадь четырехугольника 𝐴𝐵𝐶𝐷. Это равно 395.22644 и так далее.
Нас просят дать ответ с точностью до двух знаков после запятой. Итак, решающее число – шестерка. Округлив, можно сделать вывод, что площадь четырехугольника равна 395,23 квадратных сантиметра.
| ||||||||||||||
| ||||||||||||||
| ||||||||||||||
Не бойся, Кортни! Это работа для закона косинусов. Я покажу вам, как это делается с похожей геометрией, и вы можете применить те же шаги для своего вопроса: Здесь мы знаем три длины: 42, 75 и 22 и два угла: 115° и 49°. Мы хотим найти площадь четырехугольника.
Начнем с построения линии между А и С. Теперь мы разделили четырехугольник на два треугольника. Сумма площадей двух треугольников и есть площадь четырехугольника. Если мы можем определить две длины и угол между ними для каждого треугольника, мы можем использовать уравнение площади Площадь = ½xy Sin Z для вычисления площадей треугольников. Нам нужно знать длину отрезка AC для нижнего треугольника, и мы можем использовать закон косинусов для верхнего треугольника, чтобы получить это:
Нам нужен внутренний угол CAB между AC и AB, чтобы найти площадь нижнего треугольника. Мы знаем, что угол DAB равен 115 °, поэтому, если мы можем найти угол DAC, мы можем вычесть и найти угол CAB. Опять же, мы можем использовать закон косинусов для верхнего треугольника:
Таким образом, угол CAB = 115 — 15,33 = 99,67°. Теперь мы знаем две длины сторон и углы между ними для обоих треугольников, поэтому мы можем вычислить площадь четырехугольника. |


 ⓘ Высота второй колонны четырехугольника [h2]
ⓘ Высота второй колонны четырехугольника [h2] ⓘ Диагональ четырехугольника [d]
ⓘ Диагональ четырехугольника [d]

 Чем сложнее
задача, тем выше оценка.
Чем сложнее
задача, тем выше оценка.
 8.
8.