Как решать матрицы 4х4: Как вычислить определитель матрицы 4х4

Dr.HD MA 446 SM HDMI 2.0 матрица 4×4

HDMI 2.0 матрица 4×4 Dr.HD MA 446 SM — это устройство подойдет как для домашнего использования, так и для крупных сложных объектов. Его функционал позволяет решать множество задач:

• Раздавать аудио- видео- контент в разрешении 4K от 4 источников на 4 экрана (HDMI матрица)
• Или разделить аудио- видео- контент в разрешении 4K с 1 источника на 4 экрана (HDMI свитч)
• Выводить изображение с 4 источников на 1 экран в различных конфигурациях (мультикартинка)
• Выбирать разрешение, положение и варианты отображения, зумирования и отражения для каждого источника
• Моментально переключаться между источниками без задержек
• Отображать картинку в картинке
• Построить видеостену размером 2×2, 3×1 и 4×1
• А с несколькими такими устройствами можно собирать выдеостены даже из 81 экрана (9х9) любых конфигураций!
• Извлекать звук из источников сигнала (для подключения усилителей, колонок и саунбаров) и переключать их независимо друг от друга
• Выбирать настройки EDID для каждого экрана
• Управлять устройством с пульта, с кнопок на передней панели, через WEB-интерфейс, TCP/IP или RS-232

Словом, это целый комбайн для самых-самых требовательных заказчиков.  

Особенности:

• Совместимость с HDMI 2.0
• Протокол защиты HDCP 2.2 и ниже
• Поддержка видеоразрешений до 4K @60HZ 4:4:4
• Поддержка видеостены с 7 различными режимами работы
• Картинка в картинке
• Несколько режимов отображения всех источников на одном экране, в том числе функция горизонтального и вертикального поворота изображения
• Поддержка аудиоформатов семейства Dolby
• Извлечение звука
• Управление настройками EDID
• Каскадирование до 8 слоев (максимум до 81 дисплея, видеостена размером 9×9)
• Моментальное переключение между источниками без задержки и потери изображений
• Поддержка управления EDID
• Управление с пульта ДУ, кнопками с лицевой панели, по RS232, TCP / IP и WEB-интерфейс
• Металлический корпус
• Современная элементная база с дополнительной защитой
• Возможность работы в режиме 24/7
• Гарантия 2 года 

Спецификации HDMI матрицы Dr.

HD MA 446 SM:

• Версия HDMI: 2.0
• Версия HDCP: 2.2
• Полоса пропускания 18Gbps
• Видеоразрешения: 4K 60Hz YUV 4:4:4 8bit, 4K 30Hz, 1080i/p 50/60Hz, 720P
• Входные порты: 4x HDMI, 4x 3.5 mm AudioJack, 1x Phoenix RS232, 1x Ethernet
• Выходные порты: 4x HDMI, 4x 3.5 mm AudioJack, 4x RCA SPDIF, 1x 3.5 mm Jack ИК управление
• Аудио форматы: DTS-5.1, Dolby-5.1
• Защита от статики:
  • ± 8kV (по воздуху)
  • ± 4kV (при касании)
• Габариты (ДхГхВ): 262 x 163 x 36 мм
• Масса: 1440 г
• Материал корпуса: Металл
• Рабочая температура: -5°C ~ 40°C / 23°F ~ 104°F
• Температура хранения: -10°C ~ 60°C / -14°F ~ 140°F
• Относительная влажность: 5~90% RH (без конденсата)
• Питания: внешний блок 12V 3A (стандарт US/EU, сертификаты CE/FCC/UL)
• Потребляемая мощность (макс): 23W  

Варианты подключения

Как матричный HDMI коммутатор:

 

Как видеостена:

 

Варианты построения видеостены:

 

Мультикартинка:

 

Комплект поставки:

1. HDMI матрица – 1 шт
2. Пульт ДУ – 1 шт
3. Блок питания 12V/3A – 1 шт
4. Крепление – 1 шт
5. CD диск с руководством пользователя – 1 шт
6. Разъем Phoenix 3Pin – 1 шт 

Dr.

HD MA 446 SM – HDMI 2.0 матрица 4×4 и видеостена

HDMI оборудование Dr.HD оптом и в розницу. Доставка по РФ и ТС.

1. Главная
2. Каталог
3. HDMI оборудование
4. HDMI матрицы
5. HDMI 2.0 матрица 4×4 / Dr.HD MA 446 SM

Код: 005005032

Новинка осени 2022 года. Профессиональный матричный коммутатор Dr.HD MA 446 SM с мгновенным переключением источников + свитч + видеостена! Поддерживается HDMI 2.0, HDCP 2.2, 4K 60Hz, 18Gbps, 3D и возможность настройки EDID. Имеется управление по RS232 и TCP/IP.

Цена: 85 510 ₽

Безнал? Пишите сюда

 В наличии

Количество:

Купить в 1 клик

Заказать в комплекте:

• Защита HDMI интерфейсов / Dr. HD HDMI Protector(1 300 ₽)
• HDMI кабель 0.5 м Dr.HD(170 ₽)
• HDMI кабель 1 м Dr.HD(190 ₽)
• HDMI кабель 1.5 м Dr.HD(210 ₽)
• HDMI кабель 2 м Dr.HD(230 ₽)
• HDMI кабель 3 м Dr.HD(290 ₽)

Доставка и самовывоз:
— по Москве: 1-3 дня (пн-пт)
— по России: 2-8 дней (пн-пт) *
— в страны Таможенного союза: 3-12 дней *
— самовывоз: в день заказа или на следующий (пн-пт)

* Зависит от региона, страны и транспортной компании.

Это устройство подойдет как для домашнего использования, так и для крупных сложных объектов. Его функционал позволяет решать множество задач:

• Раздавать аудио- видео- контент в разрешении 4K от 4 источников на 4 экрана (HDMI матрица)
• Или разделить аудио- видео- контент в разрешении 4K с 1 источника на 4 экрана (HDMI свитч)
• Выводить изображение с 4 источников на 1 экран в различных конфигурациях (мультикартинка)
• Выбирать разрешение, положение и варианты отображения, зумирования и отражения для каждого источника
• Моментально переключаться между источниками без задержек
• Отображать картинку в картинке
• Построить видеостену размером 2×2, 3×1 и 4×1
• А с несколькими такими устройствами можно собирать выдеостены даже из 81 экрана (9х9) любых конфигураций!
• Извлекать звук из источников сигнала (для подключения усилителей, колонок и саунбаров) и переключать их независимо друг от друга
• Выбирать настройки EDID для каждого экрана
• Управлять устройством с пульта, с кнопок на передней панели, через WEB-интерфейс, TCP/IP или RS-232

Словом, это целый комбайн для самых-самых требовательных заказчиков.

 

Особенности:

• Совместимость с HDMI 2.0
• Протокол защиты HDCP 2.2 и ниже
• Поддержка видеоразрешений до 4K @60HZ 4:4:4
• Поддержка видеостены с 7 различными режимами работы
• Картинка в картинке
• Несколько режимов отображения всех источников на одном экране, в том числе функция горизонтального и вертикального поворота изображения
• Поддержка аудиоформатов семейства Dolby
• Извлечение звука
• Управление настройками EDID
• Каскадирование до 8 слоев (максимум до 81 дисплея, видеостена размером 9×9)
• Моментальное переключение между источниками без задержки и потери изображений
• Поддержка управления EDID
• Управление с пульта ДУ, кнопками с лицевой панели, по RS232, TCP / IP и WEB-интерфейс
• Металлический корпус
• Современная элементная база с дополнительной защитой
• Возможность работы в режиме 24/7
• Гарантия 2 года

 

Спецификации HDMI матрицы Dr.

HD MA 446 SM:

• Версия HDMI: 2.0
• Версия HDCP: 2.2
• Полоса пропускания 18Gbps
• Видеоразрешения: 4K 60Hz YUV 4:4:4 8bit, 4K 30Hz, 1080i/p 50/60Hz, 720P
• Входные порты: 4x HDMI, 4x 3.5 mm AudioJack, 1x Phoenix RS232, 1x Ethernet
• Выходные порты: 4x HDMI, 4x 3.5 mm AudioJack, 4x RCA SPDIF, 1x 3.5 mm Jack ИК управление
• Аудио форматы: DTS-5.1, Dolby-5.1
• Защита от статики:
  • ± 8kV (по воздуху)
  • ± 4kV (при касании)
• Габариты (ДхГхВ): 262 x 163 x 36 мм
• Масса: 1440 г
• Материал корпуса: Металл
• Рабочая температура: -5°C ~ 40°C / 23°F ~ 104°F
• Температура хранения: -10°C ~ 60°C / -14°F ~ 140°F
• Относительная влажность: 5~90% RH (без конденсата)
• Питания: внешний блок 12V 3A (стандарт US/EU, сертификаты CE/FCC/UL)
• Потребляемая мощность (макс): 23W 

 

Варианты подключения

Как матричный HDMI коммутатор:

 

Как видеостена:

 

Варианты построения видеостены:

 

Мультикартинка:

 

Комплект поставки:

1. HDMI матрица – 1 шт
2. Пульт ДУ – 1 шт
3. Блок питания 12V/3A – 1 шт
4. Крепление – 1 шт
5. CD диск с руководством пользователя – 1 шт
6. Разъем Phoenix 3Pin – 1 шт

 

Аналоги (заменители):

• HDMI матрица 4×4 / Dr. HD MX 445 SM
• HDMI матрица 4×4 с мгновенным переключением / Dr.HD MA 443 SM

 

Все HDMI матрицы Dr.HD имеют декларацию соответствия EAC и 2х летнюю гарантию, что позволяет применять их не только в бытовых условиях, но и в профессиональных инсталляциях и участвовать в тендерах.

 

Список команд для управления по RS232 —	Скачать
Инструкция для матрицы Dr.HD MA 446 SM —	Скачать
Драйверы для матрицы Dr.HD MA 446 SM —	Скачать
Утилита для управления матрицей Dr.HD MA 446 SM —	Скачать

Добавить комментарий

Этот товар, как и все остальные, представленные в нашем интернет-магазине, можно приобрести по более низкой партнерской или даже оптовой цене. Т.к. мы являемся официальными дистрибьюторами компании Dr.HD на территории РФ и стран Таможенного союза, мы готовы предоставить самые выгодные условия, самую низкую цену и официальную поддержку.

Если вы инсталляторы или интеграторы и заинтересованы в качественном и функциональном оборудовании – попробуйте HDMI оборудование Dr.HD! Мы готовы предложить продвинутые устройства по отличной цене и гибкие условия работы.

Если вы занимаетесь продажей оборудования – добро пожаловать в нашу команду! У нас широкий ассортимент, низкие оптовые цены и оперативная доставка по всей России и странам ТС.

Если вы занимаетесь закупками оборудования – найдем что предложить и вам! У нас только официальные поставки, декларации соответствия, техническое сопровождение и двухлетняя гарантия.

Мы готовы обсудить условия взаимовыгодного сотрудничества с любыми компаниями и индивидуальными предпринимателями. Мы обязательно найдем общий язык!

Скачать наш прайс-лист можно в разделе Партнерам – Прайс-лист.

Возникли вопросы? Обращайтесь:

+7 499 730-71-11

+7 499 730-73-33

 

Предыдущий← HDMI 2.0 матрица 4×4 / Dr.HD MA 447 FX ВпередHDMI 2.0 матрица 4×4 с удлинением по UTP / Dr.HD MA 446 EX90 →

Copyright MAXXmarketing GmbH
JoomShopping Download & Support

Сайт использует cookie файлы для сбора статистики. Оставаясь на сайте, Вы даете согласие на их использование.
Впрочем, Вы всегда можете их отключить в настройках своего браузера.

Вычисление определителя матрицы 4 x 4 с примерами решения

Детерминанты — это скаляры, которые получаются суммой произведений элементов квадратной матрицы и их кофакторов по определенному правилу. Определители в математике помогают нам найти сопряженную матрицу, а также обратную матрицу. Мы можем использовать определители для решения линейных уравнений с помощью метода обращения матриц. Кроме того, определители помогают найти векторное произведение двух векторов.

Что такое определитель матрицы 4×4?

Определитель матрицы 4×4 — это уникальное число, вычисляемое по специальной формуле. Если матрица имеет порядок n x n, то это квадратная матрица. Итак, здесь 4×4 — это квадратная матрица, состоящая из 4 строк и 4 столбцов. Также для квадратной матрицы A порядка \(4 \times 4 \) ее определитель записывается как |A|.

Могут быть разные способы нахождения определителей матрицы порядка \(4 \times 4 \).

Условия для того, чтобы определитель матрицы 4×4 был равен нулю

Прежде чем пытаться вычислить значение определителя матрицы 4×4, нам сначала нужно проверить, является ли значение определителя ненулевым числом.

Это можно сделать, просто проанализировав предоставленный определитель.

Некоторые случаи, когда значение определителя матрицы 4×4 равно нулю: матрица}\справа|\)

В этом случае одна из строк матрицы равна нулю, поэтому значение определителя матрицы становится равным нулю.

Случай 2:  \(\left|\begin{matrix}2&1&2&3\\6&7&6&9\\0&6&0&0\\1&2&1&4\end{matrix}\right|\)

В приведенной выше матрице, как мы видим, первый и третий столбцы имеют одинаковые значения, поэтому значение определителя матрицы \(4 \times 4 \) равно нулю.

Случай 3: \(\left|\begin{matrix}1&2&3&4\\2&5&7&3\\4&10&14&6\\3&4&2&7\end{matrix}\right|\)

В приведенном выше сценарии мы видим, что вторая и третья строки пропорциональны друг другу. Итак, значение определителя матрицы \(4\times 4\) равно нулю.

Теперь, когда мы знаем случаи, когда значение определителя может быть равно нулю, давайте проверим, как найти значение определителя для матрицы \(4 \times 4 \) в случае, если он не равен нулю.

Узнать о свойствах определителей

Что такое исключение Гаусса?

Метод исключения Гаусса также называется методом редукции строк и используется для решения линейных уравнений в линейной алгебре. Этот метод исключения на самом деле представляет собой серию операций, которые используются с матрицей, и очень полезен при нахождении ранга матрицы, обратной матрицы и даже определителя матрицы.

Чтобы выполнить это исключение, мы используем ряд алгебраических операций над матрицей, превращая все элементы ниже главной диагонали в нуль.

Мы можем использовать три вида операций над строками:

• Поменяв местами две строки: значение определителя меняет знак. Отрицательное становится положительным, а положительное становится отрицательным.
• Значение определителя остается неизменным при умножении строки на ненулевую константу.
• Значение определителя остается неизменным при добавлении или вычитании строки из любой другой строки.

Узнайте об инволютивной матрице

Свойство треугольности матрицы

Чтобы найти определитель матрицы \(4 x 4 \), мы должны хорошо знать свойство треугольности матрицы. По свойству треугольности матрицы говорят, что если каждый элемент матрицы как выше, так и ниже главной диагонали равен нулю, то значение определителя равно произведению диагональных элементов.

Теперь существует три вида треугольных матриц, мы узнаем о каждом из них ниже:

1. Верхняя треугольная матрица:  \(4 \times 4 \)Матрица называется верхней треугольной матрицей, когда все элементы ниже главной диагонали равны нулю. Или можно сказать, что все ненулевые элементы такой матрицы находятся выше главной диагонали.

Пример:

\(\left|\begin{matrix}1&2&3&4\\0&5&7&3\\0&0&4&6\\0&0&0&7\end{matrix}\right|\) — верхняя треугольная матрица.

2. Нижняя треугольная матрица: Матрица \(4 \times 4 \) называется нижней треугольной матрицей, если все элементы выше главной диагонали равны нулю. Или можно сказать, что все ненулевые элементы такой матрицы находятся ниже главной диагонали.

Пример:

\(\left|\begin{matrix}2&0&0&0\\6&7&0&0\\0&6&4&0\\1&2&1&4\end{matrix}\right|\) — нижняя треугольная матрица.

3. Диагональная матрица: \(4 \times 4 \) Матрица называется диагональной матрицей, когда все элементы, кроме главной диагонали, равны нулю.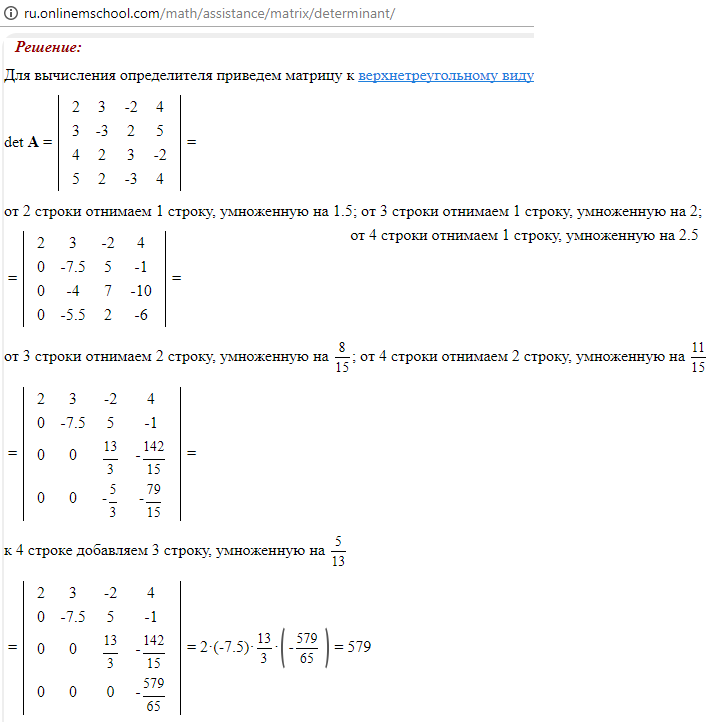 Или можно сказать, что в такой матрице все, что выше или ниже главной диагонали, равно нулю.

Пример:

\(\left|\begin{matrix}2&0&0&0\\0&7&0&0\\0&0&4&0\\0&0&0&4\end{matrix}\right|\)

Значение определителя во всех трех вышеперечисленных случаях равно произведение диагональных элементов. Поясним это на примере:

Пример: Пусть задано

\(\left|\begin{matrix}2&3&3&1\\1&5&4&3\\4&6&8&5\\-2&-3&-3&4\end{matrix}\right| \)

Мы знаем, что добавление строк и столбцов к другим строкам и столбцам того же определителя не приводит к изменению значения определителя.

С помощью операций:

\(r_2-r_1\)

\(r_3-2r_1\)

\(r_4+r_1\)

Результирующая матрица будет иметь вид:

\(\left | \begin{matrix}2&3&3&1\\0&2&1&3\\0&0&2&5\\0&0&0&5\end{matrix}\right|\)

Как мы знаем, для треугольной матрицы определитель равен произведению диагональных элементов.

Итак, |В| = 2.2.2.5 = 40.

Узнайте о применении матриц и определителей

Что такое метод расширения кофактора?

Чтобы найти определитель для матрицы \(4 \times 4 \), мы используем другой метод, который представляет собой разложение на кофакторы. {3+1}\раз\влево|\начать{матрицу}0&-2\\ 95\times\left|\begin{matrix}-1&-2\\
1&-5\end{matrix}\right|+0\right)\)

\(\det\left(A\right)\ )=\(5\times -1\times \left|\begin{matrix}-1&-2\\
1&-5\end{matrix}\right|\)

\(\det\left(A\ right)\)= (5)(-7)= -35

Узнайте о матрице кофакторов

Решенные примеры определителя матрицы 4 × 4

Вопрос 1: Найдите определитель матрицы \(B=\ влево|\начало{матрица}4&3&4&2\\8&7&5&3\\4&3&8&5\\4&3&4&3\конец{матрица}\вправо|\)

Ответ 1: Мы будем использовать эти операции на приведенной выше матрице;

\(r_3-r_1\)

\(r_2-2r_1\)

\(r_4-r_1\)

Матрица, полученная после операций, выглядит следующим образом;

\(B=\left|\begin{matrix}4&3&4&2\\0&1&3&-1\\0&0&4&3\\0&0&0&1\end{matrix}\right|\)

Матрица является верхней треугольной матрицей, поэтому определитель произведение всех диагональных элементов.

Итак, det(B)=4.1.4.1 = 16

Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.

Часто задаваемые вопросы об определителе матрицы 4 x 4

В.1 Для чего используются определители?

Ответ 1

Детерминанты используются для нахождения решений линейных уравнений, для определения того, как линейные преобразования изменяют площадь и объем, а также для изменения переменных в интегралах.

Q.2 Каковы свойства определителей?

Ответ 2 Некоторыми из важных свойств определителей являются скалярное кратное свойство, свойство всех нулей, факторное свойство, свойство пропорциональности, свойство кофакторной матрицы, свойство отражения, свойство треугольника, свойство суммы и свойство инвариантности.

Q. 3 Что такое метод обратной матрицы?

Ответ 3 Обратная матрица находится только для квадратной матрицы. Это можно сделать, просто разделив сопряжение данной матрицы на определитель данной матрицы.

Q.4 Что такое формула определителя треугольной матрицы?

Ответ 4 Для треугольной матрицы определитель равен произведению всех диагональных элементов.

В.5 Являются ли определители коммутативными?

Ответ 5 Да, умножение определителей коммутативно. Мы можем понять это на примере. Пусть A и B — две квадратные матрицы порядка \(n\times n\). det(AB)=\(det(A)\times det(B)=det(B)\times det(A)\).

Скачать публикацию в формате PDF

Читать больше сообщений

90 264

Угол между двумя плоскостями: изучите понятие, формулу и примеры решения
Среднее значение сгруппированных данных: изучите понятие, формулу, методы и примеры решения
Грех Кос Тан Значения, формулы, таблицы, приложения с примерами
Формулировка теоремы Аполлония с доказательством теоремой Пифагора, правилом косинусов и векторами
Этин: изучите его формулу, структуру, получение, свойства и применение

▷ Как найти определитель матрицы 4×4 (практика)

Мы объясним, как найти определитель матрицы 4×4 с пример. Кроме того, вы найдете решенные упражнения, чтобы вы могли попрактиковаться и в совершенстве понять, как вычислить определитель матрицы 4 × 4.

Содержание

Как найти определитель матрицы 4×4, используя операции со строками и расширение кофактора

Давайте посмотрим, как вычислить определитель матрицы 4×4, решив пример:

Первым шагом в вычислении определителя матрицы 4×4 является обнуление всех элементов столбца, кроме одного с помощью элементарные операции со строками .

Мы можем выполнять элементарные операции со строками благодаря свойствам определителей.

В этом случае в первом столбце уже есть ноль. Таким образом, мы собираемся преобразовать все записи в первом столбце в 0, кроме числа 1 (поскольку легче выполнять вычисления со строкой, в которой есть 1). Для этого мы прибавляем первую строку ко второй строке и вычитаем первую строку, умноженную на 2, из четвертой строки:

После того, как мы преобразовали в 0 все элементы, кроме одного из выбранного столбца, мы вычисляем определитель матрицы 4×4, используя расширение кофактора .

Расширение кофакторов — это метод нахождения определителей, который состоит в сложении произведений элементов столбца на их соответствующие кофакторы .

Является кофактором i, j матрицы, определяемой:

Где M _ij является минором i, j матрицы, то есть определителем, полученным в результате удаления i-й строки и j -й столбец матрицы.

Итак, мы складываем произведения элементов в первом столбце по их соответствующим кофакторам:

Члены, умноженные на 0, сокращаются, поэтому мы упрощаем их:

Итак, мы должны вычислить кофактор первой строки и первого столбца, то есть (-1), возведенное в 1+1 (1-я строка и 1-й столбец), умноженное на определитель, полученный в результате удаления первой строки и первого столбца матрицы 4×4.

И, наконец, нам просто нужно найти определитель матрицы 3×3:

Итак, мы решили определитель матрицы 4×4, используя операции со строками и разложение на кофакторы.

Практические задачи на нахождение определителя матрицы 4×4

Задача 1

Найдите определитель следующей квадратной матрицы 4-го порядка:

См. решение

Мы найдет определитель 4 Матрица × 4 с методом расширения кофактора, также называемым расширением Лапласа. Но сначала проделаем элементарные операции со строками, чтобы обнулить все элементы столбца, кроме одного:

Теперь вычисляем определитель 4×4, используя разложение кофактора:

Упрощаем термины:

И, наконец, выполняем кофактор:

 

Задача 2

Вычислить определитель следующей матрицы 4×4:

См. решение

Вычислим определитель определителя 4×4 по формуле разложения кофакторов. Но сначала проделываем элементарные операции со строками, чтобы преобразовать все элементы столбца, кроме единицы, в ноль:

Теперь мы решаем определитель 4×4 путем расширения кофактора:

Упрощаем термины:

И вычисляем кофактор третьей строки и второго столбца:

 

Задача 3

Вычислите определитель следующей матрицы 4×4:

См.