свойства экспоненты и основные формулы
Многие числа обрели свою величину и суеверное значение еще в древности. В наши дни к ним добавляются новые мифы. Существует много легенд о числе пи, немногим уступают ему в известности знаменитые числа Фибоначчи. Но, пожалуй, самым удивительным является число е, без которого не может обойтись современная математика, физика и даже экономика.
Арифметическое значение числа е равно приблизительно 2,718. Почему не точно, а приблизительно? Потому что это число иррациональное и трансцендентное, его нельзя выразить дробью с натуральными целыми числами или многочленом с рациональными коэффициентами. Для большинства расчетов указанной точности значения в 2,718 достаточно, хотя современный уровень вычислительной техники позволяет определить его значение с точностью более триллиона знаков после запятой.
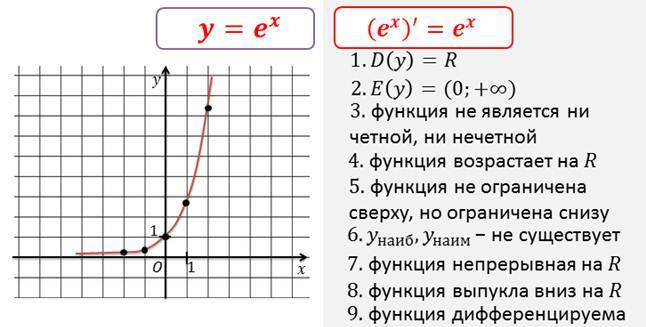
Главной особенностью числа е является то, что производная его показательной функции f (x) = ex равно значению самой функции ех. Такого необычного свойства нет больше ни у какой другой математической зависимости. Расскажем об этом чуть подробнее.
Такого необычного свойства нет больше ни у какой другой математической зависимости. Расскажем об этом чуть подробнее.
Содержание:
- Что такое предел
- Что такое производная функции
- Производная экспоненты
- Некоторые интересные факты о числе е
- Видео
Что такое предел
Вначале разберемся с понятием предела. Рассмотрим какое-нибудь математическое выражение, например, i = 1/n. Можно увидеть, что при увеличении «n «, значение «i «будет уменьшаться, а при стремлении «n» к бесконечности (которая обозначается значком ∞), «i» будет стремиться к предельному значению (называемого чаще просто пределом), равному нулю. Выражение предела (обозначаемого как lim) для рассматриваемого случая можно записать в виде lim n →∞ (1/ n) = 0 .
Существуют различные пределы для различных выражений. Одним из таких пределов, вошедших в советские и российские учебники как второй замечательный предел, является выражение lim n →∞ (1+1/ n) n . Уже в Средневековье было установлено, что пределом этого выражения является число е.
Уже в Средневековье было установлено, что пределом этого выражения является число е.
К первому же замечательному пределу относят выражение lim n →∞ (Sin n / n) = 1.
Как найти производную ex — в этом видео.
Что такое производная функции
Для раскрытия понятия производной следует напомнить что такое функция в математике. Чтобы не загромождать текст сложными определениями, остановимся на интуитивном математическом понятии функции, заключающимся в том, что в ней одна или несколько величин полностью определяют значение другой величины, если они взаимосвязаны. Например, в формуле S = π ∙ r 2 площади круга, значение радиуса r полностью и однозначно определяет площадь круга S.
В зависимости от вида, функции могут быть алгебраическими, тригонометрическими, логарифмическими и др. В них могут быть взаимосвязаны два, три и более аргументов. Например, пройденное расстояние S, которое объект преодолел с равноускоренной скоростью, описывается функцией S = 0,5 ∙ a ∙ t 2 + V ∙ t, где «t» — время движения, аргумент «а» ускорение (может быть как положительной, так и отрицательной величиной) и «V» начальная скорость движения. Таким образом, величина пройденного расстояния зависит от значений трех аргументов, два из которых («а» и «V») постоянны.
Например, пройденное расстояние S, которое объект преодолел с равноускоренной скоростью, описывается функцией S = 0,5 ∙ a ∙ t 2 + V ∙ t, где «t» — время движения, аргумент «а» ускорение (может быть как положительной, так и отрицательной величиной) и «V» начальная скорость движения. Таким образом, величина пройденного расстояния зависит от значений трех аргументов, два из которых («а» и «V») постоянны.
Покажем на этом примере элементарное понятие производной функции. Оно характеризует скорость изменения функции в данной точке. В нашем примере это будет скорость движения объекта в конкретный момент времени. При постоянных «а» и «V» она зависит только от времени «t», то есть говоря научным языком нужно взять производную функции S по времени «t».
Этот процесс называется дифференцированием, выполняется путем вычисления предела отношения прироста функции к приросту ее аргумента на ничтожно малую величину. Решения подобных задач для отдельных функций часто является непростым делом и здесь не рассматриваются.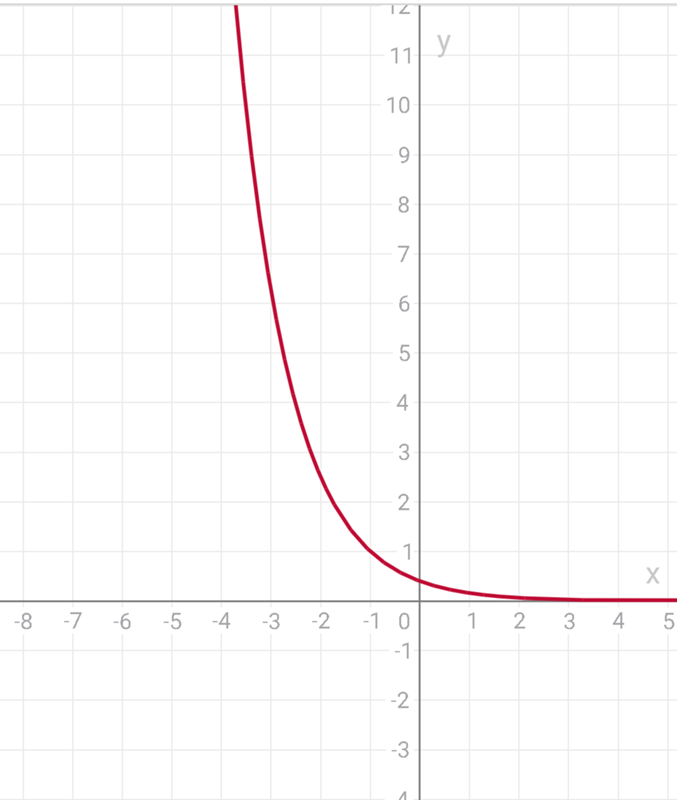 Также стоит отметить, что некоторые функции в определенных точках вообще не имеют таких пределов.
Также стоит отметить, что некоторые функции в определенных точках вообще не имеют таких пределов.
В нашем же примере производная S по времени «t» примет вид S’ = ds/dt = а ∙ t + V, из которого видно, что скорость S’ изменяется по линейному закону в зависимости от «t».
Производная экспоненты
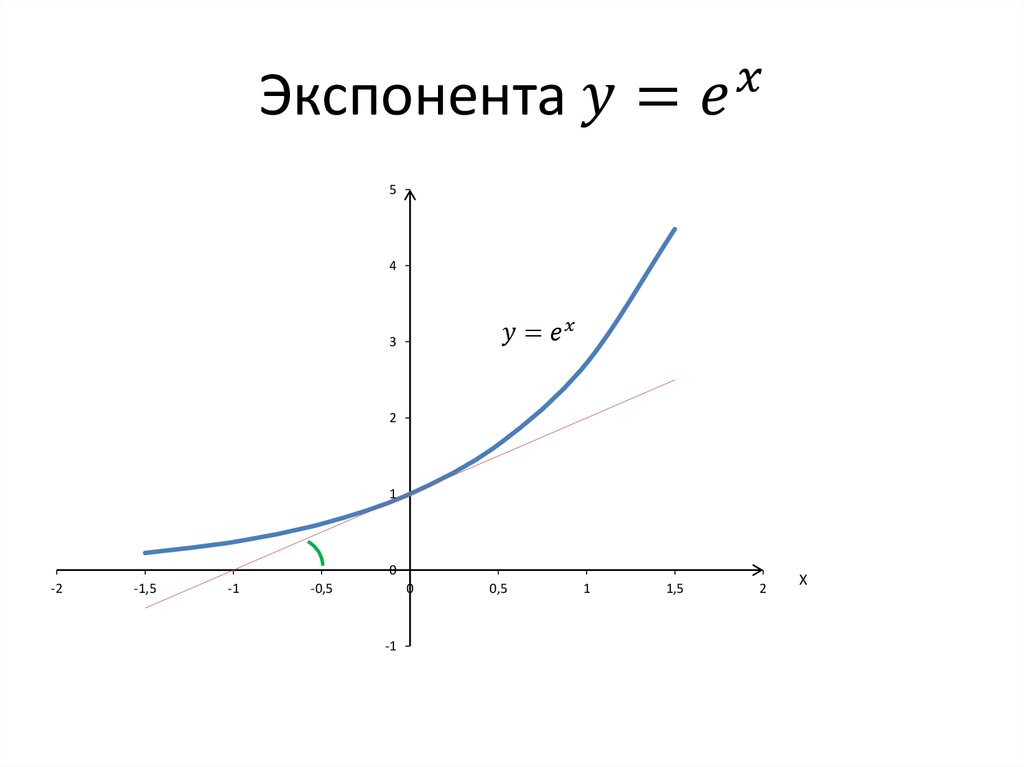
Экспонентой называется показательная функция, в качестве основания которой находится число е. Она обычно отображается в виде F (x) = ex, где показатель степени x является переменной величиной. Данная функция обладает полной дифференцируемостью во всем диапазоне вещественных чисел. С ростом x она постоянно возрастает и всегда больше нуля. Обратная к ней функция — логарифм.
Известный математик Тейлор сумел разложить эту функцию в ряд, названный его именем ex = 1 + x/1! + x 2 /2! + x 3 /3! + … в диапазоне x от — ∞ до + ∞.
Закон, базирующийся на этой функции, называется экспоненциальным. Он описывает:
Он описывает:
- возрастание сложных банковских процентов;
- увеличение популяции животных и населения планеты;
- время окоченения трупа и многое другое.
Повторим еще раз замечательное свойство данной зависимости — значение ее производной в любой точке всегда равно значению функции в этой точке, то есть (e
Приведем производные для наиболее общих случаев экспоненты:
- (eax)’ = a ∙ eax ;
- (ef (x))’ = f'(x) ∙ ef (x).
Используя данные зависимости, несложно найти производные для других частных видов этой функции.
Некоторые интересные факты о числе е
С этим числом связаны фамилии таких ученых, как Непер, Отред, Гюйгенс, Бернулли, Лейбниц, Ньютон, Эйлер, и другие. Последний собственно и ввел обозначение е для этого числа, а также нашел первые 18 знаков, используя для расчета открытый им ряд е = 1 + 1/1! + 2/2! + 3/3! …
Число e встречается в самых неожиданных местах. Например, оно входит в уравнение цепной линии, которое описывает провис каната под действием собственного веса, когда его концы закреплены на опорах.
Например, оно входит в уравнение цепной линии, которое описывает провис каната под действием собственного веса, когда его концы закреплены на опорах.
Видео
Тема видеоурока — производная показательной функции.
свойства экспоненты и основные формулы
Многие числа обрели свою величину и суеверное значение еще в древности. В наши дни к ним добавляются новые мифы. Существует много легенд о числе пи, немногим уступают ему в известности знаменитые числа Фибоначчи. Но, пожалуй, самым удивительным является число е, без которого не может обойтись современная математика, физика и даже экономика.
Арифметическое значение числа е равно приблизительно 2,718. Почему не точно, а приблизительно? Потому что это число иррациональное и трансцендентное, его нельзя выразить дробью с натуральными целыми числами или многочленом с рациональными коэффициентами. Для большинства расчетов указанной точности значения в 2,718 достаточно, хотя современный уровень вычислительной техники позволяет определить его значение с точностью более триллиона знаков после запятой.
Для большинства расчетов указанной точности значения в 2,718 достаточно, хотя современный уровень вычислительной техники позволяет определить его значение с точностью более триллиона знаков после запятой.
Главной особенностью числа е является то, что производная его показательной функции f (x) = ex равно значению самой функции ех. Такого необычного свойства нет больше ни у какой другой математической зависимости. Расскажем об этом чуть подробнее.
Содержание:
- Что такое предел
- Что такое производная функции
- Производная экспоненты
- Некоторые интересные факты о числе е
- Видео
Что такое предел
Вначале разберемся с понятием предела. Рассмотрим какое-нибудь математическое выражение, например, i = 1/n. Можно увидеть, что при увеличении «n «, значение «i «будет уменьшаться, а при стремлении «n» к бесконечности (которая обозначается значком ∞), «i» будет стремиться к предельному значению (называемого чаще просто пределом), равному нулю. Выражение предела (обозначаемого как lim) для рассматриваемого случая можно записать в виде lim n →∞ (1/ n) = 0 .
Выражение предела (обозначаемого как lim) для рассматриваемого случая можно записать в виде lim n →∞ (1/ n) = 0 .
Существуют различные пределы для различных выражений. Одним из таких пределов, вошедших в советские и российские учебники как второй замечательный предел, является выражение lim n →∞ (1+1/ n) n . Уже в Средневековье было установлено, что пределом этого выражения является число е.
К первому же замечательному пределу относят выражение lim n →∞ (Sin n / n) = 1.
Как найти производную ex — в этом видео.
Что такое производная функции
Для раскрытия понятия производной следует напомнить что такое функция в математике. Чтобы не загромождать текст сложными определениями, остановимся на интуитивном математическом понятии функции, заключающимся в том, что в ней одна или несколько величин полностью определяют значение другой величины, если они взаимосвязаны. Например, в формуле S = π ∙ r 2 площади круга, значение радиуса r полностью и однозначно определяет площадь круга S.
Например, в формуле S = π ∙ r 2 площади круга, значение радиуса r полностью и однозначно определяет площадь круга S.
В зависимости от вида, функции могут быть алгебраическими, тригонометрическими, логарифмическими и др. В них могут быть взаимосвязаны два, три и более аргументов. Например, пройденное расстояние S, которое объект преодолел с равноускоренной скоростью, описывается функцией S = 0,5 ∙ a ∙ t 2 + V ∙ t, где «t» — время движения, аргумент «а» ускорение (может быть как положительной, так и отрицательной величиной) и «V» начальная скорость движения. Таким образом, величина пройденного расстояния зависит от значений трех аргументов, два из которых («а» и «V») постоянны.
Покажем на этом примере элементарное понятие производной функции. Оно характеризует скорость изменения функции в данной точке. В нашем примере это будет скорость движения объекта в конкретный момент времени. При постоянных «а» и «V» она зависит только от времени «t», то есть говоря научным языком нужно взять производную функции S по времени «t».
Этот процесс называется дифференцированием, выполняется путем вычисления предела отношения прироста функции к приросту ее аргумента на ничтожно малую величину. Решения подобных задач для отдельных функций часто является непростым делом и здесь не рассматриваются. Также стоит отметить, что некоторые функции в определенных точках вообще не имеют таких пределов.
В нашем же примере производная S по времени «t» примет вид S’ = ds/dt = а ∙ t + V, из которого видно, что скорость S’ изменяется по линейному закону в зависимости от «t».
Производная экспоненты
Экспонентой называется показательная функция, в качестве основания которой находится число е. Она обычно отображается в виде F (x) = ex, где показатель степени x является переменной величиной. Данная функция обладает полной дифференцируемостью во всем диапазоне вещественных чисел. С ростом x она постоянно возрастает и всегда больше нуля. Обратная к ней функция — логарифм.
Известный математик Тейлор сумел разложить эту функцию в ряд, названный его именем ex = 1 + x/1! + x 2
/2! + x 3 /3! + … в диапазоне x от — ∞ до + ∞.
Закон, базирующийся на этой функции, называется экспоненциальным. Он описывает:
- возрастание сложных банковских процентов;
- увеличение популяции животных и населения планеты;
- время окоченения трупа и многое другое.
Повторим еще раз замечательное свойство данной зависимости — значение ее производной в любой точке всегда равно значению функции в этой точке, то есть (ex)’ = ex .
Приведем производные для наиболее общих случаев экспоненты:
- (eax)’ = a ∙ eax ;
- (ef (x))’ = f'(x) ∙ ef (x).
Используя данные зависимости, несложно найти производные для других частных видов этой функции.
Некоторые интересные факты о числе е
С этим числом связаны фамилии таких ученых, как Непер, Отред, Гюйгенс, Бернулли, Лейбниц, Ньютон, Эйлер, и другие. Последний собственно и ввел обозначение е для этого числа, а также нашел первые 18 знаков, используя для расчета открытый им ряд е = 1 + 1/1! + 2/2! + 3/3! …
Число e встречается в самых неожиданных местах. Например, оно входит в уравнение цепной линии, которое описывает провис каната под действием собственного веса, когда его концы закреплены на опорах.
Например, оно входит в уравнение цепной линии, которое описывает провис каната под действием собственного веса, когда его концы закреплены на опорах.
Видео
Тема видеоурока — производная показательной функции.
свойства экспоненты и основные формулы
Многие числа обрели свою величину и суеверное значение еще в древности. В наши дни к ним добавляются новые мифы. Существует много легенд о числе пи, немногим уступают ему в известности знаменитые числа Фибоначчи. Но, пожалуй, самым удивительным является число е, без которого не может обойтись современная математика, физика и даже экономика.
Арифметическое значение числа е равно приблизительно 2,718. Почему не точно, а приблизительно? Потому что это число иррациональное и трансцендентное, его нельзя выразить дробью с натуральными целыми числами или многочленом с рациональными коэффициентами. Для большинства расчетов указанной точности значения в 2,718 достаточно, хотя современный уровень вычислительной техники позволяет определить его значение с точностью более триллиона знаков после запятой.
Для большинства расчетов указанной точности значения в 2,718 достаточно, хотя современный уровень вычислительной техники позволяет определить его значение с точностью более триллиона знаков после запятой.
Главной особенностью числа е является то, что производная его показательной функции f (x) = ex равно значению самой функции ех. Такого необычного свойства нет больше ни у какой другой математической зависимости. Расскажем об этом чуть подробнее.
Содержание:
- Что такое предел
- Что такое производная функции
- Производная экспоненты
- Некоторые интересные факты о числе е
- Видео
Что такое предел
Вначале разберемся с понятием предела. Рассмотрим какое-нибудь математическое выражение, например, i = 1/n. Можно увидеть, что при увеличении «n «, значение «i «будет уменьшаться, а при стремлении «n» к бесконечности (которая обозначается значком ∞), «i» будет стремиться к предельному значению (называемого чаще просто пределом), равному нулю. Выражение предела (обозначаемого как lim) для рассматриваемого случая можно записать в виде lim n →∞ (1/ n) = 0 .
Выражение предела (обозначаемого как lim) для рассматриваемого случая можно записать в виде lim n →∞ (1/ n) = 0 .
Существуют различные пределы для различных выражений. Одним из таких пределов, вошедших в советские и российские учебники как второй замечательный предел, является выражение lim n →∞ (1+1/ n) n . Уже в Средневековье было установлено, что пределом этого выражения является число е.
К первому же замечательному пределу относят выражение lim n →∞ (Sin n / n) = 1.
Как найти производную ex — в этом видео.
Что такое производная функции
Для раскрытия понятия производной следует напомнить что такое функция в математике. Чтобы не загромождать текст сложными определениями, остановимся на интуитивном математическом понятии функции, заключающимся в том, что в ней одна или несколько величин полностью определяют значение другой величины, если они взаимосвязаны. Например, в формуле S = π ∙ r 2 площади круга, значение радиуса r полностью и однозначно определяет площадь круга S.
Например, в формуле S = π ∙ r 2 площади круга, значение радиуса r полностью и однозначно определяет площадь круга S.
В зависимости от вида, функции могут быть алгебраическими, тригонометрическими, логарифмическими и др. В них могут быть взаимосвязаны два, три и более аргументов. Например, пройденное расстояние S, которое объект преодолел с равноускоренной скоростью, описывается функцией S = 0,5 ∙ a ∙ t 2 + V ∙ t, где «t» — время движения, аргумент «а» ускорение (может быть как положительной, так и отрицательной величиной) и «V» начальная скорость движения. Таким образом, величина пройденного расстояния зависит от значений трех аргументов, два из которых («а» и «V») постоянны.
Покажем на этом примере элементарное понятие производной функции. Оно характеризует скорость изменения функции в данной точке. В нашем примере это будет скорость движения объекта в конкретный момент времени. При постоянных «а» и «V» она зависит только от времени «t», то есть говоря научным языком нужно взять производную функции S по времени «t».
Этот процесс называется дифференцированием, выполняется путем вычисления предела отношения прироста функции к приросту ее аргумента на ничтожно малую величину. Решения подобных задач для отдельных функций часто является непростым делом и здесь не рассматриваются. Также стоит отметить, что некоторые функции в определенных точках вообще не имеют таких пределов.
В нашем же примере производная S по времени «t» примет вид S’ = ds/dt = а ∙ t + V, из которого видно, что скорость S’ изменяется по линейному закону в зависимости от «t».
Производная экспоненты
Экспонентой называется показательная функция, в качестве основания которой находится число е. Она обычно отображается в виде F (x) = e
Известный математик Тейлор сумел разложить эту функцию в ряд, названный его именем ex = 1 + x/1! + x 2 /2! + x 3 /3! + … в диапазоне x от — ∞ до + ∞.
Закон, базирующийся на этой функции, называется экспоненциальным. Он описывает:
- возрастание сложных банковских процентов;
- увеличение популяции животных и населения планеты;
- время окоченения трупа и многое другое.
Повторим еще раз замечательное свойство данной зависимости — значение ее производной в любой точке всегда равно значению функции в этой точке, то есть (e x)’ = ex .
Приведем производные для наиболее общих случаев экспоненты:
- (eax)’ = a ∙ eax ;
- (ef (x))’ = f'(x) ∙ ef (x).
Используя данные зависимости, несложно найти производные для других частных видов этой функции.
Некоторые интересные факты о числе е
С этим числом связаны фамилии таких ученых, как Непер, Отред, Гюйгенс, Бернулли, Лейбниц, Ньютон, Эйлер, и другие. Последний собственно и ввел обозначение е для этого числа, а также нашел первые 18 знаков, используя для расчета открытый им ряд е = 1 + 1/1! + 2/2! + 3/3! …
Число e встречается в самых неожиданных местах. Например, оно входит в уравнение цепной линии, которое описывает провис каната под действием собственного веса, когда его концы закреплены на опорах.
Например, оно входит в уравнение цепной линии, которое описывает провис каната под действием собственного веса, когда его концы закреплены на опорах.
Видео
Тема видеоурока — производная показательной функции.
Что особенного в числе Эйлера?
В математике есть много важных констант, которые задают структуру дисциплины, например, пи и i , мнимое число, равное квадратному корню из -1. Но есть одна константа, которая не менее важна, хотя, возможно, и менее известна, — это константа Эйлера, e .
Он постоянно появляется в математике и физике, чаще всего как основание в логарифмических и экспоненциальных функциях. Он используется для расчета сложных процентов, скорости радиоактивного распада и количества времени, необходимого для разрядки конденсатора. Как говорит Стефани Райхерт, Nature Physics , «мы не можем избежать числа Эйлера».
Но откуда берется постоянная Эйлера? А что именно это это?
Что такое постоянная Эйлера?
Посмотреть полный пост на Youtube
Постоянная Эйлера, которую некоторые эксперты-математики также называют числом Эйлера, является иррациональным числом, то есть ее нельзя свести к простой дроби. Как и число пи, десятичные дроби e’ s продолжаются бесконечно, не повторяясь. Если вы хотите получить техническую информацию, это то, что e looks like to the 100th decimal point:
2.71828182845 If you’ve ever taken an entry level calculus course, you’ve probably run into Euler’s constant, since it’s the base for the натуральные логарифмы. Выглядит это так: е ln x = x . Numberphile//YouTube При построении уравнения y=e x , вы обнаружите, что наклон этой кривой в любой заданной точке также равен e x , а площадь под кривой от отрицательной бесконечности до x равна также е х . Константа Эйлера — единственное число во всей математике, которое можно подставить в уравнение y=n x , для которого эта закономерность верна. ильбуска//Getty Images История и немного запутана и включает в себя вклад трех математиков: Джона Нэпьера, Якоба Бернулли и Леонарда Эйлера. Полную версию можно найти в статье Cantor’s Paradise , публикации на Medium, посвященной математике. Для краткой версии, читайте дальше. В 17 веке Нейпир, шотландский математик, физик и астроном, начал искать более простой способ умножения очень больших чисел. Читать Сейчас скидка 13% Читать сейчас Сейчас скидка 12% Читать сейчас Пройдет еще около 70 лет, прежде чем этот список логарифмов станет ассоциироваться с показателями степени. В 1683 году швейцарский математик Якоб Бернулли открыл константу e , решая финансовую проблему, связанную со сложными процентами. Courtney Linder/PM Наконец, в 1731 году швейцарский математик Леонард Эйлер назвал число e , доказав его иррациональность, разложив его в сходящийся бесконечный ряд факториалов. ROBERT BROOK/SCIENCE PHOTO LIBRARY//Getty Images Поскольку e связаны с экспоненциальными отношениями, это число полезно в ситуациях, когда наблюдается постоянный рост. Один распространенный пример, который исследовал Бернулли, связан со сложными процентами — процентами, которые вы платите по кредиту, когда вы включаете в расчет как первоначальную основную сумму (сумму кредита), так и накопленные проценты за предыдущие периоды. Предположим, вы кладете деньги в банк, и банк ежегодно начисляет эти деньги по ставке 100 процентов. Через год у вас будет вдвое больше суммы, которую вы инвестировали. Теперь предположим, что банк начисляет проценты каждые 6 месяцев, но предлагает только половину процентной ставки, или 50 процентов. В этом случае через год вы получите в 2,25 раза больше первоначальных инвестиций. Продолжаем. Предположим, что банк предлагает 8,3 процента (1/12 от 100 процентов) процентов, начисляемых каждый месяц, или 1,9 процента (1/52 от 100 процентов) процентов, начисляемых каждую неделю. В этом случае вы получите в 2,61 и 2,69 раза больше своих инвестиций. Давайте напишем для этого уравнение. Если мы сделаем 9n, , где A = окончательная сумма, P = начальный остаток основного долга, r — процентная ставка, n — количество раз, когда проценты начисляются за определенный период времени, и t — количество прошедших периодов времени. Что произойдет, если n станет очень большим? Скажем, бесконечность большая? На этот вопрос пытался ответить Бернулли, но Эйлеру потребовалось 50 лет, чтобы прийти и решить его. Оказывается ответ иррациональное число e , что составляет около 2,71828…. Что еще можно сделать с постоянной Эйлера? Постоянная Эйлера полезна не только в финансах. Некоторые другие распространенные варианты использования включают: ☐ Теория вероятности: Если вы играете в рулетку и ставите на одно число, вероятность того, что вы проиграете в каждой игре из 37 игр, составляет около . 1/е . ☐ Расчет периода полураспада радиоактивных химических веществ. ☐ Уравнения для волн (таких как световые, звуковые и квантовые волны) в физике. Эйвери Томпсон twitter.com/physicallyavery Кортни ЛиндерЗаместитель редактора До того, как присоединиться к газете Pop Mech, Кортнитт Хоум была репортером по технологиям в Herr. Она выпускница Университета Питтсбурга, где изучала английский язык и экономику. Ее любимые темы включают, помимо прочего, гигантский кальмар, панк-рок и робототехнику. Она живет в пригороде Филадельфии со своим партнером, своей черной кошкой и башнями из книг. Термин число Эйлера (e) относится к математическому выражению основания натурального логарифма. Это представлено неповторяющимся числом, которое никогда не заканчивается. Первые несколько цифр числа Эйлера — 2,71828. Число обычно обозначается буквой e и обычно используется в задачах, связанных с экспоненциальным ростом или затуханием. Как отмечалось выше, число Эйлера используется для выражения основания натурального логарифма. E — это ряд чисел, начинающихся с 2,71828. Как и число Пи, оно не имеет конца, что означает, что оно продолжается и продолжается. Это также иррациональное число, что означает, что его нельзя представить в виде дроби. Вы можете использовать его для расчета снижения или роста определенного фактора с течением времени, например сложных процентов. Представьте, что вы даете деньги взаймы под 100% процентную ставку, начисляемую каждый год. Через год ваши деньги удвоятся. Но что, если бы процентная ставка была снижена вдвое и начислялась бы в два раза чаще? При 50% каждые шесть месяцев ваши деньги вырастут на 225% за год. По мере того, как интервал становится меньше, общая доходность становится немного выше. Если проценты рассчитываются n раз в год по ставке 100%/n, общее накопленное богатство в конце первого года будет немного больше, чем в 2,7 раза больше первоначальных инвестиций, если n Хотя обычно он ассоциируется со швейцарским математиком Леонардом Эйлером и назван в его честь, он был впервые обнаружен в 1683 году математиком Якобом Бернулли. Он пытался определить, как будет расти богатство, если проценты будут начисляться чаще, а не ежегодно. Самая важная работа, связанная с числом, была выполнена Леонардом Эйлером лишь несколько десятилетий спустя. В своей книге Introductio in Analysin Infinitorum (1748 г.) Эйлер доказал, что это иррациональное число, цифры которого никогда не повторяются. Он также доказал, что число можно представить в виде бесконечной суммы обратных факториалов: е знак равно 1 + 1 1 + 1 2 + 1 1 × 2 × 3 + 1 1 × 2 × 3 × 4 + . . . + 1 н ! e = 1 + \ frac { 1 }{ 1 } + \ frac { 1 }{ 2 } + \ frac { 1 }{ 1 \ times 2 \ times 3 } + \ frac {1 }{ 1 \ times 2 \ times 3 \times 4 } + … + \frac { 1 }{ n! }
e=1+11+21+1×2×31+1×2×3×41+…+n!1 Эйлер использовал букву e для показателей степени, но теперь эта буква широко ассоциируется с его именем. Число Эйлера (e) не следует путать с постоянной Эйлера, которая обозначается строчной гаммой (γ). Также известная как постоянная Эйлера-Маскерони, последняя связана с гармоническим рядом и имеет значение приблизительно 0,57721…9.0007 Таким образом, если бы у вас было 1000 долларов с выплатой 2% годовых с непрерывным начислением сложных процентов, через три года у вас было бы:
9{ 12 \ умножить на 3 } = \ $ 1061,78
1000 долларов США (1 + 12,02) 12 × 3 = 1061,78 долларов США Здесь разница составляет всего несколько центов, но по мере того, как наши суммы становятся больше, процентные ставки становятся выше, а количество времени увеличивается, непрерывное начисление процентов с использованием константы Эйлера становится все более и более ценным по сравнению с дискретным начислением процентов. Число Эйлера часто появляется в задачах, связанных с ростом или убыванием, где скорость изменения определяется текущим значением измеряемого числа. Число Эйлера появляется в задачах, связанных со сложными процентами. Всякий раз, когда инвестиция предлагает фиксированную процентную ставку в течение определенного периода времени, будущая стоимость этой инвестиции может быть легко рассчитана с точки зрения e. Проще говоря, число Эйлера является основанием экспоненциальной функции, скорость роста которой всегда пропорциональна текущему значению. Показательная функция e x всегда растет со скоростью e x , что не относится к другим системам счисления и значительно упрощает алгебру, связанную с показателями степени и логарифмами.3536028747135266249775724709369995957
49669676277240766303535475945713821785251664274… 
Кто открыл постоянную Эйлера?
 В частности, он хотел найти короткий путь для экспонентов. Пока Нейпир не открыл число e , он придумал список логарифмов, которые он неосознанно вычислил с константой. Он опубликовал свою работу Mirifici Logarithmorum Canonis Descriptio, в 1614 году.
В частности, он хотел найти короткий путь для экспонентов. Пока Нейпир не открыл число e , он придумал список логарифмов, которые он неосознанно вычислил с константой. Он опубликовал свою работу Mirifici Logarithmorum Canonis Descriptio, в 1614 году. Лучшие математические книги
Морские книги Бесконечные силы. Amazon
imusti Zero: Биография опасной идеи
Основные книги Искусство статистики: как учиться на данных
Mariner Books The Joy of x: A Guided Tour of Math, from One to Infinity
 Он увидел, что через все большее и большее количество интервалов его последовательность приближается к пределу (силе интереса). Бернулли записал этот предел как n продолжает расти, как e .
Он увидел, что через все большее и большее количество интервалов его последовательность приближается к пределу (силе интереса). Бернулли записал этот предел как n продолжает расти, как e . Использование константы Эйлера для расчета сложных процентов
 Вот почему вы можете делать минимальный платеж по кредитной карте каждый месяц, но никогда не погашать его полностью.
Вот почему вы можете делать минимальный платеж по кредитной карте каждый месяц, но никогда не погашать его полностью.
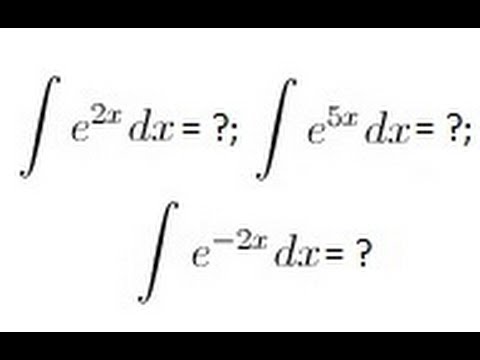
🎥 Смотрите сейчас:
Число Эйлера (e) Объяснение, как оно используется в финансах
Что такое число Эйлера (e)?
 Вы также можете интерпретировать число Эйлера как основу экспоненциальной функции, значение которой всегда равно ее производной. Другими словами, e — единственное возможное число, такое что
Вы также можете интерпретировать число Эйлера как основу экспоненциальной функции, значение которой всегда равно ее производной. Другими словами, e — единственное возможное число, такое что Ключевые выводы
Понимание числа Эйлера (e)

История числа Эйлера (e)
 Он обычно используется в широком спектре приложений, включая рост популяции живых организмов и радиоактивный распад тяжелых элементов, таких как уран, учеными-ядерщиками. Его также можно использовать в тригонометрии, вероятности и других областях прикладной математики.
Он обычно используется в широком спектре приложений, включая рост популяции живых организмов и радиоактивный распад тяжелых элементов, таких как уран, учеными-ядерщиками. Его также можно использовать в тригонометрии, вероятности и других областях прикладной математики. Число Эйлера (e) в финансах: сложные проценты
 9{rt} \\&\textbf{где:} \\&\text{FV} = \text{Будущая стоимость} \\&\text{PV} = \text{Текущая стоимость баланса или суммы} \\&e = \text{Константа Эйлера} \\&r = \text{Процентная ставка начисляется} \\&t = \text{Время в годах} \\\end{выровнено}
FV=PVertwhere:FV=Будущая стоимостьPV=Текущая стоимость баланса или сумма=Константа Эйлера=Процентная ставка начисляетсяt=Время в годах
9{rt} \\&\textbf{где:} \\&\text{FV} = \text{Будущая стоимость} \\&\text{PV} = \text{Текущая стоимость баланса или суммы} \\&e = \text{Константа Эйлера} \\&r = \text{Процентная ставка начисляется} \\&t = \text{Время в годах} \\\end{выровнено}
FV=PVertwhere:FV=Будущая стоимостьPV=Текущая стоимость баланса или сумма=Константа Эйлера=Процентная ставка начисляетсяt=Время в годах Почему число Эйлера важно?
 Одним из примеров является биология, где ожидается удвоение популяции бактерий через определенные промежутки времени. Другим случаем является радиометрическое датирование, когда ожидается, что количество радиоактивных атомов уменьшится в течение фиксированного периода полураспада измеряемого элемента.
Одним из примеров является биология, где ожидается удвоение популяции бактерий через определенные промежутки времени. Другим случаем является радиометрическое датирование, когда ожидается, что количество радиоактивных атомов уменьшится в течение фиксированного периода полураспада измеряемого элемента. Как число Эйлера используется в финансах?
Что такое число Эйлера?