Площадь треугольника, построенного на векторах — онлайн калькулятор
- Справочник
- Онлайн-калькуляторы
- Тесты с ответами
Формула площади треугольника заложена в программе и вычисляет половину модуля векторного произведения:
S=12·c
Чтобы найти площадь треугольника, необходимы задать значения двух векторов или координаты вершин треугольника. После этого вы получите готовое решение с пояснениями и ответ. Сервис используют школьники, их родители, студенты, преподаватели.
Вариант 1
- Выберите форму представления треугольника «Двумя векторами сторон».
- Введите значения векторов a и b в соответствующие поля. Отправьте задание на решение кнопкой «Рассчитать»
- Получите решение и ответ.

Вариант 2
- Выберите форму представления треугольника «Координатами точек».
- Введите координаты вершин A, B, C в соответствующие поля. Отправьте задание на решение кнопкой «Рассчитать».
- Получите решение и ответ.
Материалы, которые помогут вам лучше разобраться в теме:
- Векторы на плоскости и в пространстве — основные определения
- Координаты вектора в декартовой системе координат (ДСК)
- Нахождение длины вектора, примеры и решения
- Нахождение координат вектора через координаты точек
Ответ:
Решение
Ответ:
- list» :key=»`error-${eIdx}`» v-html=»e»/>
Похожие калькуляторы:
- Длина вектора. Модуль вектора
- Векторное произведение векторов
- Умножение вектора на число
- Угол между векторами
- Смешанное произведение векторов
- Сложение и вычитание двух векторов
- Скалярное произведение векторов
- Определение вектора по двум точкам
- Разложение вектора по базису
- Проверить являются ли вектора базисом
- Ортогональность векторов
- Компланарность векторов
- Коллинеарность векторов
- Проекция вектора на вектор
- Площадь параллелограмма, построенного на векторах
Как найти площадь треугольника, построенного на векторах
Онлайн-калькулятор позволяет учащимся готовиться к занятиям, разбираться в непонятной теме, тренироваться на примерах. Расчеты производятся бесплатно, поэтому вы сможете сэкономить деньги на репетиторе и самостоятельно осваивать материал. Моментальное решение также поможет сдать зачет или экзамен, написать контрольную на хорошую оценку. Родители смогут быстро проверить домашнее задание ребенка, а преподаватели – автоматизировать процесс создания обучающих материалов.
Расчеты производятся бесплатно, поэтому вы сможете сэкономить деньги на репетиторе и самостоятельно осваивать материал. Моментальное решение также поможет сдать зачет или экзамен, написать контрольную на хорошую оценку. Родители смогут быстро проверить домашнее задание ребенка, а преподаватели – автоматизировать процесс создания обучающих материалов.
Чтобы вычислить площадь треугольника через векторы, программа выполняет следующие действия:
- Анализирует введенные данные. Если указаны координаты точек, рассчитываются векторы a и b.
- Находит произведение векторов.
- Вычисляет модуль вектора.
- Делит результат на 2 и выдает ответ.
С помощью нашего сайта вы сможете изучить, как найти площадь треугольника не только по векторам, но и другими способами. Мы разделили калькуляторы по темам для удобного использования. Так вы быстро найдете нужную тему и получите правильный ответ. В автоматических расчетах исключена потеря данных между действиями, опечатки.
Понравился калькулятор? Поделись с друзьями!
Разделы калькуляторов
- Процент
- Решение матриц
- Точка, прямая, плоскость
- Конвертеры
- Объем фигур
- Калькуляторы площади фигур
- Решение уравнений
- Операции над векторами
- Периметр фигур
Поможем с любой работой
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Решение задач
- Отчеты по практике
Все наши услуги
Узнай бесплатно стоимость работыНе получается написать работу самому?
Доверь это кандидату наук!
Геометрия
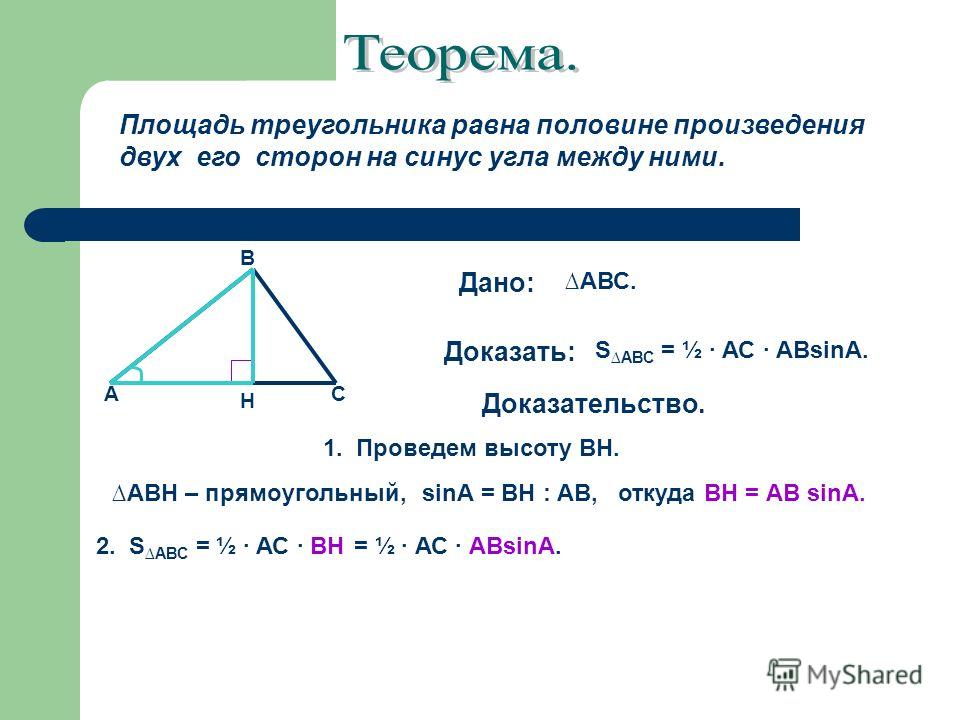
Площадь треугольника по двум сторонам и углу
Площадь плоских фигур Площадь Геометрия
Вектор.
 Определение и основные понятия
Определение и основные понятияВектор — это направленный отрезок, то есть отрезок, имеющий длину и определенное направление.
Вектора Формулы Геометрия Алгебра Теория Обозначения
Векторное произведение векторов
Векторным произведением векторов u и v называется третий вектор w, модуль которого равен произведению модулей векторов u и v на синус угла θ между ними и перпендикулярен им.
Вектора Формулы Геометрия Алгебра Теория Обозначения
Векторы
Площади и объемы Площадь Таблицы Геометрия Теория
Гексагон
Правильный шестиугольник (гексагон) — многоугольник с шестью равными сторонами.
Фигуры Математика Формулы Геометрия Теория Фигуры
Геометрические задачи на оптимизацию
Геометрия Расчёт Тригонометрия Формулы Геометрия Задачи
Декартовы координаты и векторы в пространстве
Декартовы координаты — система координат, состоящая из двух перпендикулярных осей.

Вектора Формулы Геометрия Алгебра Теория Обозначения
Калькулятор объема конуса
Объём геометрических фигур Калькулятор Расчёт Геометрия
Калькулятор объёма куба
Объём геометрических фигур Калькулятор Расчёт Геометрия
Калькулятор объёма параллелепипеда
Объём геометрических фигур Калькулятор Расчёт Геометрия
Калькулятор объема пирамиды через площадь основания и высоту
Объём геометрических фигур Калькулятор Расчёт Геометрия
Калькулятор объёма правильной пирамиды
Объём геометрических фигур Калькулятор Расчёт Геометрия
Калькулятор объёма правильной треугольной пирамиды
Объём геометрических фигур Калькулятор Расчёт Геометрия
Калькулятор объёма правильной четырёхугольной пирамиды
Объём геометрических фигур Калькулятор Расчёт Геометрия
Калькулятор объёма тетраэдра
Объём геометрических фигур Калькулятор Расчёт Геометрия
Калькулятор объема усечённого конуса
Объём геометрических фигур Калькулятор Расчёт Геометрия
Калькулятор объема усечённой пирамиды
Объём геометрических фигур Калькулятор Расчёт Геометрия
Калькулятор объёма цилиндра
Объём геометрических фигур Калькулятор Расчёт Геометрия
Калькулятор объёма шара
Объём геометрических фигур Калькулятор Расчёт Геометрия
Калькулятор объема шарового сегмента
Объём геометрических фигур Калькулятор Расчёт Геометрия
Калькулятор площади круга
Площадь плоских фигур Калькулятор Расчёт Площадь Геометрия
Калькулятор площади параллелограмма
Площадь плоских фигур Калькулятор Расчёт Площадь Геометрия
Калькулятор площади правильного многоугольника
Площадь плоских фигур Калькулятор Расчёт Площадь Геометрия
Калькулятор площади ромба
Площадь плоских фигур Калькулятор Расчёт Площадь Геометрия
Калькулятор площади элипса
Площадь плоских фигур Калькулятор Расчёт Площадь Геометрия
Квадрат
Квадрат — это правильный четырёхугольник.
 У него все стороны и углы равны между собой.
У него все стороны и углы равны между собой.Фигуры Математика Формулы Геометрия Теория Фигуры
Координаты вектора
Координатами вектора называются проекции вектора на оси координат
Вектора Формулы Геометрия Алгебра Теория Обозначения
Круг и окружность
Круг — геометрическое место точек плоскости, равноудаленных от одной заданной точки, называемой центром круга.
Фигуры Математика Формулы Геометрия Теория Фигуры
Основные фигуры планиметрии
Геометрия Геометрия 5 класс Фигуры
Параллелограмм
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.
Фигуры Математика Формулы Геометрия Теория Фигуры
Прямоугольник
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам).
Фигуры Математика Формулы Геометрия Теория Фигуры
Прямоугольный треугольник
Треугольник называют прямоугольным, если у него есть прямой угол, который равен 90 градусов.

Фигуры Математика Формулы Геометрия Теория Фигуры
Ромб
Ромб — это параллелограмм, у которого все стороны равны.
Фигуры Математика Формулы Геометрия Теория Фигуры
Скалярное произведение векторов
Скалярным произведением векторов u и v называется произведение их модулей на косинус угла между ними.
Вектора Формулы Геометрия Алгебра Теория Обозначения
Сколько соток, квадратных метров, километров и аров в одном гектаре земли? Метры, сотки, ары, гектары: значение, таблица. Как рассчитать, сколько гектаров в одной сотке или в одном квадратном метре, аре: перевод соток в гектары
Гектар — это площадь квадрата со стороной 100 м. Ар — площади квадрата со стороной в 10 м. 1 сотка это 100 квадратных метров
Площади и объемы Площадь Математика Формулы Геометрия
Сколько ягод в 1 литре?
Я́года — маленький сочный или мясистый плод, обычно кустарниковых или травянистых растений, который при употреблении в пищу не требуется откусывать или разрезать.

Площади и объемы Площадь Математика Формулы Геометрия
Сложение и вычитание векторов
Суммой двух векторов a и b называется третий вектор c, проведенный из начала a к концу b, если начало вектора b совпадает с концом вектора a. Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.
Вектора Формулы Геометрия Алгебра Теория Обозначения
Смешанное произведение векторов
Смешанным произведением трех векторов u, v и w называется скалярное произведение вектора u на векторное произведение векторов v и w
Вектора Формулы Геометрия Алгебра Теория Обозначения
Трапеция
Трапеция — четырехугольник, у которого две стороны параллельны, а две стороны не параллельны. Параллельные стороны называются основаниями трапеции, две другие — боковыми сторонами.
Фигуры Математика Формулы Геометрия Теория Фигуры
Треугольник
Треугольник — многоугольник, образованный тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.

Фигуры Математика Формулы Геометрия Теория Фигуры
Тригонометрические функции двойного, половинного и тройного аргументов
Тригонометрические функции двойного, половинного и тройного аргументов
Тригонометрия Математика Тригонометрия Формулы Геометрия Теория
Тригонометрические функции суммы и разности углов
Тригонометрические функции суммы и разности углов
Тригонометрия Математика Тригонометрия Формулы Геометрия Теория
Тригонометрические функции числового аргумента
Основным тригонометрическим тождеством в русскоязычных учебниках математики называют соотношение sin 2 α + cos 2 α = 1
Тригонометрия Математика Тригонометрия Формулы Геометрия Теория
Углы на плоскости
Геометрия Геометрия 5 класс Фигуры
Умножение вектора на число
Произведением вектора u≠0 на число λ≠0 называется вектор w, модуль которого равен |λ||u|, направление которого совпадает с вектором u при λ>0 и противоположно ему при λ
Вектора Формулы Геометрия Алгебра Теория Обозначения
Формула объема конуса
Объем конуса равен одной трети произведения площади основания на высоту
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объема куба
Объем куба равен кубу его ребра
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объёма параллелепипеда
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объема пирамиды
Объем пирамиды равен одной трети произведения площади основания на высоту
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объема цилиндра
Объем цилиндра равен произведению квадрата радиуса основания, высоты цилиндра и числа пи (3.
 1415)
1415)Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объема шара
Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула периметра круга
Периметр круга радиуса r равен удвоенному произведению радиуса r на число пи (~3.1415)
Формулы периметра Математика Тригонометрия Формулы Геометрия Теория
Формула периметра равнобедренного треугольника
Периметр равнобедренного треугольника равен сумме длин его сторон
Формулы периметра Математика Тригонометрия Формулы Геометрия Периметр
Формула периметра равностороннего треугольника
Периметр равностороннего треугольника равен тройной сумме длины его стороны
Формулы периметра Математика Тригонометрия Формулы Геометрия
Формула периметра треугольника
Периметр треугольника равен сумме длин его сторон
Формулы периметра Расчёт Математика Формулы Геометрия Периметр
Формула площади квадрата
Площадь квадрата равна квадрату его стороны.

Формулы площади Площадь Формулы Геометрия
Формула площади круга
Площадь круга равна произведению квадрата радиуса на число пи, или половине произведения длины ограничивающей его окружности на радиус.
Формулы площади Площадь Формулы Геометрия
Формула площади параллелограмма
Площадь параллелограмма равна произведению его основания (a) на высоту (h)
Формулы площади Площадь Формулы Геометрия
Формула площади правильного многоугольника
Формулы площади Площадь Формулы Геометрия
Формула площади прямоугольника
Площадь прямоугольника равна произведению его сторон
Формулы площади Площадь Формулы Геометрия
Формула площади прямоугольного треугольника
Площадь прямоугольного треугольника равна половине произведения катетов треугольника
Формулы площади Площадь Формулы Геометрия
Формула площади равнобедренного треугольника
Площадь равнобедренного треугольника равна произведению половины основания треугольника на его высоту
Формулы площади Площадь Формулы Геометрия
Формула площади равностороннего треугольника
Площадь равностороннего треугольника — половина произведения его основания на высоту
Формулы площади Площадь Формулы Геометрия
Формула площади ромба
Площадь ромба равна произведению длины его стороны на высоту (a, h), или половине произведения его диагоналей.

Формулы площади Расчёт Площадь Формулы Геометрия Фигуры
Формула площади трапеции
Площадь трапеции равна произведению полусуммы ее оснований (a, b) на высоту (h)
Формулы площади Площадь Формулы Геометрия
Формула площади треугольника
Площадь треугольника равна произведению половины основания треугольника (a) на его высоту (h)
Формулы площади Площадь Формулы Геометрия
Формула площади элипса
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи
Формулы площади Площадь Тригонометрия Формулы Геометрия
Четырёхугольник
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Фигуры Математика Формулы Геометрия Теория Фигуры
Карта сайта
В Вашем браузере отключен Javascript. Без Javascript данный сайт полноценно работать не будет.
Все онлайн калькуляторы
Матричный калькулятор онлайн
Обратная матрица онлайн
Определитель матрицы онлайн
Ранг матрицы онлайн
Инженерный калькулятор онлайн
Калькулятор дробей онлайн
Непрерывные (цепные) дроби онлайн
Онлайн калькулятор комплексных чисел
Наибольший общий делитель и наименьшее общее кратное.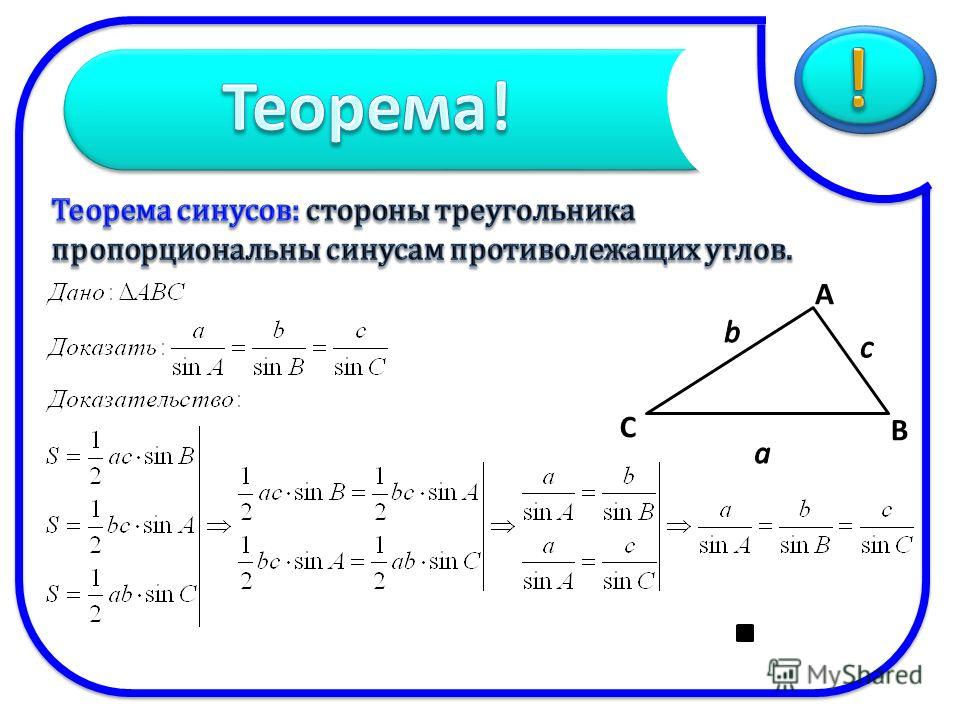 Онлайн калькулятор
Онлайн калькулятор
Перевод чисел из одной системы счисления в другую онлайн
Калькулятор процентов онлайн
Калькулятор сложных процентов онлайн
Общее решение однородной системы линейных уравнений онлайн
Общее решение неоднородной системы линейных уравнений онлайн
Метод Крамера онлайн
Метод Гаусса онлайн
Метод Жордана-Гаусса онлайн
Определитель матрицы
Обратная матрица. Нахождение обратной матрицы
Общие понятия алгебры
Группа (математика)
Кольцо (математика)
Поле (математика)
Теория чисел
Делимость чисел. Признак делимости
Наибольший общий делитель и наименьшее общее кратное. Онлайн калькулятор
Простые числа. Составные числа
Решето Эратосфена онлайн
Разложение числа на простые множители онлайн
Метод факторизации Ферма онлайн
Функция Эйлера. Доказательство
Сравнение чисел по модулю
Полная система вычетов
Малая теорема Ферма
Комплексные числа
Комплексные числа. Алгебраическая форма комплексного числа
Алгебраическая форма комплексного числа
Тригонометрическая форма комплексного числа
Линейные пространства
Линейное (векторное) пространство
Подпространство линейного пространства
Линейные операторы
Эквивалентные матрицы
Матрицы
Матрицы. Виды матриц
Сложение матриц
Умножение матриц
Умножение матрицы на число
Транспонированная матрица
Сопряженная матрица
Определитель матрицы
Обратная матрица. Нахождение обратной матрицы
Ранг матрицы
Псевдообратная матрица
Ортогональная матрица. Ортогонализация Грамма-Шмидта.
Скелетное разложение матрицы
QR-разложение матрицы онлайн
LU-разложение. LUP-разложение
Норма матрицы
Число обусловленности матрицы
Векторы
Векторы. Виды векторов
Сложение векторов
Разность векторов
Умножение вектора на число
Угол между двумя векторами
Скалярное произведение векторов
Векторное произведение векторов онлайн
Смешанное произведение векторов. Онлайн калькулятор
Онлайн калькулятор
Норма (модуль, длина) вектора
Линейная зависимость и линейная независимость векторов
Линейные уравнения
Система линейных уравнений. Общее решение
Однородная система линейных уравнений
Линейное программирование
Формы записи задачи линейного программирования
Решение задачи линейного программирования. Симплекс метод
Двойственная задача линейного программирования. Онлайн калькулятор
Двойственный симплекс метод онлайн
Симплекс метод для решения задачи линейного программирования в основной форме онлайн
Транспортная задача. Методы решения
Задача о назначениях онлайн
Теория игр. Матричные игры. Онлайн калькулятор
Многочлены и их корни
Решение квадратных уравнений онлайн
Последовательности
Числовая последовательность
Арифметическая прогрессия онлайн
Геометрическая прогрессия онлайн
Тригонометрия
Радианы и градусы онлайн
Синус и косинус. Онлайн калькулятор
Тангенс и котангенс. Онлайн калькулятор
Онлайн калькулятор
Арксинус и арккосинус. Онлайн калькулятор
Арктангенс и арккотангенс. Онлайн калькулятор
Формулы приведения тригонометрических функций онлайн
Формулы суммы и разности углов тригонометрических функций онлайн
Формулы двойного и тройного угла (аргумента) онлайн
Формулы половинного угла (аргумента) онлайн
Сумма и разность тригонометрических функций
Формулы произведения тригонометрических функций
Формулы понижения степени в тригонометрии
Универсальная тригонометрическая подстановка
Основные тригонометрические формулы
Аналитическая геометрия
Расстояние между двумя точками онлайн
Общее уравнение прямой на плоскости
Каноническое уравнение прямой на плоскости
Параметрическое уравнение прямой на плоскости
Уравнение прямой в отрезках
Нормальное уравнение прямой
Отклонение точки от прямой
Пучок прямых. Уравнение пучка прямых
Общее уравнение плоскости
Уравнение плоскости в отрезках
Нормальное уравнение плоскости
Уравнение прямой, проходящей через две точки онлайн
Проекция точки на прямую онлайн
Расстояние от точки до прямой онлайн
Расстояние между прямыми на плоскости онлайн
Расстояние между прямыми в пространстве онлайн
Точка пересечения прямых на плоскости онлайн
Точка пересечения прямых в пространстве онлайн
Точка пересечения прямой и плоскости онлайн
Линия пересечения плоскостей онлайн
Угол между прямыми онлайн
Угол между прямой и плоскостью онлайн
Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости онлайн
Уравнение плоскости онлайн
Проекция точки на плоскость онлайн
Расстояние от точки до плоскости онлайн
Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости онлайн
Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой онлайн
Уравнение плоскости, проходящей через точку и прямую онлайн
Уравнение плоскости, проходящей через данную прямую параллельно другой прямой онлайн
Уравнение плоскости, проходящей через прямую перпендикулярно заданной плоскости онлайн
Расстояние между плоскостями. Онлайн калькулятор
Онлайн калькулятор
Угол между плоскостями. Онлайн калькулятор
Геометрия
Точка (геометрия)
Прямая
Луч (геометрия)
Угол
Отрезок
Серединный перпендикуляр к отрезку
Ломаная
Пропорциональные отрезки
Аксиома параллельных прямых
Смежные углы. Свойства смежных углов
Вертикальные углы. Свойства вертикальных углов
Перпендикулярные прямые
Перпендикуляр к прямой
Параллельные прямые. Признаки параллельности прямых
Теоремы об углах, образованных двумя параллельными прямыми и секущей
Биссектриса угла. Свойства
Теорема Пифагора онлайн
Теорема, обратная теореме Пифагора
Теорема Фалеса. Доказательство
Треугольники. Признаки равенства треугольников
Подобные треугольники. Признаки подобия треугольников
Биссектриса треугольника онлайн
Серединные перпендикуляры к сторонам треугольника
Теорема о биссектрисе треугольника. Доказательство
Высота треугольника онлайн
Теорема Стюарта. Доказательство
Доказательство
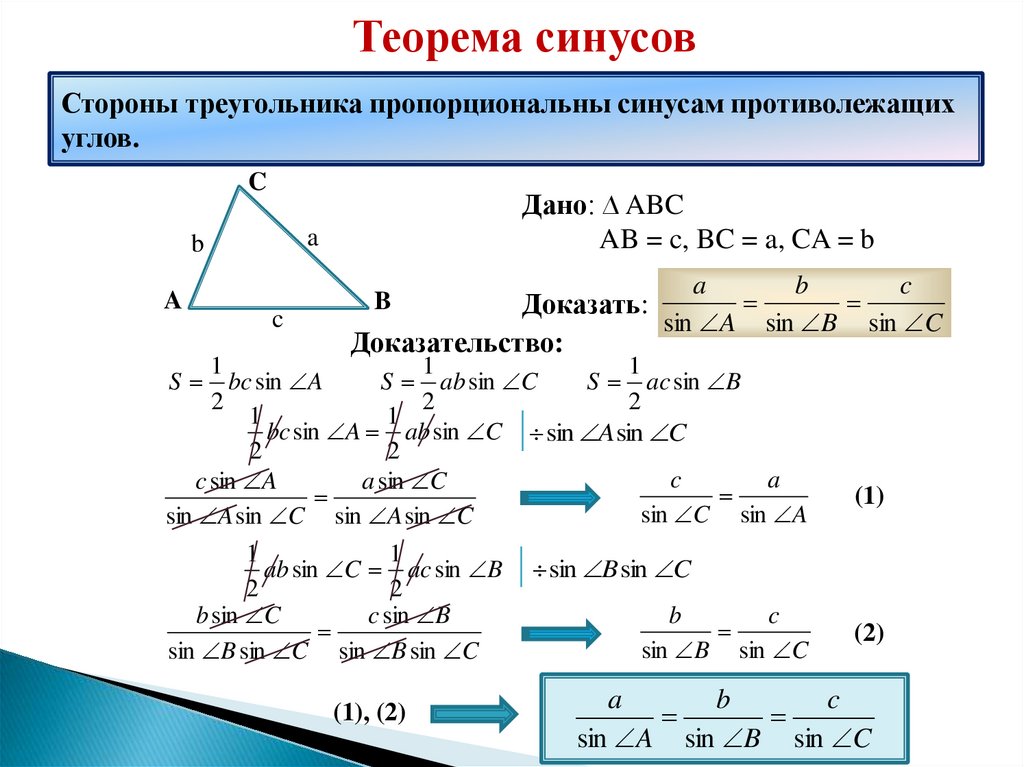
Теорема синусов. Доказательство
Теорема косинусов. Доказательство
Решение треугольников онлайн
Прямоугольный треугольник. Онлайн калькулятор
Равнобедренный треугольник. Онлайн калькулятор
Сумма углов треугольника
Внешний угол треугольника
Виды треугольников
Соотношения между сторонами и углами треугольника
Неравенство треугольника
Средняя линия треугольника
Теорема Менелая
Окружность, описанная около треугольника
Радиус описанной окружности около треугольника онлайн
Радиус описанной окружности около равнобедренного треугольника онлайн
Радиус описанной окружности около равностороннего треугольника онлайн
Радиус описанной окружности около прямоугольного треугольника онлайн
Окружность, вписанная в треугольник
Радиус вписанной в треугольник окружности онлайн
Радиус вписанной окружности в равнобедренный треугольник онлайн
Радиус вписанной окружности в равносторонний треугольник онлайн
Радиус вписанной окружности в прямоугольный треугольник онлайн
Окружность и круг. Онлайн калькулятор
Онлайн калькулятор
Взаимное расположение прямой и окружности
Касательная к окружности
Центральный угол окружности. Градусная мера дуги окружности
Вписанный угол окружности
Квадрат. Онлайн калькулятор
Прямоугольник. Онлайн калькулятор
Параллелограмм
Ромб
Сторона ромба онлайн
Высота ромба онлайн
Площадь ромба онлайн
Диагонали ромба онлайн
Трапеция. Определение, виды, свойства
Четырехугольник
Четырехугольник, вписанный в окружность
Окружность, вписанная в четырехугольник
Многоугольник
Площадь треугольника онлайн
Площадь прямоугольного треугольника онлайн
Площадь равностороннего треугольника онлайн
Площадь равнобедренного треугольника онлайн
Площадь квадрата онлайн
Площадь прямоугольника онлайн
Калькулятор площади треугольника с координатами
Создано Krishna Nelaturu
Отзыв от Rijk de Wet
Последнее обновление: 11 октября 2022 г.
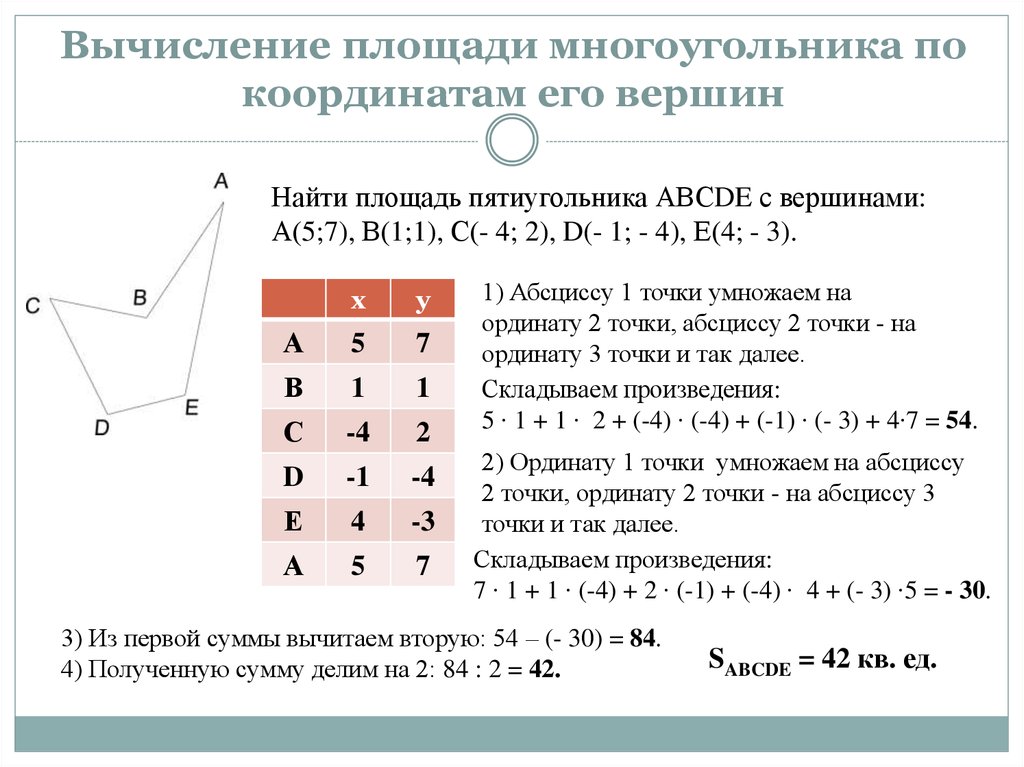
- Формула площади треугольника с вершинами 90 площадь треугольника с координатами?
- Как вычислить периметр треугольника с помощью точек?
- Как использовать этот калькулятор площади треугольника с координатами
- Другие связанные калькуляторы
- Часто задаваемые вопросы
Если вы хотите рассчитать площадь треугольника с вершинами , то этот калькулятор площади треугольника с координатами — правильный инструмент для вас! Вы также можете использовать этот калькулятор, чтобы найти периметра треугольника с вершинами . В этой статье вы узнаете:
- Какова формула площади треугольника с вершинами?
- Как найти площадь треугольника с координатами?
- Как вычислить периметр треугольника с помощью точек?
- Как определить, лежат ли три заданные точки на одной прямой?
Формула площади треугольника с вершинами
Треугольник, образованный тремя точками A(x1,y1)A(x_1, y_1)A(x1,y1), B(x2,y2)B(x_2, y_2)B( x2,y2) и C(x3,y3)C(x_3, y_3)C(x3,y3).
Формула для площади треугольника из его трех вершин задается следующим образом: \начать{выравнивать*} \text{Площадь} = \frac{1}{2} &\big\lvert x_1(y_2-y_3) + x_2(y_3-y_1) \\ &+ x_3(y_1-y_2) \big\rvert \end{align*}Area=21∣
∣x1(y2−y3)+x2(y3−y1)+x3(y1−y2)∣
∣
где:
- Area\text{ Area}Площадь равна площади треугольника ABCABCABC;
- (x1,y1)(x_1,y_1)(x1,y1) — координаты вершины AAA;
- (x2,y2)(x_2,y_2)(x2,y2) — координаты вершины BBB; и
- (x3,y3)(x_3,y_3)(x3,y3) — координаты вершины CCC;
Эта простая формула удобна для вычисления площади треугольника по трем координатам. Другой способ выразить эту же формулу через с помощью определителя . Чтобы вычислить площадь треугольника по 3 точкам:
Area=12∣111x1x2x3y1y2y3∣\text{Area} = \frac{1}{2} \begin{vmatrix} 1 и 1 и 1\\ х_1 и х_2 и х_3 \\ у_1 и у_2 и у_3 \end{vmatrix}Area=21∣
∣1×1y11×2y21×3y3∣
∣
Как найти площадь треугольника с координатами?
Для вычисления площади треугольника с его вершинами A(x₁, y₁) , B(x₂, y₂) , и C(x₃, y₃) , выполните следующие простые действия: )| .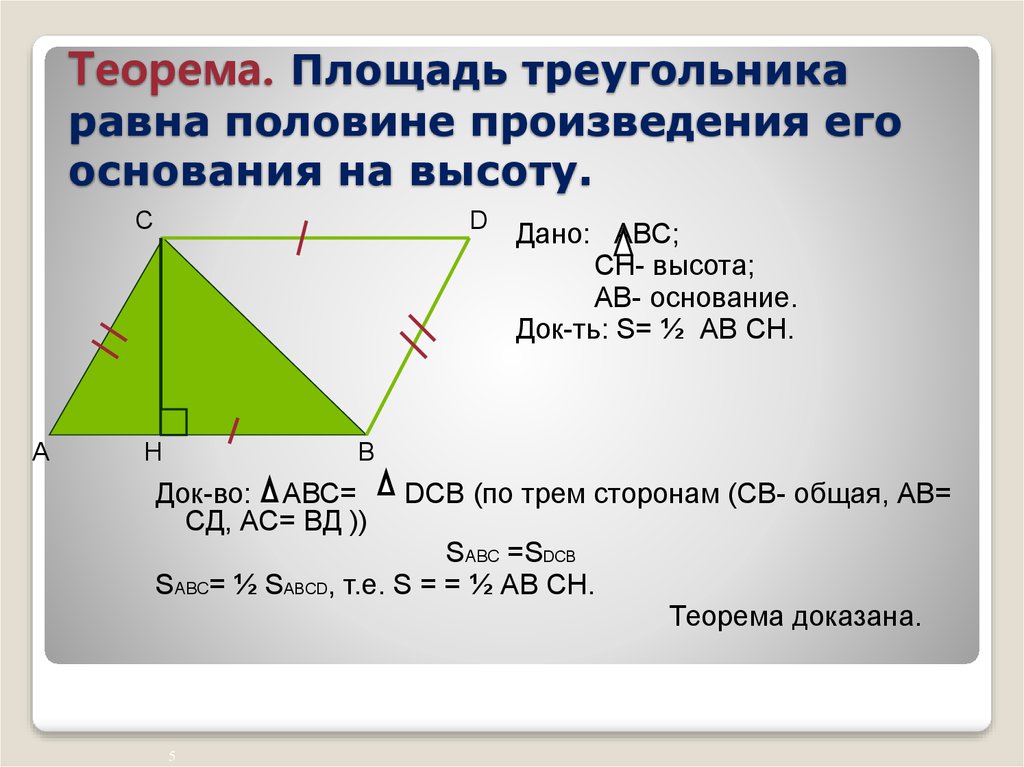
Как вычислить периметр треугольника с помощью точек?
Чтобы вычислить и найти периметр треугольника с его вершинами a (x₁, y₁) , b (x₂, y₂) и c (x₃, y₃) , выполните следующие просты формула расстояния AB = √(x₂ − x₁)² + (y₂ − y₁)² .
BC и AC используя формулу расстояния . ABC .Как использовать этот калькулятор площади треугольника с координатами
Этот калькулятор может одновременно выполнять две функции:
- Вычислять площадь треугольника по трем точкам.

- Вычислите (или найдите) периметр треугольника с точками.
Просто введите координаты вершин треугольника, а все остальное сделает этот калькулятор.
У нас есть еще калькуляторы треугольников для вас:
- Калькулятор площади треугольника;
- Калькулятор подобных треугольников;
- Калькулятор площади трехстороннего треугольника; Калькулятор
- квадратных футов треугольника;
- Калькулятор площади разностороннего треугольника;
- Калькулятор площади тупоугольного треугольника;
- Калькулятор площади косоугольного треугольника; и
- Калькулятор площади треугольника.
Часто задаваемые вопросы
Как определить, лежат ли три точки на одной прямой?
Чтобы определить, являются ли любые три точки A(x₁, y₁) , B(x₂, y₂) и C(x₃, y₃) коллинеарными, выполните следующие действия: выражение |x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂)| .
Какова площадь треугольника, образованного A(1,2), B(-1,1) и C(0,5)?
3,5 шт. Чтобы вычислить это значение самостоятельно, выполните следующие действия:
- Вычислите абсолютное значение выражения
|(1)×(1−5)+(−1)×(5−2)+(0)×( 2−1)| = |−4−3+0| = 7. - Разделите это значение на
2, чтобы получить7/2 = 3,5. - Проверьте этот результат, используя нашу площадь треугольника с калькулятором координат.
Кришна Нелатуру
Площадь треугольника с вершинами A(x₁, y₁), B(x₂, y₂), C(x₃, y₃)
Периметр
Посмотреть 18 подобных калькуляторов треугольников 🔺
30 60 90 треугольник45 45 90 треугольникПлощадь прямоугольного треугольника… Еще 15 углы, на которые они ориентированы, имеют большое значение в векторной геометрии и физике.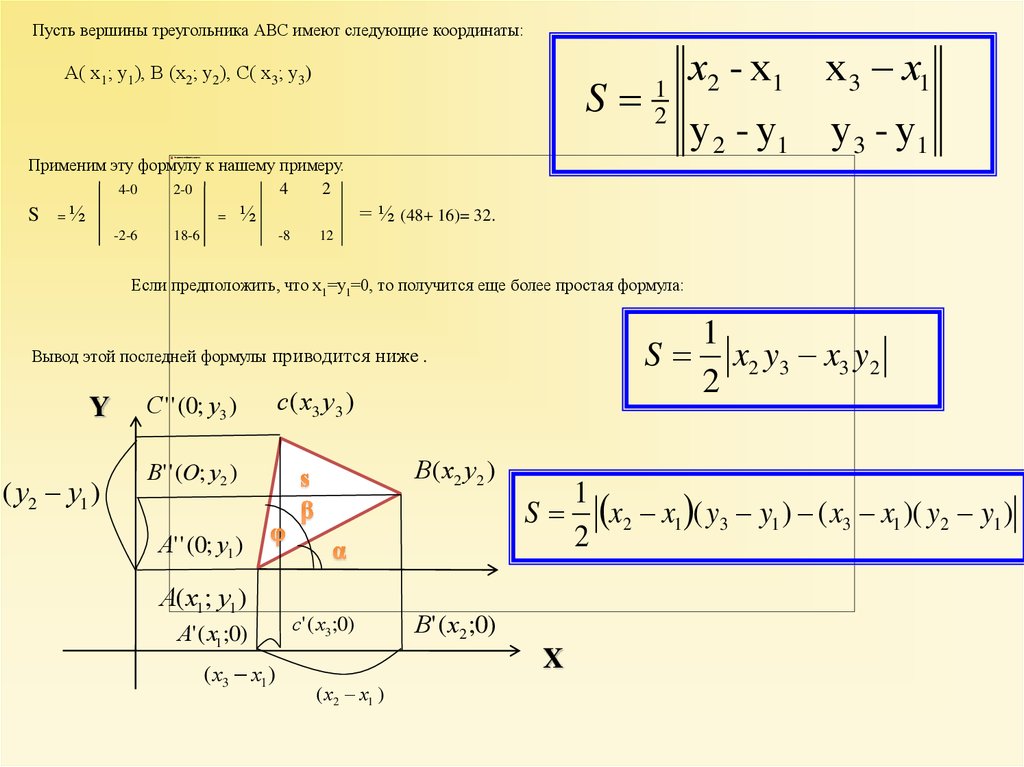 Если есть два вектора, скажем, a и b в плоскости, так что хвосты обоих векторов соединены, то между ними существует некоторый угол, и что Угол между двумя векторами определяется как:
Если есть два вектора, скажем, a и b в плоскости, так что хвосты обоих векторов соединены, то между ними существует некоторый угол, и что Угол между двумя векторами определяется как:
“ Угол между двумя векторами — это кратчайший угол, на который любой из двух векторов повернут вокруг другого вектора так, что оба вектора имеют одинаковую направление.»
Кроме того, это обсуждение сосредоточено на нахождении угла между двумя стандартными векторами, что означает, что их начало находится в точке (0, 0) в плоскости x-y.
В этой теме мы кратко обсудим следующие моменты:
- Какой угол между двумя векторами?
- Как узнать угол между двумя векторами?
- Угол между двумя двумерными векторами.
- Угол между двумя трехмерными векторами.
- Примеры.
- Проблемы.
Векторы ориентированы в разных направлениях и образуют разные углы. Этот угол существует между двумя векторами и отвечает за определение возведения векторов.
Этот угол существует между двумя векторами и отвечает за определение возведения векторов.
Угол между двумя векторами можно найти с помощью умножения векторов. Существует два типа векторного умножения, т. е. скалярное произведение и векторное произведение 9.0259 .
Скалярное произведение — это произведение или произведение двух векторов, при котором получается скалярная величина. Как следует из названия, векторное произведение или перекрестное произведение дает векторную величину из-за произведения или умножения двух векторов.
Например, если мы говорим о движении теннисного мяча, его положение описывается вектором положения, а движение — вектором скорости, длина которого указывает скорость мяча. Направление вектора объясняет направление движения. Точно так же импульс мяча также является примером векторной величины, которая равна массе, умноженной на скорость.
Иногда нам приходится иметь дело с двумя векторами, действующими на какой-либо объект, поэтому угол векторов имеет решающее значение. В реальном мире любая работающая система объединяет несколько связанных друг с другом векторов и образует между собой некоторые углы в заданной плоскости. Векторы могут быть двумерными или трехмерными. Следовательно, необходимо вычислить угол между векторами.
В реальном мире любая работающая система объединяет несколько связанных друг с другом векторов и образует между собой некоторые углы в заданной плоскости. Векторы могут быть двумерными или трехмерными. Следовательно, необходимо вычислить угол между векторами.
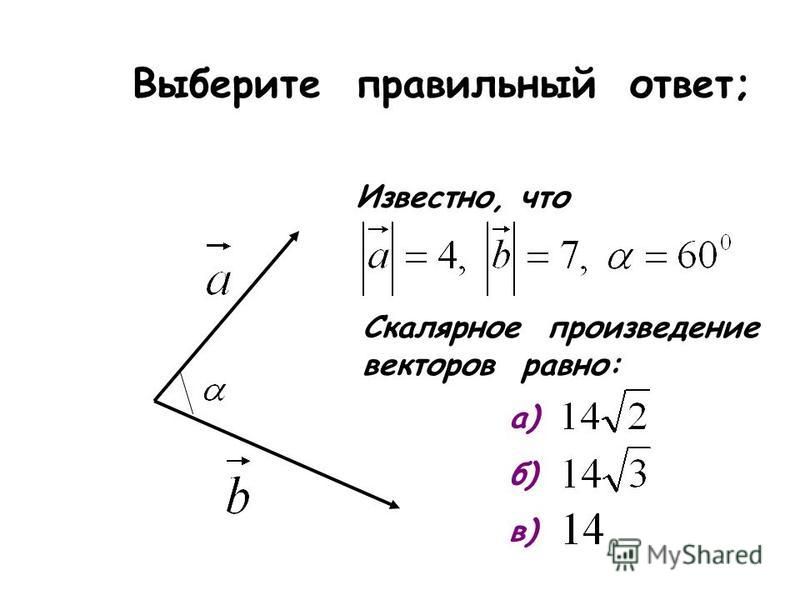
Давайте сначала обсудим скалярные произведения.
Угол между двумя векторами с использованием скалярного произведенияРассмотрим два вектора a и b , разделенные некоторым углом θ. Тогда по формуле скалярного произведения:
a.b = |a| |b|.cosθ
, где a.b — скалярное произведение двух векторов. |а| и |б| — величина векторов a и b, и θ — угол между ними.
Чтобы найти угол между двумя векторами, мы начнем с формулы скалярного произведения, которая дает косинус угла θ.
Согласно формуле скалярного произведения
а.б = |а| |b|.cosθ
Это утверждает, что скалярное произведение двух векторов a и b равно величине двух векторов a и b, умноженной на косинус угла. Чтобы найти угол между двумя векторами, a и b, мы решим угол θ,
Чтобы найти угол между двумя векторами, a и b, мы решим угол θ,
cosθ = a.b / |a|. |б|
θ = arccos ( a.b / |a| . |b| )
Итак, θ — это угол между двумя векторами.
Если вектор a = < ax , ay > и b = < bx, by >,
Тогда скалярное произведение двух векторов a и b определяется как
a.b 90 топор, ай > . < bx, by >
a.b = ax.bx + ay.by
Здесь мы можем иметь пример выполненной работы, поскольку выполненная работа определяется как сила, приложенная для перемещения объекта на некоторое расстояние. И сила, и перемещение являются векторами, и их скалярное произведение дает скалярную величину, т. е. ., раб. Совершенная работа представляет собой скалярное произведение силы и перемещения, которое можно определить как
F . д = |F| |д| cos (θ)
Где θ — угол между силой и перемещением. Например, если мы рассмотрим автомобиль, движущийся по дороге, преодолевая некоторое расстояние в определенном направлении, на автомобиль действует сила, при этом сила составляет некоторый угол θ со смещением.
Ниже приведены некоторые свойства скалярного произведения:
- Скалярное произведение коммутативно по своей природе.
- Он носит распределительный характер по сравнению с векторным сложением:
a . (b + c) = (a.b) + (a.c)
- Он неассоциативен по своей природе.
- 4. Скалярную величину можно умножить на скалярное произведение двух векторов.
в. ( а . б ) знак равно ( c а ) . б = а . ( c b)
- Скалярное произведение максимально, когда два ненулевых вектора параллельны друг другу.
- 6. Два вектора перпендикулярны друг другу тогда и только тогда, когда a . b = 0, так как скалярное произведение — это косинус угла между двумя векторами a и b, а cos ( 90 ) = 0.
- Для единичных векторов
i . я = 1
дж . j = 1
к . k = 1
- Умножение точек не подчиняется закону сокращения
a . б = а . в
а . ( b – c ) = 0
Точно так же мы можем использовать перекрестные произведения для этой цели.
Формула векторного произведения выглядит следующим образом:
a x b = |a|.|b|.sinθ. n
Давайте сначала оценим угол между двумя векторами, используя скалярное произведение.
Пример 1
Найти угол между двумя векторами, имеющими одинаковую величину, причем величина их результирующего вектора эквивалентна величине любого из заданных векторов.
Решение
Рассмотрим два вектора, A и B, , и результирующая двух векторов равна R .
Следовательно, согласно условию, указанному в вопросе:
|A| = |В| = |Р|
Теперь по закону косинусов 92 = ( 1 + cos (θ) )
1 / 2 = 1 + cos (θ)
1 / 2 – 1 = cos (θ)
-1 / 2 = cos (θ)
θ = cos -1 ( -1 / 2 )
θ = 120º
Итак, угол между двумя векторами, имеющими одинаковую величину, равен 120º.
Пример 2
Найдите угол между двумя векторами, имеющими одинаковую величину. Кроме того, вычислите величину результирующего вектора.
Решение
Дано, что
|A| = |В| 92 ( θ / 2))
|R| = 2 A cos ( θ / 2 )
Теперь для расчета результирующего угла α, который он составит с первым вектором,
tan α = ( A sin θ ) / ( A + A cos θ )
tan α = (2 A cos (θ / 2) . sin (θ / 2) / ( 2 A cos2 (θ / 2))
tan α = tan (θ / 2)
α = θ / 2
Следовательно, это показывает, что результирующая будет делить пополам угол между двумя векторами, имеющими одинаковую величину
Пример 3
Найдите угол между данными двумя векторами 92 )
|Б| = √ ( 9 + 64 + 4 )
|B| = √ ( 77 )
Теперь найдем скалярное произведение
A.B = ( 6 i + 5 j +7 k ). (3 I + 8 J + 2 K )
A.B = 18 + 40 + 14
A.B = 72
Установка в Formula of Dot Product,
72 = 72
. Вставка в Dot Product,
72 72 = 72
. (110)). (√(77)) . cos (θ)
cos (θ)
72 / (√ ( 110 x 77 )) = cos (θ)
cos (θ) = 0,78
θ = cos-1 (0,78)
θ = 51,26º
Пример 4
Познайте угол между данными двумя векторами
A = <4, 3, 2>
A
Решение
Используйте формулу скалярного произведения,
A . В = |А| |Б| . cos (θ)
Найдите величину A и B.
Итак, величина A задается как, 92 )
|Б| = √ ( 1 + 4 + 25 )
|B| = √ ( 30 )
Теперь найдем скалярное произведение
A.B = <4, 3, 2> . <1, 2, 5>
A.B = 4 + 6 + 10
A.B = 20
Подставляя формулу скалярного произведения,
20 = (√(29)) . (√(30)) . cos (θ)
20 / (√ (29 x 30)) = cos (θ)
cos (θ) = 0,677
θ = cos-1 (0,677)
θ = 42,60º
4
59 Угол между двумя векторами с помощью векторного произведения Другой метод нахождения угла между двумя векторами — это векторное произведение. Перекрестное произведение определяется как:
Перекрестное произведение определяется как:
«Вектор, который перпендикулярен как векторам, так и направлению, задается правилом правой руки.
Таким образом, векторное произведение математически представляется как
a x b = |a| |б| . sin (θ) n
Где θ — угол между двумя векторами, |a| и |б| — величины двух векторов a и b, и n — единичный вектор, перпендикулярный плоскости, содержащей два вектора a и b в направлении, заданном правилом правой руки.
Рассмотрим два вектора a и b , хвосты которых соединены вместе и, следовательно, образуют некоторый угол θ. Чтобы найти угол между двумя векторами, мы будем манипулировать вышеупомянутой формулой векторного произведения.
( a x b ) / ( |a| . |b| ) = sin (θ)
Если заданные векторы a и b параллельны друг другу, то согласно приведенной формуле крест произведение будет равно нулю, поскольку sin (0) = 0. Имея дело с перекрестным произведением, мы должны быть осторожны с направлениями.
Имея дело с перекрестным произведением, мы должны быть осторожны с направлениями.
Ниже приведены некоторые свойства перекрестного произведения:
- Перекрестное произведение является антикоммутативным по своей природе.
- Самоперекрестное произведение векторов равно нулю.
A x A = 0
- Поперечный продукт распределяется по векторному добавлению
A x ( B + C) = ( A x
........... x c )- Неассоциативный по своей природе.
- Скалярную величину можно умножить на скалярное произведение двух векторов.
c . ( a x b ) = ( c a ) x b = a x ( c b )
- Скалярное произведение максимально, когда два ненулевых вектора перпендикулярны друг другу.
- Два вектора параллельны (т. е. если угол между двумя векторами равен 0 или 180) друг другу тогда и только тогда, когда a x b = 1, так как перекрестное произведение является синусом угла между двумя векторами a и b и синуса ( 0 ) = 0 или синус (180) = 0.

- Для единичных векторов
i x i = 0
j x j = 0
k x k = 0
i x j = k
j x k = i
k x i = j
- Cross умножение не подчиняется закону сокращения
a x b = a x c
a x ( b – c ) = 0
Это некоторые свойства векторного произведения. 92) = 1/5
Теперь, подставляя в формулу,
| а х б | = |а| |б| sin θ
1 / 5 = (1) (1) sin θ
θ = sin-1 (1/ 5)
θ = 30º
Пример 6
A = 3 I - 2 J - 5 K и B = I + 4 J - 4 K + A A . A . . . . . . . . . . . . . . . . . . . . . . . . . . . + 7 92)
|б| = √( 1 + 16 + 16)
|b| = √(33)
Принимая во внимание, что величина a x b задается как
| а х б | = √ ((28)2 + (7)2 + (14))
| а х б | = √(1029)
| а х б | = 32. 08
08
Теперь, подставляя в формулу,
| а х б | = |а| |б| sin θ
32,08 = (√ (38)) (√(33)) sin θ
sin θ = 32,08 / (√ (38)) (√(33))
θ = 64,94º
Итак, угол между двумя векторами a и b равны θ = 64,94º .
Векторы могут быть как двумерными, так и трехмерными. Метод нахождения угла одинаков в обоих случаях. Единственное отличие состоит в том, что двумерный вектор имеет две координаты x и y, тогда как трехмерный вектор имеет три координаты x, y и z. В решенных выше примерах используются как двумерные, так и трехмерные векторы.
Практические задачи - Учитывая, что |A| = 3 и |В| = 5, где а . b = 7,5, найдите угол между двумя векторами.
- Вычислите угол между двумя векторами 3i + 4j – k и 2i – j + k.
- Calculate the angle between two vectors such that a = 2 i – 3 j + 1 k and b = -1 i + 0 j + 5 k где a x b = -15 i – 11 j – 3 k .

- Вычислите угол между двумя векторами так, что A = 2 I + 3 J + 5 K и B = I + 6 J - 4 K . b = 0.
- Найдите угол между заданными векторами t = (3, 4) и r = (−1, 6).
- Каким будет результирующий вектор R двух векторов A и B , имеющих одинаковую величину, если угол между ними равен 90°.
Answers - 60°
- 85.40°
- 81.36°
- 90°
- 36.30°
- 90°
All the vector diagrams are constructed by using GeoGebra.
Предыдущий урок | Главная страница | Следующий урок Дженсенмат
Добро пожаловать на Jensenmath.ca
Прокрутите вниз, чтобы найти
Бесплатный материал для всех математических курсов средней школы.
Математика для 9 класса (mth2w)
Модуль 1
Узнайте, как использовать законы экспоненты для упрощения выражений. Также узнайте, как упростить полиномиальные выражения, используя дистрибутивное свойство и собирая похожие термины.
Кликните сюда
Блок 2
Узнайте, как решать уравнения 1-й степени, используя балансовый метод и обратные операции. Изучите процесс решения простых и многоступенчатых уравнений, включая уравнения с дробями.
Кликните сюда
Блок 3
Узнайте о принципах выборки и о том, как собирать первичные данные. Затем узнайте, как смещать и анализировать взаимосвязи между переменными с помощью точечных диаграмм. Также посмотрите на тенденции в графиках расстояние-время.
Затем узнайте, как смещать и анализировать взаимосвязи между переменными с помощью точечных диаграмм. Также посмотрите на тенденции в графиках расстояние-время.
Кликните сюда
Модуль 4
Узнайте о различиях между прямыми и частичными линейными зависимостями. Затем научитесь вычислять наклон линии по графику и писать уравнение линейной зависимости.
Кликните сюда
Модуль 5
Научитесь писать уравнение прямой как в форме пересечения наклона и оси Y, так и в стандартной форме. Создайте уравнение линии, учитывая информацию о точках на линии или о параллельных или перпендикулярных линиях.
Создайте уравнение линии, учитывая информацию о точках на линии или о параллельных или перпендикулярных линиях.
Кликните сюда
Модуль 6
Узнайте о взаимосвязях между сторонами и углами в различных формах. Также узнайте о теоремах о параллельных линиях, таких как альтернативные и соответствующие углы.
Кликните сюда
Модуль 7
Узнайте, как рассчитать объем и площадь поверхности любой призмы, сферы, конуса и пирамиды.
Кликните сюда
Модуль 8
Завершите проект, который научит вас оптимизировать объем и площадь поверхности различных форм с учетом различных ограничений.
Кликните сюда
Обзор курса
Практические задачи для повторения всех концепций курса. Также включает видеоурок «Математика для 9 класса за 1 час».
Кликните сюда
Математика для 10 класса (mpm2d)
Модуль 1
Научитесь решать линейные системы с помощью графиков, замены и исключения. Также научитесь решать приложения линейных систем.
Кликните сюда
Unit 2
Изучите уравнения для средней точки, длины и для окружностей. Также научитесь писать уравнения медиан, биссектрисы и высоты треугольников.
Также научитесь писать уравнения медиан, биссектрисы и высоты треугольников.
Кликните сюда
Блок 3
Узнайте, как. умножить полиномы с помощью FOIL. Также узнайте, как в общих выражениях факторного полинома и факторных квадратичных уравнениях использовать метод суммы и произведения.
Кликните сюда
Модуль 4
Научитесь писать и преобразовывать между стандартными, вершинными и факторизованными уравнениями квадратного уравнения. Также научитесь строить квадратичные графики.
Кликните сюда
Модуль 5
Узнайте, как решать квадратные уравнения, разлагая на множители и используя квадратную формулу. Затем используйте эти стратегии для решения прикладных вопросов.
Кликните сюда
Блок 6
Узнайте о подобных треугольниках. Затем узнайте, как использовать SOHCATOA, закон синусов и закон косинуса, чтобы найти недостающие стороны и углы треугольника.
Кликните сюда
Обзор курса
Практические задачи для повторения всех концепций курса. Также включает видеоурок «Математика для 10 класса за 1 час».
Также включает видеоурок «Математика для 10 класса за 1 час».
Кликните сюда
Математика 11 класс (mcr3u)
Модуль 1
Узнайте, что такое функции и каково их обозначение. Также узнайте о свойствах квадратичных чисел и о том, как упростить радикальные выражения.
Кликните сюда
Модуль 2
Узнайте об ограничениях рациональных выражений и о том, как упростить рациональные выражения при их сложении, вычитании, умножении и делении.
Кликните сюда
Модуль 3
Узнайте, как преобразовывать различные типы функций путем отражения, растяжения, сжатия и алгебраического сдвига.
Кликните сюда
Блок 4
Узнайте об уравнениях и графиках функций экспоненциального роста и затухания. Также узнайте о процентных приложениях.
Кликните сюда
Модуль 5
Узнайте об особых треугольниках и о том, как использовать правило CAST и соответствующие углы для нахождения точных соотношений триггеров. Также узнайте, как доказать триггерные тождества.
Кликните сюда
Модуль 6
Узнайте о свойствах периодических функций и о том, как строить графики и преобразовывать функции синуса и косинуса.
Кликните сюда
Unit 7
Узнайте, как использовать формулы для арифметических и геометрических последовательностей и рядов. Также узнайте о треугольнике Паскаля и его приложениях.
Кликните сюда
Обзор курса
Практические задачи для повторения всех концепций курса. Также включает видеоурок «Математика для 11 класса за 1 час».
Кликните сюда
Расширенные функции 12 класса (mhf4u)
Модуль 1
Узнайте о свойствах полиномиальных функций, в том числе о том, как определить конечное поведение и симметрию из уравнения.
Кликните сюда
Модуль 2
Научитесь разлагать полиномиальные уравнения на множители, используя деление в длинное и синтетическое деление. Расширьте эти навыки до решения полиномиальных уравнений.
Кликните сюда
Модуль 3
Узнайте о логарифмических функциях и правилах регистрации для упрощения логарифмических выражений.
Кликните сюда
Модуль 4
Используя радианы в качестве единицы измерения углов, узнайте, как определить точные коэффициенты синхронизации и графические функции триггеров.
Кликните сюда
Модуль 5
Узнайте, как использовать тождества составного угла и двойного угла для доказательства других тригонометрических тождеств. Затем научитесь решать различные типы триггерных уравнений.
Кликните сюда
Модуль 6
Узнайте о разработке коэффициента Ньютона с помощью использования пределов и средней скорости изменения.
Кликните сюда
Блок 7
Узнайте о графиках различных рациональных функций, а также о решении рациональных уравнений и неравенств.
Кликните сюда
Обзор курса
Практические задачи для повторения всех концепций курса. Также включает видеоурок «Математика для 11 класса за 1 час».
Кликните сюда
12 класс - исчисление и векторы (mcv4u)
Модуль 1
Узнайте, как найти производную функции, используя степень, произведение, частное и цепные правила дифференцирования.
Кликните сюда
Модуль 2
Научитесь строить графики полиномиальных и рациональных функций, вычисляя первую и вторую производные для определения интервалов возрастания/убывания и интервалов вогнутости.
Кликните сюда
Модуль 3
Узнайте, как расширить свои знания о правилах производных, чтобы найти производные экспоненциальных, тригонометрических и логарифмических функций.
Кликните сюда
Модуль 4
Узнайте, как выполнять основные операции с геометрическими векторами. Также узнайте о приложениях, связанных с силой, скоростью и напряжением.
Кликните сюда
Модуль 5
Узнайте, как алгебраически представлять векторы в двух- и трехмерном пространстве. Также узнайте о точечном и перекрестном произведении векторов и их приложениях.
Также узнайте о точечном и перекрестном произведении векторов и их приложениях.
Кликните сюда
Модуль 6
Научитесь писать векторные и параметрические уравнения прямых в трехмерном пространстве. Также научитесь писать векторные и скалярные уравнения плоскостей. Затем найдите пересечения систем, включающих прямые и плоскости.
Кликните сюда
Обзор курса
Практические задачи для повторения всех концепций курса. Также включает видеоурок «Исчисление для 12 класса за 1 час».
Кликните сюда
12 класс - Управление данными (mdm4u)
Блок 1
Изучите различные способы отображения и анализа данных, таких как диаграммы, гистограммы, гистограммы и диаграммы рассеяния.
Кликните сюда
Блок 2
Узнайте, как правильно собирать первичные данные с помощью тщательно разработанных опросов и экспериментов. Узнайте о принципах выборки и источниках смещения.
Кликните сюда
Блок 3
Узнайте о показателях центральной тенденции, показателях разброса и свойствах данных с нормальным распределением.


 Определение и основные понятия
Определение и основные понятия
 У него все стороны и углы равны между собой.
У него все стороны и углы равны между собой.


 1415)
1415)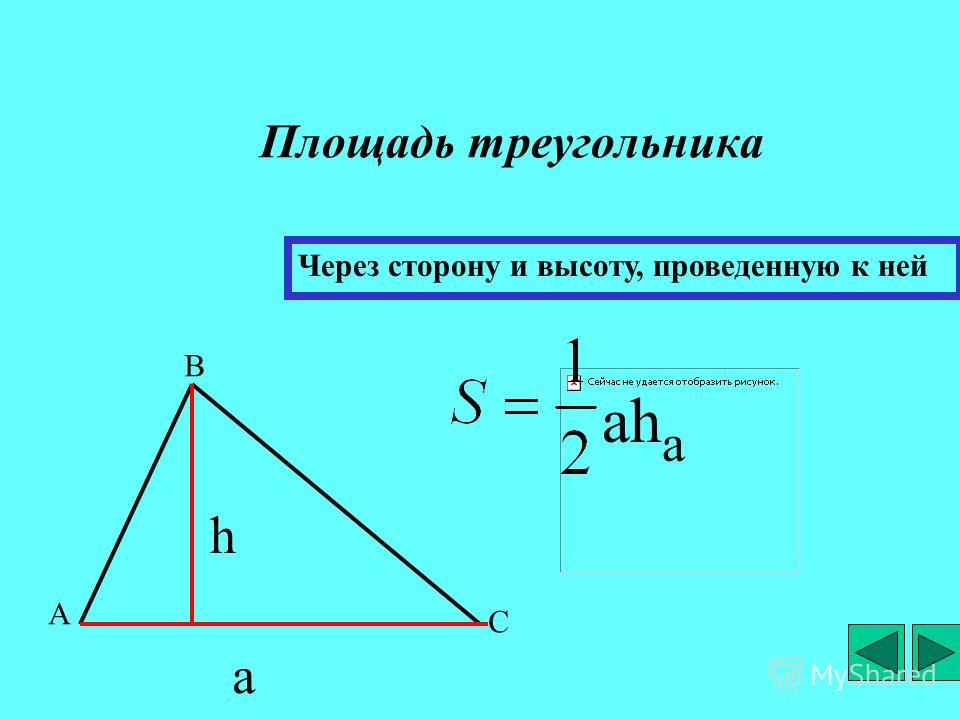


 Перекрестное произведение определяется как:
Перекрестное произведение определяется как:  Имея дело с перекрестным произведением, мы должны быть осторожны с направлениями.
Имея дело с перекрестным произведением, мы должны быть осторожны с направлениями.
 08
08
 Затем узнайте, как смещать и анализировать взаимосвязи между переменными с помощью точечных диаграмм. Также посмотрите на тенденции в графиках расстояние-время.
Затем узнайте, как смещать и анализировать взаимосвязи между переменными с помощью точечных диаграмм. Также посмотрите на тенденции в графиках расстояние-время. Создайте уравнение линии, учитывая информацию о точках на линии или о параллельных или перпендикулярных линиях.
Создайте уравнение линии, учитывая информацию о точках на линии или о параллельных или перпендикулярных линиях.
 Также научитесь писать уравнения медиан, биссектрисы и высоты треугольников.
Также научитесь писать уравнения медиан, биссектрисы и высоты треугольников.
 Также включает видеоурок «Математика для 10 класса за 1 час».
Также включает видеоурок «Математика для 10 класса за 1 час».



 Также узнайте о точечном и перекрестном произведении векторов и их приложениях.
Также узнайте о точечном и перекрестном произведении векторов и их приложениях.
