Что такое каноническое уравнение: Каноническое уравнение прямой на плоскости: теория, примеры, решение задач

Каноническое уравнение прямой на плоскости: теория, примеры, решение задач

Прямую линию в прямоугольной системе координат можно задать с помощью канонического уравнения. В этой статье мы расскажем, что это такое, приведем примеры, рассмотрим связи канонических уравнений с другими типами уравнений для этой прямой. В последнем пункте мы разберем несколько задач на закрепление темы.

Понятие канонического уравнения прямой

Допустим, что у нас есть декартова (прямоугольная) система координат, в которой задана прямая. Нам известны координаты произвольно взятой точки этой прямой M1(x1, y1), а также ее направляющего вектора a→=(ax, ay). Попробуем составить уравнение, которое описывало бы эту прямую.

Возьмем плавающую точку M(x, y). Тогда вектор M1M→ можно считать направляющим для исходной прямой. Его координаты будут равны  x-x1, y-y1 (если нужно, повторите материал о том, как правильно вычислять координаты вектора с помощью координат отдельных его точек).

Множество произвольно взятых точек M(x, y) будут определять нужную нам прямую с направляющим вектором a→=(ax, ay)  только в одном случае – если векторы M1M→ и a→=(ax, ay) будут коллинеарны по отношению друг к другу. Посмотрите на картинку: 

Таким образом, мы можем сформулировать необходимое и достаточное коллинеарности этих двух векторов:

M1M→=λ·a→, λ∈R

Если преобразовать полученное равенство в координатную форму, то мы получим:

x-x1=λ·axy-y1=λ·ay

При условии, что ax≠0 и ay≠0, получим:

x-x1=λ·axy-y1=λ·ay⇔λ=x-x1axλ=y-y1ay⇔x-x1ax=y-y1ay

Итог наших преобразований и будет каноническим уравнением прямой на плоскости. Запись вида x-x1ax=y-y1ay также называют уравнением прямой в каноническом виде.

Таким образом, с помощью уравнения x-x1ax=y-y1ay можно задать в прямоугольной системе координат на плоскости прямую, которая имеет направляющий вектор a→=(ax, ay) и проходит через точку M1(x1, y1).

Примером уравнения подобного типа является, например, x-23=y-31. Прямая, которая задана с его помощью, проходит через  M1(2, 3) и имеет направляющий вектор a→=3, 1. Ее можно увидеть на рисунке:

Из определения канонического уравнения нужно сделать несколько важных выводов. Вот они:

Определение 1

1. Если прямая, имеющая направляющий вектор a→=(ax, ay), проходит через две точки – M1(x1, y1) и M2(x2, y2), то уравнение для нее может быть записано как в виде x-x1ax=y-y1ay, так и x-x2ax=y-y2ay.

2. Если заданная прямая имеет направляющий вектор с координатами a→=(ax, ay), то множество всех ее векторов можно обозначить как μ·a→=(μ·ax, μ·ay), μ∈R, μ≠0. Таким образом, любое уравнение прямой в каноническом виде x-x1μ·ax=y-y1μ·ay будет соответствовать этой прямой.

Разберем важный пример задачи на нахождение канонического уравнения.

Пример 1

В прямоугольной системе координат на плоскости задана прямая, которая проходит через точку M1(2, -4) и имеет направляющий вектор с координатами a→=(1, -3). Запишите каноническое уравнение, описывающее данную прямую.

Решение

Для начала вспомним общий вид нужного нам канонического уравнения – x-x1ax=y-y1ay. Подставим в него имеющиеся значения x1=2, y1=-4, ax=1, ay=-3 и подсчитаем:

x-x1ax=y-y1ay⇔x-21=y-(-4)-3⇔x-21=y+4-3

Получившееся в итоге равенство и будет нужным ответом.

Ответ: x-21=y+4-3

Канонические уравнения прямой на плоскости с ax или ay, равными нулю

Если значение хотя бы одной переменной a является нулевым, то уравнение плоскости используют в первоначальном виде. Сразу две переменные нулевыми не могут быть по определению, поскольку нулевой вектор не бывает направляющим. В таком случае мы можем считать запись x-x1ax=y-y1ay условной и понимать ее как равенство ay(x-x1)=ax(y-y1).

Разберем случаи канонических уравнений на плоскости с одним нулевым a более подробно. Допустим, что x-x10=y-y1ay при ax=0, а исходная прямая будет проходить через M1(x1, y1). В таком случае она является параллельной оси ординат (если x1=0, то она будет с ней совпадать). Докажем это утверждение.

Для этой прямой вектор a→=(0, ay) будет считаться направляющим. Этот вектор является коллинеарным по отношению к координатному вектору j→=(0,1).

Если же нулевым является значение второго параметра, то есть ay=0, то мы получаем равенство вида x-x1ax=y-y10. Это уравнение описывает прямую, проходящую через M1(x1, y1), которая расположена параллельно оси абсцисс. Это утверждение верно, поскольку a→=(ax, 0) является для этой прямой направляющим вектором, а он в свою очередь является коллинеарным по отношению к координатному вектору i→=(1, 0).

Проиллюстрируем два частных случая канонического уравнения, описанные выше:

Пример 2

На плоскости задана прямая, параллельная оси Oy. Известно, что она проходит через точку M123, -17. Запишите каноническое уравнение для нее.

Решение 

Если прямая по отношению оси ординат является параллельной, то мы можем взять координатный вектор j→=(0, 1) в качестве направляющего для нее. В таком случае искомое уравнение выглядит следующим образом:

x-230=y—171⇔x-230=y+171

Ответ: x-230=y+171

Пример 3

На рисунке изображена прямая. Запишите ее каноническое уравнение.

Решение

Мы видим, что исходная прямая проходит параллельно оси Ox через точку M1(0, 3). Мы берем координатный вектор i→=(1, 0) в качестве направляющего. Теперь у нас есть все данные, чтобы записать нужное уравнение.

x-01=y-30⇔x1=y-30

Ответ: x1=y-30

Преобразование канонического уравнения прямой в другие виды уравнений

Мы уже выяснили, что в прямоугольной системе координат на плоскости заданную прямую можно описать с помощью канонического уравнения. Оно удобно для решения многих задач, однако иногда лучше производить вычисления с помощью другого типа уравнений. Сейчас мы покажем, как преобразовать каноническое уравнение в другие виды, если это требуется по ходу решения.

Стандартной форме записи канонического уравнения x-x1ax=y-y1ay можно поставить в соответствие систему параметрических уравнений на плоскости x=x1+ax·λy=y1+ay·λ. Чтобы преобразовать один вид уравнения в другой, нам надо приравнять правую и левую часть исходного равенства к параметру λ. После этого надо выполнить разрешение получившихся равенств относительно переменных x и y:

x-x1ax=y-y1ay⇔x-x1ax=y-y1ay=λ⇔⇔x-x1ax=λy-y1ay=λ⇔x=x1+ax·λy=y1+ay·λ

Покажем на примере, как именно выполняется это действие с конкретными числами.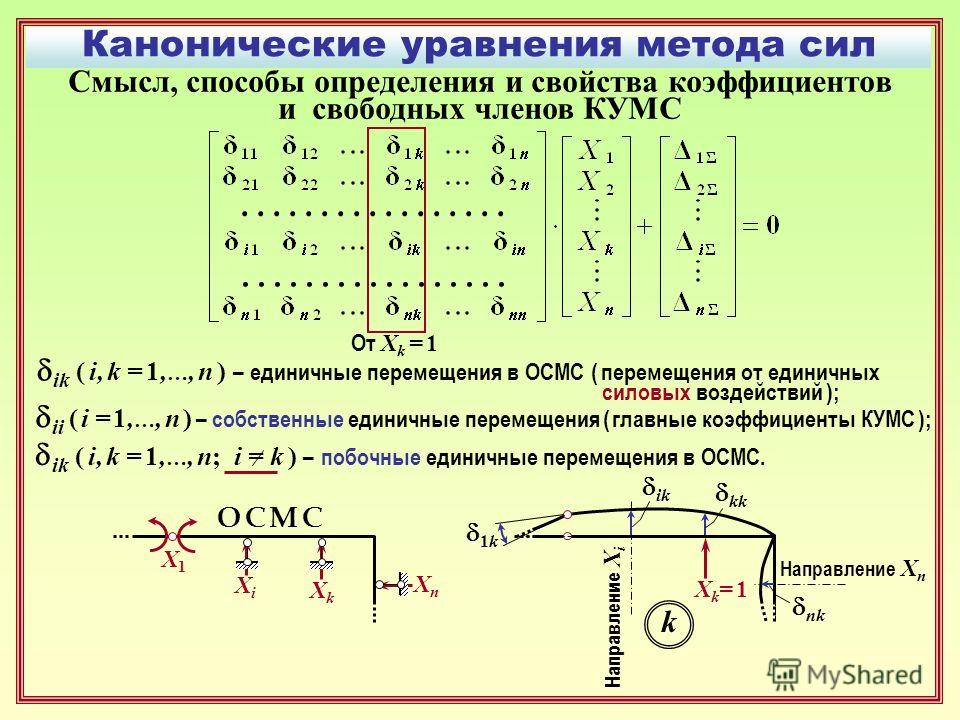

Пример 4

У нас есть прямая, заданная на плоскости с помощью канонического уравнения x+23=y-111. Запишите параметрические уравнения исходной прямой.

Решение

Сначала поставим знак равенства между отдельными частями уравнения и переменной λ и получим x+23=λy-111=λ.

Далее можно перейти к формулированию необходимых параметрических уравнений:

x+23=λy-111=λ⇔x+2=3·λy-1=11·λ⇔x=-2+3·λy=1+11·λ

Ответ: x=-2+3·λy=1+11·λ

Из канонического уравнения можно получить не только параметрические, но и общие уравнения прямой. Вспомним понятие пропорции: запись ab=cd можно представить в виде a·d=b·c с сохранением смысла. Значит, что x-x1ax=y-y1ay⇔ay(x-x1)=ax(y-y1)⇔ayx-axy-ayx1+axy1=0.

Это и есть общее уравнение прямой. Это станет более очевидно, если мы добавим в него значения параметров ay=A, -ax=B, -ayx1+axy1=C.

Пример 5

Прямая на плоскости описана с помощью канонического уравнения x-12=y+40. Вычислите общее уравнение этой прямой.

Решение 

Делаем указанные выше действия по порядку.

x-12=y+40⇔0·(x-1)=2·(y+4)⇔y+4=0

Ответ: y+4=0 .

Также из канонического уравнения мы можем получить уравнение прямой в отрезках, прямой с угловым коэффициентом или нормальное уравнение прямой, но это действие выполняется в два шага: первым делом мы получаем общее уравнение прямой, а вторым – преобразуем его в уравнение указанного типа. Разберем пример такой задачи.

Пример 6

На плоскости задана прямая с помощью уравнения x+33=y-22. Запишите уравнение этой же прямой в отрезках.

Решение

Для начала преобразуем исходное каноническое уравнение в общее уравнение прямой.

x+33=y-22⇔2·(x+3)=3·(y-2)⇔2x-3y+6+23=0

Далее переходим к формулировке уравнения прямой в отрезках.

2x-3y+6+23=0⇔2x-3y=-6+23⇔⇔2-(6+23)x-3-(6+23)y=1⇔x-6+232+y6+233=1⇔x-3+3+y33+2=1

Ответ: x-3+3+y33+2=1

Достаточно легко решить и задачу, обратную этой, т. е. привести уравнение прямой на плоскости обратно к каноническому. Допустим, у нас есть общее уравнение прямой в стандартной формулировке – Ax+By+C=0. При условии A≠0 мы можем перенести By вправо с противоположным знаком. Получим Ax+C=-By. Теперь выносим A за скобки и преобразуем равенство так:

Ax+CA=-By

Получившееся уравнение мы записываем в виде пропорции: x+CA-B=yA.

У нас получилось нужное нам каноническое уравнение прямой на плоскости.

А как сделать преобразование, если B≠0? Переносим все слагаемые, кроме Ax, вправо с противоположными знаками. Получаем, что Ax=-By-C. Выносим -B за скобки:

Ax=-By+CB

Формируем пропорцию: x-B=y+CBA

Пример 7

Есть общее уравнение прямой x+3y-1=0. Перепишите его в каноническом виде.

Решение

Оставим с левой стороны только одну переменную x. Получим:

x=-3y+1

Теперь вынесем -3 за скобки: x=-3y-13. Преобразуем равенство в пропорцию и получим необходимый ответ:

x-3=y-131

Ответ: x-3=y-131

Таким же образом мы поступаем, если нам нужно привести к каноническому виду уравнение прямой в отрезках и уравнение прямой с угловым коэффициентом.

Наиболее простая задача – переход от параметрических уравнений к каноническим. Нужно просто выразить параметр λ в системе уравнений x=x1+ax·λy=y1+ay·λ и приравнять обе части равенств. Схема решения выглядит так:

x=x1+ax·λy=y1+ay·λ⇔λ=x-x1axλ=y-y1ay⇔x-x1ax=y-y1ay

Если значение одного из параметров a будет нулевым, мы поступаем точно таким же образом.

Пример 8

Прямая на плоскости описана с помощью системы параметрических уравнений x=3+0·λy=-2-4·λ. Запишите каноническое уравнение для этой прямой.

Решение

Для начала преобразуем исходные уравнения в систему x=3+0·λy=-2-4·λ. Следующим шагом будет выражение параметра в каждом уравнении:

x=3+0·λy=-2-4·λ⇔λ=x-30λ=y+2-4

Ставим знак равенства между получившимися частями и получаем нужное нам каноническое уравнение: x-30=y+2-4

Ответ: x-30=y+2-4

Как решать задачи на составление канонических уравнений

В первую очередь канонические уравнения используются для тех задач, где нужно выяснить, принадлежит ли некоторая точка заданной прямой или нет. Вспомним, что в случае, если точка лежит на прямой, ее координаты будут удовлетворять уравнению этой прямой.

Пример 9

На плоскости задана прямая, каноническое уравнение которой имеет вид x-12=y+12-3. Выясните, лежат ли на ней точки M13, -312 и M2(5, -4).

Решение

Для проверки принадлежности необходимо подставить координаты точки в исходное уравнение и проверить, получим ли мы в итоге верное равенство.

3-12=-312+12-2⇔1=1

Результат говорит нам, что точка M13, -312 принадлежит исходной прямой.

Точно так же поступим и с координатами второй точки:

5-12=-4+12-3⇔2=76

Получившееся в итоге равенство не является верным, значит, эта точка заданной прямой не принадлежит.

Ответ: первая точка лежит на заданной прямой, а вторая нет.

Пример 10

Есть две точки M1(2, 4) и M2(-1, 3). Будет ли прямая, которая задана в той же плоскости с помощью уравнения x-20=y-32, проходить через них?

Решение

Вспомним, что запись x-20=y-32 можно понимать как 2·(x-2)=0·(y-3)⇔x-2=0. Подставим координаты заданных точек в это равенство и проверим.

Начнем с первой точки M1(2, 4) : 2-2=0⇔0=0

Равенство верное, значит, эта точка расположена на заданной прямой.

Подставляем данные второй точки: -1-2=0⇔-3=0.

Равенство неверное, значит, точка M2(-1, 3) не лежит на исходной прямой.

Ответ: через точку M1(2, 4) прямая проходит, а через M2(-1, 3) нет.

Далее мы посмотрим, какие еще типичные задачи на нахождение канонического уравнения можно встретить. Возьмем примеры с разными условиями.

Наиболее простыми являются задачи на нахождение канонического уравнения прямой на плоскости, в которых уже заданы координаты некой точки, лежащей на прямой. В первой части материала мы уже приводили пример решения такой задачи.

Чуть сложнее будет найти нужное уравнение, если нам предварительно нужно будет вычислить координаты направляющего вектора исходной прямой. Чаще всего встречаются задачи, в которой нужная прямая проходит через две точки с известными координатами.

Пример 11

Прямая на плоскости проходит через точку M1(0, -3) и через точку M2(2, -2). Сформулируйте для этой прямой канонической уравнение.

Решение

Eсли у нас есть координаты двух точек, то мы можем вычислить по ним координаты вектора M1M2→=2, 1. По отношению к прямой, чье уравнение мы составляем, он будет направляющим вектором. После этого мы можем записать следующее:

x-02=y-(-3)1⇔x2=y+31

Также можно использовать координаты второй точки. Тогда мы получим: x-22=y-(-2)1⇔x-22=y+21

Ответ: x2=y+31

Посмотрим, как нужно составлять канонические уравнения прямой на плоскости в том случае, если направляющий вектор этой прямой нужно вычислять исходя из параллельных или перпендикулярных ей прямых.

Пример 12

Известно, что точка M1(1, 3) принадлежит некоторой прямой, которая параллельна второй прямой, заданной с помощью уравнения x2=y-5. Запишите каноническое уравнение первой прямой.

Решение

Для первой прямой можно определить направляющий вектор a→=2, -5. Его можно рассматривать и в качестве направляющего для второй прямой, что следует из самого определения направляющих векторов. Это позволяет нам получить всю информацию, нужную для записи искомого уравнения: x-12=y-3-5

Ответ: x-12=y-3-5

Пример 13

Через точку M1(-1, 6) проходит прямая, которая является перпендикулярной другой прямой, определенной на плоскости с помощью уравнения 2x-4y-7=0. Запишите каноническое уравнение первой прямой.

Решение

Из данного уравнения мы можем взять координаты нормального вектора второй прямой – 2, 4. Мы знаем, что этот вектор является направляющим по отношению к первой. Тогда мы можем записать искомое уравнение:

x-(-1)2=y-64⇔x+11=y-62

Ответ: x+11=y-62

Канонические уравнения прямой в пространстве: теория, примеры, решение задач

Одним из видов уравнений прямой в пространстве является каноническое уравнение. Мы рассмотрим это понятие во всех подробностях, поскольку знать его необходимо для решения многих практических задач.

В первом пункте мы сформулируем основные уравнения прямой, расположенной в трехмерном пространстве, и приведем несколько примеров. Далее покажем способы вычисления координат направляющего вектора при заданных канонических уравнениях и решение обратной задачи. В третьей части мы расскажем, как составляется уравнение прямой, проходящей через 2 заданные точки в трехмерном пространстве, а в последнем пункте укажем на связи канонических уравнений с другими. Все рассуждения будут проиллюстрированы примерами решения задач.

Что такое каноническое уравнение прямой в пространстве

О том, что вообще из себя представляют канонические уравнения прямой, мы уже говорили в статье, посвященной уравнениям прямой на плоскости. Случай с трехмерным пространством мы разберем по аналогии.

Допустим, у нас есть прямоугольная система координат Oxyz, в которой задана прямая. Как мы помним, задать прямую можно разными способами. Используем самый простой из них – зададим точку, через которую будет проходить прямая, и укажем направляющий вектор. Если обозначить прямую буквой a, а точку M, то можно записать, что M1(x1, y1, z1) лежит на прямой a и направляющим вектором этой прямой будет a→=(ax, ay, az). Чтобы множество точек M(x, y, z) определяло прямую a, векторы M1M→ и a→ должны быть коллинеарными,

Если мы знаем координаты векторов M1M→ и a→, то можем записать в координатной форме необходимое и достаточное условие их коллинеарности. Из первоначальных условий нам уже известны координаты a→. Для того чтобы получить координаты M1M→, нам необходимо вычислить разность между M(x, y, z) и M1(x1, y1, z1). Запишем:

M1M→=x-x1, y-y1, z-z1

После этого нужное нам условие мы можем сформулировать так: M1M→=x-x1, y-y1, z-z1 и a→=(ax, ay, az): M1M→=λ·a→⇔x-x1=λ·axy-y1=λ·ayz-z1=λ·az

Здесь значением переменной λ может быть любое действительное число или ноль. Если λ=0, то M(x, y, z) и M1(x1, y1, z1)совпадут, что не противоречит нашим рассуждениям.

При значениях ax≠0, ay≠0, az≠0 мы можем разрешить относительно параметра λ все уравнения системы x-x1=λ·axy-y1=λ·ayz-z1=λ·az

Между правыми частями после этого можно будет поставить знак равенства:

x-x1=λ·axy-y1=λ·ayz-z1=λ·az⇔λ=x-x1axλ=y-y1ayλ=z-z1az⇔x-x1ax=y-y1ay=z-z1az

В итоге у нас получились уравнения x-x1ax=y-y1ay=z-z1az, с помощью которых можно определить искомую прямую в трехмерном пространстве. Это и есть нужные нам канонические уравнения.

Такая запись используется даже при нулевых значениях одного или двух параметров ax, ay, az, поскольку она в этих случаях она также будет верна. Все три параметра не могут быть равны 0, поскольку направляющий вектор a→=(ax, ay, az) нулевым не бывает.

Если один-два параметра a равны 0, то уравнение x-x1ax=y-y1ay=z-z1az носит условный характер. Его следует считать равным следующей записи:

x=x1+ax·λy=y1+ay·λz=z1+az·λ, λ∈R.

Частные случаи канонических уравнений мы разберем в третьем пункте статьи.

Из определения канонического уравнения прямой в пространстве можно сделать несколько важных выводов. Рассмотрим их.

1) если исходная прямая будет проходить через две точки  M1(x1, y1, z1) и M2(x2, y2, z2), то канонические уравнения примут следующий вид:

x-x1ax=y-y1ay=z-z1az или x-x2ax=y-y2ay=z-z2az.

2) поскольку a→=(ax, ay, az) является направляющим вектором исходной прямой, то таковыми будут являться и все векторы μ·a→=μ·ax, μ·ay, μ·az, μ∈R, μ≠0. Тогда прямая может быть определена с помощью уравнения x-x1ax=y-y1ay=z-z1az или x-x1μ·ax=y-y1μ·ay=z-z1μ·az.

Вот несколько примеров таких уравнений с заданными значениями:

Пример 1

x-32=y+1-12=zln 7

Тут x1=3, y1=-1, z1=0, ax=2, ay=-12, az=ln 7.

Пример 2

x-40=y+21=z+10

Тут M1(4, -2, -1), a→=(0, 1, 0).

Как составить каноническое уравнение прямой в пространстве

Мы выяснили, что канонические уравнения вида x-x1ax=y-y1ay=z-z1az будут соответствовать прямой, проходящей через точку M1(x1, y1, z1), а вектор a→=(ax, ay, az) будет для нее направляющим. Значит, если мы знаем уравнение прямой, то можем вычислить координаты ее направляющего вектора, а при условии заданных координат вектора и некоторой точки, расположенной на прямой, мы можем записать ее канонические уравнения.

Разберем пару конкретных задач.

Пример 3

У нас есть прямая, заданная в трехмерном пространстве с помощью уравнения x+14=y2=z-3-5. Запишите координаты всех направляющих векторов для нее.

Решение

Чтобы получить координаты направляющего вектора, нам надо просто взять значения знаменателей из уравнения. Мы получим, что одним из направляющих векторов будет a→=(4, 2, -5), а множество всех подобных векторов можно сформулировать как μ·a→=4·μ, 2·μ, -5·μ. Здесь параметр μ – любое действительное число (за исключением нуля).

Ответ: 4·μ, 2·μ, -5·μ, μ∈R,  μ≠0 

Пример 4

Запишите канонические уравнения, если прямая в пространстве проходит через M1(0, -3, 2) и имеет направляющий вектор с координатами -1, 0, 5.

Решение

У нас есть данные, что x1=0, y1=-3, z1=2, ax=-1, ay=0, az=5. Этого вполне достаточно, чтобы сразу перейти к записи канонических уравнений.

Сделаем это:

x-x1ax=y-y1ay=z-z1az⇔x-0-1=y-(-3)0=z-25⇔⇔x-1=y+30=z-25

Ответ: x-1=y+30=z-25

Эти задачи – самые простые, потому что в них есть все или почти все исходные данные для записи уравнения или координат вектора. На практике чаще можно встретить те, в которых сначала нужно находить нужные координаты, а потом записывать канонические уравнения. Примеры таких задач мы разбирали в статьях, посвященных нахождению уравнений прямой, проходящей через точку пространства параллельно заданной, а также прямой, проходящей через некоторую точку пространства перпендикулярно плоскости.

Канонические уравнения с одним или двумя a, равными нулю

Ранее мы уже говорили, что одно-два значения параметров ax, ay, az в уравнениях могут иметь нулевые значения. При этом запись x-x1ax=y-y1ay=z-z1az=λ приобретает формальный характер, поскольку мы получаем одну или две дроби с нулевыми знаменателями. Ее можно переписать в следующем виде (при λ∈R):

x=x1+ax·λy=y1+ay·λz=z1+az·λ

Рассмотрим эти случаи подробнее. Допустим, что ax=0, ay≠0, az≠0, ax≠0, ay=0, az≠0, либо ax≠0, ay≠0, az=0. В таком случае нужные уравнения мы можем записать так:

1.  В первом случае: 
   x-x10=y-y1ay=z-z1az=λ⇔x-x1=0y=y1+ay·λz=z1+az·λ⇔x-x1=0y-y1ay=z-z1az=λ

2.  Во втором случае:
   x-x1ax=y-y10=z-z1az=λ⇔x=x1+ax·λy-y1=0z=z1+az·λ⇔y-y1=0x-x1ax=z-z1az=λ

3.  В третьем случае:
   x-x1ax=y-y1ay=z-z10=λ⇔x=x1+ax·λy=y1+ay·λz-z1=0⇔z-z1=0x-x1ax=y-y1ay=λ

Получается, что при таком значении параметров нужные прямые находятся в плоскостях x-x1=0, y-y1=0 или z-z1=0, которые располагаются параллельно координатным плоскостям (если x1=0, y1=0 либо z1=0). Примеры таких прямых показаны на иллюстрации.

Следовательно, мы сможем записать канонические уравнения немного иначе.

1. В первом случае: x-x10=y-y10=z-z1az=λ⇔x-x1=0y-y1=0z=z1+az·λ, λ∈R
2. Во втором: x-x10=y-y1ay=z-z10=λ⇔x-x1=0y=y1+ay·λ, λ∈Rz-z1=0
3. В третьем: x-x1ax=y-y10=z-z10=λ⇔x=x1+ax·λ, λ∈Ry=y1=0z-z1=0

Во всех трех случаях исходные прямые будут совпадать с координатными осями или окажутся параллельными им: x1=0y1=0, x1=0z1=0, y1=0z1=0. Их направляющие векторы имеют координаты  0, 0, az, 0, ay, 0, ax, 0, 0. Если обозначить направляющие векторы координатных прямых как i→, j→, k→, то направляющие векторы заданных прямых будут коллинеарными по отношению к ним. На рисунке показаны эти случаи:

Покажем на примерах, как применяются эти правила.

Пример 5

Найдите канонические уравнения, с помощью которых можно определить в пространстве координатные прямые Oz, Ox, Oy.

Решение

Координатные векторы i→=(1, 0, 0), j→=0, 1, 0, k→=(0, 0, 1) будут для исходных прямых направляющими. Также мы знаем, что наши прямые будут обязательно проходить через точку O(0, 0, 0), поскольку она является началом координат. Теперь у нас есть все данные, чтобы записать нужные канонические уравнения.

Для прямой Ox: x1=y0=z0

Для прямой Oy: x0=y1=z0

Для прямой Oz: x0=y0=z1

Ответ: x1=y0=z0, x0=y1=z0, x0=y0=z1.

Пример 6

В пространстве задана прямая, которая проходит через точку M1(3, -1, 12). Также известно, что она расположена параллельно оси ординат. Запишите канонические уравнения этой прямой.

Решение

Учитывая условие параллельности, мы можем сказать, что вектор j→=0, 1, 0 будет для нужной прямой направляющим. Следовательно, искомые уравнения будут иметь вид:

x-30=y-(-1)1=z-120⇔x-30=y+11=z-120

Ответ: x-30=y+11=z-120

Как записать каноническое уравнение прямой, которая проходит через две заданные точки

Допустим, что у нас есть две несовпадающие точки M1(x1, y1, z1) и M2(x2, y2, z2), через которые проходит прямая. Как в таком случае мы можем сформулировать для нее каноническое уравнение?

Для начала примем вектор M1M2→ (или M2M1→) за направляющий вектор данной прямой. Поскольку у нас есть координаты нужных точек, сразу вычисляем координаты вектора:

M1M2→=x2-x1, y2-y1, z2-z1

Далее переходим непосредственно к записи канонического уравнения, ведь все нужные данные у нас уже есть. Исходная прямая будет определяться записями следующего вида:

x-x1x2-x1=y-y1y2-y1=z-z1z2-z1x-x2x2-x1=y-y2y2-y1=z-z2z2-z1

Получившиеся равенства – это и есть канонические уравнения прямой, проходящей через две заданные точки. Взгляните на иллюстрацию:

Приведем пример решения задачи.

Пример 7

в пространстве есть две точки с координатами M1(-2, 4, 1) и M2(-3, 2, -5), через которые проходит прямая. Запишите канонические уравнения для нее.

Решение

Согласно условиям, x1=-2, y1=-4, z1=1, x2=-3, y2=2, z2=-5. Нам требуется подставить эти значения в каноническое уравнение:

x-(-2)-3-(-2)=y-(-4)2-(-4)=z-1-5-1⇔x+2-1=y+46=z-1-6

Если мы возьмем уравнения вида x-x2x2-x1=y-y2y2-y1=z-z2z2-z1, то у нас получится: x-(-3)-3-(-2)=y-22-(-4)=z-(-5)-5-1⇔x+3-1=y-26=z+5-6

Ответ: x+3-1=y-26=z+5-6 либо x+3-1=y-26=z+5-6.

Преобразование канонических уравнений прямой в пространстве в другие виды уравнений

Иногда пользоваться каноническими уравнениями вида x-x1ax=y-y1ay=z-z1az не очень удобно. Для решения некоторых задач лучше использовать запись x=x1+ax·λy=y1+ay·λz=z1+az·λ. В некоторых случаях более предпочтительно определить нужную прямую с помощью уравнений двух пересекающихся плоскостей A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0. Поэтому в данном пункте мы разберем, как можно перейти от канонических уравнений к другим видам, если это требуется нам по условиям задачи.

Понять правила перехода к параметрическим уравнениям несложно. Сначала приравняем каждую часть уравнения к параметру λ и разрешим эти уравнения относительно других переменных. В итоге получим:

x-x1ax=y-y1ay=z-z1az⇔x-x1ax=y-y1ay=z-z1az⇔⇔x-x1ax=λy-y1ay=λz-z1az=λ⇔x=x1+ax·λy=y1+ay·λz=z1+az·λ

Значение параметра λ может быть любым действительным числом, ведь и x, y, z могут принимать любые действительные значения.

Пример 8

В прямоугольной системе координат в трехмерном пространстве задана прямая, которая определена уравнением x-23=y-2=z+70. Запишите каноническое уравнение в параметрическом виде.

Решение

Сначала приравниваем каждую часть дроби к λ.

x-23=y-2=z+70⇔x-23=λy-2=λz+70=λ

Теперь разрешаем первую часть относительно x, вторую – относительно y, третью – относительно z. У нас получится:

x-23=λy-2=λz+70=λ⇔x=2+3·λy=-2·λz=-7+0·λ⇔x=2+3·λy=-2·λz=-7

Ответ: x=2+3·λy=-2·λz=-7

Следующим нашим шагом будет преобразование канонических уравнений в уравнение двух пересекающихся плоскостей (для одной и той же прямой).

Равенство x-x1ax=y-y1ay=z-z1az нужно для начала представить в виде системы уравнений:

x-x1ax=y-y1ayx-x1ax=z-z1axy-y1ay=z-z1az

Поскольку pq=rs мы понимаем как p·s=q·r, то можно записать:

x-x1ax=y-y1ayx-x1ax=z-z1azy-y1ay=z-z1az⇔ay·(x-x1)=ax·(y-y1)az·(x-x1)=ax·(z-z1)az·(y-y1)=ay·(z-z1)⇔⇔ay·x-ax·y+ax·y1-ay·x1=0az·x-ax·z+ax·z1-az·x1=0az·y-ay·z+ay·z1-az·y1=0

В итоге у нас вышло, что:

x-x1ax=y-y1ay=z-z1az⇔ay·x-ax·y+ax·y1-ay·x1=0az·x-ax·z+ax·z1-az·x1=0az·y-ay·z+ay·z1-az·y1=0

Выше мы отмечали, что все три параметра a не могут одновременно быть нулевыми. Значит, ранг основной матрицы системы будет равен 2, поскольку ay-ax0az0-ax0az-ay=0 и один из определителей второго порядка не равен 0:

ay-axaz0=ax·az, ay0az-ax=ax·ay,  -ax00-ax=ax2ay-ax0az=ay·az, ay00-ay=-ay2, -ax0az-ay=ax·ayaz00az=az2, az-ax0-ay=-ay·az, 0-axaz-ay=ax·az

Это дает нам возможность исключить одно уравнение из наших расчетов. Таким образом, канонические уравнения прямой можно преобразовать в систему из двух линейных уравнений, которые будут содержать 3 неизвестных. Они и будут нужными нам уравнениями двух пересекающихся плоскостей.

Рассуждение выглядит довольно сложным, однако на практике все делается довольно быстро. Продемонстрируем это на примере.

Пример 9

Прямая задана каноническим уравнением x-12=y0=z+20. Напишите для нее уравнение пересекающихся плоскостей.

Решение

Начнем с попарного приравнивания дробей.

x-12=y0=z+20⇔x-12=y0x-12=z+20y0=z+20⇔⇔0·(x-1)=2y0·(x-1)=2·(z+2)0·y=0·(z+2)⇔y=0z+2=00=0

Теперь исключаем из расчетов последнее уравнение, потому что оно будет верным при любых x, y и z. В таком случае x-12=y0=z+20⇔y=0z+2=0.

Это и есть уравнения двух пересекающихся плоскостей, которые при пересечении образуют прямую, заданную с помощью уравнения x-12=y0=z+20

Ответ: y=0z+2=0

Пример 10

Прямая задана уравнениями x+12=y-21=z-5-3, найдите уравнение двух плоскостей, пересекающихся по данной прямой.

Решение

Приравниваем дроби попарно.

x+12=y-21=z-5-3⇔x+12=y-21x+12=z-5-3y-21=z-5-3⇔⇔1·(x+1)=2·(y-2)-3·(x+1)=2·(z-5)-3·(y-2)=1·(z-5)⇔x-2y+5=03x+2z-7=03y+7-11=0

Получаем, что определитель основной матрицы полученной системы будет равен 0:

1-20302031=1·0·1+(-2)·2·0+0·3·3-0·0·0-1·2·3-(-2)·3·1=0

Минор второго порядка нулевым при этом не будет: 1-230=1·0-(-2)·3=6. Тогда мы можем принять его в качестве базисного минора.

В итоге мы можем вычислить ранг основной матрицы системы x-2y+5=03x+2z-7=03y+z-11=0. Это будет 2. Третье уравнение исключаем из расчета и получаем:

x-2y+5=03x+2z-7=03y+z-11=0⇔x-2y+5=03x+2z-7=0

Ответ: x-2y+5=03x+2z-7=0

8.

3: Уравнения движения Гамильтона

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

9609

• Дуглас Клайн
• Университет Рочестера

9{EXC}\метка{8.18}\]

Можно продолжить изучение следствий гамильтоновой механики, взяв дифференциал времени \((8.1.3)\) даяния.

\[\frac{dH(\mathbf{q,p,}t)}{dt}=\sum_{j}\left( \dot{q}_{j}\frac{dp_{j}} }{dt } + p_ {j} \ frac {d \ dot {q} _ {j}} {dt} — \ frac {\ partial L} {\ partial q_ {j}} \ frac { dq_ {j}} {dt} -\frac{\partial L}{\partial \dot{q}_{j}}\frac{d\dot{q}_{j}}{dt} \right) -\frac{\partial L}{ \partial t}\label{8.19}\]

Вставка сопряженных импульсов \(p_{i}\equiv \frac{\partial L}{\partial \dot{q}_{i}}\) и уравнения \ref{8. 17} в уравнение \ref{8.19{EXC} \right] \dot{q}_{j}\right) -\frac{\partial L}{\partial t}\label{8.21}\]

Это обобщенная теорема об энергии , заданная уравнением \((7.8.1)\).

Полный дифференциал гамильтониана также может быть записан как

\[\frac{dH(\mathbf{q,p,}t)}{dt}=\sum_{j}\left(\frac{\partial H}{\partial p_{j}}\dot{p } _ {j} + \ frac {\ partial H} {\ partial q_ {j}} \ dot {q} _ {j} \ right) + \ frac {\ partial H} {\ partial t} \ label {8.22 }\]

Используйте уравнения \ref{8.15} и \ref{8.18} для замены \(\frac{\partial H}{\partial p_{j}}\) и \(\frac{\partial H}{\partial q_ {j}}\) в уравнении \ref{8.22} дает 9{EXC} \right] \dot{q}_{j}\right) +\frac{\partial H(\mathbf{q,p,}t)}{\partial t}\label{8.23}\]

Обратите внимание, что уравнение \ref{8.23} должно совпадать с обобщенной теоремой об энергии, т.е. уравнение \ref{8.21}. Следовательно,

\[\frac{\partial H}{\partial t}=-\frac{\partial L}{\partial t}\label{8.24}\]

Таким образом, уравнений движения Гамильтона задаются как

\[\begin{align} \dot{q}_{j} &= \frac{\partial H(\mathbf{q,p,}t)}{\partial p_{j}} \label{8.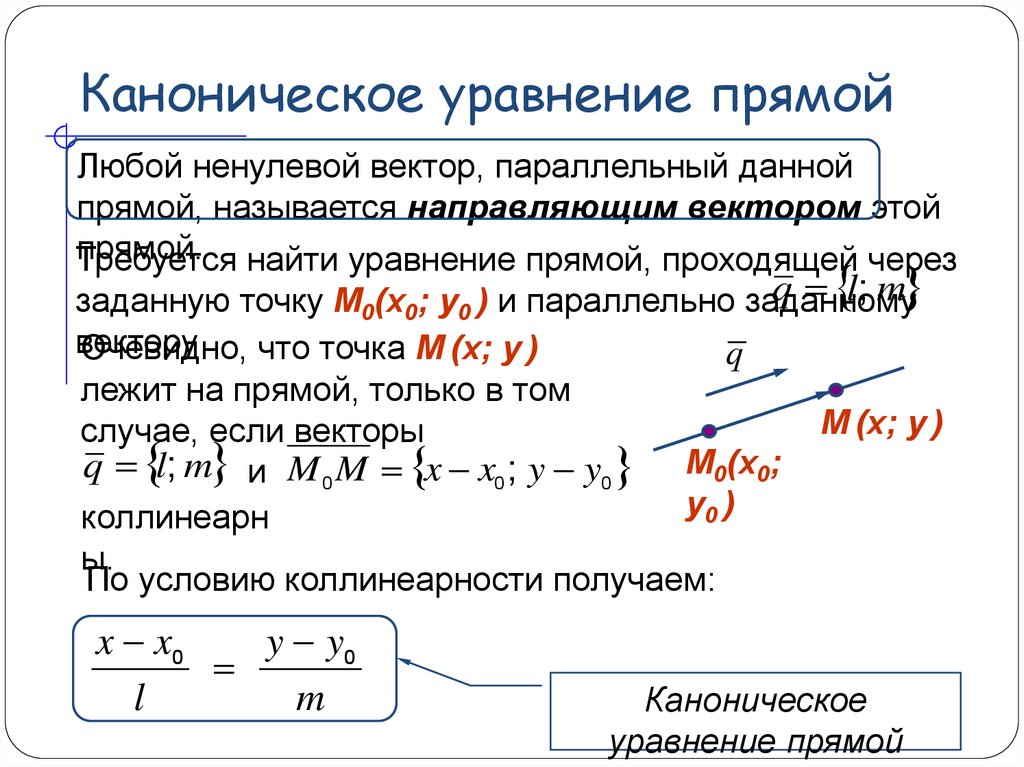 {EXC} \right] \dot{q}_{j}\right) -\frac{\ частичное L(\mathbf{q,\dot{q},}t)}{\partial t}\label{8.27}\end{align}\]

Симметрия уравнений движения Гамильтона иллюстрируется, когда множитель Лагранжа и обобщенные силы равны нулю. Затем

\[\begin{align} \dot{q}_{j} &= \frac{\partial H(\mathbf{q,p,}t)}{\partial p_{j}} \label{8.28} \\[4pt] \dot{p}_{j} &= -\frac{\partial H(\mathbf{p,q},t)}{\partial q_{j}} \label{8.29}\\ [4pt] \ frac {dH (\ mathbf {p, q}, t)} {dt} & = \ frac {\ partial H (\ mathbf {p, q}, t)} {\ partial t} = — \ frac{\ partial L (\ mathbf {\ dot {q}, q,} t)} {\ partial t} \ end {align} \ label {8.30} \] 9{EXC}\) для учета неголономных или других сил. Уравнения движения Гамильтона обычно называют каноническими уравнениями движения . Обратите внимание, что термин «канонический» не имеет ничего общего с религией или каноническим правом; причина этого названия сбила с толку многие поколения исследователей классической механики. Термин был введен Якоби в \(1837\) для обозначения простого и фундаментального набора сопряженных переменных и уравнений. Обратите внимание на симметрию двух канонических уравнений Гамильтона, а также на то, что канонические переменные \(p_{k},q_{k}\) рассматриваются как независимые канонические переменные. Координаты механики Лагранжа \((\mathbf{q, \dot{q},}t)\) заменены координатами гамильтоновой механики \((\mathbf{ q,p,}t),\) , где сопряженные импульсы \(\mathbf{p}\) считаются не зависящими от координаты \(\mathbf{q}\).

Лагранж первым вывел канонические уравнения, но не признал их основной системой уравнений движения. Гамильтон вывел канонические уравнения движения из своего фундаментального вариационного принципа, глава \(9.2\), и сделал их основой далеко идущей теории динамики. Уравнения Гамильтона дают \(2s\) дифференциальные уравнения первого порядка для \(p_{k},q_{k}\) для каждой из \(s=n-m\) степеней свободы. Уравнения Лагранжа дают \(s\) дифференциальные уравнения второго порядка для \(s\) независимых обобщенных координат \(q_{k},\dot{q}_{k}.\)

Было показано, что \(H(\mathbf{p,q},t)\) и \(L(\mathbf{\dot{q},q, }t)\) являются преобразованиями Лежандра каждого другой. Хотя лагранжева формулировка идеальна для решения численных задач классической механики, гамильтонова формулировка обеспечивает лучшую основу для концептуальных расширений на другие области физики, поскольку она записывается в терминах фундаментальных сопряженных координат, \(\mathbf{q,p} \). Гамильтониан широко используется в современной физике, включая квантовую физику, как обсуждалось в главах \(15\) и \(18\). Например, в квантовой механике существует прямая связь между классическим и квантовым представлением импульса; этого не существует для скоростей.

Понятие пространства состояний, введенное в главе \(3.3.2\), естественным образом применимо к лагранжевой механике, поскольку \((\dot{q},q)\) — это обобщенные координаты, используемые в лагранжевой механике. Понятие фазового пространства, введенное в главе \(3.3.3\), естественно применимо к гамильтонову фазовому пространству, поскольку \((p,q)\) — это обобщенные координаты, используемые в гамильтоновой механике.

---

Эта страница под названием 8. 3: Уравнения движения Гамильтона распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Дугласом Клайном посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Дуглас Клайн

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. Обобщенная теорема об энергии
   2. Уравнения движения Гамильтона
   3. источник@http://classicalmechanics. lib.rochester.edu

2.4.1 Канонические уравнения Гамильтона

2.4.1 Канонические уравнения Гамильтона
Далее: 2.4.2 Преобразование Лежандра Up: 2.4 Гамильтонов формализм и Предыдущий: 2.4 Гамильтонов формализм и Содержимое Индекс

В В разделе 2.3.4 мы столкнулись с двумя величинами, которые мы вспоминаем здесь и для которых мы теперь вводим специальные символы. Первым был номер импульс

(2.27)

которую мы обычно будем рассматривать как функцию связанный с заданной кривой . Вторым объектом стал гамильтониан .

(2. 28)

которая записывается здесь как общая функция четырех переменных, но также становится функция в одиночку при оценке вдоль кривой. Внутренний продукт знак в определении отражает тот факт, что в случай множественных степеней свободы, и являются векторами.

Переменные и называются каноническими переменными . Предположим теперь, что является экстремалью, т. е. удовлетворяет уравнение Эйлера-Лагранжа (2.18). Оказывается, дифференциальные уравнения описание эволюции из и вдоль такой кривой, если записать ее в терминах гамильтониана , принять особенно красивую форму. Для , у нас есть

Для , у нас есть где второе равенство есть уравнение Эйлера-Лагранжа. В более сжатой форме результат является

(2.29)

которая известна как система канонических уравнений Гамильтона . Эта переформулировка уравнения Эйлера-Лагранжа была предложена Гамильтоном в 1835. Поскольку мы не предполагаем здесь, что мы находимся в «не «дело или «нет » случай раздела 2.3.4, импульс и гамильтониан не обязательно должны быть постоянными вдоль экстремалей.

Важным дополнительным наблюдением является то, что частная производная в отношении является

(2.30)

где последнее равенство следует из определения (2.28) из . Это говорит о том, в дополнение к каноническим уравнениям (2.30) необходимое условие для оптимальности должно быть так имеет стационарную точку как функцию по оптимальной кривой. Делать уточнить это утверждение, подставим следующие рассуждения в Гамильтониан: произвольный ; для , соответствующее положение оптимальной кривой; для , соответствующее значение импульса . Давайте держать последний оставшийся аргумент, , как свободную переменную, и перемаркировать это как для ясности. Это дает функцию

(2.31)

Наше утверждение состоит в том, что эта функция имеет стационарную точку, когда равно , скорость оптимальной кривой при . Действительно, это сразу проверяется

(2.32)

Позже мы увидим, что в контексте принципа максимума это стационарная точка на самом деле экстремум, на самом деле, максимум. Более того, заявление относительно максимума остается верным, когда не обязательно дифференцируемый или когда принимает значения в наборе с граница и на этой границе; основное свойство дело не в том, что производная обращается в нуль, а в том, что достигает максимум в указанном выше смысле.