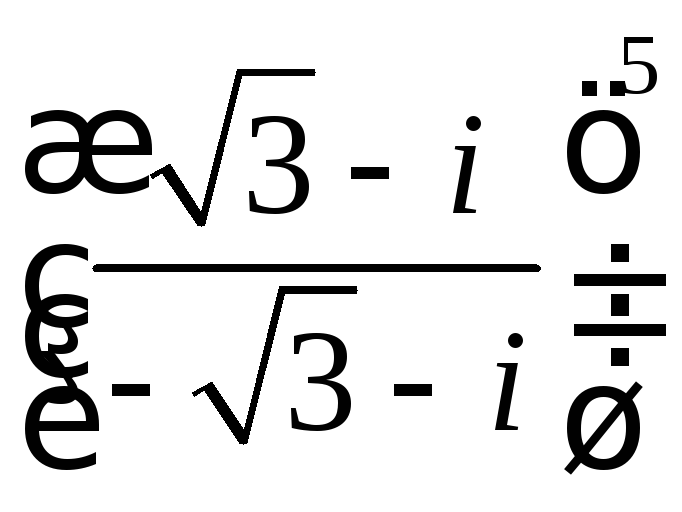3. Нахождение оригинала по изображению.
Задача 1.Найти оригинал для изображения
при помощи разложения на простейшие дроби.
Решение.Разложимна сумму простейших дробей
.
Найдем неопределенные коэффициенты A, B, C, D. Так как
,
то, приравнивая коэффициенты при одинаковых степенях , получаем
, , , .
Таким образом,
.
Свертка оригиналов.Пустьи- функции-ориентиры и, . По определению, сверткой оригиналовназывается интеграл(3.1)
По теореме сложения изображений свертки оригиналов соответствует произведение изображений
.
Задача 2.Найти свертку функцийи.
Решение.
Задача 3.Восстановить оригинал по изображениюпри помощи свертки.
Решение.Представимкак произведение двух функций и используя теорему умножения, запишем
. (см. задачу 2)
4. Решение линейных дифференциальных уравнений и систем.
Рассмотрим применение правил и теорем операционного исчисления к решению линейных дифференциальных уравнений с постоянными коэффициентами и их систем при заданных начальных условиях. Предлагаем, что искомое решение, его производные и правая часть дифференциального уравнения являются оригиналами.
Схема решения дифференциального уравнения.
Искомая функция, ее производные, входящие в данное уравнение, правая часть уравнения заменяются их изображениями. В результате получается так называемое операторное уравнение.
- Решаем операторное уравнение относительно
изображения искомой функции.

Переходим от изображения искомой функции к оригиналу.
Схема решения систем дифференциальных уравнений такая же.
Задача 1.Решить дифференциальное уравнение
, если,
Решение.Пусть- искомое решение.
.
Запишем операторное уравнение
или
.
Находим A, B, C. ,,.
Итак,
.
Задача 2.Найти решение системы дифференциальных уравнений
удовлетворяющее начальным условиям , , ,
Решение.Пусть, . Тогда
; ;;.
Преобразованная система имеет вид
Определяем , по правилу Крамера
;
Вычислим получим
Итак,
Вычислим получим
Тогда
Итак,
Рассмотрим решение дифференциальных
уравнений при нулевых начальных условиях
с использованием интеграла Дюамеля.
Интеграл Дюамеля.
Если и, то
(4.1)
или
(4.1’)
Рассмотрим линейное дифференциальное уравнение с постоянными коэффицентами
при Если
,
то получим
или , где- многочленn-ой степени;
отсюда
(4.2)
Если рассмотреть ещё одно дифференциальное уравнение, у которого правая часть равна единице,
то при тех же нулевых начальных условиях в изображениях получим уравнение
Отсюда (4.3)
Подставим (4.3) в (4.2), получим
(4.4)
Используя интеграл Дюамеля (4.1’) для и учитывая, что, получаем
(4.5)
Итак, достаточно решить уравнение с правой частью равной единице, чтобы при помощи интеграла (4.5) получить решения при различных правых частях.
Задача 3.
Найти частное решение дифференциального уравнения, используя интеграл Дюамеля:
(4.7)
Пусть , тогда
Получим уравнение для изображения
Отсюда
Возвращаясь к первоначальному уравнению для , Запишем
Следует отметить, что преимущество
операционного метода решения
дифференциальных уравнений состоит в
том, что благодаря этому методу мы
заменяем решение дифференциального
уравнения на решение алгебраического
уравнения, что сильно упрощает вычисление.
Применение методов операционного исчисления в
задачах электротехники.
Методы операционного исчисления широко используются в решениях специальных задач электротехники.
Задача1.
Включение дополнительного источника ЭДС в цепь с ненулевыми начальными условиями.
Рассмотрим электрическую цепь с ненулевыми начальными условиями (рис. 5.1), где r- сопротивление;L- индуктивность;C– ёмкость конденсатора;k– выключатель.
рис 5.1
Эта цепь характеризуется тем, что при отключении ЭДС Е в цепи происходит арядка конденсатора. После зарядки конденсатора ток в цепи становится равным нулю. Требуется найти ток i(t) после подключения к цепи дополнительной ЭДС е(t).
По второму закону Кирхгофа (алгебраическая сумма падения напряжения на сопротивлениях равна алгебраической сумме действующих в цепи ЭДС) для момента времени имеем
,
(5.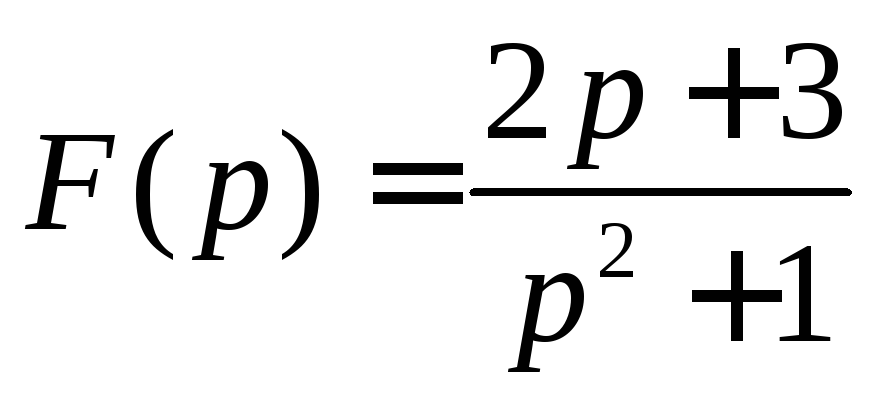 1)
1)
где — напряжение на конденсаторе;
(0) – начальное напряжение на конденсаторе, обусловленное тем, что конденсатор уже был ранее заряжен.
Решение.
Применяя к интегро-дифяфференциальному уравнению (5.1) преобразование Лапласа, запишем
где — начальный ток в цепи. Используя указанные соотношения, получаем алгебраическое уравнение в изобржениях
где неизвестной величиной является. Остальные величины известныИз (5.2) получаем
(5.3)
Рассмотрим конкретный пример. Пусть Применяя преобразование Лапласа, получаемследовательно,С учётом этих условий из (5.3) получаем
(5.4)
Замечание.Из полученного решения (5.4) следует, что, при, т.е.Это означает что за некоторое время конденсатор дополнительно зарядится и ток станет равным нулю.
Задача 2.
Определить ток в цепи, состоящей из
последовательно соединённых сопротивления
rи конденсатора С, если
в моментt=0 цепь подсоединяется
к источнику ЭДС (рис 5.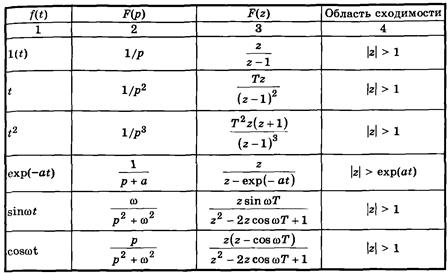 2) в виде треугольного
импульса (рис 5.3).
2) в виде треугольного
импульса (рис 5.3).
рис 5.2 рис 5.3
В задаче задано
Решение.
Используя второй закон Кирхгофа, получим интегральное уравнение для рассматриваемого контура
(5.5)
Решение уравнения (5.5) выразим при помощи интеграла Дюамеля (4.1)
(5.6)
где — решение вспомогательного уравнения
(5.7)
Применяя преобразование Лапласа, имеем
Уравнение (5.7) преобразуется к алгебраическому уравнению для нахождения J(p)
откуда(5.8)
Подставляя найденное решение (5.8) вспомогательного уравнения (5.7) в интеграл Дюамеля (5.6) получаем решение исходного уравнения (5.5)
.
Пример контрольной работы по операционному исчислению
и комплексным числам.
Вариант 1.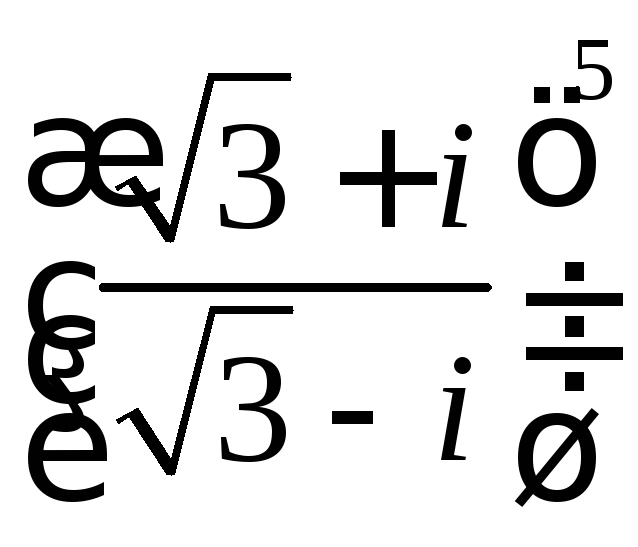
1. Восстановить оригинал по изображению:
2. Решить задачу Коши операторным методом:
.
3. Найти все значения корней
4. Представить в алгебраической форме:
5. Найти изображение оригинала, заданного графически
6. Решить систему
Вариант 2.
Решить задачу Коши операторным методом:
3. Найти все значения корней
4. Представить в алгебраической форме:
Восстановить оригинал по изображению
6. Решить систему
Вариант 3.
1. Восстановить оригинал по изображению:
2. Решить задачу Коши операторным методом:
.
3. Найти все значения корней
4. Представить в алгебраической форме:
5. Найти изображение оригинала, заданного
графически:
Найти изображение оригинала, заданного
графически:
6. Решить систему
Вариант 4.
Найти изображение функции:
Решить задачу Коши операторным методом:
3. Найти все значения корней
4. Представить в алгебраической форме:
Восстановить оригинал по изображению
6. Решить систему
Вариант 5.
1. Восстановить оригинал по изображению:
2. Решить задачу Коши операторным методом:
.
3. Найти все значения корней
а) ;
б)
4. Представить в алгебраической форме:
а); б)
5. Найти изображение оригинала, заданного графически:
6. Решить систему
Вариант 6.
Найти изображение функции:
Решить задачу Коши операторным методом:
3.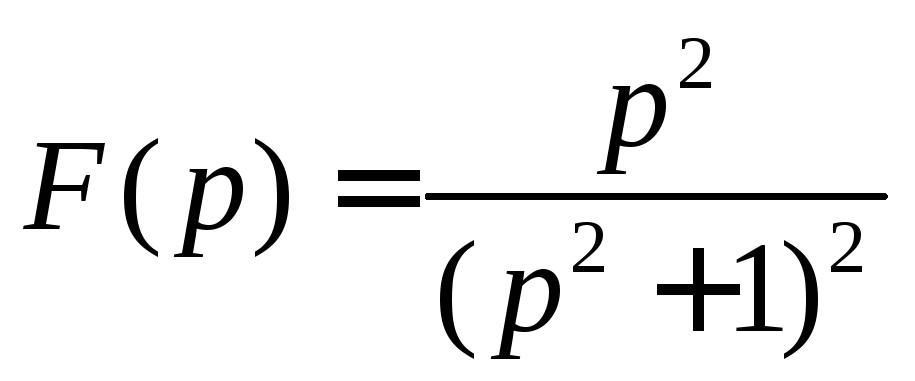 Найти все значения корней
Найти все значения корней
а) ;
б)
4. Представить в алгебраической форме:
а) ; б)
Восстановить оригинал по изображению
6. Решить систему
Вариант 7.
1. Восстановить оригинал по изображению:
2. Решить задачу Коши операторным методом:
.
3. Найти все значения корней
а) ;
б)
4. Представить в алгебраической форме:
а) ; б)
5. Найти изображение оригинала, заданного графически:
6. Решить систему
Вариант 8.
1. Найти изображение функции:
2. Решить задачу Коши операторным методом:
3. Найти все значения корней
а) ;
б)
4. Представить в алгебраической форме:
а) ;
б)
Восстановить оригинал по изображению
6. Решить систему
Решить систему
Вариант 9.
1. Восстановить оригинал по изображению:
2. Решить задачу Коши операторным методом:
.
3. Найти все значения корней
а) ;
б)
4. Представить в алгебраической форме:
а) ; б)
5. Найти изображение оригинала, заданного графически:
6. Решить систему
Вариант 10.
1. Найти изображение функции:
2. Решить задачу Коши операторным методом:
3. Найти все значения корней
а) ;
б)
4. Представить в алгебраической форме:
а) ; б)
5. Восстановить оригинал по изображению
6. Решить систему
Вариант 11.
1. Восстановить оригинал по изображению:
2. Решить задачу Коши операторным методом:
.
3. Найти все значения корней
а) ;
б)
4. Представить в алгебраической форме:
а) ; б)
5.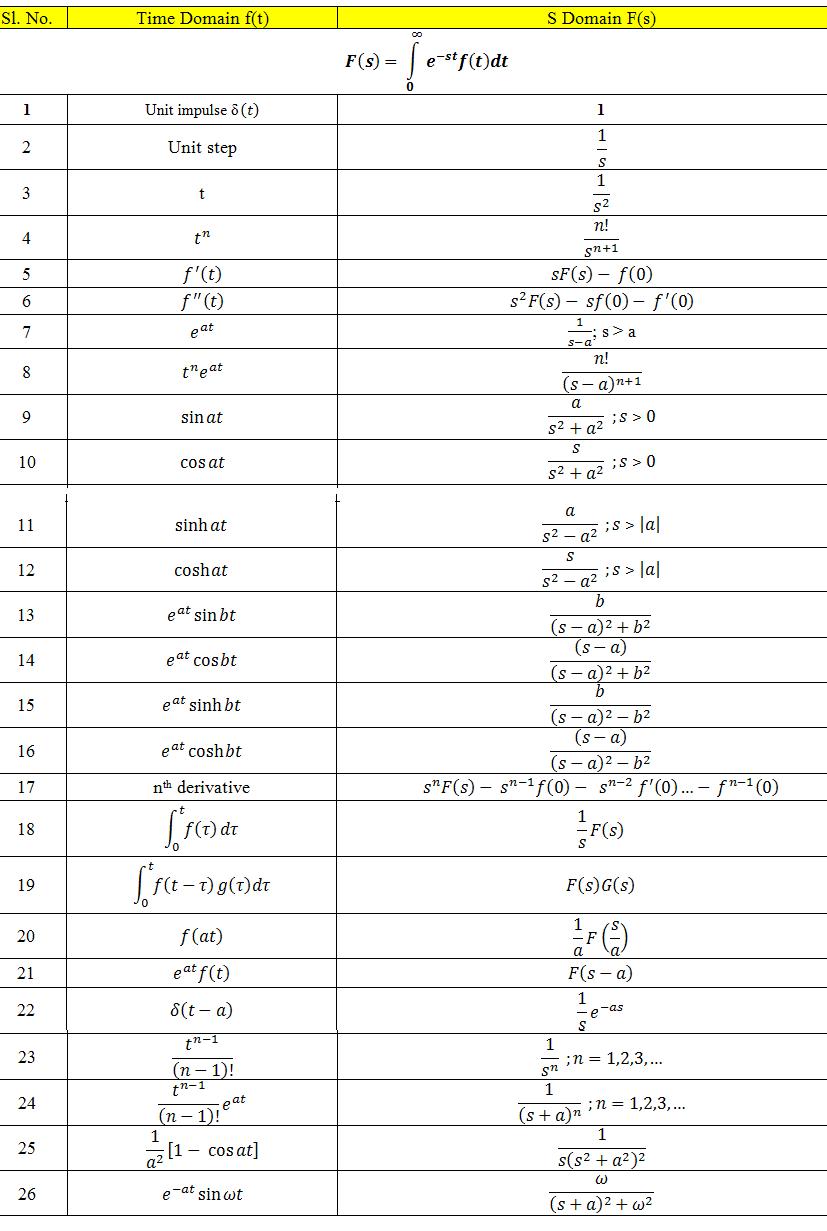 Найти изображение оригинала, заданного
графически:
Найти изображение оригинала, заданного
графически:
6. Решить систему
Вариант 12.
1. Найти изображение функции:
2. Решить задачу Коши операторным методом:
3. Найти все значения корней
а) ;
б)
4. Представить в алгебраической форме:
а) ; б)
5. Восстановить оригинал по изображению
6. Решить систему
Вариант 13.
1. Восстановить оригинал по изображению:
2. Решить задачу Коши операторным методом:
.
3. Найти все значения корней
а) ;
б)
4. Представить в алгебраической форме:
а) ; б)
5. Найти изображение оригинала, заданного графически:
6. Решить систему
Вариант 14.
1. Найти изображение функции:
2. Решить задачу Коши операторным методом:
3. Найти все значения корней
а) ;
б)
4.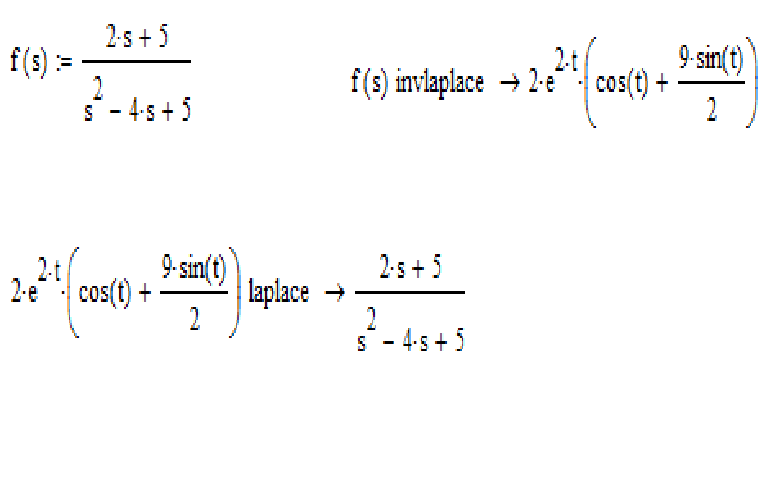 Представить в алгебраической форме:
Представить в алгебраической форме:
а) ; б)
5. Восстановить оригинал по изображению
6. Решить систему
Вариант 15.
1. Восстановить оригинал по изображению
2. Решить задачу Коши операторным методом:
3. Найти все значения корней
а) ;
б)
4. Представить в алгебраической форме:
а) ; б)
5. Найти изображение оригинала, заданного графически:
6. Решить систему
Вариант 16.
1. Найти изображение функции:
2. Решить задачу Коши операторным методом:
3. Найти все значения корней
а) ;
б)
4. Представить в алгебраической форме:
а) ; б)
5. Восстановить оригинал по изображению
6. Решить систему
Оглавление.
Введение.
Комплексные числа.

Преобразование Лапласа. Оригинал и изображение.
Нахождение оригинала по изображению.
Решение линейных дифференциальных уравнений и систем.
Применение методов операционного исчисления в задачах электротехники.
Пример контрольной работы по операционному исчислению и комплексным числам.
Литература.
Литература.
Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М.: Наука, 1981, 448с.
Сборник задач по математике для втузов. Ч.З. Под ред. А.В. Ефимова, А.С. Поспелова. М.: издательства физико-математической литературы, 2002. 576с.
Краснов М.Л., Киселев А.Н., Макаренко Г.Н. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. М.: Наука, 1981. 304с.
Глатенок И.
 В., Заварзина И.Ф. Теория
функций комплексного переменного и
операционное исчисление. М.: Московский
энергетический институт, 1989. 48с.
В., Заварзина И.Ф. Теория
функций комплексного переменного и
операционное исчисление. М.: Московский
энергетический институт, 1989. 48с.
31
Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа
Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа
ОглавлениеПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮГЛАВА 1. РЯДЫ ФУРЬЕ И ИНТЕГРАЛ ФУРЬЕ § 2. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi § 3. КОМПЛЕКСНАЯ ФОРМА РЯДА ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ § 5. РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ С ПЕРИОДОМ 2pi § 6. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИИ С ЛЮБЫМ ПЕРИОДОМ § 7. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ И ЕГО РЕШЕНИЕ МЕТОДОМ ФУРЬЕ § 8. ИНТЕГРАЛ ФУРЬЕ § 9. КОМПЛЕКСНАЯ ФОРМА ИНТЕГРАЛА ФУРЬЕ § 10. ИНТЕГРАЛ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ § 11. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ § 12. МИНИМАЛЬНОЕ СВОЙСТВО КОЭФФИЦИЕНТОВ ФУРЬЕ ГЛАВА II. ОСНОВЫ ТЕОРИИ ПОЛЯ § 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОЙ АЛГЕБРЫ § 2. ВЕКТОРНЫЕ ФУНКЦИИ СКАЛЯРНОГО ПЕРЕМЕННОГО § 3. СОПРОВОЖДАЮЩИЙ ТРЕХГРАННИК ПРОСТРАНСТВЕННОЙ КРИВОЙ § 4. СКАЛЯРНОЕ ПОЛЕ. ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ § 5. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ § 6. ВЕКТОРНОЕ ПОЛЕ § 7.  ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ§ 8. ФОРМУЛА ОСТРОГРАДСКОГО § 9 ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ § 10. ФОРМУЛА СТОКСА § 11. ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ СТОКСА. ВИХРЬ ВЕКТОРНОГО ПОЛЯ § 12. ОПЕРАЦИИ ВТОРОГО ПОРЯДКА § 13. СИМВОЛИКА ГАМИЛЬТОНА § 14. ВЕКТОРНЫЕ ОПЕРАЦИИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ ГЛАВА III. НАЧАЛЬНЫЕ СВЕДЕНИЯ ОБ АНАЛИТИЧЕСКИХ ФУНКЦИЯХ § 1. КОМПЛЕКСНЫЕ ЧИСЛА § 2. РЯДЫ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ § 3. СТЕПЕННЫЕ РЯДЫ § 4. ПОКАЗАТЕЛЬНЫЕ, ГИПЕРБОЛИЧЕСКИЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО § 5. НЕКОТОРЫЕ МНОГОЗНАЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО § 6. ПРОИЗВОДНАЯ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО § 7. АНАЛИТИЧЕСКИЕ И ГАРМОНИЧЕСКИЕ ФУНКЦИИ § 8. ИНТЕГРАЛ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО § 9. ОСНОВНАЯ ТЕОРЕМА КОШИ § 10. ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ § 11. ИНТЕГРАЛ ТИПА КОШИ § 12. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ ОТ АНАЛИТИЧЕСКОЙ ФУНКЦИИ § 13. ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ § 14.  РЯД ТЕЙЛОРА РЯД ТЕЙЛОРА§ 15. РЯД ЛОРАНА § 16. ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ АНАЛИТИЧЕСКОЙ ФУНКЦИИ § 17. ВЫЧЕТЫ § 18. ПРИНЦИП АРГУМЕНТА § 19. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ Отображение, конформное в данной точке § 20. КОНФОРМНЫЕ ОТОБРАЖЕНИЯ ОБЛАСТЕЙ Конформное отображение области на область Линейные преобразования Конформные отображения односвязных областей ГЛАВА IV. О НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЯХ § 1. ГАММА-ФУНКЦИЯ § 2. БЕССЕЛЕВЫ ФУНКЦИИ С ЛЮБЫМ ИНДЕКСОМ § 3. ФОРМУЛЫ ПРИВЕДЕНИЯ ДЛЯ БЕССЕЛЕВЫХ ФУНКЦИЙ § 4. БЕССЕЛЕВЫ ФУНКЦИИ С ПОЛУЦЕЛЫМ ИНДЕКСОМ § 5. ИНТЕГРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ § 6. АСИМПТОТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ ДЛЯ БОЛЬШИХ ЗНАЧЕНИЙ АРГУМЕНТА § 7. ИНТЕГРАЛЬНЫЙ ЛОГАРИФМ, ИНТЕГРАЛЬНЫЙ СИНУС, ИНТЕГРАЛЬНЫЙ КОСИНУС ГЛАВА V. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА § 2. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА § 3. ПРОСТЕЙШИЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА § 4. СВЕРТКА ФУНКЦИЙ § 5. 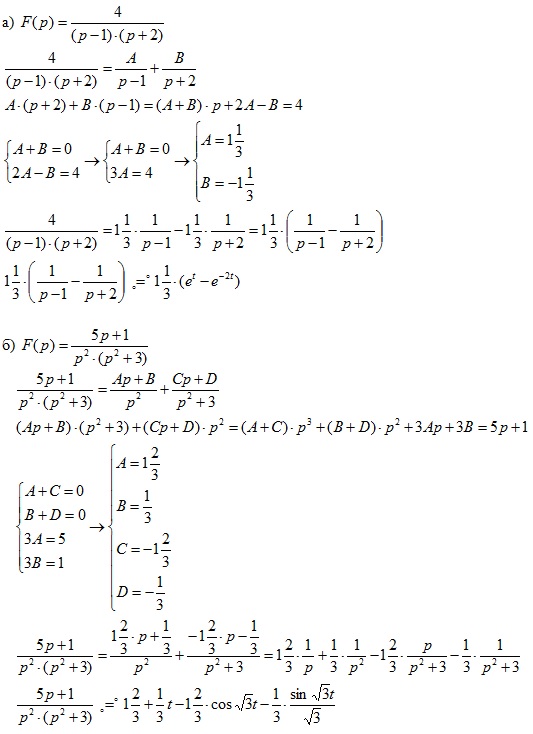 ОРИГИНАЛЫ С РАЦИОНАЛЬНЫМИ ИЗОБРАЖЕНИЯМИ ОРИГИНАЛЫ С РАЦИОНАЛЬНЫМИ ИЗОБРАЖЕНИЯМИ§ 6. ПРИЛОЖЕНИЯ К РЕШЕНИЮ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ И СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ § 7. ПРИЛОЖЕНИЕ К РЕШЕНИЮ ЛИНЕЙНЫХ УРАВНЕНИЙ В КОНЕЧНЫХ РАЗНОСТЯХ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ § 8. ОРИГИНАЛЫ С ИЗОБРАЖЕНИЯМИ, РЕГУЛЯРНЫМИ В БЕСКОНЕЧНОСТИ § 9. ИЗОБРАЖЕНИЯ НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЙ 2. Изображения функций, связанных с интегралом вероятностей 3. Изображения интегрального синуса и интегрального косинуса 4. Изображения интегралов Френеля § 10. ФОРМУЛЫ ОБРАЩЕНИЯ § 11. ДОСТАТОЧНОЕ УСЛОВИЕ ДЛЯ ТОГО, ЧТОБЫ АНАЛИТИЧЕСКАЯ ФУНКЦИЯ БЫЛА ИЗОБРАЖЕНИЕМ |
Лучшие инструменты обратного поиска изображений для поиска оригинальных источников
Когда вы найдете изображение в Google или на веб-сайте социальной сети, вы можете почувствовать необходимость сохранить копию. Существует так много веб-сайтов и ресурсов, что поиск исходного источника изображения может занять целую вечность. Но как насчет поиска альтернативных размеров, обрезанных миниатюр и других веб-сайтов, использующих это же изображение? Обратный поиск изображений вам в помощь!
Существует так много веб-сайтов и ресурсов, что поиск исходного источника изображения может занять целую вечность. Но как насчет поиска альтернативных размеров, обрезанных миниатюр и других веб-сайтов, использующих это же изображение? Обратный поиск изображений вам в помощь!
Концепция обратного поиска изображений довольно проста: вы загружаете изображение или вставляете прямой URL-адрес изображения в Интернете, и поисковая система сопоставляет формы/шаблоны, чтобы найти копии этого изображения. При достаточном терпении вы часто можете найти первоисточник, который также, вероятно, имеет самые большие размеры.
Конечно, существует множество инструментов для обычного поиска изображений по тексту. Но поиск изображений на основе изображений постепенно набирает популярность.
Я хочу представить небольшую коллекцию веб-приложений, которые вы, вероятно, сможете использовать для поиска изображений. Стоит добавить эти ссылки в закладки или сохранить их в другом месте на случай, если вы забудете гиперссылку. В настоящее время я использую эти инструменты почти постоянно. Если вам часто нужно реконструировать источник изображений, тогда эти поисковые системы станут для вас второй натурой.
В настоящее время я использую эти инструменты почти постоянно. Если вам часто нужно реконструировать источник изображений, тогда эти поисковые системы станут для вас второй натурой.
TinEye
Сначала у нас есть TinEye, продукт Idée. Обычно это мой первый ресурс, потому что у него отличный интерфейс и каталогизировано огромное количество изображений. TinEye в основном сканирует веб-сайты, написанные на английском языке, поэтому пропускает веб-сайты на восточных языках.
Но это действительно бесценный инструмент для обратного просмотра изображений. Вы можете либо загрузить изображение, либо скопировать/вставить URL-адрес изображения, чтобы найти дубликаты в другом месте. Страница результатов включает размеры изображения и URL-адрес прямого источника, по которому его можно найти. Сервис бесплатный для анонимного использования, но вы также можете зарегистрировать личный кабинет.
Кроме того, существует API-интерфейс онлайн-разработчика для доступа к их функциям на серверной части.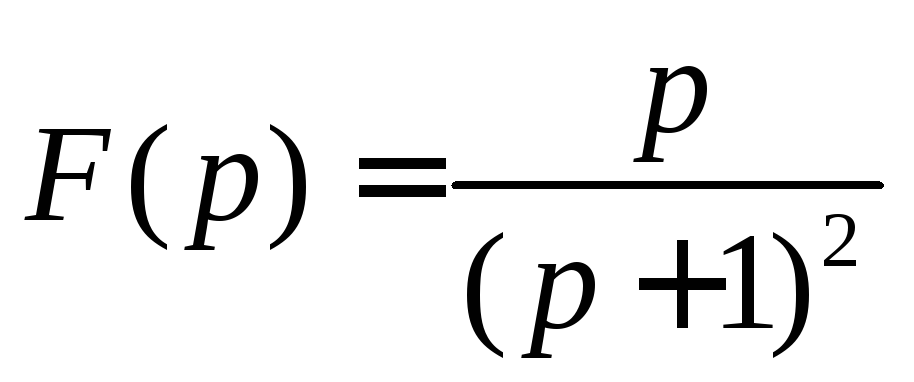 Любой, кто хочет интегрировать поиск TinEye на свой веб-сайт, может сгенерировать ключ API и приступить к работе. Это, пожалуй, самый простой инструмент для поиска изображений, который вы найдете. Я взволнован мыслью о том, где этот продукт может быть еще через 3-5 лет.
Любой, кто хочет интегрировать поиск TinEye на свой веб-сайт, может сгенерировать ключ API и приступить к работе. Это, пожалуй, самый простой инструмент для поиска изображений, который вы найдете. Я взволнован мыслью о том, где этот продукт может быть еще через 3-5 лет.
Google Reverse Images
Практически каждый, кто использует поиск Google, также знает о поиске изображений. Вы можете ввести ключевые слова, и Google выдаст большую галерею связанных фотографий со всего Интернета. Но знаете ли вы, что поиск изображений Google также может выполнять обратный поиск на основе любого изображения?
Сначала перейдите на http://images.google.com/ и найдите крошечный значок камеры в строке поиска (обычно рядом с микрофоном). Если вы наведете курсор на этот значок, появится всплывающая подсказка с надписью «Поиск по изображению». Нажмите, и поле ввода изменится, запрашивая прямой URL-адрес изображения. В качестве альтернативы вы можете нажать «Загрузить изображение», чтобы загрузить свое собственное.
На самом деле я считаю результаты поиска Google более полезными, чем TinEye. Очевидно, что Google имеет более мощные алгоритмы индексации и, таким образом, возвращает гораздо больше информации для любого типичного поиска. Вы также можете проверить размеры изображения на странице результатов вместе с внешним URL-адресом веб-сайта. Между Google и TinEye вы сможете найти источники с разных веб-сайтов.
А как насчет восточноязычных сайтов, о которых я упоминал ранее? Китайские или японские веб-сайты, такие как niconico, не могут быть проиндексированы этими поисковыми роботами. Вместо этого у нас есть еще одно отличное веб-приложение для обработки изображений на иностранном языке.
SauceNAO
Несмотря на то, что домашняя страница немного пресная, SauceNAO — лучший ресурс для поиска внешних изображений, когда от TinEye или Google ничего не приходит. SauceNAO создан для распознавания символов, отличных от латинского алфавита, и сканирования веб-сайтов на этих языках. Это веб-приложение незаменимо, когда дело доходит до поиска тех хитрых изображений, которые, кажется, не имеют альтернативных результатов.
Это веб-приложение незаменимо, когда дело доходит до поиска тех хитрых изображений, которые, кажется, не имеют альтернативных результатов.
Если вам нужны надстройки для браузера, они доступны для Google Chrome и Firefox. Они оба бесплатны для установки и предоставляют дополнительные функции, встроенные прямо в ваш веб-браузер. Я не использую SauceNAO более пары месяцев, но он быстро вошел в мой список рекомендуемых веб-приложений.
Функциональность поиска построена поверх IQDB, которая очень похожа на обратный поиск изображения. Их дизайн гораздо более простой, и в нем нет всех дополнительных вещей, которые вы заметите на странице результатов. Но полезно знать о других решениях, которые существуют.
RevIMG
Последняя система поиска изображений, о которой я хочу упомянуть, это RevIMG. Этот более уникален, потому что вы фактически указываете часть изображения для поиска. Например, вы можете загрузить коллаж из значков и обрезать его, чтобы найти только один значок в надежде найти другой дубликат в Интернете.
Дизайн немного похож на SauceNAO, но алгоритмы совсем другие. Веб-мастерам разрешено отправлять свои веб-сайты в базу данных для сканирования. Это может помочь быстрее индексировать ваши собственные изображения и ранжировать их в других поисковых системах с обратным поиском изображений. Вы можете прочитать немного больше о том, как работает RevIMG и связанных с ними ресурсах.
Примечательно, что на их веб-сайте также есть API на основе JavaScript, который можно использовать во внешних проектах. Это скорее поисковая система с подстановочными знаками, популярность которой растет, но она не может конкурировать с TinEye (пока).
Я очень надеюсь, что эти веб-приложения могут принести некоторую пользу веб-мастерам и пользователям Интернета. Я часто ловлю себя на обратном поиске, чтобы найти источник множества разных изображений. Иногда вы не можете найти никаких результатов, потому что исходный источник был удален или веб-сайт по какой-то причине просто отключился. Это довольно распространено, и это еще одна причина, по которой нам нужен онлайн-архив, сохраняющий эти URL-адреса в базе данных.
Это довольно распространено, и это еще одна причина, по которой нам нужен онлайн-архив, сохраняющий эти URL-адреса в базе данных.
Но технология есть, и она работает. Это работает чертовски хорошо, если я сам так говорю. Я часто задаюсь вопросом, насколько эти поисковые системы изображений изменятся в течение нескольких лет. Но как существующий ресурс я не мог жить без этих практичных и удобных инструментов поиска изображений.
избранный источник изображения
Автор: Хайме Моррисон
Джейме — младший. дизайнер, заинтересованный в исследованиях мобильного UI/UX и веб-разработке внешнего интерфейса с помощью фреймворков JavaScript. Он освещает общие новости и полезные ресурсы в области веб-дизайна.
6 лучших инструментов обратного поиска изображений для поиска исходного кода
Анкуш Дас в Цифровой маркетинг | Последнее обновление: 14 марта 2023 г.
Поделись на:
Сканер безопасности веб-приложений Invicti — единственное решение, обеспечивающее автоматическую проверку уязвимостей с помощью Proof-Based Scanning™.
В Интернете миллиарды изображений. Как вы проверяете их происхождение, если хотите использовать некоторые из них для своей личной или коммерческой работы?
Изображения, которые вы найдете при поиске в Google, могут быть дублированы, украденными произведениями искусства, манипулированными медиафайлами и т. д. Можете ли вы самостоятельно попытаться найти его происхождение или проверить, является ли это оригинальным изображением? Или вам нужен профессионал, который сделает это за вас?
Если вы говорите о громких юридических вопросах авторского права и другой беготне, вам наверняка понадобится помощь профессионала. Но для повседневного использования вы можете легко воспользоваться инструментом обратного поиска изображений.
Что такое обратный поиск изображения?
Обратный поиск изображения — это метод поиска источника (или других источников), из которого возникло конкретное изображение.
Если вам интересно узнать об изображении на вашем устройстве, вы можете легко использовать некоторые из инструментов, доступных для обратного поиска изображения, и найти дополнительную информацию о нем.
Некоторые варианты использования инструментов обратного поиска изображений:
- Чтобы проверить, не использует ли кто-то вашу защищенную авторским правом работу без разрешения
- Для идентификации человека или получения контактной информации в Интернете
- Для проверки подлинности изображения
- Узнать источник изображения
- Для выявления фейковых новостей
Вы можете выполнить обратный поиск изображения на своем iPhone или Android-смартфоне. Все, что вам нужно сделать, это получить доступ к веб-браузеру (компьютерному или мобильному) и загрузить изображение.
Преимущества инструмента обратного поиска изображений 👍
Инструменты обратного поиска изображений имеют ряд замечательных преимуществ.
- Проверить подлинность изображения можно бесплатно
- Экономьте время за счет ручной проверки изображения на вашем устройстве или в чьем-то профиле в социальной сети.
- Найдите бесплатные изображения, которые вы можете использовать в своей работе
- Найдите место или поселок на давно забытой фотографии на вашем чердаке
- Узнать информацию о неизвестных объектах или немаркированных продуктах
Все это, и вам не нужно тратить на это ни копейки. Я думаю, что одним из наиболее ценных преимуществ инструмента обратного поиска изображений является возможность определить, использует ли кто-то еще ваше изображение или иллюстрацию.
Я думаю, что одним из наиболее ценных преимуществ инструмента обратного поиска изображений является возможность определить, использует ли кто-то еще ваше изображение или иллюстрацию.
Кража изображений — обычное дело, и предотвратить ее часто невозможно. Следовательно, инструмент, чтобы узнать об изображении, пригодится для такой работы.
Давайте взглянем на некоторые из лучших инструментов обратного поиска изображений.
Примечание: Обычно сервисы не сохраняют ваши данные с обратным поиском по картинкам. Но, если вы ищете что-то конфиденциальное, вы можете ознакомиться с их политикой конфиденциальности, прежде чем продолжить.
TinEye
TinEye — одна из самых ценных опций, которую вы можете добавить в Chrome для быстрого поиска.
Вам нужно будет загрузить изображение или вставить URL-адрес изображения, чтобы получить дополнительную информацию с помощью TinEye. Хотя это бесплатно для начала, они предлагают корпоративные / корпоративные предложения для автоматизации отслеживания изображений и предупреждения вас, если ваше изображение используется без разрешения.
В отличие от обычного инструмента поиска изображений, он фокусируется на различных аспектах распознавания изображений и компьютерного зрения. Таким образом, вы можете интегрировать другие продукты для проверки изображений или их аутентификации во время поиска.
Обратный поиск изображений
Обратный поиск изображений сам по себе не является системой поиска изображений, но он позволяет загружать фотографии, а затем дает возможность выбирать из различных порталов обратного поиска изображений (Яндекс, Google и Bing).
Если вам нужен универсальный магазин для быстрого поиска изображения в Интернете, это может вам помочь.
Pixsy
Pixsy — интересный инструмент обратного поиска изображений, для бесплатного доступа к которому требуется регистрация.
Он позволяет импортировать изображения из различных источников, включая платформы социальных сетей и облачные сервисы хранения, что может пригодиться. Вы также можете напрямую загрузить фотографии со своего компьютера, чтобы выполнить поиск.
Подобно TinEye, Pixsy также предлагает корпоративные/бизнес-планы, позволяющие автоматизировать отслеживание и получать юридическую помощь в случае нарушения авторских прав.
Картины Google
Поиск картинок Google — самый эффективный инструмент обратного поиска, который вы можете использовать на своем рабочем столе. У них есть миллиарды изображений с миллионов веб-страниц для перечисления.
Итак, если вы не можете найти совпадение для своего изображения с помощью других инструментов, лучше всего подойдет Google Images. Вам не нужно регистрироваться для доступа к сервису, и вы можете загрузить изображение или вставить URL-адрес изображения.
В отличие от некоторых других инструментов поиска, даже если нет точных совпадений с загруженным вами изображением, вы получите множество похожих (или тематических) предложений.
Обратите внимание, что вы не сможете загружать или вставлять URL-адреса изображений при использовании мобильного браузера. Чтобы получить возможность, вам нужно запросить сайт рабочего стола из меню вашего браузера. Google может рассмотреть возможность оптимизации веб-сайта для мобильных пользователей.
Чтобы получить возможность, вам нужно запросить сайт рабочего стола из меню вашего браузера. Google может рассмотреть возможность оптимизации веб-сайта для мобильных пользователей.
Визуальный поиск Bing
Портал поиска изображений Bing не уступает Google Images. Он также предлагает «текстовый режим», в котором вы можете выбрать любой фрагмент текста на изображении, которое вы загрузили для поиска, чтобы точно определить любые результаты обратного поиска изображения.
Конечно, вы также можете попробовать преобразовать изображения в текст, но это может быть удобно.
В текстовом режиме вы получаете дополнительные преимущества, позволяющие быстро находить ориентиры, объекты и многое другое. Итак, стоит попробовать!
Поиск изображений Yahoo
Yahoo Image Search не поддерживает загрузку изображений. Таким образом, это не самый эффективный инструмент обратного поиска изображений. Однако вы можете использовать метаданные или имя файла исходного изображения для сканирования базы данных, чтобы увидеть, соответствует ли оно чему-то идентичному.


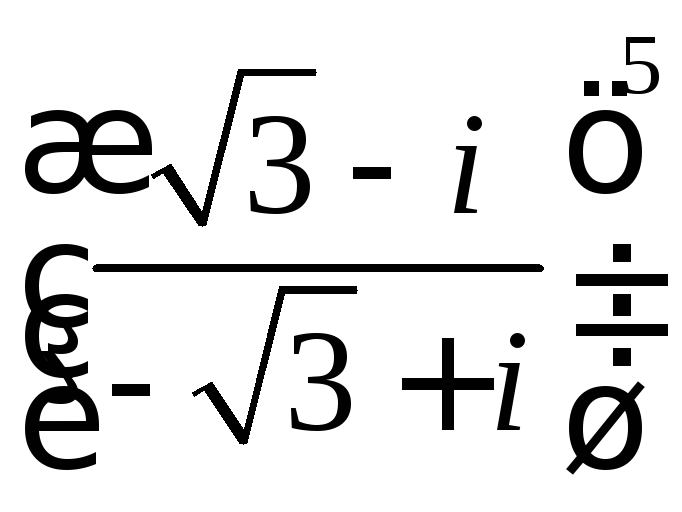
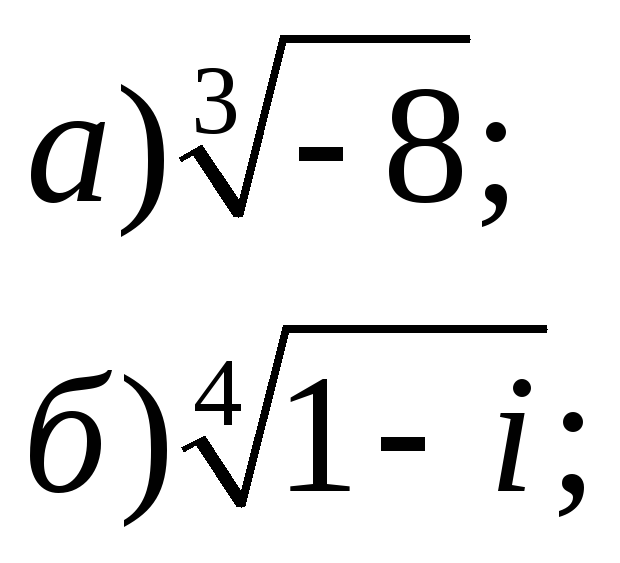 В., Заварзина И.Ф. Теория
функций комплексного переменного и
операционное исчисление. М.: Московский
энергетический институт, 1989. 48с.
В., Заварзина И.Ф. Теория
функций комплексного переменного и
операционное исчисление. М.: Московский
энергетический институт, 1989. 48с.