Урок 33. круг. окружность (центр, радиус, диаметр) — Математика — 3 класс
Математика, 3 класс
Урок №33. Круг. Окружность (центр, радиус, диаметр)
Перечень вопросов, рассматриваемых в теме:
— что такое окружность и круг?
— какие элементы имеет окружность?
— чем отличается круг от окружности?
Глоссарий по теме:
Окружность — это замкнутая кривая, все точки которой одинаково удалены от центра.
Круг – это геометрическая фигура, которая ограничена окружностью.
Радиус- это отрезок, соединяющий центр окружности с любой точкой на окружности.
Диаметр – отрезок, который соединяет две точки окружности, проходящий через центр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. с. 94-96.
2. Рудницкая В. Н. Тесты по тматематике:3 класс.
3. Рудницкая В.Н. Контрольные работы по математике:3 класс. М.: Издательство»Экзамен», 2017, с. 49-54.
4. Рудницкая В. Н. КИМ ВПР. Математика .3 класс. М.: Издательство «Экзамен», 2018, с. 77-79.
Теоретический материал для самостоятельного изучения
С незапамятных времен люди используют в своей жизни круг.
1. Около 3300 года до нашей эры стали применять гончарный круг, делать круглую посуду – тарелки, вазы, кастрюли, горшки, сковородки. У посуды есть окружность (верхний край) и круг (дно).
2. Мы не можем представить свою жизнь без машин: автобус, велосипед, швейная, машинки, самолет, луноход, различные станки, подъемный кран…Они не похожи друг на друга, но присмотримся к ним повнимательнее. Есть у них у всех похожие части – детали, и одна из них – колесо. Сначала колеса были круглые и гладкие, чтобы по земле легко катились, а потом человек придумал много разных колес.
3. Круг и окружность широко применяются в архитектуре и искусстве: круглые арки, своды, купола.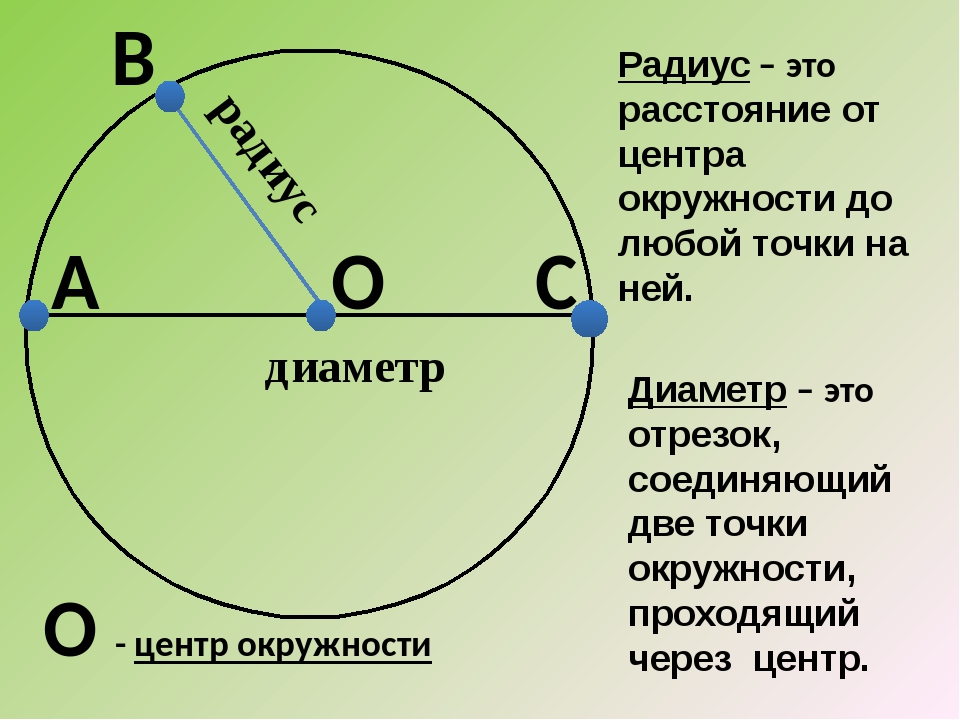 Круг – это форма кочевых шатров и поселений. Еще древние греки обнаружили, что с помощью циркуля и линейки можно построить множество фигур, включая шестиугольники, квадраты и другие правильные многоугольники, и создавать волшебные узоры.
Круг – это форма кочевых шатров и поселений. Еще древние греки обнаружили, что с помощью циркуля и линейки можно построить множество фигур, включая шестиугольники, квадраты и другие правильные многоугольники, и создавать волшебные узоры.
4. Необозрима сфера применения круга в математике: тригонометрический круг, круги Эйлера, задачи на построение, круговые диаграммы и т.д. Многие приборы имеют круглую шкалу, в математике таким прибором является транспортир .
5. Картинки с волшебными кругами люди используют в медицинских целях, когда на них смотришь, кажется, что они двигаются. Если смотреть на них несколько минут, то проходит головная боль.
6. Также человек использует круг, как универсальный символ, означающий целостность, непрерывность, первоначальное совершенство. Три концентрических круга символизируют прошлое, настоящее и будущее; три сферы земли: землю, воздух и воду.
Круг в жизни человека имеет очень важную роль, и без использования круглых предметов обойтись невозможно.
Окружность и круг – удивительно гармоничные, совершенные, простые фигуры. Окружность – единственная замкнутая кривая, которая может “скользить сама по себе”, вращаясь вокруг центра, поэтому колеса делают круглыми, а не квадратными или треугольными.
Круг – это колесо. Колесо – это прогресс – движение вперед. Если остановится колесо, то остановится колесо Истории. Остановятся все виды транспорта, остановятся все часы и механизмы, фабрики и заводы.
Круг – символ цикличности, повторяемости. Все движется по кругу.
Круг дает ощущение взаимосвязи с Космосом.
Сама природа выбирает эту удобную и компактную форму как шар и круг.
Сравним две фигуры.
На 1 рисунке видим замкнутую кривую линию, на которой находятся точки К и С на одинаковых расстояниях от точки О.Такая замкнутая кривая называется окружностью. Точка О — центр окружности. Все точки, поставленные на окружности, находятся на одинаковом расстоянии от центра!
Есть специальный инструмент, который позволяет чертить окружности – это циркуль.
На рисунке 2 видим геометрическую фигуру, которая ограничена окружностью. Эта фигура называется круг.
Вывод: окружность — граница круга; круг — часть внутри окружности. В таблице указаны отличительные признаки круга и окружности:
Если соединить любую точку окружности с ее центром, то получится отрезок, который называется радиусом.
Если соединить 2 точки окружности, проходящих через центр, получится отрезок, который называется диаметром.
Диаметр делит круг на две равные части и все диаметры у окружности равной длины.
Задания тренировочного модуля:
1. Длина радиуса составляет 6 см. Чему равен диаметр окружности?
6см; 12 см; 3см.
Правильный ответ: 12см.
2. Заполните таблицу
радиус | 4 см | 3 см | 7 дм | 5 дм |
диаметр |
Правильный ответ:
радиус | 4 см | 3 см | 7 дм | 5 дм |
диаметр | 8 см | 6 см | 14 дм | 10 дм |
Радиус окружности — что такое, формула, как найти ⚪
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.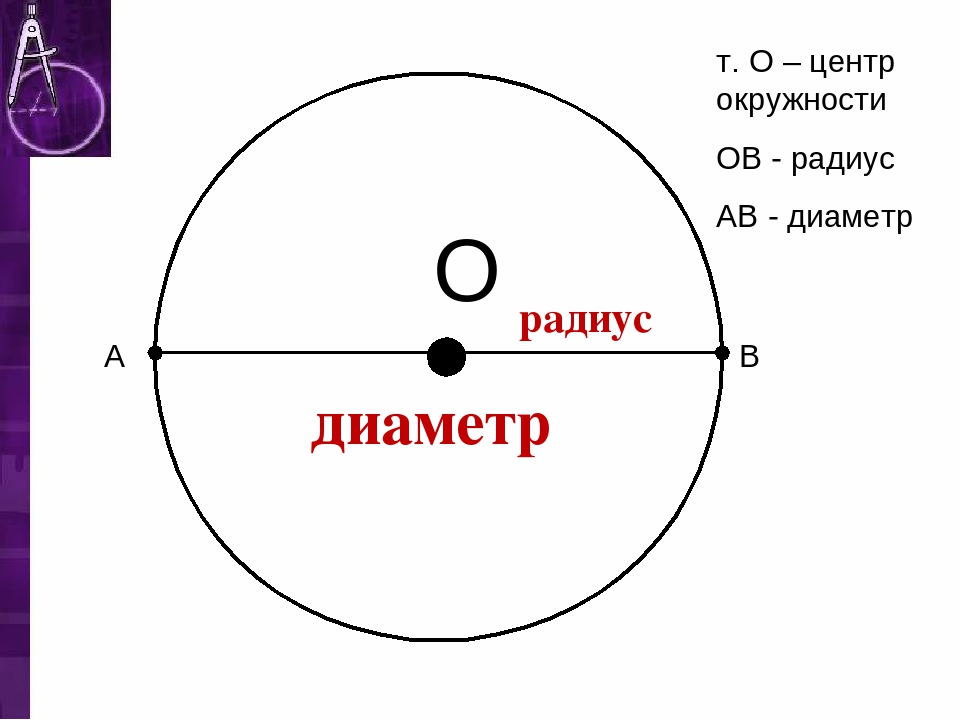
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать — как найти длину окружности?
Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.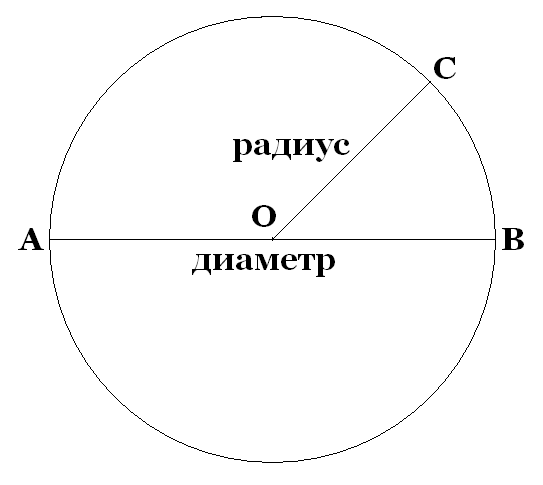
Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a2 + b2, где a, b — стороны вписанного прямоугольника.
Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
История №1005081 Знаете ли вы, что такое диаметр/радиус? Супружеская жизнь.…
Знаете ли вы, что такое диаметр/радиус? Супружеская жизнь.
Работаю за металлорежущим станком. В свое время решил поменять род деятельности и был с нуля обучен на производстве на оператора ЧПУ. Позже уже сам обучал основам других ребят. Однажды, во время объяснения одному из стажёров, заметил, что он как-то не очень воспринимает, что я ему пытаюсь втолковать:
— Ты понимаешь? Ты ж знаешь что мерили мы диаметр, а в таблицу записываем радиус? Знаешь что такое радиус?
— Нет, не знаю.
— В смысле не знаешь? Что такое диаметр же понимаешь?
— Нет.
Неожиданно? Не верится? А ведь стажёр был даже не вчерашний школьник, а выпускник Башкирского строительного колледжа по специальности промышленное и гражданское строительство!!! Позже я вспомнил, что и при моем обучение на заводе наставники мне задавали этот вопрос и тогда он показался мне глупым: «как так не знать взрослому, что такое радиус? Да это ж одна из основ всего и вся!»
«Ну наверное парень просто определений не знает <<по-учебнику>>» — подумал я и нарисовал на бумаге окружность:
— Нарисуй, где здесь радиус, где диаметр.
Стажёр рисует внутри моей окружности ещё две.
Проходив под впечатлением от открывшей мне правды весь день, лежу ночью в постели. Размышляю: в какой момент человек узнает что такое радиус/диаметр ( имеется ввиду <<не по учебнику, а своими словами>>; в бытовом смысле когда человек начинает понимать, что вот окружность, а вот тут ее радиус). И каким «типом мышления» обладать, чтобы это понимать? Обязательно математико-техническим? Ну это выяснить легко:
— Жена, просыпайся. Ты знаешь что такое радиус? Диаметр? — супруга-то у меня не технарь ни разу, а филолог-журналист.
— Ты сдурел что ли? Какой радиус, какой диаметр — час ночи! Что случилось?
— Да вот… долго объяснять. Можешь своими словами сказать, что такое радиус?
— Размер круга. Да что случилось-то? Ты что там ночью в постели меряешь?…
То есть всё-таки это не сакральные какие-то знания, хранимые от посторонних. И «не технарь», спокойно окончивший школу и с геометрией, кроме как в бытовом плане, не сталкивающийся, может в час ночи сквозь сон дать ответ, где копать, чтоб найти определение «радиуса».
Вечером следующего дня я решил выяснить, а с какого возраста человек узнает, что есть такой термин «радиус» и спросил у дочери-второкласницы («ну во втором то классе ещё вряд ли проходят, — подумал я — будет понятно, обязательно ли учиться в школе или достаточно просто по жизни внимательно смотреть по сторонам, чтобы узнать):
— Ты знаешь, что такое радиус? Или диаметр?
— Это в круге, вот точка такая, центральная, и там расстояние до линии…. — немного смутившись отвечает.
То есть ребенок во втором классе уже знает! Но… Что-то больно похоже на определение из учебника… Неужели всё-таки в школе уже проходили?
— А откуда ты знаешь? Вы уже в школе проходили?
— Нет, — улыбается — мне мама утром сказала, что ты меня обязательно спросишь сегодня и надо выучить.
+1428–
Тема: «Радиус и диаметр» Цели: Метапредметные задачи Методы и приемы организации деятельности учащихся:
МЕТОДИЧЕСКИЕ РАЗРАБОТКИ УРОКОВ
МЕТОДИЧЕСКИЕ РАЗРАБОТКИ УРОКОВ Развёрнутый план урока по теме «Замена двузначного числа суммой разрядных слагаемых» ТЕМА: «Замена двузначного числа суммой разрядных слагаемых» (ч. 1: с. 15) ЦЕЛЕВЫЕ УСТАНОВКИ:
1: с. 15) ЦЕЛЕВЫЕ УСТАНОВКИ:
Вершинина Анна Владимировна
МБОУ «СОШ 76» Урок математики ( 27) Сложение и вычитание в пределах 100. Образовательная программа: Материально-техническое обеспечение: Тип урока: Цель: Задачи: Формируемые УУД: Вершинина Анна Владимировна
ПодробнееТехнологическая карта урока
Технологическая карта урока Предмет, класс Математика, 5А Автор (ы) УМК Н. Я. Виленкин, М.; Мнемозина, 2012 год ФИО учителя, школа Страшнова Г. А. МОУ СОШ 2 Тема урока Умножение десятичных дробей на натуральные
ПодробнееI. Место предмета в учебном плане
I. Место предмета в учебном плане В Федеральном базисном образовательном плане на изучение математики в каждом классе начальной школы отводится 4 часа в неделю, всего 540 часов. II. Содержание учебного
II. Содержание учебного
Технологическая карта урока математики
АДМИНИСТРАЦИЯ ГОРОДСКОГО ОКРУГА ПОДОЛЬСК КОМИТЕТ ПО ОБРАЗОВАНИЮ Муниципальное общеобразовательное учреждение «Лицей 1» (МОУ «Лицей 1») Технологическая карта урока математики Урок математики в 6 классе
Конспект урока во 2 классе
Конспект урока во 2 классе Тема: Вычитание двузначных чисел с переходом через разряд Цель: Знакомство с приемами вычитания двузначного числа из двузначного с переходом через разряд Задачи: — познакомить
ПодробнееТехнологическая карта урока
Технологическая карта урока Общая часть Предмет Математика Класс, ФИО 1дополнительный класс Тема урока Тип урока Цель Планируемые образовательные результаты ПИСЬМЕННОЕ СЛОЖЕНИЕ ДВУЗНАЧНЫХ ЧИСЕЛ С ПЕРЕХОДОМ
ПодробнееТехнологическая карта урока
Технологическая карта урока Учитель: Кривцовой О.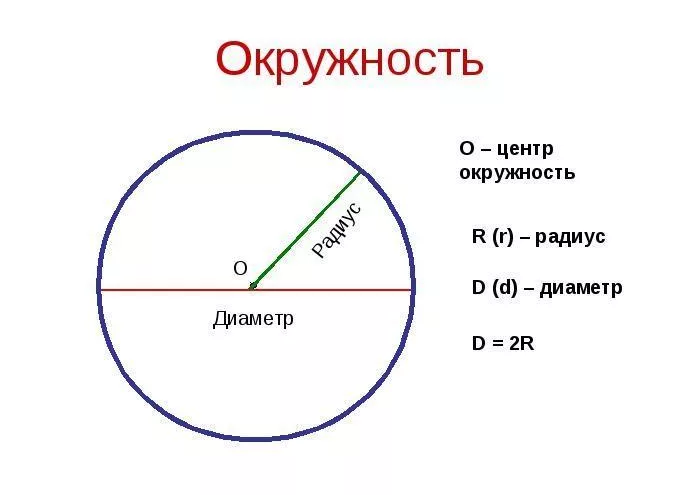 И. Класс: 2 «Б» УМК: «Школа России» Предмет: математика. Тема урока: Периметр прямоугольника. Вычисление периметра. урока: урок открытия новых знаний Место
И. Класс: 2 «Б» УМК: «Школа России» Предмет: математика. Тема урока: Периметр прямоугольника. Вычисление периметра. урока: урок открытия новых знаний Место
Предмет математика класс 2 г
Предмет математика класс 2 г Тема урока Место урока по теме (в разделе/главе) Закрепление изученного по теме «Умножение и деление» «Умножение и деление» 18 из 20 Тип урока Форма урока, форма учебной деятельности,
ПодробнееТехнологическая карта урока
Технологическая карта урока Класс: 8 Предмет: алгебра Тема урока: Погрешность и точность измерения. Дидактическая цель урока: создать условия для восприятия и осознания понятий абсолютная и относительная
ПодробнееI. Место предмета в учебном плане
I. Место предмета в учебном плане Программа составлена в соответствии с требованиями ФГОС начального общего образования и обеспечена УМК «Гармония» для 1 4 классов (автор Н. Б. Истомина). В Федеральном
Б. Истомина). В Федеральном
Технологическая карта урока
Технологическая карта урока Учитель: Класс Предмет: Авторы учебника: Тарасова Екатерина Антоновна 1Г Математика В.Н. Рудницкая, Т.В.Юдачёва (Начальная школа XXI века) Тема урока. Прибавление числа 5. Тип
ПодробнееТехнологическая карта урока
Технологическая карта урока ФИО Попенкова Татьяна Сергеевна КЛАСС 3 УМК «Начальная школа XXI век» ПРЕДМЕТ Математика ТЕМА Умножение многозначного числа на двузначное. ТИП Урок открытия нового знания. ЦЕЛЬ
Подробнее«Числовые и буквенные выражения».
Муниципальное казѐнное общеобразовательное учреждение «Дуровская средняя общеобразовательная школа» Сафоновского района Смоленской области «Числовые и буквенные выражения». Учитель математики I категории
ПодробнееТехнологическая карта урока
Технологическая карта урока Тема урока: «Описание помещения по личным впечатлениям в сочинении повествовательного характера». Класс: 6 Учитель: Филиппова И.С. Тип урока: урок развития речи Цели по содержанию:
Класс: 6 Учитель: Филиппова И.С. Тип урока: урок развития речи Цели по содержанию:
Конспект урока по математике.
Конспект урока по математике. Класс: 1 В, учитель Шелякина Н.А. Тема урока: «Дециметр». Дидактическая цель: создать условия для открытия детьми новых знаний. Тип урока: открытие новых знаний. Задачи урока:
ПодробнееТехнологическая карта урока
г. Рыбинск МОУ гимназия 18 МЦ ОС «Школа 2100» Технологическая карта урока Ф.И.О. учителя: Столовичева Елена Фёдоровна, Будилова Маргарита Валентиновна Предмет: математика Класс: 3А,3Б Тип урока: урок открытия
ПодробнееТехнологическая карта урока 50
Урок математики в 1 Д классе по теме «Решаем задачи» (УМК «Начальная школа XXI век») Учитель: Нигматуллина Татьяна Семеновна, МБОУ «СШ 21», г.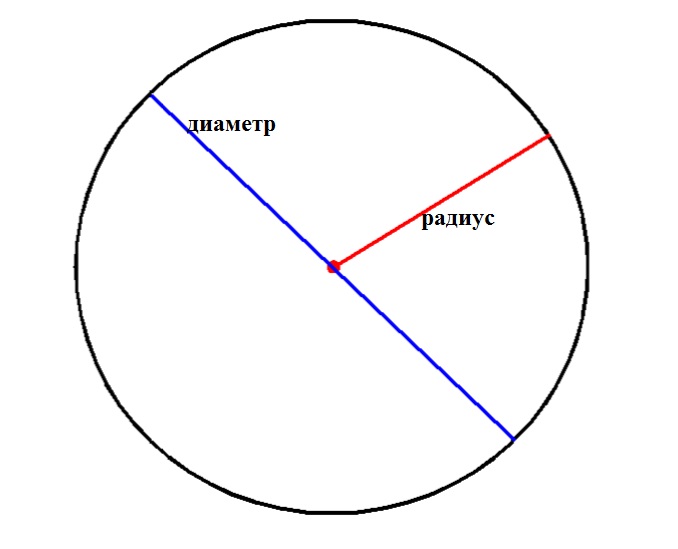 Нижневартовск. Технологическая карта урока 50 Тип урока Тема
Нижневартовск. Технологическая карта урока 50 Тип урока Тема
Технологическая карта урока математики
Технологическая карта урока математики Дата: 16 апреля 2014 года Тема: Проценты Класс: 5 Тип урока: урок изучения нового материала Цели урока: Предметные: научить учащихся находить число по его процентам
ПодробнееАННОТАЦИЯ РАБОЧЕЙ ПРОГРАММЫ
АННОТАЦИЯ РАБОЧЕЙ ПРОГРАММЫ Предмет: Русский язык Класс: 2 Количество часов по учебному плану: всего- 136часов в год (4 часа в неделю) УМК: 1. Авторская программа «Перспективная начальная школа» на основе
Подробнее3 класс. Личностные результаты
3 класс Личностные результаты У учащегося будут сформированы: навыки в проведении самоконтроля и самооценки результатов своей учебной деятельности; основы мотивации учебной деятельности и личностного смысла
ПодробнееТехнологическая карта урока по геометрии
Технологическая карта урока по геометрии Автор: Турукина Светлана Ивановна, учитель математики, МБОУ «СОШ 6» города Обнинска Предмет: Геометрия Класс: 9 класс Тип урока: урок «открытия нового знания» Тема:
Подробнее Урок математики в 1Б классе по программе «Школа России» по теме: «Задачи в два действия».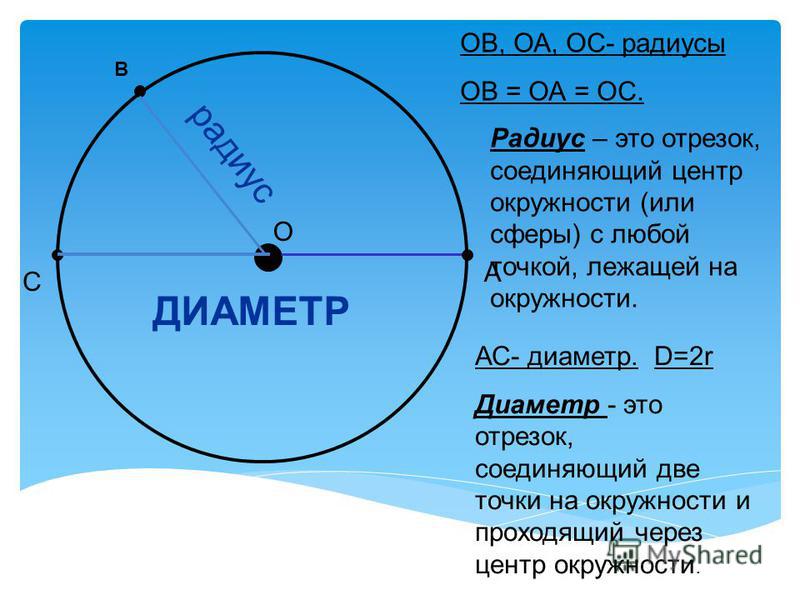 Первый урок в теме, когда дети переходят от решения задач-цепочек к решению задач в два действия. Цели деятельности
Первый урок в теме, когда дети переходят от решения задач-цепочек к решению задач в два действия. Цели деятельности
ПЛАН-КОНСПЕКТ УРОКА 1. ФИО
ПЛАН-КОНСПЕКТ УРОКА Тема: «Сложение чисел с разными знаками» 1. ФИО (полностью) Федосеева Ольга Васильевна 2. Место работы ГБОУ школа-интернат 1 г.о. Чапаевск 3. Должность Учитель математики 4. Предмет
ПодробнееМЕТОДИЧЕСКИЕ РАЗРАБОТКИ УРОКОВ
162 МЕТОДИЧЕСКИЕ РАЗРАБОТКИ УРОКОВ Конспект урока по теме «Решение текстовых задач» Тема: Решение задач на нахождение четвёртого пропорционального (ч. 1: с. 46) Целевые установки: предметные: познакомить
ПодробнееКонспект урока по предмету
Конспект урока по предмету Предмет: МАТЕМАТИКА Уровень образования: СРЕДНИЙ Тема: «ОБЪЁМ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА» Тип урока: ИЗУЧЕНИЕ И ПЕРВИЧНОЕ ЗАКРЕПЛЕНИЕ ЗНАНИЙ И СПОСОБОВ ДЕЯТЕЛЬНОСТИ. Форма
Форма
Технологическая карта урока
Технологическая карта урока Тема урока: «Прямоугольник» Класс: 5 Учитель: Рыжова Лидия Петровна Тип урока: урок «открытия» нового знания Цели по содержанию: обучающие: изучить свойства прямоугольника развивающие:
ПодробнееРабочая программа по математике 2 класс
МБОУ «Кипринская основная общеобразовательная школа» Рабочая программа по математике 2 класс Составитель: учитель нач. классов Пыстогова В. В. 2018 2019 учебный год 1 Пояснительная записка Рабочая программа
ПодробнееПояснительная записка
Пояснительная записка Данный урок является уроком открытия нового знания по теме «Свойства степени с натуральным показателем», расширяющий кругозор учащихся. Урок может быть проведён учителем, работающим
ПодробнееОкружность, круг, секущая и сектор
Окружность и круг — геометрические фигуры, взаимосвязанные между собой. Окружность есть граничная ломаная линия (кривая) круга,
Окружность есть граничная ломаная линия (кривая) круга,
Определение. Окружность — замкнутая кривая, каждая точка которой равноудалена от точки, называемой центром окружности.
Для построения окружности выбирается произвольная точка О, принятая за центр окружности, и с помощью циркуля проводится замкнутая линия.
Если точку О центра окружности соединить с произвольными точками на окружности, то все полученные отрезки будут между собой равны, и называются такие отрезки радиусами, сокращенно обозначаются латинской маленькой или большой буквой «эр» (r или R). Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Отрезок, соединяющий две точки окружности и проходящий через ее центр, называется диаметром. Диаметр состоит из двух радиусов, лежащих на одной прямой. Диаметр обозначается латинской маленькой или большой буквой «дэ» (d или D).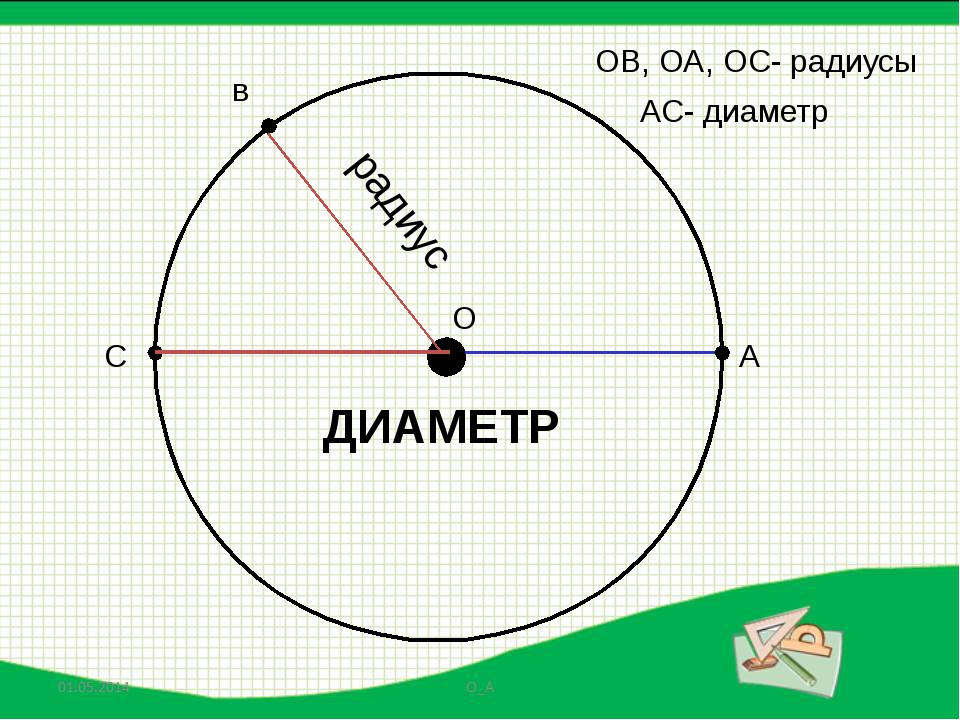
Правило. Диаметр окружности равен двум ее радиусам.
d = 2r
D = 2R
Длина окружности вычисляется по формуле и зависит от радиуса (диаметра) окружности. В формуле присутствует число ¶, которое показывает во сколько раз длина окружности больше, чем ее диаметр. Число ¶ имеет бесконечное число знаков после запятой. Для вычислений принято ¶ = 3,14.
Длина окружности обозначается латинской большой буквой «цэ» (C). Длина окружности пропорциональна ее диаметру. Формулы для расчета длины окружности по ее радиусу и диаметру:
C = ¶d
C = 2¶r
- Примеры
- Дано: d = 100 см.
- Длина окружности: C = 3,14 * 100 см = 314 см
- Дано: d = 25 мм.
- Длина окружности: С = 2 * 3,14 * 25 = 157 мм
Секущая окружности и дуга окружности
Всякая секущая (прямая линия) пересекает окружность в двух точках и делит ее на две дуги. Величина дуги окружности зависит от расстояния между центром и секущей и измеряется по замкнутой кривой от первой точки пересечения секущей с окружностью до второй.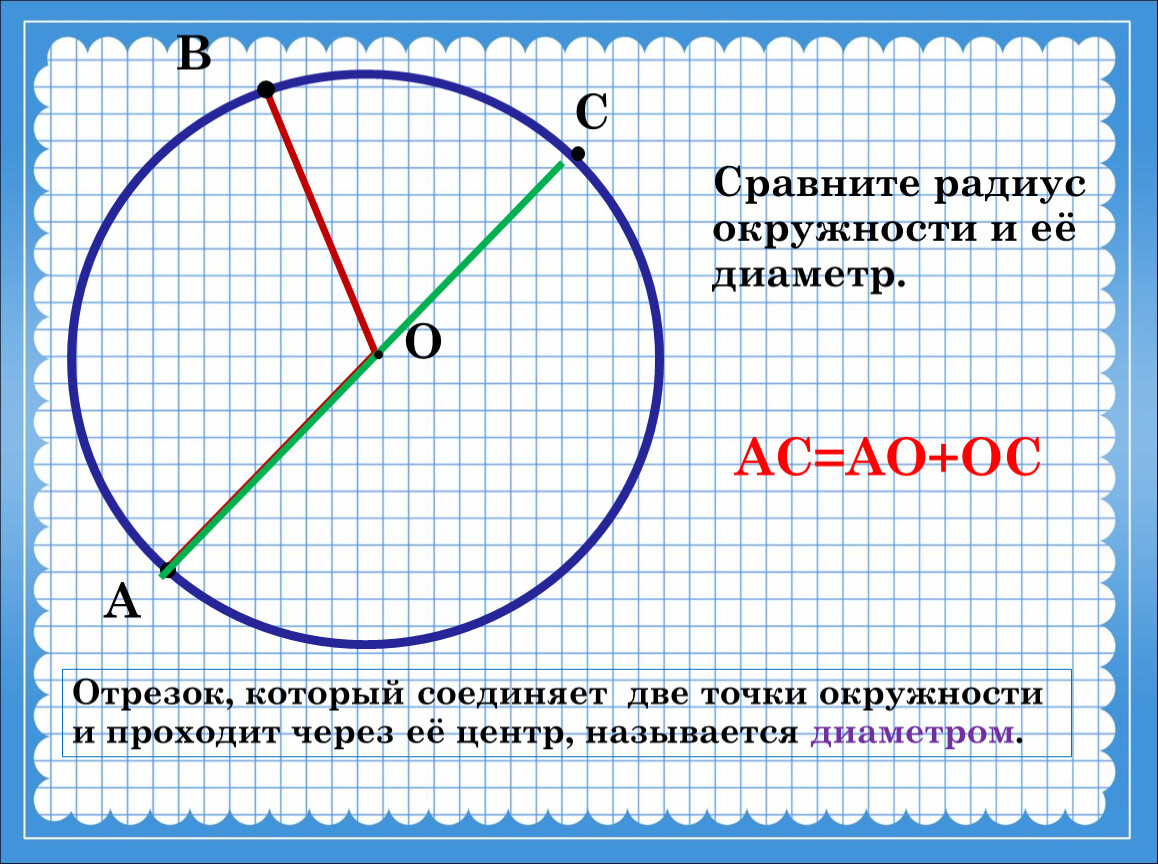
Дуги окружности делятся секущей на большую и малую, если секущая не совпадает с диаметром, и на две равные дуги, если секущая проходит по диаметру окружности.
Если секущая проходит через центр окружности, то ее отрезок, расположенный между точками пересечения с окружностью, есть диаметр окружности, или самая большая хорда окружности.
Чем дальше секущая расположена от центра окружности, тем меньше градусная мера меньшей дуги окружности и больше — большей дуги окружности, а отрезок секущей, называемый хордой, уменьшается по мере удаления секущей от центра окружности.
Определение. Кругом называется часть плоскости, лежащая внутри окружности.
Центр, радиус, диаметр окружности являются одновременно центром, радиусом и диаметром соответствующего круга.
Так как круг — это часть плоскости, то одним из его параметров является площадь.
Правило. Площадь круга (S) равна произведению квадрата радиуса ( r 2 ) на число ¶.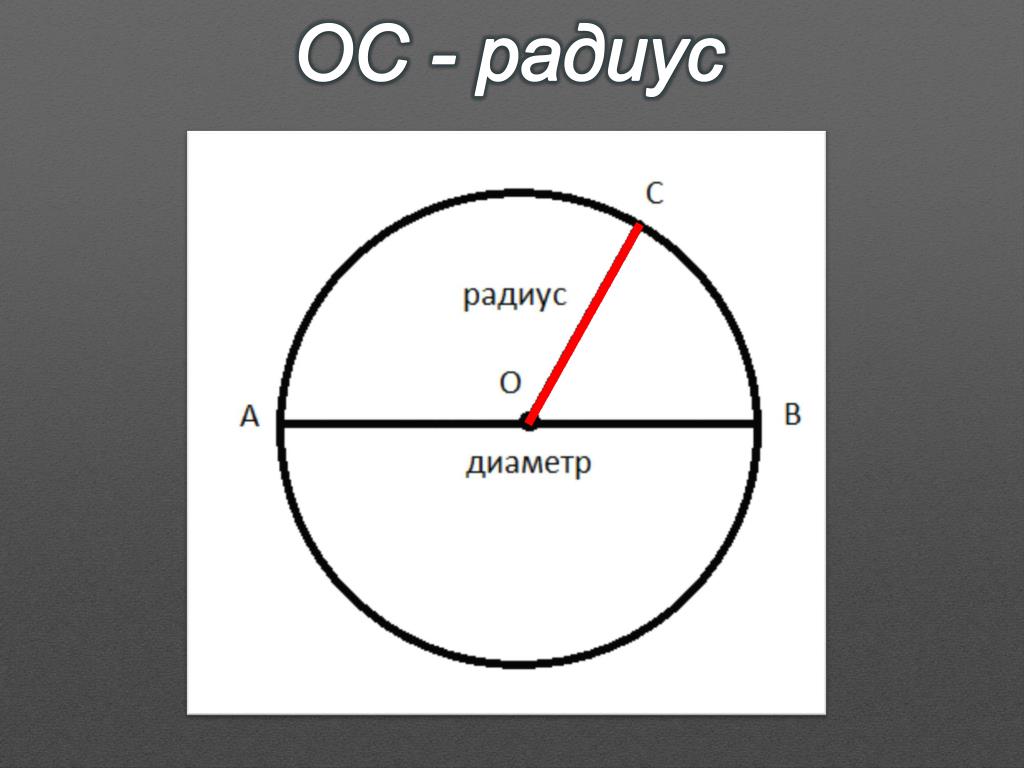
- Примеры
- Дано: r = 100 см
- Площадь круга:
- S = 3,14 * 100 см * 100 см = 31 400 см 2 ≈ 3м 2
- Дано: d = 50 мм
- Площадь круга:
- S = ¼ * 3,14 * 50 мм * 50 мм = 1 963 мм 2 ≈ 20 см 2
Если в круге провести два радиуса к разным точкам окружности, то образуется две части круга, которые называется секторами. Если в круге провести хорду, то часть плоскости между дугой и хордой называется сегментом окружности.
Определение. Сектор — это часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги. Сектор, образованный радиусами, расположенными под углом в 90° называется квадрантом.
Площадь сектора составляет только часть площади круга, и ее величина пропорциональна длине дуги m или зависит от величины центрального угла a, образованного двумя радиусами с вершиной в центре круга.
Формула для вычисления площади сектора:
где S — площадь сектора; m — длина дуги; r — радиус круга; а — угловая величина дуги (и градусах).
Диаметр и радиус — что это такое?
В жизни человек часто сталкивается с понятием окружность. Все едят с круглых тарелок, грызут круглые яблоки, катаются на велосипеде или ездят на транспорте с круглыми колесами и просто видят круглое солнце.
Понятия радиус и диаметр
Немногие задумываются, что на самом деле круг – очень сложная замкнутая фигура. Она состоит из главной точки (так называемый центр), а также из множества точек, которые идут от этого центра. Расстояние от центральной точки до окружности называют радиус. Чаще всего это понятие обозначается букой «R».
Если соединить две противоположные друг другу точки окружности и провести между ними линию, то она и будет диаметром. Диаметр обозначают символом «Ø». То есть радиус всегда будет равен половине диаметра.
Как использовать эти понятия в жизни
Вообще с этими понятиями знакомы практически все, кто учил геометрию в школе. Взрослые тоже часто сталкиваются с ними, когда помогают детям делать домашнее задание или просто проверяют его.
Также эти понятия очень часто используются в черчении, к примеру, в архитектуре, когда планируется сделать круглое окно, арку или другую круглую деталь.
В ландшафте тоже не обойтись без радиуса и диаметра, ведь именно они позволят поделить круг на несколько частей, создав яркие цветочные композиции. Последние будут не только радовать глаза, но и помогут отвлечь внимание гостей от грядок с овощами.
Во время конструирования одежды тоже часто встречаются понятия радиус и диаметр. Например, когда шьют шляпы, юбки или круглые накладные воротники.
Понятия диметр и радиус часто используются в программировании и создании сайтов. К примеру, многие создают программы для коррекции кругов (последние используются в разных сферах).
Важно обратить внимание, что понятия диаметр и радиус касаются не только круга. Круг – это фигура, которая лежит на определенной плоскости. Но в геометрии фигуры не всегда лежат на плоскости, некоторые находятся в пространстве. И понятия круг в пространстве вообще не существует, в нем используются объемные фигуры, например, эллипс, цилиндр, конус или шар. Для вычисления объема всех этих фигур тоже понадобится определять диаметр и радиус.
Круг – это фигура, которая лежит на определенной плоскости. Но в геометрии фигуры не всегда лежат на плоскости, некоторые находятся в пространстве. И понятия круг в пространстве вообще не существует, в нем используются объемные фигуры, например, эллипс, цилиндр, конус или шар. Для вычисления объема всех этих фигур тоже понадобится определять диаметр и радиус.
Другие понятия
Существует еще несколько понятий, которые могут пригодиться тем, кто работает с диаметром или радиусом:
- Дуга. Это кривая линия, которая является частью окружности. Ее измеряют в градусах. Сумма всех дуг составляет 360 градусов.
- Хорда. В отличие от кривой дуги это прямой отрезок, который соединяет две точки на окружности. Хорда отличается и диаметра – последний всегда равен двум радиусам и всегда проходит через центральную точку круга. Хорда же может быть длиннее или короче радиуса и никогда не проходит через центральную точку на круге.
- Сектор. Простыми словами, круг – это торт или пирог.
 Сектор же это треугольный кусок, который вырезается из этого пирога или торта.
Сектор же это треугольный кусок, который вырезается из этого пирога или торта. - Касательная. Это линия, которая проходит рядом с кругом так, что соприкасается только с одной точкой на окружности.
Все перечисленные выше понятия пригодятся не только тем, кто учит геометрию, но и тем, кто имеет дело с кругами в других сферах. В математике существует несколько формул, которые помогут выяснить величину любого из описанных выше понятий по заданным параметрам.
Знак диаметра
В тех случаях, когда требуется указать размер диаметра, используют знак в виде окружности с линией «Ø». Этот символ наносят перед размерным числом.
Примеры использования знака диаметра:
Знаки диаметра на деталях вращения цилиндрической и конической формы
Размеры наносимые при недостатке места
на размерной линии
Обозначение размеров при недостатке места
для стрелок
Диаметр – это длинна отрезка прямой соединяющей поверхности окружности. Отрезок диаметра, в любом случае проходит только через центр окружности. Обозначают его обычно латинской буквой «
Отрезок диаметра, в любом случае проходит только через центр окружности. Обозначают его обычно латинской буквой «D» или знаком «Ø». Если радиус окружности умножить на два, суммой будет диаметр. Все объемные тела, имеющие сферическую форму, а также те, хотя бы одно из возможных сечений которых представляет собой круг, обозначаются символами диаметра. Слово «диаметр» произошло от греческого слова «diametros» – поперечник.
Пример обозначения четырёх отверстий
с указанием диаметра
На технических чертежах диаметры обозначаются символом в виде перечеркнутой окружности «Ø». Данный знак, ставится перед размерными числами деталей, которые могут быть как цилиндрическими, так и коническими.
В сечение конус представляет собой прямоугольный треугольник, один из катетов которого параллелен или сосен телу вращения. Его параметры имеют следующими обозначениями: «D» – больший диаметр, «d» – меньший диаметр, «L» – длина. На чертеже диаметры конуса обозначаются цифрами, перед которыми ставятся знаки «
На чертеже диаметры конуса обозначаются цифрами, перед которыми ставятся знаки «Ø» а числовое значение длинны без буквенных обозначений.
К наиболее распространенным деталям с цилиндрическими поверхностями, относятся валы различного назначения. Цилиндрические тела, образованные вращением прямоугольника около одной из его сторон обозначаются диаметром. Гладкие валы имеют некоторые конструктивные особенности, и разделяются на разновидности: прямые, ступенчатые односторонние, ступенчатые двусторонние и тяжелые. К примеру, валы асинхронных двигателей, в которых ротор сопрягается с валом методом запрессовки на наибольший его диаметр, а по обеим сторонам имеются ступени под подшипники, вентиляторы, и шкивы. Двусторонние ступенчатые валы можно встретить так же в различных механизмах там, где требуются, какие либо другие конструктивные особенности. Цилиндрические детали, как правило, имеют общую максимальную длину и наружный диаметр. В зависимости от конкретной конфигурации того или иного изделия в её состав могут входить такие элементы как внутренние и наружные канавки, ступени, выточки и др. с различными диаметрами перед значениями которых ставятся знаки «
с различными диаметрами перед значениями которых ставятся знаки «Ø».
Пример нанесения знака диаметра
на сферической поверхности
К деталям с коническими поверхностями относятся инструментальные переходные втулки, у которых наружная и внутренняя поверхность конические. Такие втулки обеспечивают высокую точность центрирования и быстродействие смены инструмента с достаточной жёсткостью при использовании их на станках. Переходные втулки бывают короткие и длинные.
Конические инструментальные детали данного типа называются «конус Морзе» и делятся на номера. Углы, длины и диаметры переходных втулок можно взять из специальных таблиц. В табличных данных используются буквенные обозначения такие как – «d» меньший диаметр, «D» большой диаметр, «L» длина детали. На чертежах диаметры и длины обозначаются цифровыми значениями, причём перед числами диаметра ставится знак «Ø».
«Конус Морзе» – помимо переходных втулок применяется при изготовлении хвостовиков спиральных свёрл, концевых фрез, приспособлений и оправок. Инструментальные конусы фиксируются за счёт упругой и пластической деформации. Для реализации таких соединений в шпинделях фрезерных и токарных станков, предусмотрены конические отверстия для установки вспомогательного инструмента. Кроме того у токарного станка пиноль задней бабки имеет такое же коническое отверстие.
В технике используются большое количество деталей и их элементов для обозначения, которых используется знак диаметра. Для стандартных размеров диаметров используются параметрический ряд, в который входят стандартные размеры. При разработке технических изделий расчётные диаметры округляются до ближайших их величин. При обозначении на технических чертежах знак диаметра должен сопровождаться обозначением оси штрихпунктирной линией, что указывает на круглое сечение участка детали.
Окружности, начало координат, радиус, диаметр, окружность, пи, сектор, касательная
Определение: Окружность — это простая форма, состоящая из точек на плоскости, находящихся на заданном расстоянии от данной точки — центра.
Начало : центр круга
Радиус : расстояние от центра круга до любой точки на нем.
Диаметр : наибольшее расстояние от одного конца круга до другого.Диаметр = 2 × радиус (d = 2r).
Окружность : расстояние по окружности.
Окружность $ = \ pi \ times диаметра $.
Окружность $ = \ pi \ times d = 2 \ times \ pi \ times r $
$ \ pi $ — pi : число, равное 3,141592 … или $ \ приблизительно \ frac {22} {7} $, то есть $ \ frac {\ text {окружность}} {\ text { диаметр}} $ любой окружности.
Дуга : изогнутая линия, которая является частью окружности круга.
Дуга окружности измеряется в градусах или радианах — например: 90 ° или $ \ frac {\ pi} {2} $ — четверть круга,
180 ° или $ \ pi $ — половина круг.
Дуга меньше 360 ° (или $ 2 \ pi $), потому что это весь круг.
Хорда : отрезок линии внутри круга, который касается 2 точек на окружности.
Сектор : похож на кусок пирога (круговой клин).
Касательная : линия, перпендикулярная радиусу, которая касается ТОЛЬКО одной точки на окружности.2 $
Уголки
Центральный угол
Если длина дуги составляет $ \ theta $ градусов или радиан, то центральный угол также измеряется в $ \ theta $ (градусах или радианах).
Если вам известна длина дуги (в дюймах, ярдах, футах, сантиметрах, метрах …), вы можете найти измерение соответствующего центрального угла ($ \ theta $) по формуле:
$ \ theta = 360 \ cdot \ frac {l} {P} = \ frac {360 \ cdot l} {2 \ cdot \ pi \ cdot r} = \ frac {180 \ cdot l} {\ pi \ cdot r} $
$ l $ — длина дуги.\ circ $
Углы между двумя секущими
Случай 1: две секущие пересекают внутри окружности.
Когда две секущие пересекаются внутри круга, измерение каждого образованного угла составляет половину суммы дуг.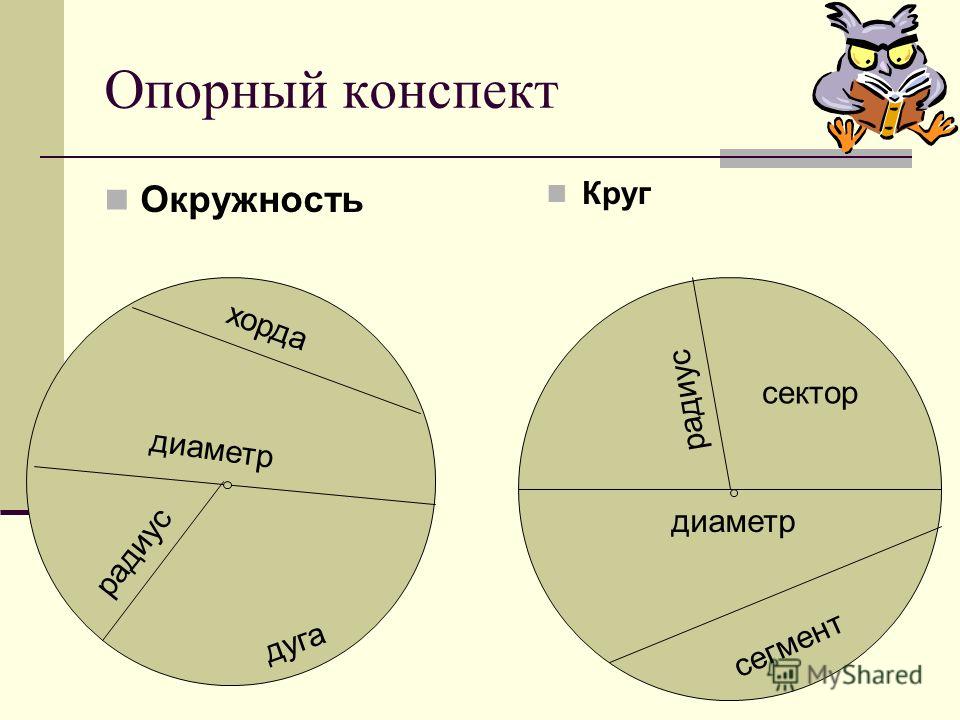
На рисунке дуга AB равна 60 °, а дуга CD — 50 °.
Таким образом, угол 1 и 2 составляют ½ (60 ° + 50 °) = 55 °.
Случай 2: две секущие пересекают за пределами окружности.
Измерение образовавшегося угла равно половине разности дуг.2) \ frac {\ theta} {360} $
Калькулятор окружности круга + руководство (и формула для его определения)
Расчет окружности объяснен
Понимание того, что такое окружность окружности и как ее вычислить, имеет решающее значение при переходе на более высокий уровень математики. В этой статье вы узнаете ответы на следующие вопросы.
- Какова длина окружности?
- Как можно рассчитать длину окружности?
Окружность круга — это расстояние по внешней стороне круга.Это как периметр других форм, например квадратов. Вы можете думать об этом как о линии, определяющей форму. Для фигур, состоящих из прямых краев, эта линия называется периметром , но для окружностей эта определяющая линия называется окружностью .
Для фигур, состоящих из прямых краев, эта линия называется периметром , но для окружностей эта определяющая линия называется окружностью .
На этой диаграмме показана длина окружности.
На окружности есть два других важных расстояния: радиус (r) и диаметр (d). Радиус, диаметр и длина окружности — три определяющих аспекта каждой окружности.Зная радиус или диаметр и число пи, вы можете вычислить длину окружности. Диаметр — это расстояние от одной стороны круга до другой в самых широких точках. Диаметр всегда проходит через центр круга. Радиус составляет половину этого расстояния. Вы также можете думать о радиусе как о расстоянии между центром круга и его краем.
На этой диаграмме показаны окружность, диаметр, центр и радиус окружности.
Как можно рассчитать длину окружности? Если вы знаете диаметр или радиус окружности, вы можете вычислить длину окружности. Для начала вспомним, что пи — это иррациональное число, записываемое символом π. π примерно равно 3,14.
Для начала вспомним, что пи — это иррациональное число, записываемое символом π. π примерно равно 3,14.
Формула для вычисления длины окружности:
Окружность окружности = π x Диаметр окружности
Обычно это записывается как C = πd. Это говорит нам о том, что длина окружности в три «с небольшим» раза больше диаметра. Мы можем видеть это на рисунке ниже:
Вы также можете вычислить длину окружности, если знаете ее радиус.Помните, что диаметр в два раза больше радиуса. Мы уже знаем, что C = πd. Если r — радиус окружности, то d = 2r. Итак, C = 2πr.
Пример 1Если круг имеет диаметр 10 см, какова его окружность?
ОтветМы знаем, что C = πd. Поскольку диаметр равен 10 см, мы знаем, что C = π x 10 см = 31,42 см (с точностью до 2 знаков после запятой).
Пример 2Если круг имеет радиус 3 м, какова его длина?
Ответ Мы знаем, что C = 2πr. Поскольку радиус равен 3 м, мы знаем, что C = π x 6m = C = 18,84 м (с точностью до 2 знаков после запятой).
Поскольку радиус равен 3 м, мы знаем, что C = π x 6m = C = 18,84 м (с точностью до 2 знаков после запятой).
Найдите недостающую длину (отмеченную знаком?) На диаграмме ниже:
ОтветНедостающая длина — это длина окружности. Зная, что диаметр на диаграмме составляет 4,3 м, и зная, что C = πd, мы можем вычислить длину окружности. Немного подумав, мы можем легко понять, что C = π x 4,3 м = 13,51 м (с точностью до 2 знаков после запятой).Недостающая длина 13,51 м.
Как рассчитать длину окружности ЗемлиВы когда-нибудь задумывались, насколько велика Земля? Что ж, с помощью числа Пи можно вычислить окружность Земли! Ученые обнаружили, что диаметр Земли составляет 12742 км. Учитывая эту информацию, какова окружность Земли? Возьмите лист бумаги и калькулятор и посмотрите, сможете ли вы решить все самостоятельно.
Опять же, мы знаем, что C = πd, и что диаметр Земли составляет 12 742 км.Используя эту информацию, мы можем вычислить длину окружности Земли как C = π x 12,742 км = 40,030 км.
Калькулятор окружности
Укажите любое значение ниже, чтобы рассчитать оставшиеся значения круга.
В то время как круг символически представляет множество разных вещей для множества разных групп людей, включая такие понятия, как вечность, безвременье и тотальность, круг по определению представляет собой простую замкнутую форму.Это набор всех точек на плоскости, которые равноудалены от данной точки, называемой центром. Его также можно определить как кривую, очерченную точкой, где расстояние от данной точки остается постоянным при перемещении точки. Расстояние между любой точкой круга и центром круга называется его радиусом, а диаметр круга определяется как наибольшее расстояние между любыми двумя точками на окружности. По сути, диаметр в два раза больше радиуса, так как наибольшее расстояние между двумя точками на окружности должно быть отрезком прямой, проходящим через центр окружности.Окружность круга может быть определена как расстояние вокруг круга или длина контура вдоль окружности.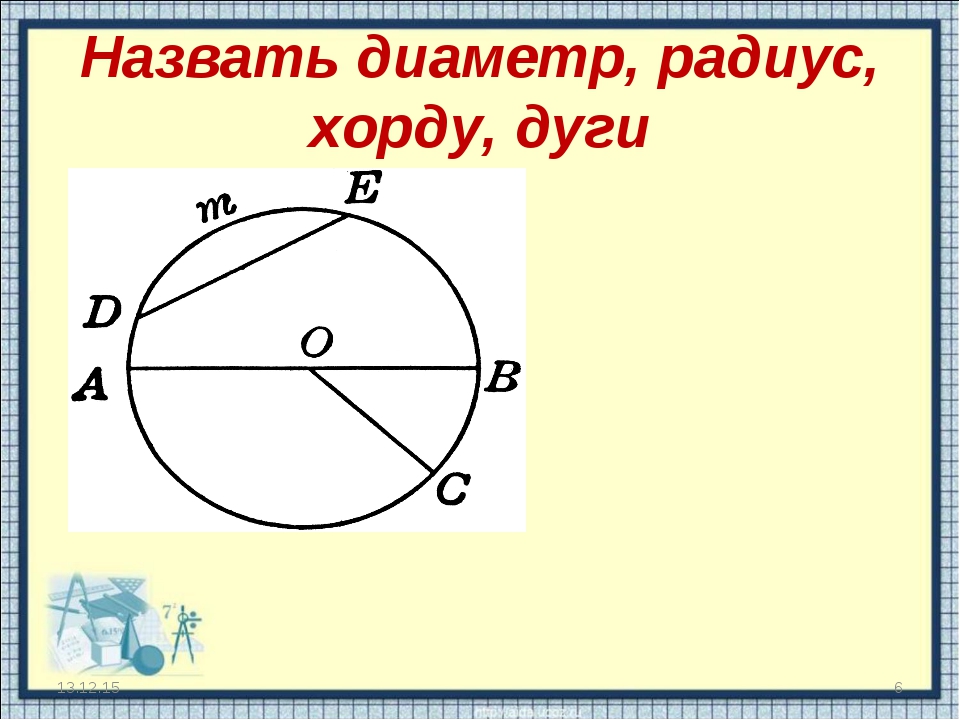 Все эти значения связаны через математическую константу π, или пи, которая представляет собой отношение длины окружности к ее диаметру и составляет приблизительно 3,14159. π — иррациональное число, означающее, что оно не может быть выражено в точности как дробь (хотя часто приближается к 22/7), а его десятичное представление никогда не заканчивается или имеет постоянный повторяющийся узор.Это также трансцендентное число, означающее, что оно не является корнем любого ненулевого многочлена с рациональными коэффициентами. Интересно, что доказательство Фердинанда фон Линдеманна в 1880 году, что π трансцендентно, наконец положило конец тысячелетнему поиску «квадратуры круга», который начался с древних геометров. Это включало попытку построить квадрат с той же площадью, что и данный круг, за конечное количество шагов, только используя циркуль и линейку. Хотя сейчас известно, что это невозможно, и представление о пылких усилиях взволнованных древних геометров, пытающихся сделать невозможное при свете свечей, может вызвать смехотворный образ, важно помнить, что именно благодаря таким людям многие математические концепции являются правильными.
Все эти значения связаны через математическую константу π, или пи, которая представляет собой отношение длины окружности к ее диаметру и составляет приблизительно 3,14159. π — иррациональное число, означающее, что оно не может быть выражено в точности как дробь (хотя часто приближается к 22/7), а его десятичное представление никогда не заканчивается или имеет постоянный повторяющийся узор.Это также трансцендентное число, означающее, что оно не является корнем любого ненулевого многочлена с рациональными коэффициентами. Интересно, что доказательство Фердинанда фон Линдеманна в 1880 году, что π трансцендентно, наконец положило конец тысячелетнему поиску «квадратуры круга», который начался с древних геометров. Это включало попытку построить квадрат с той же площадью, что и данный круг, за конечное количество шагов, только используя циркуль и линейку. Хотя сейчас известно, что это невозможно, и представление о пылких усилиях взволнованных древних геометров, пытающихся сделать невозможное при свете свечей, может вызвать смехотворный образ, важно помнить, что именно благодаря таким людям многие математические концепции являются правильными. определено сегодня.
определено сегодня.
Формулы круга
D = 2R С = 2πR А = πR 2 | где: R: радиус |
Радиус и диаметр — GED Math
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Калькулятор окружности
Если вам нужно решить какие-то геометрические упражнения, этот калькулятор окружности — то, что вам нужно. Это инструмент, специально созданный для определения диаметра, длины окружности и площади любого круга.Читайте дальше, чтобы узнать:
Это инструмент, специально созданный для определения диаметра, длины окружности и площади любого круга.Читайте дальше, чтобы узнать:
- Какое определение окружности
- Как найти длину окружности
- Как преобразовать длину окружности в диаметр
Как и все наши инструменты, калькулятор окружности работает во всех направлениях — он также вычисляет длину окружности в диаметр и может использоваться для преобразования длины окружности в радиус, окружности в площадь, радиуса в окружность, радиуса в диаметр. (да!), радиус к площади, диаметр к окружности, диаметр к радиусу (да, опять же с ракетной наукой), диаметр к площади, площадь к окружности, площадь к диаметру или площадь к радиусу.
Если вы хотите нарисовать круг на декартовой плоскости, вам может пригодиться это уравнение калькулятора окружности.
Определение окружности
Окружность круга — это линейное расстояние до края круга. Это то же самое, что и периметр геометрической фигуры, но термин «периметр» используется исключительно для многоугольников.
Окружность часто ошибочно пишется как , окружность .
Формула для определения окружности
Следующее уравнение описывает соотношение между длиной окружности и радиусом R окружности:
С = 2πR
Где π — константа, приблизительно равная 3.14159265 …
| 💡 Невозможно найти точное значение π. Это иррациональное число, поэтому мы обычно используем приближения, такие как 3,14 или 22/7. Если вам интересна эта тема, взгляните на первый миллион цифр числа π! |
Аналогичная простая формула определяет соотношение между площадью круга и его радиусом:
A = π * R²
Как найти длину окружности
- Определите радиус окружности.Допустим, он равен 14 см.
- Подставьте это значение в формулу для окружности:
C = 2 * π * R = 2 * π * 14 = 87,9646 см. - Вы также можете использовать его, чтобы найти площадь круга:
A = π * R² = π * 14² = 615,752 см².
- Наконец, вы можете найти диаметр — это просто двойной радиус:
D = 2 * R = 2 * 14 = 28 см. - Воспользуйтесь нашим калькулятором длины окружности, чтобы найти радиус, если у вас есть только длина окружности или площадь круга.
Если вы хотите рассчитать свойства трехмерного твердого тела, такого как сфера, цилиндр или конус, лучше всего использовать наш калькулятор объема.
От окружности до диаметра
Вы, наверное, заметили, что, поскольку диаметр в два раза больше радиуса, соотношение между длиной окружности и диаметром равно π:
C / D = 2πR / 2R = π
Эта пропорция (длина окружности к диаметру) является определением константы пи.Он используется во многих областях, таких как физика и математика. Например, вы можете найти его в калькуляторе центробежной силы.
FAQ
Как найти длину окружности?
Чтобы вычислить длину окружности, вам понадобится радиус окружности :
- Умножьте радиус на 2, чтобы получить диаметр.

- Умножьте результат на π или 3,14 для оценки.
- Вот и все; вы нашли окружности окружности .
Или вы можете использовать диаметр окружности :
- Умножьте диаметр на π, или на 3,14.
- Результат — окружности окружности .
Какова длина окружности?
Длина окружности равна линейному расстоянию от края окружности . Это эквивалент периметру геометрической формы, хотя этот термин периметр используется только для многоугольников.
Кто первым рассчитал длину окружности Земли?
Первым человеком, вычислившим длину окружности Земли в году, был Эратосфен, греческий математик года, в 240 году до нашей эры. Он обнаружил, что объекты в городе в Северном тропике не отбрасывают тень в полдень во время летнего солнцестояния, но это происходит в более северном месте. Зная это и расстояние между локациями, ему удалось вычислить окружность Земли.
Зная это и расстояние между локациями, ему удалось вычислить окружность Земли.
Как найти диаметр по окружности?
Если вы хотите найти диаметр по длине окружности , выполните следующие действия:
- Разделите длину окружности на π, или 3.14 для оценки.
- Вот и все; у вас есть диаметр круга .
Как найти площадь круга по окружности?
Чтобы найти площадь круга от окружности , выполните следующие действия:
- Разделите окружности на π.
- Разделите результат на 2, чтобы получить радиус окружности .
- Умножьте радиуса на себя, чтобы получить его квадрат.
- Умножьте квадрат на π или 3,14 для оценки.
- Вы нашли площадь круга из окружности .
Как найти радиус по окружности?
Чтобы найти радиус от окружности окружности, необходимо сделать следующее:
- Разделите окружности на π или 3,14 для оценки.
 В результате получился диаметр круга.
В результате получился диаметр круга. - Разделите диаметр на 2.
- Итак, вы нашли радиус круга .
Как измерить окружность?
- Вычислите длину окружности как 2 ⨉ радиус ⨉ π .
- Вычислите длину окружности как диаметра ⨉ π .
- Оберните нить вокруг объекта и измерьте ее длину.
- Используйте калькулятор окружности Omni .
Какова формула окружности?
Формула для окружности , если задан радиус окружности, будет:
Или, если дана длина окружности:
Можно оценить π как 3.14.
Какова длина окружности радиуса 1 метр?
Чтобы рассчитать длину окружности с радиусом 1 метр , просто выполните следующие действия:
- Умножьте радиус на 2, чтобы получить диаметр 2 метра.
- Умножьте результат на π или 3,14 для оценки.

- И вот; Окружность окружности радиусом 1 метр составляет 6,28 метра .
Как найти окружность цилиндра?
Чтобы найти окружность цилиндра , вы должны знать, что поперечное сечение цилиндра представляет собой круг.Если известен радиус цилиндра:
- Умножьте радиус на 2, чтобы получить диаметр.
- Умножьте результат на π или 3,14 для оценки.
- Вот и все; вы нашли окружности цилиндра .
Или вы можете использовать диаметр цилиндра :
- Умножьте диаметр на π, или на 3,14.
- В результате получается окружности цилиндра .
Как найти площадь круга с окружностью 1 метр?
Если вы хотите найти площадь круга с окружностью 1 метр , сделайте следующее:
- Разделите окружности на π.
 Это диаметр круга , в данном случае 31,8 сантиметра.
Это диаметр круга , в данном случае 31,8 сантиметра. - Разделите на 2. В результате получится радиус окружности , равный 15,9 сантиметра.
- Умножьте радиуса на себя, получив квадрат, в нашем случае 256 см².
- Умножьте на π или 3,14 для оценки.
- Вот и все; круг с окружностью 1 метр имеет площадь 795,78 см² .
Как найти радиус окружности 10 сантиметров?
Чтобы найти радиус окружности с длиной окружности 10 сантиметров , вы должны сделать следующее:
- Разделите окружности на π или 3,14 для оценки. В результате получился диаметр круга 3.18 сантиметров.
- Разделите диаметр на 2.
- И вот, радиус круга с окружностью 10 сантиметров составляет 1,59 сантиметра .
Какая единица измерения длины окружности?
Поскольку длина окружности является линейным расстоянием от края круга, она описывает длину. Таким образом, наиболее распространенными единицами измерения окружности круга являются миллиметр, сантиметр, метр для метрической системы и дюйм, фут и ярд для имперской системы .
Таким образом, наиболее распространенными единицами измерения окружности круга являются миллиметр, сантиметр, метр для метрической системы и дюйм, фут и ярд для имперской системы .
6.8: Радиус или диаметр окружности в данной области
Чтобы найти радиус, разделите площадь на пи, а затем извлеките квадратный корень.
Клара повела свою младшую сестру Грейс на пруд с рыбками в местном парке. Грейс увидела в центре пруда пенни и попросила Клару протянуть ее ей. Табличка гласила, что площадь пруда составляет 113,04 кв. Фута. Может ли Клара достать пенни, не упав в нее?
В этой концепции вы узнаете, как найти радиус (и диаметр ) окружности , если вам известна ее площадь.2 \)
Затем извлеките квадратный корень из обеих частей.
\ (6 = г \)
Ответ: r = 6. Радиус круга — 6 дюймов.
Пример \ (\ PageIndex {1} \)
Ранее вам давали задачу о Кларе и Грейс, которые находились в круглом рыбном пруду площадью 113,04 кв. 2 \)
2 \)
Затем подставьте то, что вы знаете.2 \)
Извлеките квадратный корень из обеих частей.
\ (12 = г \)
Ответ: r = 12. Радиус круга 12 метров.
Как определить площадь по диаметру — стенограмма видео и урока
Radius
Чтобы понять это, давайте посмотрим, что такое радиус круга. Радиус круга — это длина отрезка прямой от центра круга до любой точки на окружности.
Вы замечаете, как радиус соотносится с диаметром? Поскольку диаметр — это длина отрезка прямой, проходящего через центр круга от одной стороны круга до другой, на самом деле он состоит из двух радиусов.Другими словами, если d — диаметр окружности, а r — радиус окружности, то d = 2 r . Мы также можем посмотреть на это, так как радиус составляет 1/2 диаметра, или r = d /2 .
Formula
Это отличная новость! Вы понимаете почему? Все, что нам нужно сделать, это вставить r = d /2 в нашу формулу площади, и у нас есть способ найти площадь круга по его диаметру .
A = π ( d /2) 2
Решение
Если длина диаметра круга составляет d , то мы можем найти площадь A , используя следующую формулу;
A = π ( d / 2) 2
Приложение
Круги постоянно появляются в мире вокруг нас, поэтому, естественно, возможность найти площадь круга чрезвычайно полезна в реальной жизни. . Например, предположим, что вы хотите создать песчаный пляж на заднем дворе таким образом, чтобы пляж имел круглую форму.Вам нужно выяснить, сколько потребуется песка и сколько он будет стоить. Нанятые вами ландшафтные дизайнеры сообщают вам, что они определяют, сколько песка вам потребуется, исходя из площади земли, которую необходимо покрыть, и что они берут 0,50 доллара за квадратный фут.
Вы понимаете, что можете найти это место, если знаете диаметр круглого пляжа, поэтому вы выходите на улицу и измеряете диаметр круглого участка, чтобы найти, что это 42 фута. Вы возвращаетесь внутрь и берете лист бумаги, карандаш и калькулятор, чтобы найти площадь ( A ) круга, учитывая, что диаметр ( d ) равен 42. Наша первая строка утверждает, что:
Наша первая строка утверждает, что:
A = π ( d /2) 2
Мы вставляем наши известные числа во вторую строку:
A = π (42/2) 2
Мы вычисляем деление в третьей строке:
A = π (21) 2
В четвертой строке находим квадрат 21:
A = π (441)
И, наконец, приходим к выводу, что A ≈ 1385.44 .
Мы видим, что площадь вашего пляжа будет примерно 1385,44 квадратных футов. Поскольку ландшафтные дизайнеры берут 0,50 доллара за квадратный фут, вы можете рассчитать стоимость, умножив 1385,44 0,5.
Стоимость = 1385,44 ⋅ 0,5 = 692,72
Вы подсчитали, что создание пляжа на заднем дворе обойдется вам в 692,72 доллара. Ух ты! И все это благодаря знанию диаметра круга! Конечно, это всего лишь один пример того, как определение площади круга по его диаметру может проявиться в нашей жизни.Вы встретите гораздо больше, поэтому здорово, что теперь вы точно знаете, как это сделать!
Резюме урока
Диаметр окружности — это длина отрезка прямой, идущего от одной стороны окружности к другой и проходящего через центр окружности.

 Сектор же это треугольный кусок, который вырезается из этого пирога или торта.
Сектор же это треугольный кусок, который вырезается из этого пирога или торта.

 В результате получился диаметр круга.
В результате получился диаметр круга.
 Это диаметр круга , в данном случае 31,8 сантиметра.
Это диаметр круга , в данном случае 31,8 сантиметра.