Как решать уравнения с дробями
Уравнения с дробями сами по себе не трудны и очень интересны. Рассмотрим виды дробных уравнений и способы их решения.
1
Как решать уравнения с дробями – икс в числителе
В случае, если дано дробное уравнение, где неизвестное находится в числителе, решение не требует дополнительных условий и решается без лишних хлопот. Общий вид такого уравнения – x/a + b = c, где x – неизвестное, a,b и с – обычные числа.
Пример 1:
Найти x: x/5 + 10 = 70.
Для того чтобы решить уравнение, нужно избавиться от дробей. Умножаем каждый член уравнения на 5: 5x/5 + 5×10 = 70×5. 5x и 5 сокращается, 10 и 70 умножаются на 5 и мы получаем: x + 50 = 350 => x = 350 – 50 = 300.
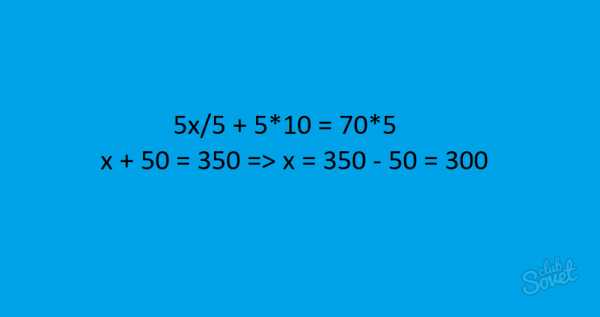
Пример 2:
Найти x: x/5 + x/10 = 90.
Данный пример – немного усложненная версия первого. Тут есть два варианта решения.
- Вариант 2: Складываем левую часть уравнения. x/5 + x/10 = 90. Общий знаменатель – 10. 10 делим на 5, умножаем на x, получаем 2x. 10 делим на 10, умножаем на x, получаем x: 2x+x/10 = 90. Отсюда 2x+x = 90×10 = 900 => 3x = 900 => x = 300.
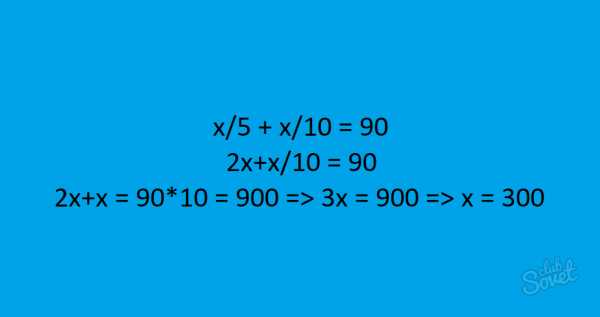
Нередко встречаются дробные уравнения, в которых иксы находятся по разные стороны знака равно. В таких ситуация необходимо перенести все дроби с иксами в одну сторону, а числа в другую.
Пример 3:
- Найти x: 3x/5 = 130 – 2x/5.
- Переносим 2x/5 направо с противоположным знаком: 3x/5 + 2x/5 = 130 => 5x/5 = 130.
- Сокращаем 5x/5 и получаем: x = 130.

2
Как решить уравнение с дробями – икс в знаменателе
Данный вид дробных уравнений требует записи дополнительных условий. Указание этих условий является обязательной и неотъемлемой частью правильного решения. Не приписав их, вы рискуете, так как ответ (даже если он правильный) могут просто не засчитать.
Общий вид дробных уравнений, где x находится в знаменателе, имеет вид: a/x + b = c, где x – неизвестное, a, b, c – обычные числа. Обратите внимание, что x-ом может быть не любое число. Например x не может равняться нулю, так как делить на 0 нельзя. Именно это и является дополнительным условием, которое мы должны указать. Это называется областью допустимых значений, сокращенно – ОДЗ.
Пример 4:
Найти x: 15/x + 18 = 21.
Сразу же пишем ОДЗ для x: x ≠ 0. Теперь, когда ОДЗ указана, решаем уравнение по стандартной схеме, избавляясь от дробей. Умножаем все члены уравнения на x. 15x/x+18x = 21x => 15+18x = 21x => 15 = 3x => x = 15/3 = 5.

Часто встречаются уравнения, где в знаменателе стоит не только x, но и еще какое-нибудь действие с ним, например сложение или вычитание.
Пример 5:
Найти x: 15/(x-3) + 18 = 21.
Мы уже знаем, что знаменатель не может равняться нулю, а значит x-3 ≠ 0. Переносим -3 в правую часть, меняя при этом знак “-” на ”+” и получаем, что x ≠ 3. ОДЗ указана.
Решаем уравнение, умножаем все на x-3: 15 + 18×(x – 3) = 21×(x – 3) => 15 + 18x – 54 = 21x – 63.
Переносим иксы направо, числа налево: 24 = 3x => x = 8.
 sovetclub.ru
sovetclub.ruКак решать уравнения с дробями
Уравнения с дробями – нестандартный вид уравнений, имеющий свои специфические особенности и тонкие моменты. Испробуем в них разобраться.
Инструкция
1. Вероятно, самый явственный момент тут – это, безусловно, знаменатель. Числовые дроби не представляют никакой угрозы (дробные уравнения, где во всех знаменателях стоят только числа, вообще будут линейными), а вот если в знаменателе стоит переменная, то это неукоснительно надобно рассматривать и прописывать. Во-первых, это значит, что значение х, обращающее в 0 знаменатель, корнем быть не может, и вообще необходимо отдельно прописать тот факт, что икс не может равняться этому числу. Даже если у вас получится, что при подстановке в числитель всё восхитительно сходится и удовлетворяет условиям. Во-вторых, мы не можем умножать либо разделять обе части уравнения на выражение, равное нулю.
2. Позже этого решение такого уравнения сводится к переносу всех его членов в левую часть так, дабы в правой остался 0.Надобно привести все члены к всеобщему знаменателю, домножив, где надобно, числители на недостающие выражения.Дальше решаем обыкновенное уравнение, написанное в числителе. Можем переносить всеобщие множители за скобки, использовать формулы сокращённого умножения, приводить сходственные, вычислять корни квадратного уравнения через дискриминант и т.д.
3. В результате должно получиться разложение на множители в виде произведения скобок (х-(i-ый корень)). Также сюда могут входить многочлены, не имеющие корней, скажем, квадратный трёхчлен с дискриминантом, меньшим нуля (если, финально, в задаче требуется обнаружить только действительные корни, как почаще каждого и бывает).Неукоснительно надобно разложить на множители и знаменатель с целью нахождения там скобок, теснее содержащихся в числителе. Если в знаменателе стоят выражения типа (х-(число)), то класснее при приведении к всеобщему знаменателю стоящие в нём скобки не перемножать “в лоб”, а оставить в виде произведения начальных примитивных выражений.Идентичные скобки в числителе и знаменателе дозволено сократить, прописав заранее, как говорилось выше, данные на х.Результат записывается в фигурных скобках, как уйма значений х, либо легко перечислением: x1=…, х2=… и т.д.
Решение уравнений – то, без чего невозможно обойтись в физике, математике, химии. Как минимум. Учимся основам их решения.
Инструкция
1. В самой всеобщей и легкой систематизации уравнения дозволено поделить по числу переменных, в них содержащихся, и по степеням, в которых эти переменные стоят.Решить уравнение значит обнаружить все его корни либо подтвердить, что их нет.Всякое уравнений имеет не больше P корней, где P – максимальная степень данного уравнения.Но часть этих корней может и совпадать. Так, скажем, уравнение х^2+2*x+1=0, где ^ – значок возведения в степень, сворачивается в квадрат выражения (х+1), то есть в произведение 2-х идентичных скобок, вся из которых даёт х=-1 в качестве решения.
2. Если в уравнении каждого одна неведомая, это значит, что вам удастся в очевидном виде обнаружить его корни (действительные либо комплексные).Для этого скорей каждого потребуются, разные реформирования: формулы сокращённого умножения, формула вычисления дискриминанта и корней квадратного уравнения, перенос слагаемых из одной части в иную, приведение к всеобщему знаменателю, умножение обоих частей уравнения на одно и тоже выражение, возведение в квадрат и другое.Реформирования, не влияющие на корни уравнения, именуются тождественными. Они применяются для облегчения процесса решения уравнения.Также вы можете взамен традиционного аналитического воспользоваться графическим способом и записать данное уравнение в виде функции, проведя после этого её изыскание.
3. Если в уравнении незнакомых огромнее одной, то вам удастся лишь выразить одну из них через иную, показав тем самым комплект решений. Таковы, скажем, уравнения с параметрами, в которых присутствует незнакомая x и параметр а. Решить параметрическое уравнение – значит для всех а выразить х через а, то есть разглядеть все допустимые случаи.Если в уравнении стоят производные либо дифференциалы незнакомых (смотри картинку), поздравляю, это дифференциальное уравнение, и здесь вам не обойтись без высшей математики).

Дабы решить задачу с дробями , необходимо обучиться делать с ними арифметические действия. Они могут быть десятичные, но почаще каждого применяются естественные дроби с числителем и знаменателем. Только позже этого дозволено переходить на решения математических задач с дробными величинами.

Вам понадобится
- – калькулятор;
- – умения свойств дробей;
- – знание изготавливать действия с дробями.
Инструкция
1. Дробью называют запись деления одного числа на другое. Нередко это сделать нацело невозможно, следственно и оставляют это действие «неоконченным . Число, которое является делимым (оно стоит над либо перед знаком дроби), именуются числителем, а второе число (под знаком дроби либо позже него) – знаменателем. Если числитель огромнее знаменателя, дробь именуется неправильной, и из нее дозволено выделить целую часть. Если числитель поменьше знаменателя, то такая дробь именуется верной, и ее целая часть равна 0.
2. Задачи с дробями делятся на несколько видов. Определите, к какому из них относится задача. Примитивный вариант – нахождение доли числа, выраженной дробью. Для решения этой задачи довольно умножить это число на дробь. Скажем, на склад завезли 8 т картошки. В первую неделю было продано 3/4 от ее всеобщего числа. Сколько картошки осталось? Дабы решить эту задачу, число 8 умножьте на 3/4. Получится 8?3/4=6 т.
3. Если надобно обнаружить число по его части, умножьте вестимую часть числа на дробь, обратную той, которая показывает какова доля данной части в числе. Скажем, 8 человек из класса составляют 1/3 от всеобщего числа учеников. Сколько детей учится в классе? От того что 8 человек это часть, которая представляет 1/3 от каждого числа, то обнаружьте обратную дробь, которая равна 3/1 либо примитивно 3. После этого для приобретения числа учеников в классе 8?3=24 ученика.
4. Когда необходимо обнаружить какую часть числа составляет одно число от иного, поделите число, которое представляет часть на то, которое является целым. К примеру, если расстояние между городами 300 км, а автомобиль проехал 200 км, какую часть данный составит от каждого пути? Поделите часть пути 200 на полный путь 300, позже сокращения дроби получите итог. 200/300=2/3.
5. Дабы обнаружить часть неведомую долю от числа, когда есть вестимая, возьмите целое число за условную единицу, и отнимите от нее знаменитую долю. Скажем, если теснее прошло 4/7 части урока, сколько еще осталось? Возьмите каждый урок как условную единицу и отнимите от нее 4/7. Получите 1-4/7=7/7-4/7=3/7.
Дроби – это математическая форма записи простого разумного числа. Она представляет собой число, которое состоит из одной либо нескольких долей единицы, может быть как в десятичном, так и в обыкновенном виде. Сегодня операции по реформированию дробей имеют большое значение не только в математике, но и в иных областях умений.
Инструкция
1. Как водится, множество обычных дробей бывают неправильными, и в таком случае они требуют определенных действий со стороны того, кто решает примеры и задачи с данной дробью.
2. Возьмите учебник со своей задачей. Наблюдательно ознакомьтесь с условием, прочитав его несколько раз, и перейдите к решению. Посмотрите, какие дроби имеются в решаемых вами действиях. Это могут быть неправильные, положительные либо десятичные дроби. Переведите верные дроби в неправильные, но при этом помните, что для записи результата все действия придется исполнить обратно, преобразовав теснее неправильную дробь в верную. У неправильной дроби число над дробной чертой (числитель) неизменно огромнее числа под чертой – знаменателя. Для того дабы сделать перевод из положительной дроби в неправильную нужно исполнить следующие шаги.
3. Умножьте знаменатель на целое число и прибавьте к полученному итогу числитель. К примеру, если дробь вида 2 целых 7/9, нужно 9 умножить на 2 и потом к 18 прибавить 7 – финальным итогом будет 25/9.
4. Произведите все нужные действия по своей задаче (сложения, вычитания, деления, умножения), применяя преобразованные дроби.Возьмите свой результат, его нужно будет представить в обычной дроби. Для этого поделите числитель на знаменатель. К примеру, если нужно перевести число 25/9 в верную дробь, поделите 25 на 9. Потому что 25 на 9 нацело не делится, в результате получается 2 целых и семь (числитель) девятых (знаменатель). Сейчас получена верная дробь, где числитель огромнее знаменателя и имеется целая часть.
5. Запишите результат задачи положительной дробью. Проведите проверку своим действиям, в случае если ее требует сделать условие задачи либо преподаватель.
jprosto.ru
Ответы@Mail.Ru: Как избавляются от знаменателя?
На фото изображение практически наразличимо. Если речь идет об избавлении от знаменателя в уравнении, нужно все числители дробей обеих частей уравнения умножить на произведение знаменателей всех дробей и сократить знаменатели.
правую часть разделить на знаменатель
домнажай все части на этот знаменательЕсли вы хотите от него избавиться, надо его кому-нибудь заказать…
тоесть все знаменатели приведи к одному и умнож все числители на него
Домножьте числитель на этот знаменатель. Они и сократятся.
touch.otvet.mail.ru
