4/5
206331441042717613615431915227898763583068286175818367293632007559999071393467889206609428828651511872512531611969768111040298985109951689741117578284143200208972902947264661890158544101751040273254974215592859366575113601285981064608384841683059318327462333533401620775630426878460698114410939232150247713385554845227341060092312030542759300802271359324530852450763711134117785123088504128696618481897541051229241985401599261730491985392719229020579008969073303317450295118929296678082691744282944442374580499904136795397583127043916055595621774601886061339032428891982637914663804363403573226824250916458908362582786247787477013497511124419773186607828934236546950716765072481453217917087511170314392465088336628935393746432945407198278440135799382252160213346448408068389250771436490086608856707014919680891316110955240401212394153740437019450837397016584873199462890625*5 > 125
значит решение неравенства будет при:
$$x
_____
\
-------ο-------
x1Таблица степеней по алгебре
На этой странице размещена таблица степеней от 2 до 10 для натуральных чисел от 1 до 20. Пример использования: находим в таблице число 9 (слева), затем во втором столбике видим квадрат числа, который равен 81. В третьем столбце таблицы значения кубов. Смотрите также: таблица квадратов, таблица корней.
Пример использования: находим в таблице число 9 (слева), затем во втором столбике видим квадрат числа, который равен 81. В третьем столбце таблицы значения кубов. Смотрите также: таблица квадратов, таблица корней.
https://uchim.org/matematika/tablica-stepenej — uchim.org
Таблица степеней
Пример: 23=8
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Свойства степени — 2 части
youtube.com/embed/4FrlQUHlDrg» frameborder=»0″ allowfullscreen=»»/>Таблица основных степеней по алгебре в компактном виде (картинка, удобно, чтобы распечатать), сверху числа, сбоку степени:
(можно открыть в новом окне, нажав на картинку)
Полную математическую таблицу можно бесплатно скачать, просто сохранив картинку выше с помощью правой кнопки мыши.
Всё для учебы » Математика в школе » Таблица степеней по алгебре
Степень с натуральным показателем
Предварительные навыкиЧто такое степень?
Степенью называют произведение из нескольких одинаковых множителей. Например:2 × 2 × 2
Значение данного выражения равно 8
2 × 2 × 2 = 8
Левую часть этого равенства можно сделать короче – сначала записать повторяющийся множитель и указать над ним сколько раз он повторяется. Повторяющийся множитель в данном случае это 2.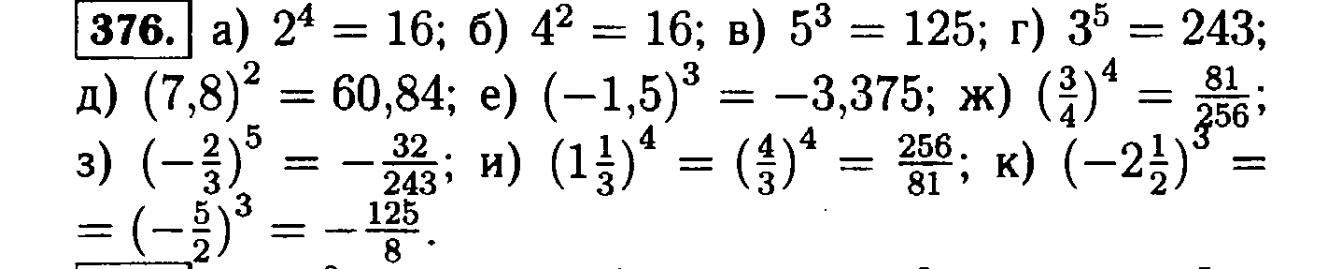 Повторяется он три раза. Поэтому над двойкой записываем тройку:
Повторяется он три раза. Поэтому над двойкой записываем тройку:
23 = 8
Это выражение читается так: «два в третьей степени равно восемь» или «третья степень числа 2 равна 8».
Короткую форму записи перемножения одинаковых множителей используют чаще. Поэтому надо помнить, что если над каким-то числом надписано другое число, то это есть перемножение нескольких одинаковых множителей.
Например, если дано выражение 53, то следует иметь ввиду, что это выражение равносильно записи 5 × 5 × 5.
А число, которое надписано над числом 5 называют показателем степени. В выражении 53 показателем степени является число 3. Показатель степени показывает сколько раз повторяется основание степени. В нашем случае основание 5 повторяется три раза
Саму операцию перемножения одинаковых множителей называют возведением в степень.
Например, если нужно найти произведение из четырёх одинаковых множителей, каждый из которых равен 2, то говорят, что число 2 возводится в четвёртую степень:
Видим, что число 2 в четвёртой степени есть число 16.
Отметим, что в данном уроке мы рассматриваем степени с натуральным показателем. Это вид степени, показателем которой является натуральное число. Напомним, что натуральными называют целые числа, которые больше нуля. Например, 1, 2, 3 и так далее.
Вообще, определение степени с натуральным показателем выглядит следующим образом:
Степень числа a с натуральным показателем n — это выражение вида an, которое равно произведению n множителей, каждый из которых равен a
Примеры:
Следует быть внимательным при возведении числа в степень. Часто по невнимательности человек умножает основание степени на показатель.
Например, число 5 во второй степени есть произведение двух множителей каждый из которых равен 5. Это произведение равно 25
Теперь представим, что мы по невнимательности умножили основание 5 на показатель 2
Получилась ошибка, поскольку число 5 во второй степени не равно 10.
Дополнительно следует упомянуть, что степень числа с показателем 1, есть само это число:
Например, число 5 в первой степени есть само число 5
Соответственно, если у числа отсутствует показатель, то надо считать, что показатель равен единице.
Например, числа 1, 2, 3 даны без показателя, поэтому их показатели будут равны единице. Каждое из этих чисел можно записать с показателем 1
А если возвести 0 в какую-нибудь степень, то получится 0. Действительно, сколько бы раз ничего не умножалось на само себя получится ничего. Примеры:
А выражение 00 не имеет смысла. Но в некоторых разделах математики, в частности анализе и теории множеств, выражение 00 может иметь смысл.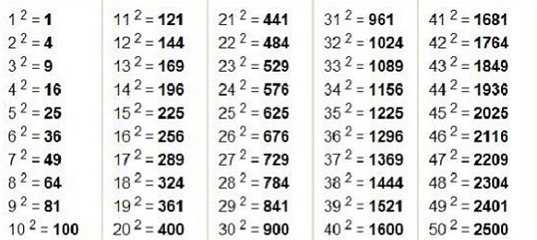
Для тренировки решим несколько примеров на возведение чисел в степени.
Пример 1.
Возвести число 3 во вторую степень.Число 3 во второй степени это произведение двух множителей, каждый из которых равен 3
32 = 3 × 3 = 9
Пример 2. Возвести число 2 в четвертую степень.
Число 2 в четвертой степени это произведение четырёх множителей, каждый из которых равен 2
24 =2 × 2 × 2 × 2 = 16
Пример 3. Возвести число 2 в третью степень.
Число 2 в третьей степени это произведение трёх множителей, каждый из которых равен 2
23 =2 × 2 × 2 = 8
Возведение в степень числа 10
Чтобы возвести в степень число 10, достаточно дописать после единицы количество нулей, равное показателю степени.
Например, возведем число 10 во вторую степень. Сначала запишем само число 10 и в качестве показателя укажем число 2
102
Теперь ставим знак равенства, записываем единицу и после этой единицы записываем два нуля, поскольку количество нулей должно быть равно показателю степени
102 = 100
Значит, число 10 во второй степени это число 100. Связано это с тем, что число 10 во второй степени это произведение двух множителей, каждый из которых равен 10
Связано это с тем, что число 10 во второй степени это произведение двух множителей, каждый из которых равен 10
102 = 10 × 10 = 100
Пример 2. Возведём число 10 в третью степень.
В данном случае после единицы будут стоять три нуля:
103 = 1000
Пример 3. Возведем число 10 в четвёртую степень.
В данном случае после единицы будут стоять четыре нуля:
104 = 10000
Пример 4. Возведем число 10 в первую степень.
В данном случае после единицы будет стоять один нуль:
101 = 10
Представление чисел 10, 100, 1000 в виде степени с основанием 10
Чтобы представить числа 10, 100, 1000 и 10000 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать число, равное количеству нулей исходного числа.
Представим число 10 в виде степени с основанием 10. Видим, что в нём один нуль.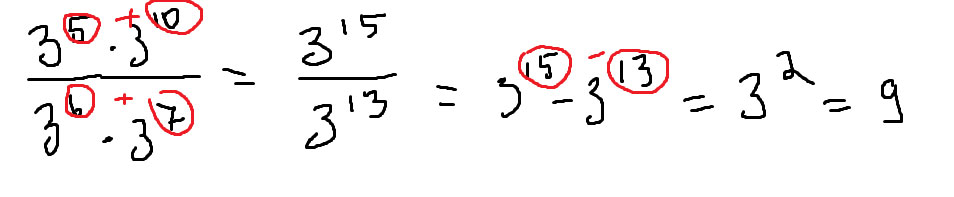 Значит, число 10 в виде степени с основанием 10 будет представлено как 101
Значит, число 10 в виде степени с основанием 10 будет представлено как 101
10 = 101
Пример 2. Представим число 100 в виде степени основанием 10. Видим, что число 100 содержит два нуля. Значит, число 100 в виде степени с основанием 10 будет представлено как 102
100 = 102
Пример 3. Представим число 1 000 в виде степени с основанием 10.
1 000 = 103
Пример 4. Представим число 10 000 в виде степени с основанием 10.
10 000 = 104
Возведение в степень отрицательного числа
При возведении в степень отрицательного числа, его обязательно нужно заключить в скобки.
Например, возведём отрицательное число −2 во вторую степень. Число −2 во второй степени это произведение двух множителей, каждый из которых равен (−2)
(−2)2 = (−2) × (−2) = 4
Если бы мы не заключили в скобки число −2, то получилось бы что мы вычисляем выражение −22, которое не равно 4. Выражение −2² будет равно −4. Чтобы понять почему, коснёмся некоторых моментов.
Выражение −2² будет равно −4. Чтобы понять почему, коснёмся некоторых моментов.
Когда мы ставим перед положительным числом минус, мы тем самым выполняем операцию взятия противоположного значения.
Допустим, дано число 2, и нужно найти его противоположное число. Мы знаем, что противоположное числу 2 это число −2. Иными словами, чтобы найти противоположное число для 2, достаточно поставить минус перед этим числом. Вставка минуса перед числом уже считается в математике полноценной операцией. Эту операцию, как было указано выше, называют операцией взятия противоположного значения.
В случае с выражением −22 происходит две операции: операция взятия противоположного значения и возведение в степень. Возведение в степень является более приоритетной операцией, чем взятие противоположного значения.
Поэтому выражение −22 вычисляется в два этапа. Сначала выполняется операция возведения в степень. В данном случае во вторую степень было возведено положительное число 2
Затем выполнилось взятие противоположного значения. Это противоположное значение было найдено для значения 4. А противоположное значение для 4 это −4
Это противоположное значение было найдено для значения 4. А противоположное значение для 4 это −4
−22 = −4
Скобки же имеют самый высокий приоритет выполнения. Поэтому в случае вычисления выражения (−2)2 сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2. В результате получается положительный ответ 4, поскольку произведение отрицательных чисел есть положительное число.
Пример 2. Возвести число −2 в третью степень.
Число −2 в третьей степени это произведение трёх множителей, каждый из которых равен (−2)
(−2)3 = (−2) × (−2) × (−2) = −8
Пример 3. Возвести число −2 в четвёртую степень.
Число −2 в четвёртой степени это произведение четырёх множителей, каждый из которых равен (−2)
(−2)4 = (−2) × (−2) × (−2) × (−2) = 16
Легко заметить, что при возведении в степень отрицательного числа может получиться либо положительный ответ либо отрицательный.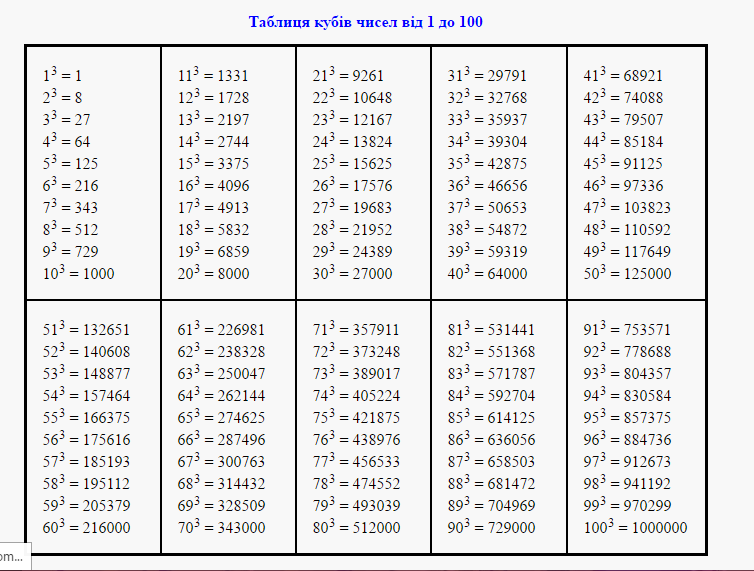 Знак ответа зависит от показателя исходной степени.
Знак ответа зависит от показателя исходной степени.
Если показатель степени чётный, то ответ будет положительным. Если показатель степени нечётный, ответ будет отрицательным. Покажем это на примере числа −3
В первом и в третьем случае показатель был нечётным числом, поэтому ответ стал отрицательным.
Во втором и в четвёртом случае показатель был чётным числом, поэтому ответ стал положительным.
Пример 7. Возвести число −5 в третью степень.
Число −5 в третьей степени это произведение трёх множителей каждый из которых равен −5. Показатель 3 является нечётным числом, поэтому мы заранее можем сказать, что ответ будет отрицательным:
(−5)3 = (−5) × (−5) × (−5) = −125
Пример 8. Возвести число −4 в четвёртую степень.
Число −4 в четвёртой степени это произведение четырёх множителей, каждый из которых равен −4. При этом показатель 4 является чётным, поэтому мы заранее можем сказать, что ответ будет положительным:
(−4)4 = (−4) × (−4) × (−4) × (−4) = 256
Нахождение значений выражений
При нахождении значений выражений, не содержащих скобки, возведение в степень будет выполняться в первую очередь, далее умножение и деление в порядке их следования, а затем сложение и вычитание в порядке их следования.
Пример 1. Найти значение выражения 2 + 52
Сначала выполняется возведение в степень. В данном случае во вторую степень возводится число 5 — получается 25. Затем этот результат складывается с числом 2
2 + 52 = 2 + 25 = 27
Пример 10. Найти значение выражения −62 × (−12)
Сначала выполняется возведение в степень. Заметим, что число −6 не взято в скобки, поэтому во вторую степень будет возведено число 6, затем перед результатом будет поставлен минус:
−62 × (−12) = −36 × (−12)
Завершаем пример, умножив −36 на (−12)
−62 × (−12) = −36 × (−12) = 432
Пример 11. Найти значение выражения −3 × 22
Сначала выполняется возведение в степень. Затем полученный результат перемножается с числом −3
−3 × 22 = −3 × 4 = −12
Если выражение содержит скобки, то сначала нужно выполнить действия в этих скобках, далее возведение в степень, затем умножение и деление, а затем сложение и вычитание.
Пример 12. Найти значение выражения (32 + 1 × 3) − 15 + 5
Сначала выполняем действия в скобках. Внутри скобок применяем ранее изученные правила, а именно сначала возводим во вторую степень число 3, затем выполняем умножение 1 × 3, затем складываем результаты возведения в степень числа 3 и умножения 1 × 3. Далее выполняется вычитание и сложение в порядке их следования. Расставим такой порядок выполнения действия над исходным выражением:
(32 + 1 × 3) − 15 + 5 = 12 − 15 + 5 = 2
Пример 13. Найти значение выражения 2 × 53 + 5 × 23
Сначала возведем числа в степени, затем выполним умножение и сложим полученные результаты:
2 × 53 + 5 × 23 = 2 × 125 + 5 × 8 = 250 + 40 = 290
Тождественные преобразования степеней
Над степенями можно выполнять различные тождественные преобразования, тем самым упрощая их.
Допустим, потребовалось вычислить выражение (23)2. В данном примере два в третьей степени возводится во вторую степень. Иными словами, степень возводится в другую степень.
В данном примере два в третьей степени возводится во вторую степень. Иными словами, степень возводится в другую степень.
(23)2это произведение двух степеней, каждая из которых равна 23
При этом каждая из этих степеней является произведением трёх множителей, каждый из которых равен 2
Получили произведение 2 × 2 × 2 × 2 × 2 × 2, которое равно 64. Значит значение выражения (23)2 или равно 64
Этот пример можно значительно упростить. Для этого показатели выражения (23)2 можно перемножить и записать это произведение над основанием 2
Получили 26. Два в шестой степени это произведение шести множителей, каждый из которых равен 2. Это произведение равно 64
Данное свойство работает по причине того, что 23 это произведение 2 × 2 × 2, которое в свою очередь повторяется два раза. Тогда получается, что основание 2 повторяется шесть раз. Отсюда можно записать, что 2 × 2 × 2 × 2 × 2 × 2 это 26
Отсюда можно записать, что 2 × 2 × 2 × 2 × 2 × 2 это 26
Вообще, для любого основания a с показателями m и n, выполняется следующее равенство:
(an)m = an × m
Это тождественное преобразование называют возведением степени в степень. Его можно прочитать так: «При возведении степени в степень основание оставляют без изменений, а показатели перемножают».
После перемножения показателей, получится другая степень, значение которой можно найти.
Пример 2. Найти значение выражения (32)2
В данном примере основанием является 3, а числа 2 и 2 являются показателями. Воспользуемся правилом возведения степени в степень. Основание оставим без изменений, а показатели перемножим:
Получили 34. А число 3 в четвёртой степени есть 81
Рассмотрим остальные преобразования.
Умножение степеней
Чтобы перемножить степени, нужно по отдельности вычислить каждую степень, и полученные результаты перемножить.
Например, умножим 22 на 33.
22 это число 4, а 33 это число 27. Перемножаем числа 4 и 27, получаем 108
22 × 33 = 4 × 27 = 108
В этом примере основания степеней были разными. В случае, если основания будут одинаковыми, то можно записать одно основание, а в качестве показателя записать сумму показателей исходных степеней.
Например, умножим 22 на 23
В данном примере основания у степеней одинаковые. В этом случае можно записать одно основание 2 и в качестве показателя записать сумму показателей степеней 22 и 23. Иными словами, основание оставить без изменений, а показатели исходных степеней сложить. Выглядеть это будет так:
Получили 25. Число 2 в пятой степени есть 32
Данное свойство работает по причине того, что 22 это произведение 2 × 2, а 23 это произведение 2 × 2 × 2. Тогда получается произведение из пяти одинаковых множителей, каждый из которых равен 2. Это произведение представимо в виде 25
Это произведение представимо в виде 25
Вообще, для любого a и показателей m и n выполняется следующее равенство:
Это тождественное преобразование носит название основного свойства степени. Его можно прочитать так: «При перемножении степеней с одинаковыми основаниями, основание оставляют без изменений, а показатели складывают».
Отметим, что данное преобразование можно применять при любом количестве степеней. Главное, чтобы основание было одинаковым.
Например, найдем значение выражения 21 × 22 × 23. Основание 2 оставим без изменений, а показатели сложим:
В некоторых задачах достаточным бывает выполнить соответствующее преобразование, не вычисляя итоговую степень. Это конечно же очень удобно, поскольку вычислять большие степени не так-то просто.
Пример 1. Представить в виде степени выражение 58 × 25
В данной задаче нужно сделать так, чтобы вместо выражения 58 × 25 получилась одна степень.
Число 25 можно представить в виде 52. Тогда получим следующее выражение:
В этом выражении можно применить основное свойство степени — основание 5 оставить без изменений, а показатели 8 и 2 сложить:
Задачу можно считать решённой, поскольку мы представили выражение 58 × 25 в виде одной степени, а именно в виде степени 510.
Запишем решение покороче:
Пример 2. Представить в виде степени выражение 29 × 32
Число 32 можно представить в виде 25. Тогда получим выражение 29 × 25. Далее можно применить основание свойство степени — основание 2 оставить без изменений, а показатели 9 и 5 сложить. В результате получится следующее решение:
Пример 3. Вычислите произведение 3 × 3, используя основное свойство степени.
Все хорошо знают, что три умножить на три равно девять, но задача требует в ходе решения воспользоваться основным свойством степени.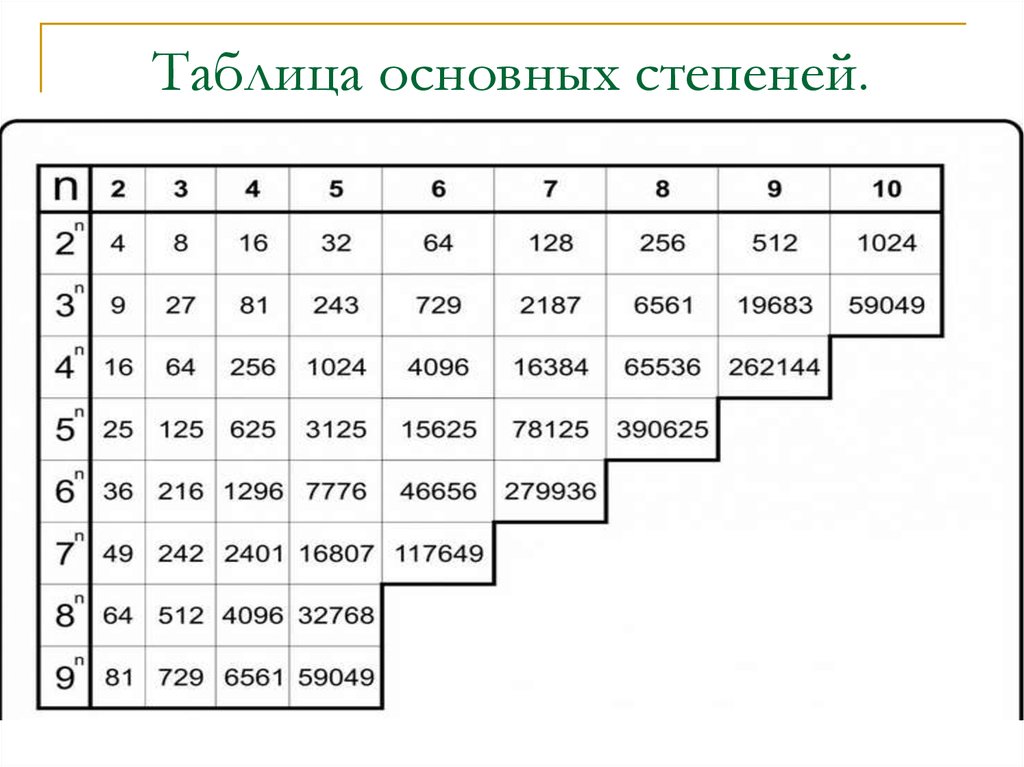 Как это сделать?
Как это сделать?
Вспоминаем, что если число дано без показателя, то показатель нужно считать равным единице. Стало быть сомножители 3 и 3 можно записать в виде 31 и 31
31 × 31
Теперь воспользуемся основным свойством степени. Основание 3 оставляем без изменений, а показатели 1 и 1 складываем:
31 × 31 = 32
Далее вычисляем значение выражения. Число 3 во второй степени равно числу 9
31 × 31 = 32 = 9
Пример 4. Вычислите произведение 2 × 2 × 32 × 33, используя основное свойство степени.
Произведение 2 × 2 заменим на 21 × 21, затем на 21 + 1, а затем на 22. Произведение 32 × 33 заменим на 32 + 3, а затем на 35
Далее вычисляем значение каждой степени и находим произведение:
Пример 5. Выполнить умножение x × x
Выполнить умножение x × x
Это два одинаковых буквенных сомножителя с показателями 1. Для наглядности запишем эти показатели. Далее основание x оставим без изменений, а показатели сложим:
Находясь у доски, не следует записывать перемножение степеней с одинаковыми основаниями так подробно, как это сделано здесь. Такие вычисления нужно выполнять в уме. Подробная запись скорее всего будет раздражать учителя и он снизит за это оценку. Здесь же подробная запись дана, чтобы материал был максимально доступным для понимания.
Решение данного примера желательно записать так:
Пример 6. Выполнить умножение x2 × x
Показатель второго сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 7. Выполнить умножение y3y2y
Показатель третьего сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 8. Выполнить умножение aa3a2a5
Показатель первого сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 9. Представить степень 38 в виде произведения степеней с одинаковыми основаниями.
В данной задаче нужно составить произведение степеней, основания которых будут равны 3, и сумма показателей которых будет равна 8. Можно использовать любые показатели. Представим степень 38 в виде произведения степеней 35 и 33
В данном примере мы опять же опирались на основное свойство степени. Ведь выражение 35 × 33 можно записать как 35 + 3, откуда 38.
Конечно можно было представить степень 38 в виде произведения других степеней. Например, в виде 37 × 31, поскольку это произведение тоже равно 38
Например, в виде 37 × 31, поскольку это произведение тоже равно 38
Представление степени в виде произведения степеней с одинаковыми основаниями это по большей части творческая работа. Поэтому не нужно бояться экспериментировать.
Пример 10. Представить степень x12 в виде различных произведений степеней с основаниями x.
Воспользуемся основным свойство степени. Представим x12 в виде произведений с основаниями x, и сумма показателей которых равна 12
Конструкции с суммами показателей были записаны для наглядности. Чаще всего их можно пропустить. Тогда получится компактное решение:
Возведение в степень произведения
Чтобы возвести в степень произведение, нужно возвести в указанную степень каждый множитель этого произведения и перемножить полученные результаты.
Например, возведём во вторую степень произведение 2 × 3. Возьмём в скобки данное произведение и в качестве показателя укажем 2
Возьмём в скобки данное произведение и в качестве показателя укажем 2
Теперь возведём во вторую степень каждый множитель произведения 2 × 3 и перемножим полученные результаты:
Принцип работы данного правила основан на определении степени, которое было дано в самом начале.
Возвести произведение 2 × 3 во вторую степень означает повторить данное произведение два раза. А если повторить его два раза, то можно получить следующее:
2 × 3 × 2 × 3
От перестановки мест сомножителей произведение не меняется. Это позволяет сгруппировать одинаковые множители:
2 × 2 × 3 × 3
Повторяющиеся множители можно заменить на короткие записи — основания с показателями. Произведение 2 × 2 можно заменить на 22, а произведение 3 × 3 можно заменить на 32. Тогда выражение 2 × 2 × 3 × 3 обращается в выражение 22 × 32.
Пусть ab исходное произведение. Чтобы возвести данное произведение в степень n, нужно по отдельности возвести множители a и b в указанную степень n
Данное свойство справедливо для любого количества множителей. Следующие выражения также справедливы:
Следующие выражения также справедливы:
Пример 2. Найти значение выражения (2 × 3 × 4)2
В данном примере нужно возвести во вторую степень произведение 2 × 3 × 4. Чтобы сделать это, нужно возвести во вторую степень каждый множитель этого произведения и перемножить полученные результаты:
Пример 3. Возвести в третью степень произведение a × b × c
Заключим в скобки данное произведение, и в качестве показателя укажем число 3
Далее возводим в третью степень каждый множитель данного произведения:
Пример 4. Возвести в третью степень произведение 3xyz
Заключим в скобки данное произведение, и в качестве показателя укажем 3
(3xyz)3
Возведём в третью степень каждый множитель данного произведения:
(3xyz)3 = 33x3y3z3
Число 3 в третьей степени равно числу 27. Остальное оставим без изменений:
Остальное оставим без изменений:
(3xyz)3 = 33x3y3z3 = 27x3y3z3
В некоторых примерах умножение степеней с одинаковыми показателями можно заменять на произведение оснований с одним показателем.
Например, вычислим значение выражения 52 × 32. Возведем каждое число во вторую степень и перемножим полученные результаты:
52 × 32 = 25 × 9 = 225
Но можно не вычислять по отдельности каждую степень. Вместо этого, данное произведение степеней можно заменить на произведение с одним показателем (5 × 3)2. Далее вычислить значение в скобках и возвести полученный результат во вторую степень:
52 × 32 = (5 × 3)2 = (15)2 = 225
В данном случае опять же было использовано правило возведения в степень произведения. Ведь, если (a × b)n = an × bn, то an × bn = (a × b)n. То есть левая и правая часть равенства поменялись местами.
То есть левая и правая часть равенства поменялись местами.
Возведение степени в степень
Это преобразование мы рассматривали в качестве примера, когда пытались понять суть тождественных преобразований степеней.
При возведении степени в степень основание оставляют без изменений, а показатели перемножают:
(an)m = an × m
К примеру, выражение (23)2 является возведением степени в степень — два в третьей степени возводится во вторую степень. Чтобы найти значение этого выражения, основание можно оставить без изменений, а показатели перемножить:
(23)2 = 23 × 2 = 26
Далее вычислить степень 26, которая равна 64
(23)2 = 23 × 2 = 26 = 64
Данное правило основано на предыдущих правилах: возведении в степень произведения и основного свойства степени.
Вернёмся к выражению (23)2. Выражение в скобках 23 представляет собой произведение из трёх одинаковых множителей, каждый из которых равен 2. Тогда в выражении (23)2 степень, находящуюся внутри скобок можно заменить на произведение 2 × 2 × 2.
Выражение в скобках 23 представляет собой произведение из трёх одинаковых множителей, каждый из которых равен 2. Тогда в выражении (23)2 степень, находящуюся внутри скобок можно заменить на произведение 2 × 2 × 2.
(2 × 2 × 2)2
А это есть возведение в степень произведения, которое мы изучили ранее. Напомним, что для возведения в степень произведения, нужно возвести в указанную степень каждый множитель данного произведения и полученные результаты перемножить:
(2 × 2 × 2)2 = 22 × 22 × 22
Теперь имеем дело с основным свойством степени. Основание оставляем без изменений, а показатели складываем:
(2 × 2 × 2)2 = 22 × 22 × 22 = 22 + 2 + 2 = 26
Как и раньше получили 26. Значение этой степени равно 64
(2 × 2 × 2)2 = 22 × 22 × 22 = 22 + 2 + 2 = 26 = 64
В степень также может возводиться произведение, сомножители которого тоже являются степенями.
Например, найдём значение выражения (22 × 32)3. Здесь показатели каждого множителя нужно умножить на общий показатель 3. Далее найти значение каждой степени и вычислить произведение:
(22 × 32)3 = 22×3 × 32×3 = 26 × 36 = 64 × 729 = 46656
Примерно тоже самое происходит при возведении в степени произведения. Мы говорили, что при возведении в степень произведения, в указанную степень возводится каждый множитель этого произведения.
Например, чтобы возвести произведение 2 × 4 в третью степень, нужно записать следующее выражение:
Но ранее было сказано, что если число дано без показателя, то показатель надо считать равным единице. Получается, что множители произведения 2 × 4 изначально имеют показатели равные 1. Значит в третью степень возводилось выражение 21 × 41. А это есть возведение степени в степень.
Перепишем решение с помощью правила возведения степени в степень. У нас должен получиться тот же результат:
Пример 2. Найти значение выражения (33)2
Основание оставляем без изменений, а показатели перемножаем:
Получили 36. Число 3 в шестой степени есть число 729
Пример 3. Выполнить возведение в степень в выражении (xy)³
Возведём в третью степень каждый множитель произведения:
Пример 4. Выполнить возведение в степень в выражении (abc)⁵
Возведём в пятую степень каждый множитель произведения:
Пример 5. Выполнить возведение в степень в выражении (−2ax)3
Возведём в третью степень каждый множитель произведения:
Поскольку в третью степень возводилось отрицательное число −2, оно было взято в скобки.
Далее нужно вычислить то, что вычисляется. В данном случае можно вычислить (−2)3 — получится −8. Буквенная часть останется без изменений:
Пример 6. Выполнить возведение в степень в выражении (10xy)2
Пример 7. Выполнить возведение в степень в выражении (−5x)3
Пример 8. Выполнить возведение в степень в выражении (−3y)4
Пример 9. Выполнить возведение в степень в выражении (−2abx)⁴
Пример 10. Упростите выражение x5 × (x2)3
Степень x5 пока оставим без изменений, а в выражении (x2)3 выполним возведение степени в степени:
x5 × (x2)3 = x5 × x2 × 3 = x5 × x6
Теперь выполним умножение x5× x6. Для этого воспользуемся основным свойством степени — основание x оставим без изменений, а показатели сложим:
x5 × (x2)3 = x5 × x2× 3 = x5 × x6 = x5 + 6 = x11
Пример 9. Найти значение выражения 43 × 22, используя основное свойство степени.
Основное свойство степени можно использовать в случае, если основания исходных степеней одинаковы. В данном примере основания разные, поэтому для начала исходное выражение нужно немного видоизменить, а именно сделать так, чтобы основания степеней стали одинаковыми.
Посмотрим внимательно на степень 43. Основание у этой степени есть число 4, которое можно представить в виде 22. Тогда исходное выражение примет вид (22)3 × 22. Выполнив возведение степени в степень в выражении (22)3, мы получим 26. Тогда исходное выражение примет вид 26 × 22, вычислить которое можно, используя основное свойство степени.
Запишем решение данного примера:
Деление степеней
Чтобы выполнить деление степеней, нужно найти значение каждой степени, затем выполнить деление обыкновенных чисел.
Например, разделим 43 на 22.
Вычислим 43, получим 64. Вычислим 22, получим 4. Теперь разделим 64 на 4, получим 16
Если при делении степеней основания окажутся одинаковыми, то основание можно оставить без изменений, а из показателя степени делимого вычесть показатель степени делителя.
Например, найдем значение выражения 23 : 22
Основание 2 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Значит, значение выражения 23 : 22 равно 2.
Данное свойство основано на умножении степеней с одинаковыми основаниями, или как мы привыкли говорить на основном свойстве степени.
Вернемся к предыдущему примеру 23 : 22. Здесь делимое это 23, а делитель 22.
Разделить одно число на другое означает найти такое число, которое при умножении на делитель даст в результате делимое.
В нашем случае, разделить 23 на 22 означает найти такую степень, которая при умножении на делитель 22 даст в результате 23. А какую степень можно умножить на 22, чтобы получить 23 ? Очевидно, что только степень 21. Из основного свойства степени имеем:
Убедиться, что значение выражения 23 : 22 равно 21 можно непосредственно вычислив само выражение 23 : 22. Для этого сначала найдём значение степени 23, получим 8. Затем найдём значение степени 22, получим 4. Разделим 8 на 4, получим 2 или 21, поскольку 2 = 21.
23 : 22 = 8 : 4 = 2
Таким образом, при делении степеней с одинаковыми основаниями выполняется следующее равенство:
Может случиться и так, что одинаковыми могут оказаться не только основания, но и показатели. В этом случае в ответе получится единица.
Например, найдём значение выражения 22 : 22. Вычислим значение каждой степени и выполним деление получившихся чисел:
При решении примера 22 : 22 также можно применить правило деления степеней с одинаковыми основаниями. В результате получается число в нулевой степени, поскольку разность показателей степеней 22 и 22 равна нулю:
В математике принято считать, что любое число в нулевой степени есть единица:
Почему число 2 в нулевой степени равно единице мы выяснили выше. Если вычислить 22 : 22 обычным методом, не используя правило деления степеней, получится единица.
Пример 2. Найти значение выражения 412 : 410
Воспользуемся правилом деления степеней. Основание 4 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
412 : 410 = 412 − 10 = 42 = 16
Пример 3. Представить частное x3 : x в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя. Показатель делителя равен единице. Для наглядности запишем его:
Пример 4. Представить частное x3 : x2 в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Деление степеней можно записывать в виде дроби. Так, предыдущий пример можно записать следующим образом:
Числитель и знаменатель дроби разрешается записывать в развёрнутом виде, а именно в виде произведений одинаковых множителей. Степень x3 можно записать как x × x × x, а степень x2 как x × x. Тогда конструкцию x3 − 2 можно будет пропустить и воспользоваться сокращением дроби. В числителе и в знаменателе можно будет сократить по два множителя x. В результате останется один множитель x
Или ещё короче:
Также, полезно уметь быстро сокращать дроби, состоящие из степеней. Например, дробь можно сократить на x2. Чтобы сократить дробь на x2 нужно числитель и знаменатель дроби разделить на x2
Деление степеней подробно можно не расписывать. Приведённое сокращение можно выполнить короче:
Или ещё короче:
Пример 5. Выполнить деление x12 : x3
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Запишем решение при помощи сокращения дроби. Деление степеней x12 : x3 запишем в виде . Далее сократим данную дробь на x3.
Пример 6. Найти значение выражения
В числителе выполним умножение степеней с одинаковыми основаниями:
Теперь применяем правило деления степеней с одинаковыми основаниями. Основание 7 оставляем без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Завершаем пример, вычислив степень 72
Пример 7. Найти значение выражения
Выполним в числителе возведение степени в степень. Сделать это нужно с выражением (23)4
Теперь выполним в числителе умножение степеней с одинаковыми основаниями:
Теперь применяем правило деления степеней с одинаковыми основаниями:
Значит, значение выражения равно 16
В некоторых примерах можно сокращать одинаковые множители в ходе решения. Это позволяет упростить выражение и само вычисление в целом.
Например, найдём значение выражения . Степень 43 запишем в виде возведения степени в степень (22)3. Тогда получим следующее выражение:
В числителе выполним возведение степени в степень. Сделать это нужно с выражением (22)3
В числителе и в знаменателе получившегося выражения содержится степень 26, которую можно сократить на 26
Видим, что в результате осталась единственная степень 32, значение которой равно 9.
Пример 8. Найти значение выражения
В знаменателе содержится произведение степеней с одинаковыми показателями. Согласно правилу возведения в степень произведения, конструкцию 75 × 45 можно представить в виде степени с одним показателем (7 × 4)5. Далее перемножим выражение в скобках, получим 285. В результате исходное выражение примет следующий вид:
Теперь можно применить правило деления степеней:
Значит, значение выражения равно 28. Запишем решение полностью:
Возведение в степень обыкновенных дробей
Чтобы возвести в степень обыкновенную дробь, нужно возвести в указанную степень числитель и знаменатель этой дроби.
Например, возведём обыкновенную дробь во вторую степень. Возьмём в скобки данную дробь и в качестве показателя укажем 2
Если не брать в скобки всю дробь, то это равносильно возведению в степень только числителя данной дроби. Иными словами, если мы хотим возвести во вторую степень дробь , мы не должны записывать это как .
Итак, чтобы вычислить значение выражения , нужно возвести во вторую степень числитель и знаменатель данной дроби:
Получили дробь в числителе и в знаменателе которой содержатся степени. Вычислим каждую степень по отдельности
Значит обыкновенная дробь во второй степени равна дроби .
Приведённое правило работает следующим образом. Дробь во второй степень это произведение двух дробей, каждая из которых равна
Мы помним, что для перемножения дробей необходимо перемножить их числители и знаменатели:
А поскольку в числителе и в знаменателе происходит перемножение одинаковых множителей, то выражения 2 × 2 и 3 × 3 можно заменить на 22 и 32 соответственно:
Откуда и получится ответ .
Вообще, для любого a и b ≠ 0 выполняется следующее равенство:
Это тождественное преобразование называют возведением в степень обыкновенной дроби.
Пример 2. Возвести дробь в третью степень
Заключим данную дробь в скобки и в качестве показателя укажем число 3. Далее возведём числитель и знаменатель данной дроби в третью степень и вычислим получившуюся дробь:
Отрицательная дробь возводится в степень таким же образом, но перед вычислениями надо определиться какой знак будет иметь ответ. Если показатель четный, то ответ будет положительным. Если показатель нечетный, то ответ будет отрицательным.
Например, возведём дробь во вторую степень:
Показатель является чётным числом. Значит ответ будет положительным. Далее применяем правило возведения в степень дроби и вычисляем получившуюся дробь:
Ответ положителен по причине того, что выражение представляет собой произведение двух сомножителей, каждый из которых равен дроби
А произведение отрицательных чисел (в том числе и рациональных) есть положительное число:
Если возводить дробь в третью степень, то ответ будет отрицательным, поскольку в данном случае показатель будет нечётным числом. Правило возведения в степень остаётся тем же, но перед выполнением этого возведения, нужно будет поставить минус:
Здесь ответ отрицателем по причине того, что выражение представляет собой произведение трёх множителей, каждый из которых равен дроби
Сначала перемножили и , получили , но затем умножив на мы получим отрицательный ответ
Пример 3. Найти значение выражения
Выполним возведение в степень обыкновенной дроби:
Далее вычислим значение получившегося выражения:
Возведение в степень десятичных дробей
При возведении в степень десятичной дроби её необходимо заключить в скобки. Например, возведём во вторую степень десятичную дробь 1,5
Допускается переводить десятичную дробь в обыкновенную и возводить в степень эту обыкновенную дробь. Решим предыдущий пример, переведя десятичную дробь в обыкновенную:
Пример 2. Найти значение степени (−1,5)3
Показатель степени является нечётным числом. Значит ответ будет отрицательным
Пример 3. Найти значение степени (−2,4)2
Показатель степени является чётным числом. Значит ответ будет положительным:
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Задание 6. Найдите значение выражения:
Решение:
Задание 7. Представьте в виде степени произведение:
Решение:
Задание 8. Представьте в виде степени произведение:
Решение:
Задание 9. Представьте в виде степени произведение:
Решение:
Задание 10. Представьте в виде степени произведение:
Решение:
Задание 11. Представьте в виде степени произведение:
Решение:
Задание 12. Представьте в виде степени произведение:
Решение:
Задание 13. Представьте в виде степени частное:
Решение:
Задание 14. Представьте в виде степени частное:
Решение:
Задание 15. Представьте в виде степени частное:
Решение:
Задание 16. Представьте в виде степени частное:
Решение:
Задание 17. Представьте в виде степени частное:
Решение:
Задание 18. Представьте в виде степени частное и найдите значение получившейся степени при x = 3 и n = 2Решение:
Задание 19. Представьте в виде степени частное:
Решение:
Задание 20. Сократите дробь на c¹Решение:
Задание 21. Представьте в виде степени следующее произведение:
Решение:
Задание 22. Представьте в виде степени следующее произведение:
Решение:
Задание 23. Представьте в виде степени следующее произведение:
Решение:
Задание 24. Представьте в виде степени следующее произведение:
Решение:
Задание 25. Представьте в виде степени следующее произведение:
Решение:
Задание 26. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 27. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 28. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 29. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 30. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 31. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 32. Представьте в виде степени следующее выражение:
Решение:
Задание 33. Представьте в виде степени следующее выражение:
Решение:
Задание 34. Представьте в виде степени следующее выражение:
Решение:
Задание 35. Представьте в виде степени следующее выражение:
Решение:
Задание 36. Представьте в виде степени следующее выражение:
Решение:
Задание 37. Представьте в виде степени следующее выражение:
Решение:
Задание 38. Найдите значение следующего выражения:
Решение:
Задание 39. Найдите значение следующего выражения:
Решение:
Задание 40. Найдите значение следующего выражения:
Решение:
Задание 41. Найдите значение следующего выражения:
Решение:
Задание 42. Найдите значение следующего выражения:
Решение:
Задание 43. Найдите значение следующего выражения:
Решение:
Задание 44. Найдите значение следующего выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Таблица кубов натуральных чисел от 1 до 209
Число в кубе (в третей степени) это результат умножения заданного числа трижды на самого себя. x3 = x • x • x (если к примеру х=3, то по формуле возведя его в куб, мы получим 33 = 3 • 3 • 3 = 27;
Пример: ab3 = 103 = 1… + …03 = 1000 …
| ab3 | …03 | …13 | …23 | …33 | …43 | …53 | …63 | …73 | …83 | …93 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0… | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |
| 1… | 1 000 | 1 331 | 1 728 | 2 197 | 2 744 | 3 375 | 4 096 | 4 913 | 5 832 | 6 859 |
| 2… | 8 000 | 9 261 | 10 648 | 12 167 | 13 824 | 15 625 | 17 576 | 19 683 | 21 952 | 24 389 |
| 3… | 27 000 | 29 791 | 32 768 | 35 937 | 39 304 | 42 875 | 46 656 | 50 653 | 54 872 | 59 319 |
| 4… | 64 000 | 68 921 | 74 088 | 79 507 | 85 184 | 91 125 | 97 336 | 103 823 | 110 592 | 117 649 |
| 5… | 125 000 | 132 651 | 140 608 | 148 877 | 157 464 | 166 375 | 175 616 | 185 193 | 195 112 | 205 379 |
| 6… | 216 000 | 226 981 | 238 328 | 250 047 | 262 144 | 274 625 | 287 496 | 300 763 | 314 432 | 328 509 |
| 7… | 343 000 | 357 911 | 373 248 | 389 017 | 405 224 | 421 875 | 438 976 | 456 533 | 474 552 | 493 039 |
| 8… | 512 000 | 531 441 | 551 368 | 571 787 | 592 704 | 614 125 | 636 056 | 658 503 | 681 472 | 704 969 |
| 9… | 729 000 | 753 571 | 778 688 | 804 357 | 830 584 | 857 375 | 884 736 | 912 673 | 941 192 | 970 299 |
| 10… | 1 000 000 | 1 030 301 | 1 061 208 | 1 092 727 | 1 124 864 | 1 157 625 | 1 191 016 | 1 225 043 | 1 259 712 | 1 295 029 |
| 11… | 1 331 000 | 1 367 631 | 1 404 928 | 1 442 897 | 1 481 544 | 1 520 875 | 1 560 896 | 1 601 613 | 1 643 032 | 1 685 159 |
| 12… | 1 728 000 | 1 771 561 | 1 815 848 | 1 860 867 | 1 906 624 | 1 953 125 | 2 000 376 | 2 048 383 | 2 097 152 | 2 146 689 |
| 13… | 2 197 000 | 2 248 091 | 2 299 968 | 2 352 637 | 2 406 104 | 2 460 375 | 2 515 456 | 2 571 353 | 2 628 072 | 2 685 619 |
| 14… | 2 744 000 | 2 803 221 | 2 863 288 | 2 924 207 | 2 985 984 | 3 048 625 | 3 112 136 | 3 176 523 | 3 241 792 | 3 307 949 |
| 15… | 3 375 000 | 3 442 951 | 3 511 808 | 3 581 577 | 3 652 264 | 3 723 875 | 3 796 416 | 3 869 893 | 3 944 312 | 4 019 679 |
| 16… | 4 096 000 | 4 173 281 | 4 251 528 | 4 330 747 | 4 410 944 | 4 492 125 | 4 574 296 | 4 657 463 | 4 741 632 | 4 826 809 |
| 17… | 4 913 000 | 5 000 211 | 5 088 448 | 5 177 717 | 5 268 024 | 5 359 375 | 5 451 776 | 5 545 233 | 5 639 752 | 5 735 339 |
| 18… | 5 832 000 | 5 929 741 | 6 028 568 | 6 128 487 | 6 229 504 | 6 331 625 | 6 434 856 | 6 539 203 | 6 644 672 | 6 751 269 |
| 19… | 6 859 000 | 6 967 871 | 7 077 888 | 7 189 057 | 7 301 384 | 7 414 875 | 7 529 536 | 7 645 373 | 7 762 392 | 7 880 599 |
| 20… | 8 000 000 | 8 120 601 | 8 242 408 | 8 365 427 | 8 489 664 | 8 615 125 | 8 741 816 | 8 869 743 | 8 998 912 | 9 129 329 |
…
Как распечатать таблицу? Левой кнопкой на мишке выделите полностью всё таблицу, на выделенном фоне нажмите правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Как пользоваться таблицей? Допустим, что Вам конкретно нужно узнать куб такого двухзначного числа, как 25, для этого в крайней левой вертикальной колонке (отмечена синим цветом) находим строчку с указанием нужных десятков — 2… , после в верхнем горизонтальном рядке ищем пункт …53 , в условном месте пересечении этих двух цифр будет находится правильный ответ, в нашем случае 15625. (Пример: 253= 2… + …53 = 15625)
Автор: Bill4iam
Опухолевые маркеры: Рак яичников (РЯ)
Для эпителиального рака яичников наиболее информативным из существующих маркеров считается муцин или СА125. Этот высокомолекулярный гликопротеид экспрессируется клетками целомического эпителия, покрывающего опухоли яичников. Функция этого антигена в норме неизвестна. Маркер неспецифичен, повышается при метастатическом поражении брюшины из опухолей других органов, при эндометриозе, в 3-м триместре беременности, при панкреатитах, циррозе печени и лимфомах.
При муцинозных опухолях более чувствительными опухолевыми маркерами являются СА72.4 или СА199. Если они повышены у пациентки на старте лечения, то дальнейший мониторинг следует проводить с использованием соответствующего опухолевого маркера.
При подозрении на рак яичников у молодых женщин и девочек-подростков с большой вероятностью может иметь место герминогенная опухоль. Ведущими маркерами при этой патологии являются АФП и ХГЧ.
Скрининг. Ввиду недостаточной чувствительности при ранних стадиях болезни и недостаточной специфичности не рекомендуется использовать СА125 для скрининга в общей популяции с целью выявления спорадических форм РЯ. Однако у женщин с наследственным синдромом РЯ или РМЖ, у которых наблюдаются мутации генов BRCA1 и BRCA2, СА125 следует определять каждые полгода в целях ранней детекции РЯ.
Диагностика. При анализе результатов СА125 важно учитывать возраст больных. У молодых женщин повышение уровня СА125 может быть связано с определёнными физиологическими состояниями (менструация, беременность), с различными воспалительными заболеваниями придатков, эндометриозом и т.п. У женщин в постменопаузе воспалительные процессы в органах таза встречаются редко, поэтому уровень СА125 выше 65 Е/мл, в особенности при наличии кистозных образований, выявленных клинически или на УЗИ, означает РЯ с вероятностью 90%. В то же время необходимо учитывать, что уровни СА125 могут быть повышенными при любых патологиях, связанных с воспалением брюшины, плевры или перикарда, и не всегда указывают на РЯ, если нет чётких клинических данных об изменениях в этом органе. Окончательный диагноз рака яичников возможен лишь при исследовании гистопатологический образцов, полученных при операции.
Прогноз. Уровни СА125 до и на различных этапах лечения могут иметь прогностическое значение. Показано, что выживаемость пациенток с СА125 до операции менее 65 Е/мл значительно выше по сравнению с больными, у которых уровни маркера превышали это значение. Уровни СА125 после 1-го, 2-го или 3-го курсов химиотерапии являются чёткими индикаторами прогноза заболевания. Показано, что концентрация СА125 выше 70 Е/мл перед 3-м курсом была связана с прогрессированием заболевания в ближайшие 12 мес. Скорость снижения СА125 после циторедуктивной операции или в ходе цитотоксической химиотерапии также может использоваться в качестве независимого прогностического фактора с целью определения необходимости в дальнейшей дополнительной химиотерапии.
Мониторинг. После потенциально радикальной операции и цитотоксической химиотерапии СА125 следует определять каждые 3 месяца с целью раннего выявления рецидива. ДУ у радикально оперированных больных должен быть снижен приблизительно в 2 раза (до 15-17 Е/мл). Устойчивое повышение уровня СА125 выше ДУ, либо сохраняющийся при повторном исследовании уровень выше нормы, являются первым подозрительным в отношении рецидива сигналом. Этот факт является основанием для проведения second look даже при незначительном повышении уровня маркера и несмотря на то, что другие диагностические процедуры могут быть отрицательными. Мониторинг с использованием СА125 является средством не только более раннего, но и более дешёвого выявления рецидива по сравнению с радиологическими процедурами. Вопрос о том, является ли повышение СА125 достаточным основанием для проведения терапии до появления симптоматики, остаётся открытым, поскольку пока нет доказательных данных о том, что её результатом будет увеличение выживаемости.
Оценка эффективности терапии. СА125 коррелирует с клиническим состоянием: его уровень повышается при прогрессировании, остаётся неизменным при стабилизации процесса и снижается при регрессии опухоли. Стабильно не снижающиеся на фоне терапии значения СА125 связаны с прогрессированием заболевания в более чем 90% случаев и показывают неэффективность терапии. При этом маркер может быть полезен как для выбора терапии, так и для изменения схемы лечения в случае её неэффективности.
Амиксин: инструкция по применению
Торговое название препарата: Амиксин®
Международное непатентованное название: Тилорон
Химическое название: дигидрохлорид 2,7-бис-[2(диэтиламино)-этокси]-флуорен-9-она
Лекарственная форма препарата: таблетки, покрытые плёночной оболочкой
Описание
Состав на одну таблетку
Фармакологические свойства
Показания к применению
Противопоказания
Применение при беременности и в период грудного вскармливания
Способ применения и дозы
Побочное действие
Передозировка
Взаимодействие с другими лекарственными средствами
Влияние на способность управлять транспортными средствами, механизмами
Форма выпуска
Срок годности
Условия хранения
Условия отпуска из аптек
Наименование и адрес производителя/организация, принимающая претензии потребителей
Таблетки, покрытые пленочной оболочкой оранжевого цвета, круглые, двояковыпуклые. На изломе оранжевого цвета, допускаются незначительные вкрапления оранжевого и белого цвета.
Состав на одну таблеткуТилорон — 60 мг или 125 мг.
Вспомогательные вещества:
ядро: крахмал картофельный – 25,500 мг или 46,000 мг, целлюлоза микрокристаллическая – 60,000 мг или 120,000 мг, повидон-К30 (коллидон 30) – 1,500 мг или 3,000 мг, кальция стеарат – 1,500 мг или 3,000 мг, кроскармеллоза натрия (примеллоза) – 1,500 мг или 3,000 мг;
оболочка: гипромеллоза (гидроксипропилметилцеллюлоза) – 3,4050 мг или 6,8100 мг, титана диоксид – 1,7815 мг или 3,5630 мг, макрогол-4000 (полиэтиленгликоль-4000) – 0,4565 мг или 0,9130 мг, полисорбат-80 (твин-80) – 0,0570 мг или 0,1140 мг, краситель хинолиновый желтый (Е 104) – 0,1235 мг или 0,2470 мг, краситель «солнечный закат» желтый (Е 110) – 0,1765 мг или 0,3530 мг.
Фармакотерапевтическая группа: противовирусное иммуностимулирующее средство – индуктор образования интерферонов.
Код АТХ: J05АХ
Фармакологические свойстваФармакодинамика.
Низкомолекулярный синтетический индуктор интерферона, стимулирующий образование в организме интерферонов всех типов (альфа, бета, гамма и лямбда). Основными продуцентами интерферона в ответ на введение тилорона являются клетки эпителия кишечника, гепатоциты, T-лимфоциты, нейтрофилы и гранулоциты. После приема препарата внутрь максимум продукции интерферона определяется в последовательности кишечник – печень – кровь через 4–24 ч. Амиксин® обладает иммуномодулирующим и противовирусным эффектом. В лейкоцитах человека он индуцирует синтез интерферона. Также он стимулирует стволовые клетки костного мозга, в зависимости от дозы усиливает антителообразование, уменьшает степень иммунодепрессии, восстанавливает соотношения T-супрессоров и T-хелперов. Препарат эффективен против различных вирусных инфекций, в том числе вирусов гриппа, других острых респираторных вирусных инфекций, вирусов гепатита и герпес-вирусов. Механизм антивирусного действия связан с ингибированием трансляции вирус-специфических белков в инфицированных клетках, в результате чего подавляется репродукция вирусов.
Фармакокинетика.
После приема внутрь препарат Амиксин® быстро всасывается из желудочно-кишечного тракта. Биодоступность – 60 %. Около 80 % препарата связывается с белками плазмы. Выводится препарат практически в неизмененном виде через кишечник (70 %) и через почки (9 %). Период полувыведения (T1/2) – 48 часов. Препарат не подвергается биотрансформации и не накапливается в организме.
В составе комплексной терапии
У детей от 7 до 18 лет:
— для лечения гриппа и других острых респираторных вирусных инфекций(ОРВИ).
У взрослых (старше 18 лет):
— лечение гриппа и других ОРВИ;
— лечение герпетической инфекции
Профилактика гриппа и других ОРВИ у взрослых:
— в составе комплексной терапии инфекционно-аллергических и вирусных.
Повышенная чувствительность к тилорону или любому другому компоненту препарата.
Беременность и период грудного вскармливания. Детский возраст до 7 лет (для дозировки 60мг), детский возраст до 18 лет (для дозировки 125мг).
Применение при беременности и в период грудного вскармливанияПрименение Амиксина® при беременности противопоказано. При необходимости применения препарата в период лактации грудное вскармливание следует прекратить.
Способ применения и дозы
Амиксин® принимают внутрь после еды.
Для детей от 7 до 18 лет:При неосложненных формах гриппа и других ОРВИ — по 60 мг 1 раз в день на 1-й, 2-й и 4-й день от начала лечения. Курсовая доза — 180 мг (3 таблетки).
Для взрослых (старше 18 лет). Для лечения гриппа и других ОРВИ – по 125 мг в сутки первые 2 дня лечения, затем по 125 мг через 48 часов. Курсовая доза Амиксина® – 750 мг (6 таблеток).
Для профилактики гриппа и других ОРВИ – по 125 мг 1 раз в неделю в течение 6 недель. На курс — 750 мг (6 таблеток).
Для лечения герпетической, цитомегаловирусной инфекции – первые двое суток по 125 мг, затем через 48 часов по 125 мг. Курсовая доза – 1,25–2,5 г (10–20 таблеток).
При лечении гриппа и других ОРВИ в случае сохранения симптомов заболевания более 4-х дней следует проконсультироваться у врача
Побочное действиеВозможны аллергические реакции, диспепсические явления, кратковременный озноб.
Если любые из указанных в инструкции побочных эффектов усугубляются, или Вы заметили любые другие побочные эффекты, не указанные в инструкции, сообщите об этом врачу.
ПередозировкаСлучаи передозировки Амиксина® не известны.
Взаимодействие с другими лекарственными средствамиСовместим с антибиотиками и лекарственными средствами традиционного лечения вирусных и бактериальных заболеваний. Клинически значимого взаимодействия Амиксина® с антибиотиками и средствами традиционного лечения вирусных и бактериальных заболеваний не выявлено.
Влияние на способность управлять транспортными средствами, механизмамиПрепарат не оказывает отрицательного влияния на способность к управлению транспортными средствами и занятиям другими потенциально опасными видами деятельности, требующими повышенной концентрации внимания и быстроты психомоторных реакций.
Форма выпуска
Таблетки, покрытые пленочной оболочкой 60 мг, 125 мг. По 6 или 10 таблеток в контурной ячейковой упаковке; по 6, 10 или 20 таблеток в полимерной банке. 1 или 2 контурные ячейковые упаковки или 1 полимерная банка вместе с инструкцией к Амиксину в пачке из картона.
Срок годности3 года. Не применять Амиксин® по истечении срока годности, указанного на упаковке.
Условия храненияВ защищенном от света месте, при температуре не выше 30 °C. Хранить Амиксин® в недоступном для детей месте.
Условия отпуска из аптекБез рецепта.
Наименование и адрес производителя/организация, принимающая претензии потребителей:При производстве на ОАО «Фармстандарт-Томскхимфарм»:
ОАО «Фармстандарт-Томскхимфарм», 634009, Россия, г. Томск, пр. Ленина, д. 211, тел./факс. (3822) 40-28-56, www.pharmstd.ru
Двигатель Duratec Ti VCT 1.6 125 л.с.| Неисправности и тюниг
Характеристика двигателя Форд Фокус 3 1.6 125 л.с.
Производство — Bridgend Engine
Годы выпуска – (2010 – наши дни)
Материал блока цилиндров – алюминий
Система питания – инжектор
Тип – рядный
Количество цилиндров – 4
Клапанов на цилиндр – 4
Ход поршня – 81,4 мм
Диаметр цилиндра – 79 мм
Степень сжатия – 11
Объем мотора – 1596 см. куб.
Мощность двигателя Форд Фокус 3 – 125 л.с. /6300 об.мин
Крутящий момент – 159Нм/4100 об.мин
Топливо – 95
Экологические нормы – Евро 5
Расход топлива — город 8 л. | трасса 4,7 л. | смешанн. 5,9 л/100 км
Расход масла – 200 г/1000 км
Сухой вес двигателя Duratec 1.6 ~90 кг.
Геометрические размеры двигателя Фокус 1.6 (ДхШхВ), мм —
Тип масла:
5W-20
5W-30
Ресурс :
1. По данным завода – 250 тыс. км.
2. На практике – 300-350 тыс. км
ТЮНИНГ
Потенциал – неизвестно
Без потери ресурса – неизвестно
Двигатель устанавливался на:
Ford C-Max
Ford Focus Mk. III
Ford Mondeo Mk IV
Ford Fiesta
Неисправности и ремонт двигателя Форд Фокус 3 Ti-VCT 125 л.с.
Двигатель Ford Focus Duratec Ti-VCT 1,6 л. 125 л.с. тот же самый Duratec Ti-VCT 1,6 105 л.с. c системой изменения фаз газораспределения, но с другими распредвалами, измененными фазами газораспределения, другим выхлопом, более ранней отсечкой, отсюда имеем прирост мощности на 20 л.с. Ресурс двигателя форда фокуса 1.6 125 л.с. по данным завода составляет 250 тыс. км. Зная, что мотор представяет собой старый 115-сильный от фокуса II, можно предположить реальный моторесурс в 300-350 тыс.
Привод ГРМ у мотора ременной, обязательно раз в 160 тыс.км. проводится замена роликов и ремня. Как и все прошлые модели 1,6 литрового движка, так же надежен, без явных слабых мест, но по словам владельцев, едет он хуже старого 1,6 115 л.с. В остальное косяки и недостатки те же, что и на предыдущих Зетеках.
Для Ford Fiesta Mk VI данный мотор выпускается в дефорсированном варианте, мощностью 120 л.с.
Тюнинг двигателя Ford Focus 1,6 125 л.с.
Доработки данного мотора 1 в 1 повторяют то, что делалось на прошлом дорестайлинговом двигателе форд фокус 2. Об этом читаем в статье тюнинг Ti-VCT 115 л.с.
РЕЙТИНГ ДВИГАТЕЛЯ: 4
<<НАЗАД
Найдите значение 125 в степени -2/3.
Мы хотим найти 125 -2/3 . Для этого нам нужно будет использовать множество правил мощности, которые мы узнали.
Во-первых, когда мы помещаем одну степень в другую, мы умножаем две степени. Например, (2 3 ) 4 (2 в степени 3, ВСЕ в степени 4) равно 2 3×4 = 2 12 .
Мы собираемся использовать это правило в обратном порядке. Мы можем переписать нашу степень, -2/3, как произведение чисел, с которыми мы умеем работать, в качестве степеней.
Примеры умений, которые мы умеем использовать:
Положительные целые числа, такие как 2 или 3: мы просто умножаем число само на себя столько раз, как обычно.
-1: мы ставим число «на единицу». Например, 3 -1 = 1/3.
Дробные степени вида 1 / n: берем корень n-й степени. Например, 4 1/2 = квадратный корень из 4 = 2.
Во-первых, мы можем исключить негатив, чтобы упростить себе жизнь, поскольку мы знаем, как работать с -1 в качестве силы.Итак, -2/3 = -1 x 2/3.
Во-вторых, мы умеем использовать дробные степени, если у них в числителе стоит 1. Итак, 2/3 = 2 x 1/3.
Собирая все вместе, получаем -2/3 = -1 * 2 * 1/3.
Теперь вернемся к нашему первоначальному вопросу!
Мы хотим найти 125 -2/3 , которые мы теперь можем переписать, используя наше правило «мощности мощности» в обратном порядке, чтобы получить ((125 1/3 ) 2 ) -1 . Поскольку мы можем умножать числа в любом порядке и при этом получать тот же результат, мы можем применять эти полномочия в любом порядке. Но, одни заказы часто бывают проще, чем другие. Мне нравится использовать отрицательные силы в последнюю очередь, потому что тогда нам не нужно работать с дробями. Также здесь я заметил интересное свойство числа 125 — это число куба! Конкретно 5 кубов! Итак, я использую степень 1/3, которая является кубическим корнем, во-первых, чтобы сделать вещи удобными и простыми для себя.
Теперь нам просто нужно выполнить наши полномочия одну за другой, чтобы ответить на вопрос.
125 1/3 = кубический корень из 125 = 5.(-2) «.
Шаг 1:
125
Упростить ———
216
Уравнение в конце шага 1:
125 ———) -2 ) ÷ 3 216
Шаг 2:
2.1 Возведение в отрицательную степень Увеличение числа до отрицательной степени означает, что на 1 больше этого числа. то же число, но теперь с положительной экспонентой. Например, x (-2) равно 1 / x (2) 2.2 Отрицательное число, возведенное в четную степень, является положительным.
Например, давайте посмотрим на (-7) 6 , где (-7), отрицательное число, увеличивается до 6, четный показатель степени:
(-7) 6 можно записать как (-7 ) • (-7) • (-7) • (-7) • (-7) • (-7)
Теперь, используя правило, согласно которому минус, умноженный на минус, равен плюс, (-7) 6 может быть записывается как (49) • (49) • (49), что, в свою очередь, может быть записано как (7) • (7) • (7) • (7) • (7) • (7) или 7 6 , что является положительный.
Мы доказали, что (-7) 6 равно (7) 6 , которое является положительным числом
Используя те же аргументы, что и выше, заменив (-7) любым отрицательным числом и заменив экспоненту 6 по любому четному показателю мы доказали, что должно было быть доказано
2.3 125 = 5 3 (-125) -2 = (5 3 ) (-2) = (5) (-6 ) 2,4 216 = 2 3 • 3 3 (216) -2 = (2 3 • 3 3 ) (-2) = (2) (-6) • (3) (-6)
Уравнение в конце шага 2:
(5) (-6) ————————————————— 3 ((2) (-6) • (3) (-6) )
Шаг 3:
(5) (-6)
Разделите ————————————————— на 3
((2) (-6) • (3) (-6) )
Показатели деления:
3.1 3 6 разделить на 3 1 = 3 (6 — 1) = 3 5
Конечный результат:
(2 6 • 3 5 )
——————— = 0,99533
5 6 Видео с вопросом: Оценка выражения с помощью рациональной базы и положительной рациональной экспоненты
Стенограмма видео
Оцените 125 по 343 в степени двух третей.
Первое, что здесь стоит отметить, это что наша дробь, две трети, является экспонентой или степенью. И это не значит, что мы умножив его на дробь 125 на 343. Для начала возьмем показатель степени этой дроби и запишем ее как показатель числителя и показатель степени знаменатель. Другими словами, мы можем использовать правило что если у нас есть дробь над в степени, это эквивалентно власть 𝑎 над степенью.Итак, для нашей ценности мы можем написать наш числитель равен 125 в степени двух третей, а наш знаменатель — 343 в степени. двух третей.
Итак, давайте упростим эти дробные показатели двух третей. Напомним, что если у нас есть значение 𝑥 в степени над, это эквивалентно корню-й степени из в степени из 𝑎. И поэтому в нашем числителе 125 в степени двух третей эквивалентно кубическому корню из 125 в квадрате.Наш знаменатель эквивалентен кубический корень из 343 в квадрате.
В числителе мы можем заметить, что это эквивалентно возведению в квадрат 125 и извлечению кубического корня. Точно так же в нашем знаменателе мы можно сначала возвести в квадрат 343, а затем извлечь кубический корень. Однако во второй форме написано оранжевым цветом будут гораздо большие числа. Поскольку мы сначала возводим 125 и затем пытаюсь найти кубический корень из этого.Если мы начнем с сначала кубический корень, а затем квадрат, наши значения не станут такими большими.
Следовательно, кубический корень из 125 даст нам пять. И поскольку тогда нам нужно возвести в квадрат В нашем числителе будет пять квадратов. И на нашем знаменателе куб корень из 343 равен семи, так как семь умножить на семь умножить на семь дает 343. А затем нам нужно возвести в квадрат что. Оценка наших квадратов тогда будет дайте нам окончательный ответ 25 из 49.
Дробные экспоненты — объяснение и примеры
Показатели — это степени или индексы. Экспоненциальное выражение состоит из двух частей: основания, обозначаемого как b, и показателя степени, обозначаемого как n. Общая форма экспоненциального выражения: b n . Например, 3 x 3 x 3 x 3 можно записать в экспоненциальной форме как 3 4 , где 3 — основание, а 4 — показатель степени. Они широко используются в алгебраических задачах, и по этой причине важно изучать их, чтобы облегчить изучение алгебры.
Правила решения дробных показателей становятся сложной задачей для многих студентов. Они будут тратить свое драгоценное время, пытаясь понять дробные показатели, но это, конечно, огромная путаница в их умах. Не волнуйся. В этой статье разобраны, что вам нужно делать, чтобы понять и решить проблемы, связанные с дробными показателями
Первый шаг к пониманию того, как решать дробные показатели, — это краткое описание того, что именно они есть, и как обращаться с показателями, когда они объединяются либо делением, либо умножением.
Что такое дробная экспонента?Дробная экспонента — это метод выражения степеней и корней вместе. Общая форма дробного показателя:
b n / m = ( m √ b ) n = m √ (b n ), позвольте нам определите некоторые термины этого выражения.
Подкоренное выражение находится под знаком корня √. В данном случае подкоренное выражение — b n
- Порядок / индекс радикала
Индекс или порядок радикала — это число, указывающее на извлекаемый корень.В выражении: b n / m = ( m √ b ) n = m √ (b n ) порядком или индексом корня является число м.
Это число, корень которого вычисляется. База обозначается буквой b.
Степень определяет, сколько раз значение корня умножается само на себя, чтобы получить основание. Обычно обозначается буквой n.
Как решить дробные экспоненты?Давайте узнаем, как решить дробные показатели с помощью приведенных ниже примеров.
Примеры
= (3 2 ) 1/2
= 3
= 2,828
4 3/2 = 4 3 × (1/2)
= √ (4 3 ) = √ (4 × 4 × 4)
= √ (64) = 8
Альтернативно;
4 3/2 = 4 (1/2) × 3
= (√4) 3 = (2) 3 =
27 4/3 = 27 4 × (1/3)
= ∛ (27 4 ) = 3 √ (531441) = 81
Альтернативно;
27 4/3 = 27 (1/3) × 4
= ∛ (27) 4 = (3) 4 = 81
- Упростить: 125 1/3
125 1/3 = ∛125
= [(5) 3 ] 1/3
= (5) 1
= 5 - Вычислить: (8/27) 4/3
(8/27) 4/3
8 = 2 3 и 27 = 3 3
Итак, (8/27) 4/3 = (2 3 /3 3 ) 4/3
= [(2/3) 3 ] 4/3
= (2/3) 4
= 2/3 × 2/3 × 2/3 × 2/3
= 16/81
Умножение членов с одинаковым основанием и дробными показателями равносильно сложению показателей.Например:
x 1/3 × x 1/3 × x 1/3 = x (1/3 + 1/3 + 1/3)
= x 1 = x
Поскольку x 1/3 подразумевает «кубический корень из x », он показывает, что если x умножить 3 раза, произведение будет x.
Рассмотрим другой случай, когда;
x 1/3 × x 1/3 = x (1/3 + 1/3)
= x 2/3 , это можно выразить as ∛x 2
Пример 2
Тренировка: 8 1/3 x 8 1/3
Решение
8 x 8 1/3 = 8 1/3 + 1/3 = 8 2/3
= ∛8 2
И поскольку кубический корень из 8 можно легко найти,
Следовательно , ∛8 2 = 2 2 = 4
Также можно встретить умножение дробных показателей, имеющих разные числа в знаменателях, в этом случае показатели складываются так же, как и дроби.
Пример 3
x 1/4 × x 1/2 = x (1/4 + 1/2)
= x (1 / 4 + 2/4)
= x 3/4
Как разделить дробную экспонентуПри делении дробной степени с тем же основанием мы вычитаем показатели степени. Например:
x 1/2 ÷ x 1/2 = x (1/2 — 1/2)
= x 0 = 1
Это означает, что любое число деление на себя эквивалентно единице, и это имеет смысл с правилом нулевой экспоненты, согласно которому любое число, возведенное в степень 0, равно единице.
Пример 4
16 1/2 ÷ 16 1/4 = 16 (1/2 — 1/4)
= 16 (2 / 4 — 1/4)
= 16 1/4
= 2
Вы можете заметить, что 16 1/2 = 4 и 16 1/4 = 2.
Отрицательное дробное число показатели степени Если n / m — положительное дробное число и x> 0;
Тогда x -n / m = 1 / x n / m = (1 / x) n / m , и это означает, что x -n / m является обратной величиной x n / м .
В целом; если основание x = a / b,
Тогда (a / b) -n / m = (b / a) n / m .
Пример 5
Рассчитать: 9 -1/2
Решение
9 -1/2
= 1/9 1/2
= (1/9) 1/2
= [(1/3) 2 ] 1/2
= (1/3) 1
= 1/3
Пример 6
Решить: (27/125) -4/3
Решение
(27/125) -4/3
= (125/27) 4/3
= (5 3 /3 3 ) 4/3
= [(5/3) 3 ] 4/3
= (5/3) 4
= (5 × 5 × 5 × 5) / (3 × 3 × 3 × 3)
= 625/81
Практические вопросы
- Оценить 8 2/3
- Разработать выражение (8a 2 б 4 ) 1/3
- Решить: a 3/4 a 4/5
- [(4 -3/2 x 2/3 y -7/4 ) / (2 3/2 x — 1/3 y 3/4 )] 2/3
- Вычислить: 5 1/2 5 3/2
- Вычислить: (1000 1/3 ) / (400 — 1/2 )
Ответы
- 4.
- 2a 2/3 b 4/3 .
- а 31/20 .
- x 2/3 / 8y 5/3
- 25.
- 200.
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби.Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — используйте косую черту «/» между числителем и знаменателем, т. Е. Для пяти сотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью i.э., 1 2/3 (с таким же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, то есть 1/2: 3 .
Десятичные числа (десятичные числа) вводятся с десятичной точкой . , и они автоматически конвертируются в дроби, то есть 1,45 .
Двоеточие : и косая черта / являются символом деления.1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целых и дробных чисел: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичные дроби: 0,625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок или порядок, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Дроби в словесных задачах:
следующие математические задачи »
Кубический корень из 125 — Как найти кубический корень из 125? [Решено]
Кубический корень из 125 равен 5. Это реальное решение уравнения x 3 = 125. Кубический корень из 125 выражается как ∛125 в радикальной форме и как (125) ⅓ или ( 125) 0,33 в экспоненциальной форме.Поскольку кубический корень из 125 представляет собой целое число, 125 — это идеальный куб.
- Кубический корень из 125: 5
- Кубический корень из 125 в экспоненциальной форме: (125) ⅓
- Кубический корень из 125 в радикальной форме: ∛125
Что такое кубический корень из 125?
Кубический корень из 125 — это число, которое при трехкратном умножении на себя дает произведение 125. Поскольку 125 можно выразить как 5 × 5 × 5.Следовательно, кубический корень из 125 = ∛ (5 × 5 × 5) = 5.
Как рассчитать значение кубического корня из 125?
Кубический корень из 125 путем простой факторизации
- Разложение на простые множители 125 равно 5 × 5 × 5
- Упрощая приведенное выше выражение: 5 3
Следовательно, кубический корень из 125, полученный путем разложения на простые множители, равен (5 × 5 × 5) 1/3 = 5.
Является ли кубический корень числа 125 иррациональным?
Нет, потому что ∛125 = ∛ (5 × 5 × 5) может быть выражено в виде p / q i.е. 5/1. Следовательно, значение кубического корня из 125 является целым (рациональным).
☛ Также проверьте:
Кубический корень из 125 решенных примеров
Пример 1. Какое значение имеет ∛125 + ∛ (-125)?
Решение:
Кубический корень -125 равен отрицательному значению кубического корня из 125.
т.е. ∛-125 = -∛125Следовательно, ∛125 + ∛ (-125) = ∛125 — ∛125 = 0
Пример 2: Объем куба равен 125 из 3 .Найдите длину стороны куба.
Решение:
Объем куба = 125 дюймов 3 = 3
⇒ a 3 = 125
Куб укореняется с двух сторон,
⇒ a = ∛125 в
Поскольку кубический корень из 125 равен 5, длина стороны куба составляет 5 дюймов.Пример 3. Найдите действительный корень уравнения x 3 — 125 = 0.
Решение:
x 3 — 125 = 0 я.е. х 3 = 125
Решение относительно x дает нам
x = ∛125, x = ∛125 × (-1 + √3i)) / 2 и x = ∛125 × (-1 — √3i)) / 2
где i называется мнимой единицей и равен √-1.
Игнорирование мнимых корней,
х = 125
Следовательно, действительный корень уравнения x 3 — 125 = 0 равен x = ∛125 = 5.
перейти к слайду перейти к слайду
Готовы увидеть мир глазами математиков?
Математика лежит в основе всего, что мы делаем.Наслаждайтесь решением реальных математических задач на живых занятиях и станьте экспертом во всем.
Забронируйте бесплатную пробную версию Класс
FAQ по Cube Root из 125
Что такое кубический корень из 125?
Мы можем выразить 125 как 5 × 5 × 5, т.е. 125 = ∛ (5 × 5 × 5) = 5. Следовательно, значение кубического корня из 125 равно 5.
Если кубический корень 125 равен 5, найдите значение 0,125 фунта стерлингов.
Представим ∛0,125 в форме p / q, т.е. ∛ (125/1000) = 5/10 = 0.5. Следовательно, значение ∛0,125 = 0,5.
Что такое кубический корень -125?
Кубический корень -125 равен отрицательному значению кубического корня из 125. Следовательно, ∛-125 = — (∛125) = — (5) = -5.
Что такое куб из кубического корня из 125?
Куб кубического корня из 125 — это само число 125, т.е. (∛125) 3 = (125 1/3 ) 3 = 125.
Является ли 125 идеальным кубом?
Число 125 при разложении на простые множители дает 5 × 5 × 5.При объединении простых множителей в группы по 3 получаем 5. Итак, кубический корень из 125 = ∛ (5 × 5 × 5) = 5 (идеальный куб).
Что такое 16 плюс 2 кубического корня 125?
Значение 125 равно 5. Итак, 16 + 2 × ∛125 = 16 + 2 × 5 = 26. Следовательно, значение 16 плюс 2 кубического корня 125 равно 26.
РешенияNCERT для математики класса 7 Глава 13
Стр. № 252:
Вопрос 1:
Найдите стоимость:
(i) 2 6 (ii) 9 3
(iii) 11 2 (iv) 5 4
Ответ:
(i) 2 6 = 2 × 2 × 2 × 2 × 2 × 2 = 64
(ii) 9 3 = 9 × 9 × 9 = 729
(iii) 11 2 = 11 × 11 = 121
(iv) 5 4 = 5 × 5 × 5 × 5 = 625
Стр. № 252:
Вопрос 2:
Экспресс следующее в экспоненциальной форме:
(я) 6 × 6 × 6 × 6 (ii) т × т
(iii) b × б × б × б (iv) 5 × 5 × 7 × 7 × 7
(в) 2 × 2 × а × a (vi) a × a × а × c × c × c × c × д
Ответ:
(я) 6 × 6 × 6 × 6 = 6 4
(ii) т × т = т 2
(iii) b × b × b × b = b 4
(iv) 5 × 5 × 7 × 7 × 7 = 5 2 × 7 3
(в) 2 × 2 × a × a = 2 2 × a 2
(vi) а × a × a × c × c × c × c × d = a 3 c 4 d
Стр. № 253:
Вопрос 3:
Экспресс следующие числа в экспоненциальной записи:
(i) 512 (ii) 343
(iii) 729 (iv) 3125
Ответ:
(я) 512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2 9
(ii) 343 = 7 × 7 × 7 = 7 3
(iii) 729 = 3 × 3 × 3 × 3 × 3 × 3 = 3 6
(iv) 3125 = 5 × 5 × 5 × 5 × 5 = 5 5
Стр. № 253:
Вопрос 4:
Идентифицировать большее число, где это возможно, в каждом из следующих пунктов?
(i) 4 3 или 3 4 (ii) 5 3 или 3 5
(iii) 2 8 или 8 2 (iv) 100 2 или 2 100
(в) 2 10 или 10 2
Ответ:
(i) 4 3 = 4 × 4 × 4 = 64
3 4 = 3 × 3 × 3 × 3 = 81
Следовательно, 3 4 > 4 3
(ii) 5 3 = 5 × 5 × 5 = 125
3 5 = 3 × 3 × 3 × 3 × 3 = 243
Следовательно, 3 5 > 5 3
(iii) 2 8 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256
8 2 = 8 × 8 = 64
Следовательно, 2 8 > 8 2
(iv) 100 2 или 2 100
2 10 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024
2 100 = 1024 × 1024 × 1024 × 1024 × 1024 × 1024 × 1024 × 1024 × 1024 × 1024
100 2 = 100 × 100 = 10000
Следовательно, 2 100 > 100 2
(в) 2 10 и 10 2
2 10 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024
10 2 = 10 × 10 = 100
Следовательно, 2 10 > 10 2
Стр. № 253:
Вопрос 5:
Выразите каждое из следующих значений как произведение степеней их простых множителей:
(i) 648 (ii) 405
(iii) 540 (iv) 3,600
Ответ:
(i) 648 = 2 × 2 × 2 × 3 × 3 × 3 × 3 = 2 3 .3 4
(ii) 405 = 3 × 3 × 3 × 3 × 5 = 3 4 . 5
(iii) 540 = 2 × 2 × 3 × 3 × 3 × 5 = 2 2 . 3 3 . 5
(iv) 3600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5 = 2 4 . 3 2 . 5 2
Видео решение для экспонентов и степеней (Страница: 253, Q.No .: 5)
Решение NCERT для математики класса 7 — показатели и степени 253, вопрос 5
Стр. № 253:
Вопрос 6:
Упростить:
(я) 2 × 10 3 (ii) 7 2 × 2 2
(iii) 2 3 × 5 (iv) 3 × 4 4
(в) 0 × 10 2 (vi) 5 2 × 3 3
(vii) 2 4 × 3 2 (viii) 3 2 × 10 4
Ответ:
(я) 2 × 10 3 = 2 × 10 × 10 × 10 = 2 × 1000 = 2000
(ii) 7 2 × 2 2 = 7 × 7 × 2 × 2 = 49 × 4 = 196
(iii) 2 3 × 5 = 2 × 2 × 2 × 5 = 8 × 5 = 40
(iv) 3 × 4 4 = 3 × 4 × 4 × 4 × 4 = 3 × 256 = 768
(в) 0 × 10 2 = 0 × 10 × 10 = 0
(vi) 5 2 × 3 3 = 5 × 5 × 3 × 3 × 3 = 25 × 27 = 675
(vii) 2 4 × 3 2 = 2 × 2 × 2 × 2 × 3 × 3 = 16 × 9 = 144
(viii) 3 2 × 10 4 = 3 × 3 × 10 × 10 × 10 × 10 = 9 × 10000 =
Стр. № 253:
Вопрос 7:
Упростить:
(i) (- 4) 3 (ii) (- 3) × (- 2) 3
(iii) (- 3) 2 × (- 5) 2 (iv) (- 2) 3 × (−10) 3
Ответ:
(я) (−4) 3 = (−4) × (−4) × (−4) = −64
(ii) (−3) × (−2) 3 = (−3) × (−2) × (−2) × (−2) = 24
(iii) (−3) 2 × (−5) 2 = (−3) × (−3) × (−5) × (−5) = 9 × 25 = 225
(iv) (−2) 3 × (−10) 3 = (−2) × (−2) × (−2) × (−10) × (−10) × (−10)
= (−8) × (−1000) = 8000
Стр. № 253:
Вопрос 8:
Сравните следующие числа:
(i) 2.7 × 10 12 ; 1,5 × 10 8
(ii) 4 × 10 14 ; 3 × 10 17
Ответ:
(i) 2,7 × 10 12 ; 1,5 × 10 8
2,7 × 10 12 > 1,5 × 10 8
(ii) 4 × 10 14 ; 3 × 10 17
3 × 10 17 > 4 × 10 14
Видео решение для экспонентов и степеней (Страница: 253, В.№: 8)
Решение NCERT для математики класса 7 — показатели и степени 253, вопрос 8
Стр. № 260:
Вопрос 1:
Использование законов экспонент, упростите и запишите ответ в экспоненциальной форме:
(i) 3 2 × 3 4 × 3 8 (ii) 6 15 ÷ 6 10 (iii) a 3 × а 2
(iv) 7 x × 7 2 (v) (vi) 2 5 × 5 5
(vii) a 4 × b 4 (viii) (3 4 ) 3
(ix) (x) 8 т ÷ 8 2
Ответ:
(i) 3 2 × 3 4 × 3 8 = (3) 2 + 4 + 8 ( a m × a n = a m + n )
= 3 14
(ii) 6 15 ÷ 6 10 = (6) 15-10 ( а м ÷ a n = a m — n )
= 6 5
(iii) a 3 × а 2 = а (3 + 2) ( а м × a n = a m + n )
= a 5
(iv) 7 x + 7 2 = 7 x + 2 ( а м × a n = a m + n )
(в) (5 2 ) 3 ÷ 5 3
= 5 2 × 3 ÷ 5 3 ( a m ) n = а мин
= 5 6 ÷ 5 3
= 5 (6 — 3) ( a м ÷ a n = a m — n )
= 5 3
(vi) 2 5 × 5 5
= (2 × 5) 5 [ a м × b м = (a × b ) м ]
= 10 5
(vii) a 4 × б 4
= ( ab ) 4 [ a m × b m = (a × b ) m ]
(viii) (3 4 ) 3 = 3 4 × 3 = 3 12 ( a m ) n = а мин
(ix) (2 20 ÷ 2 15 ) × 2 3
= (2 20-15 ) × 2 3 ( а м ÷ a n = a m — n )
= 2 5 × 2 3
= (2 5 + 3 ) ( a m × a n = a m + n )
= 2 8
(x) 8 т ÷ 8 2 = 8 ( т — 2) ( а м ÷ a n = a m — n )
Стр. № 260:
Ответ:
(я)
(ii) [(5 2 ) 3 × 5 4 ] ÷ 5 7
= [5 2 × 3 × 5 4 ] ÷ 5 7 ( a m ) n = а мин
= [5 6 × 5 4 ] ÷ 5 7
= [5 6 + 4 ] ÷ 5 7 ( а м × a n = a m + n )
= 5 10 ÷ 5 7
= 5 10-7 ( a m ÷ a n = a m — n )
= 5 3
(iii) 25 4 ÷ 5 3 = (5 × 5) 4 ÷ 5 3
= (5 2 ) 4 ÷ 5 3
= 5 2 × 4 ÷ 5 3 ( a m ) n = а мин
= 5 8 ÷ 5 3
= 5 8 — 3 ( a m ÷ a n = a m — n )
= 5 5
(iv)
= 1 × 7 × 11 5 = 7 × 11 5
(в)
(vi) 2 0 + 3 0 + 4 0 = 1 + 1 + 1 = 3
(vii) 2 0 × 3 0 × 4 0 = 1 × 1 × 1 = 1
(viii) (3 0 + 2 0 ) × 5 0 = (1 + 1) × 1 = 2
(ix)
(х)
(xi)
(xii) (2 3 × 2) 2 = ( а м × a n = a m + n )
= (2 4 ) 2 = 2 4 × 2 ( a m ) n = а мин
= 2 8
Стр. № 260:
Вопрос 3:
Скажи правду или неверно и обоснуйте свой ответ:
(я) 10 × 10 11 = 100 11 (ii) 2 3 > 5 2
(iii) 2 3 × 3 2 = 6 5 (iv) 3 0 = (1000) 0
Ответ:
(я) 10 × 10 11 = 100 11
Л.H.S. = 10 × 10 11 = 10 11 + 1 ( а м × a n = a m + n )
= 10 12
R.H.S. = 100 11 = (10 × 10) 11 = (10 2 ) 11
= 10 2 × 11 = 10 22 ( a m ) n = а мин
Как сказал Л.H.S. ≠ R.H.S.,
Следовательно, данное утверждение неверно.
(ii) 2 3 > 5 2
L.H.S. = 2 3 = 2 × 2 × 2 = 8
R.H.S. = 5 2 = 5 × 5 = 25
Как 25> 8,
Следовательно, данное утверждение неверно.
(iii) 2 3 × 3 2 = 6 5
L.H.S. = 2 3 × 3 2 = 2 × 2 × 2 × 3 × 3 = 72
Р.H.S. = 6 5 = 7776
Как сообщает L.H.S. ≠ R.H.S.,
Следовательно, данное утверждение неверно.
(iv) 3 0 = (1000) 0
L.H.S. = 3 0 = 1
R.H.S. = (1000) 0 = 1 = L.H.S.
Следовательно, данное утверждение верно.
Стр. № 261:
Вопрос 4:
Выразите каждое из следующих значений как произведение простых множителей только в экспоненциальной форме:
(i) 108 × 192 (ii) 270
(iii) 729 × 64 (iv) 768
Ответ:
(я) 108 × 192
= (2 × 2 × 3 × 3 × 3) × (2 × 2 × 2 × 2 × 2 × 2 × 3)
= (2 2 × 3 3 ) × (2 6 × 3)
= 2 6 + 2 × 3 3 + 1 ( а м × а n = а м + 91144 4 )
= 2 8 × 3 4
(ii) 270 = 2 × 3 × 3 × 3 × 5 = 2 × 3 3 × 5
(iii) 729 × 64 = (3 × 3 × 3 × 3 × 3 × 3) × (2 × 2 × 2 × 2 × 2 × 2)
= 3 6 × 2 6
(iv) 768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 = 2 8 × 3
Видео решение для экспонентов и степеней (Страница: 261, В.№: 4)
Решение NCERT для математики класса 7 — показатели и степени 261, вопрос 4
Стр. № 261:
Вопрос 5:
Упростить:
(i) (ii) (iii)
Стр. № 263:
Вопрос 1:
Напишите следующие номера в развернутых формах:
279404, г. 3006194, 2806196, 120719, 20068
Ответ:
279404 = 2 × 10 5 + 7 × 10 4 + 9 × 10 3 + 4 × 10 2 + 0 × 10 1 + 4 × 10 0
3006194 = 3 × 10 6 + 0 × 10 5 + 0 × 10 4 + 6 × 10 3 + 1 × 10 2 + 9 × 10 1 + 4 × 10 0
2806196 = 2 × 10 6 + 8 × 10 5 + 0 × 10 4 + 6 × 10 3 + 1 × 10 2 + 9 × 10 1 + 6 × 10 0
120719 = 1 × 10 5 + 2 × 10 4 + 0 × 10 3 + 7 × 10 2 + 1 × 10 1 + 9 × 10 0
20068 = 2 × 10 4 + 0 × 10 3 + 0 × 10 2 + 6 × 10 1 + 8 × 10 0
Стр. № 263:
Вопрос 2:
Найдите номер из каждой из следующих развернутых форм:
(а) 8 × 10 4 + 6 × 10 3 + 0 × 10 2 + 4 × 10 1 + 5 × 10 0
(б) 4 × 10 5 + 5 × 10 3 + 3 × 10 2 + 2 × 10 0
(в) 3 × 10 4 + 7 × 10 2 + 5 × 10 0
(г) 9 × 10 5 + 2 × 10 2 + 3 × 10 1
Ответ:
(а) 8 × 10 4 + 6 × 10 3 + 0 × 10 2 + 4 × 10 1 + 5 × 10 0
= 86045
(б) 4 × 10 5 + 5 × 10 3 + 3 × 10 2 + 2 × 10 0
= 405302
(в) 3 × 10 4 + 7 × 10 2 + 5 × 10 0
= 30705
(г) 9 × 10 5 + 2 × 10 2 + 3 × 10 1
= 0
Стр. № 263:
Вопрос 3:
Экспресс следующие числа в стандартной форме:
(я) 5, 00, 00, 000 (ii) 70, 00, 000
(iii) 3, 18, 65, 00, 000 (iv) 3, 90, 878
(в) 39087.8 (vi) 3908,78
Ответ:
(я) 50000000 = 5 × 10 7
(ii) 7000000 = 7 × 10 6
(iii) 3186500000 = 3,1865 × 10 9
(iv) 3
= 3,
× 10 5
(в) 39087,8
= 3,
× 10 4
(vi) 3908,78
= 3,
× 10 3
Стр. № 263:
Вопрос 4:
Экспресс число, фигурирующее в следующих утверждениях в стандартной форме.
(а) расстояние от Земли до Луны 384 000 000 м.
(b) Скорость света в вакууме составляет 300 000 000 м / с.
(c) Диаметр Земли составляет 1, 27, 56, 000 м.
(d) Диаметр Солнца — 1 400 000 000 м.
(e) В Галактика насчитывает в среднем 100 000 000 000 000 звезд.
(f) Возраст Вселенной оценивается примерно в 12 000 000 000 лет.
(g) Расстояние от Солнца до центра Галактики Млечный Путь. оценивается в 300, 000, 000, 000, 000, 000, 000 м.
(h) 60, 230, 000, 000, 000, 000, 000, 000 молекул содержатся в капля воды весом 1,8 гр.
(i) Земля имеет 1 353 000 000 кубических километров морской воды.
(j) Население Индии в марте 2001 г. составляло около 1 027 000 000 человек.
Ответ:
(а) 3.84 × 10 8 кв.м
(б) 3 × 10 8 м / с
(в) 1,2756 × 10 7 м
(г) 1.4 × 10 9 кв.м
(е) 1 × 10 11 звезды
(ж) 1,2 × 10 10 9000 4 года
(г) 3 × 10 20 кв.
