Геометрия: свойства треугольника — intmag24.ru
Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).
На рисунке: Треугольник ABC;
A, B, C – вершины треугольника ABC;
AB, AC, BC – стороны треугольника ABC;
∠BAC, ∠ABC, ∠ACB – углы треугольника ABC.
Содержание
- Виды треугольников
- Свойства сторон треугольника
- Свойства углов треугольника
- Свойства высоты треугольника
- Свойства медианы треугольника
- Свойства биссектрисы треугольника
- Средняя линия треугольника
- Равнобедренный треугольник
- Равносторонний треугольник
- Прямоугольный треугольник
- Треугольник и окружность
- Основные формулы
- Теорема Чевы
- Теорема Менелая
Виды треугольников
- Треугольник называется остроугольным, если все его углы острые.
- Треугольник называется тупоугольным, если один из его углов тупой.
- Треугольник называется прямоугольным, если один из его углов прямой. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
- Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
- Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
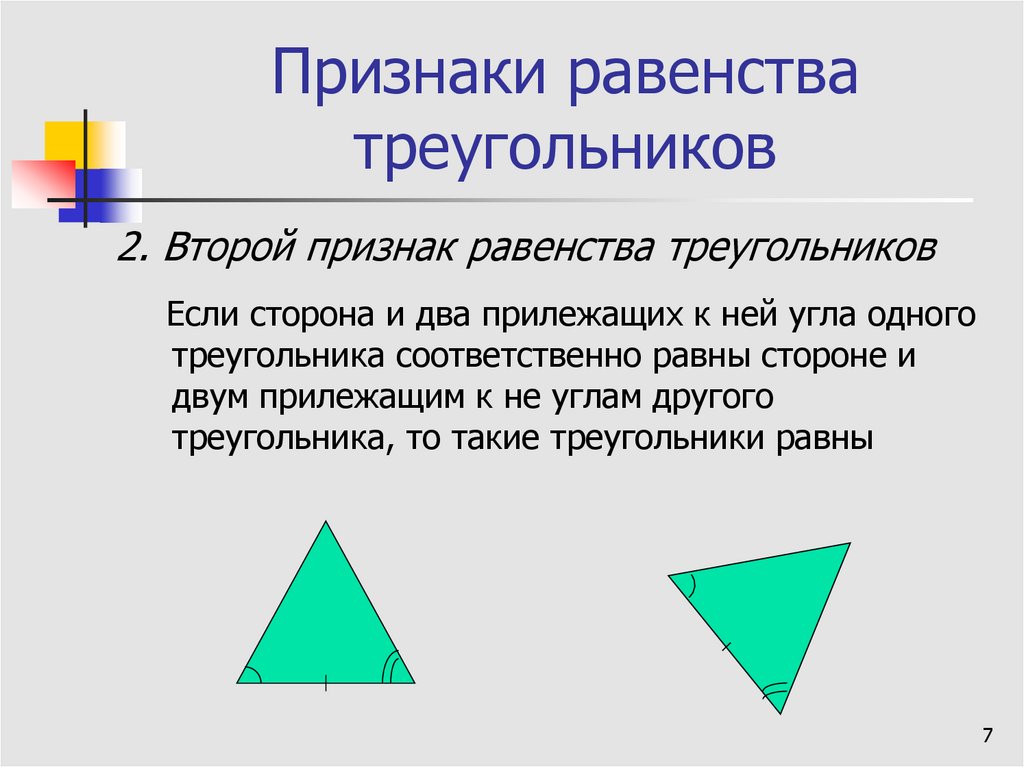
- Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны. Основные признаки равенства треугольников: по двум сторонам и углу между ними, по стороне и двум прилежащим к ней углам, по трем сторонам.
Свойства сторон треугольника
- Сумма любых двух сторон треугольника больше его третьей стороны.
На рисунке: b+c>a, a+c>b, a+b>c. - Длина каждой стороны треугольника больше разности длин двух других сторон. На рисунке: |a-b| <c, |a-c|<b, |b-c|<a.
Свойства углов треугольника
- Сумма углов треугольника равна 180°:
- В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
- Внешний угол треугольника равен сумме двух внутренних углов, с ним не смежных.
Свойства высоты треугольника
Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны. На рисунке: BD – высота треугольника ABC.
Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника. На рисунке: H – ортоцентр треугольника ABC.
Свойства медианы треугольника
Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны (AM).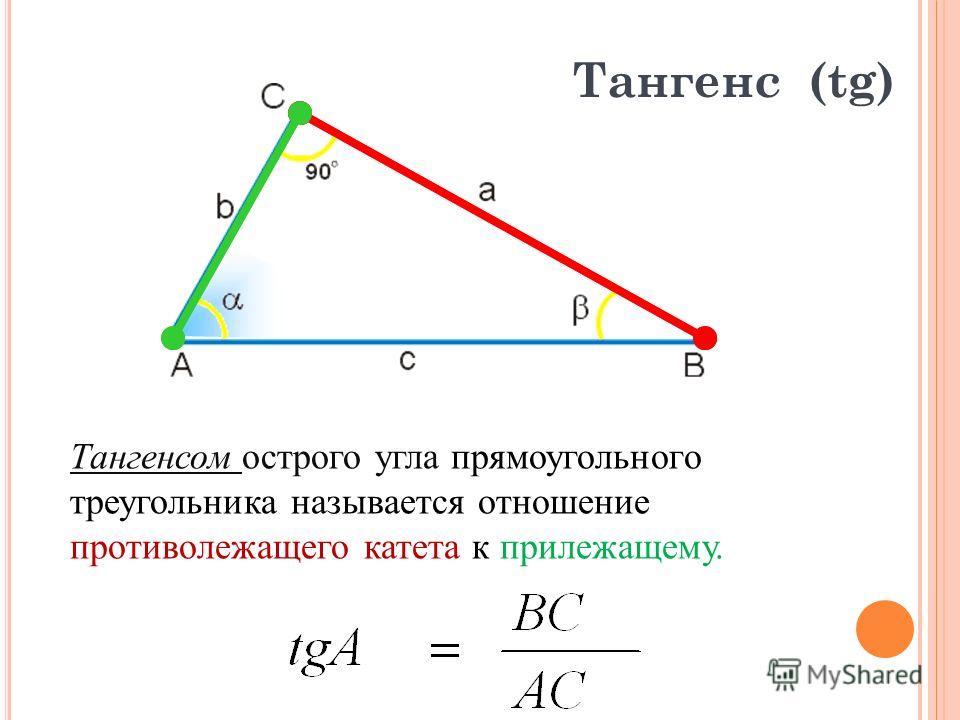
— Она делит треугольник на два равновеликих (с равными площадями) треугольника.
— Три медианы треугольника делят его на шесть равновеликих треугольников. Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины треугольника. На рисунке: AG/GA1=BG/GB1=CG/GC1=2/1.
Формула медианы:
Свойства биссектрисы треугольника
Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне. На рисунке: AL – биссектриса треугольника ABC.
Свойство биссектрисы треугольника: Отношение отрезков, на которые биссектриса делит сторону треугольника, равно отношению прилежащих к этим отрезкам сторон треугольника. На рисунке: BL/CL=AB/AC.
Биссектрисы треугольника пересекаются в одной точке. Эта точка равноудалена от всех сторон треугольника и является центром окружности, вписанной в треугольник.
Формула нахождения длины биссектрисы:
Средняя линия треугольника
Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника.
На рисунке: MN – средняя линия треугольника ABC.
Средняя линия треугольника параллельна третьей стороне треугольника и равна её половине.
На рисунке: MN||AC,MN=AC/2.
Средние линии разбивают треугольник на четыре равных треугольника, подобных исходному с коэффициентом 1/2. Треугольник из средних линий называется срединным треугольником.
На рисунке: MNP – срединный треугольник треугольника ABC.
Равнобедренный треугольник
Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
На рисунке:
AC – основание,
AB, BC – боковые стороны.
Свойства равнобедренного треугольника:
- В равнобедренном треугольнике углы при основании равны.
На рисунке: ∠BAC=∠BCA - В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
На рисунке: AD=DC, ∠ABD=∠CBD, BD⊥AC.
Признаки равнобедренного треугольника:
- Если два угла треугольника равны, то этот треугольник равнобедренный. На рисунке: ∠BAC=∠CAB⇒AB=BC.
- Если в треугольнике медиана и высота, проведённые к одной стороне, совпадают, то этот треугольник равнобедренный. На рисунке: AD=DC, BD⊥AC ⇒ AB=BC.
- Если в треугольнике медиана и биссектриса , проведённые к одной стороне, совпадают, то этот треугольник равнобедренный. На рисунке: AD=DC, ∠ABD=∠CBD ⇒ AB=BC.
- Если в треугольнике высота и биссектриса, проведённые к одной стороне, совпадают, то этот треугольник равнобедренный. На рисунке: BD⊥AC, ∠ABD=∠CBD ⇒ AB=BC.
Равносторонний треугольник
- Все стороны равностороннего треугольника равны.
- Все углы равностороннего треугольника равны 60°.
- Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
Прямоугольный треугольник
Треугольник называется прямоугольным, если один из его углов прямой. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
На рисунке: △ABC прямоугольный; AC, BC – катеты, AB – гипотенуза.
Медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.
На рисунке: ∠C=90∘,CM – медиана △ABC⇒AM=BM=CM.
Высота, проведённая к гипотенузе, делит прямоугольный треугольник на два треугольника подобных друг другу и исходному треугольнику. На рисунке: △ACH∽△CBH∽△ABC.
В прямоугольном треугольнике катет, лежащий напротив угла в 30∘, равен половине гипотенузы.
На рисунке: если ∠A=30∘⇔BC=AB/2.
Основные метрические соотношения в прямоугольном треугольнике:
Пусть в треугольнике ABC ∠C=90∘, a=BC, b=AC – катеты, c=AB – гипотенуза, h=CH – высота к гипотенузе, a1=BH, b1=AH – проекции катетов на гипотенузу. Тогда:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов ( Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов. Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы. Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы: Радиус r окружности, вписанной в прямоугольный треугольник, может быть вычислен по формуле: r=(a+b−c)/2, где a и b – катеты треугольника, c – его гипотенуза.
Калькулятор для прямоугольного треугольника поможет вычислить все его характеристики: стороны, углы, периметр и площадь, радиус вписанной и описанной окружности.
Треугольник и окружность
Около любого треугольника можно описать окружность, и только одну. Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.
Радиус описанной окружности треугольника ABC может быть вычислен по формулам: где a, b и c – длины сторон треугольника ABC, S – его площадь.
В любой треугольник можно вписать окружность, и только одну. Центром вписанной окружности треугольника является точка пересечения биссектрис треугольника.
Пусть a, b и c – длины сторон треугольника ABC и p=(a+b+c)/2 – его полупериметр. Тогда
— длины отрезков касательных из вершин A, B, C до точек касания вписанной окружности со сторонами треугольника равны p−a, p−b, p−c соответственно.
Радиус r вписанной окружности треугольника может быть вычислен по формуле: где a, b и c – длины сторон треугольника, p=(a+b+c)/2 – его полупериметр, S – площадь треугольника.
Основные формулы:
Периметр: P=a+b+c
Площадь по стороне и высоте: площадь треугольника равна половине произведения стороны треугольника на высоту, проведённую к этой стороне.
Площадь по сторонам и углу между ними: площадь треугольника равна половине произведения двух его сторон на синус угла между ними. или половине произведения катетов:
Площадь по формуле Герона (где p=(a+b+c)/2 – полупериметр, a, b, c – стороны треугольника):
Площадь по трем сторонам и радиусу вписанной окружности (где p=(a+b+c)/2 – полупериметр треугольника, r — радиус вписанной окружности): Площадь по трем сторонам и радиусу описанной окружности:
Стороны прямоугольного треугольника (Теорема Пифагора):
где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ — угол между сторонами и r — радиус вписанной окружности, R — радиус описанной окружности
Для нахождения характеристик простого, равнобедренного или равностороннего треугольника, воспользуйтесь калькулятором для треугольника.
Чтобы вычислить все характеристики прямоугольного треугольника, воспользуйтесь калькулятором для прямоугольного треугольника.
Скачать программы, которые формируют задания на нахождение периметра и площади геометрических фигур, а также неизвестных характеристик (сторон, диагоналей и др.), в том числе для: квадрата, прямоугольника, треугольника, трапеции и другие. |
Теорема Чевы
Пусть A1, B1, C1 – точки на прямых BC, AC и AB, содержащих стороны треугольника ABC. Прямые AA1, BB1 и CC1 пересекаются в одной точке тогда и только тогда, когда:
Теорема Менелая
Пусть A1, B1, C1 – точки на прямых BC, AC и AB, содержащих стороны треугольника ABC. Точки A1, B1 и C1 лежат на одной прямой тогда и только тогда, когда:
Параллелограмм в геометрии и свойства параллелограмма
Определение: параллелограмм — это четырехугольник, у которого противолежащие стороны попарно параллельны, является геометрической фигурой.
Высотой параллелограмма называется перпендикуляр, опущенный из его вершины на прямую, содержащую противолежащую ей сторону. В этой статье мы рассмотрим основные свойства параллелограмма и решим задачи, с опорой на эти свойства.
Четырехугольник ABCD — параллелограмм.
BH — высота.
Изучение этой геометрической фигуры начинается в 8 классе, однако знакомство с ней происходит еще в дошкольный период, например, когда мы видим этот четырехугольник в элементах конструктора, а можем сами получить такую фигуру, если прикрепить стороны прямоугольника не крепко и потянуть за одну из них, тогда перпендикулярность сторон нарушится и мы получим тот четырехугольник, который будем сегодня с вами изучать. Этот четырехугольник настолько популярен, что часто встречается в орнаментах и даже есть на флагах некоторых государств, например, на флаге острова Саба — островного государства в Карибском море.
Содержание
Свойства параллелограмма
Свойство 1
Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.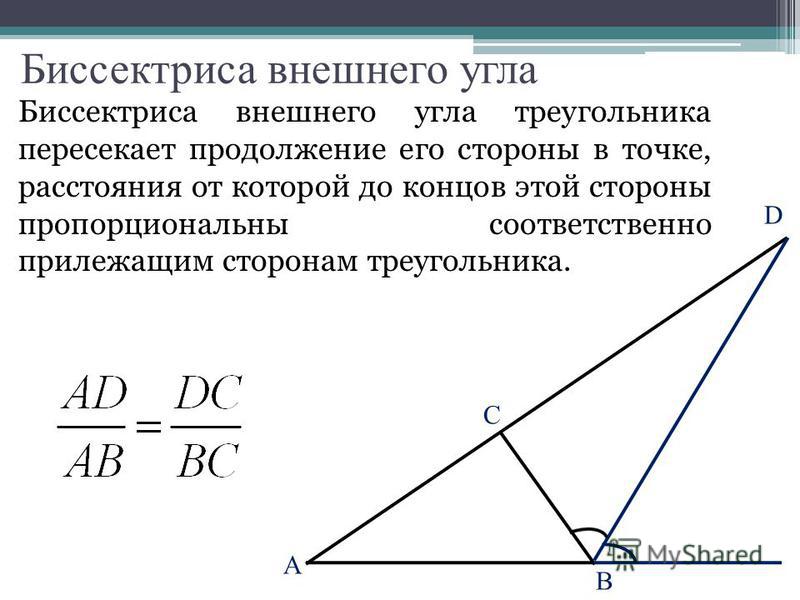
Доказательство.
Рассмотрим параллелограмм ABCD. Докажем, например, что сумма ∠A и ∠B, прилежащих к стороне AB, равна 180°.
Действительно, ∠A и ∠B являются внутренними односторонним углами при параллельных прямых АD, BC и секущей AB. В седьмом классе доказывалось, что если две параллельные прямые пересечены третьей прямой, то внутренние односторонние углы составляют в сумме 180°. Следовательно, сумма ∠А +∠B=180°. Аналогичным образом доказывается, что суммы углов параллелограмма, прилежащих к другим его сторонам, также равны 180°.
Свойство 2
У параллелограмма противоположные стороны равны и противолежащие углы равны.
Доказательство.
Рассмотрим параллелограмм ABCD. Диагональ АС разбивает его на два треугольника АВС и CDA. Эти треугольники равны по второму признаку равенства треугольников (AC — общая сторона, ∠1=∠2, ∠3=∠4 как внутренние накрест лежащие углы при двух параллельных прямых и секущей.) Из равенства треугольников следует, что AB=CD, BC=AD и ∠B=∠D.
Кроме того, ∠A=∠1+∠3=∠2+∠4=∠C.
Свойство 3
Диагонали параллелограмма в точке пересечения делятся пополам.
Доказательство.
Рассмотрим параллелограмм ABCD. Обозначим O точку пересечения диагоналей AC и BD. Треугольники AOB и COD равны по второму признаку равенства треугольников (AB=CD, ∠1=∠2, ∠3=∠4 как внутренние накрест лежащие углы при двух параллельных прямых и секущей).
Из равенства треугольников следует равенство сторон AO=OC и DO=OB. То есть диагонали точкой пересечения делятся пополам. Что и требовалось доказать.
Неправильно
В геометрии важно не только построение фигур, но и произношение их названий. Так правильно следует говорить «параллелограмм» (с двумя «л» в первом случае и с двумя «м» в конце). Неправильно писать и говорить: паралеллограм, паралелограм, в паралелограми.
Математика требует четкости во всем.
Примеры решения задач
Решим несколько задач
Задача 1
У параллелограмма две стороны равны 30 и 40 см, найдите две другие стороны.
Решение.
По второму свойству стороны данной геометрической фигуры равны, нам даны два разных числа, значит, это не противоположные стороны, а смежные. Смежные стороны четырехугольника — это те стороны, которые прилежат к одной вершине. Таким образом, мы можем сказать, что две другие стороны также будут 30 и 40 см.
Ответ: 30 см, 40 см.
Задача 2
Один из углов параллелограмма равен 45°. Найдите остальные углы параллелограмма?
Решение: Согласно первому свойству углы при одной стороне в сумме дают 180°. А также противоположные углы равны по второму свойству. Таким образом, ∠A= ∠C=45° и ∠B=∠D=180°- 45°=135°.
Ответ: 45°, 135°, 135°.
Задача 3
Диагональ параллелограмма образует с двумя его сторонами углы 15° и 35°. Найдите остальные его углы.
Решение:
Сделаем чертеж. Итак, диагональ AC делит ∠A на две части, по 15 и 35 градусов.
Вместе получается 15+35=50 градусов.
Тогда противоположный ∠C тоже будет 50 градусов по второму свойству (о равенстве сторон и противоположных углов). Так как сумма внутренних углов при одной стороне 180°, то найдем: ∠B=180°-∠A=180°-50°=130°.
Таким образом, ∠D = 130°.
Ответ: 50°, 130°, 50°, 130°.
Задача 4
Найдите углы параллелограмма, если известно, что один из его углов больше другого на 20º.
Решение:
Пусть ∠A будет x, тогда ∠B= x+20. Известно, что ∠A и ∠B в сумме дают 180°. Составим уравнение:
x+x+20=180
2x+20=180
2x=180-20
2x=160
x=80
Таким образом, один ∠A= 80°, а ∠B=100°. По второму свойству имеет ∠C=80° и ∠D=100°.
Ответ: 80°, 80°, 100°, 100°
Задача 5
Найдите стороны параллелограмма, если его периметр равен 48 см, а одна из его сторон больше другой на 4 см.
Решение:
Пусть одна сторона равна x см, тогда другая сторона x+4. Периметр — это сумма всех сторон, а стороны в данной геометрической фигуре попарно равны по второму свойству.
Составим уравнение: 2 (x+x+4)= 48. Решим это уравнение:
2x+4=24
2x=20
x=10
Значит, одна сторона 10 см, а другая сторона будет 10+4=14 см.
Ответ: 10 см и 14 см.
Задача 6
Докажите, что биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
Доказательство:
Нарисуем параллелограмм ABCD, и проведем биссектрису ∠A. Точку пересечения биссектрисы и стороны BC обозначим N. Требуется доказать, что треугольник ABN равнобедренный.
У равнобедренного треугольника две стороны равны и углы при основании равны. Так как AN биссектриса, то ∠1=∠2 и ∠2=∠3 (как внутренние накрест лежащие углы), отсюда ∠3=∠1. Таким образом, треугольник ABN равнобедренный.
Из того, что треугольник равнобедренный следует, что AB=BN. Это можно будет использовать при решении других подобных задач.
Что и требовалось доказать.
Частный случай параллелограмма
Частным случаем параллелограмма является ромб.
Ромб — это параллелограмм, у которого все стороны равны. Свойства ромба такие же как и свойства параллелограмма. Но есть и особенность — диагонали ромба перпендикулярны и являются биссектрисами его углов.
Изучением ромба мы займемся подробно в следующих статьях, а также докажем это свойство ромба о его диагоналях.
Заключение
В геометрии 8 класса о параллелограмме можно узнать — определение, свойства и по каким признакам определить, что перед вами именно эта геометрическая фигура. Например, нам дана такая задача — определите четырехугольник, если его диагонали пересекаются в точке O, которая делит их пополам и стороны данного четырехугольника попарно параллельны, то понятно о какой фигуре здесь идет речь. О вписанных и описанных окружностях в такой четырехугольник вы узнаете в девятом классе.
Свойства надо выучить, необязательно запоминать их порядок, главное знать содержание, уметь использовать в решении геометрических задач.
Что такое треугольник | Что такое определение треугольника
Содержание
Этот пост также доступен в: हिन्दी (хинди)
Существует много двумерных фигур, которые вы изучаете в геометрии, таких как квадрат, прямоугольник, круг, ромб и т.
д. Треугольник также является двумерной фигурой, имеющей три стороны, три вершины и три угла. Есть много треугольных предметов, с которыми мы сталкиваемся в повседневной жизни, таких как бутерброды, дорожные знаки, вешалки для одежды, стойка в бильярде, парусные лодки, крыши и т. д.
Давайте разберемся, что такое треугольник в геометрии и узнаем о его форме.
Что такое треугольник в геометрии?
Треугольник — это простой многоугольник с тремя сторонами, тремя вершинами и тремя внутренними углами. Это одна из основных фигур в геометрии. Треугольник обозначается символом $\triangle$. Существуют различные типы треугольников, классифицированные на основе сторон и углов. Некоторые основные понятия, такие как теорема Пифагора и тригонометрия, основаны на свойствах треугольников.
СКАЧАТЬ БЕСПЛАТНО КАРТОЧКИ ПО МАТЕМАТИКЕ:
Красиво оформленные карточки для печати, которые помогут вам запомнить все важные математические понятия и формулы.
{\circ}$.
Что такое внутренний и внешний углы треугольника?
Треугольник состоит из внутренних и внешних углов. Внутренний угол определяется как угол, образованный между двумя смежными сторонами треугольника. Внешний угол определяется как угол, образованный между стороной треугольника и смежной стороной, идущей наружу.
Внутренний угол: Внутренний угол треугольника — это угол, образованный внутри треугольной области. Всякий раз, когда мы говорим о любом угле треугольника, мы имеем в виду его внутренний угол. Внутренний угол представлен именем вершины, в которой он лежит, или тремя буквами, где средняя буква — это вершина, в которой лежит угол, а две другие представляют две другие вершины. 9{\circ}$. Это свойство называется свойством суммы углов треугольников.
Часто задаваемые вопросы
Что такое треугольник в геометрии?
Треугольник — это простой многоугольник с тремя сторонами, тремя вершинами и тремя внутренними углами. Это одна из основных фигур в геометрии. Треугольник обозначается символом $\triangle$.
Почему он называется треугольником?
Слово треугольник происходит от латинского слова triangulus 9{\circ}$ и сумма любых двух сторон больше длины третьей стороны. Точно так же разность между любыми двумя сторонами треугольника меньше длины третьей стороны.
Рекомендуемая литература
- Типы углов в математике (острые, прямые, тупые, прямые и обратные)
- Что такое угол в геометрии – определение, свойства и измерение
- Как построить касательную к окружности (с шагами) и изображения)
- Тангенс окружности – значение, свойства, примеры
- Углы в круге – значение, свойства и примеры
- Хорда круга – определение, свойства и примеры
- Как нарисовать круг (с шагами и рисунками)
- Что такое круг – части, свойства и примеры
- Как построить перпендикулярную линию (с шагами и примерами)
- Как построить параллельные линии (с шагами и примерами)
- Как построить отрезок линии (с шагами и примерами)
- Что такое коллинеарные точки в геометрии — определение , свойства и примеры
- Что такое поперечная линия в геометрии – определение, свойства и примеры
- Что такое параллельные линии в геометрии – определение, свойства и примеры
- Что такое параллельные линии в геометрии – определение, условия и примеры
- Что такое полупрямая в геометрии Геометрия – определение, свойства и примеры
- Что такое перпендикулярная линия в геометрии – определение, свойства и примеры
- Разница между аксиомой, постулатом и теоремой
- Линии в геометрии (определение, типы и примеры)
- Что такое 2D-фигуры — имена, определения и свойства
- 3D-фигуры — определение, свойства и типы
Уравнения с матрицами (с методом и примерами)
Содержание Как решать линейные уравнения с матрицамиУсловие непротиворечивости
Читать далее
Правило Крамера – определение, формулы и примеры
Содержание Что такое правило Крамера?Формула правила КрамераПравило Крамера 2 x
Читать далее
Бесплатные карточки по математике – скачать PDF для печати
Этот пост также доступен на: हिन्दी (хинди) Читать далее
Учебное пособие: основы треугольников и тригонометрии
MathComments: 0Tags: Geometry, Math, Trigonometry, Tutorial Сегодня мы собираемся начать погружение в тригонометрию.
В конце концов мы поговорим обо всем, от триггера прямоугольного треугольника до единичного круга и триггерных функций. А пока давайте начнем с самого начала: основы треугольника и тригонометрии.
Чтобы говорить о тригонометрии, мы должны быть на одной странице в отношении определенных фактов и стандартных способов мышления о треугольниках. Вот некоторые из них:
Углы
Сумма трех углов треугольника составляет 180°. Прямой угол — это угол 90°, а прямоугольный треугольник — это треугольник, содержащий прямой угол. В прямоугольном треугольнике сумма двух углов, не являющихся прямыми, должна составлять 90°. Оба эти угла называются острыми , что означает, что их мера меньше 90°.
Соглашения об именах
Для наших целей мы будем обозначать углы треугольника заглавными буквами, обычно A, B и C, а стороны — строчными буквами, обычно a, b и c. Угол А образован двумя сторонами треугольника; сторона а — это « напротив » этого угла или сторона, которая не касается угла А.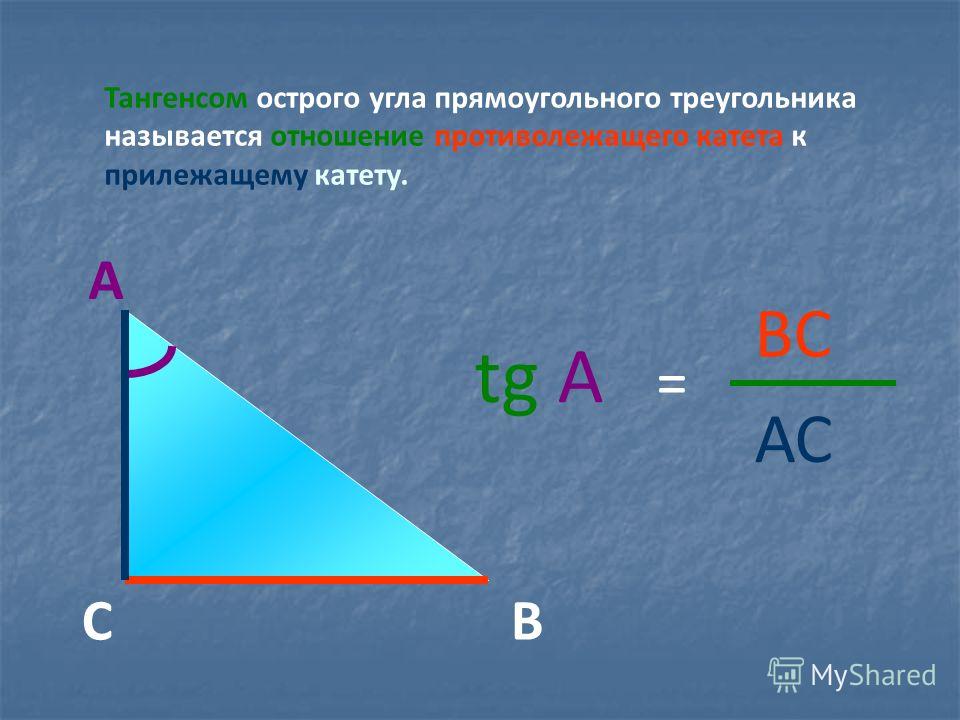
То же самое с другими сторонами и углами — если они имеют общую букву, они противоположны друг другу.
Аккуратный и полезный факт : Наименьший угол в треугольнике лежит против наименьшей стороны. Наибольший угол лежит против наибольшей стороны. И, если хотите, самый «средний» угол находится напротив стороны средней длины.
Нахождение прямоугольных треугольников
Есть несколько способов узнать, что треугольник является прямоугольным. Во-первых, если вы знаете, что конкретный угол имеет градусную меру 90 °, это прямоугольный треугольник! Иногда вы увидите маленький квадрат, втянутый в треугольник, как вы видите под углом С справа. Этот маленький квадрат означает, что две линии, которых он касается, перпендикулярны, еще один способ сказать вам, что угол с маленьким квадратом является прямым углом.
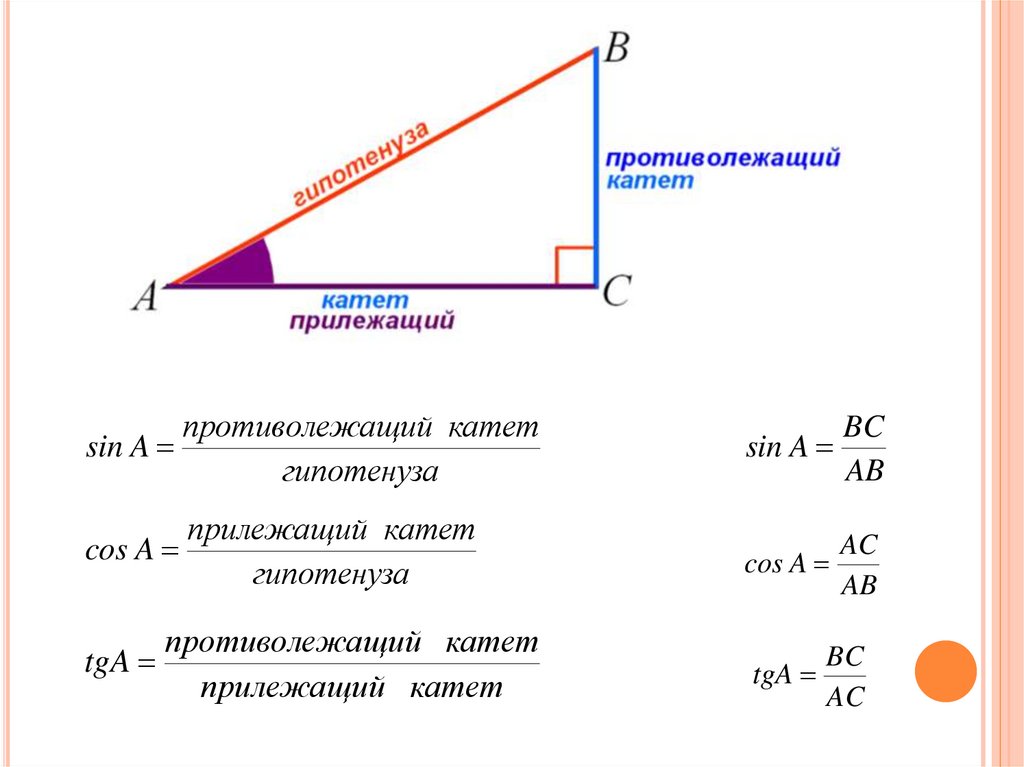
Напротив, Смежно, Гипотенуза
В прямоугольных треугольниках мы можем использовать противолежащие, смежные и гипотенузы, чтобы говорить о сторонах треугольника относительно относительно определенного угла.