Свойства степеней с примерами: Свойства степеней, действия со степенями

формулировки, доказательства, примеры, формулы степеней

Ранее мы уже говорили о том, что такое степень числа. Она имеет определенные свойства, полезные в решении задач: именно их и все возможные показатели степени мы разберем в этой статье. Также мы наглядно покажем на примерах, как их можно доказать и правильно применить на практике.

Свойства степени с натуральным показателем

Вспомним уже сформулированное нами ранее понятие степени с натуральным показателем: это произведение n-ного количества множителей, каждый из которых равен а. Также нам понадобится вспомнить, как правильно умножать действительные числа. Все это поможет нам сформулировать для степени с натуральным показателем следующие свойства:

Определение 1

1. Главное свойство степени: am·an=am+n

Можно обобщить до: an1·an2·…·ank=an1+n2+…+nk.

2. Свойство частного для степеней, имеющих одинаковые основания: am:an=am−n 

3. Свойство степени произведения: (a·b)n=an·bn

Равенство можно расширить до: (a1·a2·…·ak)n=a1n·a2n·…·akn 

4. Свойство частного в натуральной степени: (a:b)n=an:bn 

5. Возводим степень в степень: (am)n=am·n,

Можно обобщить до:(((an1)n2)…)nk=an1·n2·…·nk

6. Сравниваем степень с нулем:

• если a>0, то при любом натуральном n, an будет больше нуля;
• при a, равном 0, an также будет равна нулю;
• при a<0 и таком показателе степени, который будет четным числом 2·m, a2·m будет больше нуля;
• при a <0 и таком показателе степени, который будет нечетным числом 2·m−1, a2·m−1 будет меньше нуля.

7. Равенство an<bn будет справедливо для любого натурального n при условии, что a и b больше нуля и не равны друг другу.

8. Неравенство am>an будет верным при условии, что m и n – натуральные числа, m больше n и а больше нуля и не меньше единицы.

В итоге мы получили несколько равенств; если соблюсти все условия, указанные выше, то они будут тождественными. Для каждого из равенств, например, для основного свойства, можно поменять местами правую и левую часть: am·an=am+n — то же самое, что и am+n=am·an. В таком виде оно часто используется при упрощении выражений.

Далее мы разберем каждое свойство подробно и попробуем привести доказательства.

1. Начнем с основного свойства степени: равенство am·an=am+n будет верным при любых натуральных m и n и действительном a. Как доказать это утверждение?

Основное определение степеней с натуральными показателями позволит нам преобразовать равенство в произведение множителей. Мы получим запись такого вида:

Это можно сократить до  (вспомним основные свойства умножения). В итоге мы получили степень числа a с натуральным показателем m+n. Таким образом, am+n, значит, основное свойство степени доказано.

Разберем конкретный пример, подтверждающий это.

Пример 1

Итак, у нас есть две степени с основанием 2. Их натуральные показатели — 2 и 3 соответственно. У нас получилось равенство: 22·23=22+3=25 Вычислим значения, чтобы проверить верность этого равенства.

Выполним необходимые математические действия: 22·23=(2·2)·(2·2·2)=4·8=32 и 25=2·2·2·2·2=32

В итоге у нас вышло: 22·23=25.

Свойство доказано.

В силу свойств умножения мы можем выполнить обобщение свойства, сформулировав его в виде трех и большего числа степеней, у которых показатели являются натуральными числами, а основания одинаковы. Если обозначить количество натуральных чисел n1, n2 и др. буквой k, мы получим верное равенство:

an1·an2·…·ank=an1+n2+…+nk.

Пример 2

Пример с конкретными числами (легко посчитать самостоятельно): (2,1)3·(2,1)3·(2,1)4·(2,1)7=(2,1)3+3+4+7=(2,1)17.

2. Далее нам необходимо доказать следующее свойство, которое называется свойством частного и присуще степеням с одинаковыми основаниями: это равенство am:an=am−n, которое справедливо при любых натуральным m и n (причем m больше n) ) и любом отличном от нуля действительном a.

Для начала поясним, каков именно смысл условий, которые упомянуты в формулировке. Если мы возьмем a, равное нулю, то в итоге у нас получится деление на нуль, чего делать нельзя (ведь 0n=0). Условие, чтобы число m обязательно было больше n, нужно для того, чтобы мы могли удержаться в рамках натуральных показателей степени: вычтя n из m, мы получим натуральное число.

Если условие не будет соблюдено, у нас получится отрицательное число или ноль, и опять же мы выйдем за пределы изучения степеней с натуральными показателями.

Теперь мы можем перейти к доказательству. Из ранее изученного вспомним основные свойства дробей и сформулируем равенство так:

am−n·an=a(m−n)+n=am

Из него можно вывести: am−n·an=am

Вспомним про связь деления и умножения. Из него следует, что am−n– частное степеней am и an. Это и есть доказательство второго свойства степени.

Пример 3

Подставим конкретные числа для наглядности в показатели, а основание степени обозначим π: π5:π2=π5−3=π3

3. Следующим мы разберем свойство степени произведения: (a·b)n=an·bn при любых действительных a и b и натуральном n.

Согласно базовому определению степени с натуральным показателем мы можем переформулировать равенство так:

Вспомнив свойства умножения, запишем: . Это значит то же самое, что и an·bn.

Пример 4

23·-4254=234·-4254

Если множителей у нас три и больше, то это свойство также распространяется и на этот случай. Введем для числа множителей обозначение k и запишем:

(a1·a2·…·ak)n=a1n·a2n·…·akn

Пример 5

С конкретными числами получим следующее верное равенство: (2·(-2,3)·a)7=27·(-2,3)7·a

4. После этого мы попробуем доказать свойство частного: (a:b)n=an:bn при любых действительных a и b, если b не равно 0, а n – натуральное число.

Для доказательства можно использовать предыдущее свойство степени. Если (a:b)n·bn=((a:b)·b)n=an , а (a:b)n·bn=an, то из этого выходит, что (a:b)n есть частное от деления an на bn.

Пример 6

Подсчитаем пример: 312:-0.53=3123:(-0,5)3

5. Далее мы поговорим о свойстве возведения степени в степень: (am)n=am·n для любого действительного a и любых натуральных n и m.

Пример 7

Начнем сразу с примера: (52)3=52·3=56

А теперь сформулируем цепочку равенств, которая докажет нам верность равенства:

Если у нас в примере есть степени степеней, то это свойство справедливо для них также. Если у нас есть любые натуральные числа p, q, r, s, то верно будет:

apqys=ap·q·y·s

Пример 8

Добавим конкретики: (((5,2)3)2)5=(5,2)3·2·5=(5,2)30

6. Еще одно свойство степеней с натуральным показателем, которое нам нужно доказать, – свойство сравнения.

Для начала сравним степень с нулем. Почему an>0 при условии, что а больше 0?

Если умножить одно положительное число на другое, то мы получим также положительное число. Зная этот факт, мы можем сказать, что от числа множителей это не зависит – результат умножения любого числа положительных чисел есть число положительное. А что же такое степень, как не результат умножения чисел? Тогда для любой степени an с положительным основанием и натуральным показателем это будет верно.

Пример 9

 35>0, (0,00201)2>0 и 3491351>0

Также очевидно, что степень с основанием, равным нулю, сама есть ноль. В какую бы степень мы не возводили ноль, он останется им.

Пример 10

03=0 и 0762=0

Если основание степени – отрицательное число, тот тут доказательство немного сложнее, поскольку важным становится понятие четности/нечетности показателя. Возьмем для начала случай, когда показатель степени четный, и обозначим его 2·m, где m – натуральное число.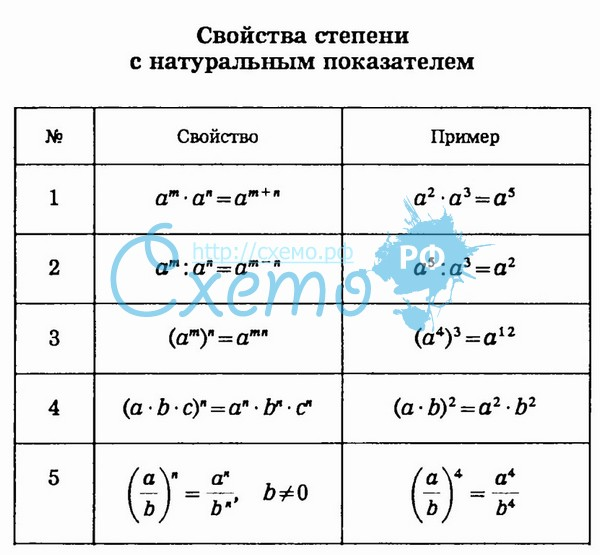

Тогда:

Вспомним, как правильно умножать отрицательные числа: произведение a·a равно произведению модулей, а, следовательно, оно будет положительным числом. Тогда  и степень a2·m также положительны.

Пример 11

Например, (−6)4>0, (−2,2)12>0 и -296>0

А если показатель степени с отрицательным основанием – нечетное число? Обозначим его 2·m−1.

Тогда  

Все произведения a·a, согласно свойствам умножения, положительны, их произведение тоже. Но если мы его умножим на единственное оставшееся число a, то конечный результат будет отрицателен.

Тогда получим: (−5)3<0, (−0,003)17<0 и -111029<0

7. Далее разберем следующее свойство, формулировка которого такова: из двух степеней, имеющих одинаковый натуральный показатель, больше та, основание которой больше (и наоборот).

Как это доказать?

an<bn– неравенство, представляющее собой произведение левых и правых частей nверных неравенств a<b. Вспомним основные свойства неравенств справедливо и an<bn.

Пример 12

Например, верны неравенства: 37<(2,2)7 и 3511124>(0,75)124

8. Нам осталось доказать последнее свойство: если у нас есть две степени, основания которых одинаковы и положительны, а показатели являются натуральными числами, то та из них больше, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше.

Докажем эти утверждения.

Для начала нам нужно убедиться, что am<an при условии, что m больше, чем n, и а больше 0, но меньше 1.Теперь сравним с нулем разность am−an

Вынесем an за скобки, после чего наша разность примет вид an·(am−n−1). Ее результат будет отрицателен (поскольку отрицателен результат умножения положительного числа на отрицательное). Ведь согласно начальным условиям, m−n>0, тогда am−n−1–отрицательно, а первый множитель положителен, как и любая натуральная степень с положительным основанием.

У нас вышло, что am−an<0 и am<an. Свойство доказано.

Осталось привести доказательство второй части утверждения, сформулированного выше: am>a справедливо при m>n и a>1. Укажем разность и вынесем an за скобки: (am−n−1).Степень an при а, большем единицы, даст положительный результат; а сама разность также окажется положительна в силу изначальных условий, и при a>1 степень am−n больше единицы. Выходит, am−an>0 и am>an, что нам и требовалось доказать.

Пример 13

Пример с конкретными числами: 37>32

Основные свойства степеней с целыми показателями

Для степеней с целыми положительными показателями свойства будут аналогичны, потому что целые положительные числа являются натуральными, а значит, все равенства, доказанные выше, справедливы и для них. Также они подходят и для случаев, когда показатели отрицательны или равны нулю (при условии, что само основание степени ненулевое).

Таким образом, свойства степеней такие же для любых оснований a и b (при условии, что эти числа действительны и не равны 0) и любых показателей m и n (при условии, что они являются целыми числами). Запишем их кратко в виде формул:

Определение 2

1. am·an=am+n 

2. am:an=am−n

3. (a·b)n=an·bn

4. (a:b)n=an:bn

5. (am)n=am·n 

6. an<bn и a−n>b−n при условии целого положительного n, положительных a и b, a<b 

7. am<an, при условии целых m и n, m>n и 0<a<1, при a>1   am>an.

Если основание степени равно нулю, то записи am и an имеют смысл только лишь в случае натуральных и положительных m и n. В итоге получим, что формулировки выше подходят и для случаев со степенью с нулевым основанием, если соблюдаются все остальные условия.

Доказательства этих свойств в данном случае несложные. Нам потребуется вспомнить, что такое степень с натуральным и целым показателем, а также свойства действий с действительными числами.

Разберем свойство степени в степени и докажем, что оно верно и для целых положительных, и для целых неположительных чисел. Начнем с доказательства равенств (ap)q=ap·q, (a−p)q=a(−p)·q, (ap)−q=ap·(−q) и (a−p)−q=a(−p)·(−q)

Условия: p=0 или натуральное число; q– аналогично.

Если значения p и q больше 0, то у нас получится (ap)q=ap·q. Схожее равенство мы уже доказывали раньше. Если p=0, то:

(a0)q=1q=1 a0·q=a0=1

Следовательно, (a0)q=a0·q

Для q=0 все точно так же:

(ap)0=1 ap·0=a0=1

Итог: (ap)0=ap·0.

Если же оба показателя нулевые, то (a0)0=10=1 и a0·0=a0=1, значит, (a0)0=a0·0.

Далее разберем равенство (a−p)q=a(−p)·q. Согласно определению степени с целым отрицательным показателем имеем a-p=1ap, значит, (a-p)q=1apq.

Вспомним доказанное выше свойство частного в степени и запишем:

1apq=1qapq

Если 1p=1·1·…·1=1 иapq=ap·q, то 1qapq=1ap·q

Эту запись мы можем преобразовать в силу основных правил умножения в a(−p)·q.

Так же: ap-q=1(ap)q=1ap·q=a-(p·q)=ap·(-q).

И (a-p)-q=1ap-q=(ap)q=ap·q=a(-p)·(-q)

Остальные свойства степени можно доказать аналогичным образом, преобразовав имеющиеся неравенства. Подробно останавливаться мы на этом не будем, укажем только сложные моменты.

Доказательство предпоследнего свойства: вспомним, a−n>b−n верно для любых целых отрицательных значений nи любых положительных a и b при условии, что a меньше b.

Тогда неравенство можно преобразовать следующим образом:

1an>1bn

Запишем правую и левую части в виде разности и выполним необходимые преобразования:

1an-1bn=bn-anan·bn

Вспомним, что в условии a меньше b, тогда, согласно определению степени с натуральным показателем: — an<bn, в итоге: bn−an>0.

an·bn в итоге дает положительное число, поскольку его множители положительны. В итоге мы имеем дробь bn-anan·bn, которая в итоге также дает положительный результат. Отсюда 1an>1bn откуда a−n>b−n, что нам и нужно было доказать.

Последнее свойство степеней с целыми показателями доказывается аналогично свойству степеней с показателями натуральными.

Основные свойства степеней с рациональными показателями

В предыдущих статьях мы разбирали, что такое степень с рациональным (дробным) показателем. Их свойства такие же, что и у степеней с целыми показателями. Запишем:

Определение 3

1. am1n1·am2n2=am1n1+m2n2 при a>0, а если m1n1>0 и m2n2>0, то при a≥0 ( свойство произведения степеней с одинаковыми основаниями).

2.am1n1:bm2n2=am1n1-m2n2 , если a>0 (свойство частного).

3. a·bmn=amn·bmn при a>0 и b>0, а если m1n1>0 и m2n2>0, то при a≥0 и (или) b≥0 (свойство произведения в дробной степени).

4. a:bmn=amn:bmn при a>0 и b>0, а если mn>0, то при a≥0 и b>0 (свойство частного в дробной степени).

5. am1n1m2n2=am1n1·m2n2 при a>0, а если m1n1>0 и m2n2>0, то при a≥0 (свойство степени в степени).

6. ap<bp при условии любых положительных a и b, a<b и рациональном p при p>0; если p<0 — ap>bp (свойство сравнения степеней с равными рациональными показателями).

7. ap<aq при условии рациональных чисел p и q, p>q при 0<a<1; если a>0 – ap>aq

Для доказательства указанных положений нам понадобится вспомнить, что такое степень с дробным показателем, каковы свойства арифметического корня n-ной степени и каковы свойства степени с целыми показателем. Разберем каждое свойство.

Согласно тому, что из себя представляет степень с дробным показателем, получим:

am1n1=am1n1 и am2n2=am2n2, следовательно, am1n1·am2n2=am1n1·am2n2

Свойства корня позволят нам вывести равенства:

am1·m2n1·n2·am2·m1n2·n1=am1·n2·am2·n1n1·n2

Из этого получаем:  am1·n2·am2·n1n1·n2=am1·n2+m2·n1n1·n2

Преобразуем:

am1·n2·am2·n1n1·n2=am1·n2+m2·n1n1·n2

Показатель степени можно записать в виде:

m1·n2+m2·n1n1·n2=m1·n2n1·n2+m2·n1n1·n2=m1n1+m2n2

Это и есть доказательство. Второе свойство доказывается абсолютно так же. Запишем цепочку равенств:

am1n1: am2n2=am1n1: am2n2=am1·n2:am2·n1n1·n2==am1·n2-m2·n1n1·n2=am1·n2-m2·n1n1·n2=am1·n2n1·n2-m2·n1n1·n2=am1n1-m2n2

Доказательства остальных равенств:

a·bmn=(a·b)mn=am·bmn=amn·bmn=amn·bmn;(a:b)mn=(a:b)mn=am:bmn==amn:bmn=amn:bmn;am1n1m2n2=am1n1m2n2=am1n1m2n2==am1m2n1n2=am1·m2n1n2==am1·m2n2·n1=am1·m2n2·n1=am1n1·m2n2

Следующее свойство: докажем, что для любых значений a и b больше 0, если а меньше b, будет выполняться ap<bp, а для p больше 0 — ap>bp

Представим рациональное число p как mn. При этом m–целое число, n–натуральное. Тогда условия p<0 и p>0 будут распространяться на m<0 и m>0. При m>0 и a<b имеем (согласно свойству степени с целым положительным показателем), что должно выполняться неравенство am<bm.

Используем свойство корней и выведем: amn<bmn

Учитывая положительность значений a и b, перепишем неравенство как amn<bmn. Оно эквивалентно ap<bp.

Таким же образом при m<0 имеем a am>bm, получаем amn>bmn значит, amn>bmn и ap>bp.

Нам осталось привести доказательство последнего свойства. Докажем, что для рациональных чисел p и q, p>q при 0<a<1 ap<aq, а при a>0 будет верно ap>aq.

Рациональные числа p и q можно привести к общему знаменателю и получить дроби m1n и m2n

Здесь m1 и m2 – целые числа, а n – натуральное. Если p>q, то m1>m2 (учитывая правило сравнения дробей). Тогда при 0<a<1 будет верно am1<am2, а при a>1 – неравенство a1m>a2m.

Их можно переписать в следующем виде:

am1n<am2nam1n>am2n

Тогда можно сделать преобразования и получить в итоге:

am1n<am2nam1n>am2n

Подводим итог: при p>q и 0<a<1 верно ap<aq, а при a>0– ap>aq.

Основные свойства степеней с иррациональными показателями

На такую степень можно распространить все описанные выше свойства, которыми обладает степень с рациональными показателями. Это следует из самого ее определения, которое мы давали в одной из предыдущих статей. Сформулируем кратко эти свойства (условия: a>0, b>0, показатели p и q– иррациональные числа):

Определение 4

1. ap·aq=ap+q 

2. ap:aq=ap−q 

3. (a·b)p=ap·bp

4. (a:b)p=ap:bp 

5. (ap)q=ap·q

6. ap<bp верно при любых положительных a и b, если a<b и p – иррациональное число больше 0; если p меньше 0, то ap>bp 

7. ap<aq верно, если p и q– иррациональные числа, p<q, 0<a<1; если a>0, то ap>aq.

Таким образом, все степени, показатели которых p и q являются действительными числами, при условии a>0 обладают теми же свойствами.

формулы, примеры с натуральным и рациональным показателем, доказательства, тема по алгебре для 7 класса

В статье рассмотрим свойства степеней с натуральным и рациональным показателями. Мы изучим формулы, приведем примеры и доказательства

Свойства степеней. Фото: SHVETS production, pixals.com

Наталия Юмагулова Учитель математики

Содержание

1. Свойства степени с натуральным показателем
2. Свойства степени с рациональным показателем
3. Доказательства свойств степеней
4. Вопросы и ответы

Михаил Васильевич Ломоносов когда-то сказал: «Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь». Действительно: степени и их свойства — важные темы, изучение которых необходимо для успешной подготовки к ЕГЭ по математике. Знание свойств степеней облегчает работу с уравнениями и функциями, где содержатся такие выражения. Внимательно их изучив, можно достаточно быстро выполнять задания, что немаловажно в процессе написания экзамена.

Свойства степени с натуральным показателем

Степенью числа a с натуральным показателем n (n>1), называют произведение n множителей, каждый из которых равен a.

Основание степени — это повторяющийся множитель. Показатель степени — это число, указывающее количество повторений. Изображение: Наталия Юмагулова.

Мы собрали свойства степени с натуральным показателем в одну таблицу. С помощью нее можно быстро выучить все формулы и подготовиться к экзамену.

Примеры

Пример №1

Выполните деление:
7¹⁴ : 7¹²

Решение:

Применим свойство частного, получим:
7¹⁴ : 7¹² = 7^14–12 =7² = 49

Пример №2

Упростите выражение:
(−b⁶)¹⁰

Решение:

Применим свойства возведения произведения в степень, возведения отрицательного числа в четную степень, возведения степени в степень, получим:
(−b⁶)¹⁰ = (−1b⁶)¹⁰ = (− 1)¹⁰ (b⁶)¹⁰ = b⁶⁰

Пример №3

Представьте в виде степени выражение:
(m⁶)^t (m^t)², где t – натуральное число

Решение:

Применим свойство возведения степени в степень, а затем свойство умножения степеней:
(m⁶)^t (m^t)² = m^6t m^2t = m^6t+2t = m^8t

это интересно

Таблица степеней

Рассказываем, как ей пользоваться и что с ее помощью можно сделать

ПОДРОБНЕЕ

Свойства степени с рациональным показателем

Примеры

Доказательства свойств степеней

Доказательство свойств степеней с дробными показателями базируется на определении степени с дробным показателем, на свойствах арифметического корня n-ой степени и на свойствах степени с целым показателем. Приведем некоторые доказательства.

1. Свойство умножения степеней

2. Свойство возведения произведения в степень

3. Следствие из свойства умножения степеней — возведение в отрицательную степень

Популярные вопросы и ответы

Почему свойства степеней изучают на алгебре в 7 классе?

Впервые ребята встречаются с понятием степени в 5-м классе. По мере знакомства и действий с одночленами и многочленами в 7-м классе необходима определенная теоретическая база, поэтому перед изучением данных тем и проходят свойства степени.

Что такое основное свойство степени?

Основным является свойство умножения степеней, так как с помощью этого правила доказываются другие свойства.

Для чего используются свойства степеней?

Эти свойства используются для упрощения числовых и буквенных выражений, то есть для их преобразования. Также они необходимы при решении уравнений и работе с функциями, где встречаются выражения со степенями.

показателей — определение, примеры | Свойства показателей степени

Показатель степени числа показывает, сколько раз число умножается само на себя. Например, 3 ⁴ означает, что 3 умножается на себя четыре раза, то есть 3 × 3 × 3 × 3 = 3 ⁴ , а здесь 4 — показатель степени числа 3. Показатель степени также известен как степень число, и в этом случае оно читается как 3 в степени 4. Показатель степени может быть целым числом, дробью, отрицательным или десятичным числом. Давайте узнаем больше о значение показателей вместе с примерами показателей в этой статье.

1.	Что такое экспоненты?
2.	Законы (свойства или правила) экспонентов
3.	Отрицательные показатели
4.	Экспоненты с дробями
5.	Десятичные степени
6.	Научное обозначение с показателями
7.	Часто задаваемые вопросы по экспонентам

Что такое экспоненты?

Показатель степени числа показывает, сколько раз число умножается само на себя. Например, 2 × 2 × 2 × 2 можно записать как 2 ⁴ , так как 2 умножается на себя 4 раза. Здесь 2 называется «основание», а 4 — «показатель степени» или «степень».

Значение показателей степени

Степень степени — это способ выражения больших чисел в степени. Например, 4, умноженное 3 раза само на себя, может быть выражено как 4 × 4 × 4 = 4 ³ , где 3 — показатель степени числа 4. Посмотрите на следующий рисунок, чтобы увидеть, как мы выражаем показатель степени числа. Он показывает, что x ⁿ означает, что x умножается сам на себя n раз.

Здесь в члене x ⁿ ,

• x называется «базой»
• n называется «показатель степени»
• x ⁿ читается как «x в степени n» (или) «x в степени n».

Вот несколько примеров показателей степени:

• 3 × 3 × 3 × 3 × 3 = 3 ⁵
• -2 × -2 × -2 = (-2) ³
• а × а × а × а × а × а = а ⁶

Показатель степени важен, потому что, когда число многократно умножается само на себя, его легко выразить в виде показателей степени. Например, проще написать 5 ⁷ вместо того, чтобы писать как 5 × 5 × 5 × 5 × 5 × 5 × 5.

Свойства показателей степени

свойства показателей степени , которые также известны как законы показателей степени, используются для решения задач, связанных с показателями степени. Эти свойства также рассматриваются как правила основных показателей. Основные свойства показателей приведены ниже.

• Закон произведения: a ^m × a ⁿ = a ^m+n
• Закон частного: а ^м /а ^н = а ^м-н
• Закон нулевой степени: a ⁰ = 1
• Закон отрицательного показателя степени: a ^-m = 1/a ^m
• Закон Силы Силы: (a ^m ) ⁿ = a ^mn
• Закон силы продукта: (ab) ^m = a ^m b ^m
• Закон степени частного: (a/b) ^m = a ^m /b ^m

Отрицательные показатели степени

Отрицательный показатель степени говорит нам, сколько раз нам нужно умножить обратное основание. Например, если известно, что a ^-n , его можно разложить как 1/a ⁿ . Это означает, что мы должны умножить обратную величину a, то есть 1/a ‘n’ раз. Отрицательные показатели степени используются при записи дробей с показателями степени. Некоторые примеры отрицательных показателей: 2 × 3 ^-9 , 7 ^-3 , 67 ^-5 и т. д. Мы можем преобразовать их в положительные показатели следующим образом:

• 2 × 3 ^-9 = 2 × (1/3 ⁹ ) = 2/3 ⁹
• 7 ^-3 = 1/7 ³
• 67 ^-5 = 1/67 ⁵

Экспоненты с дробями

Если показатель степени числа представляет собой дробь, он называется дробным показателем. Квадратные корни, кубические корни, корень n ^th являются частями дробных показателей. Число со степенью 1/2 называется квадратным корнем из основания. Точно так же число со степенью 1/3 называется кубическим корнем из основания. Некоторые примеры показателей степени с дробями: 5 ^2/3 , -8 ^1/3 , 10 ^5/6 и т. д. Мы можем записать их следующим образом:

• 5 ^2/3 = (5 ² ) 19300 = 25 ^1/3 = ∛25
• -8 ^1/3 = ((-2) ³ ) ^1/3 = -2
• 10 ^5/6 = (10 ⁵ ) ⁶ = ⁶ √10 ⁵ = ⁶ √100000

Десятичные экспоненты

Если показатель степени числа задан в десятичной форме, он известен как десятичный показатель степени. Немного сложно оценить правильный ответ любого десятичного показателя степени, поэтому мы находим приблизительный ответ для таких случаев. Десятичные показатели степени можно решить, сначала преобразовав десятичную дробь в дробную форму. Например, 4 ^1,5 можно записать как 4 ^3/2 , что можно еще упростить, чтобы получить окончательный ответ 8, то есть 4 ^3/2 = (2 ² ) ^3/2 = 2 ³ = 8.

Научное обозначение с показателями

Научная нотация — это стандартная форма записи очень больших или очень маленьких чисел. При этом числа записываются с помощью десятичных знаков и степеней 10. Говорят, что число записывается в экспоненциальном представлении, когда число от 0 до 10 умножается на степень 10. В случае числа больше, чем 1 , степень 10 будет положительным показателем, а в случае чисел меньше 1 , степень 10 будет отрицательной. Давайте разберемся с этапами записи чисел в экспоненте с экспонентами:

• Шаг 1: Поставьте десятичную точку после первой цифры числа слева. Если в числе только одна цифра без нулей, то десятичную ставить не нужно.
• Шаг 2: Умножьте это число на степень 10 так, чтобы степень была равна количеству сдвигов десятичной точки.

Следуя этим двум простым шагам, мы можем записать любое число в стандартной форме с показателями, например, 560000 = 5,6 × 10 ⁵ , 0,00736567 = 7,36567 × 10 ^-3 .

Чтобы узнать больше об использовании показателей степени при написании экспоненциального представления чисел, посетите следующие статьи:

• Как записать 2,5 миллиона в экспоненциальном представлении?
• Как записать 12 миллионов в экспоненциальном представлении?
• Как записать 0,0001 в экспоненциальном представлении?
• Какое научное обозначение для 8 миллионов?
• Как записать 13 миллионов в экспоненциальном представлении?
• Какое из следующих выражений записано в экспоненциальной записи

Советы и подсказки:

• Если дробь имеет отрицательный показатель степени, то мы берем обратную дробь, чтобы показатель степени был положительным, т. е. (a/b) ^-m = (b/a) ^м .
• Десятичные показатели степени можно решить, сначала преобразовав десятичную дробь в форму дроби, т. е. 2 ^0,5 можно записать как 2 ^1/2

☛ Связанные темы по показателям степени

Посмотрите еще несколько интересных статей, основанных на показателях степени в математике.

• Умножение показателей степени
• Экспоненциальные функции
• Экспоненциальные уравнения
• Иррациональные Показатели

 

Показатели Примеры

1. Пример 1: Найдите произведение следующих выражений: a ⁵ × b ³ × a ⁸

   Решение:

   . ^м × a ⁿ = a ^(m+n)

   Это будет a ⁵ × b ³ × a ⁸ = a ⁵⁺⁸ × b 90 90 ^{3 3 0006 × b 3 = a 13 b 3}

2. Пример 2: Найдите произведение числа 5 ⁷ × 5 ³ , используя свойства показателей степени.

   Решение:

   5 ³ × 5 ⁷ = 5 ¹⁰ (используя формулу показателей степени = a ^m × a ⁿ

   = 5

   ^m x a n

   = 5

   n

   6)

3. Пример 3: Упростите следующее выражение: p ¹² ÷ p ⁴ q.

   Решение:

   Данное выражение равно p ¹² ÷ p ⁴ q. Чтобы упростить это выражение, мы используем закон отношения показателей степени, который гласит:

   ⇒ p ¹² /p ⁴ q

   ⇒ p ^12-4 /q

   ⇒ p ⁸ /q

   9 Следовательно ÷ p ⁴ q = p ⁸ /q

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по Exponents

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по экспонентам

Что такое экспоненты в математике?

Показатель степени — это число, которое помещается над числом в виде надстрочного индекса. Другими словами, это указывает на то, что основание возведено в определенную степень. Показатель степени также называют другими именами, такими как индекс и мощность. Если m — положительное число, а n — его показатель степени, то m ⁿ означает, что m умножается само на себя n раз. Здесь m ⁿ читается как «m в степени n», и в этом случае «m» — это основание, а «n» — показатель степени.

Каковы свойства экспонент?

Свойства показателей степени — это некоторые правила, которые мы используем при решении выражений, включающих показатели степени. Эти правила помогают нам легко и быстро упрощать выражения. Несколько важных свойств экспонент перечислены ниже:

• a ^m × a ⁿ = a ^m+n
• a ^м /a ⁿ = a ^m-n
• а ⁰ = 1
• а ^-м = 1/а ^м
• ( ^м ) ⁿ = ^мн
• (ab) ^м = a ^м b ^м
• (a/b) ^м = a ^м /b ^м

Каковы примеры показателей степени?

Ниже приведены некоторые примеры показателей степени:

• 7 × 7 × 6 × 6 × 6 = 7 ² × 6 ³ . Здесь 2 и 3 — показатели степени.
• -4 × -4 × -4 × -4 = (-4) ⁴ . Здесь 4 — показатель степени.
• п × п × п × п × п = п ⁵ . Здесь 5 — показатель степени.

Как экспоненты относятся к реальной жизни?

В реальной жизни мы используем понятие экспоненты для упрощенного и краткого написания чисел. Повторное умножение можно легко записать с помощью показателей степени. Кроме того, мы используем показатель степени для записи больших чисел, например, расстояния Луны от Земли, количества бактерий, присутствующих на поверхности, и т. д.

Как добавить экспоненты?

Экспоненты не могут быть добавлены. Мы можем добавлять только одинаковые термины (термы, имеющие один и тот же показатель степени и одну и ту же переменную). Но, в случае умножения членов с одинаковыми переменными, мы прибавляем показатели степени переменной к умножению. Например, х ² × х ⁴ = х ⁽²⁺⁴⁾ = х ⁶ .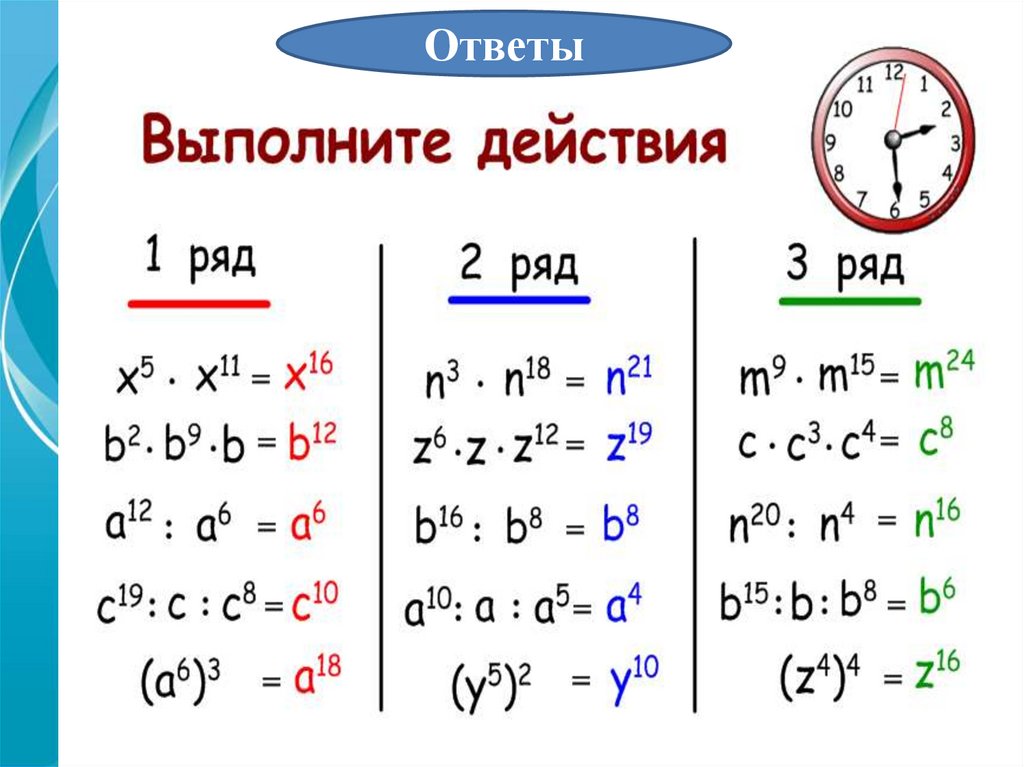 Попробуйте калькулятор сложения показателей степени от Cuemath и получите ответы быстро и легко.

Почему показатели степени важны?

Экспоненты важны для записи значений чисел в упрощенной форме. Мы знаем, что многократное сложение можно записать как умножение. Точно так же многократное умножение можно записать просто с помощью показателей степени. Показатель степени также важен, потому что, когда число многократно умножается само на себя, его легко выразить в виде показателей степени. Например, проще написать 13 ⁶ , чем записать это как 13 × 13 × 13 × 13 × 13 × 13.

Как вычислить показатели степени с помощью калькулятора степени?

«Калькулятор степени» — это онлайн-инструмент, который находит значение экспоненциального выражения. Проверьте теперь калькулятор экспоненты Cuemath и найдите значение экспоненциального выражения для заданного значения основания и экспоненты в течение нескольких секунд.

☛ Также проверьте:

• Калькулятор отрицательных показателей
• Калькулятор степени деления
• Калькулятор умножения показателей степени
• Калькулятор правил экспоненты
• Калькулятор дробей с показателями степени

Как умножать показатели степени?

Когда необходимо умножить показатели степени, мы сначала решаем числа в скобках, степень вне скобок умножается на каждую степень внутри скобок. Например, (3x ² y ³ ) ² = 3 ² x x ^{2 x 2} x y ^{3 x 2} = 9 x ^{4 6}

y

Какая польза от свойств показателей?

Свойства показателей степени широко используются в математике, особенно в алгебре. С помощью свойств показателей мы можем легко упростить выражения. Давайте разберемся в этом на примере. С помощью свойств экспоненты 2 ⁴ × 2 ⁶ можно упростить в два быстрых шага как 2 ⁴ × 2 ⁶ = 2 ^{(4 + 6)} = 2 ¹⁰ .

Каково реальное применение экспонентов?

Экспоненты имеют различные применения. Ниже перечислены несколько приложений экспонентов:

• Экспоненты широко используются в компьютерных играх, измерительных весах и т. д.
• Научные шкалы, такие как шкала рН или шкала Рихтера, основаны на показателях степени.
• Они используются при вычислении площади, объема и задач, связанных с измерением.
• Чаще всего они используются в соответствующих областях науки, техники, экономики, бухгалтерского учета и финансов.
• Они часто используются для представления памяти компьютера или ноутбука.

Как законы экспоненты используются в алгебре?

Законы экспоненты очень полезны в алгебре. Например, алгебраическую формулу (a — b) ² = a ² + b ² — 2ab можно легко записать и вычислить, применяя правила возведения в степень. Многие такие алгебраические формулы зависят только от законов показателей.

Как отрицательные показатели используются в реальной жизни?

Отрицательные показатели степени используются для записи очень маленьких чисел в реальной жизни, что означает числа со значениями от 0 до 1.

Что такое нулевой показатель?

Нулевой показатель степени означает числа, у которых показатель степени равен 0. Значения этих чисел всегда равны 1. Любое число с 0 в качестве его степени равно 1. Например, 5 ⁰ = 1, 34 ⁰ = 1, a ⁰ = 1

Полномочия?

Показатели и степени означают одно и то же. Давайте разберемся в этом на примерах. В выражении 10 ⁴ 10 — это основание, а 4 — показатель степени, и мы читаем его как 10, возведенное в степень 4. Аналогично, в 6 ³ , 6 — это основание, а 3 — показатель степени, и мы читаем это как 6, возведенное в степень 3.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочие листы по показателям [PDF]

Законы показателей

Экспоненты также называются Степенями или Индексами

Показатель степени числа говорит , сколько раз использовать число при умножении .

В этом примере: 8 ² = 8 × 8 = 64

Прописью: 8 ² можно назвать «8 во второй степени», «8 во второй степени» или просто «8 в квадрате»

Попробуйте сами:

изображения/экспонента-calc. js

Таким образом, экспонента избавляет нас от записи большого количества умножений!

Пример: a

⁷

a ⁷ = a × a × a × a × a × a × a = aaaaaaa

Обратите внимание, как мы написали буквы вместе, чтобы означать умножение? Мы будем делать это много здесь.

Пример: x

⁶ = xxxxxx

Ключ к законам

Написание всех букв является ключом к пониманию Законов

Пример: х

² х ³ = (хх)(ххх) = ххххх = х ⁵

Что показывает, что х ² х ^{3 = х}

1 6, но больше

5 что позже!

Итак, если вы сомневаетесь, просто не забудьте записать все буквы (столько, сколько вам говорит показатель степени) и посмотреть, сможете ли вы понять это.

Все, что вам нужно знать…

«Законы экспонентов» (также называемые «Правилами экспонентов») исходят из трех идей :

	Показатель степени говорит сколько раз использовать число в умножении .
	Отрицательный показатель степени означает, что делит , потому что деление 9 противоположно умножению.0018
	Дробная экспонента, такая как 1/n , означает, что извлекает корень n-й степени : х ( 1 n ) = п√х

Если вы их понимаете, то понимаете и экспоненты!

И все законы ниже основаны на этих идеях.

Законы экспонентов

Вот законы (пояснения следуют):

Право	Пример
х 1 = х	6 1 = 6
х 0 = 1	7 0 = 1
х -1 = 1/х	4 -1 = 1/4
x м x n = x м+n	x 2 x 3 = x 2+3 = x 5
x м /x n = x м-n	х 6 /х 2 = х 6-2 = х 4
(х м ) n = х м	(х 2 ) 3 = х 2×3 = х 6
(ху) н = х н у н	(ху) 3 = х 3 у 3
(x/y) n = x n /y n	(х/у) 2 = х 2 / у 2
x -n = 1/x n	х -3 = 1/х 3
И закон о дробных показателях:
х м/п  = n√x м            = (n√x) м	х 2/3  = 3√x 2            = (3√x) 2

Объяснение законов

Первые три приведенных выше закона (x ¹ = x, x ⁰ = 1 и x ^-1 = 1/x) являются лишь частью естественной последовательности показателей степени. Взгляните на это:

Пример: Степени числа 5
	.. и т.д..
5 2	1 × 5 × 5	25
5 1	1 × 5	5
5 0	1	1
5 -1	1 ÷ 5	0,2
5 -2	1 ÷ 5 ÷ 5	0,04
	.. и т.д..

Некоторое время посмотрите на эту таблицу. .. обратите внимание, что положительный, нулевой или отрицательный показатель степени на самом деле являются частью одного и того же шаблона, то есть в 5 раз больше (или в 5 раз меньше) в зависимости от того, увеличивается (или уменьшается) показатель степени.

Закон о том, что x

^m x ⁿ = x ^m+n

С x ^m x ⁿ , сколько раз мы в итоге умножаем «x»? Ответ: сначала «m» раз, затем еще «n» раз, всего «m+n» раз.

Пример: х

² х ³ = (хх)(ххх) = ххххх = х ⁵

Итак, х ² х ³ = х ^{(2+3) 900}

Закон, который х

^м /х ^н = х ^м-н

Как и в предыдущем примере, сколько раз нам нужно умножить «x»? Ответ: «m» раз, тогда уменьшите это в «n» раз (потому что мы делим), итого в «m-n» раз.

Пример: х

⁴ /х ² = (хххх) / (хх) = хх = х ²

Итак, х ⁴ /х ² = х ^{(00-2) х 2}

(Помните, что х / x = 1, поэтому каждый раз, когда вы видите x «над чертой» и одну «под чертой», вы можете отменить их. )

Этот закон также может показать вам, почему x ⁰ = 1 :

Пример: x

² /x ² = x ^2-2 = x ⁰ =1 3 3 3

Закон того, что (x

^m ) ⁿ = x ^mn

Сначала вы умножаете «m» раз. Тогда у вас есть сделать это «n» раз , всего m×n раз.

Пример: (x

³ ) ⁴ = (xxx) ⁴ = (xxx)(xxx)(xxx)(xxx) = xxxxxxxxxxxx = x ¹²

Итак (x ³

5 ) 9

= х ^3×4 = х ¹²

Закон того, что (xy)

ⁿ = x ⁿ y ⁿ

Чтобы показать, как это работает, просто подумайте о перестановке всех «x» и «y», как в этом примере:

Пример: (ху)

³ = (xy)(xy)(xy) = xyxyxy = xxxyyy = (xxx)(yyy) = x ³ y ³

Закон того, что (x/y)

ⁿ = x ⁿ /y ⁿ

Аналогично предыдущему примеру, просто переставьте «x» и «y»

Пример: (x/y)

³ = (x/y)(x/y)(x/y) = (xxx)/(yyy) = x ³ /y ³

Закон, который х

^м/п  = n√x ^м «=» (п√х) ^м

Хорошо, это немного сложнее!

Я предлагаю вам сначала прочитать дробные экспоненты, так это имеет больше смысла.

В любом случае, важная идея заключается в следующем:

x ^{1/ n} = n- -й корень x

Таким образом, дробная экспонента, такая как 4 ^3/2 , на самом деле говорит о том, что нужно сделать кубом (3) и извлечь квадратный корень из из (1/2) в любом порядке.

Просто запомните из дробей, что м/н = м × (1/н) :

Пример: x

^{( м n )}  = x ^{(м × 1 n )}  = (x ^м ) ^1/n  = n√x ^м

Порядок не имеет значения, поэтому он работает и для m/n = (1/n) × m :

Пример: x

^{( м n )}  = х ^{( 1 n × m)}  = (x ^1/n ) ^м  = (n√x) ^м

Экспоненты экспонентов .

..

Что насчет этого примера?

4 ^{3 2}

Мы делаем показатель степени в top first , поэтому мы вычисляем его следующим образом:

Начните с:		4 3 2
3 2 = 3×3:		4 9
4 9 = 4×4×4×4×4×4×4×4×4:		262144

 

Вот и все!

Если вам сложно запомнить все эти правила, то запомните это:

, вы сможете понять их, когда поймете три идеи
в верхней части этой страницы:

• Показатель степени говорит сколько раз использовать число при умножении
• Отрицательный показатель степени означает деление
• Дробная экспонента, такая как 1/n , означает, что берет корень n-й степени : х ^{( 1 n )} = п√х

 

О, еще кое-что.

.. Что, если x = 0?

Положительный показатель степени (n>0)		0 n = 0
Отрицательная экспонента (n<0)		0 -n равно undefined (поскольку деление на 0 не определено)
Показатель степени = 0		0 0 … мммм … см. ниже!

 

Странная история 0

⁰

Существуют разные аргументы в пользу правильного значения 0 ⁰

0 ⁰ может быть 1 или, возможно, 0, поэтому некоторые люди говорят, что это действительно «неопределенно»:

90

х 0 = 1, значит…	0 0 = 1
0 n = 0, значит. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт