Что значит задать множество перечислением элементов: Задать множества A и B перечислением элементов – решение и ответ

Содержание

Множества. способы задания множеств — математика, уроки

ПрактическАЯ РАБОТА

Тема: Множества. Способы задания множеств.

Цели:

ознакомиться с понятием множества;
ознакомиться со способами задания множеств;
ознакомиться с основными видами множеств.

Оснащение занятия: конспект лекций.

Порядок выполнения работы

Задание 1.

1. Ознакомиться с лекцией 1.

2. Выписать в тетрадь определения. Ответить на вопросы:

а). Какие множества называются конечными, какие бесконечными, какие пустыми? Приведите примеры конечных, бесконечных, пустых множеств.

б). Что значит задать множество?

в). Что значит задать множество пересечением элементов? Когда это можно сделать? Приведите пример множеств, заданных пересечением элементов.

г). Что значит задать множество указанием характеристического свойства элементов? Приведите примеры множеств, заданных указанием характеристического свойства элементов.

д). Дайте определение характеристического свойства элементов множества.

3. Записать в тетрадь образцы решения заданий

Лекция 1.

Тема «Множества. Способы задания множеств»

Множества.
Множество — совокупность различных элементов, мыслимая как единое целое. Элемент множества — объект А называется элементом множества, если он обладает характеристическим свойствами этого множества.
Способы задания множеств.
1) Перечислением — при перечислении множества его элементы принято заключать в фигурные скобки:
{2,4,6,…} — множество четных чисел,
{3,6,9,…}— множество чисел кратных трем.
Под многоточием в данных случаях подразумеваются все последующие числа: в первом случае — четные, а во втором — кратные трем.
2) Описание свойств — для задания (описания) некоторого множества
X, состоящего из элементов, обладающих свойством α, используют запись X={x |α(x)}. Читается как: «X — множество элементов x таких, что α(x)». Например, Y={y | y∈N и y — множество натуральных чисел, меньших 7.
Характеристическое свойство множеств.
Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, не принадлежащий ему.
Равные множества, подмножества.
Два множества A и B называются равными, если они состоят из одних и тех же элементов, т. е. если каждый элемент множества A принадлежит B и, обратно, каждый элемент B принадлежит A. Тогда пишут A = B. Таким образом, множество однозначно определяется его элементами и не зависит от порядка записи этих элементов. Например, множество из трех элементов a, b, c допускает шесть видов записи:

{a, b, c} = {a, c, b} = {b, a, c} = {b, c, a} = {c, a, b} = {c, b, a}.

Множество является подмножеством множества , если любой элемент, принадлежащий , также принадлежит . Формальное определение:

Универсальное множество.
Определение: Универсальное множество — это такое множество, которое состоит из всех элементов, а так же подмножеств множества объектов исследуемой области.
Конечные и бесконечные множества.
Множества, состоящие из бесконечного числа элементов, называются бесконечными, из конечного – конечными.
Пустое множество.
Множество, не содержащее ни одного элемента, называется пустым. ∅
Основные числовые и геометрические множества.
Z− множество целых чисел;
Q− множество рациональных чисел;
I− множество иррациональных чисел;
R− множество действительных чисел;
C− множество комплексных чисел.

Образцы решения заданий

Пример 1. Задать с помощью характеристического свойства элементов множество всех положительных чисел.

Ответ: .

Пример 2. Задать перечислением элементов множества, заданные указанием характеристического свойства элементов:

. Ответ: М = {1; 2; 3; 4}.

Пример 3. Указать стандартное обозначение множества М и изобразить его на числовой прямой:

Примеры для самостоятельного решения.

Задание 2. Выполните указанные примеры.

Приведите примеры множеств, составленных из объектов следующих видов:

а) неодушевленных предметов;

б) животных;

в) растений;

г) геометрических фигур;

д) населенных пунктов;

е) водоемов;

ж) политических деятелей.

2. Назовите элементы, принадлежащие множеству:

а) студентов вашей группы;

б) предметов, изучаемых в I семестре вашей специальности;

в) всех частей света;

г) субъектов федерации, входящих в Российскую Федерацию.

3. Пусть А – множество многоугольников. Принадлежат ли этому множеству:

а) восьмиугольник;

б) параллелограмм;

в) отрезок;

г) параллелепипед;

д) круг;

е) полукруг?

4. Множество С состоит из квадрата, круга и треугольника. Принадлежит ли этому множеству диагональ квадрата?

5. Прочитайте запись и укажите, какие из указанных высказываний истина, а какие ложь:

а) 270 N; ж) -3 Z;

б) 0 N; з) Q;

в) –3 N; и) R;

г) 1 Q; к) sin 2,3 R;

д) –7 N; л) tg R.

е) 22 N;

6. Пусть Е – множество европейских государств, А – множество азиатских государств. Какие из следующих высказываний истина, а какие – ложь?

а) Франция Е; з) Волга Е;

б) Испания Е; и) Нигерия А;

в) Монголия А; к) Гималаи А;

г) Индия А; л) Япония А;

д) Ирак Е; м) Альпы Е;

е) Турция А; н) Швеция А.

ж) Байкал А;

7. Запишите перечислением элементов следующие множества:

а) А – множество нечетных чисел на отрезке [1; 15];

б) В – множество натуральных чисел, меньших 8;

в) С – множество натуральных чисел, больших 10, но меньших 12;

г) D – множество двузначных чисел, делящихся на 10;

д) Е – множество натуральных делителей числа 18;

е) F – множество чисел, модуль которых равен .

8. Запишите перечислением элементов следующие множества:

а) множество различных букв в слове «головоломка»;

б) множества цифр числа 134433154.

9. Изобразите на числовой прямой множество решений неравенства с одним неизвестным x:

а) x 5,3;

б) x ≤ –3,8;

в) – 4,5 ≤ x

г) 2,7 ≤ x ≤ 9.

10. Выясните, множество решений какого неравенства изображено на числовой прямой в каждом случае:

11. Найдите длину каждого из следующих множеств и назовите их элементы:

а) {а}; б) {{а}}; в) ; г) {}; д) {{ a; b }, { а }}; е) {{ a; b; c}, а };
ж) {{ а }, а, }.

2) Из каких элементов состоят следующие множества:

а) множество трехзначных чисел, составленных с помощью цифр 1 и 3;

б) множество трехзначных чисел, составленных с помощью цифр 1, 3, 5, причем так, что никакие две цифры не встречаются дважды;

в) множество трехзначных чисел, составленных из цифр 1, 3, 5 так, что любые две соседние цифры различны;

г) множество трехзначных чисел, сумма цифр которых равна 5.

3) Задайте перечислением элементов множество делителей числа 36. Можно ли задать таким образом множество чисел, кратных числу 36?

Контроль знаний обучающихся:

Множества — Теория — Способы задания множеств

Множества

Способы задания множеств

1. Простым перечислением элементов

Пример. Множество отличников в классе 1а обозначим и зададим его перечислением: .
Способ задания множества перечислением его элементов не пригоден для задания бесконечных множеств и даже в случае конечных множеств часто практически нереализуем. Например, невозможно перечислить множество рыб в Тихом океане, хотя совершенно очевидно, что их число конечно.

2. Описание элементов определяющим свойством:
Множество , где означает, что элемент х обладает свойством .

Пример. Множество N₁₀ всех натуральных чисел, меньших 10 можно задать так:

Свойства элементов могут быть заданы не формально, а с помощью описания на естественном языке.

Пример. Множество слонов, множество птиц, множество рыб, множество натуральных чисел N.

Пример. В геометрии часто приходится иметь дело с множествами, заданными своими характеристическими свойствами. Так, окружность есть геометрическое место точек плоскости, равноудаленных от данной точки этой плоскости.

3. Множество может быть задано рекурсивно. В этом случае должен быть задан способ последовательного порождения его элементов.

Пример. Множество значений рекурсивной функции является рекурсивно — заданным множеством

Так,

и т.д.

Понятие рекурсивно заданного множества тесно связано с понятиями функции, алгоритма и формальной системы, которые будут изучаться далее.
При задании множеств могут возникать ошибки и противоречия. Множество задано верно, если для любого элемента можно определить, принадлежит он множеству или нет. Напротив, множество задано неправильно, если для какого-либо элемента нельзя определить его принадлежность множеству.

Пример. Определение множества A как множества, содержащего любые пять чисел, не является правильным, поскольку невозможно определить точно элементы A.

Пример. Множество всех простых чисел является правильным определением множества. Для любого числа можно определить, принадлежит ли оно этому множеству, хотя практически на это может потребоваться очень много времени.

Пример. Множество всех динозавров, живших на Земле, является множеством, заданным верно. Хотя практически невозможно определить элементы этого множества, но теоретически ясно, что если животное, когда-либо жившее на Земле, является динозавром, то оно принадлежит к этому множеству, в противном случае — нет.

Теория наборов

Каждая область исследования ищет общую терминологию и символику. Хотя можно думать о предмете, не зная его конкретного языка, невозможно общаться с другими об этом предмете без какой-либо общей системы отсчета. Таким образом, мы начнем с основных терминов и обозначений теории множеств. Теория множеств — один из краеугольных камней математики. Многие понятия математики и информатики можно удобно выразить на языке множеств. Операции могут выполняться над наборами для создания новых наборов. Хотя большинство множеств, представляющих интерес для специалистов по информатике, конечны или счетны, существуют множества с таким количеством элементов, что их невозможно перечислить.

Установить обозначение

Набор — это набор объектов, называемых элементами . Мы используем заглавных буквы

для обозначения множеств и символ ∈ для обозначения членства в множестве. Таким образом, a ∈ A означает, что объект a является членом или элементом множества A , а b ∉ A означает, что объект b не является элементом множества A . Фигурные скобки используются для обозначения множества.

Пример 1:
Если A = {фиолетовый, шартрез, жженая умбра}, то шартрез ∈ A и пурпурный ∉ A.

Дополнительные баллы:

• Повторяющиеся элементы перечисляются один раз:
Элементы в наборе не упорядочиваются; поэтому {фиалка, шартрез, жженая умбра} совпадает с {шартрез, жженая умбра, фиалка}.
• В наборе нет порядка:
Каждый элемент набора указан только один раз; излишне перечислять его снова.

Элементы и мощность

Конечное множество
Множество является конечным множеством, если оно имеет конечное число элементы. Любое множество, которое не является конечным, является бесконечным множеством.

Мощность
Пусть A — конечное множество. Количество различных элементов в Число называется его мощностью . Мощность конечного множества A обозначается |A|

Перечень

Когда элементы множества перечисляются (или перечисляются), их традиционно заключают в фигурные скобки. Например, набор двоичных цифр — {0,1}, а набор десятичных цифр — {0,1,2,3,4,5,6,7,8,9}. Выбор имени для этих наборов был бы произвольным; но было бы «логично» назвать их B и D соответственно. Выбор имени набора очень похож на выбор имени идентификатора в программировании. Некоторые большие множества можно перечислить, фактически не перечисляя все элементы. Например, буквы алфавита и целые числа от 1 до 100 могут быть описаны как

A = {a,b,c,…,x,y,z} и G ={1,2, …,99,100}. Три последовательные «точки» называются многоточием. Мы используем их, когда ясно, какие элементы включены, но не перечислены. Многоточие используется в двух других ситуациях. Чтобы перечислить положительные целые числа, мы должны написать {1,2,3,…}, указывая на то, что список можно продолжать бесконечно. Если мы хотим перечислить более общий набор, такой как целые числа от 1 до n, где n — некоторое неопределенное положительное целое число, мы могли бы написать {1,…,n}.

Стандартные символы

Часто встречающиеся наборы обычно обозначаются символами, зарезервированными только для них. Например, поскольку в этом курсе мы будем ссылаться на положительные целые числа, мы будем использовать символ $\mathbb{P} $ вместо записи {1,2,3,…}. Некоторым стандартным наборам удобно давать имена, чтобы мы могли легко обращаться к ним. Вот несколько других наборов чисел, которые мы будем часто использовать:

$ \mathbb{P} $: набор всех положительных целых чисел, {1,2,3,4,…}
$ \mathbb{N} $: набор всех неотрицательных целых чисел (натуральных чисел), {0,1,2,3,4,…}
$ \mathbb{Z} $: набор всех целые числа, {…,-3,-2,-1,0,1,2,3,…}
$ \mathbb{Q} $: множество всех рациональных чисел
$ \mathbb{ R} $: набор всех действительных чисел
$ \mathbb{C} $: набор всех комплексных чисел

иногда мы также хотим говорить о наборе без элементов ( пустой набор или нулевой набор ), обозначаемый $\emptyset $ или {} . Например, если S = {x|x ∈ $\mathbb{N} $ и x < 0}, то S = $\emptyset $. Обратите внимание, что $\emptyset$, набор без элементов, не совпадает с {$\emptyset $}, который представляет собой набор с одним элементом, где единственный элемент является пустым набором.

Обозначение Set-Builder

Другой способ описания наборов — использовать нотацию построителя наборов. Например, мы могли бы определить рациональные числа $ \mathbb{Q} $ = {…,$ \frac{1}{1},\frac{1}{2},\frac{1}{ 3},\frac{2}{3}$,…} как:
$ \mathbb{Q} $ = {a/b|a,b ∈ $ \mathbb{Z} $, b ≠ 0 }

Обратите внимание, что в описании построителя множеств для рациональных чисел :
• a/b указывает на то, что типичным элементом набора является «фракитон».
• Вертикальная черта | читается как «такой, что» или «где» и используется взаимозаменяемо с двоеточием
• a,b ∈ $\mathbb{Z}$ — сокращенный способ сказать, что a и b — целые числа.
• Запятые в математике читаются как «и»

Пример. Определите нотацию конструктора наборов для четных целых чисел. $\mathbb{2Z}$ = {…,-4,-2,0,2,4,…} 9{+}}\)|x

• Перечислите элементы $\mathbb{D}$.

• Какова мощность $\mathbb{D}$?

• Какова мощность {$\emptyset$,{a,b}}?

Подмножество

Подмножество
Пусть A и B будут множествами. Мы говорим, что A является подмножеством B тогда и только тогда, когда каждый элемент A является элементом B . Мы пишем A ⊆ B , чтобы обозначить тот факт, что A является частью B .

Установить равенство
Пусть A и B будут множествами. Мы говорим, что A равно , равному и B (обозначение A = B ), тогда и только тогда, когда каждый элемент A является элементом

B и, наоборот, каждый элемент B является элементом B . элемент А ; то есть A ⊆ B и B ⊆ A .
Правильное подмножество
Если A является подмножеством B , мы обозначаем отношение по A ⊆B . Если A ⊆ B , но A ≠ B (там является по крайней мере одним элементом B , который не является элементом A ), тогда A является правильным подмножеством B, обозначаемым A ⊂ B
Справочник
saylor academy
4.
2: Перечисления и счетные множества
Последнее обновление
Сохранить как PDF
Идентификатор страницы
121644
Richard Zach et al.
Проект Open Logic

Мы уже приводили примеры множеств, перечисляя их элементы. Давайте обсудим в более общих чертах, как и когда мы можем перечислить элементы множества, даже если это множество бесконечно.
Определение $\PageIndex{1}$: перечисление, неофициально
Неформально, перечисление множества $A$ представляет собой список (возможно, бесконечный) элементов $A$, такой что каждый элемент из $A$ появляется в списке в некоторой конечной позиции. Если $A$ имеет нумерацию, то $A$ называется счетным .
Пара слов о перечислениях:
Мы считаем перечислениями только те списки, которые имеют начало и в которых каждому элементу, кроме первого, непосредственно предшествует один элемент. Другими словами, между первым элементом списка и любым другим элементом находится только конечное число элементов. В частности, это означает, что каждый элемент перечисления имеет конечную позицию: первый элемент имеет позицию $1$, второй позицию $2$ и т. д.

У нас могут быть разные перечисления одного и того же множества $A$, отличающиеся порядком расположения элементов: $4$, $1$, $25$, $16$, $9$ перечисляет (множество) первых пяти квадратных чисел точно так же, как $1$, $4$, $9$, $16$, $25$ .
Избыточные перечисления по-прежнему являются перечислениями: $1$, $1$, $2$, $2$, $3$, $3$, … перечисляет тот же набор, что и \ (1\), $2$, $3$, … делает.
Порядок и избыточность имеют значение, когда мы определяем перечисление: мы можем перечислять положительные целые числа, начиная с $1$, $2$, $3$, $1$, …, но шаблон легче увидеть, если пронумеровать его стандартным способом: $1$, $2$, $3$, $4$, .
..
Перечисления должны иметь начало: …, $3$, $2$, $1$ не является перечислением натуральных чисел, поскольку не имеет первого элемента. Чтобы понять, как это следует из неформального определения, спросите себя: «На какой позиции в списке стоит число 76?»
Следующее не является перечислением целых положительных чисел: $1$, $3$, $5$, …, $2$, $4$, $6$, … Проблема в том, что четные числа встречаются в местах $\infty + 1$, $\infty + 2$, $\infty + 3$, а не в конечных позициях.
Пустое множество перечислимо: оно перечисляется пустым списком!
Предложение $\PageIndex{1}$
Если $A$ имеет перечисление, то оно имеет перечисление без повторений.
Доказательство. Предположим, $A$ имеет перечисление $x_1$, $x_2$,…, в котором каждый $x_i$ является элементом $A$. Мы можем удалить повторы из перечисления, удалив повторяющиеся элементы.
Например, мы можем превратить перечисление в новое, в котором мы перечисляем $x_i$, если это элемент $A$, который не входит в число $x_1$, …, $x_{i- 1}$ или удалить $x_i$ из списка, если он уже есть среди $x_1$, …, $x_{i-1}$. ◻
Последний аргумент показывает, что для того, чтобы получить хорошее представление о перечислениях и счетных множествах и доказать что-то о них, нам нужно более точное определение. Следующее обеспечивает это.
Определение $\PageIndex{2}$: перечисление, формально
Перечисление множества $A \neq \emptyset$ представляет собой любую сюръективную функцию $f \colon \PosInt \to A$.
Давайте убедим себя, что формальное определение и неформальное определение, использующее, возможно, бесконечный список, эквивалентны. Во-первых, любая сюръективная функция от $\PosInt$ до множества $A$ перечисляет $A$. Такая функция определяет перечисление, неформально определенное выше: список $f(1)$, $f(2)$, $f(3)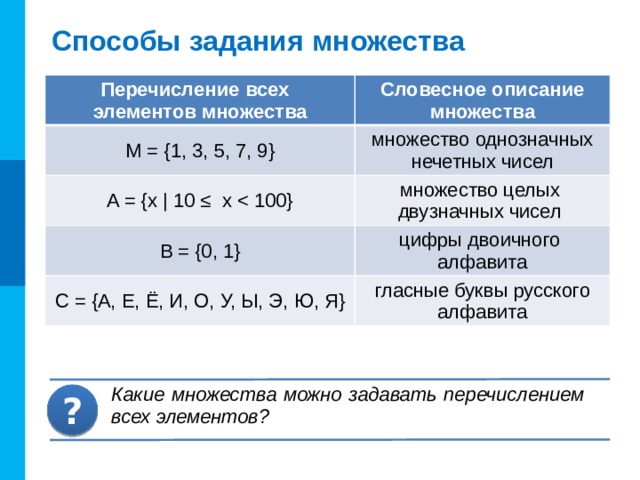$, …. Поскольку $f$ сюръективен, каждый элемент $A$ гарантированно будет значением $f(n)$ для некоторого $n \in \PosInt$. Следовательно, каждый элемент $A$ появляется в некоторой конечной позиции в списке. Поскольку функция может быть неинъективной, список может быть избыточным, но это допустимо (как отмечалось выше).
С другой стороны, для данного списка, который перечисляет все элементы $A$, мы можем определить сюръективную функцию $f\colon \PosInt \to A$, полагая $f(n)$ равным $n$-й элемент списка или последний элемент списка, если нет $n$-го элемента. Единственный случай, когда это не дает сюръективной функции, — это когда $A$ пусто, и, следовательно, список пуст. Таким образом, каждый непустой список определяет сюръективную функцию $f\colon \PosInt \to A$.
Определение $\PageIndex{3}$
Множество $A$ счетно тогда и только тогда, когда оно пусто или имеет перечисление.
Пример $\PageIndex{1}$
Функция, перечисляющая положительные целые числа ($\PosInt$) — это просто тождественная функция, заданная выражением $f(n) = n$. Функция, перечисляющая натуральные числа $\Nat$, есть функция $g(n) = n — 1$.
Пример $\PageIndex{2}$
Функции $f\colon \PosInt \to \PosInt$ и $g \colon \PosInt \to \PosInt$, заданные \[\begin{aligned } f(n) & = 2n \text{ и}\\ g(n) & = 2n+1\end{aligned}\] перечисляют четные и нечетные положительные целые числа соответственно. Однако ни одна из функций не является перечислением $\PosInt$, поскольку ни одна из них не является сюръективной. 9{n} \lceil \frac{(n-1)}{2}\rceil\) (где $\lceil x \rceil$ обозначает функцию потолка , которая округляет $x$ до ближайшего integer) перечисляет набор целых чисел $\Int$. Обратите внимание, как $f$ генерирует значения $\Int$, «перескакивая» вперед и назад между положительными и отрицательными целыми числами: \[\begin{array}{c c c c c c c c} f(1) & f(2) & f(3) & f(4) & f(5) & f(6) & f(7) & \dots \\ \\ — \lceil \tfrac{0}{2} \rceil & \lceil \tfrac{ 1}{2}\rceil & — \lceil \tfrac{2}{2} \rceil & \lceil \tfrac{3}{2} \rceil & — \lceil \tfrac{4}{2} \rceil & \ lceil \tfrac{5}{2} \rceil & — \lceil \tfrac{6}{2} \rceil & \dots \\ \\ 0 & 1 & -1 & 2 & -2 & 3 & \dots \end {array}\nonumber\] Вы также можете думать о $f$ как о определяемом регистрами следующим образом: \[f(n) = \begin{cases} 0 & \text{if $n = 1$}\\ n/2 & \text{если $n$ четно}\\ -(n-1)/2 & \text{если $n$ нечетно и $>1$} \end{cases}\nonumber\]
Задача $\PageIndex{2}$
Показать, что если $A$ и $B$ счетны, то счетно и $A \cup B$. Для этого предположим, что существуют сюръективные функции $f\colon \PosInt \to A$ и $g\colon \PosInt \to B$, и определим сюръективную функцию $h\colon \PosInt \to A \cup B$ и докажите, что оно сюръективно. Также рассмотрим случаи, когда $A$ или $B = \emptyset$.
Задача $\PageIndex{3}$
Показать, что если $B \subseteq A$ и $A$ счетно, то $B$ счетно. Для этого предположим, что существует сюръективная функция $f\colon\PosInt\to A$. Определите сюръективную функцию $g\colon \PosInt\to B$ и докажите, что она сюръективна. Что произойдет, если $B = \emptyset$?
Проблема $\PageIndex{4}$
Покажите индукцией по $n$, что если $A_1$, $A_2$, …, $A_n$ счетны, то \ (A_1 \чашка \точки \чашка A_n\). Вы можете предположить, что если два множества $A$ и $B$ счетны, то счетно и $A \cup B$.
Хотя, возможно, более естественно при перечислении элементов множества начинать отсчет с $1$-го элемента, математики предпочитают использовать для подсчета натуральные числа $\Nat$. Они говорят о $0$-м, $1$-м, $2$-м и так далее элементах списка. Соответственно, мы можем определить перечисление как сюръективную функцию от $\Nat$ до $A$. Конечно, эти два определения эквивалентны.
Proposition $\PageIndex{2}$
Существует сюръекция $f\colon \PosInt \to A$ тогда и только тогда, когда существует сюръекция $g\colon \Nat \to A$.
Доказательство. Учитывая сюръекцию $f\colon \PosInt\to A$, мы можем определить $g(n) = f(n+1)$ для всех $n \in \Nat$. Легко видеть, что выражение $g\colon \Nat \to A$ сюръективно. И наоборот, учитывая сюръекцию $g\colon \Nat\to A$, определите $f(n) = g(n+1)$. ◻
Это дает нам следующий результат:
Следствие $\PageIndex{1}$
Множество $A$ счетно тогда и только тогда, когда оно пусто или существует сюръективная функция $f\colon \Nat \to A$.
Выше мы обсуждали, что список элементов множества $A$ можно превратить в список без повторений. Это также верно для перечислений, но его немного сложнее сформулировать и строго доказать. Любая функция $f\colon \PosInt\to A$ должна быть определена для всех $n \in \PosInt$. Если имеется только конечное число элементов в $A$, то мы, очевидно, не можем иметь функцию, определенную на бесконечном числе элементов $\PosInt$, которая принимает в качестве значений все элементы $A$, но никогда не принимает одно и то же значение дважды. В этом случае, т. е. в случае, когда список без повторений конечен, мы должны выбрать другую область для $f$, только с конечным числом элементов. Отсутствие повторений означает, что $f$ должно быть инъективным. Поскольку он также сюръективен, мы ищем биекцию между некоторым конечным множеством $\{1, \dots, n\}$ или $\PosInt$ и $A$.
Предложение $\PageIndex{3}$
Если $f\colon \PosInt \to A$ сюръективно (т. е. перечисление $A$), то существует биекция $g\colon Z \to A$, где $Z$ равно $\PosInt$ или $\{1, \dots, n\}$ для некоторого $n \in \PosInt$.
Доказательство. Определим функцию $g$ рекурсивно: пусть $g(1) = f(1)$. Если $g(i)$ уже определено, пусть $g(i+1)$ будет первым значением $f(1)$, $f(2)$, … не уже среди $g(1)$,…, $g(i)$, если он есть. Если $A$ имеет только $n$ элементов, то $g(1)$,…, $g(n)$ все определены, и поэтому мы определили функцию $g\ двоеточие \{1, \dots, n\} \to A$. Если $A$ имеет бесконечно много элементов, то для любого $i$ должен быть элемент $A$ в перечислении $f(1)$, $f(2)$ , …, которого еще нет среди $g(1)$, …, $g(i)$. В этом случае мы определили функцию $g\colon\PosInt\to A$.
Функция $g$ сюръективна, так как любой элемент из $A$ находится среди $f(1)$, $f(2)$, … (поскольку $f$ является сюръективно) и, таким образом, в конечном итоге будет значением $g(i)$ для некоторого $i$. Оно также инъективно, так как если бы существовало $j < i$ такое, что $g(j) = g(i)$, то $g(i)$ уже было бы среди $g(1 )$, …, $g(i-1)$, в отличие от того, как мы определили $g$. ◻
Следствие $\PageIndex{2}$
Множество $A$ счетно тогда и только тогда, когда оно пусто или существует биекция $f\colon N \to A$, где либо $N = \Nat $ или $N = \{0, \dots, n\}$ для некоторого $n \in \Nat$.
Доказательство. $A$ счетно тогда и только тогда, когда $A$ пусто или существует сюръективное $f\двоеточие \PosInt \to A$. По предложению $\PageIndex{3}$ последнее выполняется тогда и только тогда, когда существует биективная функция $f\colon Z \to A$, где $Z = \PosInt$ или $Z = \{1, \dots, n\}$ для некоторого $n \in \PosInt$. По тому же аргументу, что и при доказательстве предложения $\PageIndex{2}$, это, в свою очередь, имеет место тогда и только тогда, когда существует биекция $g\colon N \to A$, где либо $N = \Nat $ или $N = \{0, \dots, n-1\}$. ◻
Задача $\PageIndex{5}$
Согласно определению $\PageIndex{3}$, множество $A$ перечислимо тогда и только тогда, когда $A = \emptyset$ или существует сюръективное \ (f\colon\PosInt\to A\). Также можно точно определить «счетное множество» следующим образом: множество перечислимо тогда и только тогда, когда существует инъективная функция $g\colon A \to \PosInt$. Покажите, что определения эквивалентны, т.
No related posts.