Высота трапеции определение: Все формулы высоты трапеции

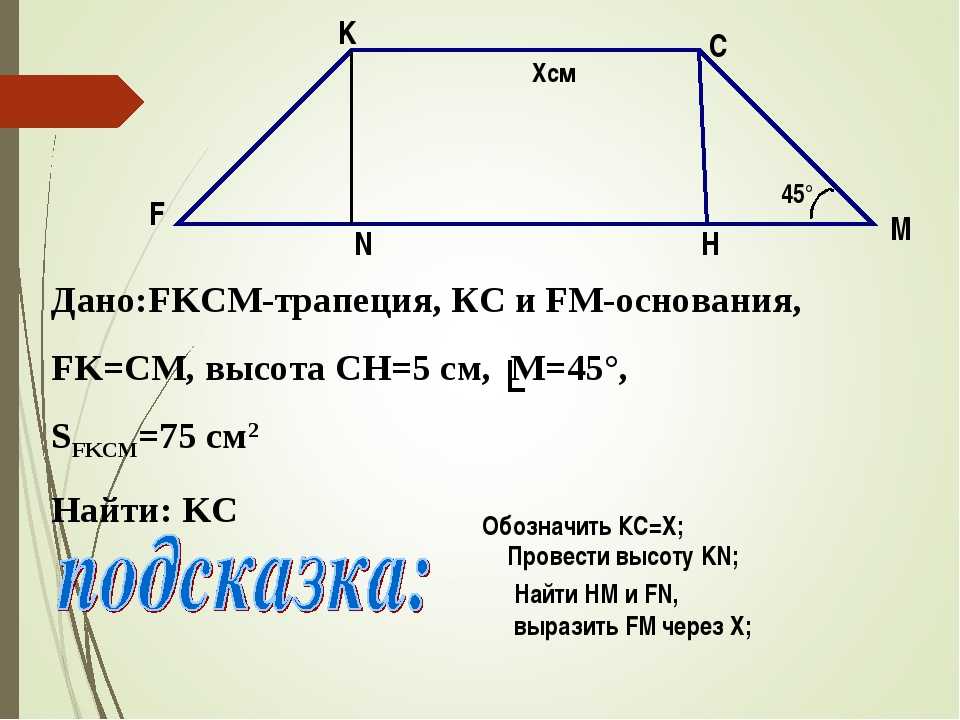
найти онлайн, формулы и примеры

Трапецией принято называть выпуклую четырёхугольную четырехугольник с парой параллельных и двумя не параллельными сторонами. Отрезки, которые создают параллельные прямы называются «основанием трапеции», две других стороны играют роль «боковой стороны трапеции». Средняя линия трапеции будет соединять два центра боковых сторон.

• Высота трапеции через боковую сторону и прилегающий угол при основании
• Высота трапеции через площадь и длины оснований
• Высота трапеции через площадь и среднию линию
• Высота трапеции через основании, диагонали и угол между диагоналями
• Высота трапеции через среднию линию, диагонали и угол между диагоналями

Как найти высоту при помощи боковой стороны и прилегающего угла при основании

Для вычисления высоты трапеции через боковую сторону и прилегающий угол при основании нужно воспользоваться нижеприведенной формулой:

h = a · sin α

где h — это искомая высота трапеции, a — известная боковая сторона, sin α — угол при основании.

Сторона (a):

ммсмдмм

Угол (α):

градусырадианыsin

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Чтобы разобраться с применением формулы, давайте рассмотрим пример. Дана некая трапеция. Нам известно, что боковая сторона равна 10 сантиметрам, а прилегающих угол составляет 30 гр. Нам нужно найти высоту данной трапеции. Для решения у нас есть вся нужная информация и формула выше. Подставляем значения в формулу: h = a · sin, h = 10 · sin 30, h = 10 · 1/2, h = 5 см

Как найти высоту трапецию при помощи длины основания и площади трапеции

Чтобы найти высоту трапеции через известные длины основания и площадь, нужно воспользоваться формулой:

h = (2S) / (a + b)

где h — это искомая высота трапеции, S — известная площадь фигуры, a и b — длины обеих оснований.

Площадь (S):

мм²см²дм²м²

Основание (a):

ммсмдмм

Основание (b):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Закрепим на примере: Нам известно, что в трапеции АВСD основания a и b равны 5 и 10 сантиметров. Площадь фигуры равна 30 квадратных сантиметров. Для решения нужно воспользоваться формулой. h = (2S) / (a + b), h = (2 х 30) / (5 + 10), h = 60 /15, h = 4 см. Высота трапеции равна 4 см.

Как найти высоту при помощи диагоналей, углу между диагоналями и средней линией трапеции

Чтобы найти высоту трапеции через среднюю линию, известные диагонали и угол между ними, нужно прибегнуть к применению выведенной формулы:

h = ((D x d) / (2m)) x sin (α)

где h — это искомая высота трапеции, D и d — известные диагонали, m — средняя линия, sin(α) — угол между диагоналями.

Диагональ (D):

ммсмдмм

Диагональ (d):

ммсмдмм

Средняя линия (m):

ммсмдмм

Угол (α):

градусырадианыsin

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Закрепим на примере: Дана трапеция с диагоналями 5 и 12 сантиметров. Известно, что средняя линия фигуры равна 6 см, а угол между диагоналями – 30 градусов. Применив формулу выше, мы сможем с легкостью найти высоту трапеции. h = ((D x d) / (2m)) x sin (α), h = ((5 x 12) / (2 х 6)) x sin (30), h = (60 /12) x 0.5, h = 2.5 см. Высота трапеции равна 2.5 см.

Как найти высоту при помощи средней линии и площади трапеции

Чтобы найти высоту трапеции через площадь и среднюю линию воспользуемся выведенной формулой:

h = (2S) / m

где h — это искомая высота трапеции, S — известная площадь фигуры, а m — средняя линия.

Площадь (S):

мм²см²дм²м²

Средняя линия (m):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Закрепим на примере: Площадь произвольной трапеции составляет 30 квадратных сантиметров. Средняя линия фигуры равна 5 см. Нужно найти высоту по формуле. h = (2S) / m, h = (2 х 30) / 5, h = 60 / 5, h = 12 см. 12 см – высота трапеции.

Как найти высоту при помощи известного основания, диагоналей трапеции и угла между диагоналями

Для нахождения высоты трапеции при помощи известного основания, диагонали и углу между диагоналями используют нижеприведенную формулу:

h = ((Dd) / (a + b)) x sin (α)

где h — это искомая высота трапеции, D и d — известные диагонали, a и b — длины обеих оснований, sin(α) — угол между диагоналями.

Диагональ (D):

мм

Диагональ (d):

ммсмдмм

Основание (a):

ммсмдмм

Основание (b):

ммсмдмм

Угол (α):

градусырадианыsin

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Закрепим на примере: В трапеции ABCD диагонали равны 10 см каждая. Известно, что сумма основ фигура равна 20 см. Угол, созданный между диагоналями – 30 градусов. Нужно найти высоту. Для этого нужно воспользоваться выше предоставленной формулой. h = ((Dd) / (a+b)) x sin (α), h = ((10 х 10) / (20)) x sin (30), h = 5 x sin (30), h = 2.5 см. Высота трапеции равна 2.5 см

Можно выделить 2 разновидности трапеции:

1. Трапеция, в которой одна из боковых сторон лежит под перпендикулярным углом с обеими основами называется прямоугольной.
2. Трапеции с равными боковыми сторонами называется равнобедренной.

Высотой трапеции принято называть отрезок, которой показывает самое короткое расстояние между верхним и нижним основанием фигуры. Существует большое количество математических задач разного уровня сложности, для решения которых активно применяют высоту. Стоит разобраться со всеми возможными формулами, которые используются для нахождения высоты трапеции.

формулы на все случаи жизни :: SYL.ru

На простой вопрос «Как найти высоту трапеции?» существует несколько ответов, и все потому, что могут быть даны разные исходные величины. Поэтому и формулы будут различаться.

Эти формулы можно запомнить, но они несложно выводятся. Нужно только применять ранее изученные теоремы.

Принятые в формулах обозначения

Во всех приведенных ниже математических записях верны такие прочтения букв.

произвольная трапеция	равнобедренная трапеция	название
а	а	нижнее основание
в	в	верхнее основание
с, d	с	боковые стороны
н	н	высота
m	m	средняя линия
d1, d2	d1	диагонали
s	s	площадь
α, β	α	углы при нижнем основании
γ, δ	γ, δ	углы на пересечении диагоналей

В исходных данных: все стороны

Для того чтобы найти высоту трапеции в общем случае потребуется воспользоваться такой формулой:

н = √(с² — (((а — в)² + с² — d²)/(2(а — в)))²). Номер 1.

Не самая короткая, но и встречается в задачах достаточно редко. Обычно можно воспользоваться другими данными.

Формула, которая подскажет, как найти высоту равнобедренной трапеции в той же ситуации, гораздо короче:

н = √(с² — (а — в)²/4). Номер 2.

В задаче даны: боковые стороны и углы при нижнем основании

Принимают, что угол α прилежит к боковой стороне с обозначением «с», соответственно угол β к стороне d. Тогда формула для того, как найти высоту трапеции, в общем виде будет такой:

н = с * sin α= d * sin β. Номер 3.

Если фигура равнобедренная, то можно воспользоваться таким вариантом:

н = с * sin α= ((а — в) / 2) * tg α. Номер 4.

Известны: диагонали и углы между ними

Обычно к этим данным присоединяются еще известные величины. Например, основания или средняя линия. Если даны основания, то для ответа на вопрос, как найти высоту трапеции, пригодится такая формула:

н = (d₁* d₂ * sin γ) / (а + в) или н = (d₁* d₂ * sin δ) / (а + в).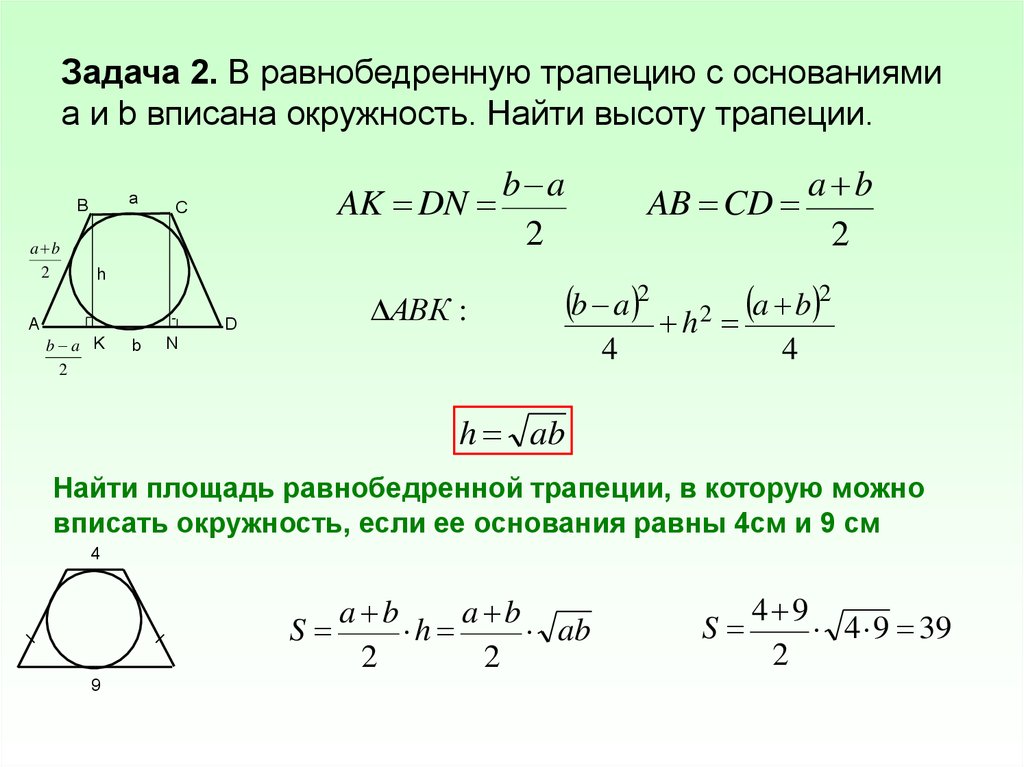 Номер 5.

Это для общего вида фигуры. Если дана равнобедренная, то запись преобразится так:

н = (d₁² * sin γ) / (а + в) или н = (d₁² * sin δ) / (а + в). Номер 6.

Когда в задаче идет речь о средней линии трапеции, то формулы для поиска ее высоты становятся такими:

н = (d₁* d₂ * sin γ) / 2m или н = (d₁* d₂ * sin δ) / 2m. Номер 5а.

н = (d₁² * sin γ) / 2m или н = (d₁² * sin δ) / 2m. Номер 6а.

Среди известных величин: площадь с основаниями или средней линией

Это, пожалуй, самые короткие и простые формулы того, как найти высоту трапеции. Для произвольной фигуры она будет такой:

н = 2S / (а + в). Номер 7.

Она же, но с известной средней линией:

н = S / m. Номер 7а.

Как ни странно, но для равнобедренной трапеции формулы будут выглядеть так же.

Задачи

№1. На определение углов при нижнем основании трапеции.

Условие. Дана равнобедренная трапеция, боковая сторона которой 5 см. Ее основания равны 6 и 12 см. Требуется найти синус острого угла.

Решение. Для удобства следует ввести обозначение. Пусть левая нижняя вершина будет А, все остальные по часовой стрелке: В, С, Д. Таким образом, нижнее основание будет обозначено АД, верхнее — ВС.

Нужно провести высоты из вершин В и С. Точки, которые укажут концы высот будут обозначены Н₁ и Н₂, соответственно. Поскольку в фигуре ВСН₁Н₂ все углы прямые, то она является прямоугольником. Это означает, что отрезок Н₁Н₂ равен 6 см.

Теперь нужно рассмотреть два треугольника. Они равны, так как являются прямоугольными с одинаковыми гипотенузами и вертикальными катетами. Отсюда следует, что и меньшие катеты у них равны. Поэтому их можно определить как частное от разности. Последняя получится от вычитания из нижнего основания верхнего.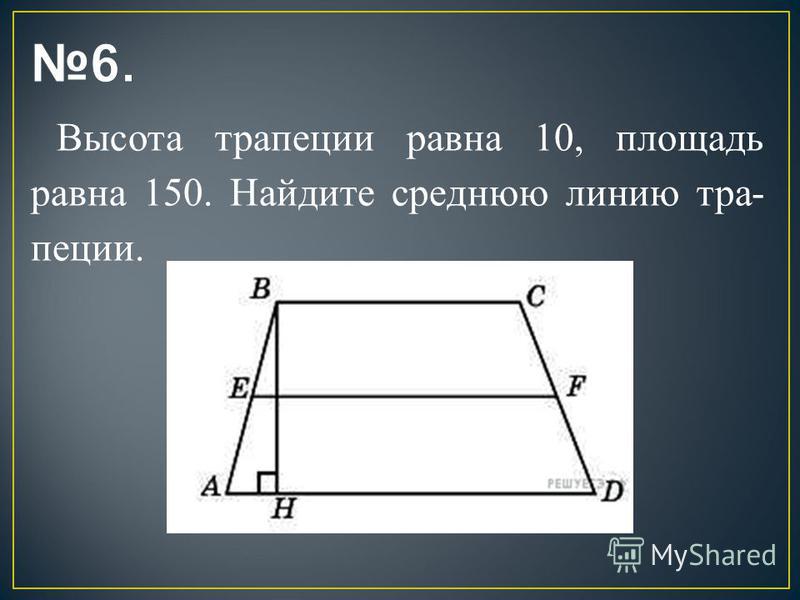 Делиться оно будет на 2. То есть 12 — 6 нужно поделить на 2. АН₁ = Н₂Д = 3 (см).

Теперь из теоремы Пифагора нужно найти высоту трапеции. Она необходима для нахождения синуса угла. ВН₁ = √(5² — 3²) = 4 (см).

Воспользовавшись знанием о том, как находится синус острого угла в треугольнике с прямым углом, можно записать такое выражение: sin α= ВН₁ / АВ = 0,8.

Ответ. Искомый синус равен 0,8.

№2. На нахождение высоты трапеции по известному тангенсу.

Условие. У равнобедренной трапеции нужно вычислить высоту. Известно, что ее основания равны 15 и 28 см. Дан тангенс острого угла: 11/13.

Решение. Обозначение вершин такое же, как в предыдущей задаче. Снова нужно провести две высоты из верхних углов. По аналогии с решением первой задачи нужно найти АН₁ = Н₂Д, которые определятся как разность 28 и 15, деленная на два. После подсчетов получается: 6,5 см.

Поскольку тангенс — это отношение двух катетов, то можно записать такое равенство: tg α= АН₁ / ВН₁. Причем это отношение равно 11/13 (по условию). Так как АН₁ известен, то можно вычислить высоту: ВН₁= (11 * 6,5) / 13. Простые расчеты дают результат в 5,5 см.

Ответ. Искомая высота равна 5,5 см.

№3. На вычисление высоты по известным диагоналям.

Условие. О трапеции известно, что ее диагонали равны 13 и 3 см. Нужно узнать ее высоту, если сумма оснований составляет 14 см.

Решение. Пусть обозначение фигуры будет таким же, как раньше. Предположим, что АС — меньшая диагональ. Из вершины С нужно провести искомую высоту и обозначить ее СН.

Теперь потребуется выполнить дополнительное построение. Из угла С нужно провести прямую, параллельную большей диагонали и найти точку ее пересечения с продолжением стороны АД. Это будет Д₁. Получилась новая трапеция, внутри которой начерчен треугольник АСД₁. Он-то и нужен для дальнейшего решения задачи.

Искомая высота окажется еще и ей же в треугольнике. Поэтому можно воспользоваться формулами, изученными в другой теме. Высота треугольника определяется как произведение числа 2 и площади, деленное на сторону, к которой она проведена. А сторона оказывается равна сумме оснований исходной трапеции. Это исходит из правила, по которому выполнено дополнительное построение.

В рассматриваемом треугольнике все стороны известны. Для удобства введем обозначения х = 3 см, у = 13 см, z = 14 см.

Теперь можно сосчитать площадь, воспользовавшись теоремой Герона. Полупериметр будет равен р = (х + у + z)/ 2 = (3 + 13 + 14) / 2 = 15 (см). Тогда формула для площади после подстановки значений будет выглядеть так: S = √(15 * (15 — 3) * (15 — 13) * (15 — 14)) = 6 √10 (см²).

Теперь нужно сосчитать высоту: н = (2 * 6 √10) / 14 = 6√10 / 7 (см).

Ответ. Высота равна 6√10 / 7 см.

№4. Для поиска высоты по сторонам.

Условие. Дана трапеция, три стороны которой равны 10 см, а четвертая 24 см. Нужно узнать ее высоту.

Решение. Поскольку фигура равнобедренная, то потребуется формула под номером 2. В нее нужно просто подставить все значения и сосчитать. Это будет выглядеть так:

н = √(10² — (10 — 24)²/4) = √51 (см).

Ответ. н = √51 см.

Площадь трапеции Определения, формулы, примеры

Трапеция — это двумерная геометрическая фигура с четырьмя сторонами, две из которых параллельны друг другу. Площадь трапеции можно рассчитать по формуле: A = 1/2 x (b1 + b2) x h, где b1 и b2 — длины параллельных сторон, а h — высота. Если вам интересно узнать, как найти площадь трапеции, прочтите пошаговое руководство, а также несколько примеров.

Что такое трапеция?

Трапеция представляет собой четырехгранную геометрическую фигуру с двумя параллельными сторонами. Две другие стороны не параллельны и называются «ногами» трапеции. Ноги трапеции могут быть любой длины, но две параллельные стороны должны быть одинаковой длины.

Формула площади трапеции

Трапеция – четырехгранная геометрическая фигура с двумя параллельными сторонами. Две другие стороны не параллельны и сходятся под углом. Площадь трапеции можно найти по формуле:

Площадь = 1/2 * (основание1 + основание2) * высота

Чтобы воспользоваться формулой, нужно знать длины всех четырех сторон трапеции. Основания — это две параллельные стороны, а высота — расстояние между основаниями.

Как вывести формулу площади трапеции

Трапеция – четырехгранная фигура, две стороны которой параллельны друг другу. Формула площади трапеции:

Площадь = 1/2 * (Основание1 + Основание2) * Высота

Чтобы вывести эту формулу, мы можем начать с прямоугольника. Прямоугольник имеет две параллельные стороны (основания) и две непараллельные стороны (катетки). Если отрезать треугольник от одного угла прямоугольника, останется трапеция.

Площадь прямоугольника: Площадь = Основание * Высота

Площадь треугольника: Площадь = 1/2 * Основание * Высота

Следовательно, площадь трапеции: Площадь = Площадь прямоугольника – Площадь треугольника
Площадь = Основание * Высота – 1/2 * Основание * Высота
Площадь = 1/2 * Основание * Высота

Примеры нахождения площади трапеции

Если вы ищете примеры нахождения площади трапеции, вы попали по адресу! В этой статье мы пошагово покажем вам, как рассчитать площадь трапеции по стандартной формуле. Мы также дадим несколько советов и приемов для запоминания формулы, а также несколько практических задач, которые помогут вам лучше понять концепцию.

Так чего же ты ждешь? Давайте начнем!

Площадь поверхности трапециевидной призмы

Трапециевидная призма представляет собой трехмерную фигуру с двумя параллельными сторонами, называемыми основаниями, и четырьмя боковыми гранями, являющимися трапециями. Площадь поверхности трапециевидной призмы равна сумме площадей ее боковых граней и двух оснований.

Чтобы найти площадь поверхности трапециевидной призмы, мы будем использовать формулу:

Площадь поверхности = (2 * Площадь основания) + (4 * Площадь боковой грани)

Где:
Площадь основания = (b1 + b2) /2 * ч
Площадь боковой грани = l * h
b1 и b2 — длины двух оснований, а h — высота. l — длина одной стороны боковой грани.

Вычисление площади поверхности трапециевидной призмы

Предполагая, что трапециевидная призма, показанная на рисунке, состоит из двух прямоугольных трапеций с основаниями b1 и b2 и высотами h, мы можем найти общую площадь поверхности призмы, складывая площади из его шести граней. Площадь каждой прямоугольной стороны равна просто bh, где b — основание, а h — высота. Их два, поэтому их общая площадь равна 2bh. Площадь каждого треугольного конца равна 1/2b?, где b — основание, а ? высота; опять же, их два, а общий вклад равен 2b?. Наконец, трапециевидные стороны дают суммарный вклад (b1+b2)h. Таким образом, общая площадь поверхности А призмы равна
A=2bh+2b?+(b_1+b_2)h=bh(2+b_1/b_2+1).

Заключение

Мы надеемся, что эта статья помогла вам понять, как найти площадь трапеции. Если у вас есть какие-либо вопросы, не стесняйтесь оставлять комментарии ниже.

Хотите рассчитать площадь трапеции? Выучите эту формулу! – Stop The Breaks

Трапеция – завораживающая вещь. Что еще более интересно, так это то, что дети, принадлежащие к Соединенным Штатам и Соединенному Королевству, будут рисовать фигуры, когда их просят нарисовать трапецию. Однако мы можем сказать, что схематическое изображение трапеции зависит от места и варьируется от места к месту. Эта статья посвящена площади трапеции.

Трапеция — определение

Первоначально трапеция была определена как четырехсторонняя фигура, у которой нет параллельных сторон. Позднее это определение считалось устаревшим.

Трапеция — замкнутая фигура, имеющая четыре стороны, две из которых параллельны друг другу. Это выпуклый многоугольник. Стороны, которые параллельны друг другу, обычно называют основаниями трапеции, а две другие стороны — катетами трапеции. Трапеция, будучи четырехугольником, имеет четыре вершины и четыре ребра. Площадь трапеции можно вычислить по формуле — ½*(Сумма длин трапеции)*перпендикулярное расстояние между основаниями. Если вы хотите узнать, как найти площадь шестиугольника и другие подобные формулы вместе с их выводами, посетите сайт Cuemath.

Вывод формулы трапеции?

Формулу площади трапеции можно вывести двумя способами:

1. С помощью параллелограмма.

2. С помощью треугольника.

Вывод формулы площади трапеции с помощью параллелограмма

Чтобы вывести формулу площади трапеции с помощью параллелограмма, нам нужно будет рассмотреть две совершенно одинаковые трапеции, причем основания каждой трапеции равны b1 и b2 и высота h.

Предположим, что A — площадь каждой из трапеций. Теперь предположим, что другая трапеция была перевернута.

Теперь вы заметите, что новая фигура, образованная размещением двух трапеций, одна из которых направлена ​​вертикально, а другая перевернута, представляет собой не что иное, как параллелограмм с основанием b1 + b2 и высотой h.

Уже известно, что формула нахождения площади параллелограмма равна основанию параллелограмма × высоте параллелограмма.

 В качестве альтернативы мы также можем сказать, что площадь параллелограмма в два раза больше площади каждой трапеции.

Площадь параллелограмма = 2×Площадь каждой трапеции = 2 A

Таким образом, 2A = (b1+b2)h

⇒ A = (b1+b2)h/2

Следовательно, формула для площади трапеция была получена с использованием концепции параллелограмма.

Вывод формулы площади трапеции с помощью треугольника

Если мы хотим вывести формулу площади трапеции с помощью треугольника, принимается во внимание трапеция с основаниями b1 и b2 и высотой h. Выполните следующие шаги, чтобы вывести формулу площади трапеции.

Шаг 1: Одну из непараллельных сторон трапеции нужно разделить пополам.

Шаг 2: От трапеции отрезается треугольная часть.

Шаг 3: Эту треугольную часть необходимо прикрепить трапецией внизу.

Доказательство 

Так как трапеция была преобразована в треугольник, площадь трапеции и треугольника будут одинаковыми, а треугольник будет иметь основание, равное (b1 + b2), и высоту, такую ​​же, как у трапеции.