Cos 2 x первообразная: ПОМОГИТЕ ПОЖАЛУЙСТА.Нужно найти первообразную функции f(x)=1/cos^2x-cos(3x-1)

Тесты по теме Первообразная онлайн — АСТ партнер

Тест по теме первообразная

Тест предназначен на проверку знаний и умений учащихся по теме «Первообразная. Таблица первообразных.

Тест по теме: «Нахождение первообразных»

Данный тест поможет закрепить знания по теме: «Нахождение первообразных».

Первообразная. Нахождение первообразной.

Тест по алгебре и началам анализа для 11 класса. ТЕСТ НАПРВЛЕН НА ПРОВЕРКУ ПЕРВИЧНОГО УСВОЕЕНИЯ МАТЕРИАЛА

Определенный интеграл и его приложения

Тест предназначен для проверки знания физического и геометрического смысла определенного интеграла, формул первообразных элементарных функций, правил вычисления интеграла, формулы Ньютона-Лейбница, уения вычислять определенный интеграл, находить площади плоских фигур

Виртуальная образовательная среда

Данный тест предназначен для оценки знаний студентов Московского государственного областного университета по предмету «Виртуальная образовательная среда»

Первообразная и ее применение

Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Первообразная» из раздела «Начала математического анализа». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 10 минут.

Тест по алгебре и началам анализа для 11 класса. ТЕСТ НАПРВЛЕН НА ПРОВЕРКУ ПЕРВИЧНОГО УСВОЕЕНИЯ МАТЕРИАЛА

Тест предназначен для проверки знания физического и геометрического смысла определенного интеграла, формул первообразных элементарных функций, правил вычисления интеграла, формулы Ньютона-Лейбница, уения вычислять определенный интеграл, находить площади плоских фигур

ТЕСТ НАПРВЛЕН НА ПРОВЕРКУ ПЕРВИЧНОГО УСВОЕЕНИЯ МАТЕРИАЛА.

Onlinetestpad. com

03.01.2019 6:36:55

2019-01-03 06:36:55

Источники:

Https://onlinetestpad. com/ru/tests/antiderivative

Тест по теме Первообразная » /> » /> .keyword { color: red; }

Тест по теме первообразная

Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного использования. Администрация сайта не проверяет возможные ошибки, которые могут встретиться в тестах.

Список вопросов теста

Вопрос 1

Найдите производную функции y=4cos2x в точке х 0 = — 3 π 4 .

Варианты ответов

Вопрос 2

Найдите промежутки возрастания функции у = х + 1 х — 1 .

Варианты ответов

Вопрос 3

Какая из данных функций является первоообразной для функциии у = 2 х 3 — 3 х 2 ?

Варианты ответов

F(x) = 0 , 5 х 4 — х 3 + 5

Вопрос 4

Какая из данных функций является первообразной для функции у = sin 2x?

Варианты ответов

F ( x ) = — 1 2 cos 2 x

F ( x ) = — cos 2 x

F ( x ) = — sin 2 x

Вопрос 5

На каком из указаанных промежутков функция F ( x ) = cos 2 x — 2 x + 1 является первообразной для f ( x ) = — 2 sin 2 x — 1 x?

Варианты ответов

Вопрос 6

Для функции у = — 1 — 2 х 2 найдите первообразную, график которой проходит через точку М(-3;12).

Варианты ответов

F ( x ) = — x — 2 3 x 3 — 2

F ( x ) = — x — 2 3 x 3 — 9

F ( x ) = 7 — x — 2 3 x 3

F ( x ) = — x — 2 3 x 3 + 9

Вопрос 7

Известно, что F1, F2, F3 — первообразные для f ( x ) = 4 x 3 — 3 x 2 на R, графики которых проходят через точки M(-1;2), N(1;4) и K(2;5) соответственно. Перечислите, в каком порядке (сверху вниз) графики этих функций пересекают ось ординат?

Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного использования. Администрация сайта не проверяет возможные ошибки, которые могут встретиться в тестах.

Вопрос 1

Найдите производную функции y=4cos2x в точке х 0 = — 3 π 4 .

Варианты ответов

Вопрос 2

Найдите промежутки возрастания функции у = х + 1 х — 1 .

Варианты ответов

Вопрос 3

Какая из данных функций является первоообразной для функциии у = 2 х 3 — 3 х 2 ?

Варианты ответов

F(x) = 0 , 5 х 4 — х 3 + 5

Вопрос 4

Какая из данных функций является первообразной для функции у = sin 2x?

Варианты ответов

F ( x ) = — 1 2 cos 2 x

F ( x ) = — cos 2 x

F ( x ) = — sin 2 x

Вопрос 5

На каком из указаанных промежутков функция F ( x ) = cos 2 x — 2 x + 1 является первообразной для f ( x ) = — 2 sin 2 x — 1 x?

Варианты ответов

Вопрос 6

Для функции у = — 1 — 2 х 2 найдите первообразную, график которой проходит через точку М(-3;12).

Варианты ответов

F ( x ) = — x — 2 3 x 3 — 2

F ( x ) = — x — 2 3 x 3 — 9

F ( x ) = 7 — x — 2 3 x 3

F ( x ) = — x — 2 3 x 3 + 9

Вопрос 7

Известно, что F1, F2, F3 — первообразные для f ( x ) = 4 x 3 — 3 x 2 на R, графики которых проходят через точки M(-1;2), N(1;4) и K(2;5) соответственно. Перечислите, в каком порядке (сверху вниз) графики этих функций пересекают ось ординат?

Тест по теме Первообразная.

Multiurok. ru

11.10.2019 17:34:08

2019-10-11 17:34:08

Источники:

Https://multiurok. ru/tests/test-po-teme-pervoobraznaia. html

Тест по теме » Первообразная и интеграл» | Тест по алгебре (11 класс) по теме: | Образовательная социальная сеть » /> » /> .keyword { color: red; }

Тест по теме первообразная

Тест можно использовать на уроке при проверке знаний и умений по теме. Тест состоит из двух вариантов и содержит критерии оценки.

Скачать:

ВложениеРазмер

test_integrirovanie_na_sayt. pdf	199.51 КБ

Подтяните оценки и знания с репетитором Учи. ру

За лето ребенок растерял знания и нахватал плохих оценок? Не беда! Опытные педагоги помогут вспомнить забытое и лучше понять школьную программу. Переходите на сайт и записывайтесь на бесплатный вводный урок с репетитором.

Вводный урок бесплатно, онлайн, 30 минут

Предварительный просмотр:

По теме: методические разработки, презентации и конспекты

Программа элективного курса по математике для 9 класса «Интеграл»

Основная задача обучения математике в школе – обеспечить прочное и сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельно.

Урок по теме «Вычисление площадей фигур с помощью определенного интеграла»

Урок изучения нового материала в 11 классе.

Интеграл

Вычисление интегралов по формуле прямоугольников.

Зачет по теме «Интеграл»

В старшей школе целесообразно проводить зачеты по основным темам курса математики. Предложенные мною билеты по теме «Интеграл» в 11 классах (профильном и общеобразовательном) – форма письм.

Научно практическая конференция «Интеграл и его применение»

Научно-практическая конференция «Интеграл и его применение» была разработана с акцентом на применение метода проектов. Во время подготовки.

Тест. Первообразная и интеграл (в 4-х вариантах).

Тест направлен на проверку знаний и умений учащихся по данной теме. Задачи теста позволяют эффективно подготовить учащихся к сдаче ЕГЭ по изученной теме. Задачи соответствуют программным требованиям. Д.

Тест можно использовать на уроке при проверке знаний и умений по теме. Тест состоит из двух вариантов и содержит критерии оценки.

ВложениеРазмер

test_integrirovanie_na_sayt. pdf	199.51 КБ

Подтяните оценки и знания с репетитором Учи. ру

За лето ребенок растерял знания и нахватал плохих оценок? Не беда! Опытные педагоги помогут вспомнить забытое и лучше понять школьную программу. Переходите на сайт и записывайтесь на бесплатный вводный урок с репетитором.

Вводный урок бесплатно, онлайн, 30 минут

Предварительный просмотр:

Предложенные мною билеты по теме Интеграл в 11 классах профильном и общеобразовательном форма письм.

Nsportal. ru

06.01.2020 8:11:13

2020-01-06 08:11:13

Источники:

Https://nsportal. ru/shkola/algebra/library/2013/02/17/test-po-teme-pervoobraznaya-i-integral

Неопределенный интеграл

Глава 5

Основной задачей дифференциального исчисления является отыскание производной заданной функции. Обратная задача — восстановление функции по известной производной, является основной задачей интегрального исчисления.

Всюду в этой главе функции рассматриваются на промежутках (конечных или бесконечных), расположенных в их области определения.

5.1 Первообразная функция и неопределенный интеграл

Определение 5.1.1. Пусть D — промежуток в R, конечный или бесконечный, f : D → R. Функция F : D → R называется первообразной функцией для функции f на D (или, проще и короче, первообразной функции f), если она дифференцируема на D и

F 0(x) = f(x), x D.

Очевидно, что если F — первообразная функции f на промежутке D, то F непрерывна на промежутке D, поскольку дифференцируема.

Например, функция F (x) = x является на R первообразная функции f(x) = 1, поскольку F (x) = x дифференцируема на R, и

F 0(x) = 1 = f(x), x R.

Аналогично, функция F (x)					= arcsin x — первообразная для функции
f(x) =	√	1		на интервале (−1, 1), так как
		1 − x	2
							1
				(arcsin x)0	=	√			, x (−1, 1).
							1 − x	2

В отличие от производной, первообразная функции не обладает свойством единственности. Например, для функции f(x) = −2 sin 2x, функции F (x) = cos 2x и Φ(x) = −2 sin2 x являются первообразными на R,

140

так как для всех x R

(cos 2x)0 = −2 sin 2x и (−2 sin2 x)0 = −4 sin x cos x = −2 sin 2x .

Естественно возникает вопрос об описании всех первообразных заданной функции.

Теорема 5.1. Пусть f : D → R. Если F(x) — первообразная на D для функции f(x), то множество всех ее первообразных на D совпадает с множеством {F (x) + C : C R}.

1). Обозначим через Jf множество всех первообразных функции f на D. Поскольку для любого числа C R функция F (x) + C дифференцируема на D и (F (x)+C)0 = f(x), x D, то функция F (x)+C, является первообразной функции f на D. Значит, {F (x) + C : C R} Jf .

2). Докажем обратное вложение, для чего рассмотрим функцию Φ(x) Jf . Введем функцию ϕ(x) = F (x) −Φ(x), x D. Тогда функция ϕ(x) дифференцируема на D и

ϕ0(x) = F 0(x) − Φ0(x) = f(x) − f(x) = 0, x D.

Откуда по критерию постоянства функции на промежутке (см. теорему 4.13) следует, что ϕ(x) ≡ C, x D, где C — некоторая постоянная. Таким оразом, F (x)−Φ(x) = C, x D, то есть Jf {F (x) + C : C R}.

Учитывая еще вложение, полученное в первой части доказательства, окончательно получаем, что Jf = {F (x) + C : C R} .

Определение 5.1.2. Пусть D — промежуток, функция f имеет на D первообразную. Совокупность всех первообразных функции f(x) на D называется неопределенным интегралом от функции f(x) на промежутке D и обозначается символом

Z

f(x) dx,

при этом x называется переменной интегрирования, f(x) — подынтегральной функцией, f(x) dx — подынтегральным выражением.

Таким образом, если F (x) — некоторая первообразная функции f(x)

на промежутке D, то	Z
		f(x) dx = F (x) + C,

где C — произвольная постоянная. Последнее равенство следует понимать как равенство двух множеств, состоящих из функций, определенных на промежутке D, причем слева — совокупность, образующая неопределенный интеграл от f(x), а справа — совокупность функций, отличающихся на D от F (x) на некоторую постоянную C.

141

Операция поиска неопределенного интеграла от заданной функции f(x) на промежутке D называется интегрированием.

Пример 5.1.1. Найти неопределенный интеграл функции f(x) = e|x| на всей числовой прямой.

При x > 0 e|x| = ex и для этой функции на интервале (0, +∞) ex является одной из ее первообразных. При x < 0 e|x| = e−x, и для этой функции на (−∞, 0) первообразной будет функция −e−x + C при любой постоянной C. Так как первообразная функции f(x) по определению 5.1.1 должна быть дифференцируемой на R, а, следовательно, непрерывной на R, то должно выполняться условие

lim ex = lim (−e−x + C),

x→+0 x→−0

то есть 1 = −1 + C, откуда C = 2. Итак, функция

F (x) =		ex,
		1,
		−e−	x	+ 2,

если x > 0, если x = 0, если x < 0

является непрерывной на R.

Докажем, что эта функция является на R первообразной функции f(x) = e|x|. Очевидно, что f0(x) = ex = e|x| для x > 0 и F 0(x) = e−x = e|x|

для x < 0. Покажем, что F 0(0) = e0 = 1:

F 0(+0) =

lim

F (x) − F (0)

=

lim

ex − 1

= 1,

x→+0

x

x→+0

x

F 0(

0) = lim

F (x) − F (0)

= lim

−e−x + 2 − 1

= 1,

−

x

→−

0

x

x

0

x

→−

то есть F 0(+0) = F 0(−0) = F 0(0) = 1 = e|0|. Следовательно,

e|x| dx = F (x) + C =

x

если x ≥ 0,

ex

+ C,

Z

e−

+ 2 + C,

если x < 0.

−

5.2 Основные свойства неопределенного интеграла

Теорема 5.2. Пусть функция f : D → R имеет первообразную на промежутке D, тогда на D

Z 0 Z

f(x) dx = f(x), x D, и d f(x) dx = f(x) dx, x D.

Действительно, если F (x) — некоторая первообразная функции f(x)

на D, то	Z

f(x) dx = F (x) + C.

142

Тогда по определению 5.1.1 для всех x D
	Z f(x) dx 0	= (F (x) + C)0 = F (x)0 = f(x),
d Z	f(x) dx = d(F (x) + C) = F 0(x)dx = Z		f(x) dx 0	dx = f(x) dx.

Теорема 5.3. Если функция f(x) дифференцируема на промежут-

ке D, то	Z

df(x) = f(x) + C.

Так как df(x) = f0(x)dx, то по определению 5. 1.2

ZZ

df(x) = f0(x) dx = f(x) + C.

Теорема 5.4. Если функции f(x) и g(x) имеют на промежутке D первообразные, то функция f(x) ± g(x) также имеет первообразную на D, причем

Z Z Z

(f(x) ± g(x)) dx = f(x) dx ± g(x) dx. (5.1)

Заметим, что равенство в формуле (5.1) следует понимать как совпадение двух множеcтв функций. Пусть F (x) и G(x) некоторые первообразные функций f(x) и g(x), соответственно, на промежутке D, то

есть Z Z

f(x) dx = F (x) + C1, g(x) dx = G(x) + C2.

Функция F (x) ± G(x) дифференцируема на D и

(F (x) ± G(x))0 = F 0(x) ± G0(x) = f(x) ± g(x), x D.

Последнее означает, что F (x) ± G(x) является первообразной функции f(x) ± g(x) на D, а поэтому

Z

(f(x) ± g(x)) dx = F (x) ± G(x) + C.

Левая часть формулы (5.1) — множество, состоящее из функций вида F (x) ±G(x) + C, а правая — из функций (F (x) + C1) ±(G(x) + C2). Ввиду произвольности постоянных C, C1, C2 эти множества совпадают, то есть справедливо равенство (5. 4).

Теорема 5.5. Если функция f(x) имеет на промежутке D первообразную и λ — число, то функция λf(x) также имеет первообразную на D, причем при λ 6= 0

Z	Z	(5.2)
λf(x) dx = λ	f(x) dx.

143

3

Подписаться І 3

Подробнее

Отчет

2 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Тамара Дж. ответил 21.03.13

Репетитор

4.9(51)

Репетиторство по математике – алгебра и исчисление (все уровни)

См. таких репетиторов

Смотрите таких репетиторов

∫ COS ² X · SIN ³ x DX = ∫ COS ² X · SINX · SIN ² X DX

Напомним: SIN ² X + COS ² X = 1 ==> sin ² x = 1 — cos ² x

   ∫ cos ² x·sinx·(1 — cos ² x)  dx  =  ∫ (cos ² x · sinx- cos ⁴ x · sinx) dx

= ∫ cos ² x · sinx dx- ∫ cos ⁴ x · sinx dx

Использование u-substitution, пусть: u = cosx, так ,   du = -sinx  dx

 ==>   ∫ cos ² x·sinx  dx  =  ∫ -1·cos ² x·(-1·sinx  dx)  =  ∫ -(u) ^{2 · 900 ) = ∫ -u 2 DU}

=-(U) ³ /3 =-(COSX) ³ /3 = -cos ³ x /3

==> ∫ cos x /3

==> ∫ Cos ⁴ x · sinx dx = ∫ -1 · cos ⁴ x · (-1 · sinx dx) = ∫ -(u) ⁴ · (du) = ∫ -u ⁴ DU

= — (U) ⁵ /5 =-(COSX) ⁵ /5 = -cos ⁵ x /5

∫ COS ² X · SINX DX-COS ⁴ X · SINX DX = ( -cos ³ x/3)-(-cos ⁵ x/5)

= -cos ³ x/3+ cos ⁵ x/5 = cos ⁵ х/5 — cos ³ х/3

Голосовать за 0 голос против

Подробнее

Отчет

Джон М. ответил 20.03.13

Репетитор

4.9 (551)

Аналитическая помощь – Письмо, Математика и др.

См. таких репетиторов 94 x][sin x], при этом вы можете использовать правило сумм, u-подстановку и правило степени для решения каждого члена, что довольно просто. Не стесняйтесь писать по электронной почте или задавать дополнительный вопрос, если это не имеет смысла. Джон

Голосовать за 0 голос против

Подробнее

Отчет

Все еще ищете помощи? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

Как делать первообразные производные — синоним

МАРКИРОВКА САМУЭЛА

КЛАСС

… Jupiterimages/Photos.com/Getty Images

Исчисление — это раздел математики, изучающий изменение одной величины по отношению к другой. В исчислении есть два процесса — дифференцирование и интегрирование. Эти процессы противоположны друг другу, и поэтому результат интегрирования дает первообразную. Есть несколько способов интегрировать функцию для получения первообразной, и это зависит от конкретной функции.

Исследуйте эту статью

• Антидовитивные простые функции
• Антидовичение продуктов
• Антидовая по замене
• Антидервижение по тригонометрическим идентификациям

12012020202020202020202020202020202021

1.

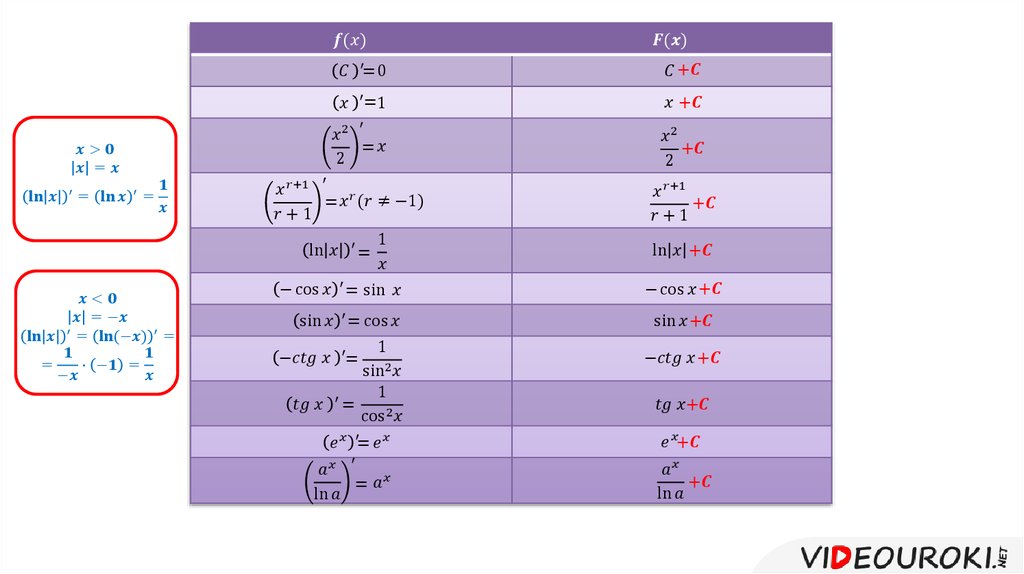
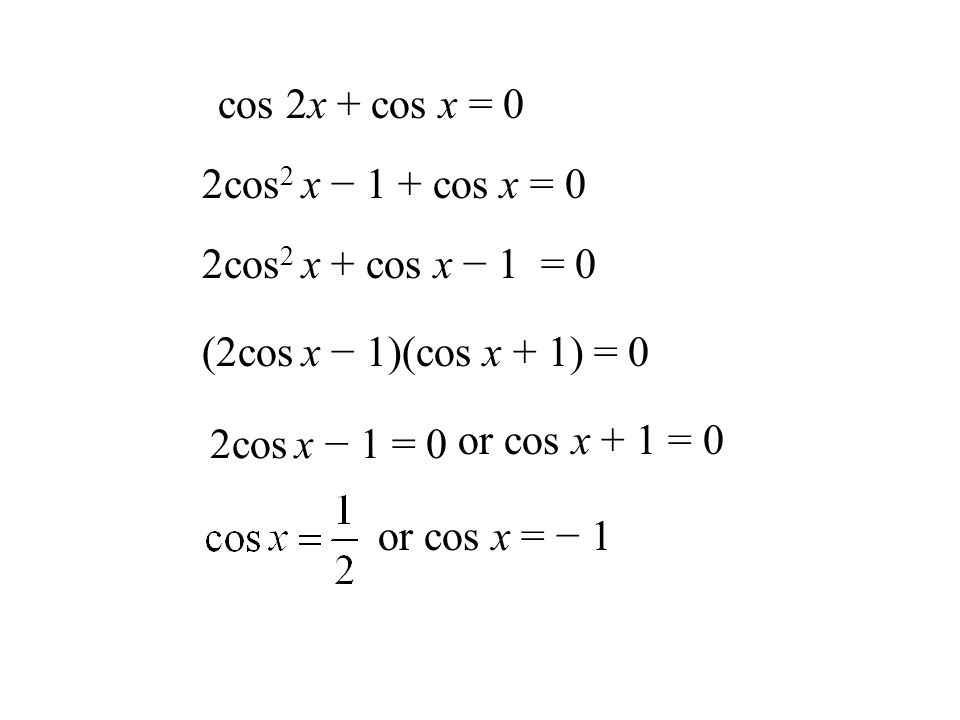Если рассматриваемая функция проста, ее следует найти в таблице первообразных. Чтобы найти первообразную определенной функции, найдите функцию в левой части таблицы и соответствующую первообразную в правой части таблицы. Например, если требуется первообразная cos(x), таблица показывает, что первообразная равна sin(x) + c.

2 Первообразная произведения

Иногда функция является произведением двух более простых функций. В этом случае таблица первообразных не даст результата. Вместо этого нужно будет выполнить некоторые простые математические действия. Метод нахождения первообразной произведения известен как интегрирование по частям. Чтобы выполнить интегрирование по частям, разделите исходное уравнение на два произведения. Например, если исходная функция y=x.cos(x), разбивается на u=x и dv/dx=cos(x). Следующим шагом будет использование таблицы первообразных для нахождения производной u и первообразной dv/dx:

u=x, поэтому производная du/dx=1

dv/dx=cos(x), следовательно, первообразная v=sin(x)

Следующее уравнение затем используется для вычисления первообразной:

Интеграл (u.