Квадратный корень посчитать онлайн: Калькулятор квадратных корней

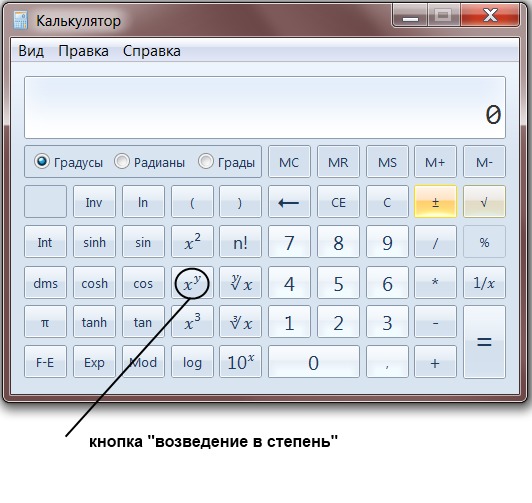
Найти квадратный корень — формула и калькулятор квадратного корня с шагами

Предположим, вас попросили найти квадратный корень из числа. Но для этого нужно знать, что такое квадраты и квадратные корни. Значение числа, умножаемого само на себя, возвращает исходное заданное число, известное как его квадратный корень. Например, предположим, что у — квадратный корень из х, тогда у2 = х. Это уравнение также можно записать в виде y = √x. Квадратный корень числа представлен символом ‘√’ Всякий раз, когда мы умножаем число само на себя, мы получаем положительное значение, равное квадрату числа. Мы вернем исходное число, найдя квадратный корень из этого положительного значения.

Квадрат 4 равен 16 или 42 = 16 и √16 = 4. Легко найти квадратный корень из 16 или подобных чисел, потому что они являются полными квадратами. Но для таких чисел, как 10, 7, 20, 24 и многих других, это становится немного сложным и расчетливым. Не существует такой формулы для нахождения квадратного корня числа. Но есть различные методы и приемы, с помощью которых можно легко вычислить квадратный корень. В разных разделах мы узнаем о них.

Представление квадратных корней

Символ, используемый для представления квадратного корня, известен как радикальный символ. ‘√’ — это символ квадратного корня. Если x — это исходное число, то √x — это квадратный корень из числа. Здесь x также известен как подкоренное число. Радикал и квадратный корень представляют одно и то же. Формула квадратного корня может быть представлена ​​следующим образом:

X = √Y, где X — квадратный корень из Y. С другой стороны, X2 = Y. Следовательно, где Y — квадрат X. 

Свойства квадратов И Квадратные корни

В математике функция квадратного корня принимает положительное значение в качестве входных данных и возвращает квадратный корень входного значения в качестве выходных данных. Следовательно, говорят, что это функция один к одному. Например,

F(а) = √а.

Предположим, что если x = 25, то возвращаемое значение будет равно 5. Ниже приведены некоторые свойства квадратов и квадратных корней.

• Число может иметь квадратный корень, если оно заканчивается четным числом нулей.

• Число может быть полным квадратом. Тогда будет и идеальный квадратный корень.

• Возможно умножение двух значений квадратного корня. Например, √2 × √3 = √6.

• Если найти квадратный корень из отрицательного числа, в результате получится комплексное число. Совершенные квадраты никогда не бывают отрицательными.

• Подкоренное число получается путем умножения двух одинаковых квадратных корней. Если вы умножите √7 × √7, вы получите 7, что является числом, не имеющим квадратного корня.

• Числа, оканчивающиеся на 1, 4, 5 и 6, будут иметь квадратный корень.

• Идеальный квадратный корень не существует для чисел, оканчивающихся на 2, 3, 7 и 8.

Простой способ найти квадратный корень из числа

Нам нужно найти квадратный корень из числа, будь то совершенный или несовершенный квадрат. Вы уже знаете, является ли это идеальным квадратом, тогда мы можем использовать метод простой факторизации, чтобы разложить на множители и легко найти квадратный корень. Для других чисел у нас есть метод деления.

Метод простой факторизации

Это один из самых простых способов найти квадратный корень из числа. Например, возьмем число 256. Теперь разобьем 256 на простые множители. Следовательно, 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2. Теперь нам нужно спарить одинаковые числа попарно и рассмотреть их только один раз, (2 × 2) × (2 × 2) × (2 × 2) × (2 × 2). Следовательно, √256 = (2 × 2 × 2 × 2) = 16, 

Метод длинного деления

Это формула квадратного корня, используемая для неполных квадратов или больших чисел. Давайте рассмотрим число 3. Это не идеальное квадратное число. На этом примере мы проиллюстрировали метод длинного деления ниже.

Запись 3 с десятичной точкой и группами из двух нулей для десятичной точки. Помещаем все это под символ длинного квадратного корня (который выглядит как деление) и начинаем делить.

1√3.00 00 00 00 00

Подставить наибольшее число, квадрат которого меньше или равен 3 и больше 3. Возвести его в квадрат и вычесть из 3, что в данном случае равно 1. 

Сведение пары нулей и умножение полученного результата на два. Следующая цифра в ответе будет помещена в конце удвоенного ответа и умножена на новую цифру. Произведение вычитается, и прибавляются еще два нуля. Мы должны продолжить этот процесс для стольких цифр точности, сколько мы хотим.

Квадратный корень из 3 дает 1,732.

Теперь рассмотрим число 24.

Решенные примеры

1. Приведите некоторые приложения формулы квадратного корня.

Ответ: Формула квадратного корня используется в геометрии, исчислении, алгебре, квадратных уравнениях, вычислениях и других математических приложениях.

2. Найдите квадратные корни из 5, 7, 9 и 11.

Ответ: Квадратные корни из 5, 7, 9 и 11 равны 2,236, 2,646, 3,0 и 3,317 соответственно.

Как найти квадратный корень из числа

Последнее обновление: 5 ноября 2021 г.

Нередко учащиеся сталкиваются с задачами, требующими нахождения квадратного корня из числа. Хотя легко полагаться на научный калькулятор или смартфон, изучение того, как находить квадратный корень вручную, может помочь понять концепцию квадратных корней на более глубоком уровне.

Существует несколько различных способов нахождения квадратов вручную, и все они были изобретены до появления калькуляторов.

В этом посте мы обсудим три метода нахождения квадратных корней вручную.

Угадай и проверь, а также разложи на простые множители — это быстрые и простые методы нахождения квадратного корня любого числа. Метод длинного деления особенно полезен при нахождении квадратных корней иррациональных чисел.

Метод №1. Угадай и проверь 

Нахождение десятичной аппроксимации квадратного корня методом предположения и проверки включает:

1. Первоначальное предположение о значении корня
2. Возведение в квадрат угаданного значения корня
3. Определение того, насколько близка догадка к числу
4. Улучшение вашего предположения путем увеличения или уменьшения угаданного квадратного корня соответственно

Поскольку применение этого метода предполагает использование определения квадратного корня, это поможет вам понять концепцию на более глубоком уровне.

Допустим, вы хотите найти √20. Поскольку √16 = 4, а √25 = 5, √20 находится между 4 и 5. Применяя метод угадывания и проверки:

1. Предположим, что √20 = 4,5.
2. 4,52 = 20,25. Следовательно, √20 < 4,5.
3. Предположим, что √20 = 4,4.
4. 4,42 = 19,36. Следовательно, √20 > 4,4.
5. Предположим, что √20 = 4,45.
6. 4,452 = 19,8025. Следовательно, √20 > 4,45.
7. Предположим, что √20 = 4,47.
8. 4,472 = 19,9809. Следовательно, √20 > 4,47.
9. Предположим, что √20 = 4,475.
10. 4,4752 = 20,02. Следовательно, √20 < 4,475.

Продолжая этот процесс, мы обнаружим, что √20 = 4,472135955.

Метод № 2. Факторизация простых чисел

Метод факторизации простых чисел включает определение того, какие числа составляют другое число. Числа, которые умножаются друг на друга, чтобы получить другое число, называются его факторами.

Чтобы найти квадратный корень любого числа с помощью этого метода, вы должны найти простые множители числа, а затем посмотреть, есть ли у него совершенные квадраты чисел (16, 49, 121 и т. д.)

Предположим, вы хотите найти √400. Сначала вы должны найти простые делители числа 400. Это можно легко сделать, постоянно деля число на простые числа.

Мы проиллюстрировали процесс деревом множителей:

Изображение: Factor-Tree-of-400.png

Простые множители равны 2, 2, 2, 2, 5 и 5. Мы Теперь нужно определить, является ли число 400 кратным идеальным квадратам.

400 = 24 * 52 = 16 * 25

Следовательно,

√400 = √16*25 = √16 *√ 25 = 4 * 5 = 20

Хотя это выглядит просто, метод становится немного сложнее, когда вы находите квадратный корень из чисел, которые не округлены, например 400

Если вы попытаетесь найти квадратный корень из 147, простые множители будут:

Image: Factor-Tree-of-147.

png

Простые множители 3, 7 и 7. Теперь мы должны определить, является ли число 400 кратным идеальным квадратам.

147 = 72 * 3 = 49 * 3

Следовательно,

√147 = √49*3 = √49 * √3 = 7*√3 = 7√3

Теперь вам потребуется дополнительное время, чтобы использовать метод догадок и проверок и найти значение √3. Мы знаем, что 12=1 и 22=4. Итак, √3 должно быть между 1 и 2.

1. Предположим, что √3 = 1,5.
2. 1,52 = 2,25. Следовательно, √3 > 1,5.
3. Предположим, что √3 = 1,7.
4. 1,72 = 2,89. Следовательно, √3 > 1,7.
5. Предположим, что √3 = 1,73.
6. 1,732 = 2,9929. Следовательно, √3 > 1,73.

Продолжая этот процесс, мы получаем √3=1,732.

7√3=7* √3 = 7*1,732 = 12,124

Следовательно,

√400 = 7√3 = 12,124

Вы также можете найти квадратные корни десятичных чисел, просто записав число в виде дроби.

и нахождение простых множителей числителя и знаменателя.

Допустим, вы хотите найти √17,64. Вы должны сначала записать это как √1764/100, а затем найти простые делители 1764 и 100. Затем вы можете разделить числа и получить ответ: 4.2.

Метод №3: Деление в длинную сторону

Метод деления в длинную может показаться сложным, но он упрощает вычисление рациональных приближений иррациональных чисел.

Вот краткая иллюстрация использования деления в большую сторону для нахождения √3.

1. Сначала найдите наибольшее число, квадрат которого меньше или равен 3. Затем используйте его как делитель и запишите остаток.
2. Поместите точку после первой цифры в частном для обозначения десятичных дробей.
3. Доведите до остатка два нуля.
4. Теперь угадайте максимально возможную цифру, чтобы при умножении на нее нового делителя произведение было меньше или равно делимому.

   No related posts.