Формулы приведения тригонометрических функций
Формулы приведения тригонометрических функцийФормулы привидения тригонометрических функций представлены в виде таблицы. Ниже находятся некоторые формулы приведения в табличном виде. Еще ниже эти формулы приведения расписаны для некоторых тригонометрических функций в виде тригонометрических тождеств.Таблицы значений тригонометрических функций находятся на другой странице.
Формулы привидения для синуса выглядят так:
sin (π/2 + α) = cos α
sin (π + α) = — sin α
sin (3π/2 + α) = — cos α
sin (π/2 — α) = cos α
sin (π — α) = sin α
sin (3π/2 — α) = — cos α
sin (2π — α) = — sin α
Формулы приведения для тригонометрической функции синус будут следующие. Синус угла пи пополам (пи/2) плюс или минус угол альфа равняется косинусу угла альфа.
Тригонометрические формулы привидения для косинуса приобретают такой вид:
cos (π/2 + α) = — sin α
cos (π + α) = — cos α
cos (3π/2 + α) = sin α
cos (π/2 — α) = sin α
cos (π — α) = — cos α
cos (3π/2 — α) = — sin α
cos (2π — α) = cos α
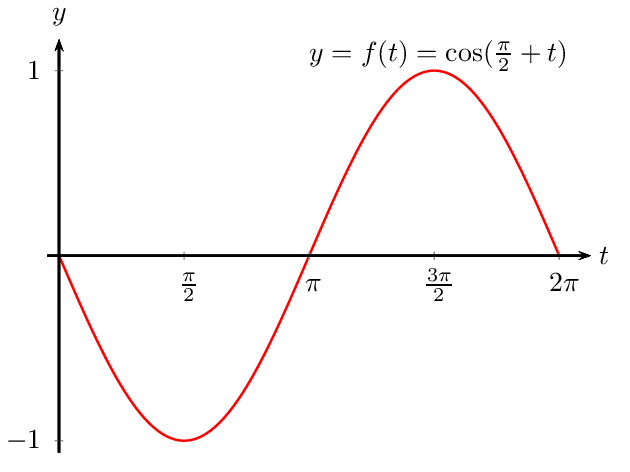
Для косинуса формулы приведения имеют следующий вид. Косинус угла пи пополам (пи/2) плюс угол альфа и косинус три вторых пи минус альфа равняются минус синусу угла альфа.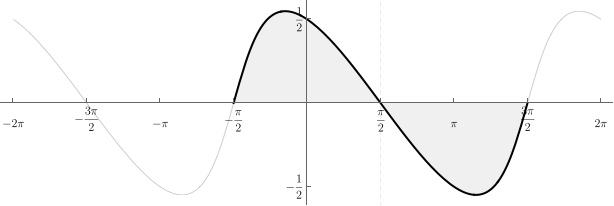
Тригонометрическая функция тангенс имеет следующие формулы привидения:
tg (π/2 + α) = — ctg α
tg (π + α) = tg α
tg (3π/2 + α) = — ctg α
tg (π/2 — α) = ctg α
tg (π — α) = — tg α
tg (3π/2 — α) = ctg α
tg (2π — α) = tg α
Тригонометрические формулы приведения функции тангенс tg. Тангенс угла пи деленное на два плюс альфа и угла три вторых пи плюс альфа приравниваются минус котангенсу угла альфа.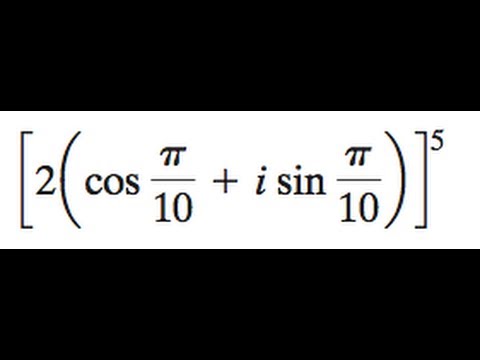 Тригонометрическая функция тангенс угла пи на два или три пи деленное на два (3/2 пи) минус альфа равна котангенсу альфа. Тангенс угла пи минус альфа равен минус тангенсу угла альфа. Формулы приведения для тангенса пи плюс альфа и тангенса два пи минус альфа равняются тангенсу угла альфа. Тригонометрические тождества. Перевод тангенса в котангенсы.
Тригонометрическая функция тангенс угла пи на два или три пи деленное на два (3/2 пи) минус альфа равна котангенсу альфа. Тангенс угла пи минус альфа равен минус тангенсу угла альфа. Формулы приведения для тангенса пи плюс альфа и тангенса два пи минус альфа равняются тангенсу угла альфа. Тригонометрические тождества. Перевод тангенса в котангенсы.
Тригонометрическая функция тангенс имеет следующие формулы привидения:
ctg (π/2 + α) = — tg α
ctg (π + α) = ctg α
ctg (3π/2 + α) = — tg α
ctg (π/2 — α) = tg α
ctg (π — α) = — ctg α
ctg (3π/2 — α) = tg αctg (2π — α) = ctg α
Формулы приведения функции котангенс ctg угла. Для угла 1/2 пи плюс альфа и угла 3/2 пи плюс альфа котангенс равняется минус тангенсу -tg угла альфа. Если в этих же выражениях угол альфа не прибавляется, а вычитается, тогда котангенс такого угла равняется тангенсу угла альфа. n arcsin a+pi n, n in Z`.
n arcsin a+pi n, n in Z`.
Отметим, что последнюю формулу иногда удобнее расписать отдельно для чётных `(n=2k, k in Z)` и нечётных `(n=2k+1, k in Z)n`. А именно
$$ x=\left[\begin{array}{l}\mathrm{arc}\mathrm{sin}a+2\pi k,\\ \pi -\mathrm{arc}\mathrm{sin}a+2\pi k, k\in Z.\end{array}\right.$$
2. `cosx=a`. Если `|a|>1`, решений нет. Если `|a|<=1`, то
`x=+- arccosa+2pin, n in Z`.
3. `»tg»x=a`. При любом `a` `x=»arctg»a+pin, n in Z`.
4. `»ctg»x=a`. При любом `a` `x=»arcctg»a+pin, n in Z`.
Отметим несколько частных случаев простейших тригонометрических уравнений, в которых ответ можно записать более просто, чем по общим формулам.
а) `sinx=1`. Тогда `x=pi/2+2pin,n in Z`.
б) `sinx=-1`. Тогда `x=-pi/2+2pin, n in Z`.
в) `cosx=0`. Тогда `x=pi/2+pin, n in Z`.
г) `cosx=-1`. Тогда `x=pi+2pin, n in Z`.
Рассмотрим несколько типовых способов решения тригонометрических уравнений.
I. 2 4x-1)-2cos4x=0`, `2cos4x(cos4x-1)=0 iff` $$ \iff \left[\begin{array}{l}\mathrm{cos}4x=1.\\ \mathrm{cos}4x=0.\end{array}\right.$$
2 4x-1)-2cos4x=0`, `2cos4x(cos4x-1)=0 iff` $$ \iff \left[\begin{array}{l}\mathrm{cos}4x=1.\\ \mathrm{cos}4x=0.\end{array}\right.$$
Если `cos4x=1`, то `4x=2pin,x=(pin)/2,ninZ`.
1. Изображаем точки
`x=(pin)/2,ninZ`, (3)
на тригонометрическом круге (рис. 4а). Геометрически их `4` штуки (для `n=0,1,2,3` – далее они повторяются).
2. Изображаем точки
`x=(pim)/3,m inZ` (4)
которые не удовлетворяют ОДЗ на тригонометрическом круге (4б). Их `6` штук (для `m=0,1,2,3,4,5` – далее они повторяются).
Видно, что совпадения точек в `(3)` и `(4)` будут при `x=pin,ninZ`. Эти значения надо исключить из решения, т. е. в ответ пойдут точки
`x=pi/2+pin,ninZ`.
С решениями уравнения
`cos4x=0`, `4x=pi/2+pin,ninZ`,
или `x=pi/8+(pin)/4,ninZ`, можно поступить аналогично, сделав отбор на тригонометрическом круге.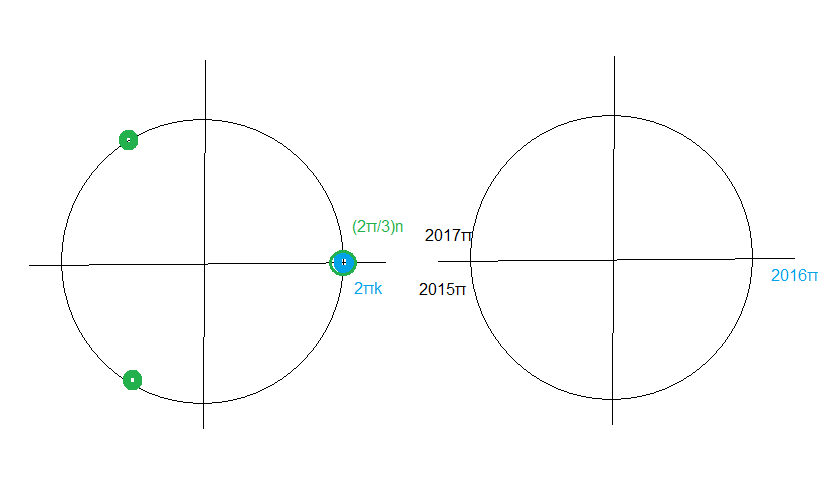 Но когда точек–решений на тригонометрическом круге много, и много точек, не входящих в ОДЗ, то удобнее воспользоваться аналитическим способом отбора решений. В данном случае точек — решений на тригонометрическом круге в серии `x=pi/8+(pin)/4,ninZ`, будет `8` штук (различные при `n=0, 1, 2, 3, 4, 5, 6, 7` – далее они повторяются), а точек, не входящих в ОДЗ на тригонометрическом круге `6`. Посмотрим, есть ли совпадения, т. е. существуют ли целые `m` и `n` такие, что
Но когда точек–решений на тригонометрическом круге много, и много точек, не входящих в ОДЗ, то удобнее воспользоваться аналитическим способом отбора решений. В данном случае точек — решений на тригонометрическом круге в серии `x=pi/8+(pin)/4,ninZ`, будет `8` штук (различные при `n=0, 1, 2, 3, 4, 5, 6, 7` – далее они повторяются), а точек, не входящих в ОДЗ на тригонометрическом круге `6`. Посмотрим, есть ли совпадения, т. е. существуют ли целые `m` и `n` такие, что
`pi/8+(pin)/4=(pim)/3 iff 1/8+n/4=m/3 iff`
`iff 3+6n=8m iff 3=2(4m-3n)`.
Последнее равенство невозможно, т. к. слева стоит нечётное число, а справа чётное.
Отметим, что и для решений уравнения `cos4x=1` отбор можно было сделать аналитически. А именно смотрим, существуют ли целые `m` и `n` такие, что `(pin)/2=(pim)/3 iff 3n=2m`. Видим, что `n` делится на `2`. Тогда `n=2k` и `m=3k,kinZ`. Т. е. из решения уравнения `cos4x=1` надо исключить `x=(pin)/2`, где `n=2k`, т. е. оставить `x=(pin)/2` с `n=2k+1,kinZ`. 2-t-3=0`. Его решение `t_1=-1` и `t_2=3/2`.
2-t-3=0`. Его решение `t_1=-1` и `t_2=3/2`.
1) `»tg»x=-1`. Следовательно, `x=-pi/4+pin,ninZ`.
2) `»tg»x=2/3`. Тогда `x=»arctg»2/3+pin,ninZ`.
б) Сделаем отбор корней, принадлежащих отрезку `[-(3pi)/2; -pi/2]`.
1) Решаем неравенство `-(3pi)/2<=-pi/4+pin<=-pi/2`. Оно равносильно неравенству `-5/4<=n<=-1/4`. Т. к. `ninZ`, то последнему неравенству удовлетворяет только `n=-1`. Итак, из серии решений `x=-pi/4+pin,ninZ`, только корень `x=-(5pi)/4 in [-(3pi)/2; -pi/2]`.2) Аналогично решаем неравенство
`-(3pi)/2<=»arctg»2/3+pin<=-pi/2`. (5)
Т. к. `ninZ`, то в силу правого неравенства `n<0`. Число `n=-1` подходит, т. к. неравенство (5) в этом случае преобразуется в неравенство `-pi/2<=»arctg»2/3<=pi/2`, что верно, `n=-2` не удовлетворяет (5), т. к. в этом случае получим `pi/2<=»arctg»2/3`, что неверно. Аналогично не подходит `n< -2`. Итак, из серии решений `x=»arctg»2/3+pin,ninZ`, только корень `(«arctg»2/3-pi)in[-(3pi)/2; -pi/2]`.
а) `x=-pi/4+pin,ninZ`; `x=»arctg»2/3+pin,ninZ`.
б) `x=-(5pi)/4` и `x=»arctg»2/3-pi`.
Найти наименьший корень уравнения `»ctg»6x-«tg»5x=1/(cos5x)`,
принадлежащий отрезку `[(8pi)/17; (40pi)/17]`.
Преобразуем данное уравнение
`(cos6x)/(sin6x)-(sin5x)/(cos5x)=1/(cos5x)`,
`(cos6x*cos5x-sin6x*sin5x)/(sin6x*cos5x)=1/(cos5x)`,
`(cos11x)/(sin6x*cos5x)=1/(cos5x)`.
Последнее уравнение равносильно `cos11x=sin6x` при условии `sin6x*cos5x!=0`.
Решаем уравнение `cos11x-sin6x=0`. Преобразуем его:
`cos11x-cos(6x-pi/2)=0` или `-2sin((17x)/2-pi/4)sin((5x)/2+pi/4)=0`.
1) Если `sin((5x)/2+pi/4)=0` то `(5x)/2+pi/4=pin,ninZ`, откуда `5x=-pi/2+2pin,ninZ`.
Эти числа не являются корнями исходного уравнения, т. к. нарушается условие `cos5x!=0`.
2) Если `sin((17x)/2-pi/4)=0`, то `x=(pi(1+4n))/(34),ninZ`. Находим, при каких `ninZ`, эти числа лежат на отрезке `[(8pi)/17;(40pi)/17]`. Решаем неравенства
`(8pi)/(17)<=(pi(1+4n))/34<=(40pi)/17 iff 15/4<=n<=79/4`.
Это однородное уравнение 1-го порядка. Оно эквивалентно уравнению `»tg»2x=-1`.
Отсюда `2x=-pi/4+pin,ninZ`, или `x=-pi/8+(pin)/2,ninZ`.
Изобразим решения на тригонометрическом круге (рис. 6). Это `4` точки (`n=0,1,2,3` — далее они повторяются).
Для этих точек надо проверить неравенство `cosx-3sinx>=0`. Ясно, что точка `x_1` удовлетворяет этому неравенству, т. к. `cosx_1>0` и `sinx_1<0`. Для точки `x_3`, диаметрально противоположной точке `x_1`, `sinx` и `cosx` меняют знак, меняет знак и выражение `(cosx-3sinx)`, и, следовательно, для `x_3` неравенство не выполняется. Точка `x_2` не удовлетворяет неравенству, т. к. `sinx_2>0`, `cosx_2>0`, но `sinx_2>cosx_2` в виду того, что `pi/4<x_2<pi/2`, так что выражение `cosx_2-3sinx_2<0`. Точка `x_4` диаметрально противоположна `x_2`. Следовательно,
`cosx_4-3sinx_4=-(cosx_2-3sinx_2)>0`,
и, значит, это решение. Учитывая, что решения имеют период `2pi`, получаем
`x=-pi/8+2pin,ninZ`; `x=11/8pi+2pin,ninZ`.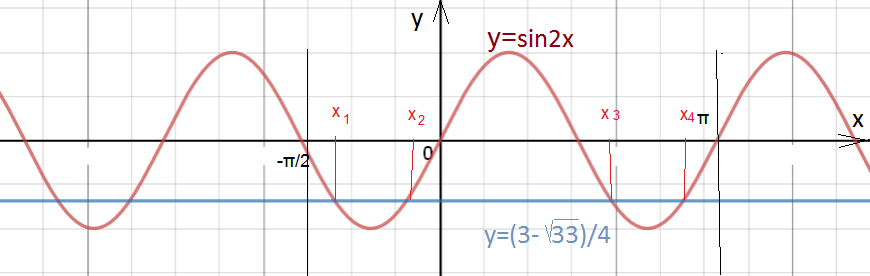
VII. Уравнения с модулем
Решить уравнение `sin3x+|sinx|=sin2x`.
Решение уравнения сводится к объединению решений двух систем.
1) $$ \left\{\begin{array}{l}\mathrm{sin}x\ge 0,\\ \mathrm{sin}3x+\mathrm{sin}x=\mathrm{sin}2x.\end{array}\right.$$
2) sinx0,sin3x-sinx=sin2x.\left\{\begin{array}{l}\sin x
Решаем первую систему. Уравнение `sin3x+sinx=sin2x` преобразуем:
`2sin2xcosx=sin2x` или `sin2x(2cosx-1)=0`.
Значит,
$$ \left[\begin{array}{l}\mathrm{sin}2x=0,\\ \mathrm{cos}x=\frac{1}{2}.\end{array}\right.$$
Изображаем решения уравнения `sin2x=0` на тригонометрическом круге: `x=(pin)/2,ninZ`, (рис. 7). В силу неравенства `sinx>=0` не подходит нижняя точка, т. е. в решения системы входят
`x=pin,ninZ`, и `x=pi/2+2pin,ninZ`.
Аналогично, изображаем на тригонометрическом круге (рис. 8) решения уравнения `cosx=1/2`. Нижняя точка не удовлетворяет неравенству `sinx>=0`. 2x-cosx-1=0`.
2x-cosx-1=0`.
Отсюда `cosx=1` или `cosx=-1/2`. На тригонометрическом круге этим уравнениям удовлетворяют соответственно точки (рис. 9 и рис. 10). Неравенству `sinx<0` удовлетворяет только одна из этих трёх точек, находящаяся в нижней полуплоскости, а именно
`x=pi/3+pi+2pin,ninZ`.
В ответе две серии решений
`x=pi/3+2pin,ninZ` и `x=pi/3+pi+2pin,ninZ`,
соответствующие двум диаметрально противоположным точкам тригонометрического круга, можно задать одной формулой:
`x=pi/3+pin,ninZ` (но это не обязательно).
`x=pin`; `x=pi/2+2pin`; `x=pi/3+pin,ninZ`.
ЕГЭ. Задание 13. Тригонометрические (и не только) уравнения
Подготовка к профильному уровню единого государственного экзамена по математике. Полезные материалы по тригонометрии, большие теоретические видеолекции, видеоразборы задач и подборка заданий прошлых лет.
Полезные материалы
Подборки видео и онлайн-курсы
Тригонометрические формулы
{2 \sin 2x}$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\dfrac{3\pi}{2}; 3\pi \right]$.
а) Решите уравнение $\sin x + \left(\cos \dfrac{x}{2} — \sin \dfrac{x}{2}\right)\left(\cos \dfrac{x}{2} + \sin \dfrac{x}{2}\right) = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\pi; \dfrac{5\pi}{2}\right]$.
а) Решите уравнение $\log_4 (\sin x + \sin 2x + 16) = 2$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -4\pi; -\dfrac{5\pi}{2} \right]$.
Подборка заданий прошлых лет
- а) Решите уравнение $\dfrac{\sin x}{\sin^2\dfrac{x}{2}} = 4\cos^2\dfrac{x}{2}$.
 2 x + \sin x = \sqrt2 \sin\left( x + \dfrac{\pi}{4} \right)$.
2 x + \sin x = \sqrt2 \sin\left( x + \dfrac{\pi}{4} \right)$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -4\pi; -\dfrac{5\pi}{2} \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $2 \sin\left( 2x + \dfrac{\pi}{3} \right) — \sqrt{3} \sin x = \sin 2x + \sqrt3$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ 2\pi; \dfrac{7\pi}{2} \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $2\sqrt3 \sin\left( x + \dfrac{\pi}{3} \right) — \cos 2x = 3\cos x — 1$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ 2\pi; \dfrac{7\pi}{2} \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $2\sin\left( 2x + \dfrac{\pi}{6} \right) — \cos x = \sqrt3\sin 2x — 1$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{5\pi}{2}; 4\pi \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $\sqrt2\sin\left( \dfrac{\pi}{4} + x \right) + \cos 2x = \sin x — 1$.
 2 x + 5\sin\left( \dfrac{\pi}{2} — x\right) — 2 = 0$.
2 x + 5\sin\left( \dfrac{\pi}{2} — x\right) — 2 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -5\pi; \ — \dfrac{7\pi}{2}\right]$. (ЕГЭ-2012, вторая волна)
Тригонометрических функций и единичная окружность
Радианы
Радианы — это еще один способ измерения углов, и величина угла может быть преобразована между градусами и радианами.
Цели обучения
Объясните определение радианов с точки зрения длины дуги единичного круга и используйте это для преобразования между градусами и радианами.
Основные выводы
Ключевые моменты
- Один радиан — это мера центрального угла окружности, при которой длина дуги равна радиусу
окружности.\ circ} {\ pi}} [/ латекс]. - Радианная мера угла — это отношение длины дуги к радиусу круга [латекс] \ displaystyle {\ left (\ theta = \ frac {s} {r} \ right)} [/ latex] . Другими словами, если [latex] s [/ latex] — это длина дуги круга, а [latex] r [/ latex] — это радиус круга, то центральный угол, содержащий эту дугу, измеряется в радианах.

Ключевые термины
- дуга : Непрерывная часть окружности круга.
- окружность : длина линии, ограничивающей круг.
- радиан : Стандартная единица измерения углов в математике. Мера центрального угла круга, который пересекает дугу, равную по длине радиусу этого круга.
Введение в радианы
Напомним, что деление круга на 360 частей дает измерение в градусах. Это произвольное измерение, и мы можем выбрать другие способы разделить круг.Чтобы найти другую единицу, представьте себе процесс рисования круга. Представьте, что вы остановились до того, как круг замкнулся. Нарисованная вами часть называется дугой. Дуга может быть частью полного круга, полного круга или более чем полного круга, представленного более чем одним полным оборотом. Длина дуги вокруг всего круга называется окружностью этого круга.
Окружность круга
[латекс] C = 2 \ pi r [/ латекс]
Если мы разделим обе части этого уравнения на [латекс] r [/ латекс], мы получим отношение длины окружности, которое всегда равно [латексу] 2 \ pi [/ латексу] к радиусу, независимо от длины радиус. Таким образом, длина окружности любого круга равна [латексу] 2 \ пи \ приблизительно в 6,28 [/ латексу] раз больше длины радиуса. Это означает, что если мы возьмем струну такой же длины, как радиус, и будем использовать ее для измерения последовательных длин по окружности, то будет место для шести полных струн и чуть больше четверти седьмой, как показано на диаграмме. ниже.
Таким образом, длина окружности любого круга равна [латексу] 2 \ пи \ приблизительно в 6,28 [/ латексу] раз больше длины радиуса. Это означает, что если мы возьмем струну такой же длины, как радиус, и будем использовать ее для измерения последовательных длин по окружности, то будет место для шести полных струн и чуть больше четверти седьмой, как показано на диаграмме. ниже.
Длина окружности по сравнению с радиусом : длина окружности чуть более чем в 6 раз превышает длину радиуса.
Это подводит нас к нашей новой угловой мере. Радиан — это стандартная единица измерения углов в математике. Один радиан — это мера центрального угла круга, который пересекает дугу, равную по длине радиусу этого круга.
Один радиан: Угол [латекс] t [/ латекс] выметает величину в один радиан. Обратите внимание, что длина перехваченной дуги равна длине радиуса круга.
Поскольку общая длина окружности круга равна [латексу] 2 \ pi [/ latex], умноженному на радиус, полный круговой поворот составляет [латекс] 2 \ pi [/ латекс] радиан. {\ circ}} [/ latex].
{\ circ}} [/ latex].
Измерение угла в радианах
Длина дуги [латекс] s [/ латекс] — это длина кривой вдоль дуги. Так же, как полная длина окружности всегда имеет постоянное отношение к радиусу, длина дуги, образованная любым заданным углом, также имеет постоянную связь с радиусом, независимо от длины радиуса.
Это соотношение, называемое радианной мерой, одинаково независимо от радиуса круга — оно зависит только от угла. Это свойство позволяет нам определять меру любого угла как отношение длины дуги [latex] s [/ latex] к радиусу [latex] r [/ latex].
[латекс] \ displaystyle {\ begin {align} s & = r \ theta \\ \ theta & = \ frac {s} {r} \ end {align}} [/ latex]
Измерительные радианы: (a) в угле 1 радиан; длина дуги равна радиусу [латекс] r [/ латекс]. (b) Угол в 2 радиана имеет длину дуги [латекс] s = 2r [/ латекс]. (c) Полный оборот составляет [латекс] 2 \ pi [/ латекс], или около 6,28 радиана.
Пример
Какова мера данного угла в радианах, если длина его дуги равна [латекс] 4 \ pi [/ latex], а радиус — [латекс] [/ латекс] 12?
Подставьте значения [latex] s = 4 \ pi [/ latex] и [latex] r = 12 [/ latex] в формулу угла:
[латекс] \ displaystyle {\ begin {align} \ theta & = \ frac {s} {r} \\ & = \ frac {4 \ pi} {12} \\ & = \ frac {\ pi} {3 } \\ & = \ frac {1} {3} \ pi \ end {align}} [/ latex]
Угол имеет размер [latex] \ displaystyle {\ frac {1} {3} \ pi} [/ latex] радиан.
Определение тригонометрических функций на единичной окружности
Определение точек на единичной окружности позволяет применять тригонометрические функции к любому углу.
Цели обучения
Используйте прямоугольные треугольники, нарисованные в единичной окружности, чтобы определить тригонометрические функции для любого угла
Основные выводы
Ключевые моменты
- Координаты [latex] x [/ latex] — и [latex] y [/ latex] в точке на единичной окружности, заданной углом [latex] t [/ latex], определяются функциями [latex] x = \ cos t [/ latex] и [latex] y = \ sin t [/ latex].{\ circ} [/ латекс].
- Единичный круг демонстрирует периодичность тригонометрических функций, показывая, что они приводят к повторяющемуся набору значений через равные промежутки времени.
Ключевые термины
- периодичность : качество функции с повторяющимся набором значений через равные промежутки времени.

- единичная окружность : окружность с центром в начале координат и радиусом 1.
- квадранты : четыре четверти координатной плоскости, образованные осями [латекс] x [/ латекс] — и [латекс] y [/ латекс].
Тригонометрические функции и единичная окружность
Мы уже определили тригонометрические функции в терминах прямоугольных треугольников. В этом разделе мы переопределим их в терминах единичной окружности. Напомним, что единичный круг — это круг с центром в начале координат и радиусом 1. Угол [латекс] t [/ латекс] (в радианах) образует дугу длиной [латекс] s [/ латекс].
Оси x- и y- делят координатную плоскость (и единичную окружность, поскольку она центрирована в начале координат) на четыре четверти, называемых квадрантами.Мы помечаем эти квадранты, чтобы имитировать направление, в котором развернется положительный угол. Четыре квадранта обозначены I, II, III и IV.
Для любого угла [latex] t [/ latex] мы можем обозначить пересечение его стороны и единичного круга его координатами, [latex] (x, y) [/ latex]. Координаты [latex] x [/ latex] и [latex] y [/ latex] будут выходными данными тригонометрических функций [latex] f (t) = \ cos t [/ latex] и [latex] f (t). = \ sin t [/ latex] соответственно. Это означает:
Координаты [latex] x [/ latex] и [latex] y [/ latex] будут выходными данными тригонометрических функций [latex] f (t) = \ cos t [/ latex] и [latex] f (t). = \ sin t [/ latex] соответственно. Это означает:
[латекс] \ displaystyle {\ begin {align} x & = \ cos t \\ y & = \ sin t \ end {align}} [/ latex]
Эти координаты показаны на диаграмме единичного круга.
Единичный круг: координаты точки на единичной окружности, центральный угол которой составляет [латекс] t [/ латекс] радиан.
Обратите внимание, что значения [latex] x [/ latex] и [latex] y [/ latex] задаются длинами двух сторон треугольника, окрашенных в красный цвет. Это прямоугольный треугольник, и вы можете видеть, как длины этих двух сторон (и значения [latex] x [/ latex] и [latex] y [/ latex]) задаются тригонометрическими функциями [latex] t [/латекс].
В качестве примера того, как это применимо, рассмотрим диаграмму, показывающую точку с координатами [latex] \ displaystyle {\ left (- \ frac {\ sqrt2} {2}, \ frac {\ sqrt2} {2} \ right)} [/ latex] по единичной окружности.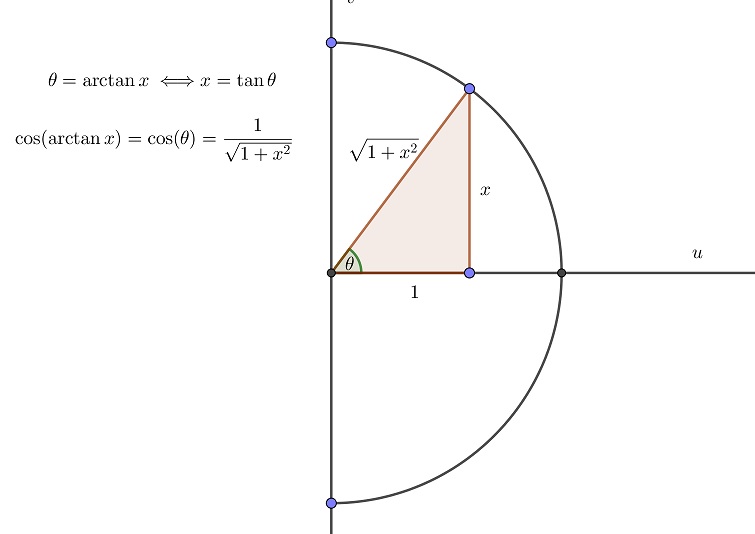
Точка на единичном круге: точка [латекс] \ displaystyle {\ left (- \ frac {\ sqrt2} {2}, \ frac {\ sqrt2} {2} \ right)} [/ latex] на единичном круге. .
Мы знаем, что для любой точки единичного круга координата [latex] x [/ latex] равна [latex] \ cos t [/ latex], а координата [latex] y [/ latex] — [latex] ] \ sin t [/ латекс]. Применяя это, мы можем определить, что [latex] \ displaystyle {\ cos t = — \ frac {\ sqrt2} {2}} [/ latex] и [latex] \ displaystyle {\ sin t = — \ frac {\ sqrt2} {2}} [/ латекс] для угла [латекс] t [/ латекс] на схеме.
Напомним, что [латекс] \ displaystyle {\ tan t = \ frac {\ sin t} {\ cos t}} [/ latex]. Применяя эту формулу, мы можем найти тангенс любого угла, обозначенного единичной окружностью. Для угла [латекс] т [/ латекс], указанного на диаграмме единичного круга, показывающего точку [латекс] \ displaystyle {\ left (- \ frac {\ sqrt2} {2}, \ frac {\ sqrt2} {2 } \ right)} [/ latex], касательная:
[латекс] \ displaystyle {\ begin {align} \ tan t & = \ frac {\ sin t} {\ cos t} \\ & = \ frac {- \ frac {\ sqrt2} {2}} {- \ гидроразрыв {\ sqrt2} {2}} \\ & = 1 \ end {align}} [/ latex]
Ранее мы обсуждали тригонометрические функции применительно к прямоугольным треугольникам.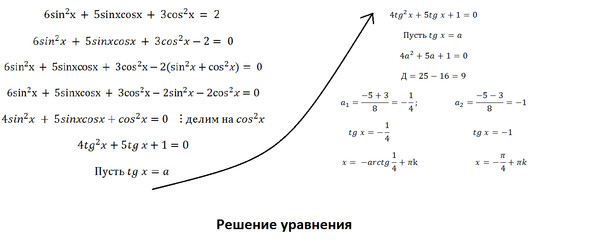 {\ circ} [/ латекс].
{\ circ} [/ латекс].
Дальнейшее рассмотрение единичного круга
Координаты определенных точек на единичной окружности и мера каждого угла в радианах и градусах показаны на диаграмме координат единичной окружности. Эта диаграмма позволяет наблюдать за каждым из этих углов, используя тригонометрические функции.
Координаты единичной окружности : Единичная окружность, показывающая координаты и угловые размеры определенных точек.
Мы можем найти координаты любой точки единичной окружности.Учитывая любой угол [латекс] t [/ латекс], мы можем найти координату [latex] x [/ latex] или [latex] y [/ latex] в этой точке, используя [latex] x = \ text {cos} t [/ latex] и [latex] y = \ text {sin} t [/ latex].
Единичный круг демонстрирует периодичность тригонометрических функций. Периодичность относится к способу, которым тригонометрические функции приводят к повторяющемуся набору значений через равные промежутки времени. Взгляните на [latex] x [/ latex] -значения координат в единичном круге выше для значений [latex] t [/ latex] от [latex] 0 [/ latex] до [latex] 2 {\ pi} [/ latex]:
[латекс] {1, \ frac {\ sqrt {3}} {2}, \ frac {\ sqrt {2}} {2}, \ frac {1} {2}, 0, — \ frac {1} {2}, — \ frac {\ sqrt {2}} {2}, — \ frac {\ sqrt {3}} {2}, -1, — \ frac {\ sqrt {3}} {2}, — \ frac {\ sqrt {2}} {2}, — \ frac {1} {2}, 0, \ frac {1} {2}, \ frac {\ sqrt {2}} {2}, \ frac { \ sqrt {3}} {2}, 1} [/ латекс]
Мы можем определить закономерность в этих числах, которые колеблются между [латекс] -1 [/ латекс] и [латекс] 1 [/ латекс]. Обратите внимание, что этот шаблон будет повторяться для более высоких значений [latex] t [/ latex]. Напомним, что эти значения [latex] x [/ latex] соответствуют [latex] \ cos t [/ latex]. Это показатель периодичности функции косинуса.
Обратите внимание, что этот шаблон будет повторяться для более высоких значений [latex] t [/ latex]. Напомним, что эти значения [latex] x [/ latex] соответствуют [latex] \ cos t [/ latex]. Это показатель периодичности функции косинуса.
Пример
Решите [латекс] \ displaystyle {\ sin {\ left (\ frac {7 \ pi} {6} \ right)}} [/ latex].
Похоже, это будет сложно решить. Однако обратите внимание, что диаграмма единичного круга показывает координаты в [latex] \ displaystyle {t = \ frac {7 \ pi} {6}} [/ latex].Поскольку координата [latex] y [/ latex] соответствует [latex] \ sin t [/ latex], мы можем идентифицировать, что
[латекс] \ displaystyle {\ sin {\ left (\ frac {7 \ pi} {6} \ right)} = — \ frac {1} {2}} [/ latex]
Специальные уголки
Единичный круг и набор правил можно использовать для вызова значений тригонометрических функций специальных углов.
Цели обучения
Объясните, как свойства синуса, косинуса и тангенса и их знаки в каждом квадранте дают свои значения для каждого из специальных углов
Основные выводы
Ключевые моменты
- Тригонометрические функции углов в единичной окружности можно запомнить и вызвать с помощью набора правил.

- Знак тригонометрической функции зависит от квадранта, в который попадает угол, и мнемоническая фраза «Умный класс триггера» используется для определения того, какие функции в каком квадранте положительны.
- Базовые углы в квадранте I используются для определения значения любого угла в квадрантах II, III или IV. Базовый угол образует тот же угол с осью [latex] x [/ latex], что и рассматриваемый угол.
- В единичную окружность включаются только функции синуса и косинуса для особых углов.Однако, поскольку тангенс получается из синуса и косинуса, его можно вычислить для любого из специальных углов.
Ключевые термины
- специальный угол : угол, кратный 30 или 45 градусам; тригонометрические функции легко записываются под этими углами.
Тригонометрические функции специальных углов
Напомним, что определенные углы и их координаты, которые соответствуют [latex] x = \ cos t [/ latex] и [latex] y = \ sin t [/ latex] для данного угла [latex] t [/ latex], можно идентифицировать на единичном круге.{\ circ} \ right)} & = 1 \\ \ end {align}} [/ latex]
Выражения для косинусных функций этих специальных углов также просты.
Обратите внимание, что, хотя только синус и косинус определяются непосредственно единичной окружностью, тангенс может быть определен как частное, включающее эти два:
[латекс] \ displaystyle {\ tan t = \ frac {\ sin t} {\ cos t}} [/ latex]
Функции касания также имеют простые выражения для каждого из специальных углов.
Мы можем наблюдать эту тенденцию на примере.{\ circ} \ right)}} \\ & = \ frac {\ frac {\ sqrt {3}} {2}} {\ frac {1} {2}} \\ & = \ frac {\ sqrt {3 }} {2} \ cdot \ frac {2} {1} \\ & = \ sqrt {3} \ end {align}} [/ latex]
Запоминание тригонометрических функций
Понимание единичной окружности и способность быстро решать тригонометрические функции для определенных углов очень полезно в области математики. Применение правил и ярлыков, связанных с единичным кругом, позволяет быстро решать тригонометрические функции. Ниже приведены некоторые правила, которые помогут вам быстро решить такие проблемы.
Признаки тригонометрических функций
Знак тригонометрической функции зависит от квадранта, в который попадает угол. Чтобы помочь запомнить, какие из тригонометрических функций положительны в каждом квадранте, мы можем использовать мнемоническую фразу «Умный класс триггера». Каждое из четырех слов во фразе соответствует одному из четырех квадрантов, начиная с квадранта I и вращаясь против часовой стрелки. В квадранте I, который является «А», все тригонометрических функций положительны.В квадранте II, «Умный», только синус является положительным. В квадранте III «Триггер» только , касательная положительна. Наконец, в квадранте IV «Класс» только , косинус положительный.
Знаковые правила для тригонометрических функций: Каждая тригонометрическая функция перечислена в тех квадрантах, в которых она положительна.
Определение значений с использованием опорных углов
Внимательно посмотрите на единичный круг и обратите внимание, что [latex] \ sin t [/ latex] и [latex] \ cos t [/ latex] принимают определенные значения, поскольку они колеблются между [latex] -1 [/ latex] и [латекс] 1 [/ латекс]. {\ circ} [/ латекс].
Для любого заданного угла в первом квадранте существует угол во втором квадранте с тем же значением синуса. Поскольку значение синуса является координатой [latex] y [/ latex] на единичной окружности, другой угол с таким же синусом будет иметь такое же значение [latex] y [/ latex], но будет иметь противоположное значение [latex] x [/ latex] -значение. Следовательно, его значение косинуса будет противоположным значению косинуса первого угла.
Аналогично, в четвертом квадранте будет угол с таким же косинусом, что и исходный угол.Угол с таким же косинусом будет иметь одно и то же значение [latex] x [/ latex], но будет иметь противоположное значение [latex] y [/ latex]. Следовательно, его значение синуса будет противоположным значению синуса исходного угла.
Как показано на диаграммах ниже, угол [латекс] \ альфа [/ латекс] имеет то же значение синуса, что и угол [латекс] t [/ латекс]; значения косинуса противоположны. Угол [латекс] \ бета [/ латекс] имеет то же значение косинуса, что и угол [латекс] t [/ латекс]; значения синуса противоположны.
[латекс] \ Displaystyle {\ begin {align} \ sin t = \ sin \ alpha \ quad & \ text {and} \ quad \ cos t = — \ cos \ alpha \\ \ sin t = — \ sin \ beta \ quad & \ text {and} \ quad \ cos t = \ cos \ beta \ end {align}} [/ latex]
Контрольные углы: На левом рисунке [латекс] t [/ latex] является контрольным углом для [латекс] \ альфа [/ латекс].{\ circ} [/ latex] или [latex] 0 [/ latex] и [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex] радиан. Для любого угла в квадранте II, III или IV существует опорный угол в квадранте I.
Контрольные углы в каждом квадранте: Для любого угла в квадрантах II, III или IV существует контрольный угол в квадранте I.
Таким образом, чтобы вызвать любой синус или косинус особого угла, вам необходимо определить его угол с осью [latex] x [/ latex], чтобы сравнить его с опорным углом.{\ circ})} \\ & = \ frac {- \ frac {\ sqrt {2}} {2}} {- \ frac {\ sqrt {2}} {2}} \\ & = — \ frac { \ sqrt {2}} {2} \ cdot — \ frac {2} {\ sqrt {2}} \\ & = 1 \ end {align}} [/ latex]
Синус и косинус как функции
Функции синуса и косинуса можно изобразить, используя значения из единичной окружности, и на обоих графиках можно наблюдать определенные характеристики.
Цели обучения
Опишите характеристики графиков синуса и косинуса
Основные выводы
Ключевые моменты
- И синусоидальную функцию [latex] (y = \ sin x) [/ latex], и косинусную функцию [latex] (y = \ cos x) [/ latex] можно изобразить, нанеся на график точки, полученные из единичной окружности, с каждая координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] представляет собой соответствующее значение функции под этим углом.
- Синус и косинус — периодические функции с периодом [латекс] 2 \ пи [/ латекс].
- И синус, и косинус имеют домен [latex] (- \ infty, \ infty) [/ latex] и диапазон [latex] [- 1, 1] [/ latex].
- График [latex] y = \ sin x [/ latex] симметричен относительно начала координат, потому что это нечетная функция, в то время как график [latex] y = \ cos x [/ latex] симметричен относительно [latex ] y [/ latex] -axis, потому что это четная функция.
Ключевые термины
- период : интервал, содержащий значения, повторяющиеся в функции.
- четная функция : непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], в которых [latex] f (-x) = f (x) [/ latex], с симметрией относительно оси [латекс] y [/ латекс].
- нечетная функция : непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], в которых [latex] f (-x) = -f (x) [/ latex] , с симметрией относительно начала координат.
- периодическая функция : непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], который повторяется через равные промежутки времени.
Графические функции синуса и косинуса
Напомним, что функции синуса и косинуса связывают значения действительных чисел с координатами [latex] x [/ latex] и [latex] y [/ latex] точки на единичной окружности. Так как же они выглядят на графике на координатной плоскости? Начнем с синусоидальной функции [latex] y = \ sin x [/ latex]. Мы можем создать таблицу значений и использовать их для построения графика. Ниже приведены некоторые значения синусоидальной функции на единичном круге, где координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] — [latex] \ sin х [/ латекс]:
[латекс] \ displaystyle {(0, 0) \ quad (\ frac {\ pi} {6}, \ frac {1} {2}) \ quad (\ frac {\ pi} {4}, \ frac { \ sqrt {2}} {2}) \ quad (\ frac {\ pi} {3}, \ frac {\ sqrt {3}} {2}) \ quad (\ frac {\ pi} {2}, 1 ) \\ (\ frac {2 \ pi} {3}, \ frac {\ sqrt {3}} {2}) \ quad (\ frac {3 \ pi} {4}, \ frac {\ sqrt {2} } {2}) \ quad (\ frac {5 \ pi} {6}, \ frac {1} {2}) \ quad (\ pi, 0)} [/ latex]
Построение точек из таблицы и продолжение по оси [latex] x [/ latex] дает форму синусоидальной функции.
График синусоидальной функции: График точек с координатами [latex] x [/ latex], являющимися углами в радианах, и координатами [latex] y [/ latex], являющимися функцией [latex] \ sin x [/ latex] .
Обратите внимание на положительные значения синуса между [latex] 0 [/ latex] и [latex] \ pi [/ latex], которые соответствуют значениям синусоидальной функции в квадрантах I и II на единичном круге, и синусоиде значения отрицательны между [латекс] \ пи [/ латекс] и [латекс] 2 \ пи [/ латекс], которые соответствуют значениям синусоидальной функции в квадрантах III и IV на единичной окружности.
Построение значений синусоидальной функции: Точки на кривой [латекс] y = \ sin x [/ latex] соответствуют значениям синусоидальной функции на единичной окружности.
Теперь давайте аналогичным образом посмотрим на функцию косинуса, [latex] f (x) = \ sin x [/ latex]. Опять же, мы можем создать таблицу значений и использовать их для построения графика. Ниже приведены некоторые значения синусоидальной функции на единичном круге, где координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] — [latex] \ cos х [/ латекс]:
[латекс] \ displaystyle {(0, 1) \ quad (\ frac {\ pi} {6}, \ frac {\ sqrt {3}} {2}) \ quad (\ frac {\ pi} {4} , \ frac {\ sqrt {2}} {2}) \ quad (\ frac {\ pi} {3}, \ frac {1} {2}) \ quad (\ frac {\ pi} {2}, 0 ) \\ (\ frac {2 \ pi} {3}, — \ frac {1} {2}) \ quad (\ frac {3 \ pi} {4}, — \ frac {\ sqrt {2}} { 2}) \ quad (\ frac {5 \ pi} {6}, — \ frac {\ sqrt {3}} {2}) \ quad (\ pi, -1)} [/ latex]
Как и в случае с функцией синуса, мы можем построить точки для построения графика функции косинуса.
График функции косинуса: Точки на кривой [latex] y = \ cos x [/ latex] соответствуют значениям функции косинуса на единичной окружности.
Поскольку мы можем вычислять синус и косинус любого действительного числа, обе эти функции определены для всех действительных чисел. Если рассматривать значения синуса и косинуса как координаты точек на единичном круге, становится ясно, что диапазон обеих функций должен быть интервалом [latex] \ left [-1, 1 \ right] [/ latex].
Определение периодических функций
На графиках для функций синуса и косинуса форма графика повторяется после [latex] 2 \ pi [/ latex], что означает, что функции являются периодическими с периодом [latex] 2 \ pi [/ latex].Периодическая функция — это функция с повторяющимся набором значений через равные промежутки времени. В частности, это функция, для которой определенный горизонтальный сдвиг, [латекс] P [/ латекс], приводит к функции, равной исходной функции:
[латекс] f (x + P) = f (x) [/ латекс]
для всех значений [latex] x [/ latex] в домене [latex] f [/ latex]. Когда это происходит, мы называем наименьший такой сдвиг по горизонтали с [latex] P> 0 [/ latex] периодом функции. На приведенной ниже диаграмме показаны несколько периодов функций синуса и косинуса.
Периоды функций синуса и косинуса: Функции синуса и косинуса являются периодическими, что означает, что определенный горизонтальный сдвиг, [latex] P [/ latex], приводит к функции, равной исходной функции: [latex] f (x + P) = f (x) [/ латекс].
Четные и нечетные функции
Еще раз взглянув на функции синуса и косинуса в домене с центром на оси [latex] y [/ latex], можно выявить симметрии. Как видно на графике синусоидальной функции, она симметрична относительно начала координат, что указывает на то, что это нечетная функция.На всем протяжении графика любые две точки с противоположными значениями [latex] x [/ latex] также имеют противоположные значения [latex] y [/ latex]. Это характерно для нечетной функции: два входа, которые являются противоположными, имеют выходы, которые также являются противоположными. Другими словами, если [латекс] \ sin (-x) = — \ sin x [/ latex].
Нечетная симметрия синусоидальной функции: Синусоидальная функция нечетная, то есть симметрична относительно начала координат.
График функции косинуса показывает, что он симметричен относительно оси y .Это указывает на то, что это четная функция. Для четных функций любые две точки с противоположными значениями [latex] x [/ latex] имеют одинаковое значение функции. Другими словами, [латекс] \ cos (-x) = \ cos x [/ latex]. Мы можем видеть из графика, что это правда, сравнивая значения [latex] y [/ latex] графика с любыми противоположными значениями [latex] x [/ latex].
Четная симметрия функции косинуса: Функция косинуса четная, что означает, что она симметрична относительно оси [latex] y [/ latex].
Касательная как функция
Характеристики касательной функции можно увидеть на ее графике.
Цели обучения
Опишите характеристики графика касательной функции
Основные выводы
Ключевые моменты
- Функция касательной не определена при любом значении [latex] x [/ latex], где [latex] \ cos x = 0 [/ latex], и ее график имеет вертикальные асимптоты при этих значениях [latex] x [/ latex] .
- Касательная — периодическая функция с периодом [латекс] \ пи [/ латекс].
- График функции касательной симметричен относительно начала координат и, следовательно, является нечетной функцией.
Ключевые термины
- периодическая функция : непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex] с набором значений, повторяющихся через равные промежутки времени.
- период : интервал, содержащий минимальный набор значений, повторяющихся в периодической функции.
- нечетная функция : непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], в которых [latex] f (-x) = -f (x) [/ latex] , и есть симметрия относительно начала координат.
- вертикальная асимптота : прямая линия, параллельная оси [латекс] y [/ латекс], к которой кривая приближается произвольно близко, когда кривая уходит в бесконечность.
Построение касательной функции
Касательная функция может быть построена на графике путем нанесения точек [latex] \ left (x, f (x) \ right) [/ latex]. Форму функции можно создать, найдя значения тангенса под определенными углами. Однако невозможно найти касательные функции для этих особых углов с единичной окружностью.Мы применяем формулу [latex] \ displaystyle {\ tan x = \ frac {\ sin x} {\ cos x}} [/ latex], чтобы определить касательную для каждого значения.
Мы можем проанализировать графическое поведение касательной функции, посмотрев на значения некоторых специальных углов. Рассмотрим точки ниже, для которых координаты [latex] x [/ latex] представляют собой углы в радианах, а координаты [latex] y [/ latex] — [latex] \ tan x [/ latex]:
[латекс] \ displaystyle {(- \ frac {\ pi} {2}, \ text {undefined}) \ quad (- \ frac {\ pi} {3}, — \ sqrt {3}) \ quad (- \ frac {\ pi} {4}, -1) \ quad (- \ frac {\ pi} {6}, — \ frac {\ sqrt {3}} {3}) \ quad (0, 0) \\ (\ frac {\ pi} {6}, \ frac {\ sqrt {3}} {3}) \ quad (\ frac {\ pi} {4}, 1) \ quad (\ frac {\ pi} {3 }, \ sqrt {3}) \ quad (\ frac {\ pi} {2}, \ text {undefined})} [/ latex]
Обратите внимание, что [latex] \ tan x [/ latex] не определено в [latex] \ displaystyle {x = — \ frac {\ pi} {2}} [/ latex] и [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ латекс].Вышеупомянутые пункты помогут нам нарисовать наш график, но нам нужно определить, как граф ведет себя там, где он не определен. Давайте рассмотрим последние четыре пункта. Мы можем определить, что значения [latex] y [/ latex] увеличиваются по мере того, как [latex] x [/ latex] увеличивается и приближается к [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex]. Мы могли бы рассмотреть дополнительные точки между [latex] \ displaystyle {x = 0} [/ latex] и [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ latex], и мы увидим, что это держит. Точно так же мы видим, что [latex] y [/ latex] уменьшается по мере приближения [latex] x [/ latex] к [latex] \ displaystyle {- \ frac {\ pi} {2}} [/ latex], потому что выходные становиться все меньше и меньше.
Напомним, что существует несколько значений [latex] x [/ latex], которые могут дать [latex] \ cos x = 0 [/ latex]. В любой такой точке [latex] \ tan x [/ latex] не определено, потому что [latex] \ displaystyle {\ tan x = \ frac {\ sin x} {\ cos x}} [/ latex]. При значениях, при которых функция касания не определена, на ее графике наблюдаются разрывы. При этих значениях график касательной имеет вертикальные асимптоты.
График функции касательной: функция касательной имеет вертикальные асимптоты в [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ latex] и [latex] \ displaystyle {x = — \ frac {\ пи} {2}} [/ латекс].
Характеристики графика касательной функции
Как и функции синуса и косинуса, тангенс является периодической функцией. Это означает, что его значения повторяются через равные промежутки времени. Период касательной функции равен [latex] \ pi [/ latex], потому что график повторяется на [latex] x [/ latex] -осных интервалах [latex] k \ pi [/ latex], где [latex] k [/ latex] — это константа. На графике функции касательной на интервале [latex] \ displaystyle {- \ frac {\ pi} {2}} [/ latex] к [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex], мы можем увидеть поведение графика за один полный цикл функции.Если мы посмотрим на
любой больший интервал, мы увидим, что характеристики графика повторяются.
График функции касательной симметричен относительно начала координат и, следовательно, является нечетной функцией. Другими словами, [latex] \ text {tan} (- x) = — \ text {tan} x [/ latex] для любого значения [latex] x [/ latex]. Любые две точки с противоположными значениями [latex] x [/ latex] дают противоположные значения [latex] y [/ latex]. Мы можем видеть, что это правда, рассматривая значения [latex] y [/ latex] графика при любых противоположных значениях [latex] x [/ latex].Рассмотрим [latex] \ displaystyle {x = \ frac {\ pi} {3}} [/ latex] и [latex] \ displaystyle {x = — \ frac {\ pi} {3}} [/ latex]. Выше мы уже определили, что [латекс] \ displaystyle {\ tan (\ frac {\ pi} {3}) = \ sqrt {3}} [/ latex] и [latex] \ displaystyle {\ tan (- \ frac { \ pi} {3}) = — \ sqrt {3}} [/ latex].
Секанс и тригонометрические функции
Тригонометрические функции имеют обратные величины, которые можно вычислить с помощью единичной окружности.
Цели обучения
Расчет значений тригонометрических функций, являющихся обратными синусу, косинусу и тангенсу
Основные выводы
Ключевые моменты
- Секущая функция обратна функции косинуса [latex] \ displaystyle {\ left (\ sec x = \ frac {1} {\ cos x} \ right)} [/ latex].Его можно найти для угла [латекс] t [/ latex], используя координату [latex] x [/ latex] связанной точки на единичной окружности: [latex] \ displaystyle {\ sec t = \ frac { 1} {x}} [/ латекс].
- Функция косеканса является обратной функцией синусоидальной функции [latex] \ displaystyle {\ left (\ csc x = \ frac {1} {\ sin x} \ right)} [/ latex]. Его можно найти для угла [латекс] t [/ latex], используя координату [latex] y [/ latex] связанной точки на единичном круге: [latex] \ displaystyle {\ csc t = \ frac { 1} {y}} [/ латекс].
- Функция котангенса является обратной функцией касательной [латекс] \ displaystyle {\ left (\ cot x = \ frac {1} {\ tan x} = \ frac {\ cos t} {\ sin t} \ right) }[/латекс]. Его можно найти для угла, используя координаты [latex] x [/ latex] и [latex] y [/ latex] соответствующей точки на единичной окружности: [latex] \ displaystyle {\ cot t = \ frac {\ cos t} {\ sin t} = \ frac {x} {y}} [/ latex].
Ключевые термины
- секанс : величина, обратная функции косинуса
- косеканс : функция, обратная синусоиде
- котангенс : величина, обратная касательной функции
Введение в взаимные функции
Мы обсудили три тригонометрические функции: синус, косинус и тангенс.Каждая из этих функций имеет обратную функцию, которая определяется обратной величиной отношения исходной тригонометрической функции. Обратите внимание, что обратные функции отличаются от обратных функций. Обратные функции — это способ работать в обратном направлении или определять угол с учетом тригонометрического отношения; они предполагают работу с теми же соотношениями, что и исходная функция.
Три взаимные функции описаны ниже.
Секант
Секущая функция обратна функции косинуса и обозначается сокращенно как [латекс] \ сек [/ латекс].
Его можно описать как отношение длины гипотенузы к длине соседней стороны в треугольнике.
[латекс] \ displaystyle {\ begin {align} \ sec x & = \ frac {1} {\ cos x} \\ \ sec x & = \ frac {\ text {hypotenuse}} {\ text {смежный}} \ end {align}} [/ latex]
Секанс легко вычислить со значениями в единичной окружности. Напомним, что для любой точки круга значение [latex] x [/ latex] дает [latex] \ cos t [/ latex] для соответствующего угла [latex] t [/ latex].Следовательно, секущая функция для этого угла равна
.[латекс] \ displaystyle {\ sec t = \ frac {1} {x}} [/ латекс]
Косеканс
Функция косеканса является обратной функцией синусоиды и обозначается сокращенно как [latex] \ csc [/ latex]. Его можно описать как отношение длины гипотенузы к длине противоположной стороны треугольника.
[латекс] \ displaystyle {\ begin {align} \ csc x & = \ frac {1} {\ sin x} \\ \ csc x & = \ frac {\ text {hypotenuse}} {\ text {напротив}} \ end {align}} [/ latex]
Как и секанс, косеканс может быть вычислен со значениями в единичной окружности.Напомним, что для любой точки круга значение [latex] y [/ latex] дает [latex] \ sin t [/ latex]. Следовательно, функция косеканса для того же угла равна
[латекс] \ Displaystyle {\ csc t = \ frac {1} {y}} [/ латекс]
Котангенс
Функция котангенса обратна функции тангенса и обозначается сокращенно как [latex] \ cot [/ latex]. Его можно описать как отношение длины соседней стороны к длине гипотенузы в треугольнике.
[латекс] \ displaystyle {\ begin {align} \ cot x & = \ frac {1} {\ tan x} \\ \ cot x & = \ frac {\ text {смежный}} {\ text {противоположный}} \ end {align}} [/ latex]
Также обратите внимание, что поскольку [latex] \ displaystyle {\ tan x = \ frac {\ sin x} {\ cos x}} [/ latex], его обратное значение равно
[латекс] \ displaystyle {\ cot x = \ frac {\ cos x} {\ sin x}} [/ latex]
Котангенс также можно вычислить со значениями в единичной окружности.Применяя координаты [latex] x [/ latex] и [latex] y [/ latex], связанные с углом [latex] t [/ latex], получаем
[латекс] \ displaystyle {\ begin {align} \ cot t & = \ frac {\ cos t} {\ sin t} \\ \ cot t & = \ frac {x} {y} \ end {align}} [/ латекс]
Вычисление взаимных функций
Теперь мы распознаем шесть тригонометрических функций, которые можно вычислить, используя значения в единичном круге. Напомним, что мы использовали значения функций синуса и косинуса для вычисления функции тангенса.Мы будем следовать аналогичному процессу для обратных функций, ссылаясь на значения в единичном круге для наших расчетов.
Например, давайте найдем значение [latex] \ sec {\ left (\ frac {\ pi} {3} \ right)} [/ latex].
Применяя [latex] \ displaystyle {\ sec x = \ frac {1} {\ cos x}} [/ latex], мы можем переписать это как:
[латекс] \ displaystyle {\ sec {\ left (\ frac {\ pi} {3} \ right)} = \ frac {1} {\ cos {\ left ({\ frac {\ pi} {3}} \ right)}}} [/ латекс]
Из единичного круга мы знаем, что [латекс] \ displaystyle {\ cos {\ left ({\ frac {\ pi} {3}} \ right)} = \ frac {1} {2}} [/ latex] .Используя это, можно найти значение [latex] \ displaystyle {\ sec {\ left (\ frac {\ pi} {3} \ right)}} [/ latex]:
[латекс] \ displaystyle {\ begin {align} \ sec {\ left (\ frac {\ pi} {3} \ right)} & = \ frac {1} {\ frac {1} {2}} \\ & = 2 \ end {align}} [/ латекс]
Остальные взаимные функции могут быть решены аналогичным образом.
Пример
Используйте единичный круг для вычисления [латекс] \ sec t [/ latex], [latex] \ cot t [/ latex] и [latex] \ csc t [/ latex] в точке [latex] \ displaystyle {\ left (- \ frac {\ sqrt {3}} {2}, \ frac {1} {2} \ right)} [/ latex].
Точка на единичном круге: Точка [латекс] \ displaystyle {\ left (- \ frac {\ sqrt {3}} {2}, \ frac {1} {2} \ right)} [/ latex] , показанный в единичном круге.
Поскольку нам известны координаты [latex] (x, y) [/ latex] точки на единичной окружности, обозначенной углом [latex] t [/ latex], мы можем использовать эти координаты для нахождения трех функций.
Напомним, что координата [latex] x [/ latex] дает значение для функции косинуса, а координата [latex] y [/ latex] дает значение для функции синуса.Другими словами:
[латекс] \ displaystyle {\ begin {align} x & = \ cos t \\ & = — \ frac {\ sqrt {3}} {2} \ end {align}} [/ latex]
и
[латекс] \ displaystyle {\ begin {align} y & = \ sin t \\ & = \ frac {1} {2} \ end {align}} [/ latex]
Используя эту информацию, можно вычислить значения обратных функций под углом [латекс] t [/ латекс]:
[латекс] \ displaystyle {\ begin {align} \ sec t & = \ frac {1} {\ cos t} \\ & = \ frac {1} {x} \\ & = \ left (\ frac {1 } {- \ frac {\ sqrt {3}} {2}} \ right) \\ & = — \ frac {2} {\ sqrt {3}} \\ & = \ left (- \ frac {2} { \ sqrt {3}} \ cdot \ frac {\ sqrt {3}} {\ sqrt {3}} \ right) \\ & = — \ frac {2 \ sqrt {3}} {3} \ end {align} } [/ латекс]
[латекс] \ displaystyle {\ begin {align} \ cot t & = \ frac {\ cos t} {\ sin t} \\ & = \ frac {x} {y} \\ & = \ left (\ frac {- \ frac {\ sqrt {3}} {2}} {\ frac {1} {2}} \ right) \\ & = \ left (- \ frac {\ sqrt {3}} {2} \ cdot \ frac {2} {1} \ right) \\ & = — \ sqrt {3} \ end {align}} [/ latex]
[латекс] \ displaystyle {\ begin {align} \ csc t & = \ frac {1} {\ sin t} \\ & = \ frac {1} {y} \\ & = \ left (\ frac {1 } {\ frac {1} {2}} \ right) \\ & = 2 \ end {align}} [/ latex]
Обратные тригонометрические функции
У каждой тригонометрической функции есть обратная функция, которую можно изобразить в виде графика. {- 1} x = y [/ latex].{-1} [/ латекс]
Введение в обратные тригонометрические функции
Обратные тригонометрические функции используются для нахождения углов треугольника, если нам заданы длины сторон. Обратные тригонометрические функции могут использоваться, чтобы определить, какой угол даст определенное значение синуса, косинуса или тангенса.
Чтобы использовать обратные тригонометрические функции, мы должны понимать, что обратная тригонометрическая функция «отменяет» то, что «делает» исходная тригонометрическая функция, как и в случае с любой другой функцией и ее обратной.{-1} (б) = а [/ латекс]. Однако функции синуса, косинуса и тангенса — это , а не взаимно однозначные функции. График каждой функции не прошел бы тест горизонтальной линии. Фактически, никакая периодическая функция не может быть взаимно однозначной, потому что каждый выход в ее диапазоне соответствует по крайней мере одному входу в каждом периоде, а количество периодов бесконечно. Как и в случае с другими функциями, которые не являются взаимно однозначными, нам нужно будет ограничить область определения каждой функции, чтобы получить новую функцию, которая является взаимно однозначной. Мы выбираем домен для каждой функции, который включает число [latex] 0 [/ latex].
Функции синуса и косинуса в ограниченных областях: (a) Функция синуса, показанная в ограниченной области [latex] \ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ справа] [/ латекс]; (b) Функция косинуса, показанная в ограниченной области [latex] \ left [0, \ pi \ right] [/ latex].
График функции синуса ограничен областью [latex] [- \ frac {\ pi} {2}, \ frac {\ pi} {2}] [/ latex] и графиком функции косинуса ограничено [латексом] [0, \ pi] [/ латексом]. График касательной функции ограничен [latex] \ left (- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right) [/ latex].
Касательная функция в ограниченной области
Функция касательной, показанная в ограниченной области [latex] \ left (- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right) [/ latex].
Эти варианты выбора ограниченных доменов в некоторой степени произвольны, но они имеют важные полезные характеристики. Каждый домен включает начало координат и некоторые положительные значения, и, что наиболее важно, каждый результат дает взаимно однозначную обратимую функцию. Обычный выбор для ограниченной области касательной функции также имеет то полезное свойство, что он распространяется от одной вертикальной асимптоты к другой, вместо того, чтобы разбиваться на части асимптотой.{-1} x \ quad \ text {имеет домен} \ quad \ left (- \ infty, \ infty \ right) \ quad \ text {и диапазон} \ quad \ left (- \ frac {\ pi} {2} , \ frac {\ pi} {2} \ right)} [/ latex]
Графики обратных тригонометрических функций
Функция синуса и функция обратного синуса (или арксинуса): функция арксинуса является отражением функции синуса относительно линии [latex] y = x [/ latex].
Чтобы найти область определения и диапазон обратных тригонометрических функций, мы меняем область определения и диапазон исходных функций.
Функция косинуса и функция обратного косинуса (или арккосинуса): Функция арккосинуса является отражением функции косинуса относительно линии [latex] y = x [/ latex].
Каждый график обратной тригонометрической функции является отражением графика исходной функции относительно линии [латекс] y = x [/ latex].
Функция тангенса и функция арктангенса (или арктангенса): Функция арктангенса является отражением функции касательной относительно линии [latex] y = x [/ latex].{-1} х = у [/ латекс].
% PDF-1.3 % 8 0 объект > эндобдж xref 8 79 0000000016 00000 н. 0000001924 00000 н. 0000002076 00000 н. 0000002105 00000 н. 0000002183 00000 п. 0000002582 00000 н. 0000002819 00000 н. 0000002848 00000 н. 0000003034 00000 н. 0000003196 00000 н. 0000003285 00000 н. 0000003937 00000 н. 0000004133 00000 п. 0000004542 00000 н. 0000004722 00000 н. 0000004744 00000 н. 0000010847 00000 п. 0000010869 00000 п. 0000016796 00000 п. 0000016818 00000 п. 0000022809 00000 п. 0000022831 00000 п. 0000028850 00000 п. 0000028872 00000 п. 0000035280 00000 п. 0000035302 00000 п. 0000035499 00000 н. 0000035802 00000 п. 0000035993 00000 п. 0000036103 00000 п. 0000036211 00000 п. 0000036532 00000 п. 0000036939 00000 п. 0000037379 00000 п. 0000037569 00000 п. 0000037960 00000 п. 0000038160 00000 п. 0000039418 00000 п. 0000039624 00000 н. 0000039779 00000 п. 0000045905 00000 п. 0000045927 00000 п. 0000052042 00000 п. 0000052065 00000 п. 0000062851 00000 п. 0000166043 00000 н. 0000166184 00000 н. 0000166325 00000 н. 0000166472 00000 н. 0000166619 00000 н. 0000166763 00000 н. 0000166907 00000 н. 0000167054 00000 н. 0000167201 00000 н. 0000167345 00000 н. 0000167489 00000 н. 0000167632 00000 н. 0000167775 00000 н. 0000168491 00000 н. 0000168638 00000 н. 0000168778 00000 н. 0000168918 00000 н. 0000169059 00000 н. 0000169202 00000 н. XX0 \ aaPt 4o_Kd & / 0_` | A _} / oʀ ** 0>
Углы квадранта До сих пор мы находили тригонометрическое функциональное значение некоторого угла в стандартной позиция, заданная некоторой точкой ( x , y ) на конечном луче.Теперь мы найдем значения тригонометрических функций для некоторых особых углов. Начнем с квадранта. углы.
Примеры квадрантных углов: 0, π / 2, π и 3π / 2. Уголки совпадающие с этими углами, конечно, тоже квадрантальны.Мы заинтересованы в поиске шести тригонометрических функциональных значений этих особых углов, и мы начнем с θ = 0. Поскольку любая точка ( x , y ) на конечном луче угла с мерой 0 имеет координату y , равную 0, мы знаем, что r = | x |, а у нас Используя аналогичный подход, мы можем найти шесть тригонометрических функциональных значений для Тригонометрические функциональные значения углов, совпадающих с 0, π / 2, π и 3π / 2 одинаковы как указано выше, и тригонометрические функциональные значения повторяются (например,g., π и 3π являются концевыми и sin (π) = sin (π + 2π) = sin (3π) = 0). Это иллюстрирует Дело в том, что тригонометрические функции периодичны. Мы обсудим это более подробно в следующий раздел. Прямоугольники Чтобы найти тригонометрические функциональные значения других специальных углов, мы переопределим шесть тригонометрические функции относительно угла прямоугольного треугольника.Рассмотрим следующие прямоугольный треугольник, Мы можем найти тригонометрические функциональные значения, используя следующие определения: , где adj, opp и hyp — короткие для стороны, прилегающей к θ , противоположной стороны θ , и гипотенуза соответственно. Вы должны убедиться, что эти новые определения последовательны. с предыдущими.Теперь рассмотрим следующий треугольник 30 ° — 60 ° — 90 °: Может быть полезно вспомнить теорему Пифагора, a 2 + b 2 = c 2 , , где a и b — катеты прямоугольного треугольника, а c — гипотенуза. С помощью выше определения тригонометрических функций, мы можем вычислить значения тригонометрических функций из θ = π / 6 (30 °) и θ = π / 3 (60 °) ас, Теперь мы найдем тригонометрические функциональные значения другого особого угла, треугольника 45 ° -45 ° -90 °, как показано на рисунке. на следующем рисунке: Используя приведенный выше треугольник, мы находим шесть тригонометрических функциональных значений: θ = π / 4 (т.е. 45 °) как, Другие специальные уголки Мы также можем найти точные тригонометрические функциональные значения некоторых других углов, которые связаны до углов θ = π / 6, θ = π / 4 и θ = π / 3 определенными способами. Чтобы посмотреть на этих других углов, мы вводим понятие опорного угла , , обозначенного как θ ‘. Вычислить опорный угол для угла с отрицательной мерой, найдите первый положительный котерминальный угол.Чтобы найти опорный угол для угла больше 360 °, найдите котерминальный угол между 0 ° и 360 °. Как только у вас есть угол θ при 0 ° ≤ θ ≤ 360 °, вы можете найти его опорный угол следующим образом:
Опорный угол используется для нахождения точных тригонометрических функциональных значений углов, которые заканчиваются за пределами первого квадранта.В частности, верно, что | триггерный ( θ ) | знак равно триггерный ( θ ‘), , где тригонометрия обозначает одну из шести тригонометрических функций. Например, предположим мы хотим найти грех (7π / 6). Сначала преобразуйте 7π / 6 радиан в градусы, так как у нас есть больше интуиции о степени меры. Поскольку 7π / 6 радиан — это то же самое, что 210 °, мы пытаются найти sin (210 °), где θ = 210 ° находится в квадранте III.Таким образом, θ ‘= 210 ° -180 ° = 30 °, где θ ‘ — опорный угол (специальный угол). Поскольку грех (30 °) = грех (π / 6) = 1 / 2, мы знаем, что грех (210 °) = грех (7π / 6) либо равно 1/2, либо -1/2. Чтобы определить, какие Во-первых, мы спрашиваем себя, является ли функция синуса положительной или отрицательной в квадранте III? Чтобы ответить на этот вопрос, напомним определение sin θ , грех θ = л / р . Поскольку координата y точки в квадранте III отрицательна, а r определяется как быть положительным, sin θ (где θ лежит в квадранте III) должен быть отрицательным. Поэтому мы сделать вывод, что,
***** В следующем разделе мы исследуем графики тригонометрических функции. Графические тригонометрические функции |
Калькулятор — cos (2 * pi / 3) — Solumaths
Сводка:
Тригонометрическая функция cos вычисляет косинус угла в радианах, градусы или градианы.
потому что онлайнОписание:
Калькулятор позволяет использовать большинство тригонометрических функций , можно вычислить косинус , синус и касательная угла через одноименные функции ..
Тригонометрическая функция косинус отмечен cos , позволяет вычислить косинус угла онлайн , можно использовать разные угловые единицы: градусы, градианы и радианы, которые являются угловыми единицами по умолчанию.
- Расчет косинуса
- Специальные значения косинуса
Косинус для вычисления угла в радианах
Калькулятор косинуса позволяет через функцию cos вычислить онлайн косинус угла в радианах, сначала необходимо выберите желаемую единицу измерения, нажав кнопку параметров модуля расчета. После этого можно приступать к расчетам.
Чтобы вычислить косинус онлайн числа «пи / 6», введите cos (`pi / 6`), после вычисления результат sqrt (3) / 2 возвращается.
Обратите внимание, что функция косинуса способна распознавать некоторые особые углы и делать расчеты со специальными связанными значениями в точной форме.
Вычислить косинус угла в градусах
Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать нужную единицу щелкнув по кнопке опций модуля расчета. После этого вы можете приступить к расчету.
Чтобы вычислить косинус 90, введите cos (90), после вычисления restults 0 возвращается.
Вычислить косинус угла в градусах
Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать желаемую единицу измерения. щелкнув по кнопке опций модуля расчета. После этого вы можете приступить к расчету.
Чтобы вычислить косинус 50, введите cos (50), после вычисления возвращается результат sqrt (2) / 2.
Обратите внимание, что функция косинуса способна распознавать некоторые особые углы и выполнять исчисление со специальными связанными точными значениями.
Косинус допускает некоторые особые значения, которые калькулятор может определять в точной форме. Вот список специальные значения косинуса :
Производная косинуса равна -sin (x).
Первообразная косинуса равна sin (x).
Функция косинуса является четной функцией для каждого действительного x: `cos (-x) = cos (x)`. Следствием для кривой, представляющей функцию косинуса, является то, что она допускает ось ординат как ось симметрии.
В калькуляторе есть решающая программа, позволяющая решать уравнение с косинусом вида cos (x) = a .Расчеты для получения результата детализированы, поэтому можно будет решить такие уравнения, как `cos (x) = 1 / 2` или же `2 * cos (x) = sqrt (2)` с шагами расчета.
Тригонометрическая функция cos вычисляет косинус угла в радианах, градусы или градианы.
Синтаксис:
cos (x), где x — мера угла в градусах, радианах или градианах.Примеры:
cos (`0`), возвращает 1Производный косинус:
Чтобы дифференцировать функцию косинуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции косинуса
Производная от cos (x) — это производная_вычислителя (`cos (x)`) = `-sin (x)`
Первоначальный косинус:
Калькулятор первообразной функции косинуса позволяет вычислить первообразную.
Первообразная от cos (x) — это первообразная_вычислителя (`cos (x)`) = `sin (x)`
Предельный косинус:
Калькулятор пределов позволяет вычислить пределы функции косинуса.
Предел для cos (x) равен limit_calculator (`cos (x)`)
Косинус обратной функции:
Функция , обратная косинусу , — это функция арккосинуса, отмеченная как arccos.
Графический косинус:
Графический калькулятор может строить функцию косинуса в интервале ее определения.
Свойство функции косинус:
Функция косинуса является четной функцией.Рассчитать онлайн с cos (косинусом)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решения практических задач (Триггер без слез)
Решения практических задач (Триггер без слез)Триггер без слез:
Авторские права 19972020 Стэн Браун, BrownMath.com
Решения для части 1: Введение
1 Найдите эти углы в градусах: (а) π / 6; (б) 2π; (c) 1 (это верно, радианные углы не обязательно дроби или кратные π).Решения :
(а) (π / 6) × (180 / π) = 30
(б) 2π × (180 / π) = 360
(в) 1 × (180 / π) = (180 / π) ≈ 57,3
2 Какое правильное определение острого угла в интервале обозначения?(а) (0, 90) (б) [0, 90]
Ответ : (0, 90) от 0 до 90 градусов за исключением 0 и 90; [0, 90] равно от 0 до 90 градусов , включая 0 и 90.Острые углы от 0 до 90 исключая , поэтому ответ (а) (0, 90).
3 Два угла треугольника — 80 и 40. Третий угол точен.Решение : внутренние углы треугольник всегда должен прибавлять к 180. 80 + 40 = 120, поэтому, чтобы сделать полные 180, третий угол должен быть 60.
4 Треугольник имеет угол 90. Две короткие стороны (рядом с этим угол) равны 5 и 12. Найдите третью сторону.Решение : Подскажите теорему Пифагора!
c = a + b
c = 5 + 12
c = 25 + 144 = 169
c = √169 = 13
5 Найдите эти углы в радианах: (а) 60 (б) 126; (в) 45.По возможности дайте точный ответ, а не десятичную дробь. приближение.
Решения :
(а) 60 + (π / 180) = π / 3.
(б) 126 × (π / 180) ≈ 2.20
(в) 45 × (π / 180) = π / 4
Обратите внимание, что вам не нужно говорить радианы, когда давая угол в радианах, хотя это было бы неправильно. В этой книге углы в градусах помечены знаком градуса (), поэтому Я скажу радианы только тогда, когда это необходимо Во избежание путаницы.
6 Кто сказал: сумма квадратных корней любых двух сторон равнобедренный треугольник равен квадратному корню из оставшихся боковая сторона? Это верно?Ответ : Это было Пугало в фильме Волшебник Оз (1939).И нет, это звучит глупо, но это чушь. Это не может быть верным для любого треугольника , равнобедренного или нет. (Вы понимаете, почему?)
7 На круглом циферблате, цифры которого являются границами каждого квадрант?Ответы : Квадрант I: 12 и 3; Квадрант II: 9 и 12; Квадрант III: 6 и 9; Квадрант IV: 3 и 6.
Решения для части 2: Шесть функций
1 Найдите все шесть функций угла 30. Найдите синус, косинус, и тангенс 60.Решение : Во-первых, вам нужна длина горизонтального боковая сторона.Вы помните теорему Пифагора: 1 + b = 2, откуда вы получаем b = √3. После этого это просто вопрос запоминания определений. Если вам нужно освежиться, вы найдете синус и косинус в уравнении 1, касательную в уравнение 4, а остальные — в уравнении 5.
грех 30 = 1/2
cos 30 = √3 / 2
загар 30 = 1 / √3 или √3 / 3
детская кроватка 30 = 1 / (1 / √3) = √3
сек 30 = 1 / (√3 / 2) = 2 / √3 или (2 √3) / 3
csc 30 = 1 / (1/2) = 2
грех 60 = √3 / 2
cos 60 = 1/2
загар 60 = √3 / 1 = √3
Поскольку 60 = 90 — 30, обратите внимание, что грех 60 = соз 30, соз 60 = грех 30 и загар 60 = детская кроватка 30.
2 Найдите sin A , sin B , tan A и tan B .Решение :
sin A = 3/5 или 0,6
sin B = 4/5 или 0,8
коричневый A = 3/4 или 0,75
загар B = 4/3 ≈ 1,33
Между прочим, A ≈ 36,87, а B ≈ 53,13.
3 A ≈ 53,13. Найдите примерную площадь треугольник. Подсказка: площадь треугольника равна основание × высота /2.Решение : У вас есть основание (5), поэтому вам просто нужна высота. Но sin A = h /3, поэтому h = 3 × sin А . Таким образом, площадь (5 × 3 × sin A ) / 2 ≈ 5,99999.
Решения для части 3: Функции специальных углов
1 (a) Нарисуйте треугольник 45-45-90 с гипотенузой 1. Обозначьте размер каждого угла и точную длину каждой стороны, а не калькулятор аппроксимации. (Подсказка: поскольку два острых угла равны, две короткие стороны должны быть равны.Это и теорема Пифагора достаточно, чтобы вы могли их найти.)(b) Нарисуйте треугольник, все стороны которого равны 1. Если все стороны равны, все углы должны быть равны. Зная, что они добавляют к 180, введите значение каждого угла. Теперь опустите перпендикуляр от вершины треугольника до середины противоположной стороны. Ты теперь есть два треугольника 30-60-90 с гипотенузой 1. Заполните точные длины коротких сторон этих двух треугольников.
Для решения остальных проблем обратитесь к этим эскизам. Если вам нужно. Дайте точные ответы, а не десятичные дроби.
Решение : Сравните свои наброски с теми, что в глава.
2 Найдите tan 45, cos 45, sin 90, cos 30, грех 30, cos 90.Ответы : загар 45 = 1; cos 45 = 1 / √2 или √2 / 2; грех 90 = 1; cos 30 = √3 / 2; грех 30 = 1/2; cos 90 = 0.
3 Найдите sin (π / 4), cos (π / 6), tan (π / 3).Ответы : sin (π / 4) = √2 / 2 или 1 / √2; соз (π / 6) = √3 / 2; загар (π / 3) = √3
4 Найдите каждый из следующих углов от подсказок, предполагая, что все углы составляют от 0 до π / 2 (от 0 до 90) включительно.Дайте каждый ответ в градусах и радианах. sin A = 0; cos B = √3 / 2; sin C = 1/2; sin D = 1; tan E = 1; cos F = 1/2; tan G = 0; загар H = √3; cos I = 1; cos Дж = 0.Ответы :
sin A = 0 ⇒ A = 0 или 0 [радиан]
cos B = √3 / 2 ⇒ B = 30 или π / 6
sin C = 1/2 ⇒ C = 30 или π / 6
sin D = 1 ⇒ D = 90 или π / 2
загар E = 1 ⇒ E = 45 или π / 4
cos F = 1/2 ⇒ F = 60 или π / 3
загар G = 0 ⇒ G = 0 или 0 [радиан]
загар H = √3 ⇒ H = 60 или π / 3
cos I = 1 ⇒ I = 0 или 0 [радиан]
cos Дж = 0 ⇒ Дж = 90 или π / 2
5 Найдите сек 60 и детскую кроватку 30.Подсказка: помните, как секанс и котангенс определяются в терминах большие три функции: синус, косинус и тангенс.Решения : сек 60 = 1 / (cos 60) = 1 / (1/2) ⇒ сек 60 = 2
детская кроватка 30 = 1 / (загар 30) = 1 / (√3 / 3) = 3 / √3 = √3 ⇒ детская кроватка 30 = √3
Вы также можете выполнить второй, используя уравнение 6:
детская кроватка 30 = загар (90-30) = загар 60 = √3
6 Найдите sin 120, cos 120 и tan 120.Решение:
грех 120 = грех (180 — 120) = √3 / 2.
cos 120 = −cos (180 — 120) = −1/2.
А как насчет касательной? У вас нет правила о добавках для этого, но у вас есть другой способ найти ответ:
загар 120 = грех 120 / соз 120 = (√3 / 2) / (-1/2) = −√3
7 Несмотря на то, что вы всегда можете получить дополнительный угол от синуса и косинуса, вы сэкономите время, если будете иметь правило для дополнения касательной. Решение последних проблем предположил, что это за правило.Доказательство: загар (180 — A ) = −tan А .
Проба:
желто-коричневый (180 — A ) = sin (180 — A ) / cos (180 — A )
желто-коричневый (180 — A ) = sin A / (−cos A )
желто-коричневый (180 — A ) = −sin A / cos A
желто-коричневый (180 — A ) = −tan A QED
8 Найдите загар 150.Решение: загар 150 = −tan (180 — 150) = −tan 30 = −√3 / 3
Решения для части 4: Решение треугольников
1 У вас есть прямоугольный треугольник ( C = 90) с короткие стороны a = 88 и b = 37.Решите треугольник.Всегда начинайте с эскиза. На эскизе справа видно прочь, что это случай с SAS, или сторона-угол-сторона. Чтобы получить третью сторону, вам нужен закон косинусов, уравнение 31.
c = a + b — 2 a b × cos C
c = 37 + 88 — 2 × 37 × 88 × cos 90
Обратите внимание на то, что, когда включенный угол C равен 90, cos C = 0, и вы только что получили пифагорейский Теорема.
c = 37 + 88
c = √37 + 88
c ≈ 95,5
Чтобы найти два угла, вы можете использовать Закон синуса, но почему бы не взять Преимущество прямого угла и использования тангенса?
загар A = 37/88 ⇒ A ≈ 22,8
Конечно, загар B = 88/37, но вы также знаете, что
A + B = 90 ⇒ B = 90 — A ⇒ В ≈ 67.2
2 (Нарисуйте эту проблему, когда будете ее читать.) В государственном парке река течет практически прямо к 1800 м. Вы хотите построить монорельс из A , один конец этот участок до точки C на дальнем берегу. Вы также хотите построить пешеходный мост от B , на другом конце этого участка реки, до той же точки C на дальнем берегу. На A угол между линиями обзора к B и C — 67.У B угол между вашим прицелом линии на A и C — 38.Какой длины должны быть монорельс и пешеходный мост?
Бонусный вопрос: если река имеет одинаковую ширину на всем протяжении протянуть от A до B , насколько он широкий?
На эскизе b — монорельс, a — подножка. мост, а w ширина реки. Поскольку вы знаете два углы и включенная сторона, это случай ASA.Хотя ты не особо заботьтесь об угле C , вы должны его найти так что вы можете использовать закон синусов, чтобы получить стороны a и b :
С = 180 — 67 — 38 = 75
Очевидно, когда я смотрел на углы A и B Я не очень их оценил! Но это хорошо, набросок достаточно близок, чтобы быть полезным.
Какова длина пешеходного моста? От Закон синуса,
a / sin A = c / sin C ⇒ a = c sin A / sin C
a = 1800 × грех 67 / грех 75
Пешеходный мост: a ≈ 1715 м
Какова длина монорельса? От Закон синуса,
b / sin B = c / sin C ⇒ b = c sin B / sin C
б = 1800 × грех 38 / грех 75
Монорельс: b ≈ 1147 м
Насколько широка река?
w = b sin A
w ≈ 1147 sin 67
Ширина реки: w ≈ 1056 м
3 Найдите другие элементы треугольника с B = 117, a = 16 см и b = 25 см.Это случай SSA (или ASS); обратитесь к таблица возможностей для SSA. Эта проблема принадлежит строке 1, столбцу 2: противоположная сторона длиннее, чем соседняя сторона, и известный угол> 90. Итак, есть одно-единственное решение.
Вы можете использовать закон синусов, чтобы найти угол A :
(sin A ) / a = (sin B ) / b
sin A = ( a / b ) sin B
sin A = (16/25) sin 117 ≈ 0.57024
A ≈ 34,8
Найдите третий угол, вычтя:
С = 180 — А — В
С ≈ 180 — 34,8 — 117
C ≈ 28,2
Наконец, используйте закон синуса, чтобы найти сторону с :
c / sin C = b / sin B
c = b sin C / sin B
c ≈ 25 sin 28.2 / грех 117
c ≈ 13,3 см
4 Очень современно выглядящая подставка представляет собой треугольную форму со сторонами 6 дюймов, 9 дюймов и 12 дюймов. Какие три угла?Это случай SSS. Во-первых, используйте Закон косинусов для определения угла A:
cos A = ( b + c — a ) / 2 b c
cos A = (9 + 12-6) / (2 × 9 × 12) = 0,875
A ≈ 29,0
Затем используйте закон синусов, чтобы найти угол B :
(sin B ) / b = (sin A ) / a ⇒ sin B = ( b / a ) sin A
sin B ≈ (9/6) sin 29.0 ≈ 0,72618
B ≈ 46,6
Наконец, вычтите два угла из 180, чтобы найти третий угол:
C = 180 — 915 12 A — B
C ≈ 180 — 29,0 — 46,6
C ≈ 104,5
Кстати, это не опечатка. A и B оба оказались округленными, но я использовал неокругленные значения, чтобы найти С . Вы никогда не должны использовать округленные числа в дальнейшем расчеты.
5После того, как вы покрасили спальню, у вас будет достаточно краски осталось, чтобы покрыть 25 футов. Вы решаете нарисовать треугольник на стене другой комнаты, как акцент. Два угла должны быть 30 и 40. Найдите третий угол и длину с трех сторон.Третий угол 180-30-40, поэтому С = 110. Сделайте свой набросок, используя эти три угла. (Я сделал это без Измерение углов, так что это не идеально. Но зарисовки не обязательно быть идеальным, просто достаточно близким.)
Найдите сторону c по уравнению 32:
с = √2 площадь × sin C / (sin A sin B )
с = √2 × 25 × sin 110 / (sin 30 sin 40)
c ≈ 12,1 футов
Тогда закон синуса дает вам другое с двух сторон:
a = c sin A / sin C
a ≈ 12,1 sin 30 / sin 110
a ≈ 6.4 фута
и
b = c sin B / sin C
b ≈ 12,1 sin 40 / sin 110
b ≈ 8,3 фут
6 Вы проезжаете 6,0 миль по прямому шоссе, затем съезжаете на съезд. Поворот направо, но угла не замечаешь.Вы едете по прямой проселочной дороге. Пройдя 9,8 миль по проселочной дороге, вы повернете 135 на правильно, на третьей дороге. (Если вы визуализируете это сверху, изменение направления на 135 соответствует углу 180 — 135 = 45 в треугольнике.)
Если предположить, что дорога идет в том же направлении, как далеко? вы должны ехать, чтобы добраться до отправной точки?
Этот набросок сложно нарисовать, потому что вы не знаете угол первого поворота. Но описание дает вам две стороны и невключенный угол; это проблемный случай SSA. Вы не знаете, где именно сторона c будет соответствовать стороне a . Если быть более точным, вы даже не знаю , встретятся ли .
Могут ли они встретиться? Ссылаясь на таблица возможностей в SSA, мы видим, что были в третьем ряду, первом столбце: соседний сторона (9.8) длиннее противоположной стороны (6.0), а известный угол (45) <90. Вычислить
h = b sin A
h = 9,8 sin 45 ≈ 6.9 миль
Что это значит? Кратчайшее расстояние от точки C до стороны c — это отрезок, который соответствует сторона c под прямым углом. Другими словами, чтобы получить от точки C к стороне c , кратчайшее возможное расстояние 6.9 миль. Но сторона у всего 6,0 миль в длину, так что она может никогда не встречал стороны c .
Эта проблема не имеет решения.
Вы выкладываете треугольную грядку для своего сада. Две стороны 40 м и 60 м, а угол между ними равен 22. Какова длина третьей стороны и какие две другие? углы?Вы знаете две стороны и угол между ними. Вы можете использовать Закон косинусов для получения третьей стороны:
a = b + c — 2 b c × cos A
a = 60 + 40 — 2 × 60 × 40 × cos 22
c ≈ √749.52 ⇒ c ≈ 27,4 м
Далее, для угла B можно использовать Закон синуса:
(sin B ) / b = (sin A ) / a ⇒ sin B = (б / а) sin A
sin B ≈ (60 / 27,4) sin 22 ≈ 0,82099
Ваш калькулятор дает около 55,2 как угол, синус которого равен 0.82099, но это выглядит не так с эскиза. Очевидно, что B должен быть тупым углом, так что помните что грех (180 — х ) = грех х , и вы вычитаете 180 — 55.2, чтобы получить
B ≈ 124,8
Видите, насколько важен эскиз? Конечно твой скетч наверное не совсем точен, поэтому вы относитесь к нему как к способу указать что-то может быть неправильным, но тогда вы ищите способ подтвердить это. В этом случае у вас есть два способа подтвердить it:
- Вы можете использовать Закон косинусов, который автоматически
учитывает тупые углы:
cos B = ( a + c — b ) / (2 a c )
cos B ≈ (27.4 + 40 — 60) / (2 × 27,4 × 40)
cos B ≈ −0,57095 ⇒ B ≈ 124,8
- Или вы можете вычислить угол C (ниже), а затем вспомнить этот угол C должно быть < B , потому что сторона c — < b . Если вы сделали C тупой, 180 — 33,2 = 146,8, было бы > B независимо от того, является ли B острым или тупым. Так C должно быть <90 и B должно быть > 90.
Теперь поверните на угол C:
(sin C ) / c = (sin A ) / a ⇒ sin C = (c / a) sin A
sin C ≈ (40 / 27,4) sin 22 ≈ 0,54732
C ≈ 33,2
Решения для Части 5: Функции под любым углом
1 В каком квадранте находится угол -868? Как насчет 42 радиана? Каковы знаки их синусов, косинусов и касательных?Решение: Твоя задача всегда — изгнать кратные 360 или 2π, чтобы вы оставались с положительным углом от 0 до 360 (от 0 до 2π).
−868 = −1080 + 212. И 212 находится между 180 и 270, так что −868 встречается в Q III.
42 радиана составляет около 13,37π, или 12π + 1,37π. 1,37π, очевидно, находится между π и 3π / 2 (1.5π), поэтому 42 (радианы) находится в III квартале.
В третьем квартале x и y отрицательны. Следовательно В Q III синус и косинус отрицательны, а тангенс положительна.
2 Перепишите, используя наименьший возможный положительный угол та же триггерная функция: (а) грех 700 (б) загар 780 (c) cos (−390.5) (Вот это радиан, так как градуса нет, но будьте осторожны! Угол равно -390,5, а не -390,5π.)Решение: (a) 700 = 360 + 340, поэтому грех 700 = грех 340. 340 в Q IV, где y отрицательно; следовательно, синус отрицательный. Базовый угол равен 20, поэтому грех 700 = −sin 20.
(б) 780 = 720 + 60, поэтому загар 780 = загар 60.
(в) −390,5 ≈ −124,3π, или −126π + 1,7π; следовательно cos (-390,5) ≈ cos 1,7π. Угол 1,7π радиан находится между 1,5π и 2π, поэтому в Q IV, где x положительно и, следовательно, косинус равен положительный.Базовый угол составляет около 2π — 1,7π ≈ 0,3π или 0,94, поэтому cos (-390,5) ≈ cos 0,94.
3 Перепишите как функцию всего A : (а) cos (720 — A ) (б) грех (43π + A )Решение: (а) 720 делится на 360, поэтому cos (720 — A ) = cos (- A ). Но cos (- A ) = cos A , и поэтому cos (720 — A ) = cos A .
(б) sin (43π + A ) = грех (42π + π + A ) = sin (π + A ).sin (π + A ) = −sin A , поэтому sin (43π + A ) = −sin A .
Решения для части 6: Квадратные идентичности
1 Если sin A = 3/4, найдите cos A .Решение :
sin² A + cos² A = 1
cos² A = 1 — sin² A = 1 — (3/4) = 1 — 9/16
cos² A = 7/16
cos А = √7 / 16 ⇒ cos A = √7 / 4 или −√7 / 4
Вы помните знак? Как только x = 9 имеет два решения, 3 и −3, поэтому любое уравнение в cos² A имеет два решения.
Это имеет смысл с точки зрения функций. Есть два углы в интервале [0, 2π) или [0, 360) где sin A = 3/4, один острый и один тупой. В острый имеет положительный косинус, а тупой — отрицательный. косинус.
2 tan B = −2√2. Найдите sec B .Решение : Поскольку эта глава посвящена в квадрате личности, вы можете быть уверены, что она существует который соединяет tan x и sec x .Но предположим, вы встретили это проблема в другом контексте?
Ну, вы знаете два тождества с касательной функцией. Определение tan B = (sin B ) / cos B , не много ли вам добра, потому что в нем смешаны синус и косинус все вместе. У вас смутные воспоминания о квадратной идентичности (если вы как и я, он тусклый), но вы также знаете, что можете воссоздать его легко, с одного личность в квадрате, которую невозможно забыть:
sin² B + cos² B = 1
У вас есть sin² B , который станет tan² B , если вы разделите обе стороны на cos² B .
(sin² B ) / cos² B + (cos² B ) / cos² B = 1 / cos² B
tan² B + 1 = sec² B
Успех! У вас есть личность, которая связывает касательную и секущие функции. Теперь можно переходить к решению проблемы.
(−2√2) + 1 = сек² B
сек² B = (4 × 2) + 1 = 9
сек B = 3
Знак вам нужен, потому что оба ( x ) и (- x ) равны x .Но делает это имеет смысл с точки зрения триггера? Да, потому что касательная отрицательна в Q II и Q IV, а секущая, имеющая то же знак как косинус, 1 по косинусу положительна в Q IV, но отрицательный в Q II.
3 загар С = √15. Найдите cos C .Решение : Подождите, что? У тебя нет тождество, соединяющее тангенс и косинус. Но у вас есть соединяя касательную и секанс, и вы знаете, что секанс на 1 больше косинус, так что вы тоже можете сделать это.
Начните с квадрата идентичности из предыдущей задачи:
tan² C + 1 = sec² C
(√15) + 1 = 15 + 1 = 16 ⇒ сек² C = 16
сек C = 4 ⇒ cos C = 1/4
4 tan D = √15, Найти sin D .Решение : Хорошо, в предыдущей задаче вы получили касательная к косинусу. Но вы уже знаете, как перейти от косинуса к синус, так что у вас есть еще одно звено в цепочке.
tan² D + 1 = sec² D
сек² D = (√15) + 1 = 16
сек D = 4 ⇒ cos D = 1/4
sin² D + cos² D = 1
sin² D = 1 — cos² D = 1 — (1/4) = 1 — 1/16 = 15/16
sin D = √15 / 4
5 Докажите: sin² x = tan² x / (tan² x + 1)Предполагается, что x ≠ π / 2 + k π, для целого числа к или 90 + 180 к , если вы предпочитаю, потому что касательная для этих углов не определена.
Проба :
желто-коричневый x = коричневый x
загар x cos x = загар x cos x
sin x = коричневый x / сек x
sin² x = tan² x / сек² x
But tan² x + 1 = sec² x , поэтому замена у вас
sin² x = tan² x / (tan² x + 1) QED
Возможны многие другие доказательства.Например, вы можете заменить tan² x с sin² x / cos² x в личность вас попросили доказать, а затем упростить дробь. Пока каждый шаг вашего доказательства действителен как в обратном, так и в обратном направлении. вперед, ваше доказательство в порядке.
Если ваше доказательство начинается с очевидной идентичности, а затем работает вперед к личности, которую мы попросили доказать, как и вышеприведенное доказательство, тогда имеет значение только то, что все шаги действительны в этом форварде направление.
Решения для части 7: формулы суммы и разности
1 Точно найдите sin (−15).Решение: Начать с −15 = 30-45
грех (-15) = грех (30−45)
грех (-15) = грех 30 соз 45 — cos 30 sin 45
грех (-15) = (1/2) (√2 / 2) — (√3 / 2) (√2 / 2) = √2 / 4 — √6 / 4
грех (-15) = (√2 — √6) / 4
Альтернативное решение: Вы также можете сделать это, используя 45-60:
грех (-15) = грех (45-60)
грех (-15) = грех 45 cos 60 — cos 45 sin 60
грех (-15) = (√2 / 2) (1/2) — (√2 / 2) (√3 / 2) = √2 / 4 — √6 / 4 = (√2 — √6) / 4
2 Найдите загар 105 точно.Решение: 105 = 60 + 45
загар 105 = загар (60 + 45)
загар 105 = (загар 60 + загар 45) / (1 — загар 60 загар 45)
загар 105 = (√3 + 1) / (1 — (√3) (1)) = (√3 + 1) / (1 — √3)
Умножить верхнюю и нижнюю на 1 + √3, чтобы получить рационализировать знаменатель:
загар 105 = (√3 + 1) / ((1 — √3) (1 + √3))
загар 105 = (3 + 2√3 + 1) / (1-3) = (4 + 2√3) / (- 2) = −2 — √3
3 Докажите: cos 2 A = 2 cos² A — 1. (Подсказка: 2 A = A + A .)Проба:
cos 2 A = cos ( A + A )
cos 2 A = cos A cos A — sin A sin A
cos 2 A = cos² A — sin² A
Но sin² A = 1 — cos² A
cos 2 A = cos² A — (1 — cos² A ) = cos² A — 1 + cos² A
cos 2 A = 2 cos² A — 1 QED
4 Докажите эти формулы из уравнения 22, используя формулы для функций суммы и разности.(а) cos (- A ) = cos A (Я сделал за вас первый шаг.)
cos (- A ) = cos (0 — А )
cos (- A ) = cos 0 cos A + sin 0 sin A
cos (- A ) = 1 cos A + 0 sin A
cos (- A ) = cos A QED
(б) tan (π + A ) = tan A
загар (π + A ) = (загар π + загар A ) / (1 — загар π загар A )
загар (π + A ) = (0 + загар A ) / (1-0 загар A )
загар (π + A ) = (загар A ) / 1
загар (π + A ) = желто-коричневый A QED
(c) sin (π — A ) = sin A
грех (π — A ) = sin π cos A — cos π sin A
грех (π — A ) = 0 cos A — (−1) sin A
грех (π — A ) = грех A QED
Решения для Части 8: Формулы двойного и половинного угла
1 Используйте формулы половинного угла, чтобы найти sin 90 и cos 90.Конечно, вы их уже знаете; эта проблема просто для практики в работе с формулами и легкими числами.Решение: : 90 — половина 180. Синус и косинус равны положительный или ноль на 90, поэтому знаки в формулах можно рассматривать как положительный.
грех (180/2) = √ (1 — cos 180) / 2 = √ (1 — (−1)) / 2 = √2 / 2
грех 90 = 1
cos (180/2) = √ (1 + cos 180) / 2 = √ (1 + (−1)) / 2 = √0 / 2
cos 90 = 0
Почему я не просил вас сделать то же самое для загар 90?
2 Воспользуйтесь формулами двойного угла, чтобы найти sin 120, cos 120, а tan 120 точно.Опять же, ты уже знать это; Вы только начинаете знакомиться с формулами.Решение: 120 — это двойное 60. sin 60 = √3 / 2, cos 60 = 1/2 и загар 60 = √3.
грех (260) = 2 sin 60 cos 60 = 2 (√3 / 2) (1/2)
грех 120 = (√3) / 2
cos (260) = 2 cos² 60 — 1 = 2 × (1/2) — 1 = (1/2) — 1
cos 120 = -1/2
загар (260) = 2 загар 60 / (1 — загар² 60) = 2 √3 / (1 — (√3)) = 2 √3 / (1-3) = 2 √3 / (−2)
загар 120 = −√3
Альтернативное решение: Вы также можете разделить:
загар 120 = грех 120 / соз 120 = (√3 / 2) / (-1/2) = −√3
3 3 A = 2 A + A .Используйте формулы двойного угла вместе с формулы для синуса или косинуса суммы, чтобы найти формулы для sin 3 A только в терминах sin A , и cos 3 A только в терминах cos A .(На самом деле это сделано позже раздел, используя другой метод.)
Решение: Сначала синус:
sin (2 A + A ) = sin 2 A cos A + cos 2 A sin A
sin 3 A = (2 sin A cos A ) cos A + (1-2 sin² A ) sin A
sin 3 A = 2 sin A cos² A + sin A — 2 sin³ A
sin 3 A = 2 sin A (1 — sin² A ) + sin A — 2 sin³ A
sin 3 A = 2 sin A — 2 sin³ A + sin A — 2 sin³ A
sin 3 A = 3 sin A — 4 sin³ A , или (3 — 4 sin² A ) sin A
Теперь косинус:
cos (2 A + A ) = cos 2 A cos A — sin 2 A sin A
cos 3 A = (2 cos² A — 1) cos A — (2 sin A cos A ) sin A
cos 3 A = 2 cos³ A — cos A — 2 sin² A cos A
cos 3 A = 2 cos³ A — cos A — 2 (1 — cos² A ) cos A
cos 3 A = 2 cos³ A — cos A — 2 cos A + 2 cos³ A
cos 3 A = 4 cos³ A — 3 cos A , или (4 cos² A — 3) cos A
4 Учитывая грех 3 A = (3 — 4 sin² A ) sin A и cos 3 A = (4 cos² A — 3) cos A , найти tan 3 A только для tan A .Проверьте себя, вычислив загар (2 A + A ).Решение:
желто-коричневый 3 A = sin 3 A / cos 3 A
желто-коричневый 3 A = ((3 — 4 sin² A ) sin A ) / ((4 cos² A — 3) cos A )
коричневый 3 A = (sin A / cos A ) (3 — 4 sin² A ) / (4 cos² A — 3)
желто-коричневый 3 A = tan A (3 — 4 sin² A ) / (4 cos² A — 3)
Разделите верх и низ на cos² A .Это, по крайней мере, избавляет of sin² A и cos² A , хотя и вводит секущие функции. (Вы помните, что 1 / cos A = сек А , верно?)
желто-коричневый 3 A = желто-коричневый A (3 сек² A — 4 tan² A ) / (4 — 3 сек² A )
Возможно, это выглядит не лучше, но раньше вам пришлось избавиться от двух нежелательных функций; теперь у вас есть только один нежелательный функция, даже если это происходит дважды.И его sec² A . Разве нет какого-то Пифагорейская идентичность с участием sec² A ? Да, есть! sin² A + cos² A = 1 ⇒ tan² A +1 = sec² A .
желто-коричневый 3 A = желто-коричневый A (3 (tan² A + 1) — 4 tan² A ) / (4 — 3 (tan² A + 1))
желто-коричневый 3 A = tan A (3 tan² A + 3-4 tan² A ) / (4–3 tan² A — 3)
желто-коричневый 3 A = желто-коричневый A (3 — tan² A ) / (1 — 3 tan² A )
Чек:
желто-коричневый (2 A + A ) = (загар 2 A + загар A ) / (1 — загар 2 A загар A )
Из уравнения 60, tan 2 A = 2 желто-коричневый A / (1 — коричневый² A ).
желто-коричневый 3 A = (2 желто-коричневый A / (1 — коричневый² A ) + коричневый A ) / (1 — (2 желтовато-коричневый A / (1 — коричневый² A )) коричневый A )
Ну вот и бардак! Очистите это, умножив верхнюю и снизу по (1 — tan² A ).
желто-коричневый 3 A = (2 желто-коричневый A + (1 — коричневый² A ) коричневый A ) / ((1 — коричневый² A ) — 2 желто-коричневый A желто-коричневый A )
желто-коричневый 3 A = (3 желтовато-коричневый A — желто-коричневый³ A ) / (1 — 3 желтовато-коричневый² A )
Вынести за скобки tan A из верхней части фракции, и он такой же, как и в первом методе:
желто-коричневый 3 A = желто-коричневый A (3 — tan² A ) / (1 — 3 tan² A )
5 Найдите точно синус, косинус и тангенс числа π / 8.Решение: π / 8 (22) составляет половину от π / 4 (45), поэтому вам нужны формулы половинного угла. И π / 8 находится в квадранте I, поэтому все значения функции будут положительными.
sin π / 8 = √ (1 — cos π / 4) / 2
грех π / 8 = √ (1 — √2 / 2) / 2 = √ (2 — √2) / 4 = () √2 — √2
Это выражение содержит вложенных радикалов . Хотя некоторые вложенные радикалы могут быть денестированы, следуя техника в Denesting Radicals (или Unnesting Radicals), эта к сожалению, нет.
cos π / 8 = √ (1 + cos π / 4) / 2
cos π / 8 = √ (1 + √2 / 2) / 2 = √ (2 + √2) / 4 = () √2 + √2
Теперь перейдем к касательной.Вы можете использовать формула полуугла, или просто разделите синус на косинус.
тангенса π / 8 = (грех π / 8) / (соз π / 8)
тангенса π / 8 = √2 — √2 / √2 + √2
Этот можно денвертировать , если умножить вершину и снизу на √2 — √2. Ты обычно делаешь это так или иначе, чтобы рационализировать знаменатель, но это приятный бонус в том, что это происходит, чтобы очистить числитель.
тангенса π / 8 = √ (2 — √2) (2 — √2) / √ (2 + √2) (2 — √2)
тангенса π / 8 = (2 — √2) / √ (4-2) = (2 — √2) / √2 = √2 — 1
Решения для Части 9: Обратные функции
1 Возможные выходные значения Arcsin x включают π / 2, но возможные выходные значения Arctan x соответствуют нет.Почему Arctan x никогда не может равняться −π / 2 или π / 2?Решение : Arctan x — это угол, тангенс которого равен x , поэтому возможные значения Arctan x — это углы в Q IV и Q I, касательные к которым могут быть взяты. Но tan −π / 2 и tan π / 2 не существует, поэтому они не являются возможными значениями Арктан х .
2 Найдите sec (Arcsin x ). Не забудьте сделать набросок, чтобы помочь вам. Выберите значение, например x = −0,7, в качестве тестового примера для Проверьте свой ответ.Решение : Если угол A равен Arcsin x , то мы можем сделайте x противоположную сторону и 1 гипотенузу. Посредством теорема Пифагора, которая делает смежную сторону √1 — х . sec A поэтому сек (Arcsin x ) = 1 / √1 — x .
В ответе нет нечетных степеней x , поэтому мы не нужно беспокоиться о знаке x .
Давайте проверим это с помощью х = -0.7: Arcsin −0,7 ≈ −44,43, а с -44,3 = 1 / cos −44,3 ≈ 1,40. 1 / √ (1 — 0,7) ≈ 1,40 также, так что формула верна, по крайней мере, для этого теста.
3 Найдите грех (Arccos 1/ x ). Не забудьте сделать набросок, чтобы помочь вам. Выберите значение, например x = 1,3, в качестве тестового примера для Проверьте свой ответ.Решение : Если угол A равен Arccos 1/ x , мы можем установить гипотенузу на x , а прилегающую сторону на 1, так что что cos A = 1/ x по мере необходимости.Третья сторона равно √ x — 1.
Что грешит А ? Это должно быть √ x — 1/ x . Но это выражение имеет нечетную степень x , поэтому нам нужно проверьте знаки. Если x отрицательно, то Arccos x будет во втором квартале. Функция синуса имеет все положительные значения в Q II, значит, у нас должен быть положительный ответ. Но как написано, дробь отрицательна, если x отрицательна, поэтому требуется знак абсолютного значения, как в примере 3.Наш окончательный ответ —
sin (Arccos 1/ x ) = √ ( x — 1) / | x |
Давайте проверим это с помощью х = -1,3: Arccos (1 / −1,3) ≈ 140,28, дюйм Q II, как ожидалось, и sin 140,28 ≈ 0,64, положительное число, например синусы всех углов в Q II. √ ((- 1,3) — 1) / | −1,3 | ≈ 0,64 тоже. Итак, формула верна, по крайней мере, для этого тестового примера даже с отрицательным x, положив угол в Q II, формула при необходимости возвращает положительное число.
Решения для части 10: Развлечение с комплексными числами
1 Экспресс в форме a + b i: (а) 62∠240 (б) 100e 1.17iРешения : (а) 62 (cos (240) + i sin (240)) ≈ −31−53,69i
(b) явно в радианах, так как градусы отсутствуют. отметка. 100 (cos (1,17) + i sin (1,17)) ≈ 39.02 + 92.08i
2 Выразите в полярной форме как в градусах, так и в радианах: (а) −42 + 17i (б) 100i (в) −14,7Решения : (а) r = √ (-42) + 17 ≈ 45,31. θ = 2 Arctan (17 / (- 42 + 45,31)) ≈ 2,76; умножьте на 180 / π, чтобы преобразовать в 157,96. Ответы: 45,31 цис 157.96 или 45,31 цис 2,76. Конечно, вы могли бы использовать любые другие формы, показанные в главе.
(b) и (c) — это пустяки, так как у вас нет
для вычисления радиуса или угла.
(б) 100i = 100∠90 или
100e iπ / 2
(в) −14,7 = 14,7∠180 или
14,7 e iπ
Решение : сначала положите −i в полярную форму, что достаточно просто, поскольку −i на отрицательной оси y : −i = 1 цис 3π / 2.Затем примените формулу, уравнение 83:
(1 цис 3π / 2) 1/3 = 1 1/3 цис (π / 2 + 2π k /3) для k = 0, 1, 2
Три угла равны π / 2, π / 2 + 2π / 3 = 7π / 6 и π / 2 + 4π / 3 = 11π / 6 = 3π / 2.
(1 цис 3π / 2) 1/3 = 1 цис π / 2, 1 цис 7π / 6, 1 цис 11π / 6.
Вы знаете точные синусы и косинусы для любого числа, кратного π / 6, так что вам не нужен ваш калькулятор, чтобы конвертировать обратно в a + b i форма:
Кубические корни из −i: я, — (√3 / 2) — (1/2) я, (√3 / 2) — (1/2) я.
Между прочим, я не только кубический корень из −i, но −i — кубический корень из я. Я позволю тебе найти два других кубических корня я себя.
4 Найдите (1.04−0.10i) 16 .Решение : Сначала представьте это число в полярной форме: r = √1,04 + 0,10 ≈ 1.044796631. Затем найти θ = 2 Арктан (-0,10 / (1,04 + 1,044796631)) ≈ −0,09585. (Мой калькулятор работает в радианах, но это не имеет значения, потому что я буду конвертировать обратно в в любом случае прямоугольный формат.) Так
(1.04−0.10i) ≈ 1,04796631 цис -0,09585
И поэтому
(1.04−0.10i) 16 ≈ 1,04796631 16 цис (-16; 0,09585)
≈ 2,016082111 цис (-1,533746354)
≈ 0,0746787−2,01469853i
Что нового
- 6 ноября 2020 г. : страница преобразована из HTML 4.01 в HTML5 и улучшено форматирование радикалов.
- 20 декабря 2016 г. : в проблеме, которая создает вложенные радикалы, добавлена ссылка на методику на этом сайте за их разрушение.
- 11.12.2016 : Добавлены решения практических задач для Часть 5; добавлены три новых доказательства в части 7.
- 29 ноября 2016 г. : добавлены три новые задачи в части 3.
- 26/27 ноя 2016 : Добавлены решения для проблем Части 7 и Части 8.
- 19/20 ноября 2017 г. : Добавлены решения для Части 1, Части 3 и Часть 6 проблемы.
- 13 ноя 2016 : Добавлены решения для проблем Части 5. (Часть 5 была изменена нумерация на Часть 4 29 ноября 2016 г.)
- 30 октября 2016 г. : Добавлены решения для проблем Части 9 и Части 10.
- 27 октября 2016 г. : новый документ (только задачи части 2).
Функция в кубе косинуса — Исчисление
Эта статья посвящена конкретной функции от подмножества действительных чисел до действительных чисел. Информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференциации и интеграции, представлена в статье.
Посмотреть полный список конкретных функций в этой вики
Для функций, включающих углы (тригонометрические функции, обратные тригонометрические функции и т. Д.) мы следуем соглашению, согласно которому все углы измеряются в радианах. Так, например, угол измеряется как.
Определение
Эта функция, обозначенная, определяется как комбинация функции куба и функции косинуса. Явно это функция:
.
Ключевые данные
График
Ниже приведено базовое изображение графика с областью, ограниченной интервалом:
Ниже представлен более крупный план, ограниченный интервалом:
Толстые красные точки представляют точки перегиба, а толстые черные точки представляют локальные экстремальные значения.
Интеграция
Первая первообразная: стандартный метод
Переписываем и затем используем интеграцию u-подстановкой, установкой. Ясно:
Установив, получаем:
Это дает нам:
Вставляя обратно, получаем:
Первая первообразная: с использованием формулы тройного угла
Альтернативный метод интеграции — использовать идентификатор:
Таким образом получаем:
Хотя этот ответ кажется отличным от другого, два первообразных на самом деле равны, как мы можем видеть, вставив вышеупомянутое первообразное выражение.3 и sin, которые могут быть антидифференцированными, с участием нового первообразного и cos. Таким образом, процедуру можно повторять до бесконечности.
Силовая серия и серия Тейлора
Вычисление степенного ряда
Мы можем использовать удостоверение личности:
У нас есть силовая серия:
Таким образом, получаем:
Объединяя, получаем:
Первые несколько терминов:
.
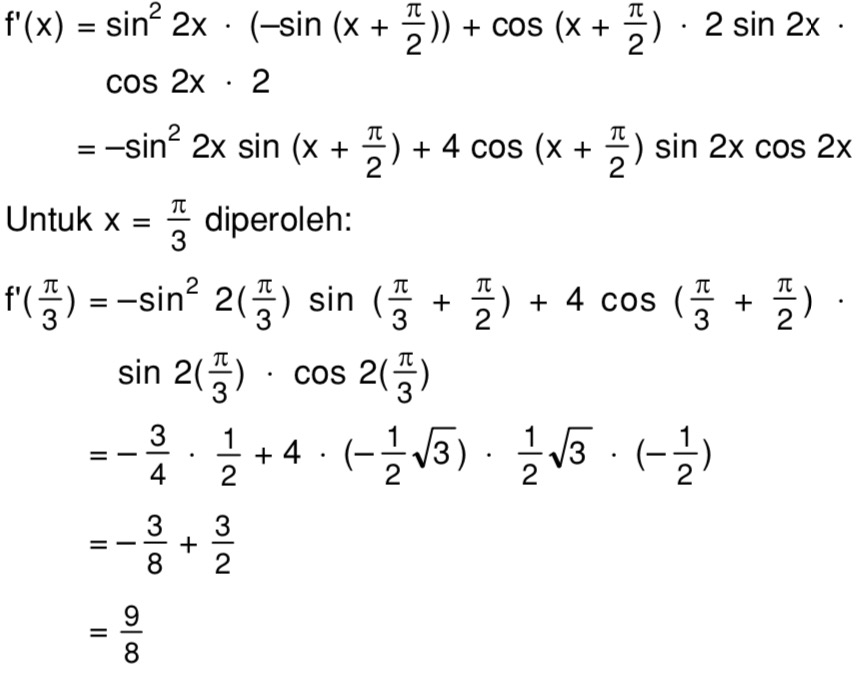 2 x + \sin x = \sqrt2 \sin\left( x + \dfrac{\pi}{4} \right)$.
2 x + \sin x = \sqrt2 \sin\left( x + \dfrac{\pi}{4} \right)$. 2 x + 5\sin\left( \dfrac{\pi}{2} — x\right) — 2 = 0$.
2 x + 5\sin\left( \dfrac{\pi}{2} — x\right) — 2 = 0$.