| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Косинус 30 градусов — справочник для студентов и школьников
ОПРЕДЕЛЕНИЕ
Косинус 30 градусов равен \(\ \frac{\sqrt{3}}{2} \) , записанный следующим образом: \(\ \cos 30^{\circ}=\frac{\sqrt{3}}{2} \)
В радианах 30 градусов соответствует \(\ \frac{\pi}{6} \) , то \(\ \cos \frac{\pi}{6}=\frac{\sqrt{3}}{2} \)
На тригонометрическом круге косинус 30 градусов расположен следующим образом (рис.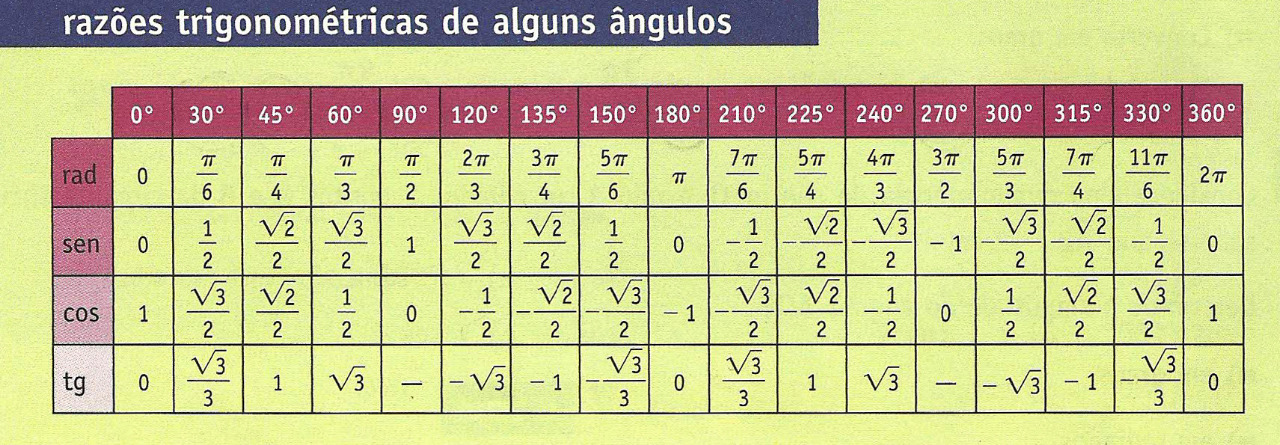 {\circ}=\frac{\sqrt{3}}{2}
\) , мы, наконец, получаем:
\(\
(\overline{a}, \overline{b})=3 \sqrt{3} \cdot 6 \cdot \frac{\sqrt{3}}{2}=27
\)
{\circ}=\frac{\sqrt{3}}{2}
\) , мы, наконец, получаем:
\(\
(\overline{a}, \overline{b})=3 \sqrt{3} \cdot 6 \cdot \frac{\sqrt{3}}{2}=27
\)
\(\ (\overline{a}, \overline{b})=27 \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Косинус 0 градусов Косинус угла Произведение синусов График синуса
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Cos 30 градусов: Значение косинуса 30 с доказательством, примерами и часто задаваемыми вопросами
Cos 30 градусов Значение косинуса, если угол прямоугольного треугольника равен 30 градусам, называется косинусом угла 30 градусов. Косинусом угла 30° называется отношение длины прилежащей стороны (рассматриваемого угла) к длине гипотенузы.
Косинусом угла 30° называется отношение длины прилежащей стороны (рассматриваемого угла) к длине гипотенузы.
В тригонометрии мы математически записываем cos 30°, и его точное значение в виде дроби равно √3/2. Поэтому запишем его в следующем виде по тригонометрии.
cos (30°) = cos π/6 = √3/2
Значение Cos 30°
Точное значение косинуса угла 30 градусов равно √5…0,86037…0,860 десятичная форма. Приблизительное значение косинуса угла 30 равно 0,8660.
Cos (30°) = 0,8660254037… ≈ 0,8660
ДоказательствоТочное значение cos π/6 можно получить с помощью трех методов, описанных ниже.
- Теоретический метод
Мы должны знать отношение сторон прямоугольного треугольника, если один из его углов равен 30°. Согласно этому свойству длина противоположной стороны равна половине длины гипотенузы (до угла 30°, т. е. перпендикуляра).
С помощью этого свойства мы вычислим точное значение косинуса угла 30 градусов.
В этом случае мы рассматриваем длину гипотенузы как «d», тогда длина противоположной стороны (до угла 30°, т. е. перпендикуляра) PQ будет «d/2». 9{2}
\Стрелка вправо\mathrm{OQ}=(\sqrt{3} / 2) \mathrm{d}
\Стрелка вправо \mathrm{OQ} / \mathrm{d}=\sqrt{3} / 2
Здесь d представляет собой длину гипотенузы.
⇒ Длина смежной стороны/гипотенуза = √3/2
Следовательно, мы можем написать, что cos (30°) = √3/2
- Практический метод
Значение косинуса угла 30° можно найти, построив прямоугольный треугольник с углом 30° с помощью геометрических инструментов.
Проведите прямую горизонтальную линию из точки G и затем постройте угол 30° с помощью транспортира.
Установите компас на любую длину с помощью линейки. Здесь компас установлен на 7,5 см. Теперь нарисуйте дугу на линии под углом 30° из точки G, и она пересечет линию в точке H.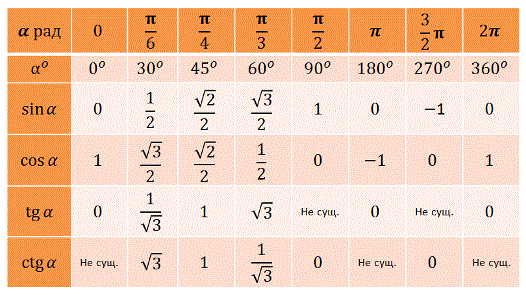 Я перпендикулярно. Таким образом, образуется прямоугольный треугольник ∆HGI.
Я перпендикулярно. Таким образом, образуется прямоугольный треугольник ∆HGI.
Теперь вычислите значение косинуса 30 градусов и для этого линейкой измерьте длину прилежащей стороны. Вы заметите, что длина соседней стороны равна 6,5 см. Длина гипотенузы в этом примере принята равной 7,5 см.
Теперь найдем отношение длин прилежащей стороны к гипотенузе и получим значение косинуса угла 30°.
cos (30°) = GI/GH = 6,5/7,5
Итак, cos (30°) = 0,866666… ≈ 0,8660 9{\circ}\right)=\sqrt{(3 / 4)}=\sqrt{3} / 2
Следовательно, мы доказали значение cos (30°), используя разные подходы.
Пример1. Вычисление: cos 30° + sin 60°
Решение:
Мы знаем, что cos (30°) = sin (60°,3) 2 0 cos (30°) + sin (60°)
= √3/2 + √3/2
= 2(√3/2)
= √3
2. Вычислить: 2 cos 30 ° – 2 sin 30°
Решение:
Мы знаем, что cos (30°) = √3/2,
и sin (30°) = 1/2
Итак, 2 cos (30°) – 2 sin (30°)
= 2 (√3/2) – 2(1/2)
= √3 – 1
Косинус 30 градусов – значение, расчет, вывод, методы и часто задаваемые вопросы
Функция косинуса в тригонометрии вычисляется путем отношения смежных катет к гипотенузе треугольника.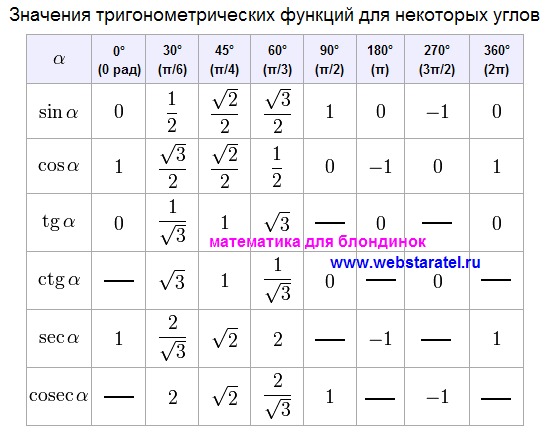 Скажем, угол прямоугольного треугольника равен 30 градусам, поэтому значение косинуса в этом конкретном угле равно делению 0,8660254037. Значение sec 30 будет точной обратной величиной значения cos 30. 9{o}) = \frac{\sqrt{3}}{2}\]
Скажем, угол прямоугольного треугольника равен 30 градусам, поэтому значение косинуса в этом конкретном угле равно делению 0,8660254037. Значение sec 30 будет точной обратной величиной значения cos 30. 9{o}) = \frac{\sqrt{3}}{2}\]
В формате дроби значение cos(30°) равно 0,8660254037. Поскольку это иррациональное число, его значение в десятичной форме равно 0,8660254037……., что примерно равно 0,866 в области математики и для решения задач. Значение cos(30°) обычно называют функцией стандартного угла в тригонометрии или тригонометрическим отношением.
Альтернативная форма Cos 30
В математике существует альтернативный формат записи cos(30°): cos(∏/6) (2∏ = 360 градусов. Итак, ∏ = 180 градусов. ∏ /6 = 180°/6 = 30°) в системе кровообращения, также выражается как cos(33) в сотенной системе. Значение cos(∏/6) и cos(33 ) равно \[\frac{\sqrt{3}}{2}\] в дробной форме и 0,8660254037……., в десятичной форме.
Доказательство для Cos 30 градусов
В математике всегда важно иметь возможность правильно вывести значение, используя ряд подходов, чтобы считать его само собой разумеющимся.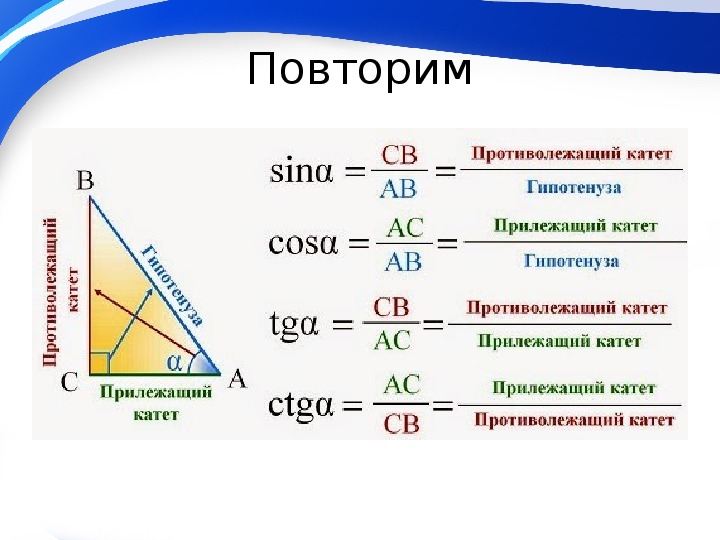 Значение cos 30 также можно узнать с помощью теоретических и практических подходов. Это геометрические методы нахождения значения cos 30, а также один тригонометрический метод, который можно использовать.
Значение cos 30 также можно узнать с помощью теоретических и практических подходов. Это геометрические методы нахождения значения cos 30, а также один тригонометрический метод, который можно использовать.
Использование теоретического подхода
Для любого прямоугольного треугольника существует прямая и установленная связь между сторонами, если угол равен 30 градусам. Длина противоположной стороны треугольника всегда равна половине длины гипотенузы. Следовательно, мы знаем значение двух сторон, гипотенузы и стороны, противоположной гипотенузе, поэтому мы можем попытаться использовать теорему Пифагора, чтобы найти значение прилежащей стороны.
Практический подход
Существует еще один способ узнать значение cos 30, это практический подход. Выполните следующие действия:
Отметьте определенную точку, скажем, P, и нарисуйте на ней горизонтальную линию.

С помощью транспортира создайте угол 30 градусов с точкой P в центре.
Начертите линию с помощью линейки, чтобы получился угол.
Нарисуйте дугу с помощью компаса на линии угла любой заданной длины и назовите ее точкой Q.
Из точки Q проведите перпендикуляр к основанию и отметьте точку пересечения основания с точкой R. выяснил.
Использование тригонометрического подхода
Используя тождество квадрата косинуса в тригонометрии, т. е. cos2θ = 1 – sin2θ , мы можем вычислить точное значение cos(33 ). Для вычисления точного значения cos(∏/6) мы должны подставить значение sin(30°) в ту же формулу.
cos(30°) = √1 – sin230°
cos(30°) = √1 – (1/2)2
cos( 30°) = √1 – (1/4)
cos(30°) = √(1 * 4 – 1)/4
cos(30°) = √(4 – 1)/4
cos( 30°) = √3/4
Следовательно, cos(30°) = √3/2
Заключение
С помощью как тригонометрического метода, так и геометрических методов (теоретический подход и практический подход) мы доказали, что значение \[cos \frac{\pi}{6}\] равно \[\frac{\sqrt{3}}{2}\] в формате дроби и 0,8660254037……, в десятичном формате , с приблизительным значением, равным 0,866.