| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.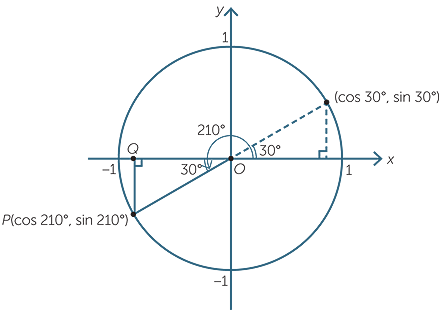 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Cos A-Cos B — формула, доказательство
LearnPracticeDownload
Cos A — Cos B, важное тождество в тригонометрии, используется для нахождения разности значений функции косинуса для углов A и B. Это одно из отличий к формулам произведения, используемым для представления разности функции косинуса для углов A и B в форме их произведения. Результат для Cos A — Cos B дается как 2 sin ½ (A + B) sin ½ (B — A).
Результат для Cos A — Cos B дается как 2 sin ½ (A + B) sin ½ (B — A).
Давайте разберемся в формуле Cos A — Cos B и ее доказательстве в деталях, используя решенные примеры.
| 1. | Что такое тождество Cos A — Cos B в тригонометрии? |
| 2. | Cos A — Cos B Отличие от формулы продукта |
| 3. | Доказательство формулы Cos A — Cos B |
| 4. | Как применять формулу Cos A — Cos B? |
| 5. | Часто задаваемые вопросы по Cos A — Cos B |
Что такое тождество Cos A — Cos B в тригонометрии?
Тригонометрическое тождество Cos A — Cos B используется для представления разности косинусов углов A и B, Cos A — Cos B в виде произведения с использованием сложных углов (A + B) и (A — B). Мы подробно изучим формулу Cos A — Cos B в следующих разделах.
Cos A — Cos B Отличие от формулы продукта
Разница Cos A — Cos B с формулой произведения в тригонометрии для углов A и B определяется как,
Cos A — Cos B = — 2 sin 1/2 (A + B) sin 1/2 (A — B)
или
Cos A — Cos B = 2 sin 1/2 (A + B) sin 1/2 (B — A)
Здесь A и B — углы, а (A + B) и (A — B) — их составные углы.
Доказательство формулы Cos A — Cos B
Мы можем дать доказательство тригонометрической формулы Cos A — Cos B, используя разложение формул cos(A + B) и cos(A — B). Как мы заявили в предыдущем разделе, мы пишем Cos A — Cos B = 2 sin ½ (A + B) sin ½ (B — A).
Предположим, что два составных угла A и B заданы как A = X + Y и B = X — Y,
⇒ Решая, получаем,
X = (A + B)/2 и Y = (A — B)/2
Мы знаем, cos(X + Y) = cos X cos Y — sin X sin Y
cos(X — Y) = cos X cos Y + sin X sin Y
cos(X + Y) — cos(X — Y) = -2 sin X sin Y
⇒ Cos A — Cos B = — 2 sin ½ (A + B) sin ½ (A — B)
⇒ Cos A — Cos B = 2 sin ½ (A + B) sin ½ (B — A)
Следовательно, доказано.
Как применять формулу Cos A — Cos B?
Мы можем применить формулу Cos A — Cos B в качестве отличия от идентичности продукта. Давайте разберемся в его применении на примере cos 60º — cos 30º. Мы решим значение данного выражения двумя способами, используя формулу и непосредственно применяя значения, и сравним результаты. Взгляните на приведенные ниже шаги.
Взгляните на приведенные ниже шаги.
- Сравните углы A и B с данным выражением, cos 60° — cos 30°. Здесь А = 60º, В = 30º.
- Решая с помощью расширения формулы Cos A — Cos B, заданной как, Cos A — Cos B = 2 sin ½ (A + B) sin ½ (B — A), мы получаем,
Cos 60° — Cos 30° = 2 sin ½ (60° + 30°) sin ½ (30° — 60°) = — 2 sin 45° sin 15° = — 2 (1/√2) ((√3 — 1)/2√2) = (1 — √3)/2. - Также мы знаем, что Cos 60° — Cos 30° = (1/2 — √3/2) = ( 1- √3)/2.
Следовательно, результат проверен.
☛ Связанные темы по Cos A + Cos B:
- Тригонометрическая таблица
- Закон косинусов
- грех кост загар
- Закон синусов
- Тригонометрические функции
Давайте рассмотрим несколько примеров, чтобы лучше понять концепцию cos A — cos B.
Примеры использования идентификатора Cos A — Cos B
Пример 1: Найдите значение cos 165° — cos 15°.

Решение:
Мы знаем, что Cos A — Cos B = 2 sin ½ (A + B) sin ½ (B — A)
Здесь A = 165°, B = 15°
cos 165° — cos 15° = -2 sin ½ (165° + 15°) sin ½ (165° — 15°)
= -2 sin 90° sin 75° = —
3 75°
= -2 sin(45° + 30°) = -2(sin 45° cos 30° + sin30° cos45°)
= -2((1/√2) (√3/2) + (1/2)(1 /√2))
= -(√3 + 1)/√2
Пример 2: Используя значения углов из тригонометрической таблицы, решить выражение: -2 sin 67,5º sin 22,5º
Решение:
Мы можем переписать данное выражение как -2 sin 67,5º sin 22,5º = -2 sin ½ (135)º sin ½ (45)º
Предполагая, что A + B = 135º, A — B = 45º и решая для A и B, мы получаем, A = 90º и B = 45º.
⇒ -2 sin ½ (135)º sin ½ (45)º = -2 sin ½ (90º + 45º) sin ½ (90º — 45º)
Мы знаем, Cos A — Cos B = 2 sin ½ (A + B) sin ½ (B — A)
-2 sin ½ (90° + 45°) sin ½ (90° — 45°) = cos 90° — cos 45° = -(1/√2).

Пример 3: Решите данное выражение, (cos x — cos 5x)/(cos 2x — cos 4x).
Решение:
У нас есть,
(cos x — cos 5x)/(cos 2x — cos 4x) = [-2 sin ½ (x + 5x) sin ½ (x — 5x)]/[- 2 sin ½ (2x + 4x) sin ½ (2x — 4x)]
= [sin 3x sin(-2x)]/[sin 3x sin(-x)]
= (-sin 3x sin 2x)/( -sin 3x sin x)
= sin 2x cosec x
Пример 4: Проверьте данное выражение, используя расширение Cos A — Cos B: cos 70° — sin 70° = √2 sin 25°
Решение:
У нас есть L.H.S. = cos 70º — sin 70º
SInce sin 70º = sin(90º — 20º) = cos 20º
⇒ cos 70º — sin 70º = cos 70º — cos 20º
Используя Cos A — Cos B = 2 B) sin ½ (B — A)
⇒ cos 70° — cos 20° = -2 sin ½ (70° + 20°) sin ½ (70° — 20°)
= -2 sin 45° sin 25°
= -√2 sin 25º
Следовательно, проверено.
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по Cos A — Cos B
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по Cos A — Cos B
Что такое Cos A — Cos B в тригонометрии?
Cos A — Cos B представляет собой тождество или тригонометрическую формулу, используемую для представления разности косинусов углов A и B, Cos A — Cos B в форме произведения с использованием сложных углов (A + B) и (A — B) ). Здесь А и В — углы.
Как использовать формулу Cos A — Cos B?
Чтобы использовать формулу Cos A — Cos B в заданном выражении, сравните разложение Cos A — Cos B = 2 sin ½ (A + B) sin ½ (B — A) с данным выражением и подставьте значения углов A и B.
Какова формула Cos A — Cos B?
Формула Cos A — Cos B для двух углов A и B может быть представлена как Cos A — Cos B = 2 sin ½ (A + B) sin ½ (B — A). Здесь (А + В) и (А — В) — сложные углы.
Здесь (А + В) и (А — В) — сложные углы.
Что такое расширение Cos A — Cos B в тригонометрии?
Расширение формулы Cos A — Cos B дается следующим образом: Cos A — Cos B = 2 sin ½ (A + B) sin ½ (B — A), где A и B — любые заданные углы.
Как доказать расширение формулы Cos A — Cos B?
Расширение Cos A — Cos B, заданное как Cos A — Cos B = 2 sin ½ (A + B) sin ½ (B — A), может быть доказано с использованием тождества произведения 2 sin X sin Y в тригонометрии. Нажмите здесь, чтобы проверить подробное доказательство формулы.
Каково применение формулы Cos A — Cos B?
Формулу Cos A — Cos B можно применять для представления разности косинусов углов A и B в виде произведения синуса (A + B) и синуса (A — B) по формуле Cos A — Cos B = 2 sin ½ (A + B) sin ½ (B — A).
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист по тригонометрии
Рабочие листы по математике и визуальный учебный план
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус (-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктический(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы | 45 | |
| 33 | Найти точное значение 92 | ||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 пи)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 пи)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 шт. |
