Google Документы – бесплатный онлайн-редактор документов
Создавайте онлайн-документы и работайте над ними совместно с другими людьми на любых устройствах. Изменения отображаются в режиме реального времени.
Попробовать Документы для работы Перейти в Документы
Нет аккаунта?
- Для личного использования
- Для работы или бизнеса
I
d
e
a
s
Преимущества Google Docs
Больше возможностей с дополнениями
В Google Документах можно работать с приложениями сторонних разработчиков. Например, можно интегрировать приложение для создания электронной подписи или инструмент для управления проектами.
Например, можно интегрировать приложение для создания электронной подписи или инструмент для управления проектами.
Работа с последней версией файла
В Google Документах каждый работает с актуальной версией документа. Изменения автоматически сохраняются в истории версий, поэтому их легко отслеживать и при необходимости отменять.
Работа в офлайн-режиме
Файлы Документов можно просматривать, создавать и редактировать даже без подключения к интернету, поэтому вы сможете продуктивно работать откуда угодно.
Безопасность, соответствие требованиям и конфиденциальность
Защита конфиденциальности пользователей
Google Документы соответствуют тем же строгим требованиям к обеспечению конфиденциальности и защите данных, которые применяются в отношении остальных корпоративных сервисов Google Cloud.
Вы управляете своими данными.
Мы не используем ваши данные из Google Документов для показа рекламы.
Мы не продаем ваши личные данные третьим лицам.
Выберите подходящий план
Google Документы входят в Google Workspace
Попробовать Документы для работы | Для личного использования (Бесплатно) | Business Standard $10. |
|---|---|---|
| Документы, Таблицы, Презентации, Формы – создание контента | done | done |
Диск – надежное облачное хранилище | 15 ГБ на пользователя | 2 ТБ на пользователя |
Общие диски для команды | remove | done |
Gmail – защищенная электронная почта | done | done |
Корпоративный адрес электронной почты | remove | done |
Meet – голосовой и видеочат | 100 участников | 150 участников |
Сохранение записей встреч на Диске | remove | done |
Admin – централизованное управление | remove | done |
Управление правилами безопасности на основе групп | remove | done |
Поддержка пользователей | Онлайн-справка и форумы сообщества | Круглосуточная онлайн-поддержка и форумы сообщества |
Совместная работа без границ
Создавайте, редактируйте и просматривайте документы с мобильного устройства, планшета или на компьютере – даже без подключения к интернету.
Шаблоны на все случаи жизни
Создавайте проектные предложения, планы продаж и многое другое на основе профессиональных шаблонов из нашей коллекции.
Проекты
Коммерческое предложение
Рецепты
Отчеты
Проекты
Коммерческое предложение
Рецепты
Отчеты
Остальные шаблоны можно найти в галерее шаблонов Google Документов.
Готовы начать?
Попробовать Документы для работы Перейти в Документы
Статья 5.
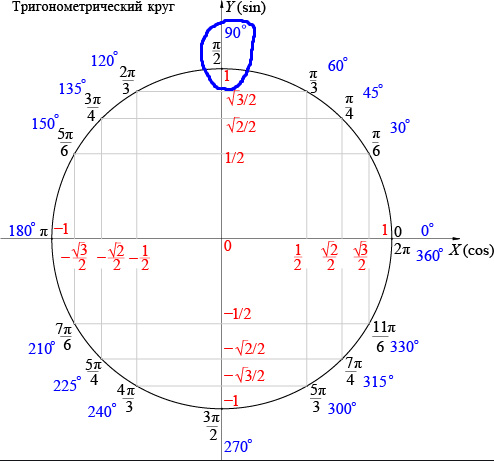 1. Медицинское освидетельствование и медицинское обследование граждан в связи с исполнением воинской обязанности, поступлением на военную службу по контракту или поступлением в мобилизационный людской резерв \ КонсультантПлюс
1. Медицинское освидетельствование и медицинское обследование граждан в связи с исполнением воинской обязанности, поступлением на военную службу по контракту или поступлением в мобилизационный людской резерв \ КонсультантПлюс- Главная
- Документы
- Статья 5.1. Медицинское освидетельствование и медицинское обследование граждан в связи с исполнением воинской обязанности, поступлением на военную службу по контракту или поступлением в мобилизационный людской резерв
Подготовлена редакция документа с изменениями, не вступившими в силу
Федеральный закон от 28.03.1998 N 53-ФЗ (ред. от 14.07.2022) «О воинской обязанности и военной службе» (с изм. и доп., вступ. в силу с 25.07.2022)
Статья 5.1. Медицинское освидетельствование и медицинское обследование граждан в связи с исполнением воинской обязанности, поступлением на военную службу по контракту или поступлением в мобилизационный людской резерв
(в ред. Федерального закона от 30.12.2012 N 288-ФЗ)
Федерального закона от 30.12.2012 N 288-ФЗ)
(см. текст в предыдущей редакции)
(введена Федеральным законом от 31.12.2005 N 199-ФЗ)
1. Граждане при постановке на воинский учет, призыве на военную службу или поступлении на военную службу по контракту, поступлении в мобилизационный людской резерв, поступлении в военные профессиональные образовательные организации и военные образовательные организации высшего образования, заключении с Министерством обороны Российской Федерации договора об обучении, предусмотренного пунктом 1 или 4 статьи 20 или пунктом 1 статьи 20.2 настоящего Федерального закона, призыве на военные сборы, прохождении альтернативной гражданской службы, а также граждане, ранее признанные ограниченно годными к военной службе по состоянию здоровья, проходят медицинское освидетельствование врачами-специалистами (терапевтом, хирургом, невропатологом, психиатром, окулистом, оториноларингологом, стоматологом) и в случае необходимости — врачами других специальностей.
(в ред. Федеральных законов от 03.04.2017 N 61-ФЗ, от 07.03.2018 N 55-ФЗ, от 03.08.2018 N 309-ФЗ)
(см. текст в предыдущей редакции)
1.1. Медицинское освидетельствование граждан, указанных в пункте 1 настоящей статьи и являющихся детьми-инвалидами, инвалидами I группы или имеющих иную группу инвалидности без указания срока переосвидетельствования, в связи с исполнением ими воинской обязанности с их согласия или с согласия их законных представителей проводится заочно на основании документов, перечень которых определяется Положением о военно-врачебной экспертизе, утверждаемым уполномоченным федеральным органом исполнительной власти.
(п. 1.1 введен Федеральным законом от 29.11.2010 N 319-ФЗ)
1.2. Медицинское освидетельствование граждан, подлежащих призыву на военную службу, имеющих основания для предоставления отсрочки от призыва на военную службу или право на освобождение от призыва на военную службу (за исключением граждан, указанных в пункте 2.1 статьи 22 и подпункте «а» пункта 1 статьи 24 настоящего Федерального закона), проводится по их заявлению.
(п. 1.2 введен Федеральным законом от 26.05.2021 N 146-ФЗ)
2. Врачи, руководящие работой по медицинскому освидетельствованию граждан, указанных в пункте 1 настоящей статьи, по результатам медицинского освидетельствования дают заключение о годности гражданина к военной службе по следующим категориям:
А — годен к военной службе;
Б — годен к военной службе с незначительными ограничениями;
В — ограниченно годен к военной службе;
Г — временно не годен к военной службе;
Д — не годен к военной службе.
3. Порядок организации и проведения медицинского освидетельствования граждан, указанных в пункте 1 настоящей статьи, определяется Положением о военно-врачебной экспертизе.
(в ред. Федеральных законов от 23.07.2008 N 160-ФЗ, от 29.11.2010 N 319-ФЗ)
(см. текст в предыдущей редакции)
4. В случае невозможности вынесения медицинского заключения о годности гражданина к военной службе по состоянию здоровья в ходе медицинского освидетельствования гражданин направляется на основании решения комиссии по постановке граждан на воинский учет или призывной комиссии, принятого по заключению врачей-специалистов, принимавших участие в медицинском освидетельствовании, на амбулаторное или стационарное медицинское обследование в медицинскую организацию государственной системы здравоохранения (за исключением медицинской организации, подведомственной федеральному органу исполнительной власти) или медицинскую организацию муниципальной системы здравоохранения, включенную в перечень медицинских организаций, проводящих медицинское обследование граждан, указанных в пункте 1 настоящей статьи, утверждаемый решением высшего должностного лица субъекта Российской Федерации (руководителя высшего исполнительного органа государственной власти субъекта Российской Федерации), в порядке, установленном Положением о военно-врачебной экспертизе.
(в ред. Федерального закона от 30.04.2021 N 131-ФЗ)
(см. текст в предыдущей редакции)
5. Гражданам при постановке на воинский учет и призыве на военную службу, признанным по результатам медицинского освидетельствования временно не годными к военной службе, при наличии медицинских показаний медицинская помощь оказывается в соответствии с законодательством в сфере охраны здоровья.
(п. 5 в ред. Федерального закона от 30.04.2021 N 131-ФЗ)
(см. текст в предыдущей редакции)
5.1. Наличие оснований для предоставления гражданам отсрочек и освобождений от призыва на военную службу по состоянию здоровья, освобождений от исполнения воинской обязанности в связи с признанием их не годными к военной службе по состоянию здоровья и правильность их предоставления проверяются призывной комиссией субъекта Российской Федерации в порядке, установленном Положением о военно-врачебной экспертизе. В случае выявления нарушений в правильности предоставления гражданам отсрочек и освобождений от призыва на военную службу по состоянию здоровья, освобождений от исполнения воинской обязанности в связи с признанием их не годными к военной службе по состоянию здоровья, предоставленных в ходе работы призывной комиссии, по решению призывной комиссии субъекта Российской Федерации проводится контрольное медицинское освидетельствование указанных граждан.
Граждане, заявившие о несогласии с заключением об их годности к военной службе по результатам медицинского освидетельствования, направляются на контрольное медицинское освидетельствование.
Граждане, не пребывающие в запасе, призванные на военную службу, перед направлением к месту военной службы проходят медицинский осмотр в целях выявления состояний и заболеваний, препятствующих прохождению военной службы по состоянию здоровья.
Порядок организации и проведения медицинского осмотра граждан, не пребывающих в запасе, призванных на военную службу, перед направлением к месту прохождения военной службы и контрольного медицинского освидетельствования граждан, получивших отсрочку или освобождение от призыва на военную службу по состоянию здоровья, граждан, получивших освобождение от исполнения воинской обязанности в связи с признанием их не годными к военной службе по состоянию здоровья, и граждан, заявивших о несогласии с заключением об их годности к военной службе по результатам медицинского освидетельствования, определяется Положением о военно-врачебной экспертизе.
(п. 5.1 введен Федеральным законом от 30.04.2021 N 131-ФЗ)
6. Финансовое обеспечение медицинского освидетельствования граждан, указанных в пункте 1 настоящей статьи, осуществляется за счет средств федерального бюджета в порядке, установленном Правительством Российской Федерации.
7. Финансовое обеспечение медицинского обследования граждан, указанных в пункте 1 настоящей статьи, осуществляется в соответствии с законодательством в сфере охраны здоровья.
(в ред. Федерального закона от 25.11.2013 N 317-ФЗ)
(см. текст в предыдущей редакции)
Статья 5. Мероприятия по обеспечению исполнения воинской обязанности, поступления на военную службу по контракту или поступления в мобилизационный людской резерв Статья 5.2. Профессиональный психологический отбор
SHAFA ᐈ Одяг, Взуття, Аксесуари, вигідні ціни в Києві у Україні
Все категории
Додати товар
Каталог
Жіночий одяг
Дитячий одяг
Чоловічий одяг
Для дому
Краса і здоров’я
Спорт і відпочинок
Дитячі товари
Зроблено в УкраїніНовинкиЗнижка дняБрендиВерхній одягПлаттяСпідниціМайки й футболкиСорочки та блузиКофтиНижня білизнаАксесуариІнші речі
Спортивний одягКостюмиКомбінезониОдяг для дому та снуСпецодягДля вагітнихВзуттяШтани та шортиПальтоПлащіКурткиШубиЖилеткиПіджаки і жакетиПуховикиПаркиДублянкиДощовикиВітровки
Короткі сукніПлаття мідіДовгі сукніВечірні сукніВесільні сукніСарафаниТуніки
Міні-спідниціМіді спідниціДовгі юбки
ФутболкиМайкиПолоТопи
СорочкиБлузиВишиванкиБоді
ДжемпериСветриКардиганиВодолазкиСвітшотиХудіПуловериТолстовкиНакидкиБолероПончоРегланиЛонгслівиЖилети
БюстгальтериТрусикиКомплектиКупальникиШкарпеткиБодіКорсетиПанчохиКолготкиПеньюариТермобілизнаПортупеї
Сумки та РюкзакиОкуляри
Головні убориПрикраси і годинникиРеменіШарфи і хусткиКраватки і метелики
Рукавички і рукавиціОбкладинки для документівПарасоліІнші аксесуариТканинні маски для обличчя
Аксесуари для телефонівПерукиВолосся для нарощуванняПрикраси для нареченоїАксесуари для окулярів
КлатчіРюкзакиДорожні валізиГаманціСумкиБананкиШоппериКрос-бодіАвоськиКартхолдериПляжні сумкиСпортивні рюкзакиСпортивні сумкиКлючниціОрганайзериАксесуари
ШапкиБейсболки і кепкиКапелюхиПанамиПов’язки на головуБеретиБандани
ПідвіскиКольє і намистаОбручіЧокериШпилькиЛанцюжкиКулониСережкиКільцяБраслетиБрошкиНабориГодинникиІнші прикрасиСережки для пірсингуШарми та кліпси
РукавичкиРукавиціМітенки
ЧохлиПопсокетиЗахисне склоЧохли для airpods
Спортивні костюмиСпортивні штаниЛосіниШортиТопиКофтиМайкиКапріКомбінезониБілизна
Гірськолижний одягЛижні курткиЛижні костюмиЛижні штаниЛижні комбінезони
Костюми з сукнеюКостюми з шортамиКостюми зі спідницеюБрючні костюми
Джинсові комбінезониБрючні комбінезониКомбінезони з шортами
Домашній одягПіжамиНочнушкиХалатиМаски для сну
Для сфери обслуговуванняМедичний одягРобочий спецодягЗахисний спецодягАкадемічний одягФормений одяг
Верхній одягПлаттяСарафаниФутболки і майкиДжинсиШтани
БілизнаІнша одягЛосіниКомбінезониКофти та світериЛонгслівиСпідниціСорочки і блузи
КолготиБандажіТрусиБюстгальтериКомплектиКупальникиХалатиПіжамиНічні сорочки
ЧеревикиБотильйониЧоботиКросівкиКедиСнікериУггіДутикиБотфортиГумові чоботиВалянкиСабоШльопанціВ’єтнамкиТуфліБалеткиЛофериОксфордиБрогиБосоніжкиСандаліСліпониМокасиниЕспадрільіКапціЧешкиАквашузиАксесуари для взуття
БрюкиДжинсиЛосіни та ЛегінсиШортиБриджі
Для дівчатокДля хлопчиківДля малюківВерхній одягКофти та светриФутболки та майки
КостюмиКолготи та шкарпеткиШтани, джинси, лосиниБлузки та сорочкиСпідниціШортиКомбінезони літні
аксесуариІнше
Нижня білизнаСукні
ВзуттяСпорт і відпочинокКурткиПальтоПлащіПуховикиШуби і дублянкиПіджаки і жакетиЖилеткиЗимові комбінезониПарки
КарнавальніСпортивніПовсякденніШкільна форма
Головні убориСумки і рюкзакиРукавички і рукавиціПрикрасиІншіРемені і підтяжкиДитячий текстиль
ПіжамиБілизняні майкиТрусиКупальникиКомплектиХалати
Кросовки і кедиБосоніжки і шльопанціТуфліЧоботи і черевикиКапціІнше взуття
Спортивний одягСпортивне взуттяСпортивні сумки та аксесуариВерхній одягПлаття
Костюми для заняття спортомСпідниці
Футболки та майкиШтани і лосиниШортиКофти
Нижня білизнаКросівкиКедиЧеревикиЧоботиТуфліСандаліКапціЧешки і балеткиАквашузи
Головні убориРукавичкиШарфи і БаффіБраслети
Рюкзаки та сумкиОкуляриГодинникиТуніки і парео
Верхній одягКофти та светриФутболки та майки
КостюмиКолготи та шкарпеткиШтани, джинси, лосиниСорочкиШортиКомбінезони літні
АксесуариІнше
Нижня білизнаВзуттяСпорт і відпочинокКурткиПальтоПлащіПуховикиШуби і дублянкиПіджаки і жакетиЖилеткиЗимові комбінезониПарки
КарнавальніСпортивніПовсякденніШкільна форма
Головні убориРюкзаки та сумкиРукавички і рукавиціПрикрасиІншіРемені і підтяжкиДитячий текстильКосметика
ПіжамиБілизняні майкиТрусиПлавки та купальні костюмиКомплектиХалати
Кросівки і кедиБосоніжки і шльопанцітуфліЧоботи і черевикиКапціІнше взуття
Спортивний одягСпортивне взуттяСпортивні сумки та аксесуариВерхній одягКостюми для заняття спортомФутболки та майкиКофти
Штани і лосиниШорти
Нижня білизнаКросівкиКедиБутсиЧеревикиТуфліСандаліКапціАквашузи
Головні убориРукавичкиШарфи і БаффіБраслети
Рюкзаки та сумкиОкуляриГодинники
Набори для хрещенняКонверти та спальні мішкиКостюми та комплектиБоді, чоловічки, пісочникиПовзунки, штани, шортиСорочечки і кофтиПінетки і царапкиПлаття, сарафани, спідниціВерхній одягВзуттяІнший одягФутболки та майкиГоловні убориТекстильКупальні костюми
Верхній одягПіджаки і костюмиКофти та СветриСорочки та теніскиФутболки та МайкиНижня білизнаВзуттяАксесуариСпортивний одягОдяг для дому та снуСпецодягТактичний одягШтани та шортиПуховикиПальтоПлащіКурткиПаркиДублянки і шубиВітровкиЖилеткиДощовики
ПіджакиДілові костюмиЖакетиСмокінгиЖилетки
ТолстовкиРегланиКофтиСветриОлімпійкиГольфиКардиганиДжемпериСвітшотиХудіПуловериЛонгсліви
СорочкиТеніскиВишиванки
ФутболкиМайкиПоло
ТрусиПлавкиКомплектиТермобілизнаШкарпетки
КросівкиТуфліМокасиниКедиЧеревикиЧоботиУггіСліпони і ЕспадрільіСандаліїШльопанціКапціІнше взуттяАквашузиГумові чоботиБутсиБорцовкиАксесуари
Сумки і РюкзакиГодинникиОкуляри
Ремені і підтяжкиГоловні убориШарфиРукавичкиКраватки і метелики
ПрикрасиІнші аксесуариПарасолькиАксесуари для окулярів
Аксесуари для телефонівСумкиРюкзакиСпортивні сумкиПортфеліБарсеткиДорожніВалізиГаманціСпортивні рюкзакиБананкиКартхолдериКлючниціАксесуари для сумок
РеменіПідтяжки
ШапкиБейсболкиКепкиКапелюхиБеретиБанданиПанамиПов’язки
Кільця і персніЛанцюжкиБраслетиЗапонкиСережки
ЧохлиПопсокетиЗахисне склоЧохли для навушників
Спортивні костюмиСпортивні штаниСпортивні шортиСпортивні футболкиСпортивні кофтиТайтсиСпортивна білизнаФутбольна форма
Гірськолижний одягВелокостюмиГідрокостюми
Лижні курткиЛижні штаниЛижні костюмиЛижні комбінезони
Домашній одягПіжамиХалатиМаски для сну
Для сфери обслуговуванняМедичний одягРобочий спецодягЗахисний спецодягАкадемічний одягФормений одягОдяг для мисливців та рибалокОдяг для бджільництва
Верхній одягШтаниФутболкиГоловні убориРукавиціВзуттяРозвантажувальні системиТактичний захистАксесуари
БрюкиДжинсиШортиБриджі
Домашній текстильПосудЗберігання та догляд за одягомДекор і дизайнГосподарські товариПобутова хіміяТовари для тваринТовари для дозвілляАксесуари для фотосесійУпаковка для подарунківКанцеляріяКнигиОсвітленняМатрациШтори і карнизиІнвентар для прибиранняМебліКилимові виробиДля кухніДля спальніДля ванноїДитячий текстильІнші товари
Текстиль для відпочинкуТканиниЧохли для диванів
СкатертиниСерветкиРушникиФартухиПодушки на стільціДоріжки на стілПрихватки
НаматрацникиПокривала
Постільна білизнаПледиПодушкиКовдриРолетиКилимкиДекоративні подушки
КомплектиПідодіяльникиНаволочкиПростирадла
РушникиКилимкиШторки
Постільна білизнаПледиНаматрацникикилимкиПелюшкиКовдриПодушкиРушникиБалдахіниПокривалаБортики в кроваткуКокони
КомплектиПідодіяльникиНаволочкиПростирадла
Пляжні рушникиПляжні підстилки
Столовий посудСервіровка столаПосуд для зберіганняКухонний посудБарні аксесуариПосуд для приготування
Посуд для чаю та кавиКухонне приладдяСтолові сервізиЧайні сервізиКелихи і фужериЧарки і стопкиСклянкиЧашкиТарілкиМискиСтравиСалатникиПіалиСтолове приладдяГлечики і графиниПосуд для суші
Килимки для столуПідставкиПідносиКреманкиСоусникиСерветниціЦукорниціТортівниціФруктовниціВази для цукерокСолонки та перечниціАксесуари
КонтейнериБаночкиПляшкиЛанч боксиТермосиТермокружкиХлібниціНабори для спеційМаслянкиЄмності для маслаБочки та діжкиКорзинки
Форми для випічки і запіканняКаструліСотейникиГусятниціСковородиНабори посудуКришки для посудуНабори приладдяЄмності для змішуванняФондюшниціПароварки
Гейзерні кавоваркиЧайники для плитиЗаварювальні чайникиТуркиПуровериФренч-пресиМлини для кавиКавникиАксесуари
НожіОбробні дошкиСушки і органайзериКухарські лопатки та ложкиКондитерські приналежностіТертки та овочерізкиКонсервні ножі і ключіМірний посудПрихватки і підставкиДрушляки і ситоПодрібнювачі і пресиВсе для приготування сушіРучна технікаАксесуари для миття посуду
Коробки для зберіганняКонтейнериКошики для білизниОрганайзериВішалкиЧохли для одягуМішки для пранняВакуумні пакети для одягуПрасувальні дошкиСушарки для білизниПрищіпки
СвічкиСвічники
Ароматичні засобиФоторамкиВазиКвіткові горщикиСкринькиСтатуеткиГодинникиКартиниДзеркалаАксесуариВесільні аксесуариШтучні квітиКлючниці настінніПодарунки та сувеніриСкретч-картиПостериІкониФурнітура для картинпанноКашпоІнтер’єрні лялькиДекоративні елементиНастінний декор
АромалампиАромадіффузориАромасашеЕфірні масла
Паперові рушникиСерветки для збиранняГубки кухонніРукавички для прибиранняПакети для сміттяТуалетний папірХарчова упаковкаОдноразовий посудВологопоглиначіГосподарські сумкиПоліетиленові пакетиАнтимоскітні сіткиГачки і кріпленняНакладки на унітаз
Для миття посудуОсвіжувачі повітря
Засоби для прибиранняПральний порошокКондиціонери для білизниВідбілювачі і засоби для виведення плямГосподарські милаСпеціалізовані засобиАксесуари для пранняЗасоби по догляду за взуттямЗасоби від комахДля посудомийних машинЗасоби для прасування
Засоби для миття підлогЗасоби для чищення ваннЗасоби для кухніЗасоби для миття віконЗасоби по догляду за побутовою технікоюЗасоби для чищення килимів
Одяг для тваринПовідці і шлейкиНашийникиСпальні місцяІграшкиПереноскиПосудДогляд та гігієнаІнструменти для грумінгуТуалетиЗагони і будкиТаблички і наклейкиКліткиГодівниці і гніздаАкваріумиУстаткування для акваріумівДогляд за акваріумомТераріуми і фаунаріумиДекорації для акваріумівКігтіточки
Картини по номерамНастільні ігри
РукоділляВсе для святаНоворічні товариТовари для паскиТовари до дня святого ВалентинаТовари для Хеллоуїна
В’язанняВалянняТовари для шиттяВишивка і бісероплетінняФурнітура для біжутеріїСкрапбукінгДля квілінгу, декупажуМалювання і творчістьШвейна фурнітураДля макрамеМатеріали для рукоділляОрганайзери для рукоділляЗаготовки
ФотофонДекор для фотозоніФотобутафоріяОб’ємні букви і цифри
КоробкиПакетиПакувальний папір і стрічкиДекор для упаковки
ЗошитиПеналиКанцелярські набориПапки для документів і зошитівОбкладинки для документівОбкладинки для зошитів і книжокПапір, фотопапірЛистівки та конвертиЗаписні книжкиФотоальбомиКалендарі
ХудожніБізнесНаукові та технічніПсихологіяПідручникиСловники і енциклопедіїБудинок і хобіКулінарні книгиЖурнали та каталогиІсторичні книгиДитячі книги
ЛюстриБраСвітильникиВуличні світильникиСпотиНастільні лампиТоршериПідсвічуванняLED-стрічкаТрекові світильникиНічникиСтудійне освітленняОсвітлення для дитячої кімнатиГірляндиРозумне освітленняБактерицидні лампиЛампочкиАксесуари для світильників
ОдноспальніПолуторніДвоспальніОртопедичніТоппериБезпружинніПружинніНадувніДитячі
КарнизиШториАксесуари для шторРулонні шториРимські шториЖалюзі
ШвабриЩітки і совкиТазиНасадки до швабриВідраВіники та щіткиСовкиКонтейнери для сміття
ШафиМеблі для офісуМ’які мебліТумбиСтелажіСтолиСтільціМеблеві гарнітуриПолиціГардеробні системиМеблі для кухніМеблева фурнітураКомодиПідставки і тумби для взуттяЛіжкаЕтажеркиДекоративна мебліШирмиБезкаркасні мебліКорпусні мебліМеблі для спальніМеблі для передпокоюМеблі для ванноїМеблі для дачіКомплектуючіПідставки для квітівЧохли для меблівДитячі меблі
КилимиКилимові доріжкиПридверні килимки
Чоловіча косметикаАксесуари для красиДекоративна косметикаПарфумиМанікюр і педикюрКосметика для волоссяКосметика для обличчяТіло і ваннаДогляд за собоюТехніка для краси
Подарункові набори косметикиДезінфікуючі засобиМедичні приладиДомашня аптекаОптикаПарфумиЗасоби для голінняЗасоби після голінняДезодорантиКосметика для тілаКосметика для обличчяКосметика для волоссяІнша косметика
Туалетна водаДухиТуалетна водаОдеколон
Спонж для макіяжуАплікатори для тінейДзеркала для макіяжуКосметичкиПензлі для макіяжуГребінціБігудіМочалки і щіткиКейси для косметикиОрганайзериАксесуари для фарбуванняПінцети для брівЩипці для завивки війІнструменти для чищення обличчя
Косметика для очейКосметика для брівКосметика для губКосметика для обличчяЗасоби для зняття макіяжуНабори декоративної косметики
Туш для війТіні для повікКонтурні олівціБаза під тініПідводка для очейКоректори для очейНакладні віїПалетки тіней
Тіні для бровТуш для брівОлівці для брівГелі для брівПомада для брівХна для брівФарба для бровей
Помада для губБлиск для губОлівці для губТінт для губБальзами для губПлампери для губ
База під макіяжРум’янаБронзериХайлайтериКонсилериПудраКоректориТональний кремІлюмінатори і шіммериBB-кремиCC-кремиПраймери для особи
ДухиТуалетна водаТестериПарфумовані спреїПарфумовані дезодорантиПарфумована водаПробники парфумівАтомайзери для духів
Лак для нігтівГель-лакиОснови під лакЗакріплювачі для лакуДекор для нігтівНакладні нігтіГелі для нігтівРідини для зняття лакуЗасоби для догляду і лікуванняІнструменти для манікюруЛампи для манікюруРемувер для кутикулиПраймери для нігтівСтартові набори для манікюру
ШампуніКондиціонериБальзамиОполіскувачіМаскиЛосьйониМасла і сироваткиСпреїКератинЗасоби від випадінняЗасоби від лупиЗахист для волоссяФарба для волосся
Стайлінг для волоссяАксесуари для волоссяТонуючі засоби для волоссяХна для волоссяОсвітлювач для волоссяОкислювачі для волоссяЗасоби для завивки волоссяРемувер для волосся
Лак для волоссяПінка для волоссяГель для фіксації волоссяВіск для волосся
Фени та плойки
Крем для обличчяМаски для обличчяБальзами для обличчяМасло для обличчяСпреї для обличчяСироватки для обличчяТермальна водаМицеллярная водаТоніки для обличчяСкраби для обличчяЗасоби для очищення обличчя
Засоби для гоління
Депіляція і шугарінгКосметика для ванни і душаДогляд за тіломКосметика для рукКосметика для нігВоскоплавиПаста для шугарингаВіск для депіляціїВоскові смужкиМатеріали для депіляції
Гель для душуМилоСкраби для тілаКосметика для інтимної гігієниСіль для ванниПіна для ванниБомбочки для ванни
Крем для тілаДезодоранти і антиперспірантиЗасоби для засмагиМасло для тіла
Крем для рукМаска для рук
Крем для нігМаска для нігДезодоранти для ніг
Догляд за порожниною ротаОсобиста гігієнаЗубні пастиЗубні щіткиЗубний порошокОполіскувачіЗубні ниткиДорожні набориЗасоби для відбілювання зубівНабори по догляду за порожниною ротаЗасоби по догляду за зубними протезами і брекетами
Ватні дискиВатні паличкиГігієнічні прокладкиТампониЗасоби для інтимної гігієниВологі серветкиПаперові носові хусточки
Жіночі подарункові набориЧоловічі подарункові набориДитячі подарункові набори
АнтисептикиДезінфектори
Медичне приладдяТонометриСтетоскопиПульсоксиметриІнгаляториТермометри медичніДомашня медтехніка
Біологічно активні речовиниПерев’язувальний матеріалБактерицидні лампиМедичні пластирі
окуляриЛінзиОправа для окулярів
Ігрові видиЗимові види спортуФітнес та аеробікаБасейн і аквафітнесБокс і єдиноборстваТренажериЕлектротранспортЗасоби пересуванняТуризм і кемпінгРиболовляНадувні мебліМузичні інструментиМ’ячіНастільний тенісБадмінтон і сквошРакетки для великого тенісуМ’ячі для великого тенісуДартсБейсбол
СанкиКовзаниКлючки і шайбиЛижіЛижні палиціЛижні кріпленняСноубордиАксесуари
ЕспандериФітнес м’ячіОбручіСкакалкиОбважнювачіДиски здоров’яБалансувальні платформиСтеп платформиРолики для пресаУпори для віджиманьСпортивні матиГімнастичні палиціСпортивні канатиФітнес джампериКільця для пілатесуМішки для кроссфітаРезинки для фітнесуГімнастичні килимкиФітнес браслети
Окуляри для плаванняШапочки для плаванняЛастиБеруші і затискачіМаски для дайвінгуТрубки для дайвінгуАксесуари
РукавиціМішки та грушіЛапи і маківариНунчакуАксесуари
БатутиГантеліБігові доріжкиГребні тренажериШведські стінкиТурнікиСилові тренажериВелотренажериОрбітреки
ЕлектровелосипедиЕлектросамокатиГіроскутериГіробордиМоноколесаЕлектроскейтиГіророликиДрифт-картиАксесуари
ВелосипедиВелоаксесуариСамокатиРоликові ковзаниСкейтбордиЗахист
НаметиСкладні мебліТуристичні килимкиСпальні мішкиРюкзакиТермопродукціяПосуд для відпочинкуМангали та барбекюАксесуари для мангалівПальникиЛіхтарикиАксесуариТактична медицина
ВудкиКотушкиШнури та волосініВоблериБлешняМ’які приманкиГачкиВертлюги і застібкиГодівниціГрузилаАксесуари
ДиваниМатрациПодушкиКругиПлатформи і плотиЛамзакиБасейниНасоси
ГітариКлавішні інструментиУдарні інструментиДухові інструментиСмичкові інструменти
Дитяча кімнатаТовари для мамХарчування і годуванняЩоденний догляд і здоров’яКоляски та автокріслаДитячі іграшкиДитячий транспортТовари для творчостіАктивний відпочинокДитячі книги
МанежіДитячі ліжечкаПартиМобіліКомоди та пеленаториШафи в дитячу кімнатуАксесуари для дитячих меблівІграшки-нічникиЯщики для іграшокСтоли для творчостіДитячі шведські стінкиДитяча безпекаНамети і вігвамиХодункиГойдалкиСтрибунки
МолоковідсосиСлінгиНабори в пологовий будинокДитячі вагиРадіоняніНакидки для годуванняЛактаційні вкладишіНакладки для годуванняПодушки для годуванняЕрго-рюкзаки
ПустушкиПляшечкиПоїльникиДитячі кухонні комбайниСтерилізатори і підігрівачіСоскиСлюнявчикиАксесуари для дитячого посудуНіблериЧохли та термосумки для пляшечокТермосиПосудСтільці для годування
Приналежності по доглядуНабори по доглядуАспіраториГорщикиВанночкиПідгузкиПелюшки
КосметикаПарфюмеріяСерветки і палочкиМаски для обличчя
Догляд для шкіриЗасоби для купанняДогляд за зубкамиНабори косметики
КоляскиАвтокріслаАксесуари для колясок і автокріселІграшки для колясок і автокрісел
ЛялькиІгрові набориІграшки для малюківМ’які іграшки
Іграшкові машинки і технікаІграшкова зброяРозвиваючі іграшки та центриРухливі ігриДитячі ігрові комплексиМузичні іграшкиПазлиІграшкові фігуркиГоловоломкиТрансформери і роботиНастільні ігри
Розвиваючі іграшкиІграшки для пляжу і пісочниціМашинки і технікаРадіокеровані іграшкиАвтомобільні трекиКолекційні моделькиЗалізниця і аксесуариМоделюванняАксесуари для моделюванняРобототехніка
Інтерактивні іграшкиДитячі комп’ютериКонструкториБізібордиСортериШнурівкиАнтистреси
Іграшки для піскуІграшки для купанняНадувні басейни та гіркиНадувні круги і жилетиНадувні матраци та м’ячіВодяні пістолетиМаски і ластиПісочниці
СамокатиВелосипедиЕлектромобіліВеломобіліЧудомобіліРоликиСкейтбордиАксесуари
Творчість в 3DМалюванняЛіпленняНабориВиготовлення прикрасНаклейки і стікериМозаїкиСкрапбукінг і кардмейкінгПлетінняВиготовлення іграшокШиття і в’язанняАплікаціїДекупажВишиванняНабори для дослідженьМузичні інструментиЗбірні моделіМольбертиДошки для малювання
Спортивний інвентарСанки та снігокатиЛедянки і тарілкиКовзаниЛижіДжампериГойдалкиБатутиЗахист
ЖінкамЧоловікамДитячі речіДля домуКраса і здоров’яДитячі товариСпорт і відпочинокНовинкиЗнижка дня
VIP-Оголошення
Vip
AdidasVip
ZARAVip
BurberryVip
NikeVip
PrimarkVip
GantVip
Brunello CucinelliVip
Vip
ClarksVip
Moon GirlVip
EcoToolsVip
Vip
HandmadeVip
Vip
HandmadeVip
Vip
Best ConnectionVip
Vip
ZARAVip
MARKS & SPENCERVip
New LookVip
ExtraVip
BonprixVip
Реклама на Шафі. Як сюди потрапити?
Як сюди потрапити?
ПОПУЛЯРНІ РУБРИКИ
Верхній одяг
- Норкові шуби
- Еко Шуби
- Зимні куртки
- Хутряні жилетки
- Куртки-косухи
- Джинсові куртки з хутром
- Зимні пальто
- Шкіряні куртки
- Демісезонні куртки
Спідниці
- Олівець
- Кльош
- До підлоги
- Трапеція
- Класика
- Плісировані
- Із завишеною талією
Сукні
- Теплі
- Коктейльна
- В’язані
- До підлоги
- На випускний
- Футляр
- Піджак
- Плісировані
- Бюстьє
Тепле взуття
- Осінні черевики
- Зимні кросівки
- Ботфорди
- Трекінгові черевики
- Зимні чоботи
- Ботильйони
- Уги
- Зимові черевики
Туфлі
- Лофери
- Відкриті
- Лодочки
- Лабутени
- Еспадрільї
- Весільні
- Оксфорди
- Балетки
- Класика
- Мокасини
- Мюлі
Всі бренди
ВИБИРАЙ ЗА БРЕНДАМИ
Ще бренди
- Thomas Sabo
Всі бренди
ПРО СЕРВІС
- 1.
 ціна – тут можна знайти модний брендовий одяг, взуття та аксесуари за доступними цінами з доставкою у будь-яке місто України;
ціна – тут можна знайти модний брендовий одяг, взуття та аксесуари за доступними цінами з доставкою у будь-яке місто України; - 2. асортимент – десятки тисяч одиниць одягу, взуття та аксесуарів розміщені в нашому каталозі;
- 3. ексклюзив – на Шафі можна знайти відмінний брендовий одяг який продають за півціни.
На Шафі є світові бренди за доступними цінами. Наприклад: Zara, H&M, Adidas, Nike
Як купити недорого класну річ на Шафі
1. Знайти в каталозі потрібний розділ або ввести запит в рядку пошуку.
2. Вибрати відповідну річ за фото та описом.
3. Якщо є питання, задати їх продавцеві тут же, на сторінці товару. Не соромтеся попросити точні виміри, додаткові фото і уточнювати стан.
4. Домовитися про спосіб оплати і про доставку в особистому листуванні з продавцем.
Забрати посилку та носити із задоволенням
Продати свої речі на Шафі — простіше простого!
Якщо ви давно шукали, де можна продати б/в речі, то ви потрапили за адресою. З Шафою ви не обмежені своїм містом – будь то Харків, Одеса чи Київ. На нашому сайті щодня тисячі покупців з усієї України готові купити сукні, парфуми, черевики та інші речі за розумними цінами.
З Шафою ви не обмежені своїм містом – будь то Харків, Одеса чи Київ. На нашому сайті щодня тисячі покупців з усієї України готові купити сукні, парфуми, черевики та інші речі за розумними цінами.
Тепер не потрібно продавати або купувати речі в соцмережах, дошках оголошень або на інших неспеціалізованих майданчиках. Спробуйте Шафу, тут набагато зручніше!
Ніколи ще не продавали в інтернеті? Ми допоможемо. Шафа, на відміну від інших майданчиків, була створена для дівчат, які розпродають свій гардероб і роблять це вперше. Почитайте нашу Довідку « Як продати одяг в інтернеті » і сміливо розміщуйте речі, що залежалися.
На Шафі є наступні розділи:
- Жіночий одяг
- Дитячий одяг
- Чоловічий одяг
- Для дому
Модний жіночій одяг у вашому місті
Ви можете знайти продавців відмінного жіночого одягу у вашому місті:
- у Дніпрі
- у Одесі
- у Харкові
- у Львові
- у Запоріжжі
- у Києві
- у Кривому Розі
- у Миколаєві
- у Вінниці
- у Житомирі
- у Чернігові
- у Сумах
- у Полтаві
- у Рівному
- у Черкасах
- у Хмельницькому
- у Кропивницькому
- у Маріуполі
- у Тернопілі
- у Херсоні
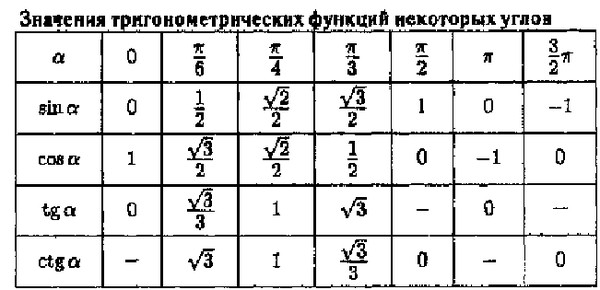
, где члены обоих вышеуказанных рядов попеременно положительные и отрицательные. {2r}(\theta)}.tan(nθ)=cos(nθ)sin(nθ)=2r≤nr=0 ∑(−1)r(2rn)cosn−2r(θ)sin2r(θ)2r+1≤nr=0∑(–1)r(2r+1n)cosn−2r−1(θ) sin2r+1(θ). 9{2r}(\theta)}}.tan(nθ)=2r≤nr=0∑(−1)r(2rn)tan2r(θ)2r+1≤nr=0∑(−1) r(2r+1n)tan2r+1(θ).
{2r}(\theta)}.tan(nθ)=cos(nθ)sin(nθ)=2r≤nr=0 ∑(−1)r(2rn)cosn−2r(θ)sin2r(θ)2r+1≤nr=0∑(–1)r(2r+1n)cosn−2r−1(θ) sin2r+1(θ). 9{2r}(\theta)}}.tan(nθ)=2r≤nr=0∑(−1)r(2rn)tan2r(θ)2r+1≤nr=0∑(−1) r(2r+1n)tan2r+1(θ).
Итак, наше доказательство завершено. □_\квадрат□
Для углов θ1,θ2,θ3,…\theta_1, \theta_2, \theta_3, \ldotsθ1,θ2,θ3,… имеем
- sin(θ1+θ2+θ3+⋯ )=cos (θ1)⋅cos(θ2)⋅cos(θ3)⋯[s1−s3+s5−s7+⋯ ]{\sin(\theta_1 + \theta_2 + \theta_3 +\cdots) = \cos(\theta_1) \ cdot \cos(\theta_2) \cdot \cos(\theta_3) \dotsm [s_1 — s_3 + s_5 — s_7 + \cdots]}sin(θ1+θ2+θ3+⋯)=cos(θ1)⋅ cos(θ2)⋅cos(θ3)⋯[s1−s3+s5−s7+⋯]
- cos(θ1+θ2+θ3+⋯ )=cos(θ1)⋅cos(θ2)⋅cos(θ3)⋯[1−s2+s4−s6+⋯ ]{ \cos(\theta_1 + \theta_2 + \theta_3 + \cdots) = \cos(\theta_1) \cdot \cos(\theta_2) \cdot \cos(\theta_3) \dotsm [1 — s_2 + s_4 — s_6 + \cdots]}cos(θ1+θ2 +θ3+⋯)=cos(θ1)⋅cos(θ2)⋅cos(θ3)⋯[1−s2+s4−s6+⋯]
- tan(θ1+θ2+θ3+⋯ )=s1−s3+s5−s7+⋯1−s2+s4−s6+⋯, {\tan(\theta_1 + \theta_2 +\theta_3 +\cdots) = \dfrac{s_1 — s_3 + s_5 — s_7 + \cdots}{1 — s_2 + s_4 — s_6 + \cdots}},tan(θ1+θ2+θ3+⋯)=1−s2+s4−s6+⋯ s1−s3+s5−s7+⋯,
, где sn = ∑ циклический загар(θ1)загар(θ2)загар(θ3)⋯загар(θn).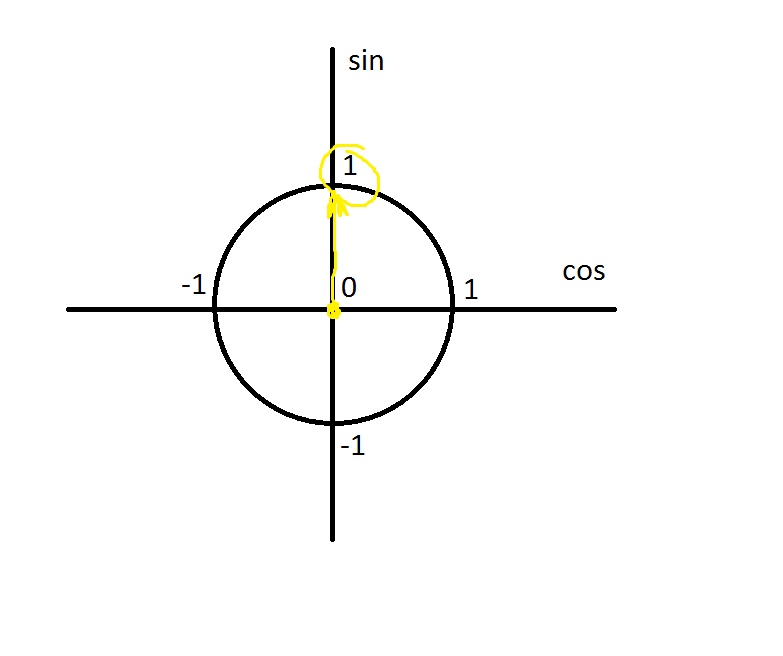 {s_n = \displaystyle \sum_\text{циклический} \tan(\theta_1) \tan(\ theta_2) \tan(\theta_3) \dotsm \tan(\theta_n)}.sn=cyclo∑tan(θ1)tan(θ2)tan(θ3)⋯tan(θn).
{s_n = \displaystyle \sum_\text{циклический} \tan(\theta_1) \tan(\ theta_2) \tan(\theta_3) \dotsm \tan(\theta_n)}.sn=cyclo∑tan(θ1)tan(θ2)tan(θ3)⋯tan(θn).
Извините. Этот раздел временно пуст. Он будет завершен как можно скорее.
Мы покажем здесь, без использования какой-либо формы ряда Тейлора, разложение sin(θ),cos(θ),tan(θ)\sin(\theta), \cos(\theta), \tan(\theta)sin(θ),cos(θ),tan(θ) через θ\thetaθ для малых θ\thetaθ. 95}{15} + \cdots}.tan(θ)=θ+3θ3+152θ5+⋯.
Извините. Этот раздел временно пуст. Он будет завершен как можно скорее.
| 1 | Найти производную — d/dx | натуральное бревно х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x 92) | |
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) по x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | предел, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Калькулятор — cos(n) — Solumaths
Cos, расчет онлайн
Резюме:
Тригонометрическая функция cos вычисляет cos угла в радианах,
градусов или градианов.
cos online
Описание:
Калькулятор позволяет использовать большинство тригонометрических функций , есть возможность вычислить косинус , синус и касательная угла через одноименные функции.
Косинус тригонометрической функции отметил cos , позволяет вычислить косинус угла онлайн , можно использовать разные угловые единицы: градусы, грады и радианы, которые по умолчанию являются угловыми единицами.
- Расчет косинуса
- Специальные значения косинуса
- Основные свойства
- `cos(-x)= cos(x)`
- `cos(x+2*k*pi)=cos(x)`
- `cos(pi-x)=-cos(x) `
- `cos(pi+x)=-cos(x)`
- `cos(pi/2-x)=sin(x)`
- `cos(pi/2+x)=-sin(x) )`
- Производная косинуса
- Первообразная косинуса
- Свойства функции косинуса
- Уравнение с косинусом
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс: котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. - Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упростить калькулятор: упростить. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус : грех. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
Последний
Самые читаемые
Самые цитируемые
- Малый школьный округ (до 2500 учащихся)
- 29 долларов США0 + $ 50 $ Огайо Плата за главу
- Средний школьный округ (2 501–9 999 учеников)
- $ 865 + 100 долларов США в Огайо Глава.
Heisenberg, W. Zur Theorie des Ferromagnetismus. Z. f.ür. физ. 49 , 619–636 (1928).
МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google ученый
Lovesey, S. W. Теория рассеяния нейтронов в конденсированных средах . (Кларендон Пресс, 1984).
Stoner, E.C. Коллективная электронная теплоемкость и спиновой парамагнетизм в металлах. Проц. Р. Соц. Лонд. сер. Математика. физ. науч. 154 , 656–678 (1936).
МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google ученый
Stoner, E.C. Коллективный электронный ферромагнетизм. Проц.
 Р. Соц. Лонд. сер. Математика. физ. науч. 165 , 372–414 (1938).
Р. Соц. Лонд. сер. Математика. физ. науч. 165 , 372–414 (1938).МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google ученый
Слейтер Дж. К. Теория ферромагнетизма: нижние энергетические уровни. Физ. 52 , 198–214 (1937).
МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google ученый
Вольфарт, Э. П. Теоретический и экспериментальный статус коллективной электронной теории ферромагнетизма. Ред. Мод. физ. 25 , 211–219 (1953).
МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google ученый
Фосетт, Э. Антиферромагнетизм СПИН-волн плотности в хроме. Ред. Мод. физ. 60 , 209–283 (1988).
ОБЪЯВЛЕНИЕ Google ученый
Линн, Дж. В. Температурная зависимость магнитных возбуждений в железе.
 Физ. Ред. B 11 , 2624–2637 (1975).
Физ. Ред. B 11 , 2624–2637 (1975).ОБЪЯВЛЕНИЕ Google ученый
Perring, T.G. et al. Высокоэнергетические спиновые волны в ОЦК-железе. г., J. Appl. физ. 69 , 6219–6221 (1991).
ОБЪЯВЛЕНИЕ Google ученый
Мук, Х.А., Линн, Дж.В. и Никлоу, Р.М. Температурная зависимость магнитных возбуждений в никеле. Физ. Преподобный Летт. 30 , 556–559 (1973).
ОБЪЯВЛЕНИЕ Google ученый
Киршнер, Дж., Ребенсторфф, Д. и Ибах, Х. Спектроскопия потерь энергии спин-поляризованных электронов высокого разрешения и стоунеровский спектр возбуждения в никеле. г. Физ. Преподобный Летт. 53 , 698–701 (1984).
ОБЪЯВЛЕНИЕ Google ученый
«>Мория, Т. Спиновые флуктуации в блуждающем электронном магнетизме г. (Спрингер-Верлаг, 1985 г.).
Сазерленд, Б. Локализация электронных волновых функций благодаря локальной топологии. Физ. Ред. B 34 , 5208–5211 (1986).
ОБЪЯВЛЕНИЕ Google ученый
Лейкам Д., Андреанов А. и Флач С. Искусственные плоские ленточные системы: от решетчатых моделей к экспериментам. Доп. Phys.: X 3 , 1473052 (2018).
Google ученый
Тан, Э., Мэй, Дж.-В. и Вен, X.-G. Высокотемпературные дробные квантовые холловские состояния.
 Физ. Преподобный Летт. 106 , 236802 (2011).
Физ. Преподобный Летт. 106 , 236802 (2011).ОБЪЯВЛЕНИЕ Google ученый
Нойпер Т., Сантос Л., Чамон К. и Мадри К. Дробные квантовые состояния Холла при нулевом магнитном поле. Физ. Преподобный Летт. 106 , 236804 (2011).
ОБЪЯВЛЕНИЕ Google ученый
Гимире, Н.Дж. и Мазин, И.И. Топология и корреляции на решетке кагоме. Нац. Матер. 19 , 137–138 (2020).
ОБЪЯВЛЕНИЕ Google ученый
Го, Х. М. и Франц, М. Топологический изолятор на решетке кагоме. Физ. B 80 , 113102 (2009).
ОБЪЯВЛЕНИЕ Google ученый
Мазин И.И. и соавт. Теоретическое предсказание сильно коррелированного металла Дирака.
 Нац. коммун. 5 , 4261 (2014).
Нац. коммун. 5 , 4261 (2014).ОБЪЯВЛЕНИЕ Google ученый
Chen, H., Niu, Q. & MacDonald, A.H. Аномальный эффект Холла, возникающий из-за неколлинеарного антиферромагнетизма. Физ. Преподобный Летт. 112 , 017205 (2014).
ОБЪЯВЛЕНИЕ Google ученый
Тасаки, Х. От ферромагнетизма Нагаоки к плоскозонному ферромагнетизму и дальше: введение в ферромагнетизм в модели Хаббарда. Прог. Теор. физ. 99 , 489–548 (1998).
ОБЪЯВЛЕНИЕ Google ученый
Бистритцер, Р. и Макдональд, А. Х. Полосы муара в скрученном двухслойном графене. Проц. Натл акад. науч. США 108 , 12233–12237 (2011).
ОБЪЯВЛЕНИЕ Google ученый
«>Кан М. и др. Фермионы Дирака и плоские зоны в идеальном металле кагоме FeSn. Нац. Матер. 19 , 163–169 (2020).
ОБЪЯВЛЕНИЕ Google ученый
Liu, Z.H. et al. Орбитально-селективные фермионы Дирака и чрезвычайно плоские зоны в металле CoSn с фрустрированной кагоме-решеткой. Нац. коммун. 11 , 4002 (2020).
ОБЪЯВЛЕНИЕ Google ученый
Кан М. и др. Топологические плоские зоны в фрустрированной решетке кагоме CoSn. Нац. коммун. 11 , 4004 (2020).
ОБЪЯВЛЕНИЕ Google ученый
«>Лин, З. и др. Плоские зоны и возникающее ферромагнитное упорядочение в решетках Кагоме Fe3Sn2. Физ. Преподобный Летт. 121 , 096401 (2018).
ОБЪЯВЛЕНИЕ Google ученый
Инь, Ж.-Х. и другие. Отрицательный магнетизм плоских зон в коррелированном магните кагомэ со спин-орбитальной связью. Нац. физ. 15 , 443–448 (2019).
Google ученый
Дитрих, О. В., Альс-Нильсен, Дж. и Пассел, Л. Рассеяние нейтронов на гейзенберговских ферромагнетиках EuO и EuS. III. Спиновая динамика EuO. Физ. Ред. B 14 , 4923–4945 (1976).
ОБЪЯВЛЕНИЕ Google ученый
«>Дай, П., Ху, Дж. и Даготто, Э. Магнетизм и его микроскопическое происхождение в высокотемпературных сверхпроводниках на основе железа. Нац. физ. 8 , 709–718 (2012).
Google ученый
Sales, B.C. et al. Электронные, магнитные и термодинамические свойства соединения кагомэ-слоя FeSn. г. Физ. Преподобный Матер. 3 , 114203 (2019).
Google ученый
Meier, W.R. et al. Переориентация антиферромагнетизма в легированном кобальтом FeSn. Физ. B 100 , 184421 (2019).
ОБЪЯВЛЕНИЕ Google ученый
«>Luo, H.Q. et al. Эволюция легирования электронами анизотропных спиновых возбуждений в BaFe2-xNixAs2. Физ. Ред. B 86 , https://doi.org/10.1103/PhysRevB.86.024508 (2012 г.).
Xing, Y., Ma, F., Zhang, L. & Zhang, Z. Селективное уплощение магнонных зон в кагоме-решетчатых ферромагнетиках с взаимодействием Дзялошинского-Мория. г. China Phys., Mech. Астрон. 63 , 107511 (2020).
ОБЪЯВЛЕНИЕ Google ученый
Chisnell, R. et al. Топологические магнонные зоны в ферромагнетике с решеткой кагоме. Физ. Преподобный Летт. 115 , 147201 (2015).

ОБЪЯВЛЕНИЕ Google ученый
Yamaguchi, K. & Watanabe, H. Исследование нейтронной дифракции FeSn. J. Phys. соц. Япония. 22 , 1210–1213 (1967).
ОБЪЯВЛЕНИЕ Google ученый
Кулшрешта С.К. и Радж П. Анизотропные сверхтонкие поля в FeSn с помощью мессбауэровской спектроскопии. J. Phys. Ф: Мет. физ. 11 , 281–291 (1981).
ОБЪЯВЛЕНИЕ Google ученый
Дай П. Антиферромагнитный порядок и спиновая динамика в сверхпроводниках на основе железа. Ред. Мод. физ. 87 , 855–896 (2015).
MathSciNet ОБЪЯВЛЕНИЯ Google ученый
ЦИТОП. http://www.bellexinternational.com/products/cytop/.
«>Johnson, J. A. et al. Связь углерод-водород в углероде почти без трения. Заяв. физ. лат. 93 , 131911 (2008 г.).
ОБЪЯВЛЕНИЕ Google ученый
Котляр Г. и др. Расчеты электронной структуры с помощью динамической теории среднего поля. Ред. Мод. физ. 78 , 865–951 (2006).
ОБЪЯВЛЕНИЕ Google ученый
Инь, З. П., Хауле, К. и Котляр, Г. Кинетические расстройства и природа магнитных и парамагнитных состояний в пниктидах и халькогенидах железа.
 Нац. Матер. 10 , 932–935 (2011).
Нац. Матер. 10 , 932–935 (2011).ОБЪЯВЛЕНИЕ Google ученый
Ewings, R. A. et al. Обновите спектрометр с времяпролетным прерывателем нейтронов MAPS. Rev. Sci. Инструм. 90 , 035110 (2019).
ОБЪЯВЛЕНИЕ Google ученый
Granroth, G. E. et al. SEQUOIA: новый спектрометр с прерывателем на SNS. J. Phys.: Conf. сер. 251 , 012058 (2010).
Google ученый
Тот, С. и Лейк, Б. Теория линейных спиновых волн для несоизмеримых магнитных структур с одним добротностью. J. Phys.: Condens. Материя 27 , 166002 (2015).
ОБЪЯВЛЕНИЕ Google ученый
Блаха, П. и др. . WIEN2k: Расширенная программа плоской волны и локальных орбиталей для расчета свойств кристаллов .
 (2019).
(2019).Пердью, Дж. П., Берк, К. и Эрнзерхоф, М. Упрощенное приближение обобщенного градиента. Физ. Преподобный Летт. 77 , 3865–3868 (1996).
ОБЪЯВЛЕНИЕ Google ученый
Хауле, К., Йи, К.-Х. и Ким, К. Динамическая теория среднего поля в рамках полнопотенциальных методов: электронная структура CeIrIn5, CeCoIn5 и CeRhIn5. г. Физ. B 81 , 195107 (2010).
ОБЪЯВЛЕНИЕ Google ученый
Хауле, К. Решатель примесей методом квантового Монте-Карло для кластерной динамической теории среднего поля и расчетов электронной структуры с регулируемой базой кластера. Физ. B 75 , 155113 (2007).
ОБЪЯВЛЕНИЕ Google ученый
Вернер П., Команак А., Медичи Л., Тройер М.
 и Миллис А. Дж. Решатель с непрерывным временем для квантовых моделей примесей. г. Физ. Преподобный Летт. 97 , 076405 (2006).
и Миллис А. Дж. Решатель с непрерывным временем для квантовых моделей примесей. г. Физ. Преподобный Летт. 97 , 076405 (2006).ОБЪЯВЛЕНИЕ Google ученый
Инь З. П., Хауле К. и Котляр Г. Спиновая динамика и симметрия орбитально-противофазного спаривания в сверхпроводниках на основе железа. Нац. физ. 10 , 845–850, http://www.nature.com/nphys/journal/v10/n11/abs/nphys3116.html#supplementary-information (2014).
Google ученый
Факультет физики и астрономии, Университет Райса, Хьюстон, Техас, США
Яофэн Се, Лебинг Чен, Тонг Чен и Пэнчэн Дай
Факультет физики и Пекинская ключевая лаборатория оптоэлектронных функциональных материалов и микронаноустройств Китайского университета Жэньминь, Пекин, Китай , STFC Rutherford Appleton Laboratory, Didcot, OX11 0QX, UK
J. Ross Stewart
Neutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, TN, USA
Matthew B. Stone, Luke L. Daemen, Erxi Фэн и Хуэйбо Цао
Центр перспективных квантовых исследований и факультет физики Пекинского педагогического университета, Пекин, Китай
Чжипин Инь
Факультет физики Техасского университета в Остине, Остин, Техас, США
Аллан Х.
 Макдональд
Макдональд- Yaofeng Xie
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Лебинг Чен
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Тонг Чен
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Qi Wang
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Qiangwei Yin
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- J. Ross Stewart
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Мэтью Б.
 Стоун
СтоунПросмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Luke L. Daemen
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Erxi Feng
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Huibo Cao
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Hechang Lei
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
- Zhiping Yin
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Allan H. MacDonald
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Pengcheng Dai
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Расчет косинуса угла в радианах
Калькулятор косинуса позволяет через функцию cos вычислить онлайн косинус угла в радианах, вы должны сначала
выберите нужную единицу, нажав на кнопку параметров расчетного модуля.
После этого можно приступать к расчетам.
Чтобы вычислить косинус онлайн от `pi/6`, введите cos(`pi/6`), после вычисления результат `sqrt(3)/2` возвращается.
Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.
Вычислить косинус угла в градусах
Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Для вычисления косинуса 90, введите cos(90), после расчета возвращает 0.
Вычислить косинус угла в градусах
Для вычисления косинуса угла в градианах необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить косинус 50, введите cos(50), после вычисления
возвращается результат `sqrt(2)/2`.
Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.
Косинус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот список специальные значения косинуса :
| cos(`2*pi`) | `1` | ||||||||||
| cos(`pi`) | `-1` | ||||||||||
| cos(`pi/2`) | `0` | ||||||||||
| cos(`pi/4`) | `sqrt(2)/2` | ||||||||||
| `1/2` | |||||||||||
| cos(`pi/6`) | `sqrt(3)/2` | ||||||||||
| cos(`2*pi/3`) | `-1/2` | ||||||||||
| cos(`3*pi/4`) | `-sqrt(2)/2` | ||||||||||
| cos(`5*pi/6`) | `- sqrt(3)/2` | ||||||||||
| cos(`0`) | `1` | ||||||||||
| cos(`-2*pi`) | `1` | ||||||||||
| cos(`-pi`) | `-1` | ||||||||||
| cos(`-pi/4`) | `sqrt(2)/2` |
| cos(`-pi/3`) | `1/2` |
| cos(`-pi/3`) (`-pi/6`) | `sqrt(3)/2` |
| cos(`-2*pi/3`) | `-1/2` |
| cos(`-3 *pi/4`) | `-sqrt(2)/2` |
| cos(`-5*pi/6`) | `-sqrt(3)/2` |
`AA x в RR, k в ZZ`,
Производная косинуса равна -sin(x).
Первообразная косинуса равна sin(x).
Функция косинуса является четной функцией для каждого действительного x, `cos(-x)=cos(x)`. Следствием для кривой, представляющей функцию косинуса, является то, что она допускает ось ординат как ось симметрии.
Калькулятор имеет решатель, который позволяет решать уравнение с косинусом формы cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `cos(x)=1/2` или же `2*cos(x)=sqrt(2)` с этапами расчета.
Синтаксис:
cos(x), где x — мера угла в градусах, радианах или градах.
Примеры:
cos(`0`), возвращает 1
Производный косинус:
Чтобы дифференцировать функцию косинуса онлайн,
можно использовать калькулятор производной, который позволяет вычислить производную функции косинуса.
Первообразная косинуса :
Калькулятор первообразной позволяет вычислить первообразную функции косинуса.
Первопроизводная cos(x) является первопроизводной(`cos(x)`)=`sin(x)`
Предел косинуса :
Калькулятор предела позволяет вычислить пределы функции косинуса.
предел cos(x) is limit(`cos(x)`)
Обратная функция косинуса :
обратная функция косинуса является функцией арккосинуса, отмеченной как arccos.
Графический косинус:
Графический калькулятор может отображать функцию косинуса в заданном интервале.
Свойство функции косинуса:
Функция косинуса является четной функцией.
Расчет онлайн с косинусом
См. также
Список связанных калькуляторов:
Напоминания о курсах, калькуляторы, упражнения и игры: Тригонометрические функции, Вещественные функции
Лагранжева интерполяция в точках Чебышева xn, ν ≡ cos (νπ/n), ν = 0(1)n; некоторые незамеченные преимущества | Компьютерный журнал
Фильтр поиска панели навигации The Computer JournalЭтот выпускЖурналы BCSИнформатикаКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации The Computer JournalЭтот выпускЖурналы BCSИнформатикаКнигиЖурналыOxford Academic Термин поиска на микросайте
Расширенный поиск
Журнальная статья
Х. Э. Зальцер
Э. Зальцер
HE Salzer
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
Компьютерный журнал , том 15, выпуск 2, май 1972 г., страницы 156–159, https://doi.org/10.1093/comjnl/15.2.156
Опубликовано:
01 мая 1972 г.
История статьи
Получено:
1 марта 1971 г.
Опубликовано:
1 мая 1972 г.
Фильтр поиска панели навигации The Computer JournalЭтот выпускЖурналы BCSИнформатикаКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации The Computer JournalЭтот выпускЖурналы BCSИнформатикаКнигиЖурналыOxford Academic Термин поиска на микросайте
Расширенный поиск
Помимо многих приложений точек Чебышева x n ν ≡ cos(νπ/ n ),ν = 0(1) n численное интегрирование и численное дифференцирование имеют преимущества при их использовании в барицентрической форме интерполяционной формулы Лагранжа и при проверке разделенными разностями. Когда n = 2 m , получаем X 2 m ,ν с меньшим, чем половина числа квадратных корней, необходимых для нахождения остальных точек Чебышева X 8 ′ 91 ,ν ≡ cos[(2ν – 1) π/2 m +1 ], ν = 1(1)2 m . Кроме того, формула барицентрической интерполяции может быть применена к решению почти минимаксной задачи, чтобы избежать обширного вычисления вспомогательных полиномов, а также в процедуре численного дифференцирования, которая удобно обходит прямое дифференцирование интерполяционного полинома.
Когда n = 2 m , получаем X 2 m ,ν с меньшим, чем половина числа квадратных корней, необходимых для нахождения остальных точек Чебышева X 8 ′ 91 ,ν ≡ cos[(2ν – 1) π/2 m +1 ], ν = 1(1)2 m . Кроме того, формула барицентрической интерполяции может быть применена к решению почти минимаксной задачи, чтобы избежать обширного вычисления вспомогательных полиномов, а также в процедуре численного дифференцирования, которая удобно обходит прямое дифференцирование интерполяционного полинома.
Этот контент доступен только в формате PDF.
© Британское компьютерное общество
© Британское компьютерное общество
Раздел выпуска:
Технические приложения
Скачать все слайды
Реклама
Цитаты
Альтметрика
Дополнительная информация о метриках
Оповещения по электронной почте
Оповещение об активности статьи
Предварительные уведомления о статьях
Оповещение о новой проблеме
Получайте эксклюзивные предложения и обновления от Oxford Academic
Ссылки на статьи по номеру
Двойной поиск контента и схема прогнозирования местоположения производителя для мобильности производителя в именованных сетях передачи данных
Факторизация значений на основе символов для MADRL
Новая схема запутывания соединений
Криптоанализ на 3D с уменьшенным числом раундов и Saturnin
CCESHP: Модель причинно-следственной согласованности пограничного хранилища на основе хэш-кольца и частичной георепликации
Реклама
Огайо CoSN – Learn21
Кто мы
Огайо CoSN является государственным отделением CoSN, Консорциума школьных сетей. Миссия и видение отделения CoSN Learn21, штат Огайо, заключается в разработке стандартов для технологических лидеров в школьных системах штата Огайо, защите новых тенденций на местном уровне и уровне штата и постоянном профессиональном развитии технологических лидеров и других руководителей округов. Мы считаем, что эти цели дополняют миссию CoSN по расширению возможностей лидеров образования для использования технологий для создания привлекательной среды обучения для всех заинтересованных сторон в школьных системах по всему штату Огайо.
Миссия и видение отделения CoSN Learn21, штат Огайо, заключается в разработке стандартов для технологических лидеров в школьных системах штата Огайо, защите новых тенденций на местном уровне и уровне штата и постоянном профессиональном развитии технологических лидеров и других руководителей округов. Мы считаем, что эти цели дополняют миссию CoSN по расширению возможностей лидеров образования для использования технологий для создания привлекательной среды обучения для всех заинтересованных сторон в школьных системах по всему штату Огайо.
В 2017 году компания Learn21 основала отделение CoSN штата Огайо. Learn21 использует свои некоммерческие ресурсы для поддержки миссии и совета директоров Ohio CoSN. Совет директоров и финансы Learn21 отделены от CoSN штата Огайо. Руководящая группа и правление CoSN в Огайо руководят финансами и миссией CoSN в Огайо.
Группа руководителей CoSN штата Огайо
Дженнифер Фрай
Председатель
Арлин Пике
Заместитель председателя
Stephen Collins
Treasurer
Rebecca Furlong
Secretary
Dustin Ruffell
Officer at Large
Brian Seymour
Officer at Large
Jennette Irish-Glass
Officer at Большой
Тодд Уэсли
Офицер на свободе
Б. Дж.1003
Дж.1003
Officer at Large
Bill Fritz
Officer at Large
Sean Whalen
Officer at Large
Mike Daugherty
Past Chair
K12 EdTech Leadership
Mentorship Program
Программа наставничества направлена на подготовку квалифицированных лидеров образовательных технологий и технических директоров. Программа поднимает планку для технологических лидеров и создает сообщество поддержки посредством наставничества и сотрудничества. Программа также направлена на информирование суперинтендантов и руководителей округов о важности должности технического директора на уровне кабинета министров. Программа управляется и спонсируется CoSN штата Огайо и поддерживается Learn21. Контакт для получения дополнительной информации: Дженнифер Фрай
18 ноября 2021 г. Веб-семинар по лидерству
16 декабря 2021 г. Веб-семинар по созданию команды и подбору персонала
20 января 2022 г. Веб-семинар по управлению бизнесом
Веб-семинар по управлению бизнесом
17 февраля 2022 г. Веб-семинар по вопросам обучения
17 марта 2022 г. Веб-семинар по этике и политике 1
21 апреля, веб-семинар по коммуникациям 19 мая 2022 г. Вебинар по управлению данными
Сертификационная программа и семинары CETL
Огайо CoSN помогает подготовить лидеров образовательных технологий к карьерному росту. Каждый год CoSN публикует опрос руководителей ИТ-отделов Edtech, и из него мы узнаем, что единого пути к роли технического директора не существует. На самом деле технические директора по всей стране проходят 2 основных пути, с 49% имеют технологическое или техническое образование, а 45% имеют образование или педагогическое образование.
CoSN удовлетворил потребности лидеров образовательных технологий, которые идут по одному из этих путей или в другом направлении, разработав структуру основных навыков технического директора K-12. Это свод знаний, на котором основан экзамен CoSN CETL®, и руководство по всему, что должен знать и делать успешный технический директор. Все профессиональные ресурсы CoSN основаны на Framework.
Все профессиональные ресурсы CoSN основаны на Framework.
Заинтересованы ли вы в получении сертификата Certified Education Technology Leader (CETL®)? Огайо CoSN проводит семинары CETL, которые обучают вас фундаментальным принципам CoSN Framework of Essentials Skills — основе аккредитованной на национальном уровне сертификации CETL®. Семинары проводятся каждую осень и весну. Если вы хотите участвовать в совместной и поддерживающей когорте для подготовки к сертификационному экзамену CETL®, свяжитесь с Майком Дотери
Кибербезопасность
Огайо CoSN признала необходимость поддерживать, формировать и направлять диалог о кибербезопасности для лидеров Огайо K12. Свяжитесь с Джоном Риццо, чтобы узнать, как вы можете присоединиться к разговору и быть в курсе.
Learn21 Ohio CoSN Conference
Learn21 Ohio CoSN Conference — это ведущая конференция лидеров образовательных технологий штата Огайо. Конференция объединяет экспертов, которые обсуждают перспективные технологические темы и возникающие технические проблемы в соответствии с инновационными практиками. Конференция проводится ежегодно осенью и собирает лидеров и партнеров образовательных технологий штата Огайо K-12 в Колумбусе, штат Огайо. Отметьте в календаре: 2–3 ноября 2022 г.
Конференция проводится ежегодно осенью и собирает лидеров и партнеров образовательных технологий штата Огайо K-12 в Колумбусе, штат Огайо. Отметьте в календаре: 2–3 ноября 2022 г.
Партнеры CoSN штата Огайо
Повышайте свою карьеру
Присоединяйтесь к CoSN штата Огайо
Консорциум школьной сети (CoSN) — это ведущая профессиональная ассоциация руководителей школьных системных технологий. CoSN предоставляет ресурсы для интеллектуального лидерства, сообщество, передовой опыт и инструменты защиты, чтобы помочь лидерам образовательных технологий добиться успеха в цифровой трансформации. Присоединяйтесь к разговору на конференции CoSN National, Огайо CoSN Conference,
и СТО клиники.
Доступ к библиотеке ресурсов, технических документов и инструментов CoSN, которые
поддерживают вашу работу.
Совершенствуйте свои лидерские навыки, так как
Ohio CoSN проводит семинары CETL
, программы наставничества, семинары
CTO и награды за лидерство.
Примите участие и станьте членом правления
Ohio CoSN.
Ежегодные членские взносы
Learn21 Ohio CoSN Conference
Learn21 Ohio CoSN Conference — это ведущая конференция лидеров образовательных технологий штата Огайо. Конференция объединяет экспертов, которые обсуждают перспективные технологические темы и возникающие технические проблемы в соответствии с инновационными практиками. Конференция проводится ежегодно осенью и собирает лидеров и партнеров образовательных технологий штата Огайо K-12 в Колумбусе, штат Огайо. Отметьте в календаре — 2–3 ноября 2022 г.
Узнать больше
Альянс по обеспечению конфиденциальности данных учащихся штата Огайо (OSDPA)Кто мы
Learn21 – это Альянс по защите данных учащихся штата Огайо (OSDPA), партнерство с Консорциумом по защите данных учащихся Access 4 Learning Community ( СДПК). Learn21 присоединился к этому консорциуму от имени всех школ штата Огайо.
Learn21 присоединился к этому консорциуму от имени всех школ штата Огайо.
Чем мы занимаемся
OSDPA предоставляет каждому округу штата Огайо бесплатное членство для доступа к общегосударственному соглашению, которое округа могут использовать для обеспечения того, чтобы поставщик знал и соблюдал национальные законы о конфиденциальности данных учащихся. Доступная для поиска база данных приложений и поставщиков, которые подписали общегосударственное соглашение по крайней мере с одной школой или округом. База данных обеспечивает прозрачность для учителей, родителей и других лиц, чтобы определить, соответствует ли приложение требованиям. Он также создает перечень используемых приложений и позволяет учителям запрашивать проверку нового приложения в их организации.
Примите участие
Примите участие в работе OSDPA, защитите свою организацию K12 и сотрудничайте с коллегами в Огайо и по всей стране. Свяжитесь с Биллом Фрицем или Дон Скьявоне для получения дополнительной информации.
Спиновые возбуждения в металлической решетке кагомэ FeSn и CoSn
Abstract
В двумерных (2D) металлических материалах с решеткой кагомэ деструктивная интерференция электронных прыжковых путей вокруг скобки кагомэ может производить почти локализованные электроны и, таким образом, электронные зоны, которые являются плоскими в импульсном пространстве. Когда ферромагнитный порядок снимает вырождение электронных зон и расщепляет их на электронные зоны со спином вверх и в меньшинстве, квазичастичные возбуждения между плоскими зонами со спином вверх и вниз должны образовывать узкий локализованный континуум Стонера со спином и возбуждением. сосуществующие с четко определенными спиновыми волнами в длинноволновом диапазоне. Здесь мы сообщаем об исследованиях неупругого рассеяния нейтронов спиновых возбуждений в антиферромагнитном FeSn и парамагнитном CoSn в металлической решетке кагоме, где эксперименты по фотоэмиссионной спектроскопии с угловым разрешением обнаружили спин-поляризованные и неполяризованные плоские полосы, соответственно, ниже уровня Ферми. Наши измерения на FeSn и CoSn выявили четко определенные спиновые волны, распространяющиеся выше 140 мэВ, и коррелированное парамагнитное рассеяние вокруг точки Γ ниже 90 мэВ соответственно. Кроме того, мы наблюдали недисперсионные возбуждения при ~170 мэВ и ~360 мэВ, возникающие в основном из-за углеводородного рассеяния CYTOP-M, используемого для приклеивания образцов к алюминиевому держателю. Таким образом, наши результаты установили эволюцию спиновых возбуждений в FeSn и CoSn и идентифицировали аномальные плоские моды, которые в течение многих лет упускались из виду сообществом, занимающимся рассеянием нейтронов.
Наши измерения на FeSn и CoSn выявили четко определенные спиновые волны, распространяющиеся выше 140 мэВ, и коррелированное парамагнитное рассеяние вокруг точки Γ ниже 90 мэВ соответственно. Кроме того, мы наблюдали недисперсионные возбуждения при ~170 мэВ и ~360 мэВ, возникающие в основном из-за углеводородного рассеяния CYTOP-M, используемого для приклеивания образцов к алюминиевому держателю. Таким образом, наши результаты установили эволюцию спиновых возбуждений в FeSn и CoSn и идентифицировали аномальные плоские моды, которые в течение многих лет упускались из виду сообществом, занимающимся рассеянием нейтронов.
Введение
Магнитные металлы поддерживают как коллективные спин-волновые (рис. 1а), так и квазичастичные (Стоунера) (рис. 1б, в) возбуждения с переворотом спина 1,2,3,4,5,6,7 . В трехмерных (3D) металлических ферромагнетиках, таких как железо 8,9 и никель 10 , полосы квазичастиц широкие, а спиновые волны четко выражены только на больших длинах волн, исчезая, когда они входят в континуум Стонера на промежуточных значениях спина.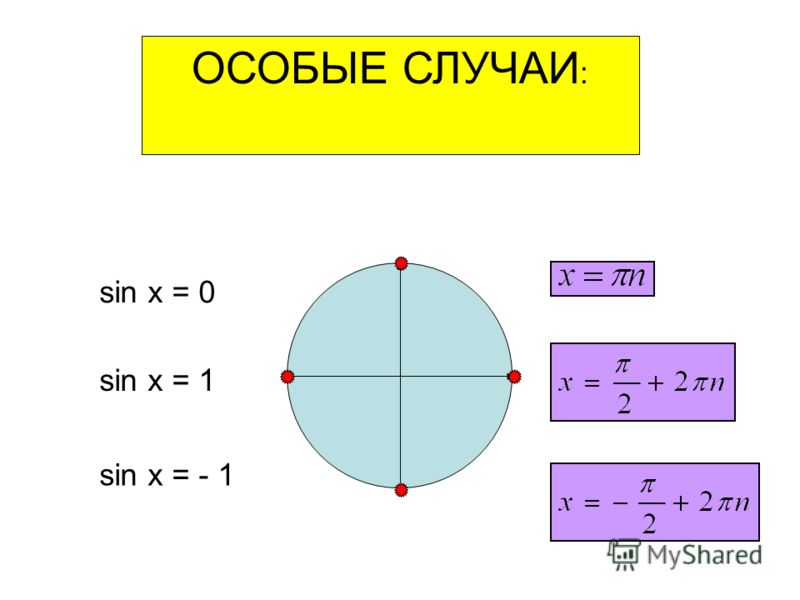 волновые импульсы (рис. 1в) 11,12,13 . В материалах с двумерной металлической решеткой кагомэ (рис. 1d–g) деструктивная интерференция путей электронных прыжков вокруг скобки кагомэ может создавать почти локализованные электроны и, следовательно, электронные полосы, которые являются плоскими в импульсном пространстве (рис. 1h–j) 14,15,16,17,18 . В сочетании со спин-орбитальной связью и магнитным порядком плоские полосы, индуцированные геометрической фрустрацией, обеспечивают идеальную платформу для новых топологических фаз 19,20,21 , ферромагнетизма 22 и сверхпроводимости 23,24 . Хотя плоские полосы ниже уровня Ферми недавно были идентифицированы в антиферромагнитном (АФ) металле кагоме FeSn 25 , парамагнитном металле кагоме CoSn 26,27 , а также в других материалах 28,29,30 , их влияние на спин-волновые и стонеровские возбуждения неизвестно.
волновые импульсы (рис. 1в) 11,12,13 . В материалах с двумерной металлической решеткой кагомэ (рис. 1d–g) деструктивная интерференция путей электронных прыжков вокруг скобки кагомэ может создавать почти локализованные электроны и, следовательно, электронные полосы, которые являются плоскими в импульсном пространстве (рис. 1h–j) 14,15,16,17,18 . В сочетании со спин-орбитальной связью и магнитным порядком плоские полосы, индуцированные геометрической фрустрацией, обеспечивают идеальную платформу для новых топологических фаз 19,20,21 , ферромагнетизма 22 и сверхпроводимости 23,24 . Хотя плоские полосы ниже уровня Ферми недавно были идентифицированы в антиферромагнитном (АФ) металле кагоме FeSn 25 , парамагнитном металле кагоме CoSn 26,27 , а также в других материалах 28,29,30 , их влияние на спин-волновые и стонеровские возбуждения неизвестно.
 1: Схематические диаграммы спиновых волн, континуума Стонера, решеточной и магнитной структур FeSn и его обозначения в обратном пространстве.
1: Схематические диаграммы спиновых волн, континуума Стонера, решеточной и магнитной структур FeSn и его обозначения в обратном пространстве. a Коллективные спиновые волны в модели Гейзенберга с локальным моментом. b , c Схематические иллюстрации возбуждений Стонера. Это возбуждение соответствует переходу от занятых состояний в полосе со спином вверх к незанятым состояниям в полосе со спином вниз. Пронумерованные стрелки в ( b ) указывают на возможные процессы рассеяния, соответствующие пронумерованным точкам ( c ) энергетического спектра одночастичных возбуждений электронно-дырочной пары. d Кристаллическая и магнитная структуры FeSn. e Top view of the kagome lattice, where J 1 , J 2 , and J c are the dominant magnetic interactions used in the Heisenberg model to fit спиновые волны FeSn. f , g 3D и 2D зоны Бриллюэна FeSn соответственно.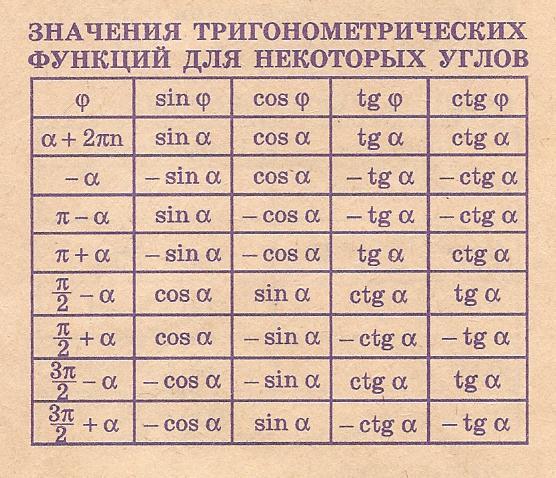 Указаны точки высокой симметрии, а шестиугольником зеленого цвета отмечена область интегрирования в обратном пространстве для получения полного магнитного рассеяния в пределах одной зоны Бриллюэна. h , i , j Схематические иллюстрации деструктивных квантовых интерференций, индуцированных электронным ограничением и плоской зоной в решетке кагоме. Прыжки электронов за пределы фиолетового шестиугольника будут запрещены из-за противофазы собственных состояний плоских зон в соседних подрешетках, что приводит к идеальной локализации электронов и плоской электронной зоне в обратном пространстве.
Указаны точки высокой симметрии, а шестиугольником зеленого цвета отмечена область интегрирования в обратном пространстве для получения полного магнитного рассеяния в пределах одной зоны Бриллюэна. h , i , j Схематические иллюстрации деструктивных квантовых интерференций, индуцированных электронным ограничением и плоской зоной в решетке кагоме. Прыжки электронов за пределы фиолетового шестиугольника будут запрещены из-за противофазы собственных состояний плоских зон в соседних подрешетках, что приводит к идеальной локализации электронов и плоской электронной зоне в обратном пространстве.
Изображение в натуральную величину
В общем случае возбуждения с переворотом спина в магнетике можно интерпретировать либо в рамках квантовой спиновой модели 1,2 с локальными моментами на каждом атомном узле (рис. 1а), либо в рамках модели Стонера 3,4,5,6,13 модель блуждающего электрона. В изолирующих ферромагнетиках, таких как EuO, магнитные возбуждения могут быть полностью описаны гамильтонианом Гейзенберга 31 со спинами в узлах решетки Eu. В ферромагнитных (ФМ) металлах магнитный порядок нарушает вырождение электронных зон, расщепляя большинство электронов со спином вверх и неосновные электроны со спином вниз (рис. 1b) 6 . Для трехмерных металлических ФМ Fe и Ni низкоэнергетические спиновые волны сильно затухают, когда они входят в широкий стонеровский континуум зонно-электронных спин-флипов, энергия которого простирается на несколько эВ (рис. 1c) 8,9,10, 11,12 . Для парамагнитного металла нет расщепления вырожденных электронных зон, хотя континуум возбуждений электронно-дырочных пар (континуум Стонера) все же может возникать, если в системе есть электронные и дырочные карманы ниже и выше уровня Ферми. В сильно коррелированных материалах, таких как сверхпроводники на основе меди и железа, тонкий баланс между кинетической энергией электронов и короткодействующими взаимодействиями может привести к спорам о том, имеет ли магнетизм локальное или блуждающее происхождение 32,33 .
В ферромагнитных (ФМ) металлах магнитный порядок нарушает вырождение электронных зон, расщепляя большинство электронов со спином вверх и неосновные электроны со спином вниз (рис. 1b) 6 . Для трехмерных металлических ФМ Fe и Ni низкоэнергетические спиновые волны сильно затухают, когда они входят в широкий стонеровский континуум зонно-электронных спин-флипов, энергия которого простирается на несколько эВ (рис. 1c) 8,9,10, 11,12 . Для парамагнитного металла нет расщепления вырожденных электронных зон, хотя континуум возбуждений электронно-дырочных пар (континуум Стонера) все же может возникать, если в системе есть электронные и дырочные карманы ниже и выше уровня Ферми. В сильно коррелированных материалах, таких как сверхпроводники на основе меди и железа, тонкий баланс между кинетической энергией электронов и короткодействующими взаимодействиями может привести к спорам о том, имеет ли магнетизм локальное или блуждающее происхождение 32,33 .
В некоторых двумерных кристаллах электроны могут удерживаться в реальном пространстве, образуя плоские полосы, например, за счет нарушения геометрической решетки 19,20,21 . Плоские полосы скрученного под магическим углом двухслойного графена 23 представляют собой один из примеров этого пути к сильной электронной корреляции 24 . Решетка кагомэ, изображенная на рис. 1h, в которой простейшая модель электронного прыжка ближайшего соседа предсказывает деструктивную фазовую интерференцию (рис. 1i), приводящую к локализации электронов в реальном пространстве и плоской электронной зоне (рис. 1j) 20 , обеспечивает второй. Недавно с помощью фотоэмиссионной спектроскопии с угловым разрешением (ARPES) в экспериментах по фотоэмиссионной спектроскопии с угловым разрешением (ARPES) 25 недавно была идентифицирована спин-поляризованная плоская электронная полоса в металле AF кагоме FeSn при энергии \(E = 230 мкм\)50 мэВ ниже уровня Ферми. FeSn представляет собой АФ типа A с антиферромагнитно связанными ФМ-плоскостями 34 , которые мы будем рассматривать как двумерные ферромагнетики. Нейтроны в принципе должны обнаруживать стонеровские возбуждения электронно-дырочной пары от плоской полосы большинства спинов ниже уровня Ферми до полос неосновных спинов вблизи или выше уровня Ферми (рис.
Плоские полосы скрученного под магическим углом двухслойного графена 23 представляют собой один из примеров этого пути к сильной электронной корреляции 24 . Решетка кагомэ, изображенная на рис. 1h, в которой простейшая модель электронного прыжка ближайшего соседа предсказывает деструктивную фазовую интерференцию (рис. 1i), приводящую к локализации электронов в реальном пространстве и плоской электронной зоне (рис. 1j) 20 , обеспечивает второй. Недавно с помощью фотоэмиссионной спектроскопии с угловым разрешением (ARPES) в экспериментах по фотоэмиссионной спектроскопии с угловым разрешением (ARPES) 25 недавно была идентифицирована спин-поляризованная плоская электронная полоса в металле AF кагоме FeSn при энергии \(E = 230 мкм\)50 мэВ ниже уровня Ферми. FeSn представляет собой АФ типа A с антиферромагнитно связанными ФМ-плоскостями 34 , которые мы будем рассматривать как двумерные ферромагнетики. Нейтроны в принципе должны обнаруживать стонеровские возбуждения электронно-дырочной пары от плоской полосы большинства спинов ниже уровня Ферми до полос неосновных спинов вблизи или выше уровня Ферми (рис. 1b) 6,13 . Поскольку рассеяние нейтронов измеряет возбуждения пары электрон-дырка, наличие плоской электронной полосы со спином вверх ниже уровня Ферми является необходимым, но недостаточным условием для наблюдения плоской полосы континуума Стонера. Вместо этого такая бездисперсионная узкая полоса возбуждения энергетического спина также требует наличия плоской электронной зоны со спином вниз выше (или вблизи) уровня Ферми 13 . К сожалению, измерения ARPES не могут дать никакой информации о такой электронной зоне выше уровня Ферми, хотя расчеты теории функционала плотности (DFT) предполагают ее наличие 25 . Для сравнения, хотя измерения ARPES также идентифицировали плоскую полосу с энергией \(E = 270 мкм\)50 мэВ ниже уровня Ферми в CoSn 26,27 , нельзя было бы ожидать наблюдения плоской полосы стонеровского континуума из-за вырожденная электронная полосовая природа системы 35 .
1b) 6,13 . Поскольку рассеяние нейтронов измеряет возбуждения пары электрон-дырка, наличие плоской электронной полосы со спином вверх ниже уровня Ферми является необходимым, но недостаточным условием для наблюдения плоской полосы континуума Стонера. Вместо этого такая бездисперсионная узкая полоса возбуждения энергетического спина также требует наличия плоской электронной зоны со спином вниз выше (или вблизи) уровня Ферми 13 . К сожалению, измерения ARPES не могут дать никакой информации о такой электронной зоне выше уровня Ферми, хотя расчеты теории функционала плотности (DFT) предполагают ее наличие 25 . Для сравнения, хотя измерения ARPES также идентифицировали плоскую полосу с энергией \(E = 270 мкм\)50 мэВ ниже уровня Ферми в CoSn 26,27 , нельзя было бы ожидать наблюдения плоской полосы стонеровского континуума из-за вырожденная электронная полосовая природа системы 35 .
В этой статье мы сообщаем об исследованиях спиновых возбуждений методом неупругого рассеяния нейтронов (ИНН) в двумерных металлических антиферромагнитных FeSn 34 решетках кагоме и парамагнитных CoSn 35 . Для FeSn наши измерения показывают хорошо выраженные спиновые волны, распространяющиеся значительно выше 140 мэВ. Однако нет никаких свидетельств узкополосного континуума Стонера, ожидаемого из расчета зонной структуры. Для CoSn существуют коррелированные парамагнитные рассеяния с центром вокруг точки Γ, простирающиеся до ~90 мэВ. Мы также наблюдаем две бездисперсионные полосы возбуждения при ~170 мэВ и ~360 мэВ в FeSn и CoSn, обусловленные в основном углеводородным рассеянием CYTOP-M (торговая марка фторполимера), обычно используемого для приклеивания образцов к алюминиевому держателю 36 . Таким образом, наши результаты установили эволюцию спиновых возбуждений в FeSn и CoSn и показали, что наблюдаемая плоская электронная полоса ниже уровня Ферми не индуцирует узкозонный континуум Стонера. Кроме того, мы идентифицировали аномальные плоские моды, возникающие в основном из-за фононного рассеяния CYTOP-M. Повторный анализ данных высокоспинового возбуждения образцов пниктида железа, склеенных с помощью CYTOP-M, подтвердил наличие плоской моды ~170 мэВ, на которую не обращали внимания в течение многих лет9.
Для FeSn наши измерения показывают хорошо выраженные спиновые волны, распространяющиеся значительно выше 140 мэВ. Однако нет никаких свидетельств узкополосного континуума Стонера, ожидаемого из расчета зонной структуры. Для CoSn существуют коррелированные парамагнитные рассеяния с центром вокруг точки Γ, простирающиеся до ~90 мэВ. Мы также наблюдаем две бездисперсионные полосы возбуждения при ~170 мэВ и ~360 мэВ в FeSn и CoSn, обусловленные в основном углеводородным рассеянием CYTOP-M (торговая марка фторполимера), обычно используемого для приклеивания образцов к алюминиевому держателю 36 . Таким образом, наши результаты установили эволюцию спиновых возбуждений в FeSn и CoSn и показали, что наблюдаемая плоская электронная полоса ниже уровня Ферми не индуцирует узкозонный континуум Стонера. Кроме того, мы идентифицировали аномальные плоские моды, возникающие в основном из-за фононного рассеяния CYTOP-M. Повторный анализ данных высокоспинового возбуждения образцов пниктида железа, склеенных с помощью CYTOP-M, подтвердил наличие плоской моды ~170 мэВ, на которую не обращали внимания в течение многих лет9.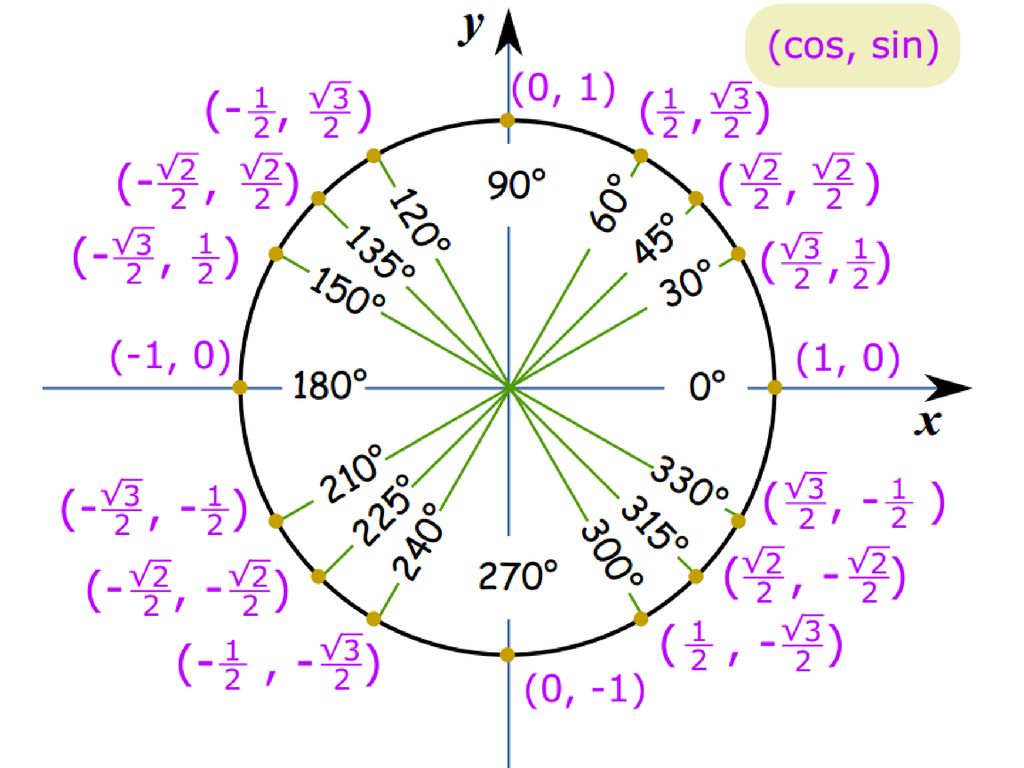 1444 37 .
1444 37 .
Результаты
Рассеяние нейтронов на FeSn
Нами проведены эксперименты по ИНС по изучению спиновых волн и поиску аномальных стонеровских возбуждений в АФ-кагоме металлическом FeSn 34 и парамагнитном CoSn 35 . Структура FeSn состоит из двумерных кагоме-сеток Fe, разделенных слоями Sn, и демонстрирует AF-порядок ниже \(T_N \приблизительно 365\) K с плоскостными FM-моментами в каждом слое, антиферромагнитно сложенными вдоль оси c ( Рис. 1г) 34 . Поскольку каждая элементарная ячейка содержит три атома Fe (рис. 1e), мы ожидаем одну акустическую и две оптические спин-волновые ветви в локальном моменте Гейзенберговского гамильтониана 34,38,39 . На рис. 1f, g показаны обратные пространства, соответствующие кристаллическим структурам FeSn, изображенным на рис. 1d, e соответственно. CoSn имеет ту же кристаллическую структуру, что и FeSn, но является парамагнитным при всех температурах 35 .
На рис. 2а показаны низкоэнергетические спиновые возбуждения, наблюдаемые в FeSn вдоль направлений высокой симметрии в ( H , K ) самолет, изображенный на рис. 1g. Мы видим почти изотропную моду спиновых волн, происходящую от точки Γ в центре ФМ-зоны, которая движется к границе зоны с ростом энергии. В направлении [ H ,0,0] к точке M акустическая мода достигает границы зоны около 90 мэВ. На рис. 2b показано изображение зависимости передачи волнового вектора ( Q ) и энергии ( E ) спиновых возбуждений вокруг М точка. Данные подтверждают, что акустические спиновые волны достигают около 90 мэВ в точке M , и обнаруживают оптическую моду спиновых волн, которая видна при энергиях между 115 и 140 мэВ и характеризуется противофазными колебаниями среди три спина подрешетки Fe. Эволюция плоскостной Q -зависимости акустических спиновых волн с увеличением энергии представлена на рис. 2e, где видны кольца спиновых волн вокруг точки Γ , которые увеличиваются с увеличением энергии. В отличие от плоскостных ЧМ спиновых волн, происходящих от Γ , энергии возбуждения которых превышают 140 мэВ (рис. 2а, д), спиновые волны вдоль оси c происходят от волновых векторов упорядочения АФ \({{{{{{{\boldsymbol{Q }}}}}}}} = (0,0,0,5 + L)\) при ( L = 0, 1) и достигают границы зоны около \(E \приблизительно 20\) мэВ (рис. 2ж) , что отражает относительно слабую связь между ферромагнитными плоскостями кагоме. Мы также наблюдаем щель легкой оси анизотропии \({\Delta}_a \приблизительно 2\) мэВ из-за одноионной магнитной анизотропии (рис. 2i, j) 34 .
В отличие от плоскостных ЧМ спиновых волн, происходящих от Γ , энергии возбуждения которых превышают 140 мэВ (рис. 2а, д), спиновые волны вдоль оси c происходят от волновых векторов упорядочения АФ \({{{{{{{\boldsymbol{Q }}}}}}}} = (0,0,0,5 + L)\) при ( L = 0, 1) и достигают границы зоны около \(E \приблизительно 20\) мэВ (рис. 2ж) , что отражает относительно слабую связь между ферромагнитными плоскостями кагоме. Мы также наблюдаем щель легкой оси анизотропии \({\Delta}_a \приблизительно 2\) мэВ из-за одноионной магнитной анизотропии (рис. 2i, j) 34 .
a Функция рассеяния нейтронов \(S({{{{{{\boldsymbol{Q}}}}}}}},E)\) при 5 K вдоль высокосимметричной линии Γ-M-K-Γ через зону Бриллюэна. Данные ниже и выше \(E = 55\) мэВ были собраны с энергией падающих нейтронов \(E_i = 100\) и 250 мэВ соответственно.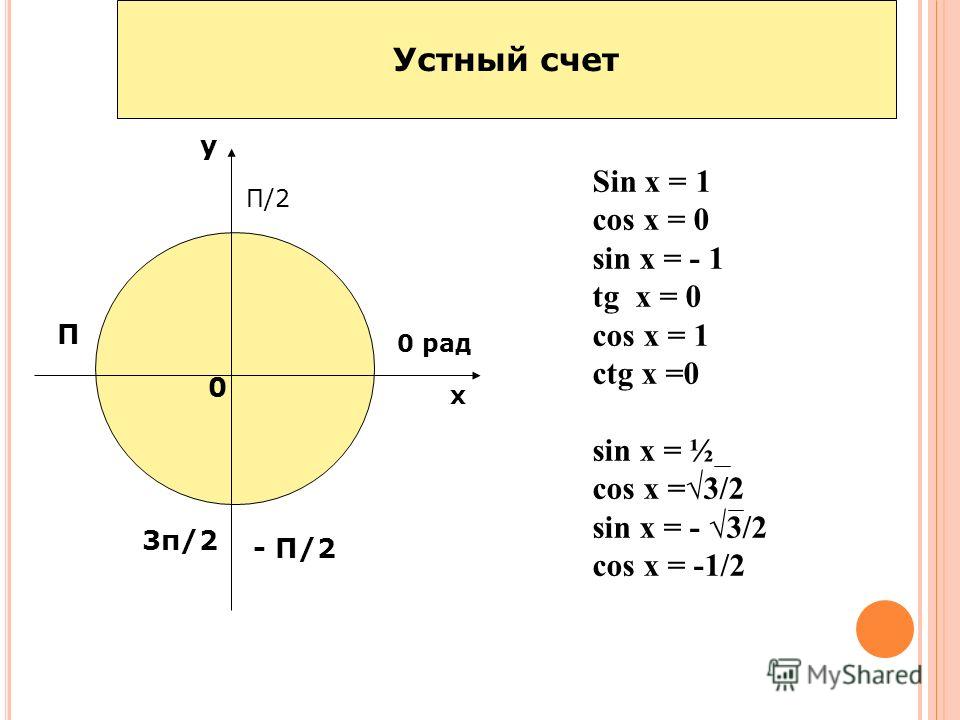 b , c Измерено \(S({{{{{{\boldsymbol{Q}}}}}}}},E)\) при 5 K вдоль высокосимметричной линии Г-М-Г . Оранжевый прямоугольник показывает диапазон интегрирования вдоль направления [ H ,0] для энергетического разреза справа. d Рассчитано \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) вдоль направления Γ-MK-Γ с использованием модели Гейзенберга. e Разрезы постоянной энергии в плоскости ( H , K ) при энергиях \(E = 10 \pm 2,25 \pm 4,45 \pm 5,80 \pm 10\) мэВ. f Разрезы с постоянной энергией подгонки \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) в модели Гейзенберга. г Измерено \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) вдоль направления [0,0, L ]. Пунктирные линии соответствуют модели Гейзенберга. h Рассчитано \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) в направлении [0,0, L ]. i , j Изображения и срезы магнитных возбуждений вблизи центра антиферромагнитной (АФ) зоны \({{{{{{{\boldsymbol{Q}}}}}}}} = (0,0,0,5) \).
b , c Измерено \(S({{{{{{\boldsymbol{Q}}}}}}}},E)\) при 5 K вдоль высокосимметричной линии Г-М-Г . Оранжевый прямоугольник показывает диапазон интегрирования вдоль направления [ H ,0] для энергетического разреза справа. d Рассчитано \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) вдоль направления Γ-MK-Γ с использованием модели Гейзенберга. e Разрезы постоянной энергии в плоскости ( H , K ) при энергиях \(E = 10 \pm 2,25 \pm 4,45 \pm 5,80 \pm 10\) мэВ. f Разрезы с постоянной энергией подгонки \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) в модели Гейзенберга. г Измерено \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) вдоль направления [0,0, L ]. Пунктирные линии соответствуют модели Гейзенберга. h Рассчитано \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) в направлении [0,0, L ]. i , j Изображения и срезы магнитных возбуждений вблизи центра антиферромагнитной (АФ) зоны \({{{{{{{\boldsymbol{Q}}}}}}}} = (0,0,0,5) \).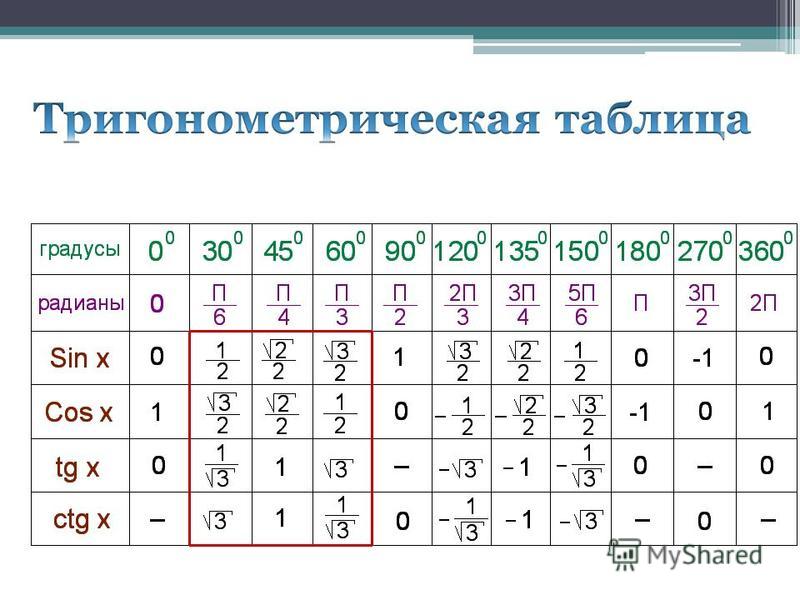 2\), где \(J_{ij}\) — магнитная обменная связь спина \({{{{{{{\boldsymbol {S}}}}}}}}_i\) и \({{{{{{{\boldsymbol{S}}}}}}}}}_j\), обменная муфта J состоит из J 1 (ближайший сосед в плоскости), J 2 (ближней ближней ближней), J (соседние ближней), J (in-Planes ближайшего соседа плоскости) (рис. 1г, д) 34 . Магнитная анизотропия представлена вторым членом, параметризованным как A . Поскольку спиновые волны имеют ФМ дисперсию в плоскости (рис. 2а, д] и внеплоскостной дисперсии АФ (рис. 2ж, и), принимаем Дж 1 , j 2 <0 и J C > 0. Предполагая, что in-Plane Easy-Easy-AXAMSIS AXISIS на сайте. ) направление 40,41 , мы определяем A ( < 0) как одноионную анизотропию. На рис. 2d, f, h показан результат нашей подгонки по методу наименьших квадратов к спин-волновым возбуждениям FeSn на рис.
2\), где \(J_{ij}\) — магнитная обменная связь спина \({{{{{{{\boldsymbol {S}}}}}}}}_i\) и \({{{{{{{\boldsymbol{S}}}}}}}}}_j\), обменная муфта J состоит из J 1 (ближайший сосед в плоскости), J 2 (ближней ближней ближней), J (соседние ближней), J (in-Planes ближайшего соседа плоскости) (рис. 1г, д) 34 . Магнитная анизотропия представлена вторым членом, параметризованным как A . Поскольку спиновые волны имеют ФМ дисперсию в плоскости (рис. 2а, д] и внеплоскостной дисперсии АФ (рис. 2ж, и), принимаем Дж 1 , j 2 <0 и J C > 0. Предполагая, что in-Plane Easy-Easy-AXAMSIS AXISIS на сайте. ) направление 40,41 , мы определяем A ( < 0) как одноионную анизотропию. На рис. 2d, f, h показан результат нашей подгонки по методу наименьших квадратов к спин-волновым возбуждениям FeSn на рис. 2a, e, g соответственно. Сплошные линии на рис. 2c и на рис. 2g представляют собой дисперсии спиновых волн, определенные из гамильтониана Гейзенберга с j 1 = −20,7 ± 3,5 МэВ, J 2 = -5,1 ± 1,3 МэВ, J 6 C J C J 98 .1186. ± 0,002 мэВ, а спин Fe \(S = 1\). Экспериментальные обменные связи FM в плоскости, полученные из этой подгонки, меньше теоретических предсказаний, в то время как обменная связь по оси c больше в два раза 34 .
2a, e, g соответственно. Сплошные линии на рис. 2c и на рис. 2g представляют собой дисперсии спиновых волн, определенные из гамильтониана Гейзенберга с j 1 = −20,7 ± 3,5 МэВ, J 2 = -5,1 ± 1,3 МэВ, J 6 C J C J 98 .1186. ± 0,002 мэВ, а спин Fe \(S = 1\). Экспериментальные обменные связи FM в плоскости, полученные из этой подгонки, меньше теоретических предсказаний, в то время как обменная связь по оси c больше в два раза 34 .
Чтобы определить, можно ли понять магнитные возбуждения FeSn в рамках гамильтониана Гейзенберга с \(S = 1\) 9{\prime\prime} (E)\) в абсолютных единицах при \(S = 1\) и 0,5 соответственно. Эти необычные флуктуационные свойства предполагают, что электронная инерционность играет роль в наблюдаемом статическом упорядоченном моменте FeSn 34 .
Рис. 3. Бездисперсионные возбуждения FeSn+CYTOP-M.
a , b Измерено \(S({{{{{{\boldsymbol{Q}}}}}}}},E)\) FeSn при 5 K вдоль [ H , H ] и [ H ,0] соответственно. Данные были собраны при энергии падающих нейтронов \(E_i = 250\) мэВ. Бездисперсионное возбуждение имеет пик около \(E = 173\) мэВ с полной шириной на полувысоте (FWHM) 24 мэВ. Энергетическое разрешение прибора при \(E = 173\) мэВ составляет около 11 мэВ. c Сокращение энергии на выбранных волновых векторах в пределах первой зоны Бриллюэна. Интенсивность рассеяния, по-видимому, уменьшается с увеличением \({{{{{{{\boldsymbol{Q}}}}}}}}\). d , e Рассчитано \(S({{{{{{\boldsymbol{Q}}}}}}}},E)\) с использованием модели Гейзенберга с теми же параметрами, что и на рис. 2. Красные пунктирные линии — соответствующие дисперсии спиновых волн, показывающие одну акустическую и две оптические спиновые волны. Вертикальные белые пунктирные линии указывают границы первой зоны Бриллюэна. f Разрез по постоянной энергии рассчитанного \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) в плоскости ( H , K ) при \(E = 170 \pm 5\) мэВ из модели Гейзенберга.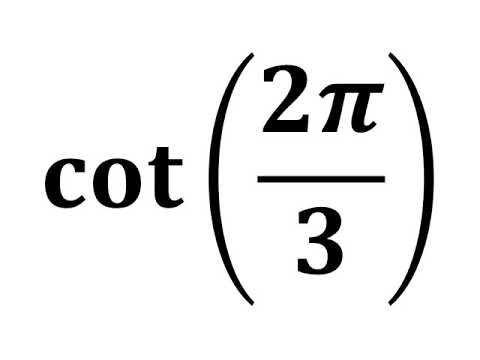 Штриховые линии — границы зоны Бриллюэна двумерной обратной решетки. g , h Измерено \(S({{{{{{\boldsymbol{Q}}}}}}}},E)\) вдоль направления [ H , H ] с падением энергия нейтрона \(E_i = 300\) мэВ и соответствующий энергетический разрез в правой части, чей \({{{{{{{\boldsymbol{Q}}}}}}}}}\)-диапазон интегрирования 9{\prime\prime} (E)\) с использованием идентичного \({{{{{{{\boldsymbol{Q}}}}}}}}}\)-интегрирования из модели Гейзенберга в предположении \(S = 1\) и \(0,5\) соответственно. Статистические ошибки в ( i ) не включают точность 30%, вызванную нормализацией стандарта ванадия. Горизонтальные и вертикальные полосы ошибок в ( c ) и ( i ) представляют \({{{{{{\boldsymbol{Q}}}}}}}}(E)\) диапазон интегрирования и статистические ошибки 1 стандартное отклонение соответственно. CYTOP-M является фторполимером, зарегистрированным под торговой маркой.
Штриховые линии — границы зоны Бриллюэна двумерной обратной решетки. g , h Измерено \(S({{{{{{\boldsymbol{Q}}}}}}}},E)\) вдоль направления [ H , H ] с падением энергия нейтрона \(E_i = 300\) мэВ и соответствующий энергетический разрез в правой части, чей \({{{{{{{\boldsymbol{Q}}}}}}}}}\)-диапазон интегрирования 9{\prime\prime} (E)\) с использованием идентичного \({{{{{{{\boldsymbol{Q}}}}}}}}}\)-интегрирования из модели Гейзенберга в предположении \(S = 1\) и \(0,5\) соответственно. Статистические ошибки в ( i ) не включают точность 30%, вызванную нормализацией стандарта ванадия. Горизонтальные и вертикальные полосы ошибок в ( c ) и ( i ) представляют \({{{{{{\boldsymbol{Q}}}}}}}}(E)\) диапазон интегрирования и статистические ошибки 1 стандартное отклонение соответственно. CYTOP-M является фторполимером, зарегистрированным под торговой маркой.
Полный размер изображения
В дополнение к четким возбуждениям спиновых волн, которые исчезают выше ~140 мэВ в FeSn (рис. 2 и 3i), мы также обнаружили аномальный Q -независимый континуум возбуждений с центром в E = 173 ± 1 мэВ с энергетической шириной около 24 мэВ. На рисунке 3a, b показаны 2D космические изображения Q — E , измеренные вдоль плоскостных направлений [ H ,0] и [ H , H ] в более широком энергетическом режиме. Разрезы энергии при разных волновых векторах в пределах первой зоны Бриллюэна показывают аналогичные результаты, указывая на то, что мода действительно Q — независимый (рис. 3в). На рисунке 3c показано, что интенсивность моды уменьшается с увеличением Q . На рис. 3d, e показаны двухмерные космические изображения Q — E вдоль плоскостных направлений [ H ,0] и [ H , H ], рассчитанные с использованием параметров магнитного обмена Гейзенберга из гамильтониана соответствует рис. 2. Хотя энергия ожидаемых вторых оптических спиновых волн аналогична энергии плоской моды, экспериментальная плоскостная Q -зависимость на рис.
2 и 3i), мы также обнаружили аномальный Q -независимый континуум возбуждений с центром в E = 173 ± 1 мэВ с энергетической шириной около 24 мэВ. На рисунке 3a, b показаны 2D космические изображения Q — E , измеренные вдоль плоскостных направлений [ H ,0] и [ H , H ] в более широком энергетическом режиме. Разрезы энергии при разных волновых векторах в пределах первой зоны Бриллюэна показывают аналогичные результаты, указывая на то, что мода действительно Q — независимый (рис. 3в). На рисунке 3c показано, что интенсивность моды уменьшается с увеличением Q . На рис. 3d, e показаны двухмерные космические изображения Q — E вдоль плоскостных направлений [ H ,0] и [ H , H ], рассчитанные с использованием параметров магнитного обмена Гейзенберга из гамильтониана соответствует рис. 2. Хотя энергия ожидаемых вторых оптических спиновых волн аналогична энергии плоской моды, экспериментальная плоскостная Q -зависимость на рис. 3a, b, c, g, h качественно отличается от теоретического гамильтониана Гейзенберга на рис. 3d, e, f. Например, оптические спиновые волны от гамильтониана Гейзенберга не должны иметь интенсивности магнитного рассеяния в пределах первой зоны Бриллюэна (рис. 3f), что явно противоречит экспериментальным данным (рис. 3g). Отметим, что плоские полосы спиновых волн могут возникать в ферромагнетиках с решеткой кагоме с взаимодействиями Дзялошинского–Мория (ДМ) 38 , но они имеют совершенно другое происхождение 39 .
3a, b, c, g, h качественно отличается от теоретического гамильтониана Гейзенберга на рис. 3d, e, f. Например, оптические спиновые волны от гамильтониана Гейзенберга не должны иметь интенсивности магнитного рассеяния в пределах первой зоны Бриллюэна (рис. 3f), что явно противоречит экспериментальным данным (рис. 3g). Отметим, что плоские полосы спиновых волн могут возникать в ферромагнетиках с решеткой кагоме с взаимодействиями Дзялошинского–Мория (ДМ) 38 , но они имеют совершенно другое происхождение 39 .
Рассеяние нейтронов на CoSn
Если плоская полоса, наблюдаемая на рис. 3а, б, возникает из-за плоской электронной полосы со спином вниз выше (или вблизи) уровня Ферми (рис. 1б), то плоской полосы в парамагнитный CoSn из-за отсутствия спин-поляризованных плоских электронных зон. Удивительно, но спектры возбуждения в CoSn снова показывают плоскую моду при ~ 170 мэВ (рис. 4а), что позволяет предположить, что моды в обоих соединениях не имеют магнитного происхождения.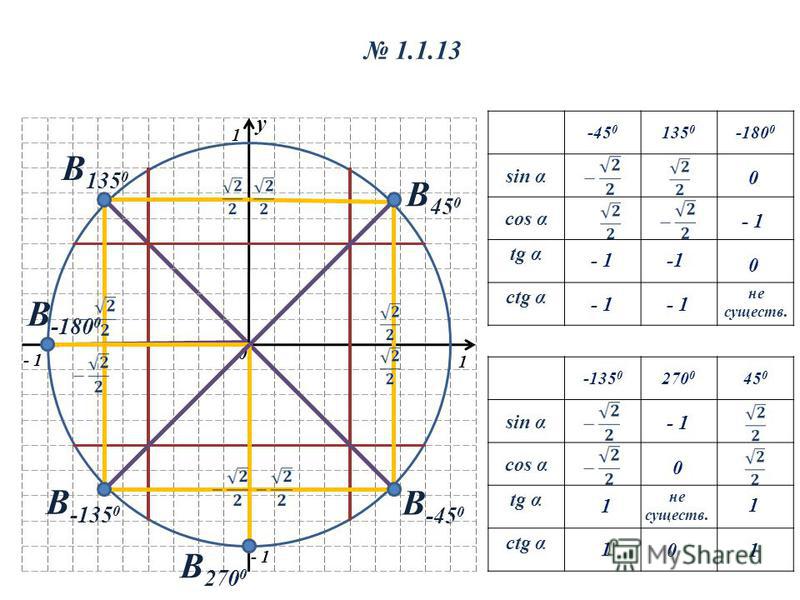 Поскольку наши образцы FeSn и CoSn наклеены на алюминиевые пластины с помощью CYTOP-M, который представляет собой аморфный фторполимер, но содержит один водород для облегчения сцепления с металлической поверхностью 36,43 , гидрогенизированные аморфные углеродные пленки, образованные между образцом и алюминиевыми пластинами, должны иметь изгибные и валентные колебания C–H, возникающие в районе 150–180 мэВ и 350–380 мэВ соответственно 44,45 . Действительно, сканирование с энергией падающего пучка нейтронов 500 мВ показывает наличие плоской моды около 350–380 мэВ (рис. 4б), тем самым подтверждая немагнитную природу плоских мод при 170 мэВ и 360 мэВ в FeSn и CoSn.
Поскольку наши образцы FeSn и CoSn наклеены на алюминиевые пластины с помощью CYTOP-M, который представляет собой аморфный фторполимер, но содержит один водород для облегчения сцепления с металлической поверхностью 36,43 , гидрогенизированные аморфные углеродные пленки, образованные между образцом и алюминиевыми пластинами, должны иметь изгибные и валентные колебания C–H, возникающие в районе 150–180 мэВ и 350–380 мэВ соответственно 44,45 . Действительно, сканирование с энергией падающего пучка нейтронов 500 мВ показывает наличие плоской моды около 350–380 мэВ (рис. 4б), тем самым подтверждая немагнитную природу плоских мод при 170 мэВ и 360 мэВ в FeSn и CoSn.
a Измерено \(S({{{{{{\boldsymbol{Q}}}}}}}},E)\) CoSn с E i = 300 мэВ при 5 K вдоль направление [ H ,0]. B Средний для порошка спектр COSN с E I = 550 МэВ при 5 К.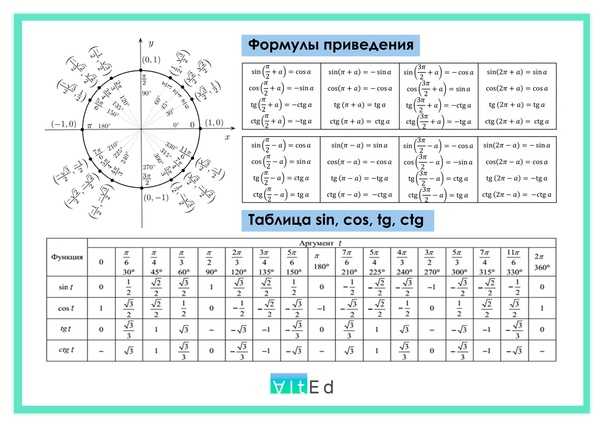 C , D Сравнение между низким уровнем переноса 1.7 ≤ Q ≤ 2,3 Å 444444447777777777774777474774774774777747747477777477777774777777477774777774777477774774777744 переданный импульс 7,7 ≤ Q ≤ 8,3 Å -1 энергетическая зависимость измеренного \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) для CoSn c и FeSn d соответственно. e , f Зависимость \(S({{{{{{\boldsymbol{Q}}}}}}}},E)\) от импульса вдоль направления [ H ,0] в точке E = 70 ± 15 мэВ для CoSn e и FeSn f соответственно. CYTOP-M является фторполимером, зарегистрированным под торговой маркой.
C , D Сравнение между низким уровнем переноса 1.7 ≤ Q ≤ 2,3 Å 444444447777777777774777474774774774777747747477777477777774777777477774777774777477774774777744 переданный импульс 7,7 ≤ Q ≤ 8,3 Å -1 энергетическая зависимость измеренного \(S({{{{{{{\boldsymbol{Q}}}}}}}},E)\) для CoSn c и FeSn d соответственно. e , f Зависимость \(S({{{{{{\boldsymbol{Q}}}}}}}},E)\) от импульса вдоль направления [ H ,0] в точке E = 70 ± 15 мэВ для CoSn e и FeSn f соответственно. CYTOP-M является фторполимером, зарегистрированным под торговой маркой.
Увеличить
Для сравнения парамагнитного рассеяния в CoSn и спиновых волн в FeSn сначала определим энергетические масштабы фононного рассеяния. Синие и красные точки на рис. 4в и г показывают энергетическую зависимость рассеяния при Q = 7,7–8,3 Å -1 и 1,7–2,3 Å -1 соответственно. При больших значениях Q в рассеянии преобладают фононы, и для обоих образцов наблюдается отсечка выше 50 мэВ.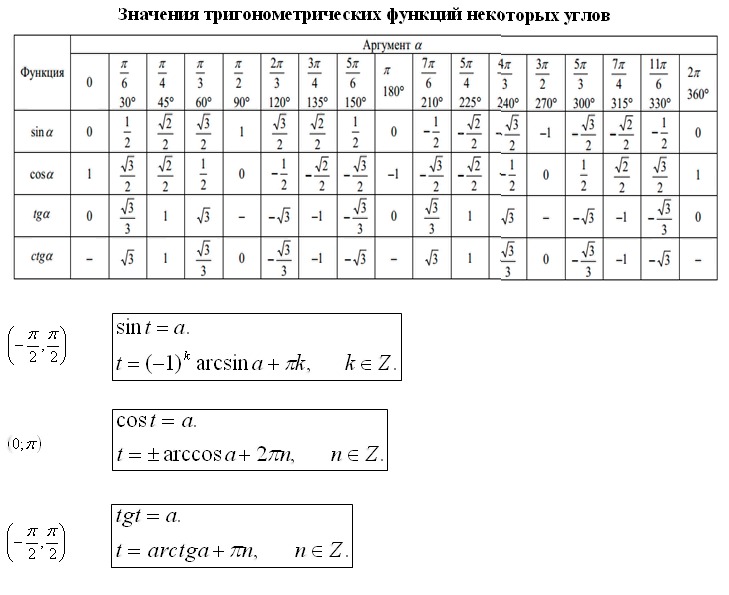 На рисунках 4e и f сравнивается зависимость рассеяния от волнового вектора выше фононного обрезания, которая показывает широкое парамагнитное рассеяние с центром вокруг точки Γ в CoSn и четкие спиновые волны в FeSn. Эти результаты позволяют предположить, что энергетический масштаб парамагнитного рассеяния в CoSn сравним со спиновыми волнами FeSn.
На рисунках 4e и f сравнивается зависимость рассеяния от волнового вектора выше фононного обрезания, которая показывает широкое парамагнитное рассеяние с центром вокруг точки Γ в CoSn и четкие спиновые волны в FeSn. Эти результаты позволяют предположить, что энергетический масштаб парамагнитного рассеяния в CoSn сравним со спиновыми волнами FeSn.
Рассеяние нейтронов на CYTOP-M
Хотя наши измерения в CoSn окончательно идентифицировали плоские моды при 170 мэВ, возникающие из-за изгибных колебательных мод C-H, эти результаты не могут окончательно установить, что мода на рис. 3a возникает полностью из CYTOP-M и существует остается возможность того, что плоская мода 170 мэВ в FeSn имеет магнитную составляющую. Чтобы проверить эти возможности, мы нанесли жидкий CYTOP-M на алюминиевые пластины, но без образца (~ 0,34 грамма), и прокалили сборку в вакуумной печи при температурах, аналогичных тем, при которых были приготовлены образцы FeSn. Результат эксперимента при 5 K показывает четкую плоскую моду при 170 мэВ, таким образом устанавливая, что затвердевший CYTOP-M вызывает рассеяние (рис. 5a, b). Наличие плоской моды при 360 мэВ на рис. 5в подтверждает, что рассеяние при 170 мэВ возникает из-за деформационной моды C–H 44,45 . На рисунке 5d показано рассеяние от жидкого CYTOP-M при комнатной температуре, где изгибная мода C–H 170 мэВ в затвердевшем CYTOP-M смещается до 150 мэВ.
5a, b). Наличие плоской моды при 360 мэВ на рис. 5в подтверждает, что рассеяние при 170 мэВ возникает из-за деформационной моды C–H 44,45 . На рисунке 5d показано рассеяние от жидкого CYTOP-M при комнатной температуре, где изгибная мода C–H 170 мэВ в затвердевшем CYTOP-M смещается до 150 мэВ.
а – в Интенсивность неупругого рассеяния нейтронов от обожженного CYTOP-M на алюминиевых пластинах при 5 К с E i = 300 д Интенсивность неупругого рассеяния нейтронов жидким CYTOP-M при комнатной температуре с E i = 300 мэВ. e , f Энергетическая зависимость измеренного \(S({{{{{{\boldsymbol{Q}}}}}}}},E)\) чистого FeSn для передачи импульса 4 ≤ Q ≤ 7 Å -1 e и 7 ≤ Q ≤ 10 Å -1 f при 5 K.Поскольку измерения в FeSn с (рис. 3а, б) и без (рис.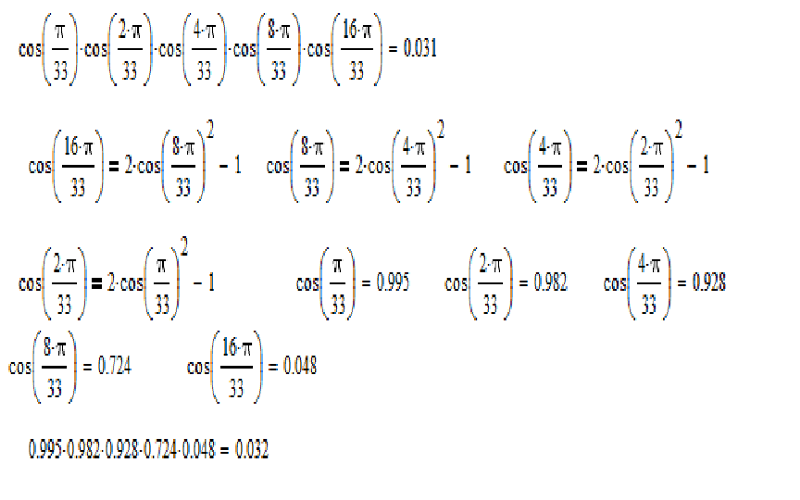 5д, е) CYTOP-M были нормализованы к абсолютным единицам, мы находим, что интегральное отношение интенсивностей моды 170 мэВ с CYTOP-M и без него составляет \((18,4 \pm 0,3)/(1,3 \pm 0,2)\), тем самым подтверждая, что большая часть сигнала при 170 мэВ связано с CYTOP-M (торговая марка фторполимера).
5д, е) CYTOP-M были нормализованы к абсолютным единицам, мы находим, что интегральное отношение интенсивностей моды 170 мэВ с CYTOP-M и без него составляет \((18,4 \pm 0,3)/(1,3 \pm 0,2)\), тем самым подтверждая, что большая часть сигнала при 170 мэВ связано с CYTOP-M (торговая марка фторполимера).
Изображение в полный размер
Рассеяние нейтронов на чистом FeSn
Для дальнейшего тестирования того, может ли чистый FeSn без CYTOP-M также быть загрязнен углеводородами, мы подготовили свежие монокристаллы FeSn и провели измерения при 5 K с использованием невыровненных монокристаллов на СЕКВОЙЯ. Мы снова обнаруживаем слабые и широкие возбуждения при 170 мэВ и 360 мэВ соответственно, что указывает на наличие дополнительного углеводородного загрязнения. При смещении нейтрона падающего пучка от образца углеводородное загрязнение все еще присутствует с аналогичным соотношением интенсивностей между модами 170 мэВ и 360 мэВ (таблица 1). Эти результаты предполагают, что рассеяние 170 мэВ может происходить только из-за изгибной моды C-H и не имеет магнитной составляющей. 2}). \) и \(d_{xy}\) орбиталей и около 4 для \(d_{xz}\) и \(d_{yz}\) орбиталей [рис. 6а]. Поскольку эти значения аналогичны значениям в сверхпроводниках на основе арсенида железа, мы заключаем, что FeSn является металлом Хунда 47 с корреляциями промежуточной прочности. На рисунке 6b показаны электронные структуры DFT + DMFT с выделенными доминирующими орбиталями Fe d в парамагнитном состоянии. Чтобы рассчитать спин-поляризованное магнитоупорядоченное состояние, мы предполагаем обменные связи FM вдоль обеих плоскостей и направлений оси c из-за небольшой обменной связи AF оси c [Рис. 2е] и простотой электронной зонной структуры в ферромагнетике. Мы находим, что увеличение массы Fe 92}\), \(d_{xz}\) и \(d_{yz}\) орбиталей в основном спиновом канале. На рис. 6c, d соответственно показаны расчетные электронные структуры FeSn со спином вверх и вниз в упорядоченном ФМ-состоянии. В дополнение к подтверждению наличия плоской электронной полосы со спином вверх примерно на 230 мэВ ниже уровня Ферми, наблюдаемой в экспериментах ARPES 25 , мы получили плоскую электронную полосу с неосновным спином примерно на 170 мэВ выше уровня Ферми.
2}). \) и \(d_{xy}\) орбиталей и около 4 для \(d_{xz}\) и \(d_{yz}\) орбиталей [рис. 6а]. Поскольку эти значения аналогичны значениям в сверхпроводниках на основе арсенида железа, мы заключаем, что FeSn является металлом Хунда 47 с корреляциями промежуточной прочности. На рисунке 6b показаны электронные структуры DFT + DMFT с выделенными доминирующими орбиталями Fe d в парамагнитном состоянии. Чтобы рассчитать спин-поляризованное магнитоупорядоченное состояние, мы предполагаем обменные связи FM вдоль обеих плоскостей и направлений оси c из-за небольшой обменной связи AF оси c [Рис. 2е] и простотой электронной зонной структуры в ферромагнетике. Мы находим, что увеличение массы Fe 92}\), \(d_{xz}\) и \(d_{yz}\) орбиталей в основном спиновом канале. На рис. 6c, d соответственно показаны расчетные электронные структуры FeSn со спином вверх и вниз в упорядоченном ФМ-состоянии. В дополнение к подтверждению наличия плоской электронной полосы со спином вверх примерно на 230 мэВ ниже уровня Ферми, наблюдаемой в экспериментах ARPES 25 , мы получили плоскую электронную полосу с неосновным спином примерно на 170 мэВ выше уровня Ферми.
Увеличенное изображение
Основываясь на измерении ARPES и вычислении DMFT, можно было бы ожидать наличия континуума Стонера с плоской полосой, возникающего из-за возбуждения квазичастиц между большинством электронов со спином вверх и меньшинством со спином вниз. Наша неспособность наблюдать такую моду означает, что такая мода, если она присутствует, должна быть намного слабее, чем спиновые волны в FeSn. Из наших измерений абсолютной интенсивности спиновых волн в FeSn мы обнаружили, что модель Гейзенберга с локальным моментом с S = 1 не может объяснить интегральную интенсивность спиновой волны, что указывает на важную роль, которую в этих материалах играют блуждающие электроны.
Хотя CYTOP-M уже более 20 лет используется специалистами по рассеянию нейтронов в качестве клея для крепления небольших образцов, о его характеристиках при высоких энергиях не сообщалось 36 . В основном это связано с трудностью переноса неупругого рассеяния нейтронов при энергиях выше 100 мэВ в традиционных реакторных источниках. Развитие технологии времени пролета нейтронов позволяет проводить измерения при энергиях значительно выше 200 мэВ. Мы еще раз проверили высокоэнергетические спиновые волны пниктида железа, обсуждавшиеся в предыдущей работе 9.1444 37,42 и обнаружили, что для образцов, склеенных CYTOP-M, наблюдается слабая зависимость Q при 170 мэВ. К счастью, поскольку магнитное рассеяние от образцов пниктида железа намного сильнее и сосредоточено вокруг определенного Q , выводы этой работы не затрагиваются. В любом случае, наша идентификация плоских изгибных и валентных колебательных мод C-H должна помочь будущим рассеивателям нейтронов отделить это рассеяние от истинного магнитного сигнала, особенно в ситуациях, когда ожидается слабое и широкое магнитное рассеяние.
В основном это связано с трудностью переноса неупругого рассеяния нейтронов при энергиях выше 100 мэВ в традиционных реакторных источниках. Развитие технологии времени пролета нейтронов позволяет проводить измерения при энергиях значительно выше 200 мэВ. Мы еще раз проверили высокоэнергетические спиновые волны пниктида железа, обсуждавшиеся в предыдущей работе 9.1444 37,42 и обнаружили, что для образцов, склеенных CYTOP-M, наблюдается слабая зависимость Q при 170 мэВ. К счастью, поскольку магнитное рассеяние от образцов пниктида железа намного сильнее и сосредоточено вокруг определенного Q , выводы этой работы не затрагиваются. В любом случае, наша идентификация плоских изгибных и валентных колебательных мод C-H должна помочь будущим рассеивателям нейтронов отделить это рассеяние от истинного магнитного сигнала, особенно в ситуациях, когда ожидается слабое и широкое магнитное рассеяние.
Методы
Синтез образцов, характеристика структуры и состава
Монокристаллы FeSn и CoSn были выращены методом самофлюса. Высокочистые Fe(Co) и Sn помещали в корундовые тигли и запаивали в кварцевые трубки с соотношением Fe(Co) : Sn = 2:98. Трубку нагревали до 1273 К и выдерживали 12 ч, затем охлаждают до 823 К (873 К) со скоростью 3 (2) К/ч. Флюс удаляли центрифугированием. И блестящие кристаллы с типичным размером около 2 × 2 × 5 мм 3 можно получить. Монокристаллическая рентгенограмма (XRD) FeSn была получена с использованием рентгеновского дифрактометра Bruker D8 с излучением Cu K α ( λ = 0,15418 нм) при комнатной температуре (рис. S1). .
Высокочистые Fe(Co) и Sn помещали в корундовые тигли и запаивали в кварцевые трубки с соотношением Fe(Co) : Sn = 2:98. Трубку нагревали до 1273 К и выдерживали 12 ч, затем охлаждают до 823 К (873 К) со скоростью 3 (2) К/ч. Флюс удаляли центрифугированием. И блестящие кристаллы с типичным размером около 2 × 2 × 5 мм 3 можно получить. Монокристаллическая рентгенограмма (XRD) FeSn была получена с использованием рентгеновского дифрактометра Bruker D8 с излучением Cu K α ( λ = 0,15418 нм) при комнатной температуре (рис. S1). .
Элементный анализ проводили с помощью энергодисперсионной рентгеновской спектроскопии (EDX) на сканирующем электронном микроскопе FEI Nano 450 (SEM). Чтобы точно определить состав FeSn, мы тщательно отполировали поверхность FeSn с помощью наждачной бумаги и провели измерения EDX на пяти кристаллах FeSn (рис. S2). Среднюю стехиометрию каждого кристалла определяли путем исследования нескольких точек (5 позиций).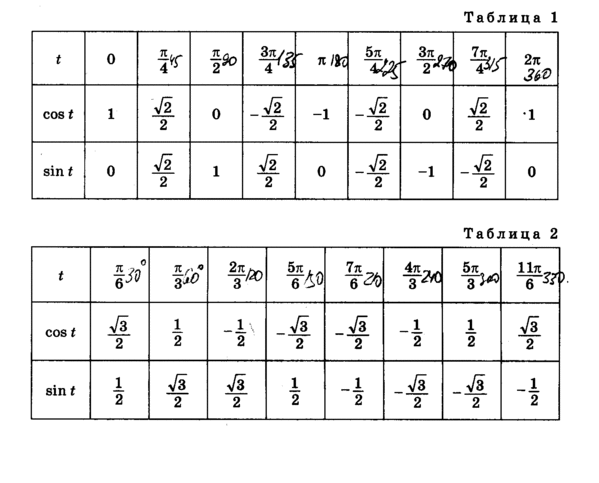 Как показано в Таблице S1, атомное соотношение Fe:Sn близко к 1:1.
Как показано в Таблице S1, атомное соотношение Fe:Sn близко к 1:1.
Для дальнейшего определения качества кристаллов и стехиометрии образцов, использованных в экспериментах по рассеянию нейтронов, мы провели эксперименты по дифракции рентгеновских лучей на монокристаллах двух частей этих образцов на дифрактометре Rigaku XtaLAB PRO, расположенном в Источнике нейтронов расщепления в Ок-Риджском национальном университете. Лаборатория (ОРНЛ). Измеренные кристаллы осторожно подвешивали в паратоновом масле и закрепляли на пластиковой петле, прикрепленной к медному штифту/гониометру (рис. S3). Данные дифракции рентгеновских лучей монокристалла были собраны с молибденом K α излучение ( λ = 0,71073 Å). Было собрано и уточнено более 2800 дифракционных пиков Брэгга с использованием анализа Ритвельда (таблица S2). Мы не находим признаков пиков сверхрешетки, указывающих на возможный порядок вакансий Fe (рис. S3). Результаты уточнения указывают на возможную вакансию Fe менее 1,5% (рис. S4), что позволяет предположить, что монокристаллы практически полностью стехиометричны.
S4), что позволяет предположить, что монокристаллы практически полностью стехиометричны.
Чтобы определить, согласуется ли фазовый переход AF в нашем образце с более ранней работой 34 были проведены измерения намагниченности в зависимости от температуры и поля. На рисунке S5 показан фазовый переход AF около 377 K в магнитном поле 0,5 и 14 T (рис. S5a и b). Зависимости намагниченности от магнитного поля для обоих направлений поля при различных температурах (рис. S5c и d) также согласуются с более ранней работой 34 .
Эксперименты по рассеянию нейтронов
Измерения INS на FeSn проводились с использованием времяпролетного спектрометра MAPS в источнике нейтронов и мюонов ISIS, Лаборатория Резерфорда Эпплтона, Великобритания 48 . Измерения INS на CoSn и FeSn также выполняются с использованием спектрометра SEQUOIA в Spallation Neutron Source, Oak Ridge National Laboratory 49 . Пятьдесят кусков монокристаллов FeSn общей массой 0,97 г были соосно совмещены на одном куске алюминиевой пластины и установлены внутри дисплекса He. На рисунке S6 показано, что мозаика выровненных монокристаллов составляет около 6 градусов. Кристаллическая структура FeSn гексагональная с пространственной группой P 6 мкм с параметрами решетки \(a = b = 5,529\ast = 2\pi ({{{{{{{\boldsymbol{a}}}}}}}} \times {{{{{{{\boldsymbol{b}}}}}}}}})/[ {{{{{{{\boldsymbol{a}}}}}}}}} \cdot \left( {{{{{{{{\boldsymbol{b}}}}}}}}} \times {{{{ {{{\boldsymbol{c}}}}}}}}} \right)]\) с \({{{{{{{\boldsymbol{a}}}}}}}}} = a{{{\ шляпа{\boldsymbol x}}}}\), \({{{{{{{\boldsymbol{b}}}}}}}}} = a(\cos 120\;{{{\шляпа{\boldsymbol x }}}} + \sin 120\;{{{\шляпа{\boldsymbol y}}}})\), \({{{{{{{\boldsymbol{c}}}}}}}}} = c {{{\шляпа{\boldsymbol z}}}}\) (рис. 1г, д). Горизонтальная плоскость рассеяния [ H ,0, L ] и данные INS были собраны с энергиями падающих нейтронов, установленными на \(E_i = 300,250,150,100,30,\) и 15 мэВ в режиме Горация, а температура установлена на 5 K. Данные по рассеянию нейтронов нормированы в абсолютные единицы с использованием ванадиевого эталона с точностью примерно 30 % 42 .
На рисунке S6 показано, что мозаика выровненных монокристаллов составляет около 6 градусов. Кристаллическая структура FeSn гексагональная с пространственной группой P 6 мкм с параметрами решетки \(a = b = 5,529\ast = 2\pi ({{{{{{{\boldsymbol{a}}}}}}}} \times {{{{{{{\boldsymbol{b}}}}}}}}})/[ {{{{{{{\boldsymbol{a}}}}}}}}} \cdot \left( {{{{{{{{\boldsymbol{b}}}}}}}}} \times {{{{ {{{\boldsymbol{c}}}}}}}}} \right)]\) с \({{{{{{{\boldsymbol{a}}}}}}}}} = a{{{\ шляпа{\boldsymbol x}}}}\), \({{{{{{{\boldsymbol{b}}}}}}}}} = a(\cos 120\;{{{\шляпа{\boldsymbol x }}}} + \sin 120\;{{{\шляпа{\boldsymbol y}}}})\), \({{{{{{{\boldsymbol{c}}}}}}}}} = c {{{\шляпа{\boldsymbol z}}}}\) (рис. 1г, д). Горизонтальная плоскость рассеяния [ H ,0, L ] и данные INS были собраны с энергиями падающих нейтронов, установленными на \(E_i = 300,250,150,100,30,\) и 15 мэВ в режиме Горация, а температура установлена на 5 K. Данные по рассеянию нейтронов нормированы в абсолютные единицы с использованием ванадиевого эталона с точностью примерно 30 % 42 .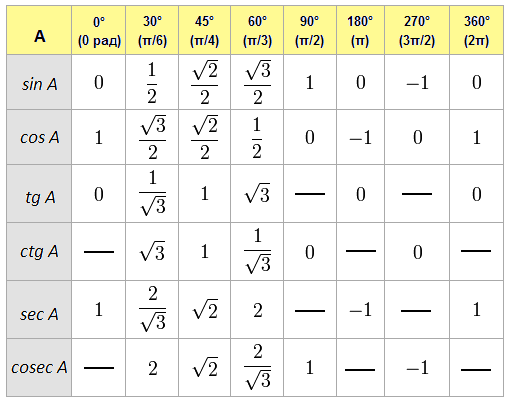
Подгонка модели Гейзенберга к спиновым волнам FeSn
Мы используем модель Гейзенберга и метод наименьших квадратов для подгонки спиновых волн FeSn (рис. S7-S9). Использовался программный пакет SpinW и Horace 9.2\) как обсуждалось в основном тексте. Обратите внимание, что в нашей подгонке гамильтониана Гейзенберга к данным о спиновых волнах мы использовали только дисперсионные соотношения из экспериментов и приняли \(S = 1\), что близко к 1,86 \(\mu _B\) на упорядоченный момент Fe 34 . Общая интенсивность от SpinW fit, если рассматривать ее в абсолютных единицах, значительно выше, чем в эксперименте (рис. 2h). Это говорит о том, что гамильтониан Гейзенберга переоценивает вклад интенсивности спиновой волны от упорядоченного момента. Сначала определим межслойную связь Дж с . Используя линейную теорию спиновых волн, мы находим, что вершина полосы спиновых волн вдоль направления оси c имеет энергию \(E_{Ltop} = 2|J_c|\), когда анизотропия A не слишком велика. Постоянная — Q , разрезанная на волновом векторе границы зоны \({{{{{{{\boldsymbol{Q}}}}}}}} = (0,0,1,75)\), показывает E Ltop = 19,0 ± 0,3 мэВ (рис. 2f), что дает J c = 9,5 ± 0,2 мэВ.
Постоянная — Q , разрезанная на волновом векторе границы зоны \({{{{{{{\boldsymbol{Q}}}}}}}} = (0,0,1,75)\), показывает E Ltop = 19,0 ± 0,3 мэВ (рис. 2f), что дает J c = 9,5 ± 0,2 мэВ.
Для оценки A отметим, что спиновая щель \({\Delta}_a \приблизительно 2\) мэВ при волновом векторе АФ \({{{{{{{\boldsymbol{Q}}}} }}}} = (0,0,0,5)\) (рис. 2з). Рассматриваются несколько типов анизотропии, как показано на рис. S7, и мы выбираем дипольную анизотропию, потому что только она может создать щель в спектре нейтронов. Предполагая, что Дж c = 9,5 мэВ, мы находим \({\Delta}_a = 8,761\sqrt {\left| A \right|}\). Расчетный параметр анизотропии равен A = 0,052 ± 0,002 мэВ. Присутствие A приведет к сдвигу E Ltop на 0,1 мэВ, и поэтому его можно безопасно игнорировать при подгонке магнитных обменных муфт в плоскости.
, чтобы соответствовать обменам в плоскости J 1 и J 2 , мы используем константу- E CUTS вдоль.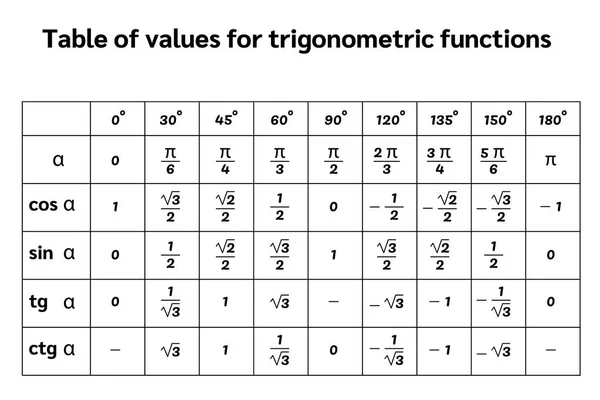 H ] направлений для энергий спиновых волн 15–80 мэВ. Подгонка по Гауссу используется для извлечения положения пика спиновой волны. Мы повторяем [ J 1 , J 2 ], calculate every dispersion, and calculate the square error between calculation and experiment of each [ J 1 , J 2 ] конфигурации (рис. S7). Чтобы сузить диапазон J 1 и J 2 , мы подгоняем часть мод оптических спиновых волн в точке M (рис. S8). Константа- Q разрез, интегрирующий между [ H , H ] = (−0,1, 0,1), [ H , 0] = [0,4, 0,6], и L = [−1, 3] используется в качестве подгонки данные (рис. 2в, д, ж). Режим ошибки наименьшего квадрата используется для получения наилучшего соответствия, предоставляя J 1 = −20,7 ± 3,5 МэВ и J 2 = –5,1 ± 1,3 я, что подтверждает.
H ] направлений для энергий спиновых волн 15–80 мэВ. Подгонка по Гауссу используется для извлечения положения пика спиновой волны. Мы повторяем [ J 1 , J 2 ], calculate every dispersion, and calculate the square error between calculation and experiment of each [ J 1 , J 2 ] конфигурации (рис. S7). Чтобы сузить диапазон J 1 и J 2 , мы подгоняем часть мод оптических спиновых волн в точке M (рис. S8). Константа- Q разрез, интегрирующий между [ H , H ] = (−0,1, 0,1), [ H , 0] = [0,4, 0,6], и L = [−1, 3] используется в качестве подгонки данные (рис. 2в, д, ж). Режим ошибки наименьшего квадрата используется для получения наилучшего соответствия, предоставляя J 1 = −20,7 ± 3,5 МэВ и J 2 = –5,1 ± 1,3 я, что подтверждает. данных.
данных.
Обратите внимание, что планки ошибок этих параметров оцениваются следующим образом: Сначала вычислите ошибку наименьших квадратов, используя параметр наилучшего соответствия 9.1786 J 0 и обозначим его как R 0 ; затем определите параметр J 0 ’ , когда квадратичные значения ошибки дают 2R 0 , а планка ошибки дается как ΔJ = | J 0 ’ — J 0 |. Этот диапазон ошибок дает 68-процентный доверительный интервал, что означает, что если невязка аппроксимации имеет гауссово распределение, расчет, созданный диапазоном [ J 0 — ΔJ , J 0 + ΔJ ] может покрыть 68% точек данных (1σ ins, т.е.
Расчеты DFT+DMFT
Электронные структуры и спиновая динамика FeSn в парамагнитном и магнитоупорядоченном состояниях рассчитаны с использованием метода DFT+DMFT 46 . Часть теории функционала плотности основана на полнопотенциальном линейном методе присоединенных плоских волн, реализованном в Wien2K 51 . Для обменно-корреляционного функционала 52 используется приближение обобщенного градиента Пердью–Берка–Эрнзергофа. DFT+DMFT был реализован поверх Wien2K и подробно описан до 53 . В расчетах DFT+DMFT электронный заряд рассчитывался самосогласованно по матрице плотности DFT+DMFT. Квантовая проблема примесей решалась квантовым методом Монте-Карло с непрерывным временем (CTQMC) 54,55 с Хаббардом U = 4,0 эВ и связью по правилу Хунда Дж = 0,7 эВ как в парамагнитном, так и в магнитоупорядоченном состоянии. Уравнение Бете-Солпитера используется для вычисления динамической спиновой восприимчивости, где голая восприимчивость вычисляется с использованием сходящейся функции Грина DFT + DMFT, а двухчастичная вершина напрямую выбирается с использованием метода CTQMC после достижения полной самосогласованности матрицы плотности DFT + DMFT.
Часть теории функционала плотности основана на полнопотенциальном линейном методе присоединенных плоских волн, реализованном в Wien2K 51 . Для обменно-корреляционного функционала 52 используется приближение обобщенного градиента Пердью–Берка–Эрнзергофа. DFT+DMFT был реализован поверх Wien2K и подробно описан до 53 . В расчетах DFT+DMFT электронный заряд рассчитывался самосогласованно по матрице плотности DFT+DMFT. Квантовая проблема примесей решалась квантовым методом Монте-Карло с непрерывным временем (CTQMC) 54,55 с Хаббардом U = 4,0 эВ и связью по правилу Хунда Дж = 0,7 эВ как в парамагнитном, так и в магнитоупорядоченном состоянии. Уравнение Бете-Солпитера используется для вычисления динамической спиновой восприимчивости, где голая восприимчивость вычисляется с использованием сходящейся функции Грина DFT + DMFT, а двухчастичная вершина напрямую выбирается с использованием метода CTQMC после достижения полной самосогласованности матрицы плотности DFT + DMFT. 56 . Для магнитоупорядоченного состояния усредненная функция Грина каналов со спином вверх и вниз используется для вычисления затравочной восприимчивости. В парамагнитном состоянии на несколько мэВ выше уровня Ферми располагается электронная плоская полоса доминирующих \(d_{xz}\) и \(d_{yz}\) орбитальных символов (рис. 6б). В магнитном состоянии взаимодействие спинового обмена приводит к расщеплению этой электронной плоской зоны примерно на 400 мэВ, где плоская полоса со спином вверх смещается примерно до -230 мэВ (рис. 6c), тогда как плоская полоса со спином вниз смещается вверх. до ~170 мэВ (рис. 6d). Экспериментальная кристаллическая структура (пространственная группа P6/9В расчетах используется 1786 ммм , № 191) FeSn с параметрами решетки \(a = b = 5,297{\AA}\) и \(c = 4,481{\AA}\). На рисунке S10 показаны зонные структуры FeSn с орбитальным разрешением в парамагнитном, магнитоупорядоченном состоянии со спином вверх и вниз. Мы также отмечаем, что возможный дефицит железа ~ 1,2% в FeSn, полученный в результате рентгеноструктурного анализа (таблица S2), не изменит зонную структуру.
56 . Для магнитоупорядоченного состояния усредненная функция Грина каналов со спином вверх и вниз используется для вычисления затравочной восприимчивости. В парамагнитном состоянии на несколько мэВ выше уровня Ферми располагается электронная плоская полоса доминирующих \(d_{xz}\) и \(d_{yz}\) орбитальных символов (рис. 6б). В магнитном состоянии взаимодействие спинового обмена приводит к расщеплению этой электронной плоской зоны примерно на 400 мэВ, где плоская полоса со спином вверх смещается примерно до -230 мэВ (рис. 6c), тогда как плоская полоса со спином вниз смещается вверх. до ~170 мэВ (рис. 6d). Экспериментальная кристаллическая структура (пространственная группа P6/9В расчетах используется 1786 ммм , № 191) FeSn с параметрами решетки \(a = b = 5,297{\AA}\) и \(c = 4,481{\AA}\). На рисунке S10 показаны зонные структуры FeSn с орбитальным разрешением в парамагнитном, магнитоупорядоченном состоянии со спином вверх и вниз. Мы также отмечаем, что возможный дефицит железа ~ 1,2% в FeSn, полученный в результате рентгеноструктурного анализа (таблица S2), не изменит зонную структуру.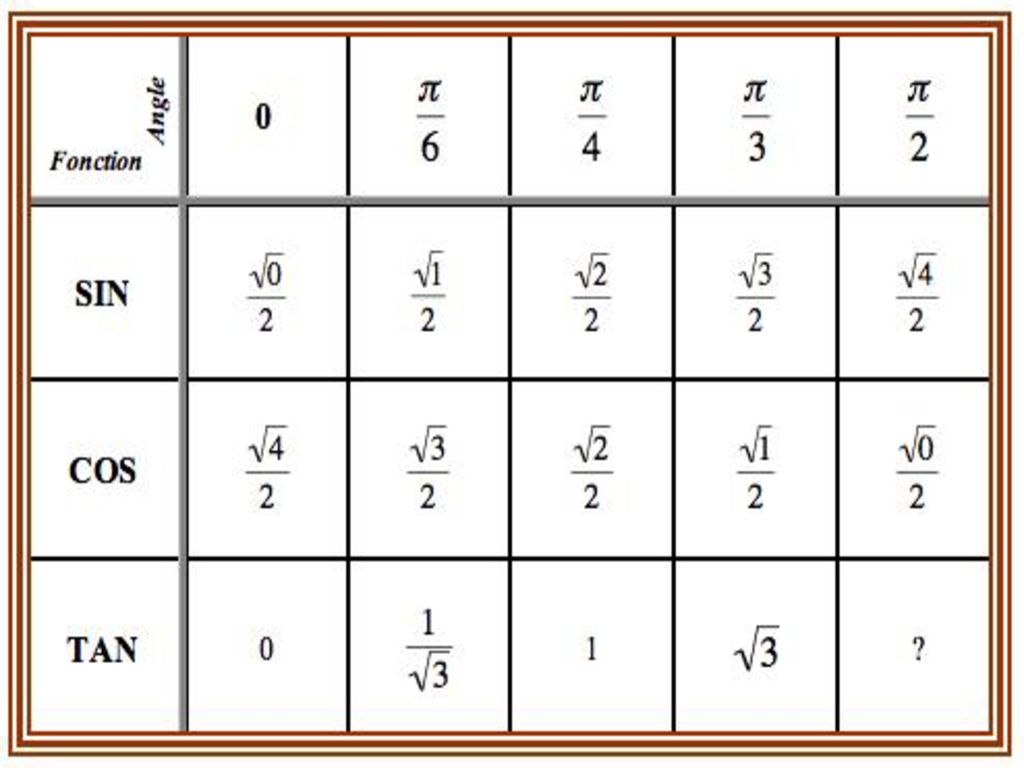
Измерение поглощения инфракрасного излучения
Чтобы определить, имеет ли теплозащита экспериментов SEQUOIA органическое покрытие, мы вырезали небольшой кусок защиты сразу после эксперимента и провели измерение спектра поглощения инфракрасного излучения. Спектр на рис. S11 показывает явные признаки органического покрытия на фольге, подвергшейся воздействию загрязняющего вещества. Режимы 1072, 1038 и 960 см −1 в области отпечатков пальцев спектра однозначно указывают на растяжения Si–O–Si (силоксановые группы). Сильный пик при 1128 см -1 также может быть отнесен к участкам Si-R (R = арил). Очень сильная острая мода при 1240 см –1 характерна для симметричной моды деформации Ch4 в связях Si–Ch4. Ожидаемый диапазон частот составляет 1240–1290 см −1 . Электроположительные металлы, присоединенные к Si, имеют тенденцию смещать этот пик к более высоким частотам, тогда как для силоксанов полоса появляется на нижнем конце. Режим на 1462 см -1 является либо модой ножниц -Ch3, либо, что более вероятно, модой асимметричной деформации -Ch4.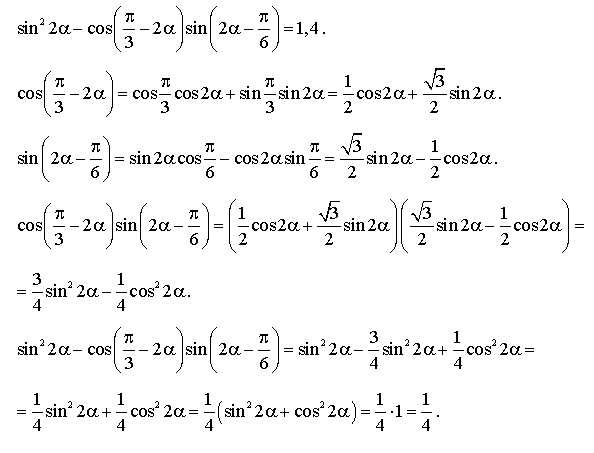 Наличие связей C–H подтверждается существованием сильной полосы поглощения с тремя четкими, относительно резкими модами чуть ниже 3000 см –1 (симметричные и антисимметричные отрезки C–H). Эта информация указывает на то, что загрязнителем является полисилоксановый материал, вероятно, силиконовое масло, случайно загрязнившее вакуумную систему SEQUOIA. Происхождение этого загрязнения неизвестно: смазка или электроизоляционный материал вокруг силовых или сигнальных кабелей. Очень интенсивная мода на 1728 см -1 , несомненно, является модой растяжения карбонила. Он может быть частью боковой группы полисилоксановой цепи (например, карбинольной группы, используемой для модификации гидрофобных/гидрофильных свойств масла). Дальнейших попыток определить точную молекулярную структуру полимерного материала не предпринималось.
Наличие связей C–H подтверждается существованием сильной полосы поглощения с тремя четкими, относительно резкими модами чуть ниже 3000 см –1 (симметричные и антисимметричные отрезки C–H). Эта информация указывает на то, что загрязнителем является полисилоксановый материал, вероятно, силиконовое масло, случайно загрязнившее вакуумную систему SEQUOIA. Происхождение этого загрязнения неизвестно: смазка или электроизоляционный материал вокруг силовых или сигнальных кабелей. Очень интенсивная мода на 1728 см -1 , несомненно, является модой растяжения карбонила. Он может быть частью боковой группы полисилоксановой цепи (например, карбинольной группы, используемой для модификации гидрофобных/гидрофильных свойств масла). Дальнейших попыток определить точную молекулярную структуру полимерного материала не предпринималось.
Доступность данных
Данные, подтверждающие графики в этой статье и другие результаты этого исследования, можно получить у соответствующих авторов по обоснованному запросу.
Наличие кода
Коды, использованные для расчетов ДПФ+ДПФ в этом исследовании, можно получить у соответствующих авторов по обоснованному запросу.
Ссылки
Киршнер, Дж. Прямой и обменный вклады в неупругое рассеяние спин-поляризованных электронов на железе. Физ. Преподобный Летт. 55 , 973–976 (1985).
ОБЪЯВЛЕНИЕ Google ученый
Цао, Ю. и др. Нетрадиционная сверхпроводимость в сверхрешетках графена под магическим углом. Природа 556 , 43–50 (2018).
ОБЪЯВЛЕНИЕ Google ученый
Ye, L. et al. Массивные фермионы Дирака в ферромагнитном металле кагоме. Природа 555 , 638–642 (2018).
ОБЪЯВЛЕНИЕ Google ученый
Кеймер Б., Кивелсон С.А., Норман М.Р., Учида С. и Заанен Дж. От квантовой материи к высокотемпературной сверхпроводимости в оксидах меди. Природа 518 , 179–186 (2015).
ОБЪЯВЛЕНИЕ Google ученый
Рул К.С., Крот Р.А. и Ю Д. Какой клей выбрать? Исследование нейтронного рассеяния различных клеящих материалов и их влияние на фоновое рассеяние. г., J. Appl. Кристаллогр. 51 , 1766–1772 (2018).
Google ученый
Heitz, T., Drévillon, B., Godet, C. & Bourée, J.E. Количественное исследование связи C-H в полимероподобных аморфных углеродных пленках с использованием инфракрасной эллипсометрии in situ. Физ. B 58 , 13957–13973 (1998).
ОБЪЯВЛЕНИЕ Google ученый
Скачать ссылки
Благодарности
Мы хотим выразить нашу искреннюю признательность рецензентам, участвовавшим в рецензировании этой статьи, в том числе тем, кто участвовал во время первоначальной подачи нашей статьи в другой журнал в Nature Portfolio. В частности, мы хотели бы поблагодарить рецензента № 2 в этом журнале, так как его информативный отчет вдохновил нас на проведение измерений CoSn, выявив первоначальные неверные интерпретации данных и дав результаты, представленные сейчас в опубликованной статье.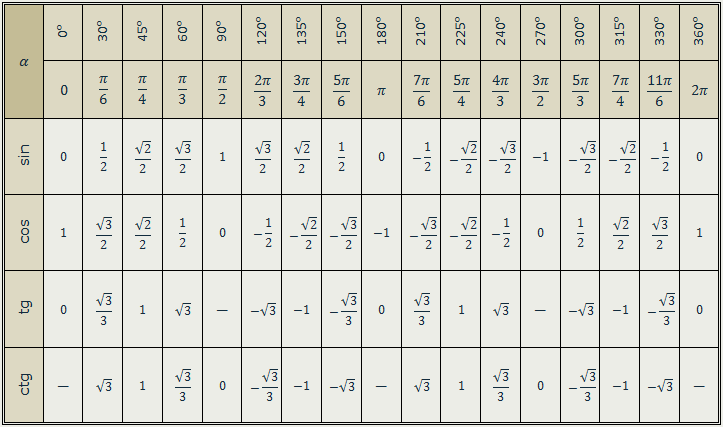 Работа по рассеянию нейтронов и синтезу материалов FeSn/CoSn в Райсе была поддержана US DOE-DE-SC0012311 и Фондом Роберта А. Уэлча в рамках гранта № C-1839.(ПД) соответственно. З.П.И. был поддержан NSFC (грант № 11674030), фондами фундаментальных исследований для центральных университетов (грант № 310421113), грантом Национальной ключевой программы исследований и разработок Китая 2016YFA0302300. В расчетах использовались высокопроизводительные вычислительные кластеры в BNU в Чжухай и Национальном суперкомпьютерном центре в Гуанчжоу. HL был поддержан Национальной ключевой программой исследований и разработок Китая (гранты № 2018YFE0202600, 2016YFA0300504), Национальным фондом естественных наук Китая (№ 11774423, 11822412), фондами фундаментальных исследований центральных университетов и исследовательскими фондами Renmin. Китайский университет (RUC) (18XNLG14, 19XNLG17). А.Х.М. была поддержана Министерством энергетики США, Управлением науки, фундаментальных энергетических наук в рамках премии № DE-SC0019481 и Фондом Уэлча в рамках премии TBF1473.
Работа по рассеянию нейтронов и синтезу материалов FeSn/CoSn в Райсе была поддержана US DOE-DE-SC0012311 и Фондом Роберта А. Уэлча в рамках гранта № C-1839.(ПД) соответственно. З.П.И. был поддержан NSFC (грант № 11674030), фондами фундаментальных исследований для центральных университетов (грант № 310421113), грантом Национальной ключевой программы исследований и разработок Китая 2016YFA0302300. В расчетах использовались высокопроизводительные вычислительные кластеры в BNU в Чжухай и Национальном суперкомпьютерном центре в Гуанчжоу. HL был поддержан Национальной ключевой программой исследований и разработок Китая (гранты № 2018YFE0202600, 2016YFA0300504), Национальным фондом естественных наук Китая (№ 11774423, 11822412), фондами фундаментальных исследований центральных университетов и исследовательскими фондами Renmin. Китайский университет (RUC) (18XNLG14, 19XNLG17). А.Х.М. была поддержана Министерством энергетики США, Управлением науки, фундаментальных энергетических наук в рамках премии № DE-SC0019481 и Фондом Уэлча в рамках премии TBF1473. Э.Ф. и Х.К. признаем поддержку премии Министерства энергетики США в области ранней карьеры KC0402010 по контракту DE-AC05-00OR22725.
Э.Ф. и Х.К. признаем поддержку премии Министерства энергетики США в области ранней карьеры KC0402010 по контракту DE-AC05-00OR22725.
Информация об авторе
Авторы и организации
Авторы
Взносы
P. D. и HL задумали проект. QW, QY и HL подготовили образцы. Эксперименты по рассеянию нейтронов проводились Y.F.X., J.R.S., M.B.S. и анализировались Y.F.X., L.C. с помощью T.C. и П.Д. Рентгенодифракционные измерения монокристалла были выполнены Е.Ф. и Х.К. Расчеты DFT+DMFT были выполнены Z.P.Y. L.L.D провел измерения инфракрасной спектроскопии. Статья была написана P.D., Y.F.X., Z.P.Y., L.C., H.L. и A.H.M. Все авторы сделали комментарии.
D. и HL задумали проект. QW, QY и HL подготовили образцы. Эксперименты по рассеянию нейтронов проводились Y.F.X., J.R.S., M.B.S. и анализировались Y.F.X., L.C. с помощью T.C. и П.Д. Рентгенодифракционные измерения монокристалла были выполнены Е.Ф. и Х.К. Расчеты DFT+DMFT были выполнены Z.P.Y. L.L.D провел измерения инфракрасной спектроскопии. Статья была написана P.D., Y.F.X., Z.P.Y., L.C., H.L. и A.H.M. Все авторы сделали комментарии.
Авторы переписки
Переписка с Хэчан Лэй или Пэнчэн Дай.
Заявление об этике
Конкурирующие интересы
Авторы не заявляют об отсутствии конкурирующих интересов.
Дополнительная информация
Информация о рецензировании Communications Physics благодарит анонимных рецензентов за их вклад в рецензирование этой работы. Доступны отчеты рецензентов.
Примечание издателя г. Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.

 80 USD
80 USD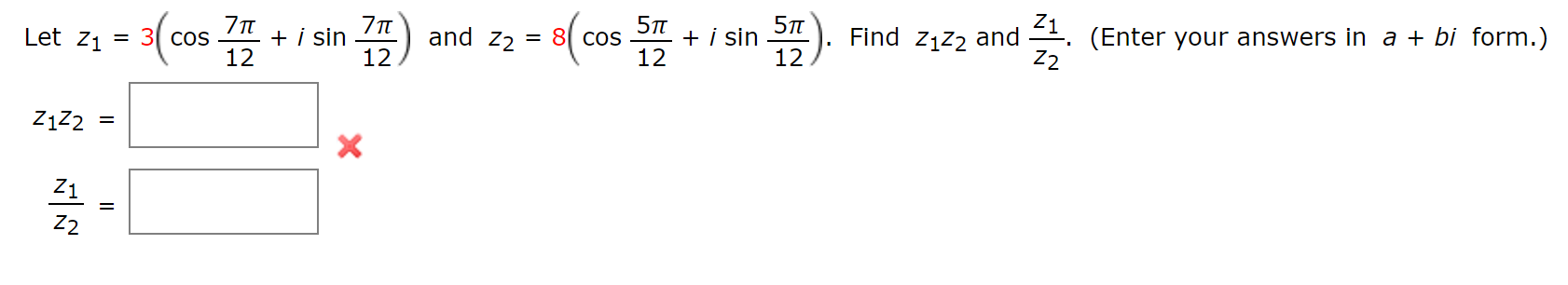 ціна – тут можна знайти модний брендовий одяг, взуття та аксесуари за доступними цінами з доставкою у будь-яке місто України;
ціна – тут можна знайти модний брендовий одяг, взуття та аксесуари за доступними цінами з доставкою у будь-яке місто України;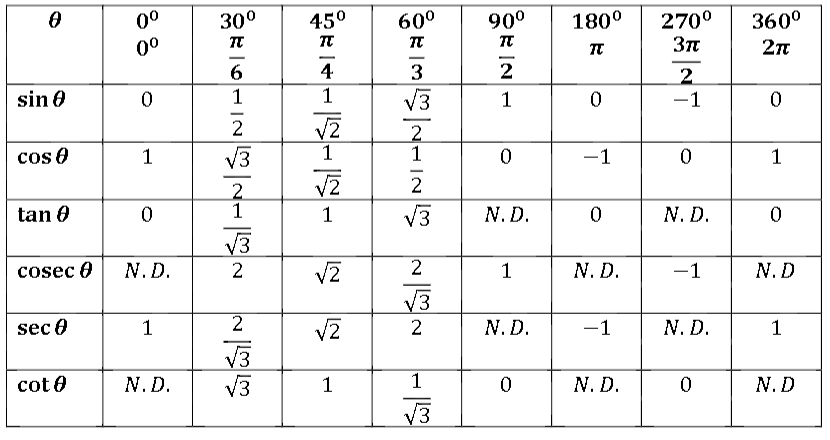 Р. Соц. Лонд. сер. Математика. физ. науч. 165 , 372–414 (1938).
Р. Соц. Лонд. сер. Математика. физ. науч. 165 , 372–414 (1938). Физ. Ред. B 11 , 2624–2637 (1975).
Физ. Ред. B 11 , 2624–2637 (1975). Физ. Преподобный Летт. 106 , 236802 (2011).
Физ. Преподобный Летт. 106 , 236802 (2011). Нац. коммун. 5 , 4261 (2014).
Нац. коммун. 5 , 4261 (2014).
 Нац. Матер. 10 , 932–935 (2011).
Нац. Матер. 10 , 932–935 (2011). (2019).
(2019). и Миллис А. Дж. Решатель с непрерывным временем для квантовых моделей примесей. г. Физ. Преподобный Летт. 97 , 076405 (2006).
и Миллис А. Дж. Решатель с непрерывным временем для квантовых моделей примесей. г. Физ. Преподобный Летт. 97 , 076405 (2006). Макдональд
Макдональд Стоун
Стоун