Тригонометрические функции произвольных углов. Теоремы синусов и косинусов 8 класс онлайн-подготовка на Ростелеком Лицей
Основные тригонометрические тождества
Тригонометрические функции (синус, косинус, тангенс, котангенс) однозначно определяют острый угол. Это значит, что если нам известно значение хотя бы одной из этих функций, то мы можем найти и сам острый угол, и значение оставшихся трех тригонометрических функций (см. рис. 1).
Рис. 1. Взаимосвязь тригонометрических функций
Взаимосвязь тригонометрических функций:
Например, глядя на определения тангенса и котангенса, легко заметить, что:
Потому что , и наоборот.
Можно переписать в эквивалентном виде:
Если мы знаем, что , то сразу скажем: . Нам даже не надо искать само значение угла.
Кроме того, несложно заметить, что:
И аналогично:
Мы уже почти научились по значению одной тригонометрической функции угла находить остальные. Нужно только связать между собой синус и косинус.
Нужно только связать между собой синус и косинус.
Вспомним, что для прямоугольного треугольника верна теорема Пифагора:
Чтобы перейти к формулам для синуса и косинуса, разделим обе части этого равенства на . Получим:
Откуда, по определению:
Можно получить и другие формулы, связывающие тригонометрические функции одного угла. Например, если мы хотим связать тангенс и косинус, то, взяв формулу
, поделим обе части на , получим:
Откуда:
Аналогично можно получить формулу:
Полученные нами формулы называются основными тригонометрическими тождествами. С их помощью можно, зная значение одной из тригонометрических функций острого угла, найти значения трех остальных. С примером решения такой задачи можно ознакомиться ниже.
Вычисление значений тригонометрических функций
Предположим, что нам известно значение синуса острого угла:
Найдем значения остальных тригонометрических функций этого угла.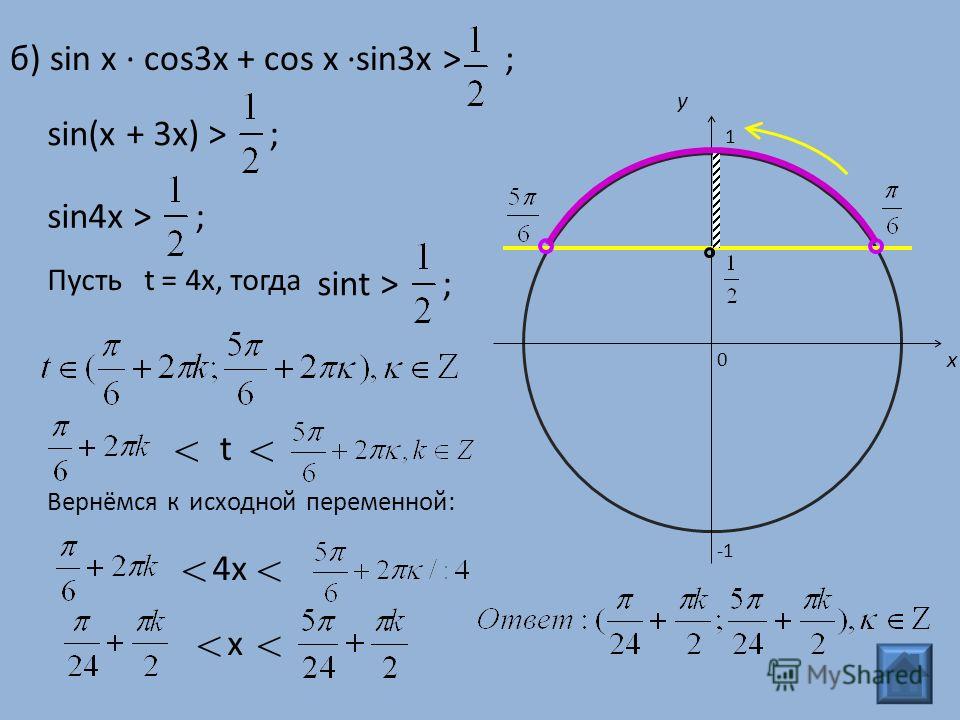
Зная синус, несложно найти косинус, используя формулу:
Подставляем, получаем:
Поскольку косинус острого угла, по определению, – это отношение длин двух сторон, то он может принимать только положительные значения. Значит,
Теперь найти тангенс и котангенс не составит проблем:
Можно было действовать и по-другому, например найти котангенс через синус, используя формулу:
Потренируйтесь самостоятельно находить значения остальных тригонометрических функций острого угла по известному тангенсу или котангенсу.
Возникает вопрос: зачем нужно рассматривать целых четыре функции, если можно использовать одну, а все остальные при необходимости выражать через эту одну?
Конечно, можно. Вопрос только в удобстве. Если какая-то конструкция часто используется, то ее удобно обозначить отдельно, а также вывести ее свойства, чтобы использовать их при решении конкретных задач.
К примеру, длину можно было бы измерять только в метрах. Но расстояние между городами или размеры телефона в них измерять не очень удобно. Не говоря уже про размеры бактерий или расстояния между планетами. Поэтому люди используют разные единицы измерения для одной и той же величины (миллиметры, километры, дюймы, мили, световые года и т. д.) в зависимости от удобства при решении той или иной задачи (см. рис. 2).
Но расстояние между городами или размеры телефона в них измерять не очень удобно. Не говоря уже про размеры бактерий или расстояния между планетами. Поэтому люди используют разные единицы измерения для одной и той же величины (миллиметры, километры, дюймы, мили, световые года и т. д.) в зависимости от удобства при решении той или иной задачи (см. рис. 2).
Рис. 2. Использование различных единиц измерения
Такая же ситуация с тригонометрическими функциями – оказалось, что эти соотношения используются настолько часто, что удобнее ввести и изучать их отдельно, чем выражать через одно.
Более того, можно ввести и другие тригонометрические функции, но они не прижились именно из-за того, что редко встречаются при решении практических задач. Подробнее о них ниже.
vetkaДругие тригонометрические функции
Наблюдательный человек заметит, что при определении тригонометрических функций мы перебрали не все комбинации (см. рис. 3): можно гипотенузу разделить на каждый из катетов.
Рис. 3. Взаимосвязь тригонометрических функций
Взаимосвязь тригонометрических функций:
Действительно, можно ввести еще две функции – секанс и косеканс:
Несложно заметить, что мы получили функции, обратные синусу и косинусу.
В наше время эти функции практически не используют. Слишком просто их заменить синусом и косинусом. Кстати, по этой причине в некоторой литературе не выписываются свойства для котангенса – считается, что его проще выражать через тангенс.
На самом деле, никакой принципиальности в том, чтобы использовать именно эти, а не другие функции, нет. Просто при решении различных задач чаще встречались именно выражения, содержащие синусы, косинусы, тангенсы и котангенсы, поэтому им дали отдельные названия и их подробно изучают.
Диапазон значений синуса и косинуса угла
Какие значения могут принимать тригонометрические функции? Рассмотрим . Поскольку мы определяли синус для острых углов прямоугольных треугольников, то угол может принимать значение от до . Формально, не включая эти значения. Но угол может сколь угодно близко к ним приближаться.
Формально, не включая эти значения. Но угол может сколь угодно близко к ним приближаться.
Зафиксируем гипотенузу и уменьшим угол почти до нуля (см. рис. 4).
Рис. 4. Уменьшенный почти до угол при зафиксированной гипотенузе
Почти до нуля уменьшится и катет . А вместе с ним и :
Поэтому можем определить:
Если начать увеличивать (см. рис. 5), то будет увеличиваться и катет , а вместе с ним будет увеличиваться и значение синуса.
Рис. 5. Увеличенный почти до угол
Чем ближе к будет угол, тем ближе катет будет к гипотенузе . Значит:
Поэтому можем определить:
Значение синуса не может превышать – это его максимальное значение. Больше синус быть не может.
Попробуйте самостоятельно провести аналогичные рассуждения для косинуса острого угла и убедиться, что он будет убывать с увеличением угла от до . И максимальное значение:
Минимальное значение:
Такие выводы можно сделать сразу, используя полученное на прошлом уроке свойство:
Диапазон значений тангенса и котангенса угла
Рассмотрим теперь значения тангенса и котангенса. Будем увеличивать угол от до . Катет будет меняться от до . С катетом все с точностью до наоборот: от до .
Будем увеличивать угол от до . Катет будет меняться от до . С катетом все с точностью до наоборот: от до .
Получается, что:
Поэтому можем определить:
А :
Но мы знаем, что деление на не определено. Как же быть? Если проследить изменение значений тангенса, то заметно, что они неограниченно растут при приближении угла к . Поэтому можно сказать, что: . Но поскольку у нас нет такого числа, как бесконечность, говорят, что не существует или, по-другому, не определен.
не определен
Это вполне согласуется с уже полученными свойствами. Действительно:
Поскольку деление на не определено, то и должен быть не определен.
С котангенсом все аналогично. Несложно получить:
– не определен
Расширение диапазона углов для синуса и косинуса
Мы ввели тригонометрические функции, чтобы заменить непосредственное измерение углов измерением длин. И сделали это для острых углов, т. к. использовали свойства прямоугольных треугольников.
к. использовали свойства прямоугольных треугольников.
Вспомним, что математика имеет инструментальный характер. Чтобы инструмент был удобным, мы можем расширять или дополнять его. При этом обычно это делается так, чтобы свойства расширенных инструментов совпадали со свойствами уже существующих (или не противоречили им). Именно поэтому мы расширили значения тригонометрических функций для углов и , которые не являются острыми.
Но углы могут быть и больше (например, в тупоугольном треугольнике) (см. рис. 6).
Рис. 6. Угол больше в тупоугольном треугольнике
И хочется расширить наш удобный инструмент измерения углов с помощью линейных измерений на произвольный угол (от до ), сохранив при этом все полученные нами свойства (например, основные тригонометрические тождества).
Стороны угла можно продлить сколь угодно далеко. Для измерения длин нам необходимо их ограничить. Когда угол был острый, мы использовали для этих целей прямоугольный треугольник. Для произвольного угла можно использовать еще одну простую фигуру – окружность.
Для произвольного угла можно использовать еще одну простую фигуру – окружность.
Для острых углов от размера прямоугольного треугольника ничего не зависело, т. к. все прямоугольные треугольники с равным острым углом подобны (см. рис. 7).
Рис. 7. Подобные прямоугольные треугольники с равным острым углом
Поскольку любые две окружности подобны (см. рис. 8), то от размера окружности тоже ничего зависеть не будет.
Рис. 8. Окружности подобны
Поэтому можем выбрать в качестве эталона окружность радиуса (см. рис. 9) (или, как ее еще называют, единичную окружность).
Рис. 9. Единичная окружность
Можно сказать и по-другому: какую бы окружность мы ни взяли – можно обозначить ее радиус за – значения тригонометрических функций от этого не изменятся.
Итак, начертим единичную окружность с центром в вершине рассматриваемого угла.
Рассмотрим декартову систему координат, начало которой совпадает с центром этой окружности и, соответственно, вершиной угла. А ось направлена вдоль одной из сторон этого угла (рис. 10).
А ось направлена вдоль одной из сторон этого угла (рис. 10).
Рис. 10. Тригонометрическая окружность
Тогда вершины угла – это точки: , и подвижная точка на окружности, координаты которой будут зависеть от величины угла (рис. 11).
Рис. 11. Точки на тригонометрической окружности
Точка может двигаться по часовой стрелке к точке (угол равен ) (см. рис. 12) или против часовой стрелки до точки как бы с другой стороны (угол равен ) (см. рис. 13).
Рис. 12. Точка двигается по часовой стрелке к точке (угол равен )
Рис. 13. Точка двигается против часовой стрелки до точки с другой стороны (угол равен )
Понятно, что точка однозначно задает угол, и наоборот – каждому углу соответствует ровно одна такая точка. Поэтому нам достаточно следить за положением (координатами) этой точки, чтобы определять величину угла.
Как мы уже говорили, главная задача при расширении инструмента – чтобы сохранялись его свойства. Посмотрим, как будут выглядеть уже известные нам тригонометрические функции острого угла. Понятно, что им соответствует расположение точки в первой четверти.
Понятно, что им соответствует расположение точки в первой четверти.
Построим прямоугольный треугольник, чтобы воспользоваться определением. Для этого опустим перпендикуляр из точки на ось (см. рис. 14).
Рис. 14. Построенный прямоугольный треугольник
По определению: синус угла – это отношение противолежащего катета к гипотенузе (радиусу окружности, который мы считаем равным ).
Получаем, что – ордината точки . Аналогично получаем, что – абсцисса точки .
Таким образом, можно дать новое определение синуса и косинуса угла – это координаты и точки : . Это определение позволяет нам его использовать для любых углов, при этом для острых углов оно совпадает с ранее введенным.
Попробуем вычислить значение синуса и косинуса, например . При пересечении двух прямых образуется четыре угла. Но, как мы знаем, по любому из них можно однозначно восстановить все остальные (см. рис. 15):
Рис. 15. По одному из углов можно восстановить все остальные
Поэтому логично ожидать, что синусы и косинусы таких углов будут обладать какими-то особыми свойствами.
Свойства синуса и косинуса для произвольных углов
Отметим точку и точку (см. рис. 16).
Рис. 16. Отмеченные точки и
Несложно заметить, что прямоугольные треугольники, которые получились, равны (гипотенузы – радиусы, острые углы по ) (см. рис. 17).
Рис. 17. Полученные равные прямоугольные треугольники
Значит, у этих двух точек равны ординаты и равны по модулю, но противоположны по знаку абсциссы. Используя введенное определение, получаем, что:
Несложно обобщить эти свойства для произвольных углов:
Попробуйте самостоятельно доказать похожие свойства:
Обратите внимание, что, расширив тригонометрические функции на углы больше мы получили, что значение синуса и косинуса может быть отрицательным. Однако несложно видеть, что в силу определения оно по модулю не может быть больше .
Нас будут интересовать значения тригонометрических функций для углов треугольника, которые могут быть от до . Им будут соответствовать точки окружности первой и второй четверти (см. рис. 18).
Им будут соответствовать точки окружности первой и второй четверти (см. рис. 18).
Рис. 18. Первая и вторая четверти тригонометрической окружности
Ординаты этих точки всегда будут положительными, т. е. синус может принимать значения только в интервале , а вот абсцисса точек второй четверти отрицательна. Поэтому косинус острого угла всегда будет положительным, а тупого – отрицательным.
Расширение диапазона углов для тангенса и котангенса
Мы расширили определение синуса и косинуса. А что же с тангенсом и котангенсом?
Как мы уже говорили, расширение инструмента должно сохранять его свойства.
Мы знаем, что:
Раз мы определили: , , то должно выполняться:
Можем принять полученные формулы в качестве определения для тангенса и котангенса.
Мы узнаем, что тангенс и котангенс для острых углов – положительные, несложно получить, что для тупых углов они будут отрицательными (если одно из чисел положительно, другое отрицательно, то их отношение будет отрицательным).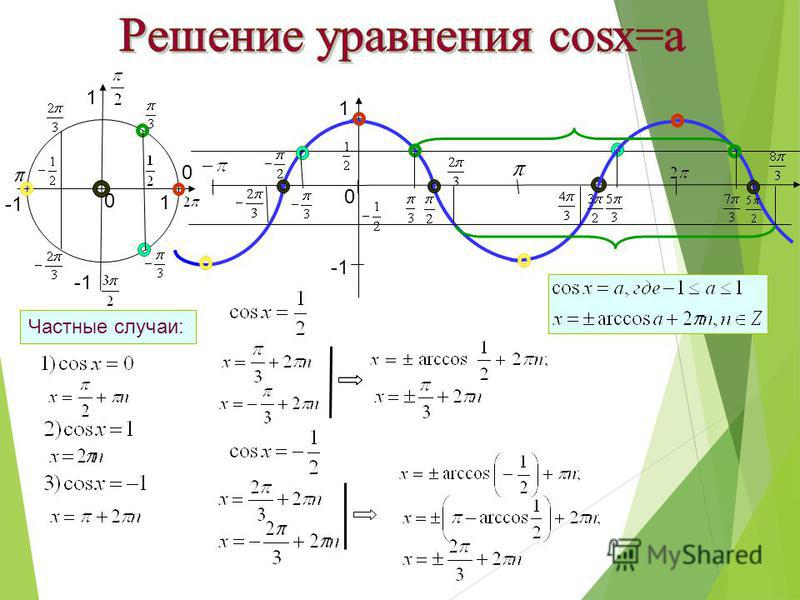
Например:
Обратите внимание, что:
Это неслучайное совпадение:
Мы использовали полученные ранее свойства для синуса и косинуса.
Попробуйте, используя их, самостоятельно вывести аналогичные формулы для:
Основные тригонометрические тождества
Будут ли верны для расширенных тригонометрических функций основные тождества?
Очевидно, да, т. к. мы через них определили тангенс и котангенс. Перемножим эти два равенства, получим еще одно тождество:
Чуть сложнее с тождеством:
Используем определение (см. рис. 19):
Рис. 19. Тригонометрические функции на единичной окружности
Обратите внимание, что и – это длины катетов прямоугольного треугольника для точки из любой четверти (см. рис. 20).
Рис. 20. и – длины катетов прямоугольного треугольника для точки из любой четверти
Значит, для них выполняется теорема Пифагора:
Т.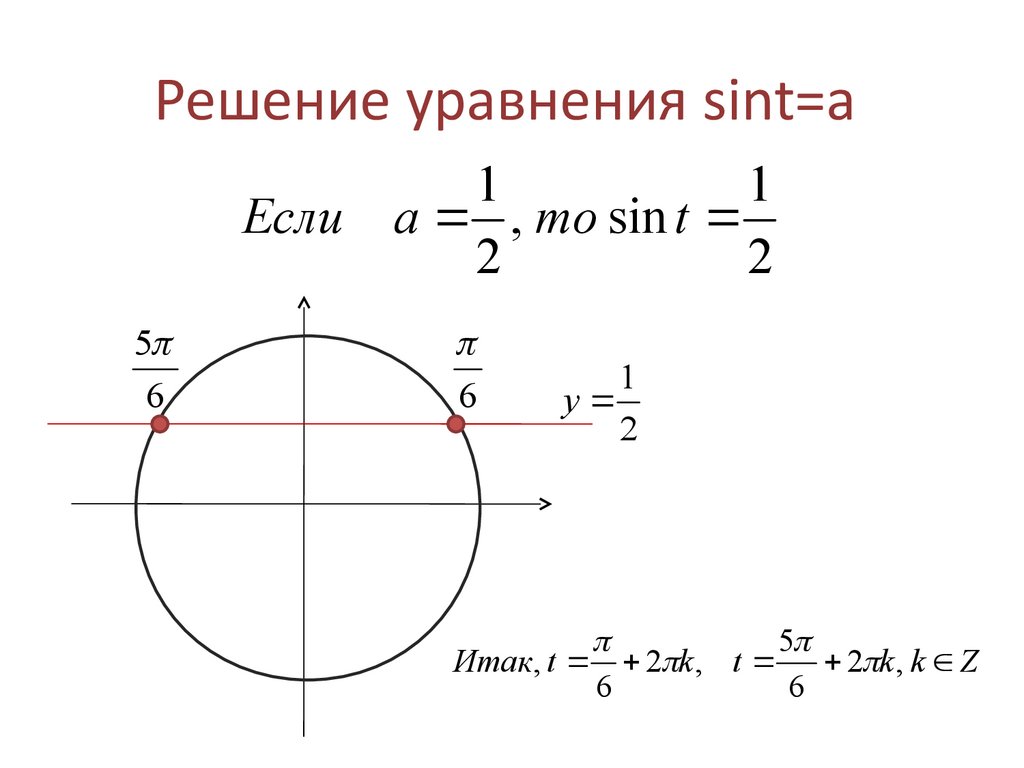 е.:
е.:
Значит, для любых углов.
Следующие тождества докажите самостоятельно, используя уже доказанные тождества:
Теорема синусов
Итак, мы расширили инструмент тригонометрических функций и можем использовать их не только для острых углов. Воспользуемся этим инструментом.
Мы знаем формулу для вычисления площади треугольника через длину его стороны и высоты, которая к ней проведена (см. рис. 21):
Рис. 21. Произвольный треугольник со стороной и проведенной к ней высотой
Но высота – это дополнительный элемент, который может быть неизвестен (а его измерение на практике затруднено). Поэтому хочется иметь формулу, позволяющую находить площадь треугольника только с использованием его основных элементов – углов и треугольников. Попробуем избавиться от высоты в формуле: .
Рассмотрим остроугольный треугольник (см. рис. 22).
Рис. 22. Рассматриваемый остроугольный треугольник
В нем все три высоты лежат внутри. Проведем любую из них (см. рис. 23) и воспользуемся определением синуса острого угла в прямоугольном треугольнике:
Проведем любую из них (см. рис. 23) и воспользуемся определением синуса острого угла в прямоугольном треугольнике:
Рис. 23. Остроугольный треугольник со стороной и проведенной к ней высотой
Откуда:
Несложно получить аналогичные формулы:
В прямоугольном треугольнике (см. рис. 24) ситуация с острыми углами аналогична:
Рис. 24. Рассматриваемый прямоугольный треугольник
А для прямого угла :
Наконец, в тупоугольном треугольнике (см. рис. 25) все аналогично для острых углов :
Рис. 25. Рассматриваемый тупоугольный треугольник
Рассмотрим тупой угол . Проведем высоту :
Откуда:
(по доказанному нами свойству синуса).
Итак, мы доказали, что для любого треугольника:
В первых двух выражениях мы видим одинаковые ненулевые множители . Попробуем сократить на них:
Или, если переписать в виде пропорции:
Аналогично можно получить:
Или, обобщая:
Это равенство означает, что если в треугольнике делить длину стороны на синус противолежащего угла, то всегда будем получать одно и то же значение. Или иначе: стороны треугольника пропорциональны синусам противолежащих углов.
Или иначе: стороны треугольника пропорциональны синусам противолежащих углов.
Это равенство носит название теоремы синусов. Это полезный инструмент, который позволяет нам находить значение недостающих элементов треугольника (например, по двум углам и стороне найти значение еще одной стороны).
Можно ли вычислить значение этих дробей? Имеет ли оно какой-то геометрический смысл?
Опишем около треугольника окружность. Через центр проведем диаметр . Углы и опираются на одну и ту же окружность, следовательно, они равны: (см. рис. 26).
Рис. 26. Равные углы и , опирающиеся на одну и ту же окружность
Раз углы равны, то равны и синусы: . Тогда:
Но треугольник является прямоугольным (угол вписанный, опирается на диаметр), поэтому:
Подставив это выражение в правую часть равенства, получим:
Т. е. все три отношения из теоремы синуса равны диаметру описанной окружности вокруг треугольника:
Очевидно, что наши рассуждения доказывают и саму теорему синусов.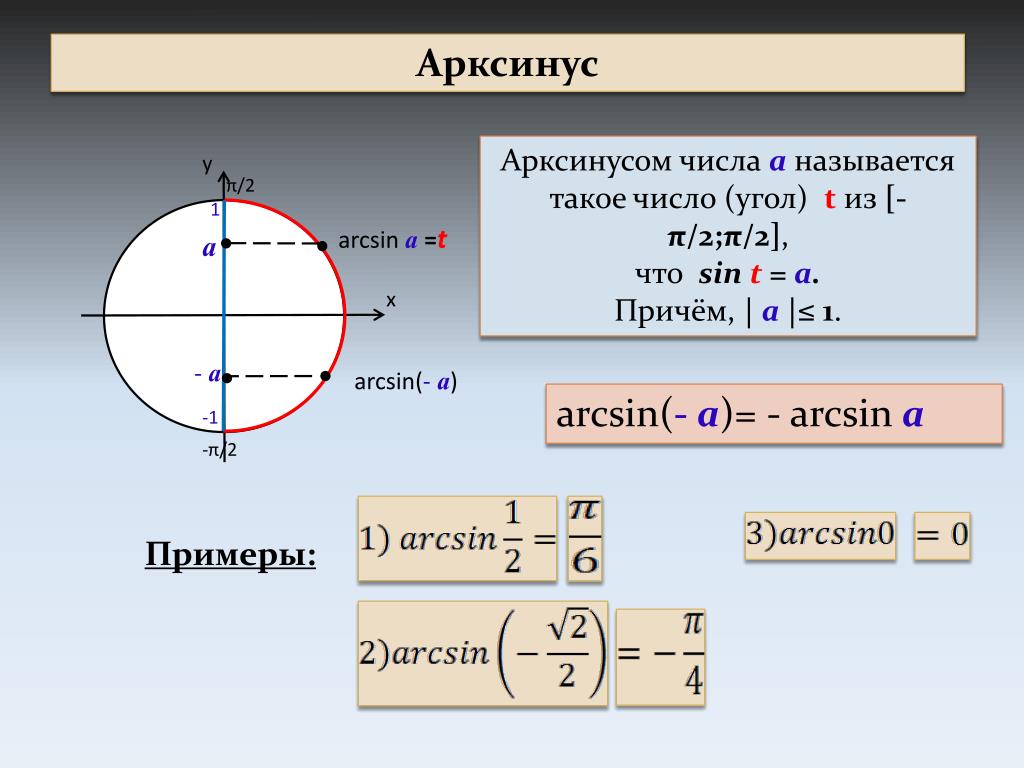 Ведь все три отношения для нашего треугольника равны диаметру описанной окружности, а значит, равны и друг другу.
Ведь все три отношения для нашего треугольника равны диаметру описанной окружности, а значит, равны и друг другу.
ГМТ, из которых данный отрезок виден под одним и тем же углом
Рассмотрим все треугольники с основанием BC, вписанные в данную окружность (см. рис. 27).
Рис. 27. Рассматриваемые треугольники с основанием BC, вписанные в окружность
По теореме синусов:
Т. к. для всех таких треугольников будут равны и , то для них будут равны и .
Как мы уже знаем, синусы углов треугольника будут равны в двух случаях:
Первый вариант выполняется для точек верхней дуги окружности, второй – нижней (рис. 28).
Рис. 28. Первый случай выполняется для точек верхней дуги окружности, второй – для нижней точки
Несложно доказать и обратное утверждение: если любая точка лежит вне окружности, то , т. е. из нее отрезок не будет виден под углом .
Таким образом, геометрическим местом точек, из которых данный отрезок виден под данным углом, будет дуга окружности. А если точнее, то, в силу симметрии, две дуги окружности (это ГМТ еще называют «уши Чебурашки») (рис. 29).
А если точнее, то, в силу симметрии, две дуги окружности (это ГМТ еще называют «уши Чебурашки») (рис. 29).
Рис. 29. ГМТ «уши Чебурашки»
Этот факт можно использовать, например, для расположения зрителей в зале – чтобы все имели одинаковый угол обзора сцены.
Теорема косинусов
Рассмотрим еще один инструмент, который поможет нам находить неизвестные элементы треугольника. Мы уже оценили, насколько полезна теорема Пифагора для вычисления длины неизвестной стороны прямоугольного треугольника. Но хочется иметь аналогичный инструмент для произвольного треугольника.
Вот треугольник с острым углом . Обозначим длины его сторон малыми буквами . Из вершины проведем высоту (см. рис. 30) (для определенности будем считать, что она лежит внутри треугольника, случай тупоугольного треугольника разберите самостоятельно – все рассуждения там аналогичны).
Рис. 30. Рассматриваемый треугольник с проведенной высотой
Тогда, из определения:
По теореме Пифагора:
Уберем на чертеже лишние построения и посмотрим на полученное тождество:
Рис.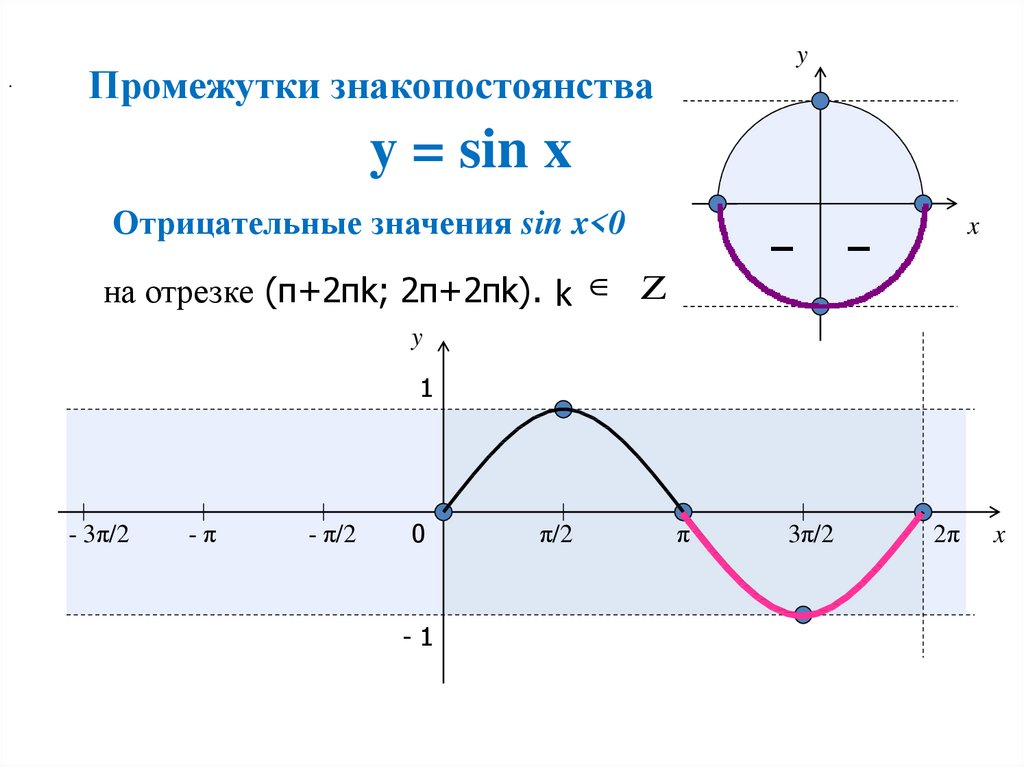 31. Рассматриваемый треугольник
31. Рассматриваемый треугольник
Квадрат стороны треугольника равен сумме квадратов двух других минус удвоенное произведение этих сторон, умноженное на косинус угла между ними.
Это утверждение носит название теоремы косинусов. По виду она очень похожа на теорему Пифагора для прямоугольных треугольников. На самом деле, теорема косинусов – это и есть обобщенная теорема Пифагора для произвольного треугольника.
Действительно, воспользуемся теоремой косинусов для прямоугольных треугольников:
Но, как мы знаем, , поэтому получаем теорему Пифагора:
Теорема Пифагора – частный случай теоремы косинусов для прямоугольных треугольников.
Можно ли тогда теорему Пифагора доказывать, используя теорему косинусов? Нет. Ведь при доказательстве теоремы косинусов мы использовали теорему Пифагора. Получится замкнутый круг: мы доказали через , а через .
Заключение
Теоремы синусов и косинусов – удобные инструменты для решения задач: для нахождения недостающих элементов в треугольниках. С их помощью можно находить неизвестные стороны и углы треугольников. На ближайших уроках мы обязательно потренируемся это делать.
С их помощью можно находить неизвестные стороны и углы треугольников. На ближайших уроках мы обязательно потренируемся это делать.
Список литературы
1. Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия, 8 класс. Учебник. – М.: «Просвещение», 2018.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия, 8 класс. Учебник. – М.: «Просвещение», 2018.
3. Мерзляк А.Г., Полонский В.Б., Якир М.С. Геометрия, 8 класс. Учебник. – М.: издательский центр «ВЕНТАНА-ГРАФ», 2018
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-портал cleverstudents.ru (Источник)
2. Интернет-портал calc.ru (Источник)
3. Интернет-портал yaklass.ru (Источник)
Домашнее задание
1. Упростить выражение:
2. Каким является треугольник со сторонами – остроугольным, тупоугольным или прямоугольным?
3. Найти биссектрисы треугольника, если одна из его сторон равна , а прилежащие к этой стороне углы и .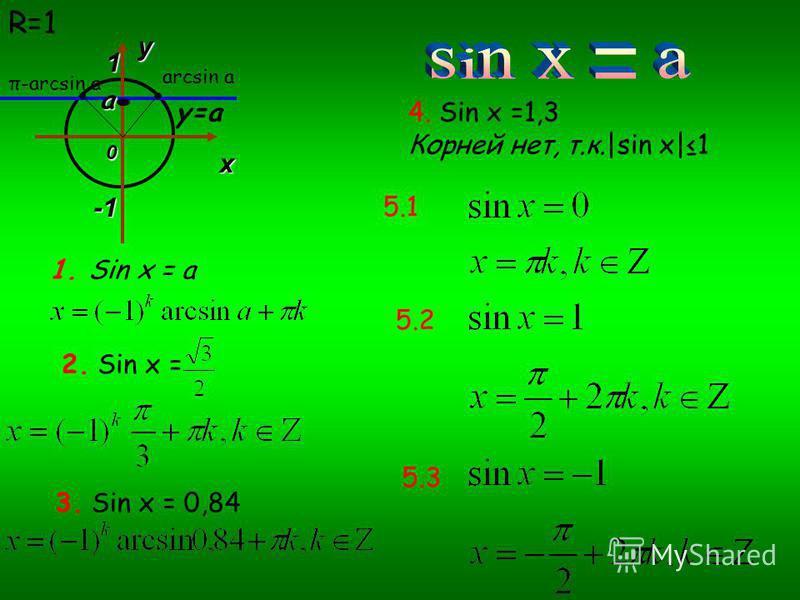
Решение тригонометрических уравнений — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Решение тригонометрических уравнений
2. Содержание
Простейшиетригонометрические
уравнения
Простейшие
тригонометрические
неравенства
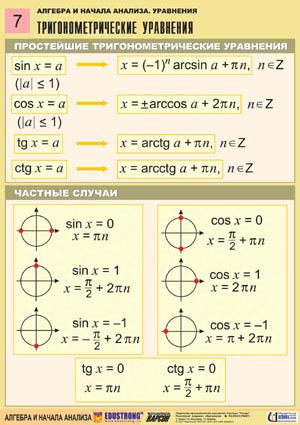
3. Простейшие тригонометрические уравнения
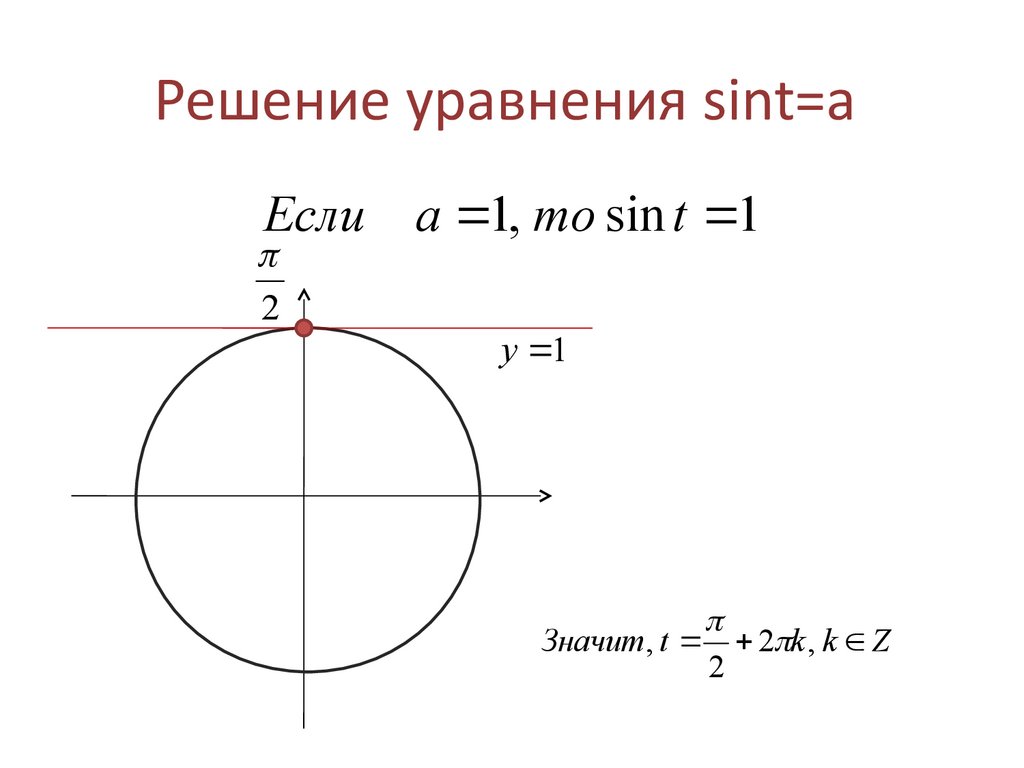
Определение арксинусаУравнение sin t = a
Определение арккосинуса
Уравнение cos t = a
Определение арктангенса
Уравнение tg t = a
Определение арккотангенса
Уравнение ctg t = a
Примеры
4.
 Определение арксинусаАрксинусом числа а называется
Определение арксинусаАрксинусом числа а называетсятакой угол из промежутка [− 0,5π; 0,5π],
синус которого равен а, где lаl ≤ 1.
arcsin a = t , sin t = a
где t [− 0,5π; 0,5π]
а [− 1; 1]
аrcsin(- a) = -arcsina, а [− 1; 1]
5. Уравнение sin t = а
Уравнениеπ − arcsin a
sin t = а
у
1
а
arcsin a
π−t
−1
t
0
−1
1
x
Уравнение
sin t = а
C учетом периодичности:
t = arcsin a + 2πn, n Z
t = π − arcsin a + 2πn, n Z
Объединив в одну формулу:
t = (−1)n arcsin a + πn, n Z
Пример
1 частный случай
y
1
−1
π
sin t = 0
1
0
x
0
t = πn, n Z
−1
2 частный случай
y
1 π
2
sin t = 1
−1
π
t = + 2πn, n Z
2
0
−1
1
x
3 частный случай
y
1
sin t = − 1
−1
0
π
t = − + 2πn, n Z
−1 2
−1
π
−
2 −1
1
x
10. Определение арккосинуса
Арккосинусом числа а называетсятакой угол из промежутка [ 0; π],
косинус которого равен а, где lаl ≤ 1.
arccos a = t , cos t = a
где t [ 0; π]
а [− 1; 1]
arccos(- a) = п-arccosa, a [-1; 1]
11. Уравнение cos t = а
у1
arccos a
t
−1
0
−t
а
1 x
− arccos a
−1
Уравнение
cos t = а
C учетом периодичности:
t = arccos a + 2πn, n Z
t = − arccos a + 2πn, n Z
Объединив в одну формулу:
t=+
arccos
a
+
2πn,
n Z
−
Пример
1 частный случай
y
π 1
2
cos t = 0
x
−1
0
π
−
2 −1
1
π
t = + πn, n Z
2
2 частный случай
y
cos t = 1
−1
1
0
t = 2πn, n Z
−1
0
1
x
3 частный случай
y
1
π
−1
cos t = − 1
x
0
1
t = π + 2πn, n Z
−1
16. Определение арктангенса
Арктангенсом числа а называетсятакой угол из промежутка (− 0,5π; 0,5π),
тангенс которого равен а.
arctg a = t , tg t = a
где t (− 0,5π; 0,5π)
arctg (−a) = − arctg a
17.
 Уравнение tg t = аУравнение
Уравнение tg t = аУравнениеу
1
arctg a
t
−1
0
t = arctga + πn, n Z
Пример
−1
1
Линия тангенсов
а
tg t = а
x
18. Определение арккотангенса
Арккотангенсом числа а называетсятакой угол из промежутка (0; π),
котангенс которого равен а.
arcсtg a = t , сtg t = a
где t (0; π)
arсctg (−a) = π − arcсtg a
19. Уравнение сtg t = а
у1
Линия котангенсов
arcсtg a
−1
t
0
x
1
а
t = arcсtg a + πn, n Z
Пример
−1
20. Примеры
Пример 3.√3
sin x = −
2
1
cos x =
2
tg x = − 1
Пример 4.
ctg x = √3
Пример 1.
Пример 2.
√3
Пример 1 sin t = 2
√3
t=
arcsin
+ πn, n Z
2
π
n
t = (−1)
+ πn, n Z
3
π
n
Ответ: (−1)
+ πn, n Z
3
(−1)n
1
Пример 2 cos x =
2
x =+
−
x=+
−
1
arccos 2 + 2πn, n Z
π
+ 2πn, n Z
3
Ответ:
π
+ + 2πn, n Z
−3
23.
 Пример tg x = − 1x = arctg (− 1) + πn, n Z
Пример tg x = − 1x = arctg (− 1) + πn, n Zπ
x = − + πn, n Z
4
π
Ответ: − 4 + πn, n Z
24. Пример сtg x =
√3x = arсctg √3 + πn, n Z
π
x = + πn, n Z
6
Ответ:
π
+
πn,
n Z
6
25. Простейшие тригонометрические неравенства
Неравенство sin x ≥ aНеравенство cos x < a
Неравенство tg x > a
Неравенство ctg x ≤ a
Примеры
26. Неравенство sin x ≥ a
y3
0
-1
-2
-3
π
2π
2π+arcsin a
a 1
π-arcsin a
-π
-π-arcsin a
-2π+arcsin a
-2π
y=а
sin x ≥ a
arcsin a
y = sin x
2
x
Неравенство sin x ≥ a
arcsin a ≤ x ≤ π − arcsin a
C учетом периодичности:
arcsin a + 2πn ≤ x ≤ π − arcsin a +
+ 2πn, n Z
Ответ:
[arcsin a + 2πn; π − arcsin a + 2πn], n Z
28. Неравенство cos x < a
−2π−arccos a-2π
−2π+arccos a
-π
cos x < a
−arccos a
0
-1
-2
-3
π
2π x
2π +arccos a
2
2π−arccos a
y=а
arccos a
Неравенство cos x < a
y
3
y = cos x
a
Неравенство cos x < a
arccos a < x < 2π − arccos a
C учетом периодичности:
arccos a + 2πn < x < 2π − arccos a +
+ 2πn, n Z
Ответ:
(arccos a + 2πn; 2π − arccos a + 2πn), n Z
30.
 Неравенство tg x > aНеравенство tg x > a
Неравенство tg x > aНеравенство tg x > a3
-2π
— 3π
2
arctg a
2
-π
π
-2
y=а
1
0
-1
-2 a
-3
-4
y = tg x
2π+arctg a
4
-π+arctg a
-2π+arctg a
tg x > a
π+arctg a
y
π
2
π
3π
2
2π
x
Неравенство tg x > a
π
arctg a < x <
2
C учетом периодичности:
π
arctg a + πn < x < 2 + πn, n Z
Ответ:
π
(arctg a + πn;
+ πn), n Z
2
32. Неравенство ctg x ≤ a
yy = ctg x
4
a 3
ctg x ≤ a
2
-1
-2
-3
-4
arcctg a
0
π
2π
2π+arcctg a
-π
π+arcctg a
1
-π+arcctg a
-2π+arcctg a
-2π
y=а
x
Неравенство ctg x ≤ a
arcctg a ≤ x < π
C учетом периодичности:
arcctg a + πn < x < π + πn, n Z
Ответ:
[arctg a + πn; π+ πn), n Z
34. Примеры
Пример 1.Пример 2.
Пример 3.
Пример 4.
1
sin x ≥
2
√3
sin x < −
2
1
cos x ≤
2
√2
cos x >
2
1
sin x ≥
2
Пример 1:
y
3
2
y = sin x
0,5
3π
11π
— — 7π
6 2 6
1
π 0 π π 5π
2 -1 6 2 6
-2
-3
y = 0,5
3π
2
13πx
6
1
Пример 1: sin x ≥ .

2
π
5π
≤
x
≤
6
6
C учетом периодичности:
π
5π
+ 2πn ≤ x ≤
+ 2πn, n Z
6
6
Ответ:
5π
π
+ 2πn; 6 + 2πn , n Z
6
37. Пример 2: sin x < −
Пример 2:y
√3
sin x < −
2
3
2
— 7π
3
-2π
— 2π — π
1
3 3 0
-π
√3
-1
2
-2
-3
4π 7π
3 3
π
x
2π
√3
Пример 2: sin x < − .
2
π
2π
−
<x<−
3
3
C учетом периодичности:
π
2π
− 3 + 2πn < x < − 3 + 2πn, n Z
Ответ:
π
2π
− + 2πn; − + 2πn , n Z
3
3
39. Пример 3: cos x ≤ .
1cos x ≤ 2 .
Пример 3:
y
3
2
y = 0,5
-7π-2π- 5π
3
3
-π
y = cos x
0,5
π
π
x
0
π
2π
5π
7π
-1 3
3
1 3
3
cos x ≤
2
-2
-3
1
Пример 3: cos x ≤ 2 .
π
5π
≤
x
≤
3
3
C учетом периодичности:
π
5π
+
2πn
≤
x
≤
+
2πn,
n Z
3
3
Ответ:
5π
π
+ 2πn; 3 + 2πn , n Z
3
41.
 Пример 4: cos x > . √2
Пример 4: cos x > . √2cos x > .
2
Пример 4:
y
3
√2
y=
2
9π
7π
4 — 4
-π
√2
2
π
— 0
4
-2
-3
2
π
4
y = cos x
π
7π
4
9πx
4
√2
Пример 4: cos x >
.
2
π
π
− 4 <x< 4
C учетом периодичности:
π
π
− + 2πn < x <
+ 2πn, n Z
4
Ответ:
π
π
− + 2πn;
+ 2πn , n Z
4
4
English Русский Правила
404 Cтраница не найдена
Размер:
AAA
Изображения Вкл. Выкл.
Обычная версия сайта
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Уравнение sinx=a
Напомним,
что уравнение, которое содержит переменную под знаком тригонометрических
функций, называется тригонометрическим уравнением. Уравнения вида
, , и , где –
переменная, а число , называются простейшими
тригонометрическими уравнениями. На этом уроке мы с вами подробно
рассмотрим решение уравнений вида .
Уравнения вида
, , и , где –
переменная, а число , называются простейшими
тригонометрическими уравнениями. На этом уроке мы с вами подробно
рассмотрим решение уравнений вида .
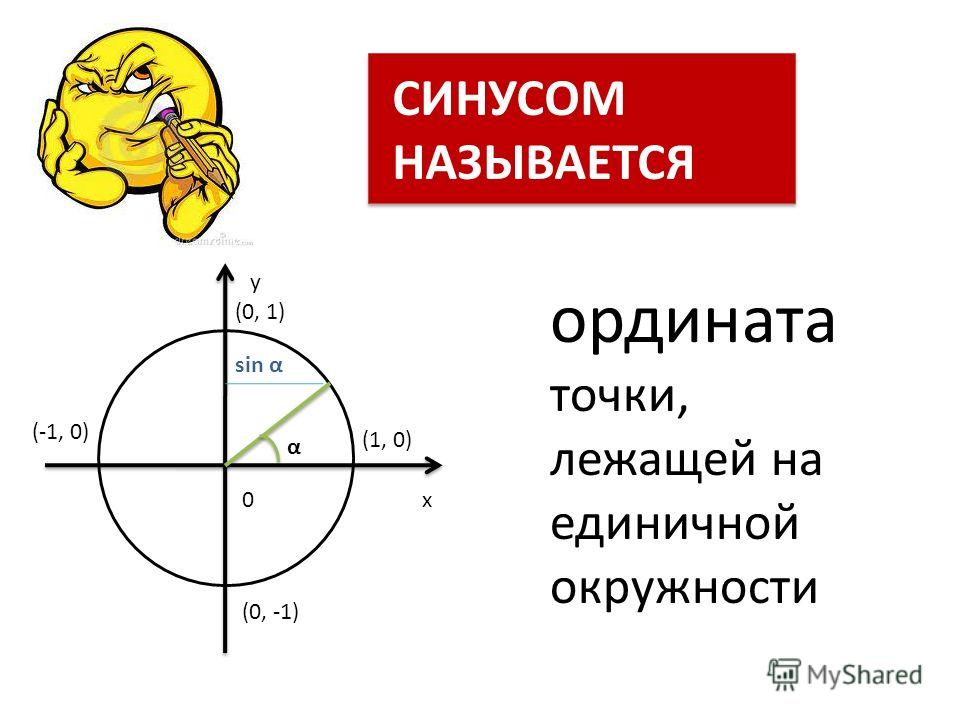
Вы уже знаете, что синусом угла называется ордината точки , полученной поворотом точки вокруг начала координат на угол . При этом не забудем отметить, что так как координаты и точек единичной окружности удовлетворяют неравенствам и , то для справедливо неравенство . Из этого следует, что уравнение имеет корни только при .
Так как же решают такие уравнения? Давайте рассмотрим два уравнения: и .
Чтобы найти х в первом уравнении, нам нужно ответить на вопрос, чему равен синус точки . Для этого нам достаточно вспомнить таблицу значений синуса.
Тогда
. Давайте покажем
это на единичной окружности. Отметим точку . У этой точки,
как и у любой другой, есть свои координаты. Если мы опустим перпендикуляр из
точки на ось ординат,
то попадём в .
Если мы опустим перпендикуляр из
точки на ось ординат,
то попадём в .
А теперь вернёмся ко второму уравнению . Чтобы найти х в этом уравнении, нам нужно ответить на вопрос, синус каких точек равен .
Давайте ненадолго отвлечёмся от тригонометрии. Начертим координатную плоскость. А теперь найдём все те точки, у которых ордината равна . Несложно догадаться, что таких точек будет бесконечное множество и все они будут лежать на горизонтальной прямой, проходящей через точки с ординатой, равной .
А
теперь вернёмся к тригонометрии. Нас будут интересовать все точки, которые
лежат на единичной окружности и пересекаются горизонтальной прямой, проходящей
через точки, имеющие ординату, равную . Заметим, что
наша прямая пересекает единичную окружность в двух точках – и . Исходя из
таблицы значений синуса, точка получается из
начальной точки поворотом на угол
, а точка – поворотом на
угол . Тогда решением нашего
уравнения будут два корня и . Но ведь в эти точки
мы можем попасть не по одному разу. Если мы сделаем полный оборот по единичной
окружности, то снова попадём в эти точки. Сделав ещё полный оборот, снова
попадём в эти точки и так далее. Тогда окончательным решением нашего уравнения
будет серия корней:
Тогда решением нашего
уравнения будут два корня и . Но ведь в эти точки
мы можем попасть не по одному разу. Если мы сделаем полный оборот по единичной
окружности, то снова попадём в эти точки. Сделав ещё полный оборот, снова
попадём в эти точки и так далее. Тогда окончательным решением нашего уравнения
будет серия корней:
Второй корень мы можем переписать как . Как правило, эти два корня совмещают и записывают как .
Заметим, что если , то из последней формулы получаем: , а если , то из последней формулы получаем: .
Вообще, при решении уравнений вида возможны четыре случая.
Первый
случай: . Раскрывая
модуль, имеем . В этом случае на
единичной окружности будут располагаться две точки – и , ординаты которых
равны а. Эти точки получаются путём поворота начальной точки на угол и соответственно.
Тогда решения уравнения можно записать в
виде: , и . Заметим, что эти
точки симметричны относительно оси ординат.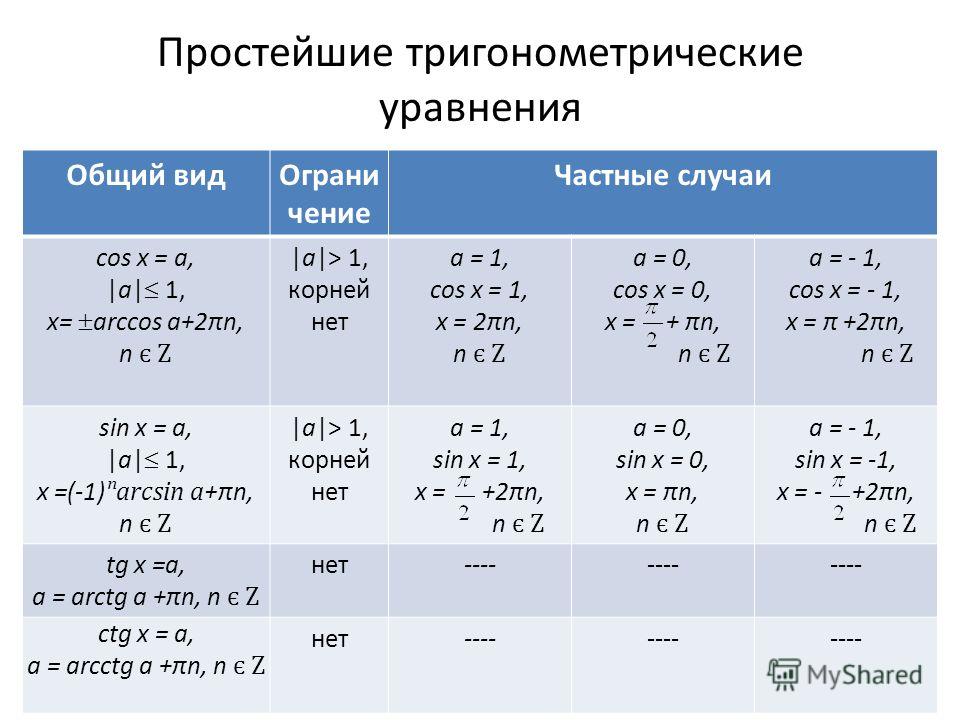 Следовательно, . Чаще всего эти
серии решений объединяют в одну формулу: .
Следовательно, . Чаще всего эти
серии решений объединяют в одну формулу: .
Например, решим следующие уравнения и . Ординату, равную , имеют две точки единичной окружности. Так как , то угол , а тогда угол . Следовательно, все корни уравнения можно найти по формуле . При чётном n получим первую серию решений, при нечётном – вторую.
Перейдём ко второму уравнению . Ординату, равную , имеют две точки единичной окружности. Так как , то угол , а тогда угол . Следовательно, все решения уравнения можно найти по формуле .
Обратите внимание, каждое из уравнений и имеет бесконечное множество корней. Однако на отрезке каждое из этих уравнений имеет только один корень. Так, , – это корень уравнения , а , – это корень уравнения . Число называют арксинусом числа . Записывают так: . Число называют арксинусом числа . Записывают так: .
Кстати,
«арксинус» в переводе с латинского означает «дуга» и «синус». Это обратная
функция.
Это обратная
функция.
Вообще, уравнение , где , на отрезке имеет только один корень. Если , то этот корень заключён в промежутке ;
если же , то корень располагается в промежутке .
Этот корень называют арксинусом числа а и обозначают так .
Запомните! Арксинусом числа а, , называется такое число , синус которого равен а.
, если и
Например, , так как , . , так как , .
Возвращаясь к нашему уравнению , где , можно утверждать, что все корни уравнения можно найти по формуле: .
Запомните! Для любого справедлива формула . Эта формула позволяет находить значения арксинусов отрицательных чисел через значения арксинусов положительных чисел.
Например, .
Второй
случай: . Раскрывая модуль,
имеем и . Поскольку для справедливо
неравенство , то понятно, что
в этом случае уравнение не будет иметь
корней.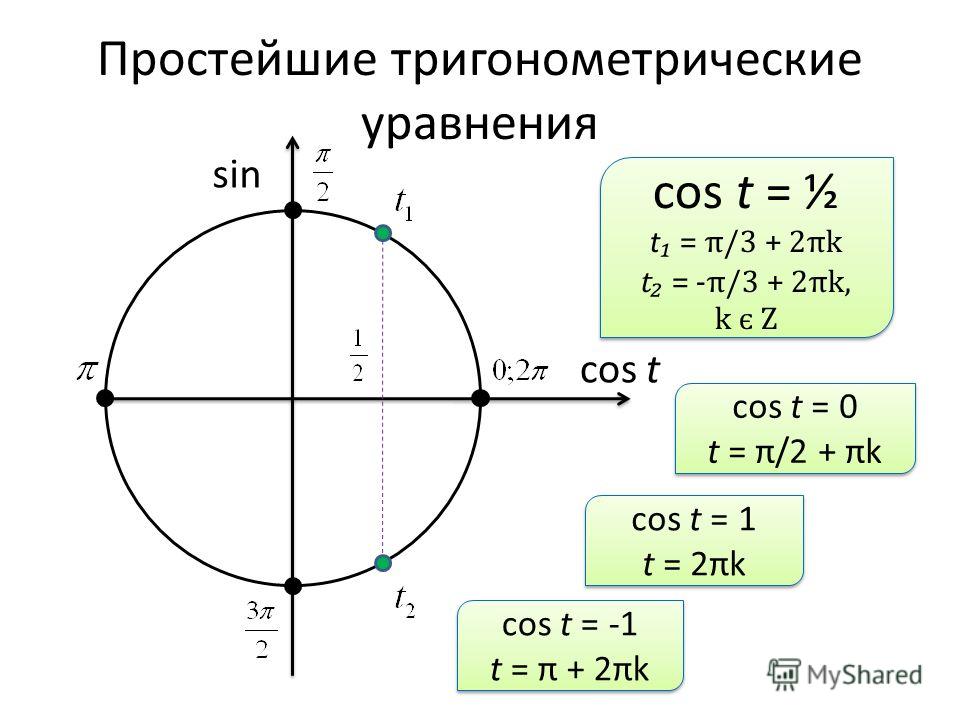
Например, уравнения и не имеют корней.
Третий случай (частный): . В этом случае есть две точки тригонометрической окружности, которые имеют ординату, равную 0. Точка представляет все числа вида , а точка – все числа вида . Заметим, что две записанные серии решений уравнения можно выразить одной формулой: . Так как при получится первая серия решений , а при – .
И последний, четвёртый случай (тоже частный): . Раскрывая модуль, имеем , и . В этом случае горизонтальные прямые, проходящие через точки, имеющие ординаты, равные –1 и 1, будут касаться единичной окружности в точках с координатами (0;1) и (0;–1). Эти точки получаются путём поворота начальной точки на угол и . Тогда уравнение имеет серию решений: . А решением уравнения будет следующее: .
А теперь давайте приступим к практической части нашего урока.
Задание. Решите
уравнение .
Решение. Для начала преобразуем уравнение. Единицу перенесём в правую часть, затем разделим обе части равенства на –2. Получим . По формуле нахождения корней уравнения , имеем . . Отсюда . Перенесём 4 в правую часть равенства. Затем разделим обе части равенства на 3. Отсюда х равен: .
Формулы двойного угла — значения функций, свойства и примеры решений » Kupuk.net
На уроках математики школьники 8−11 классов изучают интегралы, знакомятся с таблицей значений аргумента (переменная). Через формулу двойного угла (ФДУ) выражаются косинус, синус, тангенс, котангенс с произведением 2α. В основе находится тригонометрическая функция угла альфа. Чтобы её отобразить на графике, используются координаты и окружность.
Способы преобразования
Чтобы понять, как выражаются тригонометрические функции двойных углов, необходимо воспользоваться их записью в виде nα, где n принадлежит натуральному числу.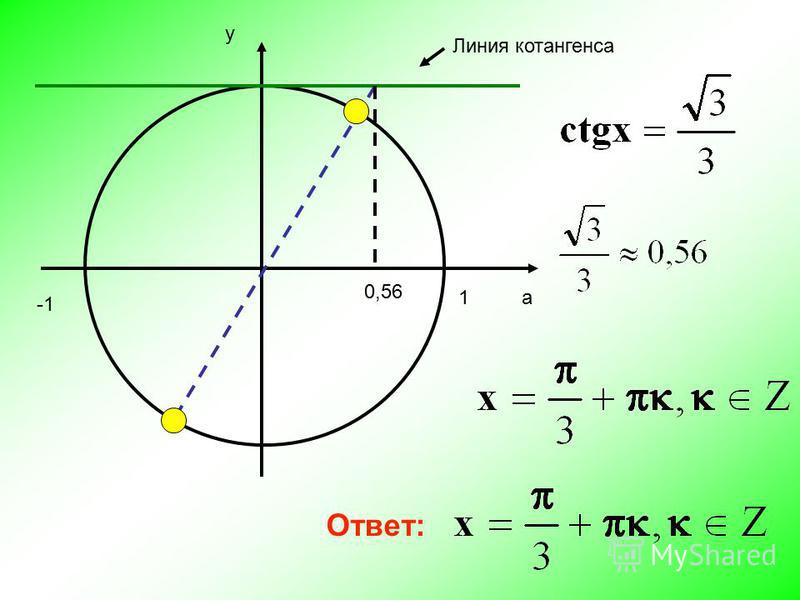 Значение основного выражения отображается математически без скобок. Используя это свойство, можно составить следующее уравнение: sin nα = sin (nα).
Значение основного выражения отображается математически без скобок. Используя это свойство, можно составить следующее уравнение: sin nα = sin (nα).
Для приведения произведения sin nα х sin nα, используется аналогичное свойство. Выражение можно упростить до 2 (n sin α). Основой тождества является n sin α. В математике используются и другие равенства:
В геометрии и алгебре чаще применяются следующие известные формулы: синус2α = cos2α — sin2α, cos2α = 1 − 2·sin2α. Можно разложить производные sin и cos, если угол имеет любой градус. Решение тангенса потребуется, если в основе задачи находится tg2α, при этом значение угла отлично от суммы π4 и π2. Частный случай, когда в задании есть целое число z, а α ≠ π4 + π2·z. Если рассматривать для котангенса ФДУ при любом альфа, ctg2α не определён на промежутке π2. Для косинуса двойного угла характерна тройная запись.
Для косинуса двойного угла характерна тройная запись.
Доказательства равенств
Чтобы подтвердить уравнения на сложение, вычитание и умножение, понадобится подойти к доказательству комплексным способом. Используя формулы синуса с плюсом для углов (α+β) и косинуса для β и α, получится синусα·косинусβ+косинусα·синусβ. Пример для вычитания: соsα ·cosβ-синусα·синусβ.
При вычислении разницы следует придерживаться аналогичного принципа. Результат будет следующим: косинус (α+α) равен двойному значению косинуса минус двойное значение синуса. Формула двойного угла косинуса и синуса доказана. При решении задач из дидактических материалов используются и другие уравнения при положительном и отрицательном значении альфа, при нуле либо половинном π.
Для их доказательства необходимо находить корень из числа z, возводить целое значение в квадрат либо иную степень. Чтобы определиться с ходом решения, необходимо следить за графиком функции:
Чтобы определиться с ходом решения, необходимо следить за графиком функции:
- возрастанием;
- понижением.
Сложные действия вычисляются с помощью калькулятора. Если задача состоит из нескольких частей, для нахождения результата потребуется преобразовать первичное уравнение в более простое. Используются следующие равенства:
- косинус2α=1−2⋅синус2α;
- косинус 2α=2·косинус2α — 1.
Их можно привести к косинус2α — синус2α. Если заменить единицу суммой квадратов, тогда sin2α + cos2α = 1. Получается, что синус2α + косинус2α = 1. Подставив данные, выходит: 1 − 2·sin2α.
Чтобы доказать ФДУ котангенса, применяется равенство ctg2α = cos2αsin2α. Преобразовав данные, получится для tg2α равенство 2·sinα·cosαcos2α — sin2α. Разделив выражение на cos2α, отличное от нуля, получится, что tgα определен. Другое выражение поделится на sin2α. Значение sin2α ≠ 0 будет иметь смысл при любом α, если ctg2α имеет смысл.
Другое выражение поделится на sin2α. Значение sin2α ≠ 0 будет иметь смысл при любом α, если ctg2α имеет смысл.
Решение задач
Для убеждения в справедливости 2α для α=30° применяется значение тригонометрических функций для углов. Если α=30°, тогда 2α будет соответствовать 60°. Необходимо проверить значение sin 60° = 2·sin 30°·cos 30°, cos 60° = cos2 30° — sin2 30°. Если подставить данные, получится подробная функция: tg 60°= 2·tg 30°1 — tg2 30° и ctg 60° = ctg230° — 12·ctg 30°.
Так как sin 30° = 12, cos 30° = 32, tg 30° = 33, ctg 30° = 3 и sin 60° = 32, cos 60° = 12, tg 60° = 3, ctg 60° = 33, тогда выводится следующее: 2·sin 30°·cos 30° = 2·12·32 = 32, cos230° — sin230° = (32)2-(12)2 = 12,2·tg 30°1-tg230° = 2·321 — (33) = 3 и ctg230° — 12·ctg 30° = (3)2 − 12·3 = 33.
Задача 1: дан угол, отличный от 2α, например 3π5. Нужно найти его значение. Решение: угол 3π5 необходимо преобразовать. Получается α = 3π5:2 = 3π10.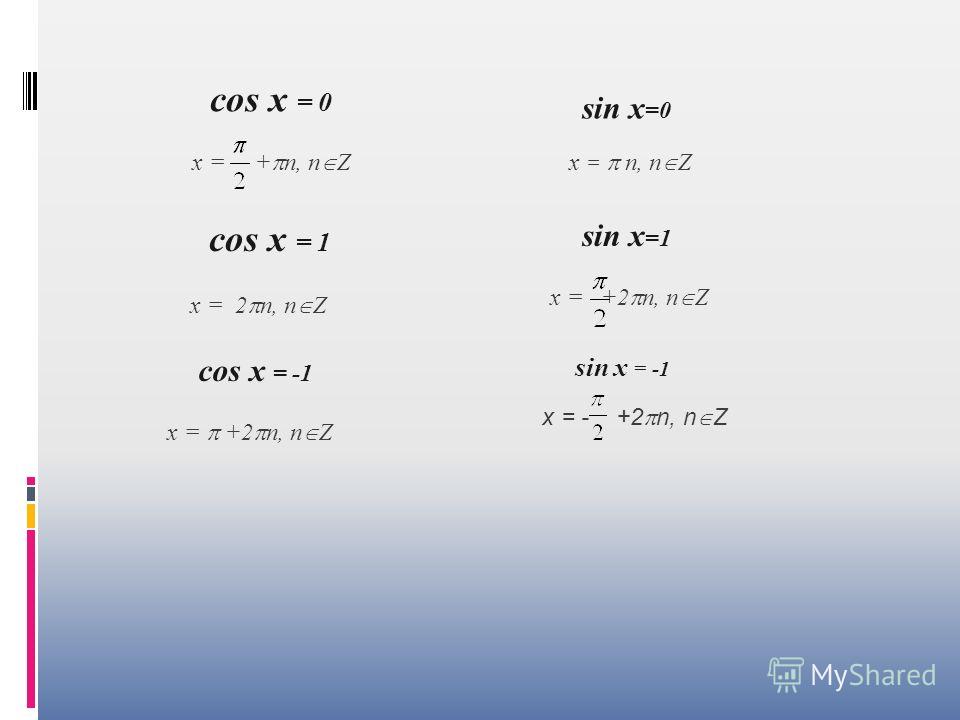 Из результата следует, что ФДУ для косинуса принимает следующий вид: cos3π5 = cos23π10 — sin23π10.
Из результата следует, что ФДУ для косинуса принимает следующий вид: cos3π5 = cos23π10 — sin23π10.
Задача 2: необходимо представить sin2α3 через функции, когда α = 6. Решение: заменить 2α3 = 4·α6. Если подставить данные, получится sin2α3. Выражая через функцию, принимая формулу двойного угла, записывается выражением: sin2α3 = 2·sinα3·cosα3. Используя cosα3, применяя sin2α2, получится результат sin2α3 = 4·sinα6·cos3α6 − 4·sin3α6·cosα6.
Тождества при других значениях
На практике студенты высших учебных заведений математических факультетов встречаются с задачами, для решения которых применяются формулы тройного, четверного и другого угла. В их основе находятся тригонометрические функции. Чтобы их вывести, используются формулы сложения двойного угла: sin3α = sin (2α+α) = 3·sinα·cos2α — sin3α.
При замене cos2α на 1-sin2α формула примет новый вид: sin3α = 3·sinα-4·sin3α.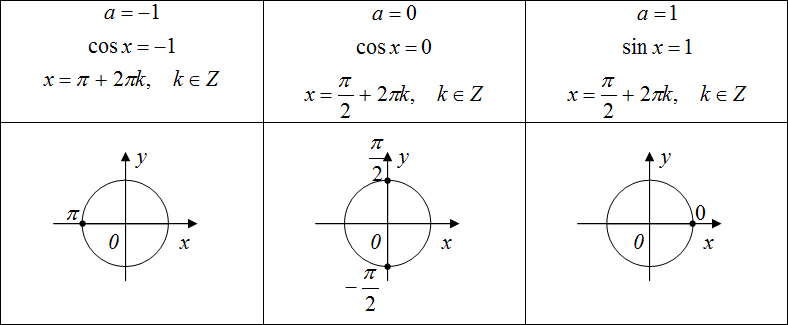 По аналогичной схеме приводится формула косинуса тройного угла: косинус3α = косинус (2α+α) = косинус3α — 3·синус2α·косинусα.
По аналогичной схеме приводится формула косинуса тройного угла: косинус3α = косинус (2α+α) = косинус3α — 3·синус2α·косинусα.
При замене sin2α на 1-cos2α, получится формула вида cos3α = -3·cosα+4·cos3α. С помощью полученных равенств преобразовывается формула тройного угла для тангенса и котангенса: tg3α = sin3αcos3α = ctg3α — 3·ctgα3·ctg2α — 1.
По такой же методике выводятся формулы четвёртой степени. Значение 4α нужно представить в виде 2·2α. Равенство выводится с помощью ФДУ дважды. Для получения равенства пятой степени представляется значение угла 5α в виде 3α+2α.
Такая сумма позволяет использовать формулы двойного и тройного углов с целью преобразования в конечный результат. По аналогичной схеме преобразовываются разные степени тригонометрических функций, но их применяют в тригонометрии редко.
Область применения
Чтобы определить значение тригонометрической функции (ТФ), рассматривается окружность с радиусом в единицу и диаметрами, взаимно перпендикулярными. Для вычислений потребуется отложить от точки, принадлежащей окружности, дуги любых длин. Они будут положительными, если их отложить против часовой стрелки.
Для вычислений потребуется отложить от точки, принадлежащей окружности, дуги любых длин. Они будут положительными, если их отложить против часовой стрелки.
Отрицательное значение принимают те, которые размещены по часовой стрелке. Если конец дуги имеет длину f, тогда проекция радиуса на любом диаметре примет значение косинуса дуги. Под аргументом понимается число, которое рассматривается геометрически как f либо радианная мера угла. Если аргумент ТФ взят за угол, тогда его значение выражается и в градусах.
Доказано, что значение острых углов больше нуля, но меньше p/2. Для таких величин ТФ рассматривается как отношение катетов к гипотенузе. Эти элементы принадлежат прямоугольному треугольнику. Название связано с наличием угла в 90 градусов. Для решения задач с тригонометрическими функциями используется и теорема Пифагора, в основе которой находится свойство прямоугольного треугольника: квадрат гипотенузы равен сумме квадратов катетов.
Дуга делит окружность на несколько частей.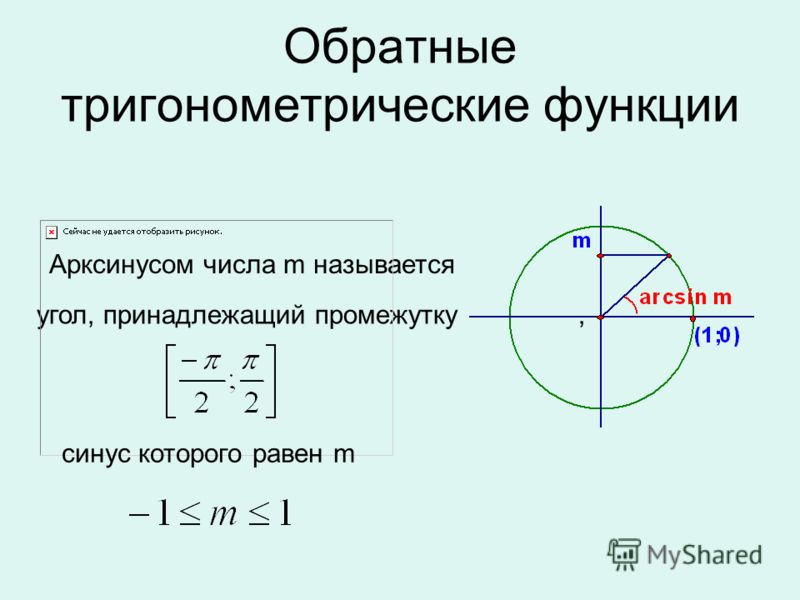 Углы, размещенные в первой четверти, больше нуля, во второй косинус меньше, но синус больше, в третьей ТФ меньше 0, а в четвёртой получаются значения, противоположные второй. Для построения окружности потребуется циркуль, а для измерения углов транспортир.
Углы, размещенные в первой четверти, больше нуля, во второй косинус меньше, но синус больше, в третьей ТФ меньше 0, а в четвёртой получаются значения, противоположные второй. Для построения окружности потребуется циркуль, а для измерения углов транспортир.
Для получения точного чертежа рекомендуется наносить данные на миллиметровую бумагу либо тетрадь в клетку.
Преобразование тригонометрических выражений в математике с примерами решения и образцами выполнения
Оглавление:
Преобразования тригонометрических выражений опираются на следующие основные формулы:
- основные тригонометрические тождества
- формулы приведения
- формулы суммы и разности аргументов
- формулы двойного аргумента
- формулы тройного аргумента
- формулы половинного аргумента
- формулы преобразования суммы (разности) тригонометрических функций в произведение
- формулы преобразования произведения тригонометрических функций в сумму (разность)
Задача:
На плоскости даны две точки и . Найти расстояние АВ между ними.
Найти расстояние АВ между ними.
Решение:
На рис. 125 изображен случай, когда и . Мы же будем вести рассуждения, справедливые для любого случая расположения точек A и В. Заметим, что и . По теореме Пифагора из прямоугольного треугольника АСВ имеем
или
Так как и , то
откуда имеем
Пример:
Найти расстояние между точками А (7, —2) и В (4, — 6).
Решение:
По формуле (114.1) имеем
Пример:
Найти расстояние между точками С (2, —1) и D (3, 1).
Решение:
По формуле (114.1) имеем
Косинус суммы и разности двух аргументова) Косинус разности. Предположим, что углы и удовлетворяют следующим двум условиям:
Предположим, что углы и удовлетворяют следующим двум условиям:
На рис. 126 изображены углы и . Точки А, В и С лежат на единичной окружности (OA = OB = ОС = 1). Заметим, что .
Кроме системы координат Оху будем рассматривать еще новую систему координат Ох’у’, полученную из старой поворотом на угол .
В дальнейшем будем использовать тот факт, что расстояние ВС между точками В и С, вычисленное в старой системе координат Оху и в новой системе координат Ох’у’, будет одинаково.
В системе координат Оху точка В имеет координаты , а точка С — координаты . По формуле (114.1) имеем
В системе координат Ох’у’ точка В имеет координаты (1, 0), а точка С — координаты . По формуле (114.1) найдем
По формуле (114.1) найдем
Приравняв правые части формул (115.1) и (115.2), получим выражение для косинуса разности двух углов:
Мы доказали теорему:
Косинус разности двух углов равен произведению косинуса первого угла на косинус второго плюс произведение синуса первого угла на синус второго.
Заметим, что ограничения, наложенные на углы и условиями 1) и 2), можно снять. В самом деле, допустим, что снято ограничение ; , налагаемое на углы и условиями 1), и мы имеем: и , где k, m = 0, ±1, ±2, … , или и . Положив , , получим и . Без ограничения общности будем считать, что . (Ниже будет показано, что условие 2) не существенно.)
Итак, углы и , удовлетворяют условиям 1) и 2), при которых была доказана теорема. Следовательно,
Подставив вместо и их значения, получим
Воспользовавшись периодичностью синуса и косинуса, придем к формуле (115.3). Мы показали, что условие 1) не существенно.
Допустим теперь, что, вопреки условию 2), , т. е. . Воспользовавшись четностью косинуса, будем иметь
Итак, доказана общность формулы (115.3), т. е. ее справедливость при любых углах и .
б) Косинус суммы. Так как формула (115.3) справедлива для любых двух углов и , то, заменив в ней на , получим
Воспользовавшись четностью косинуса и нечетностью синуса, будем иметь
Мы доказали теорему:
Косинус суммы двух углов равен произведению косинуса первого угла на косинус второго минус произведение синуса первого угла на синус второго.
Пример:
Вычислить .
Решение:
Формулы (115.3) и (115.4), как и все выводимые в дальнейшем соотношения для тригонометрических функций, сохраняют свою силу и для тригонометрических функций числового аргумента. Вообще, в дальнейшем мы уже не будем всякий раз указывать, как понимается аргумент тригонометрической функции (как угол или как число).
Синус суммы и разности двух аргументова) Синус суммы.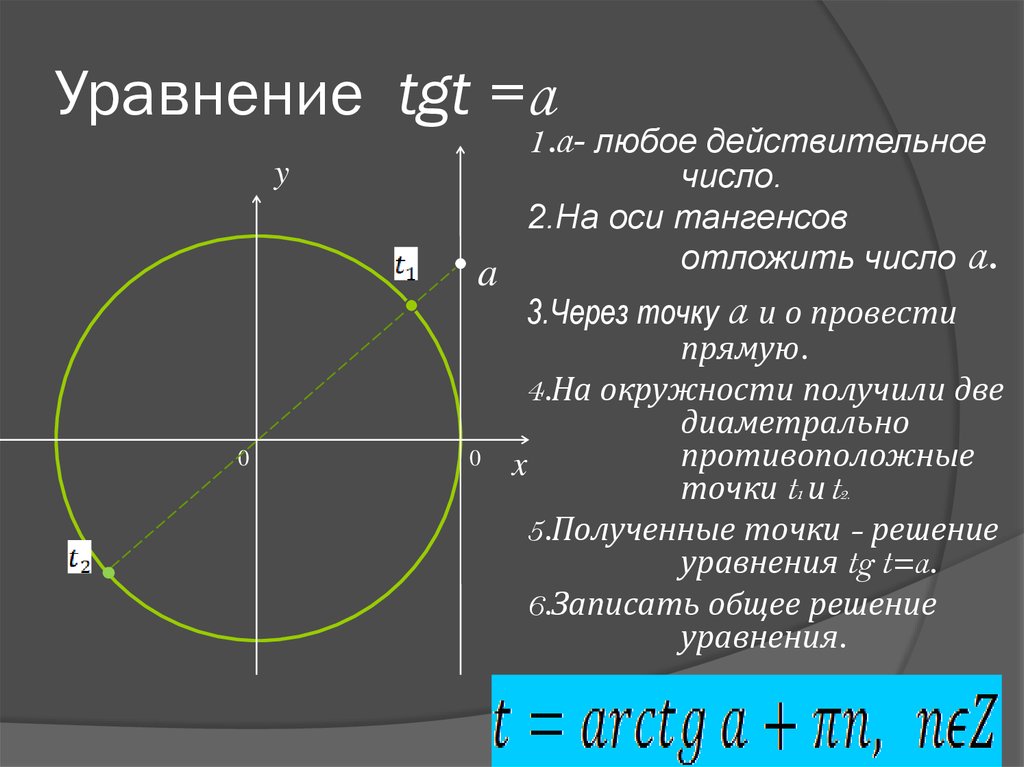 Воспользовавшись формулой приведения (105.2), будем иметь
Воспользовавшись формулой приведения (105.2), будем иметь
К правой части последнего равенства применим формулу (115.3):
Итак,
Мы доказали теорему:
Синус суммы двух аргументов равен произведению синуса первого аргумента на косинус второго плюс произведение косинуса первого аргумента на синус второго.
б) Синус разности. Выводится формула
и формулируется соответствующая теорема.
Пример:
Вычислить sin 105°.
Решение:
Тангенс суммы и разности двух аргументова) Тангенс суммы. При всех допустимых значениях аргументов и имеет место формула
Доказательство:
Па основании формул (116.1) и (115.4) имеем
Разделив почленно числитель и знаменатель дроби, стоящей в правой части, на произведение cosaeosp (мы предполагаем, что оно отлично от нуля), получим (117.1).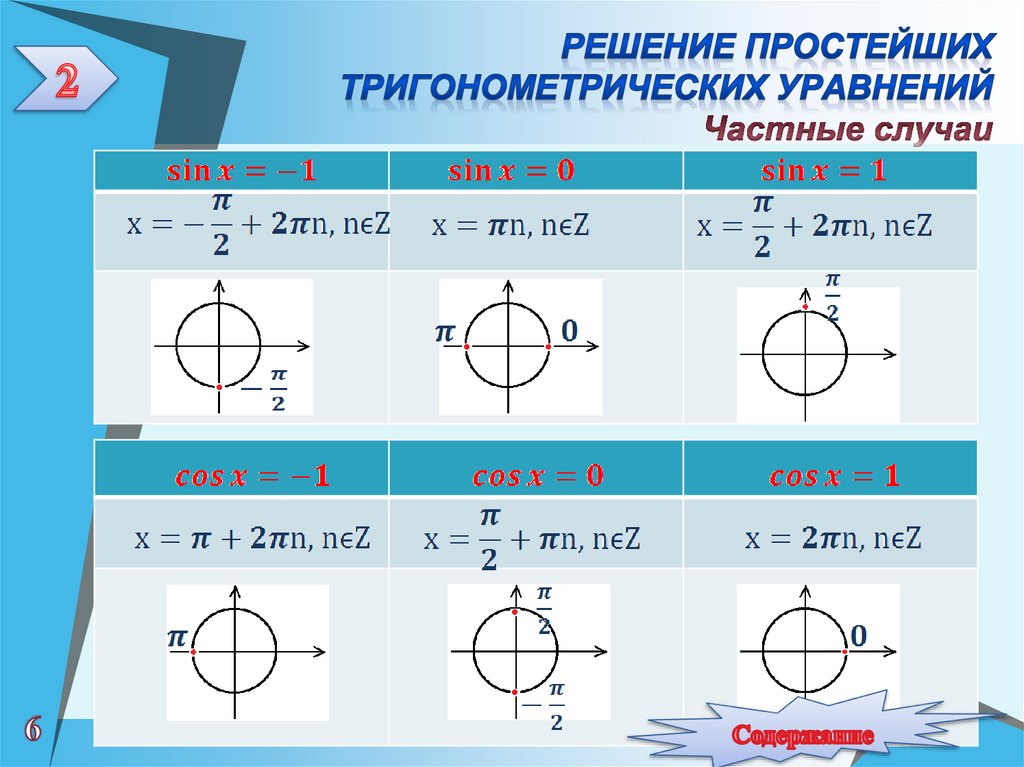
б) Тангенс разности. Аналогично можно вывести формулу
Пример:
Вычислить tg 105°.
Решение:
Пример:
Вычислить .
Решение:
О формулах сложения для нескольких аргументовЕсли возникает необходимость найти тригонометрическую функцию трех (или более) слагаемых, то это можно сделать, последовательно применив выведенные в пп. 115—117 формулы. Например:
и
Формулы для двойного и половинного аргументаВыражение и через степени и
119. Тригонометрические функции двойного аргумента. Положив в формулах (116.1), (115.4) и (117.1) , мы получаем следующие формулы:
Синус двойного аргумента равен удвоенному произведению синуса и косинуса данного аргумента.
Косинус двойного аргумента равен разности квадратов косинуса и синуса данного аргумента.
Пример:
Упростить выражение
Решение:
Мы уже решали этот пример в п. 99. Используя формулы (99.9), (99.10) и (119.1), имеем
Подставив (119.5) и (119.6) в (119.4), получаем
Замечание:
Формулы (119.5) и (119.6) можно получить и так:
Формулы (119.1) — (119.3) можно использовать для любого аргумента , считая его двойным для аргумента . Например:
и т. д.
Пример:
Упростить выражение .
Решение:
Умножим числитель и знаменатель на tg(a/2) и заменим tga по формуле (119.9), тогда получим
Пример:
Доказать, что
Решение:
Заметим, что
Преобразуя левую часть тем же способом и далее, получим последовательно
Тождество доказано.
Выражение через степени при натуральном числе
Выражение и через степени и при натуральном числе n.
Случай, когда n = 2, дан формулами (119.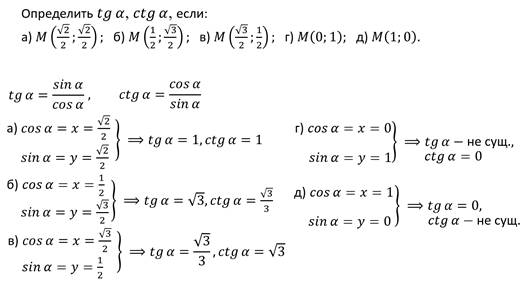 1), (119.2). Выразим теперь , , , и вообще , через и . Укажем на два способа получения соответствующих формул. Покажем, например, как получаются формулы для и .
1), (119.2). Выразим теперь , , , и вообще , через и . Укажем на два способа получения соответствующих формул. Покажем, например, как получаются формулы для и .
Первый способ. Представляем в виде и используем формулу (116.1), а затем используем формулы (119.1) и (119.2):
Итак,
В правую часть формулы (120.1) входят sin а и cos а; заменив на , придем к следующей формуле:
которая содержит в правой части только степени sin а. Аналогичные формулы можно получить для cos За:
Заметим, что формулы (120.1) и (120.2) являются частным случаем формулы (118.1), когда в последней . Формулы же (120.3) и (120.4) — частный случай формулы (118.2).
Второй способ. Воспользуемся результатами, полученными в алгебре при изучении комплексных чисел. На основании формулы Муавра (п. 17)
для случая, когда n = 3, имеем
Два комплексных числа равны тогда и только тогда, когда равны соответственно их действительные и мнимые части. Теперь из равенства
Теперь из равенства
отделяя (и соответственно приравнивая) действительную и мнимую части, получим формулы
и
В общем случае для получения sin na и cos na можно поступать также двумя способами: либо применять последовательно теоремы сложения (первый способ), либо пользоваться формулой Муавра (второй способ).
Пример:
Упростить выражение
Решение:
Применив формулы (120.1) и (120.3), получим
В конце решения примера мы воспользовались формулами (119.2), (99.1) и (119.1).
Тригонометрические функции половинного аргументаЧасто бывает необходимо, зная тригонометрические функции аргумента , найти тригонометрические функции аргумента . Выведем соответствующие формулы. Мы имеем
Присоединим к этой формуле основное тригонометрическое тождество:
Сложив почленно (119.8) и (121.1), получим
Вычитая (119.8) из (121.1), получим
Из тождеств (121. 2) и (121.3) соответственно имеем
2) и (121.3) соответственно имеем
Разделив почленно тождество (121.3) на (121.2), приходим к тождеству
Из последнего тождества имеем
Применяя формулы (121.4), (121.5) и (121.7), следует всякий раз заботиться о знаке, который нужно взять перед радикалом.
Для вычисления tg (а/2) могут быть использованы и формулы, выражающие tg (a/2) через cos а и sin а рационально. Выведем эти формулы:
Итак,
Так как всегда (формула (121.8) имеет смысл только при 1 + cos a > 0), то из (121.8) можно заключить, что знак во всех случаях совпадает со знаком sin а.
Итак,
Из последней формулы также ясно, что знак совпадает со знаком sin а, ибо всегда .
Пример:
Найти sin 22°30′, cos 22°30 и tg 22°30 .
Решение:
Мы знаем, что . Следовательно, применяя формулы (121.5), (121.4) и (121.9), получим
Пример:
Дано: , где . Найти и .
Решение:
Сначала находим
Так как , то , a .
Применяя формулы (121.5), (121.4) и беря в них радикалы с соответствующими знаками, получим
Пример:
Доказать тождество
Решение:
Так как ctg а = cos a/sin а, то достаточно доказать, что
На основании формул приведения и (99.2) имеем
Применяя формулу (121.2), получим
Далее получаем
(Мы применили сначала формулу (119.1), приняв за данный аргумент , а за удвоенный аргумент , а затем формулу приведения (105.1).) Следовательно, тождество доказано.
Выражение основных тригонометрических функций аргумента a через tg (a/2)Иногда требуется основные тригонометрические функции (sin a, cos a, tg a и ctg а) выразить рационально через tg (a/2). Покажем, например, как это делается для sin а. Используя тождества
Покажем, например, как это делается для sin а. Используя тождества
можно писать
Разделив числитель и знаменатель дроби, стоящей в правой части последнего равенства, почленно на , получим
Используя тождество , можно доказать, что
Соответствующая формула для tg a приводилась нами в п. 119:
Зная tg a можно получить формулу
Замечание. Формулы (122.1)—(122.4) имеют смысл для всех значений аргумента , кроме , где n — целое число.
Пример:
Дано . Найти sin a, cos a и tg a.
Решение:
На основании формулы (122.1) имеем
Аналогично . tg a уже проще искать так: .
Пример:
Вычислить , если .
Решение:
На основании формул (122.1) и (122.2) находим
Далее,
Преобразование в сумму выраженийПреобразование в сумму выражений вида , и
Основные формулы. Вернемся к формулам (116.1) и (116.2):
Вернемся к формулам (116.1) и (116.2):
Сложив эти тождества почленно и разделив на 2, получим
Выполнив аналогичные действия с формулами (115.3) и (115.4):
получим
Вычтем из (115.3) почленно (115.4) и разделим на 2; получим
Примеры:
Иногда при решении примеров, имея произведения тригонометрических функций, например функций аргументов и , бывает полезно перейти к полусуммам или к полуразностям соответствующих тригонометрических функций.
Пример:
Упростить
Решение:
Мы решали этот пример в п. 120, используя формулы (120.1) и (120.3) для sin 3a и cos 3a. Покажем теперь, как можно этот же пример решить, используя формулу (123.1). Заметим, что
Используя только что полученные соотношения, будем иметь
(В конце решения примера мы воспользовались формулами п. 119.)
Пример:
Упростить
Решение:
Преобразовав произведение, стоящее в знаменателе, получаем
Знаменатель преобразуем при помощи формулы приведения
Числитель же преобразуем так:
Тогда
Пример:
Вычислить А = sin20°sin40°sin80°. Решение. Заметим, что
Решение. Заметим, что
Далее,
так как , а .
Преобразование в произведение суммвида , и
125. Основные формулы. При вычислении различных выражений, содержащих тригонометрические функции, с помощью таблиц логарифмов и логарифмической линейки удобно иметь дело с произведениями, а не с суммами. Выведем ряд формул, которые позволяют от сумм переходить к произведениям.
а) Сумма синусов. Запишем формулу (123.1) в виде
и положим в ней и . Заметим, что и ; следовательно,
Сумма двух синусов равна удвоенному произведению синуса полусуммы на косинус полуразности их аргументов.
Пример:
Пример:
б) Разность синусов. Заменив в формуле (125.1) на , получим, учитывая нечетность синуса,
Разность двух синусов равна удвоенному произведению синуса полуразности на косинус полусуммы их аргументов.
Пример:
Пример:
в) Сумма косинусов.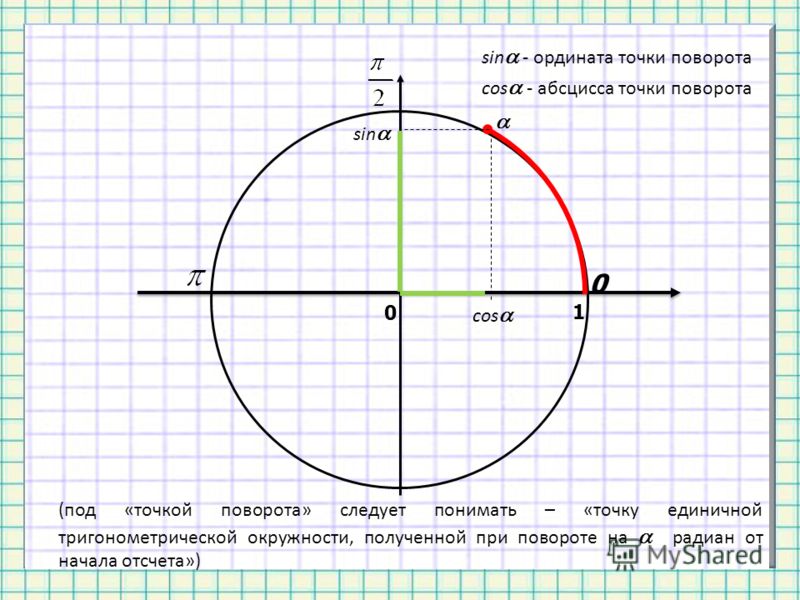 Запишем формулу (123.2) в виде
Запишем формулу (123.2) в виде
и положим в ней и . Мы уже видели, что и ; следовательно,
Сумма двух косинусов равна удвоенному произведению косинуса полусуммы на косинус полуразности их аргументов.
Пример:
cos 52°30′ + cos 16°30′ = 2 cos 34°30′ cos 18°.
Пример:
cos0,8 + cos2,8 — 2cos1,8cos1.
г) Разность косинусов. Из формулы (123.3), аналогично предыдущему, получается формула
Разность двух косинусов равна удвоенному произведению синуса полусуммы на синус обратной полуразности их аргументов.
Пример:
Пример:
cos 1,6 — cos 1,4 = —2 sin 1,5 sin 0,1.
д) Сумма тангенсов. Перейдя к синусам и косинусам, получим
Итак,
Пример:
Пример:
е) Разность тангенсов. Заменив в формуле (125.5) на , будем иметь, учтя четность косинуса и нечетность тангенса,
Пример:
Преобразовать по формуле (125.6) и вычислить, используя таблицу тригонометрических функций (приложение II),
tg 0,55 — tg 0,15.
Решение:
В нашей таблице нет значений функций для аргументов 0,55 и 0,15, поэтому, воспользовавшись формулой (123.2), перейдем к полусумме косинусов, но уже от аргументов, которые имеются в таблице:
Теперь имеем
Пример:
Замечание:
Последние две формулы (125.5) и (125.6) имеют смысл для аргументов и , отличных от , где n — целое число.
Примеры:
Пример:
Преобразовать в произведение выражение .
Решение:
Заменив по формуле приведения на , перейдем к сумме косинусов и воспользуемся формулой (125.3):
Пример:
Преобразовать в произведение .
Решение:
Перейдя к и , получим
Пример:
Привести к виду, удобному для логарифмирования,
Peшeние:
Заменив ctg 60° по формуле приведения на tg 30° и воспользовавшись формулой (126.1), получим
Далее, будем иметь
Последнее выражение можно упростить, если заметить, что , а sin 80° = cos 10°. Теперь будем иметь
Пример:
Привести к виду, удобному; для логарифмирования,
Решение:
Воспользовавшись формулой (125. 3), получим
3), получим
Согласно формуле (120.4)
откуда
и мы имеем
Пример:
Доказать тождество
Решение:
Заметим, что (см. (121.2)) и . После этого преобразуем левую часть предполагаемого тождества:
Следовательно, наше тождество доказано. Мы исключили из рассмотрения те значения аргумента а, при которых выражение или, что то же самое, равно нулю.
Пример:
Проверить, что tg 9°—tg 27° — tg 63° + tg 81° = 4.
Решение:
Заменив по формуле приведения tg 81° на ctg 9°, а tg 63° на ctg 27° и воспользовавшись формулой (126.1), получим
Заметив, что cos 36° = sin 54°, мы приходим к равенству 4 = 4. Итак, tg 9°—tg 27° — tg 63° + tg 81° = 4 .
Итак, tg 9°—tg 27° — tg 63° + tg 81° = 4 .
Некоторые суммы бывает возможно свести к произведениям, если соответствующим образом ввести вспомогательный аргумент. Проиллюстрируем этот прием на отдельных примерах.
Преобразование в произведение выражения . Мы предполагаем, что и . Постараемся подобрать аргумент и положительный множитель так, чтобы было
Возведя в квадрат обе части равенств (127.1) и сложив полученные равенства почленно, будем иметь
откуда и
(В качестве мы берем арифметическое значение корня.) После этого вспомогательный аргумент можно найти из соотношений
Теперь будем иметь
Итак,
Формулу (127.4) можно получить и так:
Положив теперь
мы придем к формуле (127. 4).
4).
Замечание:
Тот факт, что такой аргумент существует, доказан в п. 100 .
Пример 1. Представить в виде произведения выражение .
Решение:
Здесь , и . Следовательно,
Теперь полагаем
и .
В качестве аргумента можно взять, например, . Окончательно имеем
Пример:
Представить в виде произведения выражение .
Решение:
В этом примере а = 1 и b = 1, следовательно, . Теперь поступаем, как в общем случае:
Положим и .
В качестве аргумента можно взять, например, . После этого получим
Преобразование в произведение выражений и при .
1) Рассмотрим выражение . Запишем его следующим образом:
Так как, по предположению, , то можно положить . Теперь будем иметь
Пример:
Преобразовать в произведение .
Решение:
Положим .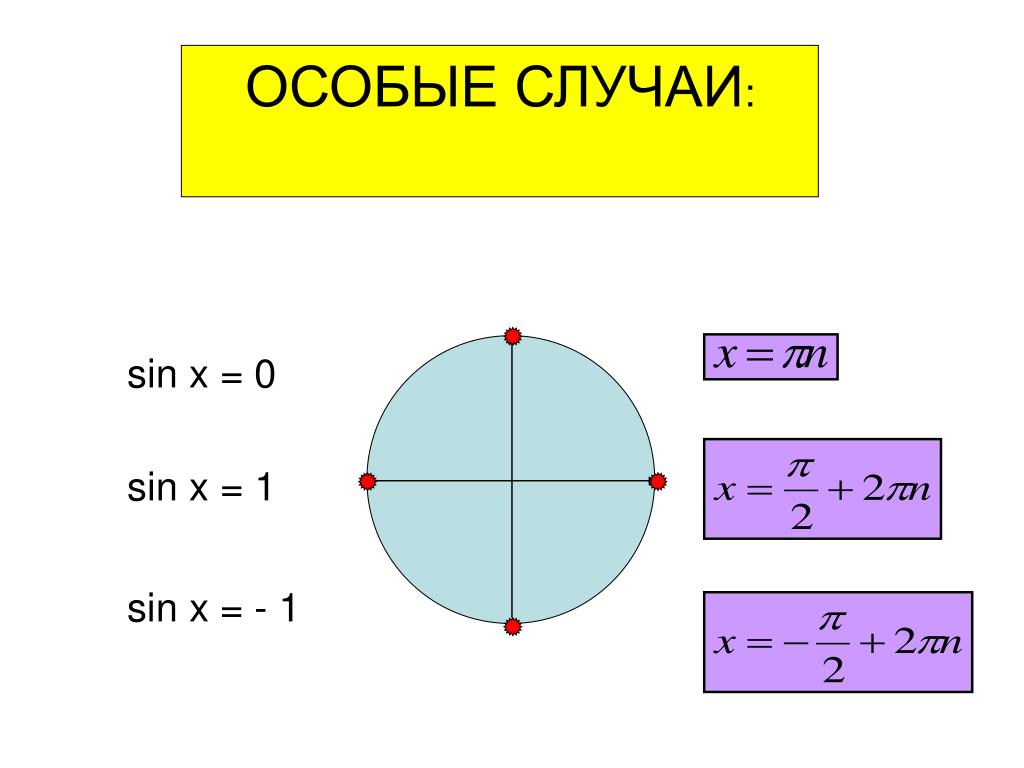 В качестве можно, например, взять , и мы получим
В качестве можно, например, взять , и мы получим
2) Рассмотрим выражение . Запишем его следующим образом:
Так как, по предположению, , то можно положить . Теперь будем иметь
Пример:
Преобразовать в произведение
Решение:
Положим . В качестве можно, например, взять , и мы получим
Пример:
Преобразовать в произведение . Решение.
Положим . В качестве можно, например, взять , и мы будем иметь
Преобразование в произведение выражения . Рассмотрим выражение , где . Запишем его следующим образом:
Так как тангенс изменяется в пределах от до , то при любых а и b можно положить , и мы получим
Пример:
Преобразовать в произведение . Решение.
Положим . В качестве можно, например, взять , и мы будем иметь
Пример:
Преобразовать в произведение .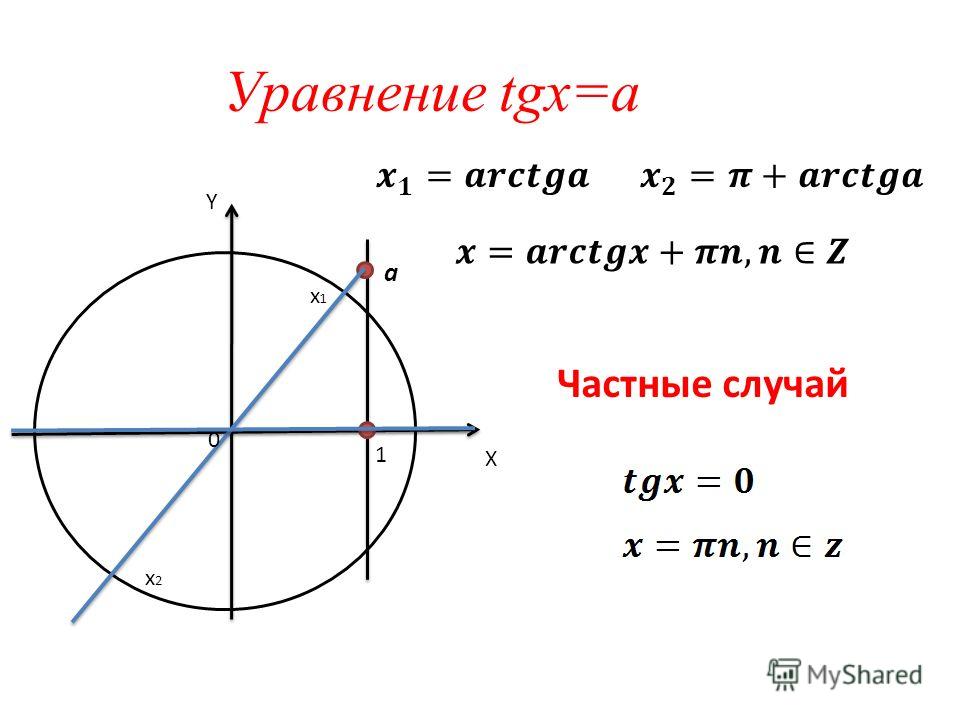 Решение.
Решение.
Положим . В качестве можно, например, взять , и мы получим
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Правило синусов (закон синусов)
Пи Хан Го, Мэй Ли, Махиндра Джейн, а также
способствовал
Содержимое
- Правило синусов
- Примеры
- Неоднозначный случай
- Расширенное правило синусов
Дан треугольник ABC ABC ABC с соответствующими длинами сторон a, b a, ba, b и c cc:
правило синусов или закон синусов является следующим тождеством:
asin(A)=bsin(B)=csin(C). \ frac { a} {\ sin (A)} = \ frac {b} {\ sin (B)} = \ frac {c} {\ sin (C)}. грех (А) а = грех (В) б = грех (С) с.
\ frac { a} {\ sin (A)} = \ frac {b} {\ sin (B)} = \ frac {c} {\ sin (C)}. грех (А) а = грех (В) б = грех (С) с.
Докажем первое тождество
asin(A)=bsin(B). \frac { a}{ \sin (A)} = \frac {b}{\sin (B)}. грех (А) а = грех (В) б.
Второе равенство доказывается аналогично.
Проведя высоту треугольника hhh от вершины ССС до противоположной стороны, мы можем выразить высоту hhh двумя разными способами:
- Во-первых, у нас есть sinA=гипотенуза напротив=hb\sin A = \frac{\text{противоположная}}{\text{гипотенуза}} = \frac{h}{b}sinA=hypotenuseopposite=bh, откуда следует h=bsin(A).h = b\sin(A).h=bsin(A).
- Кроме того, sinB=гипотенуза напротив=ha\sin B = \frac{\text{противоположная}}{\text{гипотенуза}} = \frac{h}{a}sinB=hypotenuseopposite=ah, что подразумевает h = asin(B).h = a\sin(B).h=asin(B).
Приравнивая эти значения hhh, мы получаем
bsin(A)=asin(B)asin(A)=bsin(B).\begin{выровнено} б \sin(A) &= a \sin(B) \\ \frac{a}{\sin(A)} &= \frac{b}{\sin(B)}.
\end{align}bsin(A)sin(A)a=asin(B)=sin(B)b.
Проведя высоту hhh из двух других вершин, мы можем аналогичным образом показать второе равенство. □_\квадрат□ 9\круг)} \\ \ гидроразрыва {1}{\ \ гидроразрыва {1} {2}\ } &= \ гидроразрыва {b}{\ \ гидроразрыва {\ sqrt {2}} {2}\} \\ \frac{2 \cdot \sqrt{2}}{2}&= b. \end{выровнено}sin(A)asin(30∘)1 21 122⋅2=sin(B)b=sin(45∘)b= 22b= б.
Следовательно, b=2b= \sqrt{2}b=2. □_\квадрат□
Обычно правило синусов применяется для определения треугольника ABC ABCABC по некоторым его сторонам и углам. Неоднозначный случай относится к сценариям, в которых есть 2 различных треугольника, удовлетворяющих такой конфигурации. Это происходит, когда нам дан угол-сторона-сторона, как показано на диаграмме ниже: 9\circ} sin46∘10=sin13∘9, что явно неверно, подразумевая, что такого треугольника не существует. Следовательно, не существует возможного треугольника, соответствующего этим критериям. □_\квадрат□
0 1 2 Недостаточно информации
Стороны треугольника равны a,b,a,b,a,b и ccc, а противоположные им углы равны A,B,A,B,A,B и C,C,C , соответственно.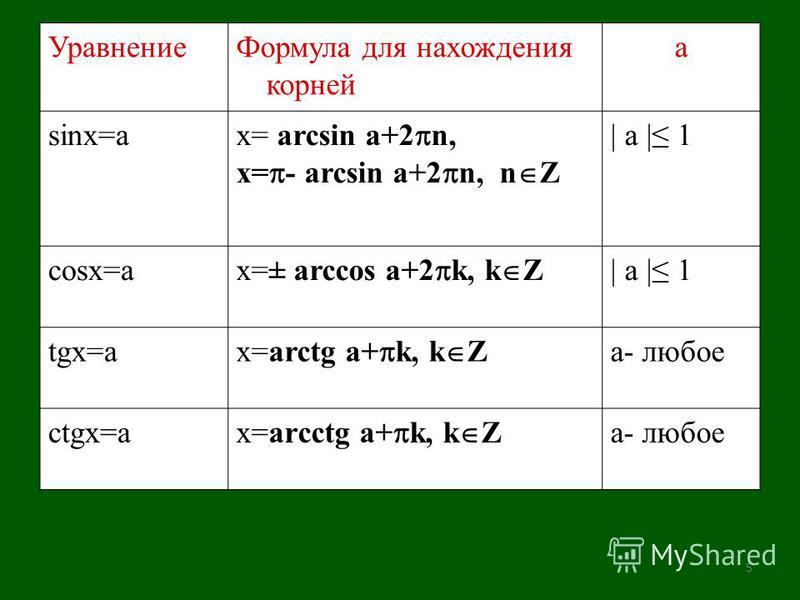 Учитывая a = 3, b = 8, a = 3, b = 8, a = 3, b = 8 и sinA = 513, \ sin { A } = \ frac { 5 }{ 13 }, sin A = 135 , какое количество треугольников можно составить из данных?
Учитывая a = 3, b = 8, a = 3, b = 8, a = 3, b = 8 и sinA = 513, \ sin { A } = \ frac { 5 }{ 13 }, sin A = 135 , какое количество треугольников можно составить из данных?
Расширенное правило синусов представляет собой отношение, связывающее стороны треугольника с синусом соответствующих углов и радиусом описанной окружности. Выписка выглядит следующим образом:
Дан треугольник ABC ABC ABC с соответствующими длинами сторон a, b a, ba, b и c cc и R RR как радиус описанной окружности треугольника ABC ABCABC, мы имеем следующее:
asinA=bsinB=csinC=2R. \ frac { a} {\ sin A} = \ frac {b} {\ sin B} = \ frac {c} {\ sin C} = 2R. sinAa=sinBb=sinCc=2R.
Примечание: Утверждение без третьего равенства часто называют правилом синусов. Связь между правилом синусов и радиусом описанной окружности треугольника ABCABCABC расширяет его до расширенного правила синусов. \circ — \alpha180∘−α, и, таким образом, sinBOD=sinα \sin BOD = \sin \alphasinBOD=sinα . Таким образом,
\circ — \alpha180∘−α, и, таким образом, sinBOD=sinα \sin BOD = \sin \alphasinBOD=sinα . Таким образом,
∣BD‾∣ ∣OB‾∣=sinα ⟹ asinα=2R. □ \ frac {\ \ lvert \ overline {BD} \ rvert \ }{\ lvert \ overline {OB} \ rvert} = \ sin \ alpha \ подразумевает \ frac {a} {\ sin \ alpha} = 2R. \, _\квадрат ∣OB∣ ∣BD∣ =sinα⟹sinαa=2R.□
Докажите, что площадь треугольника ABC ABCABC равна abc4R. \ frac {abc} {4R}. 4Rabc.
Пусть D DD основание перпендикуляра из A AA в BC‾ \overline{BC}BC. Используя BC‾ \overline{BC}BC в качестве основания и AD‾ \overline{AD}AD в качестве высоты, площадь треугольника равна 12a⋅∣AD‾∣ \frac {1}{2} a \cdot \lvert \overline{AD}\rvert21a⋅∣AD∣. Из прямоугольного треугольника CAD CADCAD, sinγ=∣AD‾∣b \sin\gamma = \frac {\lvert\overline{AD}\rvert} {b}sinγ=b∣AD∣. Таким образом, площадь треугольника равна 12a⋅∣AD‾∣=12absinγ \frac {1}{2} a \cdot \lvert\overline{AD}\rvert = \frac {1}{2} a b \sin \gamma21a⋅∣AD∣=21absinγ, который часто цитируют.
Теперь, используя расширенное правило синусов, мы имеем csinγ=2R \frac {c}{\sin \gamma} = 2Rsinγc=2R, и, таким образом, площадь треугольника равна
12absinγ=12abc2R=abc4R. □ \frac {1}{2} a b \sin \gamma = \frac {1}{2} a b \frac {c}{2R} = \frac {abc} {4R}. \ _\квадрат 21absinγ=21ab2Rc=4Rabc. □
В море плавает сферический буй с надводной частью высотой h=18 см, h =18\text{ см}h=18 см и радиусом r=24 см,r = 24\text{ см},r =24 см, как показано ниже:
Каков радиус этого буя?
Цитировать как: Правило синусов (закон синусов). Brilliant.org . Извлекаются из https://brilliant.org/wiki/sine-rule/
исчисление — что такое синус вещественного числа
Попробуйте этот ответ, сначала просто взглянув на изображения (щелкните средней кнопкой мыши, чтобы увеличить в новой вкладке).
Если этого недостаточно, попробуйте прочитать описание.
Где ввод в радианах:
Представьте себе круг, как черный ниже: Для удобства назовем направление вверх на этой диаграмме «север».
Представьте, что вы сидите на круге у красной точки в автомобиле с очень точным одометром.
Вы можете представить, что транспортное средство — это вагон поезда, а черный кружок — это путь, если это поможет.
Теперь представьте, что вы путешествуете по кругу и очерчиваете оранжевую дугу.
Предположим, вы остановились в какой-то момент. Показания одометра х .
(Вы можете представить, что это мили, километры, мегаметры или другие общие единицы, которые кто-то решил назвать «радианами».)
«Синус» x — это расстояние, которое вам придется пройти на юг, чтобы достичь исходной широты.
Другими словами, «синус» x — это то, как далеко вы находитесь на север от горизонтальной синей линии.
Если вы прошли более половины круга и находитесь в «южной» половине, это расстояние будет отрицательным числом.
Если вы прошли ровно половину круга или весь круг, это будет 0.
Если вы прошли четверть пути, это будет 1.
Если вы прошли три четверти пути, это будет -1.
Радиус круга — это расстояние между центром и любой точкой на его краю. (Тот факт, что это постоянное значение, делает его кругом.)
Центр этого круга находится в месте пересечения синих линий, а расстояние от этого центра до красной точки (точки на внешнем краю круга) равно 1.
Это означает, что радиус этой окружности равен 1.
(Любая окружность с радиусом 1 получает специальное название «единичная окружность», но на самом деле вам не нужно знать это, чтобы понять это объяснение.)
Диаметр круга (расстояние от центра круга до середины) всегда в два раза больше радиуса.
Следовательно, диаметр этого круга равен 2.
$\pi$ определяется как отношение диаметра круга к его длине окружности (расстоянию вокруг внешнего края круга).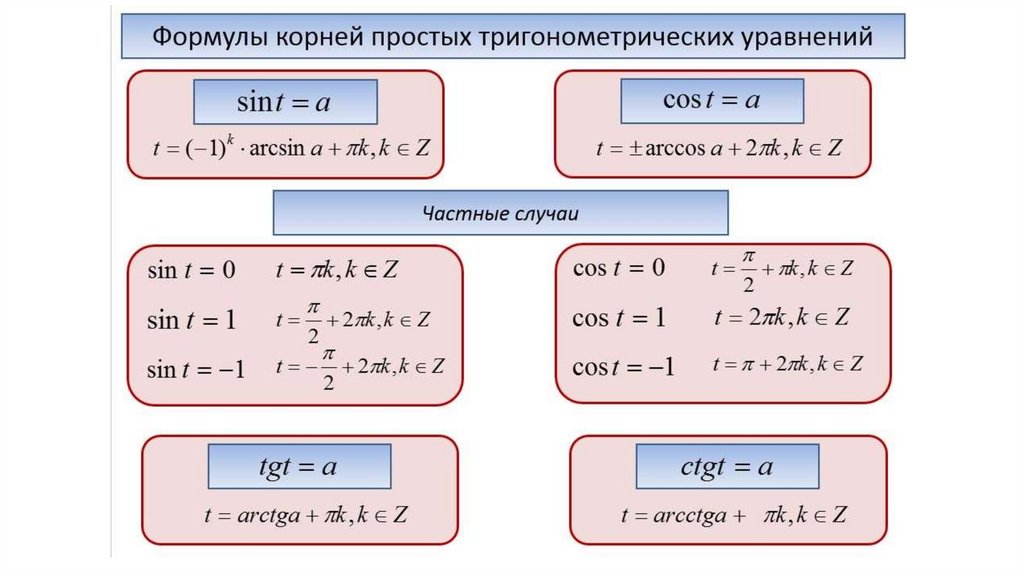 Так как $\pi$ = окружности / диаметра, окружности = диаметра * $\pi$, а длина окружности этого круга равна 2$\pi$.
Так как $\pi$ = окружности / диаметра, окружности = диаметра * $\pi$, а длина окружности этого круга равна 2$\pi$.
Как только одометр покажет 2$\pi$, вы вернетесь туда, откуда начали. Если вы продолжите движение, вы будете отслеживать тот же путь, и для каждого показания одометра расстояние, которое вам придется пройти на юг, чтобы достичь той же широты, с которой вы начали, точно такое же, как когда ваш одометр показывал 2 $\pi$ меньше, чем сейчас. Другими словами, значение синуса будет точно таким же, как и в прошлый раз, когда вы были там.
Вот почему функция синуса является периодической (это означает, что она повторяется).
$sin(x) = sin(x-2\pi) = sin(x+2\pi)$.
Где ввод в градусах:
Представьте себе круг, как черный ниже:
Для удобства назовем направление вверх на этой диаграмме севером.
Представьте, что в точке пересечения синих линий стоит обелиск, который виден отовсюду на круге.
Представьте, что вы сидите на круге у красной точки, в одной единице к востоку от обелиска.
Представьте, что линия между этим обелиском и вашей отправной точкой постоянно отмечена тем, что я назову «положительной горизонтальной осью».
Теперь представьте, что вы путешествуете по кругу и очерчиваете оранжевую дугу.
Предположим, вы остановились в какой-то точке и провели фиолетовую линию между тем, где вы находитесь, и обелиском. Назовем угол, который проходит от положительной горизонтальной оси к этой линии, $\theta$.
«Синус» $\theta$ — это расстояние, которое вам придется пройти на юг, чтобы достичь исходной широты.
Другими словами, «синус» $\theta$ показывает, как далеко вы находитесь на север от горизонтальной синей линии.
Если вы прошли более половины круга и находитесь в «южной» половине, это расстояние будет отрицательным числом.
Если вы прошли ровно половину круга или весь круг, это будет 0.
Если вы прошли одну четверть пути, это будет 1.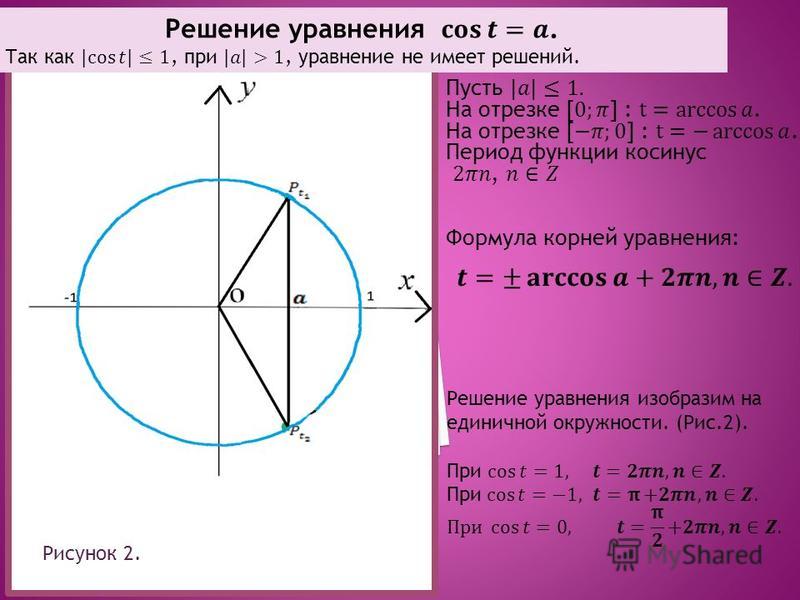
Если вы прошли три четверти пути, это будет -1.
Как только вы вернетесь к тому, с чего начали, $\theta$ будет равно 360 градусам, потому что в круге 360 градусов (по определению).
Если вы продолжите движение, вы будете отслеживать тот же путь, и для точки, которую вы достигнете снова, значение синуса будет точно таким же, как и в прошлый раз, когда вы были там.
Вот почему функция синуса является периодической (это означает, что она повторяется).
$sin(\theta) = sin(\theta-360°) = sin(\theta+360°)$.
Дополнительное пояснение: косинус
В обоих примерах косинус от x, или $\theta$, — это расстояние, которое вам придется пройти « на запад », чтобы достичь вертикальной синей линии.
Другими словами, это то, как далеко вы находитесь «на восток» от вертикальной синей линии.
Если вы нарисовали горизонтальную линию между концом дуги и вертикальной синей линией, это будет длина этой линии.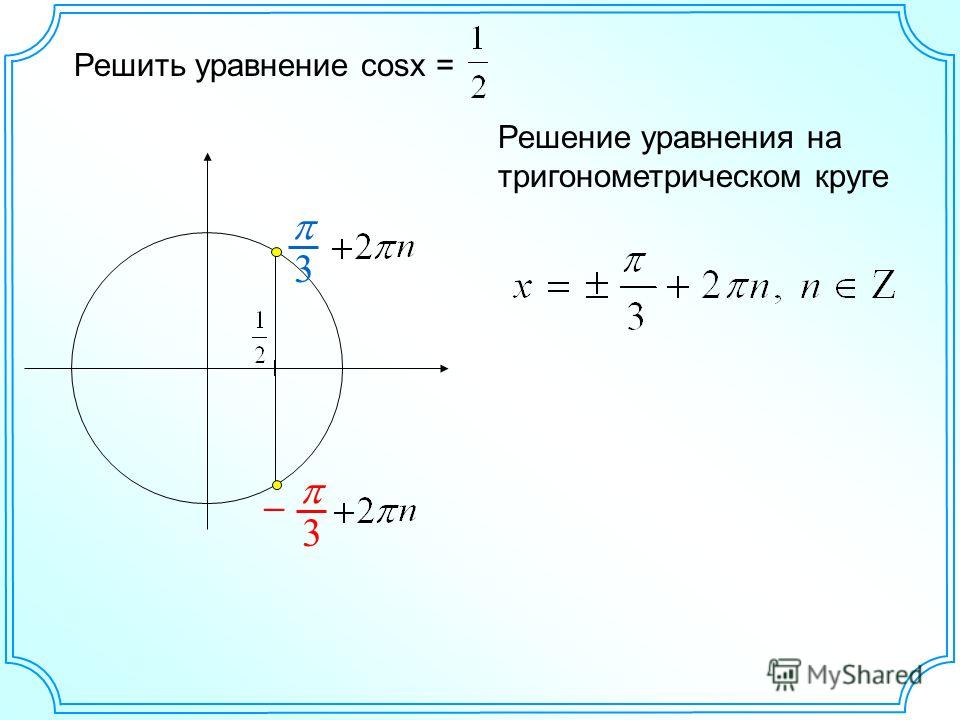
Это длина синей стороны треугольника на второй диаграмме выше (где длина дуги по-прежнему равна x ).
В начальной точке это 1.
В «западной» половине круга это отрицательное число.
Если вы прошли ровно половину пути, будет -1.
Если вы прошли четверть круга или три четверти круга, это будет 0,9.0151 Косинус периодичен так же, как и синус; вы могли бы последовательно написать «cos» вместо «sin» в приведенных выше строках формулы (которые имеют два знака =), и каждый из них все равно будет правильным.
Математики называют местонахождение обелиска «происхождением», но я решил не использовать этот термин здесь, чтобы избежать путаницы с более распространенным определением «происхождения», а именно «где вы начали», потому что это относится к другое место в повествовании, лежащем в основе этого ответа. Я также сделал альтернативную версию второй диаграммы, в которой вместо этого используется «происхождение».
В этой публикации также используется слово «линия» в нескольких местах, где «отрезок линии» был бы более правильным; Я думаю, что смысл понятен в контексте, и используемый здесь язык лучше облегчает понимание.
Особые тригонометрические углы – объяснение и примеры
Обычно нам нужно использовать калькулятор для вычисления значений тригонометрических функций угла, если мы не имеем дело с специальными тригонометрическими углами . Потому что точно оценить тригонометрические функции для большинства углов невозможно. Но верно ли это для всех углов? Ответ нет — не всегда.
Специальные тригонометрические углы — 30 o , 45 o и 60 o — генерируют довольно простые тригонометрические значения. Мы можем точно вычислить тригонометрические функции для этих специальных углов без калькулятора.
Ожидается, что после изучения этого урока мы изучим концепции, лежащие в основе этих вопросов, и будем готовы давать точные, конкретные и последовательные ответы на эти вопросы.
- Что такое специальные тригонометрические углы?
- Как решать тригонометрические специальные углы?
- Как мы можем решать актуальные задачи, используя специальные тригонометрические углы?
Цель этого урока — прояснить любую путаницу, которая может у вас возникнуть в отношении понятий, связанных с тригонометрическими специальными углами.
Что такое специальные тригонометрические углы?
Существуют определенные углы, которые обеспечивают простые и точные тригонометрические значения. Эти особые углы известны как тригонометрические особые углы . Это 30 o , 45 o и 60 o .
Что в них такого особенного?
Потому что легко «точно» вычислить тригонометрическую функцию без использования калькулятора для этих углов. Эти углы имеют сравнительно чистые значения, предлагающие нам многое для решения математических задач. Мы используем эти значения, чтобы дать точных ответов для определения значений многих тригонометрических соотношений.
В этом уроке мы будем использовать два «особых прямоугольных треугольника», чтобы обсудить особых ангелов .
- 45 o – 45 o – 90 o треугольник — также известный как равнобедренный треугольник — представляет собой особый треугольник с углами 45 или , 45 или и 90 или .

- 30 o – 60 o – 90 o треугольник – еще один особый треугольник с углами 30 o , 60 o 90 8 9 o и 8
Эти специальные треугольники обладают уникальной способностью давать нам точные и простые ответы при работе с тригонометрическими функциями.
Хорошо, что вы уже знакомы с этими особыми треугольниками, как мы обсуждали их на наших уроках геометрии. Мы просто будем использовать их для решения тригонометрических специальных углов и определения тригонометрических отношений этих специальных углов. 9{\ circ } $
$ \ sin $
$ {\ frac {1} {2}} $
$ {\ frac { 1} {\ sqrt {2}}} $
$ {\ frac {\ sqrt {3}} {2}} $
$ \ cos $
$ {\ frac {\ sqrt {3}} {2}} $
$ {\ frac { 1} {\ sqrt {2}}} $
$ {\ frac {1} {2}} $
$ \ tan $
8$ {\ frac { 1} {\ sqrt {3}}} $
$1$
$\sqrt{3}$
$\csc$
$2$
$\sqrt{2}$
${ \frac { 2}{\sqrt{3}}}$
$\sec$
${\frac { 2}{\sqrt{3}}}$
$\ sqrt{2}$
$2$
$\cot$
$\sqrt{3}$
\:+2$= $2\влево(\frac{1}{4}\right)+\:3\:\влево(\frac{3}{4}\right)\:+\:6 \:\left(\frac{1}{3}\right)\:+2$
= $\frac{1}{2}+\frac{9}{4}+2+2$
= $\frac{1}{2}+\frac{9}{4}+4$
= $\frac{27}{4}$
math package — math — Go Packages
Пакет math содержит основные константы и математические функции.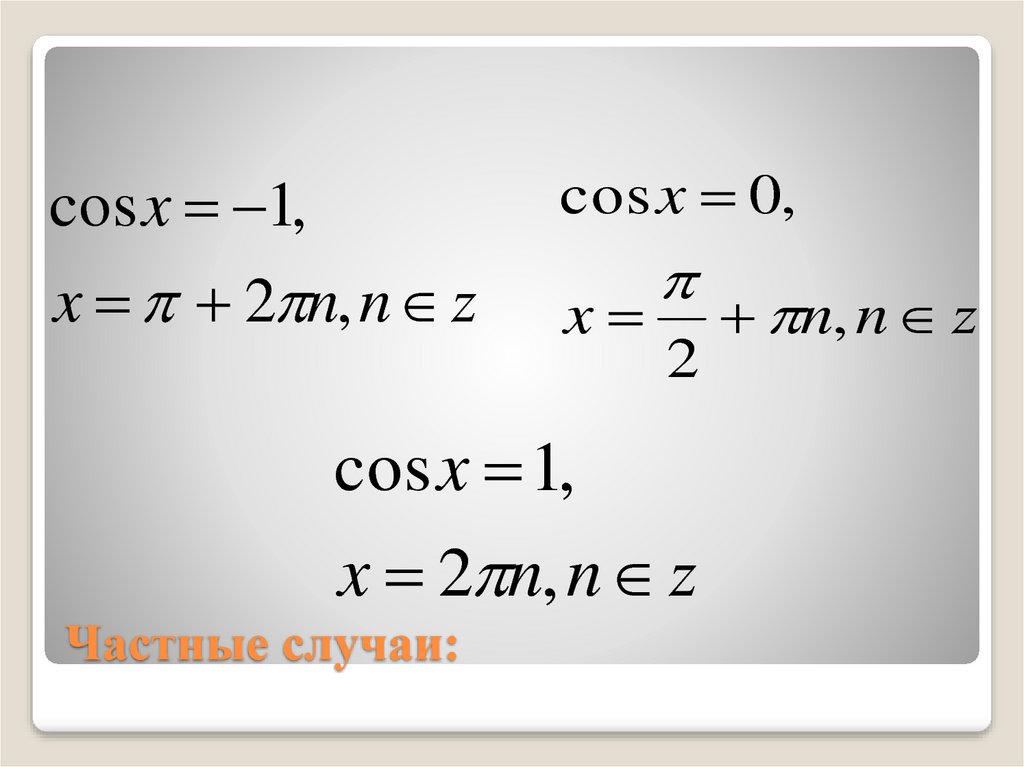
Этот пакет не гарантирует идентичных по битам результатов для разных архитектур.
- Константы
- func Abs(x float64) float64
- func Acos(x float64) float64
- функция Acosh(x float64) float64
- функция Asin(x float64) float64
- функция Asinh(x float64) float64
- func Atan(x float64) float64
- функция Atan2(y, x float64) float64
- func Atanh(x float64) float64
- func Cbrt(x float64) float64
- func Ceil(x float64) float64
- func Copysign(f, знак float64) float64
- функция Cos(x float64) float64
- func Cosh(x float64) float64
- func Dim(x, y float64) float64
- функция Erf(x float64) float64
- функция Erfc(x float64) float64
- функция Erfcinv(x float64) float64
- функция Erfinv(x float64) float64
- функция Exp(x float64) float64
- функция Exp2(x float64) float64
- func Expm1(x float64) float64
- функция FMA(x, y, z float64) float64
- func Float32bits(f float32) uint32
- func Float32frombits(b uint32) float32
- func Float64bits(f float64) uint64
- func Float64frombits(b uint64) float64
- func Floor(x float64) float64
- func Frexp(f float64) (frac float64, exp int)
- func Gamma(x float64) float64
- func Hypot(p, q float64) float64
- функция Ilogb(x float64) целое число
- func Inf(sign int) float64
- func IsInf (f float64, знак int) bool
- func IsNaN(f float64) (bool)
- функция J0(x float64) float64
- функция J1(x float64) float64
- func Jn(n int, x float64) float64
- func Ldexp(frac float64, exp int) float64
- func Lgamma(x float64) (lgamma float64, целочисленный знак)
- журнал функций (x float64) float64
- функция Log10(x float64) float64
- функция Log1p(x float64) float64
- функция Log2(x float64) float64
- функция Logb(x float64) float64
- функция Max(x, y float64) float64
- функция Min(x, y float64) float64
- func Mod(x, y float64) float64
- func Modf(f float64) (int float64, frac float64)
- функция NaN() float64
- func Nextafter(x, y float64) (r float64)
- func Nextafter32(x, y float32) (r float32)
- func Pow(x, y float64) float64
- func Pow10(n int) float64
- func Remainder(x, y float64) float64
- func Round(x float64) float64
- функция RoundToEven(x float64) float64
- func Signbit (x float64) bool
- функция Sin(x float64) float64
- func Sincos(x float64) (sin, cos float64)
- функция Sinh(x float64) float64
- функция Sqrt(x float64) float64
- func Tan(x float64) float64
- func Tanh(x float64) float64
- func Trunc(x float64) float64
- функция Y0(x float64) float64
- функция Y1(x float64) float64
- функция Yn(n int, x float64) float64
- Абс
- Акос
- Акош
- Асин
- Асинь
- Атан
- Атан2
- Атан
- ЦБ
- Потолок
- Копирайтинг
- Кос
- Кош
- Размер
- Опыт
- Опыт2
- Эксперимент1
- Этаж
- Журнал
- Журнал10
- Журнал2
- Мод.

- Модификация
- Пау
- Пау10
- Остаток
- Раунд
- RoundToEven
- Грех
- Синкос
- Синь
- кв.
- Тан
- Танх
- Транк
Просмотр исходного кода
константа ( E = 2,718281828453536028747135266249775724709369995957496696763 // https://oeis.org/A001113 Пи = 3,1415
589746264338327950288419716939937510582097494459 // https://oeis.org/A000796 Фи = 1,618033988749894848204586834365638117720300576286213544862 // https://oeis.org/A001622 Sqrt2 = 1,41421356237309504880168872420969807856967187537694807317667974 // https://oeis.org/A002193 SqrtE = 1,64872127070012814684865078781416357165377610071014801157507931 // https://oeis.org/A019774 SqrtPi = 1,772453850602729816748334114518279754945612238712821380779 // https://oeis.org/A002161 SqrtPhi = 1,272019649514068964252422461737471560804184009624861664038 // https://oeis.org/A139339 Ln2 = 0,6180559945309417232121458176568075500134360255254120680009// https://oeis.org/A002162 Log2E = 1 / Ln2 Ln10 = 2,3025850045684017968436420760110148862877297603332790 // https://oeis.org/A002392 Log10E = 1 / Ln10 )
Математические константы.
Просмотр исходного кода
константа ( MaxFloat32 = 0x1p127 * (1 + (1 - 0x1p-23)) // 3.402823466385288598117041834845160e+38 SmallestNonzeroFloat32 = 0x1p-126 * 0x1p-23 // 1.4012984643248170701280e-45 MaxFloat64 = 0x1p1023 * (1 + (1 - 0x1p-52)) // 1,79769583289
86231570814527423731704356798070e+308 SmallestNonzeroFloat64 = 0x1p-1022 * 0x1p-52 // 4,940656458412465441765687
22137236505980e-324 )Предельные значения с плавающей запятой. Max — это наибольшее конечное значение, представляемое типом. SmallestNonzero — это наименьшее положительное ненулевое значение, представляемое типом.
Просмотр исходного кода
константа ( MaxInt = 1<<(intSize-1) - 1 MinInt = -1 << (intSize - 1) МаксИнт8 = 1<<7 - 1 Мининт8 = -1 << 7 MaxInt16 = 1<<15 - 1 Мининт16 = -1 << 15 MaxInt32 = 1<<31 - 1 MinInt32 = -1 << 31 MaxInt64 = 1<<63 - 1 Мининт64 = -1 << 63 MaxUint = 1<Целочисленные предельные значения.
Этот раздел пуст.
func Abs(x float64) float64Abs возвращает абсолютное значение x.
Особые случаи:
Абс(±Инф) = +Инф Абс(NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { x := math.Abs(-2) fmt.Printf("%.1f\n", х) y := math.Abs(2) fmt.Printf("%.1f\n", у) }Выход: 2.0 2.0func Acos(x float64) float64Acos возвращает арккосинус x в радианах.
Особый случай:
Acos(x) = NaN, если x < -1 или x > 1Пример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f", math.Acos(1)) }Выход: 0,00func Acosh(x float64) float64Acosh возвращает гиперболический арккосинус x.
Особые случаи:
Акош(+Инф) = +Инф Acosh(x) = NaN, если x < 1 Акош(NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f", math.Acosh(1)) }
Выход: 0,00func Asin(x float64) float64Asin возвращает арксинус x в радианах.
Особые случаи:
Asin(±0) = ±0 Asin(x) = NaN, если x <-1 или x > 1Пример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f", math.Asin(0)) }Выход: 0,00func Asinh(x float64) float64Asinh возвращает обратный гиперболический синус x.
Особые случаи:
Asinh(±0) = ±0 Asinh(±Inf) = ±Inf Асинх (NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f", math.Asinh(0)) }Выход: 0,00func Atan(x float64) float64Atan возвращает арктангенс x в радианах.
Особые случаи:
Атан(±0) = ±0 Атан(±Inf) = ±Pi/2Пример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f", math.Atan(0)) }
Выход: 0,00func Atan2(y, x float64) float64Atan2 возвращает арктангенс y/x, используя знаки двойки для определения квадранта возвращаемого значения.
Особые случаи (по порядку):
Atan2(y, NaN) = NaN Атан2(NaN, х) = NaN Атан2(+0, х>=0) = +0 Атан2(-0, х>=0) = -0 Атан2(+0, х<=-0) = +Пи Atan2(-0, x<=-0) = -Pi Atan2(y>0, 0) = +Pi/2 Atan2(y<0, 0) = -Pi/2 Atan2(+Inf, +Inf) = +Pi/4 Atan2(-Inf, +Inf) = -Pi/4 Atan2(+Inf, -Inf) = 3Pi/4 Atan2(-Inf, -Inf) = -3Pi/4 Атан2(у, +Инф) = 0 Atan2(y>0, -Inf) = +Pi Atan2(y<0, -Inf) = -Pi Atan2(+Inf, x) = +Pi/2 Atan2(-Inf, x) = -Pi/2Пример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f", math.Atan2(0, 0)) }Выход: 0,00func Atanh(x float64) float64Atanh возвращает аркгиперболический тангенс x.
Особые случаи:
Атанх(1) = +Инф Атанг (±0) = ±0 Атанх(-1) = -Инф Atanh(x) = NaN, если x < -1 или x > 1 Атан (NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f", math.Atanh(0)) }
Выход: 0,00func Cbrt(x float64) float64Cbrt возвращает кубический корень из x.
Особые случаи:
Cbrt(±0) = ±0 Cbrt(±Inf) = ±Inf Cbrt(NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f\n", math.Cbrt(8)) fmt.Printf("%.2f\n", math.Cbrt(27)) }Выход: 2.00 3.00func Ceil(x float64) float64Ceil возвращает наименьшее целочисленное значение, большее или равное x.
Особые случаи:
Потолочное (±0) = ±0 Потолок(±Inf) = ±Inf Потолок (NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { c := math.Ceil(1.49) fmt.Printf("%.1f", с) }Выход: 2.0func Copysign(f, sign float64) float64Copysign возвращает значение с величиной f и знак знака.
Пример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f", math.Copysign(3.2, -1)) }
Выход: -3,20func Cos(x float64) float64Cos возвращает косинус аргумента x в радианах.
Особые случаи:
Cos(±Inf) = NaN Cos(NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f", math.Cos(math.Pi/2)) }Выход: 0,00func Cosh(x float64) float64Cosh возвращает гиперболический косинус x.
Особые случаи:
Кош(±0) = 1 Кош(±Инф) = +Инф Кош (NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f", math.Cash(0)) }Выход: 1,00func Dim(x, y float64) float64Dim возвращает максимальное значение x-y или 0.
Особые случаи:
Тусклый (+Inf, +Inf) = NaN Dim(-Inf, -Inf) = NaN Dim(x, NaN) = Dim(NaN, x) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f\n", math.Dim(4, -2)) fmt.Printf("%.2f\n", math.Dim(-4, 2)) }
Выход: 6.00 0,00func Erf(x float64) float64Erf возвращает функцию ошибки x.
Особые случаи:
Erf(+Inf) = 1 Эрф(-Инф) = -1 Erf(NaN) = NaNfunc Erfc(x float64) float64Erfc возвращает дополнительную функцию ошибки x.
Особые случаи:
Erfc(+Inf) = 0 Erfc(-Inf) = 2 Erfc(NaN) = NaNfunc Erfcinv(x float64) float64Erfcinv возвращает значение, обратное Erfc(x).
Особые случаи:
Erfcinv(0) = +Inf Erfcinv(2) = -Inf Erfcinv(x) = NaN, если x < 0 или x > 2 Erfcinv(NaN) = NaNfunc Erfinv(x float64) float64Erfinv возвращает обратную функцию ошибки x.
Особые случаи:
Erfinv(1) = +Inf Erfinv(-1) = -Inf Erfinv(x) = NaN, если x < -1 или x > 1 Erfinv(NaN) = NaNfunc Exp(x float64) float64Exp возвращает e**x, экспоненту x с основанием e.
Особые случаи:
Exp(+Inf) = +Inf Exp(NaN) = NaNОчень большие значения переполняются до 0 или +Inf. Очень маленькие значения уменьшаются до 1.
Пример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f\n", math.Exp(1)) fmt.Printf("%.2f\n", math.Exp(2)) fmt.Printf("%.2f\n", math.Exp(-1)) }Выход: 2,72 7,39 0,37func Exp2(x float64) float64Exp2 возвращает 2**x, экспоненту x с основанием 2.
Особые случаи аналогичны Exp.
Пример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f\n", math.Exp2(1)) fmt.Printf("%.2f\n", math.Exp2(-3)) }Выход: 2.00 0,12func Expm1(x float64) float64Expm1 возвращает e**x - 1, экспоненту x минус 1 с основанием e. Это более точно, чем Exp(x) - 1, когда x близок к нулю.
Особые случаи:
Expm1(+Inf) = +Inf Выражение1(-Inf) = -1 Expm1(NaN) = NaNОчень большие значения переполняются до -1 или +Inf.
Пример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.6f\n", math.Expm1(0.01)) fmt.Printf("%.6f\n", math.Expm1(-1)) }Выход: 0,010050 -0,632121func FMA(x, y, z float64) float64FMA возвращает значение x * y + z, рассчитанное только с одним округлением. (То есть FMA возвращает слитое умножение x, y и z.)
func Float32bits(f float32) uint32Float32bits возвращает двоичное представление IEEE 754 f, со знаковым битом f и результатом в той же битовой позиции. Float32bits(Float32frombits(x)) == x.
func Float32frombits(b uint32) float32Float32frombits возвращает число с плавающей запятой, соответствующее к двоичному представлению IEEE 754 b со знаковым битом b и результат в той же битовой позиции. Float32frombits(Float32bits(x)) == x.
func Float64bits(f float64) uint64Float64bits возвращает двоичное представление IEEE 754 f, со знаковым битом f и результатом в той же битовой позиции, и Float64bits(Float64frombits(x)) == x.
func Float64frombits(b uint64) float64Float64frombits возвращает число с плавающей запятой, соответствующее к двоичному представлению IEEE 754 b со знаковым битом b и результат в той же битовой позиции. Float64frombits(Float64bits(x)) == x.
func Floor(x float64) float64Floor возвращает наибольшее целочисленное значение, меньшее или равное x.
Особые случаи:
Этаж(±0) = ±0 Этаж (±Inf) = ±Inf Этаж (NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { c := math.Floor(1.51) fmt.Printf("%.1f", с) }Выход: 1,0func Frexp(f float64) (frac float64, exp int)Frexp разбивает f на нормализованную дробь и целочисленная степень двойки. Он возвращает frac и exp, удовлетворяющие f == frac × 2**exp, с абсолютным значением frac в интервале [½, 1).
Особые случаи:
Частотвыр(±0) = ±0, 0 Frexp(±Inf) = ±Inf, 0 Частотное выражение (NaN) = NaN, 0func Gamma(x float64) float64Gamma возвращает гамма-функцию x.
Особые случаи:
Гамма(+Инф) = +Инф Гамма(+0) = +Inf Гамма (-0) = -Inf Gamma(x) = NaN для целых чисел x < 0 Гамма (-Inf) = NaN Гамма (NaN) = NaNfunc Hypot(p, q float64) float64Hypot возвращает Sqrt(p*p + q*q), избегая ненужное переполнение и недополнение.
Особые случаи:
Гипотеза(±Inf, q) = +Inf Гипот(р, ±Inf) = +Inf Гипот (NaN, q) = NaN Гипот(р, NaN) = NaNfunc Ilogb(x float64) intIlogb возвращает двоичный показатель степени x как целое число.
Особые случаи:
Ilogb(±Inf) = MaxInt32 Ilogb(0) = MinInt32 Ilogb(NaN) = MaxInt32func Inf(sign int) float64Inf возвращает положительную бесконечность, если знак >= 0, и отрицательную бесконечность, если знак < 0.
func IsInf(f float64, sign int) boolIsInf сообщает, является ли f бесконечностью в соответствии со знаком. Если знак > 0, IsInf сообщает, является ли f положительной бесконечностью.
Если sign < 0, IsInf сообщает, является ли f отрицательной бесконечностью. Если знак == 0, IsInf сообщает, равно ли f бесконечности.
func IsNaN(f float64) (является логическим)IsNaN сообщает, является ли f значением IEEE 754 «не число».
func J0(x float64) float64J0 возвращает функцию Бесселя первого рода нулевого порядка.
Особые случаи:
J0(±Inf) = 0 J0(0) = 1 J0(NaN) = NaNfunc J1(x float64) float64J1 возвращает функцию Бесселя первого рода первого порядка.
Особые случаи:
J1(±Inf) = 0 J1(NaN) = NaNfunc Jn(n int, x float64) float64Jn возвращает функцию Бесселя первого рода порядка n.
Особые случаи:
Jn(n, ±Inf) = 0 Jn(n, NaN) = NaNfunc Ldexp(frac float64, exp int) float64Ldexp является обратным значением Frexp. Он возвращает frac × 2**exp.
Особые случаи:
Ldexp(±0, exp) = ±0 Ldexp(±Inf, exp) = ±Inf Ldexp(NaN, exp) = NaNfunc Lgamma(x float64) (lgamma float64, знак int)Lgamma возвращает натуральный логарифм и знак (-1 или +1) Gamma(x).
Особые случаи:
Lгамма(+Inf) = +Inf Lgamma(0) = +Inf Lgamma(-integer) = +Inf Lgamma(-Inf) = -Inf Lгамма(NaN) = NaNfunc Log(x float64) float64Log возвращает натуральный логарифм x.
Особые случаи:
Лог(+Инф) = +Инф Журнал (0) = -Inf Лог(х <0) = NaN Журнал (NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { х := math.Log(1) fmt.Printf("%.1f\n", х) y := math.Log(2,7183) fmt.Printf("%.1f\n", у) }Выход: 0,0 1,0func Log10(x float64) float64Log10 возвращает десятичный логарифм x. Особые случаи такие же, как и для Log.
Пример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.1f", math.Log10(100)) }Выход: 2.0func Log1p(x float64) float64Log1p возвращает натуральный логарифм 1 плюс его аргумент x. Он более точен, чем Log(1 + x), когда x близок к нулю.
Особые случаи:
Log1p(+Inf) = +Inf Log1p(±0) = ±0 Log1p(-1) = -Inf Log1p(x <-1) = NaN Log1p(NaN) = NaNfunc Log2(x float64) float64Log2 возвращает двоичный логарифм x. Особые случаи такие же, как и для Log.
Пример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.1f", math.Log2(256)) }Выход: 8,0func Logb(x float64) float64Logb возвращает двоичный показатель степени x.
Особые случаи:
Logb(±Inf) = +Inf Логб(0) = -Инф Logb(NaN) = NaNfunc Max(x, y float64) float64Max возвращает большее из значений x или y.
Особые случаи:
Макс(х, +Инф) = Макс(+Инф, x) = +Инф Макс (х, NaN) = Макс (NaN, х) = NaN Макс(+0, ±0) = Макс(±0, +0) = +0 Макс (-0, -0) = -0func Min(x, y float64) float64Min возвращает меньшее из значений x или y.
Особые случаи:
Мин.(x, -Inf) = Мин.(-Inf, x) = -Inf Мин (х, NaN) = Мин (NaN, х) = NaN Мин.(-0, ±0) = Мин.(±0, -0) = -0
func Mod(x, y float64) float64Mod возвращает остаток x/y с плавающей запятой. Величина результата меньше y и его знак совпадает со знаком х.
Особые случаи:
Mod(±Inf, y) = NaN Mod(NaN, у) = NaN Mod(x, 0) = NaN Mod(x, ±Inf) = x Mod(x, NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { c := math.Mod(7, 4) fmt.Printf("%.1f", с) }Выход: 3.0func Modf(f float64) (int float64, frac float64)Modf возвращает целые и дробные числа с плавающей запятой эта сумма к f. Оба значения имеют тот же знак, что и f.
Особые случаи:
Modf(±Inf) = ±Inf, NaN Modf(NaN) = NaN, NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { int, frac:= math.Modf(3.14) fmt.Printf("%.2f, %.2f\n", целое число, дробь) int, frac = math.Modf(-2.71) fmt.Printf("%.2f, %.2f\n", целое число, дробь) }
Выход: 3,00, 0,14 -2,00, -0,71функция NaN() float64NaN возвращает значение IEEE 754 «не число».
func Nextafter(x, y float64) (r float64)Nextafter возвращает следующее представляемое значение float64 после x по направлению к y.
Особые случаи:
Следующий после(х, х) = х Далее после (NaN, у) = NaN Далее после (x, NaN) = NaNfunc Nextafter32(x, y float32) (r float32)Nextafter32 возвращает следующее представляемое значение float32 после x по направлению к y.
Особые случаи:
Nextafter32(х, х) = х Nextafter32(NaN, у) = NaN Nextafter32(x, NaN) = NaNfunc Pow(x, y float64) float64Pow возвращает x**y, экспоненту y с основанием x.
Особые случаи (по порядку):
Pow(x, ±0) = 1 для любого x Pow(1, y) = 1 для любого y Pow(x, 1) = x для любого x Pow(NaN, у) = NaN Pow(x, NaN) = NaN Pow(±0, y) = ±Inf для y нечетное целое число < 0 Pow(±0, -Inf) = +Inf Pow(±0, +Inf) = +0 Pow(±0, y) = +Inf для конечного y < 0 и нечетного целого числа Pow(±0, y) = ±0 для y нечетное целое число > 0 Pow(±0, y) = +0 для конечного y > 0 и нечетного целого числа Pow(-1, ± Inf) = 1 Pow(x, +Inf) = +Inf для |x| > 1 Pow(x, -Inf) = +0 для |x| > 1 Pow(x, +Inf) = +0 для |x| < 1 Pow(x, -Inf) = +Inf для |x| < 1 Pow(+Inf, y) = +Inf для y > 0 Pow(+Inf, y) = +0 для y < 0 Pow(-Inf, y) = Pow(-0, -y) Pow(x, y) = NaN для конечного x < 0 и конечного нецелого yПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { c := math.Pow(2, 3) fmt.Printf("%.1f", с) }
Выход: 8,0func Pow10(n int) float64Pow10 возвращает 10**n, экспоненту n с основанием 10.
Особые случаи:
Pow10(n) = 0 для n < -323 Pow10(n) = +Inf для n > 308Пример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { c := math.Pow10(2) fmt.Printf("%.1f", с) }Выход: 100,0функция Остаток ¶
func Remainder(x, y float64) float64Remainder возвращает остаток x/y с плавающей запятой IEEE 754.
Особые случаи:
Остаток(±Inf, y) = NaN Остаток (NaN, у) = NaN Остаток (х, 0) = NaN Остаток (x, ± Inf) = x Остаток (x, NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.1f", math.Remainder(100, 30)) }Выход: 10,0func Round(x float64) float64Round возвращает ближайшее целое число, округляя половину от нуля.
Особые случаи:
Раунд(±0) = ±0 Раунд(±Inf) = ±Inf Раунд (NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { p := math.Round(10.5) fmt.Printf("%.1f\n", p) n := math.Round(-10,5) fmt.Printf("%.1f\n", n) }Выход: 11,0 -11,0func RoundToEven(x float64) float64RoundToEven возвращает ближайшее целое число, округляя связи до четных.
Особые случаи:
RoundToEven(±0) = ±0 RoundToEven(±Inf) = ±Inf RoundToEven(NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { u := math.RoundToEven(11.5) fmt.Printf("%.1f\n", и) d := math.RoundToEven(12.5) fmt.Printf("%.1f\n", д) }Выход: 12,0 12,0func Signbit(x float64) boolSignbit сообщает, является ли x отрицательным или отрицательным нулем.
func Sin(x float64) float64Sin возвращает синус аргумента x в радианах.
Особые случаи:
Sin(±0) = ±0 Sin(±Inf) = NaN Грех (NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f", math.Sin(math.Pi)) }
Выход: 0,00func Sincos(x float64) (sin, cos float64)Sincos возвращает Sin(x), Cos(x).
Особые случаи:
Sincos(±0) = ±0, 1 Sincos(±Inf) = NaN, NaN Синкос (NaN) = NaN, NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { sin, cos := math.Sincos(0) fmt.Printf("%.2f, %.2f", sin, cos) }Выход: 0,00, 1,00func Sinh(x float64) float64Sinh возвращает гиперболический синус x.
Особые случаи:
Sin(±0) = ±0 Синх(±Инф) = ±Инф Sin(NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f", math.Sinh(0)) }Выход: 0,00func Sqrt(x float64) float64Sqrt возвращает квадратный корень из x.
Особые случаи:
Кв.(+Инф.) = +Инф. Кв.кв.(±0) = ±0 Sqrt(x <0) = NaN Квадрат(NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { константа ( а = 3 б = 4 ) c := math.Sqrt(a*a + b*b) fmt.Printf("%.1f", с) }
Выход: 5,0func Tan(x float64) float64Tan возвращает тангенс аргумента x в радианах.
Особые случаи:
Тангенс(±0) = ±0 Tan(± Inf) = NaN Тан (NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f", math.Tan(0)) }Выход: 0,00func Tanh(x float64) float64Tanh возвращает гиперболический тангенс x.
Особые случаи:
Танх(±0) = ±0 Tanh(±Inf) = ±1 Тан (NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f", math.Tanh(0)) }Выход: 0,00func Trunc(x float64) float64Trunc возвращает целочисленное значение x.
Особые случаи:
Trunc(±0) = ±0 Trunc(±Inf) = ±Inf Trunc (NaN) = NaNПример ¶основной пакет импорт ( "ФМТ" "математика" ) основная функция () { fmt.Printf("%.2f\n", math.Trunc(math.Pi)) fmt.Printf("%.2f\n", math.Trunc(-1.2345)) }
Выход: 3.00 -1,00func Y0(x float64) float64Y0 возвращает функцию Бесселя нулевого порядка второго рода.
Особые случаи:
Y0(+Inf) = 0 Y0(0) = -Инф Y0(x < 0) = NaN Y0(NaN) = NaNfunc Y1(x float64) float64Y1 возвращает функцию Бесселя первого порядка второго рода.
Особые случаи:
Y1(+Inf) = 0 Y1(0) = -Инф Y1(x < 0) = NaN Y1(NaN) = NaNfunc Yn(n int, x float64) float64Yn возвращает функцию Бесселя порядка n второго рода.
Особые случаи:
Yn(n, +Inf) = 0 Yn(n ≥ 0, 0) = -Inf Yn(n < 0, 0) = +Inf, если n нечетно, -Inf, если n четно Yn(n, x < 0) = NaN Yn(n, NaN) = NaNЭтот раздел пуст.
Задание 1. Изучение синусоидальных кривых
Задание 1. Изучение синусоидальных кривыхЗадание 1. Изучение синусоидальных кривых Кристина Данбар, UGA
В этом задании мы будем исследуя график уравненияс использованием разных значений a, b, и с.
В приведенном выше уравнении
- и есть амплитуда синусоиды
- б есть период синусоиды
- с есть фаза сдвиг синусоиды
Что такое амплитуда синусоиды? Амплитуда синусоиды равна ее высоте.
Что такое период синусоида? Период синусоиды равен длине одного цикла кривой. Естественный период синуса кривая 2π. Итак, коэффициент б =1 эквивалентен периоду 2π. Чтобы получить период синусоиды для любого коэффициента b , просто разделите 2π на коэффициент b , чтобы получить новый период кривой.
Коэффициент b и период синусоиды имеют обратную зависимость, так как b получается меньше, длина одного цикла кривой становится больше.
Точно так же, как вы увеличиваете b , период уменьшится.
Что такое фазовый сдвиг из синусоида? Фазовый сдвиг синусоидальной кривой кривая смещается от нуля. Если фазовый сдвиг равен нулю, кривая начинается в начале координат, но может двигаться влево или вправо в зависимости от фазового сдвига. Отрицательный фазовый сдвиг указывает движение вправо, а положительный фазовый сдвиг указывает на движение влево.
Давайте посмотрим на график y = sin x.
Глядя на график, помните, что числовое значение π составляет приблизительно 3,1416, поэтому 2π составляет приблизительно 6,2832.
На графике выше
Амплитуда а равна 1. Это означает, что высота графика будет равна 1, а вершина первого "горб" равен 1.
Период b имеет коэффициент 1, поэтому период равен (2π)/1 или просто 2π.
Фазовый сдвиг c равен ноль, поэтому кривая начинается в начале координат.
Вернуться на мою домашнюю страницу.
Давайте рассмотрим синусоиду с разными амплитуды.
Мы уже видели случай, когда амплитуда равна 1; это на графике выше. Как насчет других амплитуды?
у = 2 sin x
у = 5 sin x
у = -1 sin x
Чем отличается приведенный выше график? Это имеет коэффициент а = -1. Что это значит? Мы видим, что самая высокая точка кривой по-прежнему равна 1, но первый выступ равен -1 вместо 1. По сути, мы перевернули график.
Теперь давайте посмотрим на несколько различных синусоидальных графиков.
вместе.
Вернуться на мою домашнюю страницу.
Давайте рассмотрим синусоиду с разными периоды.
Мы уже видели случай, когда коэффициент b равен 1; это на графике выше. Как насчет другие периоды?
Помните, б коэффициент и период кривой находятся в обратной зависимости.
у = грех (2x) Коэффициент b на приведенном выше графике равен 2, поэтому период синусоиды изменился в 1/2 раза, в результате чего новый период π, или около 3,14.
у = sin (0,5x)
Для графика выше коэффициент b = 1/2, так что период синусоиды будет в два раза больше, чем обычно, или 4π.
у = грех (3x)
Обратите внимание, что новый период составляет 1/3 исходного период, равный 2π/3, что составляет примерно 2.09. Теперь давайте рассмотрим несколько различных синусоидальных графики вместе, с разными периодами.
Вернуться на мою домашнюю страницу.
Рассмотрим синусоиду с фазой сдвиг.
Обычно синусоида не имеет фазы сдвига, поэтому переменная c равна 0. Это означает, что синусоида начинается с источник, как показано на первом графике в верхней части этой страницы.
Что делать, если с не равно нулю?
у = грех (х + п)
На приведенном выше графике y = sin (x + π) , график был сдвинут на единицу π слева. 
На самом деле положительный фазовый сдвиг c фактически указывает на сдвиг влево. давайте посмотрим на некоторые другие примеры:
у = грех (х + 1)
Синусоида сместилась на одну единицу в оставил.
у = грех (х + π/2)
Кривая сместилась на π/2 единицы влево. Напомним, что π/2 примерно равно 1,57.
Что делать, если переменная c отрицательный?
у = грех (х - 1)
Кривая сместилась на 1 единицу вправо.
у = грех (х - №/2)
Давайте посмотрим вместе на несколько фазовых сдвигов:
Примечание: Фазовый сдвиг π будет выглядеть точно так же, как фазовый сдвиг -π.

у = грех (х + π)
у = грех (х - π)
Вернуться на мою домашнюю страницу.
В приведенных выше упражнениях мы выяснили, что происходит с синусоидой, когда мы варьируем коэффициенты a, b и c индивидуально. Что делать, если вы изменили более одного за раз?
у = 2 sin (2x)
а = 2 б=2 с=0
Амплитуда равна 2, а период равен 2π/2, или π. Фазового сдвига нет.
у = 2 sin (2x -1)
а = 2 б = 2 с = -1
Амплитуда равна 2, а период равен 2π/2, или π. Вся кривая сдвинута на одну единицу вправо.
у = 3 sin (2x + 2)
а = 3 б = 2 с = 2
Амплитуда равна 3, как и следовало ожидать. период графика равен 2π/2, или π. Мы ожидали, что фазовый сдвиг будет на две единицы влево, но мы видим, что Это не относится к делу. Почему? Поскольку фазовый сдвиг связан с Период. Период графика равен 1/2 его первоначального размера, а поэтому фазовый сдвиг также будет равен 1/2 коэффициента c или 1. Это показано на графике выше.
y = 0,5 sin (0,5x -3)
а = 0,5 б = 0,5 с = -3
Амплитуда равна 0,5, что мы ясно видим на график. Коэффициент b равен 0,5, поэтому период синусоиды вдвое больше. как обычно, или 4π (примерно 12,57). Так как период кривой в два раза больше, чем обычно фазовый сдвиг будет в два раза больше коэффициента с, или на 6 единиц к Правильно.
Вернуться на мою домашнюю страницу.
Не хотите ли вы решить несколько практических задач? Кликните сюда.
Unit Circle: Функции синуса и косинуса
Результаты обучения
- Найдите значения функции для синуса и косинуса особых углов.
- Определение области определения и диапазона функций синуса и косинуса.
- Используйте опорные углы для оценки тригонометрических функций.
- Вычислите значения синуса и косинуса с помощью калькулятора.
Чтобы определить наши тригонометрические функции, мы начнем с рисования единичной окружности с центром в начале координат и радиусом 1, как показано на рисунке 2. Угол (в радианах), который пересекает [латекс]t[/латекс], образует дуга длиной [латекс]s[/латекс]. Используя формулу [латекс]s=rt[/латекс] и зная, что [латекс]r=1[/латекс], мы видим, что для единичного круга [латекс]s=t[/латекс].
Напомним, что оси x- и y- делят координатную плоскость на четыре четверти, называемые квадрантами. Мы помечаем эти квадранты, чтобы имитировать направление положительного угла. Четыре квадранта обозначены I, II, III и IV.
Для любого угла [латекс]t[/латекс] мы можем пометить пересечение конечной стороны и единичной окружности его координатами [латекс]\влево(х,у\вправо)[/латекс]. Координаты [латекс]х[/латекс] и [латекс]у[/латекс] будут выходами тригонометрических функций [латекс]f\left(t\right)=\cos t[/латекс] и [латекс] f\left(t\right)=\sin t[/latex] соответственно. Это означает [латекс]x=\cos t[/латекс] и [латекс]у=\sin t[/латекс].
Рис. 2. Единичная окружность, центральный угол которой равен [латекс]t[/латекс] радианам
A Общее примечание: Единичная окружность
Единичная окружность имеет центр в точке [латекс]\влево(0,0\вправо)[/латекс] и радиус [латекс]1[/латекс] . В единичном круге длина пересекаемой дуги равна радианной мере центрального угла [латекс]1[/латекс].
Пусть [латекс]\влево(х,у\вправо)[/латекс] будет концом единичной окружности дуги с длиной дуги [латекс]s[/латекс]. Координаты [латекс]\влево(х,у\вправо)[/латекс] этой точки можно описать как функции угла.
Определение функций синуса и косинуса
Теперь, когда мы пометили нашу единичную окружность, мы можем узнать, как координаты [латекс]\влево(х,у\вправо)[/латекс] соотносятся с длиной дуги и углом . Функция синуса связывает действительное число [latex]t[/latex] с y -координатой точки, где соответствующий угол пересекает единичную окружность. Точнее, синус угла [latex]t[/latex] равен y -значению конечной точки на единичной окружности дуги длины [latex]t[/latex]. На рисунке 2 синус равен [latex]y[/latex]. Как и все функции, синусоидальная функция имеет вход и выход. Его вход является мерой угла; его выход y -координата соответствующей точки на единичной окружности.
Функция косинуса угла [latex]t[/latex] равна x -значению конечной точки единичной окружности дуги длины [latex]t[/latex].
{2} [ /латекс]. Имейте в виду, что многие калькуляторы и компьютеры не распознают стенографию. Если вы сомневаетесь, используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер.
Общее примечание: функции синуса и косинуса
Если [latex]t[/latex] является вещественным числом и точка [latex]\left(x,y\right)[/latex] на единичной окружности соответствует угол [латекс]t[/латекс], затем
[латекс]\cos t=x[/латекс]
[латекс]\sin t=y[/латекс]
Как: Дана точка
P [латекс]\влево(х,у\вправо)[/латекс] на единичной окружности, соответствующей углу [латекс]t[/латекс], найдите синус и косинус.
- Синус [latex]t[/latex] равен y -координата точки [latex]P:\sin t=y[/latex].
- Косинус [latex]t[/latex] равен x -координате точки [latex]P: \text{cos}t=x[/latex].
Пример 1. Нахождение значений функций для синуса и косинуса
Точка [latex]P[/latex] — это точка на единичной окружности, соответствующая углу [latex]t[/latex], как показано на рис.
4. Найдите [латекс]\cos\left(t\right)[/latex] и [латекс]\text{sin}\left(t\right)[/latex].
Рисунок 4
Показать решение
Попробуйте
Некоторый угол [latex]t[/latex] соответствует точке на единичной окружности в точке [latex]\left(-\frac{\sqrt{2}}{2},\frac{\ sqrt{2}}{2}\right)[/latex], как показано на рисунке 5. Найдите [latex]\cos t[/latex] и [latex]\sin t[/latex].
Рисунок 5
Показать решение
Нахождение синусов и косинусов углов на оси
Для четырехугольных углов соответствующая точка на единичной окружности приходится на 9{2}t=1[/latex], известный как Пифагорейская идентичность .
Мы можем использовать тождество Пифагора, чтобы найти косинус угла, если мы знаем синус, или наоборот. Однако, поскольку уравнение дает два решения, нам нужно дополнительное знание угла, чтобы выбрать решение с правильным знаком.
Если мы знаем квадрант, в котором находится угол, мы можем легко выбрать правильное решение.
Общее примечание: Пифагорейская идентичность
Пифагорейская идентичность 9{2}t=1[/latex]
Как сделать: Зная синус некоторого угла [latex]t[/latex] и его положение в квадранте, найдите косинус [latex]t[/latex].
- Подставить известное значение [латекс]\sin\left(t\right)[/латекс] в тождество Пифагора.
- Найдите [латекс]\cos\left(t\right)[/латекс].
- Выберите решение с соответствующим знаком для значений x в квадранте, где находится [латекс]t[/латекс].
Пример 3. Нахождение косинуса по синусу или синуса по косинусу
Если [латекс]\sin \left(t\right)=\frac{3}{7}[/latex] и [latex]t[/latex] находится во втором квадранте, найти [latex]\cos \ влево(т\вправо)[/латекс].
Показать решение
Попробуйте
Если [латекс]\cos \left(t\right)=\frac{24}{25}[/latex] и [латекс]t[/латекс] находится в четвертом квадранте, найдите [латекс ]\sin\left(t\right)[/латекс].
Показать решение
Попробуйте
Нахождение синусов и косинусов специальных углов
Мы уже изучили некоторые свойства специальных углов, например преобразование радианов в градусы. Мы также можем вычислить синусы и косинусы специальных углов, используя 9\circ [/latex] треугольник является равнобедренным треугольником, поэтому координаты x- и y соответствующей точки на окружности совпадают. Поскольку значения x- и y одинаковы, значения синуса и косинуса также будут равны. Рис. 9 Это означает, что радиус лежит вдоль линии [латекс]у=х[/латекс]. Радиус единичной окружности равен 1. Итак, прямоугольный треугольник, образованный под линией [latex]y=x[/latex], имеет стороны [latex]x[/latex] и [latex]y\text{ }\left (y=x\right)[/latex], а радиус = 1,9{2}=\frac{1}{2}\\ x=\pm \frac{1}{\sqrt{2}}\end{gathered}[/latex]
В квадранте I [latex]x= \frac{1}{\sqrt{2}}[/latex].
При [латекс]t=\frac{\pi }{4}[/латекс] или 45 градусов,
[латекс]\начало{собрано}\влево(х,у\вправо)=\влево(х, x\right)=\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right) \\ x=\frac{1}{\sqrt{2 }},y=\frac{1}{\sqrt{2}}\\ \cos t=\frac{1}{\sqrt{2}},\sin t=\frac{1}{\sqrt{2 }} \end{gathered}[/latex]
Если мы затем рационализируем знаменатели, то получим
9\circ [/latex], как показано на рисунке 12.
Рисунок 11
Рисунок 12
Поскольку все углы равны, стороны также равны. Вертикальная линия имеет длину [latex]2y[/latex], и поскольку все стороны равны, мы также можем заключить, что [latex]r=2y[/latex] или [latex]y=\frac{1}{2 }р[/латекс]. Поскольку [латекс]\sin t=y[/латекс] ,
[латекс]\sin \left(\frac{\pi }{6}\right)=\frac{1}{2}r[/latex]
А так как [latex]r=1[/latex] в нашем 9\circ [/латекс]. Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника [латекс]ABC[/латекс] имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичной окружности, длина всех сторон должна быть равна 1.
Рисунок 13
Угол [латекс]ABD[/латекс] равен 30°. Итак, если число двойное, угол [латекс]АВС[/латекс] равен 60°. [latex]BD[/latex] является серединным перпендикуляром к [latex]AC[/latex], поэтому он делит [latex]AC[/latex] пополам. Это означает, что [latex]AD[/latex] — это [latex]\frac{1}{2}[/latex] радиус, или [latex]\frac{1}{2}[/latex].
Обратите внимание, что [latex]AD[/latex] — это 9\circ [/latex] равны [латекс]\left(\frac{1}{2},\frac{\sqrt{3}}{2}\right)\[/latex], поэтому мы можем найти синус и косинус.
[латекс]\begin{собран}\влево(x,y\вправо)=\влево(\frac{1}{2},\frac{\sqrt{3}}{2}\right) \\ x =\ frac {1} {2}, y = \ frac {\ sqrt {3}} {2} \\ \ cos t = \ frac {1} {2}, \ sin t = \ frac {\ sqrt {3 }}{2} \end{gathered}[/latex]
Теперь мы нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичной окружности. В таблице ниже приведены эти значения.
Угол 0 [латекс]\frac{\pi }{6}[/латекс], или 30° [латекс]\frac{\pi }{4}[/латекс], или 45° [латекс]\frac{\pi }{3}[/латекс], или 60° [латекс]\frac{\pi }{2}[/латекс], или 90° Косинус 1 [латекс]\frac{\sqrt{3}}{2}[/латекс] [латекс]\frac{\sqrt{2}}{2}[/латекс] [латекс]\фракция{1}{2}[/латекс] 0 Синус 0 [латекс]\фракция{1}{2}[/латекс] [латекс]\frac{\sqrt{2}}{2}[/латекс] [латекс]\frac{\sqrt{3}}{2}[/латекс] 1 На рисунке 14 показаны общие углы в первом квадранте единичной окружности.

.0023 специальные углы , обращаемся к компьютеру или калькулятору. Имейте в виду : Большинство калькуляторов можно установить в режим «градусы» или «радианы», которые сообщают калькулятору единицы измерения для входного значения. Когда мы оцениваем [латекс]\cos \left(30\right)[/латекс] на нашем калькуляторе, он будет оценивать его как косинус 30 градусов, если калькулятор находится в режиме градусов, или как косинус 30 радиан, если калькулятор находится в радианном режиме.
Как: Зная угол в радианах, используйте графический калькулятор, чтобы найти косинус.
- Если в калькуляторе есть режимы в градусах и в радианах, установите его в режим в радианах.
- Нажмите клавишу COS.
- Введите значение угла в радианах и нажмите клавишу закрытия скобок «)».
- Нажмите ВВОД.
Пример 4. Использование графического калькулятора для нахождения синуса и косинуса
Вычислите значение [latex]\cos \left(\frac{5\pi }{3}\right)[/latex] с помощью графического калькулятора или компьютера.
Показать решение
Попробуйте
Вычислить [латекс]\sin\left(\frac{\pi }{3}\right)[/latex].
Показать решение
Определение области определения и диапазона функций синуса и косинуса
Теперь, когда мы можем найти синус и косинус угла, нам нужно обсудить их области определения и диапазоны. Каковы области определения функций синуса и косинуса? То есть, каковы наименьшее и наибольшее числа, которые могут быть входными данными функций? Поскольку углы меньше 0 и углы больше [латекс]2\пи [/латекс] все еще могут быть изображены на единичном круге и имеют реальные значения [латекс]x,y[/латекс] и [латекс]r[/ латекс], нет нижнего или верхнего предела углов, которые могут быть входными данными для функций синуса и косинуса.
Входными данными для функций синуса и косинуса является вращение от положительной x -ось, и это может быть любое действительное число.
Каковы диапазоны функций синуса и косинуса? Каковы наименьшее и максимальное возможные значения их выхода? Мы можем увидеть ответы, исследуя единичный круг , как показано на рисунке 15. Границы координаты x равны [латекс]\лево[-1,1\право][/латекс]. Границы координаты y также равны [латекс]\влево[-1,1\вправо][/латекс]. Таким образом, диапазон функций синуса и косинуса составляет [латекс]\влево[-1,1\вправо][/латекс].
Рисунок 15
Мы обсудили нахождение синуса и косинуса для углов в первом квадранте, но что, если наш угол находится в другом квадранте? Для любого заданного угла в первом квадранте существует угол во втором квадранте с таким же значением синуса. Поскольку значением синуса является координата y на единичной окружности, другой угол с таким же синусом будет иметь такое же значение y , но противоположное значение x .
Следовательно, его значение косинуса будет противоположно значению косинуса первого угла.
Аналогично, в четвертом квадранте будет угол с тем же косинусом, что и исходный угол. Угол с тем же косинусом будет иметь то же значение x , но будет иметь противоположное значение y . Следовательно, его значение синуса будет противоположно значению синуса исходного угла.
Как показано на рисунке 16, угол [латекс]\альфа [/латекс] имеет то же значение синуса, что и угол [латекс]t[/латекс]; значения косинуса противоположны. Угол [латекс]\бета [/латекс] имеет то же значение косинуса, что и угол [латекс]t[/латекс]; значения синуса противоположны.
[латекс]\begin{array}{ccc}\sin \left(t\right)=\sin \left(\alpha \right)\hfill & \text{and}\hfill & \cos \left(t \right)=-\cos \left(\alpha \right)\hfill \\ \sin \left(t\right)=-\sin \left(\beta \right)\hfill & \text{and}\hfill & \cos \left(t\right)=\cos \left(\beta \right)\hfill \end{array}[/latex]
Рисунок 16
острый угол, [латекс]t[/латекс], образованный конечной стороной угла [латекс]t[/латекс] и горизонтальной осью.
\circ \mathrm{-t}|[/латекс]. 9\circ [/latex], как показано на рис. 18.
рис. 18
Показать решение
Попробуйте
Найдите базовый угол [латекс]\фракция{5\пи }{3}[/латекс].
Показать решение
Использование опорных углов
Теперь давайте еще раз рассмотрим колесо обозрения, представленное в начале этого раздела. Предположим, всадник делает снимок, остановившись в двадцати футах над уровнем земли. Затем всадник вращается на три четверти круга. Какова новая высота всадника? Чтобы ответить на такие вопросы, как этот, нам нужно оценить функции синуса или косинуса при углах, превышающих 90 градусов или под отрицательным углом . Опорные углы позволяют вычислять тригонометрические функции для углов вне первого квадранта. Их также можно использовать для нахождения [латексных]\левых(х,у\правых)[/латексных] координат для этих углов. Мы будем использовать опорный угол угла поворота в сочетании с квадрантом, в котором лежит конечная сторона угла.
Использование опорных углов для вычисления тригонометрических функций
Мы можем найти косинус и синус любого угла в любом квадранте, если знаем косинус или синус его опорного угла. Абсолютные значения косинуса и синуса угла такие же, как у опорного угла. Знак зависит от квадранта исходного угла. Косинус будет положительным или отрицательным в зависимости от знака числа 9.0068 x - значения в этом квадранте. Синус будет положительным или отрицательным в зависимости от знака значений и в этом квадранте.
Общее примечание: использование опорных углов для нахождения косинуса и синуса
Углы имеют косинусы и синусы с тем же абсолютным значением, что и их опорные углы. Знак (положительный или отрицательный) можно определить по квадранту угла.
Как сделать: по заданному углу в стандартном положении найдите опорный угол, а также косинус и синус исходного угла.
- Измерьте угол между конечной стороной заданного угла и горизонтальной осью.
Это опорный угол.
- Определите значения косинуса и синуса опорного угла.
- Присвойте косинусу тот же знак, что и значениям x в квадранте исходного угла.
- Присвойте синусу тот же знак, что и y -значения в квадранте исходного угла.
Пример 6. Использование опорных углов для нахождения синуса и косинуса 9\circ \right)[/латекс].
б. Используйте опорный угол [латекс]-\frac{\pi }{6}[/латекс], чтобы найти [латекс]\cos\left(-\frac{\pi }{6}\right)[/латекс] и [латекс]\sin\left(-\frac{\pi}{6}\right)[/латекс].
Показать решение
Попробуйте
Использование опорных углов для нахождения координат
Теперь, когда мы научились находить значения косинуса и синуса для специальных углов в первом квадранте, мы можем использовать симметрию и опорные углы для заполнения значений косинуса и синуса для остальные специальные углы на единичной окружности. Они показаны на рисунке 19.
. Потратьте время, чтобы узнать [латексные]\левые(х,у\правые)[/латексные] координаты всех основных углов в первом квадранте.
Помимо изучения значений специальных углов, мы можем использовать эталонные углы для нахождения [латексных]\левых(х,у\правых)[/латексных] координат любой точки на единичной окружности, используя то, что мы знаем об эталонных углы вместе с тождествами
[латекс]\begin{gathered}x=\cos t \\ y=\sin t \end{gathered}[/latex]
Сначала находим опорный угол, соответствующий заданному угол. Затем мы берем значения синуса и косинуса опорный угол , и присвойте им знаки, соответствующие y – и x -значениям квадранта.
Как сделать: Зная угол точки на окружности и радиус окружности, найдите [латекс]\влево(х,у\вправо)[/латекс] координаты точки.
- Найдите исходный угол, измерив наименьший угол относительно оси x .
- Найдите косинус и синус опорного угла.
- Определите соответствующие знаки для [latex]x[/latex] и [latex]y[/latex]
в данном квадранте.Пример 7. Использование единичной окружности для поиска координат
Найдите координаты точки на единичной окружности под углом [latex]\frac{7\pi }{6}[/latex].
Показать решение
Попробуйте
Найдите координаты точки на единичной окружности под углом [latex]\frac{5\pi }{3}[/latex].
Показать решение
Ключевые уравнения
Косинус [латекс]\cos t=x[/латекс] 9{2}t=1[/латекс] Ключевые понятия
- Нахождение значений функции для синуса и косинуса начинается с рисования единичной окружности с центром в начале координат и радиусом в 1 единицу.
- Используя единичную окружность, синус угла [latex]t[/latex] равен y -значению конечной точки единичной окружности дуги длины [latex]t[/latex], тогда как косинус угла угол [latex]t[/latex] равен x -значению конечной точки.
- Значения синуса и косинуса наиболее непосредственно определяются, когда соответствующая точка на единичной окружности попадает на ось.
- Когда известен синус или косинус, мы можем использовать тождество Пифагора, чтобы найти другой. Тождество Пифагора также полезно для определения синусов и косинусов специальных углов.
- Калькуляторы и программы для построения графиков полезны для нахождения синусов и косинусов, если известна правильная процедура ввода информации.
- Областью определения функций синуса и косинуса являются все действительные числа.
- Диапазон функций синуса и косинуса: [латекс]\влево[-1,1\вправо][/латекс].
- Синус и косинус угла имеют то же абсолютное значение, что и синус и косинус исходного угла.
- Знаки синуса и косинуса определяются из значений x и y в квадранте исходного угла.
- Опорный угол угла — это угол размера, [latex]t[/latex],
образованный конечной стороной угла [latex]t[/latex] и горизонтальной осью.

 ru
ru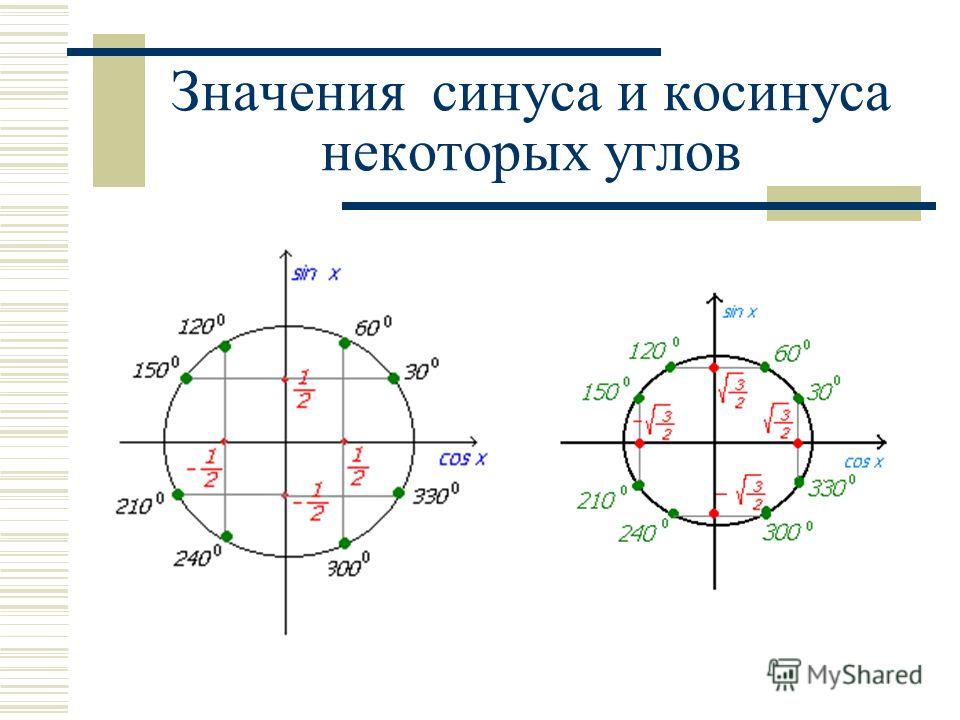 \end{align}bsin(A)sin(A)a=asin(B)=sin(B)b.
\end{align}bsin(A)sin(A)a=asin(B)=sin(B)b. Теперь, используя расширенное правило синусов, мы имеем csinγ=2R \frac {c}{\sin \gamma} = 2Rsinγc=2R, и, таким образом, площадь треугольника равна
Теперь, используя расширенное правило синусов, мы имеем csinγ=2R \frac {c}{\sin \gamma} = 2Rsinγc=2R, и, таким образом, площадь треугольника равна

 org/A139339
Ln2 = 0,6180559945309417232121458176568075500134360255254120680009// https://oeis.org/A002162
Log2E = 1 / Ln2
Ln10 = 2,3025850045684017968436420760110148862877297603332790 // https://oeis.org/A002392
Log10E = 1 / Ln10
)
org/A139339
Ln2 = 0,6180559945309417232121458176568075500134360255254120680009// https://oeis.org/A002162
Log2E = 1 / Ln2
Ln10 = 2,3025850045684017968436420760110148862877297603332790 // https://oeis.org/A002392
Log10E = 1 / Ln10
) 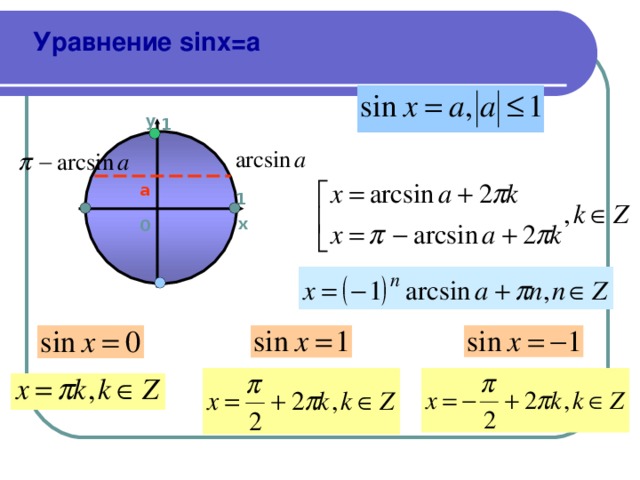
 Printf("%.2f", math.Acosh(1))
}
Printf("%.2f", math.Acosh(1))
}
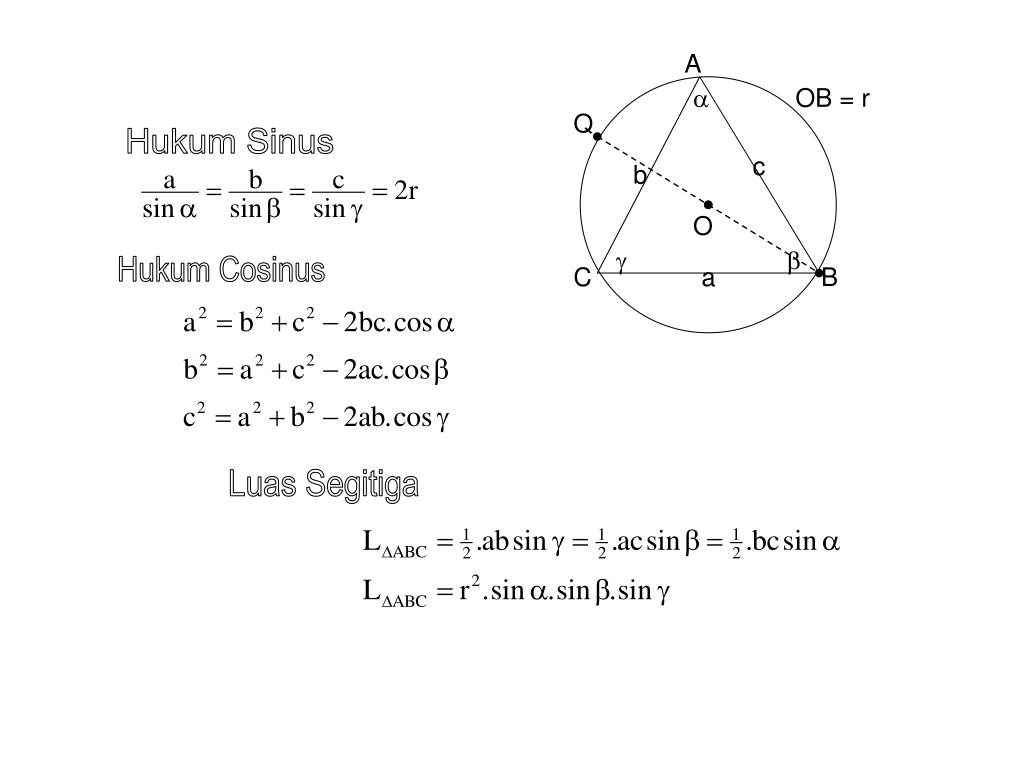 2f", math.Atan(0))
}
2f", math.Atan(0))
}
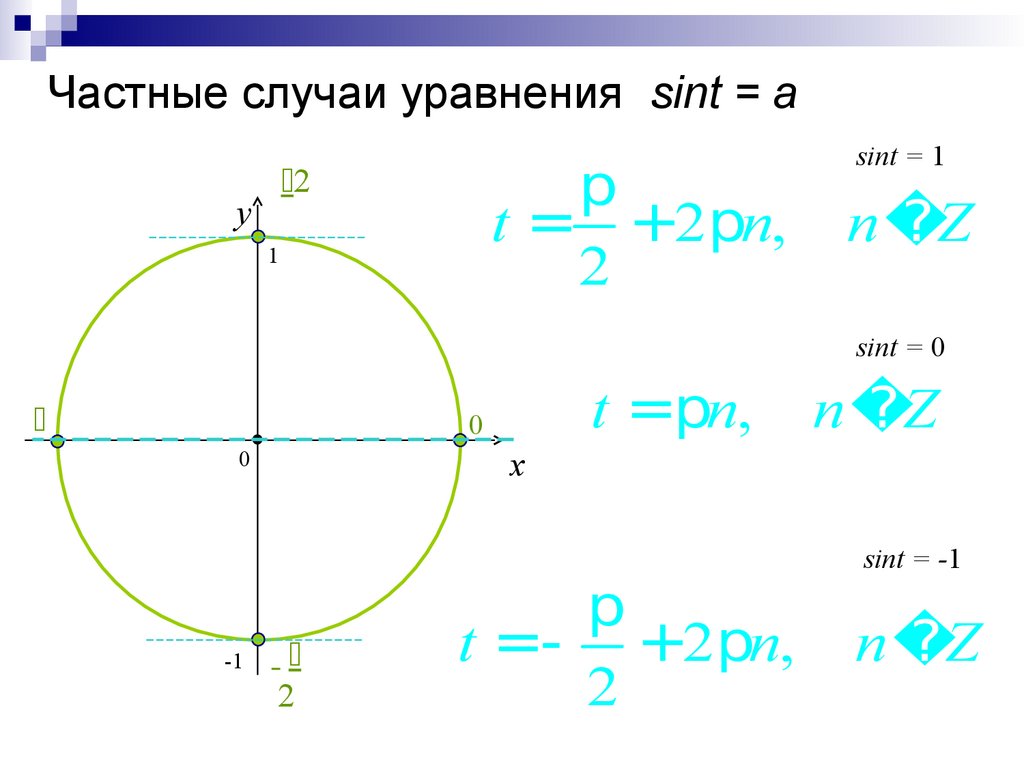 Printf("%.2f", math.Atanh(0))
}
Printf("%.2f", math.Atanh(0))
}
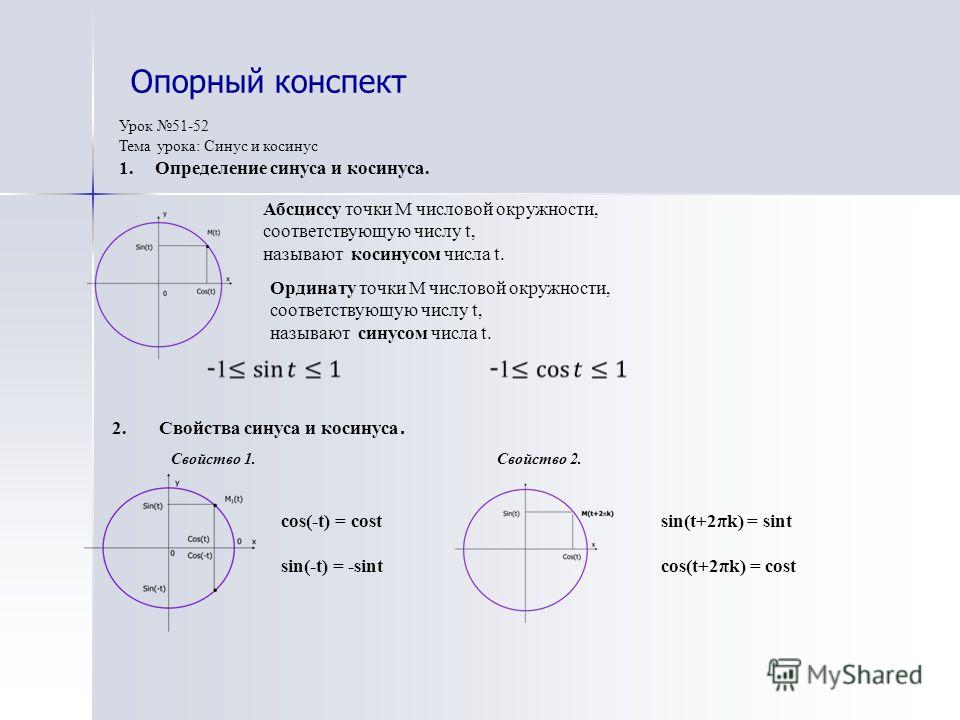 Printf("%.2f", math.Copysign(3.2, -1))
}
Printf("%.2f", math.Copysign(3.2, -1))
}
 Printf("%.2f\n", math.Dim(4, -2))
fmt.Printf("%.2f\n", math.Dim(-4, 2))
}
Printf("%.2f\n", math.Dim(4, -2))
fmt.Printf("%.2f\n", math.Dim(-4, 2))
}




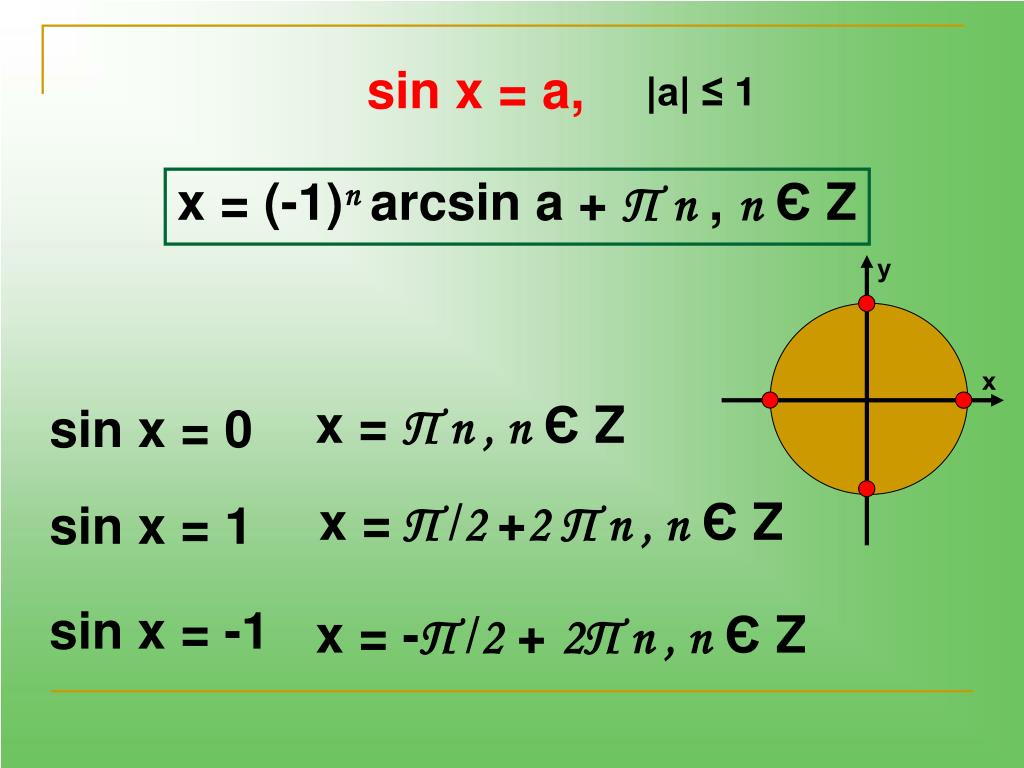 Если sign < 0, IsInf сообщает, является ли f отрицательной бесконечностью.
Если знак == 0, IsInf сообщает, равно ли f бесконечности.
Если sign < 0, IsInf сообщает, является ли f отрицательной бесконечностью.
Если знак == 0, IsInf сообщает, равно ли f бесконечности.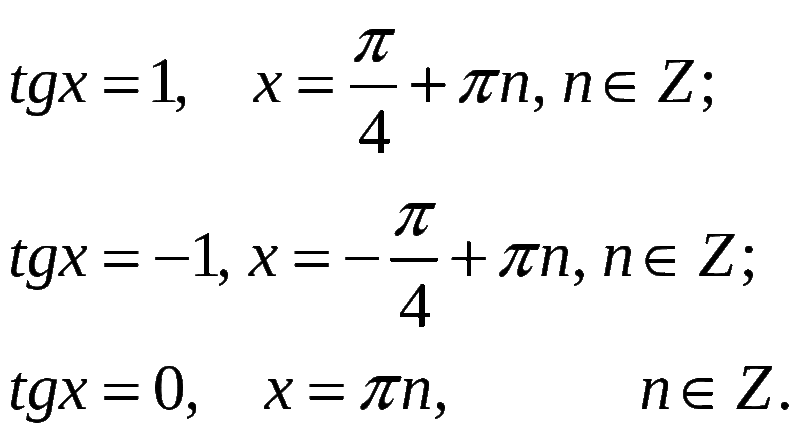
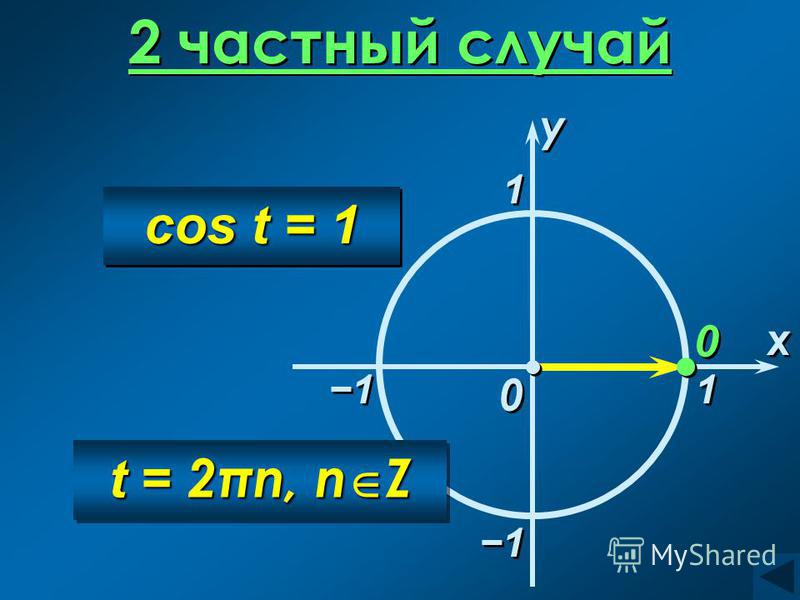
 (-Inf, x) = -Inf
Мин (х, NaN) = Мин (NaN, х) = NaN
Мин.(-0, ±0) = Мин.(±0, -0) = -0
(-Inf, x) = -Inf
Мин (х, NaN) = Мин (NaN, х) = NaN
Мин.(-0, ±0) = Мин.(±0, -0) = -0
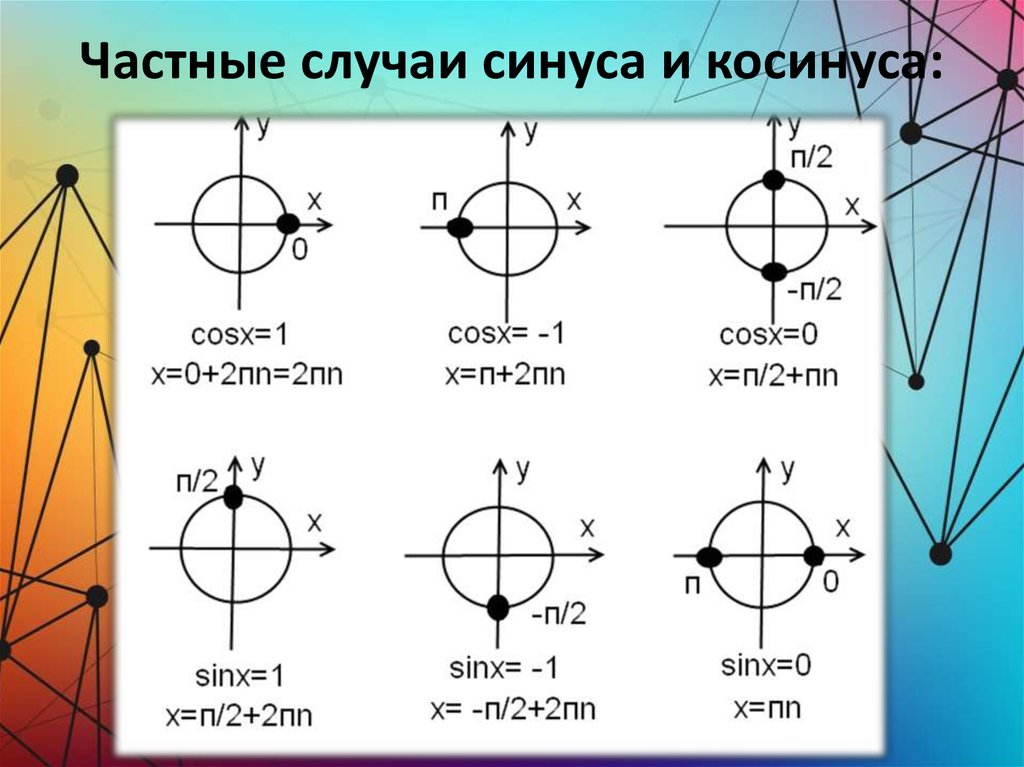 Printf("%.2f, %.2f\n", целое число, дробь)
}
Printf("%.2f, %.2f\n", целое число, дробь)
}
 Pow(2, 3)
fmt.Printf("%.1f", с)
}
Pow(2, 3)
fmt.Printf("%.1f", с)
}

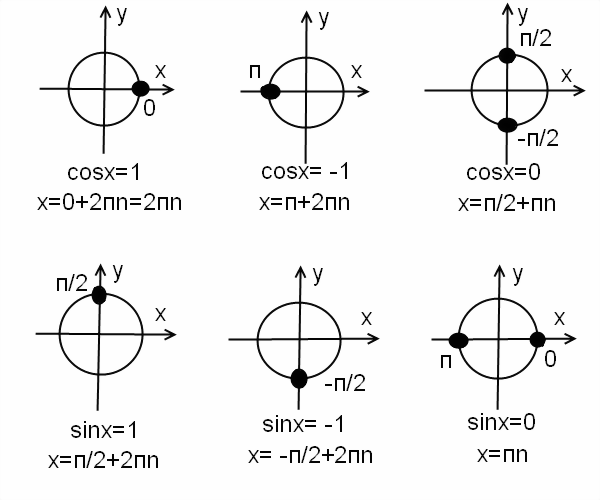 Printf("%.2f", math.Sin(math.Pi))
}
Printf("%.2f", math.Sin(math.Pi))
}
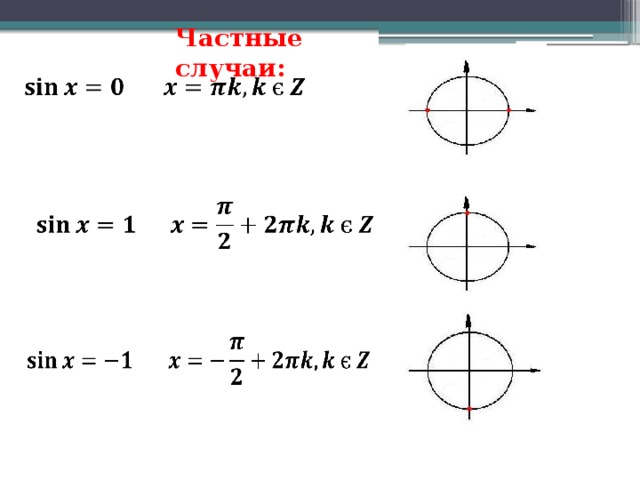 Sqrt(a*a + b*b)
fmt.Printf("%.1f", с)
}
Sqrt(a*a + b*b)
fmt.Printf("%.1f", с)
}
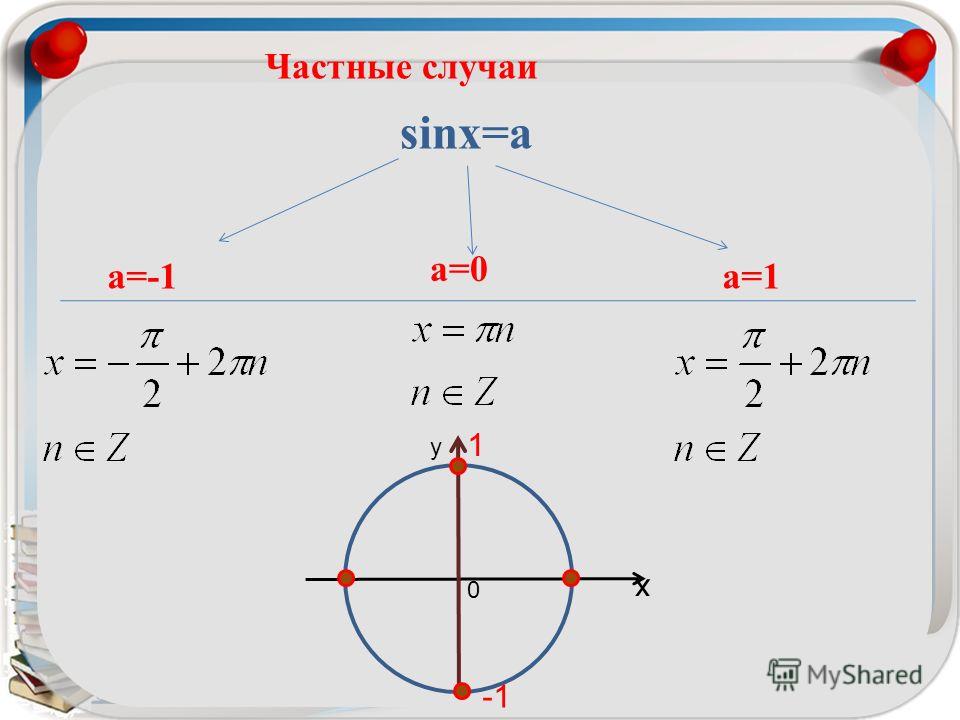 Printf("%.2f\n", math.Trunc(math.Pi))
fmt.Printf("%.2f\n", math.Trunc(-1.2345))
}
Printf("%.2f\n", math.Trunc(math.Pi))
fmt.Printf("%.2f\n", math.Trunc(-1.2345))
}

 Точно так же, как
вы увеличиваете b , период уменьшится.
Точно так же, как
вы увеличиваете b , период уменьшится.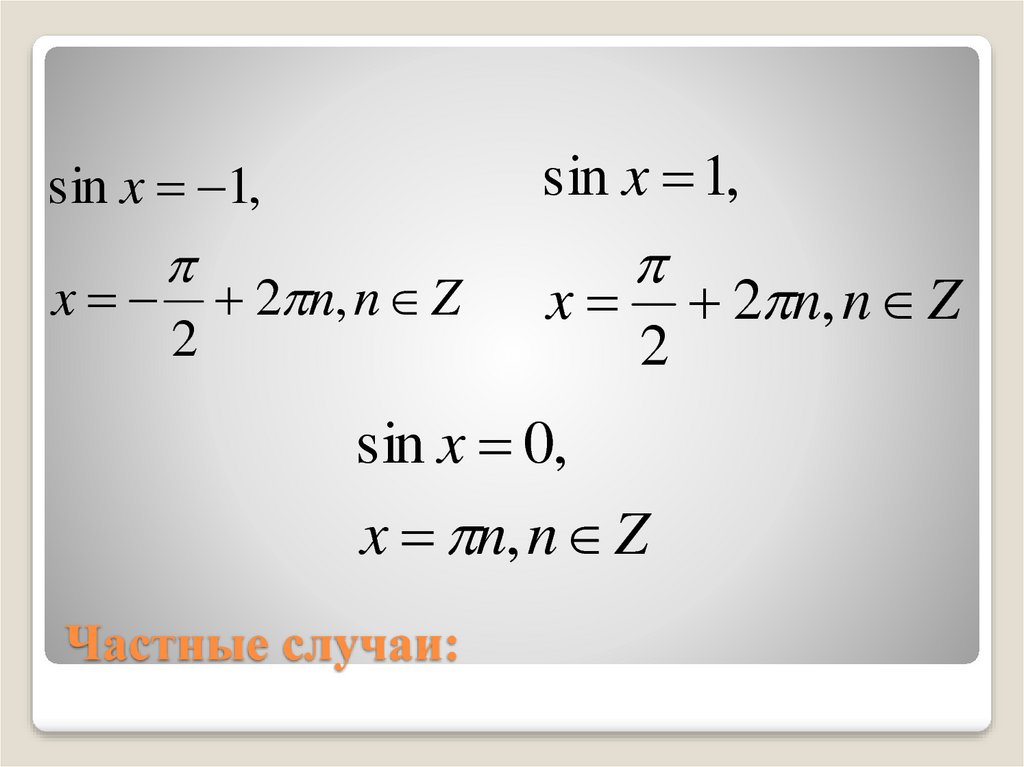
 вместе.
вместе.


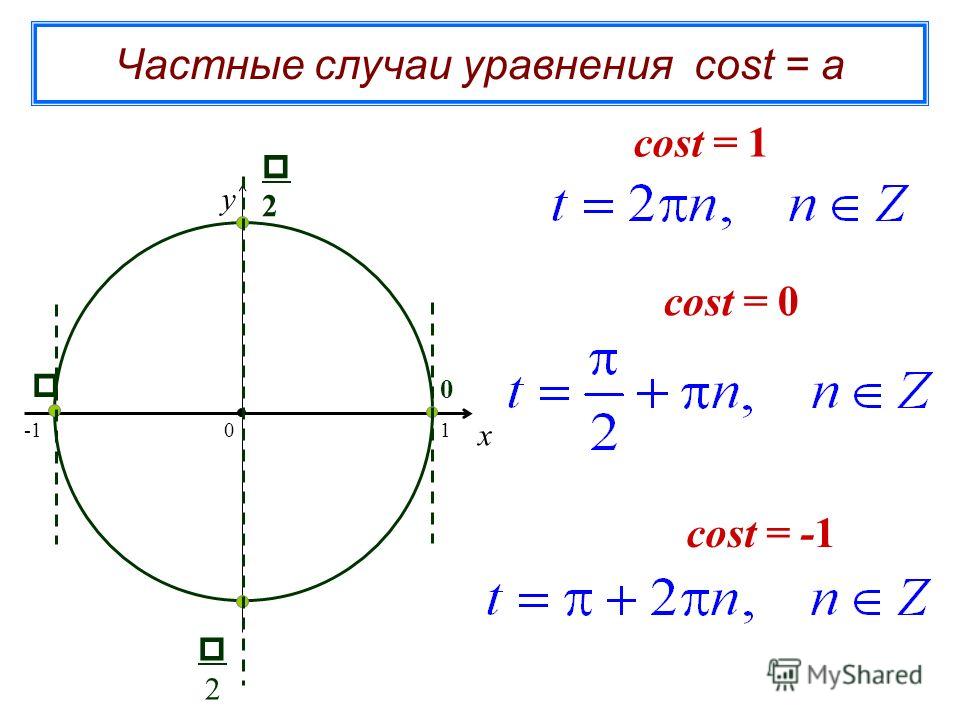


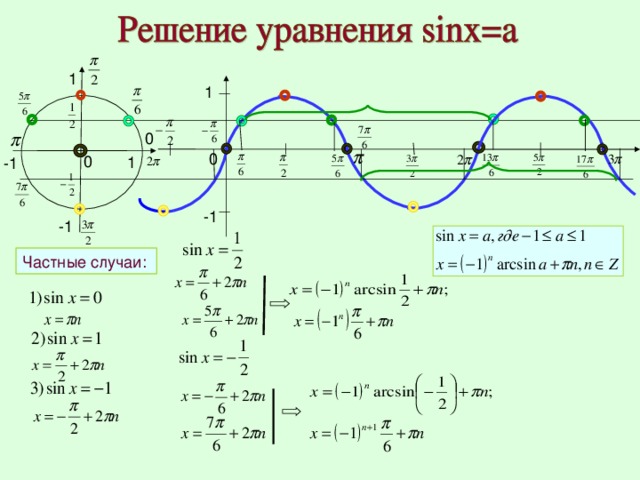
 {2} [ /латекс]. Имейте в виду, что многие калькуляторы и компьютеры не распознают стенографию. Если вы сомневаетесь, используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер.
{2} [ /латекс]. Имейте в виду, что многие калькуляторы и компьютеры не распознают стенографию. Если вы сомневаетесь, используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер.