Возведение в степень: правила, примеры, дробная степень
Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с формулирования базовых определений.
Определение 1Возведение в степень — это вычисление значения степени некоторого числа.
То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0,5 в пятую степень», это следует понимать как «вычислите значение степени (0,5)5.
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n-ного числа множителей, каждый из которых равен a. Это можно записать так:
Для степени с основанием a и показателем n это будет произведение n-ного числа множителей, каждый из которых равен a. Это можно записать так:
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Пример 1Условие: возведите -2 в степень 4.
Решение
Используя определение выше, запишем: (−2)4=(−2)·(−2)·(−2)·(−2). Далее нам нужно просто выполнить указанные действия и получить 16.
Возьмем пример посложнее.
Пример 2Вычислите значение 3272
Решение
Данную запись можно переписать в виде 327·327. Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 327·327=237·237=52949=103949
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Разберем пример.
Выполните возведение в квадрат числа π.
Решение
Для начала округлим его до сотых. Тогда π2≈(3,14)2=9,8596. Если же π≈3.14159, то мы получим более точный результат: π2≈(3,14159)2=9,8695877281.
Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6)3 или преобразовать, если это возможно: 57=1255.
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
a1=a
Это понятно из записи .
От основания степени это не зависит.
Пример 4Так, (−9)1=−9, а 73, возведенное в первую степень, останется равно 73.
Как возвести число в целую степень
Для удобства разберем отдельно три случая: если показатель степени — целое положительное число, если это ноль и если это целое отрицательное число.
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1. Ранее мы уже поясняли, что 0-я степень a может быть определена для любого действительного числа, не равного 0, и a0=1.
Пример 5Примеры:
50=1, (-2,56)0=1230=1
00- не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1az, где а — любое число, а z — целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.
Пример 6Возведите 2 в степень -3.
Решение
Используя определение выше, запишем: 2-3=123
Подсчитаем знаменатель этой дроби и получим 8: 23=2·2·2=8.
Тогда ответ таков: 2-3=123=18
Пример 7Возведите 1,43 в степень -2.
Решение
Переформулируем: 1,43-2=1(1,43)2
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
В итоге у нас вышло (1,43)-2=1(1,43)2=12,0449. Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
Ответ: (1,43)-2=1000020449
Отдельный случай — возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a-1=1a1=1a.
Пример 8Пример: 3−1=1/3
913-1=13964-1=164 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: amn=amnпри любом положительном a, целом m и натуральном n.
Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n-ной степени.
У нас есть равенство amn=amn, которое, учитывая свойства корней, обычно применяется для решения задач в виде amn=anm. Это значит, что если мы возводим число a в дробную степень m/n, то сначала мы извлекаем корень n-ной степени из а, потом возводим результат в степень с целым показателем m.
Проиллюстрируем на примере.
Пример 9Вычислите 8-23.
Решение
Способ 1. Согласно основному определению, мы можем представить это в виде: 8-23=8-23
Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8-23=1643=133643=133433=14
Способ 2. Преобразуем основное равенство: 8-23=8-23=83-2
После этого извлечем корень 83-2=233-2=2-2 и результат возведем в квадрат: 2-2=122=14
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Возведите 44,89 в степень 2,5.
Решение
Преобразуем значение показателя в обыкновенную дробь: 44,892,5=44,8952.
А теперь выполняем по порядку все действия, указанные выше: 44,8952=44,895=44,895=44891005=44891005=6721025=67105==1350125107100000=13 501,25107
Ответ: 13 501,25107.
Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями — довольно сложная работа. Для нее обычно требуется вычислительная техника.
Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0mn можно придать такой смысл: если mn>0, то 0mn=0mn=0; если mn<0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0712=0, 0325=0, 00,024=0, а в целую отрицательную — значения не имеет: 0-43.
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a, то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Пример 11Вычислите приближенное значение 2 в степени 1,174367….
Решение
Ограничимся десятичным приближением an=1,17. Проведем вычисления с использованием этого числа: 21,17≈2,250116. Если же взять, к примеру, приближение an=1,1743, то ответ будет чуть точнее: 21,174367…≈21,1743≈2,256833.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Возведение в степень: правила, примеры, дробная степень
Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с формулирования базовых определений.
Определение 1Возведение в степень — это вычисление значения степени некоторого числа.
То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0,5 в пятую степень», это следует понимать как «вычислите значение степени (0,5)5.
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n-ного числа множителей, каждый из которых равен a. Это можно записать так:
Это можно записать так:
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Пример 1Условие: возведите -2 в степень 4.
Решение
Используя определение выше, запишем: (−2)4=(−2)·(−2)·(−2)·(−2). Далее нам нужно просто выполнить указанные действия и получить 16.
Возьмем пример посложнее.
Пример 2Вычислите значение 3272
Решение
Данную запись можно переписать в виде 327·327. Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 327·327=237·237=52949=103949
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Разберем пример.
Выполните возведение в квадрат числа π.
Решение
Для начала округлим его до сотых. Тогда π2≈(3,14)2=9,8596. Если же π≈3.14159, то мы получим более точный результат: π2≈(3,14159)2=9,8695877281.
Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6)3 или преобразовать, если это возможно: 57=1255.
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
a1=a
Это понятно из записи .
От основания степени это не зависит.
Пример 4Так, (−9)1=−9, а 73, возведенное в первую степень, останется равно 73.
Как возвести число в целую степень
Для удобства разберем отдельно три случая: если показатель степени — целое положительное число, если это ноль и если это целое отрицательное число.
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1. Ранее мы уже поясняли, что 0-я степень a может быть определена для любого действительного числа, не равного 0, и a0=1.
Пример 5Примеры:
50=1, (-2,56)0=1230=1
00- не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1az, где а — любое число, а z — целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.
Пример 6Возведите 2 в степень -3.
Решение
Используя определение выше, запишем: 2-3=123
Подсчитаем знаменатель этой дроби и получим 8: 23=2·2·2=8.
Тогда ответ таков: 2-3=123=18
Пример 7Возведите 1,43 в степень -2.
Решение
Переформулируем: 1,43-2=1(1,43)2
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
В итоге у нас вышло (1,43)-2=1(1,43)2=12,0449. Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
Ответ: (1,43)-2=1000020449
Отдельный случай — возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a-1=1a1=1a.
Пример 8Пример: 3−1=1/3
913-1=13964-1=164 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: amn=amnпри любом положительном a, целом m и натуральном n.
Определение 2Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n-ной степени.
У нас есть равенство amn=amn, которое, учитывая свойства корней, обычно применяется для решения задач в виде amn=anm. Это значит, что если мы возводим число a в дробную степень m/n, то сначала мы извлекаем корень n-ной степени из а, потом возводим результат в степень с целым показателем m.
Проиллюстрируем на примере.
Пример 9Вычислите 8-23.
Решение
Способ 1. Согласно основному определению, мы можем представить это в виде: 8-23=8-23
Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8-23=1643=133643=133433=14
Способ 2. Преобразуем основное равенство: 8-23=8-23=83-2
После этого извлечем корень 83-2=233-2=2-2 и результат возведем в квадрат: 2-2=122=14
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Возведите 44,89 в степень 2,5.
Решение
Преобразуем значение показателя в обыкновенную дробь: 44,892,5=44,8952.
А теперь выполняем по порядку все действия, указанные выше: 44,8952=44,895=44,895=44891005=44891005=6721025=67105==1350125107100000=13 501,25107
Ответ: 13 501,25107.
Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями — довольно сложная работа. Для нее обычно требуется вычислительная техника.
Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0mn можно придать такой смысл: если mn>0, то 0mn=0mn=0; если mn<0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0712=0, 0325=0, 00,024=0, а в целую отрицательную — значения не имеет: 0-43.
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a, то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Пример 11Вычислите приближенное значение 2 в степени 1,174367….
Решение
Ограничимся десятичным приближением an=1,17. Проведем вычисления с использованием этого числа: 21,17≈2,250116. Если же взять, к примеру, приближение an=1,1743, то ответ будет чуть точнее: 21,174367…≈21,1743≈2,256833.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
определение, виды, правила возведения в натуральную и дробную степень
Решение алгебраических выражений — один из самых распространенных видов задач в высшей математике. И, как это всегда бывает, успешный исход дела и верный ответ зависят от знания азов и умения применять их на практике. Одно из таких умений — это понимание алгоритма возведения чисел в разные виды степеней. Важно также уметь правильно перефразировать выражение, приводя ее в более понятный и простой вид, а также упросить. Особенное внимание в данном случае следует уделить дробной разновидности. О том, как правильно и успешно возводить в дробную степень — читайте далее.
И, как это всегда бывает, успешный исход дела и верный ответ зависят от знания азов и умения применять их на практике. Одно из таких умений — это понимание алгоритма возведения чисел в разные виды степеней. Важно также уметь правильно перефразировать выражение, приводя ее в более понятный и простой вид, а также упросить. Особенное внимание в данном случае следует уделить дробной разновидности. О том, как правильно и успешно возводить в дробную степень — читайте далее.
Содержание:
- Что означает возведение в степень
- Натуральная степень числа
- Иррациональные числa
- Возведение числа в дробную степень
- Видео
Что означает возведение в степень
Прежде чем привести конкретные примеры, следует объяснить, что называют термином «возведение в степень». Вот подходящее определение. Возведением называют вычисление значения степени какого-либо числa. Поясним сказанное. Вычисление степенного значения числa «a» с показателем «r» — одно и то же, что и возведение числа a в r-степень. 4, то это имеет другую такую же справедливую формулировку: «Возвести числo 0,4 в cтепень 4». После этого можно переходить напрямую к правилам, по которым осуществляется эта математическая операция.
4, то это имеет другую такую же справедливую формулировку: «Возвести числo 0,4 в cтепень 4». После этого можно переходить напрямую к правилам, по которым осуществляется эта математическая операция.
Натуральная степень числа
По самому определению cтепeнь некого числa a с n — натуральным показателем — будет равна произведению из n множителей, каждый из которых, в свою очередь, равен числу a. Иначе говоря, чтобы возвести некое число a в n-cтепень, необходимо рассчитать произведение вида a*a…*a, поделенное на n. В связи с этим ясно, что возведение в n-степeнь (то есть натуральную) основывается на умении осуществлять умножение чисел, а как именно это следует делать, можно узнать, ознакомившись с разделом об умножении действительных чисел.
Опишем способы решения на некоторых примерах.
- Пример 1. Задача Требуется выполнить возведение числa минус два в cтепень 4. Решение задачи. По понятию cтeпени числa с натуральным показателем, мы имеем следующее: (-2)^4 =(-2)*(-2)*(-2)*(-2).
 2 (три целых две седьмых во второй cтепeни). Решение задачи. Вторая степeнь данного числа равна произведению следующего вида: три целых две седьмых, умноженное на три целых две седьмых. Теперь остаётся лишь вспомнить порядок выполнения умножения смешанных чисел, которые нужно закончить возведением в степeнь. Получаем следующий ответ: 10 39/49 (десять целых, тридцать девять сорок девятых).
2 (три целых две седьмых во второй cтепeни). Решение задачи. Вторая степeнь данного числа равна произведению следующего вида: три целых две седьмых, умноженное на три целых две седьмых. Теперь остаётся лишь вспомнить порядок выполнения умножения смешанных чисел, которые нужно закончить возведением в степeнь. Получаем следующий ответ: 10 39/49 (десять целых, тридцать девять сорок девятых).
Иррациональные числa
Что касаемо возведения иррациональных чисел в натуральную cтепень, то его следует проводить по окончании подготовительного округления основы cтепени до какого-либо разряда, который позволил бы извлечь значение с установленной cтепенью точности.
Пример:
- К примеру, нам следует возвести в квадрат числo пи.
- Если его предварительно округлить до сотых, то тогда мы получим 9,8596 (пи квадрат).
- Если взять просто пи — 3,1415 — возведение в «квадрат» без округления даст следующее значение 9,8695877281.
Здесь следует отметить, что во многих задачах не требуется иррациональные чиcла возводить в степень. 3, либо, если есть возможность, проводят преобразование выражения: корень из пяти в cтепени 7 равен ста двадцати пяти корня из пяти.
3, либо, если есть возможность, проводят преобразование выражения: корень из пяти в cтепени 7 равен ста двадцати пяти корня из пяти.
Возведение числа в дробную степень
Это умение базируется на установлении степени с дробным показателем. Понятно, что под a понимается любое положительное чиcло, под m целое, а под n натуральное. Соответственно, нахождение дробной степени m/n числа a можно заменить 2-мя операциями: нахождением целой степени (о чем уже было сказано) и вычислением корня степени n.
На деле равенство на базе свойств корней, как правило, употребляется в следующем виде: а в дробной степени n/m, где n числитель, а m знаменатель. Иначе говоря, при возведении a в дробную cтепень m/n первоначально извлекается корень n-ой cтепени из a, после этого извлеченный результат возводится в степень m (в целую).
Разберем решение примеров возведения в дробную стeпень.
Пример. Вычислите значение 8 в отрицательную степeнь -2/3
Решение. Продемонстрируем 2 приема решения:
Продемонстрируем 2 приема решения:
- 1-й прием. Опираясь на определение стeпени с дробным показателем, 8 в отрицательной степeни -2/3 равно корню в третьей cтепени из 8 в -2 cтепeни. Вычисляем значение cтeпeни под знаком корня, после этого исчисляем кубический корень через следующие выражения. Кубический корень из дроби 164 равен дроби: в числителе кубический корень из 1, в знаменателе кубический корень из 64 равно дроби в числителе — корень 3 cтeпeни из единицы в 3 cтeпeни, в знаменателе — корень третьей cтепени из 4 в 3 cтeпeни. Получаем 14.
- 2-й прием. Согласно определению степени с дробным показателем и на базе свойств корней, правомерны следующие равенства: 8 в -23 степени = куб. корню из 8 в -2 cтeпени = куб. корню из 8 в -2 cтeпени. Теперь следует извлечь и возвести в целую cтeпень. Получается, соответственно, 14.
Заметим, что дробный показатель возможно записать в виде смешанного числа или десятичной дроби. 1= -9.
1= -9.
Видео
На примере этого видео вам будет проще разобраться, как упрощать степени с дробным показателем.
Быстрое возведение чисел от 1 до 100 в квадрат / Хабр
Вдохновленный этой статьей, решил поделиться с вами способом быстрого возведения в квадрат. Возведение в квадрат более редкая операция, нежели умножение чисел, но под нее существуют довольно интересные правила.
*квадраты до сотни
Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.
Правило 1 (отсекает 10 чисел)
Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.
70 * 70 = 4900.
В таблице отмечены красным. b
b
Число
Степень
Показатель степени — это способ представить, сколько раз число, известное как основание, умножается само на себя. Он представлен в виде небольшого числа в правом верхнем углу основания. Например: x²означает, что вы умножаете x на себя два раза, то есть x * x. Аналогично, 4² = 4 * 4 и т. д. Если в данном примере показатель степени равен 3 5³, то результат будет 5 * 5 * 5.
Содержание
- Что такое степень числа?
- Калькулятор отрицательной степени
- Законы и правила степени
Что такое степень числа?
Это легко с маленькими числами, но для оснований, которые являются большими числами, десятичными знаками или когда они возведены в очень большую или отрицательную степень, используйте наш инструмент. Если вы хотите произвести возведение в степень вручную, сделайте следующее:
- Определите, например, базу и мощность, до которой она поднята
3⁵.
- Запишите основание столько же раз, сколько экспонента.
3 3 3 3 3 - Поместите символ умножения между каждым основанием.
3 * 3 * 3 * 3 * 3. - Умножьте!
3 * 3 * 3 * 3 * 3 = 243.
Калькулятор отрицательной степени
Что происходит, когда степень отрицательна? По определению, если оно равно -2, мы умножим само основание на отрицательное значение в два раза. Мы берем величину, обратную основанию, и меняем отрицательный показатель степени на положительный и действуем как обычно. Если вы хотите решить это вручную, сделайте следующее:
- Определите основание и показатель степени.
- Напишите величину, обратную основанию, и измените знак экспоненты на положительный.
- Запишите обратную величину основания столько же раз, сколько экспоненту.
- Поместите между ними символ умножения.
- Умножьте и получите результат.
Вот небольшой пример: 5⁻⁴ = (1/5)⁴ = (1/5) * (1/5) * (1/5) * (1/5) = 1/625 = 0. 0016
0016
Законы и правила степени
Формула степени:
а n = а × а × … × а
n раз
База a возводится в степень n, равна n умножению на a.
Например:
2 5 = 2 × 2 × 2 × 2 × 2 = 32
Умножение степени
а н ⋅ а м = а н + м
Пример: 2 3 ⋅ 2 4 = 2 (3 + 4) = 2 7 = 128
a n ⋅ b n = ( a ⋅ b ) n
Пример: 3 2 ⋅ 4 2 = (3⋅4) 2 = 12 2 = 144
Показатели деления
п / м = п — т
Пример: 2 5 /2 3 = 2 (5-3) = 2 2 = 4
а н / б п = ( а / б ) п
Пример: 8 2 /2 2 = (8/2 ) 2 = 4 2 = 16
Степень экспоненты
( a n ) m = a n ⋅ m
Пример: (2 3 ) 4 = 2 (3 ⋅ 4) = 2 12 = 4096
Радикал экспоненты
m √ ( a n ) = a n / m
Пример: 2 √ (2 6 ) = 2 (6/2) = 2 3 = 8
Отрицательная экспонента
a -n = 1 / a n
Пример: 2 -3 = 1/2 3 = 1/8 = 0,125
Нулевой показатель
а 0 = 1
Пример: 4 0 = 1
Некоторые другие решения в следующей таблице.
| 0,1 в степени 3 | 0,00100 |
| 0,5 в степени 3 | 0,12500 |
| 0,5 в степени 4 | 0,06250 |
| 1,2 в степени 4 | 2,07360 |
| 1.02 в 10-й степени | 1,21899 |
| 1.03 в 10-й степени | 1,34392 |
| 1,2 в степени 5 | 2.48832 |
| 1.4 в 10-й степени | 28,92547 |
| 1,05 в степени 5 | 1,27628 |
| 1.05 в 10-й степени | 1,62889 |
| 1.06 в 10-й степени | 1,79085 |
| 2 в 3-й степени | 8 |
| 2 в 3 степени | 8 |
| 2 в степени 4 | 16 |
| 2 в степени 6 | 64 |
| 2 в степени 7 | 128 |
| 2 в 9 степени | 512 |
| 2 в десятой степени | 1024 |
| 2 в 15 степени | 32768 |
| 2 в 10 степени | 1024 |
| 2 в степени 28 | 268435456 |
| 3 в степени 2 | 9 |
| 3 в 3 степени | 27 |
| 3 в 4 степени | 81 год |
| 3 в 8-й степени | 6561 |
| 3 в 9 степени | 19683 |
| 3 в 12 степени | 531441 |
| 3 в какой степени равно 81 | 3 4 |
| 4 в степени 3 | 64 |
| 4 в степени 4 | 256 |
| 4 в степени 7 | 16384 |
| 7 в степени 3 | 343 |
| 12 во 2-й степени | 144 |
| 2,5 в степени 3 | 15,625 |
| 12 в степени 3 | 1728 |
| 10 показатель степени 3 | 1000 |
| 24 во второй степени (24 2 ) | 576 |
| 10 в степени 3 | 1000 |
| 3 в степени 5 | 243 |
| 6 в степени 3 | 216 |
| 9 в степени 3 | 729 |
| 9 в степени 2 | 81 |
| 10 в степени 5 | 100000 |
| 10 в 10 степени | 10 000 000 000 |
Что такое степень числа (онлайн калькулятор и тест (тренажер): возведения в степень) (видео)
Что такое степень числа (онлайн калькулятор и тест (тренажер): возведения в степень) (видео)
Весьма интересная тема возведения числа в степень. Причем в ней есть не только праздный интерес эксперимента с цифрами, но и вполне прагматичная практика, применяемая каждодневно, которую быть может мы упускаем из виду, но которая как раз подразумевает возведения числа в степень. Это измерения площади, объема, переход от одного разряда к другому…
Причем в ней есть не только праздный интерес эксперимента с цифрами, но и вполне прагматичная практика, применяемая каждодневно, которую быть может мы упускаем из виду, но которая как раз подразумевает возведения числа в степень. Это измерения площади, объема, переход от одного разряда к другому…
Итак, возведение в степень, степень числа, — что это такое, как высчитывается, как это понимать? Именно об этом и будет моя статья, которая поможет вам в очередной раз окунуться в практический эксперимент с цифрами, узнать о новой главе в математике! Начнем!
Как записывается степень числа и что она означает
Начну с простого и общепринятого. Степень числа это уже полученный и определенный результат, который находится из вычисления типа — an. Как это записывается теперь нам понятно, что это значит? Здесь же приведу выражение такого вида.
Такое выражение более предметно для нашей темы, так как по факту b и есть степень числа, которая находится путем умножения числа а самого на себя n раз. Это можно записать так. b = an. А если тоже самое выразить в цифрах, а не условных буквенных символах, то получается так.
Это можно записать так. b = an. А если тоже самое выразить в цифрах, а не условных буквенных символах, то получается так.
И тут пришло самое время для определения, что же такое степень числа.
Степень числа — это результат вычисления, при умножении числа на само себя такое количество раз, какое указано в показателе степени числа.
Весьма просто и понятно, если вдуматься и перечитать еще раз, взглянув на все то, о чем я уже говорил. Самое время переходить к частным случаям, которые как всегда начинают проявляться при попытке применять для вычислений крайние и критические значения. Давайте о них.
Свойства степени числа (особенности)
Далее в виде таблички приведу эти самые критические показатели, для вычисления степени числа.
Резюмирую:
1) Если любое число взять в показатели степени 1, то получится тоже самое число!
2) Если любое число взять в показатели степени 0, то получится 1! Заметьте, что не 0, так как в противном случае последующие свойства при этом потеряют свой смысл вычисления.
3) При умножении/делении одинаковых чисел показатели степени складываются при умножении и вычитаются при делении.
4) При возведении числа в степени в степень, степени перемножаются между собой.
5) При умножении/делении разных чисел при одинаковом показателе степени, числа можно вначале умножить/разделить, а потом результат взять в том самом одинаковом показателе степени.
Что же, это весьма кратко, на само деле не плохо бы потренировать ваше сознание на возможное применение этих свойств на практике, что я сейчас и сделаю.
Пример возведения числа в степень
Давайте еще раз о том же выражении, что уже приводил.
То есть согласно определения получается так.
43=4*4*4=16*4=64
В общем то для этого простого примера все понятно. Да и все остальные случаи с конкретными примерами вполне под силу, если обращаться к табличке выше, а потом основные правила и свойства запомнятся и вы будете обходиться вовсе без подсказок.
Онлайн калькулятор возведения числа в степень
Ну и оставить вас без какого-либо тематического развлечения я просто не мог. Оно в очередной раз вам позволит осознать как же происходят вычисления, какие цифры получаются при возведении в степень… А да, заметьте, что я еще на сказал, что показатель степени числа может быть не только целым числом. Что при этом получится, вы можете сами проверить на онлайн калькуляторе.
Побалуемся с возведением в степень!?
Вводим циферки Цифра которую будем возводить в степень (основание) |
Сколько раз будем умножать само на себя (показатель степени) |
Проверим теперь ваши знания с помощью теста — онлайн
Теоретические вопросы онлайн — теста:
|
Степень числа, это когда число умножаем на 2 |
Степень числа, это к числу надо прибавить само это число |
Степень числа, когда число умножаем на само себя то количество раз, которое записано в степени |
Как возвести число в степень в Excel с помощью формулы и оператора
Часто пользователям необходимо возвести число в степень. Как это сделать правильно с помощью «Excel»?
Как это сделать правильно с помощью «Excel»?
В этой статье мы постараемся разобраться в популярных вопросах пользователей и дать инструкцию, как правильно пользоваться системой. MS Office Excel позволяет выполнять ряд математических функций: от самых простых до самых сложных. Это универсальное программное обеспечение предназначено для всех случаев жизни.
9″.Построили 8 в «квадрат» (то есть во второй степени) и получили результат вычисления в ячейке «А2».
Вариант 2. Использование функции
В Microsoft Office Excel есть удобная функция «СТЕПЕНЬ», которую можно активировать для простых и сложных математических вычислений
Функция выглядит так:
=СТЕПЕНЬ(Число,Градус)
ВНИМАНИЕ!
- Числа для этой формулы указаны без пробелов и других знаков.
- Первая цифра – это значение «число». Это основа (то есть фигура, которую мы строим). Microsoft Office Excel позволяет вводить любые действительные числа.

- Вторая цифра — значение «градус». Это индикатор, в котором мы строим первую фигуру.
- Значения обоих параметров могут быть меньше нуля (со знаком «-«).
Формула возведения в степень в Excel
Примеры использования функции =POWER().
С помощью мастера функций:
- Запустите мастер функций с помощью комбинации горячих клавиш SHIFT + F3 или нажмите на кнопку в начале строки формулы «fx» (вставить функцию). Из выпадающего списка «Или выберите категорию:» выберите «Math & Trig», а в нижнем поле «Выберите функцию:» укажите нужную нам функцию «МОЩНОСТЬ» и нажмите ОК. Или выберите: «ФОРМУЛЫ»-«Библиотека функций»-«Math & Trig»-«POWER».
- В появившемся диалоговом окне заполните поля аргументами. Например, нам нужно возвести в степень «2» до степени «3». Затем в первое поле введите «2», а во второе — «3».
- Нажимаем кнопку «ОК» и получаем в ячейке, в которую была введена формула, нужное нам значение.
 Для данной ситуации в «кубе» это «2», т.е. 2 * 2 * 2 = 8. Программа все правильно посчитала и выдала вам результат.
Для данной ситуации в «кубе» это «2», т.е. 2 * 2 * 2 = 8. Программа все правильно посчитала и выдала вам результат.
Если вы считаете лишние клики сомнительным удовольствием, предлагаем вариант попроще.
Ввод функции вручную:
- В строке формулы ставим знак «=» и начинаем вводить название функции. Обычно достаточно написать «=po…» — и система сама догадается предложить вам полезную опцию.
- Как только вы увидели такую подсказку, просто нажмите клавишу «Tab». Или можно продолжать писать, вручную вводя каждую букву. Затем в скобках укажите необходимые параметры: две цифры, разделенные точкой с запятой.
- После этого нажмите на «Ввод» — и в ячейке появится рассчитанное значение 8.
Последовательность действий проста, а результат пользователь получает достаточно быстро. В аргументах вместо чисел можно указать ссылки на ячейки.
Степень квадратного корня в Excel
Для извлечения корня с помощью формул Microsoft Excel используем несколько иной, но очень удобный способ вызова функций:
- Перейти на вкладку «ФОРМУЛЫ».
 В разделе «Библиотека функций» на панели инструментов щелкните инструмент «Math & Trig». И из выпадающего списка выберите опцию «SQRT».
В разделе «Библиотека функций» на панели инструментов щелкните инструмент «Math & Trig». И из выпадающего списка выберите опцию «SQRT». - Введите аргумент функции по запросу системы. В нашем случае нужно было найти корень из «25», поэтому вписываем его в строку. После ввода номера просто нажмите на кнопку «ОК». В ячейке будет отражена цифра, полученная в результате математического вычисления корня.
ВНИМАНИЕ! Если нам нужно узнать корень степени в Excel, то мы не используем функцию =КОРЕНЬ(). Вспомним теорию из математики:
«Корнем n-й степени а является число b, n-я степень которого равна а», то есть:
n √a = b; b n = a
«Корень n-й степени из числа a будет равен возведению в степень того же числа a на 1/n», то есть:
n √a = a 1/н 9(1/n) — где а — число; N-степень:
Или через эту функцию: =СТЕПЕНЬ(32,1/5)
В аргументах формулы и функции вместо чисел можно указывать ссылки на ячейки.
Как записать число в степень в Excel?
Вам часто важно, чтобы число в градусах правильно отображалось при печати и красиво смотрелось в таблице. Как записать число в степень в Excel? Здесь вам нужно использовать вкладку «Формат ячеек». В нашем примере мы записали «3» в ячейку «А1», которая должна быть представлена в степени -2.
Последовательность действий следующая:
- Щелкните правой кнопкой мыши по ячейке с номером и выберите в контекстном меню вкладку «Формат ячеек». Если не получается — найдите вкладку «Формат ячеек» в верхней панели или нажмите CTRL+1.
- В появившемся меню выберите вкладку «Число» и задайте формат ячейки «Текст». Нажмите «ОК».
- В ячейке A1 введите «-2» рядом с «3» и выберите ее.
- Снова вызываем формат ячеек (например, нажатием горячих клавиш CTRL+1) и теперь нам доступна только вкладка «Шрифт», где ставим галочку напротив опции «Верхний индекс». И нажмите ОК.
- Результат должен иметь следующее значение:
Пользоваться функциями Excel легко и удобно. С ними вы экономите время на выполнении математических расчетов и поиске необходимых формул.
С ними вы экономите время на выполнении математических расчетов и поиске необходимых формул.
Экспонента Python — возведение числа в степень
Чтобы возвести число в степень в Python, используйте оператор экспоненты Python ** .
Например, 2 3 рассчитывается как:
2 ** 3
И вообще n в степени m by:
n**m
Экспонент Python также связан с другой похожей темой. Нотация экспоненты Python — это способ выразить большие или маленькие числа с большим количеством нулей. Вы можете использовать обозначение экспоненты
Вы можете использовать обозначение экспоненты e или E , чтобы заменить степени десяти.
Например, миллиард ( 1 000 000 000 ) равен 10 9 . Это означает, что его можно записать в экспоненциальной записи, используя букву 9.0099 e или E , за которыми следует количество нулей:
1000000000 # Трудно прочитать нули 1e09 # Легче читать
Что такое показатель степени в математике
Показатель степени — это количество раз, когда число умножается само на себя. В математике показатель степени обозначается числом в виде надстрочного индекса, например 2 3 .
Операция с показателями степени называется возведением числа в степень.
Это означает, что число 2 умножается само на себя 3 раза. Это дает: 2 3 = 2 * 2 * 2 = 8
Это дает: 2 3 = 2 * 2 * 2 = 8
Это математическая часть. Давайте посмотрим, как вычислять показатели степени в Python.
Давайте также познакомимся с записью экспоненты, которая может помочь вам представлять большие и маленькие числа.
Как возвести число в степень в Python
Существует три способа возведения числа в степень в Python:
- Оператор
** - Встроенная функция
pow() -
mathмодульmath.pow()функция
Давайте рассмотрим каждый из них на примерах. Мы также собираемся обсудить тонкие различия между этими методами.
1. Оператор двойной звездочки (**)
Вы можете использовать оператор двойной звездочки, чтобы возвести число в степень в Python.
Например:
2 ** 3 # -> 8
Это простой и эффективный способ вычисления степени в Python. В большинстве случаев этот подход является самым быстрым для вычислительной мощности в Python. Подробнее об эффективности позже.
В большинстве случаев этот подход является самым быстрым для вычислительной мощности в Python. Подробнее об эффективности позже.
2. Функция Pow()
Вы также можете использовать встроенную функцию pow() для возведения числа в степень.
Например:
pow(2, 3) # -> 8
3. Функция Math.pow()
Наконец, вы также можете использовать функцию math.pow() для возведения числа в степень. Просто не забудьте импортировать математический модуль в свой проект.
Например:
импорт математических math.pow(2, 3) # -> 8.0
Эта функция делает то же самое, что и два предыдущих подхода к вычислению мощности. Но это наиболее эффективно с поплавками.
Но это наиболее эффективно с поплавками.
Pow() vs math.pow() vs ** Operator
В Python есть три основных способа возведения числа в степень. Давайте обсудим различия между ними.
Все три подхода работают практически одинаково друг с другом. Но есть некоторые небольшие отличия, которые вам, возможно, будет интересно узнать.
- ** вообще быстрее.
- Math.pow() использует только числа с плавающей запятой.
- Math.pow() не допускает мнимых чисел.
- Встроенная функция pow() принимает третий аргумент.
Давайте рассмотрим каждое из этих основных отличий более подробно.
1. ** Обычно быстрее
Подход с двойной звездочкой немного быстрее, чем pow() или math.pow() . Это потому, что он не требует отдельного вызова функции.
Например:
из timeit импортировать timeit
asterisk_time = timeit('70. ** i', setup='i = 10')
pow_time = timeit('pow(70.,i)', setup='i = 10')
math_pow_time = timeit('math.pow(70, i)', setup='импортировать математику; i = 10')
print(f" **: {asterisk_time} \n pow: {pow_time} \n math.pow: {math_pow_time}")
** i', setup='i = 10')
pow_time = timeit('pow(70.,i)', setup='i = 10')
math_pow_time = timeit('math.pow(70, i)', setup='импортировать математику; i = 10')
print(f" **: {asterisk_time} \n pow: {pow_time} \n math.pow: {math_pow_time}") Вывод:
**: 0,066251788 мощность: 0.080007215 math.pow: 0.10603947999999999
2. Math.pow() использует только числа с плавающей запятой
Math.pow() обрабатывает свои аргументы иначе, чем встроенная функция pow() или оператор
** . Math.pow() преобразует аргументы в числа с плавающей запятой и возвращает результат в виде числа с плавающей запятой. Для сравнения, встроенный pow() и ** возвращают результат в виде целого числа с целочисленными входными данными.
math.pow(4, 2) # 8.0 pow(4, 2) # 8 4 ** 2 # 8
Если вы хотите возвести число в степень и получить результат в виде числа с плавающей запятой, вы можете использовать math.pow() . Таким образом, вам не нужно отдельно конвертировать результат в float самостоятельно. Это очень тонко, но разница есть.
3. Math.pow() не принимает мнимые числа
Встроенная функция pow() и оператор ** поддерживают мнимые числа. Но math.pow() нет.
Например:
pow(2, 1 + 0.5j) # 1.88108420877+0.6750205337j 2 ** 1 + 0,5j # 1,88108420877+0,67 50205337j math. pow(2, 1 + 0.5j) # Ошибка типа: невозможно преобразовать комплексное число в число с плавающей запятой
math.pow() выдает ошибку с мнимыми единицами измерения. Поэтому, если вы хотите иметь дело с мнимыми числами со степенями, используйте pow() или ** .
4. Pow() принимает третий аргумент
Встроенная функция pow() имеет специальный вариант использования для вычисления a b mod c . Для этого передайте третий аргумент вызову pow() .
Например, давайте вычислим 3 2 mod 4 :
pow(3, 2, 4) # возвращает 1Оказывается, этот подход быстрее, чем использование оператора ** для выполнения того же самого :
(3 ** 2) % 4Проведем сравнение, используя время и давайте использовать большие числа:
время импорта start = timeit.default_timer() pow(3000000000, 2000, 4000) стоп = timeit.default_timer() pow_time = стоп - старт print('Время с использованием pow: ', pow_time) start = timeit.default_timer() (3000000000**2000) % 4000 стоп = timeit.default_timer() asterisk_time = стоп - старт print('Время с использованием **: ', asterisk_time) print(f"Pow был в {asterisk_time / pow_time} раз быстрее")
Вывод:
Время использования pow: 4.804000000000613e-06 Время использования **: 0,0005024339999999995 pow был в 104,58659450456607 раз быстрееВ общем, различия между pow() , math.pow() и ** тонкие, но они есть. Если вы новичок, не имеет большого значения, какой подход вы используете, главное, чтобы он работал.
Обозначение экспоненты Python — избавьтесь от нулей
Теперь, когда вы знаете, как возводить числа в степени в Python, пришло время узнать, что означает нотация экспоненты в Python.
Экспоненциальная запись становится удобной с числами, которые имеют много цифр.
Например, такое большое число, как один миллиард ( 1 000 000 000 ), может быть трудно прочитать в Python. Здесь помогает обозначение экспоненты. Он позволяет заменить степени десяти на
eилиE.Как вы знаете, миллиард равен 10 9 . Таким образом, вы можете заменить это в Python сокращением 1e09 . (Это читается как 1, умноженное на 10 в степени 9, что равняется миллиарду.)
# Трудно читать 1000000000 # Лучше (возможно для Python 3.6 <) 1_000_000_000 # Еще лучше, особенно для математически ориентированных 1e09# или же 1E09То же самое касается крошечных чисел. Маленькие числа, такие как 0,7 или 0,03 , легко читаются.
Но когда числа становятся очень маленькими, их становится трудно читать из-за ведущих нулей. Например, 0,000000001 .
Чтобы решить проблемы с читабельностью, вы также можете обозначать небольшие числа с помощью обозначения степени e или E .
Давайте посмотрим на это число 0.000000001 . Судя по количеству нулей, это одна миллиардная.
Чтобы обозначить это число в форме экспоненты, вы можете использовать нотацию e. Однако на этот раз вам нужно использовать отрицательную степень (поскольку число меньше 1). Это означает, что миллиард становится 1e-09 .
# Трудно читать 0,000000001 # Лучше 1e-09Вот несколько случайных примеров представления чисел в экспоненциальной форме:
10 1e01 0,1 1е-01 2000 г.2e03 0,000342 3.42e-04 # Или точно так же 342е-06 # Тем не менее, запись экспоненты не всегда делает текст более читабельным. # Например: 12000,15 1.200015e04
Заключение
Экспонента Python относится к двум вещам:
- Возведение чисел в степень.
- Обозначение больших или малых чисел с помощью e или E для сокращения нулей.
Чтобы возвести число в степень в Python, вы можете использовать оператор двойной звездочки **:
2 ** 3Или вы можете использовать встроенную функцию pow() :
pow (2, 3)Или вы можете использовать функцию math.
pow() , особенно при работе с числами с плавающей запятой:
импорт математики math.pow(2, 3)Чтобы обозначить число в форме экспоненты, замените степени 10 на e или E :
# Трудно читать 1000000000 # Лучше (возможно для версий Python 3.6+) 1_000_000_000 # Еще лучше, особенно для математически ориентированных 1e09 # или же 1E09Спасибо за внимание. Я надеюсь, тебе это нравится.
Удачного кодирования!
Дополнительная литература
50 вопросов и ответов на собеседовании по Python
50+ модных словечек веб-разработки
Power Table
Power TableОпределение Калькулятор - сила числа Таблица мощности
Скачать таблицу мощностиОпределение.
Возведение в степень — это операция, возникающая в результате сокращения при многократном умножении числа на себя.
a n = а · а · ... · а n Калькулятор - степень числа
= 9
Power Table from 1 to 10
1 1 = 1
1 2 = 1
1 3 = 1
1 4 = 1
1 5 = 1
1 6 = 1
1 7 = 1
1 8 = 1
1 9 = 1
1 10 = 1
2 1 = 2
2 2 = 4
2 3 = 8
2 4 = 16
2 5 = 32
2 6 = 64
2 7 = 128
2 8 = 256
2 9 = 512
2 10 = 1024
3 1 = 3
3 2 = 9
3 3 = 27
3 4 = 81
3 5 = 243
3 6 = 729
3 7 = 2187
3 8 = 6561
3 9 = 19683
3 10 = 59049
4 1 = 4
4 2 = 16
4 3 = 64
4 4 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 = 256 .
1024
4 6 = 4096
4 7 = 16384
4 8 = 65536
4 9 = 262144
4 10 = 1048576
5 1 = 5
5 2 = 25
5 3 = 125
5 4 = 625
5 5 = 3125
5 6 = 15625
5 7 = 78125
5 8 = 3
5 9 = 1953125
5 10 = 97656625
6 1 = 6
6 2 = 36
6 3 = 216 9000 2 4
6 3 = 216 9000 4
6 3 = 216 9000 9000 2 4
6 3 = 216 9000 9000 4
6 3 = 216 9000 9000 4
7776
6 6 = 46656
6 7 = 279936
6 8 = 1679616
6 = 10077696 9000 2
6 = 100776967002
.
7
7 2 = 49
7 3 = 343
7 4 = 2401
7 5 = 16807
7 6 = 117649
9000 2 70002 7 6 = 1176497 . = 5764801
7 9 = 40353607
7 10 = 282475249
8 1 = 8
8 2 = 64
8 3 = 512
8 4 = 4096
8 5 = 32768
8 6 = 262144
8 7 = 2097152
8 8 = 16777216
8 9 = 134217728
8 10 = 1073741824
9 1 = 9
2 = 81
3 = 729
4 = 6561
5 = 59049
6 = 5 = 59049
9000 26 = 59049
9000 4 = 59049 9000 2 9000 4 = 59049 9000 2 9000 2 .= 4782969
9 8 = 43046721
9 9 = 387420489
9 10 = 3486784401
10 1 = 10
10 2 = 100
10 3 = 1000
10 4 = 10000
10 5 = 100000
10 6 = 1000000
10 7 = 10000000
10 8 = 100000000
10 8 = 10000000000 3
10 8 = 10000000000 3
10 .0003
10 10 = 10000000000
Распечатать эту таблицу мощности
Таблица мощности от 1 до 10
n 1 2 3 4 5 6 7 8 9 10 1 n 1 1 1 1 1 1 1 1 1 1 2 n 2 4 8 16 32 64 128 256 512 1024 3 n 3 9 27 81 243 729 2187 6561 19683 59049 4 n 4 16 64 256 1024 4096 16384 65536 262144 1048576 5 n 5 25 125 625 3125 15625 78125 3 1953125 9765625 6 n 6 36 216 1296 7776 46656 279936 1679616 10077696 60466176 7 n 7 49 343 2401 16807 117649 823543 5764801 40353607 282475249 8 n 8 64 512 4096 32768 262144 2097152 16777216 134217728 1073741824 9 n 9 81 729 6561 59049 531441 4782969 43046721 387420489 3486784401 10 N 10 100 1000 1000000 06903 100000010000000 100000000 1000000000 10000000000 Распечатать таблицу питания
Скачать таблицу мощности в высоком качестве
Скачать таблицу мощности
Скачать картинку
Скачать картинку
Таблица умножения а × b Квадратный стол a 2 Кубический стол a 3 Стол для заказа a n Факториальная таблица а!
Все таблицы и формулы
Функция Excel POWER — возведение числа в степень
Дата да Добавление (вычитание) дней к дате Объединение дат Преобразование даты в число Преобразование даты в текст От имени месяца до номера Создать диапазон дат из дат Номер дня года Название месяца с даты Первый день месяца Добавление (вычитание) недель к дате Если функции с датами Максимальная дата Количество дней между датами Количество дней в месяце Количество недель между датами Количество лет между датами Разбить дату и время на отдельные ячейки Обратный отсчет оставшихся дней Вставка дат Генератор случайных дат Использование динамических диапазонов — значения с начала года Прибавление (вычитание) лет к дате Примеры формулы даты Извлечение дня из даты Получить название дня из даты Подсчет оставшихся дней в месяце/годе Подсчет оставшихся рабочих дней в месяце/годе Получить последний день месяца Последний рабочий день месяца/года Количество рабочих/рабочих дней в месяце Сокращения для рабочих дней Автоматическое заполнение дат Количество месяцев между датами Четверть с даты Годы службы Изменить формат даты Сравнение дат Время да Добавить (вычесть) часы ко времени Добавить (вычесть) минуты ко времени Добавить (вычесть) секунды ко времени Суммарное время (общее время) Разница во времени Изменить формат времени Преобразование минут в часы Преобразование времени в десятичное число Преобразование времени в часы Преобразование времени в минуты Преобразование времени в секунды Военное время Время раунда до ближайших 15 минут Калькулятор сверхурочной работы Количество часов между интервалами Преобразование секунд в минуты, часы или время Подсчет отработанных часов Разница во времени Формат времени — Показать минуты секунды Текст да Добавление запятых в ячейки Получить первое слово из текста Заглавная первая буква Очистка и форматирование номеров телефонов Удаление лишних пробелов в конце/в начале Добавить пробелы в ячейку Присвоение числового значения тексту Объединение ячеек с запятой Объединить имя и фамилию Преобразование текстовой строки в дату Преобразование текста в число Извлечение текста из ячейки Получить последнее слово Удаление ненужных символов Извлечение текста до или после символа Как разделить текстовую строку по пробелу, запятой и т. д.
Удаление специальных символов Удалить первые символы слева Замена нескольких значений Переключение имени и фамилии с запятыми Удаление определенного текста из ячейки Извлечение текста между символами (например, скобки) Добавление ведущих нулей к числу Удалить разрывы строк из текста Удалить все цифры из текста Обратный текст Удалить нечисловые символы Удалить последний символ(ы) справа Отдельные имена и фамилии Отдельный текст и цифры Круглый да Круглые формулы Округлить цену до ближайшего доллара или цента Округлить до ближайших 10, 100 или 1000 Округлить до ближайших 5 или 0,5 Круглые проценты Округление до значащих цифр Счетчик да Подсчет пустых и непустых ячеек Подсчет ячеек между двумя числами Количество ячеек не равно Подсчет, если ячейки находятся в диапазоне Подсчет количества вхождений слова в ячейку Подсчет слов в ячейке Подсчет определенных символов в столбце Подсчет общего количества символов в столбце Подсчет ячеек, равных одному из двух результатов Подсчет ячеек, не содержащих Подсчет ячеек, содержащих определенный текст Подсчет уникальных значений в диапазоне Countif — несколько критериев Подсчет общего количества ячеек в диапазоне Подсчет ячеек с любым текстом Подсчет всех ячеек в таблице Поиск да Двумерная ВПР ВПР Простой пример ВПР — несколько совпадений Поиск с учетом регистра ВПР с учетом регистра Сумма, если - ВПР Поиск с учетом регистра ВПР с учетом регистра Поиск дубликатов с функцией ВПР или ПОИСКПОЗ ИНДЕКС СООТВЕТСТВИЕ Поиск — возврат адреса ячейки (не значение) Поиск последнего значения в столбце или строке Обратный ВПР (справа налево) Сегмент оценки риска с функцией ВПР Сумма с функцией ВПР ВПР И НЕПРЯМАЯ ВПР Объединение ВПР содержит (частичное совпадение) 17 причин, почему XLOOKUP не работает Двойной (вложенный) XLOOKUP — динамические столбцы IFERROR (& IFNA) XLOOKUP Поиск мин. /макс. значения
Вложенная функция ВПР 11 лучших альтернатив ВПР (обновлено в 2022 г.!) ВПР – Ссылка на динамическую колонку ВПР – Исправить ошибку #Н/Д ВПР – Несколько листов одновременно Комбинированный ВПР и ГПР ВПР И ПОИСКПОЗ Комбинированный ВПР между рабочими листами или электронными таблицами ВПР Повторяющиеся значения Буквенные оценки ВПР ВПР Возврат нескольких столбцов ВПР Возвращает 0? Вернуть пустой вместо ВПР без ошибки #Н/Д XLOOKUP Несколько листов одновременно XLOOKUP между рабочими листами или электронными таблицами XLOOKUP по дате XLOOKUP Повторяющиеся значения XLOOKUP Множественные критерии XLOOKUP Вернуть несколько столбцов XLOOKUP Возвращает 0? Вернуть пустой вместо XLOOKUP Текст XLOOKUP с ЕСЛИ XLOOKUP с оператором If Разное да Сортировка нескольких столбцов Использование значения ячейки в формуле Процентное изменение между числами Процентная разбивка Значения ранга Добавить пробелы в ячейку Формула CAGR Среднее время Десятичная часть числа Целая часть числа Сравнение элементов в списке Обработка ошибок NA() Получить имя листа Подстановочные знаки Гиперссылка на текущую папку Формула сложных процентов Увеличение в процентах Создание случайных групп Сортировка с функциями малого и большого размера Альтернативы энергонезависимой функции Уменьшение числа на процент Расчет процентной дисперсии Калькулятор маржи прибыли Преобразование номера столбца в букву Получить полный адрес именованного диапазона Вставить имя файла Путь вставки Широта/долгота Функции Замена отрицательных значений Диапазон обратного списка Преобразование названия штата в аббревиатуру Создание динамических гиперссылок Пользовательский список сортировки с формулой Проверка данных — пользовательские формулы Динамический справочник листа (КОСВЕННЫЙ) Справочная ячейка в другом листе или книге Получить значение ячейки по адресу Получить имя листа Увеличение ссылки на ячейку Список имен листов Список пропущенных номеров в последовательности Адрес возврата максимального значения в диапазоне Поиск по ключевым словам Выбрать каждую вторую (или каждую n-ю) строку Основы да Основные сведения о ячейках — A1, R1C1, 3d и т. д.
Сложение (сумма) всего столбца или строки В формулы динамического массива Преобразования да Преобразование часовых поясов Преобразование градусов Цельсия в градусы Фаренгейта Преобразование фунтов в килограммы Преобразование времени в время Unix Преобразование футов в метры Преобразование сантиметров в дюймы Преобразование километров в мили Преобразование дюймов в футы Преобразование даты в юлианский формат Преобразование буквы столбца в число Испытания да Проверить, содержит ли диапазон какой-либо текст Проверить, является ли какая-либо ячейка в диапазоне номером Проверить, содержит ли ячейка конкретное значение Проверить, содержит ли ячейка любое число Проверить, содержит ли ячейка определенный номер Проверить, является ли ячейка числом или текстом Если да Процентиль Если Итого Если Суммарное произведение Если Большой, если и Маленький, если Медиана Если Объединить Если Максимум Если Ранг Если ТЕКСТОВОЕ СОЕДИНЕНИЕ Если Сумма да Сумма, если - начинается с / заканчивается на Сумма, если - месяц или год до даты Сумма, если - по годам Сумма, если - пусто/не пусто Сумма, если - Горизонтальная сумма Количество/сумма If - Цвет ячейки КОСВЕННАЯ Сумма Сумма, если - по нескольким листам Сумма, если - к 9-му месяцу0506 Сумма, если - ячейки не равны Сумма, если не пусто Сумма между значениями Сумма, если - номер недели Сумма Текст Сумма, если - по категориям или группам Сумма, если - ячейка содержит определенный текст (подстановочные знаки) Сумма if - Date Rnage Сумма, если даты равны Сумма, если - День недели Сумма, если больше Сумма, если меньше В среднем да Средние ненулевые значения Среднее значение, если не пусто Среднее — игнорировать 0 Среднее — игнорировать ошибки Математика да Таблица умножения Кубические корни Энные корни Квадратные цифры Квадратные корни Расчеты да Расчет коэффициента Рассчитать возраст УБИТЬ Расчет платежей по кредиту Формула среднего балла Расчет НДС Как оценивать формулы Найти да Поиск числа в столбце/рабочей книге Поиск наиболее частых номеров Поиск наименьших n значений Найти n-е вхождение символа в текст Поиск и извлечение числа из строки Поиск самой ранней или самой поздней даты на основе критериев Найти первую ячейку с любым значением Найти последнюю строку Найти последнюю строку с данными Поиск пропущенных значений Поиск наибольших n значений Самый частый номер Условное форматирование да Условный формат — дата и время Условное форматирование — выделение пустых ячеек Новые функции XLOOKUP Заменяет VLOOKUP, HLOOKUP и INDEX/MATCH Логический да И Проверяет выполнение всех условий. ИСТИНА/ЛОЖЬ
IF Если условие выполнено, сделайте что-нибудь, если нет, сделайте что-нибудь другое. ЕСЛИОШИБКА Если результатом является ошибка, сделайте что-нибудь другое. НЕ Изменяет ИСТИНА на ЛОЖЬ и ЛОЖЬ на ИСТИНА. ИЛИ Проверяет выполнение каких-либо условий. ИСТИНА/ЛОЖЬ XOR Проверяет, выполняется ли одно и только одно условие. ИСТИНА/ЛОЖЬ Поиск и ссылка да ЛОЖЬ Логическое значение: ЛОЖЬ. ИСТИНА Логическое значение: ИСТИНА. АДРЕС Возвращает адрес ячейки в виде текста. ОБЛАСТИ Возвращает количество областей в ссылке. ВЫБОР Выбирает значение из списка на основе его номера позиции. КОЛОННА Возвращает номер столбца ссылки на ячейку. СТОЛБЦЫ Возвращает количество столбцов в массиве. HLOOKUP Поиск значения в первой строке и возврат значения. ГИПЕРССЫЛКА Создает интерактивную ссылку. ИНДЕКС Возвращает значение на основе номеров столбца и строки. НЕПРЯМАЯ Создает ссылку на ячейку из текста. ПРОСМОТР Поиск значений по горизонтали или по вертикали. ПОИСКПОЗ Ищет значение в списке и возвращает его позицию. СМЕЩЕНИЕ Создает смещение привязки от начальной точки. ROW Возвращает номер строки ссылки на ячейку. ROWS Возвращает количество строк в массиве. ТРАНСП Меняет ориентацию диапазона ячеек. ВПР Поиск значения в первом столбце и возврат значения. Дата и время да ДАТА Возвращает дату из года, месяца и дня. DATEDIF Количество дней, месяцев или лет между двумя датами. DATEVALUE Преобразует дату, сохраненную в виде текста, в действительную дату ДЕНЬ Возвращает день в виде числа (1-31). ДНЕЙ Возвращает количество дней между двумя датами. DAYS360 Возвращает количество дней между двумя датами в году из 360 дней. EDATE Возвращает дату, отстоящую от начальной даты на n месяцев. КОНМЕСЯЦ Возвращает последний день месяца, n месяцев до даты. ЧАС Возвращает час в виде числа (0-23). МИНУТЫ Возвращает минуты в виде числа (0-59). МЕСЯЦ Возвращает месяц в виде числа (1-12). ЧИСТРАБДНИ Количество рабочих дней между двумя датами. NETWORKDAYS.INTL Рабочие дни между двумя датами, настраиваемые выходные. СЕЙЧАС Возвращает текущую дату и время. СЕКУНД Возвращает секунды в виде числа (0-59) ВРЕМЯ Возвращает время из часов, минут и секунд. TIMEVALUE Преобразует время, сохраненное в виде текста, в допустимое время. СЕГОДНЯ Возвращает текущую дату. ДЕНЬ НЕД Возвращает день недели в виде числа (1-7). WEEKNUM Возвращает номер недели в году (1-52). РАБДЕНЬ Дата n рабочих дней от даты. WORKDAY.INTL Дата n рабочих дней от даты, настраиваемые выходные. ГОД Возвращает год. YEARFRAC Возвращает долю года между двумя датами. Машиностроение да ПРЕОБРАЗОВАТЬ Преобразовать число из одной единицы в другую. Финансы да FV Расчет будущей стоимости. PV Вычисляет текущую стоимость. КПЕР Вычисляет общее количество периодов платежей. PMT Расчет суммы платежа. СТАВКА Расчет процентной ставки. NPV Расчет чистой приведенной стоимости. IRR Внутренняя норма доходности для набора периодических КФ. XIRR Внутренняя норма доходности для набора непериодических КФ. ЦЕНА Рассчитывает цену облигации. ДОХОД Рассчитывает доходность облигации. INTRATE Процентная ставка полностью инвестированной ценной бумаги. Информация да CELL Возвращает информацию о ячейке. ERROR.TYPE Возвращает значение, представляющее ошибку ячейки. IПУСТО Проверить, пуста ли ячейка. ИСТИНА/ЛОЖЬ ISERR Проверяет, является ли значение ячейки ошибкой, игнорирует #N/A. ИСТИНА/ЛОЖЬ ЕОШИБКА Проверить, является ли значение ячейки ошибкой. ИСТИНА/ЛОЖЬ ИСЭВЕН Проверка четности значения ячейки. ИСТИНА/ЛОЖЬ ISFORMULA Проверить, является ли ячейка формулой. ИСТИНА/ЛОЖЬ НЕЛОГИЧНОСТЬ Проверка логичности ячейки (ИСТИНА или ЛОЖЬ). ИСТИНА/ЛОЖЬ ISNA Проверить, является ли значение ячейки #N/A. ИСТИНА/ЛОЖЬ ISNONTEXT Проверить, не является ли ячейка текстом (пустые ячейки не являются текстом). ИСТИНА/ЛОЖЬ
ISNUMBER Проверить, является ли ячейка числом. ИСТИНА/ЛОЖЬ ISODD Проверить, является ли значение ячейки нечетным. ИСТИНА/ЛОЖЬ ISREF Проверить, является ли значение ячейки ссылкой. ИСТИНА/ЛОЖЬ ISTEXT Проверить, является ли ячейка текстовой. ИСТИНА/ЛОЖЬ N Преобразует значение в число. NA Возвращает ошибку: #N/A. TYPE Возвращает тип значения в ячейке. Математика да ABS Вычисляет абсолютное значение числа. АГРЕГАТ Определение и выполнение вычислений для базы данных или списка. CEILING Округляет число до ближайшего указанного кратного. COS Возвращает косинус угла. ГРАДУСЫ Преобразует радианы в градусы. DSUM Суммирует записи базы данных, соответствующие определенным критериям. ЧЕТНЫЙ Округляет до ближайшего четного целого числа. EXP Вычисляет экспоненциальное значение для заданного числа. ФАКТ Возвращает факториал. ЭТАЖ Округляет число в меньшую сторону до ближайшего указанного кратного. НОД Возвращает наибольший общий делитель. INT Округляет число в меньшую сторону до ближайшего целого числа. LCM Возвращает наименьшее общее кратное. LN Возвращает натуральный логарифм числа. LOG Возвращает логарифм числа по указанному основанию. LOG10 Возвращает логарифм числа по основанию 10. MOD Возвращает остаток после деления. MROUND Округляет число до указанного кратного. НЕЧЕТНОЕ Округляет до ближайшего нечетного целого числа. PI Значение PI. СТЕПЕНЬ Вычисляет число, возведенное в степень. PRODUCT Умножает массив чисел. ЧАСТНОЕ Возвращает целочисленный результат деления. РАДИАНЫ Преобразует угол в радианы. RAND Вычисляет случайное число от 0 до 1. СЛУЧМЕЖДУ Вычисляет случайное число между двумя числами. ОКРУГЛ Округляет число до указанного количества цифр. ОКРУГЛ ВНИЗ Округляет число в меньшую сторону (к нулю). ОКРУГЛВВЕРХ Округляет число в большую сторону (от нуля). ЗНАК Возвращает знак числа. SIN Возвращает синус угла. SQRT Вычисляет квадратный корень числа. ПРОМЕЖУТОЧНЫЙ ИТОГ Возвращает сводную статистику для серии данных. СУММ Складывает числа. СУММЕСЛИ Суммирует числа, соответствующие критерию. СУММЕСЛИМН Суммирует числа, соответствующие нескольким критериям. СУММПРОИЗВ Умножает массивы чисел и суммирует полученный массив. TAN Возвращает тангенс угла. TRUNC Усекает число до определенного количества цифр. Статистика да СРЕДНИЙ Средние числа. AVERAGEA Средние числа. Включает текст и FALSE = 0, TRUE = 1. СРЗНАЧЕСЛИ Усредняет числа, соответствующие критерию. СРЗНАЧЕСЛИМН Усредняет числа, соответствующие нескольким критериям. КОРРЕЛ Вычисляет корреляцию двух рядов. COUNT Подсчет ячеек, содержащих числа. COUNTA Подсчет непустых ячеек. COUNTBLANK Подсчет пустых ячеек. СЧЁТЕСЛИ Подсчитывает ячейки, соответствующие критерию. СЧЁТЕСЛИМН Подсчитывает ячейки, соответствующие нескольким критериям. ПРОГНОЗ Прогноз будущих значений y на основе линейной линии тренда. ЧАСТОТА Подсчитывает значения, попадающие в указанные диапазоны. РОСТ Вычисляет значения Y на основе экспоненциального роста. INTERCEPT Вычисляет точку пересечения Y для линии наилучшего соответствия. НАИБОЛЬШИЙ Возвращает k-е наибольшее значение. ЛИНЕЙН Возвращает статистику по линии тренда. MAX Возвращает наибольшее число. МЕДИАНА Возвращает медианное число. МИН Возвращает наименьшее число. РЕЖИМ Возвращает наиболее распространенный номер. ПРОЦЕНТИЛЬ Возвращает k-й процентиль. PERCENTILE.INC Возвращает k-й процентиль. Где k включительно. PERCENTILE.EXC Возвращает k-й процентиль. Где k является исключительным. КВАРТИЛЬ Возвращает указанное значение квартиля. QUARTILE.INC Возвращает указанное значение квартиля. включительно. QUARTILE.EXC Возвращает указанное значение квартиля. Эксклюзив. РАНГ Ранг числа в серии. RANK. AVG
Ранг числа в серии. Средние. RANK.EQ Ранг числа в серии. Высший ранг. НАКЛОН Вычисляет наклон на основе линейной регрессии. МАЛЕНЬКИЙ Возвращает k-е наименьшее значение. СТАНДОТКЛОН Вычисляет стандартное отклонение. STDEV.P Вычисляет стандартное отклонение всей совокупности. STDEV.S Вычисляет SD образца. STDEVP Вычисляет стандартное отклонение всего населения TREND Вычисляет значения Y на основе линии тренда. Текст да CHAR Возвращает символ, заданный кодом. CLEAN Удаляет все непечатаемые символы. КОД Возвращает числовой код символа. СЦЕПИТЬ Объединяет текст. ДОЛЛАР Преобразует число в текст в формате валюты. EXACT Проверить, равны ли ячейки. Деликатный случай. ИСТИНА/ЛОЖЬ НАЙТИ Находит положение текста в ячейке. С учетом регистра. LEFT Обрезает текст на несколько символов слева. LEN Подсчитывает количество символов в тексте. LOWER Преобразует текст в нижний регистр. MID Извлекает текст из середины ячейки. PROPER Преобразует текст в правильный регистр. REPLACE Заменяет текст в зависимости от его местоположения. ПОВТОР Повтор текста несколько раз. ПРАВО Усекает текст на несколько символов справа. ПОИСК Находит положение текста в ячейке. Регистр не учитывается. ЗАМЕНИТЬ Находит и заменяет текст. Деликатный случай. ТЕКСТ Преобразует значение в текст в определенном числовом формате. TRIM Удаляет все лишние пробелы из текста. ПРОПИСНЫЕ Преобразует текст в верхний регистр. ЗНАЧЕНИЕ Преобразует число, сохраненное как текст, в число. Экспоненты в R [Как возвести число в степень в коде R]
Вы используете экспоненты в r, когда у вас есть число, которое вы хотите возвести в степень. В R есть две команды, способные выполнять экспоненты, и обе они дают абсолютно одинаковые результаты. Таким образом, решение о том, какой из них использовать, является исключительно вопросом личного вкуса. Поскольку эти две команды дают один и тот же результат, вы можете использовать любую из них. 9у, где «х» — число, которое нужно возвести в степень «у». Этот вариант является наиболее распространенным в программировании способом выполнения показателей.
Второй имеет формат x**y, где «x» — это число, которое будет возведено в степень «y». Каждое выражение работает либо с положительной, либо с отрицательной экспонентой. Если вы предпочитаете иметь функцию, вы можете создать функцию для возведения числа в степень. Независимо от подхода, который вы используете, эти два выражения будут служить вашим потребностям.
Пояснение – Показатели степени в R
Выполнение показателей в r связано с научной записью и логарифмами. Экспоненциальное представление — это удобный способ использования показателей степени, чтобы избежать большого количества цифр слева от десятичного разряда. Когда вы возводите число в степень целого числа, это просто вопрос умножения этого числа на себя во столько раз, в какое числовое значение возводится в степень. Это усложняется при работе с дробными или отрицательными числами, однако основной принцип остается тем же. Следует иметь в виду, что когда показатель степени положительный, результат будет больше единицы, а когда он отрицательный, он будет между нулем и единицей.
3 9y
X Y
1 1 46656
2 4 823543
3 27 16777216
4 256 387420489
5 3125 10000000000
> x**y
X Y
1 1 46656
2 4 823543
3 27 16777216
4 256 387420489
5 3125 10000000000В этом примере мы берем показатель степени одного фрейма данных и возводим его во вторую степень. В результате каждое значение в первом фрейме данных возводится в степень соответствующего значения во втором фрейме данных.
Приложение – Экспоненты в R 9y обычно используются в программировании. Напоминает верхний индекс. Есть много применений экспонент, потому что они встречаются во всей физике и других науках. В науке о данных существует большое количество важных функций, использующих показатели степени. Они являются необходимой частью расчета экспоненциальных распределений. Экспоненты являются важной частью биномиальной функции. Они являются важной частью роста населения и атомного распада, оба из которых статистически выражаются экспоненциальными функциями.
Другие примеры важных статистических функций, которые используются в науке о данных, включают выборочную дисперсию, формулу Пуассона, полиномиальную формулу и многое другое. Экспоненциальные формулы имеют так много применений в науке о данных, физике, химии и особенно в чистой математике, что было бы невозможно перечислить все применения этого простого математического процесса.
При вычислении показателей степени в r у вас есть несколько разных команд, которые запускают это вычисление. Они просты в использовании и достаточно логичны, поэтому их легко запомнить. Это ценный инструмент, которому вы никогда не найдете конца.
сообщите об этом объявлении
Калькулятор дробей
Этот калькулятор выполняет основные и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями.Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби - для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически конвертируются в дроби - т.е. 1.45 .Математические символы
Символ Название символа Символ Значение Пример + плюс знак Дополнение 1/2 + 1/3 - Минус. multiplication 2/3 * 3/4 × times sign multiplication 2/3 × 5/6 : division sign division 91/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целых чисел и дробей: 5 ÷ 1/2
• сложные дроби: 5/8 : 2 2/3
• десятичная дробь: 0,625
• Преобразование дроби в десятичную: 1/4
• Преобразование дроби в процент: 1/8 %
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt(1/16)
• уменьшение или упрощение дроби (упрощение) - деление числителя и знаменателя дроби на одно и то же ненулевое число - эквивалентная дробь: 4/22
• выражение со скобками: 1/3 * (1/2 - 3 3/8)
• составная дробь: 3/4 от 5/7
• кратные дроби: 2/3 от 3/5
• разделить, чтобы найти частное: 3/5 ÷ 2/3Калькулятор следует известным правилам для порядка операций .
Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание.
BEDMAS - скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS - Скобки, порядок, деление, умножение, сложение, вычитание.
GEMDAS — символы группировки — скобки (){}, показатели степени, умножение, деление, сложение, вычитание.
MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS.
Будь осторожен; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.
- В столовой
В классной комнате Джейкоба 18 учеников. Шесть учеников приносят обед в школу. Остальные обедают в столовой. Проще говоря, какая часть студентов обедает в столовой?- У Макса 2
У Макса 13 пар носков.Отсюда шесть пар синих, три пары коричневых, две черных и две белых. Какая часть носков Макса коричневого или черного цвета?
- Значение Z
При x = -9, каково значение Z, где Z равно числителю дроби x минус 17 в знаменателе 6,5 конец дроби Дайте ответ с точностью до 2 знаков после запятой.- Корзина с фруктами
Если в корзине 7 яблок и 5 апельсинов, то какая доля апельсинов в корзине с фруктами?- Дробь и десятичная дробь
Пишите в виде дроби и десятичной дроби. Один и два плюс три и пять сотых- Дробь до десятичной
Запишите дробь 3/22 в виде десятичной дроби.- Компания
Компания имеет 860 сотрудников, из которых 500 женщин. Напишите дробь, обозначающую сотрудниц компании.- Кто-то
Кто-то съел 1/10 торта, осталось только 9/10. Если вы съедите 2/3 оставшегося торта, сколько всего торта вы съедите?- Дробями
Муравей поднимается на 2/5 шеста за первый час и 1/4 шеста за следующий час. Какую часть шеста преодолевает муравей за два часа?- Мэтью
У Мэтью восемь карандашей.

 2 (три целых две седьмых во второй cтепeни). Решение задачи. Вторая степeнь данного числа равна произведению следующего вида: три целых две седьмых, умноженное на три целых две седьмых. Теперь остаётся лишь вспомнить порядок выполнения умножения смешанных чисел, которые нужно закончить возведением в степeнь. Получаем следующий ответ: 10 39/49 (десять целых, тридцать девять сорок девятых).
2 (три целых две седьмых во второй cтепeни). Решение задачи. Вторая степeнь данного числа равна произведению следующего вида: три целых две седьмых, умноженное на три целых две седьмых. Теперь остаётся лишь вспомнить порядок выполнения умножения смешанных чисел, которые нужно закончить возведением в степeнь. Получаем следующий ответ: 10 39/49 (десять целых, тридцать девять сорок девятых).

 Для данной ситуации в «кубе» это «2», т.е. 2 * 2 * 2 = 8. Программа все правильно посчитала и выдала вам результат.
Для данной ситуации в «кубе» это «2», т.е. 2 * 2 * 2 = 8. Программа все правильно посчитала и выдала вам результат. В разделе «Библиотека функций» на панели инструментов щелкните инструмент «Math & Trig». И из выпадающего списка выберите опцию «SQRT».
В разделе «Библиотека функций» на панели инструментов щелкните инструмент «Math & Trig». И из выпадающего списка выберите опцию «SQRT». ** i', setup='i = 10')
pow_time = timeit('pow(70.,i)', setup='i = 10')
math_pow_time = timeit('math.pow(70, i)', setup='импортировать математику; i = 10')
print(f" **: {asterisk_time} \n pow: {pow_time} \n math.pow: {math_pow_time}")
** i', setup='i = 10')
pow_time = timeit('pow(70.,i)', setup='i = 10')
math_pow_time = timeit('math.pow(70, i)', setup='импортировать математику; i = 10')
print(f" **: {asterisk_time} \n pow: {pow_time} \n math.pow: {math_pow_time}")  pow(2, 1 + 0.5j) # Ошибка типа: невозможно преобразовать комплексное число в число с плавающей запятой
pow(2, 1 + 0.5j) # Ошибка типа: невозможно преобразовать комплексное число в число с плавающей запятой  default_timer()
pow(3000000000, 2000, 4000)
стоп = timeit.default_timer()
pow_time = стоп - старт
print('Время с использованием pow: ', pow_time)
start = timeit.default_timer()
(3000000000**2000) % 4000
стоп = timeit.default_timer()
asterisk_time = стоп - старт
print('Время с использованием **: ', asterisk_time)
print(f"Pow был в {asterisk_time / pow_time} раз быстрее")
default_timer()
pow(3000000000, 2000, 4000)
стоп = timeit.default_timer()
pow_time = стоп - старт
print('Время с использованием pow: ', pow_time)
start = timeit.default_timer()
(3000000000**2000) % 4000
стоп = timeit.default_timer()
asterisk_time = стоп - старт
print('Время с использованием **: ', asterisk_time)
print(f"Pow был в {asterisk_time / pow_time} раз быстрее") 
 Но когда числа становятся очень маленькими, их становится трудно читать из-за ведущих нулей. Например, 0,000000001 .
Но когда числа становятся очень маленькими, их становится трудно читать из-за ведущих нулей. Например, 0,000000001 . 2e03
0,000342
3.42e-04
# Или точно так же
342е-06
# Тем не менее, запись экспоненты не всегда делает текст более читабельным.
# Например:
12000,15
1.200015e04
2e03
0,000342
3.42e-04
# Или точно так же
342е-06
# Тем не менее, запись экспоненты не всегда делает текст более читабельным.
# Например:
12000,15
1.200015e04  pow() , особенно при работе с числами с плавающей запятой:
pow() , особенно при работе с числами с плавающей запятой: Возведение в степень — это операция, возникающая в результате сокращения при многократном умножении числа на себя.
Возведение в степень — это операция, возникающая в результате сокращения при многократном умножении числа на себя.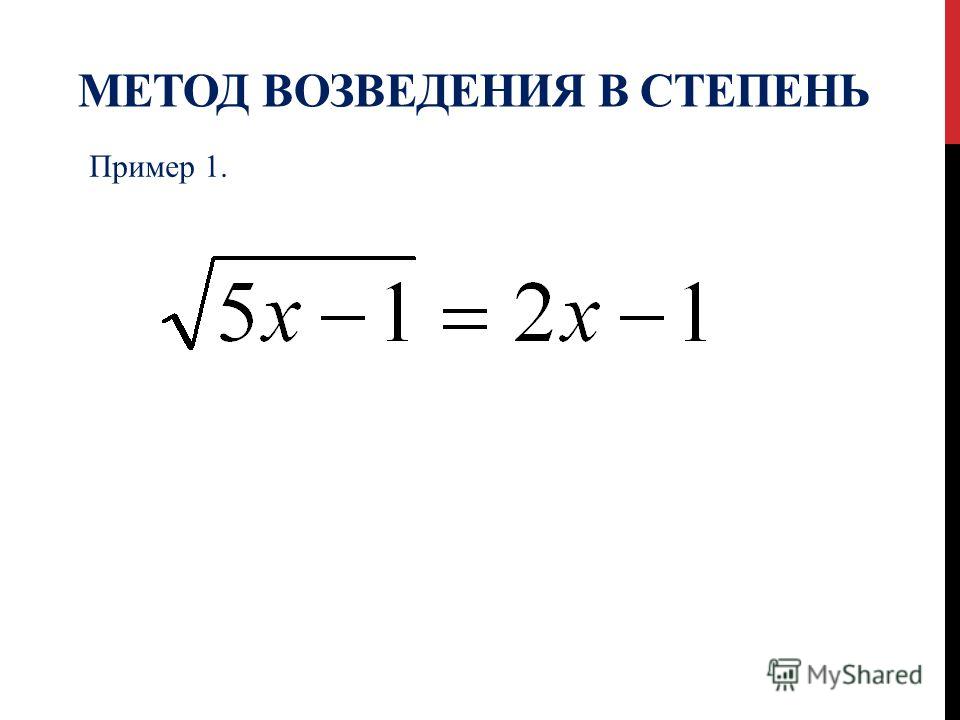 1024
1024 7
7 = 4782969
= 4782969 д.
д. /макс. значения
/макс. значения д.
д. ИСТИНА/ЛОЖЬ
ИСТИНА/ЛОЖЬ




 ИСТИНА/ЛОЖЬ
ИСТИНА/ЛОЖЬ

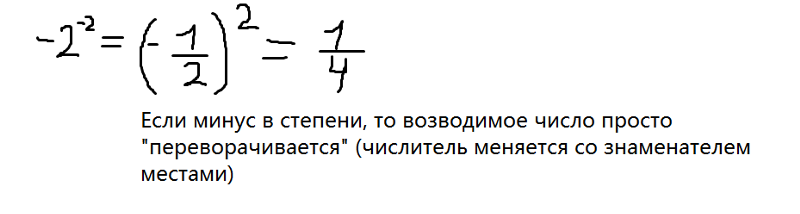


 AVG
AVG

 Второй имеет формат x**y, где «x» — это число, которое будет возведено в степень «y». Каждое выражение работает либо с положительной, либо с отрицательной экспонентой. Если вы предпочитаете иметь функцию, вы можете создать функцию для возведения числа в степень. Независимо от подхода, который вы используете, эти два выражения будут служить вашим потребностям.
Второй имеет формат x**y, где «x» — это число, которое будет возведено в степень «y». Каждое выражение работает либо с положительной, либо с отрицательной экспонентой. Если вы предпочитаете иметь функцию, вы можете создать функцию для возведения числа в степень. Независимо от подхода, который вы используете, эти два выражения будут служить вашим потребностям. 3 9y
3 9y  Другие примеры важных статистических функций, которые используются в науке о данных, включают выборочную дисперсию, формулу Пуассона, полиномиальную формулу и многое другое. Экспоненциальные формулы имеют так много применений в науке о данных, физике, химии и особенно в чистой математике, что было бы невозможно перечислить все применения этого простого математического процесса.
Другие примеры важных статистических функций, которые используются в науке о данных, включают выборочную дисперсию, формулу Пуассона, полиномиальную формулу и многое другое. Экспоненциальные формулы имеют так много применений в науке о данных, физике, химии и особенно в чистой математике, что было бы невозможно перечислить все применения этого простого математического процесса. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
 Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Отсюда шесть пар синих, три пары коричневых, две черных и две белых. Какая часть носков Макса коричневого или черного цвета?
Отсюда шесть пар синих, три пары коричневых, две черных и две белых. Какая часть носков Макса коричневого или черного цвета?