формулы cos, sin, tg, ctg
Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.
Тригонометрические тождестваsin2a+cos2a=1tgα=sinαcosα, ctgα=cosαsinαtgα·ctgα=1tg2α+1=1cos2α, ctg2α+1=1sin2α
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.
Формулы приведенияsinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα, cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα, ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα, cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα, ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα, ctg3π2-α+2πz=tgα
Формулы приведения являются следствием периодичности тригонометрических функций.
Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.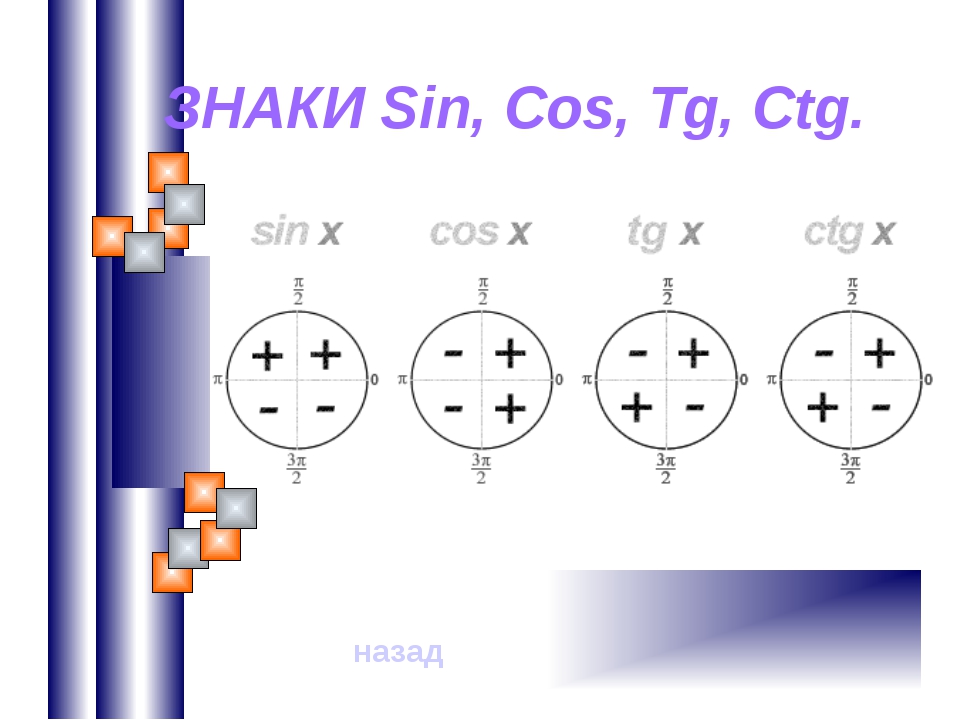
sinα±β=sinα·cosβ±cosα·sinβcosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβtgα±β=tgα±tgβ1±tgα·tgβctgα±β=-1±ctgα·ctgβctgα±ctgβ
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Формулы кратного угла: двойного, тройного и т.д.
Формулы двойного и тройного углаsin2α=2·sinα·cosαcos2α=cos2α-sin2α, cos2α=1-2sin2α, cos2α=2cos2α-1tg2α=2·tgα1-tg2α сtg2α=сtg2α-12·сtgα sin3α=3sinα·cos2α-sin3α, sin3α=3sinα-4sin3αcos3α=cos3α-3sin2α·cosα, cos3α=-3cosα+4cos3αtg3α=3tgα-tg3α1-3tg2αctg3α=ctg3α-3ctgα3ctg2α-1
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеФормулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα
Формулы понижения степени
Формулы понижения степениsin2α=1-cos2α2cos2α=1+cos2α2sin3α=3sinα-sin3α4cos3α=3cosα+cos3α4sin4α=3-4cos2α+cos4α8cos4α=3+4cos2α+cos4α8
Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
для четных n
sinnα=Cn2n2n+12n-1∑k=0n2-1(-1)n2-k·Ckn·cos((n-2k)α)cosnα=Cn2n2n+12n-1∑k=0n2-1Ckn·cos((n-2k)α)
для нечетных n
sinnα=12n-1∑k=0n-12(-1)n-12-k·Ckn·sin((n-2k)α)cosnα=12n-1∑k=0n-12Ckn·cos((n-2k)α)
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Сумма и разность тригонометрических функцийsinα+sinβ=2sinα+β2·cosα-β2sinα-sinβ=2sinα-β2·cosα+β2cosα+cosβ=2cosα+β2·cosα-β2cosα-cosβ=-2sinα+β2·sinα-β2, cosα-cosβ=2sinα+β2·sinβ-α2
Произведение тригонометрических функций
Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
sinα·sinβ=12·(cos(α-β)-cos(α+β))cosα·cosβ=12·(cos(α-β)+cos(α+β))sinα·cosβ=12·(sin(α-β)+sin(α+β))
Универсальная тригонометрическая подстановка
Все основные тригонометрические функции — синус, косинус, тангенс и котангенс, — могут быть выражены через тангенс половинного угла.
Универсальная тригонометрическая подстановкаАвтор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
формулы cos, sin, tg, ctg
Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.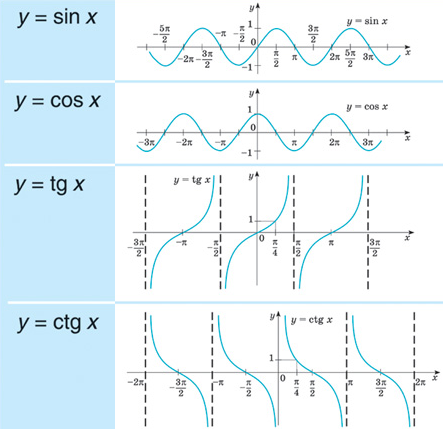
sin2a+cos2a=1tgα=sinαcosα, ctgα=cosαsinαtgα·ctgα=1tg2α+1=1cos2α, ctg2α+1=1sin2α
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.
Формулы приведенияsinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα, cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα, ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα, cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα, ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα, ctg3π2-α+2πz=tgα
Формулы приведения являются следствием периодичности тригонометрических функций.
Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
Тригонометрические формулы сложенияsinα±β=sinα·cosβ±cosα·sinβcosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβtgα±β=tgα±tgβ1±tgα·tgβctgα±β=-1±ctgα·ctgβctgα±ctgβ
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Формулы кратного угла: двойного, тройного и т.д.
Формулы двойного и тройного углаsin2α=2·sinα·cosαcos2α=cos2α-sin2α, cos2α=1-2sin2α, cos2α=2cos2α-1tg2α=2·tgα1-tg2α сtg2α=сtg2α-12·сtgα sin3α=3sinα·cos2α-sin3α, sin3α=3sinα-4sin3αcos3α=cos3α-3sin2α·cosα, cos3α=-3cosα+4cos3αtg3α=3tgα-tg3α1-3tg2αctg3α=ctg3α-3ctgα3ctg2α-1
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеФормулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα
Формулы понижения степени
Формулы понижения степениsin2α=1-cos2α2cos2α=1+cos2α2sin3α=3sinα-sin3α4cos3α=3cosα+cos3α4sin4α=3-4cos2α+cos4α8cos4α=3+4cos2α+cos4α8
Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Общий вид формул понижения степенидля четных n
sinnα=Cn2n2n+12n-1∑k=0n2-1(-1)n2-k·Ckn·cos((n-2k)α)cosnα=Cn2n2n+12n-1∑k=0n2-1Ckn·cos((n-2k)α)
для нечетных n
sinnα=12n-1∑k=0n-12(-1)n-12-k·Ckn·sin((n-2k)α)cosnα=12n-1∑k=0n-12Ckn·cos((n-2k)α)
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
sinα+sinβ=2sinα+β2·cosα-β2sinα-sinβ=2sinα-β2·cosα+β2cosα+cosβ=2cosα+β2·cosα-β2cosα-cosβ=-2sinα+β2·sinα-β2, cosα-cosβ=2sinα+β2·sinβ-α2
Произведение тригонометрических функций
Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
Формулы произведения тригонометрических функцийsinα·sinβ=12·(cos(α-β)-cos(α+β))cosα·cosβ=12·(cos(α-β)+cos(α+β))sinα·cosβ=12·(sin(α-β)+sin(α+β))
Универсальная тригонометрическая подстановка
Все основные тригонометрические функции — синус, косинус, тангенс и котангенс, — могут быть выражены через тангенс половинного угла.
sinα=2tgα21+tg2α2cosα=1-tg2α21+tg2α2tgα=2tgα21-tg2α2ctgα=1-tg2α22tgα2
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
Тригонометрические выражения и тригонометрические формулы [wiki.eduVdom.com]
subjects:mathematics:тригонометрические_выражения_и_формулы
Отметим на координатной оси Ох справа от точки О точку А и построим окружность с центром в точке О и радиусом ОА (так называемым начальным радиусом).
Окружность с центром в точке О и радиусом ОА
Рис.1
Пусть при повороте на угол a против часовой стрелки начальный радиус ОА переходит в радиус ОВ.
Тогда:
Синусом (sin α) угла α называется отношение ординаты точки В к длине радиуса.
Косинусом (cos α) угла α называется отношение абсциссы точки В к длине радиуса.

Тангенсом (tg α) угла α называется отношение ординаты точки В к ее абсциссе.
Котангенсом (ctg α) угла α называется отношение абсциссы точки В к ее ординате.
Секанс определяется как sec α = 1/(cos α)
Косеканс определяется как cosec α = 1/(sin α)
В западной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x
Если координаты точки В равны x и y, то:
$$\sin{\alpha} = \frac{y}{R}\;;\; \cos{\alpha} = \frac{x}{R}\;;\; {\rm tg}\, \alpha = \frac{y}{x}\;;\; {\rm ctg}\, \alpha = \frac{x}{y}$$
Таблица значений sin α, cos α, tg α, ctg α
Приведем таблицу значений тригонометрических функций некоторых углов (прочерк сделан, когда выражение не имеет смысла):
| Таблица значений sin α, cos α, tg α, ctg α | ||||||||
| 0º | 30º | 45º | 60º | 90º | 180º | 270º | 360º | |
|---|---|---|---|---|---|---|---|---|
| 0 рад | $\frac{\pi}{6}$ | $\frac{\pi}{4}$ | $\frac{\pi}{3}$ | $\frac{\pi}{2}$ | $\pi$ | $\frac{3\pi}{2}$ | $2\pi$ | |
| $\sin \alpha$ | 0 | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | 1 | 0 | -1 | 0 |
| $\cos \alpha$ | 1 | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | 0 | -1 | 0 | 1 |
| $\textrm{tg}\, \alpha$ | 0 | $\frac{1}{\sqrt{3}}$ | 1 | $\sqrt{3}$ | — | 0 | — | 0 |
| $\textrm{ctg}\, \alpha$ | — | $\sqrt{3}$ | 1 | $\frac{1}{\sqrt{3}}$ | 0 | — | 0 | — |
Свойства sin, cos, tg и ctg
Свойства синуса (sin), косинуса (cos), тангенса(tg) и котангенса(ctg):
Определение знака
Если α-угол I или II координатной четверти, то sin α > 0;
Если α-угол III или IV координатной четверти, то sin α < 0;
Если α-угол I или IV координатной четверти, то cos α > 0;
Если α-угол II или III координатной четверти, то cos α < 0;
Если α-угол I или III координатной четверти, то tg α > 0 и ctg α > 0;
Если α-угол II или IV координатной четверти, то tg α < 0 и ctg α < 0.

Синус, тангенс и котангенс — нечетные функции; косинус — четная функция.
Для чётной функции справедливо равенство: y(-x) = y(x). Примеры чётных функций: y = cos(x), y = x2.
Для НЕчётной функции справедливо равенство: y(-x) = -y(x). Примеры НЕчётных функций: y = sin(x), y = x.
При изменении угла на целое число оборотов значения тригонометрических функций не меняются.
1 радиан — это мера центрального угла, которому соответствует длина дуги, равная длине радиуса окружности.
Связь радианов с градусами: $1° =\frac{\pi}{180}\text{рад; 1 рад }=\frac{180°}{\pi}$.
Основные тригонометрические тождества
Формулы приведения
| X | $\frac{\pi}{2}-\alpha$ | $\frac{\pi}{2}+\alpha$ | $\pi-\alpha$ | $\pi+\alpha$ | $\frac{3\pi}{2}-\alpha$ | $\frac{3\pi}{2}+\alpha$ | $2\pi-\alpha$ | $2\pi+\alpha$ |
|---|---|---|---|---|---|---|---|---|
| sin x | cos α | cos α | sin α | -sin α | -cos α | -cos α | -sin α | sin α |
| cos x | sin α | -sin α | -cos α | -cos α | -sin α | sin α | cos α | cos α |
| tg x | ctg α | -ctg α | -tg α | tg α | ctg α | -ctg α | -tg α | tg α |
| ctg x | tg α | -tg α | -ctg α | ctg α | tg α | -tg α | -ctg α | ctg α |
Формулы сложения
Формулы двойного угла
Формулы двойного угла или двойного аргумента:
Формулы половинного аргумента
Формулы половинного аргумента (для sin и cos — формулы понижения степени):
Формулы суммы и разности
Формулы произведения
Соотношения между sin x, cos x и tg(x/2)
Один из способов использования: свести всё к tg(x/2) и путём замены получить обычное алгебраическое выражение.
Простейшие тригонометрические уравнения
Дополнительно
subjects/mathematics/тригонометрические_выражения_и_формулы.txt · Последние изменения: 2021/03/24 18:37 — ¶
Таблица тригонометрических значений углов: синус, косинус, тангенс, котангенс
Ниже представлена таблица со значениями синусов (sin), косинусов (cos), тангенсов (tg) и котангенсов (ctg) углов от 0 до 360 градусов (или от 0 до 2π).
| α° | α | sin α | cos α | tg α | ctg α |
| 0° | 0 | 0 | 1 | 0 | — |
| 30° | π/6 | 1/2 | √3/2 | 1/√3 | √3 |
| 45° | π/4 | √2/2 | √2/2 | 1 | 1 |
| 60° | π/3 | √3/2 | 1/2 | √3 | 1/√3 |
| 90° | π/2 | 1 | 0 | — | 0 |
| 120° | 2π/3 | √3/2 | -1/2 | -√3 | -1/√3 |
| 135° | 3π/4 | √2/2 | -√2/2 | -1 | -1 |
| 150° | 5π/6 | 1/2 | -√3/2 | -1/√3 | -√3 |
| 180° | π | 0 | -1 | 0 | — |
| 210° | 7π/6 | -1/2 | -√3/2 | 1/√3 | √3 |
| 225° | 5π/4 | -√2/2 | -√2/2 | 1 | 1 |
| 240° | 4π/3 | -√3/2 | -1/2 | √3 | 1/√3 |
| 270° | 3π/2 | -1 | 0 | — | 0 |
| 300° | 5π/3 | -√3/2 | 1/2 | -√3 | -1/√3 |
| 315° | 7π/4 | -√2/2 | √2/2 | -1 | -1 |
| 330° | 11π/6 | -1/2 | √3/2 | -1/√3 | -√3 |
| 360° | 2π | 0 | 1 | 0 | — |
microexcel. ru
ru
Тригонометрические тождества и преобразования
Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций:Простейшие тригонометрические тождества
Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств.
Частное от деления косинуса угла альфа на синус того же угла равно котангенсу этого же угла (Формула 2)
Секанс угла равен единице, деленной на косинус этого же самого угла (Формула 3)
Сумма квадратов синуса и косинуса одного и того же угла равна единице (Формула 4). см. также доказательство суммы квадратов косинуса и синуса.
Сумма единицы и тангенса угла равна отношению единицы к квадрату косинуса этого угла (Формула 5)
Единица плюс котангенс угла равна частному от деления единицы на синус квадрат этого угла (Формула 6)
Произведение тангенса на котангенс одного и того же угла равно единице (Формула 7).
Преобразование отрицательных углов тригонометрических функций (четность и нечетность)
Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.
Как видно, косинус и секанс является четной функцией, синус, тангенс и котангенс — нечетные функции.
Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).
Косинус «минус альфа» даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.
Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)
Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами:
Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла) в одинарный происходит по следующим правилам:
Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла
Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла
Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица
Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла
Тангенс двойного угла равен дроби, числитель которой — удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла.
Котангенс двойного угла равен дроби, числитель которой — квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла
Формулы универсальной тригонометрической подстановки
Указанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции ( sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем α/2 .Данные формулы называются формулами универсальной тригонометрической подстановки. Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще.
Тригонометрические тождества преобразования половины угла
Указанные ниже формулы тригонометрического преобразования половинной величины угла к его целому значению.
Значение аргумента тригонометрической функции α/2 приводится к значению аргумента тригонометрической функции α.
Тригонометрические формулы сложения углов
cos (α — β) = cos α · cos β + sin α · sin β
sin (α + β) = sin α · cos β + sin β · cos α
sin (α — β) = sin α · cos β — sin β · cos α
cos (α + β) = cos α · cos β — sin α · sin β
Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:
Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.
Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.
Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.
Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.
Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.
Формулы преобразования суммы или разности тригонометрических функций
Выражения, представляющие собой сумму вида sin α + sin β можно преобразовать с помощью следующих формул:Формулы тройного угла — преобразование sin3α cos3α tg3α в sinα cosα tgα
Иногда необходимо преобразовать тройную величину угла так, чтобы аргументом тригонометрической функции вместо 3α стал угол α.
В этом случае можно воспользоваться формулами (тождествами) преобразования тройного угла:
Формулы преобразования произведения тригонометрических функций
Если возникает необходимость преобразовать произведение синусов разных углов косинусов разных углов или даже произведения синуса на косинус, то можно воспользоваться следующими тригонометрическими тождествами:В этом случае произведение функций синуса, косинуса или тангенса разных углов будет преобразовано в сумму или разность.
Формулы приведения тригонометрических функций
Пользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце — угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90) = cos α .
См. также Полный список формул приведения тригонометрических функций.
| Угол |
α + 90 α + π/2 |
α + 180 α + π |
α + 270 α + 3π/2 |
90 — α π/2- α |
180 — α π- α |
270 — α 3π/2- α |
360 — α 2π- α |
| sin | cos α | -sin α | -cos α | cos α | sin α | -cos α | -sin α |
| cos | -sin α | -cos α | sin α | sin α | -cos α | -sin α | cos α |
| tg | -ctg α | tg α | -ctg α | ctg α | -tg α | ctg α | -tg α |
| ctg | -tg α | ctg α | -tg α | tg α | -ctg α | tg α | -ctg α |
Формулы приведения / Блог / Справочник :: Бингоскул
Таблица формул приведения
Два правила формул приведения
- при 900 и при 2700 (в виде (π/2 ±a) или (3*π/2 ±a)) — функция меняется на кофункцию (sin на cos либо в обратную сторону, tg на ctg либо в обратную).

- при 1800 и при 3600 (в виде (π ±a) или (2*π ±a)) — функция НЕ изменяется.
2 способа запоминания формул приведения
1. «Правило лошади»:
- Если мы откладываем угол от вертикальной оси, лошадь говорит «да» (киваем головой вдоль оси OY) и приводимая функция меняет свое название: синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс.
- Если мы откладываем угол от горизонтальной оси, лошадь говорит «нет» (киваем головой вдоль оси OХ) и приводимая функция не меняет свое название.
- Знак правой части равенства совпадает со знаком приводимой функции, стоящей в левой части равенства.
2. Использование четности и периодичности.
нечетная функция
- sin (-α) = -sin α
- tg (-α) = -tg α
- сtg (-α) = -сtg α
четная функция
Тригонометрические функции (синус, косинус, тангенс, котангенс) являются периодическими:
- sin α, cos α — периодические функции с наименьшим положительным периодом 2π: sin(α+2kπ) = sin α,cos(α+2kπ) = cos α, k ∈ Z.

- tg α, ctg α — периодические функции с наименьшим положительным периодом π: tg(α+kπ) = tgα, ctg(α+kπ) = ctg α, k ∈ Z.
Формулы приведения в виде списка
sin
- sin(900 — α) = cos α
- sin (900 + α) = cos α
- sin (1800 — α) = sin α
- sin (1800 + α) = -sin α
- sin (2700 — α) = -cos α
- sin (2700 + α) = -cos α
- sin (3600 — α) = -sin α
- sin (3600 + α) = sin α
cos
- cos (900 — α) = sin α
- cos (900 + α) = -sin α
- cos (1800 — α) = -cos α
- cos (1800 + α) = -cos α
- cos (2700 — α) = -sin α
- cos (2700 + α) = sin α
- cos (3600 — α) = cos α
- cos (3600 + α) = cos α
tg
- tg(900 — α) = ctg α
- tg (900 + α) = -ctg α
- tg (1800 — α) = -tg α
- tg (1800 + α) = tg α
- tg (2700 — α) = ctg α
- tg (2700 + α) = -ctg α
- tg (3600 — α) = -tg α
- tg (3600 + α) = tg α
ctg
- ctg (900 — α) = tg α
- ctg (900 + α) = -tg α
- ctg (1800 — α) = -ctg α
- ctg (1800 + α) = ctg α
- ctg (2700 — α) = tg α
- ctg (2700 + α) = -tg α
- ctg (3600 — α) = -ctg α
- ctg (3600 + α) = ctg α
Угол альфа α находится в интервале 0 — 90°.
Знаки основных тригонометрических функций в зависимости от четверти
Дополнительный материал: Формулы тригонометрии
Смотри также: Основные формулы по математике
Внеклассный урок — Синус, косинус, тангенс
Синус, косинус, тангенс, котангенс острого угла. Тригонометрические функции.
Синус острого угла α прямоугольного треугольника – это отношение противолежащего катета к гипотенузе.
Обозначается так: sin α.
Косинус острого угла α прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.
Обозначается так: cos α.
Тангенс острого угла α – это отношение противолежащего катета к прилежащему катету.
Обозначается так: tg α.
Котангенс острого угла α – это отношение прилежащего катета к противолежащему.
Обозначается так: ctg α.
Синус, косинус, тангенс и котангенс угла зависят только от величины угла.
Правила:
Катет b, противолежащий углу α, равен произведению гипотенузы на sin α: b = c · sin α Катет a, прилежащий к углу α, равен произведению гипотенузы на cos α: a = c · cos α Катет b, противоположный углу α, равен произведению второго катета на tg α: b = a · tg α Катет a, прилежащий к углу α, равен произведению второго катета на ctg α: a = b · ctg α |
Основные тригонометрические тождества в прямоугольном треугольнике:
(α – острый угол, противолежащий катету b и прилежащий к катету a. Сторона с – гипотенуза. β – второй острый угол).
b |
sin2 α + cos2 α = 1
|
α + β = 90˚
|
a | 1 |
cos α = sin β
|
b | 1 |
sin α = cos β
|
a | 1 1 |
tg α = ctg β |
sin α |
|
|
При возрастании острого угла sin α и tg α возрастают, а cos α убывает.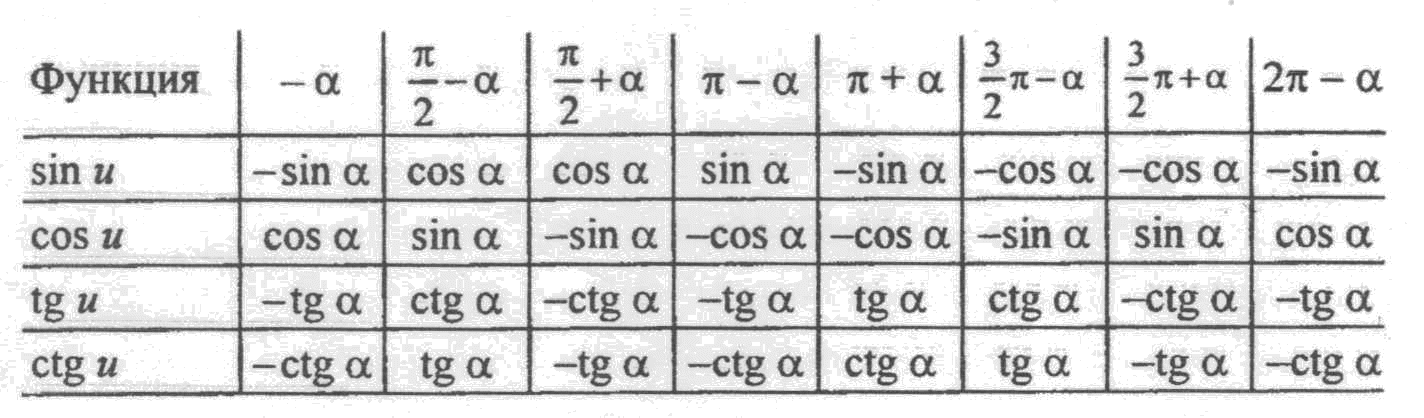
Для любого острого угла α:
sin (90° – α) = cos α
cos (90° – α) = sin α
Пример-пояснение:
Пусть в прямоугольном треугольнике АВС
АВ = 6,
ВС = 3,
угол А = 30º.
Выясним синус угла А и косинус угла В.
Решение.
1) Сначала находим величину угла В. Тут все просто: так как в прямоугольном треугольнике сумма острых углов равна 90º, то угол В = 60º:
В = 90º – 30º = 60º.
2) Вычислим sin A. Мы знаем, что синус равен отношению противолежащего катета к гипотенузе. Для угла А противолежащим катетом является сторона ВС. Итак:
BC 3 1
sin A = —— = — = —
AB 6 2
3) Теперь вычислим cos B. Мы знаем, что косинус равен отношению прилежащего катета к гипотенузе. Для угла В прилежащим катетом является все та же сторона ВС. Это значит, что нам снова надо разделить ВС на АВ – то есть совершить те же действия, что и при вычислении синуса угла А:
BC 3 1
cos B = —— = — = —
AB 6 2
В итоге получается:
sin A = cos B = 1/2.
Или:
sin 30º = cos 60º = 1/2.
Из этого следует, что в прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла – и наоборот. Именно это и означают наши две формулы:
sin (90° – α) = cos α
cos (90° – α) = sin α
Убедимся в этом еще раз:
1) Пусть α = 60º. Подставив значение α в формулу синуса, получим:
sin (90º – 60º) = cos 60º.
sin 30º = cos 60º.
2) Пусть α = 30º. Подставив значение α в формулу косинуса, получим:
cos (90° – 30º) = sin 30º.
cos 60° = sin 30º.
(Подробнее о тригонометрии — см.раздел Алгебра)
Тригонометрические формулы
1. Тождества тригонометрических функций одного и того же аргумента:
2. Значения тригонометрических функций в определенных точках:
| α ° | 0 | 30 | 45 | 60 | 90 | 180 | 270 | 360 |
|---|---|---|---|---|---|---|---|---|
| sin (α) | 0 | 12 | 22 | 32 | 1 | 0 | -1 | 0 |
| cos (α) | 1 | 32 | 22 | 12 | 0 | -1 | 0 | 1 |
| тг (α) | 0 | 13 | 1 | 3 | – | 0 | – | 0 |
| карат (α) | – | 3 | 1 | 13 | 0 | – | 0 | – |
3.Четность или нечетность:
4. Знаки в кварталах:
| Триг. функция | Quater | |||
|---|---|---|---|---|
| I | II | III | IV | |
| sin (α) | + | + | – | – |
| cos (α) | + | – | – | + |
| тг (α) | + | – | + | – |
| карат (α) | + | – | + | – |
5.Формулы приведения:
| β = | 90 ± α | 180 ± α | 270 ± α | 360 ± α |
|---|---|---|---|---|
| sin (β) | cos (α) | ∓sin (α) | -cos (α) | ± sin (α) |
| cos (β) | ∓sin (α) | -cos (α) | ± sin (α) | cos (α) |
| тг (β) | ∓ctg (α) | ± tg (α) | ∓ctg (α) | ± tg (α) |
| ктг (β) | ∓тг (α) | ± ctg (α) | ∓тг (α) | ∓ctg (α) |
6.Решение простейших тригонометрических уравнений:
sin (x) = a x = (-1) n arcsin (a) + n π, n = 0, 1 … ∈ Z
cos (x) = a ⇔ x = ± arccos (a) + 2 n π, n = 0, 1 … ∈ Z
tg (x) = a ⇔ x = arctg (a) + n π, n = 0, 1 … ∈ Z
7. Формулы суммирования и вычитания:
sinαβsinαcosβcosαsinβ sinαβsinαcosβcosαsinβ cosαβcosαcosβsinαsinβ cosαβcosαcosβsinαsinβ8.Формулы двойного угла:
9. Формулы тройного угла:
10. Формулы преобразования суммы и разности:
а) Преобразование суммы и разности одинаковых тригонометрических функций под разными углами:
Синусоидальные преобразования:
sinαsinβ2sinαβ2cosαβ2 sinαsinβ2sinαβ2cosαβ2Косинусных преобразований:
cosαcosβ2cosαβ2cosαβ2 cosαcosβ2sinαβ2sinαβ2Касательных преобразований:
tgαtgβsinαβcosαcosβ tgαtgβsinαβcosαcosβпреобразований котангенса:
ctgαctgβsinβαsinαsinβ ctgαctgβsinβαsinαsinβб) Преобразование суммы и разности различных тригонометрических функций под разными углами:
sinαcosβ2sinαβ2π4cosαβ2π4 sinαcosβ2sinαβ2π4cosαβ2π4c) Особые формулы:
AsinαBcosαA2B2sinαarctgBA sinαsin2α…sinnαsin12n1αsinnα2sinα2 cosαcos2α … cosnαcos12n1αsinnα2sinα211. Формулы преобразования произведения тригонометрических функций:
sinαsinβcosαβcosαβ2 sinαcosβsinαβsinαβ2 cosαcosβcosαβcosαβ212. Редукция тригонометрических функций по степенным формулам:
13. Выражение тригонометрических функций тангенсом половинного угла:
ttgα2sinα1cosα1cosαsinα1cosα1cosα
Все основные формулы тригонометрических тождеств
Тригонометрические тождества для синуса, косинуса, тангенса и котангенса:
sin (2α), cos (2α), tg (2α), ctg (2α)
Обозначения для синуса, косинуса, тангенса и котангенса:
sin (3α), cos (3α), tg (3α), ctg (3α)
Тригонометрические тождества для синуса, косинуса, тангенса и котангенса:
sin (α / 2), cos (α / 2), tg (α / 2), ctg (α / 2)
sin 3 (α), cos 3 (α), tg 3 (α), ctg 3 (α)
sin 2 (α), cos 2 (α), tg 2 (α), ctg 2 (α)
Формулы для синуса, косинуса, тангенса и котангенса:
sin (α + β), cos (α + β), tg (α + β), ctg (α + β)
Формулы для синуса, косинуса, тангенса и котангенса:
sin (α- β), cos (α- β), tg (α- β), ctg (α- β)
Тригонометрия: sin, cos, tg, ctg.
Trigonometria este știința care se ocupă cu măsurarea unghiurilor unui triunghi. Unghiurile se pot măsura fie cu raportorul, fie cu ajutorul unor funcții numite funcții trigonometrice . Trigonometria este des utilizată в географии, навигации, физике, астрономии и топографии. Cu ajutorul trigonometriei putem Calcula distanțele dintre orașe și putem întocmi hărți точный.
Funciile trigonometrice pe care le vom studia se aplică în triunghiul dreptunghic.
fign figura de mai jos avem o pârtie de ski și la fiecare 100 de m parcurși, înălțimea pârtiei ( h ) scade cu 5 m. Notăm cu x unghiul pe care pârtia îl face cu orizontala. N fiecare punct, raportul dintre înălțimea pârtiei și distanța rămasă de parcurs până la baza pârtiei este constant :
Фото предоставлено Schior: PixabayDe aici putem trage următoarea clozie: în triunghiurile dreptunghice care con18in acelai unghi ascuțit x, raportul dintre cateta opusă unghiului x i lungimiliste de luxe, indir.Acest raport se va numi sinusul unghiului x . N Continuous Vom Defini și alte rapoarte trigonometrice, luând in caurare laturi ale triunghiului dreptunghic.
Sinusul unui unghi x Este raportul dintre cateta opusă i ipotenuză.
Cosinusul unui unghi x Este raportul dintre cateta alăturată i ipotenuză.
Tangenta unui unghi x Este raportul dintre cateta opusă i cateta alăturată.
Cotangenta unui unghi x Este raportul dintre cateta alăturată i cateta opusă.
Sinusul, cosinusul, tangenta și cotangenta se numesc funcții trigonometrice .
Iată tabelul cu valorile funcțiilor trigonometrice ale unghiurilor uzuale:
Funciile trigonometrice uzualeProbleme rezolvate cu funcții trigonometrice
Проблема 1
Fie ABC un triunghi dreptunghic в A.Dacă AB = 3 см și AC = 4 см, aflați sinusul unghiului B.
Адрес:
Aflăm mai lungimea ipotenuzei BC cu Teorema lui Pitagora. Обțинем ВС = 5 см. Sinusul unghiului B este raportul dintre cateta opusă AC și ipotenuza BC.
sin B = AC / BC = 4/5.
Проблема 2
Fie ABC un triunghi dreptunghic în A. Dacă AB = 6 см și BC = 12 см, aflați măsura unghiului B.
Адрес:
Cunoaștem cateta alăturată unghiului B i ipotenuza.Vom Calcula cosinusul unghiului B:
cosB = AB / BC = 6/12 = 1/2. Prin urmare, unghiul B are măsura de 60 de grade (vezi tabelul funcțiilor trigonometrice uzuale).
Калькулятор тригонометрии. Простой способ найти sin, cos, tan, cot
Этот калькулятор тригонометрии поможет вам в двух популярных случаях, когда необходима тригонометрия. Если вы хотите найти значения синуса, косинуса, тангенса и их обратных функций, используйте первую часть калькулятора. Ищете недостающую сторону или угол в прямоугольном треугольнике с помощью тригонометрии? Наш инструмент — тоже беспроигрышный вариант! Введите 2–3 заданных значения во второй части калькулятора, и вы в мгновение ока найдете ответ.Прокрутите вниз, если хотите узнать больше о тригонометрии и о том, где ее можно применить.
Есть много других инструментов, полезных при решении задач тригонометрии. Ознакомьтесь с двумя популярными тригонометрическими законами: калькуляторами закона синусов и закона косинусов, которые помогают решить любой вид треугольника. Если вы хотите узнать больше о тригонометрических функциях, перейдите к нашим специальным инструментам:
Что такое тригонометрия?
Тригонометрия — это раздел математики. Само слово происходит от греческих языков trignon (что означает «треугольник») и metron («мера»).Как следует из названия, тригонометрия имеет дело в основном с углами и треугольниками ; в частности, он определяет и использует отношения и соотношения между углами и сторонами в треугольниках. Таким образом, основное приложение — решение треугольников, в частности прямоугольных, а также любого другого типа треугольника, который вам нравится.
Тригонометрия имеет различных приложений: от повседневных задач, таких как вычисление высоты или расстояния между объектами, до спутниковой навигационной системы, астрономии и географии.Кроме того, функции синуса и косинуса являются фундаментальными для описания периодических явлений — благодаря им мы можем описывать колебательные движения (как простой маятник) и волны, такие как звук, вибрация или свет.
Тригонометрия и тригонометрические функции используются во многих различных областях науки и техники, если упомянуть лишь некоторые из них: музыка, акустика, электроника, медицина и медицинская визуализация, биология, химия, метеорология, электрика, машиностроение и гражданское строительство, даже экономика. Тригонометрические функции действительно все вокруг нас!
Калькулятор триггеров нахождение sin, cos, tan, cot, sec, csc
Чтобы найти тригонометрические функции угла, введите выбранный угол в градусах или радианах.Под калькулятором появятся шесть самых популярных триггерных функций — три основных: синус, косинус и тангенс, а также их обратные величины: косеканс, секанс и котангенс. Кроме того, если угол острый, будет отображаться прямоугольный треугольник, который может помочь вам понять, как могут быть интерпретированы функции.
Чтобы найти недостающие стороны или углы прямоугольного треугольника, все, что вам нужно сделать, это ввести известные переменные в калькулятор тригонометрии. Вам нужны только два заданных значения в случае:
- одна сторона и один угол
- с двух сторон
- площадь и одна сторона
Помните, что если вы знаете два угла, этого недостаточно, чтобы найти стороны треугольника.Два треугольника, имеющие одинаковую форму (что означает, что они имеют равные углы), могут иметь разные размеры (не одинаковую длину стороны) — такая связь называется подобием треугольника . Если стороны имеют одинаковую длину, то треугольники равны равным .
Что такое тригонометрия?
Тригонометрия — это исследование отношений внутри треугольника . Для прямоугольных треугольников соотношение между любыми двумя сторонами всегда одинаково и задается в виде тригонометрических соотношений, cos, sin и tan.Тригонометрия также может помочь найти некоторую недостающую треугольную информацию , например правило синуса.
Сложна ли тригонометрия?
Поначалу тригонометрияможет быть сложной задачей, но после некоторой практики вы ее освоите! Вот несколько советов по тригонометрии: Обозначьте гипотенузу, смежную и противоположную на вашем треугольнике, чтобы помочь вам выяснить, какую идентичность использовать, и запомните мнемонику SOHCAHTOA для тригонометрических отношений!
Для чего используется тригонометрия?
Тригонометрия используется для поиска информации обо всех треугольниках и, в частности, прямоугольных треугольниках.Поскольку треугольника повсюду в природе , тригонометрия используется вне математики, в таких областях, как строительство, физика, химическая инженерия и астрономия.
Кто изобрел тригонометрию?
Поскольку тригонометрия — это взаимосвязь между углами и сторонами треугольника, никто не придумал ее , она все равно была бы там, даже если бы никто об этом не знал! Первыми, кто открыл часть тригонометрии, были древние египтяне и вавилоняне , но Евклид и Архемид первыми подтвердили идентичность, хотя они сделали это с помощью форм, а не алгебры.
Какой уровень у тригонометрии?
Тригонометрия — это , которые обычно преподают подросткам в возрасте 13-15 лет , что составляет классы 8 и 9 в США и лет 9 и 10 в Великобритании. Точный возраст преподавания тригонометрии зависит от страны, школы и способностей учеников.
Best Excel Tutorial — Как использовать триггерные функции в Excel?
Тригонометрия — это раздел математики, изучающий отношения между элементами (сторонами и углами) треугольника.Теперь вы можете вспомнить многие тригонометрические формулы и уравнения, которые вы выучили в школе или колледже. Некоторые из них: cot x = 1 / tanx, шесть x / cos x = tan x, sin (900-x) — cos x и так далее. Excel предлагает ряд встроенных функций, связанных с тригонометрией. Эти тригонометрические функции можно использовать для решения сложных тригонометрических выражений.
Главное, что вам нужно учитывать при решении тригонометрических выражений, это то, что Excel выполняет вычисления с учетом значения угла в радианах, а не в градусах.Возможно, вы знаете, что sin 900 = 1. Таким образом, если вы введете формулу SIN (90) в Excel, результатом будет 0,893997, а не 1, потому что Excel считает 90 как 90 радиан, а не 90 градусов. Если вы хотите найти синус 90 градусов, вам следует сначала преобразовать градусы в радианы, а затем использовать формулу SIN, доступную в Excel. Не волнуйтесь, мы узнаем, как использовать тригонометрические функции в Excel за считанные минуты.
Excel предоставляет функции для синуса (sin), косинуса (cos), тангенса (tan), гиперболического синуса (sinh), гиперболического косинуса (cosh) и гиперболического тангенса (tanh).Excel не предоставляет функции для секанса (сек), косеканса (косеканс), котангенса (cot) и их гиперболических аналогов. Однако вы можете рассчитать эти функции, используя базовые функции (синус и косинус). Excel также предлагает функции для преобразования угла из радианов в градусы и наоборот.
Использование тригонометрических функций в Excel
Откройте Excel и сохраните файл как trig-functions.xlsx. Введите «Угол (градусы)» в A1, «Угол (радианы)» в B1, «SIN» в C1, «COS» в D1, «TAN» в E1, «COSEC» в F1, «SEC» в G1 и « СОТ »в h2.Также введите «0» в A2, «30» в A3, «45» в A4, «60» в A5, «90» в A6, «180» в A7, «270» в A8 и «360» в A9. При вводе данных не следует вводить двойные кавычки. Вы можете отформатировать эти тексты и сделать их жирными. Теперь ваш экран будет выглядеть так:
Щелкните ячейку B2 и перейдите к Formulas (главное меню) -> Math & Trig (в группе Function Library ).
Прокрутите вниз и выберите функцию РАДИАНЫ , чтобы получить такой экран:
После щелчка внутри пространства для ввода значения (обведено красным) щелкните ячейку A2.
Нажмите ОК, и ячейка B2 будет иметь значение 0.
Щелкните ячейку B2, скопируйте формулу (CTRL + C) и вставьте ее (CTRL + V) в ячейки B3, B4, B5, B6, B7. , B8 и B9. Если вы опытный пользователь Excel, вы можете просто перетащить формулу в ячейки вместо копирования и вставки. Теперь ваш экран будет выглядеть так:
Щелкните ячейку C2 и перейдите к Formulas -> Math & Trig (в группе Function Library ).Выберите функцию SIN и, щелкнув внутри пробела для ввода значения, щелкните ячейку B2. Щелкните ОК. Скопируйте формулу в ячейку C2 и вставьте ее в ячейки C3 – C9. Теперь ваш экран будет выглядеть так:
Щелкните ячейку D2 и перейдите к Formulas -> Math & Trig (в группе Function Library ). Выберите функцию COS и, щелкнув внутри пробела для ввода значения, щелкните ячейку B2. Щелкните ОК. Скопируйте формулу в ячейку D2 и вставьте в ячейки с D3 по D9.Теперь ваш экран будет выглядеть так:
Щелкните ячейку E2 и перейдите к Formulas -> Math & Trig (в группе Function Library ). Выберите функцию TAN и, щелкнув внутри пробела для ввода значения, щелкните ячейку B2. Щелкните ОК. Скопируйте формулу в ячейку E2 и вставьте в ячейки E3 – E9. Теперь ваш экран будет выглядеть так:
Как уже упоминалось, нет встроенных функций для расчета значений COSEC, SEC и COT.Вы должны рассчитать их, используя следующие основные функции:
cosec x = 1 / sin x
sec x = 1 / cos x
cot x = 1 / tan x
Щелкните ячейку F2 и щелкните внутри формулы Полоса (обведена красным) и введите формулу «= 1 / C2» (без двойных кавычек). Скопируйте формулу в ячейку F2 и вставьте в ячейки с F3 по F9. Теперь ваш экран будет выглядеть так:
Щелкните ячейку G2, щелкните внутри строки формул и введите формулу «= 1 / D2» (без двойных кавычек).Скопируйте формулу в ячейку G2 и вставьте в ячейки G3 — G9. Теперь ваш экран будет выглядеть так:
Щелкните ячейку h3, щелкните внутри строки формул и введите формулу «= 1 / E2» (без двойных кавычек). Скопируйте формулу в ячейку h3 и вставьте в ячейки с h4 по H9. Теперь ваш экран будет выглядеть так:
Вы можете округлить полученные значения до двух или трех десятичных знаков, чтобы получить более реалистичные результаты. Измените все формулы в ячейках C, D, E, F, G и H таким образом, чтобы новая формула стала = ОКРУГЛ (существующая формула, 3) .Например, формула в ячейке C4 принимает вид = ОКРУГЛ (SIN (B4), 3) , где существующая формула была = SIN (B4) . Вы также можете заменить все ошибки (# DIV / 0!) На * и просто предоставить описание где-нибудь на том же листе, указав, что * означает undefined. Теперь ваш экран будет выглядеть так:
Точно так же вы можете найти значение sinh, cosh и tanh, используя формулы SINH, COSH и TANH, и вычислить cosech, sech и coth из sinh, cosh и tanh.
Дополнительная литература: Как использовать интегральную функцию? Как рассчитать стандартное отклонение?
Теория — Тригонометрия
Теория — ТригонометрияТРИГОНОМЕТРИЯ
Des formules générales
грех 2 а + cos 2 а = 1;
tg a = грех / cos a; ctg a = потому что / sin a;
tg a ctg а = 1;
tg 2 a + 1 = 1 / cos 2 a; ctg 2 а + 1 = 1 / sin 2 а;
Des formules d’addition
cos (a — b) = потому что cos b + грех грех б;
cos (a + b) = потому что cos b — грех грех б;
грех (а — б) = грех cos b — грех б cos a;
грех (а + б) = грех cos b + грех б cos a;
tg (a + b) = (tg a + tg b) / (1 — тг а тг б);
tg (a — b) = (тг а — tg b) / (1 + тг а тг б);
Des formules de сокращение
Avec les sinus
sin (-x) = — sinx;
sin (360k + x) = sin (2p k + x) = sin x, «к, k Î Z;
грех (90 0 — х) = грех (р / 2 — х) = cosx;
грех (90 0 + х) = грех (р / 2 + х) = cos x;
грех (180 0 — х) = грех (р — х) = грех х;
грех (180 0 + х) = грех (р + х) = — грех х;
грех (270 0 — х) = грех (3p / 2 — х) = -cos x;
грех (270 0 + х) = грех (3p / 2 + x) = cos x;
грех (360 0 — х) = грех (2р — х) = -sin x;
грех (360 0 + х) = грех (2р + х) = грех х;
Avec les косинус
cos (-x) = cos x;
cos (360k + x) = cos (2p k + x) = cos x, «к, k Î Z;
cos (90 0 — x) = cos (p / 2 — x) = грех х;
cos (90 0 + x) = cos (p / 2 + x) = — грех х;
cos (180 0 — x) = cos (p — x) = — cos x;
cos (180 0 + x) = cos (p + x) = — cos x;
cos (270 0 — x) = cos (3p / 2 — x) = -sin x;
cos (270 0 + x) = cos (3p / 2 + x) = грех х;
cos (360 0 — x) = cos (2p — x) = cos x;
cos (360 0 + x) = cos (2p + x) = cosx;
Avec les tangentes et al. котангенты
tg (-x) = — tg x;
tg (180k + x) = tg (p k + x) = tg x, «к, k Î Z;
tg (90 0 — x) = tg (p / 2 — x) = ctg x;
tg (90 0 + x) = tg (p / 2 + x) = — ctg x;
tg (180 0 — x) = tg (p — x) = — tg x;
tg (180 0 + x) = tg (p + x) = tg Икс ;
Формулы для сомнений и др. différences de sinus et de cosinus
грех а + грех b = 2sin ((a + Би 2) cos ((a — Би 2)
грех а — грех b = 2sin ((а — Би 2) cos ((a + б) / 2)
cos a + грех b = 2cos ((a + Би 2) cos ((a — Би 2)
cos a — грех b = — 2sin ((а — Би 2) грех ((а + б) / 2)
Формулы с аргументами двойной
грех 2a = 2sina cosa = (сина + cosa) 2 — 1 = 1 — (сина — cosa) 2
cos 2a = cos 2 а- грех 2 а = 2 cos 2 a-1 = 1 — 2sin 2 а
tg 2 a = 2 tga / (1 — тг 2 а)
Формулы с аргументами moitié
cos 2 a / 2 = (1 + cosa) / 2;
sin 2 a / 2 = (1 — cosa) / 2.
Возвращение
tg = cos sin ctg = tg sin2 = 1 cos 2 cos 2 = 1 sin2
1 TRIGONOMETRIA Тригонометрия a háromszögek szögei és oldalai közötti összefüggésekkel foglalkozik. A trigonometrikus összefüggések a geometriában minden területén használhatóak, hiszen minden sokszög véges számú háromszögre bontható fel.Tartalom Szögfüggvények … Értelmezés derékszögű háromszögekben … Szögfüggvények összefüggései … Koszinusz és szinusz tétel … 3 Háromszög területkázézplete … Tangens tgx … 6 Kotangens ctgx … 7 Ívmérték (radián) … 7 Egységkör … 8 Trigonometrikus egyenletek megoldása Trigonometrikus egyenletek Trigonometrikus egyenlőtlenségek … 11
. Szögfüggvények Értelmezés derékszögű háromszögekben Két derékszögű háromszög hasonlóságát teljesen meghatározza egyik szögük nagysága, ígyzezylenigetik megae.Ezeket аз arányokat hagyományosan аз ismert szög szögfüggvényeivel írhatjuk le. Ma 4 szögfüggvényt használunk (𝑠𝑖𝑛; 𝑐𝑜𝑠; 𝑡𝑔; 𝑐𝑡𝑔), bár a háromszög három oldalából 6 arányt tudunk felírni a koszinusz reciproka (szekáns: 𝑠𝑒𝑐) és a szinuszik. Szinusz: грех вал szemközti befogó Koszinusz: соз вал szomszédos befogó Tangens: Т.Г. вал szomszédos befogó 𝑏 Kotangens: CTG átfogó átfogó вал szemközti befogó вал szomszédos befogó вал szemközti befogó 𝑎 𝑐 𝑏 𝑐 𝑎 𝑏 𝑎 виду 6 trigonometrikus függvény jelentése, ábrázolása és jellemzése , kiegészítve az Inverz és hiperbolikus függvényekkel: [matematikam.hu / konyv / 09] Szögfüggvények összefüggései A sin és cos értékei mindig 1 és 1 közé esnek: 1 sin 1 és 1 cos 1 A sin az egész kifejezés négyzetét jelenti sinzban (грех), der , 14 hanem 180 (lásd «Radián» rész) sin tg cos cos ctg tg ctg ctg tg sin + cos 1 sin 1 cos sin 1 cos cos 1 sin cos 1 sin 1 sin 1 Egyenletmegoldáskor, mikor számológéppel 𝑠𝑖𝑛 és 𝑐𝑜𝑠 alapjázán viss , figyelnünk kell arra, hogy a számológép csak az egyik eredményt adja meg, a másikat magunknak kell megkeresni.Ezt tehetjük a függvény képe vagy egységkör segítségével, de talán egyszerűbb, ha megjegyezzük, hogy a szinusz két eredménye (𝑥1; 𝑥) egymást 180 -ra egélenezízízízígével,. És természetesen nem feledkezhetünk meg a periódusról sem (sin és cos esetén + k, míg tg és ctg esetén + k).
3 Koszinusz és szinusz tétel A derékszögű háromszögekre vonatkozó Pitagorasz-tétel (a + b c) általánosítása tetszőleges általános háromszögekre.Az oldalak és szögek betűzése: az a, b, c oldallal szemközt rendre az ,, szögek vannak. Cos-tétel: a b + c bc cos b a + c ac cos c a + b ab cos A tétel alkalmazható, ha ismerjük a háromszög három oldalát, vagy két oldalát és az általuk közrezárt szöget. Sin-tétel: Tetszőleges háromszögben az oldalak úgy aránylanak egymáshoz, mint az oldalakkal szemközti szögek szinuszai. Az arány (a: b: c sin: sin: sin) segítségével felírható összefüggések: a sin b sin b sin a sin a sin c sin c sin a sin b sin c sin c sin b sin abc sin sin sin sin a sin b sin c Alkalmazható a tétel, ha ismerünk egy oldal és szög párt, illetve még egy szöget vagy oldalt.A nagyobb oldallal szemközti szög meghatározásakor két megoldást is kaphatunk, mert egy adott (1-nél kisebb) szinuszértékhez egy hegyes- és egy tompaszög is tartozigel mörzik, mezérésigell. Háromszög területképletek Általános területképletek: T amabmbcmc Hérón-képlet: T s (sa) (sb) (sc) (s K a + b + c) Trigonometrikus területképletek: Be- és sin körés abc R köréírt körének sugara T rsr beírt körének sugara; (s K) Bármely hegyesszögű háromszögben egy oldal hosszának — это szemközti szög szinuszának aránya állandó.Эз аз állandó körülírt köre átmérőjének reciproka. sin a sin b sin c 1 R R köréírt körének sugara 3
4 Szögfüggvények ábrázolása és jellemzése Szinusz sin x Az f (x) sin x függvény jellemzése: ÉT: x R; 1] zh .: x k k Z szélsőérték: max hely: x + k k Z max érték: y 1 min hely: x 3 + k k Z min érték: y 1 monotonitás: szig. пн. nő: [+ k; + k] k Z szig. пн. csökken: [3 + k; + k] k Z paritás: páratlan, nem páros konvexitás: konkáv: [0 + k; + k] k Z конвекс: [+ k; + k] k Z periódus: грех x függvényt eltolva (+) -vel, cos x függvény képét kapjuk meg.4
5 Koszinusz cos x Az f (x) cos x függvény jellemzése: ÉT: x R ÉK: y [1; 1] zh .: x + k k Z szélsőérték: max hely: x k k Z max érték: y 1 min hely: x + k k Z min érték: y 1 monotonitás: szig. пн. nő: [+ k; + k] k Z szig. пн. csökken: [+ k; 3 + k] k Z paritás: páros, nem páratlan konvexitás: konkáv: [+ k; + k] k Z конвекс: [3 + k; + k] k Z periódus: A cos x függvényt eltolva () -vel, грех x függvény képét kapjuk meg. 5
6 Tangens tg x Az f (x) tg x függvény jellemzése: ÉT: x R \ {+ k} k Z ÉK: y R zh.: x k k Z szélsőérték: nincsen monotonitás: szig. пн. nő аз ÉT-на паритас: паратлан, нем парос конвекситас: конкав:] + к; 0 + k] k Z конвекс: [0 + k; + k [k Z periódus: Az f (x) tg x aszimptotái az + k egyenesek. k Z 6
7 Kotangens ctg x Az f (x) ctg x függvény jellemzése: ÉT: x R \ {k} k Z ÉK: y R zh .: x + k k Z szélsőérték: nincsen monotonitás: szig. пн. csökken аз ÉT-on paritás: páratlan, nem páros konvexitás: konkáv:] + k; 0 + k] k Z конвекс: [0 + k; + k [k Z periódus: Az f (x) ctg x aszimptotái az k egyenesek.k Z Ívmérték (radián) A radián vagy ívmérték a síkszögek egyik mértékegysége, amelyet a rad szimbólummal jelölnek. Dimenzió nélküli mértékegység, mivel két hosszúság hányadosa. Radián :, fok: A radián sugárnyi hosszúságú ívhosszhoz tartozó középponti szög. Átváltás radián és szög között: Amennyiben radiánban számolunk, a nem 3,14 -et, hanem 180 -ot jelent! 7
8 Egységkör Egységkör (egység sugarú kör) segítségével szemléltethetjük a szögfüggvények kapcsolatait.Аз egység sugarú körben a sin értékei a sugár (szög) és a körív metszéspontjának koordinátáiból olvasható le, a sin -t az y 0, tehát a második koordináta jelö les sgyzöként (szög). Аз egység sugarú körben a cos értékei a sugár (szög) — это körív metszéspontjának koordinátáiból olvasható le, a cos -t az x 0, tehát az első koordináta jelöli onkézögz () cosy szög. 8
9 Az egység sugarú körben a tg értékei a sugár (szög) és a kör jobb oldalán lév, y tengellyel párhuzamos érintője metszéspontjának koordinátáhörben a tg értékei a sugár (szög) és a kör jobb oldalán lévő, y tengellyel párhuzamos érintője metszéspontjának koordinátá, egy szög tangense.Az egység Sugarú körben a ctg értékei a sugár (szög) és a kör felett lévő, x tengellyel párhuzamos érintője metszéspontjának koordinátáiból olvasható le, aztgálés égá 9
10 Segítség néhány nevezetes sin és cos érték leolvasására az egység sugarú körben. Tehát pl. 30 esetén: sin 1 cos 3 Trigonometrikus egyenletek megoldása A trigonometrikus egyenletek megoldásához a legtöbb esetben használnunk kell a trigonometrikus összefüggéseket.Középszinten аз addíciós tételeket nem kell ismerni, de az alapösszefüggéseket mindenképp érteni kell, illetve a szögfüggvények periodikusságából adódó megoldáshalmazt ismerni kell. Trigonometrikus egyenletek A hagyományos egyenletmegoldás lépéseit itt is használhatjuk, de törekednünk kell a következőekre: Az első cél, hogy az egyenletben lehetőleg cshatzöjfögéleggs. tg sin cos tg 1 ctg ctg cos sin ctg 1 tg sin + cos 1 sin 1 cos sin 1 cos cos 1 sin cos 1 sin Következő lépésnek arra törekszünk, hogy az egyenlet egyik oldalán önmagában szerepeljen a szönystíggv.10
11 Ezután számológéppel kifejezhető az ismeretlen (vagy az ismeretlent tartalmazó kifejezés) értéke Figyelnünk kell arra, hogy a számológép sin és Ezt tehetjük a függvény képe vagy egységkör segítségével, de talán egyszerűbb, ha megjegyezzük, hogy a szinusz két eredménye (x 1; x) egymást 180 -ra egészímészígés ki.Szinusz esetén: x 180 x 1 Koszinusz esetén: x x 1 Végül természetesen nem feledkezhetünk meg a periódus hozzácsapásáról sem. Szinusz és koszinusz esetén + K K Z Тангенс és kotangens esetén + K K Z Trigonometrikus egyenlőtlenségek megoldás ELSO феле аз egyenlőtlenségre vonatkozó szabályokat betartva (Negativ számmal ВАЛО szorzás vagy osztás esetén reláció megfordul) ugyanúgy zajlik, Mintha egyenletekkel dolgoznánk. Végső lépésnél azonban függvényként érdemes ábrázolni az egyenletet, является kapott megoldásokat ábrázolva leolvashatjuk a kívánt eredményt (интерваллумот, pontokat vagy).Témakörhöz tartozó levezetett mintafeladatok szerepelnek и «Matematika kidolgozott példák» könyvben, részletes magyarázattal! 11
.